Abstract
We study global and local geometry of forms on odd symplectic BV supermanifolds, constructed from the total space of the bundle of 1-forms on a base supermanifold. We show that globally 1-forms are an extension of vector bundles defined on the base supermanifold. In the holomorphic category, we prove that this extension is split if and only if the super Atiyah class of the base supermanifold vanishes. This is equivalent to the existence of a holomorphic superconnection: we show how this condition is related to the characteristic non-split geometry of complex supermanifolds. From a local point of view, we prove that the deformed de Rham double complex naturally arises as a de-quantization of the de Rham/Spencer double complex of the base supermanifold. Following Ševera, we show that the associated spectral sequence yields semidensities on the BV supermanifold, together with their differential in the form of a super BV Laplacian.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Batalin–Vilkovisky formalism (henceforth the “BV formalism”) was originally designed in the early 1980’s as a tool to deal with the perturbative quantization of gauge theories. Nowadays, its importance goes far beyond its original purpose: the BV formalism has grown into one of the foundational languages of contemporary theoretical and mathematical physics [7, 8, 10, 14, 21], with several applications also to pure mathematics [8, 23].
It was Albert Schwarz in [24] who first elucidated the geometric framework that lies at the basis of the BV formalism, by recognizing the crucial role played by supergeometry. The BV formalism builds upon the BRST formalism, that in turn introduced a new point of view on the so-called Faddeev–Popov procedure. In particular, the BRST formalism identifies the space of fields of a gauge theory with “functions” on a supermanifold  , typically constructed as the split supermanifold generated by an action Lie algebroid
, typically constructed as the split supermanifold generated by an action Lie algebroid  associated to a Lie group action
associated to a Lie group action  , so that
, so that  is trivialized as
is trivialized as  . In this framework, ghost fields are not just byproducts of an integration procedure, as in the Faddeev–Popov procedure. Instead, they are conceptually understood as proper geometric data: odd sections of
. In this framework, ghost fields are not just byproducts of an integration procedure, as in the Faddeev–Popov procedure. Instead, they are conceptually understood as proper geometric data: odd sections of  related to the generators of the Chevalley–Eilenberg algebra
related to the generators of the Chevalley–Eilenberg algebra  resolving the (infinitesimal) gauge symmetry \({\mathfrak {g}}.\) The BV formalism enhances the above “BRST package” by crucially allowing symplectic geometry to enter the picture: starting from
resolving the (infinitesimal) gauge symmetry \({\mathfrak {g}}.\) The BV formalism enhances the above “BRST package” by crucially allowing symplectic geometry to enter the picture: starting from  , one constructs a canonically associated (odd) symplectic supermanifold
, one constructs a canonically associated (odd) symplectic supermanifold  as the total space supermanifold of the (parity-shifted) cotangent bundle
as the total space supermanifold of the (parity-shifted) cotangent bundle  . This is called BV space or BV supermanifold. Functions on
. This is called BV space or BV supermanifold. Functions on  are given by polynomial functions on the fibers of
are given by polynomial functions on the fibers of  , that is
, that is  . This means that if in the BRST setting the local \(n\,{|}\,m\) coordinates \((x^i\!, \theta ^\alpha )\) of
. This means that if in the BRST setting the local \(n\,{|}\,m\) coordinates \((x^i\!, \theta ^\alpha )\) of  are identified with the fields \(x^i\) and the ghosts \(\theta ^\alpha \) of the related physical theory, in the BV setting these get supplemented by another set of \(m\,{|}\,n\) coordinates \(( q_\alpha \,{|}\, p_i)\), accounting for the fiber directions of
are identified with the fields \(x^i\) and the ghosts \(\theta ^\alpha \) of the related physical theory, in the BV setting these get supplemented by another set of \(m\,{|}\,n\) coordinates \(( q_\alpha \,{|}\, p_i)\), accounting for the fiber directions of  and identified with the so-called anti-fields \(p_i\) and anti-ghosts \(q_\alpha \). In a similar fashion as above, whereas the odd ghosts \(\theta _\alpha \) provided a homological resolution for the gauge symmetry, the new odd generators in
and identified with the so-called anti-fields \(p_i\) and anti-ghosts \(q_\alpha \). In a similar fashion as above, whereas the odd ghosts \(\theta _\alpha \) provided a homological resolution for the gauge symmetry, the new odd generators in  —the anti-fields \(q_i\)’s—provide a homological (Koszul–Tate) resolution of the critical locus of the action
—the anti-fields \(q_i\)’s—provide a homological (Koszul–Tate) resolution of the critical locus of the action  , showing once again the vicinity of the formalism with a homological or, better, derived geometric point of view.
, showing once again the vicinity of the formalism with a homological or, better, derived geometric point of view.
Generally speaking, the most interesting aspects of supergeometry are those which do not arise as a generalization of the ordinary commutative theory, but instead force us to revise our classical geometric intuition and to confront ourselves with unexpected new features. These new features are both of local and global nature. Locally, the geometry of forms on supermanifolds and the related integration theory present the most peculiar non-trivial novelties: the failure of a trivial generalization of Poincaré duality leads to the introduction of a new kind of forms, which are crucial for the purpose of a meaningful integration theory and for this reason are called integral forms. On the other hand, globally, complex supermanifolds can be non-split or non-projected: this means that they cannot be reconstructed from ordinary geometric data, but instead they are genuinely new geometric spaces living a life of their own.
In this paper we relate these two aspects, by starting from the geometry of forms arising from a BV supermanifold of the type of  above. More precisely, the paper is organized as follows. In Sect. 2 we recall the main definitions of the supergeometric objects and constructions that we will use. We then address the global aspects related to the geometry of forms on BV supermanifolds in Sect. 3. In particular, we prove that 1-forms on
above. More precisely, the paper is organized as follows. In Sect. 2 we recall the main definitions of the supergeometric objects and constructions that we will use. We then address the global aspects related to the geometry of forms on BV supermanifolds in Sect. 3. In particular, we prove that 1-forms on  -type supermanifolds are an extension of vector bundles defined on the base supermanifold, Theorem 3.2. For real supermanifolds we show in Theorem 3.4 that this extension is always split and the splitting corresponds to a reduction of the structural symplectic supergroup. More interestingly, building upon a projection to (the cohomology of) the base supermanifold of
-type supermanifolds are an extension of vector bundles defined on the base supermanifold, Theorem 3.2. For real supermanifolds we show in Theorem 3.4 that this extension is always split and the splitting corresponds to a reduction of the structural symplectic supergroup. More interestingly, building upon a projection to (the cohomology of) the base supermanifold of  , Theorem 3.3, in the case of complex supermanifolds we show that the extension is split if and only if the super Atiyah class of the base supermanifold vanishes, corresponding to the existence of a holomorphic connection, Theorem 4.3. We then show how this condition is related to the characteristic non-split or non-projected geometry of complex and algebraic supermanifolds in Theorem 4.9 and we comment on future perspectives in this context. Several examples spanning different levels of sophistication are discussed in Sect. 5. From a local point of view, in Sect. 6, we focus on the geometry related to the symplectic nature of the supermanifold
, Theorem 3.3, in the case of complex supermanifolds we show that the extension is split if and only if the super Atiyah class of the base supermanifold vanishes, corresponding to the existence of a holomorphic connection, Theorem 4.3. We then show how this condition is related to the characteristic non-split or non-projected geometry of complex and algebraic supermanifolds in Theorem 4.9 and we comment on future perspectives in this context. Several examples spanning different levels of sophistication are discussed in Sect. 5. From a local point of view, in Sect. 6, we focus on the geometry related to the symplectic nature of the supermanifold  and we show that the associated deformed de Rham double complex—whose differentials are given by the odd symplectic form and the de Rham differential—naturally arises as a de-quantization of the de Rham/Spencer double complex associated to the base supermanifold. Following Ševera, we show in Theorem 6.13 that the related spectral sequence yields semidensities on the odd symplectic BV supermanifold and their differential in the form of a super BV Laplacian.
and we show that the associated deformed de Rham double complex—whose differentials are given by the odd symplectic form and the de Rham differential—naturally arises as a de-quantization of the de Rham/Spencer double complex associated to the base supermanifold. Following Ševera, we show in Theorem 6.13 that the related spectral sequence yields semidensities on the odd symplectic BV supermanifold and their differential in the form of a super BV Laplacian.
2 Main definitions: local and global data
In this section we recollect the definitions of the main geometric objects that will be used throughout the paper. For thorough introductions to the geometry of supermanifolds the reader is suggested to refer to the books [2, 18]. The recent [22] offers a detailed account of the geometry of forms on supermanifolds. We let  be a smooth, analytic or algebraic supermanifold of dimension \(p\,{|}\,q\) with structure sheaf given by
be a smooth, analytic or algebraic supermanifold of dimension \(p\,{|}\,q\) with structure sheaf given by  and we denote by
and we denote by  its reduced space, which is an ordinary (commutative smooth, analytic or algebraic) manifold of dimension p with structure sheaf
its reduced space, which is an ordinary (commutative smooth, analytic or algebraic) manifold of dimension p with structure sheaf  . We will denote by
. We will denote by  and
and  the even, respectively, odd part of the structure sheaf with respect to its \(\mathbb {Z}_2\)-gradation, and likewise for other sheaves or vector bundles introduced in the following. We define
the even, respectively, odd part of the structure sheaf with respect to its \(\mathbb {Z}_2\)-gradation, and likewise for other sheaves or vector bundles introduced in the following. We define  be the tangent sheaf of
be the tangent sheaf of  . This is a locally-free sheaf of (left)
. This is a locally-free sheaf of (left)  -modules of rank \(p\,{|}\,q\): if we let U be an open set in the topological space
-modules of rank \(p\,{|}\,q\): if we let U be an open set in the topological space  underlying
underlying  and \(x_a \,{:}{=}\,\,z_i \,{|}\, \theta _\alpha \) for \(i = 1, \ldots , p\) and \(\alpha = 1, \ldots , q\) be a system of local coordinates over U for
and \(x_a \,{:}{=}\,\,z_i \,{|}\, \theta _\alpha \) for \(i = 1, \ldots , p\) and \(\alpha = 1, \ldots , q\) be a system of local coordinates over U for  , then
, then

where  is the structure sheaf of
is the structure sheaf of  and the local generators \(\partial _{z_i}\)’s are even and the \(\partial _{\theta _\alpha }\)’s are odd. Given the tangent sheaf as defined above, we can immediately introduce two related sheaves. The first one is the cotangent sheaf
and the local generators \(\partial _{z_i}\)’s are even and the \(\partial _{\theta _\alpha }\)’s are odd. Given the tangent sheaf as defined above, we can immediately introduce two related sheaves. The first one is the cotangent sheaf  , which is the dual of
, which is the dual of  , i.e.
, i.e.  . The second one is the parity shifted tangent sheaf
. The second one is the parity shifted tangent sheaf  , which is a locally-free sheaf of
, which is a locally-free sheaf of  -module of rank \(q\,{|}\,p\). With reference to the above trivialization over U, the parity shifted tangent sheaf is locally generated as follows:
-module of rank \(q\,{|}\,p\). With reference to the above trivialization over U, the parity shifted tangent sheaf is locally generated as follows:

where we stress that the local generators \(\pi \partial _{\theta }\)’s are even and the \(\pi \partial _{z}\)’s are odd. Sections of the parity-shifted tangent sheaf are called \(\Pi \)-vector fields or vector fields for short. We call the dual of the parity-shifted tangent sheaf the sheaf of 1-forms on  and we denote it as
and we denote it as  . This is a locally-free sheaf of (right)
. This is a locally-free sheaf of (right)  -modules of rank \(q\,{|}\,p\): over an open set U one has the trivialization
-modules of rank \(q\,{|}\,p\): over an open set U one has the trivialization

where the local generators \(d\theta \)’s are even and the dz’s are odd. The duality paring between  and
and  over U reads \(dx_a (\pi \partial _{x_b}) = \delta _{ab}\) for any a, b both even or odd. The name sheaf of 1-forms is in some sense justified by the fact that in supergeometry it is customary take the de Rham differential to be an odd morphism, so that one indeed has a sheaf morphism
over U reads \(dx_a (\pi \partial _{x_b}) = \delta _{ab}\) for any a, b both even or odd. The name sheaf of 1-forms is in some sense justified by the fact that in supergeometry it is customary take the de Rham differential to be an odd morphism, so that one indeed has a sheaf morphism  which satisfies the \(\mathbb {Z}_2\)-graded Leibniz rule. Application of the (super)symmetric power functor
which satisfies the \(\mathbb {Z}_2\)-graded Leibniz rule. Application of the (super)symmetric power functor  to the sheaf of 1-forms
to the sheaf of 1-forms  and to
and to  yields respectively the algebra of forms and \(\Pi \)-vector fields on
yields respectively the algebra of forms and \(\Pi \)-vector fields on  . A section of
. A section of  is called a k-form and a section of
is called a k-form and a section of  is called a (k-)\(\Pi \)-polyfield or k-polyfield for short. In this context the de Rham differential lifts to the exterior derivative
is called a (k-)\(\Pi \)-polyfield or k-polyfield for short. In this context the de Rham differential lifts to the exterior derivative  , which is an odd derivation of
, which is an odd derivation of  , i.e. it obeys the \(\mathbb {Z}_2\)-graded Leibniz rule in the form
, i.e. it obeys the \(\mathbb {Z}_2\)-graded Leibniz rule in the form
where \(\omega \) and \(\eta \) are two generic forms in  and where we have denoted by \(|\omega |\) the \(\mathbb {Z}_2\)-degree, henceforth parity of \(\omega \). Further, it is easy to see that the exterior derivative is nilpotent: the pair
and where we have denoted by \(|\omega |\) the \(\mathbb {Z}_2\)-degree, henceforth parity of \(\omega \). Further, it is easy to see that the exterior derivative is nilpotent: the pair  defines a sheaf of dg-algebras, the de Rham complex of
defines a sheaf of dg-algebras, the de Rham complex of  .
.
As it is well known, differential forms are not suitable for integration in a supergeometric setting [18]: this leads to the introduction of a second complex, which is “dual” to the de Rham complex. This is the so-called complex of integral forms, which are defined as sections of the tensor product of sheaves  , where
, where  is the Berezinian sheaf of
is the Berezinian sheaf of  , see [18, 21, 22], which substitutes the notion of canonical sheaf of an ordinary manifold and whose sections are tensor densities. The interested reader can refer to [18] or the recent [5] and [22] for a construction ab initio of the differential for integral forms.
, see [18, 21, 22], which substitutes the notion of canonical sheaf of an ordinary manifold and whose sections are tensor densities. The interested reader can refer to [18] or the recent [5] and [22] for a construction ab initio of the differential for integral forms.
After this preliminary recollections of definitions, conventions and notations we introduce one of the main objects under study in this paper.
Definition 2.1
(BV supermanifold \(\textsf{M}\)) Let  be a smooth, analytic or algebraic supermanifold of dimension \(p\,{|}\,q\) and let
be a smooth, analytic or algebraic supermanifold of dimension \(p\,{|}\,q\) and let  be its sheaf of 1-forms. We call
be its sheaf of 1-forms. We call  the \(p+q \,{|}\, p + q\)-dimensional supermanifold defined as a ringed space by the pair
the \(p+q \,{|}\, p + q\)-dimensional supermanifold defined as a ringed space by the pair  , where the topological space
, where the topological space  is given by the total space
is given by the total space  of the vector bundle
of the vector bundle  of rank \(p+q\) endowed with its canonical topology, and the structure sheaf \({\mathcal {O}}_{\tiny {{\textsf{M}}}}\) is defined as
of rank \(p+q\) endowed with its canonical topology, and the structure sheaf \({\mathcal {O}}_{\tiny {{\textsf{M}}}}\) is defined as  , where
, where  is taken with its
is taken with its  -module structure.
-module structure.
Remark 2.2
Notice that the canonical topology on the total space of a vector bundle is defined locally via the product topology, and then glueing along the transition functions: the related quotient topology is the desired topology on the total space of the vector bundle.
Remark 2.3
The previous definition says that “functions” on \({\textsf{M}}\) are polynomial functions on the fibers  , i.e. they are polyfields having shifted parity. Locally, on open sets of the kind
, i.e. they are polyfields having shifted parity. Locally, on open sets of the kind  for U an open set in
for U an open set in  , one has that
, one has that

for even and odd fiber coordinates  and \(\mathbb {K}\) the field of real or complex numbers. In the following subsection we will give an explicit local description via transition functions.
and \(\mathbb {K}\) the field of real or complex numbers. In the following subsection we will give an explicit local description via transition functions.
Remark 2.4
A notational remark is in order. Indeed, in the introduction of the paper we have denoted the supermanifold \({\textsf{M}}\) defined above in Definition 2.1 with  , to distinguish it from the supermanifold
, to distinguish it from the supermanifold  arising in the context of the BRST formalism. In the following we will always consider the supermanifold
arising in the context of the BRST formalism. In the following we will always consider the supermanifold  .
.
2.1 Local description
It is worth to provide a local description of \({\textsf{M}}\) in terms of transition functions of its local coordinates. We let \((U, x_a)\) be a local chart for the \(p\,{|}\,q\)-dimensional supermanifold  , where we stress that the index a spans both even and odd local coordinates. Then \((\pi ^{-1} (U), x_a, p_a)\) is a chart for \({\textsf{M}}\) with
, where we stress that the index a spans both even and odd local coordinates. Then \((\pi ^{-1} (U), x_a, p_a)\) is a chart for \({\textsf{M}}\) with
The following is immediate.
Lemma 2.5
(Transition functions of \({{\textsf{M}}}\)) Let \((U, x_a)\) and \((V, z_b)\) be two charts on  with \(U \cap V \ne \varnothing \), and let \((\pi ^{-1}(U), x_a, p_a)\) and \((\pi ^{-1} (V), z_b, q_b)\) be the corresponding open sets on \({\textsf{M}} \). Then the transition functions of \({{\mathsf {{M}}}}\) read
with \(U \cap V \ne \varnothing \), and let \((\pi ^{-1}(U), x_a, p_a)\) and \((\pi ^{-1} (V), z_b, q_b)\) be the corresponding open sets on \({\textsf{M}} \). Then the transition functions of \({{\mathsf {{M}}}}\) read

Proof
The first ones are obvious, being the transition functions on  . For the latter, it is enough to observe that from \(d z_b = dx_a (\partial _{x_a} z_b)\) it follows that
. For the latter, it is enough to observe that from \(d z_b = dx_a (\partial _{x_a} z_b)\) it follows that

where we have made use of the definition of \(q_b\) in the last step. \(\square \)
3 The geometry of forms: split and non-split extensions
We now study the geometry of the cotangent sheaf  of the supermanifold \({\textsf{M}}\). Note that this is a locally-free sheaf of
of the supermanifold \({\textsf{M}}\). Note that this is a locally-free sheaf of  -modules of rank \(p+q \,{|}\, p+q\). We can characterize its transition functions thanks to Lemma 2.5.
-modules of rank \(p+q \,{|}\, p+q\). We can characterize its transition functions thanks to Lemma 2.5.
Lemma 3.1
(Transition functions of  ) Let \({\textsf{M}} \) be defined as above and let \((dx_a, dp_a)\) and \((dz_b, dq_b)\) be two local bases of
) Let \({\textsf{M}} \) be defined as above and let \((dx_a, dp_a)\) and \((dz_b, dq_b)\) be two local bases of  on the open sets \(\pi ^{-1} (U)\) and \(\pi ^{-1}(V)\) on \({\textsf{M}} \) with \(U \cap V \ne \varnothing \). Then the transition functions of
on the open sets \(\pi ^{-1} (U)\) and \(\pi ^{-1}(V)\) on \({\textsf{M}} \) with \(U \cap V \ne \varnothing \). Then the transition functions of  read
read
Proof
The first ones are obvious. For the transition functions of the dp’s we observe that we have
The first summand reads

The second summands reads

\(\square \)
The previous lemma describes  locally in terms of its transition functions, but it yields information also on its global geometry, as the following shows.
locally in terms of its transition functions, but it yields information also on its global geometry, as the following shows.
Theorem 3.2
( as extension of vector bundles) Let \({\textsf{M}} \) be defined as above. Then the canonical exact sequence
as extension of vector bundles) Let \({\textsf{M}} \) be defined as above. Then the canonical exact sequence

induces the isomorphism  . In particular,
. In particular,  is an extension of locally-free sheaves
is an extension of locally-free sheaves

Proof
We work in the same setting of Lemma 3.1. We first observe that the transformations of equation (3.1) identify the sections \((dx_a)\)’s as a local basis of  (notice the slight abuse of notation). The first summand in the transformations given by equation (3.2) identifies the transformations of the parity-reversed dual of
(notice the slight abuse of notation). The first summand in the transformations given by equation (3.2) identifies the transformations of the parity-reversed dual of  , as the \(dp_a\) have opposite parity with respect to the \(dx_a\). This is hence identified with
, as the \(dp_a\) have opposite parity with respect to the \(dx_a\). This is hence identified with  . The second summand in (3.2) gives the off-diagonal term of the extension of
. The second summand in (3.2) gives the off-diagonal term of the extension of  with
with  . \(\square \)
. \(\square \)
It follows from the previous theorem that in order to study the geometry of  one needs to consider the cohomology group
one needs to consider the cohomology group

which controls the splitting of the exact sequence (3.4), that will be called  -extension in the rest of the paper. For ease of reading, we have deferred to the appendix a very concrete construction of the Ext-group related to an extension, which highlights the structure of the representatives in the above cohomology group in terms of the transition functions of the vector bundles involved. As we shall see, this concrete approach will play a significant role in what follows.
-extension in the rest of the paper. For ease of reading, we have deferred to the appendix a very concrete construction of the Ext-group related to an extension, which highlights the structure of the representatives in the above cohomology group in terms of the transition functions of the vector bundles involved. As we shall see, this concrete approach will play a significant role in what follows.
It is convenient to re-express this Ext-group appearing in (3.5) as a cohomology group computed on the supermanifold  —and hence on
—and hence on  —instead of \({\textsf{M}}\).
—instead of \({\textsf{M}}\).
Theorem 3.3
(Projection to  ) Let
) Let  be a smooth, analytic or algebraic supermanifold, and let \({\mathsf {{M}}} \) be constructed as above with
be a smooth, analytic or algebraic supermanifold, and let \({\mathsf {{M}}} \) be constructed as above with  its projection map. Then one has the following natural isomorphism:
its projection map. Then one has the following natural isomorphism:

Proof
First, notice that

Since in the given hypotheses,  is an affine morphism, then by Leray’s spectral sequence
is an affine morphism, then by Leray’s spectral sequence

Finally, by projection formula applied to \(R^i \pi _{*} \)—in the case \(i=0\) (see [13, p. 253]) we have

Further, since  as
as  -modules, this can be rewritten as
-modules, this can be rewritten as

Finally, the linear dependence on p in the second summand of (3.2) shows that this extension class appears in degree one only in  , i.e. in the summand
, i.e. in the summand  of the above direct image, so that one finds
of the above direct image, so that one finds

The conclusions follow observing that

and that  , so that
, so that

\(\square \)
The above theorem can be applied to smooth real supermanifolds, as to show the existence of a reduction of the structure group of  . To this end, following [18, Chapter 4, Section 10], we recall that the structure group of
. To this end, following [18, Chapter 4, Section 10], we recall that the structure group of  is given by the symplectic supergroup \(\Pi \text {Sp} (p+q\,{|}\,p+q)\), that can be understood as the stabilizer of the “metric” in
is given by the symplectic supergroup \(\Pi \text {Sp} (p+q\,{|}\,p+q)\), that can be understood as the stabilizer of the “metric” in  given by the odd symplectic form \(\omega \)—whose related geometry will be discussed in Sect. 6, see Definition 6.6.
given by the odd symplectic form \(\omega \)—whose related geometry will be discussed in Sect. 6, see Definition 6.6.
Theorem 3.4
(Splitting & reduction of symplectic supergroup) Let  be a smooth supermanifold and let
be a smooth supermanifold and let  be the smooth supermanifold associated to
be the smooth supermanifold associated to  as defined above. Then the following are true:
as defined above. Then the following are true:
-
(1)
The
 -extension
-extension 
is split, i.e.
 non-canonically.
non-canonically. -
(2)
There exists a reduction of the structure group of
 as follows:
as follows: 
where \(\Pi { {\text {Sp}}}(p+q\,{|}\,p+q)\) is the symplectic supergroup.
Proof
For the first point it is enough to observe that the existence of a smooth partition of unity in the smooth category leads to the exactness of the Čech cochain complex of any sheaf in degree \(i > 0\), which is therefore fine, thus soft and acyclic. Applying this to  yields the conclusion, i.e.
yields the conclusion, i.e.

The second point follows from the first one and Theorem 6.14 in Appendix, which generalizes to the \({\mathbb {Z}}_2\)-graded context. To this end it is enough to observe that the structure of the transition functions as in (A.4) follows from Lemma 3.1. \(\square \)
Remark 3.5
It is to be noted that the above splitting is non-canonical. It would be interesting to see if it is possible to classify or provide constraints on smooth supermanifolds such that the above reduction of the structure group is possible via a suitable choice of charts.
4 Connections and obstructions: the super Atiyah class
Theorem 3.4 proves the existence of a splitting for the  -extension in the smooth category: this fact could have been easily inferred directly from equation (3.5). On the other hand, the “projection” result of Theorem 3.3 allows for a very nice interpretation when working in the complex analytic or algebraic category, where sheaves admit non-trivial higher cohomologies and the splitting of the
-extension in the smooth category: this fact could have been easily inferred directly from equation (3.5). On the other hand, the “projection” result of Theorem 3.3 allows for a very nice interpretation when working in the complex analytic or algebraic category, where sheaves admit non-trivial higher cohomologies and the splitting of the  -extension is far from obvious. Quite the contrary, we will see that in general the conditions under which the
-extension is far from obvious. Quite the contrary, we will see that in general the conditions under which the  -extension splits are quite restrictive. To this end, in the following we restrict ourselves to work on complex supermanifolds in the holomorphic category: the reader shall see that everything holds true also in the algebraic category.
-extension splits are quite restrictive. To this end, in the following we restrict ourselves to work on complex supermanifolds in the holomorphic category: the reader shall see that everything holds true also in the algebraic category.
Definition 4.1
(Affine connection on  ) Let
) Let  be a complex supermanifold and let
be a complex supermanifold and let  be the (holomorphic) tangent sheaf of
be the (holomorphic) tangent sheaf of  An affine connection on
An affine connection on  is an even morphism of sheaves of \({\mathbb {C}}\)-vector spaces
is an even morphism of sheaves of \({\mathbb {C}}\)-vector spaces  such that it satisfies the Leibniz rule
such that it satisfies the Leibniz rule

for any  and
and  , where
, where  is the even de Rham differential, see [18].
is the even de Rham differential, see [18].
Obstructions to the existence of an affine connection on a complex supermanifold [2, 3, 11, 17] can be established in same fashion of the original Atiyah’s result [1] for ordinary complex manifolds. We spell out the main points of the construction following [2], which is very close to the original [1].
First, one defines the sheaf of 1-jets of  . One starts introducing the sheaf of \({\mathbb {C}}\)-vector spaces given by
. One starts introducing the sheaf of \({\mathbb {C}}\)-vector spaces given by

for U an open set of  Notice that sections of
Notice that sections of  are 1-forms valued in the tangent bundle. The sheaf
are 1-forms valued in the tangent bundle. The sheaf  can be endowed with the structure of sheaf of
can be endowed with the structure of sheaf of  -modules as follows: let
-modules as follows: let  and
and  . One defines the product
. One defines the product

where  is the even de Rham differential, see again [18]. One can then verify that the sequence of sheaves of
is the even de Rham differential, see again [18]. One can then verify that the sequence of sheaves of  -modules given by
-modules given by

where \( \alpha (\tau ) \,{:}{=}\,(0, \tau )\), and \(\beta ((X, \tau )) = X\), is exact. Notice that since  is locally-free, then the sequence (4.2) is locally split, hence there exists a covering \(\{U_a \}_{a \in I}\) such that
is locally-free, then the sequence (4.2) is locally split, hence there exists a covering \(\{U_a \}_{a \in I}\) such that  and
and  are free and
are free and

which guarantees that  is locally-free. On the other hand, due to the non-trivial
is locally-free. On the other hand, due to the non-trivial  -module structure of the sheaf of 1-jets of
-module structure of the sheaf of 1-jets of  , the previous short exact sequence of locally-free sheaves of
, the previous short exact sequence of locally-free sheaves of  -modules (4.2)—henceforth 1-jets short exact sequence—does not necessarily split. Applying the functor
-modules (4.2)—henceforth 1-jets short exact sequence—does not necessarily split. Applying the functor  , and taking the long exact sequence in cohomology one gets
, and taking the long exact sequence in cohomology one gets

We call this long exact sequence in cohomology the 1-jets long exact cohomology sequence. We can thus give the following definition.
Definition 4.2
(Super Atiyah class) Let  be a complex supermanifold and let
be a complex supermanifold and let  be its tangent sheaf. We define the Atiyah class
be its tangent sheaf. We define the Atiyah class  of
of  to be the image of the identity map
to be the image of the identity map  via the 1-connecting homomorphism \(\delta \) in the 1-jets long exact cohomology sequence, i.e.
via the 1-connecting homomorphism \(\delta \) in the 1-jets long exact cohomology sequence, i.e.

The following theorem is adapted from [1] to the super-setting, and it shows how the super Atiyah class is related to the existence of an affine connection on the complex supermanifold  .
.
Theorem 4.3
(Pseudo-Atiyah) Let  be a complex supermanifold and let
be a complex supermanifold and let  be the tangent sheaf of
be the tangent sheaf of  , then:
, then:
-
(1)
the 1-jets short exact sequence (4.2) splits if and only if there exists an affine connection on
 ;
; -
(2)
there exists an affine connection on
 if and only if
if and only if  is trivial.
is trivial.
In particular, let \(\{U_i\}_{i \in I}\) be an open covering for  and \(\{ g_{ij} \}_{i, j \in I}\) be the transition functions of
and \(\{ g_{ij} \}_{i, j \in I}\) be the transition functions of  on the intersections \(U_i \cap U_j\), then the Atiyah class of
on the intersections \(U_i \cap U_j\), then the Atiyah class of  is represented by the Čech 1-cocycle
is represented by the Čech 1-cocycle

Proof
The first point is the crucial one. First, we let \(\nabla \) be an affine connection on  and we define the morphism
and we define the morphism  by \(j (X) \,{:}{=}\,(X, \nabla X)\). Notice that \(s_{\nabla }\) is a well-defined morphism of sheaves of
by \(j (X) \,{:}{=}\,(X, \nabla X)\). Notice that \(s_{\nabla }\) is a well-defined morphism of sheaves of  -modules, as
-modules, as

by equation (4.1). By definition of the 1-jets short exact sequence (4.2), one has that the surjective morphism  is given by \(\beta ((X, \tau )) = X\). Therefore
is given by \(\beta ((X, \tau )) = X\). Therefore  , which implies that the affine connection \(\nabla \) determines a splitting \(s_{\nabla } \) of the 1-jets short exact sequence, i.e.
, which implies that the affine connection \(\nabla \) determines a splitting \(s_{\nabla } \) of the 1-jets short exact sequence, i.e.

Vice versa, let the 1-jets short exact sequence (4.2) be split. Then there exists a morphism of sheaves of  -modules
-modules  such that
such that  . We let then
. We let then  be defined by \(p ((X, \tau )) = \tau \). Notice that p is \({\mathbb {C}}\)-linear, but not
be defined by \(p ((X, \tau )) = \tau \). Notice that p is \({\mathbb {C}}\)-linear, but not  -linear. Let us then define
-linear. Let us then define  It is immediate that \(\nabla ^{(s)}\) is \({\mathbb {C}}\)-linear. Finally, it satisfies the Leibniz rule, indeed
It is immediate that \(\nabla ^{(s)}\) is \({\mathbb {C}}\)-linear. Finally, it satisfies the Leibniz rule, indeed

for any  and
and  It follows that \(\nabla ^{(s)}\) defines an affine connection.
It follows that \(\nabla ^{(s)}\) defines an affine connection.
The second point of the theorem depends on the first one. Let  . Then, by definition
. Then, by definition  . By exactness, it follows from the 1-jets long cohomology exact sequence (4.3)
. By exactness, it follows from the 1-jets long cohomology exact sequence (4.3)

that there exists an element  such that
such that  , where \(\beta \) is the surjection in 1-jets short exact sequence (4.2), which therefore splits. By the previous point of the theorem, this is equivalent to the existence of an affine connection on
, where \(\beta \) is the surjection in 1-jets short exact sequence (4.2), which therefore splits. By the previous point of the theorem, this is equivalent to the existence of an affine connection on  .
.
Vice versa, let  be such that it admits an affine connection. Then the 1-jets short exact sequence is split by the previous point of the theorem. This implies that there exists a map
be such that it admits an affine connection. Then the 1-jets short exact sequence is split by the previous point of the theorem. This implies that there exists a map  such that
such that  . It follows that
. It follows that  belongs to the image of the map
belongs to the image of the map  and hence
and hence  i.e.
i.e.  .
.
For the last point, we let \(\{U_i \}_{i\in I}\) be an open covering of  and \(\{g_{ij} \}_{i, j \in I}\) be the transition functions of
and \(\{g_{ij} \}_{i, j \in I}\) be the transition functions of  on the intersections \(U_i \cap U_j\). For the sake of notation, compositions of maps are left understood in what follows. A Čech 1-cocycle representation of the class
on the intersections \(U_i \cap U_j\). For the sake of notation, compositions of maps are left understood in what follows. A Čech 1-cocycle representation of the class  in terms of \(\{g_{ij} \}_{i,j \in I} \) can be obtained by letting \(\nabla _i \) be the (flat) connection on
in terms of \(\{g_{ij} \}_{i,j \in I} \) can be obtained by letting \(\nabla _i \) be the (flat) connection on  which is determined by a fixed trivialization relative to \(\{ U_i\}_{i\in I}.\) In particular, following [1] and [2] we let
which is determined by a fixed trivialization relative to \(\{ U_i\}_{i\in I}.\) In particular, following [1] and [2] we let

where \(\phi _i \) is a trivialization on \(U_i\), and we define

by
Observing that  , one computes
, one computes

This simplifies to

where we have used the Leibniz rule applied to  . It follows that
. It follows that

Finally, upon using  , one checks that
, one checks that  , i.e. it defines a Čech 1-cocycle in the cohomology of
, i.e. it defines a Čech 1-cocycle in the cohomology of  . \(\square \)
. \(\square \)
Remark 4.4
With reference to the last part of Theorem 4.3, one can notice that a local holomorphic connection can be written in the form  in a trivialization
in a trivialization  with
with  a matrix-valued holomorphic 1-form on \(U_i\). These can be patched together to form a globally defined (holomorphic) affine connection if and only if
a matrix-valued holomorphic 1-form on \(U_i\). These can be patched together to form a globally defined (holomorphic) affine connection if and only if

that can be rearranged as

Then, in view of Theorem 4.3, the left-hand side is (a Čech 1-cocycle representing) the Atiyah class of  , and equation (4.5) can be written as
, and equation (4.5) can be written as

where the right-hand side is the Čech coboundary of  . This shows via Čech cohomology that local connections can be patched together if and only if
. This shows via Čech cohomology that local connections can be patched together if and only if  providing a different proof of the second point of Theorem 4.3 in a local-to-global fashion, as it is customary in Čech cohomology.
providing a different proof of the second point of Theorem 4.3 in a local-to-global fashion, as it is customary in Čech cohomology.
Remark 4.5
Further, notice that the same construction as above can be carried out for any locally-free sheaf  on
on  , not only the tangent sheaf
, not only the tangent sheaf  . In this respect the non-vanishing of the corresponding Atiyah class, which we still denote as
. In this respect the non-vanishing of the corresponding Atiyah class, which we still denote as  , is an obstruction to define a holomorphic connection on
, is an obstruction to define a holomorphic connection on  .
.
The previous Theorem 4.3 allows to identify the obstruction to splitting the  -extension.
-extension.
Theorem 4.6
(\(\Omega ^{1}_{ \tiny {{\textsf{M}}}}\) and the Atiyah class) Let  be a complex supermanifold and let \({\mathsf {{M}}}\) be constructed as above. Then the
be a complex supermanifold and let \({\mathsf {{M}}}\) be constructed as above. Then the  -extension
-extension

is split if and only if  is trivial. In particular, the short exact sequence is split if and only if
is trivial. In particular, the short exact sequence is split if and only if  admits an affine connection.
admits an affine connection.
Proof
By the previous Theorem 3.3 obstructions to splitting the short exact sequences lie indeed in  . By Lemma 6.14 and the structure of the transition functions given in Theorem 3.1 one sees that the obstructions are represented as Čech 1-cocycles by elements of the form
. By Lemma 6.14 and the structure of the transition functions given in Theorem 3.1 one sees that the obstructions are represented as Čech 1-cocycles by elements of the form  , (where the \(g_{ij}\)’s are the transition functions of the tangent sheaf
, (where the \(g_{ij}\)’s are the transition functions of the tangent sheaf  ), which is identified with the Atiyah class
), which is identified with the Atiyah class  by (4.4). \(\square \)
by (4.4). \(\square \)
We now aim to relate the splitting of the short exact sequence (4.6) to the geometry of the complex supermanifold  . To this end we first recall some basic constructions specific to the theory of complex supermanifolds, see [5] or [18]. To each complex supermanifold is attached the short exact sequence
. To this end we first recall some basic constructions specific to the theory of complex supermanifolds, see [5] or [18]. To each complex supermanifold is attached the short exact sequence

where  is the sheaf of nilpotent sections in
is the sheaf of nilpotent sections in  and
and  is the structure sheaf of the reduced space
is the structure sheaf of the reduced space  —and ordinary complex manifold—of the supermanifold
—and ordinary complex manifold—of the supermanifold  . If (4.7) splits, then the supermanifold
. If (4.7) splits, then the supermanifold  is said to be projected, because the splitting corresponds to the existence of a “projection” morphism
is said to be projected, because the splitting corresponds to the existence of a “projection” morphism  such that
such that  , if
, if  is the canonical embedding of the reduced space
is the canonical embedding of the reduced space  into the supermanifold
into the supermanifold  . Moreover, the quotient
. Moreover, the quotient  defines a locally-free sheaf of
defines a locally-free sheaf of  -modules of rank q —where q is the odd dimension of
-modules of rank q —where q is the odd dimension of  —and whose sections are seen to be odd. We call the quotient
—and whose sections are seen to be odd. We call the quotient  the fermionic sheaf of
the fermionic sheaf of  and we denote it by
and we denote it by  . We say that the supermanifold
. We say that the supermanifold  is split if its structure sheaf is globally isomorphic to the sheaf of exterior algebras
is split if its structure sheaf is globally isomorphic to the sheaf of exterior algebras  over
over  . Notice that a split supermanifold is in particular projected. The corresponding obstruction theory to splitting a supermanifold is currently a compelling active research topic, see for example [3, 22].
. Notice that a split supermanifold is in particular projected. The corresponding obstruction theory to splitting a supermanifold is currently a compelling active research topic, see for example [3, 22].
In this context, the fundamental obstruction class to splitting a supermanifold  is given by a class
is given by a class

If  is non-vanishing then
is non-vanishing then  is non-projected and in particular non-split. Whereas the fundamental obstruction class is always defined, higher obstruction classes
is non-projected and in particular non-split. Whereas the fundamental obstruction class is always defined, higher obstruction classes

for \(i\geqslant 1\) are defined if and only if all of the previous ones are vanishing, see the discussion in [11] for example.
A different criterion, actually a sufficient condition, for the existence of a splitting of a supermanifold, has been given by Koszul in [17], relating the question about the splitting of  to the existence of an affine connection on it.
to the existence of an affine connection on it.
Theorem 4.7
(Koszul) Let  be a complex supermanifold. If
be a complex supermanifold. If  admits an affine connection, then it is split. In particular, the affine connection defines a unique splitting of the supermanifold.
admits an affine connection, then it is split. In particular, the affine connection defines a unique splitting of the supermanifold.
Proof
See [17], recently reviewed in [3].\(\square \)
This result can in turn be related with a recent result by Donagi and Witten [11]. Indeed, when restricted to the reduced space, the tangent and cotangent sheaf  and
and  split into a direct sum of an even and an odd part. The latter is isomorphic to the fermionic sheaf or its dual in the case of the cotangent and tangent sheaf respectively. More precisely, one finds
split into a direct sum of an even and an odd part. The latter is isomorphic to the fermionic sheaf or its dual in the case of the cotangent and tangent sheaf respectively. More precisely, one finds

In this spirit, one of the key results in [11] concerns the decomposition of the Atiyah class of  upon restriction of the tangent sheaf to the reduced manifold
upon restriction of the tangent sheaf to the reduced manifold  .
.
Theorem 4.8
(Donagi & Witten) Let  be a complex supermanifold. Then, the restriction
be a complex supermanifold. Then, the restriction  of the tangent sheaf to
of the tangent sheaf to  induces the following decomposition of the cohomology group
induces the following decomposition of the cohomology group  :
:

In particular, with respect to the above decomposition the Atiyah class  decomposes as follows:
decomposes as follows:

where  is the Atiyah class of the tangent sheaf of
is the Atiyah class of the tangent sheaf of  ,
,  is first obstruction class, and
is first obstruction class, and  is the Atiyah class of the fermionic sheaf.
is the Atiyah class of the fermionic sheaf.
Proof
See [11]. \(\square \)
This result together with Koszul’s Theorem 4.7 leads to the following for the geometry of  .
.
Theorem 4.9
(Splitting of  ) Let
) Let  be a complex supermanifold and let \({\mathsf {{M}}}\) be constructed as above. Then any of the following is an obstruction to split
be a complex supermanifold and let \({\mathsf {{M}}}\) be constructed as above. Then any of the following is an obstruction to split  -extension (4.6):
-extension (4.6):
-
(1)
 , i.e.
, i.e.  does not admit a holomorphic connection;
does not admit a holomorphic connection; -
(2)
 , i.e.
, i.e.  does not admit a holomorphic connection;
does not admit a holomorphic connection; -
(3)
 , i.e.
, i.e.  is non-projected or non-split.
is non-projected or non-split.
In particular, a necessary condition for the  -extension to split is that
-extension to split is that  is a split supermanifold.
is a split supermanifold.
Proof
The  -extension is split if and only if the Atiyah class of
-extension is split if and only if the Atiyah class of  vanishes by Theorem 4.6 and the three obstructions to split the
vanishes by Theorem 4.6 and the three obstructions to split the  -extension follow from the decomposition at the Atiyah class given in (4.8) of Theorem 4.8. Finally, the vanishing of the Atiyah class implies the existence of an affine connection, which is equivalent to the existence of a splitting for
-extension follow from the decomposition at the Atiyah class given in (4.8) of Theorem 4.8. Finally, the vanishing of the Atiyah class implies the existence of an affine connection, which is equivalent to the existence of a splitting for  by Theorem 4.7.\(\square \)
by Theorem 4.7.\(\square \)
We conclude this section with some general remarks and speculation on the nature of the super Atiyah class for a complex supermanifold.
Remark 4.10
(Super Atiyah class & super characteristic classes) It should be clear by the above considerations that the vanishing of the super Atiyah class provides a very strong constraint on the geometry of a complex or algebraic supermanifold. Namely, the following is an immediate consequence of the Koszul’s result, Theorem 4.7, and the very definition of split supermanifold.
Corollary 4.11
Let  be a complex supermanifold of dimension \(n\,{|}\,m\) such that
be a complex supermanifold of dimension \(n\,{|}\,m\) such that  , then
, then  is split. In particular all of the obstruction classes to splitting
is split. In particular all of the obstruction classes to splitting  vanish, i.e. for any \(i = 1, \ldots , \lfloor m/2 \rfloor \),
vanish, i.e. for any \(i = 1, \ldots , \lfloor m/2 \rfloor \),

This, together with Theorem 4.8, should make apparent the existence of a close relation between the super Atiyah class and the obstructions to splitting a complex supermanifold (see also the recent [3] in this regard).
It should be stressed indeed that, in a classical setting, for a compact complex Kähler manifold X, the Atiyah class of tangent bundle contains information about all the Chern classes \(c_k (X) = c_{k} ({\textsf{T}}_X)\) of the manifold [15]. In particular, if X admits a holomorphic connections, i.e. the Atiyah class of \({\textsf{T}}_X\) vanishes, then all the Chern classes vanish as well, i.e. \(c_k (X) = 0\) for any \(k>0\). It can be reasonably conjectured that, in a very similar fashion, also on a complex supermanifold  the Atiyah class of the tangent bundle
the Atiyah class of the tangent bundle  contains information about all of the characteristic classes related to
contains information about all of the characteristic classes related to  . The difference relies in that among these are to be counted not only the Atiyah classes of the reduced manifold
. The difference relies in that among these are to be counted not only the Atiyah classes of the reduced manifold  and of the fermionic sheaf
and of the fermionic sheaf  —as seen in Theorem 4.8—and hence the related Chern classes, but also all of the obstruction classes to splitting the supermanifold, which indeed arises as well from the tangent bundle
—as seen in Theorem 4.8—and hence the related Chern classes, but also all of the obstruction classes to splitting the supermanifold, which indeed arises as well from the tangent bundle  of the supermanifold. Whereas the fundamental obstruction
of the supermanifold. Whereas the fundamental obstruction  arises from the super Atiyah class upon restriction to
arises from the super Atiyah class upon restriction to  [11], it is quite reasonable to imagine that higher obstruction classes would arise upon allowing for higher fermionic terms in the filtration of
[11], it is quite reasonable to imagine that higher obstruction classes would arise upon allowing for higher fermionic terms in the filtration of  by the ideal sheaf of nilpotent sections
by the ideal sheaf of nilpotent sections  of the supermanifold
of the supermanifold

and thus considering the restriction of  to the canonical superscheme contained in
to the canonical superscheme contained in  defined by the pair
defined by the pair  for \(\ell > 1\), i.e.
for \(\ell > 1\), i.e.

5 Examples and further results
In this section we discuss and comment some examples. First, it is obvious that the complex supermanifold \({\mathbb {C}}^{n|m}\) admits a splitting for the  -extension for any values of n and m.
-extension for any values of n and m.
Example 5.1
(\({\mathbb {C}}^{n|m}\)) Let  be the complex supermanifold with structure sheaf given by
be the complex supermanifold with structure sheaf given by  and let \({\textsf{M}}\) be the supermanifold constructed from \({\mathbb {C}}^{n|m}\) as in Definition 2.1. Then, for any n and m the
and let \({\textsf{M}}\) be the supermanifold constructed from \({\mathbb {C}}^{n|m}\) as in Definition 2.1. Then, for any n and m the  -extension is split.
-extension is split.
This follows from the fact that the tangent bundle \({\textsf{T}}_{{\mathbb {C}}^{n|m}}\) of \({\mathbb {C}}^{n|m}\) is trivial, and as such it admits a connection. Then, by Theorem 4.3 its super Atiyah class \({{\mathfrak {A}}}{{\mathfrak {t}}} ({\textsf{T}}_{{\mathbb {C}}^{n|m}})\) is trivial, and in turn, by Theorem 4.6 the  -extension related to \({\mathbb {C}}^{n|m}\) splits.
-extension related to \({\mathbb {C}}^{n|m}\) splits.
A way more interesting example is provided by complex Lie supergroups—the reader is suggested to refer to [26] for the relevant definitions.
Example 5.2
(Complex Lie supergroups  ) Let
) Let  be a complex Lie supergroup. Then
be a complex Lie supergroup. Then  admits a holomorphic connection and hence it is split. In particular, if \({\textsf{M}}\) is the supermanifold constructed from
admits a holomorphic connection and hence it is split. In particular, if \({\textsf{M}}\) is the supermanifold constructed from  as in Definition 2.1, the
as in Definition 2.1, the  -extension splits.
-extension splits.
The result follows from the fact that, as in the ordinary theory, a complex Lie supergroup is parallelizable, i.e. its tangent bundle  is trivial. Just like in the ordinary theory this depends on the existence of a group structure on the supermanifold
is trivial. Just like in the ordinary theory this depends on the existence of a group structure on the supermanifold  . In turn, since the tangent bundle
. In turn, since the tangent bundle  of
of  is trivial, then
is trivial, then  admits a connection. It follows from Theorem 4.7 that
admits a connection. It follows from Theorem 4.7 that  is split and from Theorems 4.3 and 4.6 that the related
is split and from Theorems 4.3 and 4.6 that the related  -extension splits.
-extension splits.
It is to be stressed that the case of homogeneous supermanifolds, i.e. quotients of Lie supergroups by some closed Lie sub-(super)group, is more delicate: indeed, complex homogeneous supermanifolds can indeed be non-split, thus not admitting holomorphic connection, see [26].
We now move to (complex) projective superspaces \({{\mathbb {C}}}{{\mathbb {P}}}^{\,n|m}\), which are defined as the complex supermanifolds given by the pair  where
where  . Notice that according to the discussion after Theorem 4.6 above, complex projective superspaces \({{\mathbb {C}}}{{\mathbb {P}}}^{\,n|m}\) are by definition split supermanifolds, in particular their fermionic sheaf reads
. Notice that according to the discussion after Theorem 4.6 above, complex projective superspaces \({{\mathbb {C}}}{{\mathbb {P}}}^{\,n|m}\) are by definition split supermanifolds, in particular their fermionic sheaf reads  . See [4] for a dedicated paper.
. See [4] for a dedicated paper.
Example 5.3
(\({{\mathbb {C}}}{{\mathbb {P}}}^{\,n|m}\)) Let \({{\mathbb {C}}}{{\mathbb {P}}}^{\,n|m}\) be any complex projective superspace and let \({\mathsf {{M}}}\) be the supermanifold constructed from \({{\mathbb {C}}}{{\mathbb {P}}}^{\,n|m}\) as above. Then, for any value of \(n\geqslant 1\) and \(m\geqslant 0\) the  -extension is not split.
-extension is not split.
The result can be seen to follow from point (1) of Theorem 4.9. For this, one needs to prove that projective spaces \({{\mathbb {C}}}{{\mathbb {P}}}^{\,n}\) do not admit affine holomorphic connections. For \(n \geqslant 1\) the (dual of the) Euler exact sequence tensored by  reads
reads
Here all tensor products are over  . In the case \(n > 1\) one computes
. In the case \(n > 1\) one computes
It follows that long cohomology sequence associated to (5.1) reads
and injectivity of the map implies that \({{\mathfrak {A}}}{{\mathfrak {t}}} ({\textsf{T}}_{{{\mathbb {C}}}{{\mathbb {P}}}^n}) \ne 0\). In the case of \({{\mathbb {C}}}{{\mathbb {P}}}^1\), one has that  and
and  . The long cohomology exact sequence reads
. The long cohomology exact sequence reads
Alternatively, one can just observe that for a line bundle the Atiyah class equals the Chern class, i.e. \({{\mathfrak {A}}}{{\mathfrak {t}}} ({\textsf{T}}_{{{\mathbb {C}}}{{\mathbb {P}}}^1}) = c ({\textsf{T}}_{{{\mathbb {C}}}{{\mathbb {P}}}^1})\) and \(c ({\textsf{T}}_{{{\mathbb {C}}}{{\mathbb {P}}}^1}) = c_1 ({\textsf{T}}_{{{\mathbb {C}}}{{\mathbb {P}}}^1}) = 2,\) see [15]. It then follows from Theorem 4.9 that the  -extension related to \({{\mathbb {C}}}{{\mathbb {P}}}^{\,n|m}\) does not split.
-extension related to \({{\mathbb {C}}}{{\mathbb {P}}}^{\,n|m}\) does not split.
Remark 5.4
Note that in the ordinary complex geometric setting, the vanishing of the Atiyah class \({{\mathfrak {A}}}{{\mathfrak {t}}}({E}) \) of a certain (Hermitian holomorphic) vector bundle E on a compact complex manifold X is equivalent for the vector bundle E to be flat. More precisely, the class of the curvature  of the Chern connection
of the Chern connection  of the vector bundle E corresponds to its Atiyah class \({{\mathfrak {A}}}{{\mathfrak {t}}} (E)\). This result is by no means true in a complex supergeometric setting. Indeed all of the Calabi–Yau projective superspaces \({{\mathbb {C}}}{{\mathbb {P}}}^{\,n|n+1}\) for \(n\geqslant 1\) admit a flat Chern connection via a generalization of the Fubini–Study metric [20], but none of them have vanishing super Atiyah class as shown above.
of the vector bundle E corresponds to its Atiyah class \({{\mathfrak {A}}}{{\mathfrak {t}}} (E)\). This result is by no means true in a complex supergeometric setting. Indeed all of the Calabi–Yau projective superspaces \({{\mathbb {C}}}{{\mathbb {P}}}^{\,n|n+1}\) for \(n\geqslant 1\) admit a flat Chern connection via a generalization of the Fubini–Study metric [20], but none of them have vanishing super Atiyah class as shown above.
Another interesting example is provided by the possibly easiest—yet non-trivial—complete intersection in \({{\mathbb {C}}}{{\mathbb {P}}}^{\,2|2}\), corresponding to the super conic  cut out by the equation
cut out by the equation
The supergeometry related to the above equation in projective superspace is non-trivial and not that well-known outside an audience of experts in supergeometry. To help the reader make sense and appreciate this example, we have opted to discuss some of the more peculiar aspects of the geometry of the super conic in Appendix B. We thus refer to it for more information. Here we content ourselves to say that the resulting \(1\,{|}\,2\)-dimensional supermanifold is notably isomorphic to the non-projected supermanifold constructed out of the following three data

where the non-zero obstruction class  is seen via the isomorphism
is seen via the isomorphism  . We have already seen that the Atiyah class of \({{\mathbb {C}}}{{\mathbb {P}}}^1\) is non-zero in Example 5.3, moreover the rank 2 vector bundle
. We have already seen that the Atiyah class of \({{\mathbb {C}}}{{\mathbb {P}}}^1\) is non-zero in Example 5.3, moreover the rank 2 vector bundle  is obviously not flat, and hence it has a non-trivial Atiyah class. We can thus conclude that
is obviously not flat, and hence it has a non-trivial Atiyah class. We can thus conclude that  -extension related to the super conic
-extension related to the super conic  is totally obstructed in the sense of Theorem 4.9, i.e. all of the obstructions in the points (1)–(3) in the statement of Theorem 4.9 are non-zero. We summarize this in the following.
is totally obstructed in the sense of Theorem 4.9, i.e. all of the obstructions in the points (1)–(3) in the statement of Theorem 4.9 are non-zero. We summarize this in the following.
Example 5.5
(Super conic  ) Let
) Let  be the complete intersection given by the equation \(X_0^2 + X_1^2 + X_2^2 + \Theta _1 \Theta _2 = 0\) in \({{\mathbb {C}}}{{\mathbb {P}}}^{\,2|2}\) and let \({\mathsf {{M}}}\) be the supermanifold constructed from
be the complete intersection given by the equation \(X_0^2 + X_1^2 + X_2^2 + \Theta _1 \Theta _2 = 0\) in \({{\mathbb {C}}}{{\mathbb {P}}}^{\,2|2}\) and let \({\mathsf {{M}}}\) be the supermanifold constructed from  as above. Then the related
as above. Then the related  -extension is not split.
-extension is not split.
Finally, let us consider a slightly trickier example, namely that of a super elliptic curve  modeled on an ordinary elliptic curve
modeled on an ordinary elliptic curve  and whose rank 3 fermionic sheaf is given by the direct sum
and whose rank 3 fermionic sheaf is given by the direct sum  . We further assume that the fundamental obstruction class
. We further assume that the fundamental obstruction class  is vanishing, i.e.
is vanishing, i.e.  in the isomorphism
in the isomorphism  . Under these hypotheses one has that all of the points (1)–(3) in Theorem 4.9 are indeed satisfied since also
. Under these hypotheses one has that all of the points (1)–(3) in Theorem 4.9 are indeed satisfied since also  . Nonetheless, the
. Nonetheless, the  -extension related to
-extension related to  might still be non-split, since
might still be non-split, since  is projected but not necessarily split as a complex supermanifold. Indeed the higher obstruction to split
is projected but not necessarily split as a complex supermanifold. Indeed the higher obstruction to split  takes values in the cohomology group
takes values in the cohomology group  which is computed to be isomorphic to \({\mathbb {C}}^{\oplus 3}\). A non-vanishing class obstruction class
which is computed to be isomorphic to \({\mathbb {C}}^{\oplus 3}\). A non-vanishing class obstruction class  would correspond to odd transition functions of the kind \(\theta _i \mapsto \theta _i + c_i \theta _1 \theta _2 \theta _3\) for some complex number \(c_i\). In this case, if
would correspond to odd transition functions of the kind \(\theta _i \mapsto \theta _i + c_i \theta _1 \theta _2 \theta _3\) for some complex number \(c_i\). In this case, if  is a non-split supermanifold, the
is a non-split supermanifold, the  -extension related to
-extension related to  is also non-split. The upshot of the example is that in the case of supermanifolds of odd dimension greater than 2, the presence of higher obstruction classes to split a supermanifold
is also non-split. The upshot of the example is that in the case of supermanifolds of odd dimension greater than 2, the presence of higher obstruction classes to split a supermanifold  is quite a delicate issues. This is summarized in the following.
is quite a delicate issues. This is summarized in the following.
Example 5.6
(Super elliptic curve of dimension \(1\,{|}\,3\)) Let  be a supermanifold of dimension \(1\,{|}\,3\) such that
be a supermanifold of dimension \(1\,{|}\,3\) such that  for E an elliptic curve (over \({\mathbb {C}}\)) and
for E an elliptic curve (over \({\mathbb {C}}\)) and  and let its fundamental obstruction class
and let its fundamental obstruction class  be zero. Then the higher obstruction to split
be zero. Then the higher obstruction to split 

is defined and fully determines the geometry of  . In particular,
. In particular,  is also an obstruction to split the the
is also an obstruction to split the the  -extension related to
-extension related to  , i.e. if
, i.e. if  is non-split, then the
is non-split, then the  -extension does not split as well.
-extension does not split as well.
6 Local theory: forms, natural operators and cohomology
In this section we study forms and natural, i.e. globally defined and invariant, operators acting on  in the smooth and holomorphic category. We start by making contact between our framework and the setting developed by the author and collaborators in [5], where differential and integral forms on a real or complex supermanifold
in the smooth and holomorphic category. We start by making contact between our framework and the setting developed by the author and collaborators in [5], where differential and integral forms on a real or complex supermanifold  are recovered in a unified fashion starting from the triple tensor product of natural sheaves on
are recovered in a unified fashion starting from the triple tensor product of natural sheaves on  given by
given by  , where
, where  is the sheaf of differential operators on
is the sheaf of differential operators on  . Notice that due to the pivotal presence of
. Notice that due to the pivotal presence of  this is a non-commutative construction, better than just super-commutative.
this is a non-commutative construction, better than just super-commutative.
This triple tensor product is acted upon by two globally defined mutually commuting operators \({\hat{d}}\) and \({\hat{\delta }}\), see [5]

and as such it yields a double complex of sheaves,  . Differential and integral forms, together with their differentials and Poincaré lemmas are recovered via the two natural spectral sequences—we call them \(E^{{\hat{d}}}_i\) and \(E^{{\hat{\delta }}}_i\), depending on whether we are starting computing the cohomology with respect of \({\hat{d}} \) or \({\hat{\delta }}\)—related to this double complex
. Differential and integral forms, together with their differentials and Poincaré lemmas are recovered via the two natural spectral sequences—we call them \(E^{{\hat{d}}}_i\) and \(E^{{\hat{\delta }}}_i\), depending on whether we are starting computing the cohomology with respect of \({\hat{d}} \) or \({\hat{\delta }}\)—related to this double complex  . In particular, the following holds true.
. In particular, the following holds true.
Theorem 6.1
([5]) Let  be a real or complex supermanifold. Then the spectral sequences \(E_i^{{\hat{\delta }}}\) and \(E_i^{{\hat{d}}}\) related to the double complex
be a real or complex supermanifold. Then the spectral sequences \(E_i^{{\hat{\delta }}}\) and \(E_i^{{\hat{d}}}\) related to the double complex 
-
(1)
yield the differential forms and integral forms on
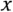 at the first page, i.e.
at the first page, i.e. 
-
(2)
both converge to the locally constant sheaf
 for \({\mathbb {K}}\) the real or complex numbers at the second page, i.e.
for \({\mathbb {K}}\) the real or complex numbers at the second page, i.e. 
A consequence of the above is that the hypercohomologies of differential and integral forms are isomorphic, and both coincide with the Rham cohomology of the reduced manifold, see also the recent [22].
Corollary 6.2
([5]) Let  be a real supermanifold. Then the hypercohomologies of (the sheaf of) differential forms
be a real supermanifold. Then the hypercohomologies of (the sheaf of) differential forms  and integral forms
and integral forms  are isomorphic. In particular, one finds
are isomorphic. In particular, one finds

One the main ingredients of the above construction is the non-commutative sheaf of differential operator  . To
. To  is canonically associated a sheaf of super-commutative
is canonically associated a sheaf of super-commutative  -algebras, by considering the filtration
-algebras, by considering the filtration  by the degree of the differential operators for any \(i \geqslant 0\). This is given by the quotient
by the degree of the differential operators for any \(i \geqslant 0\). This is given by the quotient

It is not hard to see that  . In this way, a “de-quantization” of the above triple tensor product reads
. In this way, a “de-quantization” of the above triple tensor product reads

This sheaf of super-commutative  -algebras can be put in relation with the sheaf
-algebras can be put in relation with the sheaf  , seen as a sheaf of
, seen as a sheaf of  -modules. Indeed one can observe that the
-modules. Indeed one can observe that the  -extension (3.4) is always locally split, so that over an open set \(\pi ^{-1} (U)\) of \({\textsf{M}}\) for U an open set in
-extension (3.4) is always locally split, so that over an open set \(\pi ^{-1} (U)\) of \({\textsf{M}}\) for U an open set in  , one has
, one has

This holds true globally for a real supermanifold, as proved above. It follows that

to be compared to (6.1) above. Using the decomposition (6.2), the action of the de Rham differential  can be given in an open set \(\pi ^{-1} (U)\) with local coordinate \( x_a\) and \(p_a\) as follows:
can be given in an open set \(\pi ^{-1} (U)\) with local coordinate \( x_a\) and \(p_a\) as follows:

where  ,
,  and
and  . The sum over a is left understood.
. The sum over a is left understood.
Theorem 6.3
(Homology of \({\textsf{d}}\) / Poincaré lemma) Let \({\mathsf {{M}}}\) be defined as above and let  the de Rham differential. Then
the de Rham differential. Then

where  is the sheaf of locally-constant functions on \({\mathsf {{M}}}\) for \({\mathbb {K}}\) the real or complex numbers.
is the sheaf of locally-constant functions on \({\mathsf {{M}}}\) for \({\mathbb {K}}\) the real or complex numbers.
Proof
Given the action of the de Rham differential \({\textsf{d}}\) in (6.3), the result follows from the ordinary Poincaré lemma for supermanifolds, see for example [22].\(\square \)
6.1 Odd symplectic form and its cohomology
Let us keep working in the smooth or holomorphic category and let us now consider the (non-degenerate) odd 2-form  where the index a runs over both even and odd coordinates. We first observe the following.
where the index a runs over both even and odd coordinates. We first observe the following.
Lemma 6.4
(Global definition on \(\omega \)) The odd 2-form  is invariant, i.e. coordinate independent.
is invariant, i.e. coordinate independent.
Proof
We use the coordinate transformations of Lemma 3.1. One finds that

and it is easy to verify that the contribution of the second term is zero.\(\square \)
Another way to see that \(\omega \) is actually invariant is to introduce its primitive form \( \eta \,{:}{=}\,(-1)^{|x_a| + 1} dx_a p_a. \)
Lemma 6.5
(Primitive form of \(\omega \) ) The primitive form of \(\omega \) is invariant, moreover one has \({\textsf{d }} \eta = \omega \). In particular, \(\omega \) is invariant.
Proof
Using again the the transformations of Lemma 3.1, it is enough to compute

Clearly \({\textsf{d}} \eta = \omega \). Since both \({\textsf{d}}\) and \(\eta \) are invariant so is \(\omega \).\(\square \)
The previous results allow to give the following definition, see for example [16, 25] or the dedicated chapter in the recent book [19].
Definition 6.6
(Odd symplectic form / odd symplectic supermanifold) We call \(\omega \,{:}{=}\,\sum _a dx_a dp_a\) the odd symplectic form associated to \({\mathsf {{M}}}\). In particular, we say that the pair \(({\textsf{M}}, \omega )\) defines an odd symplectic supermanifold.
Remark 6.7
Notice that with respect to the definition of odd symplectic supermanifolds available in the literature [25], the supermanifold \({\textsf{M}}\) is constructed by starting from a supermanifold  and a vector bundle on it, better than from an ordinary manifold X and a vector bundle on it: in this sense it is a “generalized” odd symplectic supermanifold.
and a vector bundle on it, better than from an ordinary manifold X and a vector bundle on it: in this sense it is a “generalized” odd symplectic supermanifold.
Left multiplication by the odd symplectic form \(\omega = \sum _a dx_a dp_a\) induces a well-defined invariant operator  whose action with respect to the above decomposition is given by
whose action with respect to the above decomposition is given by

Such as the de Rham differential \({\textsf{d}}\), also the multiplication by the odd symplectic form  is nilpotent. We compute its homology in the next theorem.
is nilpotent. We compute its homology in the next theorem.
Theorem 6.8
(Homology of \({\textsf{s}}\)) Let \({\mathsf {{M}}}\) be defined as above and let  be the left multiplication by the odd symplectic form. Then
be the left multiplication by the odd symplectic form. Then

as a sheaf of  -modules.
-modules.
Proof
We need to construct a homotopy for the operator \({\textsf{s}}.\) Using the above local decomposition,  can be represented by the sheaf of vector spaces generated by the elements
can be represented by the sheaf of vector spaces generated by the elements  where
where  and for monomials \(\eta = dx^I \) and \(F = dp^J\) for multi-indices I and J.
and for monomials \(\eta = dx^I \) and \(F = dp^J\) for multi-indices I and J.
On the other hand, one can observe that the decomposition (6.2) coincides with  , and in view of this, the action of the operator \({\textsf{s}}\) reads
, and in view of this, the action of the operator \({\textsf{s}}\) reads

as \(dp^J\) corresponds to \(\partial ^J\) and \(dp_a\) corresponds to \(\partial _{x_a}\), having used the local splitting of the  -extension. Notice that f is not touched by \({\textsf{s}}\). We thus introduce the following local operator:
-extension. Notice that f is not touched by \({\textsf{s}}\). We thus introduce the following local operator:

We prove that this is a homotopy for the operator \({\textsf{s}}.\) In particular, one finds that

The summands in the previous expression read

where n is the even and m is the odd dimension of  and \(\hbox {deg}_0\) and \(\hbox {deg}_1\) is the even and odd degree of \(\eta = dx^I\) and \(F = \partial ^J\). It follows that the above sum (6.4) gives
and \(\hbox {deg}_0\) and \(\hbox {deg}_1\) is the even and odd degree of \(\eta = dx^I\) and \(F = \partial ^J\). It follows that the above sum (6.4) gives

The homotopy \({\textsf{h}}\) fails if and only if one has \(\hbox {deg}_0 (\eta ) = \hbox {deg}_0 (\partial ^J) = 0\), \(\hbox {deg}_1 (\eta ) = n\) and \(\hbox {deg}_1 (\partial ^J) = m\), so that the non-zero element in homology takes the form  , where f is any section of the structure sheaf
, where f is any section of the structure sheaf  .\(\square \)
.\(\square \)
The above theorem has the following corollary.
Corollary 6.9
Let \({\mathsf {{M}}}\) be defined as above and let  be the left multiplication by the odd symplectic form. Then the homology of \(\text {\textsf{s}}\) is naturally isomorphic to the pull-back of the Berezinian sheaf on
be the left multiplication by the odd symplectic form. Then the homology of \(\text {\textsf{s}}\) is naturally isomorphic to the pull-back of the Berezinian sheaf on  , i.e.
, i.e.

Proof
Allowing for the above identifications and the usual slight abuse of notation concerning the pull-backs, it is enough to observe that  generates the Berezinian sheaf of the supermanifold
generates the Berezinian sheaf of the supermanifold  , see [21] for details on this construction of the Berezinian sheaf. \(\square \)
, see [21] for details on this construction of the Berezinian sheaf. \(\square \)
Remark 6.10
The above result can be related to the notion of (super) semidensities, see [16, 19, 25]. Indeed the  -extension exact sequence (3.4) allows to easily compute the Berezinian sheaf
-extension exact sequence (3.4) allows to easily compute the Berezinian sheaf  of the supermanifold \({\textsf{M}}\). Taking the Berezinians, the short exact sequence (3.4) yields
of the supermanifold \({\textsf{M}}\). Taking the Berezinians, the short exact sequence (3.4) yields

Observing that for any sheaf  on
on  one has
one has  , one sees that
, one sees that  hence
hence

Defining the sheaf of semidensities  of the supermanifold \({\textsf{M}}\) to be the locally-free sheaf of
of the supermanifold \({\textsf{M}}\) to be the locally-free sheaf of  -modules whose sections are “square roots” of the sections of the Berezinian sheaf, i.e.
-modules whose sections are “square roots” of the sections of the Berezinian sheaf, i.e.  , it follows from (6.6) that
, it follows from (6.6) that  . In turn, the above (6.5) can be re-written as
. In turn, the above (6.5) can be re-written as

where the sheaf of semidensities is seen as a sheaf of  -modules. Notice that reducing to the underlying ordinary manifold
-modules. Notice that reducing to the underlying ordinary manifold  one would find
one would find  , which is the ordinary notion for semidensities of odd symplectic supermanifolds constructed out of an ordinary manifold
, which is the ordinary notion for semidensities of odd symplectic supermanifolds constructed out of an ordinary manifold  , see for example [19] and [25].
, see for example [19] and [25].
6.2 Deformed de Rham complex and BV Laplacian
Now, the crucial observation, originally due to Ševera in [25], is that the nilpotent operators \({\textsf{d}}\) and \({\textsf{s}}\) commutes with each other. This holds true also in the present setting, as the following shows.
Lemma 6.11
(\({{{\textsf{d}}}}\) commutes with \({{{\textsf{s}}}}\)) Let \({\mathsf {{d}}}\) and \({\mathsf {{s}}}\) be the de Rham differential and the multiplication by the odd symplectic form, then \([\, {\mathsf {{d}}}, {\mathsf {{s}}} \, ] = 0\). In particular the triple  defines a double complex.
defines a double complex.
Proof
This is a local check. Using the above decomposition, one computes

which concludes the proof.\(\square \)
It follows from the previous Lemma 6.11 that, in particular, \({\textsf{d}}\) acts on the homology of \({\textsf{s}}\). This leads to the following definition.
Definition 6.12
(Deformed de Rham complex / spectral sequence  ) We call the double complex
) We call the double complex  the deformed de Rham (double) complex of \({\textsf{M}}\). We denote with
the deformed de Rham (double) complex of \({\textsf{M}}\). We denote with  the related spectral sequence \((E_i, \delta _i) \) that starts with the differential \(\delta _1 = {\textsf{s}}\) and we call it deformed de Rham spectral sequence.
the related spectral sequence \((E_i, \delta _i) \) that starts with the differential \(\delta _1 = {\textsf{s}}\) and we call it deformed de Rham spectral sequence.
Let us now study the deformed de Rham spectral sequence  .
.
Theorem 6.13
(Semidensities & super BV operator) Let  be defined as above. Then
be defined as above. Then
-
(1)
the first page of the spectral sequence
 is isomorphic to semidensities on
is isomorphic to semidensities on  , i.e.
, i.e. 
-
(2)
the second differential \(\delta _2 \) of the spectral sequence
 is zero. In particular, the second page of the spectral sequence
is zero. In particular, the second page of the spectral sequence  is given again by
is given again by 
-
(3)
the third differential \(\delta _3\) of the spectral sequence
 is—up to exact terms—the super BV Laplacian
is—up to exact terms—the super BV Laplacian
where
 is a section of
is a section of  and
and  is a section of
is a section of  . In particular, the spectral sequence converges at page three, which is isomorphic to the locally constant sheaf on
. In particular, the spectral sequence converges at page three, which is isomorphic to the locally constant sheaf on  , i.e.
, i.e. 
A representative of this homology class if given by

Proof
The first point of the theorem is just Corollary 6.9. As for the second point, notice that the corresponding differential is given by the induced action of the de Rham differential \({\textsf{d}}\) on  . Referring to Theorem 6.8, one can observe that the induced action of \({\textsf{d}}\) maps to a zero-homotopic cohomology. More in particular, for immediate use, one can observe that for any
. Referring to Theorem 6.8, one can observe that the induced action of \({\textsf{d}}\) maps to a zero-homotopic cohomology. More in particular, for immediate use, one can observe that for any  , one has
, one has

where  can be taken to be of the form
can be taken to be of the form  .
.
The third differential can be easily inferred by noticing that, formally,  , so that in particular, when acting on an element of
, so that in particular, when acting on an element of  one finds, upon the previous observation
one finds, upon the previous observation

Taking  as above it is easy to compute that
as above it is easy to compute that

We now look for a homotopy for this operator. To this end, without loss of generality, we let  be of the form \(f (x,p)\,{:}{=}\,g_I(x) p^I \) for \(x_a = x_1 \ldots x_{n} \,|\, x_{n+1} \ldots x_{n+m}\) even and odd coordinates of
be of the form \(f (x,p)\,{:}{=}\,g_I(x) p^I \) for \(x_a = x_1 \ldots x_{n} \,|\, x_{n+1} \ldots x_{n+m}\) even and odd coordinates of  and I a multi-index. We claim that the homotopy for
and I a multi-index. We claim that the homotopy for  is given by
is given by

where \(t \in [0,1]\), \({\textsf{P}}^*_t g (x) = g(tx) \) and \(\ell _f\) is a constant, which depends on f, that will be fixed later. An attentive computation yields the following:

This gives the following condition on \(\ell _f\) as to have a homotopy:
which yields

Observing that \(\deg _{0} (p^I) \geqslant 0\), \(0\leqslant \deg _{1 } (p^I) \leqslant n\) and \(0\leqslant \deg _{1} (g_I) \leqslant m\), one sees that the homotopy fails only for \(\deg _{0} (p^I) = 0\), \(\deg _{1} (p^1) = n \) and \(\deg _{1} (g_I) = m\). One thus finds that \(f(x, p) = x_{n+1} \ldots x_{n+m} p_{1} \ldots p_{n}\) so that

with \(k \in {\mathbb {R}}\) or \(k \in {\mathbb {C}}\) is a representative for  . Finally, it is easy to see that the representative is \({\textsf{d}}\)-closed, so that it yields zero when acted by all the higher differentials, concluding the proof.\(\square \)
. Finally, it is easy to see that the representative is \({\textsf{d}}\)-closed, so that it yields zero when acted by all the higher differentials, concluding the proof.\(\square \)
6.3 Remarks and outlooks
The above Theorem 6.13 extends to a “fully” supergeometric context the beautiful Ševera’s result [25] for odd symplectic supermanifolds, with possibly the bonus of showing explicitly the homotopy (6.8) of the super BV Laplacian—which is seen here as a morphism of sheaves—together with the related representative in sheaf cohomology (6.7). It is to be noted that the form of the homotopy shown above is somewhat general, as the structure of odd nilpotent operators in supergeometry often consists of a “multiplication” of an even and an odd part, such as the BV Laplacian above or the de Rham differential—notice indeed that the related complexes of integral forms and of differential forms are quasi-isomorphic, see Theorem 6.2. Similar structures for homotopies of differentials can be found also in [5, 14, 21, 22].
Finally, a remark—or better a warning—about the holomorphic category is in order. Let us consider a generic smooth supermanifold  admitting a closed non-degenerate odd 2-form \(\omega \), i.e. an odd symplectic supermanifold
admitting a closed non-degenerate odd 2-form \(\omega \), i.e. an odd symplectic supermanifold  . Then, by a well-known result due to Schwarz the supermanifold
. Then, by a well-known result due to Schwarz the supermanifold  is globally symplectomorphic to the “standard” odd symplectic supermanifold constructed as \({\textsf{M}}\) above, starting from the reduced space
is globally symplectomorphic to the “standard” odd symplectic supermanifold constructed as \({\textsf{M}}\) above, starting from the reduced space  of
of  , and endowed with its standard odd symplectic form \(\sum _i dx_i dp_i\), see [24]. The proof of this fact heavily relies on that every smooth supermanifold is in fact split, hence it is itself the total space of a certain vector bundle whose fibers have odd parity. It is then natural to ask what happens in the holomorphic category, where complex supermanifolds can in fact be non-split. In particular, one can ask the following question: does Schwarz’s result hold true in the holomorphic category as well? In other words, is it possible to find an example of complex supermanifold admitting a closed non-degenerate odd 2-form which is not globally isomorphic to a supermanifold of the kind of \({\textsf{M}}\) for some manifold
, and endowed with its standard odd symplectic form \(\sum _i dx_i dp_i\), see [24]. The proof of this fact heavily relies on that every smooth supermanifold is in fact split, hence it is itself the total space of a certain vector bundle whose fibers have odd parity. It is then natural to ask what happens in the holomorphic category, where complex supermanifolds can in fact be non-split. In particular, one can ask the following question: does Schwarz’s result hold true in the holomorphic category as well? In other words, is it possible to find an example of complex supermanifold admitting a closed non-degenerate odd 2-form which is not globally isomorphic to a supermanifold of the kind of \({\textsf{M}}\) for some manifold  ? Clearly, a non-split complex supermanifold admitting a globally defined odd non-degenerate closed 2-form would provide such a counterexample to Schwarz result. This suggests, in turn, the following question: do the obstruction classes to splitting a complex supermanifold also obstruct the existence of a globally-defined odd non-degenerate closed 2-form? We leave these questions to future works.
? Clearly, a non-split complex supermanifold admitting a globally defined odd non-degenerate closed 2-form would provide such a counterexample to Schwarz result. This suggests, in turn, the following question: do the obstruction classes to splitting a complex supermanifold also obstruct the existence of a globally-defined odd non-degenerate closed 2-form? We leave these questions to future works.
References
Atiyah, M.F.: Complex analytic connections in fibre bundles. Trans. Amer. Math. Soc. 85(1), 181–207 (1957)
Bartocci, C., Bruzzo, U., Hernández Ruipérez, D.: The Geometry of Supermanifolds. Mathematics and its Applications, vol. 71. Kluwer, Dordrecht (1991)
Bettadapura, K.; Koszul’s splitting theorem and the super Atiyah class (2020). ArXiv:2009.00177
Cacciatori, S.L., Noja, S.: Projective superspaces in practice. J. Geom. Phys. 130, 40–62 (2018)
Cacciatori, S.L., Noja, S., Re, R.: The universal de Rham/Spencer double complex on a supermanifold. Doc. Math. 27, 489–518 (2022)
Catenacci, R., Cremonini, C., Grassi, P.A., Noja, S.: On forms, cohomology, and BV Laplacians in odd symplectic geometry. Lett. Math. Phys. 111(2), 44 (2021)
Cattaneo, A.S., Schiavina, M.: BV-BFV approach to general relativity: Palatini–Cartan–Holst action. Adv. Theor. Math. Phys. 23(8), 2025–2059 (2020)
Chas, M., Sullivan, D.: String topology (1999). ArXiv:math/9911159
Costello, K., Gwilliam, O.: Factorization Algebras in Quantum Field Theory. Vol 1. New Mathematical Monographs, vol. 31. Cambridge University Press, Cambridge (2017)
Donagi, R., Witten, E.: Super Atiyah classes and obstructions to splitting of supermoduli space. Pure Appl. Math. Q. 9(4), 739–788 (2013)
Donagi, R., Witten, E.: Supermoduli space is not projected. In: Donagi, R., et al. (eds.) String-Math 2012. Proceedings of Symposia in Pure Mathematics, vol. 90, pp. 19–72. American Mathematical Society, Providence (2015)
Getzler, E.: Batalin-Vilkovisky algebras and two-dimensional topological field theories. Commun. Math. Phys. 159(2), 265–285 (1994)
Hartshorne, R.: Algebraic Geometry. Graduate Texts in Mathematics, vol. 52. Springer, New York (1977)
Hernández Ruipérez, D., Muñoz Masqué, J.: Construction intrinsèque du faisceau de Berezin d’une variété graduée. C. R. Acad. Sci. Paris Sér. I Math. 301(20), 915–918 (1985)
Huybrechts, D.: Complex Geometry. Universitext. Springer, Berlin (2005)
Khudaverdian, H.M.: Semidensities on odd symplectic supermanifolds. Commun. Math. Phys. 247(2), 353–390 (2004)
Koszul, J.-L.: Connections and splittings of supermanifolds. Differential Geom. Appl. 4(2), 151–161 (1994)
Manin, Yu.I.: Gauge Field Theory and Complex Geometry. Grundlehren der mathematischen Wissenschaften, vol. 289. Springer, Berlin (1988)
Mnev, P.: Quantum Field Theory: Batalin–Vilkovisky Formalism and its Applications. University Lecture Series, vol. 72. American Mathematical Society, Providence (2019)
Noja, S., Cacciatori, S.L., Dalla Piazza, F., Marrani, A., Re, R.: One-dimensional super Calabi-Yau manifolds and their mirrors. J. High Energy Phys. 2017(4), 94 (2017)
Noja, S., Re, R.: A note on super Koszul complex and the Berezinian. Ann. Mat. Pura Appl. 201(1), 403–421 (2022)
Noja, S.: On the geometry of forms on supermanifolds (2021). ArXiv:2111.12841
Pantev, T., Toën, B., Vaquié, M., Vezzosi, G.: Shifted symplectic structures. Publ. Math. Inst. Hautes Études Sci. 117, 271–328 (2013)
Schwarz, A.: Geometry of Batalin–Vilkovisky quantization. Commun. Math. Phys. 155(2), 249–260 (1993)
Ševera, P.: On the origin of the BV operator on odd symplectic supermanifolds. Lett. Math. Phys. 78(1), 55–59 (2006)
Vishnyakova, E.G.: On complex Lie supergroups and split homogeneous supermanifolds. Transform. Groups 16(1), 265–285 (2011)
Acknowledgements
The author wish to thank the anonymous referee for attentive and useful comments on this manuscript. Further, the author is grateful to John Huerta and Johannes Walcher for fruitful remarks and to Riccardo Re for helpful conversations and collaboration on related projects.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC-2181/1-390900948 (the Heidelberg STRUCTURES Cluster of Excellence).
Appendices
Appendix A: Extensions of sheaves
For the sake of readability of the paper we recall that an extension of sheaves on a manifold X is a short exact sequence of sheaves

In particular, we say that  is an extension of
is an extension of  by
by  . It is well known from homological algebra that extensions are classified up to equivalence via their cohomology classes
. It is well known from homological algebra that extensions are classified up to equivalence via their cohomology classes  . In particular, we say that an extension is split if is equivalent to the trivial extension, i.e. if
. In particular, we say that an extension is split if is equivalent to the trivial extension, i.e. if  in (A.1), i.e. \(\pi \) has the property that
in (A.1), i.e. \(\pi \) has the property that  . Notice that if
. Notice that if  and
and  are locally-free sheaves on X, then one has
are locally-free sheaves on X, then one has  , so that in particular
, so that in particular  .
.
We will now compute explicitly the above \(\text {Ext}\)-functor. We will work in a general setting—over a smooth, analytic or algebraic manifold X—following an ordinary diagram chasing argument. Since (A.1) is always locally split, i.e.  on an open set U in X, then there exists a basis \({\underline{c}}^U = \{ c^U_1\!, \ldots , c^U_{n+m}\}\) of
on an open set U in X, then there exists a basis \({\underline{c}}^U = \{ c^U_1\!, \ldots , c^U_{n+m}\}\) of  such that \(\underline{a}^U = \{c^U_1\!, \ldots , c_n^U \}\) is a basis of
such that \(\underline{a}^U = \{c^U_1\!, \ldots , c_n^U \}\) is a basis of  and \(\underline{b}^U = \{ j(c^U_{n+1}), \ldots j(c^U_{n+m})\}\) is a basis of
and \(\underline{b}^U = \{ j(c^U_{n+1}), \ldots j(c^U_{n+m})\}\) is a basis of  .
.
If now U and V are two open sets in X such that \(U \cap V \ne 0\), and \({\underline{c}}^U\) and \({\underline{c}}^V\) are the related local bases on U and V respectively, then we consider a coordinate transformation of the following form (see for example the transition functions of Theorem 3.1 in the main text):
where  ,
,  and
and  The class
The class  is defined applying the contravariant functor
is defined applying the contravariant functor  to the short exact sequence (A.1), obtaining
to the short exact sequence (A.1), obtaining

We have  . In order to explicitly compute this, we use a covering having open sets U and V with \(U\cap V \ne \emptyset \). In particular, we describe the element
. In order to explicitly compute this, we use a covering having open sets U and V with \(U\cap V \ne \emptyset \). In particular, we describe the element  on the open set U as
on the open set U as  , where we have introduced \(\{ \partial ^U_{a_i}\}_{i=1}^n\), the basis dual to \(\{ a_i\}_{i=1}^n\) on U. Notice that here \({\underline{a}}^U\) is looked at as a row vector and \(\partial ^U_{{\underline{a}}}\) is looked at as a column vector, so that in particular, their transformation in an intersection reads \({\underline{a}}^U = {\underline{a}}^V \!A\) and \(\partial ^U_{{\underline{a}}} = A^{-1} \partial ^V_{{\underline{a}}}\), or analogously \(\partial ^{U t}_{{\underline{a}}}\! = \partial ^{V t}_{{\underline{a}}} (A^{-1})^{t}\). It follows that indeed
, where we have introduced \(\{ \partial ^U_{a_i}\}_{i=1}^n\), the basis dual to \(\{ a_i\}_{i=1}^n\) on U. Notice that here \({\underline{a}}^U\) is looked at as a row vector and \(\partial ^U_{{\underline{a}}}\) is looked at as a column vector, so that in particular, their transformation in an intersection reads \({\underline{a}}^U = {\underline{a}}^V \!A\) and \(\partial ^U_{{\underline{a}}} = A^{-1} \partial ^V_{{\underline{a}}}\), or analogously \(\partial ^{U t}_{{\underline{a}}}\! = \partial ^{V t}_{{\underline{a}}} (A^{-1})^{t}\). It follows that indeed  .
.
We now look at the transformation of the dual basis \(\partial ^U_{{\underline{c}}}\) of \( \underline{c}^U\), which we decompose—with a slight abuse of notation—as \(\partial ^U_{{\underline{c}}} = (\partial ^U_{{\underline{a}}}, \partial ^U_{{\underline{b}}})\). We have that
In particular, it follows that
Let us now consider the liftings of  and their difference
and their difference  written with respect to the bases on V. We find
written with respect to the bases on V. We find

We observe that \(\varphi _{UV} \) can be naturally interpreted as a section  , whose associated matrix with respect to the bases \({\underline{a}}^V\) and \({\underline{b}}^V\) is given by
, whose associated matrix with respect to the bases \({\underline{a}}^V\) and \({\underline{b}}^V\) is given by  More in general, given a open covering
More in general, given a open covering  of X, the cohomology class
of X, the cohomology class  is represented by the cocycle \(\{ \varphi _{ij} \}_{i, j \in I}\), such that
is represented by the cocycle \(\{ \varphi _{ij} \}_{i, j \in I}\), such that

which is represented by the matrix \(-CB^{-1}\) on in intersection \(U_i \cap U_j\), with respect to the bases of  and
and  chosen on \(U_j\).
chosen on \(U_j\).
Now, if \([\xi ] \equiv 0 \) in cohomology, the related Čech cocycle is actually a coboundary, i.e.
for two open sets \(U\cap V \ne \varnothing \) and where  and
and  . In particular, choosing bases on U and V, in terms of matrix representatives, one pose \(\varphi _U \,{:}{=}\,\underline{a}^U [M_U] \partial ^U_{{\underline{b}}}\) and
. In particular, choosing bases on U and V, in terms of matrix representatives, one pose \(\varphi _U \,{:}{=}\,\underline{a}^U [M_U] \partial ^U_{{\underline{b}}}\) and  and
and  . Changing coordinates from U to V in \(\varphi _U\) one has
. Changing coordinates from U to V in \(\varphi _U\) one has  . Substituting these in (A.2) one gets the matrix identity
. Substituting these in (A.2) one gets the matrix identity
which in turn can be rewritten as
Recalling that in (non-abelian) Čech cohomology, by definition, two 1-cocycles \(\{ g_{ij} \}_{i<j}\) and \(\{ g^{\prime }_{ij}\}_{i<j}\) are cohomologous if \(g_{ij}^\prime = h_i g_{ij} h_j^{-1}\) for some 0-cochains \(\{ h_i \}_{i \in I}\), then in the present case for the sheaf  , it is enough to consider, say on \(U_i = V\)
, it is enough to consider, say on \(U_i = V\)
so that, in turn \(h_V g_{VU} g_{U}^{-1}\) reads
upon using equation (A.3) in the last equality. We summarize the above discussion in the following theorem.
Theorem 6.14
Let  be an extension of
be an extension of  by
by  as in (A.1) with transition functions of the form
as in (A.1) with transition functions of the form
for A and B transition functions of  and
and  respectively, upon choosing local bases. Then \({[\xi ] \in }\) Ext\({}^1 ({\mathcal {B}}, {\mathcal {A}})\) is represented by a 1-cocycle valued in
respectively, upon choosing local bases. Then \({[\xi ] \in }\) Ext\({}^1 ({\mathcal {B}}, {\mathcal {A}})\) is represented by a 1-cocycle valued in  given by \([-CB^{-1}]\) with respect to the chosen bases of
given by \([-CB^{-1}]\) with respect to the chosen bases of  and
and  . In particular, if \([\xi ] \equiv 0\), then the structure group of the
. In particular, if \([\xi ] \equiv 0\), then the structure group of the  reduces to GL
reduces to GL  GL
GL  .
.
Appendix B: Geometry of the super conic
For a better understanding of Example 5.5, we briefly spell out in this appendix some details of the geometry of the complex supermanifold  cut out by the equation
cut out by the equation
where the X’s and the \(\Theta \)’s denote homogeneous even and odd coordinates of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,2|2}\) respectively. The above Eq. (B.1) defines a \(1\,{|}\,2\)-dimensional (complex) supermanifold. Further it is easy to observe that, setting the odd homogeneous coordinates to zero, one is left with the equation
which defines a conic in \({{\mathbb {C}}}{{\mathbb {P}}}^2\), implying that the reduced manifold of  is isomorphic to \({{\mathbb {C}}}{{\mathbb {P}}}^1\), that is
is isomorphic to \({{\mathbb {C}}}{{\mathbb {P}}}^1\), that is  . We will show that the super conic
. We will show that the super conic  is indeed isomorphic to a non-projected supermanifold of dimension \(1\,{|}\,2\) having \({{\mathbb {C}}}{{\mathbb {P}}}^1\) as reduced manifold.
is indeed isomorphic to a non-projected supermanifold of dimension \(1\,{|}\,2\) having \({{\mathbb {C}}}{{\mathbb {P}}}^1\) as reduced manifold.
It is not hard to classify all of the non-projected \(1\,{|}\,2\)-dimensional complex supermanifolds over \({{\mathbb {C}}}{{\mathbb {P}}}^1\). Indeed the following fundamental Theorem holds true, see [18, Proposition 9, Chapter 4, Section 2].
Theorem B.1
(Supermanifolds of dimension \({n}\,{|}\,2\)) Let  be a complex supermanifold of dimension \(n\,{|}\,2\). Then
be a complex supermanifold of dimension \(n\,{|}\,2\). Then  is defined up to isomorphism by the triple
is defined up to isomorphism by the triple  where
where  is the reduced manifold of
is the reduced manifold of  ,
,  is a locally-free sheaf of
is a locally-free sheaf of  -modules of rank 2—the fermionic sheaf of
-modules of rank 2—the fermionic sheaf of  —and
—and  is the fundamental obstruction
is the fundamental obstruction  .
.
Notice that since the odd dimension is 2, no higher obstruction classes can appear.
Remark B.2
Concretely, in presence of a non-zero obstruction class, the (even) transition functions coming from the underlying manifold  get a correction coming from
get a correction coming from  as they are lifted to
as they are lifted to  . More precisely, if \(\{{U}_i \}_{i \in I}\) is an open covering of
. More precisely, if \(\{{U}_i \}_{i \in I}\) is an open covering of  such that in a certain intersection \({U}_i \cap {U}_j\) the transition functions of
such that in a certain intersection \({U}_i \cap {U}_j\) the transition functions of  are given by certain (holomorphic) functions \(z_{ij}^{\ell } = z_{ij}^{\ell } ({\underline{z}}_j)\) for \(\ell = 1, \ldots , n,\) then the even transition functions of a non-projected n|2-dimensional supermanifold will be given explicitly by
are given by certain (holomorphic) functions \(z_{ij}^{\ell } = z_{ij}^{\ell } ({\underline{z}}_j)\) for \(\ell = 1, \ldots , n,\) then the even transition functions of a non-projected n|2-dimensional supermanifold will be given explicitly by

where the z’s and the \(\theta \)’s are respectively even and odd local coordinates for  , and where \( \omega _{ij}\) is a derivation acting on \(z_{ij}^\ell \) and taking values in
, and where \( \omega _{ij}\) is a derivation acting on \(z_{ij}^\ell \) and taking values in  —hence the \(\theta \)’s can only appear in
—hence the \(\theta \)’s can only appear in  through their product, thus respecting parity.
through their product, thus respecting parity.
Now, keeping fixed  , Theorem B.1 yields the following result for non-projected of dimension \(1\,{|}\,2\).
, Theorem B.1 yields the following result for non-projected of dimension \(1\,{|}\,2\).
Theorem B.3
(Non-projected \(1\,{|}\,2\)-dimensional supermanifolds over \({{\mathbb {C}}}{{\mathbb {P}}}^1\)) Every non-projected \(1\,{|}\,2\)-dimensional supermanifold  over \({{\mathbb {C}}}{{\mathbb {P}}}^1\) is characterised up to isomorphism by a triple
over \({{\mathbb {C}}}{{\mathbb {P}}}^1\) is characterised up to isomorphism by a triple  where
where  is a locally-free sheaf of
is a locally-free sheaf of  -modules of rank 2 such that
-modules of rank 2 such that

with \(m+n =\ell \), \(\ell \leqslant 4\) and  is a non-zero cohomology class
is a non-zero cohomology class  .
.
Proof
First by the Birkhoff–Grothendieck splitting theorem, see [13], every locally-free sheaf of  -modules of any rank is isomorphic to a direct sum of invertible sheaves, that in turn are all of the form
-modules of any rank is isomorphic to a direct sum of invertible sheaves, that in turn are all of the form  for some \(k \in {\mathbb {Z}}\) (recall that
for some \(k \in {\mathbb {Z}}\) (recall that  ), i.e. if we let
), i.e. if we let  be a locally-free sheaf of
be a locally-free sheaf of  -modules of rank n, then we have
-modules of rank n, then we have  uniquely up to permutation of the terms in direct sum at the right hand side of the isomorphism. It follows that in our case we have
uniquely up to permutation of the terms in direct sum at the right hand side of the isomorphism. It follows that in our case we have  .
.
Finally, observing that  and that
and that  , one finds that
, one finds that

For the supermanifold  to be non-projected the cohomology in (B.3) should be non-zero, which amounts to require that \( m+n \leqslant 4\). Posing \(\ell \,{:}{=}\,m+n \leqslant 4\) and
to be non-projected the cohomology in (B.3) should be non-zero, which amounts to require that \( m+n \leqslant 4\). Posing \(\ell \,{:}{=}\,m+n \leqslant 4\) and  a non-zero class in
a non-zero class in  , one concludes using Theorem B.3. \(\square \)
, one concludes using Theorem B.3. \(\square \)
We now focus on a particular choice of supermanifold in the “family” singled out above, namely we choose \(n= m = -2\). Notice that in this case one has a one-dimensional obstruction space, i.e.  .
.
Definition B.4
(Supermanifold \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_{\omega } \)) We denote by \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \), the supermanifold arising from the triple \(({{\mathbb {C}}}{{\mathbb {P}}}^1\!, {\mathcal {F}}, \omega ) \), with  and \(\omega \) a non-zero class in
and \(\omega \) a non-zero class in  .
.
In order to prove that the supermanifold \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \) is actually isomorphic to the super conic  , we need to find the transition functions of \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \). To this end, let us work with the standard open covering of \({{\mathbb {C}}}{{\mathbb {P}}}^1\) given by \(U = (U_0, U_1)\) where \(U_i \,{:}{=}\,\{ X_i \ne 0\}\), if \([X_0 \,{:}\, X_1]\) are the homogeneous coordinates of \({{\mathbb {C}}}{{\mathbb {P}}}^1\). Then one has
, we need to find the transition functions of \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \). To this end, let us work with the standard open covering of \({{\mathbb {C}}}{{\mathbb {P}}}^1\) given by \(U = (U_0, U_1)\) where \(U_i \,{:}{=}\,\{ X_i \ne 0\}\), if \([X_0 \,{:}\, X_1]\) are the homogeneous coordinates of \({{\mathbb {C}}}{{\mathbb {P}}}^1\). Then one has

for  the nilpotent sheaf of \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \) (note that since we are working in odd dimension 2 one has
the nilpotent sheaf of \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \) (note that since we are working in odd dimension 2 one has  ). Accordingly, on unique intersection \(U_0 \cap U_1\) one finds
). Accordingly, on unique intersection \(U_0 \cap U_1\) one finds

Passing to the fermionic sheaf  , we denote by \((\theta _i)_{i = 1, 2}\) a local basis of
, we denote by \((\theta _i)_{i = 1, 2}\) a local basis of  on \({U}_0\) and by \((\psi _i)_{i= 1, 2} \) a local basis of
on \({U}_0\) and by \((\psi _i)_{i= 1, 2} \) a local basis of  on \({U}_1\) respectively, so that one can write
on \({U}_1\) respectively, so that one can write
where the \(\pi \)’s are there to remember the odd parity, since  for
for  the sheaf of nilpotent sections in
the sheaf of nilpotent sections in  . The transition functions in the intersection \(U_0 \cap U_1\) are therefore given by
. The transition functions in the intersection \(U_0 \cap U_1\) are therefore given by

These identify also the product \(\theta _1 \theta _2\) (and \(\psi _1 \psi _2\)) with a section of  This is enough to give the correction to the even part of the transition functions of the non-projected supermanifold \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \) given by the presence of a non-zero obstruction class
This is enough to give the correction to the even part of the transition functions of the non-projected supermanifold \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \) given by the presence of a non-zero obstruction class  . Indeed, working with the previous conventions, one can explicitly identify
. Indeed, working with the previous conventions, one can explicitly identify

for \(\lambda \in {\mathbb {C}}\)—in our case \(\lambda \ne 0.\) Notice that \(X_0 X_1 \ne 0\) in \(U_1 \cap U_1\), also—with abuse of notation—we will take the liberty of suppressing the index of the intersection as there is a single one of them. The previous (B.5) can be rewritten as follows:

where we have identified the sections in the intersection \(U_0 \cap U_1\) via \(w^3 = (X_0 /X_1)^3\), \(\psi _1 \psi _2 = 1 / X^4_1\) and \(\partial _z = X^2_0\). Notice indeed that the section of the tangent sheaf \(\partial _z \in {\textsf{T}}_{{{\mathbb {C}}}{{\mathbb {P}}}^1}\) satisfies the transformation law \(\partial _{z} = -w^2 \partial _w\) and hence it has a double zero at \([0\,{:}\,1] \in {{\mathbb {C}}}{{\mathbb {P}}}^1\), so that it can be identified with the section \(X^2_0\) of  . It follows that plugging equations (B.4) and (B.6) into the general expression (B.2), one finds that the even transition functions of \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \) reads
. It follows that plugging equations (B.4) and (B.6) into the general expression (B.2), one finds that the even transition functions of \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \) reads

for some non-zero complex number \(\lambda \), that we will simply set to 1 in what follows. Indeed, it is true in general that choosing  for some \(\lambda \in {\mathbb {C}}^*\) defines an isomorphic extension of
for some \(\lambda \in {\mathbb {C}}^*\) defines an isomorphic extension of  by
by  —however the isomorphism is not the identity on
—however the isomorphism is not the identity on  and
and  . We summarize the previous discussion in the following lemma.
. We summarize the previous discussion in the following lemma.
Lemma B.5
(Transition functions of \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \)) Let \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \) be the non-projected supermanifold defined as above. Then in the (unique) intersection \(U_0 \cap U_1\) the transition functions read

We now want to embed \({{\mathbb {C}}}{{\mathbb {P}}}^{1|2}_\omega \) in a projective superspace, namely in \({{\mathbb {C}}}{{\mathbb {P}}}^{\,2|2}\). In order to do this, we need to find an ample line bundle  of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \) which allows for such an embedding. In the case of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \) it is easy to define
of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \) which allows for such an embedding. In the case of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \) it is easy to define  using the standard covering of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}\) given by \(\{U_0, U_1 \}\) introduced above and then giving the expression of the unique transition function in the intersection \(U_0 \cap U_1\). Namely, we consider the following:
using the standard covering of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}\) given by \(\{U_0, U_1 \}\) introduced above and then giving the expression of the unique transition function in the intersection \(U_0 \cap U_1\). Namely, we consider the following:

where \(({e}_{ U_0 }, {e}_{ U_1})\) are the basis or frames of  on \(U_0\) and \(U_1\).
on \(U_0\) and \(U_1\).
Remark B.6
A comment is in order here. Indeed, as in the ordinary case, one can always describe a line bundle  on a supermanifold
on a supermanifold  by giving an open covering \(\{ U_i \}_{i \in I}\) of
by giving an open covering \(\{ U_i \}_{i \in I}\) of  and the transition functions \(\{ g_{ij}\}_{i, j \in I}\) between two local frames \(e_{U_i} \) and \(e_{U_j}\) in the intersections \(U_i \cap U_j\) for \(i, j \in I\), so that \(e_{U_i} = g_{ij} e_{U_j}\). In this fashion one has indeed the correspondence
and the transition functions \(\{ g_{ij}\}_{i, j \in I}\) between two local frames \(e_{U_i} \) and \(e_{U_j}\) in the intersections \(U_i \cap U_j\) for \(i, j \in I\), so that \(e_{U_i} = g_{ij} e_{U_j}\). In this fashion one has indeed the correspondence  , where we stress that \(g_{ij}\) takes values in
, where we stress that \(g_{ij}\) takes values in  for any \(i,j \in I,\) since the transition functions need to be even, hence parity-preserving. Further, compatibility on triple intersections gives a cocycle condition, i.e. the transition functions \(\{ g_{ij}\}_{i, j \in I}\) define classes in
for any \(i,j \in I,\) since the transition functions need to be even, hence parity-preserving. Further, compatibility on triple intersections gives a cocycle condition, i.e. the transition functions \(\{ g_{ij}\}_{i, j \in I}\) define classes in  . This observation leads to the super-analog of the usual identification of the Picard group
. This observation leads to the super-analog of the usual identification of the Picard group  of isomorphy classes of line bundle on a complex manifold X with
of isomorphy classes of line bundle on a complex manifold X with  : in the case of a supermanifold
: in the case of a supermanifold  we have instead
we have instead  . Along this line of thought, the explicit form of the transition functions (B.7) of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \) comes in handy to verify that the previous definition (B.8) of
. Along this line of thought, the explicit form of the transition functions (B.7) of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \) comes in handy to verify that the previous definition (B.8) of  is well-posed. Indeed, one can check that the transition function defines an element in the cohomology group \(H^1 (|{{\mathbb {C}}}{{\mathbb {P}}}^1|, {{\mathcal {O}}}^*_{{{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega , 0} )\), which is identified with the Picard group
is well-posed. Indeed, one can check that the transition function defines an element in the cohomology group \(H^1 (|{{\mathbb {C}}}{{\mathbb {P}}}^1|, {{\mathcal {O}}}^*_{{{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega , 0} )\), which is identified with the Picard group  of the supermanifold \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \). More in general, the transition functions (B.7) allow to compute, via Čech cohomology, the full Picard group of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \). Namely, one finds that the Picard group of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \) is made of lifts of line bundles on \({{\mathbb {C}}}{{\mathbb {P}}}^{1}\)—recall that
of the supermanifold \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \). More in general, the transition functions (B.7) allow to compute, via Čech cohomology, the full Picard group of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \). Namely, one finds that the Picard group of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \) is made of lifts of line bundles on \({{\mathbb {C}}}{{\mathbb {P}}}^{1}\)—recall that  —and a continuous part. Namely, one finds
—and a continuous part. Namely, one finds  .
.
Getting back to the line bundle  defined in (B.8), the transition functions allow to verify that the following are global sections:
defined in (B.8), the transition functions allow to verify that the following are global sections:


Let us check, for instance, that \(X_2\) is a global section:

It is immediate to find the equation satisfied by these global sections using their local definitions. Working on \(U_0\), for example one has
and we leave to the reader to write down the corresponding map \(\varphi :{{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \rightarrow {{\mathbb {C}}}{{\mathbb {P}}}^{\,2|2}\) and check that it defines an embedding whose image is given by the equation
Finally, in order to conclude the verification that  is actually isomorphic to the supermanifold
is actually isomorphic to the supermanifold  , one can bring the Eq. (B.9) in the form (B.1) via a transformation in
, one can bring the Eq. (B.9) in the form (B.1) via a transformation in  —the supergroup of automorphisms of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,2|2}\). Namely, this is achieved by the transformation
—the supergroup of automorphisms of \({{\mathbb {C}}}{{\mathbb {P}}}^{\,2|2}\). Namely, this is achieved by the transformation

We summarize the previous—rather informal—discussion in the following lemma.
Lemma B.7
(Super conic) The complex supermanifold  cut out by the equation
cut out by the equation
is isomorphic to the \(1\,{|}\,2\)-dimensional supermanifold \({{\mathbb {C}}}{{\mathbb {P}}}^{\,1|2}_\omega \), determined (up to isomorphism) by the triple  , where \(\omega \) is a non-zero cohomology class in \(H^1 (|{{\mathbb {C}}}{{\mathbb {P}}}^1|, {\mathsf {{T}}}_{{{\mathbb {C}}}{{\mathbb {P}}}^1} (-4))\).
, where \(\omega \) is a non-zero cohomology class in \(H^1 (|{{\mathbb {C}}}{{\mathbb {P}}}^1|, {\mathsf {{T}}}_{{{\mathbb {C}}}{{\mathbb {P}}}^1} (-4))\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Noja, S. On BV supermanifolds and the super Atiyah class. European Journal of Mathematics 9, 19 (2023). https://doi.org/10.1007/s40879-023-00603-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40879-023-00603-6



 -extension
-extension 
 non-canonically.
non-canonically. as follows:
as follows: 
 ;
; if and only if
if and only if  is trivial.
is trivial. , i.e.
, i.e.  does not admit a holomorphic connection;
does not admit a holomorphic connection; , i.e.
, i.e.  does not admit a holomorphic connection;
does not admit a holomorphic connection; , i.e.
, i.e.  is non-projected or non-split.
is non-projected or non-split. at the first page, i.e.
at the first page, i.e. 
 for
for 
 is isomorphic to semidensities on
is isomorphic to semidensities on  , i.e.
, i.e. 
 is zero. In particular, the second page of the spectral sequence
is zero. In particular, the second page of the spectral sequence  is given again by
is given again by 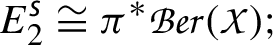
 is—up to exact terms—the super BV Laplacian
is—up to exact terms—the super BV Laplacian
 is a section of
is a section of  and
and 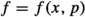 is a section of
is a section of  . In particular, the spectral sequence converges at page three, which is isomorphic to the locally constant sheaf on
. In particular, the spectral sequence converges at page three, which is isomorphic to the locally constant sheaf on  , i.e.
, i.e. 