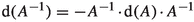Geodesic flows of c-projectively equivalent metrics are quantum integrable

Abstract

Given two c-projectively equivalent metrics on a Kähler manifold, we show that canoncially constructed Poisson-commuting integrals of motion of the geodesic flow, linear and quadratic in momenta, also commute as quantum operators. The methods employed here also provide a proof of a similar statement in the case of projective equivalence. We also investigate the addition of potentials, i.e. the generalization to natural Hamiltonian systems. We show that commuting operators lead to separation of variables for Schrödinger’s equation.

1 C-projective geometry, integrals and quantization rules

Definition 1.1

A Kähler manifold (of arbitrary signature) is a manifold ${\mathscr {M}}^{2n}$ of real dimension 2n endowed with the following objects:

• a (pseudo-)Riemannian metric g and its associated Levi-Civita connection $\nabla$,

• a complex structure J, i.e. an endomorphism on the space of vector fields with $J^2=-\textrm{Id}$,

• g and J must be compatible in the sense that $g(JX, Y)=-g(X,JY)$ and $\nabla J =0$,

• we denote by ${\Omega }$ the two-form ${\Omega }(X,Y)=g(JX,Y)$.

Definition 1.2

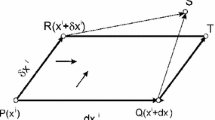
A regular curve $\gamma :I\rightarrow {\mathscr {M}}$ is called J-planar if there exist functions $A,B:I\rightarrow {\mathbb {R}}$ such that

(1)

is fulfilled on I. Here ${\dot{\gamma }}$ denotes the tangent vector to $\gamma$.

This is a natural generalization of geodesics on (pseudo-)Riemannian manifolds that in arbitrary parametrization are solutions of the equation . Similarly, the property of a curve to be J-planar survives under reparametrization.

Definition 1.3

Let $g,{\tilde{g}}$ be two Kähler metrics (of arbitrary signature) on $({\mathscr {M}},J)$. They are called c-projectively equivalent if and only if every J-planar curve of g is also a J-planar curve of ${\tilde{g}}$. (If every J-planar curve of g is also a ${\widetilde{J}}$-planar curve of ${\tilde{g}}$ and vice versa then the complex structures $J, {\widetilde{J}}$ coincide up to a sign, so we did not restrict ourselves in defining c-projective equivalence for the case where both metrics are Kähler w.r.t. the same complex structure.)

This is the Kähler analogue of projective equivalence on (pseudo-)Riemannian manifolds and it was proposed by Otsuki and Tashiro [13]. For a thorough introduction to c-projective geometry see [4]. For completeness, we recall the definition of projective equivalence, since Theorem 2.3 is the projective analogue of Theorem 2.2. Since their proofs run in parallel, all statements about the projective setting will be phrased as remarks placed after their c-projective counterparts.

Definition 1.4

Let $g,{\tilde{g}}$ be two (pseudo-)Riemannian metrics on a manifold ${\mathscr {M}}$. They are called projectively equivalent if and only if every unparametrized geodesic of g is also an unparametrized geodesic of ${\tilde{g}}$.

1.1 The tensor A

Theorem 1.5

(see [6], and also [4, Section 5]) Two (pseudo-)Riemannian metrics $g, {\tilde{g}}$ that are Kähler on a manifold $({\mathscr {M}},J)$ are c-projectively equivalent if and only if the tensor

$$\begin{aligned} A^i_j \overset{\textrm{def}}{=}\biggl |\frac{\det {\tilde{g}}}{\det g}\biggr |^{\frac{1}{2(n+1)}}{\tilde{g}}^{il}g_{lj},\quad \text {where} \;\; {\tilde{g}}^{il} {\tilde{g}}_{lm}=\delta ^i_m, \end{aligned}$$

satisfies the equation

$$\begin{aligned} \nabla _k A_{ij}&= \lambda _i g_{jk} + \lambda _j g_{ik} +{\bar{\lambda }}_i {\Omega }_{jk} + {\bar{\lambda }}_j {\Omega }_{ik}, \end{aligned}$$

(2)

where

$$\begin{aligned} \lambda&\overset{\textrm{def}}{=} \frac{1}{4}\,\textrm{tr}\,A, \quad \lambda _i \overset{\textrm{def}}{=} \nabla _i \lambda \quad \text {and} \quad {\bar{\lambda }}_i=J^j_i \lambda _j. \end{aligned}$$

Here and throughout the rest of the paper we use the Einstein sum convention. An index preceded by a comma is meant to indicate a covariant derivative. Raising and lowering indices is always by means of g: $\lambda ^i=g^{ij}\lambda _j$, where $g^{is} g_{sj}= \delta ^i_j$. A covariant (c-)projectively equivalent metric ${\tilde{g}}$, as stated above will be the sole exception: ${\tilde{g}}^{is} {\tilde{g}}_{sj}=\delta ^i_j$.

Remark 1.6

(projective case [2]) Two (pseudo-)Riemannian metrics $g, {\tilde{g}}$ on a manifold ${\mathscr {M}}$ are projectively equivalent if and only if the tensor

$$\begin{aligned} A^i_j \overset{\textrm{def}}{=}\biggl |\frac{\det {\tilde{g}}}{\det g}\biggr |^{\frac{1}{n+1}}{\tilde{g}}^{il}g_{lj},\quad \text {where} \;\; {\tilde{g}}^{il} {\tilde{g}}_{lm}=\delta ^i_m, \end{aligned}$$

(3)

satisfies the equation

$$\begin{aligned} \nabla _k A_{ij}= \lambda _i g_{jk} + \lambda _j g_{ik} \quad \text {with}\;\; \lambda \overset{\textrm{def}}{=} \frac{1}{2}\,\textrm{tr}\,A, \;\; \lambda _i \overset{\textrm{def}}{=} \nabla _i \lambda . \end{aligned}$$

(4)

Definition 1.7

We shall call Hermitian (g-self-adjoint and J-commuting) solutions of (2) c-projectively compatible or simply c-compatible with (g, J). Likewise, symmetric solutions of (4) shall be called projectively compatible or simply compatible with g.

1.2 Conserved quantities of the geodesic flow

Throughout this paper we shall canonically identify symmetric contravariant tensors with polynomials on $T^*{\mathscr {M}}$ via the isomorphisms $^\flat$ and $^\#$:

$$\begin{aligned} \begin{aligned} ^\flat&:T^{a_1\ldots a_l} \mapsto T^{a_1\ldots a_l} p_{a_1} \ldots p_{a_l},\\ ^\#&:T^{a_1\ldots a_l} p_{a_1} \ldots p_{a_l} \mapsto T^{(a_1\ldots a_l)}. \end{aligned} \end{aligned}$$

By the parentheses we mean symmetrisation with the appropriate combinatorial factor: $T^{(a_1\ldots a_l)}=1/l! \sum _{(b_1\ldots b_l)=\pi (a_1\ldots a_l)}^{}T^{b_1 \ldots b_l}$, where $\pi$ means any permutation.

Let (g, J, A) be c-compatible on ${\mathscr {M}}$ and consider the one-parameter family

(5)

Throughout this paper the root is to be taken in such a way that we simply halve the powers of the eigenvalues in . This is well defined because all eigenvalues of A are of even multiplicity. In particular, can be negative and it is smooth also near points where . With the tensors $\overset{\scriptscriptstyle t}{K}$ we associate the functions $\overset{\scriptscriptstyle t}{I}:T^* {\mathscr {M}}\rightarrow {\mathbb {R}}$

$$\begin{aligned} \overset{\scriptscriptstyle t}{I}\ \overset{\textrm{def}}{=} \ \overset{\scriptscriptstyle t}{K}{}^{ij} p_i p_j. \end{aligned}$$

(6)

Theorem 1.8

(Topalov [14], see also [4, Section 5]) Let (g, J, A) be c-compatible. Then for any pair of real numbers (v, w) the quantities $\overset{\scriptscriptstyle v}{I}$ and $\overset{\scriptscriptstyle w}{I}$ Poisson-commute, i.e. $\{\overset{\scriptscriptstyle v}{I},\overset{\scriptscriptstyle w}{I}\}=0$.

Remark 1.9

The quantities $\overset{\scriptscriptstyle t}{K}$ are well-defined for all values of t: if we denote by 2n the dimension of the manifold, then $\overset{\scriptscriptstyle t}{K}$ is a polynomial of degree $n-1$. This is a consequence of $J^2=-\textrm{Id}$, the antisymmetry of J with respect to g, the commutativity of A with J and the construction of $\overset{\scriptscriptstyle t}{K}$ from A. In particular the coefficient of $t^{n-1}$ of $\overset{\scriptscriptstyle t}{K}{}^{ij}$ is $g^{ij}$, which can be easily confirmed when looking at (5) in a frame such that A is in Jordan normal form.

Remark 1.10

(projective case) Let (g, A) be compatible. We shall define

for the projective case. Then for any pair $s,t \in {\mathbb {R}}$ the quantities $\overset{\scriptscriptstyle s}{I}\ \, \overset{\textrm{def}}{=} \, \overset{\scriptscriptstyle s}{K}{}^{ij} p_i p_j$ and $\overset{\scriptscriptstyle t}{I}\ \, \overset{\textrm{def}}{=} \, \overset{\scriptscriptstyle t}{K}{}^{ij} p_i p_j$ are commuting integrals of the geodesic flow for g [2, 12]. The projective and the c-projective cases differ merely by the power of the determinant.

For a c-compatible structure (g, J, A) there also exists a one-parameter family of commuting integrals of the geodesic flow that are linear in momenta given by

(7)

The commutation relations

$$\begin{aligned} \{\overset{\scriptscriptstyle t}{L},\overset{\scriptscriptstyle s}{I}\}=0 \end{aligned}$$

(8)

also hold. The number of functionally independent integrals within the family $\overset{\scriptscriptstyle t}{I}$ is equal to the degree of the minimal polynomial of A. The number of functionally independent integrals within $\overset{\scriptscriptstyle t}{L}$ is equal to the number of nonconstant eigenvalues of A. Furthermore the integrals $\overset{\scriptscriptstyle t}{I}$ are functionally independent from $\overset{\scriptscriptstyle t}{L}$, see [4, Section 5]. Thus the canonically constructed integrals are sufficient in number for Liouville-integrability of the geodesic flow if all eigenvalues of A are non-constant (then they are automatically pairwise different and each eigenvalue is of multiplicity two [4, Lemma 5.16]).

1.3 Quantization rules and commutators of operators

We adopt the quantization rules introduced by Carter [5] and Duval and Valent [7, Section 3]. The formulae they give construct differential operators that are independent of coordinate choice and symmetric with respect to the scalar product (the bar indicates complex conjugation)

$$\begin{aligned} \langle \phi ,\psi \rangle = \int _{{\mathscr {M}}} {\bar{\varphi }}\psi \end{aligned}$$

on the completion of the space ${\mathscr {H}}({\mathscr {M}})$ of compactly supported half-densities on ${\mathscr {M}}$. For more details and a reasoning we refer to [5, 7] and the references therein. It is sufficient for our purposes to recall the quantization formulae they give: for a homogeneous polynomial $P_m:T^*{\mathscr {M}}\rightarrow {\mathbb {R}}$ of degree m we construct its symmetric contravariant tensor via $^\#$ and compose with the covariant derivative:

(9)

For polynomials that are not homogeneous the quantization shall be done by quantizing the homogeneous parts and adding the results. So far we have been considering polynomials of degree two on the cotangent bundle of degree at most two and covariant tensors of valence at most (2, 0). These correspond to differential operators of degree at most 2. But the commutator of two such second order operators generally is an operator of order three. Later on we can facilitate the expression for the commutator of the quantum operators of two polynomials of degree two by using the quantum operator of the Poisson bracket of the two polynomials of degree two.

2 Results

The main result of this paper is a quantum version of Theorem 1.8: using the quantization rules (9) from [5] and [7] we construct differential operators from symmetric covariant tensors and show that these differential operators commute.

Let (g, J, A) be c-compatible and $\overset{\scriptscriptstyle t}{K}, \overset{\scriptscriptstyle t}{I}$ denote the associated Killing tensors and integrals of the geodesic flow. By (9) their associated quantum operators are

(The different letters I and K must not confuse the reader, for $\overset{\scriptscriptstyle t}{I}{}^\# = \overset{\scriptscriptstyle t}{K}$.)

Remark 2.1

Recalling Remark 1.9, $\overset{\scriptscriptstyle t}{{\widehat{I}}}$ is a polynomial of degree $n-1$ in t and its lead coefficient is $-{\Delta }_g$, the negative of the Laplace–Beltrami operator of g.

Theorem 2.2

Let (g, J, A) be c-compatible. Then for any pair (v, w) the operators $\overset{\scriptscriptstyle v}{{\widehat{I}}}$ and $\overset{\scriptscriptstyle w}{{\widehat{I}}}$ commute, i.e. ${[\overset{\scriptscriptstyle v}{{\widehat{I}}},\overset{\scriptscriptstyle w}{{\widehat{I}}}]=0}$.

This is a new result for both the Riemannian as well as the pseudo-Riemmanian case.

Theorem 2.3

Let (g, A) be projectively compatible. Then for any pair (v, w) the operators $\overset{\scriptscriptstyle v}{{\widehat{I}}}$ and $\overset{\scriptscriptstyle w}{{\widehat{I}}}$ commute, i.e. ${[\overset{\scriptscriptstyle v}{{\widehat{I}}},\overset{\scriptscriptstyle w}{{\widehat{I}}}]=0}$.

Remark 2.4

Theorem 2.3 was already proven by Matveev [10, 11]. The proof that we give however uses only $C^3$-smoothness whereas the original proof used $C^8$. The proof that will be given here runs in parallel with the proof of Theorem 2.2. A series of remarks to the proof of Theorem 2.2 will thus provide the proof of Theorem 2.3, giving the intermediate steps for the projective case and pointing out the analogues and differences.

We then improve the result of Theorem 2.2 by adding potential terms to these second order differential operators, finding commuting quantum observables for certain natural Hamiltonian systems.

Theorem 2.5

Let (g, J, A) be c-compatible. Let

be as in Theorem 2.2. Let

(10)

be the differential operators associated with the canonical Killing vector fields of g. Let $\overset{\textrm{nc}}{E}=\{\varrho _1, \ldots , \varrho _r\}$ be the set of non-constant eigenvalues of A. Let $\overset{\textrm{c}}{E}=\{\varrho _{r+1}, \ldots , \varrho _{r+R}\}$ be the set of constant eigenvalues and $E=\overset{\textrm{nc}}{E}\cup \overset{\textrm{c}}{E}$. Denote by $m(\varrho _{i})$ the algebraic multiplicity of $\varrho _i$. Let the family of potentials $\overset{\scriptscriptstyle t}{U}$, parametrized by t, be given by

$$\begin{aligned} \overset{\scriptscriptstyle t}{U}=\sum _{i=1}^{r+R} \prod _{\varrho _l \in E \setminus \{\varrho _i\}}^{} \frac{(t-\varrho _l)^{m(\varrho _l)/2}}{(\varrho _i-\varrho _l)^{m(\varrho _l)/2}}\, (t-\varrho _i)^{m(\varrho _i)/2-1} f_i \end{aligned}$$

(11)

with for all $l=1,\ldots , r+R$ and with $\textrm{d}f_l$ proportional to $\textrm{d}\varrho _l$ for all l for which $\varrho _l$ is non-constant. Let associated operators $\overset{\scriptscriptstyle t}{{\widehat{U}}}$ act on functions by mere multiplication, i.e. for any point p we have $(\overset{\scriptscriptstyle t}{{\widehat{U}}}(f))(p)=\overset{\scriptscriptstyle t}{U}(p) f(p)$. Then the operators

$$\begin{aligned} \overset{\scriptscriptstyle t}{{\widehat{Q}}}\ \overset{\textrm{def}}{=}\ \overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}, \quad \overset{\scriptscriptstyle t}{{\widehat{L}}} \end{aligned}$$

(12)

commute within the one-parameter-families as well as crosswise, i.e. for all values of $t,s \in {\mathbb {R}}$:

$$\begin{aligned}{}[\overset{\scriptscriptstyle t}{{\widehat{Q}}},\overset{\scriptscriptstyle s}{{\widehat{Q}}}] = [\overset{\scriptscriptstyle t}{{\widehat{Q}}},\overset{\scriptscriptstyle s}{{\widehat{L}}}] = [\overset{\scriptscriptstyle t}{{\widehat{L}}},\overset{\scriptscriptstyle s}{{\widehat{L}}}] = 0. \end{aligned}$$

(13)

Remark 2.6

Recalling Remark 1.9, $\overset{\scriptscriptstyle t}{{\widehat{Q}}}$ is a polynomial of degree $n-1$ in t, whose lead coefficient is the Schrödinger operator $-{\Delta }_g + {\widehat{U}}$, where U is simply a name introduced for the lead coefficient of $\overset{\scriptscriptstyle t}{U}$.

Remark 2.7

Since is a Killing vector field for any choice of the real parameter t [4, Section 5], we have .

Remark 2.8

1. We do not discuss whether the $\overset{\scriptscriptstyle t}{U}$ are smooth at all points of the manifold. Smoothness is guaranteed at points that have a neighbourhood in which the number of different eigenvalues is constant (see Definition 2.11 of regular points below), provided that the $f_i$ are smooth.

2. Formula (11) generally allows $\overset{\scriptscriptstyle t}{U}$ to be complex-valued. The conditions under which $\overset{\scriptscriptstyle t}{U}$ is real for any choice of $t\in {\mathbb {R}}$ are the following: for any real eigenvalue $\varrho _i$ of A the corresponding function $f_i$ must be real-valued. For all pairs $(\varrho _i, \varrho _j=\bar{\varrho _i})$ of complex-conjugate eigenvalues of A the corresponding functions $f_i$ and $f_j$ must be complex conjugate to each other: $f_i = {\bar{f}}_j$.

3. The potentials that are admissible to be added to the quantum operators are the same that may be added to the Poisson commuting integrals. In the proof we show that the quantization imposes no stronger conditions on the potential than classical integrability and then use the the conditions imposed by the Poisson-brackets to find the allowed potentials.

Theorem 2.9

Let (g, J, A) be c-compatible and A semi-simple. Let $\overset{\scriptscriptstyle t}{{\widehat{I}}}$, $\overset{\scriptscriptstyle t}{{\widehat{L}}}$ be as in Theorem 2.5. Then, for the operators

$$\begin{aligned} \overset{\scriptscriptstyle t}{{\widehat{Q}}}\ \overset{\textrm{def}}{=}\ \overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}, \quad \overset{\scriptscriptstyle t}{{\widehat{L}}} \end{aligned}$$

(14)

the commutation relations $[\overset{\scriptscriptstyle t}{{\widehat{Q}}},\overset{\scriptscriptstyle s}{{\widehat{Q}}}] = [\overset{\scriptscriptstyle t}{{\widehat{Q}}},\overset{\scriptscriptstyle s}{{\widehat{L}}}] = 0$ are satisfied if and only if the potentials are of the form (11) with the sole exception that a function of t alone may be added to $\overset{\scriptscriptstyle t}{U}$.

A result similar to Theorems 2.5 and 2.9 for projective geometry has been published in [2, Theorem 8]. Lemma 3.15 explains how this theorem is similar in nature to the ones at hand.

Corollary 2.10

Let (g, J, A), $\overset{\scriptscriptstyle t}{{\widehat{I}}}$, $\overset{\scriptscriptstyle t}{{\widehat{L}}}$, $\overset{\scriptscriptstyle t}{{\widehat{U}}}$ be as in Theorem 2.5. Let ${\widehat{I}}_{(l)}, {\widehat{L}}_{(l)}, {\widehat{U}}_{(l)}$ be the coefficients of $t^l$ in $\overset{\scriptscriptstyle t}{{\widehat{I}}}, \overset{\scriptscriptstyle t}{{\widehat{L}}}, \overset{\scriptscriptstyle t}{{\widehat{U}}}$ respectively. Then the commutation relations

$$\begin{aligned} \begin{aligned} \bigl [\overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}, {\widehat{I}}_{(l)} + {\widehat{U}}_{(l)}\bigr ]&=\bigl [\overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}, {\widehat{L}}_{(l)}\bigr ] = \bigl [\overset{\scriptscriptstyle t}{{\widehat{L}}}, {\widehat{I}}_{(m)} + {\widehat{U}}_{(m)}\bigr ]\\&= \bigl [\overset{\scriptscriptstyle t}{{\widehat{L}}}, {\widehat{L}}_{(l)}\bigr ]= \bigl [\overset{\scriptscriptstyle t}{{\widehat{L}}}, {\widehat{I}}_{(m)} + {\widehat{U}}_{(m)}\bigr ] = 0, \end{aligned} \end{aligned}$$

(15)

$$\begin{aligned} \bigl [{\widehat{I}}_{(l)} + {\widehat{U}}_{(l)}, {\widehat{I}}_{(m)} + {\widehat{U}}_{(m)}\bigr ] = \bigl [{\widehat{L}}_{(l)},{\widehat{L}}_{(m)}\bigr ] = \bigl [{\widehat{I}}_{(l)} + {\widehat{U}}_{(l)}, {\widehat{L}}_{(m)}\bigr ] = 0 \end{aligned}$$

(16)

hold true for any value of t and any values $l,m \in \{1, \ldots , n-1\}$.

Equations (16) are equivalent to

$$\begin{aligned} \bigl [\overset{\scriptscriptstyle t}{{\widehat{I}}} + \overset{\scriptscriptstyle t}{{\widehat{U}}}, \overset{\scriptscriptstyle s}{{\widehat{I}}} + \overset{\scriptscriptstyle s}{{\widehat{U}}}\bigr ] = \bigl [\overset{\scriptscriptstyle t}{{\widehat{L}}},\overset{\scriptscriptstyle s}{{\widehat{L}}}\bigr ] = \bigl [\overset{\scriptscriptstyle t}{{\widehat{I}}} + \overset{\scriptscriptstyle t}{{\widehat{U}}}, \overset{\scriptscriptstyle s}{{\widehat{L}}}\bigr ] = 0. \end{aligned}$$

(17)

Equations (15), (16), (17) remain true if a function of t alone is added to $\overset{\scriptscriptstyle t}{{\widehat{U}}}$ and constants $c_{(l)}$ are added to ${\widehat{U}}_{(l)}$. If all eigenvalues of A are non-constant and $\overset{\scriptscriptstyle t}{{\widehat{I}}}, \overset{\scriptscriptstyle t}{{\widehat{V}}}$ are as in Theorem 2.5 then no other than the described ${\widehat{U}}_{(l)}$ can be found such that the commutation relations above hold.

Lastly, we shall show how the search for common eigenfunctions of the operators can be reduced to differential equations in lower dimension in appropriate coordinates around regular points. In particular, if all eigenvalues of A are non-constant we can reduce it to ordinary differential equations only. Moreover, the case where all eigenvalues of A are non-constant provides an example of reduced separability of Schrödinger’s equation as described in [1].

Definition 2.11

Let (g, J, A) be c-compatible. A point $x \in {\mathscr {M}}$ is called regular with respect to A if in a neighbourhood of x the number of different eigenvalues of A is constant and for each eigenvalue $\varrho$ either $\textrm{d}\varrho \ne 0$ or $\varrho$ is constant in a neighbourhood of x. The set of regular points shall be denoted by ${\mathscr {M}}^0$.

Definition 2.12

Let (g, J, A) be c-compatible on ${\mathscr {M}}$. A local normal coordinate system for ${\mathscr {M}}$ is a coordinate system where (g, J, A) assume the form of Example 2.13. Existence of such coordinates in the neighbourhood of regular points is guaranteed by [3, Theorem 1.6].

Example 2.13

(General example for c-compatible structures $(g,J,\omega ,A)$ [3, Example 5]) Let $2n\geqslant 4$ and consider an open subset W of ${\mathbb {R}}^{2n}$ of the form for open subsets $V,U\subseteq {\mathbb {R}}^r$, $S_\gamma \subseteq {\mathbb {R}}^{4m_{c_\gamma }}$ for $\gamma \,{=}\,1,\ldots , L$ and $S_\gamma \,{\subseteq }\, {\mathbb {R}}^{2m_{c_\gamma }}$ for $\gamma \,{=}\,L\,{+}\,1, \ldots , L\,{+}\,Q$. Let $t_1,\dots , t_l$ be the coordinates on V and let the coordinates on U be separated into l complex coordinates $z_1, \ldots ,z_l$ and q real coordinates $x_{l+1}, \ldots , x_{l+q}$ and introduce the tuple $(\chi _1, \ldots , \chi _r)=(z_1, {\bar{z}}_1, \ldots , z_l, {\bar{z}}_l, x_{l+1}, \ldots , x_{l+q})$. Suppose the following data is given on these open subsets:

• Kähler structures $(g_\gamma , J_\gamma , \omega _\gamma )$ on $S_\gamma$ for $\gamma =1, \ldots , L+Q$.

• For each $\gamma =1, \ldots , L+Q$, a parallel Hermitian endomorphism $A_\gamma :TS_\gamma \rightarrow TS_\gamma$ for $(g_\gamma , J_\gamma )$. For $\gamma =1,\ldots , L$, A has a pair of complex conjugate eigenvalues $c_\gamma , {\bar{c}}_\gamma$ of equal algebraic multiplicity $m(c_\gamma )=m({\bar{c}}_\gamma )$. For $\gamma =L+1,\ldots , L+Q$, A has a single real eigenvalue $c_\gamma$ of algebraic multiplicity $m(c_\gamma )$.

• Holomorphic functions $\sigma _j(z_j)$ for $1\leqslant j\leqslant l$ and smooth functions $\sigma _j(x_j)$ for $l+1\leqslant j\leqslant r$.

Moreover, we choose one-forms $\alpha _1, \ldots , \alpha _r$ on that satisfy

(18)

where $A_{\gamma }^{r-i}$ denotes the $(r-i)\textrm{th}$ power of $A_\gamma$.

To facilitate the expressions for the c-compatible structure that will be constructed, the following expressions shall be introduced: the tuple $E = (\varrho _1,\ldots , \varrho _n) = (\sigma _1, {\bar{\sigma }}_1,\ldots ,\sigma _l, {\bar{\sigma }}_l, \sigma _{l+1}, \ldots , \sigma _{l+q}, c_1, \bar{c_1}, \ldots ,c_L,{\bar{c}}_L,c_{L+1}, \ldots , c_{L+Q})$ contains the designated eigenvalues for A. Their algebraic multiplicities shall be denoted by $(m(\varrho _l),l\,{=}\,1,\ldots ,r\,{+}\,R)\,{=}\,(2,\ldots ,2 , m(c_1), m({\bar{c}}_1), \ldots )$. The non-constant eigenvalues shall be collected in order in $\overset{\textrm{nc}}{E}=(\varrho _1,\ldots , \varrho _r)=(\sigma _1, \bar{\sigma _1},\ldots , \sigma _l, \ldots , {\bar{\sigma }}_l, \sigma _{l+1}, \ldots , \sigma _{l+q})$ and the collection of constant eigenvalues shall be referenced as . The quantity ${\Delta }_i$ for $i=1,\ldots ,r$ is given by ${\Delta }_i = \prod _{\varrho \in \overset{\textrm{nc}}{E}\setminus \{\varrho _i\}}^{}(\varrho _i -\varrho )$. The function $\mu _i$ denotes the elementary symmetric polynomial of degree i in the variables $\overset{\textrm{nc}}{E}$ and $\mu _i(\widehat{\varrho _s})$ denotes the elementary symmetric polynomial of degree i in the variables . We shall further define the one-forms $\vartheta _1, \ldots , \vartheta _r$ on W via $\vartheta _i = \textrm{d}t_i +\alpha _i$.

Suppose that at every point of W the elements of $\overset{\textrm{nc}}{E}$ are mutually different and different from the constants $c_1, {\bar{c}}_1, \ldots , c_{L+Q}$ and their differentials are non-zero. Then $(g,\omega , J)$ given by the formulae

(19)

(20)

is Kähler, where $(\varepsilon _1, \ldots , \varepsilon _{2l}, \varepsilon _{2l+1}, \ldots , \varepsilon _r)=(-1/4, \ldots , -1/4, \pm 1, \ldots , \pm 1)$ determine the signature of g.

With local coordinates $\overset{\scriptscriptstyle \gamma }{y}$ on $S_\gamma$ we write $\alpha _i = \sum _{\gamma ,q}^{} \overset{\scriptscriptstyle \gamma }{\alpha }_{iq} \textrm{d}\overset{\scriptscriptstyle \gamma }{y}_q$ and . Then the endomorphism A given by

(21)

is c-compatible with $(g,J,\omega )$.

Remark 2.14

($\omega$ as an exterior derivative) The formula for $\omega$ in (19) can at least locally be expressed in a very concise manner: Since $A_\gamma$ is parallel and $\omega _\gamma$ is closed for all $\gamma =1,\ldots ,L+Q$, we can at least locally find a one-form $\alpha _0$ on S such that

Then if we define the one-form $\vartheta _0$ on W simply as $\vartheta _0=\alpha _0$, it is easy to check that

$$\begin{aligned} \omega =\textrm{d}\sum _{i=0}^r \mu _i \vartheta _i. \end{aligned}$$

Theorem 2.15

([3, Theorem 1.6 / Example 5]) Suppose (g, J, A) are c-compatible on ${\mathscr {M}}$ of real dimension 2n. Assume that in a small neighbourhood $W \subseteq {\mathscr {M}}^0$ of a regular point, A has

• $r=2l+q$ non-constant eigenvalues on W which separate into l pairs of complex-conjugate eigenvalues $\varrho _1 ,{\bar{\varrho }}_1 , \ldots , \varrho _{l} , {\bar{\varrho }}_{l} :W \rightarrow {\mathbb {C}}$ and q real eigenvalues $\varrho _{l+1} , \ldots ,\varrho _{l+q} :W \rightarrow {\mathbb {R}}$,

• $R=2L+Q$ constant eigenvalues which separate into L pairs of complex conjugated eigenvalues $c_1, {\bar{c}}_1, \ldots , c_L, {\bar{c}}_L$ and Q real eigenvalues $c_{L+1}, \ldots , c_{L+Q}$,

then the Kähler structure $(g,J,\omega )$ and A are given on W by the formulas of Example 2.13.

A local description of Kähler structures $(g,J, \omega )$ with Riemannian signature that admit a Hermitian solution of 4 goes back to [1], using the language of Hamiltonian 2-forms.

Theorem 2.16

Let (g, J, A) be c-compatible on ${\mathscr {M}}$. Let A be semi-simple and let all constant eigenvalues be real. Let $(g,J,\omega ,A)$ be given by the formulas of Example 2.13 and adopt the naming conventions of Example 2.13.

Let $\psi$ be a simultaneous eigenfunction of

and

for all t, where

$$\begin{aligned} \overset{\scriptscriptstyle t}{U}=\sum _{i=1}^{r+R} \prod _{\varrho _l \in E \setminus \{\varrho _i\}}^{} \frac{(t-\varrho _l)^{m(\varrho _l)/2}}{(\varrho _i-\varrho _l)^{m(\varrho _l)/2}}\, (t-\varrho _i)^{m(\varrho _i)/2-1} f_i \end{aligned}$$

(22)

with for all $l=1,\ldots , r+R$ and with $\textrm{d}f_l$ proportional to $\textrm{d}\varrho _l$ for all l for which $\varrho _l$ is non-constant. Then there exist constants ${\tilde{\lambda }}_0, \ldots , {\tilde{\lambda }}_{r+R-1}, \omega _1,\ldots ,\omega _r$, such that $\psi$ satisfies the following ODE:

(23)

for $q=1,\ldots , r$, where the $\lambda _i$ are given by

and $\psi$ also fulfills the partial differential equations:

(24)

for $\gamma =r+1,\ldots , r+R$.

The converse is also true: If a function $\psi$ satisfies equations (23) and (24) for some constants ${\tilde{\lambda }}_0, \ldots , {\tilde{\lambda }}_{r+R-1}, \omega _1,\ldots ,\omega _r$, then it is an eigenfunction of $\overset{\scriptscriptstyle t}{{\widehat{Q}}}$ and $\overset{\scriptscriptstyle t}{{\widehat{L}}}$.

A particular application of Theorem 2.16 is in the treatment of the Laplace–Beltrami operator in the case where the number of integrals is maximal: if ${\mathscr {M}}$ is compact and Riemannian its eigenfunctions provide means to construct a countable basis in $L^2({\mathscr {M}})$, see e.g. [8]. Because the integrals are self-adjoint and commute pairwise as well as with the Laplace–Beltrami operator they leave each others eigenspaces invariant and thus there exists a countable basis of $L^2({\mathscr {M}})$ that consists of simultaneous eigenfunctions of the commuting operators. In our case, since ${\Delta }$ is within the span of our one-parameter family of operators we can find such basis by solving the simultaneous eigenvalue problems corresponding to the integrals only. In the case where all eigenvalues of A are non-constant this reduces to ODE.

3 Proof of the results

3.1 Basic facts

We shall provide some formulae that will be used throughout the proof of Theorem 2.2. We will be mainly working with (2). Unless it is stated otherwise we are working in the c-projective setting with only some remarks providing the analogue formulae for the projective setting.

We start by computing the covariant derivative of . By using Jacobi’s formula , we get

(25)

Equation (2) was used to expand the covariant derivative of A and then the properties of J interacting with g were exploited to obtain this.

Lemma 3.1

([4, Section 5]) A and thus $t \textrm{Id} - A$ and $(t \textrm{Id}-A)^{-1}$ are self-adjoint with respect to $\nabla ^2 \lambda$: ${A^{-1}}^j_l\lambda _{j,k} = {A^{-1}}^j_k\lambda _{j,l}$. The last claim is of course true only if $(t \textrm{Id}-A)^{-1}$ exists.

That is, if we consider the second derivative of $\lambda$ in the way that it maps two vector fields $\xi , \eta$ to a scalar function on ${\mathscr {M}}$ then we have $\nabla ^2 \lambda (A\xi ,\eta )=\nabla ^2 \lambda (\xi ,A\eta )$ for all $(\xi ,\eta )$.

Proof of Lemma 3.1

Without loss of generality we may assume that A is invertible. Otherwise we may choose $\varepsilon$ such that $\varepsilon \textrm{Id} - A$ is invertible. Then we can apply the same procedure that we will apply to $\ln \det A$ to $\ln \det (\varepsilon \textrm{Id} -A)$ instead. We can therefrom show that $(\varepsilon \textrm{Id} -A)^{-1}$ is self-adjoint with respect to $\nabla ^2 \lambda$. And thus by linear algebra $\varepsilon \textrm{Id} -A$ and consequentially A are also $\nabla ^2 \lambda$-self-adjoint.

Now to the main argument: We compute the second covariant derivative of $\ln \det A$ using (25), (2), the general identity as well as the antisymmetry of J with respect to g:

$$\begin{aligned} \begin{aligned} \frac{1}{4} \nabla _k \nabla _l \ln \det A = \lambda _j {A^{-1}}^j_p g^{ps} \lambda _s&{A^{-1}}^q_l g_{qk} + \lambda _j {A^{-1}}^j_k {A^{-1}}^q_l \lambda _q \\&+ \lambda _j {A^{-1}}^j_p g^{ps} \bar{\lambda }_s {A^{-1}}^q _l {\Omega }_{qk}\\&- \lambda _j {A^{-1}}^j_p J^p_k \bar{\lambda }_q {A^{-1}}^q_l +{A^{-1}}^j_l \lambda _{j,k}. \end{aligned} \end{aligned}$$

(26)

The left-hand side is symmetric with respect to (k, l). The first, second and fourth terms on the right-hand side are symmetric as well. The third term vanishes. Consequently the last term must be symmetric as well. Thus $A^{-1}$ is self-adjoint with respect to $\nabla ^2 \lambda$. By means of linear algebra, the self-adjointness with respect to $\lambda _{j,k}$ is also true for $(t \textrm{Id} -A)$ or $(t \textrm{Id}-A)^{-1}$. The latter of course is only true, provided that t is not chosen to be within the spectrum of A. This concludes the proof of Lemma 3.1.$\square$

Remark 3.2

(projective setting) The formula $A^j_l\lambda _{j,k} = A^j_k\lambda _{j,l}$ is true for the projective setting as well. Performing the same computations as in Lemma 3.1 gives the intermediate results and $\frac{1}{2}\nabla _k \nabla _l \ln \det A = \lambda _j {A^{-1}}^j_p g^{ps} \lambda _s {A^{-1}}^q_l g_{qk} + \lambda _j {A^{-1}}^j_k {A^{-1}}^q_l \lambda _q +{A^{-1}}^j_l \lambda _{j,k}$ to which the same logic is applied as in the c-projective case.

Lemma 3.3

Let S be an endomorphism on the space of vector fields on ${\mathscr {M}}$ with the following properties: , , and . Then the formula

$$\begin{aligned} R^r_{\ ijk} A_{rl} S^{ij} - R^r_{\ ijl} A_{rk} S^{ij}= 0 \end{aligned}$$

(27)

is valid.

The sign of the Riemann tensor is chosen so that $R^i_{\ jkl} = \partial _k {\Gamma }^i_{lj} -\partial _l {\Gamma }^i_{kj} +{\Gamma }^i_{ks}{\Gamma }^s_{lj} - {\Gamma }^i_{ls}{\Gamma }^s_{kj}$. It is obviously not essential for the formula but the proof would need a few changes in the signs.

Proof of Lemma 3.3

In the proof we reuse and extend the ideas used in the proof of equation (12) in [9]. We inspect the second derivative of A:

$$\begin{aligned} \begin{aligned} R^r_{\ jkl} A_{ir} + R^r_{\ ikl} A_{rj}&= (\nabla _l \nabla _k - \nabla _k \nabla _l) A_{ij} \\&= \lambda _{i,l} g_{jk} - \lambda _{i,k} g_{jl} +\lambda _{j,l} g_{ik} -\lambda _{j,k}g_{il}\\&\qquad \qquad +{\bar{\lambda }}_{i,l} {\Omega }_{jk} - {\bar{\lambda }}_{i,k} {\Omega }_{jl} +{\bar{\lambda }}_{j,l} {\Omega }_{ik} - {\bar{\lambda }}_{j,k}{\Omega }_{il}. \end{aligned} \end{aligned}$$

(28)

The first equality is the Ricci identity and is true for any (0, 2)-tensor. The second equality comes from differentiating (2). We continue by adding the equation with itself three times after performing cyclic permutations of (j, k, l). The three terms rising from the first term on the left-hand side of (28) vanish due to the Bianchi identity. On the right-hand side only terms involving ${\bar{\lambda }}$ remain:

(29)

${}+(i \,{\leftrightarrow }\, j)$ means that the preceding term is to be added again, but with indices i and j interchanged. We now multiply this equation with $S^{ij}$. Since S is g-self-adjoint and commutes with J, we have ${\bar{\lambda }}_{i,j} S^{ij}=0$. Using this and using again that S commutes with J, the right-hand side simplifies as follows:

$$\begin{aligned} \begin{aligned} R^r_{\ ikl} A_{rj} S^{ij} + R^r_{\ ijk} A_{rl} S^{ij}+ R^r_{\ ilj} A_{rk} S^{ij} = 4 \bigl (S^j_k \lambda _{j,l} - S^j_l \lambda _{j,k}\bigr ). \end{aligned} \end{aligned}$$

is g-self-adjoint because S and A are g-self-adjoint and commute. As a consequence, we have that $R^r_{\ ikl} A_{rj} S^{ij}$ vanishes on the left-hand side. Further utilizing the symmetry of the curvature tensor as well as the self-adjointness of S with respect to $\nabla ^2 \lambda$ we reach the desired result:

$$\begin{aligned} R^r_{\ ijk} A_{rl} S^{ij} - R^r_{\ ijl} A_{rk} S^{ij}= 0. \end{aligned}$$

$\square$

Remark 3.4

(projective case) In the projective case Lemma 3.3 also holds true. The procedure involves the same steps as in the proof of Lemma 3.3. Removing the terms involving ${\Omega }$ from (28) gives the intermediate step for the projective case. Equation (29) trivially simplifies to $R^r_{\ ikl} A_{rj} + R^r_{\ ijk} A_{rl} + R^r_{\ ilj} A_{rk}=0$. After multiplication with $S^{ij}$ the first term vanishes with the same argument as in the c-projective case and the result is obtained. Since the proof of Corollary 3.5 involves only linear algebra, the arguments are exactly the same in the projective and the c-projective case.

Corollary 3.5

Linear algebra applied to (27) provides the formula

$$\begin{aligned} {(v \textrm{Id} - A)^{-1}}^{lr} R^k_{\ jir}S^{ij} - {(v \textrm{Id} - A)^{-1}}^{kr} R^{l}_{\ jir}S^{ij}=0. \end{aligned}$$

(30)

Proof

Consider the endomorphism $R^r_{\ ijl} S^{ij}$ on the space of vector fields. Raising and lowering indices in (27) shows that it commutes with A. Consequently it also commutes with $(v \textrm{Id} -A)$ and thus with $(v \textrm{Id} -A)^{-1}$. Standard index manipulations using the symmetries of the curvature tensor imply the result.$\square$

3.2 Proof of Theorem 2.2

The family $\overset{\scriptscriptstyle t}{{\widehat{I}}}$ is a polynomial in t and therefore continuous. It is therefore sufficient to show that the commutator vanishes for all v and w that are not in the spectrum of A. Otherwise we can consider two sequences $(v_n)_{n\in {\mathbb {N}}}$ and $(w_n)_{n\in {\mathbb {N}}}$ where none of the elements of the sequence are in the spectrum of A and that converge to v and w. Then for each of the pairs $(v_n,w_m)$ from the sequences the commutator $[\overset{v_n}{{\widehat{I}}},\overset{w_m}{{\widehat{I}}}]$ will vanish and consequently it will vanish in the limit $(m,n)\rightarrow \infty$.

Equations (3.12), (3.13) and (3.14) in [7] give us the general formula for the commutator of two operators formed from arbitrary homogeneous polynomials $P_2, Q_2$ of degree two on $T^*{\mathscr {M}}$:

(31)

Here $\{P_2,Q_2\}$ is the Poisson bracket of the two homogeneous polynomials $P_2$ and $Q_2$ (of degree two) on $T^*{\mathscr {M}}$. $\{P_2,Q_2\}$ is a polynomial of degree three in momenta. We recall that the “hat” over $\{P_2,Q_2\}$ is explained in (9): This polynomial is mapped to a differential operator according to

where for a given polynomial $P_3$ the quantities $P_3^{jkl}$ are chosen so that they are symmetric and $P_3= P_3^{jkl}p_j p_k p_l$.

The tensor $B^{kl}_{P_2 , Q_2}$ is given by the formula

$$\begin{aligned} \begin{aligned} B^{jk}_{P_2 , Q_2}=P^{l[j}\nabla _l \nabla _m Q^{k] m}&+ P^{l[j} R^{k]}_{\ mnl} Q^{mn} - (P \,{\leftrightarrow }\, Q) \\&- \nabla _l P^{m[j}\nabla _m Q^{k] l} -P^{l[j}R_{lm} Q^{k] m}. \end{aligned} \end{aligned}$$

(32)

The brackets around the indices mean taking the antisymmetric part. In the third term $\nabla _l$ acts only on P. The subtraction of $(P\,{\leftrightarrow }\, Q)$ is meant to act upon the two leftmost terms. For the two rightmost terms the antisymmetrization w.r.t. $(j \,{\leftrightarrow }\, k)$ is the same as if one were to antisymmetrize these terms w.r.t. $(P\,{\leftrightarrow }\, Q)$. For formula (32) the sign of $R^i_{\ jkl} = \partial _k {\Gamma }^i_{lj} -\partial _l {\Gamma }^i_{kj} +{\Gamma }^i_{ks}{\Gamma }^s_{lj} - {\Gamma }^i_{ls}{\Gamma }^s_{kj}$ is important. But the reader may forget about it at once because it is not needed for our further investigations, as will be seen in the upcoming Lemmas 3.8 and 3.10.

We plug the operators $\overset{\scriptscriptstyle v}{{\widehat{I}}}$ and $\overset{\scriptscriptstyle w}{{\widehat{I}}}$ into formula (31). Using Theorem 1.8 by Topalov we get

(33)

Remark 3.6

$i\widehat{\{P_2,Q_2\}}$ in formula (31) is a differential operator of order three while the other term on the right-hand side is a differential operator of order one. Therefore it is a necessary condition for the quantities $\overset{\scriptscriptstyle v}{I}$ and $\overset{\scriptscriptstyle w}{I}$ to Poisson-commute in order for their associated differential operators to commute. This is of course a well-known fact.

Remark 3.7

(projective case) The fact that $\overset{\scriptscriptstyle t}{K}$ is a family of Killing tensors polynomial of degree ${n-1}$ in t and that their corresponding quadratic polynomials on $T^*{\mathscr {M}}$ Poisson commute pairwise can be found in [2]. Employing this instead of Theorem 1.8 brings proof in the projective case to the point where only equation (34) needs to be verified.

It remains to prove that

$$\begin{aligned} \begin{aligned} \nabla _j B^{jk}_{\overset{\scriptscriptstyle v}{I}\ , \overset{\scriptscriptstyle w}{I}}&=\nabla _j\Bigl (\bigl (\overset{\scriptscriptstyle v}{K}{}^{l[j}\nabla _l \nabla _m \overset{\scriptscriptstyle w}{K}{}^{ k] m} - (v\,{\leftrightarrow }\, w) \bigr ) - \nabla _l \overset{\scriptscriptstyle v}{K}{}^{m[j}\nabla _m \overset{\scriptscriptstyle w}{K}{}^{k] l}\\&\qquad + \bigl (\overset{\scriptscriptstyle v}{K}{}^{l[j} R^{k]}_{\ mnl} \overset{\scriptscriptstyle w}{K}{}^{mn} - (v\,{\leftrightarrow }\, w) \bigr ) -\overset{\scriptscriptstyle v}{K}{}^{l[j}R_{lm} \overset{\scriptscriptstyle w}{K}{}^{ k] m}\Bigr )=0. \end{aligned} \end{aligned}$$

(34)

The proof will be split into three steps: first we show that $\overset{\scriptscriptstyle v}{K}{}^{l[j} R^{ k]}_{\ mnl} \overset{\scriptscriptstyle w}{K}{}^{mn} - (v\,{\leftrightarrow }\, w) = 0$. In the second step we show that $\overset{\scriptscriptstyle v}{K}{}^{l[j}R_{lm} \overset{\scriptscriptstyle w}{K}{}^{k] m}=0$. This will be done in Lemmas 3.8 and 3.10. These will reduce (34) to

$$\begin{aligned} \nabla _j\bigl (\overset{\scriptscriptstyle v}{K}{}^{l[j}\nabla _l \nabla _m \overset{\scriptscriptstyle w}{K}{}^{k] m} - (v\,{\leftrightarrow }\, w) - \nabla _l \overset{\scriptscriptstyle v}{K}{}^{m[j}\nabla _m \overset{\scriptscriptstyle w}{K}{}^{k] l}\bigr )=0 \end{aligned}$$

(35)

which we will show in the last step.

Lemma 3.8

$\overset{\scriptscriptstyle v}{K}{}^{l[j} R^{ k]}_{\ mnl} \overset{\scriptscriptstyle w}{K}{}^{mn} - (v\,{\leftrightarrow }\, w) =0$.

Proof of Lemma 3.8

It follows from Lemma 3.1 that in Corollary 3.5 we may take , i.e. $S^{ij}=\overset{\scriptscriptstyle w}{K}{}^{ij}$. Plugging this into equation (30) and multiplying with gives

$$\begin{aligned} {2 \overset{\scriptscriptstyle v}{K}{}^{l[j} R^{ k]}_{\ mnl} \overset{\scriptscriptstyle w}{K}{}^{mn}=0}. \end{aligned}$$

(36)

Interchanging v and w, subtracting the result from this and dividing by 2 proves Lemma 3.8.$\square$

Remark 3.9

(projective case) Lemma 3.8 is true in the projective and c-projective cases. The proof for the projective case only requires to take and multiplying with instead of .

Lemma 3.10

$\overset{\scriptscriptstyle v}{K}{}^{l[j}R_{lm} \overset{\scriptscriptstyle w}{K}{}^{ k] m}=0$

Proof of Lemma 3.10

If we let $S=\textrm{Id}$ in Corollary 3.5, then in formula (30) the multiplication with $S^{ij}=g^{ij}$ means contraction of the Riemann tensor to the negative of the Ricci tensor. Raising and lowering indices yields that $(v \textrm{Id} - A)^{-1}$ commutes with the Ricci tensor when both are considered as endomorphisms on the space of vector fields:

$$\begin{aligned} {(v \textrm{Id} - A)^{-1}}{}^{r}_l R^k_{r} - {(v \textrm{Id} - A)^{-1}}{}^{k}_r R^{r}_{l}=0. \end{aligned}$$

(37)

Of course, $(w \textrm{Id} -A)^{-1}$ commutes with $(v \textrm{Id} - A)^{-1}$ and the Ricci tensor as well, so by multiplying (37) with ${(w \textrm{Id} - A)^{-1}}{}^l_j$ and using the commutativity gives

$$\begin{aligned} {(w \textrm{Id} - A)^{-1}}{}^k_r R^r_{l} {(v \textrm{Id} - A)^{-1}}{}^{l}_j - {(v \textrm{Id} - A)^{-1}}{}^{k}_r R^{r}_{l} {(w \textrm{Id} - A)^{-1}}{}^l_j=0. \end{aligned}$$

(38)

After multiplication of (38) with and raising and lowering indices, Lemma 3.10 is proven.$\square$

Remark 3.11

(projective case) Replacing the multiplication of with is the only difference between the proof of Lemma 3.10 in the projective and c-projective cases.

Having established Lemmas 3.8 and 3.10 we now compute the terms ${\overset{\scriptscriptstyle v}{K}{}^{l[j}\nabla _l \nabla _m \overset{\scriptscriptstyle w}{K}{}^{k] m}}- (v \,{\leftrightarrow }\, w)$ and $\nabla _m\overset{\scriptscriptstyle v}{K}{}^{l[j}\nabla _l \overset{\scriptscriptstyle w}{K}{}^{k] m}$ separately and then show that (35) is fulfilled to prove Theorem 2.2.

We introduce a shorthand notation:

$$\begin{aligned} {\Lambda }=\textrm{grad}\,\lambda =(g^{ij} \lambda _j), \quad {\bar{{\Lambda }}}=J \textrm{grad}\,\lambda , \quad \overset{\scriptscriptstyle t}{M}{}^{}_{}=(t \textrm{Id} -A)^{-1} \end{aligned}$$

for any t outside the spectrum of A.

We get

in the same way as we have obtained formula (25). Using this, the general matrix identity and (2), the covariant derivative of the Killing tensor $\overset{\scriptscriptstyle t}{K}$ evaluates to

$$\begin{aligned} \begin{aligned} \nabla _k \overset{\scriptscriptstyle t}{K}{}^{jl}&=\sqrt{\det (t \textrm{Id} -A)}\, \bigl [{}-2 \overset{\scriptscriptstyle t}{M}{}^{s}_{k} \lambda _s\, \overset{\scriptscriptstyle t}{M}{}^{j}_{r}g^{rl} +\overset{\scriptscriptstyle t}{M}{}^{j}_{p} \lambda ^p \overset{\scriptscriptstyle t}{M}{}^{l}_{k}\\&\qquad \qquad \qquad \qquad \qquad +\overset{\scriptscriptstyle t}{M}{}^{j}_{k}\ \overset{\scriptscriptstyle t}{M}{}^{l}_{q}\lambda ^q-\overset{\scriptscriptstyle t}{M}{}^{j}_{p} g^{ps} {\bar{\lambda }}_s \overset{\scriptscriptstyle t}{M}{}^{l}_{q}J^q_k-\overset{\scriptscriptstyle t}{M}{}^{l}_{r}g^{rq}{\bar{\lambda }}_q \overset{\scriptscriptstyle t}{M}{}^{j}_{p}J^p_k\bigr ]. \end{aligned} \end{aligned}$$

(39)

Contracting the indices k and l we get

(40)

For the derivative of this expression we receive

(41)

We shall denote by $(\overset{\scriptscriptstyle w}{M}{}^{}_{}{\Lambda })^k$ the k-th component of $\overset{\scriptscriptstyle w}{M}{}^{}_{}({\Lambda })$. Now multiplying the previous equation with $\overset{\scriptscriptstyle v}{K}{}^{lj}$ and antisymmetrizing with respect to $(j \,{\leftrightarrow }\, k)$ and $(v \,{\leftrightarrow }\, w)$ gives

(42)

Here $({\Lambda } \,{\leftrightarrow }\,{\bar{{\Lambda }}})$ indicates that the previous bracket shall be added with ${\Lambda }$ replaced by ${\bar{{\Lambda }}}$, $(j \,{\leftrightarrow }\, k)$ indicates antisymmetrization with respect to j and k, likewise for $(v\,{\leftrightarrow }\, w)$. In (42) the terms from (41) involving second derivatives of $\lambda$ have cancelled out as a consequence of Lemma 3.1. When forming the right-hand side expression of (42) the terms of the second to the last row of (41) cancel each other out after the antisymmetrization $(j\,{\leftrightarrow }\, k)$ due to $(v \textrm{Id}-A)$ and $(w \textrm{Id}-A)$ commuting and being self-adjoint to g.

Remark 3.12

(projective case) To get the formula for $\overset{\scriptscriptstyle v}{K}{}^{l[j}\nabla _l \nabla _m \overset{\scriptscriptstyle w}{K}{}^{ k] m} - (v \,{\leftrightarrow }\, w)$ in the projective case we perform the same steps, using (4) instead of the c-projective formula (2). The next three equations give projective analogues of the formulae (39), (41) and (42):

(43)

(44)

general matrix identity

which reads $\overset{\scriptscriptstyle v}{M}{}^{}_{} - \overset{\scriptscriptstyle w}{M}{}^{}_{}= (w-v) \overset{\scriptscriptstyle v}{M}{}^{}_{}\overset{\scriptscriptstyle w}{M}{}^{}_{}$ in our shorthand, as well as the trace applied to this matrix identity we expand (42):

$$\begin{aligned} \overset{\scriptscriptstyle v}{K}{}^{l[j}\nabla _l \nabla _m \overset{\scriptscriptstyle w}{K}{}^{ k] m} - (v \,{\leftrightarrow } w)&= \frac{1}{2}\sqrt{\det (v \textrm{Id}-A)}\sqrt{(w\textrm{Id}-A)} \cdot \bigl [\bigl [\bigl [(w-v)^{-1} \\&\begin{aligned}&\bigl [2 (\overset{\scriptscriptstyle v}{M}{}^{}_{} {\Lambda })^j (\overset{\scriptscriptstyle w}{M}{}^{}_{}{}^2 {\Lambda })^k - 2 (\overset{\scriptscriptstyle w}{M}{}^{}_{} {\Lambda })^j (\overset{\scriptscriptstyle w}{M}{}^{}_{}{}^2 {\Lambda })^k \\&+2(\overset{\scriptscriptstyle v}{M}{}^{}_{}\overset{\scriptscriptstyle w}{M}{}^{}_{} {\Lambda })^j (\overset{\scriptscriptstyle w}{M}{}^{}_{}{\Lambda })^k - 2(\overset{\scriptscriptstyle w}{M}{}^{}_{}{}^2 {\Lambda })^j (\overset{\scriptscriptstyle w}{M}{}^{}_{}{\Lambda })^k\\&-(\overset{\scriptscriptstyle v}{M}{}^{}_{}{\Lambda })^j (\overset{\scriptscriptstyle w}{M}{}^{}_{}{\Lambda })^k \textrm{tr} (\overset{\scriptscriptstyle w}{M}{}^{}_{}) +(\overset{\scriptscriptstyle w}{M}{}^{}_{}{\Lambda })^j (\overset{\scriptscriptstyle w}{M}{}^{}_{}{\Lambda })^k \textrm{tr} (\overset{\scriptscriptstyle w}{M}{}^{}_{})\bigr ]\bigr ]\\&-(v \,{\leftrightarrow }\, w) \bigr ]-(j\,{\leftrightarrow }\, k)\bigr ] +({\Lambda }\,{\leftrightarrow }\,{\bar{{\Lambda }}}). \end{aligned} \end{aligned}$$

We strike out terms that cancel after antisymmetrization w.r.t.$\ (j\,{\leftrightarrow }\, k)$:

$$\begin{aligned}&\begin{aligned} =&\,\frac{1}{2}\sqrt{\det (v \textrm{Id}-A)}\sqrt{\det (w \textrm{Id}-A)} \cdot \bigl [\bigl [ (w-v)^{-1}\\&\cdot \bigl [2 (\overset{\scriptscriptstyle v}{M}{}^{}_{} {\Lambda })^j (\overset{\scriptscriptstyle w}{M}{}^{}_{}{}^2 {\Lambda })^k + 2(\overset{\scriptscriptstyle v}{M}{}^{}_{}\overset{\scriptscriptstyle w}{M}{}^{}_{} {\Lambda })^j (\overset{\scriptscriptstyle w}{M}{}^{}_{}{\Lambda })^k \\&-(\overset{\scriptscriptstyle v}{M}{}^{}_{}{\Lambda })^j (\overset{\scriptscriptstyle w}{M}{}^{}_{}{\Lambda })^k \textrm{tr} (\overset{\scriptscriptstyle w}{M}{}^{}_{})\bigr ]\\&-(v \,{\leftrightarrow }\, w) \bigr ]-(j\,{\leftrightarrow }\, k)\bigr ] +({\Lambda }\,{\leftrightarrow }\,{\bar{{\Lambda }}}). \end{aligned} \end{aligned}$$

We expand $(v \,{\leftrightarrow }\, w)$ and $(j \,{\leftrightarrow }\, k)$. The sign of the antisymmetrization is caught in the prefactor $(w-v)^{-1}$:

We can now apply $\overset{\scriptscriptstyle v}{M}{}^{}_{} - \overset{\scriptscriptstyle w}{M}{}^{}_{}= (w-v) \overset{\scriptscriptstyle v}{M}{}^{}_{}\overset{\scriptscriptstyle w}{M}{}^{}_{}$ and in the opposite direction as before, pairing terms (1,8), (2,7), (3,6), (4,5), (9,12), (10,11) in the bracket:

(45)

Remark 3.13

(projective case) Performing the same steps on (44) gives

(46)

for the projective scenario.

We have now worked $\overset{\scriptscriptstyle v}{K}{}^{l[j}\nabla _l \nabla _m \overset{\scriptscriptstyle w}{K}{}^{ k] m} - (v \,{\leftrightarrow }\, w)$ into a suitable form. From (39) we now compute $\nabla _m\overset{\scriptscriptstyle v}{K}{}^{l[j}\nabla _l \overset{\scriptscriptstyle w}{K}{}^{ k] m}$:

(47)

In this equation $(j\,{\leftrightarrow }\, k)$ yields the same result as $(v\,{\leftrightarrow }\, w)$.

Remark 3.14

(projective case) By means of (43) the projective analogue of (47) evaluates to

(48)

We see that the right-hand side expression is equal to the right-hand side expression of (46). Thus if we plug (46) and (48) into (35) then both terms cancel each other and (35) is satisfied without even having to carry out the differentiation, concluding the proof of Theorem 2.3. The fact that in the projective case $B^{jk}_{\overset{\scriptscriptstyle v}{I}\ , \overset{\scriptscriptstyle w}{I}}$ vanishes, whereas in the c-projective case $\nabla _j B^{jk}_{\overset{\scriptscriptstyle v}{I}\ , \overset{\scriptscriptstyle w}{I}}$ vanishes but $B^{jk}_{\overset{\scriptscriptstyle v}{I}\ , \overset{\scriptscriptstyle w}{I}}$ does not is the most significant difference between the projective and the c-projective cases.

We now compare (45) and (47): they are the same except that the first is symmetric with respect to $({\Lambda } \,{\leftrightarrow }\, {\bar{{\Lambda }}})$ while the latter is antisymmetric. Subtracting both consequently yields

(49)

It remains to show that (35) is fulfilled, that is to apply $\nabla _j$ to this expression and show that it vanishes. In the computation we use

• the compatibility condition (2),

• Jacobi’s formula for the derivative of the determinant,

• 

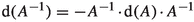
to expand the left-hand side expression of (35). We then immediately strike out terms that vanish individually due to the self-adjointness of A with respect to g and the antisymmetry of J with respect to g:

$$\begin{aligned} \nabla _j\bigl (\overset{\scriptscriptstyle v}{K}{}^{l[j}\nabla _l \nabla _m \overset{\scriptscriptstyle w}{K}{}^{ k] m}{} & {} - (v \,{\leftrightarrow }\, w)-\nabla _m\overset{\scriptscriptstyle v}{K}{}^{l[j}\nabla _l \overset{\scriptscriptstyle w}{K}{}^{ k] m}\bigr )\nonumber \\{} & {} = {}-2 \sqrt{\det (v \textrm{Id}-A)}\sqrt{\det (w \textrm{Id}-A)}\nonumber \\{} & {} \qquad \cdot \bigl [2 g(\overset{\scriptscriptstyle v}{M}{}^{}_{}\overset{\scriptscriptstyle w}{M}{}^{}_{}{\bar{{\Lambda }}}, \overset{\scriptscriptstyle v}{M}{}^{}_{}\overset{\scriptscriptstyle w}{M}{}^{}_{}{\bar{{\Lambda }}}) (\overset{\scriptscriptstyle w}{M}{}^{}_{}{\Lambda }- \overset{\scriptscriptstyle v}{M}{}^{}_{} {\Lambda })^k\nonumber \\{} & {} \qquad \qquad -2 g(\overset{\scriptscriptstyle v}{M}{}^{}_{} \overset{\scriptscriptstyle w}{M}{}^{}_{} {\bar{{\Lambda }}}, \overset{\scriptscriptstyle w}{M}{}^{}_{} {\bar{{\Lambda }}} - \overset{\scriptscriptstyle v}{M}{}^{}_{} {\bar{{\Lambda }}}) (\overset{\scriptscriptstyle v}{M}{}^{}_{} \overset{\scriptscriptstyle w}{M}{}^{}_{} {\Lambda })^k\nonumber \\{} & {} \qquad \qquad +2 g({\bar{{\Lambda }}}, \overset{\scriptscriptstyle v}{M}{}^{}_{} \overset{\scriptscriptstyle w}{M}{}^{}_{} {\bar{{\Lambda }}})\bigr ](\overset{\scriptscriptstyle v}{M}{}^{}_{} \overset{\scriptscriptstyle w}{M}{}^{}_{}(\overset{\scriptscriptstyle w}{M}{}^{}_{}{\Lambda }- \overset{\scriptscriptstyle v}{M}{}^{}_{} {\Lambda }))^k\nonumber \\{} & {} \qquad -2 g({\bar{{\Lambda }}}, \overset{\scriptscriptstyle w}{M}{}^{}_{} {\bar{{\Lambda }}} - \overset{\scriptscriptstyle v}{M}{}^{}_{} {\bar{{\Lambda }}}) (\overset{\scriptscriptstyle v}{M}{}^{}_{}{}^2 \overset{\scriptscriptstyle w}{M}{}^{}_{}{}^2 {\Lambda })^k\nonumber \\{} & {} \qquad + {\bar{\lambda }}_s g^{ls} \overset{\scriptscriptstyle v}{M}{}^{m}_{l} \overset{\scriptscriptstyle w}{M}{}^{t}_{m} \overset{\scriptscriptstyle v}{M}{}^{j}_{t} {\bar{\lambda }}_{p,j} g^{pq} \overset{\scriptscriptstyle w}{M}{}^{k}_{q}\nonumber \\{} & {} \qquad - {\bar{\lambda }}_s g^{ls} \overset{\scriptscriptstyle w}{M}{}^{m}_{l} \overset{\scriptscriptstyle v}{M}{}^{t}_{m} \overset{\scriptscriptstyle w}{M}{}^{j}_{t} {\bar{\lambda }}_{p,j} g^{pq} \overset{\scriptscriptstyle v}{M}{}^{k}_{q}\nonumber \\{} & {} \qquad + {\bar{\lambda }}_s g^{ps} \overset{\scriptscriptstyle v}{M}{}^{j}_{p} {\bar{\lambda }}_{t,j} g^{tr} \overset{\scriptscriptstyle w}{M}{}^{l}_{r} \overset{\scriptscriptstyle v}{M}{}^{m}_{l} \overset{\scriptscriptstyle w}{M}{}^{k}_{m}\nonumber \\{} & {} \qquad - {\bar{\lambda }}_s g^{ps} \overset{\scriptscriptstyle w}{M}{}^{j}_{p} {\bar{\lambda }}_{t,j} g^{tr} \overset{\scriptscriptstyle v}{M}{}^{l}_{r} \overset{\scriptscriptstyle w}{M}{}^{m}_{l} \overset{\scriptscriptstyle v}{M}{}^{k}_{m}\nonumber \\{} & {} \qquad + \textrm{tr} (\overset{\scriptscriptstyle v}{M}{}^{}_{} \overset{\scriptscriptstyle w}{M}{}^{}_{}) \cdot \bigl [g({\bar{{\Lambda }}}, \overset{\scriptscriptstyle v}{M}{}^{}_{} \overset{\scriptscriptstyle w}{M}{}^{}_{} {\bar{{\Lambda }}}) (\overset{\scriptscriptstyle w}{M}{}^{}_{} {\Lambda } - \overset{\scriptscriptstyle v}{M}{}^{}_{} {\Lambda })^k\nonumber \\{} & {} \qquad - g({\bar{{\Lambda }}}, \overset{\scriptscriptstyle w}{M}{}^{}_{} {\bar{{\Lambda }}} - \overset{\scriptscriptstyle v}{M}{}^{}_{} {\bar{{\Lambda }}}) (\overset{\scriptscriptstyle v}{M}{}^{}_{} \overset{\scriptscriptstyle w}{M}{}^{}_{} {\Lambda })^k\nonumber \\{} & {} \qquad + {\bar{\lambda }}_s g^{ps} \overset{\scriptscriptstyle v}{M}{}^{j}_{p} {\bar{\lambda }}_{t,j} g^{tr} \overset{\scriptscriptstyle w}{M}{}^{k}_{r} - {\bar{\lambda }}_s g^{ps} \overset{\scriptscriptstyle w}{M}{}^{j}_{p} {\bar{\lambda }}_{t,j} g^{tr} \overset{\scriptscriptstyle v}{M}{}^{k}_{r}\bigr ]. \end{aligned}$$

(50)

As a consequence of Lemma 3.1 the terms involving second derivatives of $\lambda$ cancel each other out in this expression. The other terms cancel each other out after applying $\overset{\scriptscriptstyle v}{M}{}^{}_{} - \overset{\scriptscriptstyle w}{M}{}^{}_{}= (w-v) \overset{\scriptscriptstyle v}{M}{}^{}_{}\overset{\scriptscriptstyle w}{M}{}^{}_{}$. Thus Theorem 2.2 is proven.

3.3 Addition of potential: Proof of Theorems 2.5 and 2.9

3.3.1 Four equivalent problems

Let (g, J, A) be c-compatible.

Lemma 3.15

Let $K= g^{ij}p_i p_j$,

and

as well as the corresponding differential operators according to the quantization rules stated earlier.

Then the following four problems are equivalent: describe all functions U, $\overset{\scriptscriptstyle t}{U}$, such that

• (1) $\{\overset{\scriptscriptstyle s}{I}+\overset{\scriptscriptstyle s}{U}, K+U\}=0$ and $\{\overset{\scriptscriptstyle s}{I}+\overset{\scriptscriptstyle s}{U}, \overset{\scriptscriptstyle t}{L}\}=0$ for all $t,s \in {\mathbb {R}}$,

• (2) $[\overset{\scriptscriptstyle s}{{\widehat{I}}}+\overset{\scriptscriptstyle s}{{\widehat{U}}}, {\widehat{K}}+{\widehat{U}}]=0$ and $[\overset{\scriptscriptstyle s}{{\widehat{I}}}+\overset{\scriptscriptstyle s}{{\widehat{U}}}, \overset{\scriptscriptstyle t}{{\widehat{L}}}]=0$ for all $t,s \in {\mathbb {R}}$,

• (3) $\{\overset{\scriptscriptstyle s}{I}+\overset{\scriptscriptstyle s}{U}, \overset{\scriptscriptstyle t}{I}+\overset{\scriptscriptstyle t}{U}\}=0$ and $\{\overset{\scriptscriptstyle s}{I}+\overset{\scriptscriptstyle s}{U}, \overset{\scriptscriptstyle t}{L}\}=0$ for all $t,s \in {\mathbb {R}}$,

• (4) $[\overset{\scriptscriptstyle s}{{\widehat{I}}}+\overset{\scriptscriptstyle s}{{\widehat{U}}}, \overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}]=0$ and $[\overset{\scriptscriptstyle s}{{\widehat{I}}}+\overset{\scriptscriptstyle s}{{\widehat{U}}}, \overset{\scriptscriptstyle t}{{\widehat{L}}}]=0$ for all $t,s \in {\mathbb {R}}$.

Proof of Lemma 3.15

To do so, we show that

• i. $\{\overset{\scriptscriptstyle t}{I}+\overset{\scriptscriptstyle t}{U}, K+U\}=0$ for all $t\in {\mathbb {R}}$ $\Leftrightarrow$ $[\overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}, {\widehat{K}}+{\widehat{U}}]=0$ for all $t \in {\mathbb {R}}$ $\Leftrightarrow$ $\overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial U}{\partial x^i}= \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^j}$ for all $t \in {\mathbb {R}}$,

• ii. $\{\overset{\scriptscriptstyle t}{I}+\overset{\scriptscriptstyle t}{U}, K+U\}=0$ for all $t\in {\mathbb {R}} \Leftrightarrow \{\overset{\scriptscriptstyle t}{I}+\overset{\scriptscriptstyle t}{U}, \overset{\scriptscriptstyle s}{I}+\overset{\scriptscriptstyle s}{U}\}=0$ for all $s,t \in {\mathbb {R}}$,

• iii. $\{\overset{\scriptscriptstyle t}{I}+\overset{\scriptscriptstyle t}{U}, \overset{\scriptscriptstyle s}{I}+\overset{\scriptscriptstyle s}{U}\}=0$ for all $s,t \in {\mathbb {R}}$ $\Leftrightarrow$ $[\overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}, \overset{\scriptscriptstyle s}{{\widehat{I}}}+\overset{\scriptscriptstyle s}{{\widehat{U}}}]=0$ for all $s,t \in {\mathbb {R}}$ $\Leftrightarrow$ $\overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle s}{U}}{\partial x^i}={\overset{\scriptscriptstyle s}{K}{}^i_j} \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^i}$ for all $s,t\in {\mathbb {R}}$,

• iv. $\{\overset{\scriptscriptstyle t}{I}+\overset{\scriptscriptstyle t}{U}, \overset{\scriptscriptstyle s}{L}\}=0$ for all $t,s \in {\mathbb {R}}$ $\Leftrightarrow$ $[\overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}, \overset{\scriptscriptstyle s}{{\widehat{L}}}]=0$ for all $t,s \in {\mathbb {R}}$ $\Leftrightarrow$ $\textrm{d}\overset{\scriptscriptstyle t}{U}\ (\overset{\scriptscriptstyle s}{V})=0$ for all $s,t \in {\mathbb {R}}$.

It is implied that all equations are to hold for all choices of its parameters, we shall not specify it each and every time again.

To iii: We use the linearity of the commutator:

$$\begin{aligned}{}[\overset{\scriptscriptstyle s}{{\widehat{I}}}+\overset{\scriptscriptstyle s}{{\widehat{U}}},\overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}] =[\overset{\scriptscriptstyle s}{{\widehat{I}}},\overset{\scriptscriptstyle t}{{\widehat{I}}}]+[\overset{\scriptscriptstyle s}{{\widehat{I}}},\overset{\scriptscriptstyle t}{{\widehat{U}}}]+[\overset{\scriptscriptstyle s}{{\widehat{U}}},\overset{\scriptscriptstyle t}{{\widehat{I}}}]+[\overset{\scriptscriptstyle s}{{\widehat{U}}},\overset{\scriptscriptstyle t}{{\widehat{U}}}]. \end{aligned}$$

(51)

The term $[\overset{\scriptscriptstyle s}{{\widehat{I}}},\overset{\scriptscriptstyle t}{{\widehat{I}}}]$ vanishes due to Theorem 2.2 and $[\overset{\scriptscriptstyle s}{{\widehat{U}}},\overset{\scriptscriptstyle t}{{\widehat{U}}}]$ vanishes trivially since the operators corresponding to the potentials act merely by multiplication. In [7] or by direct computation we have $[\overset{\scriptscriptstyle s}{{\widehat{I}}},\overset{\scriptscriptstyle t}{{\widehat{U}}}] = \widehat{\{\overset{\scriptscriptstyle s}{I}, \overset{\scriptscriptstyle t}{U}\}}$. Consequently $[\overset{\scriptscriptstyle s}{{\widehat{I}}}+\overset{\scriptscriptstyle s}{{\widehat{U}}},\overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}]= \widehat{\{\overset{\scriptscriptstyle s}{I}, \overset{\scriptscriptstyle t}{U}\}}+\widehat{\{\overset{\scriptscriptstyle s}{U}, \overset{\scriptscriptstyle t}{I}\}}$. Since quantization is a linear map and only the zero polynomial is mapped to a vanishing differential operator, we have that $[\overset{\scriptscriptstyle s}{{\widehat{Q}}},\overset{\scriptscriptstyle t}{{\widehat{Q}}}]=0$ if and only if $\{\overset{\scriptscriptstyle s}{I}, \overset{\scriptscriptstyle t}{U}\}+\{\overset{\scriptscriptstyle s}{U}, \overset{\scriptscriptstyle t}{I}\}=0$. This in turn is true if and only if $\{\overset{\scriptscriptstyle s}{I}, \overset{\scriptscriptstyle t}{U}\}^\#+\{\overset{\scriptscriptstyle s}{U}, \overset{\scriptscriptstyle t}{I}\}^\#=0$. Expressing this in terms of $\overset{\scriptscriptstyle t}{K}, \overset{\scriptscriptstyle t}{U}, \overset{\scriptscriptstyle s}{K}, \overset{\scriptscriptstyle s}{U}$ and lowering an index and rearranging terms yields $\overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle s}{U}}{\partial x^i}=\overset{\scriptscriptstyle s}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^i}$. Likewise using the fact that $\{\overset{\scriptscriptstyle s}{I}, \overset{\scriptscriptstyle t}{I}\}=0$, we have $\{\overset{\scriptscriptstyle t}{I}+\overset{\scriptscriptstyle t}{U}, \overset{\scriptscriptstyle s}{I}+\overset{\scriptscriptstyle s}{U}\}= \{\overset{\scriptscriptstyle s}{I}, \overset{\scriptscriptstyle t}{U}\}+\{\overset{\scriptscriptstyle s}{U}, \overset{\scriptscriptstyle t}{I}\}$.

Statement i can be seen analogously to iii, since K lies in the span of $\overset{\scriptscriptstyle t}{K}$.

To ii: It suffices to show the equivalence of the rightmost equations of items i and iii: Fix an arbitrary value for t in $\overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle s}{U}}{\partial x^i}=\overset{\scriptscriptstyle s}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^i}$ and choose pairwise different values $(s_1,\ldots , s_n)$ for s. Add the resulting equations, weighting the $i\textrm{th}$ equation with $(-1)^{n-1} \mu _{n-1}({\widehat{s}}_i) / { \prod _{i \ne j}(s_i-s_j)}$. Here $\mu _{n-1}({\widehat{s}}_i)$ is the elementary symmetric polynomial of degree $n-1$ in the variables $(s_1,\ldots ,s_{i-1},s_{i+1},\ldots , s_n)$. On the right-hand side this gives the coefficient of $s^{n-1}$ of $\overset{\scriptscriptstyle s}{K}$ which is the identity operator (when considered as a (1,1)-tensor) acting on the differential of $\overset{\scriptscriptstyle t}{U}$. On the left hand side we identify the sum $\sum _{i=1}^{n}(-1)^{n-1} \mu _{n-1}({\widehat{s}}_i)/\bigl ( \prod _{i \ne j}(s_i-s_j)\bigr ) \frac{\partial \overset{s_i}{U}}{\partial x^i}$ with the differential of U and thus arrive at $\overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial U}{\partial x^i}= \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^j}$. For the other direction, consider two arbitrary values s and t and the equations

(52)

We muliply the first equation with $\overset{\scriptscriptstyle s}{K}{}^j_k$, and use the commutativity of $\overset{\scriptscriptstyle t}{K}$ with $\overset{\scriptscriptstyle s}{K}$ (again considered as mapping one-forms to one-forms):

$$\begin{aligned} \overset{\scriptscriptstyle t}{K}{}^j_k\overset{\scriptscriptstyle s}{K}{}^i_j \frac{\partial U}{\partial x^i}= \overset{\scriptscriptstyle s}{K}{}^j_k\frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^j}. \end{aligned}$$

(53)

Now we can use the second equation of (52) to replace $\overset{\scriptscriptstyle s}{K}{}^i_j \frac{\partial U}{\partial x^i}$ with $\frac{\partial \overset{\scriptscriptstyle s}{U}}{\partial x^j}$ arriving back at $\overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle s}{U}}{\partial x^i}=\overset{\scriptscriptstyle s}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^i}$, as we desired.

To iv: Whenever one applies the quantization rules (9) to a linear polynomial $\overset{\scriptscriptstyle s}{L}$ and a polynomial $\overset{\scriptscriptstyle t}{I}$ of second degree in the momentum variables on $T^* {\mathscr {M}}$ and takes the commutator of the operators, then combining equations (3.8) and (3.9) from [7] gives us the formula

$$\begin{aligned} \begin{aligned}{}[\overset{\scriptscriptstyle t}{{\widehat{I}}}, \overset{\scriptscriptstyle s}{{\widehat{L}}}] = i \widehat{\{\overset{\scriptscriptstyle t}{I}, \overset{\scriptscriptstyle s}{L}\ \}}- \frac{i}{2} \,\nabla _j \bigl (\overset{\scriptscriptstyle t}{K}{}^{jk} \nabla _k (\nabla _l \overset{\scriptscriptstyle s}{V}{}^l)\bigr ). \end{aligned} \end{aligned}$$

(54)

It can be obtained via explicit calculation. The second term on the right-hand side of (54) acts on functions by mere multiplication. It vanishes in our case because $\overset{\scriptscriptstyle t}{V}$ is a Killing vector field and thus divergence free. To show that the first term on the right-hand side of (54) vanishes we use that . So, we must show that $\{\overset{\scriptscriptstyle t}{I}, \overset{\scriptscriptstyle s}{V}\}^\#$ vanishes in order for $\widehat{\{\overset{\scriptscriptstyle t}{I}, \overset{\scriptscriptstyle s}{L}\ \}}$ to vanish. Inspection of the components of $\{\overset{\scriptscriptstyle t}{I}, \overset{\scriptscriptstyle s}{L}\}^\#$ reveals that they are simply the components of the Lie derivative of $\overset{\scriptscriptstyle t}{K}$ with respect to $\overset{\scriptscriptstyle t}{V}$:

$$\begin{aligned} (\{\overset{\scriptscriptstyle t}{I}, \overset{\scriptscriptstyle s}{V}\}^\#)^{jk} = {\overset{\scriptscriptstyle s}{V}{}^i} \partial _i {\overset{\scriptscriptstyle t}{K}{}^{jk}} - \partial _i ( {\overset{\scriptscriptstyle s}{V}{}^j} ) {\overset{\scriptscriptstyle t}{K}{}^{ik}} - \partial _i ( {\overset{\scriptscriptstyle s}{V}{}^k} ) {\overset{\scriptscriptstyle t}{K}{}^{ji}} = ({\mathscr {L}}_{\overset{\scriptscriptstyle s}{V}} \overset{\scriptscriptstyle t}{K})^{jk}. \end{aligned}$$

Applying the Leibniz rule gives

From this we see that, since the flow of $\overset{\scriptscriptstyle s}{V}$ preserves A (and thus $\det A$ and functions thereof) [3, Lemma 2.2] and since $\overset{\scriptscriptstyle s}{V}$ also is a Killing vector field, the term $\widehat{\{\overset{\scriptscriptstyle t}{I}, \overset{\scriptscriptstyle s}{V}\}}$ in (54) vanishes. Using this, a direct calculation immediately reveals that both $\{\overset{\scriptscriptstyle t}{I}+\overset{\scriptscriptstyle t}{U}, \overset{\scriptscriptstyle s}{L}\}=0$ and $[\overset{\scriptscriptstyle t}{{\widehat{I}}}+\overset{\scriptscriptstyle t}{{\widehat{U}}}, \overset{\scriptscriptstyle s}{{\widehat{L}}}]=0$ reduce to the same expression, namely $\textrm{d}\overset{\scriptscriptstyle t}{U} (\overset{\scriptscriptstyle s}{V})=0$ for all $s,t \in {\mathbb {R}}$. $\square$

Lemma 3.16

Let (g, J, A) be c-compatible and $\overset{\scriptscriptstyle t}{K}$ be defined as in (5). Consider a simply connected domain where the number of different eigenvalues of A is constant. Let A be semi-simple. Let $\overset{\textrm{nc}}{E}=\{\varrho _1, \ldots , \varrho _r\}$ be the set of non-constant eigenvalues of A. Let $\overset{\textrm{c}}{E}=\{\varrho _{r+1}, \ldots , \varrho _{r+R}\}$ be the set of constant eigenvalues and $E=\overset{\textrm{nc}}{E}\cup \overset{\textrm{c}}{E}$. Denote by $m(\varrho _i)$ the algebraic multiplicity of $\varrho _i$. Let U be a function such that $\overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial U}{\partial x^i}$ is exact for all values of t and let $\overset{\scriptscriptstyle t}{U}$ be such that

$$\begin{aligned} \overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial U}{\partial x^i}= \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^j} \end{aligned}$$

(55)

is satisfied for all values of t. Then up to addition of a function of the single variable t the family of functions $\overset{\scriptscriptstyle t}{U}(t,x)$ may be written as

$$\begin{aligned} \overset{\scriptscriptstyle t}{U}=\prod _{\varrho _l \in \overset{\textrm{c}}{E}}^{} (t-\varrho _l)^{m(\varrho _l) /2-1}\,\overset{\scriptscriptstyle t}{{\widetilde{U}}} \end{aligned}$$

(56)

where $\overset{\scriptscriptstyle t}{{\widetilde{U}}}$ is a polynomial of degree $r-1$ in t. Equally $\overset{\scriptscriptstyle t}{U}$ can be written as

$$\begin{aligned} \overset{\scriptscriptstyle t}{U}=\sum _{i=1}^{r+R} \prod _{\varrho _l \in E\setminus \{\varrho _i\}}^{} \frac{(t-\varrho _l)^{m(\varrho _l)/2}}{(\varrho _i-\varrho _l)^{m(\varrho _l)/2}}\, (t-\varrho _i)^{m(\varrho _i)/2-1} f_i \end{aligned}$$

(57)

where $f_i$ are functions on ${\mathscr {M}}$. The functions $f_i$ may however not be chosen arbitrarily.

Proof of Lemma 3.16

Because we assumed that A is semi-simple, we can factorize $\overset{\scriptscriptstyle t}{K}$ into ${\overset{\scriptscriptstyle t}{K}=\prod _{l=1}^{r+R} (t-\varrho _l) ^{m_l/2-1} \overset{\scriptscriptstyle t}{{\widetilde{K}}}}$, with $\overset{\scriptscriptstyle t}{{\widetilde{K}}}$ being a polynomial of degree $r+R-1$.

$$\begin{aligned} \prod _{\varrho _l \in \overset{\textrm{c}}{E}}^{} (t-\varrho _l) ^{m(\varrho _l)/2-1} \overset{\scriptscriptstyle t}{{\widetilde{K}}}{}^i_j \frac{\partial U}{\partial x^i} =\frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^i} \quad \text {for all}\;\; t\in {\mathbb {R}}. \end{aligned}$$

(58)

We used that for the non-constant eigenvalues $\varrho _1, \ldots , \varrho _r$ the multiplicities are 2 [3, Lemma 2.2]. Thus in the product on the left-hand side all factors corresponding to non-constant eigenvalues are equal to 1. We observe that upon addition of a function of the single variable t to $\overset{\scriptscriptstyle t}{U}$ the equation above is still satisfied. This allows us to choose an arbitrary point $x_0$ and an arbitrary function $U_0 (t)$ and assume that $\overset{\scriptscriptstyle t}{U}(x_0,t)=U_0 (t)$. Since the left-hand side of (58) is a polynomial in t and is exact for all t, each of the coefficients must be exact. This allows us to integrate the terms of (58) individually:

(59)

The last step of this calculation makes use of the fact that if $\varrho _l$ is of multiplicity $m_l \geqslant 4$ then $\varrho _l$ is constant [3, Lemma 2.2]. The integral is meant to be taken along any path connecting $x_0$ and x and the ${\widetilde{K}}_{(i)}$ is the coefficient of $t^i$ in $\overset{\scriptscriptstyle t}{{\widetilde{K}}}$. Again $\overset{\scriptscriptstyle t}{{\widetilde{K}}}$ and ${\widetilde{K}}_{(i)}$ are considered as (1, 1) tensors mapping one-forms to one-forms. So for any value of t the value of $\overset{\scriptscriptstyle t}{U}$ at x is uniquely defined by its value at $x_0$ and the function U. Formula (59) proves the claim that $\overset{\scriptscriptstyle t}{U}$ can be written in the form (56) where on the right-hand side $U_0(t)$ takes the role of the possible addition of a function of t alone. Evidently, we have $\overset{\scriptscriptstyle t}{{\widetilde{U}}}(x)=\sum _{i=0}^{r+R} t^i \int _{x_0}^{x}{\widetilde{K}}_{(i)}(\textrm{d}U)$. Since $\overset{\scriptscriptstyle t}{{\widetilde{U}}}$ is a polynomial of degree $r+R-1$ it is uniquely defined by its values at the $r+R$ different eigenvalues of A. Via the Lagrange interpolation formula we have

$$\begin{aligned} \overset{\scriptscriptstyle t}{{\widetilde{U}}}=\sum _{i=1}^{r+R} \prod _{\varrho _l \in E\setminus \{\varrho _i\}}^{} \frac{(t-\varrho _l)}{(\varrho _i-\varrho _l)} \,{\tilde{f}}_i \end{aligned}$$

(60)

for some functions ${\tilde{f}}_i$. Introducing $f_i=\prod _{\varrho _l \in E\setminus \{\varrho _i\}} (\varrho _i-\varrho _l)^{m(\varrho _l)/2 -1} {\tilde{f}}_i$ the potential U can be written as

$$\begin{aligned} \overset{\scriptscriptstyle t}{U}=\sum _{i=1}^{r+R} \prod _{\varrho _l \in E\setminus \{\varrho _i\}}^{} \frac{(t-\varrho _l)^{m(\varrho _l)/2}}{(\varrho _i-\varrho _l)^{m(\varrho _l)/2}}\, (t-\varrho _i)^{m(\varrho _i)/2-1} f_i \end{aligned}$$

(61)

concluding the proof of Lemma 3.16. $\square$

Lemma 3.17

Let (g, J, A) be c-compatible and $\overset{\scriptscriptstyle t}{K}$ as in (5). Let A be semi-simple. Let $\overset{\textrm{nc}}{E}=\{\varrho _1, \ldots , \varrho _r\}$ be the set of non-constant eigenvalues of A. Let $\overset{\textrm{c}}{E}=\{\varrho _{r+1}, \ldots , \varrho _{r+R}\}$ be the set of constant eigenvalues and $E=\overset{\textrm{nc}}{E}\cup \overset{\textrm{c}}{E}$. The multiplicity of $\varrho _l$ is denoted by $m(\varrho _l)$. Let

$$\begin{aligned} \overset{\scriptscriptstyle t}{U}=\sum _{i=1}^{r+R} \prod _{\varrho _l \in E\setminus \{\varrho _i\}}^{} \frac{(t-\varrho _l)^{m(\varrho _l)/2}}{(\varrho _i-\varrho _l)^{m(\varrho _l)/2}}\, (t-\varrho _i)^{m(\varrho _i)/2-1} f_i \end{aligned}$$

(62)

and let

$$\begin{aligned} \overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial U}{\partial x^i}= \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^j} \end{aligned}$$

(63)

be satisfied for all values of t. Then for all values of i the relation must be satisfied. In other words: The differentials of the functions $f_i$ are eigenvectors of A with eigenvalues $\varrho _i$, where A is considered as to map one-forms to one-forms.

Proof of Lemma 3.17

We consider $\overset{\scriptscriptstyle t}{K}$ as a (1, 1) tensor field. Using our assumption that A is semi-simple we rewrite equation (63) in terms of the quantities $\overset{\scriptscriptstyle t}{{\widetilde{U}}}$, $\tilde{f_i}$ and $\overset{\scriptscriptstyle t}{{\widetilde{K}}}$ defined by

Then we use the fact that eigenvalues of multiplicity $m_l \geqslant 4$ are constant [3, Lemma 2.2] and equation (63) transforms into

$$\begin{aligned} \overset{\scriptscriptstyle t}{{\widetilde{K}}} (\textrm{d}U) = \textrm{d}\overset{\scriptscriptstyle t}{{\widetilde{U}}} \end{aligned}$$

(64)

by dividing out the common factors.

The right-hand side can be rewritten: consider $\overset{\scriptscriptstyle t}{{\widetilde{U}}}$ where, rather than choosing a constant value for the parameter t we fill in the $l\textrm{th}$ eigenvalue of A. Then we have $\overset{\varrho _l}{{\widetilde{U}}}= {\tilde{f}}_l$. Taking the differential and rearranging the terms gives

$$\begin{aligned} \textrm{d}{\tilde{f}}_l - \frac{\partial \overset{\scriptscriptstyle t}{{\widetilde{U}}}}{\partial t}\bigg |_{t=\varrho _l} \textrm{d}\varrho _l =\textrm{d}\overset{\varrho _l}{{\widetilde{U}}} - \frac{\partial \overset{\scriptscriptstyle t}{{\widetilde{U}}}}{\partial t}\bigg |_{t=\varrho _l} \textrm{d}\varrho _l = \textrm{d}\overset{\scriptscriptstyle t}{{\widetilde{U}}}|_{t=\varrho _l}. \end{aligned}$$

(65)

We evaluate (64) at $t=\varrho _l$ and plug in (65):

$$\begin{aligned} \overset{\varrho _l}{{\widetilde{K}}} (\textrm{d}U)= \textrm{d}{\tilde{f}}_l - \frac{\partial \overset{\scriptscriptstyle t}{{\widetilde{U}}}}{\partial t}\bigg |_{t=\varrho _l} \textrm{d}\varrho _l. \end{aligned}$$

(66)

Because we assumed A to be semi-simple we can decompose $\textrm{d}U$ into one-forms $\upsilon _l$ such that . From the definition of $\overset{\scriptscriptstyle t}{{\widetilde{K}}}$ we have that , again because we assumed A to be semi-simple. Evaluating at $t=\varrho _k$ yields

(67)

In particular this means that if $k\ne l$ then $\overset{\varrho _k}{{\widetilde{K}}}(\textrm{d}\varrho _l)$ is zero. Plugging this into 66 we get that on the left hand side only $\overset{\varrho _l}{{\widetilde{K}}}(\textrm{d}U)=\overset{\varrho _l}{{\widetilde{K}}}(\upsilon _l)$, which we express via (67):

(68)

Since [3, Lemma 2.2] and we have that . The way in which ${\tilde{f}}_l$ was constructed then implies , concluding the proof of Lemma 3.17.$\square$

Lemma 3.18

Let (g, J, A) be c-compatible, $\overset{\scriptscriptstyle t}{K}$ as in (5) and $\overset{\scriptscriptstyle t}{V}$ as in (7). $\overset{\textrm{nc}}{E}= \{\varrho _1, \ldots , \varrho _r\}$ denotes the set of non-constant eigenvalues of A. $\overset{\textrm{c}}{E}=\{\varrho _{r+1}, \ldots , \varrho _{r+R}\}$ denotes the set of constant eigenvalues and $E=\overset{\textrm{nc}}{E}\cup \overset{\textrm{c}}{E}$. The multiplicity of $\varrho _l$ is denoted by $m(\varrho _l)$. Let

$$\begin{aligned} \overset{\scriptscriptstyle t}{U}=\sum _{i=1}^{r+R} \prod _{\varrho _l \in E\setminus \{\varrho _i\}}^{} \frac{(t-\varrho _l)^{m(\varrho _l)/2}}{(\varrho _i-\varrho _l)^{m(\varrho _l)/2}}\, (t-\varrho _i)^{m(\varrho _i)/2-1} f_i. \end{aligned}$$

(69)

Let furthermore for all values of $l=1, \ldots , r+R$. Let $\textrm{d}\overset{\scriptscriptstyle t}{U}\ (\overset{\scriptscriptstyle s}{V})=0$ be satisfied for all values of $s,t \in {\mathbb {R}}$. Then $\textrm{d}\overset{\scriptscriptstyle t}{U} (\overset{\scriptscriptstyle s}{V})=0$ is satisfied for all values of $s,t \in {\mathbb {R}}$ if and only if for each eigenvalue $\varrho _k$ of A the differential $\textrm{d}f_k$ is proportional to $\textrm{d}\varrho _k$ at all points where $\textrm{d}\varrho _k \ne 0$.

Corollary 3.19

If $\varrho _l$ is a non-constant real eigenvalue and $\textrm{d}\varrho _l\ne 0$ in the neighbourhood of a given point then locally $f_l$ can be expressed as a smooth function of $\varrho _l$. Likewise if $\varrho _l$ is a non-constant complex eigenvalue and $\textrm{d}\varrho _l\ne 0$ in the neighbourhood of a given point then locally $f_l$ can be expressed as a holomorphic function of $\varrho _l$.

Proof of Lemma 3.18

The condition $\textrm{d}\overset{\scriptscriptstyle t}{U} (\overset{\scriptscriptstyle s}{V})=0$ for all $s,t\in {\mathbb {R}}$ is equivalent to , because . From (69) we see that $\textrm{d}\overset{\scriptscriptstyle t}{U}$ involves (with some coefficients) only the differentials of the eigenvalues of A and the differentials of the functions $f_i$. Thus $\textrm{d}\overset{\scriptscriptstyle t}{U}(J \textrm{grad}\, \varrho _i)$ is a linear combination of $\textrm{d}\varrho _j$ and $\textrm{d}f_j$ applied to $J \textrm{grad}\, \varrho _i$. But $\textrm{d}\varrho _j (J \textrm{grad}\, \varrho _i)$ is zero for all values of i, j: if $i=j$, then $\textrm{d}\varrho _j (J \textrm{grad}\, \varrho _i)=0$ due to the fact that J is antisymmetric with respect to g and if $i\ne j$ then $\textrm{d}\varrho _j (J \textrm{grad}\, \varrho _i)=0$, because A is g-self-adjoint and $\textrm{grad}\, \varrho _i$ and $\textrm{grad}\, \varrho _j$ are eigenvectors of A with different eigenvalues. Thus $\textrm{d}\overset{\scriptscriptstyle t}{U}(J \textrm{grad}\, \varrho _i)$ is a linear combination of $\{\textrm{d}f_j (J \textrm{grad}\, \varrho _i), j=1,\ldots , r+R\}$. But because we assumed that for all l, and because $A \textrm{grad}\, \varrho _i = \varrho _i \textrm{grad}\,\varrho _i$ [3, Lemma 2.2] and A commutes with J and is g-self-adjoint we get that $\textrm{d}\overset{\scriptscriptstyle t}{U}(J\textrm{grad}\,\varrho _i)$ is some coefficient times $\textrm{d}f_i(J \textrm{grad}\,\varrho _i)$.

From (69) we see that this coefficient is

$$\begin{aligned} \prod _{\varrho _l \in E\setminus \{\varrho _i\}}^{} \frac{(t-\varrho _l)^{m(\varrho _l)/2}}{(\varrho _i-\varrho _l)^{m(\varrho _l)/2}} \,(t-\varrho _i)^{m(\varrho _i)/2-1}. \end{aligned}$$

But for a given value of t this can only vanish at points on ${\mathscr {M}}$ where t is equal to an eigenvalue of A. So at each point on the manifold we can choose a value for t such that this expression is non-zero and thus $\textrm{d}f_i (J\textrm{grad}\,\varrho _i)$ must vanish for all values of i. If we consider a value i such that $\varrho _i$ is constant then $\textrm{d}f_i (J\textrm{grad}\, \varrho _i)=0$ is trivially satisfied. If $\varrho _i$ is non-constant then its multiplicity is 2 [3, Lemma 2.2] and at all points where $\textrm{d}\varrho _i \ne 0$ the set $\{\textrm{grad}\, \varrho _i, J\textrm{grad}\,\varrho _i\}$ is an orthogonal basis of the $\varrho _i$-eigenspace of A. It follows that at such points $\textrm{d}f_i$ may be written as a linear combination of $\textrm{d}\varrho _i$ and . Plugging this decomposition into $\textrm{d}f_i (J\textrm{grad}\, \varrho _i)=0$ we conclude that $\textrm{d}f_i$ is proportional to $\textrm{d}\varrho _i$ at all points where $\textrm{d}\varrho _i\ne 0$ and Lemma 3.18 is proven. $\square$

Lemma 3.20

Let (g, J, A) be c-compatible. $\overset{\textrm{nc}}{E}=\{\varrho _1, \ldots , \varrho _r\}$ denotes the set of non-constant eigenvalues of A. $\overset{\textrm{c}}{E}=\{\varrho _{r+1}, \ldots , \varrho _{r+R}\}$ denotes the set of constant eigenvalues and $E=\overset{\textrm{nc}}{E}\cup \overset{\textrm{c}}{E}$. The multiplicity of $\varrho _l$ is denoted by $m(\varrho _l)$. Let

$$\begin{aligned} \overset{\scriptscriptstyle t}{K}{}^{ij} \overset{\textrm{def}}{=}\sqrt{\det (t \textrm{Id} - A)}\, {(t\textrm{Id}-A)^{-1}}^i_l \,g^{lj}, \quad \overset{\scriptscriptstyle t}{V}{}^j = J^j_k g^{ki} \nabla _i \sqrt{\det (t \textrm{Id} -A)} \end{aligned}$$

and

$$\begin{aligned} \overset{\scriptscriptstyle t}{U}=\sum _{i=1}^{r+R} \prod _{\varrho _l \in E\setminus \{\varrho _i\}}^{} \frac{(t-\varrho _l)^{m(\varrho _l)/2}}{(\varrho _i-\varrho _l)^{m(\varrho _l)/2}}\, (t-\varrho _i)^{m(\varrho _i)/2-1} f_i \end{aligned}$$

(70)

with for all $l=1,\ldots , r$ and $\textrm{d}f_l$ proportional to $\textrm{d}\varrho _l$ for all l for which $\varrho _l$ is non-constant.

Then

$$\begin{aligned} \overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle s}{U}}{\partial x^i} = \overset{\scriptscriptstyle s}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^i}\quad \text {for all}\;\; s,t \in {\mathbb {R}}\quad \text {and} \quad \textrm{d}\overset{\scriptscriptstyle t}{U}\ (\overset{\scriptscriptstyle s}{V})=0\quad \text {for all}\;\; s,t \in {\mathbb {R}}. \end{aligned}$$

(71)

Proof of Lemma 3.20

$\textrm{d}\overset{\scriptscriptstyle t}{U}\ (\overset{\scriptscriptstyle s}{V})=0$ for all $s,t \in {\mathbb {R}}$ is fulfilled because $\textrm{d}f_i$ and $\textrm{d}\varrho _i$ evaluate to zero when applied to $J \textrm{grad}\,\varrho _j$ for all $i,j=1,\ldots , r+R$.

To see $\overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle s}{U}}{\partial x^i} = \overset{\scriptscriptstyle s}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^i}$, we compute $\textrm{d}\overset{\scriptscriptstyle t}{U}$ using the fact that non-constant eigenvalues of A are of multiplicity 2 [3, Lemma 2.2]:

(72)

Considering $\overset{\scriptscriptstyle s}{K}$ as a (1, 1)-tensor mapping one-forms to one-forms and using that for all $i=1, \ldots , r$: and we have

(73)

Again we consider $\overset{\scriptscriptstyle s}{K}$ as a (1, 1)-tensor acting on the differential of $\overset{\scriptscriptstyle t}{U}$. By combining (72) and (73) and using that the non-constant eigenvalues have multiplicity 2 we get

(74)

The right-hand side is apparently symmetric when exchanging s and t and as a consequence $\overset{\scriptscriptstyle t}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle s}{U}}{\partial x^i}=\overset{\scriptscriptstyle s}{K}{}^i_j \frac{\partial \overset{\scriptscriptstyle t}{U}}{\partial x^i}$ is fulfilled, concluding the proof of Lemma 3.20.$\square$

Proof of Theorem 2.5

The theorem results as a combination of the proofs of Lemmata 3.15 and 3.20.$\square$

Proof of Theorem 2.9

Combining the proofs of Lemmata 3.15, 3.16, 3.17, 3.18 and 3.20.$\square$

3.4 Proof of Theorem 2.16: common eigenfunctions

We first show that $\psi$ is an eigenfunction of $\overset{\scriptscriptstyle s}{{\widehat{L}}}$ for all values of s if and only if it is an eigenfunction of $\partial _{t_i}$ for all values of i. A direct computation from (19), (20), (21) shows that

(75)

Now suppose that $\psi$ is an eigenfunction of $\overset{\scriptscriptstyle s}{{\widehat{L}}}$ for all values of s and denote the eigenvalue by $\overset{\scriptscriptstyle s}{\omega }$. Then $\overset{\scriptscriptstyle s}{\omega }$ must be a polynomial in s of degree $r+R-1$, because $\overset{\scriptscriptstyle s}{{\widehat{L}}}$ is a polynomial in s of degree $r+R-1$. From the equation above we see that $\overset{\scriptscriptstyle s}{\omega }$ must have a zero of order $m(\varrho _p)/2$ at $s=\varrho _p$ for all constant eigenvalues $\varrho _p$. Thus we can write $\overset{\scriptscriptstyle s}{\omega }=\prod _{\varrho _p \in \overset{\textrm{c}}{E}}^{}(s-\varrho _p)^{m(\varrho _p)/2}\sum _{q=1}^{r} s^{r-q} i \omega _q$. But because polynomials are equal if and only if all their coefficients are equal we get that $\overset{\scriptscriptstyle s}{{\widehat{L}}} \psi = \overset{\scriptscriptstyle s}{\omega }$ for all $s \in {\mathbb {R}}$ if and only if $i \partial _{t_q} \psi = \omega _q \psi$ for $q=1, \ldots , r$.

To obtain the other separated equations we work with the family of second order differential operators $\overset{\scriptscriptstyle s}{K}$. Since the metric is not given in terms of the coordinate basis and the one-forms $\alpha$ and $\vartheta$ are not unique it poses an obstruction to using the standard formula for the Laplacian and $\overset{\scriptscriptstyle t}{{\widehat{K}}}$. The workaround is quick and simple though.

Let $\{X_i, i=1,\ldots , n\}$ be a set of n linearly independent differentiable vector fields on a manifold ${\mathscr {M}}^n$ and denote by its dual basis, i.e. $\beta ^i (X_j) = \delta ^i_j$. We shall denote by T the matrix relating the coordinate vector fields $\partial _i$ and the vector fields $X_i$: $T^i_j X_i = \partial _j$. Then for an arbitrary symmetric (2, 0)-tensor the following formula is easily obtained via the product rule for partial derivatives:

$$\begin{aligned} \begin{aligned} \frac{1}{\sqrt{|{\det g} |}} \,\partial _i \sqrt{|{\det g} |} \,\overset{\scriptscriptstyle s}{K}{}^{ij} \partial _j&= \frac{\det T}{\sqrt{| {\det g} |}}\, X_s\, \frac{\sqrt{| {\det g} |}}{\det T}\, T^s_i \overset{\scriptscriptstyle s}{K}{}^{ij} T^k_j X_j \\&\quad - X_s(T^s_i) \overset{\scriptscriptstyle s}{K}{}^{ij} T^k_j X_k + \frac{X_s(\det T)}{\det T}\, T^s_i \overset{\scriptscriptstyle s}{K}{}^{ij} T^k_j X_j \end{aligned} \end{aligned}$$

(76)

where on the right-hand side the X’s are to be interpreted as the directional derivative in the sense $X_s = (T^{-1})^i_s\, \partial _i$ and in the last two terms is meant as to only act on the expression in the parentheses.

The quantity $\frac{\det g}{\det T^2}$ is simply the determinant of the matrix with $(i,j)\textrm{th}$ component $g(X_i,X_j)$ and $T^s_i \overset{\scriptscriptstyle s}{K}{}^{ij} T^k_j$ are the components of in the basis $\{X_i, i=1,\ldots , n\}$. If $\{X_i,i = 1,\ldots , n\}$ are the coordinate vector fields belonging to some coordinate system then the last two terms cancel out and one arrives at the well-known fact that the left-hand side expression is independent of the choice of coordinates.

In our case we choose $(X_i) = \bigl (\partial _{\chi _i}, \partial _{t_i}, \partial _{\overset{\scriptscriptstyle \gamma }{y}_i} - \sum _{p=1}^{r} \overset{\scriptscriptstyle \gamma }{\alpha }_{pi} \partial _{t_p}\bigr )$. The dual basis consists of the one-forms $(\textrm{d}\chi _i, \textrm{d}t_i + \alpha _i , \textrm{d}\overset{\scriptscriptstyle \gamma }{y}_i)$. Taking i as the column index and j as the row index we have the components $T^i_j$ given by

$$\begin{aligned} \left( \begin{array}{c|c|c} \textrm{Id} &{} 0 &{} 0\\ \hline 0 &{} \textrm{Id} &{} 0 \\ \hline 0 &{} * &{} \textrm{Id} \end{array} \right) , \end{aligned}$$

where the $*$-block contains the components of $\alpha _l$ as the $l\textrm{th}$ column and the $\textrm{Id}$-blocks are of dimensions equal to the number of $\chi$-, t- and y-coordinates.

From this we can conclude that $X_s (T^s_i)= (T^{-1})^j_s \partial _j T^s_i=0$ because the one-forms $\alpha$ do not depend on the t-variables. Furthermore, $\det T=1$ and thus $X_s(\det T)=0$ for all values of s.

For our specific case (76) simplifies to

$$\begin{aligned} \begin{aligned} \frac{1}{\sqrt{|{\det g} |}}\, \partial _i \sqrt{|{\det g} |}\, \overset{\scriptscriptstyle s}{K}{}^{ij} \partial _j = \frac{\det T}{\sqrt{| {\det g} |}}\, X_s \,\frac{\sqrt{| {\det g} |}}{\det T}\, T^s_i \overset{\scriptscriptstyle s}{K}{}^{ij} T^k_j X_j . \end{aligned} \end{aligned}$$

(77)

Here $\frac{\sqrt{|{\det g}|}}{\det T}$ is the determinant of the matrix of g in the basis $(\textrm{d}\chi _i, \textrm{d}t_i, \textrm{d}\overset{\scriptscriptstyle \gamma }{y_i})$ and $T^s_i K^{ij} T^k_j$ is the matrix of in the basis $(X_i)$. These quantities can be obtained from the formulae (19), (20) and (21). We can then express the vector fields $(X_i)$ in terms of the coordinate basis to get the following result (we use that $A_\gamma = \varrho _{\gamma } \textrm{Id}$, because we assumed that A is semi-simple and that all constant eigenvalues are real):

$$\begin{aligned}&\nabla _i \overset{\scriptscriptstyle s}{K}{}^{ij} \nabla _j = \frac{1}{\sqrt{|{\det g} |}}\, \partial _i \sqrt{|{\det g} |} \, \overset{\scriptscriptstyle s}{K}{}^{ij} \partial _j\nonumber \\&=\sum _{\varrho _k \in \overset{\textrm{nc}}{E}}^{} \frac{\prod _{\varrho _l \in \overset{\text {}}{E}\setminus \{\varrho _k\}} (s-\varrho _l)^{m(\varrho _l)/2}}{\varepsilon _k {\Delta }_k \prod _{\varrho _\gamma \in \overset{\textrm{c}}{E}}^{} (\varrho _\gamma - \varrho _k)^{m(\varrho _\gamma )/2} \varrho _k'}\, \partial _{\chi _k} \varrho _k' \prod _{\varrho _\gamma \in \overset{\textrm{c}}{E}}\! (\varrho _\gamma - \varrho _k)^{m(\varrho _\gamma )/2} \partial _{\chi _k}\nonumber \\&\qquad +\!\! \sum _{i,j=1}^{r} \sum _{\varrho _k \in \overset{\textrm{nc}}{E}}^{} \frac{\varepsilon _k (- \varrho _k)^{2r-i-j}}{{\Delta }_k (\varrho _k ')^2} \prod _{\varrho _l \in E\setminus \{\varrho _k\}}\!\!\! (s- \varrho _l)^{m(\varrho _l)/2} \partial _{t_i} \partial _{t_j}\nonumber \\&\qquad +\!\! \sum _{\gamma :\varrho _\gamma \in \overset{\textrm{c}}{E}}^{}\! \frac{1}{\sqrt{|\det g_\gamma |}} \, \partial _{\overset{\scriptscriptstyle \gamma }{y}_i} \sqrt{|{\det g_\gamma }|} \biggl (\prod _{\varrho _l\in E}(s-\varrho _l)^{m(\varrho _l)/2} (s \textrm{Id} -A_\gamma )^{-1}\nonumber \\&\!\! \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \prod _{\varrho _k \in \overset{\textrm{nc}}{E}} (A_\gamma - \varrho _k \textrm{Id})^{-1} g_\gamma ^{-1}\biggr )^{ij} \partial _{\overset{\scriptscriptstyle \gamma }{y}_j}\nonumber \\&\qquad -\!\! \sum _{\gamma :\varrho _\gamma \in \overset{\textrm{c}}{E}}^{} \frac{1}{\sqrt{|\det g_\gamma |}}\, \partial _{\overset{\scriptscriptstyle \gamma }{y}_i} \sqrt{|\det g_\gamma |} \bigg (\prod _{\varrho _l\in E}(s-\varrho _l)^{m(\varrho _l)/2} (s \textrm{Id} -A_\gamma )^{-1}\nonumber \\&\!\! \prod _{\varrho _k \in \overset{\textrm{nc}}{E}} (A_\gamma - \varrho _k \textrm{Id})^{-1} g_\gamma ^{-1}\bigg )^{ij} \sum _{q=1}^{r}\overset{\scriptscriptstyle \gamma }{\alpha }_{qj} \partial _{t_q}\nonumber \\&-\!\! \sum _{\gamma :\varrho _\gamma \in \overset{\textrm{c}}{E}}^{} \!\! \bigg (\prod _{\varrho _l\in E}(s-\varrho _l)^{m(\varrho _l)/2} (s \textrm{Id} -A_\gamma )^{-1}\!\! \prod _{\varrho _k \in \overset{\textrm{nc}}{E}} (A_\gamma - \varrho _k \textrm{Id})^{-1} g_\gamma ^{-1}\bigg )^{ij} \sum _{q=1}^{r}\overset{\scriptscriptstyle \gamma }{\alpha }_{qi} \partial _{t_q} \partial _{\overset{\scriptscriptstyle \gamma }{y}_j}\nonumber \\&-\!\! \sum _{\gamma :\varrho _\gamma \in \overset{\textrm{c}}{E}}^{} \! \bigg (\prod _{\varrho _l\in E}(s-\varrho _l)^{m(\varrho _l)/2}(s \textrm{Id} -A_\gamma )^{-1} \!\!\prod _{\varrho _k \in \overset{\textrm{nc}}{E}}\! (A_\gamma - \varrho _k \textrm{Id})^{-1} g_\gamma ^{-1}\bigg )^{ij} \sum _{p,q=1}^{r} \!\!\overset{\scriptscriptstyle \gamma }{\alpha }_{qi}\overset{\scriptscriptstyle \gamma }{\alpha }_{pj} \partial _{t_q} \partial _{t_p}.\nonumber \\ \end{aligned}$$

(78)

If now we suppose that $\psi$ simultaneously satisfies the family of eigenvalue equations

$$\begin{aligned} - \nabla _i \overset{\scriptscriptstyle s}{K}{}^{ij} \nabla _j \psi + \overset{\scriptscriptstyle s}{U}\ \psi = \overset{\scriptscriptstyle s}{\lambda }\ \psi \end{aligned}$$

(79)

then the left-hand side is a polynomial in s and for the equations to hold $\overset{\scriptscriptstyle s}{\lambda }$ must be a polynomial of degree $n-1$ in s as well and we shall write $\overset{\scriptscriptstyle s}{\lambda }=\sum _{l=0}^{n-1} \lambda _l s^l$. Because of our assumption that all constant eigenvalues are real and that A is semi-simple, we have $A_\gamma = c_\gamma \textrm{Id}= \varrho _{r+\gamma } \textrm{Id}$ for $\gamma =1 ,\ldots , R$. Thus for all values of $\gamma$ where $m(\varrho _{\gamma })>2$ the left-hand side of $-\nabla _j \overset{\scriptscriptstyle s}{K}{}^{jk} \nabla _k \psi + \overset{\scriptscriptstyle s}{U}\ \psi = \overset{\scriptscriptstyle s}{\lambda }\ \psi$ has a zero of multiplicity $m(\varrho _{\gamma })/2-1$ at $s=\varrho _{\gamma }$. We can thus write $\overset{\scriptscriptstyle s}{\lambda }=\prod _{\varrho _{\gamma }\in \overset{\textrm{c}}{E}}^{} (s-\varrho _{\gamma })^{m(\varrho _{\gamma })/2-1}\overset{\scriptscriptstyle s}{{\tilde{\lambda }}}$ where $\overset{\scriptscriptstyle s}{{\tilde{\lambda }}}$ is a polynomial of degree ${r+R-1}$ in s. $\overset{\scriptscriptstyle s}{{\tilde{\lambda }}}$ can be written as $\overset{\scriptscriptstyle s}{{\tilde{\lambda }}}=\sum _{j=0}^{r+R-1} s^j {\tilde{\lambda }}_j$. Because we assumed that the eigenvalue equation (79) is satisfied for all values of s we can split (79) into n equations, one for each coefficient. We choose a non-constant eigenvalue $\varrho _k \in \overset{\textrm{nc}}{E}$ and multiply the equation for the coefficient of $s^l$ with $\varrho _k^l$. We do this for all n equations and add them up. If we use $\nabla _i \overset{\scriptscriptstyle s}{K}{}^{ij} \nabla _j=\frac{1}{\sqrt{|{\det g} |}} \partial _i \sqrt{|{\det g} |} \overset{\scriptscriptstyle s}{K}{}^{ij} \partial _j$ in (79) then the result of these steps is equal to replacing $\nabla _i \overset{\scriptscriptstyle s}{K}{}^{ij} \nabla _j \psi$ via (78) and substituting s with $\varrho _k$. We end up with

$$\begin{aligned} \begin{aligned}&\frac{-1}{\varepsilon _k \varrho _k '}\,\partial _{\chi _k} \varrho _k' \prod _{\varrho _{\gamma } \in \overset{\textrm{c}}{E}} (\varrho _{k} - \varrho _{\gamma })^{m(\varrho _{\gamma })/2} \partial _{\chi _k} \psi \\&\quad - \sum _{i,j=1}^{r} \frac{\varepsilon _k (-\varrho _k)^{2r-i-j}}{(\varrho _k')^2}\prod _{\varrho _{\gamma }\in \overset{\textrm{c}}{E}}^{}(\varrho _k - \varrho _{\gamma })^{m(\varrho _{\gamma })/2} \partial _{t_i} \partial _{t_j} + f_r \psi = \sum _{i=0}^{n-1} \lambda _i \varrho _k^i. \end{aligned} \end{aligned}$$

(80)

Because $\partial _{t_q}\psi =i \omega _q \psi$, $\psi$ satisfies the ordinary differential equations that have been claimed.

To obtain the separated partial differential equations that we have claimed we divide $-\nabla _j {\overset{\scriptscriptstyle s}{K}{}^{jk}} \nabla _k \psi + \overset{\scriptscriptstyle s}{U}\ \psi = \overset{\scriptscriptstyle s}{\lambda }\ \psi$ by $\prod _{\varrho _{\gamma }\in \overset{\textrm{c}}{E}}^{} (s-\varrho _{\gamma })^{m(\varrho _{\gamma })/2-1}$. Then we choose a constant eigenvalue $\varrho _{\gamma }$ and evaluate the result at $s=\varrho _{\gamma }\in \overset{\textrm{c}}{E}$ in the same way as before:

(81)

Again: using $\partial _{t_i}\psi =i \omega _i \psi$ gives us the desired result.

The last thing to prove is to show that if $\psi$ fulfills (23) and (24) for some constants ${\tilde{\lambda }}_0, \ldots , {\tilde{\lambda }}_{r+R-1}, \omega _1,\ldots ,\omega _r$ then it is also an eigenfunction of $\overset{\scriptscriptstyle s}{{\widehat{K}}}$ for all real values s. To do so, we use $\partial _{t_i}\psi =i \omega _i \psi$ to obtain (80) and (81) from (23) and (24). Then for all non-constant eigenvalues $\varrho _k$ we multiply the corresponding equation of (23) by

and for each constant eigenvalue $\varrho _{\gamma }$ we multiply the corresponding equation of (81) by

$$\begin{aligned} \prod _{\varrho _i \in E\setminus \{\varrho _\gamma \}}\biggl (\frac{s-\varrho _i}{\varrho _k - \varrho _i}\biggr ) \prod _{\varrho _i \in \overset{\textrm{c}}{E}} (s- \varrho _{\gamma })^{m_\gamma /2 -1} \end{aligned}$$

and add up the results. Then we use the product rule for differentiation and the lagrange interpolation formula for polynomials and arrive at $\overset{\scriptscriptstyle s}{{\widehat{K}}} \psi = \sum _{k=1}^{n-1}\lambda _k s^k \psi$. Theorem 2.16 is proven.

4 Summary

We have generalized the integrals that Topalov [14] found for the geodesic flow of c-compatible structures (g, J, A) to certain natural Hamiltonian systems. We have proven that these integrals also commute in the quantum sense. The result was then generalized to a class of natural Hamiltonian systems: in the case where the tensor A is semi-simple we have described all potentials that may be added to the kinetic energy term such that the resulting functions on $T^* {\mathscr {M}}$ still Poisson-commute pairwise and their quantum operators commute pairwise as well. The potentials that are admissible in the quantum problem are the same as in the classic case. In the case that A is not semi-simple we could present some potentials that may be added to the kinetic energy such that the modified integrals still commute in both the classical and the quantum sense; it is however not clear whether there exist more and this shall be subject to further investigation. We have tackled the question of the separation of variables for common eigenfunctions of the constructed differential operators in the case where A is semi-simple and all constant eigenvalues are real. If all eigenvalues of A are non-constant we get complete reduction to ordinary differential equations. The case where A has constant non-real eigenvalues or Jordan blocks still needs investigation.