Abstract
The goal of the paper is to develop a systematic approach to the study of (possibly degenerate) singularities of integrable systems and their structural stability. Following Nguyen Tien Zung, as the main tool, we use “hidden” system-preserving torus actions near singular orbits. We give sufficient conditions for the existence of such actions and show that they are persistent under integrable perturbations. We find toric symmetries for several infinite series of singularities and prove, as an application, structural stability of Kalashnikov’s parabolic orbits with resonances in the real-analytic case. We also classify all Hamiltonian k-torus actions near a singular orbit on a symplectic manifold \(M^{2n}\) (or on its complexification) and prove that the normal forms of these actions are persistent under small perturbations. As a by-product, we prove an equivariant version of the Vey theorem (Amer J Math 100(3):591–614, 1978) about local symplectic normal form of nondegenerate singularities.

Similar content being viewed by others
Notes
Indeed, it follows from Theorem 3.10 that the action of generators \(\psi ^a :=p(\gamma ^a)\) of \(\Gamma \) on V has the form

for some
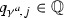 . Here
. Here  is a generating set of the lattice \(p^{-1}(\Gamma )\subset {\mathbb {R}}^r\), \(p:{\mathbb {R}}^r\rightarrow (S^1)^r\) denotes the projection. Since \(p^{-1}(\Gamma )\) is a lattice in \({\mathbb {R}}^r\), there exists a unique linear map \({\mathbb {R}}^r\rightarrow {\mathbb {R}}^{n-r}\) sending
is a generating set of the lattice \(p^{-1}(\Gamma )\subset {\mathbb {R}}^r\), \(p:{\mathbb {R}}^r\rightarrow (S^1)^r\) denotes the projection. Since \(p^{-1}(\Gamma )\) is a lattice in \({\mathbb {R}}^r\), there exists a unique linear map \({\mathbb {R}}^r\rightarrow {\mathbb {R}}^{n-r}\) sending 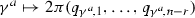 , \(1\leqslant a\leqslant r\). Clearly, this linear map has the form \(\gamma \mapsto (\langle m_1,\gamma \rangle ,\dots ,\langle m_{n-r},\gamma \rangle )\), \(\gamma \in {\mathbb {R}}^r\), for some \(m_1,\dots ,m_{n-r}\in {\mathbb {R}}^r\). From the short exact sequence \(0\rightarrow 2\pi {{\mathbb {Z}}}^r\rightarrow p^{-1}(\Gamma )\rightarrow \Gamma \rightarrow 0\), we conclude that
, \(1\leqslant a\leqslant r\). Clearly, this linear map has the form \(\gamma \mapsto (\langle m_1,\gamma \rangle ,\dots ,\langle m_{n-r},\gamma \rangle )\), \(\gamma \in {\mathbb {R}}^r\), for some \(m_1,\dots ,m_{n-r}\in {\mathbb {R}}^r\). From the short exact sequence \(0\rightarrow 2\pi {{\mathbb {Z}}}^r\rightarrow p^{-1}(\Gamma )\rightarrow \Gamma \rightarrow 0\), we conclude that 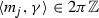 , provided that \(\gamma \in 2\pi {{\mathbb {Z}}}^r\). Therefore
, provided that \(\gamma \in 2\pi {{\mathbb {Z}}}^r\). Therefore 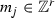 . This proves (11).
. This proves (11).
References
Bau, T., Zung, N.T.: Singularities of integrable and near-integrable Hamiltonian systems. J. Nonlinear Sci. 7(1), 1–7 (1997)
Bochner, S.: Compact groups of differentiable transformations. Ann. Math. 46(3), 372–381 (1945)
Bolsinov, A.V., Fomenko, A.T.: Integrable Hamiltonian Systems. Chapman & Hall/CRC, Boca Raton (2004)
Bolsinov, A., Guglielmi, L., Kudryavtseva, E.A.: Symplectic invariants for parabolic orbits and cusp singularities of integrable systems. Philos. Trans. Roy. Soc. A 376(2131), Art. No. 20170424 (2018)
Bolsinov, A.V., Richter, P.H., Fomenko, A.T.: The method of loop molecules and the topology of the Kovalevskaya top. Sb. Math. 191(2), 151–188 (2020)
Broer, H.W., Chow, S.-N., Kim, Y., Vegter, G.: A normally elliptic Hamiltonian bifurcation. Z. Angew. Math. Phys. 44(3), 389–432 (1993)
Chaperon, M.: Géométrie différentielle et singularités de systèmes dynamiques. Astérisque, No. 138–139 (1986)
de Verdière, Y.C.: Singular Lagrangian manifolds and semiclassical analysis. Duke Math. J. 116(2), 263–298 (2003)
Dellnitz, M., Melbourne, I.: The equivariant Darboux theorem. In: Allgower, E.L., et al. (eds.) Exploiting Symmetry in Applied and Numerical Analysis. Lectures in Applied Mathematics, vol. 29, pp. 163–169. American Mathematical Society, Providence (1993)
Desolneux-Moulis, N.: Singular Lagrangian foliation associated to an integrable Hamiltonian vector field. In: Dazord, P., Weinstein, A. (eds.) Symplectic Geometry, Groupoids, and Integrable Systems. Mathematical Sciences Research Institute Publications, vol. 20, pp. 129–136. Springer, New York (1991)
Duistermaat, J.J.: Bifurcations of periodic solutions near equilibrium points of Hamiltonian systems. In: Salvadori L. (eds.) Bifurcation Theory and Applications. Lecture Notes in Mathematics, vol. 1057. Springer, Berlin (1984)
Dullin, H.R., Ivanov, A.V.: Another look at the saddle-centre bifurcation: vanishing twist. Phys. D 211(1–2), 47–56 (2005)
Efstathiou, K., Giacobbe, A.: The topology associated with cusp singular points. Nonlinearity 25(12), 3409–3422 (2012)
Eliasson, L.H.: Normal forms for Hamiltonian systems with Poisson commuting integrals—elliptic case. Comment. Math. Helv. 65(1), 4–35 (1990)
Fomenko, A.T.: Symplectic topology of completely integrable Hamiltonian systems. Russian Math. Surveys 44(1), 181–219 (1989)
Garay, M.D.: An isochore versal deformation theorem. Topology 43(5), 1081–1088 (2004)
Giacobbe, A.: Infinitesimally stable and unstable singularities of 2-degrees of freedom completely integrable systems. Regul. Chaotic Dyn. 12(6), 717–731 (2007)
Golubitsky, M., Stewart, I.: Generic bifurcation of Hamiltonian systems with symmetry. Phys. D 24(1), 391–405 (1987)
Guillemin, V., Sternberg, S.: A normal form for the moment map. In: Sternberg, S. (ed.) Differential Geometric Methods in Mathematical Physics. Reidel, Dordrecht (1984)
Hanßmann, H.: Local and Semi-local Bifurcations in Hamiltonian Dynamical Systems—Results and Examples. Lecture Notes in Mathematics, vol. 1893. Springer, Berlin (2007)
Ito, H.: Action-angle coordinates at singularities for analytic integrable systems. Math. Z. 206(3), 363–407 (1991)
Kalashnikov, V.V.: Typical integrable Hamiltonian systems on a four-dimensional symplectic manifold. Izv. Math. 62(2), 261–285 (1998)
Kantonistova, E.O.: Topological classification of integrable Hamiltonian systems in a potential field on surfaces of revolution. Sb. Math. 207(3–4), 358–399 (2016)
Karshon, Y., Tolman, S.: Classification of Hamiltonian torus actions with two dimensional quotients. Geom. Topol. 18(2), 669–716 (2014)
Karshon, Y., Ziltener, F.: Hamiltonian group actions on exact symplectic manifolds with proper momentum maps are standard. Trans. Amer. Math. Soc. 370(2), 1409–1428 (2018)
Knörrer, H.: Singular fibres of the momentum mapping for integrable Hamiltonian systems. J. Reine Angew. Math. 355, 67–107 (1985)
Kozlov, I., Oshemkov, A.: Integrable systems with linear periodic integral for the Lie algebra \(e(3)\). Lobachevskii J. Math. 38(6), 1014–1026 (2017)
Kudryavtseva, E.A.: An analogue of the Liouville theorem for integrable Hamiltonian systems with incomplete flows. Dokl. Math. 86(1), 527–529 (2012)
Kudryavtseva, E.A., Lepskii, T.A.: The topology of Lagrangian foliations of integrable systems with hyperelliptic Hamiltonian. Sb. Math. 202(3), 373–411 (2011)
Kudryavtseva, E., Martynchuk, N.: Existence of a smooth Hamiltonian circle action near parabolic orbits (2021). arXiv:2106.04838
Kudryavtseva, E.A., Oshemkov, A.A.: Bifurcations of integrable mechanical systems with magnetic field on surfaces of revolution. Chebyshevskiĭ Sb. 21(2), 244–265 (2020) (in Russian)
Lerman, L.M.: Isoenergetical structure of integrable Hamiltonian systems in an extended neighborhood of a simple singular point: three degrees of freedom. In: Lerman, L., et al. (eds.) Methods of Qualitative Theory of Differential Equations and Related Topics, Advances in the Mathematical Sciences, vol. 48, pp. 219–242. American Mathematical Society, Providence (2000)
Lerman, L.M., Umanskii, Ya.L.: The structure of a Poisson action of \({\mathbb{R}}^2\) on a four-dimensional symplectic manifold. I. Selecta Math. Soviet. 6(4), 365–396 (1987)
Lerman, L.M., Umanskiĭ, Ya.L.: Classification of four-dimensional integrable Hamiltonian systems and Poisson actions of \({\mathbb{R}}^2\) in extended neighborhoods of simple singular points. I. Russian Acad. Sci. Sb. Math. 77(2), 511–542 (1994)
Marle, C.-M.: Sous-variétés de rang constant d’une variété symplectique. In: IIIe Rencontre de Géométrie du Schnepfenried, vol. 1. Astérisque, vols. 107–108, pp. 69–86. Société Mathématique de France, Paris (1983)
Marle, C.-M.: Modéle d’action hamiltonienne d’un groupe de Lie sur une variété symplectique. Rend. Sem. Mat. Univ. Politec. Torino 43(2), 227–251 (1985)
Mineur, H.: Sur les systèmes mécaniques dans lesquels figurent des paramétres fonctions du temps. Étude des systèmes admettant \(n\) intégrales premieres uniformes en involution. Extension à ces systèmes des conditions de quantification de Bohr-Sommerfeld. Journal de l’Ecole Polytechnique, Série III, 143ème année, 173–191 and 237–270 (1937)
Mir, P., Miranda, E.: Rigidity of cotangent lifts and integrable systems. J. Geom. Phys. 157, Art. No. 103847 (2020)
Miranda, E.: Integrable systems and group actions. Cent. Eur. J. Math. 12(2), 240–270 (2014)
Miranda, E., Zung, N.T.: Equivariant normal form for nondegenerate singular orbits of integrable Hamiltonian systems. Ann. Sci. Ecole Norm. Sup. 37(6), 819–839 (2004)
Moser, J.: On the volume elements on a manifold. Trans. Amer. Math. Soc. 120(2), 286–294 (1965)
Oshemkov, A.A., Tuzhilin, M.A.: Integrable perturbations of saddle singularities of rank 0 of integrable Hamiltonian systems. Sb. Math. 209(9), 1351–1375 (2018)
Poincaré, H.: Les Méthodes Nouvelles de la Mécanique Céleste. Gautier-Villars, Paris Vol. 1 (1892), 2 (1893), 3 (1899)
Shabat, B.V.: Introduction to Complex Analysis, Part II: Functions of Several Variables. Translations of Mathematical Monographs, vol. 110. American Mathematical Society, Providence (1992)
van der Meer, J.-C.: The Hamiltonian Hopf Bifurcation. Lecture Notes in Mathematics, vol. 1160. Springer, Berlin (1985)
Varchenko, A.N., Givental’, A.B.: Mapping of periods and intersection form. Funct. Anal. Appl. 16(2), 83–93 (1982)
Vey, J.: Sur certaines systèmes dynamiques séparables. Amer. J. Math. 100(3), 591–614 (1978)
Wassermann, G.: Classification of singularities with compact abelian symmetry. In: Singularities. Banach Center Publications, vol. 20, pp. 475–498. PWN, Warsaw (1988)
Weinstein, A.: Lectures on Symplectic Manifolds. Regional Conference Series in Mathematics, vol. 29. American Mathematical Society, Providence (1977)
Zung, N.T.: Decomposition of nondegenerate singularities of integrable Hamiltonian systems. Lett. Math. Phys. 33(3), 187–193 (1995)
Zung, N.T.: Symplectic topology of integrable Hamiltonian systems, I: Arnold–Liouville with singularities. Compositio Math. 101(2), 179–215 (1996)
Zung, N.: A note on degenerate corank-one singularities of integrable Hamiltonian systems. Comment. Math. Helv. 75(2), 271–283 (2000)
Zung, N.T.: A la recherche des tores perdus. Habilitation Thesis. Université Montpellier (2001). https://tel.archives-ouvertes.fr/tel-00001283
Zung, N.T.: Actions toriques et groupes d’automorphismes de singularités de systèmes dynamiques intégrables. C. R. Math. Acad. Sci. Paris 336(12), 1015–1020 (2003)
Zung, N.T.: Torus actions and integrable systems. In: Bolsinov, A.V., Fomenko, A.T., Oshemkov, A.A. (eds.) Topological Methods in the Theory of Integrable Systems, pp. 289–328. Cambridge Scientific Publications, Cambridge (2006)
Acknowledgements
The author is grateful to Alexey Bolsinov for helpful comments on Cartan subalgebras of the Lie algebra  and valuable suggestions on a preliminary version of the paper, to Andrey Oshemkov for the useful discussion on proving extendability of homomorphisms to a circle from a finite subgroup of a torus (cf. (11)), to Stefan Nemirovski for helpful comments on topologies on the spaces of analytic functions, and to the referees for useful comments which helped to improve the paper.
and valuable suggestions on a preliminary version of the paper, to Andrey Oshemkov for the useful discussion on proving extendability of homomorphisms to a circle from a finite subgroup of a torus (cf. (11)), to Stefan Nemirovski for helpful comments on topologies on the spaces of analytic functions, and to the referees for useful comments which helped to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the Russian Science Foundation (Project 17-11-01303).
Rights and permissions
About this article
Cite this article
Kudryavtseva, E.A. Hidden toric symmetry and structural stability of singularities in integrable systems. European Journal of Mathematics 8, 1487–1549 (2022). https://doi.org/10.1007/s40879-021-00501-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-021-00501-9
Keywords
- Integrable system
- Hamiltonian torus action
- Degenerate singularity of integrable system
- Structural stability





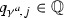 . Here
. Here  is a generating set of the lattice
is a generating set of the lattice 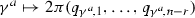 ,
, 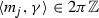 , provided that
, provided that 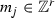 . This proves (
. This proves (