Abstract
An elliptic Newton flow is a dynamical system that can be interpreted as a continuous version of Newton’s iteration method for finding the zeros of an elliptic function f. Previous work focuses on structurally stable flows (i.e., the phase portraits are topologically invariant under perturbations of the poles and zeros for f), including a classification/representation result for such flows in terms of Newton graphs (i.e., cellularly embedded toroidal graphs fulfilling certain combinatorial properties). The present paper deals with non-structurally stable elliptic Newton flows determined by pseudo Newton graphs (i.e., cellularly embedded toroidal graphs, either generated by a Newton graph, or the so-called nuclear Newton graph, exhibiting only one vertex and two edges). Our study results into a deeper insight in the creation of structurally stable Newton flows and the bifurcation of non-structurally stable Newton flows. As it requires the classification of all third order Newton graphs, we present this classification.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Motivation; recapitulation of earlier results
In order to clarify the context of the present paper, we recapitulate some earlier results.
1.1 Elliptic Newton flows; structural stability
The results in the following four subsections, can all be found in our paper [4].
1.1.1 Planar and toroidal elliptic Newton flows
Let f be an elliptic (i.e., meromorphic, doubly periodic) function of order  on the complex plane \({\mathbb {C}}\) with \((\omega _{1}, \omega _{2})\), \(\mathrm{Im}\,{\omega _{2}}/{\omega _{1}} >0\), as basic periods spanning a lattice
on the complex plane \({\mathbb {C}}\) with \((\omega _{1}, \omega _{2})\), \(\mathrm{Im}\,{\omega _{2}}/{\omega _{1}} >0\), as basic periods spanning a lattice  .
.
The planar elliptic Newton flow\(\overline{\mathcal {N} }(f)\) is a \(C^{1}\)-vector field on \({\mathbb {C}}\), defined as a desingularized versionFootnote 1 of the planar dynamical system, \(\mathcal {N}(f)\), given by

On a non-singular, oriented \(\overline{\mathcal {N} }(f)\)-trajectory  we have:
we have:
-
 , and
, and  is a strictly decreasing function on t.
is a strictly decreasing function on t.
So that the \(\overline{\mathcal {N} }(f)\)-equilibria are of the form:
-
a stable star node (attractor); in the case of a zero for f, or
-
an unstable star node (repellor); in the case of a pole for f, or
-
a saddle; in the case of a critical point for f (i.e., \(f'\) vanishes, but f not).
For an (un)stable node the (outgoing) incoming trajectories intersect under a non-vanishing angle \({\Delta }/{k}\), where \(\Delta \) stands for the difference of the  -values on these trajectories, and k for the multiplicity of the corresponding (pole) zero. The saddle in the case of a simple critical point (i.e., \(f''\) does not vanish) is orthogonal and the two unstable (stable) separatrices constitute the “local” unstable (stable) manifold at this saddle.
-values on these trajectories, and k for the multiplicity of the corresponding (pole) zero. The saddle in the case of a simple critical point (i.e., \(f''\) does not vanish) is orthogonal and the two unstable (stable) separatrices constitute the “local” unstable (stable) manifold at this saddle.
Functions such as f correspond to meromorphic functions on the torus \(T(\Lambda )\) . So, we can interpret \(\overline{\mathcal {N} }(f)\) as a global \(C^{1}\)-vector field, denotedFootnote 2
. So, we can interpret \(\overline{\mathcal {N} }(f)\) as a global \(C^{1}\)-vector field, denotedFootnote 2 , on the Riemann surface \(T(\Lambda )\) and it is allowed to apply results for \(C^{1}\)-vector fields on compact differential manifolds, such as certain theorems of Poincaré–Bendixon–Schwartz (on limiting sets) and those of Baggis–Peixoto (on \(C^{1}\)-structural stability).
, on the Riemann surface \(T(\Lambda )\) and it is allowed to apply results for \(C^{1}\)-vector fields on compact differential manifolds, such as certain theorems of Poincaré–Bendixon–Schwartz (on limiting sets) and those of Baggis–Peixoto (on \(C^{1}\)-structural stability).
It is well known that the function f has precisely r zeros and r poles (counted by multiplicity) on the half open / half closed period parallelogram \(P_{\omega _{1}, \omega _{2}}\) given by

Denoting these zeros and poles by \(a_{1}, \dots ,a_{r} \), resp. \(b_{1}, \dots ,b_{r} \), we haveFootnote 3 (cf. [8]):

and thus

where  and
and  are the zeros, resp. poles for f on \(T(\Lambda )\) and
are the zeros, resp. poles for f on \(T(\Lambda )\) and  stands for the congruency class \(\mathrm{mod} \, \Lambda \) of a number in \({\mathbb {C}}\). Conversely, any pair
stands for the congruency class \(\mathrm{mod} \, \Lambda \) of a number in \({\mathbb {C}}\). Conversely, any pair  that fulfils (1) determines (up to a multiplicative constant) an elliptic function with
that fulfils (1) determines (up to a multiplicative constant) an elliptic function with  and
and  as zeros resp. poles in
as zeros resp. poles in  .
.
1.1.2 The topology \(\tau _{0}\)
It is not difficult to see that the functions f, and also the corresponding toroidal Newton flows, can be represented by the set of all ordered pairs  of congruency classes \(\mathrm{mod} \, \Lambda \) (with
of congruency classes \(\mathrm{mod} \, \Lambda \) (with  , \(i=1, \dots , r\)) that fulfil (2).
, \(i=1, \dots , r\)) that fulfil (2).
This representation space can be endowed with a topology, say \(\tau _{0}\), induced by the Euclidean topology on \({\mathbb {C}}\), that is natural in the following sense: Given an elliptic function f of order r and \(\varepsilon >0\) sufficiently small, a \(\tau _{0}\)-neighborhood \({\mathcal {O}}\) of f exists such that for any g in \({\mathcal {O}}\), the zeros (poles) for g are contained in \(\varepsilon \)-neighborhoods of the zeros (poles) for f.
\(E_{r}(\Lambda )\) is the set of all functions f of order r on \(T(\Lambda )\) and \(N_{r}(\Lambda )\) the set of corresponding flows  . By X(T) we mean the set of all \(C^{1}\)-vector fields on T, endowed with the \(C^{1}\)-topology (cf. [6]).
. By X(T) we mean the set of all \(C^{1}\)-vector fields on T, endowed with the \(C^{1}\)-topology (cf. [6]).
The topology \(\tau _{0}\) on \(E_{r}(\Lambda )\) and the \(C^{1}\)-topology on X(T) are matched by: The map is\(\tau _{0}\text {-}C^{1}\)-continuous.
is\(\tau _{0}\text {-}C^{1}\)-continuous.
1.1.3 Canonical forms of elliptic Newton flows
The flows  and
and  in \(N_{r}(\Lambda )\) are called conjugate, denoted
in \(N_{r}(\Lambda )\) are called conjugate, denoted  , if there is a homeomorphism from T onto itself mapping maximal trajectories of
, if there is a homeomorphism from T onto itself mapping maximal trajectories of  onto those of
onto those of  , thereby respecting the orientations of these trajectories. Conjugate flows are considered as equal, since we focus on qualitative aspects of the phase portraits.
, thereby respecting the orientations of these trajectories. Conjugate flows are considered as equal, since we focus on qualitative aspects of the phase portraits.
For a given f in \(E_{r}(\Lambda )\), let the lattice  be arbitrary. Then there is a function \(f^{*}\) in
be arbitrary. Then there is a function \(f^{*}\) in  such that
such that

In fact, the linear isomorphism \({\mathbb {C}} \rightarrow {\mathbb {C}}:(\omega _{1},\omega _{2}) \mapsto (\omega _{1}^{*},\omega _{2}^{*})\); \(\mathrm{Im}\,{\omega _{2}^{*}}/{\omega _{1}^{*}} >0,\) transforms \(\Lambda \) into  and the pair
and the pair  , determining f, into
, determining f, into  fixing \(f^{*}\) in
fixing \(f^{*}\) in  ; if
; if  then this linear isomorphism is unimodular.
then this linear isomorphism is unimodular.
It is always possible to chooseFootnote 4 , where \((1, \tau )\) is a reducedFootnote 5 pair of periods for \(f^{*}\) and to subsequently apply the linear transformation \((1,\tau ) \mapsto (1,i)\), so that we even may assume that (1, i) is a pair of reduced periods for the corresponding elliptic function on \(\Lambda _{1,i}\).
, where \((1, \tau )\) is a reducedFootnote 5 pair of periods for \(f^{*}\) and to subsequently apply the linear transformation \((1,\tau ) \mapsto (1,i)\), so that we even may assume that (1, i) is a pair of reduced periods for the corresponding elliptic function on \(\Lambda _{1,i}\).
Consequently, unless strictly necessary, we suppress the role of \(\Lambda \) and write: \(E_{r}(\Lambda )=E_{r}\), \(T(\Lambda )=T\) and \(N_{r}(\Lambda )=N_{r}\).
1.1.4 Structural stability
The flow  in \(N_{r}\) is called \(\tau _{0}\)-structurally stable, if there is a \(\tau _{0}\)-neighborhood \({\mathcal {O}}\) of f, such that for all \(g \in {\mathcal {O}} \) we have:
in \(N_{r}\) is called \(\tau _{0}\)-structurally stable, if there is a \(\tau _{0}\)-neighborhood \({\mathcal {O}}\) of f, such that for all \(g \in {\mathcal {O}} \) we have:  ; the set of all \(\tau _{0}\)-structurally stable flows
; the set of all \(\tau _{0}\)-structurally stable flows  is denoted by \(\widetilde{N}_{r}\).
is denoted by \(\widetilde{N}_{r}\).
-
\(C^{1}\)-structural stability for
 implies \(\tau _{0}\)-structural stability for
implies \(\tau _{0}\)-structural stability for  ; see Sect. 1.1.2. So, when discussing structurally stable toroidal Newton flows we may skip the adjectives \(\tau _{0}\) and \(C^{1}\)
; see Sect. 1.1.2. So, when discussing structurally stable toroidal Newton flows we may skip the adjectives \(\tau _{0}\) and \(C^{1}\) -
A structurally stable
 has precisely 2r different simple saddles (all orthogonal).
has precisely 2r different simple saddles (all orthogonal).
Note that if  is structurally stable, then also
is structurally stable, then also  is, because we have
is, because we have  . [Duality]
. [Duality]
The main results obtained in [4] are:
-
 in
in  iff the function f is non-degenerateFootnote 6. [Characterization]
iff the function f is non-degenerateFootnote 6. [Characterization] -
The set of all non-degenerate functions of order r is open and dense in the set \(E_{r}\). [Genericity]
1.2 Classification and representation of structurally stable elliptic Newton flows
The following three subsections describe shortly the main results from our paper [5].
1.2.1 The graphs \(\mathcal {G}(f )\) and \(\mathcal {G}^{*}(f)\)
For the flow  in
in  we define the connected multigraphFootnote 7\(\mathcal {G}(f )\) of order r on T by:
we define the connected multigraphFootnote 7\(\mathcal {G}(f )\) of order r on T by:
-
vertices are the r zeros for f;
-
edges are the 2r unstable manifolds at the critical points for f;
-
faces are the r basins of repulsion of the poles for f.
Similarly, we define the toroidal graph \(\mathcal {G}^{*}(f)\) at the repellors, stable manifolds and basins of attraction for  . Apparently, \(\mathcal {G}^{*}(f)\) is the geometrical dual of \(\mathcal {G}(f)\); see Figs. 1 and 2.
. Apparently, \(\mathcal {G}^{*}(f)\) is the geometrical dual of \(\mathcal {G}(f)\); see Figs. 1 and 2.
The following features of \(\mathcal {G}(f)\) reflect the main properties of the phase portraits of  :
:
-
\(\mathcal {G}(f )\) is cellularly embedded, i.e., each face is homeomorphic to an open \({\mathbb {R}}^2\)-disk;
-
all (anti-clockwise measured) angles at an attractor in the boundary of a face that span a sector of this face, are strictly positive and sum up to \(2\pi \); [A-property]
-
the boundary of each \(\mathcal {G}(f )\)-face—as subgraph of \(\mathcal {G}(f )\)—is Eulerian, i.e., admits a closed facial walk that traverses each edge only once and goes through all vertices. [E-property]
The anti-clockwise permutation on the embedded edges at vertices of \(\mathcal {G}(f )\) induces a clockwise orientation of the facial walks on the boundaries of the \(\mathcal {G}(f )\)-faces; see Fig. 2. On its turn, the clockwise orientation of \(\mathcal {G}(f )\)-faces gives rise to a clockwise permutation on the embedded edges at \(\mathcal {G}^*(f )\)-vertices, and thus to an anti-clockwise orientation of \(\mathcal {G}^*(f )\). In the sequel, all graphs of the type \(\mathcal {G}(f ),\mathcal {G}^*(f )\), are always oriented in this way, see Fig. 2. Hence, by duality,

It follows that also \(\mathcal {G}^*(f )\) is cellularly embedded and fufills the E- and A-properties.
1.2.2 Newton graphs
A connected multigraph \(\mathcal {G}\) in T with r vertices, 2r edges and r faces is called a Newton graph (of order r) if this graph is cellularly embedded and moreover, the E- and A-properties (possibly under suitable local redrawing) hold.
It is proved that the dual \(\mathcal {G}^*\) of a Newton graph \(\mathcal {G}\) is also Newtonian (of order r). The anti-clockwise (clockwise) permutations on the edges of \(\mathcal {G}\) at its vertices endow a clockwise (anti-clockwise) orientation of the \(\mathcal {G}\)-faces and, successively, an anti-clockwise (clockwise) orientation of the \(\mathcal {G}^*\)-faces, cf. Fig. 2.
-
Apparently \(\mathcal {G}(f )\) and \(\mathcal {G}^*(f )\) are Newton graphs.
The main results obtained in [5] are:
-
If
 and
and  are structurally stable and of the same order, then
are structurally stable and of the same order, then 
-
Given a clockwise oriented Newton graph \(\mathcal {G}\) of order r, there exists a structurally stable Newton flow
 such that \(\mathcal {G}(f_{\mathcal {G}}) \sim \mathcal {G}\) and thus (\(\mathcal {H}\) is another clockwise oriented Newton graph)
such that \(\mathcal {G}(f_{\mathcal {G}}) \sim \mathcal {G}\) and thus (\(\mathcal {H}\) is another clockwise oriented Newton graph) 
Here the symbol \(\sim \) between flows stands for conjugacy, and between graphs for equivalency (i.e., an orientation preserving isomorphism).
The graph \(\mathcal {G}(f )\) is, so to say, the principal part of the phase portrait of the structurally stable flow  and determines, in a qualitative sense, the whole phase portrait; see Figs. 1 and 2 for an illustration. In accordance with our philosophy (“focus on qualitative aspects”), conjugate flows are considered as equal. Note however, that by the above classification we have:
and determines, in a qualitative sense, the whole phase portrait; see Figs. 1 and 2 for an illustration. In accordance with our philosophy (“focus on qualitative aspects”), conjugate flows are considered as equal. Note however, that by the above classification we have:  iff
iff  which is in general not true.Footnote 8 Nevertheless, from our point of view it is reasonable to consider the dual flows
which is in general not true.Footnote 8 Nevertheless, from our point of view it is reasonable to consider the dual flows  and
and  as equal (since the phase portraits are equal, up to the orientation of the trajectories). So, the problem of classifying structurally stable elliptic Newton flows is reduced to the classification (under equivalency and duality) of Newton graphs.
as equal (since the phase portraits are equal, up to the orientation of the trajectories). So, the problem of classifying structurally stable elliptic Newton flows is reduced to the classification (under equivalency and duality) of Newton graphs.
1.2.3 Criteria for the A- and E-properties
Let \(\mathcal {G}\) be a cellularly embedded multigraph of order r in T. There is a simple criterion available for \(\mathcal {G}\) to fulfil the A-property. In order to formulate this criterion, we denote the vertices and faces of \(\mathcal {G}\) by \(v_i\) and  respectively, \(i, j=1, \dots ,r\). Now, let J be a subset of \(\{ 1, \dots ,r\}\) and denote the subgraph of \(\mathcal {G}\), generated by all vertices and edges incident with the faces
respectively, \(i, j=1, \dots ,r\). Now, let J be a subset of \(\{ 1, \dots ,r\}\) and denote the subgraph of \(\mathcal {G}\), generated by all vertices and edges incident with the faces  , \(j \in J\), by \(\mathcal {G}(J)\).The set of all vertices in \(\mathcal {G}(J)\) is denoted by \(V(\mathcal {G}(J))\). Then
, \(j \in J\), by \(\mathcal {G}(J)\).The set of all vertices in \(\mathcal {G}(J)\) is denoted by \(V(\mathcal {G}(J))\). Then
where  stands as usual for cardinality. As a by-product we have:
stands as usual for cardinality. As a by-product we have:
-
Under the A-property, the set
 of exterior \(\mathcal {G}(J)\)-vertices (i.e., vertices in \(\mathcal {G}(J)\) that are also adjacent to \(\mathcal {G}\)-faces, but not in \(\mathcal {G}(J)\)), is non-empty.
of exterior \(\mathcal {G}(J)\)-vertices (i.e., vertices in \(\mathcal {G}(J)\) that are also adjacent to \(\mathcal {G}\)-faces, but not in \(\mathcal {G}(J)\)), is non-empty. -
If \(r=2\), the A-property always holds and if \(r=3\) the E-property implies the A-property (cf. [5, Lemma 3.17]).
Let \(\mathcal {G}\) be a cellularly embedded multigraph of order r in T. We consider the rotation system\(\Pi \) for \(\mathcal {G}\):

where the local rotation system\(\pi _{v}\) at v is the cyclic permutation of the edges incident with v such that \(\pi _{v}(e)\) is the successor of e in the anti-clockwise ordering around v. Then, the boundaries of the faces of \(\mathcal {G}\) are formally described by \(\Pi \)-walks as: If  stands for an edge, with end vertices \(v'\) and \(v''\) we define a \(\Pi \)-walk (facial walk), say w, on \(\mathcal {G}\) as follows:
stands for an edge, with end vertices \(v'\) and \(v''\) we define a \(\Pi \)-walk (facial walk), say w, on \(\mathcal {G}\) as follows:
Consider an edge  and the closed walk
and the closed walk  , which is determined by the requirement that, for \(i=1, \dots , \ell \), we have \(\pi _{v_{i+1}}(e_{i})=e_{i+1}\), where
, which is determined by the requirement that, for \(i=1, \dots , \ell \), we have \(\pi _{v_{i+1}}(e_{i})=e_{i+1}\), where  and \(\ell \) is minimal.Footnote 9 [Face transversal procedure]
and \(\ell \) is minimal.Footnote 9 [Face transversal procedure]
Each edge occurs either once in two different \(\Pi \)-walks, or twice (with opposite orientations) in only one \(\Pi \)-walk. \(\mathcal {G}\) has the E-property iff the first possibility holds for all \(\Pi \)-walks. The dual \(\mathcal {G}^{*}\) admits a loopFootnote 10 iff the second possibility occurs at least in one of the \(\Pi \)-walks. The following observation will be referred to in the sequel:
-
Under the E-property for \(\mathcal {G}\), each \(\mathcal {G}\)-edge is adjacent to different faces; in fact, any \(\mathcal {G}\)-edge, say e, determines precisely one \(\mathcal {G}^{*}\)-edge \(e^{*}\) (and vice versa) so that there are 2r “intersections” \(s=(e, e^{*} )\) of \(\mathcal {G}\)- and \(\mathcal {G}^{*}\)-edges.
Consider an abstract graph \({\mathbb {P}} (\mathcal {G})\) with vertices represented by the pairs \(s=(e, e^{*})\) and by the \(\mathcal {G}\)- and \(\mathcal {G}^{*}\)-vertices. Two of the vertices in \({\mathbb {P}} (\mathcal {G})\) are connected iff they are represented by points incident with the same edges in \(\mathcal {G}\) or \(\mathcal {G}^{*}\)\({\mathbb {P}} (\mathcal {G})\) admits a cellular embedding in T (cf. [5]), which will be referred to as to the distinguished graph with as faces the so-called canonical regions (cf. Fig. 1). Following [10],
with as faces the so-called canonical regions (cf. Fig. 1). Following [10],  determines a \(C^{1}\)-structurally stable flow \(X(\mathcal {G})\) on T. We proved that, if the A-property holds as well, \(X(\mathcal {G})\) is topologically equivalent with a structurally stable elliptic Newton flow of order r (cf. [5, Section 4]).
determines a \(C^{1}\)-structurally stable flow \(X(\mathcal {G})\) on T. We proved that, if the A-property holds as well, \(X(\mathcal {G})\) is topologically equivalent with a structurally stable elliptic Newton flow of order r (cf. [5, Section 4]).
By the Heffter–Edmonds–Ringel rotation principle, the graph \(\mathcal {G}\) is uniquely determined up to an orientation preserving isomorphism by its rotation system. In fact, consider for each \(\Pi \)-walk w of length l, a so-called \(\Pi \)-polygon in the plane with l sides labelled by the edges of w, so that each polygon is disjoint from the other polygons. These polygons can be used to construct (patching them along identically labelled sides) an orientable surface S and in S a 2-cell embedded graph \(\mathcal {H}\) with faces determined by the polygons. Then S is homeomorphic to T and \(\mathcal {H}\) isomorphic with \(\mathcal {G}\). The clockwise oriented \(\Pi \)-walks of \(\mathcal {G}\) determine a clockwise rotation system \(\Pi ^{*}\) for \(\mathcal {G}^{*}\) that—by the face traversal procedure—leads to anti-clockwise oriented \(\Pi ^{*}\)-walks for \(\mathcal {G}^{*}\)
2 Classification of Newton graphs of order 3
Let \(\mathcal {G}\) be an arbitrary Newton graph of order r, and \(\mathcal {G}^{*}\) its geometrical dual. The vertices and faces of \(\mathcal {G}\) are denoted by \(v_{i}\), respectively by \(F_{r+i}\), \(i=1, \dots , r\). The \(\mathcal {G}^{*}\)-vertex “located” in \(F_{r+i}\) is denoted by \(v^{*}_{r+i}\), and the \(\mathcal {G}^{*}\)-face that “contains” \(v_{i}\) by \(F^{*}_{i}\). In forthcoming figures, the vertices \(\mathcal {G}\) and \(\mathcal {G}^{*}\) will be indicated by their indices in combination with the symbols \(\circ \) and \({\bullet }\) respectively, i.e.,  , and
, and  . This induces an indexation of the faces of \(\mathcal {G}\) and \(\mathcal {G}^{*}\) as follows:
. This induces an indexation of the faces of \(\mathcal {G}\) and \(\mathcal {G}^{*}\) as follows:  and
and  . The degrees of the \(\mathcal {G}\)- and \(\mathcal {G}^{*}\)-vertices are denoted by \(\delta _{i}=\mathrm{deg}\,v_{i}\), resp. \(\delta ^{*}_{i}=\mathrm{deg}\,v^{*}_{r+i}\). Put \(\delta =(\delta (\mathcal {G}))=(\delta _{1}, \dots ,\delta _{r})\) and
. The degrees of the \(\mathcal {G}\)- and \(\mathcal {G}^{*}\)-vertices are denoted by \(\delta _{i}=\mathrm{deg}\,v_{i}\), resp. \(\delta ^{*}_{i}=\mathrm{deg}\,v^{*}_{r+i}\). Put \(\delta =(\delta (\mathcal {G}))=(\delta _{1}, \dots ,\delta _{r})\) and  .
.
Lemma 2.1
\(1 < \delta _{i} \leqslant 2r\), \(1 < \delta ^{*}_{i} \leqslant 2r\),  .
.
Proof
By assumption \(\mathcal {G}\) does not admit loops, whereas this is also true for \(\mathcal {G}^{*}\) (since \(\mathcal {G}\) has the E-property). The A-property for the Newton graphs \(\mathcal {G}\) and \(\mathcal {G}^{*}\) ensures the non-existence of vertices for \(\mathcal {G}\) and \(\mathcal {G}^{*}\) of degree 1. \(\square \)
Hence there are 4r faces (canonical regions) in  (cf. Sect. 1.2.3).
(cf. Sect. 1.2.3).
As Newton graphs of order 3 are leading examples at our considerations how to handle non-structurally stable flows, we now present their classification using the results from [5]. In particular, we use that, since \(r=3\), the E-property already implies that \(\mathcal {G}\) is a Newton graph (cf. Sect. 1.2.3). So, from now on, let \(\mathcal {G}\) be a third order Newton graph. We denote the \(\mathcal {G}\)-edges by a, b, c, d, e, f, and the corresponding \(\mathcal {G}^{*}\)-edges by \(a^{*} b^{*} c^{*} d^{*} e^{*} f^{*}\) The  -vertices represented by \((a,a^{*}), (b,b^{*}), \dots \) will be denoted by respectively \(a, b, \dots \)
-vertices represented by \((a,a^{*}), (b,b^{*}), \dots \) will be denoted by respectively \(a, b, \dots \)
We distinguish between the following three possibilities with respect to the boundaries (\(\Pi \)-walks) of \(\mathcal {G}\)-faces:
Case 1: The boundary of one of the \(\mathcal {G}\)-faces, say \(\partial F_{4}\), has six edges, i.e., \(\delta ^{*}_{4}=6\).
Case 2: The boundary of one of the \(\mathcal {G}\)-faces, say \(\partial F_{4}\), has five edges, i.e., \(\delta ^{*}_{4}=5\).
Case 3: Each boundary of the faces in \(\mathcal {G}\) and \(\mathcal {G}^{*}\) has four edges, i.e.,  .
.
By Lemma 2.1, Cases 1, 2 and 3 are mutually exclusive and cover all possibilities. First we should check whether there exist graphs \(\mathcal {G}\) that fulfil the conditions in the above cases, and, even so, to what extent \(\mathcal {G}\) is determined by these conditions.
Ad Case 1: Because of the E-property, and since \(\mathcal {G}\) has no loops, it is necessary for the existence of \(\mathcal {G}\) that the \(\Pi \)-walk \(w_{F_{4}}\) of a possible face \(F_{4}\) fulfils one of the following conditions:
Subcase 1.1: Traversing \(w_{F_{4}}\) once, each vertex appears precisely twice.
Subcase 1.2: Traversing \(w_{F_{4}}\) once, there is one vertex (say \(v_{1}\)) appearing three times, one (say \(v_{2}\)) appearing twice, and one (say \(v_{3}\)) showing up only once.
The (clockwise oriented) \(\Pi \)-polygon for \(\partial F_{4}\) has six sides, labelled \(a, b, \dots , f\), and six “corner points”, labelled by the vertices \(v_{1},v_{2},v_{3}\) (repetitions necessary). Identifying points related to the same \(\mathcal {G}\)-vertex, brings us back to \(w_{F_{4}}\). Assume that the cyclic permutations of the edges in \(w_{F_{4}}\) that are incident with the same vertex are oriented anti-clockwise (cf. the conventions in Sect. 1.2.2). In order to ensure that a walk on the boundary of a face is a \(\Pi \)-walk one must verify that this walk begins and ends with the same vertex and that this vertex is incident with same edge. In the notation of a \(\Pi \)-walk this is stipulated by placing this edge—in the last position—between brackets, see e.g. (3) and (4).
In Subcase 1.1 there are precisely two different—up to relabelling—possibilities for \(w_{F_{4}}\) according to the schemes (see Fig. 3):

or

First, we focus on \(w_{F_{4}}\) given by Scheme (3), see Fig. 3 (a). In the (anti-clockwise) cyclic permutation of the \(w_{F_{4}}\)-edges, incident with the same vertex, these edges occur in pairs, determining a (positively oriented) sector of \(F_{4}\). As an edge is always adjacent to two different faces (cf. Sect. 1.2.3), two \(F_{4}\)-sectors at the same \(v_{i}\) are separated by facial sectors (at \(v_{i}\)) not belonging to \(F_{4}\) (cf. Fig. 3 (a)). Since, moreover, the graph we are looking for, admits altogether twelve facial sectors, the cyclic permutation of the edges at \(v_{i}\) are as indicated in Fig. 3 (a) and constitute a rotation system that—up to equivalency and relabelling—determines the graph, say \(\mathcal {G}\), uniquely.
With the aid of the rotation system in Fig. 3 (a) and applying the face traversal procedure, as sketched in Sect. 1.2.3, we find the closed walks  and
and  defining the two other \(\mathcal {G}\)-faces, say \(F_{5}\), resp. \(F_{6}\). (Note that each edge occurs twice in different walks, but with opposite orientation.) Gluing together the facial polygons corresponding to \(F_{4},F_{5}\) and \(F_{6}\), according to equally labelled sides and corner points, gives rise to the plane representations of \(\mathcal {G}\) in Fig. 4 (a). [Heffter–Edmonds–Ringel]
defining the two other \(\mathcal {G}\)-faces, say \(F_{5}\), resp. \(F_{6}\). (Note that each edge occurs twice in different walks, but with opposite orientation.) Gluing together the facial polygons corresponding to \(F_{4},F_{5}\) and \(F_{6}\), according to equally labelled sides and corner points, gives rise to the plane representations of \(\mathcal {G}\) in Fig. 4 (a). [Heffter–Edmonds–Ringel]
From Fig. 4 (a) it follows that the rotation system for \(\mathcal {G}^{*}\) is as depicted in Fig. 5. With the aid of this figure we find, again by the face traversal procedure, the following closed subwalks in \(\mathcal {G}^{*}\):  ,
,  and
and  , defining the \(\mathcal {G}^{*}\)-faces \(F_{1}^{*},F_{2}^{*},F_{3}^{*}\) respectively. (Note that each edge occurs twice in different walks, but with opposite orientation.) Gluing together the facial polygons corresponding to these faces according to equally labelled sides and corner points, yields the plane representations of \(\mathcal {G}^{*}\) in Fig. 4 (a).
, defining the \(\mathcal {G}^{*}\)-faces \(F_{1}^{*},F_{2}^{*},F_{3}^{*}\) respectively. (Note that each edge occurs twice in different walks, but with opposite orientation.) Gluing together the facial polygons corresponding to these faces according to equally labelled sides and corner points, yields the plane representations of \(\mathcal {G}^{*}\) in Fig. 4 (a).
The rotation systems for \(\mathcal {G}^{*}\) according to Scheme (3)
If we start from a \(\Pi \)-walk for \(F_{4}\), according to Scheme (4), we find (by the same argumentation as above) plane representations for \(\mathcal {G}\) and \(\mathcal {G}^{*}\); see Fig. 4 (b).
Note that in all graphs in Fig. 4 the anti-clockwise (clockwise) orientation of the cyclic permutations of edges incident with the same vertex induces a clockwise (anti-clockwise) orientation of the faces.
In Subcase 1.2 there is precisely one—up to relabelling—possibility for \(w_{F_{4}}\) according to the scheme:

In this case however, there are three pairs of \(\mathcal {G}\)-edges at \(v_{1}\) determining (positively measured) sectors of \(F_{4}\). So, reasoning as in Subcase 1.1, there are two possibilities for the (anti clockwise) cyclic permutations of the \(\mathcal {G}\)-edges at \(v_{1}\) (and thus also two different rotation systems; see Fig. 6).
Starting from Fig. 6 (a) and applying the face traversal procedure, we find the facial walks  and
and  , which together with Scheme (5) define the faces \(F_{5},F_{6}\) and \(F_{4}\) respectively. Reasoning as in Subcase 1.1, we arrive at the plane realizations of \(\mathcal {G}\) and \(\mathcal {G}^{*}\) as depicted in Fig. 7 (a). In the case of Fig. 6 (b) the facial walks
, which together with Scheme (5) define the faces \(F_{5},F_{6}\) and \(F_{4}\) respectively. Reasoning as in Subcase 1.1, we arrive at the plane realizations of \(\mathcal {G}\) and \(\mathcal {G}^{*}\) as depicted in Fig. 7 (a). In the case of Fig. 6 (b) the facial walks  and
and  , together with Scheme (5), define the faces \(F_{5},F_{6}\) and \(F_{4}\) respectively. Reasoning as in Subcase 1.1, we obtain the plane representations for \(\mathcal {G}\) and \(\mathcal {G}^{*}\) as depicted in Fig. 7 (b).
, together with Scheme (5), define the faces \(F_{5},F_{6}\) and \(F_{4}\) respectively. Reasoning as in Subcase 1.1, we obtain the plane representations for \(\mathcal {G}\) and \(\mathcal {G}^{*}\) as depicted in Fig. 7 (b).
Note that both graphs \(\mathcal {G}\) in Fig. 7 are self-dual (cf. footnote 8 or note that \(\delta (\mathcal {G})= \delta (\mathcal {G}^{*})\) and use [5, Lemma 3.5]). However, by inspection of their rotation systems, one sees that they are not equivalent (cf. Sect. 1.2.3).
Ad Case 2: Because the \(\Pi \)-walk of \(F_{4}\) has no loops and consists of an Euler trail on the five edges of \(\mathcal {G}\), there is only one—up to relabelling—possibility for \(w_{F_{4}}\) (see Fig. 8 (a)):

In contradistinction with the previous Case 1, now there is one edge, namely f, that is not contained in \(w_{F_{4}}\). This edge must connect either \(v_{1}\) to \(v_{2}\) (\(f:v_{1} \leftrightarrow v_{2}\)), or \(v_{1}\) to \(v_{3}\) ( ), or \(v_{2}\) to \(v_{3}\) (
), or \(v_{2}\) to \(v_{3}\) ( ); cf. Fig. 8 (b) where we show the part of the abstract graph \({\mathbb {P}} (\mathcal {G})\) underlying
); cf. Fig. 8 (b) where we show the part of the abstract graph \({\mathbb {P}} (\mathcal {G})\) underlying  that is determined by \(\partial F_{4}\). To begin with, we focus on the first two subcases.
that is determined by \(\partial F_{4}\). To begin with, we focus on the first two subcases.
Taking into account the various positions of f with respect to local sectors of \(F_{4}\) at \(v_{1}\) and \(v_{2}\) (when  ), respectively \(v_{1}\) and \(v_{3}\) (when \(f:v_{1} \leftrightarrow v_{3}\)), we find four respectively two possibilities for the rotation systems; see Fig. 9. The subcases \(f:v_{1} \leftrightarrow v_{3}\) and
), respectively \(v_{1}\) and \(v_{3}\) (when \(f:v_{1} \leftrightarrow v_{3}\)), we find four respectively two possibilities for the rotation systems; see Fig. 9. The subcases \(f:v_{1} \leftrightarrow v_{3}\) and  are not basically different.Footnote 11 So, we may neglect the case \(f:v_{2} \leftrightarrow v_{3}\). Reasoning as in Case 1, the rotation systems in Fig. 9 yield the possible planar representations of \(\mathcal {G}\) and \(\mathcal {G}^{*}\); see Fig. 10. Note that—by inspection of their rotation systems—all graphs \(\mathcal {G}\) in this figure are different under orientation preserving isomorphisms, whereas only in the cases of Fig. 10 (c), (d) these graphs are equal w.r.t. an orientation reversing isomorphism (apply the relabelling introduced in footnote 11). Apparently, the graphs \(\mathcal {G}\) and \(\mathcal {G}^{*}\) (and thus also \(\mathcal {G}^{*}\) and \(\mathcal {G}\)) in Fig. 10 (a), resp. Fig. 10 (e), are equal (under an orientation preserving isomorphism). The graphs \(\mathcal {G}\) in Fig. 10 (b)–(d), (f) are self-dual.
are not basically different.Footnote 11 So, we may neglect the case \(f:v_{2} \leftrightarrow v_{3}\). Reasoning as in Case 1, the rotation systems in Fig. 9 yield the possible planar representations of \(\mathcal {G}\) and \(\mathcal {G}^{*}\); see Fig. 10. Note that—by inspection of their rotation systems—all graphs \(\mathcal {G}\) in this figure are different under orientation preserving isomorphisms, whereas only in the cases of Fig. 10 (c), (d) these graphs are equal w.r.t. an orientation reversing isomorphism (apply the relabelling introduced in footnote 11). Apparently, the graphs \(\mathcal {G}\) and \(\mathcal {G}^{*}\) (and thus also \(\mathcal {G}^{*}\) and \(\mathcal {G}\)) in Fig. 10 (a), resp. Fig. 10 (e), are equal (under an orientation preserving isomorphism). The graphs \(\mathcal {G}\) in Fig. 10 (b)–(d), (f) are self-dual.
Ad Case 3: Without loss of generality, there are a priori two possibilities for the \(\Pi \)-walks of an arbitrary face, say \(F_{4}\); see Fig. 11 (a), (b). By inspection of the corresponding partial graph \({\mathbb {P}} (\mathcal {G})\), the first possibility is ruled out. So, we focus on Fig. 11 (b). Recall that two facial sectors at the same vertex \(v_{i}\) are separated by facial sectors (at \(v_{i}\)) not belonging to \(F_{4}\) and that in the actual case we have  . So, we find the rotation systems and the distribution of “local facial sectors” as depicted in Fig. 11 (b), where the roles of both e, f and \(F_{5},F_{6}\) may be interchanged. Now, by the face traversal procedure we find: Apart from relabelling and equivalency, there is only one (self-dual) graph possible, Fig. 12.
. So, we find the rotation systems and the distribution of “local facial sectors” as depicted in Fig. 11 (b), where the roles of both e, f and \(F_{5},F_{6}\) may be interchanged. Now, by the face traversal procedure we find: Apart from relabelling and equivalency, there is only one (self-dual) graph possible, Fig. 12.
Now the representation result from Sect. 1.2.2 and the remark there about dual flows, together with the above analysis of the third order Newton graphs yields:
Theorem 2.2
(Classification of third order Newton flows)
-
Apart from conjugacy and duality, there are precisely nine possibilities for the third order structurally stable elliptic Newton flows. These possibilities are characterized by the Newton graphs in Fig. 13.
-
If we add to Fig. 13 the duals of the graphs in Fig. 13 (a), (b), (e), we obtain a classification under merely conjugacy, containing twelve different possibilities.
Remark 2.3
(Case \(r=2\)) By similar (even easier) arguments as used in the above Case \(r=3\), it can be proved that—up to equivalency—there is only one (self-dual) possibility for the second order Newton graphs; see Fig. 14. For a different approach, see [5, Corollary 2.13].
3 Pseudo Newton graphs
Throughout this section, let \(\mathcal {G}_{r}\) be a Newton graph of order r.
Due to the E-property, we know that an arbitrary edge of \(\mathcal {G}_{r}\) is contained in precisely two different faces. If we delete such an edge from \(\mathcal {G}_{r}\) and merge the involved faces \(F_{1}, F_{2}\) into a new face, say \(F_{1,2}\), we obtain a toroidal connected multigraph (again cellularly embedded) with r vertices, \(2r-1\) edges and \(r-1\) faces: \(F_{1,2}\), \(F_{3}, \dots , F_{r}\).
If \(r=2\), then this graph has only one face.
If \(r>2\), put \(J=\{1,2\}\), thus \(\varnothing \ne J \subsetneq \{1, \dots ,r \}\). Then, we know, by the A-property (cf. Sect. 1.2.3), that the set  of exterior \(\mathcal {G}(J)\)-vertices is non-empty. Let
of exterior \(\mathcal {G}(J)\)-vertices is non-empty. Let  , thus \(v \in \partial F_{1,2} \). Hence, v is incident with an edge, adjacent only to one of the faces \(F_{1},F_{2}\). Delete this edge and obtain the “merged face” \(F_{1,2,3}\).
, thus \(v \in \partial F_{1,2} \). Hence, v is incident with an edge, adjacent only to one of the faces \(F_{1},F_{2}\). Delete this edge and obtain the “merged face” \(F_{1,2,3}\).
If \(r=3\), the result is a graph with only one face.
If \(r >3\), put \(J=\{1,2,3 \}\). By the same reasoning as used in the case \(r=3\), it can be shown that \(\partial F_{1,2,3}\) contains an edge belonging to another face than \(F_{1}, F_{2}\) or \(F_{3}\), say \(F_{4}\). Delete this edge and obtain the “merged face” \(F_{1,2,3,4}\). And so on. In this way, we obtain—in \(r-1\) steps—a connected cellularly embedded multigraph, say \(\check{\mathcal {G}}_{r}\), with r vertices, \(r+1\) edges and only one face.
Obviously, \(\check{\mathcal {G}}_{r}\) contains vertices of degree \(\geqslant 2\). Let us assume that there exists a vertex for \(\check{\mathcal {G}}_{r}\), say v, with \(\mathrm{deg}\,v=1\). If we delete this vertex from \(\check{\mathcal {G}}_{r}\), together with the edge incident with v, we obtain a graph with \(r-1\) vertices, r edges and one face. If this graph contains also a vertex of degree 1, we proceed successively. The process stops after L steps, resulting into a (connected, cellularly embedded) multigraph, say  . This graph admits \(\rho =r-L\) vertices (each of degree \(\geqslant 2\)), \(\rho +1\) edges and one face.
. This graph admits \(\rho =r-L\) vertices (each of degree \(\geqslant 2\)), \(\rho +1\) edges and one face.
ApparentlyFootnote 12 we have: \(L<r-1\) and thus \( \leqslant \rho \leqslant r.\) In particular: If \(r=2\), then \(\rho =2\) and \(L=0\). If \(r=3\), then \(\rho =3\) and \(L=0\), or \(\rho =2\) and \(L=1\); see Fig. 15.
From Fig. 14, it follows that \(\mathcal {G}_{2}\) is unique (up to equivalency). From the forthcoming Corollary 3.2 it follows that also \(\check{\mathcal {G}}_{2}\) is unique. However, a graph \(\check{\mathcal {G}}_{r}\), \(r>2\), is not uniquely determined by \(\mathcal {G}_{r}\), as will be clear from Fig. 15, where \(\mathcal {G}_{3}\) is a Newton graph (cf. Sect. 1.2.3 or Fig. 13 (c)).
Lemma 3.1
For the graphs  we have:
we have:
- \((\mathrm{a}_{1})\) :
-
Either, two vertices are of degree 3, and all other vertices of degree 2, or
- \((\mathrm{a}_{2})\) :
-
one vertex is of degree 4, and all other vertices of degree 2.
- \((\mathrm{b})\) :
-
There is a closed, clockwise oriented facial walk, say w, of length \(2(\rho +1)\) such that, traversing w, each vertex v shows up precisely \(\mathrm{deg}\,v\) times. Moreover, w is divided into subwalks \(W_{1},W_{2}, \dots \), connecting vertices of degree \(>2\) that, apart from these begin- and endpoints, contain only, if any, vertices of degree 2.
- \((\mathrm{c}_{1})\) :
-
If \(e_{1}e_{2} \cdots e_{s}\) is a walk of type \(W_{i}\), then also \( W_{i}^{-1}:=e_{s}^{-1} \cdots e_{2}^{-1}e_{1}^{-1}\), where e and \(e^{-1}\) stand for the same edge, but with opposite orientation.
- \((\mathrm{c}_{2})\) :
-
The subwalks \(W_{i}\) and \(W_{i}^{-1}\) are not consecutive in w.
- \((\mathrm{c}_{3})\) :
-
In case \((\mathrm{a}_{1})\), there are precisely six subwalks of type \(W_{i}\), each of them connecting different vertices (of degree 3). In fact there holds: \(w=W_{1}W_{2}W_{3}W_{1}^{-1}W_{2}^{-1}W_{3}^{-1}\).
- \((\mathrm{c}_{4})\) :
-
In case \((\mathrm{a}_{2})\), there are precisely four subwalks of type \(W_{i}\), each of them containing at least one vertex of degree 2. In fact we have: \(w=W_{1}W_{2}W_{1}^{-1}W_{2}^{-1}\).
Proof
(a): Each edge of  contributes precisely twice to the set
contributes precisely twice to the set  . It follows:
. It follows:

Put  , \(i=1,2,3, \dots \) Then (6) yields:
, \(i=1,2,3, \dots \) Then (6) yields:

Note that one uses here also that  has \(\rho \) vertices and all these vertices have degree \(\geqslant 2\). Thus, either \(k_{2}=\rho -2\), \(k_{3}=2\), \(k_{i} =0\) if \(i \ne 2, 3\), or \(k_{2}=\rho -1\), \(k_{4}=1\), \(k_{i} =0\) if \(i \ne 2, 4\).
has \(\rho \) vertices and all these vertices have degree \(\geqslant 2\). Thus, either \(k_{2}=\rho -2\), \(k_{3}=2\), \(k_{i} =0\) if \(i \ne 2, 3\), or \(k_{2}=\rho -1\), \(k_{4}=1\), \(k_{i} =0\) if \(i \ne 2, 4\).
(b): The geometrical dual  of
of  has only one vertex. So, all edges of
has only one vertex. So, all edges of  are loops. Hence, in the facial walk w of
are loops. Hence, in the facial walk w of  , each edge shows up precisely twice (with opposite orientation), cf. Sect. 1.2.3. Thus w has length \(2(\rho +1)\). By the face traversal procedure, each facial sector of
, each edge shows up precisely twice (with opposite orientation), cf. Sect. 1.2.3. Thus w has length \(2(\rho +1)\). By the face traversal procedure, each facial sector of  is encountered once and—at a vertex v—there are \(\mathrm{deg}\,v\) many of such sectors. Application of (\(\mathrm{a}_{1}\)) and (\(\mathrm{a}_{2}\)) yields the second part of the assertion.
is encountered once and—at a vertex v—there are \(\mathrm{deg}\,v\) many of such sectors. Application of (\(\mathrm{a}_{1}\)) and (\(\mathrm{a}_{2}\)) yields the second part of the assertion.
(\(\hbox {c}_{1}\)): Let  be a subwalk of w with \(\mathrm{deg}\,v=2\). Both \(e_{1}^{-1}\) and \(e_{2}^{-1}\) occur precisely once in w, and
be a subwalk of w with \(\mathrm{deg}\,v=2\). Both \(e_{1}^{-1}\) and \(e_{2}^{-1}\) occur precisely once in w, and  is a subwalk of w.
is a subwalk of w.
(\(\hbox {c}_{2}\)): If the subwalk \(W=e_{1}e_{2} \cdots e_{s}\) and its inverse are consecutive, then—by the face traversal procedure—\(e_{1}^{-1}v_{1} e_{1}\) or \(e_{s}v_{s}e_{s}^{-1}\) are subwalks of the facial walk w. In the first case, \(v_{1}\) is both begin- and endpoint of \(e_{1}\); in the second case, \(v_{s}\) is both begin- and endpoint of \(e_{s}\). This would imply that  has a loop which is excluded by construction of this graph.
has a loop which is excluded by construction of this graph.
(c\(_{3}\)): Note that, traversing w once, each of the two vertices of degree 3 is encountered thrice. Suppose that the begin en and points of one of the subwalks \(W_{1},W_{2}, \dots \), say \(W_{1},\) coincide. Then, this also holds for the subwalk \(W_{1}^{-1}\) being—by (\(c_{2}\))—not adjacent to \(W_{1}\). So, traversing w once, this common begin/endpoint is encountered at least four times; in contradiction with our assumption. The assertion is an easy consequence of (\(\hbox {a}_{1}\)) and (\(\hbox {c}_{2}\)).
(\(\hbox {c}_{4}\)): Traversing w once, the vertex of degree 4 is encountered four times. In view of (\(\hbox {a}_{2}\)) and (\(\hbox {c}_{2}\)), we find four closed subwalks of w namely: \(W_{1}, W_{1}^{-1}\) (not adjacent) and \(W_{2}, W_{2}^{-1}\) (not adjacent). Finally we note that each of these subwalks must contain at least one vertex of degree 2 (since  has no loops). \(\square \)
has no loops). \(\square \)
An analysis of its rotation system learns that  is determined by its facial walk w, and thus also by the subwalks \(W_{1}W_{2}W_{3}\) (in case (a\(_{1}\))) or \(W_{1}W_{2}\) (in case (a\(_{2}\))). In fact, only the length of the subwalks \(W_{i} \) matters.
is determined by its facial walk w, and thus also by the subwalks \(W_{1}W_{2}W_{3}\) (in case (a\(_{1}\))) or \(W_{1}W_{2}\) (in case (a\(_{2}\))). In fact, only the length of the subwalks \(W_{i} \) matters.
Corollary 3.2
The graphs \(\widehat{\mathcal {G}}_{2}\) and \(\widehat{\mathcal {G}}_{3}\) can be described as follows:
-
By Lemma 3.1 it follows that \(\widehat{\mathcal {G}}_{2}\) does not have a vertex of degree 4. So, \(\widehat{\mathcal {G}}_{2}\) is of the form as depicted in Fig. 16-a\(_{1}\), where each subwalk \(W_{i}\) admits only one edge. Hence, there is—up to equivalency—only one possibility for \(\widehat{\mathcal {G}}_{2}\). Compare also Fig. 14.
-
It is easily verified that—in Fig. 17—each graph (on solid and dotted edges) is a Newton graph (cf. Sect. 1.2.3). Hence, in case \(\rho =3\), both alternatives in Lemma 3.1 (a) occur. An analysis of their rotation systems learns that the three graphs with only solid edges in Fig. 17 (a)–(c) are equivalent, but not equivalent with the graph on solid edges in Fig. 17 (d). In a similar way it can be proved that the graphs in Fig. 17 expose all possibilities (up to equivalency) for \(\widehat{\mathcal {G}}_{3}\).
Definition 3.3
(Pseudo Newton graphs) Cellularly embedded toroidal graphs, obtained from \(\mathcal {G}_{r}\) by deleting edges and vertices in the way as described above, are called pseudo Newton graphs (of order r).
Apparently, a pseudo Newton graph is not a Newton graph by itself.
The only second order pseudo Newton graph is  ; see Figs. 14 and 16-a\(_{1}\) (with \(W_{i}\) single edges). In the case of third order pseudo Newton graphs (\(L=0\) or 1) we have:
; see Figs. 14 and 16-a\(_{1}\) (with \(W_{i}\) single edges). In the case of third order pseudo Newton graphs (\(L=0\) or 1) we have:
-
If \(L=1\), the graph \(\check{\mathcal {G}}_{3}\) admits a vertex v of deg 1. Deleting v together with the adjacent edge e, we obtain the unique graph \(\check{\mathcal {G}}_{2}\). The two possibilities for the original \(\check{\mathcal {G}}_{3}\) (caused by how e is attached to \(\check{\mathcal {G}}_{2}\)) are mutually equivalent (as follows from their rotation systems). By inspection (see Fig. 13 (d)), we find out that our graph is Newtonian indeed.
-
If \(L=0\) the graph \(\check{\mathcal {G}}_{3}\) is of the type \(\widehat{\mathcal {G}}_{3}\) so that by Corollary 3.2 there are two different possibilities (see Fig. 17 (a), (d)), both being Newtonian.
This is used further on; see Fig. 24 where we pictured these three possibilities.
Remark 3.4
If we delete from  an arbitrary edge, the resulting graph remains connected, but the “alternating sum of vertices, edges and face” equals \(+1\). Thus one obtains a graph that is not cellularly embedded.
an arbitrary edge, the resulting graph remains connected, but the “alternating sum of vertices, edges and face” equals \(+1\). Thus one obtains a graph that is not cellularly embedded.
Definition 3.5
A nuclear Newton graph is a cellularly embedded graph in T with one vertex and two edges.
Apparently a nuclear Newton graph is connected and admits one face and two loops. In particular such a graph has a trivial rotation system. Hence, all nuclear Newton graphs are topologically equivalent and since they expose the same structure as the pseudo Newton graphs  , they will be denoted by \(\widehat{\mathcal {G}}_{1}\). Note that a nuclear Newton graph fulfils the A-property (but certainly not the E-property). Consequently, a graph of the type \(\widehat{\mathcal {G}}_{1}\) is not a Newton graph. Nevertheless, nuclear Newton graphs will play an important role because, in a certain sense, they “generate” certain structurally stable Newton flows. This will be explained in the sequel.
, they will be denoted by \(\widehat{\mathcal {G}}_{1}\). Note that a nuclear Newton graph fulfils the A-property (but certainly not the E-property). Consequently, a graph of the type \(\widehat{\mathcal {G}}_{1}\) is not a Newton graph. Nevertheless, nuclear Newton graphs will play an important role because, in a certain sense, they “generate” certain structurally stable Newton flows. This will be explained in the sequel.
4 Nuclear elliptic Newton flow
Throughout this section, let f be an elliptic function with—viewed to as to a function on \(T=T(\Lambda (\omega _{1}, \omega _{2}))\)—only one zero and one pole, both of order \(r, r\geqslant 2\). Our aim is to derive the result on the corresponding (so-called nuclear) Newton flow  that was already announced in [4, Remark 5.1]. To be more precise:
that was already announced in [4, Remark 5.1]. To be more precise:
All nuclear Newton flows—of any order r—are conjugate, in particular each of them has precisely two saddles (simple) and there are no saddle connections.
When studying—up to conjugacy—the flow  , we may assume (cf. Sect. 1.1.3) that \(\omega _{1}=1\), \(\omega _{2}=i\), thus \(\Lambda =\Lambda _{1,i}\). In particular, the period pair (1, i) is reduced. We represent f (and thus
, we may assume (cf. Sect. 1.1.3) that \(\omega _{1}=1\), \(\omega _{2}=i\), thus \(\Lambda =\Lambda _{1,i}\). In particular, the period pair (1, i) is reduced. We represent f (and thus  ), by the \(\Lambda \)-classes
), by the \(\Lambda \)-classes  , where a, resp. b, stands for the zero, resp. pole, for f, situated in the period parallelogram \(P(=P_{1,i})\). Due to (1), (2) we have
, where a, resp. b, stands for the zero, resp. pole, for f, situated in the period parallelogram \(P(=P_{1,i})\). Due to (1), (2) we have

We may assume that a, b are not on the boundary \(\partial P\) of P. Since the period pair (1, i) is reduced, the images under f of the P-sides \(\gamma _{1}\) and \(\gamma _{2}\) are closed Jordan curves (use the explicit formula for \(\lambda ^{0}\) as presented in footnote 3). From this, we find that the winding numbers \(\eta (f(\gamma _{1}))\) and \(\eta (f(\gamma _{2}))\) can—a priori—only take the values \(-1, 0\) or \(+1\). The combination \((\eta (f(\gamma _{1})),\eta (f(\gamma _{2})))=(0, 0)\) is impossible (because \(a \ne b\)). The remaining combinations lead, for each value of \(r=2,3, \dots \), to eight different values for b each of which giving rise, together with a, to eight pairs of classes \(\mathrm{mod} \, \Lambda \) that fulfil (1), determining flows in \(N_{r}(\Lambda )\), cf. Fig. 18, where we assumed—under a suitable translation of P—that \(a=0\).
Note that the derivative \(f'\) is elliptic of order \(r+1\). Since there is on P only one zero for f (of order r), the function f has two critical points, i.e., saddles for  , counted by multiplicity.
, counted by multiplicity.
The eight pairs (a, b) that possibly determine a nuclear Newton flow are subdivided into two classes, each containing four configurations (a, b) (see Fig. 19):
Class 1:\(a=0\), b on a side of the period square P.
Class 2:\(a=0\), b on a diagonal of the period square P, but not on \(\partial P\).
Apparently, two nuclear Newton flows represented by configurations in the same class are related by a unimodular transformation on the period pair (1, i), and are thus conjugate, see Sect. 1.1.3. So, it is enough to study nuclear Newton flows, possibly represented by (0, 1 / r) or \((0, ({1+i})/{r})\).
\(\underline{\hbox {The configuration }(a, b), a=0, b={1}/{r}}\): The line \(\ell _{1}\) between 0 and 1, and the line \(\ell _{2}\) between i / 2 and \(1+ {i}/{2}\), are axes of mirror symmetry with respect to this configuration (cf. Fig. 20 (a)). By the aid of this symmetry and using the double periodicity of the supposed flow, it is easily proved that this configuration cannot give rise to a desired nuclear Newton flow.
\(\underline{\hbox {The configuration }(a, b), a=0, b=({1+i})/{r}}\): The line \(\ell \) between 0 and \(({1+i})/{2}\) is an axis of mirror symmetry with respect to this configuration (cf. Fig. 20 (b)). So the two saddles of the possible nuclear Newton flow are situated either on the diagonal of P through \(({1+i})/{r}\), or not on this diagonal but symmetric with respect to \(\ell _{1}\). The first possibility can be ruled out (by the aid of the symmetry w.r.t. \(\ell \) and using the double periodicity of the supposed flow). So it remains to analyze the second possibility. (Note that only in the case where \(r=2\), also the second diagonal of P yields an axis of mirror symmetry.)
We focus on Fig. 21, where the only relevant configuration determining a (planar) flow  , is depicted. By symmetry, the \(\ell \)-segments between 0 and \(({1+i})/{r}\), and between \(({1+i})/{r}\) and \(1+i\) are
, is depicted. By symmetry, the \(\ell \)-segments between 0 and \(({1+i})/{r}\), and between \(({1+i})/{r}\) and \(1+i\) are  -trajectories connecting the pole \(({1+i})/{r}\), with the zeros 0 and \(1+i\). Since on the
-trajectories connecting the pole \(({1+i})/{r}\), with the zeros 0 and \(1+i\). Since on the  -trajectories the
-trajectories the  values are constant, we may arrange the argument function on \({\mathbb {C}}\) so that on the segment between \(({1+i})/{r}\) and \(1+i\) we have
values are constant, we may arrange the argument function on \({\mathbb {C}}\) so that on the segment between \(({1+i})/{r}\) and \(1+i\) we have  . We put \(\mathrm{arg}\,f(\sigma _{1})=\alpha \), thus \(0<\alpha <1\) and
. We put \(\mathrm{arg}\,f(\sigma _{1})=\alpha \), thus \(0<\alpha <1\) and  . Note that at the zero / pole for f, each value of
. Note that at the zero / pole for f, each value of  appears r times on equally distributed incoming (outgoing)
appears r times on equally distributed incoming (outgoing)  -trajectories. By the aid of this observation, together with the symmetry and periodicity of f, we find out that the phase portrait of
-trajectories. By the aid of this observation, together with the symmetry and periodicity of f, we find out that the phase portrait of  is as depicted in Fig. 21, where the entries in the boxes stand for the constant values of
is as depicted in Fig. 21, where the entries in the boxes stand for the constant values of  on the unstable manifolds of
on the unstable manifolds of  . In particular, there are no saddle connections.
. In particular, there are no saddle connections.
Remark 4.1
(Canonical form of the phase portrait of a nuclear Newton flow) The qualitative features of the phase portrait of  in Fig. 21 rely on the values of r and \(\alpha \). Put \(\beta ={1}/{2}+\alpha -{1}/{r}\) and \(\gamma ={1}/{r}- 2 \alpha \). Since all angles \(\alpha , \beta \) and \(\gamma \) are strictly positive, we have \(0< \alpha < {1}/({2r})\). Note that if \(r=2\), by symmetry w.r.t. both the diagonals of P, we have \(\alpha =\beta ={1}/{8}\); \(\gamma ={1}/{4}\), see Fig. 22; in this case
in Fig. 21 rely on the values of r and \(\alpha \). Put \(\beta ={1}/{2}+\alpha -{1}/{r}\) and \(\gamma ={1}/{r}- 2 \alpha \). Since all angles \(\alpha , \beta \) and \(\gamma \) are strictly positive, we have \(0< \alpha < {1}/({2r})\). Note that if \(r=2\), by symmetry w.r.t. both the diagonals of P, we have \(\alpha =\beta ={1}/{8}\); \(\gamma ={1}/{4}\), see Fig. 22; in this case  is just
is just  , with \(\wp \) the Weierstrass’ \(\wp \)-function (lemniscate case, cf. [1]). This is also clear from Fig. 18, cf. also [3].
, with \(\wp \) the Weierstrass’ \(\wp \)-function (lemniscate case, cf. [1]). This is also clear from Fig. 18, cf. also [3].
Altogether we conclude:
Lemma 4.2
All nuclear elliptic Newton flows of the same order r are mutually conjugate.
For f an elliptic function of order r with—on T—only one zero and pole we now define:
Definition 4.3
\(\mathcal {H}_{r}(f)\) is the graph on T with as vertex, edges and face respectively:
-
the zero for f on T (as attractor for
 );
); -
the unstable manifolds for
 at the two critical points for f;
at the two critical points for f; -
the basin of repulsion for
 of a pole for f on T (as a repellor for
of a pole for f on T (as a repellor for  ).
).
From Fig. 21 it is evident that \(\mathcal {H}_{r}(f)\) is a cellularly embedded pseudo graph (loops and multiple edges permitted). This graph is referred to as to the nuclear Newton graph for  . By Lemma 4.2, the graphs \(\mathcal {H}_{r}(f)\), are—up to equivalency—unique, and will be denoted by \(\mathcal {H}_{r}\) (cf. the comment on Definition 3.5).
. By Lemma 4.2, the graphs \(\mathcal {H}_{r}(f)\), are—up to equivalency—unique, and will be denoted by \(\mathcal {H}_{r}\) (cf. the comment on Definition 3.5).
If a, b (both in  ) are of Class 2 (i.e., the configuration (a, b) determines a nuclear flow with a and b as zero resp. pole of order r), we introduce the doubly periodic functions:
) are of Class 2 (i.e., the configuration (a, b) determines a nuclear flow with a and b as zero resp. pole of order r), we introduce the doubly periodic functions:
where the summation takes place over all points in lattice  .
.
We define the planar flow \(\underline{\mathcal {N}}(f)\) by

Lemma 4.4
The flow \(\underline{\mathcal {N}}(f)\) is smooth on \({\mathbb {C}}\) and exhibits the same phase portrait as \(\overline{\mathcal {N}}(f)\), but its attractors (at zeros for f) and its repellors (at the poles for f) are all generic, i.e., of the hyperbolic type.
Proof
Since \(r\geqslant 2\) (thus \(4r-4 \geqslant 4\)), series of the type as under the square root in (7) are uniform convergent in each compact subset of \({\mathbb {C}} \backslash (a+ \Lambda \cup b+\Lambda )\). From this, together with the smoothness of \(\overline{\mathcal {N}}(f)\) on \({\mathbb {C}}\), it follows that \(\underline{\mathcal {N}}(f)\) is smooth outside the union of \(a+ \Lambda \) and \(b+ \Lambda \). Special attention should be paid to the lattice points. Here the smoothness of \(\underline{\mathcal {N}}(f)\) as well as the genericity of its attractors and repellors follows by a careful (but straightforward) analysis of the local behaviour of \(\underline{\mathcal {N}}(f)\) around these points; cf. the explicit expression for \(\overline{\mathcal {N}}(f)\) in footnote 1 and note that zeros and poles are of order r. Since outside their equilibria \(\underline{\mathcal {N}}(f)\) and \(\overline{\mathcal {N}}(f)\) are equal—up to a strictly positive factor—their portraits coincide. \(\square \)
Corollary 4.5
All nuclear Newton flows of arbitrary order are mutually conjugate.
Proof
Let \(\underline{N}(f)\) be arbitrary. Because all its equilibria are generic and there are no saddle connections, this flow is \(C^{1}\)-structurally stable. The embedded graph \(\mathcal {H}_{r}\) , together with its geometrical dual \(\mathcal {H}_{r}(f)^{*}\) forms the so-called distinguished graph that determines—up to an orientation preserving homeomorphism—the phase portrait of \(\underline{N}(f)\) (cf. [10, 11] and Sect. 1.2.3). This distinghuished graph is extremely simple, giving rise to only four distinghuished sets (see Fig. 21). This holds for any flow of the type \(\underline{N}(f)\). Now, application of Peixoto’s classification theorem for \(C^{1}\)-structurally stable flows on T yields the assertion. \(\square \)
, together with its geometrical dual \(\mathcal {H}_{r}(f)^{*}\) forms the so-called distinguished graph that determines—up to an orientation preserving homeomorphism—the phase portrait of \(\underline{N}(f)\) (cf. [10, 11] and Sect. 1.2.3). This distinghuished graph is extremely simple, giving rise to only four distinghuished sets (see Fig. 21). This holds for any flow of the type \(\underline{N}(f)\). Now, application of Peixoto’s classification theorem for \(C^{1}\)-structurally stable flows on T yields the assertion. \(\square \)
We end up with a comment on the nuclear Newton graph \(\mathcal {H}(f_{\omega _{1}, \omega _{2}})\), \(\mathrm{Im}\,{\omega _{2}}/{\omega _{1}} >0\), where \((\omega _{1}, \omega _{2})\), is related to the period pair (1, i) by the unimodular transformation
Thus \((p_{1}, p_{2})\) and \((q_{1}, q_{2})\) are co-prime, and

Our aim is to describe \(\mathcal {H}(f_{\omega _{1}, \omega _{2}})\) as a graph on the canonical torus  . In view of Lemma 4.2, the two edges of \(\mathcal {H}(f_{\omega _{1}, \omega _{2}})\) are closed Jordan curves on T, corresponding to the unstable manifolds of \(\overline{\mathcal {N}}(f_{\omega _{1},\omega _{2}})\) at the two critical points for f that are situated in the period parallelogram \(P_{\omega _{1}, \omega _{2}}\). These unstable manifolds connect
. In view of Lemma 4.2, the two edges of \(\mathcal {H}(f_{\omega _{1}, \omega _{2}})\) are closed Jordan curves on T, corresponding to the unstable manifolds of \(\overline{\mathcal {N}}(f_{\omega _{1},\omega _{2}})\) at the two critical points for f that are situated in the period parallelogram \(P_{\omega _{1}, \omega _{2}}\). These unstable manifolds connect  with
with  , and
, and  respectively. Hence, one of the \(\mathcal {H}(f_{\omega _{1}, \omega _{2}}) \)-edges wraps \(p_{1}\) times around T in the direction of the period 1 and \(p_{2}\) times around T in the direction of the period i, whereas the other edge wraps \(q_{1}\) times around this torus in the 1-direction respectively \(q_{2}\) times in the i-direction. See also Fig. 23, where we have chosen for f the Weierstrass \(\wp \)-function (lemniscate case), i.e., \(r=2\), \(a=0\) and \(\omega _{1}=3+i\), \(\omega _{2}=2+i\). Compare also Fig. 22.
respectively. Hence, one of the \(\mathcal {H}(f_{\omega _{1}, \omega _{2}}) \)-edges wraps \(p_{1}\) times around T in the direction of the period 1 and \(p_{2}\) times around T in the direction of the period i, whereas the other edge wraps \(q_{1}\) times around this torus in the 1-direction respectively \(q_{2}\) times in the i-direction. See also Fig. 23, where we have chosen for f the Weierstrass \(\wp \)-function (lemniscate case), i.e., \(r=2\), \(a=0\) and \(\omega _{1}=3+i\), \(\omega _{2}=2+i\). Compare also Fig. 22.
5 The bifurcation and creation of elliptic Newton flows
In this section we discuss the connection between pseudo Newton graphs and Newton flows. In order not to blow up the size of our study, we focus—after a brief introduction—on the cases \(r=2, 3\). However, even from these simplest cases we get some flavor of what we may expect when dealing with a more general approach.
We consider functions \(g \in E_{r}\) with r simple zeros and only one pole (of order r); such functions exist, cf. Sect. 1.1.1. The set of all these functions is denoted by \( E_{r}^{1}\) and will be endowed with the relative topology induced by the topology \(\tau _{0}\) on \(E_{r}\). Since the derivative \(g'\) of g is elliptic of order \(r+1\), the zeros for g being simple, there are \(r+1\) critical points for g (counted by multiplicity).
We consider the set \(N^{1}_{r}\) of all toroidal Newton flows  . Such a flow is \(C^{1}\)-structurally stable (thus also \(\tau _{0}\)-structurally stable) if and only if (cf. Sect. 1.1.4 and [10, 11]):
. Such a flow is \(C^{1}\)-structurally stable (thus also \(\tau _{0}\)-structurally stable) if and only if (cf. Sect. 1.1.4 and [10, 11]):
-
1.
All saddles are simple (thus generic).
-
2.
There are no “saddle connections”.
-
3.
The repellor at the pole for g is generic.
In general none of these conditions is fulfilled. We overcome this complication as follows:
Ad 1. Under suitably chosen—but arbitrarily small—perturbations of the zeros and poles of g, thereby preserving their multiplicities,  turns into a Newton flow with only simple (thus \(r+1\)) saddles (cf. [4, Lemma 5.7], case \(A=r\), \(B=1\)).
turns into a Newton flow with only simple (thus \(r+1\)) saddles (cf. [4, Lemma 5.7], case \(A=r\), \(B=1\)).
Ad 2. Possible saddle connections can be broken by “adding to g a suitably chosen, but arbitrarily small constant” (cf. [4, proof of Theorem 5.6 (2)]).
Ad 3. With the aid of a suitably chosen additional damping factor to  , the pole of g may be viewed to as generic for the resulting flow; cf. the proof of Lemma 4.4. (Note that the simple zeros for g yield already generic equilibria).
, the pole of g may be viewed to as generic for the resulting flow; cf. the proof of Lemma 4.4. (Note that the simple zeros for g yield already generic equilibria).
This opens the possibility to adapt g and  in such a way that for “almost all” functions g the flow
in such a way that for “almost all” functions g the flow  is structurally stable (see Sect. 1.1.4, and [4, Theorem 5.6]). More formally:
is structurally stable (see Sect. 1.1.4, and [4, Theorem 5.6]). More formally:
The set of functionsgin \( E_{r}^{1}\),with
of functionsgin \( E_{r}^{1}\),with structurally stable, is\(\tau _{0}\)-open and -dense in \( E_{r}^{1}\).
structurally stable, is\(\tau _{0}\)-open and -dense in \( E_{r}^{1}\).
From now on, we assume that  is structurally stable and define the multigraph \(\mathcal {G}_{r}(g)\) on T as follows:
is structurally stable and define the multigraph \(\mathcal {G}_{r}(g)\) on T as follows:
-
Vertices: r zeros for g (i.e., stable star nodes for
 ).
). -
Edges: \(r+1\) unstable manifolds at the critical points for g (orthogonal saddles for
 ).
). -
Face: the basin of repulsion of the unstable star node at the pole for g.
Note that \(\mathcal {G}_{r}(g)\) has no loops (since the zeros for g are simple). It is easily seen that \(\mathcal {G}_{r}(g)\) is cellularly embedded (cf. [5, proof of Lemma 2.9]). Because \(\mathcal {G}_{r}(g)\) has only one face, the geometrical dual \(\mathcal {G}_{r}(g)^{*}\) admits merely loops and the \(\Pi \)-walk for the \(\mathcal {G}_{r}(g)\)-face consists of \(2(r+1)\) edges, each occurring twice, be it with opposite orientation; here the orientation on the \(\Pi \)-walk is induced by the anti-clockwise orientation on the embedded \(\mathcal {G}_{r}(g)^{*}\)-edges at the pole for g. In the case where \(\mathcal {G}_{r}(g)\) admits a vertex of degree 1, we delete this vertex together with the adjacent edge, resulting into a cellularly embedded graph on \(r-1\) vertices, r edges and only one face. If this graph has a vertex of degree 1, we repeat the procedure, and so on. The process stops after  steps, resulting into a connected, cellularly embedded multigraph with
steps, resulting into a connected, cellularly embedded multigraph with  vertices (merely of degree \(>1\)), \(\rho \) edges and one face.
vertices (merely of degree \(>1\)), \(\rho \) edges and one face.
Now, we ask whether the graphs \(\mathcal {G}_{r}(g)\),  , are indeed pseudo Newtonian, i.e., do they originate from a Newton graph? And even so, can all pseudo Newton graphs be represented by elliptic Newton flows?
, are indeed pseudo Newtonian, i.e., do they originate from a Newton graph? And even so, can all pseudo Newton graphs be represented by elliptic Newton flows?
In the sequel we present an (affirmative) answer to these questions in the cases \(r=2,3\).
Lemma 5.1
If \(r=2\) or 3, then \(\mathcal {G}_{r}(g)\),  , is a pseudo Newton graph \(\check{\mathcal {G}}_{r}\).
, is a pseudo Newton graph \(\check{\mathcal {G}}_{r}\).
Proof
Firstly we note that from the proof of Lemma 3.1 it follows: Any cellularly embedded graph with two vertices (merely of degree \(>1\)), three edges and one face, must be equivalent with \(\widehat{\mathcal {G}}_{2}\); if this graph has three vertices (merely of degree \(>1\)), four edges and one face, it must be equivalent with the graphs in either Fig. 17 (a) or (d) (solid edges).
\(\underline{\hbox {Case} \,r=2}\): If there is a vertex of degree 1, then two (of the three) edges would connect the other vertex to itself. This is impossible since \(\check{\mathcal {G}}_{2}(g)\) does not admit loops. By our preambule, \(\mathcal {G}_{2}(g)\) is equivalent with the unique (cf. Sect. 2) pseudo Newton graph  .
.
\(\underline{\hbox {Case} \,r=3}\): If all vertices have degree \(> 1\), we apply our preambule and find the pseudo Newton graphs in Fig. 24 (b), (c) as possibilities. If v is a vertex of degree 1, we delete v together with its adjacent edge and distinguish between:
(i) The resulting graph has again a vertex of degree 1. Then two (of the four edges) would connect the third vertex to itself, which is impossible because \(\mathcal {G}_{2}(g)\) has no loops.
(ii) The resulting graph has no vertices of degree 1. Applying our preambule to the original \(\mathcal {G}_{r}(g)\), we find that the latter graph is pseudo Newtonian as depicted in Fig. 24 (a).
(Note that in Fig. 24 the values of degree \(v_{i}\) discriminate between the three possibilities.) \(\square \)
The above reasoning in the case \(r=3\) does not imply that each of the graphs in Fig. 24 can be realized by a Newton flow. So we need
Lemma 5.2
If \(r=2\) or 3, then each pseudo Newton graph of the type \(\check{\mathcal {G}}_{r}\) or \(\widehat{\mathcal {G}}_{r}\) can be realized as \(\mathcal {G}_{r}(g)\),  .
.
Proof
\(\underline{r=2}\): Follows from the proof of Lemma 5.1.
\(\underline{r=3}\): The local phase portrait around the attractor  of \(\overline{\mathcal {N}} (f)\) in Fig. 21 is depicted in the forthcoming Fig. 26. Recall that v is the only zero for f and a star node for \(\overline{\mathcal {N}} (f)\); also \(\alpha >0\), \(\alpha +\gamma ={1}/{r} -\alpha \) and \(\alpha +\beta +\gamma ={1}/{2}\). Thus we have: \(\beta > {1}/({2r})\) so that the combined angle \(\beta +\beta \) in Fig. 26 spans an arc greater than
of \(\overline{\mathcal {N}} (f)\) in Fig. 21 is depicted in the forthcoming Fig. 26. Recall that v is the only zero for f and a star node for \(\overline{\mathcal {N}} (f)\); also \(\alpha >0\), \(\alpha +\gamma ={1}/{r} -\alpha \) and \(\alpha +\beta +\gamma ={1}/{2}\). Thus we have: \(\beta > {1}/({2r})\) so that the combined angle \(\beta +\beta \) in Fig. 26 spans an arc greater than  .
.
Now the idea is: To split off from the third order zero v for f a simple zero (\(v_{1}\)) (“Step 1”), and thereupon, to split up the remaining double zero (\(v'_{1}\)) into two simple ones (\(v_{2},v_{3}\)) (“Step 2”), in such a way that by an appropriate strategy, the resulting functions give rise to Newton flows with associated graphs, determining each of the three possible types in Fig. 24.
\(\underline{\text {Ad Step 1}}\): We perturb the original function f into an elliptic function g with one simple (\(v_{1}\)) and one double (\(v'_{1}\) ) zero (close to each other), and one third order pole \(w_{1}\) (thus closeFootnote 13 to the third order pole w of f). The original flow  perturbs into a flow
perturbs into a flow  with \(v_{1}\) and \(v'_{1}\) as attractors and \(w_{1}\) as repellor. When \(v_{1}\) tends to \(v'_{1}\), the perturbed function g will tend to f, and thus the perturbed flow
with \(v_{1}\) and \(v'_{1}\) as attractors and \(w_{1}\) as repellor. When \(v_{1}\) tends to \(v'_{1}\), the perturbed function g will tend to f, and thus the perturbed flow  to
to  , cf. Sect. 1.1.2. In particular, when the splitted zeros are sufficiently close to each other and the circle \(C_{1}\) that encloses an open disk \(D_{1}\) with center \(v'_{1}\), is chosen sufficiently small, \(C_{1}\) is a global boundary (cf. [7]) for the perturbed flow
, cf. Sect. 1.1.2. In particular, when the splitted zeros are sufficiently close to each other and the circle \(C_{1}\) that encloses an open disk \(D_{1}\) with center \(v'_{1}\), is chosen sufficiently small, \(C_{1}\) is a global boundary (cf. [7]) for the perturbed flow  . It follows that, apart from the equilibria \(v_{1}\) and \(v'_{1}\) (both of Poincaré index 1) the flow
. It follows that, apart from the equilibria \(v_{1}\) and \(v'_{1}\) (both of Poincaré index 1) the flow  exhibits on \(D_{1}\) one other equilibrium (with index \(-1\)): a simple saddle, say c (cf. [2]). From this, it follows (cf. Sect. 1.1.1) that the phase portrait of
exhibits on \(D_{1}\) one other equilibrium (with index \(-1\)): a simple saddle, say c (cf. [2]). From this, it follows (cf. Sect. 1.1.1) that the phase portrait of  around \(v_{1}\) and \(v'_{1}\) is as sketched in Fig. 25 (a), where the local basin of attraction for \(v_{1}\) is shaded and intersects \(C_{1}\) under an arc with length approximately 1 / 3.
around \(v_{1}\) and \(v'_{1}\) is as sketched in Fig. 25 (a), where the local basin of attraction for \(v_{1}\) is shaded and intersects \(C_{1}\) under an arc with length approximately 1 / 3.
On the (compact!) complement \(T \backslash D_{1}\) this flow has one repellor (\(w_{1}\)) and two saddles. The repellor may be considered as hyperbolic (by the suitably chosen damping factor, cf. the proof of Lemma 4.4), whereas the saddles are distinct and thus simple (because  has two simple saddles, say \(\sigma _{1},\sigma _{2}\), depending continuously on \(v_{1}\) and \(v'_{1}\)). Hence, the restriction of
has two simple saddles, say \(\sigma _{1},\sigma _{2}\), depending continuously on \(v_{1}\) and \(v'_{1}\)). Hence, the restriction of  to \(T \backslash D_{1}\) is \(\varepsilon \)-structurally stable (cf. [10]). So, we may conclude that, if \(v_{1}\) (chosen sufficiently close to \(v'_{1}\)) turns around \(v'_{1}\), the phase portraits outside \(D_{1}\) of the perturbed flows undergo a change that is negligible in the sense of the \(C^{1}\)-topology. Therefore, we denote the equilibria of
to \(T \backslash D_{1}\) is \(\varepsilon \)-structurally stable (cf. [10]). So, we may conclude that, if \(v_{1}\) (chosen sufficiently close to \(v'_{1}\)) turns around \(v'_{1}\), the phase portraits outside \(D_{1}\) of the perturbed flows undergo a change that is negligible in the sense of the \(C^{1}\)-topology. Therefore, we denote the equilibria of  on \(T \backslash D_{1}\) by \(w_{1},\sigma _{1},\sigma _{2}\) (i.e., without reference to \(v_{1}\)). We move \(v_{1}\) around a small circle, centered at \(v'_{1}\) and focus on two positions (I, II) of \(v_{1}\), specified by the position of \(v_{1}\) w.r.t. the symmetry axis l. See Fig. 26 in comparison with Fig. 27, where we sketched some trajectories of the phase portraits of \(\overline{\mathcal {N}} (g)\) on \(D_{1}\).
on \(T \backslash D_{1}\) by \(w_{1},\sigma _{1},\sigma _{2}\) (i.e., without reference to \(v_{1}\)). We move \(v_{1}\) around a small circle, centered at \(v'_{1}\) and focus on two positions (I, II) of \(v_{1}\), specified by the position of \(v_{1}\) w.r.t. the symmetry axis l. See Fig. 26 in comparison with Fig. 27, where we sketched some trajectories of the phase portraits of \(\overline{\mathcal {N}} (g)\) on \(D_{1}\).
\(\underline{\text {Ad Step 2}}\): We proceed as in Step 1. Splitting \(v'_{1}\) into \(v_{2}\) and \(v_{3}\) (sufficiently close to each other) yields a perturbed elliptic function h, and thus a perturbed flow  . Consider a circle \(C_{2}\), centered at the mid-point of \(v_{2}\) and \(v_{3}\), that encloses an open disk \(D_{2}\) containing these points. If we choose \(C_{2}\) sufficiently small, it is a global boundary of
. Consider a circle \(C_{2}\), centered at the mid-point of \(v_{2}\) and \(v_{3}\), that encloses an open disk \(D_{2}\) containing these points. If we choose \(C_{2}\) sufficiently small, it is a global boundary of  . Reasoning as in Step 1, we find out that
. Reasoning as in Step 1, we find out that  has on \(D_{2}\) two simple attractors (\(v_{2},v_{3}\)) and one simple saddle: d (close to the mid-point of \(v_{2}\) and \(v_{3}\); cf. Fig. 25 (b)), where the local basin of attraction for \(v_{3}\) is shaded and intersects \(C_{2}\) under an arc with length approximately 1 / 2. Moreover, as for
has on \(D_{2}\) two simple attractors (\(v_{2},v_{3}\)) and one simple saddle: d (close to the mid-point of \(v_{2}\) and \(v_{3}\); cf. Fig. 25 (b)), where the local basin of attraction for \(v_{3}\) is shaded and intersects \(C_{2}\) under an arc with length approximately 1 / 2. Moreover, as for  in Step 1, the flow
in Step 1, the flow  is \(\varepsilon \)-structurally stable outside \(D_{2}\). So, we may conclude that, if \(v_{2}\) and \(v_{3}\) turn (in diametrical position) around their mid-point, the phase portraits outside \(D_{2}\) of the perturbed flows undergo a change that is negligible in the sense of \(C^{1}\)-topology. Therefore, we denote the equilibria of
is \(\varepsilon \)-structurally stable outside \(D_{2}\). So, we may conclude that, if \(v_{2}\) and \(v_{3}\) turn (in diametrical position) around their mid-point, the phase portraits outside \(D_{2}\) of the perturbed flows undergo a change that is negligible in the sense of \(C^{1}\)-topology. Therefore, we denote the equilibria of  on \(T \backslash D_{2}\) by \(v_{1}, w_{1}, c, \sigma _{1}\), and \(\sigma _{2}\) (i.e., without reference to \(v_{2}\) and \(v_{3}\)).
on \(T \backslash D_{2}\) by \(v_{1}, w_{1}, c, \sigma _{1}\), and \(\sigma _{2}\) (i.e., without reference to \(v_{2}\) and \(v_{3}\)).
Finally, for \(v_{1}\) in the position of Fig. 27(I) we choose the pair (\(v_{2},v_{3}\)) as in Fig. 28(I); and for \(v_{1}\) in the position of Fig. 27(II), we distinguish between two possibilities: Fig. 28 (IIa) and (IIb). Note that, with these choices of \(v_{1},v_{2},v_{3}\) each of the obtained functions has three simple zeros and one triple pole. Moreover, the four saddles are simple and not connected, whereas the three zeros are simple as well. So the graph of the associated Newton flow is well defined and has only one face, four edges and three vertices. Recall that the various values of degree \(v_{i}\) discriminate between the three possibilities for the graphs of type \(\check{\mathcal {G}}_{3}\)). Now inspection of Fig. 28 yields the assertion. \(\square \)
Up till now, we paid attention to pseudo Newton graphs with only one face (i.e., of type \(\check{\mathcal {G}}_{r}\) or \(\widehat{\mathcal {G}}_{r}\), \(r=2,3\)). If \(r=2\), these are the only possibilities.
If \(r=3\), there are also pseudo Newton graphs (denoted by \(\underline{\mathcal {G}}\)) with two faces and angles summing up to 1 or 2. When the boundaries of any pair of the original \(\mathcal {G}_{3}\)-faces have a subwalk in common, these walks have length 1 or 2. (Use the A-property and cf. Fig. 13.) So, when two \(\mathcal {G}_{3}\)-faces are merged, the resulting \(\underline{\mathcal {G}}\)-face admits either only vertices of degree \(\geqslant 2\)or one vertex of degree 1.Footnote 14 From now on, we focus on the Newton graphs as exposed in Fig. 13 (a), (d) (since all other Newton graphs (in Fig. 13) can be dealt with in the same way, there is no loss of generality). Then the two \(\underline{\mathcal {G}}\)-faces under consideration are  ) and \(\underline{F}_{\,8}:=F_{5}\); see Fig. 29 (in comparison with Fig. 13 (a), (d).
) and \(\underline{F}_{\,8}:=F_{5}\); see Fig. 29 (in comparison with Fig. 13 (a), (d).
We consider the distinguished graph  of \(\underline{\mathcal {G}}\) and its dual \(\underline{\mathcal {G}}^{*}\) see Sect. 1.2.3. Following Peixoto [10, 11] we claim that
of \(\underline{\mathcal {G}}\) and its dual \(\underline{\mathcal {G}}^{*}\) see Sect. 1.2.3. Following Peixoto [10, 11] we claim that  determines a \(C^{1}\)-structurally stable toroidal flow \(X(\underline{\mathcal {G}})\) with canonical regions as depictedFootnote 15 in Fig. 30. As equilibria for \(X(\underline{\mathcal {G}})\) we have: three stable and two unstable proper nodes (corresponding to the \(\underline{\mathcal {G}}\)-resp. \(\underline{\mathcal {G}}^{*}\)-vertices) and five orthogonal saddles (corresponding to the pairs \((e, e^{*})\) of \(\underline{\mathcal {G}}\)- and \(\underline{\mathcal {G}}^{*}\)-edges). Basically arguing as in our paper [5] (proof of Theorem 4.1), it can be shown that \(X(\underline{\mathcal {G}})\) is equivalent with an elliptic Newton flow generated by a function on three simple zeros, one double and one simple pole and five simple critical points; cf.Footnote 16 Figure 30. As an elliptic Newton flow, \(X(\underline{\mathcal {G}})\) is not (\(\tau _{0}\)-)structurally stable, since \(\underline{\mathcal {G}}\) is not Newtonian, cf. Sect. 1.2.2. However, by the aid of a suitably chosen damping factor, cf. Lemma 4.4 (preambule), and within the class \(N^{2}_{3}\) of all elliptic Newton flows generated by the class \(E^{2}_{3}\) of functions on three simple zeros, on one double and one simple pole and on five simple critical points, the structurally stable species constitute a \(\tau _{0}\)-open and -dense subset (\( \widetilde{E}^{2}_{3}\)) of \(E^{2}_{3}\).
determines a \(C^{1}\)-structurally stable toroidal flow \(X(\underline{\mathcal {G}})\) with canonical regions as depictedFootnote 15 in Fig. 30. As equilibria for \(X(\underline{\mathcal {G}})\) we have: three stable and two unstable proper nodes (corresponding to the \(\underline{\mathcal {G}}\)-resp. \(\underline{\mathcal {G}}^{*}\)-vertices) and five orthogonal saddles (corresponding to the pairs \((e, e^{*})\) of \(\underline{\mathcal {G}}\)- and \(\underline{\mathcal {G}}^{*}\)-edges). Basically arguing as in our paper [5] (proof of Theorem 4.1), it can be shown that \(X(\underline{\mathcal {G}})\) is equivalent with an elliptic Newton flow generated by a function on three simple zeros, one double and one simple pole and five simple critical points; cf.Footnote 16 Figure 30. As an elliptic Newton flow, \(X(\underline{\mathcal {G}})\) is not (\(\tau _{0}\)-)structurally stable, since \(\underline{\mathcal {G}}\) is not Newtonian, cf. Sect. 1.2.2. However, by the aid of a suitably chosen damping factor, cf. Lemma 4.4 (preambule), and within the class \(N^{2}_{3}\) of all elliptic Newton flows generated by the class \(E^{2}_{3}\) of functions on three simple zeros, on one double and one simple pole and on five simple critical points, the structurally stable species constitute a \(\tau _{0}\)-open and -dense subset (\( \widetilde{E}^{2}_{3}\)) of \(E^{2}_{3}\).
Altogether, we find:
Theorem 5.3
Any pseudo Newton graph of order r, \(r=2, 3\), represents an elliptic Newton flow of order r.
In Lemma 5.2 we proved: the third order nuclear Newton flow creates—by splitting up (“bifurcating”) zeros—all structurally stable elliptic Newton flows in \(N^{1}_{3}\). We claim:
-
The structurally stable Newton flows in \(N^{1}_{3}\) create—by splitting up triple poles into a double and a single one—all structurally stable Newton flows in \(N^{2}_{3}\).
-
The structurally stable Newton flows in \(N^{2}_{3}\) create—by splitting up double poles into two single ones—all structurally stable Newton flows in \(N_{3}\).
This can be proved by the same technique as used in the proof of Lemma 5.2 (use \(\varepsilon \)-structural stability and the A-property to implant in an appropriate way the unstable manifold at the saddle that arises from splitting up of a multiple pole).
Notes
In fact, we consider the \(C^{1}\)-system
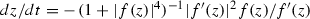 : a continuous version of Newton’s damped iteration method for finding zeros for f.
: a continuous version of Newton’s damped iteration method for finding zeros for f.Occasionally, we will refer to
 as to a toroidal (elliptic) Newton flow.
as to a toroidal (elliptic) Newton flow.In fact
 , where
, where 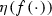 stands for winding numbers of the curves \(f(\gamma _{1})\) and \(f(\gamma _{2})\) with \(\gamma _{i}\) the sides of \(P_{\omega _{1}, \omega _{2}}\) spanned by \(\omega _{i}\), \(i=1, 2\) (cf. [8]).
stands for winding numbers of the curves \(f(\gamma _{1})\) and \(f(\gamma _{2})\) with \(\gamma _{i}\) the sides of \(P_{\omega _{1}, \omega _{2}}\) spanned by \(\omega _{i}\), \(i=1, 2\) (cf. [8]).\(\tau \) satisfies \(\text {Im}\, \tau > 0\), \(| \tau | \geqslant 1\),
 , \(\text {Re}\, \tau \leqslant 0\) if \(| \tau |=1\).
, \(\text {Re}\, \tau \leqslant 0\) if \(| \tau |=1\).A pair \((\omega _{1}^{*},\omega _{2}^{*})\) of basic periods for \(f^{*}\) is called reduced if \(|\omega _{1}^{*}|\) is minimal among all periods for \(f^{*}\) whereas \(| \omega _{2}^{*} |\) is minimal among all periods \(\omega \) for \(f^{*}\) with the property \(\mathrm{Im}\,{\omega }/{\omega _{1}^{*}} >0\).
i.e., all zeros, poles and critical points for f are simple, and no critical points are connected by
 -trajectories; the set of all such functions is denoted by
-trajectories; the set of all such functions is denoted by  .
.The graph \(\mathcal {G}(f )\) has no loops, basically because the zeros for f are simple.
If
 , and thus \(\mathcal {G}(f ) \sim \mathcal {G}({1}/{f})\), we call the flow
, and thus \(\mathcal {G}(f ) \sim \mathcal {G}({1}/{f})\), we call the flow  and also the graph \(\mathcal {G}(f )\)self-dual. More generally, \(\mathcal {G}\) is called self-dual if
and also the graph \(\mathcal {G}(f )\)self-dual. More generally, \(\mathcal {G}\) is called self-dual if 
Apparently, such “minimal” l exists since \(\mathcal {G}\) is finite. In fact, the first edge which is repeated in the same direction when traversing w, is \(e_1\) (cf. [9]).
Note that by assumption \(\mathcal {G}\) has no loops.
Relabelling
 , \(a \leftrightarrow b\) and \(c \leftrightarrow e\), transforms the two configurations in Fig. 9 (e), (f) into configurations that generate (anti-clockwise oriented) rotation systems describing the case \(f:v_{2} \leftrightarrow v_{3}\).
, \(a \leftrightarrow b\) and \(c \leftrightarrow e\), transforms the two configurations in Fig. 9 (e), (f) into configurations that generate (anti-clockwise oriented) rotation systems describing the case \(f:v_{2} \leftrightarrow v_{3}\).Assume \(L=r-1\).Then
 , \(\rho =1\), would be a connected subgraph of \(\mathcal {G}\), with two edges and one vertex; this contradicts the fact that \(\mathcal {G}\) has no loops. Compare the forthcoming Definition 3.5.
, \(\rho =1\), would be a connected subgraph of \(\mathcal {G}\), with two edges and one vertex; this contradicts the fact that \(\mathcal {G}\) has no loops. Compare the forthcoming Definition 3.5.Use property (1).
The E-property holds not always for \(\underline{\mathcal {G}}\): Only if there is a \(\underline{\mathcal {G}}\)-vertex of degree 1, the dual \(\underline{\mathcal {G}}^{*}\) admits a contractible loop (corresponding with the edge adjacent to this vertex); all other \(\underline{\mathcal {G}}^{*}\)-loops—if there are any—are non-contractible.
The picture in the r.h.s. of Fig. 30 corresponds to a canonical region in the \(\underline{\mathcal {G}}\)-face with angles summing up to 1, determining the simple pole for \(X(\underline{\mathcal {G}})\), cf. also Fig. 1. The other two pictures correspond to the \(\underline{\mathcal {G}}\)-face with angles summing up to 2, determining the double pole for \(X(\underline{\mathcal {G}})\).
References
Abramowitz, A., Stegun, I.A. (eds.): Handbook of Mathematical Functions. Dover Books on Mathematics. Dover, New York (1965)
Guillemin, V., Pollack, A.: Differential Topology. Prentice Hall, Englewood Cliffs (1974)
Helminck, G.F., Kamphof, F.H., Streng, M., Twilt, F.: The qualitative behaviour of Newton flows for Weierstrass\(^{\prime }\) \(\wp \)-functions. Complex Var. Theory Appl. 47(10), 867–880 (2002)
Helminck, G.F., Twilt, F.: Newton flows for elliptic functions I. Structural stability: characterization & genericity. Complex Var. Elliptic Equ. 63(6), 815–835 (2018)
Helminck, G.F., Twilt, F.: Newton flows for elliptic functions II. Structural stability: classification and representation. Eur. J. Math 3(3), 691–727 (2017)
Hirsch, M.W.: Differential Topology. Texts in Mathematics, vol. 33. Springer, New York (1976)
Jongen, H.T., Jonker, P., Twilt, F.: Nonlinear Optimization in Finite Dimensions. Nonconvex Optimization and Its Applications, vol. 47. Kluwer, Dordrecht (2000)
Markushevich, A.I.: Theory of Functions of a Complex Variable, vol. III. Prentice Hall, Englewood Cliffs (1967)
Mohar, B., Thomassen, C.: Graphs on Surfaces. John Hopkins Studies in the Mathematical Sciences. John Hopkins University Press, Baltimore (2001)
Peixoto, M.M.: Structural stability on two-dimensional manifolds. Topology 1(2), 101–120 (1962)
Peixoto, M.M.: On the classification of flows on \(2\)-manifolds. In: Peixoto, M.M. (ed.) Dynamical Systems, pp. 389–419. Academic Press, New York (1973)
Acknowledgements
The authors would like to thank the referee for a careful reading of the manuscript and various constructive remarks.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Helminck, G.F., Twilt, F. Newton flows for elliptic functions III & IV. European Journal of Mathematics 5, 1364–1395 (2019). https://doi.org/10.1007/s40879-018-0289-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0289-y
Keywords
- Dynamical system
- Desingularized elliptic Newton flow
- Structural stability
- Elliptic function
- Phase portrait
- Newton graph (elliptic-, nuclear-, pseudo-)
- Cellularly embedded toroidal (distinguished) graph
- Face traversal procedure
- Angle property
- Euler property
- Hall condition



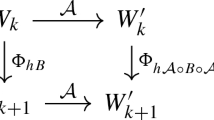
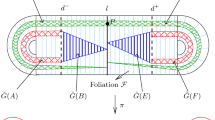
 , and
, and  is a strictly decreasing function on t.
is a strictly decreasing function on t. implies
implies  ; see Sect.
; see Sect.  has precisely 2r different simple saddles (all orthogonal).
has precisely 2r different simple saddles (all orthogonal). in
in  iff the function f is non-degenerate
iff the function f is non-degenerate
 for a pole (zero) of f
for a pole (zero) of f and
and  are structurally stable and of the same order, then
are structurally stable and of the same order, then 
 such that
such that 

 of exterior
of exterior 






















 );
); at the two critical points for f;
at the two critical points for f; of a pole for f on T (as a repellor for
of a pole for f on T (as a repellor for  ).
).


 ).
). ).
).

 around the zero
around the zero  for f;
for f; 
 on
on 
 on
on 


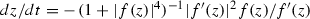 : a continuous version of Newton’s damped iteration method for finding zeros for f.
: a continuous version of Newton’s damped iteration method for finding zeros for f. as to a toroidal (elliptic) Newton flow.
as to a toroidal (elliptic) Newton flow. , where
, where 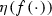 stands for winding numbers of the curves
stands for winding numbers of the curves  ,
,  -trajectories; the set of all such functions is denoted by
-trajectories; the set of all such functions is denoted by 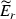 .
. , and thus
, and thus  and also the graph
and also the graph 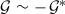
 ,
,  ,
,