Abstract
Sufficient conditions on a shift invariant probability measure on the base of a suspension flow \(\{S_t\}\) over a countable alphabet Markov shift are stated under which the corresponding \(\{S_t\}\)-invariant measure is a measure with maximal entropy.
Similar content being viewed by others
1 Introduction
The present paper is motivated by the study in [1, 2] of a measure with maximal entropy for the Teihmüller flow on the moduli space of Abelian differentials. The following result was obtained there: a measure with maximal entropy for this flow exists, is unique, and moreover, it is the well-known invariant measure constructed by H. Masur and W. Veech in the 80th. In several steps the problem reduces to the investigation of a measure with maximal entropy for a suspension flow over a countable alphabet Markov shift. Our argument can be briefly presented as follows. Veech [12] found the entropy of the Teihmüller flow with respect to the Masur–Veech measure and expressed it in terms of the genus g of the corresponding Riemann surface and the number n of punctures (in the moduli space context, the surface itself is not fixed, but g and n are). For the measure \(\mu \) obtained by transferring the Masur–Veech measure to the phase space of the suspension flow in question (more exactly to its base), we discovered some properties in terms of this flow alone, independently of the origin of \(\mu \). Using the existence of an invariant measure with these properties, we evaluated the topological entropy (the maximum of the measure theoretic entropies) of the suspension flow, which turned out to coincide with the Veech entropy. This immediately implied our main result.
Now the following natural question arises: if Veech’s entropy result [12] have not been known, would it be possible to deduce it directly from the properties of the measure, without resorting to the Teihmüller flow itself? In other words, taking into account that our evaluation of the topological entropy is valid not only for the specific suspension flow related to the Teihmüller flow, but for every suspension flow that has an invariant measure with the above properties, is it true that the entropy of this flow with respect to such a measure coincides with its topological entropy? It could seem that the whole information contained in the assumptions on \(\mu \) was already used in [2]. In fact this is not true. In the present paper we are based on the same assumptions as in [2], but exploit them in a different way (see the proof of Theorem 2.10 below).
2 Definitions and results
We start from some more or less standard definitions.
Definition 2.1
A one-to-one bi-measurable transformation T of a measurable space \((X,{\fancyscript{B}})\) onto itself is called an automorphism, a group of automorphisms \(T^t\), \(t\in {\mathbb {Z}}\), is called a cascade (a discrete time dynamical system); a continuous parameter group of automorphisms \(T^t\), \(t\in {\mathbb {R}}\), is called a flow (a continuous time dynamical system). Two dynamical systems, \((X_1,{\fancyscript{B}}_1,\{T_1^t\})\) and \((X_2,{\fancyscript{B}}_2,\{T_2^t\})\), are called isomorphic if there is a one-to-one epimorphic bi-measurable map \({\Phi }:X_1\rightarrow X_2\) such that  for all t. (For the discrete time dynamical systems, it is sufficient to check the last equation for \(t=1\).)
for all t. (For the discrete time dynamical systems, it is sufficient to check the last equation for \(t=1\).)
We often have to deal with a dynamical system \((X,{\fancyscript{B}},\{T^t\})\) endowed with a \(\{T^t\}\)-invariant probability measure \(\mu \) on X. We will call the quadruple \((X,{\fancyscript{B}},\{T^t\},\mu )\) a dynamical system with invariant measure.
Definition 2.2
Two dynamical systems with invariant measure, \((X_1,{\fancyscript{B}}_1,\{T_1^t\},\mu _1)\) and \((X_2,{\fancyscript{B}}_2, \{T_2^t\},\mu _2)\), are called isomorphic if there are sets \(X'_1\in {\fancyscript{B}}_1, X'_2\in {\fancyscript{B}}_2\) invariant with respect to all \(T_1^t\) and all \(T_2^t\), respectively, such that \(\mu _1(X'_1)=\mu _2(X'_2)=1\) and the restrictions \(\bigl (X'_1,{\fancyscript{B}}_1|_{X'_1},\{T_1^t\}|_{X'_1}\bigr )\) and \(\bigl (X'_2,{\fancyscript{B}}_2|_{X'_2}, \{ T_2^t\}|_{X'_2}\bigr )\) are isomorphic in the sense of Definition 2.1.
In what follows we will usually drop \({\fancyscript{B}}\) from the notation of a dynamical system.
A suspension flow (or special flow) over an automorphism T is defined as follows (see, e.g., [4, 8]).
Definition 2.3
Let T be an automorphism of a measurable space \((X,{\fancyscript{B}})\), and \(f:X\rightarrow (c,\infty ), c>0\), be a Borel measurable function. We set

For \(t\ge 0\) and every  , we define a map \(S_t\) by
, we define a map \(S_t\) by

where n is such that
For \(t<0\) we set \(S_t=(S_{-t})^{-1}\). For the suspension flow thus obtained we will use the notation (T, f). The space X and the function f are often called the base of the suspension flow and the roof function, respectively.
The notion of a suspension flow is an abstract version of the Poincare transversal surface idea. Suspension constructions (flows and cascades) over countable alphabet Markov shifts turn out to be a powerful tool in the study of some classes of smooth dynamical systems on manifolds [1, 2, 6, 10].
For an automorphism T of X and for \(x\in X, C\subset X\), we set

and for the suspension flow \(\{S_t\}=(T,f)\), we set

\(\tau (x,C)\) is clearly the first approach time of the set C by the point x under the action of the cascade \(\{T^n\}\), while \(\widetilde{\tau }(x,C)\) can be a little inaccurately treated as the first approach time of the set C by the point x under the action of the flow (T, f) (we put \(\tau (x,C)=\infty \) if x will never approach C).
We are mainly interested in suspension flows over topological (or symbolic) Markov shifts.
Definition 2.4
Let \(G=(V,E)\) be a directed graph with vertex set V and edge set  . One defines the two-sided infinite path space \(X(G)=X\) of G by
. One defines the two-sided infinite path space \(X(G)=X\) of G by

and introduces the topology of pointwise convergence in X(G) (every \(x\in X\) is a function from \({\mathbb {Z}}\) to V) and the (left) shift transformation T by
This T, which is clearly a homeomorphism of X, is called the topological (or symbolic) Markov shift with alphabet V. If \(G=(V,E)\) is a complete graph, i.e.,  , the shift T on X(G) is called a full shift or a topological (symbolic) Bernoulli shift.
, the shift T on X(G) is called a full shift or a topological (symbolic) Bernoulli shift.
In what follows we assume that V is countable and G is connected as a directed graph. Let

We impose the following conditions on f: f(x) does not depend on \(x_i\) with \(i<0\) and
Remark 2.5
While the former condition can be essentially relaxed, it enables us to use results from [2], where this condition is present. In contrast, the latter condition, which is also present in [2], is significant.
Denote the family of all T-invariant Borel probability measures on X by \({\fancyscript{I}}(T)\) and set

(here and below we write \(\mu (f)\) instead of  ),
),

If  , it generates, in a canonical way, a probability measure
, it generates, in a canonical way, a probability measure  on
on  that is invariant w.r.t. the suspension flow \(\{S_t\}=(T,f)\).
that is invariant w.r.t. the suspension flow \(\{S_t\}=(T,f)\).
For  , denote the entropy of T with respect to \(\mu \) by \(h_\mu (T)\) and the entropy of the flow (T, f) with respect to the measure
, denote the entropy of T with respect to \(\mu \) by \(h_\mu (T)\) and the entropy of the flow (T, f) with respect to the measure  by
by  .
.
Definition 2.6
Let

We say that \(h_{\text {top}}(T,f)\) is the topological entropy of the flow (T, f) and that every measure  with
with

is a maximal measure for (T, f).
Remark 2.7
The justification for the above definition of the topological entropy of (T, f) is that, in the case of a finite alphabet Markov shift, this quantity would really be the topological entropy of this suspension flow.
Remark 2.8
It is known [2] that in the situation we are going to study, a maximal measure is unique, but even in quite simple cases it does not necessarily exist.
In order to state the main result of this paper we have to give the following definition.
Definition 2.9
Given a graph \(G=(V,E)\) as above, we call a sequence \(w=(v_0,v_1,\) \(\dots ,v_{n-1})\) with \(v_i\in V, (v_i,v_{i+1})\in E\) a path (or a word) of length \(|w|=n\) in G. We call such w a simple word if \((v_0,v_1,\dots ,v_k)\ne (v_{n-k},v_{n-k+1},\dots ,v_n)\) unless \(k=n\). We denote the set of all words in G by W(G).
If \(w=(v_0,v_1,\dots ,v_k)\) and \(w'=(v'_0,v'_1,\dots ,v'_l)\) are two words in G such that \(v_k=v'_0\), then their concatenation \(ww'=(v_0,v_1,\dots ,v_k,v'_1,\dots ,v'_l)\) is also a word in G. We write \(w'\subset w\) if \(v_{r+i}=v'_i\) for some \(r\ge 0\) and \(i=0,1,\dots ,l\). For every \(w\in W(G)\), we denote the cylinder \(C_w=\{x\in X:(x_0,\dots ,x_{|w|-1})=w\}\) by \(C_w\).
The next theorem is the main result of the paper. To state it we have to introduce the following four conditions on a measure  :
:
-
(a)
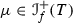 , i.e., \(\mu (C)>0\) for all open nonempty \(C\subset X\).
, i.e., \(\mu (C)>0\) for all open nonempty \(C\subset X\). -
(b)
\(\mu \) is ergodic, i.e., the transformation T is ergodic with respect to the measure \(\mu \).
-
(c)
\(H_\mu (\xi )<\infty \), where \(\xi \) is the partition of X into one-dimensional cylinders \(C_v, v\in V\), and \(H_\mu (\xi )\) is the entropy of this partition with respect to \(\mu \).
-
(d)
There exist a constant \(s\ge 0\), a function \(\kappa :{\mathbb {Z}}_+\rightarrow {\mathbb {R}}_+\), and an arbitrary long simple word \(w\in W(G)\) such that \(\lim _{r\rightarrow \infty }\kappa (r)=0\) and, for all \(\widehat{w}\in W(G)\) satisfying the conditions \(w\widehat{w}w\in W(G), \widehat{w}\not \subset w\) and \(\mu \)-almost all \(x\in C_{ww\widehat{w}}\), the inequality
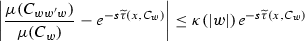
holds. Each word \(\widehat{w}\) satisfying two last conditions will be called w-admissible, we denote the set of such words by \(\widehat{A}_w\).
Theorem 2.10
Let (X, T) be an infinite alphabet Markov shift determined by a connected graph \(G=(V,E)\) and f be a function with summable variations defined on X(G) such that f(x) depends on \(x_0,x_1,\dots \) only and \(f(x)\ge c>0\). Assume that a measure  satisfies conditions (a)–(d). Then \(\overline{\mu }\) is a maximal measure for the suspension flow (T, f).
satisfies conditions (a)–(d). Then \(\overline{\mu }\) is a maximal measure for the suspension flow (T, f).
Remark 2.11
This theorem is close to [2, Theorem 2.2]. In particular, the conclusions of these theorems coincide. But their assumptions are different: instead of the equality  , we assume that \(H_{\overline{\mu }}(\xi )<\infty \). The second assumption seems to be much less restrictive and purely technical. It is quite possible that it can be rejected. As to the first assumption, we derive it from the other assumptions of Theorem 2.10. Moreover, there is good reason to believe that the sufficient conditions on the maximal measure stated in the theorem are close to necessary ones.
, we assume that \(H_{\overline{\mu }}(\xi )<\infty \). The second assumption seems to be much less restrictive and purely technical. It is quite possible that it can be rejected. As to the first assumption, we derive it from the other assumptions of Theorem 2.10. Moreover, there is good reason to believe that the sufficient conditions on the maximal measure stated in the theorem are close to necessary ones.
Theorem 2.10 will be proved in Sect 4. In Sect. 3 we state and in part prove some auxiliary facts.
3 Main lemmas
Lemma 3.1
Let (T, f) be a suspension flow over an infinite alphabet topological Bernoulli shift (X, T), where f(x) depends only on \(x_0\), i.e., there exists a function \(f_0:V\rightarrow [c,\infty ), c>0\), such that \(f(x)=f_0(x_0), x\in X\). Let

Then
-
(i)
\(h_{\mathrm{top}}(T,f)\) is the unique solution to the equation
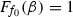 if this equation is solvable, otherwise
if this equation is solvable, otherwise 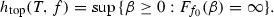
-
(ii)
(T, f) has a maximal measure \(\mu _{\mathrm{max}}\) if and only if there exists a number \(\beta _0>0\) such that

This measure is unique and is the Bernoulli measure such that
 .
.
Statement (i) is [2, Lemma 2.7] (see also [5]), statement (ii) can be derived from (i) or from [11, Theorem 3].
Lemma 3.2
Let (T, f) be a suspension flow as in Lemma 3.1 and \(h=h_{\mathrm{top}}(T,f)\). Then, for the function  ,
,
\((g_0\) corresponds to g in the same way as \(f_0\) corresponds to f).
Proof
From Lemma 3.1 (i) it follows that either  or
or  . Clearly in both cases (2) holds.\(\square \)
. Clearly in both cases (2) holds.\(\square \)
Lemma 3.3
Let (T, f) be a suspension flow over an infinite alphabet topological Bernoulli shift (X, T) and \(\inf _{x\in X}f(x)\ge c>0\). Assume that for every \(v\in V\), every pair \(x,x'\in C_v\), and some \(\delta \in [0,c/2]\), we have
Then there exists a function \(g:X\rightarrow [0,\infty )\) such that
-
\((\alpha ) \, \,g(x)=g_0(x_0)\) for some function \(g_0:V\rightarrow [0,\infty )\);
-
\((\beta )\,\, |g(x)-f(x)|\le \delta , x\in X\);
-
\((\gamma )\,\, h_{\mathrm{top}}(T,f)=h_{\mathrm{top}}(T,g)\).
Proof
Let

Clearly
Hence

Moreover,
We want to show that the function  is continuous in \(t\in [0,c/2]\). For \(t'\in [0,c/4]\), we obviously have
is continuous in \(t\in [0,c/2]\). For \(t'\in [0,c/4]\), we obviously have

In the same way and for the same \(t,t'\), we obtain

From (5) and (6) the continuity required follows.
Now, using (3), (4) and the assumption \(\delta \le c/2\), we can find a point \(t_0\in [0,\delta ]\) such that

It is evident that the function \(g(x)=f^+(x)-t_0, x\in X\), satisfies conditions \((\alpha )\)–\((\gamma )\) above.\(\square \)
The following lemma (see [6]) will be used in the end of the next section.
Lemma 3.4
Let \(\{\mu _n, n\ge 0\}\) be a sequence of T-invariant probability measures on \(X=X(G)\), see Introduction. Assume that there exist two sequences, \(r_n\) and \(\alpha _n, r_n\in {\mathbb {N}}, \alpha _n\in {\mathbb {R}}_+, n\in {\mathbb {N}}\), and a constant \(h\ge 0\) such that

for all cylinders \(C\subset X\) of the form \(C=C_{\widetilde{w}}\), where \(\widetilde{w}\) is a word in G of length \(|\widetilde{w}|= r_n\). Then \(h_{\mu _0}(T)\ge h\).
4 Proof of Theorem 2.10
We divide the proof into several steps.
1. For a simple word \(w\in W(G)\), we set

i.e., \(C^\infty _w\) is the set of the points \(x\in X\) that approaches \(C_w\) infinitely many times under the action of both T and \(T^{-1}\). This set is clearly measurable and T-invariant. So one can consider the restriction \(T|_{C^\infty _w}\) and the suspension flow \(\bigl (T|_{C^\infty _w},f|_{C^\infty _w}\bigr )\).
Let \(C'_w=C^\infty _w\cap C_w\) and \(T_{C'_w}\) be the transformation induced by T on \(C'_w\) (the first return map).
The following statements are rather simple and essentially known (see Lemma 2.8 and the proof of Theorem 2.2 in [2]).
Proposition 4.1
The dynamical system \((C'_w,T_{C'_w})\) is isomorphic to the Bernoulli shift with alphabet \(A_w\), consisting of all words \(w\widehat{w}w\in W(G)\), where \(w\not \subset \widehat{w}\).
Proof
Taking into account the simplicity of w, one sees that every point \(x\in C'_w\) is a sequence \((x_i)_{i\in {\mathbb {Z}}}\) such that, for each \(k\in {\mathbb {Z}}\), there exists \(i_k=i_k(x)\in {\mathbb {Z}}\) with the following properties: 1) \(i_0=0,\) 2) \(i_{k+1}\ge i_k+|w|,\) 3) \((x_{i_k},\dots ,x_{i_k+|w|-1})=w,\) 4) \((x_{i_k+|w|-1},\dots ,x_{i_{k+1}})=\widehat{w}\). It is clear, that \(T_{C'_w}x\) is the left shift of x by \(|w|+|\widehat{w}_k|-2=i_{k+1}-i_k-1\) steps. We assign the sequence \({\Phi }_wx=(w\widehat{w}_kw)_{k\in {\mathbb {Z}}}\) to x and observe that \({\Phi }_w\) is a continuous one-to-one map from \(C'_w\) to \((A_w)^{{\mathbb {Z}}}\). Moreover, \({\Phi }_wT_{C'_w}x=T^{|w|+|\widehat{w}_k|-2}{\Phi }_wx\).\(\square \)
Let

(See (1) for the definition of \(\tau (x,C_w\)).)
Proposition 4.2
If \(w\widehat{w}w\in A_w\) and \(x,x'\in C_{w\widehat{w}w}\), then

Proposition 4.3
The suspension flows \(\bigl (T|_{C^\infty _w},f|_{C^\infty _w}\bigr )\) and \((T_{C'_w},f_w)\) are isomorphic.
Proof
By Definition 2.3 the flow \(\bigl (T|_{C^\infty _w},f|_{C^\infty _w}\bigr )\) acts on the space \((C_w^\infty )_f\) that consists of the pairs (x, u), where \(x\in C_w^\infty , 0\le u<f(x)\). For every such a pair, we set

It is easy to see that \(\widetilde{\Phi }_w:(x,u)\mapsto (x',u')\) is a bi-measurable one-to-one map of \((C_w^\infty )_f\) to \((C'_w)_f\) that takes \(\bigl (T|_{C^\infty _w},f|_{C^\infty _w}\bigr )\) to \((T_{C'_w},f_w)\).\(\square \)
Corollary 4.4
\(h_{\mathrm{top}}\bigl (T|_{C^\infty _w},f|_{C^\infty _w}\bigr )= h_{\mathrm{top}}(T_{C'_w},f_w)=h_{\mathrm{top}}(T,f)\).
Proof
The first equality is obvious, the second one follows from the fact that the supremum in Definition 2.6 can be taken over  , see, e.g., [2, Lemma 2.9].\(\square \)
, see, e.g., [2, Lemma 2.9].\(\square \)
Denote the sequence space \((A_w)^{{\mathbb {Z}}}\) by \(Y_w\), its elements by \(y=(y_i)_{i\in {\mathbb {Z}}}\), and the one step left shift on \(Y_w\) by \(\sigma \). Proposition 4.1 implies that the suspension flow \((T_{C'_w},f_w)\) is isomorphic to the suspension flow \((\sigma ,\varphi ^w)\), where
Denote the right hand side of (8) by \(\delta _w\). By (8) and (9)
for all \(y,y'\in Y_w\) with \(y_0=y'_0\).
2. Let \({\fancyscript{W}}(G)\) be the set of simple words for which condition (d) on the measure \(\overline{\mu }\) (see Introduction) is satisfied. For each \(w\in {\fancyscript{W}}(G)\), we will introduce two probability measures, \(\mu ^w\) and \(\nu ^w\), on \(Y_w\). To define \(\mu ^w\) we note that \(\overline{\mu }(C_w)>0\) (see condition (a) on \(\overline{\mu }\)) and hence \(\overline{\mu }(C'_w)>0\). Now denote  where
where  is the normalized restriction of \(\overline{\mu }\) to \(C'_w\).
is the normalized restriction of \(\overline{\mu }\) to \(C'_w\).
To define \(\nu ^w\), we first observe that by the definition of the functions \(f_w\) and \(\varphi ^w\) the condition (d) on \(\overline{\mu }\) can be rewritten in the form

for all \(a\in A_w\) and \(\mu ^w\)-almost all \(y\in C_a\).
Now choose \(w\in {\fancyscript{W}}(G)\) such that

(the latter inequality follows from the definition of \(\varphi ^w\)). Then we can apply Lemma 3.3 to find a function \(\psi ^w\) on \(Y_w\) such that:
-
\((\alpha _w)\,\,\psi ^w(y)=\psi ^w_0(y_0)\) for some function \(\psi ^w_0:A_w\rightarrow [0,\infty )\);
-
\((\beta _w)\,\,|\psi ^w(y)-\varphi ^w(y)|\le \delta _w, y\in Y_w\);
-
\((\gamma _w)\,\, h_{\mathrm{top}}(\sigma ,\varphi ^w)=h_{\mathrm{top}}(\sigma ,\psi ^w)\).
The next proposition is a statement of [2, Theorem 2.2 (i)], one can observe that only conditions (a), (b) and (d) on the measure \(\overline{\mu }\) are used in its proof.
Proposition 4.5
Under the conditions of Theorem 2.10 the equation \(s=h_{\mathrm{top}}(T,f)\) holds.
We now perturb a little the function \(\psi ^w\) to add one useful property to \((\alpha _w)\)–\((\gamma _w)\).
Proposition 4.6
If |w| is large enough, then there exists a number \(r_w\) such that

Proof
For every \(a\in A_w\), we can choose a point \(y_a\in C_a\) such that

(see (10)) and hence

By \((\alpha _w), (\beta _w)\) and (14)

Summing up (15) over a and taking into account Lemmas 3.1, 3.2, Proposition 4.4 and the fact that \(\mu ^w\) is a probability measure, we obtain
If we now set

then (11)–(13) will clearly hold.\(\square \)
Corollary 4.7
For any \(\varepsilon >0\), there exists a word \(w=w_\varepsilon \in {\fancyscript{W}}(G)\) so long that one can find a function \(\psi ^w:Y_w\rightarrow (0,\infty )\) with the following properties:

This follows immediately from Proposition 4.6 due to the properties of the function \(\psi ^w\) there (see \((\alpha _w)\)–\((\gamma _w)\) above) and the fact that

(for the new function we use the same notation \(\psi ^w\)).
From now on we assume that \(\varepsilon \) and \(w=w_\varepsilon \) as in Corollary 4.7 are fixed, unless otherwise stated.
We define \(\nu ^w\) to be the Bernoulli measure on \(Y_w\) with

Let us show that the measures \(\mu ^w\) and \(\nu ^w\) are in some sense close to each other. From (10) and the definition of \(\nu ^w\), for every \(a\in A_w\), one obtains

Taking w still longer if necessary, from (19), (16) and the condition on \(\kappa (|w|)\) we obtain
From (16) and (20) we see that \(\nu ^w(\psi ^w)<\infty \). Hence Lemma 3.1 and Proposition 4.5 combined with (18) show that \(\nu ^w\) is the maximal measure for the suspension flow \((\sigma ,\psi ^w)\).
3. We now carry over the measures \(\nu ^w\) and \(\mu ^w\) to X with the help of the map \({\Phi }_w^{-1}\) (see the proof of Proposition 4.1). So we set

We also have  (see step 2 of this proof).
(see step 2 of this proof).
From the definition of \({\Phi }_w\) it follows that \(\nu '_w\) is a probability measure on \(C'_w\), and (20) can be rewritten, for every \(\widehat{w}\in \widehat{A}_w\), as

The next goal is to extend \(\nu '_w\) to the whole X. We first observe that

Moreover, the sets \(T^i\bigl (C'_w\cap C_{w\widehat{w}w}\bigr )\) do not intersect each other when \(\widehat{w}\in \widehat{A}_w\) and \(i=0,1,\dots ,|w|+|\widehat{w}|-3\). It is easy to check that

where \(C^\infty _w\) is defined in (7).
Taking into account (22), we introduce a measure \(\nu _w^\infty \) on \(C^\infty _w\) by

It is clear that the measure \(\nu _w^\infty \) is thus well-defined (as a measure on X) and T-invariant. Besides, replacing \(\nu '_w\) by  on the right hand side of (23) yields the measure
on the right hand side of (23) yields the measure  on the left hand side.
on the left hand side.
Compare \(\overline{\mu }_w^\infty (C_w^\infty )\) and \(\nu _w^\infty (C_w^\infty )\). Since \(\overline{\mu }\) is an ergodic measure and \(C_w^\infty \) is a T-invariant set of positive measure, we have \(\overline{\mu }(C_w^\infty )=1\), i.e.,

Hence, by (21), (23), and the definition of \(\overline{\mu }{}'_w\),

We denote the normalized version of \(\nu _w^\infty \) by \(\overline{\nu }_w\), i.e., \(\overline{\nu }_w=\nu _w^\infty /\nu _w^\infty (C^\infty _w)\).
Our next goal is to show that some finite-dimensional distributions of the T-invariant probability measures \(\overline{\nu }_w\) and \(\overline{\mu }\) are close to each other.
By the definition of \(\overline{\nu }_w\) and \(\nu _w^\infty \)

Since \(\overline{\mu }\) is an ergodic measure, one can everywhere replace \(\overline{\mu }(C'_w)\) by \(\overline{\mu }(C_w)\) and \(\overline{\mu }(C'_w\cap C_{w\widehat{w}w})\) by \(\overline{\mu }(C_{w\widehat{w}w})\). From this, using (21) and (24), we obtain

Notice that \(\overline{\nu }_w\) is also an ergodic measure. Indeed, by Proposition 4.1 the dynamical system \((C'_w,T_{C'_w},\nu '_w)\) is isomorphic to the Bernoulli shift \((Y_w,\sigma ,\nu ^w)\) and hence ergodic. But \((X,T,\overline{\nu }_w)\) is by construction an integral automorphism over \((C'_w,T_{C'_w},\nu '_w)\), which is known to be ergodic together with the automorphism in the base. Therefore (25) can be rewritten in the form

Consider an arbitrary word \(\widetilde{w}\) in G and denote the set of pairs \((\widehat{w},i)\) such that
by \(\widehat{A}_{w,\widetilde{w}}\). Since \(\overline{\mu }(C_w^\infty )=1, \overline{\mu }\)-almost every point x of the cylinder \(C_{\widetilde{w}}\) belongs to \(C_w^\infty \). For such x, there exists a unique pair \((\widehat{w},i)\in \widehat{A}_{w,\widetilde{w}}\) such that \(x\in T^iC_{w\widehat{w}w}\). Thus the cylinders \(C_{\widetilde{w}}\cap T^iC_{w\widehat{w}w}\) with \((\widehat{w},i)\in \widehat{A}_{w,\widetilde{w}}\) constitute a \(\overline{\mu }\)-mod 0 partition of \(C_{\widetilde{w}}\). Assume that \(|\widetilde{w}|\le |w|\). Then either \(C_{\widetilde{w}}\cap T^iC_{w\widehat{w}w}=\emptyset \), or \(T^iC_{w\widehat{w}w}\subset C_{\widetilde{w}}\). Hence

For the same reasons a similar formula holds for the measure \(\overline{\nu }_w\) in place of \(\overline{\mu }\). Moreover, in both sums on the right hand side the same terms equal zero, while the non-zero terms equal \(\overline{\mu }(C_{w\widehat{w}w})\) and \(\overline{\nu }_w(C_{w\widehat{w}w})\), respectively. Hence by (26), for every \(\widetilde{w}\) with \(|\widetilde{w}|\le |w|\),

where the last inequality holds when \(\varepsilon \le 1/3\).
4. Now we are going to compare the integrals \(\overline{\nu }_w(f)\) and \(\overline{\mu }(f)\). Using properties of f, one can find a number \(n(\varepsilon )\in {\mathbb {N}}\) and a function \(f_\varepsilon \) such that \(f_\varepsilon (x)\) depends on \(x_0,\dots ,x_{n(\varepsilon )}\) only and \(|f(x)-f_\varepsilon (x)|\le \varepsilon \) for all \(x\in X\). Then

The function \(f_\varepsilon \) is chosen so that it is constant on every cylinder of the form \(C_{\widetilde{w}}\), where \(|\widetilde{w}|=n(\varepsilon )\). We number these cylinders: \(C_{\widetilde{w}_1},C_{\widetilde{w}_2},\dots \), and denote the value of \(f_{\varepsilon }\) on \(C_{\widetilde{w}_i}\) by \(f_{\varepsilon ,i}, i=1,2,\dots \) Now, by (27), (28), and the definition of \(f_\varepsilon \),

which can be made arbitrary small by choosing a small \(\varepsilon \).
By the definition of the measure \(\nu ^w\) it is a maximal measure for the suspension flow \((\sigma ,\psi ^w)\), i.e.,

(For the last equality see (17).) Using (16), we obtain

(For the definition of \(\psi ^w\) see step 3 of this proof.) Hence

By Propositions 4.1 and 4.3 the suspension flows \((\sigma ,\varphi ^w)\) and \((T_{C'_w},f_w)\) are isomorphic. From this it follows that
and that the suspension flows with invariant measures \((\sigma ,\varphi ^w,\nu ^w)\) and \((T,f,\overline{\nu }_w)\) are isomorphic as well (see the definition of the measure \(\overline{\nu }_w\)). The latter fact together with (29) imply that

5. It remains to estimate \(h_{\overline{\mu }}(T)\) from below.
We take an arbitrary sequence of positive numbers \(\varepsilon (n)\le 1/3, n\ge 1\), such that \(\lim _{n\rightarrow \infty }\varepsilon (n)=0\) and denote \(w_n=w_{\varepsilon (n)}\) (see Corollary 4.7). Let also

Without loss of generality we can assume that \(|w_n|\rightarrow \infty \) as \(n\rightarrow \infty \). Using (28), (27), and (30) with \(\varepsilon =\varepsilon (n)\), it is easy to check that the assumptions of Lemma 3.4 are satisfied. By this lemma  , so that
, so that
But the opposite inequality holds for every measure from  . Thus the proof is completed.
. Thus the proof is completed.
References
Bufetov, A.I., Gurevich, B.M.: On the measure with maximum entropy for the Teichmüller flow on the moduli space of Abelian differentials. Funct. Anal. Appl. 42(3), 224–226 (2008)
Bufetov, A.I., Gurevich, B.M.: Existence and uniqueness of the measure of maximal entropy for the Teichmüller flow on the moduli space of Abelian differentials. Sb. Math. 202(7), 935–970 (2011)
Buzzi, J., Sarig, O.: Uniqueness of equilibrium measures for countable Markov shifts and multidimensional piecewise expanding maps. Ergodic Theory Dynam. Systems 23(5), 1383–1400 (2003)
Cornfeld, I.P., Fomin, S.V., Sinai, Ya.G.: Ergodic Theory. Grundlehren der Mathematischen Wissenschaften, vol. 245. Springer, Berlin (1982)
Gurevich, B.M.: A variational characterization of one-dimensional countable state Gibbs random fields. Z. Wahrsch. Verw. Gebiete 68(2), 205–242 (1984)
Gurevich, B.M.: Weak approximation of an invariant measure and a low boundary of the entropy (2014). arXiv:1408.1609
Gurevich, B., Katok, S.: Arithmetic coding and entropy for the positive geodesic flow on the modular surface. Mosc. Math. J. 1(4), 569–582 (2001)
Katok, A., Hasselblatt, B.: Introduction to the Modern Theory of Dynamical Systems. Encyclopedia of Mathematics and its Applications, vol. 54. Cambridge University Press, Cambridge (1995)
Sarig, O.M.: Bernoulli equilibrium states for surface diffeomorphisms. J. Mod. Dyn. 5(3), 593–608 (2011)
Sarig, O.M.: Symbolic dynamics for surface diffeomorphisms with positive entropy. J. Amer. Math. Soc. 26(2), 341–426 (2013)
Savchenko, S.V.: Special flows constructed from countable topological Markov chains. Funct. Anal. Appl. 32(1), 32–41 (1998)
Veech, W.A.: The Teichmüller geodesic flow. Ann. Math. 124(3), 441–530 (1986)
Author information
Authors and Affiliations
Corresponding author
Additional information
The work is supported in part by the RFBR Grants 13-01-12410 and 14-01-00379.
Rights and permissions
About this article
Cite this article
Gurevich, B. On a measure with maximal entropy for a suspension flow over a countable alphabet Markov shift. European Journal of Mathematics 1, 545–559 (2015). https://doi.org/10.1007/s40879-015-0056-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-015-0056-2



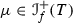 , i.e.,
, i.e., 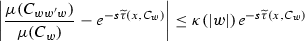
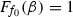 if this equation is solvable, otherwise
if this equation is solvable, otherwise 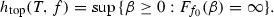

 .
.