Abstract
We prove that every continuous function \(f:E\rightarrow Y\) depends on countably many coordinates if \(E\) is an \((\aleph _1,\aleph _0)\)-invariant pseudo-\(\aleph _1\)-compact subspace of a product of topological spaces and \(Y\) is a space with a regular \(G_\delta \)-diagonal. Using this fact for any \(\alpha <\omega _1\), we construct an \((\alpha +1)\)-embedded subspace of a completely regular space which is not \(\alpha \)-embedded.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
If \(P\) is a property of functions, then by \(P(X)\) (\(P^*(X)\)) we denote the collection of all real-valued (bounded) functions on a topological space \(X\) with the property \(P\). By the symbol \(C\) we denote the property of continuity. Let \(B_\alpha \) be the property of being a function of \(\alpha \)-th Baire class, where \(0\le \alpha <\omega _1\).
Recall that a subset \(A\) of \(X\) is called functionally closed
\((\)open\()\)
in
\(X\) if there is \(f\in C^*(X)\) with \(A=f^{-1}(0)\) ( ). The system of all functionally open (closed) subsets of \(X\) we denote by \({\fancyscript{G}}_0^*\) (\({{\fancyscript{F}}}_0^*\)). Assume that the classes \({\fancyscript{G}}_\xi ^*\) and \({{\fancyscript{F}}}_\xi ^*\) are defined for all \(\xi <\alpha \), where \(0<\alpha <\omega _1\). Then, if \(\alpha \) is odd, the class \({\fancyscript{G}}_\alpha ^*\) (\({{\fancyscript{F}}}_\alpha ^*\)) consists of all countable intersections (unions) of sets of lower classes, and, if \(\alpha \) is even, the class \({\fancyscript{G}}_\alpha ^*\) (\({{\fancyscript{F}}}_\alpha ^*\)) consists of all countable unions (intersections) of sets of lower classes. The classes \({{\fancyscript{F}}}_\alpha ^*\) for odd \(\alpha \) and \({\fancyscript{G}}_\alpha ^*\) for even \(\alpha \) are said to be functionally additive, and the classes \({{\fancyscript{F}}}_\alpha ^*\) for even \(\alpha \) and \({\fancyscript{G}}_\alpha ^*\) for odd \(\alpha \) are called functionally multiplicative. A set \(A\) is called functionally measurable if \(A\in \bigcup _{0\le \alpha <\omega _1}({{\fancyscript{F}}}_\alpha ^*\cup {\fancyscript{G}}_\alpha ^*)\). Notice that the \(\sigma \)-algebra of functionally measurable subsets of \(X\) is also called the \(\sigma \)
-algebra of Baire sets.
). The system of all functionally open (closed) subsets of \(X\) we denote by \({\fancyscript{G}}_0^*\) (\({{\fancyscript{F}}}_0^*\)). Assume that the classes \({\fancyscript{G}}_\xi ^*\) and \({{\fancyscript{F}}}_\xi ^*\) are defined for all \(\xi <\alpha \), where \(0<\alpha <\omega _1\). Then, if \(\alpha \) is odd, the class \({\fancyscript{G}}_\alpha ^*\) (\({{\fancyscript{F}}}_\alpha ^*\)) consists of all countable intersections (unions) of sets of lower classes, and, if \(\alpha \) is even, the class \({\fancyscript{G}}_\alpha ^*\) (\({{\fancyscript{F}}}_\alpha ^*\)) consists of all countable unions (intersections) of sets of lower classes. The classes \({{\fancyscript{F}}}_\alpha ^*\) for odd \(\alpha \) and \({\fancyscript{G}}_\alpha ^*\) for even \(\alpha \) are said to be functionally additive, and the classes \({{\fancyscript{F}}}_\alpha ^*\) for even \(\alpha \) and \({\fancyscript{G}}_\alpha ^*\) for odd \(\alpha \) are called functionally multiplicative. A set \(A\) is called functionally measurable if \(A\in \bigcup _{0\le \alpha <\omega _1}({{\fancyscript{F}}}_\alpha ^*\cup {\fancyscript{G}}_\alpha ^*)\). Notice that the \(\sigma \)-algebra of functionally measurable subsets of \(X\) is also called the \(\sigma \)
-algebra of Baire sets.
An important role in the extension theory play \(z\)-embedded sets (a subset \(A\) of a topological space \(X\) is called \(z\)
-embedded in \(X\) if for any functionally closed set \(F\) in \(A\) there exists a functionally closed set \(B\) in \(X\) such that \(B\cap A=F\)). In [8] for any \(\alpha <\omega _1\) the notion of an \(\alpha \)
-embedded set was introduced, i.e. such a set \(A\subseteq X\) that every its subset \(B\) of functionally multiplicative class \(\alpha \) in \(A\) is the restriction on \(A\) of some set of functionally multiplicative class \(\alpha \) in \(X\). Obviously, the class of \(0\)-embedded sets coincides with the class of \(z\)-embedded sets. It is not hard to verify that any \(\alpha \)-embedded set is \(\beta \)-embedded if \(\alpha \le \beta \) [8, Proposition 2.5]. The converse statement is not true as [8, Theorem 2.6] shows: there is a \(1\)-embedded subset \(E\) of the product  , \(X_t=\mathbb N\) for all \(t\in [0,1]\), which is not \(0\)-embedded in \(X\). Here we generalize this result and show that for any \(\alpha <\omega _1\) there exists a set \(E\subseteq X\) which is \((\alpha +1)\)-embedded but not \(\alpha \)-embedded in \(X\).
, \(X_t=\mathbb N\) for all \(t\in [0,1]\), which is not \(0\)-embedded in \(X\). Here we generalize this result and show that for any \(\alpha <\omega _1\) there exists a set \(E\subseteq X\) which is \((\alpha +1)\)-embedded but not \(\alpha \)-embedded in \(X\).
A convenient tool in the investigation of properties of \(\alpha \)-embedded subsets \(E\) of \(\prod _{t\in T}X_t\) is the fact that under some conditions on \(E\) every continuous function \(f:E\rightarrow {\mathbb {R}}\) depends on countably many coordinates (see definitions in Sect. 2). Mazur introduced in [10] sets invariant under projection (see Definition 2.1 (a)) and proved that every continuous function \(f:E\rightarrow Y\) depends on countably many coordinates if \(E\subseteq \mathrm{\Sigma }(a)\) for some \(a\in E\) and \(E\) is invariant under projection, \(X_t\) is a metrizable separable space for each \(t\in T\) and \(Y\) is a Hausdorff space with a \(G_\delta \)-diagonal. Engelking [5] established the same result in the case when \(E\) is a set which is invariant under composition (see Definition 2.1 (b)) which is contained in \(\mathrm{\Sigma }(a)\) for some \(a\in E\), \(X_t\) is a \(T_1\)-space with countable base for each \(t\in T\) and \(Y\) is a Hausdorff space in which every one-point set is \(G_\delta \) (see also [7]). Noble and Ulmer [11] obtained the dependence of a continuous function \(f:E\rightarrow Y\) on countably many coordinates if \(E\) is a subset of a pseudo-\(\aleph _1\)-compact space \(\prod _{t\in T}X_t\), which contains \(\sigma (a)\) for some \(a\in E\) and \(Y\) is a space with a regular \(G_\delta \)-diagonal. The result of Noble and Ulmer was generalized by Comfort and Gotchev in [2]. Here we consider the so-called \((\aleph _1,\aleph _0)\)-invariant subsets of products and, developing the methods of Mazur and of Noble and Ulmer, we show that every continuous function \(f:E\rightarrow Y\) depends on countably many coordinates if \(E\) is an \((\aleph _1,\aleph _0)\)-invariant pseudo-\(\aleph _1\)-compact subspace of \(\prod _{t\in T}X_t\) and \(Y\) is a space with a regular \(G_\delta \)-diagonal.
2 Some properties of pseudo-\(\aleph _1\)-compact invariant sets
Let \((X_t:t\in T)\) be a family of non-empty topological spaces, \(X=\prod _{t\in T}X_t\) and let \(a=(a_t)_{t\in T}\) be a fixed point of \(X\). For \(S\subseteq T\) we denote by \(p_S\) the projection \(p_S:X\rightarrow \prod _{t\in S}X_t\), where \(p_S(x)=(x_t)_{t\in S}\) for each \(x=(x_t)_{t\in T}\in X\); by \(x_S^a\) we denote the point with coordinates \((y_t)_{t\in T}\), where \(y_t=x_t\) if \(t\in S\) and \(y_t=a_t\) if  . For a basic open set \(U=\prod _{t\in T}U_t\subseteq X\) let \(N(U)=\{t\in T: U_t\ne X_t\}\).
. For a basic open set \(U=\prod _{t\in T}U_t\subseteq X\) let \(N(U)=\{t\in T: U_t\ne X_t\}\).
Definition 2.1
A set \(E\subseteq X\) is called
-
(a)
invariant under projection [10] if \(x_S^a\in E\) for any \(x\in E\) and \(S\subseteq T\);
-
(b)
invariant under composition [5] if for any \(x,y\in E\) and \(S\subseteq T\) we have \(z=(z_t)_{t\in T}\in E\), where \(z_t=x_t\) for every \(t\in S\) and \(z_t=y_t\) for every
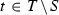 .
.
Clearly, every set \(E\) invariant under composition is invariant under projection for any \(a\in E\).
Following Engelking [5], Hušek in [7, p. 132] introduced a notion of \(\kappa \)-invariant set for \(\kappa \ge \aleph _0\).
Definition 2.2
A set \(E\) is called \(\kappa \)
-invariant if for any \(x,y\in E\) and \(S\subseteq T\) with \(|S|<\kappa \) there is a point \(z\in E\) such that \(z_t=x_t\) for every \(t\in S\) and \(z_t=y_t\) for every  .
.
Developing the above-mentioned concepts of Mazur and Hušek, we introduce the following notions.
Definition 2.3
Let \(\aleph _i\) and \(\aleph _j\) be infinite cardinals, \(E\subseteq X\) and \(a\in E\). Then \(E\) is called
-
\(\aleph _i\) -invariant with respect to \(a\) if \(x_S^a\in E\) for every \(x\in E\) and \(S\subseteq T\) with \(|S|<\aleph _i\);
-
\((\aleph _i,\aleph _j)\) -invariant with respect to \(a\) if \(x_{S_1}^a\in E\) and \(x_{T\setminus S_2}^a\in E\) for any point \(x\in E\) and for any sets \(S_1,S_2\subseteq T\) with \(|S_1|<\aleph _i\) and
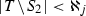 .
.
Obviously, every set \((\aleph _i,\aleph _j)\)-invariant with respect to \(a\) is \(\aleph _i\)-invariant with respect to \(a\).
Definition 2.4
A topological space \(X\) is said to be
-
pseudo- \(\aleph _1\) -compact if any locally finite family of open subsets of \(X\) is at most countable;
-
hereditarily pseudo- \(\aleph _1\) -compact if each subspace of \(X\) is pseudo-\(\aleph _1\)-compact.
It is easy to check that continuous mappings preserve pseudo-\(\aleph _1\)-compactness.
The following theorem gives a characterization of pseudo-\(\aleph _1\)-compactness of \(\aleph _0\)-invariant sets and is an analogue of the similar result of Noble and Ulmer [11, Corollary 1.5] for products.
Theorem 2.5
Let \((X_t:t\in T)\) be a family of topological spaces, \(X=\prod _{t\in T}X_t\), \(a\in X\) and let \(E\subseteq X\) be an \(\aleph _0\)-invariant set with respect to \(a\). Then the following conditions are equivalent:
-
(i) \(E\) is pseudo-\(\aleph _1\)-compact;
-
(ii) for any finite non-empty set \(S\subseteq T\) and for any uncountable family \((U_i:i\in I)\) of open sets \(U_i\) in \(X\) with \(U_i\cap E\ne \emptyset \) the family \(\bigl (p_S(U_i\cap E):i\in I\bigr )\) is not locally finite in \(p_S(E)\).
Proof
(i) \(\Rightarrow \) (ii) Let \(S\subseteq T\) be a finite non-empty set, \((U_i:i\in I)\) be an uncountable family of basic open sets \(U_i\) in \(X\) with \(U_i\cap E\ne \varnothing \) and let \(V_i=p_S(U_i\cap E)\) for each \(i\in I\). If the family \((V_i:i\in I)\) is locally finite in \(p_S(E)\), then the family \(\bigl (p_S^{-1}(V_i)\cap E:i\in I\bigr )\) is locally finite in \(E\) and \(U_i\cap E\subseteq p_S^{-1}(V_i)\cap E\) for each \(i\in I\), which contradicts pseudo-\(\aleph _1\)-compactness of \(E\).
(ii) \(\Rightarrow \) (i) Consider an uncountable family \(\bigl (U_i=\prod _{t\in T} U_i^t:i\in I\bigr )\) of basic open sets in \(X\) such that \(U_i\cap E\ne \varnothing \) for all \(i\in I\). By Šanin’s lemma [12] we choose a finite set \(Z\) and uncountable set \(J\subseteq I\) such that \(N(U_i)\cap N(U_j)=Z\) for all distinct \(i,j\in J\).
Let \(V_i=p_Z(U_i\cap E)\) for all \(i\in J\). It follows from (ii) that the family \((V_i:i\in J)\) has a cluster point \(v\in p_Z(E)\). Take \(y\in E\) such that \(v=p_Z(y)\) and put \(x=y_Z^a\). We shall show that \(x\) is a cluster point of \((U_i\cap E:i\in J)\). Indeed, let \(W=\prod _{t\in T}W_t\) be a basic open neighborhood of \(x\) in \(X\) and \(V=\prod _{t\in Z}W_t\cap p_Z(E)\). Choose such infinite set \(K\subseteq J\) that \(V\cap V_i\ne \varnothing \) and \(N(W)\cap N(U_i)\subseteq Z\) for all \(i\in K\). Take an arbitrary \(i\in K\) and a point
\(b\in V\cap V_i\). Consider a point \(c\in U_i\cap E\) with
\(b=p_Z(c)\) and put \(d=c_{Z\cup N(U_i)}^a\). Clearly,
\(d\in U_i\). Since \(E\) is
\(\aleph _0\)-invariant with respect to
\(a\) and \(c\in E\),
\(d\in E\). Moreover, \(p_Z(d)=p_Z(c)=b\in V\) and
\(d_t=a_t\in W_t\) for every  . Therefore,
\(d\in W\). Hence,
\(d\in W\cap E\cap U_i\).\(\square \)
. Therefore,
\(d\in W\). Hence,
\(d\in W\cap E\cap U_i\).\(\square \)
The example below shows that condition (ii) in the previous theorem cannot be weakened to the following: the set \(p_S(E)\) is pseudo- \(\aleph _1\) -compact for any non-empty finite set \(S\subseteq T\).
Example
There exists a set \(E\subseteq \prod _{t\in T}X_t\), \((\aleph _1,\aleph _1)\)-invariant with respect to a point \(a\in E\) such that \(p_S(E)\) is pseudo- \(\aleph _1\)-compact for any non-empty finite set \(S\subseteq T\), but \(E\) is not pseudo-\(\aleph _1\)-compact.
Proof
Let \(T=[0,1]\),  be the Niemytzki plane [6, p. 21],
\(X_t=\{0,1\}\) for each
\(t\in (0,1]\), \(X=\prod _{t\in T}X_t\) and let
\(a=(a_t)_{t\in T}\in X\), where
\(a_t=0\) for each \(t\in (0,1]\) and
\(a_0=(0,0)\). For each \(t\in (0,1]\) define
\(y^{(t)}=\bigl (y^{(t)}_s\bigr ){}_{s\in T}\) and
\(z^{(t)}=\bigl (z^{(t)}_s\bigr ){}_{s\in T}\in X\) as follows:
be the Niemytzki plane [6, p. 21],
\(X_t=\{0,1\}\) for each
\(t\in (0,1]\), \(X=\prod _{t\in T}X_t\) and let
\(a=(a_t)_{t\in T}\in X\), where
\(a_t=0\) for each \(t\in (0,1]\) and
\(a_0=(0,0)\). For each \(t\in (0,1]\) define
\(y^{(t)}=\bigl (y^{(t)}_s\bigr ){}_{s\in T}\) and
\(z^{(t)}=\bigl (z^{(t)}_s\bigr ){}_{s\in T}\in X\) as follows:

Consider the \((\aleph _1,\aleph _1)\)-invariant set

with respect to the point \(a\). Observe that for any finite set
\(S\subseteq [0,1]\) the sets
\(p_S\bigl (\{y^{(t)}:t\in (0,1]\}\bigr )\) and
\(p_S\bigl (\{z^{(t)}:t\in (0,1]\}\bigr )\) are finite and the set
 is separable. Hence, \(E\) satisfies the condition mentioned above. But
\(\bigl (\{y^{(t)}\}:t\in (0,1]\bigr )\) is a locally finite family of open sets in
\(E\). Therefore, \(E\) is not pseudo-\(\aleph _1\)-compact.
is separable. Hence, \(E\) satisfies the condition mentioned above. But
\(\bigl (\{y^{(t)}\}:t\in (0,1]\bigr )\) is a locally finite family of open sets in
\(E\). Therefore, \(E\) is not pseudo-\(\aleph _1\)-compact.
\(\square \)
3 Dependence of continuous mappings on countably many coordinates
Definition 3.1
Let \(E\subseteq \prod _{t\in T}X_t\). We say that a function \(f:E\rightarrow Y\) depends on a set \(S\subseteq T\) [3, p. 231] if for all \(x,y\in E\) the equality \(p_S(x)=p_S(y)\) implies \(f(x)=f(y)\). If \(|S|\le \aleph _0\) then we say that \(f\) depends on countably many coordinates. Similarly, \(E\) depends on \(S\) if for all \(x\in E\) and \(y\in X\) with \(p_S(x)=p_S(y)\) we have \(y\in E\).
Definition 3.2
We say that a space \(Y\) has a regular \(G_\delta \) -diagonal [14] if there exists a sequence \((G_n)_{n=1}^\infty \) of open subsets of \(Y^2\) such that

We denote \(\sigma (a)=\bigl \{x\in X:|t\in T:x_t\ne a_t|<\aleph _0\bigr \}\) as in [4].
Theorem 3.3
Let \(Y\) be a space with a regular \(G_\delta \)-diagonal, \((X_t:t\in T)\) be a family of topological spaces, \(X=\prod _{t\in T}X_t\), \(a\in X\) and let \(E\subseteq X\) be a pseudo-\(\aleph _1\)-compact subspace which is \((\aleph _1,\aleph _0)\)-invariant with respect to \(a\). Then for any continuous mapping \(f:E\rightarrow Y\) there exist a countable set \(T_0\subseteq T\) and a continuous mapping \(f_0:p_{T_0}(E)\rightarrow Y\) such that  . In particular, \(f\) depends on countably many coordinates.
. In particular, \(f\) depends on countably many coordinates.
Proof
Let \((G_n)_{n=1}^\infty \) be a sequence of open sets in \(Y^2\) which satisfies (1) and let \(f:E\rightarrow Y\) be a continuous function. Denote by \(T_0\) the set of all \(t\in T\) for which there exist points \(x^t,y^t\in E\cap \sigma (a)\) such that
Assume that \(T_0\) is uncountable and choose an uncountable subset \(B\subseteq T_0\) and a number \(n_0\in \mathbb N\) such that

Using the continuity of \(f\) at \(x^t\) and \(y^t\) for every \(t\in B\), we find open basic neighborhoods \(U^t\) and \(V^t\) of \(x^t\) and \(y^t\), respectively, such that


Since \(E\) is pseudo-\(\aleph _1\)-compact and the family \((V^t\cap E:t\in B)\) is uncountable, there exists a point \(x^*\in E\) such that for any basic open neighborhood \(W\) of \(x^*\) the set \(C_W=\{t\in B: V^t\cap E\cap W\ne \varnothing \}\) is infinite. The continuity of \(f\) at \(x^*\) implies that there is an basic open neighborhood \(W\) of \(x^*\) such that  . Notice that
. Notice that  . Fix \(t\in C\) and \(y\in V^t\cap E\cap W\). Let \(x=y^a_{T\setminus \{t\}}\). Then (2) and (3) imply that \(x\in U^t\). Since \(E\) is \((\aleph _1,\aleph _0)\)-invariant with respect to \(a\), \(x\in E\). Moreover, \(x\in W\), since \(t\not \in N(W)\). Then \((f(x),f(y))\in G_{n_0}\), which contradicts (4). Hence, the set \(T_0\) is countable.
. Fix \(t\in C\) and \(y\in V^t\cap E\cap W\). Let \(x=y^a_{T\setminus \{t\}}\). Then (2) and (3) imply that \(x\in U^t\). Since \(E\) is \((\aleph _1,\aleph _0)\)-invariant with respect to \(a\), \(x\in E\). Moreover, \(x\in W\), since \(t\not \in N(W)\). Then \((f(x),f(y))\in G_{n_0}\), which contradicts (4). Hence, the set \(T_0\) is countable.
We show that \(f\) depends on \(T_0\). To do this it is sufficient to check the equality \(f(x)=f(x^a_{T_0})\) for every \(x\in E\). Consider the case \(x\in E\cap \sigma (a)\). Let  . Then
. Then
Now let \(x\in E\). Notice that \(E\cap \sigma (a)\) is a dense set in \(E\). Indeed, if \(b=(b_t)_{t\in T}\in E\) and \(W\) is a basic open neighborhood of \(b\) in \(X\), then \(b^a_{N(W)}\in W\cap E\cap \sigma (a)\). Hence, there exists a net \((x_i)\) of points \(x_i\in E\cap \sigma (a)\) such that \(\lim _i x_i=x\). Then \(\lim _i (x_i)^a_{T_0}=x^a_{T_0}\). It follows from continuity of \(f\) that

Consider the function \(f_0:p_{T_0}(E)\rightarrow Y\) defined by \(f_0(z)=f(x)\) if \(z=p_{T_0}(x)\) for \(x\in E\). Observe that \(f_0\) is defined correctly, because \(f\) depends on \(T_0\). It remains to prove that \(f_0\) is continuous on \(p_{T_0}(E)\). Fix \(z\in p_{T_0}(E)\) and a net \((z_i)\) of points \(z_i\in p_{T_0}(E)\) such that \(\lim _i z_i=z\). Take \(x\in E\) and \(x_i\in E\) with \(z=p_{T_0}(x)\) and \(z_i=p_{T_0}(x_i)\). Let \(y_i=(x_i)^a_{T_0}\) and \(y=x^a_{T_0}\). Then \(y_i,y\in E\) and \(\lim _i y_i=y\). Moreover, since \(f\) is continuous at \(y\), we have
Hence, \(f_0\) is continuous at \(z\).\(\square \)
Notice that the proof of dependence of \(f\) on \(T_0\) in Theorem 3.3 is similar to the proof of [1, Lemmas 2.27 (a) and 2.32].
Theorem 3.4
Let \((X_t:t\in T)\) be an uncountable family of topological spaces, \(X=\prod _{t\in T}X_t\), \(a\in X\) and let \(E\subseteq X\) be an \((\aleph _1,\aleph _0)\)-invariant set with respect to \(a\). Consider the following conditions:
-
(i) \(E\) is pseudo-\(\aleph _1\)-compact;
-
(ii) for any space \(Y\) with a regular \(G_\delta \)-diagonal and for any continuous mapping \(f:E\rightarrow Y\) there exist a countable set \(T_0\subseteq T\) and a continuous mapping \(f_0:p_{T_0}(E)\rightarrow Y\) such that
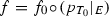 ;
; -
(iii) for any continuous function \(f:E\rightarrow {\mathbb {R}}\) there exist a countable set \(T_0\subseteq T\) and a continuous mapping \(f_0:p_{T_0}(E)\rightarrow {\mathbb {R}}\) such that
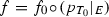 .
.
Then (i) \(\Rightarrow \) (ii) \(\Rightarrow \) (iii).
If \(E\) is completely regular and
-
(iv) for any non-empty open set \(U\) in \(E\) there exists an uncountable set \(T_U\subseteq T\) such that for every \(t\in T_U\) there are \(y^{(t)}=\bigl (y^{(t)}_s\bigr ){}_{s\in T}\) and \( z^{(t)}=\bigl (z^{(t)}_s\bigr ){}_{s\in T}\in U\) with \(y^{(t)}_t\ne z^{(t)}_t\) and \(y^{(t)}_s= z^{(t)}_s\) for every
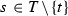 ,
,
then (iii) \(\Rightarrow \) (i).
Proof
The implication (i) \(\Rightarrow \) (ii) follows from Theorem 3.3, whereas the implication (ii) \(\Rightarrow \) (iii) is obvious.
(iii) \(\Rightarrow \) (i) Suppose that \(E\) is not pseudo-\(\aleph _1\)-compact and choose a locally finite in \(E\) family \((U_\alpha :\alpha <\omega _1)\) of non-empty open sets \(U_\alpha \). Note that \(U_\alpha \) may be taken to be disjoint. Indeed, let \((V_i:i\in I)\) be a locally finite family of non-empty open subsets of \(E\) with \(|I|>\aleph _0\). For every \(i\in I\) we choose a non-empty open set \(W_i\subseteq V_i\) and a finite set \(J_i\subseteq I\) such that \(W_i\subseteq \bigcap _{j\in J_i}V_j\) and \(W_i\cap V_j=\emptyset \) for all  . Since \(i\in J_i\) for every \(i\in I\), \(\bigcup _{i\in I}J_i=I\). Now we take a uncountable set \(I_0\subseteq I\) such that all sets \(J_i\) from the family \((J_i:i\in I_0)\) are different. Then the uncountable family \((W_i:i\in I_0)\) consists of mutually disjoint elements.
. Since \(i\in J_i\) for every \(i\in I\), \(\bigcup _{i\in I}J_i=I\). Now we take a uncountable set \(I_0\subseteq I\) such that all sets \(J_i\) from the family \((J_i:i\in I_0)\) are different. Then the uncountable family \((W_i:i\in I_0)\) consists of mutually disjoint elements.
Since \(E\) is completely regular, we may assume that all sets \(U_\alpha \) are functionally open. For every \(\alpha <\omega _1\) take a continuous function \(f_\alpha :E\rightarrow [0,1]\) such that \(U_\alpha =f_\alpha ^{-1}((0,1])\). Since \(T_{U_\alpha }\) is uncountable, we may construct a family \((t_\alpha :\alpha <\omega _1)\) of distinct points \(t_\alpha \in T_{U_\alpha }\). According to (iv) we choose for every \(\alpha <\omega _1\) points \(y^{(\alpha )}=\bigl (y^{(\alpha )}_s\bigr ){}_{s\in T}\), \(z^{(\alpha )}=\bigl (z^{(\alpha )}_s\bigr ){}_{s\in T}\in U_\alpha \) such that \(y^{(\alpha )}_{t_\alpha }\ne z^{(\alpha )}_{t_\alpha }\) and \(y^{(\alpha )}_s= z^{(\alpha )}_s\) for every  . Now for every \(\alpha <\omega _1\) we choose a continuous function \(g_\alpha :E\rightarrow [0,1]\) such that \(g_\alpha \bigl (y^{(\alpha )}\bigr )=1\) and \(g_\alpha \bigl (z^{(\alpha )}\bigr )=0\).
. Now for every \(\alpha <\omega _1\) we choose a continuous function \(g_\alpha :E\rightarrow [0,1]\) such that \(g_\alpha \bigl (y^{(\alpha )}\bigr )=1\) and \(g_\alpha \bigl (z^{(\alpha )}\bigr )=0\).
Consider the continuous function \(f:E\rightarrow [0,1]\),  . Since sets \(U_\alpha \) are mutually disjoint,
. Since sets \(U_\alpha \) are mutually disjoint,

Hence, \(f\bigl (y^{(\alpha )}\bigr )\ne f\bigl (z^{(\alpha )}\bigr )\) for every \(\alpha <\omega _1\). Since the set \(\{t_{\alpha }:\alpha <\omega _1\}\) is uncountable, the function \(f\) does not satisfy (iii).\(\square \)
4 Functionally measurable sets
Proposition 4.1
Let \(E\) be a subset of \(X=\prod _{t\in T}X_t\) such that for any continuous function \(f:E\rightarrow {\mathbb {R}}\) there exist a countable set \(T_0\subseteq T\) and a continuous mapping \(f_0:p_{T_0}(E)\rightarrow {\mathbb {R}}\) with  and let \(0\le \alpha <\omega _1\). Then for any set \(A\) of functionally additive \((\)multiplicative\()\) class \(\alpha \) in \(E\) there exists a countable set \(T_0\subseteq T\) such that \(A\) depends on \(T_0\) and \(p_{T_0}(A)\) is of functionally additive \((\)multiplicative\()\) class \(\alpha \) in \(p_{T_0}(E)\).
and let \(0\le \alpha <\omega _1\). Then for any set \(A\) of functionally additive \((\)multiplicative\()\) class \(\alpha \) in \(E\) there exists a countable set \(T_0\subseteq T\) such that \(A\) depends on \(T_0\) and \(p_{T_0}(A)\) is of functionally additive \((\)multiplicative\()\) class \(\alpha \) in \(p_{T_0}(E)\).
Proof
Let \(\alpha =0\). We consider the case when a set \(A\) is functionally open in \(E\). Then \(A=f^{-1}((0,+\infty ))\) for some continuous function \(f:E\rightarrow {\mathbb {R}}\). Take a countable set \(T_0\subseteq T\) and a continuous mapping \(f_0:p_{T_0}(E)\rightarrow {\mathbb {R}}\) with  . Then the set \(p_{T_0}(A)=f_0^{-1}((0,+\infty ))\) is functionally open in \(p_{T_0}(E)\). Moreover, if \(x\in A\) and \(y\in E\) with \(p_{T_0}(x)=p_{T_0}(y)\), then \(f(y)=f(x)>0\). Therefore, \(y\in A\) which implies that \(A\) depends on \(T_0\).
. Then the set \(p_{T_0}(A)=f_0^{-1}((0,+\infty ))\) is functionally open in \(p_{T_0}(E)\). Moreover, if \(x\in A\) and \(y\in E\) with \(p_{T_0}(x)=p_{T_0}(y)\), then \(f(y)=f(x)>0\). Therefore, \(y\in A\) which implies that \(A\) depends on \(T_0\).
Assume that the assertion is true for all \(\alpha <\beta \) and consider a set \(A\) of functionally additive class \(\alpha \) in \(E\). Then \(A=\bigcup _{n=1}^\infty A_n\), where \(A_n\) is of functionally multiplicative class \(\alpha _n<\alpha \) for every \(n\). By the assumption, for every \(n\) there exists a countable set \(T_n\subseteq T\) such that \(A_n\) depends on \(T_n\) and \(p_{T_n}(A_n)\) belongs to functionally multiplicative class \(\alpha _n\) in \(p_{T_n}(E)\). Notice that \(p_{T_0}(A_n)\) is of functionally multiplicative class \(\alpha _n\) in \(p_{T_0}(E)\) for every \(n\). Then \(p_{T_0}(A)=\bigcup _{n=1}^\infty p_{T_0}(A_n)\) is of functionally additive class \(\alpha \) in \(p_{T_0}(E)\).\(\square \)
Definition 4.2
Let \(0\le \alpha <\omega _1\). A space \(X\) is called \(\alpha \) -universal if any subset of \(X\) is \(\alpha \)-embedded in \(X\).
Clearly, every perfectly normal space is \(\alpha \)-universal for any \(\alpha <\omega _1\).
Proposition 4.3
Let \(0\le \alpha <\omega _1\), \((X_t)_{t\in T}\) be a family of topological spaces such that every countable subproduct is \(\alpha \)-universal, \(X=\prod _{t\in T}X_t\) and let \(E\subseteq X\) be such a set as in Proposition 4.1. Then \(E\) is an \(\alpha \)-embedded set in \(X\).
Proof
Let \(A\subseteq E\) be a set of functionally multiplicative class \(\alpha \) in \(E\). According to Proposition 4.1 there exists a countable set \(T_0\subseteq T\) such that \(A\) depends on \(T_0\) and \(A_0=p_{T_0}(A)\) is of functionally multiplicative class \(\alpha \) in \(E_0=p_{T_0}(E)\). Since \(X_0=\prod _{t\in T_0}X_t\) is \(\alpha \)-universal, the set \(E_0\) is \(\alpha \)-embedded in \(X_0\). Hence, there exists a set \(B_0\) of functionally multiplicative class \(\alpha \) in \(X_0\) such that \(B_0\cap E_0=A_0\). Let \(B=p_{T_0}^{-1}(B_0)\). Then \(B\) is of functionally multiplicative class \(\alpha \) in \(X\), because the mapping \(p_{T_0}\) is continuous. Moreover, it is easy to see that \(B\cap E=A\).\(\square \)
Proposition 4.4
Let \(0\le \alpha <\omega _1\), \(X=\prod _{t\in T}X_t\) be a pseudo-\(\aleph _1\)-compact space, where \((X_t)_{t\in T}\) is a family of spaces such that every countable subproduct is \(\alpha \)-universal and hereditarily pseudo-\(\aleph _1\)-compact. Then any functionally measurable set \(E\subseteq X\) is \(\alpha \)-embedded in \(X\).
Proof
Consider a functionally measurable set \(E\subseteq X\). Without loss of generality, we may assume that \(E\) belongs to functionally multiplicative class \(\beta \) for some \(0\le \beta <\omega _1\). Take a function \(f\in B_\beta (X)\) such that \(E=f^{-1}(0)\). Since \(X\) is pseudo-\(\aleph _1\)-compact, [11, Theorem 2.3] implies that there exists a countable set \(T_0\subseteq T\) such that for all \(x\in E\) and \(y\in X\) the equality \(p_{T_0}(x)=p_{T_0}(y)\) implies that \(y\in E\). Let \(E_0=p_{T_0}(E)\). Then

Since \(\prod _{t\in T_0\cup S} X_t\) is a hereditarily pseudo-\(\aleph _1\)-compact space,  is pseudo-\(\aleph _1\)-compact space for any finite set
is pseudo-\(\aleph _1\)-compact space for any finite set  . Hence, by [11, Corollary1.5] the set \(E\) is pseudo-\(\aleph _1\)-compact. Therefore, \(E\) satisfy the condition of Proposition 4.1 by Theorem 3.3 applied to the whole product
. Hence, by [11, Corollary1.5] the set \(E\) is pseudo-\(\aleph _1\)-compact. Therefore, \(E\) satisfy the condition of Proposition 4.1 by Theorem 3.3 applied to the whole product  . It remains to use Proposition 4.3.\(\square \)
. It remains to use Proposition 4.3.\(\square \)
The following result implies a positive answer to [8, Question 8.1].
Corollary 4.5
Let \((X_t)_{t\in T}\) be a family of separable metrizable spaces. Then every functionally measurable subset of \(X=\prod _{t\in T} X_t\) is \(\alpha \)-embedded in \(X\) for any \(0\le \alpha <\omega _1\).
Proof
The statement follows from Proposition 4.4 and the fact that any countable product of separable metrizable spaces is separable and metrizable, consequently, \(\alpha \)-universal and hereditarily pseudo-\(\aleph _1\)-compact.\(\square \)
5 The construction of \(\alpha \)-embedded sets
Theorem 5.1
For every \(0\le \alpha <\omega _1\) there exists a completely regular space \(X\) with an \((\alpha +1)\)-embedded subspace \(E\subseteq X\) which is not \(\alpha \)-embedded.
Proof
Fix \(\alpha <\omega _1\). Let \(X_0=[0,1]\), \(X_t=\mathbb N\) for every \(t\in (0,1]\), \(Y=\prod _{t\in (0,1]}X_t\) and  .
.
According to [9, p. 371] there exists a set \(A_1\subseteq [0,1]\) of additive class \(\alpha \) which does not belong to multiplicative class \(\alpha \). Let  . For \(i=1,2\) put
. For \(i=1,2\) put

It is easy to see that \(F_1\) and \(F_2\) are closed disjoint subsets of \(Y\). Let  for \(i=1,2\) and \(E=B_1\cup B_2\). Then \(B_1\) and \(B_2\) are disjoint closed subsets of \(E\).
for \(i=1,2\) and \(E=B_1\cup B_2\). Then \(B_1\) and \(B_2\) are disjoint closed subsets of \(E\).
Claim 5.2
The set \(B_i\) is \(\alpha \)-embedded in \(X\) for every \(i=1,2\).
Proof
We show that \(B_1\) is pseudo-\(\aleph _1\)-compact (for the set \(B_2\) we argue verbatim). Since \(A_1\) is separable, it is enough to check that \(F_1\) is pseudo-\(\aleph _1\)-compact. Notice that the set \(F_1\) is \((\aleph _1,\aleph _1)\)-invariant with respect to the point \(a=(a_t)_{t\in (0,1]}\), where \(a_t=1\) for every \(t\in (0,1]\). Since for any finite set \(S\subseteq (0,1]\) the space \(\prod _{t\in S}X_t\) is countable, the set \(F_1\) satisfies condition (ii) of Theorem 2.5. Then by Theorem 2.5 the set \(F_1\) is pseudo-\(\aleph _1\)-compact.
Now observe that each set \(B_i\) is \((\aleph _1,\aleph _1)\)-invariant with respect to the point \(a^i=(a_t^i)_{t\in [0,1]}\), where \(a_t^i=i\) for all \(t\in (0,1]\) and \(a_0^i\in A_i\). It remains to apply Theorem 3.3 and Proposition 4.3. \(\blacksquare \)
Claim 5.3
The set \(E\) is not \(\alpha \)-embedded in \(X\).
Proof
Assume the contrary and choose a set \(H\) of functionally multiplicative class \(\alpha \) in \(X\) such that \(H\cap E=B_1\). It follows from Proposition 4.1 that there is a countable set \(S=\{0\}\cup T\), where \(T\subseteq (0,1]\), such that \(H\) depends on \(S\). Let \(y_0\in Y\) be such that \(p_T(y_0)\) is a sequence of distinct natural numbers which are not equal to \(1\) or \(2\). Take \(y_1\in F_1\) and \(y_2\in F_2\) with \(p_T(y_0)=p_T(y_1)=p_T(y_2)\). Then for all \(x\in A_1\) we have \((x,y_1)\in H\) and, consequently, \((x,y_0)\in H\). Moreover, for all \(x\in A_2\) we have \((x,y_2)\not \in H\) and, consequently, \((x,y_0)\not \in H\). Hence,  . Therefore,
. Therefore,  is of functionally multiplicative class \(\alpha \) in \(X\), which implies that the set \(A_1\) belongs to functionally multiplicative class \(\alpha \) in \([0,1]\), a contradiction. \(\blacksquare \)
is of functionally multiplicative class \(\alpha \) in \(X\), which implies that the set \(A_1\) belongs to functionally multiplicative class \(\alpha \) in \([0,1]\), a contradiction. \(\blacksquare \)
Claim 5.4
The set \(E\) is \((\alpha +1)\)-embedded in \(X\).
Proof
Let \(C\) be a set of functionally multiplicative class \((\alpha +1)\) in \(E\). Denote  for \(i=1,2\). Then \(E_1\) is of functionally additive class \(\alpha \) and \(E_2\) is of functionally multiplicative class \(\alpha \) in \(X\). For \(i=1,2\) put \(C_i=C\cap B_i\). Since each of the sets \(C_i\) is of functionally multiplicative class \((\alpha +1)\) in the \(\alpha \)-embedded set \(B_i\) in \(X\), there exists a set \(D_i\) of functionally multiplicative class \((\alpha +1)\) in \(X\) such that \(D_i\cap B_i=C_i\). Let \(D=(D_1\cap E_1)\cup (D_2\cap E_2)\). Then \(D\) is a set of functionally multiplicative class \((\alpha +1)\) in \(X\) and \(D\cap E=C\).\(\blacksquare \)
for \(i=1,2\). Then \(E_1\) is of functionally additive class \(\alpha \) and \(E_2\) is of functionally multiplicative class \(\alpha \) in \(X\). For \(i=1,2\) put \(C_i=C\cap B_i\). Since each of the sets \(C_i\) is of functionally multiplicative class \((\alpha +1)\) in the \(\alpha \)-embedded set \(B_i\) in \(X\), there exists a set \(D_i\) of functionally multiplicative class \((\alpha +1)\) in \(X\) such that \(D_i\cap B_i=C_i\). Let \(D=(D_1\cap E_1)\cup (D_2\cap E_2)\). Then \(D\) is a set of functionally multiplicative class \((\alpha +1)\) in \(X\) and \(D\cap E=C\).\(\blacksquare \)
This completes the proof.\(\square \)
Notice that the sets \(F_i\) were first defined by Stone [13] in his proof of non-normality of the uncountable power \(\mathbb N^\tau \) of the space \(\mathbb N\) of natural numbers.
References
Comfort, W.W., Gotchev, I.S.: Functional dependence on small sets of indices. Sci. Math. Jpn. 69(3), 363–377 (2009)
Comfort, W.W., Gotchev, I.S.: Continuous mappings on subspaces of products with the \(\kappa \)-box topology. Topol. Appl. 156(16), 2600–2608 (2009)
Comfort, W.W., Negrepontis, S.A.: Chain Conditions in Topology. Cambridge Tracts in Mathematics, vol. 79. Cambridge University Press, Cambridge (2008)
Corson, H.H.: Normality in subsets of product spaces. Am. J. Math. 81(3), 785–796 (1959)
Engelking, R.: On functions defined on Cartesian products. Fund. Math. 59, 221–231 (1966)
Engelking, R.: General Topology, 2nd edn. Sigma Series in Pure Mathematics, vol. 6. Heldermann, Berlin (1989)
Hušek, M.: Mappings from Products. Topological Structures, vol. 2. Mathematical Centre Tracts, vol. 115, pp. 131–145. Mathematisch Centrum, Amsterdam (1979)
Karlova, O.: On \(\alpha \)-embedded sets and extension of mappings. Comment. Math. Univ. Carol. 54(3), 377–396 (2013)
Kuratowski, K.: Topology, vol. I. Academic Press/PWN, New York (1966)
Mazur, S.: On continuous mappings on Cartesian products. Fund. Math. 39, 229–238 (1952)
Noble, N., Ulmer, M.: Factoring functions on Cartesian products. Trans. Am. Math. Soc. 163, 329–339 (1972)
Šanin, N.: On the product of topological spaces. Trudy Mat. Inst. Steklov, vol. 24. Acad. Sci. USSR, Moscow–Leningrad (1948) (in Russian)
Stone, A.H.: Paracompactness and product spaces. Bull. Am. Math. Soc. 54(10), 977–982 (1948)
Zenor, P.: On spaces with regular \(G_\delta \)-diagonals. Pac. J. Math. 40(3), 759–763 (1972)
Acknowledgments
The authors express gratitude to the referees for careful reading and comments that helped to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
The paper was submitted on August 23, 2013 to the Central European Journal of Mathematics, but in spite of positive referees’ reports the manuscript was withdrawn due to financial demand for publication and resubmitted to the European Journal of Mathematics.
Rights and permissions
About this article
Cite this article
Karlova, O., Mykhaylyuk, V. On \(\alpha \)-embedded subsets of products. European Journal of Mathematics 1, 160–169 (2015). https://doi.org/10.1007/s40879-014-0018-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-014-0018-0



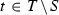 .
.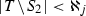 .
.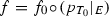 ;
;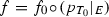 .
.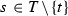 ,
,