Introduction

The development of shockless compression experimental capabilities marked a key departure from more traditional shock loading platforms. In shock compression the entropy generated by the shock results in significant heating, and in the case of most metals impact stresses on the order of several hundred GPa are sufficient to cause melting. Shockless (or ramp) compression, on the other hand, utilizes finite loading rates to continuously drive the material to a peak state orders of magnitude more slowly than the near-instantaneous rise of a shock. The subsequent compression is close to isentropic, or quasi-isentropic, with deviations arising from the irreversible processes associated with plastic work. Thus, ramp compression results in a low-temperature thermodynamic trajectory that enables loading to extreme pressures without melting.

There are a variety of applications for which shockless compression experiments can provide valuable insights. For example, an understanding of how metals compress to high energy density (HED) conditions, typically defined as pressures \(>100\) GPa, is required for modeling a range of applications from descriptions of stellar and planetary interiors to planetary formation dynamics to inertial confinement fusion implosions [1]. High precision ramp compression data can also be used in the development of standards. In dynamic experiments, waves are often transmitted from a well-characterized standard to an unknown material and the properties of the standard are required to interpret the data [2]. Similarly, in static diamond anvil cell (DAC) experiments, a standard is generally required to deduce the pressure within the cell. With the development of two-stage DACs, researchers are reaching pressures of over 600 GPa [3, 4], and the quality of the pressure standard is paramount to the interpretation of these experiments.

Ramp compression experiments generally investigate the compression of a solid state, so a description of the material’s strength is required for a complete description of the stress state. Most planar dynamic experiments probe propagation of longitudinal stress waves under conditions of uni-axial srain. A longitudinal stress wave can be decomposed into hydrostatic and deviatoric components (see Eq. 2), so a description of the deviatoric (strength) contribution is required to translate the measured response to paths in thermodynamic space; a practical example is reduction of the measured loading path to the room temperature isotherm [5], which can then be used in equation-of-state (EOS) development or as a DAC standard. Conversely, the strength model plays a key role in simulations of many of the applications mentioned previously, so high fidelity data are required to establish a predictive capability for these phenomena.

In this article we present new results from shockless compression strength experiments on four high density metals: tantalum (Ta), platinum (Pt), gold (Au), and iridium (Ir). An ongoing effort at Sandia National Laboratories is developing these materials as standards for use in both dynamic and static compression experiments. In Sect. 2 we discuss the experimental configuration and observables. Section 3 applies an established analysis technique to the data and then presents a novel analysis approach based on the calibration of numerical simulations. In both methods, the emphasis is on the extraction of the deviatoric response near the peak compression state and quantifying these results for ease of future use in standards development. Some discussion is provided in Sect. 4 and we conclude in Sect. 5.

Experimental Method

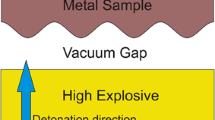
Pulsed power machines generate extreme electrical currents over very small timescales. The world’s largest pulsed power machine, the Z accelerator [6], has been adapted to convert \(10's\) of megamps of current rising over \(100's\) of nanoseconds into a mechanical pressure wave to drive dynamic materials experiments [7, 8]. One such experimental configuration has been designed to maximize sensitivity to the material strength [9, 10], a simplified representation of which is given in Fig. 1.

Fig. 1
figure 1

One-dimensional configuration resulting from a typical Z strength experiment. Current flows between a pair of parallel electrodes and generates a magnetically driven ramp-release wave. The experimental observables are the velocity of the electrode/window interface on the left and sample/window interface on the right

Full size image

As illustrated in Fig. 1, current flows through an anode-cathode gap created by a pair of parallel electrodes, generally either aluminum or copper. The current induces a magnetic field and, through the Lorentz force, a propogating stress wave. One of the electrodes is arranged in the so-called drive configuration (left side of Fig. 1), in which a single-crystal lithium fluoride (LiF) window is glued to the electrode, and the VISAR [11] diagnostic is used to measure the velocity of this interface. The other electrode is arranged in the sample configuration (right side of Fig. 1) in which the sample of interest is sandwiched between the electrode and LiF window; VISAR monitors the sample/LiF interface velocity. Characteristic dimensions are similar to what was reported previously for the early Ta experiments [10], with all new experiments utilizing copper electrodes between 1.75–2 mm thick, samples nominally 1.5–2.2 mm thick, and LiF windows 6 mm thick. Copper is preferred over aluminum for these multi-megabar experiments to avoid the complication of modeling the solid–solid phase transitions in Al over this pressure regime [12].

Through proper selection of the electrode thickness and careful shaping of the time-dependent current pulse, the stress wave will run out ahead of the magnetic diffusion front and then remain shockless as it propagates through the sample and into the window. This type of shockless (or ramp) loading results in compression of the sample to the peak state in \(\sim 100\) ns. Beyond peak, the current pulse will naturally decay resulting in a reversal of the loading direction and subsequent decompression of the sample. As will be shown in the following section, the loading reversal provides the sensitivity in the observed sample measurement to its high pressure strength.

Table 1 Summary of ambient properties
Full size table

To give a sense for relative strengths expected across the four metals, a summary of their ambient properties are given in Table 1. The sample densities, \(\rho _0\), are from immersion measurements, while the shear modulus, \(G_0\), and its normalized pressure derivative, \(A = \frac{1}{G_0} \frac{\partial G}{\partial P}\), are estimated from single crystal elastic data [13]. The initial strength, \(Y_0\), for Ta, Au, and Pt, are the values reported for the Steinberg–Cochrane–Guinan (SCG) strength model [14]. Since the SCG \(Y_0\) values are not reported for Ir and little dynamic strength data exists in the literature, \(Y_0\) was estimated from the average of the range reported for the compressive strength of commercial purity Ir in the Granta database [15]. This high Ir strength is consistent with low temperature quasi-static and Kolsky bar experiments [16], and these experiments do not exhibit a strong strain rate sensitivity which may suggest this is a reasonable representation of the higher rate Z experiments. Based on the values in Table 1 we were expecting to measure significantly lower strengths in the Au and Pt high pressure Z experiments.

Experimental Results and Analysis

Velocity Profiles

A total of 15 experiments were conducted to examine the strength of Ta, Au, Pt, and Ir at multi-megabar pressures. The majority of the experiments contained Ta samples, resulting in 15 velocity measurements spanning peak pressures from \(\sim \) 50–350 GPa. The Au, Pt, and Ir measurements consist of 3–4 velocities at two different peak pressures: \(\sim \) 200 and 300 GPa in Au and 150 and 300 GPa in Pt and Ir. A summary of the measured velocities is shown in Fig. 2 where the profiles are arbitrarily shifted in time for clarity. All of the measurements illustrate shockless compression except for one of the velocities for Ta, Pt, and Ir. This experiment, Z3322, contained a sample of each material, but there was an anomaly in the current delivery resulting in shock formation early in the measured velocity. The shocks are diagnosed through a combination of forward simulations and measured rise-times at the limiting temporal resolution of the VISAR system (\(< 1\) ns). The shocks are most visible in the highest velocity Pt and Ir profiles, which show a relatively weak shock at early times (\(\sim \) 3.45 \(\mu \) s) followed by shockless compression up to peak. The impact of this shock formation on the experimental interpretation is discussed in the following section. While very steep towards the middle of the measured Au velocities, we do not believe the Au shocked since a rise-time of several ns was accurately tracked with the VISAR diagnostic. Regardless, if this is a shock, forward simulations suggest it occurred extremely close to the window interface and there was no noticeable effect on the analysis described in the following section.

Fig. 2
figure 2

Experimental measurements of the sample/window interface velocity

Full size image

Self Consistent Lagrangian Analysis (SCLA)

SCLA is a method developed to extract an estimate of a quantity related to the material strength from experiments in which the loading direction is reversed. The process begins with Lagrangian Analysis (LA), an approach which, broadly speaking, can be applied to stress wave measurements at different Lagrangian positions to infer the material response [17]. Here, we take LA to mean the simplified application to the two measured velocities described in Fig. 1. We refer to [9] for the approximations and details associated with our application, and only briefly summarize the results. The primary output of the LA is the sample’s Lagrangian wavespeed, \(c_L\), as a function of the particle (or mass) velocity, u, measured from the evolution of the in-situ particle velocity temporal histories at the front and back of the sample. These velocities are estimated from the two experimentally measured velocities in combination with numerical simulation [9]. The longitudinal stress in the loading direction, \(\sigma _x\), and Cauchy (engineering) strain, \(\varepsilon \), are determined through integration of the conservation of momentum and mass equations, respectively:

$$\begin{aligned} d\sigma _x = \rho _0c_Ldu, \quad \quad d\varepsilon = \frac{du}{c_L}. \end{aligned}$$
(1)

A summary of the Lagrangian analysis for each of the measured velocity profiles is given in Fig. 3. The qualitative nature of each profile is the same. At low particle velocity (\(<0.1\) mm\(/\mu \) s) the deformation is elastic, so the observed Lagrangian wavespeed corresponds to the longitudinal elastic wavespeed. Analogous to the Hugoniot elastic limit (HEL), this has been referred to as the ramp elastic limit (REL) for these types of shockless compression experiments [18]. Beyond the REL, the deformation transitions to plastic flow, so the observed wavespeed up to the peak particle velocity is the bulk wavespeed. Upon loading reversal the particle velocity begins to decrease, which results in another elastic-plastic transition as the material is driven from its upper (loading) yield surface to the lower (unloading) yield surface. This transition manifests in Fig. 3 as a jump up to the elastic wavespeed at the peak state, followed by a smooth transition back to fully plastic deformation. As has been observed in multiple studies, the experimentally observed transition is not perfectly elastic and has a so-called quasi-elastic or anelastic response [9, 19,20,21,22] which results in the triangular nature of the observed wavespeeds.

Fig. 3
figure 3

Wavespeed profiles extracted through Lagrangian analysis of the measured velocities shown in Fig. 2

Full size image

The self-consistent (SC) portion of SCLA refers to the technique used to estimate material strength from LA. The technique was originally applied to shock-release and shock–reshock experiments [19] before being adapted to the ramp-release configuration of interest here [9, 21, 23]. The fundamental assumption in this analysis is that the material obeys either a von Mises or Tresca yield criterion, Y. The uniaxial strain loading conditions in these experiments combined with the yield criterion leads to [24]

$$\begin{aligned} \sigma _x = P + \frac{4}{3}\tau , \end{aligned}$$
(2)

where P is the mean stress, and \(\tau \) is the equivalent shear stress defined as \(2\tau = Y = \sigma _x - \sigma _y\), and \(\sigma _y = \sigma _z\) are the lateral components of stress. Substituting the definition of the bulk and longitudinal sound speeds, rearranging Eq. 2 in differential form, and integrating results in [9, 21, 25]

$$\begin{aligned} \Delta \tau = \frac{3}{4}\rho _0\int _{u_{peak}}^{u_{trans}} \left[c_L^2(u) - c_b^2(u)\right]\frac{du}{c_L(u)} \end{aligned}$$
(3)

where \(c_b\) is the bulk wavespeed. Eq. 3 represents the integration from the beginning of the loading reversal (start of elastic deformation) to the transition to complete plastic deformation. In the context of a yield surface, this change in shear stress represents its transition from the upper yield surface to the lower surface, so if these surfaces are symmetric then Eq. 3 represents the yield strength. A conceptual illustration of this integration is given in Fig. 4, which is an idealization of one of these experiments. The arrows in the measured curve in Fig. 4 represent increasing time, as the material deformation is initially elastic before transitioning to the plastic wavespeed for the majority of loading. At peak compression and upon loading reversal, the wavespeed jumps up to the elastic value associated with the peak state and then smoothly transitions back down to the plastic wavespeed. The shaded region within the measured curve represents Eq. 3, which is the quantitative metric of interest extracted from SCLA.

Fig. 4
figure 4

Conceptual illustration of the SCLA analysis. The change in shear stress is related to the integration of the wavespeed between the measured loading and unloading profiles. Different approximation can be made to correct for the lost area of integration due to attenuation in the peak particle velocity

Full size image

The remaining features of Fig. 4 represent different assumptions relating to how \(\Delta \tau \) from Eq. 3 is corrected for attenuation. Since these experiments do not contain a steady peak state and the intially elastic release wave travels faster than the plastic compression wave, the peak decays (attenuates) as the stress pulse propagates. Subsequently, the Lagrangian analysis only captures the lower (sample output) peak velocity, so a correction is required to estimate the missing higher velocity portion of the material response. Fig. 4 shows two different assumptions to calculate this correction. The first, labeled as correction 1, is what has been reported previously [26]:

$$\begin{aligned} \Delta \tau _{Att1} = \frac{3}{8} \rho _0 \left[c_L^2(u_1)-c_b^2(u_1)\right]\frac{\Delta u}{\bar{c}}, \end{aligned}$$
(4)

where the longitudinal elastic and bulk wavespeeds are evaluated at the peak particle velocity, \(u_1\), \(\Delta u\) is the amount of attenuation, and \(\bar{c}\) is the average of the two wavespeeds at peak particle velocity. This correction originates from previous calculations of Eq. 3 in which the quasi-elastic portion of the wavespeed is assumed to be linear function of strain [21, 26], allowing for a simple estimate of the total integral (including attenuation).

As an alternative attenuation correction, labeled correction 2 in Fig. 4, we also explore the direct integration of Eq. 3 assuming \(c_L\) and \(c_b\) increase at equal rates across \(\Delta u\):

$$\begin{aligned} \Delta \tau _{Att2} = \frac{3}{4} \rho _0 \left[c_L^2(u_1)-c_b^2(u_1)\right]\frac{\Delta u}{c(u_1)}. \end{aligned}$$
(5)

In practice, correction 2 is roughly a factor of two larger than correction 1 and the approximations should bound the problem reasonably well. As such, both corrections are calculated and assessment of their performance will be made through comparisons with the second analysis method described in Sect. 3.3.

After the addition of the attenuation correction to Eq. 3 to formulate the final \(\Delta \tau \), a few other relevant metrics can be obtained from SCLA [9]. The average strain over the integration range can be used to calculate the average longitudinal stress and Eq. 2 can then be used to estimate the average pressure. In addition to strain, stress and pressure at the peak state, estimates of the shear modulus can be made assuming the peak wavespeed repesents the true longitudinal elastic velocity [27]:

$$\begin{aligned} G=\frac{3}{4}\rho _0(1-\varepsilon _{peak})(c_{L,peak}^2-c_{b,peak}^2). \end{aligned}$$
(6)
Table 2 Summary of the Gaussian distributions used in the Monte Carlo uncertainty quantification of the SCLA method
Full size table

SCLA does not lend itself to a simple uncertainty propagation, so a Monte Carlo method is used to quantify the errors [10]. Uncorrelated normal distributions are used to represent the errors in the relevant analysis parameters and the entire SCLA is performed (independently for each measurement) for each instantiation of a random draw from these distributions. Ten thousand Monte Carlo samples were taken and statistics were calculated based on the subsequent distributions in the strength metrics. A summary of the Gaussian distributions used for the uncertainty quantification is given in Table 2. The first four parameters in Table 2 represent typical experimental uncertainties for shockless compression experiments on the Z machine, while the last three represent uncertainties which factor into the hydrocode simulations used to perform the window correction [9]. As has been shown previously, the SCLA result only weakly depends on the model choice in the simulations insofar as the model reasonably represents the experiment. The electrode and window materials utilize well-established standards [10, 28], while the sample material takes advantage of the calibrations described later in Sect. 3.3, which couple a simple yield model to Johnson et al.’s anelastic model [20] to describe the anelastic release. These calibrations, by construction, provide an excellent representation of the wave interactions (ie. window correction), but relatively large distributions are applied to the yield strength and anelastic parameters to produce variations which encompass the measured velocities to ensure model choice is not significantly influencing the SCLA. The simulation parameter scalings refer to: (1) global multiplication of the magnetic field boundary condition (ie. drive uncertainty) which has been determined previously [29], (2) the initial strength (\(Y_0\)) which propagates linearly to high pressures (see Eq. 8), and (3) the linear anelastic theory constants \(B(L/b)^2\) and \(B/(nb^2)\) described in [20]. These latter constants describe the quasi-elastic nature of the measured velocity profiles and are calibrated as hyperparameters through the method described in Sect. 3.3.

The SCLA results for all of the experiments are summarized in Figs. 5 and 6 and in Table 3. Fig. 5 contains the results of both attenuation corrections, where for most of the experiments there is not a significant difference to within the estimated errors. The exception is the Ir data where the higher wavespeeds result in significantly more attenuation. In this case, the second attenuation correction is more consistent with the Bayes calibrations described later in Sec. 3.3. Additionally, we find synthetic analyses of the forward simulations, analagous to those described in [9] are also most consistent with this second correction. As such, we take Eq. 5 as the more appropriate approximation for these data, and so this is the value reported in Table 3.

The effect of the shocks on experiment Z3322 manifest as the regions of constant wavespeed in the Ta, Pt, and Ir profiles at particles velocites just under 0.5 mm/\(\mu \) s in Fig. 3. From a practical point of view, this region is far from the SCLA integration, so it does not affect the interpretation of strength. Further, examination of the temperature rise from the simulations described in Sect. 3.3, suggest Pt was the worst offender but still only had a temperature increase of \(\sim \) 125 K over the shockless compression path. Thus, the thermodynamic trajectories were not significantly altered, so the shocks are negligible. This assertion if further corroborated with the Ta data, where there are no measurable differences in the inferred strength in other experiments (Z3249, for example) which contained no shocks and were compressed to similar peak pressures.

Table 3 Summary of the self-consistent Lagrangian analysis (SCLA). \(\Delta \tau \) represents the total value which is the sum of Eqs. 3 and 5
Full size table
Fig. 5
figure 5

Estimated strength for the SCLA and Bayes calibration methods for each of the materials tested. SCLA1 and SCLA2 refer to the attenuation corrections described in Fig. 4 and Eqs. 4 and 5, respectively. The uncertainties in SCLA2 represent the standard error, and are comparable to SCLA1 which are not shown for clarity. The Bayes calibration is represented by the mean, maximum a posteriori (MAP), and credible intervals of the propagated posterior distributions; the 68% credible intervals effectively represent the standard error

Full size image
Fig. 6
figure 6

Estimated shear modulus from the SCLA analysis. Corresponding dashed lines are the SCG model with parameters reported in Table 1

Full size image

The shear modulus for each measurement, estimated through Eq. 6 is shown in Fig. 6. The dashed lines represent the SCG model [14], parameters of which are determined from single crystal data [13] and summarized in Table 1. These lines were constructed using the average stress-density response given by the Lagrangian analysis for each material. The SCG model for the cold shear modulus is given by

$$\begin{aligned} G = G_0 \left[ 1+A \frac{P}{\Bigl (\frac{\rho }{\rho _0}\Bigr )^{1/3}} \right] , \end{aligned}$$
(7)

and is commonly used to estimate the pressure scaling of the strength models, where \(\frac{Y}{Y_0} \sim \frac{G}{G_0}\). The data suggest, albeit with relatively large uncertainties, the SCG model form and estimated parameters extrapolate reasonably to multi-megabar pressures. The notable exception is Ir, which suggests the A in Table 1 is too large. Of the values reported for the four metals in [13], only Ir contains an estimate for A instead of a true measurement. Further, for the wide range of metals examined in [13] the difference between this estimate and experiment were \(\sim 25\%\). Thus, it is not unreasonable to assume errors in the Ir value of \(25\%\), and dropping A by this amount results in excellent agreement with the data.

Bayesian Calibration

As an alternative analysis approach, it is possible to calibrate the sample material strength directly through the forward simulation configuration shown in Fig. 1. Bayesian calibration frameworks are being actively developed specifically for these types of dynamic experiments in which velocimetry is the primary diagnostic and a predictive simulation capability exists [29, 30]. There are two features of Bayesian approaches which are appealing for this application. First, this is a well-established and rigorous statistical technique which provides probability distributions for the calibration parameters. In this case, the calibration parameters refer to parameters of the yield strength model, so uncertainty quantification is inherently included. Second, it is possible to incorporate all of the uncertain parameters factoring into the simulations and the Bayesian framework allows for inference of all of these parameters. By simultaneously calibrating over multiple experiments, it is possible to reduce some of the experimental uncertainties beyond their measured values to give smaller uncertainties than conventional frequentist statistical methods. An example of this feature follows for the Ta results.

A potential drawback of the calibration approach is that it requires the specification of a yield model form. In this work, we chose a simplified two parameter Steinberg–Cochrane–Guinan (SCG) form [14] analogous to Eq. 7:

$$\begin{aligned} Y = Y_0 \left[ 1+A \frac{P}{\Bigl (\frac{\rho }{\rho _0}\Bigr )^{1/3}} \right] . \end{aligned}$$
(8)

This model was chosen with the philosophy that the primary mechanism being probed in these experiments is the pressure dependence, and the SCG form has been shown to have appropriate limiting behaviors at low and high pressures [14]. Since all of the experiments are conducted at comparable loading rates, we are not explicitly accounting for rate effects. Similarly, since these are shockless compression experiments the temperature effects are expected to be minimal. The simulations described later in this section, for example, which have \(100\%\) conversion of plastic work into heat, suggest peak temperatures are bounded by the Ta experiments and are between 500 and 1200K (only \(\sim 10\%\) of the melt temperature). Further, with the exception of Ta, there are only two experiments available for each material. Given the extremely limited data it is not possible to uniquely identify parameters from a more complicated model [31]. For example, there is insufficient data to distinguish between strain and pressure hardening, so we neglect the strain hardening terms and assume \(Y_0\) is closer to the saturated value (\(Y_{max}\) in the full SCG model [14]). Thus, this model is known to be insufficient to describe all of the relevant physics, but it is a useful tool to capture the gross features and conditions sampled in these experiments.

The details of establishing the 1D simulation capability for each experiment such as determination of the magnetic field boundary condition, material models used for the standards, and verification of the mesh and artificial viscosity convergence are given in [10]. The EOS for the sample material is critically important to the accuracy of the simulations, and this was generated as part of the SCLA described in Sec. 3.2. Summarizing briefly, the Lagrangian Analysis provides the material response on the loading path (see Fig. 3) and SCLA provides an estimate of the material strength, so the measured loading path can be reduced to an isentrope [5]. This isentrope is then used within the Mie–Grüneisen approximation as the reference curve to form the EOS used in the forward simulations [32]; the thermal EOS parameters are estimated based on ambient measurements. Iteration over this entire procedure is then performed until self-consistency between the EOS and strength are obtained. Thus, there was a consistency built-in to the SCLA and calibration analyses, but this is not necessarily required. The first iteration of SCLA, for example, used default material models (Sesame 93524 EOS [33] and SCG model [14]) and produced results which are comparable to the final reported values in Table 3.

Once the simulation capability is established, all that remains is to define the uncertain parameters along with their prior probability distributions and then perform the Bayesian calibration. The prior distributions used in this analysis are the same as those given in Table 2 with the exception of the strength scale, where, instead, both parameters of Eq. 8 are incorporated. For all materials, uniform distributions of \([0,2]\; GPa\) were used for \(Y_0\) and \([0,150] \; TPa^{-1}\) were used for A. These values were confirmed prior to the calibration to be more than sufficient to cover the range of possible solutions for all four metals.

We refer to [29] for the details of calibration implementation, and only note a few of the design choices used here. First, Monte Carlo sampling was used to select 10, 000 points from the prior distributions and for each instantiation a simulation was run for the entire set of experiments. Training data was extracted from each simulation by extracting the simulated window velocity waveform over a time range that starts when loading (prior to peak) reaches \(92.5\%\) of peak velocity, and ends when unloading (after peak) decreases to \(77.5\%\) of peak velocity. This velocity was then discretized into 500 points spaced equally in time. The range was selected to encompass the elastic-plastic transition associated with the loading reversal in order to maximize the sensitivity of the calibration to the strength parameters.

With these training data in-hand, a surrogate model (emulator) was constructed, which is required to perform the calibration in a practical amount of time. As in [29], the surrogate model is constructed using Gaussian Processes, and we utilize the likelihood scaling approach to account for autocorrelation between the 500 velocity points. Markov Chain Monte Carlo (MCMC) was used to sample from the posterior distribution of all of the uncertain parameters. The MCMC chains were run to 100, 000 samples with adaptive sampling to ensure proper convergence and mixing.

Fig. 7
figure 7

Subset of the velocities in Fig. 2 showing only a single profile at each pressure for clarity. The 95% credible intervals from the Bayes calibration are shown as the shaded regions which completely encompass the experimental measurements

Full size image

Coverage of the velocity profiles as a result of the calibration are shown in Fig. 7. We emphasize that while the time base is ’arbitrary’, the relative timing between the drive and sample measurements is maintained so there are no time shifts between the experimental and simulated velocities. Figure 7 also illustrates the efficacy of the selected velocity ranges in capturing the nature of the velocity reversal all the way through the transition to complete plastic unloading. Since the credible intervals represent complete coverage of the measured velocities, this suggests there are not any significant modeling discrepancies. This is not to say that the physics of the models is correct, only that the simulations are capable of matching the measurements to within the experimental uncertainties.

The posterior distributions for the strength model parameters are shown in Fig. 8. These posteriors represent the dramatic difference between the amount of information available for each material. In the case of Ta, the calibration is performed against 15 different velocity profiles. With this amount of data, we are able to distinguish between the material properties of interest (\(Y_0, A\)) which are fixed across all of the profiles, and the other uncertainties unique to each profile, such as the electrode and sample thicknesses, relative timing, and the magnetic field boundary condition scaling. In other words, simultaneous calibration across all 15 velocity profiles allows for inference of the experimental uncertainties (thus reducing those errors), which, in turn, provides significantly better inference of \(Y_0\) and A beyond the traditional \(\sqrt{N}\) scaling, where N is the number of experiments. We find the magnetic field drive scaling posteriors generally drop a factor of 2 to 0.2% while thickness and timing uncertainties remain about the same. This is similar to previous calibrations [29] where the drive scaling is the dominant uncertainty, making it the most identifiable.

Fig. 8
figure 8

Posterior distributions for the strength model parameters from the Bayesian calibration where the plot limits represent the uniform prior distributions. Ten contour intervals are shown, so each color level roughly represents \(10\%\) increases in the probability distribution (ie. the bright region is an \(\sim 10\%\) interval while the dark outer contour encompasses the entire distribution). Since the Au, Pt, and Ir distributions are highly non-normal, fits to the mean and confidence intervals in Fig. 5 were performed; these fits are represented by the points

Full size image

In the case of Au, Pt, and Ir, the calibration is performed over 3 or 4 profiles encompassing only 2 distinct peak pressures. As a result, there is not enough information to uniquely distinguish between \(Y_0\), A and the field scaling uncertainty. In the Bayesian setting, this is problematic because it is possible to bias \(Y_0\) and A if the field scaling is not inferred correctly. As such, we utilize a modularization approach [29] where the posteriors for the experimental uncertainties are not updated and we simply sample from their prior distributions at each step within the MCMC. Thus, the experimental errors are propagated (but not reduced) which results in unbiased but possibly overly conservative error estimates for \(Y_0\) and A.

Propagation of the posteriors shown in Fig. 8 through the strength model (Eq. 8) results in the mean and credible intervals shown in Fig. 5. Credible intervals of 68% are shown which can be interpreted as the standard errors, allowing for direct comparison with the SCLA errors. For Ta, we find the calibration results in a relatively tight interval, but agrees extremely well with the SCLA results. The only region of poor agreement is near 100 GPa, where the SCLA errors are on the fringe of the calibration intervals. This may suggest a deficiency in our simple strength model, but the general trends are captured correctly so we did not pursue a more sophisticated model. As expected from the limited amount of experiments, the intervals for Au, Pt, and Ir are quite large. However, it is encouraging to see good agreement with the SCLA points in terms of both the means and uncertainties. This gives further confidence in the robustness of the calibration approach, even in a regime where the data are extremely sparse. As noted previously, the calibration results are also used to inform the attenuation approximation. The calibrations are most consistent with the approximation in Eq. 5 (SCLA2) for all four metals, so this attenuation approximation is taken to be the better SCLA estimate.

In addition to the mean and credible intervals, the maximum a posteriori (MAP) solution is also shown in Fig. 5. The MAP solution represents the global maximum (or mode) of the posterior distributions in Fig. 8. Given the highly non-normal distributions for Au, Pt, and Ir, the MAP solution can be significantly different from mean. As shown in Fig. 5, however, the resulting pressure dependence of the strength between the MAP and mean are surprisingly similar. The exception is the Au calibration, where the MAP solution is softer but provides better agreement with the lower pressure SCLA results. This emphasizes the broad nature of the posterior distributions in that very different combinations of \(Y_0\) and A can result in equally valid fits to the experiments. More data, as with Ta, is required to uniquely constrain the parameter set.

Table 4 is provided to facilitate reproduction of the intervals shown in Fig. 5. The reported values for Ta are a direct reflection of the posterior distribution shown in Fig. 8, which is well-represented by a bivariate normal distribution. Unfortunately, it is much more difficult to represent the highly non-normal distributions for the other materials in a simple form. As such, fits for the strength model (Eq. 8) were performed for the mean as well as the upper and lower bounds for each interval in Fig. 5. The points arising for these deterministic fits are shown in Fig. 8 to emphasize these fits only reproduce the \(Y-P\) response and are reasonable solutions within the distribution, but do not reflect the true posteriors. For completeness, the MAP solution is also included as the first set of bold values in Table 4. As described previously, these MAP values correspond to the highest probabilities (bright gold regions) in Fig. 8 and are not necessarily consistent with the mean or credible interval fits.

Table 4 Summary of the Bayes calibration posteriors in Fig. 8
Full size table

Discussion

As mentioned previously in Sect. 2, we were expecting to measure significantly lower strengths in Au and Pt when compared to Ta and Ir. However, as shown in Fig. 5 the strengths across the four metals were remarkably similar. To put this in context, the calibration intervals are plotted along with the SCG model for each material in Fig. 9. The SCG model curves (dashed lines) for Ta, Au, and Pt use the reported values in [14]; since Ir parameters do not exist, the values in Table 1 are used and the strain hardening parameters are set to 0. As illustrated, for all of the metals the measured strength is higher than the SCG model prediction, especially for Pt and Au.

Fig. 9
figure 9

Calibration results from Fig. 5 where solid lines represent the mean and the corresponding shaded regions are the \(68\%\) credible interval. Dashed lines represent the SCG model

Full size image

Since pressure effects are not the only mechanism probed in the Z experiments, it is difficult to identify the origin of the discrepancies in Fig. 9. The Z experiments consist of 1D uniaxial strain deformation such that increases in pressure are directly proportional to a corresponding increase in plastic strain. Thus, there is a convolution of pressure and strain hardening in these data and we do not have the information necessary to separate these effects. For context, the average strains reported in Table 3 are close to the total strain (within a few percent), so values between 0.2 and 0.5 are representative. Additionally, while the strain-rates across the experiments are comparable, there is not enough known across these metals about the interplay between strain, strain rate, and the thermodynamic conditions accessed in these experiments to understand the results. The SCG model, for example, is rate-independent so it could be a simple matter of deficiencies in the model or the choice of data used for parameterization. As a parameterization example, the SCG values for \(Y_{max}\) are 0.23 and \(0.34\; GPa\) for Au and Pt, respectively, which are an order of magnitude larger than the \(Y_0\)’s in Table 1. These values represent the strength associated with saturated strain hardening and are in much better agreement with the Z calibrations, particularly the MAP values. Thus, it is possible there is an issue with how strain hardening is being accounted for within our simple framework. Specifically, it is possible the rate-dependence of the strain hardening is not being captured correctly by the SCG model and the evolution towards a saturated value is much faster in these high rate Z experiments. Alternatively, the simple form of the calibration model, which does not include strain hardening, may be insufficient to properly model the response and so the calibration results could be strongly biased. Consequently, it is not clear how much physical meaning can be attributed to \(Y_0\) and A, so care should be taken with these types of comparisons.

One path to better understanding the results in Fig. 9 is to examine a broader range of experiments and modern theoretical calculations to understand the relevant deformation mechanisms and how they contribute to the overall observed response. This type of holistic approach was recently applied to Ta [34]. Ta has been studied using a variety dynamic strengh platforms, and by incorporating experimental data spanning the range of strains and strain rates it is possible to isolate the pressure contribution. In this Ta work [34], it was found assuming the pressure dependence of the strength scales linearly with the pressure dependence of the shear modulus (ie. the self-similarity between Eqs. 7 and 8) is inconsistent with the high pressure Z strength data. The additional Au, Pt, and Ir data presented here suggest similar trends: the model for the shear moduli are in reasonable agreement with the data, but there is a significant difference in the pressure dependence of the strength. However, this is far from conclusive and more data across a range of experimental platforms will likely be required to understand the results.

Conclusions

Experiments were performed on Sandia’s Z machine to assess the multi-megabar strength of four high-Z metals: Ta, Pt, Au, and Ir. Magnetic loading was used to perform ramp-release compression experiments. By measuring the material behavior during loading reversal, quantitative estimates of the strength were made using both an established analytic method as well as a novel calibration approach based on forward modeling. Both methods produce similar results, and we find all four metals can support shear stresses on the order of several GPa at strain rates of \(\sim 5 \times 10^5\)/s to peak pressures of up to 400 GPa, which is significantly higher than predicted. A more thorough examination of the Ta data suggests the higher strength is due to a non-linear scaling of the strength with shear modulus [34]. The qualitative similarities in the data presented here across the four metals may suggest this larger pressure hardening behavior is not unique to Ta or BCC metals.