Multi-component Reliability Inference in Modified Weibull Extension Distribution and Progressive Censoring Scheme

Abstract

The statistical inference of multi-component reliability stress–strength system with nonidentical-component strengths is considered for the modified Weibull extension distribution in the presence of progressive censoring samples. For this aim, we study the estimation of multi-component reliability parameter in classical and Bayesian inference. So we derive some point and interval estimates such as maximum likelihood estimation, asymptotic confidence intervals, uniformly minimum variance unbiased estimation, approximate and exact Bayes estimation and highest posterior density intervals. Comparing of different estimates is provided by employing the Monte Carlo simulation, the mean squared error and coverage probabilities. Finally, one real data is utilized to illustrate the applicability of this new model.

1 Introduction

The Weibull distribution, which introduced by Swedish physicist [25], is one of the most commonly used lifetime distributions for modeling data in reliability, engineering, finance, hydrology, physics and environmental studies. This distribution is very flexible in modeling failure time data, as the corresponding failure rate function can be increasing, constant or decreasing. On the other hand, for complex system, the failure rate function can often be of bathtub shape and modeling of this system is so important in reliability analysis. For this reason, the modified Weinull extension (MWEx) with bathtub shaped failure rate function was proposed by Xie et al. [26]. Since its inception from 2002, the MWEx distribution has received a considerable amount of attention from the statistical community, with over 560 citations to date. Its versatility and effectiveness in a variety of situations have been portrayed in numerous books and papers. The probability density function (PDF) and cumulative distribution function (CDF) of this distribution are, respectively,

$$\begin{aligned} f(x)&=\lambda \beta \left( \frac{x}{\alpha }\right) ^{\beta -1}e^{\left( \frac{x}{\alpha }\right) ^\beta +\lambda \alpha \left( 1-e^{\left( \frac{x}{\alpha }\right) ^\beta }\right) }, \end{aligned}$$

(1)

$$\begin{aligned} F(x)&=1-e^{\lambda \alpha \left( 1-e^{\left( \frac{x}{\alpha }\right) ^\beta }\right) }, \end{aligned}$$

(2)

where $\alpha ,~\beta ,~\lambda >0$. Herein we denote a MWEx distribution with the parameters $\alpha$, $\beta$ and $\lambda$ by MWEx($\alpha ,\beta ,\lambda$). It is notable that MWEx is a general distribution where some most distributions can be obtained from it. In following, we explain about two of them: first one is Weibull distribution and the second one is Chen’s distribution, see Chen [8]. The Weibull distribution can be obtained as a special case of this distribution when $\alpha$ is so small that $1-e^{(\frac{x}{\alpha })^\beta }$ is approximately equal to $-(\frac{x}{\alpha })^\beta$. The particular case of the MWEx distribution for $\alpha =1$ is Chen’s distribution. The failure rate function (FRF) of MWEx distribution is

$$\begin{aligned} h(x)&=\lambda \beta \left( \frac{x}{\alpha }\right) ^{\beta -1}e^{(\frac{x}{\alpha })^\beta }, \end{aligned}$$

which depends only on the shape parameter $\beta$. The HF increases if $\beta \ge 1$ and is bathtub shaped if $\beta <1$. Some possible shapes of the PDF and the FRF of MWEx distribution are shown in Fig. 1.

Fig. 1

Shape of failure rate (left) and probability density (right) functions of MWEx distribution

The main contribution in the paper is the study in the context of Weibull extension model, there are other related works. For example, a new five parameter distribution, known as the modified beta flexible Weibull extension distribution, is derived and studied by Abubakari et al. [1]. Kamal and Ismail [12] considered the flexible Weibull Extension-Burr XII distribution. Nassar et al. [19] introduced a new extension of Weibull distribution, called Alpha logarithmic transformed Weibull distribution that provides better fits than some of its known generalizations. Peng and Yan [20] introduced a new extended Weibull distribution with one scale parameter and two shape parameters. Also, a new distribution as the exponentiated modified Weibull extension distribution has been considered by Sarhan and Apaloo [24].

Type-I and Type-II censoring schemes are two most fundamental schemes in many different censoring schemes. In these schemes, removing of the active units during the tests is not possible, whereas the removal of surviving units during the test can be pre-planned and intentional in order to save time and cost associated with test. For this and many other reasons, the progressive censoring is introduced. Combining the Type-II and progressive censoring schemes leads to consider progressive Type-II censoring scheme. Recently, this scheme was very successful in applications. Under this scheme, on a life test, N units are placed and before hand the experimenter decides n be the number of failures to be observed. So, at the first failure time, $R_1$ units randomly are removed from $N-1$ surviving units. At the second failure time, from the $N-R_1-1$ remaining units, $R_2$ units randomly are removed from the experiment. By continuing this process, finally, at the $n-$th failure time, all the remaining surviving units $R_n=N-n-R_1-\cdots -R_{n-1}$ randomly are removed from the experiment. So, in a progressive Type-II censoring scheme n is the number of failure time observations, $\{X_1,\ldots ,X_n\}$ is the censoring sample, and $\{N,n,R_1,\ldots ,R_n\}$ is the progressive censoring scheme, such that $R_1+\cdots +R_n+n=N$. Clearly, Type-II progressive censoring scheme can be converted to the conventional Type-II right censoring scheme (by $R_1=\cdots =R_{n-1}=0$ and $R_n=N-n$) and complete sampling case (by $R_1=\cdots =R_n=0$ and $N=n$). We propose that the reader refers to the book of Balakrishnan and Aggarwala [4], for more details on progressively censoring and relevant references.

Inference about stress–strength parameter is one of the interest and fundamental problems in reliability analysis. This parameter is shown by $R=P(Y<X)$, where Y and X are known as stress and strength and they are two independent random variables. Obviously, the system is reliable so long as the strength X is greater than its stress Y. This parameter has many applicable in different fields. For example, in clinical studies in medicine, if X and Y are the response of the control group to a therapeutic approach and the response of the treated group, respectively (see [11]), then R can be seen as the measure of treatment effect. The link between statistics and reliability theory leads to estimate of the stress–strength parameter, starting with the pioneering work of [6]. From that time, many researchers have studied inference on the reliability parameter from the classical and Bayesian points of views. Very recently, Al-Babtain et al. [2] considered Bayesian and non-Bayesian reliability estimation of stress–strength model for power-modified Lindley distribution. Sabry et al. [23] discussed Monte Carlo simulation of stress–strength model and reliability estimation for extension of the exponential distribution. Also, Metwally et al. [18] studied reliability analysis of the new exponential inverted Topp–Leone distribution with applications. About the multi- stress–strength reliability, Yousef and Almetwally [28] investigated multi- stress–strength reliability based on progressive first failure for Kumaraswamy model in Bayesian and non-Bayesian approaches. Also, Almetwally et al. [3] studied optimal plan of multi-stress–strength reliability Bayesian and non-Bayesian methods for the alpha power exponential model using progressive first failure. Moreover, about the fuzzy reliability approach, Sabry et al. [22] considered inference of fuzzy reliability model for inverse Rayleigh distribution. Also, Meriem et al. [17] introducing the Power XLindley distribution studied statistical inference, fuzzy reliability and COVID-19 application.

Reliability scientists, a system with more than one component, have called a multi-component system. In such system, there is one common stress component and k strength independent and identical components. Obviously, the system is reliable so long as at least s from k strength components exceed its stress. This model has received a great deal of attention, in recently years and is known as G system: s-out-of-k. Many examples can be given of multi-component systems. For instance, consider one G system: the 4 out of 8 as functioning V-8 engine of an automobile. In this system, the car can be derived if only four cylinders are firing. However, the automobile cannot be driven, if less than four cylinders are fired. Also, for another example, consider a suspension bridge. In this case, heavy traffic, wind loading, corrosion, etc., can be considered as stresses and the k number of vertical cable pairs can be considered as strengths. In this situation, the bridge breaks down, if a minimum s number of vertical cables are damaged. A more homely but complicated example of a multi-component system would be a music (stero Hi-Fi) system consisting of an FM tuner and record changer in parallel; connected in series with an amplifier and speakers (with the two speakers, say A and B) connected in parallel. Bhattacharyya and Johnson [5] firstly have presented this model as follows:

$$\begin{aligned} R_{s,k}&=\sum _{p=s}^{k}\left( {\begin{array}{c}k\\ p\end{array}}\right) \int _{-\infty }^{\infty }\big (1-F_X(y)\big )^p\big (F_X(y)\big )^{k-p}\textrm{d}F_Y(y), \end{aligned}$$

(3)

where the strength variables $(X_1,\ldots ,X_k)$ are independent and identically distributed with the CDF $F_X(\cdot )$ and stress variable Y has the CDF $F_Y(\cdot )$. Recently, this model has attracted a lot of attention and has been considered for complete and censored samples by some authors, for instance [14, 15].

As we saw, this assumption that the strengths are of i.i.d should be considered in every applications and this condition is not available in many practical situations, when the system component structures are different. The readers can see Farahmand et al. [10], for more details. So, in following, we try to focus on multi-component stress–strength models with nonidentical random strengths.

In following, one system with $\textbf{k}=(k_1,\ldots ,k_m)$ strength components is studied. In such systems, the components have nonidentical distributions so that the i-th component, $i=1,\ldots ,m$, follows a distribution with CDF $F_X(\cdot )$ and all of this strength variables are affected by a common stress Y with CDF $F_Y(\cdot )$. Obviously, this system is reliable so long as at least $\textbf{s}=(s_1,\ldots ,s_m)$ from $\textbf{k}$ strength components exceed its stress. Rasethuntsa and Nadar [21] have improved 3 to derive one suitable model as follows:

$$\begin{aligned} R_{\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\dots \sum _{p_m=s_m}^{k_m}\left( \prod _{l=1}^m\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \right) \int _{-\infty }^{\infty }\prod _{l=1}^m\left( \big (1-F_l(y)\big )^{p_l}\big (F_l(y)\big )^{k_l-p_l}\right) \textrm{d}F_Y(y). \end{aligned}$$

(4)

In very recently paper, Kohansal et al. [16] studied this model, for two components of strength variables. But, now, we consider this model for m components strength variables. So, we assume that the i-th strength component follows a MWEx($\alpha ,\beta ,\lambda _i$), for $i=1,\ldots ,m$, and the stress Y follows a MWEx($\alpha ,\beta ,\lambda$) distribution.

Accordingly, we continue the paper as follows. In Sect. 2, when the common parameters are unknown, the point statistical estimation of $R_{\textbf{s},\textbf{k}}$ is considered, so that, we obtain the MLE and Bayesian estimation are obtained. Because the lack of explicit from, we approximate the Bayesian estimation by Markov Chain Monte Carlo (MCMC) method. Also, in view of interval estimation, we studied the asymptotic and HPD intervals. In Sect. 3, when the common parameters are known, the statistical estimation of $R_{\textbf{s},\textbf{k}}$ is considered, so that, we obtain the MLE, exact Bayesian estimation, UMVUE, asymptotic and HPD intervals. In Sect. 4, we use the Numerical simulation results to compare the theoretical methods and Sect. 5, we consider the general case, when all parameters are different and unknown. In Sect. 6, one real data is utilized to illustrative the applicability of this new model. Finally, we conclude the paper in Sect. 7.

2 Inference on $R_{\textbf{s},\textbf{k}}$ with Unknown Common Parameters

In many empirical data analysis, the common parameters values of strengths and stress variables are approximately same. So, in such situations, we assume that they are equal. Also, some estimations, in other cases spatially the case with known common parameters, can be obtained from this case. In other advantages of this case, we can pointed the extent of estimations.

2.1 MLE of $R_{\textbf{s},\textbf{k}}$

Now, we suppose that $X_1\sim \textrm{MWEx}(\alpha ,\beta ,\lambda _1)$, $X_2\sim \textrm{MWEx}(\alpha ,\beta ,\lambda _2)$, $\ldots$, $X_m\sim \textrm{MWEx}(\alpha ,\beta ,\lambda _m)$ and $Y\sim \textrm{MWEx}(\alpha ,\beta ,\lambda )$ are independent random variables. Using Eqs. (1) and (2), we can obtain the multi-component reliability with nonidentical-component strengths in (4) as follows:

$$\begin{aligned} R_{\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\int _0^\infty e^{\big (\sum \limits _{l=1}^{m}\lambda _l p_l\big )\alpha (1-e^{(\frac{y}{\alpha })^\beta })}\prod _{l=1}^m\bigg (1-e^{\lambda _l\alpha (1-e^{(\frac{y}{\alpha })^\beta })}\bigg )^{k_l-p_l}\nonumber \\&\quad \times \lambda \beta (\frac{y}{\alpha })^{\beta -1} e^{\lambda \alpha (1-e^{(\frac{y}{\alpha })^\beta })+(\frac{y}{\alpha })^\beta }\textrm{d}y~~~{Put: t=e^{\alpha (1-e^{(\frac{y}{\alpha })^\beta })}}\nonumber \\&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\lambda \int _0^1 t^{\sum \limits _{l=1}^{m}\lambda _l p_l+\lambda -1} \prod _{l=1}^{m}\bigg ((1-t^\lambda _l)^{k_l-p_l}\bigg )\textrm{d}t\nonumber \\&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\lambda \int _0^1 t^{\sum \limits _{l=1}^{m}\lambda _l p_l+\lambda -1} \prod _{l=1}^{m}\bigg (\sum _{q_l=0}^{k_l-p_l}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) (-1)^{q_l}t^{\lambda _lq_l}\bigg )\textrm{d}t\nonumber \\&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )\nonumber \\&\quad \times (-1)^{\sum \limits _{l=1}^{m}q_l}\lambda \int _0^1 t^{\sum \limits _{l=1}^{m}\lambda _l (p_l+q_l)+\lambda -1}\textrm{d}t\nonumber \\&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )\nonumber \\&\quad \times (-1)^{\sum \limits _{l=1}^{m}q_l} \frac{\lambda }{\sum \limits _{l=1}^{m}\lambda _l (p_l+q_l)+\lambda }. \end{aligned}$$

(5)

Now, to derive the MLE of $R_{\textbf{s},\textbf{k}}$, we use the invariance property, so, first, we obtain the MLE’s unknown parameters $\alpha ,~ \beta ,~ \lambda _1,~ ,\ldots ,~ \lambda _m,~ \lambda$. With n system on the life-testing experiment, we construct the likelihood function. So, the observed samples can be provided as follows:

$$\begin{aligned} {\mathop {Y=\left[ \begin{array}{c} Y_{1} \\ \vdots \\ Y_{n} \end{array} \right] }\limits ^{\text {Observed stress variables}}} ~~\text{ and }~~~~~ {\mathop {X_l=\left[ \begin{array}{ccc} X^{(l)}_{11} &{}\quad \ldots &{}\quad X^{(l)}_{1k_l} \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ X^{(l)}_{n1} &{}\quad \ldots &{}\quad X^{(l)}_{nk_l} \end{array}\right] }\limits ^{\text {Observed strength variables}}},~ l=1,\ldots ,m. \end{aligned}$$

In following, we assume that $\{Y_{1},\ldots ,Y_n\}$ is progressive censoring sample from $\textrm{MWEx}(\alpha ,\beta ,\lambda )$ with the $\{N,n,S_1,\ldots ,S_n\}$ censoring scheme. Also, $\{X^{(l)}_{i1},\ldots ,X^{(l)}_{ik_l}\}$, $i=1,\ldots ,n$, $l=1,\ldots ,m$ is progressive censoring sample from $\textrm{MWEx}(\alpha ,\beta ,\lambda _i)$ with the $\{K_l,k_l,R^{(l)}_{i1},\ldots ,R^{(l)}_{ik_l}\}$ censoring scheme, where $i=1,\ldots ,n$, $l=1,\ldots ,m$. Therefore, we write the likelihood function of $\lambda _1,~ ,\ldots ,~ \lambda _m,$ and $\lambda$, $\alpha$, $\beta$ as

$$\begin{aligned} L(\lambda _1,\ldots ,\lambda _m,\lambda ,\alpha ,\beta |\text {data})&\propto \prod _{i=1}^{n}\bigg (\prod _{l=1}^{m}\Big (\prod _{j_l=1}^{k_l}f_l(x^{(l)}_{ij_l})\big (1-F_l(x^{(l)}_{ij_l})\big )^{R^{(l)}_{ij_l}}\Big )\bigg )\nonumber \\&\quad \times f_Y(y_{i})\big (1-F_Y(y_{i})\big )^{S_i}. \end{aligned}$$

About the advantage of this likelihood function, we can say that this is a general function, so that, some other likelihood functions case can be obtained from it as follows:

• $R^{(l)}_{ij_l}=0,~S_i=0$ $\Rightarrow$ $R_{\textbf{s},\textbf{k}}$ in complete sample case.

• $\textbf{k}=(k_1,k_2,0,\ldots ,0)$ $\Rightarrow$ $R_{\textbf{s},\textbf{k}}$ with two nonidentical-component in the progressive censoring case.

• $\textbf{k}=(k,0,\ldots ,0)$ $\Rightarrow$ $R_{s,k}$ in the progressive censoring case.

• $\textbf{k}=(k_1,k_2,0,\ldots ,0)$, $R^{(l)}_{ij_l}=0,~S_i=0$ $\Rightarrow$ $R_{\textbf{s},\textbf{k}}$ with two nonidentical-component in complete sample case.

• $\textbf{k}=(k,0,\ldots ,0)$, $R^{(l)}_{ij_l}=0,~S_i=0$ $\Rightarrow$ $R_{s,k}$ in complete sample case.

• $\textbf{k}=(1,0,\ldots ,0)$ $\Rightarrow$ $R=P(X<Y)$ in the progressive censoring case.

• $\textbf{k}=(1,0,\ldots ,0)$, $R^{(l)}_{ij_l}=0,~S_i=0$ $\Rightarrow$ $R=P(X<Y)$ in complete sample case.

We can obtain the likelihood function, based on observed data, as

$$\begin{aligned}&L(\lambda _1,\ldots ,\lambda _m,\lambda ,\alpha ,\beta |\text {data})\propto \Big (\prod _{l=1}^{m}\lambda _l^{nk_l}\Big )\beta ^{n(\sum \limits _{l=1}^{m}k_l+1)}\lambda ^n\times \Big (\prod _{i=1}^{n}\prod _{l=1}^{m}\prod _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^{\beta -1}\Big )\nonumber \\&\quad \times \Big (\prod _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta -1}\Big )\times e^{\sum \limits _{i=1}^{n}\sum \limits _{l=1}^{m}\sum \limits _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^{\beta }+\sum \limits _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta }}\times e^{\alpha \big (\sum \limits _{l=1}^{m}\lambda _lA_l(\alpha ,\beta )+\lambda B(\alpha ,\lambda )\big )}, \end{aligned}$$

(6)

where

$$\begin{aligned} A_l(\alpha ,\beta )&=\sum _{i=1}^{n}\sum _{j_l=1}^{k_l}\big (R^{(l)}_{ij_l}+1\big )\big (1-e^{(\frac{x^{(l)}_{ij_l}}{\alpha })^\beta }\big ),~l=1,\ldots ,m, \end{aligned}$$

(7)

$$\begin{aligned} B(\alpha ,\beta )&=\sum _{i=1}^{n}\big (S_i+1\big )\big (1-e^{(\frac{y_i}{\alpha })^\beta }\big ). \end{aligned}$$

(8)

To obtain the MLEs of unknown parameters, after deriving the log-likelihood function from (6), we should solve together the following equations:

$$\begin{aligned} \frac{\partial \ell }{\partial \lambda _l}&=\frac{nk_l}{\lambda _l}+\alpha A_l(\alpha ,\beta ),~l=1,\ldots ,m,\quad \frac{\partial \ell }{\partial \lambda }=\frac{n}{\lambda }+\alpha B(\alpha ,\beta ), \end{aligned}$$

(9)

$$\begin{aligned} \frac{\partial \ell }{\partial \beta }&=\frac{n}{\beta }\left( \sum \limits _{l=1}^{m}k_l+1\right) +\sum _{i=1}^{n}\sum _{l=1}^{m}\sum _{j_l=1}^{k_l}\log \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )+\sum _{i=1}^{n}\log \big (\frac{y_i}{\alpha }\big )\nonumber \\&\quad +\sum _{i=1}^{n}\sum _{l=1}^{m}\sum _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta \log \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )\bigg (1-\alpha \lambda _l\Big (R^{(l)}_{ij_l}+1\Big )e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta }\bigg )\nonumber \\&\quad +\sum _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^\beta \log \big (\frac{y_i}{\alpha }\big )\bigg (1-\alpha \lambda \Big (S_i+1\Big )e^{\big (\frac{y_i}{\alpha }\big )^\beta }\bigg ), \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial \ell }{\partial \alpha }&=\frac{-n(\beta -1)}{\alpha }(\sum \limits _{l=1}^{m}k_l+1)-\frac{\beta }{\alpha }\bigg (\sum _{i=1}^{n}\sum _{l=1}^{m}\sum _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta +\sum _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^\beta \bigg )\nonumber \\&\quad +\sum _{i=1}^{n}\sum _{l=1}^{m}\sum _{j_l=1}^{k_l}\lambda _l\Big (R^{(l)}_{ij_l}+1\Big )\bigg (1-e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta }+\beta \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta }\bigg )\nonumber \\&\quad +\lambda \sum _{i=1}^{n}\Big (S_i+1\Big )\bigg (1-e^{\big (\frac{y_i}{\alpha }\big )^\beta }+\beta \big (\frac{y_i}{\alpha }\big )^\beta e^{\big (\frac{y_i}{\alpha }\big )^\beta }\bigg ) \end{aligned}$$

(11)

The MLEs of $\lambda _1,~\ldots ,\lambda _m,~ \lambda , ~\alpha ,~ \beta$, presented by ${\widehat{\lambda }}_1,~\ldots ,{\widehat{\lambda }}_m,~ {\widehat{\lambda }},~{\widehat{\alpha }},~ {\widehat{\beta }}$, can be obtained from simultaneous solution of equations (9), (10) and (11), using one numerical method such as Newton–Raphson algorithm. Finally, the invariance property of MLE concludes that the MLE of $R_{\textbf{s},\textbf{k}}$, presented by $\widehat{R}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}$, can be obtained as

$$\begin{aligned} \widehat{R}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )\nonumber \\&\quad \times (-1)^{\sum \limits _{l=1}^{m}q_l} \frac{\widehat{\lambda }}{\sum \limits _{l=1}^{m}\widehat{\lambda }_l (p_l+q_l)+\widehat{\lambda }}. \end{aligned}$$

(12)

2.2 Asymptotic Confidence Interval

We provide the asymptotic confidence interval of $R_{\textbf{s},\textbf{k}}$, in this section. For such aim, firstly, using the multivariate central limit theorem, we derive the asymptotic distribution of unknown parameters $\lambda _1,~\ldots ,\lambda _m,~\lambda , ~\alpha ,~ \beta$, and then later, using delta method, we derive the asymptotic distribution and asymptotic confidence interval of $R_{\textbf{s},\textbf{k}}$.

It is noted that the expected Fisher information matrix $J(\theta ) = -E(I(\theta ))$ prepares the asymptotic variances and covariances of the parameter vector $\theta$. In this presented, $\theta =(\lambda _1,\ldots ,\lambda _m,\lambda ,\alpha ,\beta )$ is a vector of unknown parameters and $I(\theta ) = [I_{ij}]=[{\partial ^2\ell }/{(\partial \theta _i\partial \theta _j)}]$, $i,j=1,\ldots ,m+3$, is the observed Fisher information matrix. From the $I(\theta )$ elements, obviously, we cannot obtain $J(\theta )$ elements easily. So, we use the observed Fisher information matrix instead of expected Fisher information matrix. The elements of $I(\theta )$ matrix are as follows:

$$\begin{aligned} I_{l,l}&=\frac{nk_l}{\lambda _l^2},~l=1,\ldots ,m,\quad I_{m+1,m+1}=\frac{n}{\lambda ^2},\quad I_{l,k}=0,~l,k=1,\ldots ,m+1, l\ne k\\ I_{l,m+2}&=-\sum _{i=1}^{n}\sum _{j_l=1}^{k_l}\Big (R^{(l)}_{ij_l}+1\Big )\Big (1-e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta }+\beta \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta }\Big ),~l=1,\ldots ,m,\\ I_{m+1,m+2}&=-\sum _{i=1}^{n}\Big (S_i+1\Big )\Big (1-e^{\big (\frac{y_i}{\alpha }\big )^\beta }+\beta \big (\frac{y_i}{\alpha }\big )^\beta e^{\big (\frac{y_i}{\alpha }\big )^\beta }\Big ),\\ I_{l,m+3}&=\alpha \sum _{i=1}^{n}\sum _{j_l=1}^{k_l}\Big (R^{(l)}_{ij_l}+1\Big )\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta \log \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big ) e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta },~l=1,\ldots ,m,\\ I_{m+1,m+3}&=\alpha \sum _{i=1}^{n}\Big (S_i+1\Big )\big (\frac{y_i}{\alpha }\big )^\beta \log \big (\frac{y_i}{\alpha }\big ) e^{\big (\frac{y_i}{\alpha }\big )^\beta },\\ I_{m+2,m+3}&=-\frac{n}{\alpha }(\sum \limits _{l=1}^{m}k_l+1)-\frac{1}{\alpha }\bigg (\sum _{i=1}^{n}\sum _{l=1}^{m}\sum _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta \Big (1+\beta \log \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )\Big )\\&\quad +\sum _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^\beta \Big (1+\beta \log \big (\frac{y_i}{\alpha }\big )\Big )\bigg )\\&\quad +\sum _{i=1}^{n}\sum _{l=1}^{m}\sum _{j_l=1}^{k_l}\lambda _l\Big (R^{(l)}_{ij_l}+1\Big )\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta }\bigg (\beta \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta \log \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )\\&\quad +\beta \log \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )-\log \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )+1\bigg )\\&\quad +\lambda \sum _{i=1}^{n}\Big (S_i+1\Big )\big (\frac{y_i}{\alpha }\big )^\beta e^{\big (\frac{y_i}{\alpha }\big )^\beta }\bigg (\beta \big (\frac{y_i}{\alpha }\big )^\beta \log \big (\frac{y_i}{\alpha }\big )+\beta \log \big (\frac{y_i}{\alpha }\big )-\log \big (\frac{y_i}{\alpha }\big )+1\bigg ),\\ I_{m+2,m+2}&=\frac{n(\beta -1)}{\alpha ^2}(\sum \limits _{l=1}^{m}k_l+1)+\frac{\beta }{\alpha ^2}(1+\frac{1}{\alpha })\bigg (\sum _{i=1}^{n}\sum _{l=1}^{m}\sum _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta +\sum _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^\beta \bigg )\\&\quad -\frac{\beta }{\alpha }\sum _{i=1}^{n}\sum _{l=1}^{m}\sum _{j_l=1}^{k_l}\lambda _l\Big (R^{(l)}_{ij_l}+1\Big )\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta }\bigg (\beta \big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta +\beta -1\bigg )\\&\quad -\frac{\lambda \beta }{\alpha }\sum _{i=1}^{n}\Big (S_i+1\Big )\big (\frac{y_i}{\alpha }\big )^\beta e^{\big (\frac{y_i}{\alpha }\big )^\beta }\bigg (\beta \big (\frac{y_i}{\alpha }\big )^\beta +\beta -1\bigg ),\\&I_{m+3,m+3}=-\frac{n}{\beta ^2}(\sum \limits _{l=1}^{m}k_l+1)\\&\quad +\sum _{i=1}^{n}\sum _{l=1}^{m}\sum _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta \log ^2\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )\bigg (1-\alpha \lambda _l\Big (R^{(l)}_{ij_l}+1\Big ) e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^\beta }\Big (\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )+1\Big )\bigg )\\&\quad +\sum _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^\beta \log ^2\big (\frac{y_i}{\alpha }\big )\bigg (1-\alpha \lambda \Big (S_i+1\Big ) e^{\big (\frac{y_i}{\alpha }\big )^\beta }\Big (\big (\frac{y_i}{\alpha }\big )+1\Big )\bigg ). \end{aligned}$$

From the multivariate central limit theorem, it can be concluded that

$$\begin{aligned} ({\widehat{\lambda }}_1,{\widehat{\lambda }}_2,\ldots ,{\widehat{\lambda }}_m,{\widehat{\lambda }},{\widehat{\alpha }},{\widehat{\beta }}) \sim N_{m+3}((\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda ,\alpha ,\beta ),\mathbf {I^{-1}}(\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda ,\alpha ,\beta )), \end{aligned}$$

where $\textbf{I}(\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda ,\alpha ,\beta ) = \left[ I_{i,j} \right] ,~ i,j=1,\ldots ,m+3$, is a symmetric matrix, in which $I_{i,j}$ are given in the above equations. Also, $\mathbf {I^{-1}}(\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda ,\alpha ,\beta )=\frac{[b_{i,j}]}{\text{ det }\big (\textbf{I}(\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda ,\alpha ,\beta )\big )},~ i,j=1,\ldots ,m+3$, in which $b_{ij}$ is the elements of ${adj }(\textbf{I}(\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda ,\alpha ,\beta ))$.

Now, from the delta method, it can be concluded that

$$\begin{aligned} \widehat{R}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}\sim N(R_{\textbf{s},\textbf{k}},B), \end{aligned}$$

where, $B=\mathbf {b^TI^{-1}}(\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda ,\alpha ,\beta )\textbf{b}$, in which

$$\begin{aligned}{} & {} \textbf{b} = \left[ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _1}~~ \cdots ~~ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _m} ~~ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda } ~~ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \alpha }~~\frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \beta }\right] ^T\\ {}{} & {} =\left[ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _1}~~ \cdots ~~ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _m} ~~ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda } ~~ 0~~0\right] ^T, \end{aligned}$$

with

$$\begin{aligned} \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _l}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )\nonumber \\&\quad \times (-1)^{\sum \limits _{l=1}^{m}q_l+1} \frac{\lambda (p_l+q_l)}{\big (\sum \limits _{l=1}^{m}\lambda _l (p_l+q_l)+\lambda \big )^2},~ l=1,\ldots ,m, \end{aligned}$$

(13)

$$\begin{aligned} \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda }&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )\nonumber \\&\quad \times (-1)^{\sum \limits _{l=1}^{m}q_l} \frac{\sum \limits _{l=1}^{m}\lambda _l (p_l+q_l)}{\big (\sum \limits _{l=1}^{m}\lambda _l (p_l+q_l)+\lambda \big )^2}. \end{aligned}$$

(14)

So,

$$\begin{aligned} B&=\Big (\text{ det }\big (\textbf{I}(\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda ,\alpha ,\beta )\big )\Big )^{-1}\left[ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _1}~~ \cdots ~~ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _m} ~~ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda } ~~ 0~~0\right] \\&\quad \times \left[ \begin{array}{ccccccc} b_{1,1} &{} b_{1,2} &{} \cdots &{} b_{1,m} &{} b_{1,m+1} &{} b_{1,m+2} &{} b_{1,m+3} \\ &{} b_{2,2} &{} \cdots &{} b_{2,m} &{} b_{2,m+1} &{} b_{2,m+2} &{} b_{2,m+3} \\ &{} &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ &{} &{} &{} b_{m,m} &{} b_{m,m+1} &{} b_{m,m+2} &{} b_{m,m+3}\\ &{} &{} &{} &{} b_{m+1,m+1} &{} b_{m+1,m+2} &{} b_{m+1,m+3}\\ &{} &{} &{} &{} &{} b_{m+2,m+2} &{} b_{m+2,m+3}\\ &{} &{} &{} &{} &{} &{} b_{m+3,m+3} \end{array} \right] \left[ \begin{array}{c} \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _1}\\ \vdots \\ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _m}\\ \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda }\\ 0\\ 0 \end{array} \right] \\&=\Big (\text{ det }\big (\textbf{I}(\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda ,\alpha ,\beta )\big )\Big )^{-1}\\&\quad \times \bigg ({\sum \limits _{j=1}^{m}\sum \limits _{i=1 }^{m}\frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _j}\frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _i}b_{j,i}+\frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda }\big (\sum \limits _{i=1}^{m}\frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _i}b_{i,m+1}\big )^2+\big (\frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda }\big )^2b_{m+1,m+1}}\bigg ). \end{aligned}$$

Consequently, we construct a $100(1-\eta )\%$ asymptotic confidence interval for $R_{\textbf{s},\textbf{k}}$ as

$$\begin{aligned} (\widehat{R}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}-z_{1-\frac{\eta }{2}}\sqrt{\widehat{B}},\widehat{R}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}+z_{1-\frac{\eta }{2}}\sqrt{{\widehat{B}}}), \end{aligned}$$

where $z_{\eta }$ is 100$\eta$-th percentile of N(0, 1).

2.3 Bayes Estimation of $R_{\textbf{s},\textbf{k}}$

In this section, under the squared error loss function, we infer the Bayesian estimation and corresponding credible intervals for $R_{\textbf{s},\textbf{k}}$, assuming that the unknown parameters are the independent gamma random variables. So, we consider the prior distributions of the parameters as

$$\begin{aligned} \lambda _l&\sim \Gamma (a_l,b_l):~ \pi _l(\lambda _l)\propto \lambda _l^{a_l-1}e^{-b_l\lambda _l},~ l=1,\ldots ,m,\\ \lambda&\sim \Gamma (a_{m+1},b_{m+1}):~\pi _{m+1}(\lambda )\propto \lambda ^{a_{m+1}-1}e^{-b_{m+1}\lambda },\\ \alpha&\sim \Gamma (a_{m+2},b_{m+2}):~\pi _{m+2}(\alpha )\propto \alpha ^{a_{m+2}-1}e^{-b_{m+2}\alpha },\\ \beta&\sim \Gamma (a_{m+3},b_{m+3}):~\pi _{m+3}(\beta )\propto \beta ^{a_{m+3}-1}e^{-b_{m+3}\beta }. \end{aligned}$$

By this selection, we write the joint posterior density function of $\lambda _1,~\cdots ,\lambda _m,~ \lambda , ~\alpha ,~ \beta$ by

$$\begin{aligned} \pi (\lambda _1,\ldots ,\lambda _m,\lambda ,\alpha ,\beta |\text {data})&\propto L(\lambda _1,\ldots ,\lambda _m,\lambda ,\alpha ,\beta |\text {data})\nonumber \\&\quad \Big (\prod _{l=1}^{m}\pi _l(\lambda _l)\Big )\pi _{m+1}(\lambda )\pi _{m+2}(\alpha )\pi _{m+3}(\beta ). \end{aligned}$$

(15)

After some calculations, we conclude that the Bayes estimations of the unknown parameters cannot be obtained in a closed form, from (15), so that we should approximate the Bayesian estimations. For this, we propose the MCMC method. For this aim, by simplifying equation (15), we can rewrite it as follows:

$$\begin{aligned}&\pi (\lambda _1,\ldots ,\lambda _m,\lambda ,\alpha ,\beta |\text {data})\propto \Big (\prod _{l=1}^{m} \lambda _l^{nk_l+a_l-1}e^{-\lambda _l\big (b_l-\alpha A_l(\alpha ,\beta )\big )}\Big )\\&\quad \times \Big (\lambda ^{n+a_{m+1}-1}e^{-\lambda \big (b_{m+1}-\alpha B(\alpha ,\beta )\big )}\Big )\\&\quad \times \Big (\prod _{i=1}^{n}\prod _{l=1}^{m}\prod _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^{\beta -1}\Big )\times \Big (\prod _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta -1}\Big )\times \alpha ^{a_{m+2}-1}e^{-b_{m+2}\alpha }\\&\quad \times e^{\sum \limits _{i=1}^{n}\sum \limits _{l=1}^{m}\sum \limits _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^{\beta }+\sum \limits _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta }}\times \beta ^{a_{m+3}+n(\sum \limits _{l=1}^{m}k_l+1)-1}e^{-b_{m+3}\beta }, \end{aligned}$$

where $A_l(\cdot ,\cdot )$, $l=1,\ldots ,m$ and $B(\cdot ,\cdot )$ are given in (7) and (8), respectively. So, we can obtain the posterior PDFs of the parameters as

$$\begin{aligned}&\lambda _l|\alpha ,\beta ,\text {data}\sim \Gamma (nk_l+a_l,b_l-\alpha A_l(\alpha ,\beta )),~l=1,\ldots ,m,\\&\lambda |\alpha ,\beta ,\text {data}\sim \Gamma (n+a_{m+1},b_{m+1}-\alpha B(\alpha ,\beta )),\\&\pi (\alpha |\lambda _1,\ldots ,\lambda _m,\lambda ,\beta ,\text {data})\propto \alpha ^{a_{m+2}-1}\times \Big (\prod _{i=1}^{n}\prod _{l=1}^{m}\prod _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^{\beta -1}\Big )\\&\times \Big (\prod _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta -1}\Big )\times e^{\sum \limits _{i=1}^{n}\sum \limits _{l=1}^{m}\sum \limits _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^{\beta }+\sum \limits _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta }}\times e^{-b_{m+2}\alpha +\sum \limits _{l=1}^{m}\lambda _l\alpha _lA_l(\alpha ,\beta )+\lambda \alpha B(\alpha ,\lambda )}\\&\pi (\beta |\lambda _1,\ldots ,\lambda _m,\lambda ,\alpha ,\text {data})\propto \beta ^{a_{m+3}+n(\sum \limits _{l=1}^{m}k_l+1)-1}\times \Big (\prod _{i=1}^{n}\prod _{l=1}^{m}\prod _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^{\beta -1}\Big )\\&\times \Big (\prod _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta -1}\Big )\times e^{\sum \limits _{i=1}^{n}\sum \limits _{l=1}^{m}\sum \limits _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^{\beta }+\sum \limits _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta }}\times e^{-b_{m+3}\beta +\sum \limits _{l=1}^{m}\lambda _l\alpha _lA_l(\alpha ,\beta )+\lambda \alpha B(\alpha ,\lambda )}. \end{aligned}$$

Because the posterior PDFs of $\lambda _l,~l=1,\ldots ,m$ and $\lambda$ are gamma distributions, we generate random samples from them, easily. But, the posterior PDFs of $\alpha$ and $\beta$ are not well-known distributions. So, we use Metropolis–Hastings method, to generate random samples from them. Therefore, the Gibbs sampling algorithm can be implemented by the following:

• $\mathbf {1.}$ Begin with initial values $(\lambda _{1(0)},\ldots ,\lambda _{m(0)},~\lambda _{(0)},~ \alpha _{(0)},~\beta _{(0)})$.

• $\mathbf {2.}$ Set $t=1$.

• $\mathbf {3.}$ Generate $\alpha _{(t)}$ from $\pi (\alpha |\lambda _{1(t-1)},\ldots ,\lambda _{m(t-1)},\lambda _{(t-1)},\beta _{(t-1)},\text {data})$ using Metropolis–Hastings method, with $N(\alpha _{(t-1)},1)$ as proposal distribution.

• $\mathbf {4.}$ Generate $\beta _{(t)}$ from $\pi (\beta |\lambda _{1(t-1)},\ldots ,\lambda _{m(t-1)},\lambda _{(t-1)},\alpha _{(t-1)},\text {data})$ using Metropolis–Hastings method, with $N(\beta _{(t-1)},1)$ as proposal distribution.

• $\mathbf {5:m+4.}$ Generate $\lambda _{l(t)}$ from $\Gamma (nk_l+a_l,b_l-\alpha _{(t-1)}A_l(\alpha _{(t-1)},\beta _{(t-1)}))$, $l=1,\ldots ,m$.

• $\mathbf {m+5.}$ Generate $\lambda _{(t)}$ from $\Gamma (n+a_{m+1},b_{m+1}-\alpha _{(t-1)}B(\alpha _{(t-1)},\beta _{(t-1)})$.

• $\mathbf {m+6.}$ Evaluate the value

  $$\begin{aligned} R_{(t)\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )\\&\quad \times (-1)^{\sum \limits _{l=1}^{m}q_l} \frac{\lambda _{(t)}}{\sum \limits _{l=1}^{m}\lambda _{l(t)} (p_l+q_l)+\lambda _{(t)}}. \end{aligned}$$

• $\mathbf {m+7.}$ Set $t = t +1$.

• $\mathbf {m+8.}$ Repeat T times in Steps 3 : m+7.

Finally, we obtain the Bayesian estimation of $R_{\textbf{s},\textbf{k}}$ as follows:

$$\begin{aligned} \widehat{R}_{\textbf{s},\textbf{k}}^{\textrm{MC}}=\frac{1}{T}\sum _{t=1}^{T}R_{(t)\textbf{s},\textbf{k}}. \end{aligned}$$

(16)

Moreover, a $100(1-\eta )\%$ HPD credible interval of $R_{\textbf{s},\textbf{k}}$ can be provided, using the idea of Chen and Shao [9] as follows. First, sort $R_{(1)\textbf{s},\textbf{k}},\ldots ,R_{(T)\textbf{s},\textbf{k}}$ as $R_{((1)\textbf{s},\textbf{k})},\ldots ,R_{((T)\textbf{s},\textbf{k})}$ and then construct all the $100(1-\eta )\%$ confidence intervals of $R_{\textbf{s},\textbf{k}}$, as:

$$\begin{aligned} (R_{((1)\textbf{s},\textbf{k})},R_{(([T(1-\eta )])\textbf{s},\textbf{k})}),\ldots ,(R_{(([T\eta ])\textbf{s},\textbf{k})},R_{((T)\textbf{s},\textbf{k})}), \end{aligned}$$

where [T] symbolizes the largest integer less than or equal to T. The HPD credible interval of $R_{\textbf{s},\textbf{k}}$ is the shortest length interval.

3 Inference on $R_{\textbf{s},\textbf{k}}$ Known Common Parameters

When the common parameters values of strengths and stress variables are known, obtaining the estimations have less computational complexity than the case which considered in previous section. Moreover, due to the diverse and nice estimations, this case is very popular with researchers.

3.1 MLE of $R_{\textbf{s},\textbf{k}}$

Suppose that $\{Y_{1},\ldots ,Y_n\}$ is progressive censoring sample from $\textrm{MWEx}(\alpha ,\beta ,\lambda )$ with $\{N,n,S_1,\ldots ,S_n\}$ censoring scheme. Also, $\{X^{(l)}_{i1},\ldots ,X^{(l)}_{ik_l}\}$, $i=1,\ldots ,n$, $l=1,\ldots ,m$ is progressive censoring sample from $\textrm{MWEx}(\alpha ,\beta ,\lambda _i)$ with $\{K_l,k_l,R^{(l)}_{i1},\ldots ,R^{(l)}_{ik_l}\}$ censoring scheme, where $i=1,\ldots ,n$, $l=1,\ldots ,m$. Now, assuming that $\alpha$ and $\beta$ are known, from Sect. 2.1, we obtain the MLE of $R_{\textbf{s},\textbf{k}}$ by

$$\begin{aligned} \widehat{R}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )\nonumber \\&\quad \times (-1)^{\sum \limits _{l=1}^{m}q_l} \bigg (1+\sum \limits _{l=1}^{m}(p_l+q_l)\frac{k_lB(\alpha ,\beta )}{A_l(\alpha ,\beta )}\bigg )^{-1}. \end{aligned}$$

(17)

About the asymptotic confidence interval, when the common parameters $\alpha$ and $\beta$ are known, the Fisher information matrix can be obtained by

$$\begin{aligned} \textbf{I}(\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda )=\left\{ \begin{array}{lr} I_{ij} &{} i=j, \\ 0 &{} i\ne j, \end{array} \right. i,j=1,\ldots ,m+1. \end{aligned}$$

As $\textbf{I}(\lambda _1,\lambda _2,\ldots ,\lambda _m,\lambda )$ is a diagonal square matrix, so, similar to Sect. 2.2, we can obtain the asymptotic distribution of $R_{\textbf{s},\textbf{k}}$ as ${\widehat{R}}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}\sim N(R_{\textbf{s},\textbf{k}},C),$ where

$$\begin{aligned} C=\sum _{j=1}^{m} \left( \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _j}\right) ^2\frac{1}{I_{j,j}}+\left( \frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda }\right) ^2\frac{1}{I_{m+1,m+1}}, \end{aligned}$$

in which $\frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda _j}$ and $\frac{\partial R_{\textbf{s},\textbf{k}}}{\partial \lambda }$ are given in (13) and (14), respectively. Consequently, we construct a $100(1-\eta )\%$ asymptotic confidence interval for $R_{\textbf{s},\textbf{k}}$ as

$$\begin{aligned} (\widehat{R}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}-z_{1-\frac{\eta }{2}}\sqrt{\widehat{C}},\widehat{R}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}+z_{1-\frac{\eta }{2}}\sqrt{\widehat{C}}), \end{aligned}$$

where $z_{\eta }$ is 100$\eta$-th percentile of N(0, 1).

3.2 UMVUE of $R_{\textbf{s},\textbf{k}}$

Suppose that $\{Y_{1},\ldots ,Y_n\}$ is progressive censoring sample from $\textrm{MWEx}(\alpha ,\beta ,\lambda )$ with $\{N,n,S_1,\ldots ,S_n\}$ censoring scheme. Also, $\{X^{(l)}_{i1},\ldots ,X^{(l)}_{ik_l}\}$, $i=1,\ldots ,n$, $l=1,\ldots ,m$ is progressive censoring sample from $\textrm{MWEx}(\alpha ,\beta ,\lambda _i)$ with $\{K_l,k_l,R^{(l)}_{i1},\ldots ,R^{(l)}_{ik_l}\}$ censoring scheme, where $i=1,\ldots ,n$, $l=1,\ldots ,m$. Now, assuming that $\alpha$ and $\beta$ are known, we write the likelihood function by

$$\begin{aligned}&L(\lambda _1,\ldots ,\lambda _m,\lambda ,\alpha ,\beta |\text {data})\propto \Big (\prod _{l=1}^{m}\lambda _l^{nk_l}\Big )\beta ^{n(\sum \limits _{l=1}^{m}k_l+1)}\lambda ^n\times \Big (\prod _{i=1}^{n}\prod _{l=1}^{m}\prod _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^{\beta -1}\Big )\nonumber \\&\quad \times \Big (\prod _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta -1}\Big )\times e^{\sum \limits _{i=1}^{n}\sum \limits _{l=1}^{m}\sum \limits _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha }\big )^{\beta }+\sum \limits _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta }}\times e^{\alpha \Big (\sum \limits _{l=1}^{m}\lambda _lA_l(\alpha ,\beta )+\lambda B(\alpha ,\lambda )\Big )}, \end{aligned}$$

(18)

where $A_l(\alpha ,\beta )$, $l=1,\ldots ,m$ and $B(\alpha ,\beta )$ are given in (7) and (8), respectively. We note that, from (18), when the parameters $\alpha$ and $\beta$ are known, $A_l(\alpha ,\beta )$, $l=1,\ldots ,m$ and $B(\alpha ,\beta )$ are complete sufficient statistics for $\lambda _l$, $l=1,\ldots ,m$ and $\lambda$, respectively.

We obtain one progressive censoring samples from the exponential distribution with mean $\frac{1}{\lambda }$, by considering the transformation $Y^*_{i}=\alpha \Big (e^{\big (\frac{Y_{i}}{\alpha }\big )^\beta }-1\Big ),~i=1,\dots ,n$. Now, using them, define the following variables:

$$\begin{aligned} Z_1&=NY^*_{1},\\ Z_2&=(N-S_1-1)(Y^*_{2}-Y^*_{1}),\\&\vdots \\ Z_{n}&=(N-\sum _{i=1}^{n}S_i-n+1)(Y^*_{n}-Y^*_{n-1}). \end{aligned}$$

We conclude that, from Cao and Cheng [7], $Z_1,\ldots ,Z_n$ are independent and identically distributed, with mean of $\frac{1}{\lambda }$, from the exponential distribution and so, $B(\alpha ,\beta )=\sum \limits _{i=1}^{n}Z_i$ follow one gamma distribution with parameters n and $\lambda$, symbolically $B(\alpha ,\beta )\sim \Gamma (n,\lambda )$.

Lemma 1

Let $X^{(l)*}_{ij_l}=\alpha \Big (e^{\big (\frac{X^{(l)}_{ij_l}}{\alpha }\big )^\beta }-1\Big )$, $j_l=1,\ldots ,k_l$, $l=1,\ldots ,m$, $i=1,\ldots ,n$. The conditional PDFs of $Y^*_{1}$ given $B(\alpha ,\beta )=b$, $X^{(l)*}_{11}$ given $A_l(\alpha ,\beta )=a_l$ are, respectively, as follows:

Proof

Just like the method provided in [15], the lemma can be proved. $\square$

Theorem 1

Applying the complete sufficient statistics of $A_l(\alpha ,\beta )$, $l=1,\ldots ,m$ and $B(\alpha ,\beta )$ for $\lambda _l$, $l=1,\ldots ,m$ and $\lambda$, respectively, we obtain the UMVUE of $\psi (\lambda _1,\ldots ,\lambda _m,\lambda )=\frac{\lambda }{\sum \limits _{l=1}^{m}(p_l+q_l)\lambda _l+\lambda }$, which presented by ${\widehat{\psi }}_U(\lambda _1,\ldots ,\lambda _m,\lambda )$, is as

where

$$\begin{aligned}&\text{ Case } \text{ I: }~~ \frac{b}{N}<\min \left\{ \frac{a_l}{(p_l+q_l)N},~l=1,\ldots ,m\right\} ,\\&\text{ Case } \text{ II } \text{- } \text{ Case } \text{ m+1: }~~ \frac{a_l}{(p_l+q_l)N}\\ {}&<\min \left\{ \frac{b}{N},\frac{a_j}{(p_j+q_j)N},~ j\ne l, j=1,\ldots ,m\right\} ,~ l=2,\ldots ,m+1. \end{aligned}$$

Proof

We can see easily that $Y^*_{1}$ follows an exponential distribution with mean $\frac{1}{\lambda N}$ and $X^{(l)*}_{11}$, $l=1,\ldots ,m$ follow exponential distributions with mean $\frac{1}{\lambda _l K_l}$, $l=1,\ldots ,m$, respectively. So,

$$\begin{aligned} \phi (X^{(1)*}_{11}, \cdots , X^{(m)*}_{11}, Y^*_{1})=\left\{ \begin{array}{ll} 1&{} ~ K_lX^{(l)*}_{11}>N(p_l+q_l)Y^*_{1},~ l=1,\ldots ,m\\ \\ 0&{} ~ \text{ Otherwise }, \end{array} \right. \end{aligned}$$

is an unbiased estimation of $\psi (\lambda _1,\ldots ,\lambda _m,\lambda )$. Now, using the Rao–Blackwell theorem, we have

$$\begin{aligned}&{\widehat{\psi }}_U(\lambda _1,\ldots ,\lambda _m,\lambda )=E\Big (\phi (X^{(1)*}_{11},\ldots , X^{(m)*}_{11}, Y^*_{1})|A_1(\alpha ,\beta )\\&\quad =a_1,\ldots ,A_m(\alpha ,\beta )=a_m,B(\alpha ,\beta )=b\Big )\\&=\int \idotsint \limits _{{\mathcal {A}}}f_{X^{(1)*}_{11}|A_1(\alpha ,\beta )=a_1}(x_1)\cdots f_{X^{(m)*}_{11}|A_m(\alpha ,\beta )=a_m}(x_m)f_{Y^*_{1}|B(\alpha ,\beta )=b}(y)\textrm{d}x_1\cdots \textrm{d}x_m\textrm{d}y, \end{aligned}$$

where

$$\begin{aligned} {{\mathcal {A}}}=\left\{ (x_1,\ldots ,x_m,y):0<y<\frac{b}{N}, 0<x_l<\frac{a_l}{K_l}, K_lx_l>N(p_l+q_l)y, l=1,\ldots ,m\right\} , \end{aligned}$$

and the functions under integral are given in Lemma 1. We continue the proof for Case I as

$$\begin{aligned} {\widehat{\psi }}_U(\lambda _1,\ldots ,\lambda _m,\lambda )&=\int _0^{\frac{b}{N}}\int _{\frac{(p_m+q_m)Ny}{K_m}}^{\frac{a_m}{K_m}}\cdots \int _{\frac{(p_1+q_1)Ny}{K_1}}^{\frac{a_1}{K_1}}\frac{K_1(nk_1-1)(a_1-K_1x_1)^{nk_1-2}}{a_1^{nk_1-2}}\times \cdots \\&\quad \times \frac{K_m(nk_m-1)(a_m-K_mx_m)^{nk_m-2}}{a_m^{nk_m-1}}\times \frac{N(n-1)(b-Ny)^{n-2}}{b^{n-1}}\textrm{d}x_1\cdots \textrm{d}x_m\textrm{d}y\\&\quad =\int _0^{\frac{b}{N}}\Big (\int _{\frac{(p_m+q_m)Ny}{K_m}}^{\frac{a_m}{K_m}}\frac{K_m(nk_m-1)(a_m-K_mx_m)^{nk_m-2}}{a_m^{nk_m-1}}\textrm{d}x_m\Big )\\&\quad \times \cdots \times \Big (\int _{\frac{(p_1+q_1)Ny}{K_1}}^{\frac{a_1}{K_1}}\frac{K_1(nk_1-1)(a_1-K_1x_1)^{nk_1-2}}{a_1^{nk_1-2}}\textrm{d}x_1\Big )\\&\quad \times \frac{N(n-1)(b-Ny)^{n-2}}{b^{n-1}}\textrm{d}y \\&\quad =\frac{N(n-1)}{b}\int _0^{\frac{b}{N}}\Big (1-(p_m+q_m)\frac{N}{a_m}y\Big )^{nk_m-1}\times \cdots \times \Big (1-(p_1+q_1)\frac{N}{a_1}y\Big )^{nk_1-1}\\&\quad \times \Big (1-\frac{N}{b}y\Big )^{n-2}\textrm{d}y\quad \left\{ \text{ Put: }~~ t=\frac{Ny}{b}\right\} \\&\quad =(n-1)\int _0^1(1-t)^{n-2}\Big (1-(p_m+q_m)\frac{b}{a_m}t\Big )^{nk_m-1}\Big (1-(p_1+q_1)\frac{b}{a_1}t\Big )^{nk_1-1}\textrm{d}t\\&\quad =(n-1)\int _0^1(1-t)^{n-2}\Big (\sum _{j_m=0}^{nk_m-1}(-1)^{j_m}\left( {\begin{array}{c}nk_m-1\\ j_m\end{array}}\right) \big ((p_m+q_m)\frac{b}{a_m}t\big )^{j_m}\Big )\times \cdots \\&\quad \times \Big (\sum _{j_1=0}^{nk_1-1}(-1)^{j_1}\left( {\begin{array}{c}nk_1-1\\ j_1\end{array}}\right) \big ((p_1+q_1)\frac{b}{a_1}t\big )^{j_1}\Big )\textrm{d}t\\&\quad =\sum \limits _{j_1=0}^{nk_1-1}\cdots \sum \limits _{j_m=0}^{nk_m-1}(-1)^{\sum \limits _{l=1}^{m}j_l}\Big (\prod _{l=1}^{m}\big (\frac{p_l+q_l}{a_l}\big )^{j_l}\Big )\times \frac{\left( {\begin{array}{c}nk_1-1\\ j_1\end{array}}\right) \cdots \left( {\begin{array}{c}nk_m-1\\ j_m\end{array}}\right) }{\left( {\begin{array}{c}n+\sum \limits _{l=1}^{m}j_l-1\\ \sum \limits _{l=1}^{m}j_l\end{array}}\right) }. \end{aligned}$$

For other cases, the results can be obtained in a similar methods. $\square$

So, the UMVUE of $R_{\textbf{s},\textbf{k}}$ presented by $\widehat{R}^U_{\textbf{s},\textbf{k}}$ can be obtained by

$$\begin{aligned} \widehat{R}^U_{\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )\nonumber \\&\quad \times (-1)^{\sum \limits _{l=1}^{m}q_l}\widehat{\psi }_U(\lambda _1,\ldots ,\lambda _m,\lambda ). \end{aligned}$$

(19)

3.3 Bayes Estimation of $R_{\textbf{s},\textbf{k}}$

In this section, under the squared error loss function, we infer the Bayesian estimation and corresponding credible intervals for $R_{\textbf{s},\textbf{k}}$, assuming that the unknown parameters are the independent gamma random variables. So, we consider the prior distributions of the parameters as

$$\begin{aligned} \lambda _l&\sim \Gamma (a_l,b_l):~ \pi _l(\lambda _l)\propto \lambda _l^{a_l-1}e^{-b_l\lambda _l},~ l=1,\ldots ,m,\\ \lambda&\sim \Gamma (a_{m+1},b_{m+1}):~\pi _{m+1}(\lambda )\propto \lambda ^{a_{m+1}-1}e^{-b_{m+1}\lambda }. \end{aligned}$$

By this selection, we can write the joint posterior density function of $\lambda _1,~\cdots ,\lambda _m,~ \lambda$ by

$$\begin{aligned} \pi (\lambda _1,\ldots ,\lambda _m,\lambda |\alpha ,\beta ,\text {data})&=\frac{\Big (\prod \limits _{l=1}^{m}\mu _l^{\nu _l}\Big ) \mu ^{\nu }}{\Big (\prod \limits _{l=1}^{m}\Gamma (\nu _l)\Big ) \Gamma (\nu )}\times \Big (\prod _{l=1}^{m}\lambda _l^{\nu _l-1}\Big )\lambda ^{\nu -1} e^{-\sum \limits _{l=1}^{m}\lambda _{l}\mu _l-\lambda \mu }, \end{aligned}$$

(20)

where

$$\begin{aligned} \mu _l&=b_l-\sum _{i=1}^{n}\sum _{j_l=1}^{k_l}\big (R^{(l)}_{ij_l}+1\big )\big (1-e^{(\frac{x^{(l)}_{ij_l}}{\alpha })^\beta }\big ),~l=1,\ldots ,m,\quad \mu =b_{m+1}\\&\quad -\sum _{i=1}^{n}\big (S_i+1\big )\big (1-e^{(\frac{y_i}{\alpha })^\beta }\big ),\\ \nu _l&=nk_l+a_l,\quad \nu =n+a_{m+1}. \end{aligned}$$

We obtain the Bayes estimation of $R_{\textbf{s},\textbf{k}}$ under the squared error loss function, by solving the following multiple integral

$$\begin{aligned} {\widehat{R}}^B_{\textbf{s},\textbf{k}}&=\int _0^\infty \int _0^\infty \cdots \int _0^\infty R_{\textbf{s},\textbf{k}}\pi (\lambda _1,\ldots ,\lambda _m,\lambda |\alpha ,\beta ,\text{ data})\textrm{d}\lambda _1\cdots \textrm{d}\lambda _m \textrm{d}\lambda \nonumber \\&\quad =\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )(-1)^{\sum \limits _{l=1}^{m}q_l}\nonumber \\&\quad \times \int _{0}^\infty \int _{0}^\infty \cdots \int _{0}^\infty \frac{\lambda }{\sum \limits _{l=1}^{m}\lambda _l (p_l+q_l)+\lambda }\pi (\lambda _1,\ldots ,\lambda _m,\lambda |\alpha ,\beta ,\text{ data})\textrm{d}\lambda _1\cdots \textrm{d}\lambda _m \textrm{d}\lambda . \end{aligned}$$

(21)

Now, let us put the integral part in (21) by ${\mathcal {B}}$. So, We can simplify ${\mathcal {B}}$ by employing (20), as follows:

$$\begin{aligned} {\mathcal {B}}&=\int _{0}^\infty \int _{0}^\infty \cdots \int _{0}^\infty {{{\mathcal {C}}}_1}\times \frac{\Big (\prod \limits _{l=1}^{m}\lambda _l^{\nu _l-1}\Big )\lambda ^{\nu }}{\sum \limits _{l=1}^{m}\lambda _l (p_l+q_l)+\lambda }\times e^{-\sum \limits _{l=1}^{m}\lambda _{l}\mu _l-\lambda \mu }\textrm{d}\lambda _1\cdots \textrm{d}\lambda _m \textrm{d}\lambda , \end{aligned}$$

where ${{{\mathcal {C}}}_1}=\frac{\Big (\prod \limits _{l=1}^{m}\mu _l^{\nu _l}\Big ) \mu ^{\nu }}{\Big (\prod \limits _{l=1}^{m}\Gamma (\nu _l)\Big ) \Gamma (\nu )}$. Now, define the following variables:

$$\begin{aligned} \left. \begin{array}{l} \theta _1=\frac{\lambda _1 (p_1+q_1)}{\sum \limits _{l=1}^{m}\lambda _l (p_l+q_l)+\lambda },\\ \vdots \\ \theta _m=\frac{\lambda _m (p_m+q_m)}{\sum \limits _{l=1}^{m}\lambda _l (p_l+q_l)+\lambda },\\ Z=\sum \limits _{l=1}^{m}\lambda _l (p_l+q_l)+\lambda . \end{array}\right\} \Rightarrow \left\{ \begin{array}{lll} \lambda _1=\frac{\theta _1 z }{p_1+q_1},\\ \vdots \\ \lambda _m=\frac{\theta _m z }{p_m+q_m},\\ \lambda =z\big (1-\sum \limits _{l=1}^{m}\theta _l\big ). \end{array}\right. \end{aligned}$$

In this case, $0<\sum \limits _{l=1}^{m}\theta _l<1$, $z>0$ and the Jacobian is

$$\begin{aligned} |J(\theta _1,\ldots ,\theta _m,z)|=\left| \begin{array}{cccccc} \frac{z}{p_1+q_1}&{}0&{}0&{}\cdots &{}0&{}\frac{\theta _1}{p_1+q_1} \\ 0&{}\frac{z}{p_2+q_2}&{}0&{}\cdots &{}0&{}\frac{\theta _2}{p_2+q_2} \\ \vdots &{}\vdots &{}\vdots &{}\cdots &{}\vdots &{}\vdots \\ 0&{}0&{}0&{}\cdots &{}\frac{z}{p_m+q_m}&{}\frac{\theta _m}{p_m+q_m} \\ -z&{}-z&{}-z&{}\cdots &{}-z&{}1-\sum \limits _{l=1}^{m}\theta _l \end{array}\right| =\frac{z^{m}}{\prod \limits _{l=1}^{m}(p_l+q_l)}. \end{aligned}$$

So, by this transformation, assuming that ${{\mathcal {D}}}=\{(\theta _1,\ldots ,\theta _m):~0<\sum \limits _{l=1}^{m}\theta _l<1\}$, we can write

$$\begin{aligned} {\mathcal {B}}&=\idotsint \limits _{{\mathcal {D}}} \int _0^\infty {{\mathcal {C}}}_1\frac{\prod \limits _{l=1}^{m}\theta _l^{\nu _l-1}}{\prod \limits _{l=1}^{m}(p_l+q_l)^{\nu _l}}\times z^{\sum \limits _{l=1}^{m}\nu _l+\nu -1}\big (1-\sum \limits _{l=1}^{m}\theta _l\big )^\nu \nonumber \\&\quad \times e^{-z\Big (\sum \limits _{l=1}^{m}\frac{\theta _l\mu _l}{p_l+q_l}+\big (1-\sum \limits _{l=1}^{m}\theta _l\big )\mu \Big )}\textrm{d}z\textrm{d}\theta _1\cdots \textrm{d}\theta _m\nonumber \\&\quad =\idotsint \limits _{{\mathcal {D}}} {{\mathcal {C}}}_1\frac{\Big (\prod \limits _{l=1}^{m}\theta _l^{\nu _l-1}\Big )\Gamma \big (\sum \limits _{l=1}^{m}\nu _l+\nu \big )\big (1-\sum \limits _{l=1}^{m}\theta _l\big )^\nu }{\Big (\prod \limits _{l=1}^{m}(p_l+q_l)^{\nu _l}\Big )\Big (\sum \limits _{l=1}^{m}\frac{\theta _l\mu _l}{p_l+q_l}+\big (1-\sum \limits _{l=1}^{m}\theta _l\big )\mu \Big )^{\sum \limits _{l=1}^{m}\nu _l+\nu }}\textrm{d}\theta _1\cdots \textrm{d}\theta _m\nonumber \\&\quad =\idotsint \limits _{{\mathcal {D}}} {{\mathcal {C}}}_2 \Big (\prod \limits _{l=1}^{m}\theta _l^{\nu _l-1}\Big )\big (1-\sum \limits _{l=1}^{m}\theta _l\big )^\nu \big (1-\sum \limits _{l=1}^{m}\theta _lw_l\big )^{-\big (\sum \limits _{l=1}^{m}\nu _l+\nu \big )}\textrm{d}\theta _1\cdots \textrm{d}\theta _m, \end{aligned}$$

(22)

where

$$\begin{aligned} {{\mathcal {C}}}_2&=\frac{\Big (\prod \limits _{l=1}^{m}(1-w_l)^{\nu _l}\Big )\Gamma \big (\sum \limits _{l=1}^{m}\nu _l+\nu \big )}{\Big (\prod \limits _{l=1}^{m}\Gamma \big (\nu _l\big )\Big )\Gamma (\nu )},~ w_l=1-\frac{\mu _l}{\mu (p_l+q_l)}, l=1,\ldots ,m. \end{aligned}$$

The final integral, represented by (22), can be solved immediately using one numerical method in most of standard software programs. So, we can obtain the Bayes estimation of $R_{\textbf{s},\textbf{k}}$ as

$$\begin{aligned} \widehat{R}^B_{\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )(-1)^{\sum \limits _{l=1}^{m}q_l}\times {{\mathcal {B}}}. \end{aligned}$$

(23)

As obtaining the Bayes estimation from (23) needs to solve the numerical integrals, so, like as Sect. 2.3, when parameters $\alpha$ and $\beta$ are known, we derive the posterior PDFs of the parameters as

$$\begin{aligned} \lambda _l|\alpha ,\beta ,\text {data}&\sim \Gamma (nk_l+a_l,b_l-A_l(\alpha ,\beta )),~l=1,\ldots ,m,\\ \lambda |\alpha ,\beta ,\text {data}&\sim \Gamma (n+a_{m+1},b_{m+1}-B(\alpha ,\beta )). \end{aligned}$$

Now, we employ the Gibbs sampling method as follows to obtain the MCMC Bayes estimation and HPD credible intervals. So

• $\mathbf {1.}$ Begin with initial values $(\lambda _{1(0)},\ldots ,\lambda _{m(0)},~\lambda _{(0)})$.

• $\mathbf {2.}$ Set $t=1$.

• $\mathbf {3:m+2.}$ Generate $\lambda _{l(t)}$ from $\Gamma (nk_l+a_l,b_l-A_l(\alpha _{(t-1)},\beta _{(t-1)}))$, $l=1,\ldots ,m$.

• $\mathbf {m+3.}$ Generate $\lambda _{(t)}$ from $\Gamma (n+a_{m+1},b_{m+1}-B(\alpha _{(t-1)},\beta _{(t-1)})$.

• $\mathbf {m+4.}$ Evaluate the value

  $$\begin{aligned} R_{(t)\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m} \sum _{q_1=0}^{k_1-p_1}\cdots \sum _{q_m=0}^{k_m-p_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\times \Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l-p_l\\ q_l\end{array}}\right) \Big )\\&\quad \times (-1)^{\sum \limits _{l=1}^{m}q_l} \frac{\lambda _{(t)}}{\sum \limits _{l=1}^{m}\lambda _{l(t)} (p_l+q_l)+\lambda _{(t)}}. \end{aligned}$$

• $\mathbf {m+5.}$ Set $t = t +1$.

• $\mathbf {m+6.}$ Repeat T times in Steps 3 : m+5.

Finally, we obtain the Bayesian estimation of $R_{\textbf{s},\textbf{k}}$ as follows:

$$\begin{aligned} \widehat{R}_{\textbf{s},\textbf{k}}^{\textrm{MC}}=\frac{1}{T}\sum _{t=1}^{T}R_{(t)\textbf{s},\textbf{k}}. \end{aligned}$$

(24)

Moreover, just like as presented in Sect. 2.3, a $100(1-\eta )\%$ HPD credible interval of $R_{\textbf{s},\textbf{k}}$, can be provided.

4 Simulation Experiments

In this section, we employ the Monte Carlo simulation studies to compare the different estimations. In point estimates, comparing is done based on mean square errors (MSEs) and in interval estimates comparing is done based on average confidence lengths (AL) and coverage percentages (CP). We suppose the simulated system has two strength components so that, the stress random variable is $Y\sim \text {MWEx}(\alpha ,\beta ,\lambda )$ and strength components are $X_i\sim \text {MWEx}(\alpha ,\beta ,\lambda _i),~ i=1,2,3$. It is noted that we implement simulation study for different censoring schemes presented in Table 1 and we generate 2000 samples to derive the simulation results.

Table 1 Different censoring schemes

Table 2 Results of the point and interval estimates of $R_{\textbf{s},\textbf{k}}$, when common parameters are unknown

Table 3 Results of the point and interval estimates of $R_{\textbf{s},\textbf{k}}$, when common parameters are known

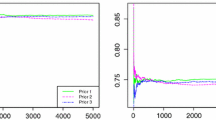
When the common parameters are unknown, we obtain the simulation results based on $(\alpha ,\beta )=(2,3)$ and $(\lambda _1,\lambda _2,\lambda _3,\lambda )=(2,3,2,4)$. Also, in this case, the repetition numbers in Gibbs sampling algorithm are $T=3000$. Moreover, we employ two priors as

$$\begin{aligned} \text{ Prior } \text{1 }:~ a_l&=0,~b_l=0,~ \text {Prior 2}:~ a_l=0.2,~b_l=0.5,~ l=1,\ldots ,6. \end{aligned}$$

In this case, we obtain the MLE and Bayes estimate of $R_{\textbf{s},\textbf{k}}$ from (12) and (16), respectively. Also, we derive $95\%$ asymptotic and HPD intervals for $R_{\textbf{s},\textbf{k}}$. The results are given in Table 2.

When the common parameters are known, we obtain the simulation results based on $(\lambda _1,\lambda _2,\lambda _3,\lambda )=(3,1.5,3,2)$. Also, in this case, the repetition numbers in Gibbs sampling algorithm is $T=3000$. Moreover, we employ two priors as

$$\begin{aligned} \text{ Prior } \text{3 }:~ a_l&=0,~b_l=0,~ \text {Prior 4}:~ a_l=0.25,~b_l=0.45,~ l=1,\ldots ,4. \end{aligned}$$

In this case, we obtain the MLE, UMVUE, exact and MCMC Bayes estimates of $R_{\textbf{s},\textbf{k}}$ from (17), (19), (23) and (24), respectively. Also, we derive $95\%$ asymptotic and HPD intervals for $R_{\textbf{s},\textbf{k}}$. The results are given in Table 3.

The simulation study, from Tables 2 and 3, has the following conclusions:

• In comparison with point estimations, Bayes estimations perform better than the others and in the Bayes estimates, informative priors perform than the non-informative ones, based on MSEs.

• In comparison with interval estimations, Bayes estimations have better performance than the others and in the Bayes estimates, informative priors have better performance than the non-informative ones, based on ALs and CPs.

• By increasing n, for fixed $\textbf{s}$ and $\textbf{k}$, MSEs and ALs decrease and CPs increase.

• By increasing in $\textbf{k}$, for fixed $\textbf{s}$ and n, MSEs and ALs decrease and CPs increase.

The two last conclusions may occur due to the fact that by increasing the sample sizes, more information is gathered.

5 General Case

In analyzing of the real data set, researcher usually faces the general case, when the common parameters are different. So, studying this case is very important. On the other hand, some formulas in Sect. 2 can be obtained from this case.

5.1 MLE of $R_{\textbf{s},\textbf{k}}$

We suppose that $X_1\sim \textrm{MWEx}(\alpha _1,\beta _1,\lambda _1)$, $X_2\sim \textrm{MWEx}(\alpha _2,\beta _2,\lambda _2)$, $\cdots$, $X_m\sim \textrm{MWEx}(\alpha _m,\beta _m,\lambda _m)$ and $Y\sim \textrm{MWEx}(\alpha ,\beta ,\lambda )$ are independent random variables. Using the equation (1) and (2), we can obtain the multi-component reliability with nonidentical-component strengths in (4) as follows:

$$\begin{aligned} R_{\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\int _0^\infty e^{\sum \limits _{l=1}^{m}\lambda _l p_l\alpha _l(1-e^{(\frac{y}{\alpha _l})^{\beta _l}})}\\&\quad \times \prod _{l=1}^m\bigg (1-e^{\lambda _l\alpha _l(1-e^{(\frac{y}{\alpha _l})^{\beta _l}})}\bigg )^{k_l-p_l} \lambda \beta (\frac{y}{\alpha })^{\beta -1} e^{\lambda \alpha (1-e^{(\frac{y}{\alpha })^\beta })+(\frac{y}{\alpha })^\beta }\textrm{d}y. \end{aligned}$$

Now, similar to Sect. 2, we can obtain the likelihood function, based on observed data, as

$$\begin{aligned}&L(\lambda _1,\ldots ,\lambda _m,\lambda ,\alpha _1,\ldots ,\alpha _m,\alpha ,\beta _1,\ldots ,\beta _m,\beta |\text {data})\propto \Big (\prod _{l=1}^{m}\big (\lambda _l\beta _l\big )^{nk_l}\Big )\big (\beta \lambda \big )^{n}\\&\qquad \times \Big (\prod _{i=1}^{n}\prod _{l=1}^{m}\prod _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l-1}\Big )\times \Big (\prod _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta -1}\Big )\\&\qquad \times e^{\sum \limits _{i=1}^{n}\sum \limits _{l=1}^{m}\sum \limits _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l}+\sum \limits _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta }}\times e^{\sum \limits _{l=1}^{m}\lambda _l\alpha _lA_l(\alpha _l,\beta _l)+\alpha \lambda B(\alpha ,\lambda )}, \end{aligned}$$

where $A_l(\cdot ,\cdot )$, $l=1,\ldots ,m$ and $B(\cdot ,\cdot )$ are given in (7) and (8), respectively. To obtain the MLEs of unknown parameters, after deriving the log-likelihood function from the above function, we should solve together the following equations:

$$\begin{aligned} \frac{\partial \ell }{\partial \lambda _l}&=\frac{nk_l}{\lambda _l}+\alpha _l A_l(\alpha _l,\beta _l),~l=1,\ldots ,m,\quad \frac{\partial \ell }{\partial \lambda }=\frac{n}{\lambda }+\alpha B(\alpha ,\beta ),\\\ \frac{\partial \ell }{\partial \beta _l}&=\frac{nk_l}{\beta _l}+\sum _{i=1}^{n}\sum _{j_l=1}^{k_l}\log \left( \frac{x^{(l)}_{ij_l}}{\alpha _l}\right) +\sum _{i=1}^{n}\sum _{j_l=1}^{k_l}\left( \frac{x^{(l)}_{ij_l}}{\alpha _l}\right) ^\beta \log \left( \frac{x^{(l)}_{ij_l}}{\alpha _l}\right) \\&\quad \times \bigg (1-\alpha _l\lambda _l\Big (R^{(l)}_{ij_l}+1\Big )e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l}}\bigg ),~l=1,\ldots ,m,\\ \frac{\partial \ell }{\partial \beta }&=\frac{n}{\beta }+\sum _{i=1}^{n}\log \left( \frac{y_i}{\alpha }\right) +\sum _{i=1}^{n}\left( \frac{y_i}{\alpha }\right) ^\beta \log \left( \frac{y_i}{\alpha }\right) \bigg (1-\alpha \lambda \Big (S_i+1\Big )e^{\big (\frac{y_i}{\alpha }\big )^{\beta }}\bigg ) \\\ \frac{\partial \ell }{\partial \alpha _l}&=-\frac{nk_l(\beta _l-1)}{\alpha _l}-\frac{\beta _l}{\alpha _l}\sum _{i=1}^{n}\sum _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l}\\&\quad +\sum _{i=1}^{n}\sum _{j_l=1}^{k_l}\lambda _l\Big (R^{(l)}_{ij_l}+1\Big )\bigg (1-e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l}}+\beta _l\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l} e^{\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l}}\bigg ),~ l=1,\ldots ,m,\\ \frac{\partial \ell }{\partial \alpha }&=-\frac{n(\beta -1)}{\alpha }-\frac{\beta }{\alpha }\sum _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta }\lambda \sum _{i=1}^{n}\Big (S_i+1\Big )\bigg (1-e^{\big (\frac{y_i}{\alpha _l}\big )^{\beta }}+\beta \big (\frac{y_i}{\alpha }\big )^{\beta } e^{\big (\frac{y_i}{\alpha _l}\big )^{\beta }}\bigg ) \end{aligned}$$

The MLEs of the unknown parameters can be obtained from simultaneous solution of the above equations, using one numerical method such as Newton–Raphson algorithm. Finally, the invariance property of MLE conclude that the MLE of $R_{\textbf{s},\textbf{k}}$, presented by ${\widehat{R}}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}$, can be obtained as

$$\begin{aligned} \widehat{R}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\int _0^\infty e^{\sum \limits _{l=1}^{m}{\widehat{\lambda }}_l p_l{\widehat{\alpha }}_l(1-e^{(\frac{y}{{\widehat{\alpha }}_l})^{{\widehat{\beta }}_l}})}\nonumber \\&\quad \times \prod _{l=1}^m\bigg (1-e^{{\widehat{\lambda }}_l{\widehat{\alpha }}_l(1-e^{(\frac{y}{{\widehat{\alpha }}_l})^{{\widehat{\beta }}_l}})}\bigg )^{k_l-p_l} {\widehat{\lambda }}{\widehat{\beta }} (\frac{y}{{\widehat{\alpha }}})^{{\widehat{\beta }}-1} e^{{\widehat{\lambda }}{\widehat{\alpha }}(1-e^{(\frac{y}{{\widehat{\alpha }}})^{{\widehat{\beta }}}})+(\frac{y}{{\widehat{\alpha }}})^{{\widehat{\beta }}}}\textrm{d}y. \end{aligned}$$

(25)

5.2 Bayes Estimation of $R_{\textbf{s},\textbf{k}}$

In this section, under the squared error loss function, we infer the Bayesian estimation and corresponding credible intervals for $R_{\textbf{s},\textbf{k}}$, assuming that the unknown parameters are the independent gamma random variables. So, we consider the prior distributions of the parameters as

$$\begin{aligned} \lambda _l&\sim \Gamma (a_l,b_l),~ l=1,\ldots ,m,\quad \lambda \sim \Gamma (a_{m+1},b_{m+1}),\\\ \alpha _l&\sim \Gamma (c_l,d_l),~ l=1,\ldots ,m,\quad \alpha \sim \Gamma (a_{m+2},b_{m+2}),\\\ \beta _l&\sim \Gamma (e_l,f_l),~ l=1,\ldots ,m,\quad \beta \sim \Gamma (a_{m+3},b_{m+3}). \end{aligned}$$

Similar to Sect. 2.3, we can obtain the posterior PDFs of the parameters as

$$\begin{aligned}&\lambda _l|\alpha _l,\beta _l,\text {data}\sim \Gamma (nk_l+a_l,b_l-\alpha _l A_l(\alpha _l,\beta _l)),~l=1,\ldots ,m,\\&\lambda |\alpha ,\beta ,\text {data}\sim \Gamma (n+a_{m+1},b_{m+1}-\alpha B(\alpha ,\beta )),\\&\pi (\alpha _l|\lambda _l,\beta _l,\text {data})\propto \alpha _l^{c_l-1}\\&\times \Big (\prod _{i=1}^{n}\prod _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l-1}\Big ) e^{-d_l\alpha _l+\sum \limits _{i=1}^{n}\sum \limits _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l}+\lambda _l\alpha _lA_l(\alpha _l,\beta _l)},~ l=1,\ldots ,m,\\&\pi (\alpha |\lambda ,\beta ,\text {data})\propto \alpha ^{a_{m+2}-1}\times \Big (\prod _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta -1}\Big ) e^{-b_{m+2}\alpha +\sum \limits _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta }+\lambda \alpha B(\alpha ,\beta )},\\&\pi (\beta _l|\lambda _l,\alpha _l,\text {data})\propto \beta _l^{nk_l+e_l-1} \\&\times \Big (\prod _{i=1}^{n}\prod _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l-1}\Big ) e^{-f_l\beta _l+\sum \limits _{i=1}^{n}\sum \limits _{j_l=1}^{k_l}\big (\frac{x^{(l)}_{ij_l}}{\alpha _l}\big )^{\beta _l}+\lambda _l\alpha _lA_l(\alpha _l,\beta _l)},~ l=1,\ldots ,m,\\&\pi (\beta |\lambda ,\alpha ,\text {data})\propto \beta ^{n+a_{m+3}-1}\times \Big (\prod _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta -1}\Big ) e^{-b_{m+3}\beta +\sum \limits _{i=1}^{n}\big (\frac{y_i}{\alpha }\big )^{\beta }+\lambda \alpha B(\alpha ,\beta )}. \end{aligned}$$

Because the posterior PDFs of $\lambda _l,~l=1,\ldots ,m$ and $\lambda$ are gamma distributions, we generate random samples from them, easily. But, the posterior PDFs of $\alpha _l,~\beta _l,~l=1,\ldots ,m$, $\alpha$ and $\beta$ are not well-known distributions. So, we use Metropolis–Hastings method, to generate random samples from them. Therefore, the Gibbs sampling algorithm can be implemented by the following:

• $\mathbf {1.}$ Begin with initial values $(\lambda _{1(0)},\ldots ,\lambda _{m(0)},\lambda _{(0)}, \alpha _{1(0)},\ldots ,\alpha _{m(0)},\alpha _{(0)},\beta _{1(0)},\ldots ,\beta _{m(0)},\beta _{(0)})$.

• $\mathbf {2.}$ Set $t=1$.

• $\mathbf {3:m+2.}$ Generate $\alpha _{l(t)}$ from $\pi (\alpha _l|\lambda _{l(t-1)},\beta _{l(t-1)},\text {data})$ using Metropolis–Hastings method, with $N(\alpha _{l(t-1)},1)$, $l=1,\ldots ,m$ as proposal distribution.

• $\mathbf {m+3.}$ Generate $\alpha _{(t)}$ from $\pi (\alpha |\lambda _{(t-1)},\beta _{(t-1)},\text {data})$ using Metropolis–Hastings method, with $N(\alpha _{(t-1)},1)$ as proposal distribution.

• $\mathbf {m+4:2m+3.}$ Generate $\beta _{l(t)}$ from $\pi (\beta _l|\lambda _{l(t-1)},\alpha _{l(t-1)},\text {data})$ using Metropolis–Hastings method, with $N(\beta _{l(t-1)},1)$, $l=1,\ldots ,m$ as proposal distribution.

• $\mathbf {2m+4.}$ Generate $\beta _{(t)}$ from $\pi (\beta |\lambda _{(t-1)},\alpha _{(t-1)},\text {data})$ using Metropolis–Hastings method, with $N(\beta _{(t-1)},1)$ as proposal distribution.

• $\mathbf {2m+5:3m+4.}$ Generate $\lambda _{l(t)}$ from $\Gamma (nk_l+a_l,b_l-\alpha _{l(t-1)}A_l(\alpha _{l(t-1)},\beta _{l(t-1)}))$, $l=1,\ldots ,m$.

• $\mathbf {3m+5.}$ Generate $\lambda _{(t)}$ from $\Gamma (n+a_{m+1},b_{m+1}-\alpha _{(t-1)}B(\alpha _{(t-1)},\beta _{(t-1)})$.

• $\mathbf {3m+6.}$ Evaluate the value

  $$\begin{aligned} R_{(t)\textbf{s},\textbf{k}}&=\sum _{p_1=s_1}^{k_1}\cdots \sum _{p_m=s_m}^{k_m}\Big (\prod _{l=1}^{m}\left( {\begin{array}{c}k_l\\ p_l\end{array}}\right) \Big )\int _0^\infty e^{\sum \limits _{l=1}^{m}\lambda _{l(t)} p_l\alpha _{l(t)}\left( 1-e^{\left( \frac{y}{\alpha _{l(t)}}\right) ^{\beta _{l(t)}}}\right) }\\&\quad \times \prod _{l=1}^m\bigg (1-e^{\lambda _{l(t)}\alpha _{l(t)}\left( 1-e^{\left( \frac{y}{\alpha _{l(t)}}\right) ^{\beta _{l(t)}}}\right) }\bigg )^{k_l-p_l}\\&\lambda _{l(t)}\beta _{l(t)} \left( \frac{y}{\alpha _{l(t)}}\right) ^{\beta _{l(t)}-1} e^{\lambda _{l(t)}\alpha _{l(t)}\left( 1-e^{\left( \frac{y}{\alpha _{l(t)}}\right) ^{\beta _{l(t)}}}\right) +\left( \frac{y}{\alpha _{l(t)}}\right) ^{\beta _{l(t)}}}\textrm{d}y. \end{aligned}$$

• $\mathbf {3m+7.}$ Set $t = t +1$.

• $\mathbf {3m+8.}$ Repeat T times in Steps 3 : 3m+7.

Finally, we obtain the Bayesian estimation of $R_{\textbf{s},\textbf{k}}$ as follows:

$$\begin{aligned} \widehat{R}_{\textbf{s},\textbf{k}}^{\textrm{MC}}=\frac{1}{T}\sum _{t=1}^{T}R_{(t)\textbf{s},\textbf{k}}. \end{aligned}$$

(26)

Moreover, just like as presented in Sect. 2.3, a $100(1-\eta )\%$ HPD credible interval of $R_{\textbf{s},\textbf{k}}$, can be provided.

6 Real Data Analysis

In this section, we analyze one real data set, for illustrative aims. The data which is considered in this section demonstrates the breaking strengths of jute fiber at 10 mm, 15 mm and 20 mm gauge lengths and can be founded in [27]. Recently, this data is investigated by Kang et al. [13] as a stress–strength model for exponential distribution. Now, we suppose that a system contains two different gauge lengths of jute fiber, so that the jute fiber at 10 mm and 15 mm gauge lengths is considered as the strength and the jute fiber at 10 mm gauge lengths is the stress of the system. Therefore, we set that $X_1$, $X_2$ and Y denote the jute fiber with length 10 mm, 15 mm and 20 mm, respectively. So, the observations of $X_1$, $X_2$ and Y can be considered, respectively, as follows:

$$\begin{aligned}&{\left[ \begin{array}{ccccc} 693.73 &{}\quad 704.66 &{}\quad 232.83 &{}\quad 778.17 &{}\quad 126.06\\ 637.66 &{}\quad 383.43 &{}\quad 151.48 &{}\quad 108.94 &{}\quad 50.16\\ 671.49 &{}\quad 183.16 &{}\quad 257.44 &{}\quad 727.23 &{}\quad 291.27\\ 101.15 &{}\quad 376.42 &{}\quad 163.40 &{}\quad 141.38 &{}\quad 700.74\\ 262.90 &{}\quad 353.24 &{}\quad 422.11 &{}\quad 43.93 &{}\quad 590.48\\ 212.13 &{}\quad 303.90 &{}\quad 506.60 &{}\quad 530.55 &{}\quad 177.25 \end{array}\right] },\\&{\left[ \begin{array}{ccccc} 594.40 &{}\quad 202.75 &{}\quad 168.37 &{}\quad 574.86 &{}\quad 225.65\\ 76.38 &{}\quad 156.67 &{}\quad 127.81 &{}\quad 813.87 &{}\quad 562.39\\ 468.47 &{}\quad 135.09 &{}\quad 72.24 &{}\quad 497.94 &{}\quad 355.56\\ 569.07 &{}\quad 640.48 &{}\quad 200.76 &{}\quad 550.42 &{}\quad 748.75\\ 489.66 &{}\quad 678.06 &{}\quad 457.71 &{}\quad 106.73 &{}\quad 716.30\\ 42.66 &{}\quad 80.40 &{}\quad 339.22 &{}\quad 70.09 &{}\quad 193.42 \end{array}\right] }, {\left[ \begin{array}{c} 71.46\\ 113.85\\ 578.62\\ 707.36\\ 547.44\\ 48.01 \end{array} \right] }. \end{aligned}$$

To simplify calculations, we re-normalized the data on a scale of 0 to 1. We noted that this work has no effect on statistical inference. Now, first, we have fitted the MWEx distribution on the three data sets, separately and obtained the results as follows. For $X_1$, ${\widehat{\alpha }}_1=1.4390$, ${\widehat{\beta }}_1=1.5830$, ${\widehat{\lambda }}_1=2.8930$ and the p-value$=0.7635$. For $X_2$, ${\widehat{\alpha }}_2=1.0670$, ${\widehat{\beta }}_2=1.4710$, ${\widehat{\lambda }}_2=2.1701$ and the p-value$=0.2410$. For Y, ${\widehat{\alpha }}=0.9700$, ${\widehat{\beta }}=1.0810$, ${\widehat{\lambda }}=1.3447$ and the p-value$=0.4819$. From the p-values, we conclude that the MWEx distribution gives suitable fits for $X_1$, $X_2$ and Y data sets. The estimated parameters for different data sets show that only the general case can be considered for analyzing of them. For these three data sets, we provide the empirical distribution functions and PP-plots in Fig. 2.

Fig. 2

Empirical distribution function (left) and the PP-plot (right) for $X_1$ (first row), for $X_2$ (middle row) and for Y (third row)

For complete data set, putting $\textbf{s}=(2,2)$ and $\textbf{k}=(5,5)$, we obtain the MLEs of $\alpha _1$, $\beta _1$, $\lambda _1$, $\alpha _2$, $\beta _2$, $\lambda _2$, $\alpha$, $\beta$, $\lambda _1$ and ${\widehat{R}}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}$ by 1.4930, 1.5830, 2.8930, 1.0670, 1.4710, 2.1701, 0.9700, 1.0810, 1.3447 and 0.5463, respectively. Also, with non-informative priors, we obtain ${\widehat{R}}^{\textrm{MC}}_{\textbf{s},\textbf{k}}$ and the corresponding 95$\%$ HPD interval by 0.5449 and (0.2658, 0.8290), respectively.

Now, we generate two different censoring progressive scheme as follows:

$$\begin{aligned} \text{ Scheme } \text{1: }~&R^{(1)}=R^{(2)}=[0,0,1,0],~~S=[0,0,1,0,0],~~ (\textbf{k}=(4,4), \textbf{s}=(2,2)).\\ \text{ Scheme } \text{2: }~&R^{(1)}=R^{(2)}=[0,1,1],~~~~~S=[1,0,0,1],~~~~~(\textbf{k}=(3,3), \textbf{s}=(1,1)). \end{aligned}$$

For Scheme 1, we obtain the MLEs of $\alpha _1$, $\beta _1$, $\lambda _1$, $\alpha _2$, $\beta _2$, $\lambda _2$, $\alpha$, $\beta$, $\lambda _1$ and ${\widehat{R}}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}$ by 1.2500, 1.8520, 2.4146, 1.2600, 1.3930, 2.5659, 1.8410, 0.9270, 1.2359 and 0.4891, respectively. Also, with non-informative priors, we obtain ${\widehat{R}}^{\textrm{MC}}_{\textbf{s},\textbf{k}}$ and the corresponding 95$\%$ HPD interval by 0.5119 and (0.1959, 0.7893), respectively. For Scheme 2, we obtain the MLEs of $\alpha _1$, $\beta _1$, $\lambda _1$, $\alpha _2$, $\beta _2$, $\lambda _2$, $\alpha$, $\beta$, $\lambda _1$ and ${\widehat{R}}^{\textrm{MLE}}_{\textbf{s},\textbf{k}}$ by 0.8430, 2.6120, 0.5292, 0.8870, 1.8510, 0.7164, 0.9220, 1.1840, 1.1563 and 0.8039, respectively. Also, with non-informative priors, we obtain $\widehat{R}^{\textrm{MC}}_{\textbf{s},\textbf{k}}$ and the corresponding 95$\%$ HPD interval by 0.7417 and (0.3315, 0.9707), respectively.

To see the effect of hyper-parameters, we obtain the Bayes estimates and HPD intervals of ${\widehat{R}}^{\textrm{MC}}_{\textbf{s},\textbf{k}}$ with informative priors. The hyper-parameters can be obtained using re-sampling method by $a_1=3.48$, $b_1=0.91$, $a_2=5.04$, $b_2=2.01$, $a_3=1.33$, $b_3=0.83$, $c_1=6.94$, $d_1=4.21$, $c_2=4.37$, $d_2=2.34$, $c_3=4.42$, $d_3=2.46$, $e_1=75.41$, $f_1=45.92$, $e_2=53.35$, $f_2=35.19$, $e_3=6.33$ and $f_3=4.75$. So, for complete data, we obtain $\widehat{R}^{\textrm{MC}}_{\textbf{s},\textbf{k}}$ and the corresponding 95$\%$ HPD interval is equal to 0.5367 and (0.2985, 0.7402), respectively. Also, for Scheme 1, we obtain ${\widehat{R}}^{\textrm{MC}}_{\textbf{s},\textbf{k}}$ and the corresponding 95$\%$ HPD interval is equal to 0.5167 and (0.2286, 0.7275), respectively. Moreover, for Scheme 2, we obtain ${\widehat{R}}^{\textrm{MC}}_{\textbf{s},\textbf{k}}$ and the corresponding 95$\%$ HPD interval is equal to 0.7731 and (0.3791, 0.9341), respectively.

With comparing the different point and interval estimates, it seems that the estimates in Scheme 1 perform better than in Scheme 2. Moreover, we observe that HPD intervals with informative priors are smaller than the non-informative ones. So, it is reasonable that we should use the informative priors, if they are available.

7 Conclusion

In this paper, the statistical inference of multi-component stress–strength system with nonidentical-component strengths is studied, for the MWEx distribution, in the presence of the progressive censoring scheme. For this aim, we derived some point and interval estimations in classical and Bayesian inference, such as MLE, UMVUE, asymptotic and HPD intervals. Also, we considered these estimations in some cases, when the common parameters are unknown, known and in general case.

The theoretical methods are compared with Monte Carlo simulation study. The important results can be described as follows. The Bayes estimates performed better than the classical ones. Also, in Bayesian estimates, the performance of informative priors is better than the non-informative ones, in terms of point and interval estimates.