Skip to main content
SpringerLink
Log in

Some More Solutions of Caudrey–Dodd–Gibbon Equation Using Optimal System of Lie Symmetries

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

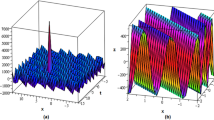
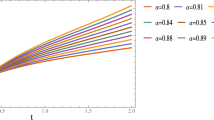
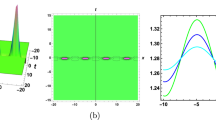
This paper investigates (\(1+1\))-dimensional Caudrey–Dodd–Gibbon equation (CDG) for the invariance properties, optimal system and group invariant solutions. The Lie point symmetries, geometric vector field, commutation table of Lie algebra and various similarity reductions are obtained by virtue of the invariance criteria of the Lie symmetry analysis. By utilizing the Lie symmetry reduction, the (\(1+1\))-dimensional Caudrey–Dodd–Gibbon equation (CDG) will be reduced to a number of ordinary differential equations. The group invariant solutions and new closed form solutions are obtained in the shapes of dynamical structures of solitary waves. Some of the obtained closed form solutions are absolutely new in formulation and entirely different from the earlier studies (Wazwaz in Appl Math Comput 174:289–299, 2006; Bibi et al. in Adv Differ Equ 2019:89, 2019). The dynamical behavior of the derived solutions is analyzed physically through 3D, 2D-graphics and corresponding contour plots.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Fu, Z.T., Liu, S.K., Liu, S.D., Zhao, Q.: New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations. Phys. Lett. A 290, 72–76 (2001)

    MathSciNet  MATH  Google Scholar 

  2. Kudryashov, N.A.: Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Soliton Fractals 24(5), 1217–1231 (2005)

    MathSciNet  MATH  Google Scholar 

  3. Malik, A., Chand, F., Kumar, H., Mishra, S.C.: Exact solutions of the Bogoyavlenskii equation using the multiple \((\frac{G^{\prime }}{G})\)-expansion method. Comput. Math. Appl. 64(9), 2850–2859 (2012)

    MathSciNet  MATH  Google Scholar 

  4. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    MATH  Google Scholar 

  5. Ma, W.X., Zhang, L.: Lump solutions with higher-order rational dispersion relations. Pramana J. Phys. 94, 43 (2020)

    Google Scholar 

  6. Chen, S.J., Yin, Y.H., Ma, W.X., Lu, X.: Abundant exact solutions and interaction phenomena of the (2+1)-dimensional YTSF equation. Anal. Math. Phys. 9, 2329–2344 (2019)

    MathSciNet  MATH  Google Scholar 

  7. Wang, M., Zhou, Y., Li, Z.: Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 216, 67–75 (1996)

    MATH  Google Scholar 

  8. Kumar, H., Malik, A., Chand, F.: Soliton solutions of some nonlinear evolution equations with time-dependent coefficients. Pramana J. Phys. 80(2), 361–367 (2013)

    Google Scholar 

  9. Kumar, H., Malik, A., Chand, F., Mishra, S.C.: Exact solutions of nonlinear diffusion reaction equation with quadratic, cubic and quartic nonlinearities. Indian J. Phys. 86(9), 819–827 (2012)

    Google Scholar 

  10. Ma, W.X., Lee, J.H.: A transformed rational function method and exact solutions to the dimensional Jimbo–Miwa equation. Chaos Solitons Fractals 42, 1356–1363 (2009)

    MathSciNet  MATH  Google Scholar 

  11. Ma, W.X., Huang, T., Zhang, T.: A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 82, 065003 (2010)

    MATH  Google Scholar 

  12. Ma, W.X., Fan, E.: Linear superposition principle applying to Hirota bilinear equations. Comput. Math. Appl. 61, 950–959 (2011)

    MathSciNet  MATH  Google Scholar 

  13. Kumar, H., Malik, A., Chand, F.: Analytical spatiotemporal soliton solutions to (3 + 1)-dimensional cubic–quintic nonlinear Schrödinger equation with distributed coefficients. J. Math. Phys. 53(10), 103704 (2012)

    MathSciNet  MATH  Google Scholar 

  14. Ma, W.X.: A refined invariant subspace method and applications to evolution equations. Sci. China Math. 55, 1769–1778 (2012)

    MathSciNet  MATH  Google Scholar 

  15. Ma, W.X.: Interaction solutions to Hirota–Satsuma–Ito equation in (2 + 1)-dimensions. Front. Math. China 14, 619–629 (2019)

    MathSciNet  MATH  Google Scholar 

  16. Ma, W.X.: Lump and interaction solutions to linear PDEs in 2 + 1 dimensions via symbolic computation. Mod. Phys. Lett. B 33, 1950457 (2019)

    MathSciNet  Google Scholar 

  17. Yang, J.Y., Ma, W.X.: Lump solutions to the BKP equation by symbolic computation. Int. J. Mod. Phys. B 30, 1640028 (2016)

    MathSciNet  MATH  Google Scholar 

  18. Kumar, S., Kumar, D.: Solitary wave solutions of (3+1)-dimensional extended Zakharov–Kuznetsov equation by Lie symmetry approach. Comput. Math. Appl. 77, 2096–2113 (2019)

    MathSciNet  Google Scholar 

  19. Kumar, D., Kumar, S.: Some new periodic solitary wave solutions of (3+1)-dimensional generalized shallow water wave equation by Lie symmetry approach. Comput. Math. Appl. 78, 857–877 (2019)

    MathSciNet  Google Scholar 

  20. Aiyer, R.N., Fuchssteiner, B., Oevel, W.: Solitons and discrete eigenfunctions of the recursion operator of non-linear evolution equations: I. The Caudrey–Dodd–Gibbon–Sawada–Kotera equations. J. Phys. A: Math. Gen. 19, 3755–3770 (1986)

    MATH  Google Scholar 

  21. Lou, S.Y.: Twelve sets of symmetries of the Caudrey–Dodd–Gibbon–Sawada–Kotera equation. Phys. Lett. A 175, 23–26 (1993)

    MathSciNet  Google Scholar 

  22. Xu, Y.G., Zhou, X.W., Yao, L.: Solving the fifth order Caudrey–Dodd–Gibbon (CDG) equation using the exp-function method. Appl. Math. Comput. 206, 70–73 (2008)

    MathSciNet  MATH  Google Scholar 

  23. Salas, A.: Exact solutions for the general fifth KdV equation by the exp function method. Appl. Math. Comput. 205, 291–297 (2008)

    MathSciNet  MATH  Google Scholar 

  24. Caudrey, P.J., Dodd, R.K., Gibbon, J.D.: A new hierarchy of Korteweg De Vries equation. Proc. R. Soc. Lond. A 351, 407–422 (1976). https://doi.org/10.1098/rspa.1976.0149

    Article  MathSciNet  MATH  Google Scholar 

  25. Wazwaz, A.M.: Analytic study of the fifth order integrable nonlinear evolution equations by using the tanh method. Appl. Math. Comput. 174, 289–299 (2006)

    MathSciNet  MATH  Google Scholar 

  26. Wazwaz, A.M.: Multiple-soliton solutions for the fifth order Caudrey–Dodd–Gibbon (CDG) equation. Appl. Math. Comput. 197, 719–724 (2008)

    MathSciNet  MATH  Google Scholar 

  27. Bibi, S., Ahmed, N., Faisal, I., Din, S.T., Rafiq, M., Khan, U.: Some new solutions of the Caudrey–Dodd–Gibbon (CDG) equation using the conformable derivative. Adv. Differ. Equ. 2019, 89 (2019)

    MathSciNet  MATH  Google Scholar 

  28. Karaagac, B.: A numerical approach to Caudrey–Dodd–Gibbon equation via collocation method using quintic B-Spline basis. J. Appl. Eng. Math. 9(1), 1–8 (2019)

    Google Scholar 

  29. Jiang, B., Bi, Q.: A study on the bilinear Caudrey–Dodd–Gibbon equation. J. Nonlinear Anal. Theory Methods Appl. 72(12), 4530–4533 (2010)

    MathSciNet  MATH  Google Scholar 

  30. Chen, H., Xu, Z., Dai, Z.: Breather soliton and cross two-soliton solutions for the fifth order Caudrey–Dodd–Gibbon (CDG) equation. Int. J. Num. Methods Heat Fluid Flow 25(3), 651–655 (2015)

    MathSciNet  MATH  Google Scholar 

  31. Olver, P.J.: Applications of Lie Groups to Differential Equations. Springer, New York (1993)

    MATH  Google Scholar 

  32. Bluman, G.W., Cole, J.D.: Similarity Methods for Differential Equations. Springer, New York (1974)

    MATH  Google Scholar 

  33. Bluman, G.W., Kumei, S.: Symmetries and Differential Equations. Springer, New York (1989)

    MATH  Google Scholar 

  34. Bluman, G., Cheviakov, A.: Applications of Symmetry Methods to Partial Differential Equations. Springer, New York (2010)

    MATH  Google Scholar 

  35. Kumar, M., Tanwar, D.V.: On Lie symmetries and invariant solutions of \((2+1)\)-dimensional Gardner equation. Commun. Nonlinear Sci. Numer. Simul. 69, 45–57 (2019)

    MathSciNet  Google Scholar 

  36. Kumar, S., Kumar, A.: Lie symmetry reductions and group invariant solutions of (2+1)-dimensional modified Veronese web equation. Nonlinear Dyn. 98, 1891–1903 (2019)

    MATH  Google Scholar 

  37. Ovsiannikov, L.V.: Group Analysis of Differential Equations. Academic Press, New York (1982)

    MATH  Google Scholar 

  38. Sahoo, S., Garai, G., Saha Ray, S.: Lie symmetry analysis for similarity reduction and exact solutions of modified KdV–Zakharov–Kuznetsov equation. Nonlinear Dyn. 87(3), 1995–2000 (2017)

    MathSciNet  MATH  Google Scholar 

  39. Sahoo, S., Ray, S.S.: Lie symmetry analysis and exact solutions of (3 + 1)-dimensional Yu–Toda–Sasa–Fukuyama equation in mathematical physics. Comput. Math. Appl. 73, 253–260 (2017)

    MathSciNet  MATH  Google Scholar 

  40. Arora, R., Chauhan, A.: Lie symmetry analysis and some exact solutions of (2+1)-dimensional KdV–Burgers equation. Int. J. Appl. Comput. Math. 5, 15 (2019)

    MathSciNet  MATH  Google Scholar 

  41. Arora, R., Chauhan, A.: Lie symmetry reductions and solitary wave solutions of modified equal width wave equation. Int. J. Appl. Comput. Math. 4, 122 (2018)

    MathSciNet  MATH  Google Scholar 

  42. Apeanti, W.O., Lu, D., Yaroz, D., Akuamoah, S.W.: Dispersive traveling wave solutions of nonlinear optical wave dynamical models. Mod. Phys. Lett. B 33, 1950120 (2019)

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, SGTB Khalsa College, University of Delhi, Delhi, 110007, India

    Dharmendra Kumar

  2. Department of Mathematics, Faculty of Mathematical Sciences, University of Delhi, Delhi, 110007, India

    Sachin Kumar

Authors
  1. Dharmendra Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sachin Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dharmendra Kumar.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, D., Kumar, S. Some More Solutions of Caudrey–Dodd–Gibbon Equation Using Optimal System of Lie Symmetries. Int. J. Appl. Comput. Math 6, 125 (2020). https://doi.org/10.1007/s40819-020-00882-7

Download citation

  • Published:

  • DOI: https://doi.org/10.1007/s40819-020-00882-7

Keywords

Search

Navigation