Introduction

The task of located DC operating points of integrated electrical circuits is one of the most important task in electrical circuit simulation. Such analysis includes finding the solutions for a nonlinear algebraic equation system (NAEs). The complexity of the NAEs, depends on the density of transistor fabricated on a wafer of silice and the mathematical model used to represent the behavior of the transistor. The above causes the presence of multiple points of operation where the method used most often is the Newton–Raphson (NR) which is not capable to locate multiple points of operation. The main reason for the use of NR method is its quadratic convergence however the starting point must be close to the solution. Alternative methods to NR are the homotopy methods, such methods are used to locate multiple DC solutions and perhaps all the solutions if the path has more than one solution [1–3]. Continuation methods or homotopy methods have shown promise in solving computational problems associated with the simulation of circuits containing transistors. To employ the homotopy methods we embed a continuation parameter \(\lambda \) into a set non-linear equation system. When the continuation parameter \(\lambda \) is set to zero then the system is reduced to equations that can be solved easily. Homotopy equations are continuously deformed until reaching the solution of the original system of equations. For example for finding the solution of a set of nonlinear equations \(F(x)=0,\) where \(F{\text {:}}\,R^{n} \rightarrow R^{n}\) is smooth using the continuation method. In general, this method involves incorporating the continuation parameter into a set of nonlinear equations \(H(x,\,\lambda ),\) where \(H{\text {:}}\,R^{n+1} \rightarrow R^{n}\) [4–7]. The computational efficiency of homotopy methods depends on the homotopy formulation as well as the curve-tracing algorithm and the initial point [4, 5, 7–11]. The usefulness of homotopy methods depends on the type of a circuits descriptive equations. Such methods are becoming a viable alternative in circuit simulation, where they can be used to resolve convergence difficulties and to find multiple operation points. These methods are slower than conventional methods but their speed can often be improved by careful implementation [12–17].

In this paper is organizable in the following sections, first the introduction is submitted, we briefly explain the characteristics of the Newton homotopy used in this proposed work is present in “Newton Homotopy” section, later to trace the curve of homotopy is used the spherical method explained in “The Spherical Algorithm” section, proposed methodology to change the radius of the spheres in the spherical method is presented in “Proposed Methodology to Accelerate the Course of the Curve on the Spherical Algorithm” section, numerical examples are solved using the proposed methodology in “Numerical Examples” section, finally the discussion of results and conclusions are shown in “Discussion” and “Conclusions” sections, respectively.

Newton Homotopy

The operating point problem for a DC network is formulated as a system of non-linear equations to be solved \(F(x)=0.\) The Newton homotopy has similar properties to the NR method, meaning that every homotopy path in the regular domain crosses at the same solution point. The Newton homotopy [11, 18] is described by the following set of nonlinear equations:

(1)

In circuit simulation applications, \(x \in R^{n}\) is the vector of node voltages, F(x) gives the set of Kirchhoff’s Current Law equations at each node, where \(\lambda \in R\) is called the continuation parameter and \(g(x_{0})\) is F(x) assessed at the initial point.

The solutions in DC are founded at \(\lambda =1\) on the solution curve, changing the start point \(g(x_{0})\) we can trace the another solution curves. If the starting point is selected properly then it possible find all solutions of the system [18].

The Spherical Algorithm

Tracing solution curves is a problem encountered in homotopy methods, where is required suitable path-tracking techniques. The curve tracing algorithm can be divided in two types; the first is based on the predictor–corrector algorithm whereas the second are piecewise-linear algorithms [19]. These algorithm are sophisticated and very efficient, notwithstanding these curve algorithm tracing algorithms are not widely used in practical applications; difficulties primarily linked to the implementation of these algorithms are the theory and programming. The spherical algorithm (SA) based predictor–corrector algorithm is used for geometrically clear interpretation besides its easy implementation in programming [20–23]. The SA algorithm consists of trace the curve using spheres of dimension \(n+1,\) where \(n+1\) is the number of variables of the equation system to be solved and continuation parameter. For tracing solution curves a starting point is chosen as the same point used wherein, the center of the first sphere; then spheres are traced following the shape of the curve using predictor–corrector algorithm as shown in Fig. 1.

Fig. 1
figure 1

Path tracking using spheres

Full size image

Equation (2) that describe the sphere with center at C and radius r is expressed by:

$$\begin{aligned} S(X)=\left( x_{1}-c_{1}\right) ^{2}+\left( x_{2}-c_{2}\right) ^{2}+\cdots +\left( x_{n+1}-c_{n+1}\right) ^{2}-r^{2}=0. \end{aligned}$$
(2)

The equation of the sphere is update at every iteration using the new center at C(\(c_{1},\,c_{2},\ldots ,c_{n+1}\)). The homotopy is applied to equilibrium equations F(x) to obtain a equation system increased as (3) with \(n+1\) equations and \(n+1\) variables.

$$\begin{aligned} \begin{array}{l} H_{1}\left( F_{1}(x),\,\lambda \right) =0,\\ H_{2}\left( F_{2}(x),\,\lambda \right) =0,\\ \vdots \\ H_{n}\left( F_{n}(x),\,\lambda \right) =0,\\ S\left( x_{1},\,x_{2},\ldots ,x_{n},\,\lambda \right) =0. \end{array} \end{aligned}$$
(3)

To follow the tracing solutions, the spheres are plotted using the predictor–corrector algorithm, where the predictor is calculated as a sum of vectors and the predictor point is used to find the correction point by solving the system of equations as (3).

Predictor–Corrector

  • The predictor point is given using the Fig. 1, where the center of the first sphere \(o_{1}\) and the center of the consecutive sphere \(o_{2}\) are used to obtain the step predictor.

  • The corrector point uses NR method, setting as a starting point the predictor point and solving (3), where can be localized at least two solutions: one lies in the forward direction \(o_{4}\) and the other in the backward direction \(o_{2}\) (see Fig. 2). The forward solution can be considered as a success of the algorithm, nonetheless if the backward solution is obtained, the algorithm fails; such case of failure is known as “reversion” phenomenon of the SA. To solve reversion problem is applied the calculus the angles of their normal vector to a sphere for the solutions \(o_{2}\) and \(o_{4},\) instead of comparing \(o_{2}\) and \(o_{4}\) directly, we use the angles of their normal vectors for an efficient comparison. After detecting the reversion phenomenon, we have to modify the corrector step by increasing the radius a \(\delta r\) (where \(\delta r\) is an increase of the radius) inducing the corrector step to converge to the forward solution [23, 24] (Fig. 3).

  • Find zero strategy the finding zero strategy should start after the trajectory crosses solution line \(\lambda =1\) [25, 26]. A functional way consist by monitoring the change of sign of \(\Delta \lambda \) after the corrector step. This procedure is realized by multiplying \(\Delta \lambda \) of two consecutive predictor steps.

    $$\begin{aligned} \textit{sign}\left( \Delta \lambda _{j+1}\Delta \lambda _{j}\right) \ne -1. \end{aligned}$$
    (4)

  • Interpolate solutions when the trajectory crosses the line solution the point \((k_{1},\,k_{2})\) are taken to implement multidimensional interpolation to approximate the solution. Interpolation is performed using the command “ArrayInterpolation” language Maple [24].

Fig. 2
figure 2

Sphere intersecting with the curve at two points

Full size image
Fig. 3
figure 3

Reversion strategy proposed

Full size image

Proposed Methodology to Accelerate the Course of the Curve on the Spherical Algorithm

Homotopy methods are characterized by slowness to the path tracking. We want to solve the system of equations \(H(x\cdot \lambda )=0,\) using Newton homotopy and for tracking the solution curve use the SA. Size radius for spheres is fixed for the SA was reported in [21]. Therefore making the radius of each sphere varies according to the form of the solution curve (see Fig. 4).

Fig. 4
figure 4

Spherical algorithm

Full size image

As the first step of the proposed methodology is to calculate the radius of curvature by

$$\begin{aligned} \rho =\left| \frac{(1+(x_{i}^{\prime })^{2})^{\frac{3}{2}}}{x_{i}^{\prime \prime }}\right| , \end{aligned}$$
(5)

where \(x_{i}^{\prime },\,x_{i}^{\prime \prime }\) are numerical derivatives of first and second order, respectively evaluated for current iteration. Numerical approximation for the first derivative is used in calculating the radius of curvature by

$$\begin{aligned} x_{i}^{\prime }=\frac{x_{i}-x_{i-1}}{h}, \end{aligned}$$
(6)

where \(x_{i}\) and \(x_{i-1}\) are current iteration and preceding iteration, respectively, h is the Euclidean distance between them. The second-order derivative also used to calculate the radius of curvature can be analogously calculated as:

$$\begin{aligned} x_{i}^{\prime \prime }=\frac{x_{i}^{\prime }-x_{i-1}^{\prime }}{h}, \end{aligned}$$
(7)

where \(x_{i}^{\prime }\) is the first derivative evaluated in the current iteration and \(x_{i-1}^{\prime }\) is first order derivative evaluated in the previous iteration (see Fig. 5).

Fig. 5
figure 5

Proposed variable radius

Full size image

Using (7) and (6) can be calculated (5) for each variable \(x_{1},\,x_{2},\ldots ,x_{n}\) corresponds to the number of system variables. Then is used arithmetic mean for the radius of curvature is given by

$$\begin{aligned} \rho _{av}=\frac{\rho _{x_{1}}+\rho _{x_{2}}+\cdots +\rho _{x_{n}}}{n}. \end{aligned}$$
(8)

The radius of the sphere expressed as the variable r is calculated using the hyperbolic tangent function (9)

$$\begin{aligned} r=f\left( \rho _{av}\right) =\tanh \left( \rho _{av}\right) =\frac{e^{\rho _{av}}-e^{-\rho _{av}}}{e^{\rho _{av}}+e^{-\rho _{av}}}. \end{aligned}$$
(9)

The function there are also a pair of horizontal asymptotes is know as a sigmoid function and is a bounded differentiable real function that is defined for all real input values and has a positive derivative at each point. Figure 6 shows the function behavior, using as parameters the radius of curvature.

Fig. 6
figure 6

Hyperbolic tangent function

Full size image

Equation (8) is a hyperbolic tangent function used to find the value of the radius of the sphere. To accelerate change radio size can increase the hyperbolic function exponent using a constant K by

$$\begin{aligned} r=f\left( \rho _{av}\right) =\frac{e^{K\rho _{av}}-1}{e^{K\rho _{av}}+1}, \end{aligned}$$
(10)

where K is an integer that allows the function to have is an abrupt change in the range of allowed values. At each iteration the curvature radius is calculated to obtain the radius of the sphere suitable to trace homotopy curve during the course of the bend solution.

Numerical Examples

For exemplify the effectiveness of the methodology of fixed radius versus variable radius, three study case are submitted.

Case Study with Two Variables

The first study case is a circuit with a two diodes, one voltage source (E) an a resistor (R) as shown in Fig. 7. In where the range of the radius of the hypersphere is taking of 0.009–0.1, knowing that most of the time the radius size will have the most value.

Fig. 7
figure 7

Two tunnel diode circuit

Full size image

The mathematical expression that represents the non-linear model having the form of a polynomial:

$$\begin{aligned} g_{1}\left( v_{1}\right)= & {} 2.5v_{1}^{3}-10.5v_{1}^{2}+11.8v_{1};\nonumber \\ g_{2}\left( v_{2}\right)= & {} 0.43v_{2}^{3}-2.69v_{2}^{2}+4.56v_{2}. \end{aligned}$$
(11)

Using Kirchhoff laws, we obtain the equilibrium equation system:

(12)

The formulation used in this work is the Newton homotopy (12), then spherical method with fixed radius is applied, for this first example the radio fixed size is \(r=0.03.\) For the same example, we change the variable radius methodology proposed in this work, for which a range of possible values for the radius of the sphere where the minimum value is the fixed value of radius 0.3 and the maximum value is 0.1 to avoid jumps between solution path. We can see Fig. 8, the result of comparison between fixed radius and the methodology of variable radius.

Fig. 8
figure 8

a Radius size constant. b Radius size variable

Full size image

Comparing the same curve solution but in the Fig. 8a using fixed radius display a curve as solid lines while for Fig. 8b points are drawn wide apart because the radius of the sphere is changed with respect to changes in the curve form solution. Table 1 shows the results as the computation time and the total number of iterations. The result shows advantages in the use of fixed radius regarding sphere of variable radius. For this case study all solutions were successfully found as shown in Table 2.

Table 1 Numerical results for the first case study
Full size table
Table 2 All solutions found for the first case study
Full size table

Case Study with 14 Variables

The following circuit is described by a system of nonlinear equations with 14 variables \(I_{E},\,v_{1},\,v_{2},\,v_{3},\,v_{4},\,v_{5},\,v_{6},\,v_{7},\,v_{8},\,v_{9},\,v_{10},\,v_{11},\,v_{12},\,v_{13}.\) This circuit contain four transistor and one diode as shown in Fig. 9.

Fig. 9
figure 9

Example circuit with 14 variables

Full size image

The equilibrium equations are obtained from the modified nodal analysis by:

$$\begin{aligned} f_{1}= & {} \frac{37}{20,000} v_{1} - \frac{1}{4000} v_{2}-\frac{1}{4000} v_{6} -\frac{1}{1000} v_{9} -\frac{1}{4000} v_{12} -\frac{1}{10,000} v_{13} +I_{E}, \\ f_{2}= & {} -\frac{1}{40,000} v_{1} + \frac{3}{8000} v_{2}+ \frac{3}{8000} v_{5} +9.90E-09 \exp ^{40v_{4}-40v_{3}}\nonumber \\&\quad +1E-10-1E-08 \exp ^{40v_{4}-40v_{2}}, \\ f_{3}= & {} \frac{1}{100}v_{3}-1E-08 \exp ^{40v_{4}-40v_{3}} + 9.90 E-09+1E-10 \exp ^{40v_{4}-40v_{2}}, \\ f_{4}= & {} \frac{1}{8000}v_{4}-\frac{1}{8000}v_{6}+1E-10 \exp ^{40v_{4}-40v_{3}}-1E-08+9.90E \nonumber \\&-09\exp ^{40v_{4}-40v_{2}},\\ f_{5}= & {} \frac{1}{8000} v_{2}+\frac{1}{8000} v_{5} +1E-10 \exp ^{40 v_{5}-40v_{7}} -1E-08 \nonumber \\&\quad +9.90 E-09\exp ^{40v_{5}- 40v_{6}}, \nonumber \\ f_{6}= & {} \frac{1}{4000} v_{1} - \frac{1}{8000} v_{4}+ \frac{3}{8000}v_{6} +9.90E-09 \exp ^{40v_{5}-40v_{7}}\nonumber \\&\quad +1.010E-08 \exp ^{40v_{5}-40v_{6}} -1E-08 \exp ^{40v_{8}-40v_{6}},\\ f_{7}= & {} \frac{1}{100} v_{7}-1E-08 \exp ^{40v_{5}-40v_{7}}+9.90E-09+1E-10 \exp ^{40v_{5}-40v_{6}},\\ f_{8}= & {} \frac{1}{30,000}v_{8}-\frac{1}{30,000}v_{9}+1E-08 \exp ^{40v_{8}-40v_{6}} -1.E-08, \end{aligned}$$
$$\begin{aligned} f_{9}= & {} \frac{1}{1000}v_{1}-\frac{1}{30,000}v_{8}+\frac{31}{30,000}v_{9}+9.90E-09\exp ^{40v_{11}-40v_{10}}+1E-10\nonumber \\&\quad +1E-08 \exp ^{40v_{11}-40v_{9}},\\ f_{10}= & {} \frac{1}{100}v_{10}-1E-08 \exp ^{40v_{11}-40v_{10}}+9.90E-09\nonumber \\&\quad +1E-10 \exp ^{40v_{11}-40v_{9}},\\ f_{11}= & {} \frac{1}{10,000}v_{11}-\frac{1}{10,000}v_{12}+1e-10 \exp ^{40v_{11}-40v_{10}} -1E-08\nonumber \\&\quad +9.9E-09\exp ^{40v_{11}-40v_{9}},\\ f_{12}= & {} -\frac{1}{4000}v_{1}-\frac{1}{10,000}v_{11}+\frac{7}{20,000}v_{12}+9.9E-12\exp ^{40v_{13}}+1E-10\nonumber \\&\quad -1E-08 \exp ^{40v_{13}-40v_{12}}, \\ f_{13}= & {} -\frac{1}{10,000}+\frac{11}{10,000}v_{13}+1E-10\exp ^{40v_{13}}-1E-08\nonumber \\&\quad +9.90E-09 \exp ^{40v_{13}-40v_{12}},\\ f_{14}= & {} v_{1}-12. \end{aligned}$$

The exponential function in the Ebers–Moll is used. Then Newton homotopy is applied to embedding the continuation parameter \(\lambda \) into a set of nonlinear equations \(H(x,\,\lambda )\) and then curve is traced using proposed methodology, we obtain the solution in Tables 3 and 4.

Table 3 Solutions second case study
Full size table
Table 4 Solutions second case study
Full size table

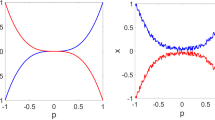
While the CPU time also is reduced for fixed radius and variable radius respectively. The projection of variable versus the \(\lambda \) parameter can be graphed, Fig. 10 shows \(I_{E}\) and \(v_{13}.\)

Fig. 10
figure 10

a Radius size constant. b Radius size variable

Full size image

Case Study with 18 Variables

Consider the following case study containing 6 transistors, 3 diodes and 18 resistors; the Fig. 11 shows the circuit. In this example, we applied the proposed algorithm to the same Newton homotopy function as above example, we choose a starting point as \((-15,\,-15,\,-15,\,-15,\,-15,\,-15,\,-15,-15,\,-15,\,-15,\,-15,\,-15,\,-15,\,-15,\,-15,-15,\,-15,\,-15).\) Tables 5 and 6 shows results of tracing the homotopy path, where can be see a clear decrease in the number of iterations and consequently also the computation time is reduced. A solution was found using a starting point without a methodology, however using other starting points probably to find other paths.

Fig. 11
figure 11

Six transistor multistate circuit

Full size image
Table 5 Solutions third case study
Full size table
Table 6 Solutions third case study
Full size table

The solution founded is plotting as a projection of the variables \(v_{1}\) and \(v_{17}\) versus \(\lambda \) parameter (see Fig. 12).

Fig. 12
figure 12

a Radius size constant. b Radius size variable

Full size image

Discussion

Proposed methodology has been applied in three circuits with different number of variables in which the number of iterations is reduced. Numerical derivatives are calculated in each iteration to obtain the radius of curvature, which changes while the curve goes through the nonlinearities own of the system of equations to be solved. Then the value for the radius of curvature is used in hyperbolic tangent function to change the radius of the spheres in the path of the homotopy curve. Tables 1, 2, 3, 4, 5, and 6 show the results of varying radius methodology where the number of iterations is decreased compared to a fixed radius methodology for SA. Numerical results is useful to solve examples with 2, 14 and 18 variables achieving the reduction of the number of iterations in each case study. In a future work will be necessary to include a proposal to find a path connecting all solutions and improve the results obtained. Nonetheless finding a curve with all connected solutions is presented as an area of opportunity to work on the starting point of homotopy.

Conclusions

The radius of curvature provides sufficient information on the prediction of how the curve will behave in the next iteration. Then the SA has been adapted to the variable-radius conforming to the shape of the curve. Using three study cases describing the behavior of electrical circuits, we show the use of variable radius for spheres in the SA yields better computation times in the simulations because the less number of iterations in each simulation. In the first case study all solutions are found while in the following case studies solutions depend strongly on the starting point.