Flexible Setup Cost and Deterioration of Products in a Supply Chain Model

Abstract

Product reliability is of significant importance in today’s technological world. People rely more and more upon the sustained functioning of machinery and complex equipments for purposes such as health, economic welfare, safety, to name just a few. Thus, in a business arena, it is critical to assess the reliability of new products. In this model, a two echelon supply chain model with variable setup cost and deterioration cost are analyzed. The setup cost is directly proportional and the deterioration rate is inversely proportional to reliability. Algebraical procedure has been employed to obtain the optimal solution of this model. The objective is to minimize the total cost of the entire system by considering reliability as a decision variable. Some numerical examples, sensitivity analysis, and graphical representations are considered to illustrate the model.

Introduction

A supply chain management (SCM) involves the movement and storage of raw materials and finished goods from point of origin to point of consumption. SCM obtains its importance in global market and network economy as organizations rely increasingly on effective supply chains or networks. Recently, Cárdenas-Barrón and Treviño-Garza [1] developed an excellent model for an optimal solution to a three echelon supply chain network. Chung et al. [2] discussed an inventory model with non-instantaneous receipt and exponentially deteriorating items for an integrated three layer supply chain system under two levels of trade credit policy. Taleizadeh and Cárdenas-Barrón [3] developed a metaheuristic algorithm for SCM problems.

In this direction, Goyal [4] developed a single supplier-single buyer integrated inventory model. Banerjee [5] derived a joint economic lot size model for the purchaser and the vendor with lot-for-lot policy. Hill [6] discussed a single-vendor single-buyer integrated production-inventory model as a general policy. Viswanathan and Piplani [7] explained a coordinating supply chain inventory through common replenishment epochs. Yang and Wee [8] derived an economic lot size model in an integrated vendor–buyer inventory system without derivatives. Sarkar and Majumder [9] developed an integrated vendor–buyer supply chain model with vendor’s setup cost reduction. Sarkar et al. [10] proposed a continuous review inventory model with setup cost reduction, quality improvement, and a service level constraint. Sarkar et al. [11] discussed an inventory model with quality improvement and setup cost reduction under controllable lead time.

Kim and Ha [12] proposed a just-in-time (JIT) lot size model to enhance the buyer–supplier linkage. They explained about the single-setup multiple-delivery (SSMD) policy. They proved that SSMD policy is more effective than single-setup single-delivery (SSSD) policy. Khouja [13] presented an optimizing inventory decisions in a multi-stage multi-customer supply chain model. Cárdenas-Barrón [14] discussed a note on optimizing inventory decisions in a multi-stage multi-customer supply chain model. Cárdenas-Barrón [15] developed an optimal manufacturing batch-size with rework in a single-stage production system. Cárdenas-Barrón [16] discussed an algebraical procedure to optimize different types of economic order quantity/economic production quantity (EOQ/EPQ) model with the help of basic algebra.

Yan et al. [17] extended Kim and Ha’s [12] model with a constant deterioration rate. Widyadana and Wee [18] developed an EPQ model for deteriorating items with preventive maintenance policy and random machine breakdown. Teng et al. [19] derived an economic lot size model of the integrated vendor–buyer inventory system without using any derivative. Teng et al. [20] extended an inventory model for buyer–distributor–vendor supply chain with backlogging without derivatives. Chung and Cárdenas-Barrón [21] found out a complete solution procedure for the EOQ and EPQ inventory models with linear and fixed backorder costs. Sett et al. [22] developed a two-warehouse inventory model with increasing demand and time varying deterioration. They considered the maximum lifetime of products. Sarkar and Saren [23] established a partial trade-credit model for retailer with exponentially deterioration. Sarkar et al. [24] considered a deteriorating inventory model with trade-credit policy for fixed lifetime products.

The process of degradation of items over time is basically perceived as deterioration. Ghare and Schrader [25] were the first authors to consider exponential deterioration in an inventory model. Covert and Philip [26] later discussed an EOQ model for deteriorating items with Weibull distribution. Misra [27] proposed an optimal production lot size model with deterioration function. Goyal [28] developed an economic ordering policy for deteriorating items over an infinite time horizon. Dutta and Pal [29] proposed an order-level inventory system with a power demand pattern and variable deterioration rate. Raafat [30] made a literature survey on continuously deteriorating inventory model. The inventory models with different types of deteriorating rates were extended by Chang and Dye [31], Skouri and Papachristos [32], Skouri et al. [33], Sarkar [34], Sarkar et al. [35], Sarkar and Sarkar [36–38], etc.

Reliability is the ability of a system to perform adequately and maintain its function under routine circumstances. More reliability implies less deteriorating rate of the manufactured items. Thus, the system has to be more reliable to reduce the production of defective items. Sarkar et al. [39] explained an economic manufacturing quantity (EMQ) model with optimal reliability, production lot size, and safety stock. Sarkar [40] explained an inventory model with reliability in an imperfect production process. Sarkar et al. [41] developed an EMQ model with price and time dependent demand under the effect of reliability and inflation. See Table 1 for the contribution of our paper.

Table 1 Comparison between the author’s contributions

Recently, Sarkar [42] developed a SCM model with fixed setup cost and deterioration cost which is an extension of Yan et al.’s [17] model. This study extends Sarkar’s [42] model by considering reliability as a decision variable. Setup cost is directly proportional and the deterioration rate is inversely proportional to the reliability. Therefore, with the increase in reliability the setup cost increases and the deterioration rate decreases. By using algebraical procedure, we minimize the total system cost and obtain a closed-form solution. There is absolutely no need to use calculus. The orientation of the paper is as follows: “Model Formulation” section contains the model formulation. In “Numerical Examples” section, the model is illustrated by using numerical examples. Finally-in “Conclusions” section, the conclusions and the future extensions of the model have been made.

Model Formulation

Following notation are used to develop the model.

Notation

Decision Variables

$q$ :

Delivery lot size (units)

$N$ :

Number of deliveries per production-batch, $N \ge 1$

$R$ :

Reliability

Parameters

$S$ :

Setup cost for a production batch ($/setup)

$S_{o}$ :

Initial setup cost for a production batch ($/setup)

$S_{1}$ :

Variable setup cost for a production batch ($/setup)

$A$ :

Ordering cost for the buyer ($/order)

$A_{b}$ :

Area under the buyer’s inventory level

$A_{s}$ :

Area under the supplier’s inventory level time

$D$ :

Demand (units/ year)

$K$ :

Transportation cost per delivery ($/delivery)

$d$ :

Deterioration rate

$M$ :

Deterioration cost per unit ($/unit)

$HC_{s}$ :

Holding cost for the supplier ($/unit/year)

$HC_{b}$ :

Holding cost for the buyer ($/unit/year)

$Q$ :

Production lot size per batch-cycle (units)

$P$ :

Production rate (unit/year)

$V_{c}$ :

Unit variable cost for order handling and receiving ($/unit)

$T$ :

Duration of inventory cycle (year)

$\lambda$ :

Proportionality constant

$\theta$ :

Proportionality constant

$t_{1}$ :

Production time duration for the supplier (year)

$t_{2}$ :

Non-production time duration for the supplier (year)

$t_{3}$ :

Duration between the two successive deliveries (year)

$TC$ :

Total cost of the system ($/year)

We consider the following assumptions to develop the model.

• (1) Single type of item is produced by the production-inventory system.

• (2) Setup cost $S$ and deterioration cost $M$ depend on the reliability parameter $R$.

• (3) Information regarding the inventory position and demand of the buyer are given to the supplier.

• (4) Production rate is greater than demand, i.e., $P>D$.

• (5) Handling and transportation costs are paid by the buyer.

• (6) Shortage and backlogging are not considered.

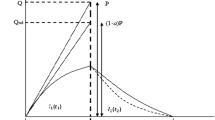
A SSMD production is considered in this research. The quantity ordered by the buyer is manufactured at a time and the ready products are delivered after a fixed time interval over multiple deliveries in an equal amount. The splitting of the order quantity into multiple lots is consistent with JIT implementation. The average total cost of the production-inventory model is developed for the buyer’s and the supplier’s which is then minimized. Without any loss of generality, we consider that the products arrive at the exact time when the items from the previous delivery has just been depleted. Two inventory versus time graphs for the buyer and the supplier, respectively are shown in Figs. 1 and 2. The total time span $T$ is divided into two components: $t_{1}$, the production time duration for the supplier and $t_{2}$, the non-production time duration for the supplier. $t_{3}$ is considered as the time duration between the two successive deliveries. We now separately calculate the buyer’s and the supplier’s inventory cost.

Fig. 1

Buyer’s inventory model. Adopted from Sarkar [42]

Fig. 2

Supplier’s inventory model. Adopted from Sarkar [42]

Inventory Cost for the Buyer

There are three well-known conditions which must prevail for the algebraic method to be used as an appropriate optimization method to minimize a function comprised by several functions and each function with one and more variables. These conditions are that:

• (1) Functions must be positive functions;

• (2) Product of the functions must be a constant;

• (3) When these functions are equalized; the system of equations can be solved.

Let $x$ be the number of deteriorating items during the time span $t_{3}$, then the delivery lot size is given by

$$\begin{aligned} q=x+Dt_{3} \end{aligned}$$

The delivery lot size $q$ is divided into two components: $Dt_{3}$ and $x$. $Dt_{3}$ is for the consumption and $x$ represents the number of deteriorating items. Since the deterioration rate is small, its square and higher powers can be neglected. Hence, during time interval $t_{3},\,x$ can be treated as the deterioration of $q$ units.

Therefore,

$$\begin{aligned} q=t_{3}\left( D+\frac{dq}{2}\right) , \end{aligned}$$

   (see for instance Yan et al. [17])

and

$$\begin{aligned} q=\frac{T}{N}\left( D+\frac{dq}{2}\right) ,\, \quad \hbox { because } \, \frac{T}{N}=t_{3} \end{aligned}$$

Now

$$\begin{aligned} q = x+Dt_{3} \end{aligned}$$

implies

$$\begin{aligned} \frac{1}{T}=\frac{D}{Nq}+\frac{d}{2N} \end{aligned}$$

(1)

i.e.,

$$\begin{aligned} \frac{q}{2}=\frac{Nq}{dT}-\frac{D}{d} \end{aligned}$$

Again the total deterioration for the buyer is obtained as

$$\begin{aligned} dA_{b}=Nq-DT \end{aligned}$$

which implies

$$\begin{aligned} A_{b}=\frac{\big (Nq-DT\big )}{d} \end{aligned}$$

i.e.,

$$\begin{aligned} \frac{A_{b}}{T}=\frac{q}{2} \end{aligned}$$

(2)

We consider that the deterioration rate $d$ is inversely proportional to reliability, i.e., $d\propto \frac{1}{R}$ which indicates $d=\frac{\theta }{R}$. Now the relevant costs for the buyer’s are

• (1) Ordering cost per unit time $= \frac{A}{T}$

• (2) Holding cost per unit per unit time $=\frac{HC_{b} A_{b}}{T}$

• (3) Deterioration cost per unit time $=\frac{MdA_{b}}{T}=\frac{\theta MA_{b}}{RT}$

• (4) Transportation cost and handling cost per unit time $=\frac{(NK+V_{c}Nq)}{T}$

Therefore, the buyer’s total cost function is obtained as

$$\begin{aligned} TC_{b}= \frac{1}{T}\big [A+HC_{b}A_{b}+\frac{\theta M}{R}A_{b}+NK+V_{c}Nq \big ] \end{aligned}$$

Using (1) and (2), the buyer’s total cost function becomes

$$\begin{aligned} TC_{b}=\left( \frac{D}{Nq}+\frac{\theta }{2NR}\right) \big (A+NK+V_{c}Nq\big )+\frac{q}{2}\left[ HC_{b}+\frac{\theta M}{R}\right] \end{aligned}$$

Inventory Cost for the Supplier

Suppose $y$ represents the number of deteriorating units for the supplier which can be symbolized as $y=dA_{s}$. $y+dqT/2$ denotes the total number of deteriorating items for the entire SCM. We have $Q=Nq+y$ and $t_{1}=\frac{Q}{P}$. Considering the initial and the total inventory for the entire SCM, we obtain

$$\begin{aligned} y+\frac{dqT}{2}=\frac{dT}{2P}\big \{2Dq+\big (Nq+y\big )\big (P-D\big )\big \} \end{aligned}$$

 hence,

$$\begin{aligned} A_{s}= & {} \frac{y}{d} \nonumber \\= & {} qT\left( \frac{D}{P}+\frac{N-1}{2}-\frac{DN}{2P}\right) \end{aligned}$$

(3)

We consider that the variable setup cost $S_{1}$ is directly proportional to reliability $R$, i.e., $S_{1}\propto R$. Then $S$ can be written as $S=S_{o}+\lambda R$ where $S_{1}=\lambda R$. Now the relevant costs for the supplier’s are

• (1) Setup cost per unit time $=\frac{S}{T}=\frac{S_{o}+\lambda R}{T}$

• (2) Holding cost per unit per unit time $=\frac{HC_{s} A_{s}}{T}$

• (3) Deterioration cost per unit time $=\frac{\theta MA_{s}}{RT}$

Now the equation for the supplier’s total cost function can be written as

$$\begin{aligned} TC_{s} = \frac{1}{T}\left( {S_{o}+\lambda R}+HC_{s}A_{s}+\frac{\theta M}{R}A_{s}\right) \end{aligned}$$

Using (1) and (3), the supplier’s total cost function is

$$\begin{aligned} TC_{s}= & {} \left( \frac{D}{Nq}+\frac{\theta }{2NR}\right) \big (S_{o}+\lambda R\big ) +q\left( HC_{s}+\frac{\theta M}{R} \right) \left( \frac{D}{P}+\frac{N-1}{2}-\frac{DN}{2P}\right) \end{aligned}$$

Integrated Inventory Cost for the Entire SCM

The total average cost for the entire SCM is $TC(q,N,R)=TC_{b}+TC_{s}$

$$\begin{aligned} TC(q,N,R)= & {} \left( \frac{D}{Nq}+\frac{\theta }{2NR}\right) \big [A+\big (S_{o}+\lambda R\big )+NK+V_{c}Nq\big ] +\frac{q}{2}\left( HC_{b}+\frac{\theta M}{R}\right) \nonumber \\&+\left( HC_{s}+\frac{\theta M}{R}\right) \left\{ \frac{(2-N)D}{P}+N-1\right\} \end{aligned}$$

(4)

Minimum Order Quantity

The required ordered quantity that makes the SSDM policy superior to single-delivery policy is obtained from the savings. Substituting $N=1$ in (4) and subtracting that result from (4), we obtain

$$\begin{aligned} SV(q,N,R)= & {} \left( \frac{D}{q}+\frac{\theta }{2R}\right) \big \{A+\big (S_{o}+\lambda R\big )\big \}\left( 1-\frac{1}{N}\right) \nonumber \\&+ \frac{q}{2}\left( HC_{s}+\frac{\theta M}{R}\right) (N-1)\left( \frac{D}{P}-1\right) \end{aligned}$$

(5)

We note that as $N=1$, the saving vanishes. It can be shown that (5) is concave and increases at a diminishing rate as the ordered quantity increases which implies that larger ordered quantity indicates more benefit for the supplier and the buyer over a long term contract. The minimum ordered quantity that makes the SSMD policy favorable over the single-delivery policy is obtained by solving $SV(q,N,R) \ge 0$ for $q$.

Therefore, $SV(q,N,R) \ge 0$ gives

$$\begin{aligned} q^{2}N\big (HC_{s}R+\theta M\big )\big (D-P\big )+\big (A+S_{o}+\lambda R\big )P\big (\theta q+2RD\big )\ge 0 \end{aligned}$$

(6)

The left hand side (LHS) of the inequality is quadratic in $q$. Considering the equality and solving for $q$ (suppose, the roots are $q_{1}$ and $q_{2}$), the LHS of the inequality gives

$$\begin{aligned} q_{1}= & {} \frac{1}{2N(HC_{s}R+\theta M)(P-D)}\Big \{P\theta \big (A+S_{o}+\lambda R\big )\nonumber \\&+ \sqrt{\big [\theta \big (A+S_{o}+\lambda R\big )P\big ]^{2}-8NDPR\big (HC_{s}R+\theta M\big )\big (D-P\big )\big (A+S_{o}+\lambda R\big )}~\Big \} \end{aligned}$$

Since $(D-P)$ is always less than zero therefore, without any loss of generality, $q_{1}$ acquires a positive value.

$$\begin{aligned} q_{2}= & {} \frac{1}{2N\big (HC_{s}R+\theta M\big )(P-D)}\Big \{-\big (P\theta \big (A+S_{o}+\lambda R\big )\big ) \\&+ \sqrt{\big [\theta \big (A+S_{o}+\lambda R\big )P\big ]^{2}-8NDPR\big (HC_{s}R+\theta M\big )\big (D-P\big )\big (A+S_{o}+\lambda R\big )}~\Big \} \end{aligned}$$

In order to find the nature of the root given by $q_{2}$, we take into consideration “Descartes’ rule of signs” which indicates that the equation $q^{2}N(HC_{s}R+\theta M)(D-P)+(A+S_{o}+\lambda R)P(\theta q+2DR)=0$ has only one positive real root given by $q_{1}$ and hence, $q_{2}$ is neglected.

From (4), we have

$$\begin{aligned} TC(q,N,R)= & {} \frac{q}{2}\left[ \left( HC_{b}+\frac{\theta M}{R}\right) +\left( HC_{s}+\frac{\theta M}{R}\right) \left( \frac{(2-N)D}{P}+N-1\right) +\frac{V_{c}\theta }{R}\right] \\&+ \frac{1}{q}\left[ \frac{D}{N}\big (A+S_{o}+\lambda R+NK\big )\right] +DV_{c}+\frac{\theta }{2NR}\big (A+S_{o}+\lambda R+NK\big ) \end{aligned}$$

[See Appendix A for optimization calculation by calculus.]

When $N$ and $R$ are fixed, $TC$ can be written in the symbolic form as

$$\begin{aligned} TC(q)=x_{1}q+\frac{x_{2}}{q}+x_{3}=\frac{x_{1}}{q}\left( q-\sqrt{\frac{x_{2}}{x_{1}}}\right) ^{2}+2\sqrt{x_{1}x_{2}}+x_{3} \end{aligned}$$

where

$$\begin{aligned} x_{1}= & {} \frac{1}{2}\left[ \left( HC_{b}+\frac{\theta M}{R}\right) +\left( HC_{s}+\frac{\theta M}{R}\right) \left( \frac{(2-N)D}{P}+N-1\right) +\frac{V_{c}\theta }{R}\right] \\ x_{2}= & {} \left[ \frac{D}{N}\big (A+S_{o}+\lambda R+NK\big )\right] \end{aligned}$$

and

$$\begin{aligned} x_{3}=DV_{c}+\frac{\theta }{2NR}\big (A+S_{o}+\lambda R+NK\big ) \end{aligned}$$

Now the expression $f(q)=x_{1}q+\frac{x_{2}}{q}+x_{3} =\big (\sqrt{x_{1}q}\big )^{2}+\left( \sqrt{\frac{x_{2}}{q}}\right) ^{2}+x_{3}= \left( \sqrt{x_{1}q}-\sqrt{\frac{x_{2}}{q}}\right) ^{2}+2\sqrt{x_{1}x_{2}}+x_{3}$ attains its minimum when $q = \sqrt{\frac{x_{2}}{x_{1}}}$, (See for instance Sarkar [42]) and the minimum cost is $2\sqrt{x_{1}x_{2}}+x_{3}$.

Therefore, $TC(q)$ is the minimum when

$$\begin{aligned} q= & {} \sqrt{\frac{x_{2}}{x_{1}}} \\= & {} \sqrt{\frac{2RDP\big (A+S_{o}+\lambda R+NK\big )}{N\big [\big (PRHC_{b}+\theta MP\big )+\big (HC_{s}R+\theta M\big )\big \{\big (2-N\big )D+PN-P\big \}+V_{c}\theta P\big ]}} \\ \end{aligned}$$

and the minimum cost is

$$\begin{aligned} TC(q)= & {} 2\sqrt{x_{1}x_{2}}+x_{3}\nonumber \\= & {} \Bigg [2\left\{ \left( HC_{b}+\frac{\theta M}{R}\right) +\left( HC_{s}+\frac{\theta M}{R}\right) \left( \frac{(2-N)D}{P}+N-1\right) +\frac{V_{c}\theta }{R}\right\} \nonumber \\&\left\{ \frac{D}{N}\big (A+S_{o}+\lambda R+NK\big )\right\} \Bigg ]^{1/2}+DV_{c}+\frac{\theta }{2NR}\big (A+S_{o}+\lambda R+NK\big ) \end{aligned}$$

(7)

When $q$ and $R$ are fixed

$$\begin{aligned} TC(N)= & {} N\frac{q}{2}\left( \frac{P-D}{P}\right) \left( HC_{s}+\frac{\theta M}{R}\right) +\frac{1}{N}\left( \frac{D}{q}+\frac{\theta }{2R}\right) \big (A+S_{o}+\lambda R\big ) \nonumber \\&+ \frac{q}{2}\left[ \left( HC_{s}+\frac{\theta M}{R}\right) \left( \frac{2D-P}{P}\right) +\left( HC_{b}+\frac{\theta M}{R}\right) \right] \nonumber \\&+ \left( \frac{D}{q}+\frac{\theta }{2R}\right) \big (K+V_{c}q\big ) \end{aligned}$$

(8)

which can be written in the symbolic form as

$$\begin{aligned} TC(N)=x_{4}N+\frac{x_{5}}{N}+x_{6} \end{aligned}$$

where

$$\begin{aligned} x_{4}= & {} \frac{q}{2}\left( \frac{P-D}{P}\right) \left( HC_{s}+\frac{\theta M}{R}\right) \\ x_{5}= & {} \left( \frac{D}{q}+\frac{\theta }{2R}\right) \big (A+S_{o}+\lambda R\big ) \end{aligned}$$

and

$$\begin{aligned} x_{6} = \frac{q}{2}\left[ \left( HC_{s}+\frac{\theta M}{R}\right) \left( \frac{2D-P}{P}\right) +\left( HC_{b}+\frac{\theta M}{R}\right) \right] +\left( \frac{D}{q}+\frac{\theta }{2R}\right) \big (K+V_{c}q\big ). \end{aligned}$$

$TC(N)$ is the minimum when

$$\begin{aligned} N= & {} \sqrt{\frac{x_{5}}{x_{4}}} \nonumber \\= & {} \sqrt{\frac{P\big (2RD+\theta q\big )\big (A+S_{o}+\lambda R\big )}{q^{2}\big (P-D\big )\big (HC_{s}R+\theta M\big )}} \end{aligned}$$

(9)

and the minimum cost is

$$\begin{aligned} TC(N)= & {} 2\sqrt{x_{4}x_{5}}+x_{6}\nonumber \\= & {} \sqrt{2q\left( \frac{P-D}{P}\right) \left( HC_{s}+\frac{\theta M}{R}\right) \left( \frac{D}{q}+\frac{\theta }{2R}\right) \big (A+S_{o}+\lambda R\big )} \nonumber \\&+ \frac{q}{2}\left[ \left( HC_{s}+\frac{\theta M}{R}\right) \left( \frac{2D-P}{P}\right) +\left( HC_{b}+\frac{\theta M}{R}\right) \right] \nonumber \\&+ \left( \frac{D}{q}+\frac{\theta }{2R}\right) \big (K+V_{c}q\big ) \end{aligned}$$

(10)

When $q$ and $N$ are fixed

$$\begin{aligned} TC(R)= & {} R\frac{\lambda D}{Nq}+\frac{1}{R}\left[ \frac{\theta }{2N}\big \{A+S_{o}+NK+V_{c}Nq\big \}+\frac{\theta Mq}{2}\left\{ \frac{(2-N)D}{P}+N\right\} \right] \nonumber \\&+ \frac{D}{Nq}\big \{A+S_{o}+NK+V_{c}Nq\big \}+\frac{\theta \lambda }{2N}\nonumber \\&+ \frac{q}{2}\left[ HC_{b}+HC_{s}\left\{ \frac{(2-N)D}{P}+N-1\right\} \right] \end{aligned}$$

(11)

The above equation can be written in the form

$$\begin{aligned} TC(R)=x_{7}R+\frac{x_{8}}{R}+x_{9} \end{aligned}$$

where

$$\begin{aligned} x_{7}= & {} \frac{\lambda D}{Nq}\\ x_{8}= & {} \left[ \frac{\theta }{2N}\big \{A+S_{o}+NK+V_{c}Nq\big \}+\frac{\theta Mq}{2}\left\{ \frac{(2-N)D}{P}+N\right\} \right] \end{aligned}$$

and

$$\begin{aligned} x_{9}= & {} \frac{D}{Nq}\big \{A+S_{o}+NK+V_{c}Nq\big \}+\frac{\theta \lambda }{2N} \\&+ \frac{q}{2}\left[ HC_{b}+HC_{s}\left\{ \frac{(2-N)D}{P}+N-1\right\} \right] \end{aligned}$$

Therefore, $TC(R)$ is the minimum when

$$\begin{aligned} R= & {} \sqrt{\frac{x_{8}}{x_{7}}}\nonumber \\= & {} \sqrt{\frac{\theta q\big [P\big \{A+S_{o}+NK+V_{c}Nq\big \}+MNq\big \{(2-N)D+NP\big \}\big ]}{2PD\lambda }} \end{aligned}$$

(12)

and the minimum cost is

$$\begin{aligned} TC(R)= & {} 2\sqrt{x_{7}x_{8}}+x_{9} \nonumber \\= & {} \sqrt{\frac{2\lambda D}{Nq}\left[ \frac{\theta }{N}\big \{A+S_{o}+NK+V_{c}Nq\big \}+\theta Mq\left\{ \frac{(2-N)D}{P}+N\right\} \right] }\nonumber \\&+ \frac{D}{Nq}\big \{A+S_{o}+NK+V_{c}Nq\big \}+\frac{\theta \lambda }{2N}\nonumber \\&+ \frac{q}{2}\left[ HC_{b}+HC_{s}\left\{ \frac{(2-N)D}{P}+N-1\right\} \right] \end{aligned}$$

(13)

Optimal Interval of the Lot Size

By our assumption $N$, the number of deliveries per production batch-cycle, must be greater than or equal to 1 and from the expression for optimum $q,\, N$ attains its upper bound at $N=1$, i.e.,

$$\begin{aligned} q \le \sqrt{\frac{2PDR\big (A+S_{o}+\lambda R+K\big )}{R\big \{PHC_{b}+DHC_{s}\big \}+\theta \big \{ M\big (D+P\big )+V_{c}P\big \}}} \end{aligned}$$

As $N$, the number of deliveries per production batch-cycle increases, the corresponding lot size value $q$ decreases hence, from the equation of optimum lot size, we obtain

$$\begin{aligned} q\ge \sqrt{\frac{2PDR\big (A+S_{o}+\lambda R+NK\big )}{\big \{HC_{b}R+\theta \big (M+V_{c}\big )\big \}\{2D+N\big (P-D\big )\}N}} \end{aligned}$$

Solution Procedure

In this model, we obtain the total cost $TC$, the delivery lot size $q$, the number of deliveries per production batch $N$, and the reliability parameter $R$. If the value of $N$, given by (9) is not an integer, then we choose $N$ in such a way which gives $\hbox {min}\{TC(N^{+}), TC(N^{-})\}$ for the model where $N^{+}$ and $N^{-}$ represent the closest integers larger or smaller than the optimal $N^{*}$. We then substitute the value of $N^{*},\, q^{*}$ and $R^{*}$ in $TC(q^{*},N^{*},R^{*})$ and obtain the optimal minimal cost given by $TC$.

Numerical Examples

Example 1

The values of the following parameters are to be taken in appropriate units: $P = 13{,}000$ units/year, $S_{o}$ = $ 200/batch, $HC_{b}$ = $ 7/unit/year, $HC_{s}$ = $ 6/unit/year, $D = 9000$ units/year, $A$ = $ 25/order, $K=$ $ 10/delivery, $V_{c}$ = $ 1/unit, $M$ = $ 10/unit, $\theta =0.1$, $\lambda =90$. Then, the optimal solution is {$TC$ = $13873.6/year, $N=12/$production batch-cycle, $q = 126.82$ units, $R=0.79$}. See Figs. 3, 4, 5 for optimality of the cost function.

Fig. 3

Total cost versus lot size and reliability when number of deliveries per production is fixed

Fig. 4

Total cost versus number of deliveries per production and reliability when lot size is fixed

Fig. 5

Total cost versus number of deliveries per production and lot size when reliability is fixed

We compare our model with that of Sarkar [42] by using the same parametric values.

Example 2

The values of the following parameters are to be taken in appropriate units: $P = 10{,}000$ units/year, $S_{o}$ = $800/batch, $HC_{b}$ =$ 7/unit/year, $HC_{s}$ =$ 6/unit/year, $D = 4800$ units/year, $A$ = $25/order, $K$=$ 50/delivery, $V_{c}$ =$ 1/unit, $M$ =$ 50/unit, $\theta =0.02$, $\lambda =250$. Then, the optimal solution is {$TC=$ $14,198.2/year, $N=6/$production batch-cycle, $q = 246.39$ units, $R=0.86$}.

(In Sarkar [42] $S_{o}=C,\, HC_{b}=H_{B},\, HC_{s}=H_{S},\, K=F,\, V_{c}=V$, and $M=C_{d}$).

Sensitivity Analysis

We now study the effects of changes in parameters such as $A, S_{0},HC_{b},HC_{s},K,V_{c}$, and $M$ on the total cost. The sensitivity analysis is performed by changing each of the parameters by $-50, -25, +25$, and $+50\,\%$ taking one parameter at a time while keeping the remaining parameters unchanged.

From Table 2, the discussion of sensitivity analysis of the key parameters are as follows:

• If the ordering cost increases, then material handelling cost, shipping cost, placing order’s cost increase; as a result the total relevant cost increases. From the above table, we may conclude that total cost is minor sensitive to changes in ordering cost.

• If the setup cost increases, then the total cost also increases. Negative change in setup cost reduce more in total cost than the positive change in it.

• Increasing value of holding cost increases the total cost. From Table 2, we can see that the negative and positive change in holding cost gives approximately same amount of change in the total cost function.

• If we increase the transportation cost, then the total cost increases.

• If the unit variable cost for order handling and receiving increases while all the other parameters remain unchanged, the expected total cost tends to increase. From Table 2, it can be concluded that the negative and positive change in it gives same amount of change in total cost. This is the most sensitive cost than others in this model.

• Increase in deterioration cost indicates increase in total deteriorate items. Therefore increasing deterioration cost increase the total cost.

Conclusions

This paper discussed the effect of reliability on setup cost and deterioration rate. An algebraical procedure was used to minimize the cost for the entire SCM model and obtained a closed-form solution. The main contribution of the model was to obtain the minimum cost with integer number of deliveries, optimal lot size, and reliability by using algebraical procedure. The proposed procedure for the computation of the total cost of the SCM can be easily done without any tedious calculation. An illustrative numerical example and a numerical comparison of this model with that of Sarkar [42] were provided. Some graphical representations were considered to illustrate the model. We proved that our model gave more savings than Sarkar [42]. The model is useful where the reduction of setup cost is possible and deterioration is present. This model can be further extended to a multi-item production process with variable transportation cost, demand, and deterioration rate.

Table 2 Sensitivity analysis for the key parameters

Appendix

Taking fast order partial derivatives of $TC(q,N,R)$ and equating to zero, we obtain

$$\begin{aligned} \frac{\partial TC}{\partial q}= & {} \frac{1}{2}\Bigg [\frac{M\theta }{R}+\frac{V_{c}\theta }{R}+C_{b}+\left( \frac{D(2-N)}{P}+N-1\right) \left( \frac{M\theta }{R}+C_{s}\right) \Bigg ] \\&-\frac{D(A+KN+R\lambda +S_{0})}{Nq^2} \\= & {} 0 \\ \Rightarrow q= & {} \sqrt{\frac{2RDP(A+S_{o}+\lambda R+NK)}{N\big [\big (PRHC_{b}+\theta MP\big )+\big (HC_{s}R+\theta M\big )\big \{\big (2-N\big )D+PN-P\big \}+V_{c}\theta P\big ]}} \\ \frac{\partial TC}{\partial N}= & {} \frac{DK}{Nq}+\frac{K\theta }{2NR}+\frac{1}{2}q\left( 1-\frac{D}{P}\right) \left( \frac{M\theta }{R}+C_{s}\right) -\frac{D\big (A+NK+R\lambda +S_{0}\big )}{N^2q} \\&- \frac{\theta }{2NR^2}\big (A+KN+r\lambda +S_{0}\big )=0 \\ \Rightarrow N= & {} \sqrt{\frac{P\big (2RD+\theta q\big )\big (A+S_{o}+\lambda R\big )}{q^{2}\big (P-D\big )\big (HC_{s}R+\theta M\big )}} \\ \frac{\partial TC}{\partial R}= & {} \frac{q}{2}\left[ -\frac{M\theta }{R^2}-\frac{\theta M}{R^2}\left( \frac{(2-N)D}{P}+N-1\right) -\frac{V_{c}\theta }{R^2}\right] \\&+\frac{D\lambda }{Nq}-\frac{\theta }{2NR^2}\big (A+S_{0}+NK\big )=0 \\ \Rightarrow R= & {} \sqrt{\frac{\theta q\big [P\big \{A+S_{o}+NK+V_{c}Nq\big \}+MNq\big \{\big (2-N\big )D+NP\big \}\big ]}{2PD\lambda }} \end{aligned}$$