Introduction

The investigation of the exact particular solutions of the nonlinear system of partial differential equations (PDEs) plays important role to provide useful information towards our understanding of the complex physical phenomenon involved. Special exact solutions of the system of nonlinear PDEs are of great interest; these solutions play a major role in designing, analyzing and testing numerical methods for solving special initial and/or boundary-value problems. Lie’s method provide an efficient way of finding exact particular solutions of nonlinear PDEs (see Ames [1], Bluman and Cole [2] and Bluman and Kumei [3]). Using classical or non-classical Lie-symmetries we are able to obtain a large class of similarity solutions to the nonlinear evolution equations. Besides similarity methods, another use of Lie symmetries admitted by given PDEs consists in introducing some invertible point transformations that map the original system to an equivalent one, admitting special solutions [4]. Using this procedure, Donato and Oliveri [5] obtained exact solutions to axisymmetric MHD equations, Pandey et al. [6] and Pandey [7] obtained exact solutions of magnetogasdynamic equations and perfect gas involving shocks, Raja Sekhar and Sharma obtained similarity solutions of the modified shallow water equations and discussed Riemann problem in the case of ideal magnetogasdynamics (see, [8] and [9]). In [10] various classes of exact solutions to ideal magnetogasdynamic equation of a perfect gases are determined by introducing some transformations, referred to as substitution principle, that map the given equations to an equivalent form. In [11] new similarity solutions of the Boiti–Leon–Pempinelli system are obtained. For non-ideal and magnetogasdynamic flows the author refers to the research papers [12, 13] and [14], and for nonlinear wave propagation in quasilinear hyperbolic systems, the reader is refer to the book by Sharma [15].

In present paper, we have used Lie’s method to obtain exact solution to the equations of non-ideal magnetogasdynamics. The Lie group of transformations admitted by the governing system are obtained using the procedure outlined in [2] and [3]. The symmetries at hand enables us to reduce the governing system to an equivalent form through the use appropriate canonical variables. The equivalent system is then solved which yield exact particular solution, that exhibits space-time dependence, to the original system [4]. The exact particular solution of the governing system, which exhibits space-time dependence, is used to study the evolution of the weak discontinuities. The influence of magnetic field strength and the van der Waals excluded volume on the evolution of the discontinuity wave are studied in detail.

Basic Equations and Lie Group Analysis

Assuming the electrical conductivity to be infinite and the direction of magnetic field orthogonal to the trajectories of the gas particles, the basic equations for the one-dimensional cylindrically symmetric motion in magnetogasdynamics, can be written in the form

$$\begin{aligned} \begin{aligned}&\rho _{t} + u\rho _{x} + \rho u_{x} +\frac{\rho u}{x} =0,\\&u_{t} + u u_{x} +\rho ^{-1} (p_{x} + h_{x}) =0,\\&p_{t} +up_{x} + \rho a^{2}\left( u_{x} + \frac{u}{x} \right) =0,\\&h_{t} + u h_{x} + 2hu_{x} + \frac{2hu}{x} =0, \end{aligned} \end{aligned}$$
(1)

where \(\rho \) is the density, \(u\) the particle velocity in the \(x\)-direction being radial in cylindrically symmetric flows, \(p\) the pressure, \(h\) the magnetic pressure defined as \( h= \mu H^{2}/2 \) with \(\mu \) as magnetic permeability and \(H\) the axial magnetic field; the entity \( \displaystyle a = \left( \frac{\gamma p}{\rho (1- b \rho )} \right) ^{1/2}\) is the equilibrium speed of sound with \(\gamma \) as the specific heats ratio lying in the region \(1<\gamma <2\) and \(b\) is the van der Waals excluded volume. The equation of state is given by

$$\begin{aligned} p (1-b\rho )= \rho RT, \end{aligned}$$

where \(R\) and \(T\) are respectively the gas constant and the temperature. Equations (1) are a quasilinear system of first order PDEs with two independent variables and four dependent variables. In order to determine a similarity solution, we seek a one parameter Lie group of transformation

$$\begin{aligned} t^{*}&= t+ \epsilon \xi _{1}( x,t,\rho ,u,p,h)+ {\mathcal {O}}(\epsilon ^{2}),\quad x^{*}= x + \epsilon \xi _{2} (x,t,\rho ,u,p,h)+ {\mathcal {O}}(\epsilon ^{2}),\nonumber \\ \rho ^{*}&= \rho + \epsilon \phi _{1} ( x,t,\rho ,u,p,h)+ {\mathcal {O}}(\epsilon ^{2}),\quad u^{*}= u + \epsilon \phi _{2}(x,t,\rho ,u,p,h)+ {\mathcal {O}}(\epsilon ^{2}),\\ p^{*}&= p + \epsilon \phi _{3}( x,t,\rho ,u,p,h)+ {\mathcal {O}}(\epsilon ^{2}),\quad h^{*}= h+ \epsilon \phi _4(x,t,\rho ,u,p,h)+ {\mathcal {O}}(\epsilon ^{2}),\qquad \nonumber \end{aligned}$$
(2)

where the infinitesimals \(\xi _{1},\, \xi _{2},\,\phi _{1},\,\phi _{2},\, \phi _{3}\) and \(\phi _4\) are to be determined in such a way the system (1), are invariant with respect to the transformations (2). We introduce the notation \(x_{1} = t,\, x_{2} = x,\, u_{1} = \rho ,\, u_{2} = u,\, u_{3} =p,\, u_4 = h\) and \(P^{i}_{j} = \frac{\partial u_{i}}{\partial x_{j}}\), where \(i=1,2,3,4\) and \(j=1,2.\) The system (1) which can be represented as

$$\begin{aligned} G_{r} (x_{j}, u_{i}, P^{i}_{j})=0, \quad r=1,2,3,4 \end{aligned}$$
(3)

is said to be invariant under the infinitesimal group of transformations (2) if and only if

$$\begin{aligned} Y G_{r} =0, \, \hbox {when}\, G_{r} =0, \quad r=1,2,3,4 \end{aligned}$$
(4)

where Y is the extended infinitesimal operator of the group of transformations (2) and is given by

$$\begin{aligned} Y= \xi ^{j} \frac{\partial }{\partial x_{j}} + \eta ^{i} \frac{\partial }{\partial u_{i}} + \beta ^{i}_{j} \frac{\partial }{\partial P^{i}_{j}}, \end{aligned}$$
(5)

with \(\xi ^{1} = \xi _{1},\,\xi ^{2} = \xi _{2},\,\eta ^{1} = \phi _{1},\,\eta ^{2} = \phi _{2},\,\eta ^{3} = \phi _{3},\,\eta ^{4} = \phi _4\) and

$$\begin{aligned} \beta ^{i}_{j} = \frac{\partial \eta ^{i} }{\partial x_{j}} +\frac{\partial \eta ^{i} }{\partial u_{k}}P^{k}_{j} - \frac{\partial \xi ^l }{\partial x_{j}} P^{i}_{l} - \frac{\partial \xi ^{l} }{\partial x_{n}} P^{i}_{l} P^{n}_{j}, \end{aligned}$$
(6)

where \(i=1,2,3,4;\, j=1,2;\,k=1,2,3,4;\,l=1,2\); and \(n=1,2,3,4\). Here repeated indices imply summation convention.

Equation (4) implies

$$\begin{aligned} \xi ^{j} \frac{\partial G_{r} }{\partial x_{j}} + \eta ^{i} \frac{\partial G_{r} }{\partial u_{i}} + \beta ^{i}_{j} \frac{\partial G_{r} }{\partial P^{i}_{j}} =0 \quad \hbox {when} \quad G_{r} =0, \quad r=1,2,3,4. \end{aligned}$$
(7)

Substitution of \(\beta ^{i}_{j}\) from (6) into (7) yields an identity in \(P^{k}_{j}\) and \(P^{i}_{l} P^{n}_{j}\); hence we equate to zero the coefficients of \(P^{k}_{j}\) and \(P^{i}_{l} P^{n}_{j}\) to obtain a system of first-order linear partial differential equations in the infinitesimals \(\xi _{1},\,\xi _{2},\,\phi _{1},\,\phi _{2},\,\phi _{3}\) and \(\phi _{4}\). This system, called the system of determining equations of the group of transformations, is solved to find the invariance group of transformations.

We apply the above mentioned procedure to the system (1); it is found that a one-parameter Lie group of transformations that leaves the system (1) invariant has the following infinitesimal operators,

$$\begin{aligned} X_{1}&= 2x\frac{\partial }{\partial x}+ t\frac{\partial }{\partial t} + u\frac{\partial }{\partial u} + 2p \frac{\partial }{\partial p}+ 2h\frac{\partial }{\partial h},\\ X_{2}&= x\frac{\partial }{\partial x}+ u\frac{\partial }{\partial u}+ 2p\frac{\partial }{\partial p} + 2h \frac{\partial }{\partial h}, \\ X_{3}&= \frac{\partial }{\partial t}. \end{aligned}$$

For the above infinitesimal generators we have the following commutator table:

 

\( X_{1}\)

\(X_{2} \)

\(X_{3}\)

\(X_{1}\)

0

0

\(-X_{3}\)

\(X_{2}\)

0

0

\( 0 \)

\(X_{3}\)

\( X_{3}\)

\(0\)

0

Exact Solutions

The knowledge of the Lie point symmetries admitted by a system of PDEs may be employed to characterize classes of invariant solutions. But, one may look for the introduction of suitable transformations allowing one to map the given system of PDEs to an equivalent form for which classes of exact solutions may be found. Let us now consider the infinitesimal generators \(X_{1}\) and \(X_{2}\) admitted by the system (1), from the commutator table it can be verified that the infinitesimal generators \(X_{1}\) and \(X_{2}\) commute, that is,

$$\begin{aligned}{}[X_{1}, X_{2}] = X_{1} ~X_{2} -X_{2} X_{1} =0, \end{aligned}$$

which means that the operators \(X_{1}\) and \(X_{2}\) generates a 2-dimensional abelian sub-algebra. Since the system is invariant under the group generated by \(X_{1}\), we introduce a set of canonical variables, defined by,

$$\begin{aligned} X_{1} {\tilde{\tau }} =1, \quad X_{1} {\tilde{\eta }} =0, \quad X_{1} {\tilde{S}} =0, \quad X_{1} {\tilde{U}} =0, \quad X_{1} {\tilde{P}} =0, \quad X_{1} {\tilde{R}} =0. \end{aligned}$$
(8)

The characteristic conditions associated with (8) yield the following transformations of variables

$$\begin{aligned} \tilde{\tau } = \ln {t}, \quad \tilde{\eta } = {\frac{x}{t^{2}}},\quad \tilde{S}= \rho ,\quad \tilde{U}= u \frac{1}{t},\quad \tilde{P}=p\frac{1}{t^{2}},\quad \tilde{R} = h \frac{1}{t^{2}}. \end{aligned}$$
(9)

We now express \(X_{2}\) in terms of the new variables, and choose a second set of canonical variables \(\tau ,\, \eta , \,S,\, U,\, P\) and \(R\), allowing one to express the generator as translation in \(\eta \) to obtain following transformation in the flow variables :

$$\begin{aligned} \tau&= \ln {t}, \quad \eta = \ln {\frac{x}{t^{2}}},\quad \rho = S(\tau , \eta ),\quad u= \frac{x}{t}\,U(\tau , \eta ),\quad p=\frac{x^{2}}{t^{2}} P(\tau , \eta ),\nonumber \\ h&= \frac{x^{2}}{t^{2}}R(\tau , \eta ), \end{aligned}$$
(10)

to the following autonomous form, (see [4, 6]):

$$\begin{aligned} \begin{aligned}&\frac{\partial S}{\partial \tau } + (U-2)\frac{\partial S}{\partial \eta } + S \frac{\partial U}{\partial \eta } +2SU=0,\\&S\frac{\partial U}{\partial \tau } + S(U-2)\frac{\partial U}{\partial \eta } + \frac{\partial P}{\partial \eta } +\frac{\partial R}{\partial \eta }+ 2P + 2R+2SU(U-1) =0,\\&\frac{\partial P}{\partial \tau } + (U-2) \frac{\partial P}{\partial \eta } + \frac{\gamma P}{1-b S} \left( \frac{\partial U}{\partial \eta } + 2U\right) + 2P(U-1)=0,\\&\frac{\partial R}{\partial \tau } + (U-2) \frac{\partial R}{\partial \eta } + 2R\left( \frac{\partial U}{\partial \eta } + 2U\right) + 2R(U-1)=0. \end{aligned} \end{aligned}$$
(11)

It may be noted that unlike the original system (1), the autonomous system (11) can be solved completely when \(U \equiv \) constant. Thus, when \(U = U_{0}\), the first third and the fourth of the equations (11) yield

$$\begin{aligned} S&= \tilde{S}_{0}(\zeta ) \exp (-2 U_{0} \tau ), \, P = \tilde{P}_{0}(\zeta ) \frac{\exp (2(U_{0} - 1)\tau ) }{(\exp (2U_{0} \tau ) - bS_{0} (\zeta ) )^{\gamma }},\nonumber \\ R&= \tilde{R}_{0}(\zeta ) \exp ((2-6U_{0})\tau ), \end{aligned}$$
(12)

where \(\tilde{S}_{0}(\zeta ),\,\tilde{P}_{0}(\zeta )\) and \(\tilde{R}_{0}(\zeta )\) are arbitrary function of \(\zeta \) defined by

$$\begin{aligned} \zeta = \tau - \frac{1}{U_{0} -2} \eta . \end{aligned}$$

Using (12) into the second of the equations (11) we get the following compatibility condition:

$$\begin{aligned}&\frac{\exp (2(U_{0} - 1)\tau ) }{(\exp (2U_{0} \tau ) - b\tilde{S}_{0} (\zeta ) )^{\gamma }} \left\{ -\frac{1}{(U_{0}-2)} \tilde{P}_{0}^{\prime }(\zeta )\right. \nonumber \\&\quad \left. +\tilde{P}_{0}(\zeta )\left( 2- \frac{\gamma b \tilde{S}_{0}^{\prime }(\zeta ) }{(U_{0}-2)(\exp (2U_{0} \tau ) - b\tilde{S}_{0} (\zeta ) )^{\gamma }}\right) \right\} \nonumber \\&\quad - \exp ((2-6U_{0})\tau )\left( \frac{1}{(U_{0}-2)} \tilde{R}_{0}^{\prime }(\zeta ) +2\tilde{R}_{0}(\zeta ) \right) 2\tilde{S}_{0} U_{0}(U_{0} -1) =0. \end{aligned}$$
(13)

Particular solution: When \(\tilde{S}_{0} (\zeta )=\) constant (say, \(S_{0}\)) and \(U_{0} =1\), we have from (13)

$$\begin{aligned} \tilde{P}_{0}^{\prime }(\zeta ) + 2\tilde{P}_{0}(\zeta ) =0 \hbox { and } \tilde{R}_{0}^{\prime }(\zeta ) + 2\tilde{R}_{0}(\zeta ) =0, \end{aligned}$$

which on solving gives

$$\begin{aligned} \tilde{P}_{0}(\zeta ) = P_{0} \exp \left( -2 \zeta \right) , \quad \tilde{R}_{0}(\zeta ) = R_{0} \exp \left( -2 \zeta \right) , \end{aligned}$$
(14)

where \(P_{0}\) and \(R_{0}\) are arbitrary constant. Thus, in view of the equations (10), (12) and (14), the solution of the system (1) can be expressed as follows (in dimensionless form ):

$$\begin{aligned} \rho (t, x) = \hat{\rho } \left( \frac{t}{t_{0}}\right) ^{-2},\quad u(t, x) = \frac{x}{t}, \quad p(x,t)= \frac{\hat{p}}{\left( (t/t_{0})^{2} - b\hat{\rho }\right) ^{\gamma }},\quad h = \hat{h} \left( \frac{t}{t_{0}}\right) ^{-4}, \qquad \end{aligned}$$
(15)

where \(\hat{\rho },~\hat{p}\) and \(\hat{h}\) are some reference constant values. In the absence of real gas \(i.e.,\,b=0\), the solution obtained here is same as that obtained in [5] and [10]. In the above particular solution, the particle velocity exhibits linear dependence on the spatial coordinate, such a state has been discussed by Pert [16], Sharma et al. [17] and Clarke [18]; Pert showed that such a form of the velocity distribution is useful in modelling the free expansion of polytropic gases, and it is attained in the limit of large time.

Evolution of the Weak Discontinuity

The governing system (1) can be written in the form

$$\begin{aligned} V_{t} + AV_{x} = B, \end{aligned}$$
(16)

where \( V= {(\rho ,u,p,h)}^{tr},\,B= (-\rho u/x, 0, -\gamma pu/x, 2hu/x )^{tr}\)

$$\begin{aligned} A= \left( \begin{array}{cccc} u &{} \rho &{} 0 &{} 0 \\ 0 &{} u &{} \rho ^{-1} &{} \rho ^{-1}\\ 0 &{} \rho a^{2} &{} u &{} 0 \\ 0 &{} 2h &{} 0 &{} u \end{array}\right) . \\ \end{aligned}$$

The matrix \(A\) has the following eigenvalues

$$\begin{aligned} \lambda ^{(1)}=u+C,\quad \lambda ^{(2)}=u \,(\hbox {double root}),\quad \lambda ^{(3)}= u-C \end{aligned}$$
(17)

with the corresponding left and right eigenvectors may be written as follows:

$$\begin{aligned} \begin{aligned}&l^{(1)}= \,(0, \rho C, 1 , 1),\quad d^{(1)}={\left( \rho C^{-1}, 1, \rho a^{2} C^{-1}, 2h C^{-1} \right) }^{tr},\\&l^{(2,1)}= (a^{2},0, -1,0),\quad d^{(2,1)}={(1,0,0,0 )}^{tr},\\&l^{(2,2)}= \left( 0,0, -2h,\rho a^{2}\right) ,\quad d^{(2,2)}={(0,0,1,-1 )}^{tr},\\&l^{(3)}= (0, -\rho C, 1 , 1),\quad d^{(3)}={\left( -\rho C^{-1}, 1,-\rho a^{2} C^{-1},-2h C^{-1} \right) }^{tr}, \end{aligned} \end{aligned}$$
(18)

where \(a=(\gamma p/\rho )^{1/2}\) is the sound speed,\(\,C={(a^{2}+k^{2})}^{1/2}\) the magneto-acoustic speed with, \(k= {(2h/\rho )}^{1/2}\) as the Alfven speed.

Fig. 1
figure 1

Evolution of \(C^{1}\) discontinuity wave influenced by the van der Waals excluded volume \(b, b=0.1\) (dashed line), \(b=0.8\) (dotted line). a discussed the behaviour when \(\pi _{0}>0\), b when \(-\pi _{c}\le \pi _{0} <0,\) while c when \(\pi _{0} < -\pi _{c} <0 \)

Full size image
Fig. 2
figure 2

Evolution of \(C^{1}\) discontinuity wave influenced by the magnetic field \(\hat{h} ,\,\hat{h}=0.1\) (dashed line), \(\hat{h}=0.8\) (dotted line). a discussed the behaviour when \(\pi _{0} >0\), b when \(-\pi _{c}\le \pi _{0} <0,\) while c when \(\pi _{0} < -\pi _{c} <0 \)

Full size image

Let us consider that the \(C^{1}\) discontinuity is propagating along the characteristic curve determined by \(\,{dx}/{dt}= \lambda ^{(1)}\,\) originating from the point \((x_{0}, t_{0})\), then the transport equation for the \(C^{1}\) discontinuity is given by (see [19–21] and [22])

$$\begin{aligned}&l^{(1)}\left\{ \frac{d\Lambda }{dt}+ (V_{x} +\Lambda )\left( \nabla \lambda ^{(1)}\right) \Lambda \right\} + {\left( \left( \nabla l^{(1)}\right) \Lambda \right) }^{tr} \frac{dV}{dt} + \left( l^{(1)}\Lambda \right) \left( \left( \nabla \lambda ^{(1)}\right) V_{x} + \lambda ^{(1)}_{x}\right) \nonumber \\&\quad -\left( \nabla \left( l^{(1)}B\right) \right) \Lambda =0, \end{aligned}$$
(19)

where \(\Lambda \), which denotes the jump in \(U_{x}\) across the \(C^{1}\) discontinuity, is collinear to the right eigenvector \(d^{(1)}\), that is, \(\Lambda = {\tilde{\pi }}(t)d^{(1)}\) with \({\tilde{\pi }}(t)\) as the amplitude of the \(C^{1}\) wave. Using (16), (17), (18), and (15) in (19), we obtain the following transport equation for the wave amplitude:

$$\begin{aligned} \frac{d\pi }{d \tau }+ \Theta _{1}(\tau ) {\pi ^{2}}+ \Theta _{2} (\tau , x) \pi =0,\,\frac{dx}{d\tau } = \frac{x}{\tau } + f_{1}(\tau ), \end{aligned}$$
(20)

where \(\pi , \tau , \Theta _{1}\) and \(\Theta _{2}\) are dimensionless quantities defined by \(\pi = \tilde{\pi } t_{0},\,\tau = t/t_{0},\)

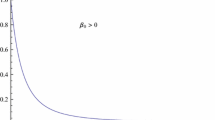
$$\begin{aligned} \Theta _{1}(\tau )&= \frac{ \gamma (\gamma +1)\hat{p}\tau ^{8} (\tau ^{2} -b \hat{\rho })^{-(\gamma +1)} + {6\hat{h}(\tau ^{2} -b \hat{\rho })}}{2\gamma \hat{p} \tau ^{6} (\tau ^{2} -b \hat{\rho })^{-\gamma } + 4\hat{h} \tau ^{2} - 2b\hat{p}\hat{h} },\,\\ \Theta _{2}(\tau , x)&= -\frac{1}{2x} f_{1}(\tau ) + \frac{f_{2}(\tau )}{f_{3}(\tau )},\\ f_{1}(\tau )&= \sqrt{\frac{\gamma \hat{p}\tau ^{6} \left( \tau ^{2} -b \hat{\rho }\right) ^{-(\gamma +1)}+ 2\hat{h}}{\hat{\rho }\tau ^{2}}},\\ f_{2}(\tau )&= 6 \hat{h}- \gamma \hat{p} \tau ^{8} \left( \tau ^{2} -b \hat{\rho }\right) ^{- (\gamma +2)} \left( 2\gamma -7-\frac{2b\hat{\rho }}{\tau ^{2}}\right) ,\\ f_{3}(\tau )&= \tau \left( 2\hat{h}+ \gamma \hat{p} \tau ^{6} \left( \tau ^{2} -b\hat{\rho }\right) ^{-(\gamma +1)}\right) . \end{aligned}$$

The transport equations (20) has a solution of the form \(\pi (\tau ) = \pi _{0} K_{1}(\tau )/ (1+ \pi _{0} K_{2}(\tau ) ),\) where \( K_{1}(\tau ) = \exp (-\int _{1}^{\tau }\Theta _{2}(x(s), s)ds )\) and \(K_{2}(\tau ) = \int _{1}^{\tau }\Theta _{1}(s^{'})ds^{'} ( \int _{1}^{s^{'}} -\Theta _{2}(x(s), s)ds )ds^{'} .\) Both the integrals are finite and continuous in \([1, \infty )\) for the functions \(\Theta _{1} \) and \(\Theta _{2}\). It then follows that an expansion wave (that is, \(\pi _{0} > 0\)) decays and dies out eventually; the corresponding situation is illustrated by the curves in Fig. 1(a) and Fig 2(a), which shows that the real gas and the magnetic field effects serve to enhance the decaying rate. However, a compression wave (that is, \(\pi _{0} < 0\)) culminates into a shock in a finite time only when the magnitude of the initial amplitude is greater than a critical value \(\pi _{c}\). The corresponding situation is illustrated by curves in the Fig.  1(b), Fig 1(c), Fig. 2(b) and Fig. 2(c). It is shown that the real gas effects serves to hasten the onset of the shock that however the magnetic field resists the shock formation in the sense that the effect of magnetic field is to enhance the shock formation time (see, Fig. 1(c) and  2(c)). The computed results are in agreement with the analytical results (see, Courant and Friedrichs [23]).

Conclusion

Exact particular solution to the equations of non-ideal magnetogasdynamics are obtained using the invariance of the system under one parameter Lie group of continuous transformations with commuting generators. The solution obtained is used to study the evolutionary behaviour of the \(C^{1}\) discontinuity waves. The effect of van-der Waals excluded volume and the magnetic field strength on the behaviour of these discontinuity waves is studied in detail and some interesting out comes are obtained such as, an increase in the van der Waals excluded volume serves to hasten the onset of a shock wave while the magnetic field strength has an opposite effect in the shock formation i.e., an increase in the magnetic field strength delays the shock formation time. However, when \((\pi _{0}>0)\) and \(-\pi _{c} \le \pi _{0}<0\) in both the cases the wave decays eventually and an increase in \(b\) and \(\hat{h}\) enhances the decaying of the weak discontinuities. To the best of my knowledge such a study in the case of non-ideal magnetogasdynamics has not be done previously.