Entrance Region Flow in Concentric Annuli with Rotating Inner Wall for Herschel–Bulkley Fluids

Abstract

A finite difference analysis of the entrance region flow of Herschel–Bulkley fluids in concentric annuli with rotating inner wall has been carried out. The analysis is made for simultaneously developing hydrodynamic boundary layer in concentric annuli with the inner cylinder assumed to be rotating with a constant angular velocity and the outer cylinder being stationary. A finite difference analysis is used to obtain the velocity distributions and pressure variations along the radial direction. With the Prandtl boundary layer assumptions, the continuity and momentum equations are solved iteratively using a finite difference method. Computational results are obtained for various non-Newtonian flow parameters and geometrical considerations. A significant asymmetry is found in the entrance region which is gradually reduced as the flow develops. For smaller values of aspect ratio and higher values of Herschel–Bulkley number the flow is found to stabilize more gradually. Comparison of the present results with the results available in literature for various particular cases has been done and found to be in agreement.

Introduction

The problem of entrance region flow in concentric annuli with rotating inner wall for non-Newtonian fluids is of practical importance in engineering applications such as the design of cooling systems for electric machines, compact rotary heat exchangers and combustion chambers, axial-flow turbo machinery and polymer processing industries. In the nuclear reactor field, laminar flow conditions occur when the coolant flow rates are reduced during periods of low power operation. Many important industrial fluids are non-Newtonian in their flow characteristics and are referred to as rheological fluids. These include blood, various suspensions such as coalwater or coal-oil slurries, glues, inks, foods, polymer solutions, paints and many others. The fluid considered here is the Herschel–Bulkley model, which is the most frequently used one in non-Newtonian fluid flow problems.

The problem of entrance region flow of non-Newtonian fluids in an annular cylinders has been studied by various authors. Mishra and Kumar [1] studied the flow of the Bingham plastic in the concentric annulus and obtained the results for boundary layer thickness, centre core velocity, pressure drop. Batra and Das [2] developed the stress–strain relation for the Casson fluid in the annular space between two coaxial rotating cylinders where the inner cylinder is at rest and outer cylinder rotating. Maia and Gasparetto [3] applied finite difference method for the Power-law fluid in the annuli and found difference in the entrance geometries. Sayed-Ahmed and Hazem [4] applied finite difference method to study the laminar flow of a power-law fluid in the concentric annulus.

The Herschel–Bulkley model represents the empirical combination of Bingham and power-law fluids. The constitutive equation for these fluids is given by [5] as

$$\begin{aligned} \tau =\tau _{0}+k \left( \frac{\partial u}{\partial r}\right) ^{n} \end{aligned}$$

(1)

where $\tau$ is the shear stress, $\tau _{0}$ is the yield stress, k is the coefficient of fluidity, n is the flow index of the model.

Manglik and Fang [6] numerically investigated the flow of non-Newtonian fluids through annuli. The problem of laminar heat transfer convection for Herschel–Bulkley within concentric annular ducts has been studied by Vaina et al. [7] with the help of integral transform method considering the plug flow region. Round and Yu [8] analyzed the developing flows of Herschel–Bulkley fluids through concentric annuli. Soares et al. [9] has taken up the problem of heat transfer in a fully developed flow of Herschel–Bulkley materials through annular spaces, with insulated outer wall and uniform heat flux at inner wall. Khaled et al. [10] analyzed the laminar flow of a Herschel–Bulkley fluid over an axisymmetric sudden expansion. Nouar et al. [11] reported the results of numerical analysis of the thermal convection for Herschel–Bulkley fluids. Numerical modeling of helical flow of viscoplastic fluid in eccentric annuli has been done by Hussain and Sharif [12]. The study of heat transfer to viscoplastic materials flowing axially through concentric annuli has been investigated by Soares et al. [13]. Kandasamy et al. [14] investigated the entrance region flow of heat transfer in concentric annuli for Herschel–Bulkley fluids and presents the velocity distributions, temperature and pressure in the entrance region. Poole and Chhabra [15] reported the results of a systematic numerical investigation of developing laminar pipe flow of yield stress fluids. Recently, Pai and Kandasamy [16] have investigated the entrance region flow of Herschel–Bulkley fluid in an annular cylinder without making prior assumptions on the form of velocity profile within the boundary layer region.

Further, entropy generation in Non-Newtonian fluids due to heat and mass transfer in the entrance region of ducts has been investigated by Galanis and Rashidi [17]. Rashidi et al. [18] analyzed the pulsatile flow through annular space bounded by outer porous cylinder and an inner cylinder of permeable material. Moreover, Rashidi et al. [19] studied the investigation of heat transfer in a porous annulus with pulsating pressure gradient by homotopy analysis method.

In the present work, the problem of entrance region flow of Herschel–Bulkley fluid in concentric annuli with rotating inner wall has been investigated. The analysis has been carried out under the assumption that the inner cylinder is rotating and the outer cylinder is at rest. With the prandtl boundary layer assumptions, the equations of conservation of mass and momentum are discretized and solved using linearized implicit finite difference technique. The system of non-linear algebraic equations thus obtained has been solved by the Newton-Raphson iterative method for simultaneous non-linear equations. The development of axial velocity profile, radial velocity profile, tangential velocity profile and pressure drop in the entrance region have been determined for different values of non-Newtonian flow characteristics and geometrical parameters. The effects of these on the velocity profiles and pressure drop have been discussed.

Formulation of the Problem

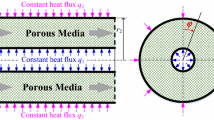
The geometry of the problem is shown in Fig. 1. The Herschel–Bulkley fluid enters the horizontal concentric annuli with inner and outer radii $R_{1}$ and $R_{2}$, respectively, from a large chamber with a uniform flat velocity profile $u_{0}$ along the axial direction z and with an initial pressure $p_{0}$. The inner cylinder rotates with an angular velocity $\omega$ and the outer cylinder is at rest. The flow is steady, laminar, incompressible, axisymmetric with constant physical properties and the absence of body forces. We consider a cylindrical polar coordinate system with the origin at the inlet section on the central axis of the annulus, the z-axis along the axial direction and the radial direction r perpendicular to the z-axis.

Fig. 1

Geometry of the problem

Under the above assumptions and with the usual Prandtl boundary layer assumptions [20], the governing equations in polar coordinate system (r, $\theta$, z) for a Herschel–Bulkley fluid in the entrance region are:

$$\begin{aligned}&\hbox {Continuity equation: }\ \frac{\partial (rv)}{\partial r}+ \frac{\partial (ru)}{\partial z}=0\end{aligned}$$

(2)

$$\begin{aligned}&r-\hbox {momentum equation: }\ \frac{w^{2}}{r}=\frac{1}{\rho }\frac{\partial p}{\partial r} \end{aligned}$$

(3)

$$\begin{aligned}&\theta -\hbox {momentum equation: }\ v \frac{\partial w}{\partial r}+u\frac{\partial w}{\partial z}+\frac{vw}{r}=\frac{1}{\rho r^{2}}\frac{\partial }{\partial r} \left( r^{2} \left( \tau _{0}+k \left[ r \frac{\partial }{\partial r}\left( \frac{w}{r}\right) \right] ^{n}\right) \right) \end{aligned}$$

(4)

$$\begin{aligned}&z-\hbox {momentum equation: }\ v \frac{\partial u}{\partial r}+u\frac{\partial u}{\partial z}=-\frac{1}{\rho }\frac{\partial p}{\partial z}+ \frac{1}{\rho r}\frac{\partial }{\partial r}\left( r\left[ \tau _{0}+k \left( \frac{\partial u}{\partial r}\right) ^{n}\right] \right) \end{aligned}$$

(5)

where u, v, w are the velocity components in z, r, $\theta$ directions respectively, $\rho$ is the density of the fluid and p is the pressure.

The boundary conditions of the problem are given by

$$\begin{aligned} \text {for }z&\ge 0 \text { and }r=R_{1}, v=u=0 \text { and } w=\omega R_{1} \nonumber \\ \text {for } z&\ge 0 \text { and } r=R_{2}, v=u=w=0 \nonumber \\ \text {for } z&= 0 \text { and } R_{1}<r<R_{2}, u=u_{0} \nonumber \\ \text {at } z&= 0, p=p_{0} \end{aligned}$$

(6)

Using the boundary conditions (6), the continuity equation (2) can be expressed in the following integral form:

$$\begin{aligned} \int ^{R_{1}}_{R_{2}}2 \pi rudr=\pi (R_{2}^{2}-R_{1}^{2})u_{0} \end{aligned}$$

(7)

Introducing the following dimensionless variables and parameters,

$$\begin{aligned}&R=\frac{r}{R_{2}}, U=\frac{u}{u_{0}}, V=\frac{\rho vR_{2}}{\mu _{r}}, W=\frac{w}{\omega R_{1}}, N=\frac{R_{1}}{R_{2}}, P=\frac{p-p_{0}}{\rho u_{0}^{2}}, Z=\frac{2z(1-N)}{R_{2} Re}\\&Y_{h}=\frac{\tau _{0}}{k}\left( \frac{R_{2}}{u_{0}}\right) ^{n}, T_{a}=\frac{2\omega ^{2}\rho ^{2}R_{1}^{2}(R_{2}-R_{1})^{3}}{\mu _{r}^{2}(R_{1}+R_{2}) } \,where\, \mu _{r}=k\left( \frac{\omega R_{1}}{R_{2}}\right) ^{n},\\&Re=\frac{2\rho (R_{2}-R_{1})u_{0}}{\mu _{r}} \end{aligned}$$

Here $Y_{h}$ is the Hershel–Bulkley number, $Re$ Reynolds number, $T_{a}$ Taylors number, $\mu _{r}$ is know as reference viscosity and N is known as aspect ratio of the annulus.

Equations (2)–(5) and (7) in the dimensionless form are given by

$$\begin{aligned}&\frac{\partial V}{\partial R}+\frac{V}{R}+\frac{\partial U}{\partial Z}=0\end{aligned}$$

(8)

$$\begin{aligned}&\frac{W^{2}}{R}=\frac{Re^{2}(1-N)}{2(1+N)T_{a}}\frac{\partial P}{\partial R}\end{aligned}$$

(9)

$$\begin{aligned}&V \frac{\partial W}{\partial R}+U\frac{\partial W}{\partial Z}+\frac{VW}{R}=\frac{2}{R}\left( \frac{\partial W}{\partial R}-\frac{W}{R}\right) ^{n}+n\left( \frac{\partial W}{\partial R}-\frac{W}{R}\right) ^{n-1} \nonumber \\&\quad \left( \frac{\partial ^{2} W}{\partial R^{2}}-\frac{1}{R}\frac{\partial W}{\partial R}+\frac{W}{R^{2}}\right) +\frac{2Y_{h}}{R}\end{aligned}$$

(10)

$$\begin{aligned}&V \frac{\partial U}{\partial R}+U\frac{\partial U}{\partial Z}=-\frac{\partial P}{\partial Z}+\frac{1}{R}\left( \frac{\partial U}{\partial R}\right) ^{n}+ n\left( \frac{\partial U}{\partial R}\right) ^{n-1}\frac{\partial ^{2} U}{\partial R^{2}}+\frac{Y_{h}}{R} \end{aligned}$$

(11)

and

$$\begin{aligned}&2\int _N^{1}RUdR=(1-N^{2}) \end{aligned}$$

(12)

The boundary conditions (6) in the dimensionless form are:

$$\begin{aligned} \text { for } Z&\ge 0 \text { and } R=N, V=U=0 \text { and }W=1 \nonumber \\ \text { for } Z&\ge 0 \text { and } R=1, V=U=W=0 \nonumber \\ \text { for } Z&= 0 \text { and } N<R<1, U=1 \nonumber \\ \text { at } Z&= 0, P=0 \end{aligned}$$

(13)

Numerical Solution

The numerical analysis and the method of solution can be considered as an indirect extension of the work of [21]. Considering the mesh network of Fig. 2, the following difference representations are made.

Fig. 2

Grid formation for finite-difference representations

Here $\Delta R$ and $\Delta Z$ represents the grid size along the radial and axial directions respectively.

$$\begin{aligned}&\displaystyle V_{i+1,j+1}=V_{i,j+1}\left( \frac{N+i\Delta R}{N+(i+1)\Delta R}\right) -\frac{\Delta R}{4\Delta Z}\left( \frac{2N+(2i+1)\Delta R}{N+(i+1)\Delta R}\right) x\nonumber \\&\displaystyle \left( U_{i+1,j+1}+U_{i,j+1}-U_{i+1,j}-U_{i,j}\right) \end{aligned}$$

(14)

$$\begin{aligned}&\displaystyle \frac{W_{i,j+1}^{2}}{N+i\Delta R}=\frac{(1-N)Re^{2}}{2T_{a}(1+N)}\frac{P_{i,j+1}-P_{i-1,j+1}}{\Delta R} \end{aligned}$$

(15)

$$\begin{aligned}&V{i,j}\left[ \frac{W_{i+1,j+1}+W_{i+1,j}-W_{i-1,j}-W_{i-1,j+1}}{4\Delta R}\right] +U{i,j}\left[ \frac{W_{i,j+1}-W_{i,j}}{\Delta Z}\right] \nonumber \\&\quad +\frac{V_{i,j}W_{i,j}}{N+i\Delta R}=\frac{2}{N+i\Delta R}\left[ \frac{W_{i+1,j+1}+W_{i+1,j}-W_{i-1,j}-W_{i-1,j+1}}{4\Delta R}- \frac{W_{i,j}}{N+i\Delta R}\right] ^{n} \nonumber \\&\quad +\,n \left[ \frac{W_{i+1,j+1}+W_{i+1,j}-W_{i-1,j}-W_{i-1,j+1}}{4\Delta R}-\frac{W_{i,j}}{N+i\Delta R} \right] ^{n-1} \nonumber \\&\quad *\,\left( \frac{W_{i+1,j+1}+W_{i+1,j}-2W_{i,j+1}-2W_{i,j}+W_{i-1,j}+W_{i-1,j+1}}{2(\Delta R)^{2}}\right. \nonumber \\&\quad \left. -\frac{W_{i+1,j+1}+W_{i+1,j}-W_{i-1,j}-W_{i-1,j+1}}{(N+i\Delta R)4\Delta R} +\frac{W_{i,j}}{(N+i\Delta R)^{2}}\right) +\frac{2Y_{h}}{N+i\Delta R}\end{aligned}$$

(16)

$$\begin{aligned}&P_{i,j+1}+U_{i-1,j+1}\left[ -\frac{\Delta Z}{2\Delta R}V_{i,j}-\frac{n\Delta Z}{2^{n-1}(\Delta R)^{n+1}}(U_{i+1,j+1}-U_{i-1,j+1})^{n-1}\right] \nonumber \\&\quad +\,U_{i,j+1}\left[ U_{i,j}+\frac{n\Delta Z}{2^{n-2}(\Delta R)^{n+1}}(U_{i+1,j+1}-U_{i-1,j+1})^{n-1}\right] \nonumber \\&\quad +\,U_{i+1,j+1}\left[ \frac{\Delta Z}{2\Delta R}V_{i,j}-\frac{n\Delta Z}{2^{n-1}(\Delta R)^{n+1}}(U_{i+1,j+1}-U_{i-1,j+1})^{n-1}\right] \nonumber \\&\quad -\frac{\Delta Z}{N+i\Delta R}\left( \frac{U_{i+1,j+1}-U_{i-1,j+1}}{2 \Delta R}\right) ^{n}=P_{i,j}+U^{2}_{i,j}+\frac{Y_{h}(\Delta Z)}{N+i\Delta R} \end{aligned}$$

(17)

where i $=$ 0 at R $=$ N and i $=$ m at R $=$ 1.

The application of trapezoidal rule to equation (12) gives

$$\begin{aligned}&\frac{\Delta R}{2}(NU_{0,j}+U_{m,j})+\Delta R\sum _{i=1}^{m-1}U_{i,j}(N+i\Delta R)=\left( \frac{1-N^{2}}{2}\right) \end{aligned}$$

The boundary condition (13) gives $U_{0,j}=U_{m,j}=0$ and the above equation reduces to

$$\begin{aligned}&\Delta R\sum _{i=1}^{m-1}U_{i,j}(N+i\Delta R)=\left( \frac{1-N^{2}}{2}\right) \end{aligned}$$

(18)

The set of difference Eqs.(14)–(18) have been solved by the iterative procedure. Starting at the j $=$ 0 column (annulus entrance cross section) and applying Eq.(16) for $1\le i\le m-1$, we get a system of non-linear algebraic equations. This system has been solved by using Newton-Raphson method to obtain the values of the velocity component W at the second column j $=$ 1. Then applying Eqs. (15) and (17) for $1\le i\le m-1$ and Eq.(18), we get a system of non-linear equations. Again solving this system by Newton-Raphson method, we obtain the values of the velocity component U and the pressure P at the second column j $=$ 1. Finally, the values of the velocity component V at the second column j $=$ 1 are obtained from Eq.(14) by Gauss-Jordan method using the known values of U. Repeating this procedure, we can advance, column by column, along the axial direction of the annulus until the flow becomes axially and tangentially fully developed.

Results and Discussion

Numerical calculations have been performed for all admissible values of Herschel–Bulkley number $Y_{h}$, flow index n and aspect ratio N. The ratio of Reynolds number to Taylor number $Rt=Re^{2}/T_{a}=20 ,10, \Delta Z=0.02, 0.03$ and $\Delta R=0.1, 0.05$ have been fixed for N $=$ 0.3 and 0.8 respectively. The velocity profiles and pressure distribution along radial direction have been plotted for N $=$ 0.3, 0.8; n $=$ 0.5, 1, 1.5 and $Y_{h}$ $=$ 0, 10, 20, 30.

Figures 3–8 show the development of the tangential velocity profile component W for N $=$ 0.3 and 0.8, for values of n as 0.5, 1, and 1.5 and for different values of Herschel–Bulkley numbers $Y_{h}$. The values of tangential velocity decrease from the inner wall to outer wall of the annulus. It is found that with the increase of aspect ratio N, the tangential velocity profile increases. That is, the tangential velocity is more when the gap of the annuli is small. Also, it is observed that the value of W increases with the increasing value of flow index n. Further, it is found that with the increase of Herschel–Bulkley number, the tangential velocity profile increases. This means, the tangential velocity tends to increase for the thick viscous fluids when the inner cylinder is rotating. The effect of the parameter Rt is negligible for the tangential velocity.

Fig. 3

Tangential Velocitys for N $=$ 0.3, n $=$ 0.5, $\Delta R = 0.1,\Delta Z = 0.02$ and Rt $=$ 20

Fig. 4

Tangential Velocitys for N $=$ 0.3, n $=$ 1, $\Delta R=0.1, \Delta Z=0.02$ and Rt $=$ 20

Fig. 5

Tangential Velocitys for N $=$ 0.3, n $=$ 1.5, $\Delta R=0.1, \Delta Z=0.02$ and Rt $=$ 20

Fig. 6

Tangential Velocitys for N $=$ 0.8, n $=$ 0.5, $\Delta R=0.05, \Delta Z=0.03$ and Rt $=$ 10

Fig. 7

Tangential Velocitys for N $=$ 0.8, n $=$ 1, $\Delta R=0.05, \Delta Z=0.03$ and Rt $=$ 10

Fig. 8

Tangential Velocitys for N $=$ 0.8, n $=$ 1.5, $\Delta R=0.05, \Delta Z=0.03$ and Rt $=$ 10

Figures 9–14 show the development of the axial velocity profile component U for N $=$ 0.3 and 0.8 and for the value of n chosen as 0.5, 1, and 1.5, for different values of the Herschel–Bulkley numbers $Y_{h}$. It is found that increasing the flow index n, the axial velocity component U increases at all values of Herschel–Bulkley numbers $Y_{h}$ and the velocity profile develops faster as n increases. It indicates that the axial velocity is more for shear thinning fluids $(n>1)$ and for shear thickening fluids $(n<1)$ the axial velocity component is less. Also, it is observed that the velocity profile takes the parabolic form as n tends to 1 with Herschel–Bulkley number $Y_{h}$ being zero (Newtonian fluid).

Fig. 9

Axial Velocity Profiles for N $=$ 0.3, n $=$ 0.5, $\Delta R=0.1, \Delta Z=0.02$ and Rt $=$ 20

Fig. 10

Axial Velocity Profiles for N $=$ 0.3, n $=$ 1, $\Delta R=0.1, \Delta Z=0.02$ and Rt $=$ 20

Fig. 11

Axial Velocity Profiles for N $=$ 0.3, n $=$ 1.5, $\Delta R=0.1, \Delta Z=0.02$ and Rt $=$ 20

Fig. 12

Axial Velocity Profiles for N $=$ 0.8, n $=$ 0.5, $\Delta R=0.05, \Delta Z=0.03$ and Rt $=$ 10

Fig. 13

Axial Velocity Profiles for N $=$ 0.8, n $=$ 1, $\Delta R=0.05, \Delta Z=0.03$ and Rt $=$ 10

Fig. 14

Axial Velocity Profiles for N $=$ 0.8, n $=$ 1.5, $\Delta R=0.05, \Delta Z=0.03$ and Rt $=$ 10

The radial velocity profile component V for N $=$ 0.3 and 0.8 when n $=$ 1, at different sections of the axial direction Z are shown in Figs. 15–16. The values of radial velocity are negative in the region near the outer wall since it is in the opposite direction to the radial coordinate R and it has positive values near the inner wall because it has the same direction of the radial coordinate. This phenomena is due to the rotation of the inner cylinder of the annuli. It is noted here that the radial velocity components purely depends on the axial coordinate.

Fig. 15

Radial Velocity Profiles for N $=$ 0.3, $\Delta R=0.1$, n $=$ 1 and Rt $=$ 20

Fig. 16

Radial Velocity Profiles for N $=$ 0.8, $\Delta R=0.05$, n $=$ 1 and Rt $=$ 10

Figures 17–22 show the distribution of the pressure P along the radial coordinate R for N $=$ 0.3 and 0.8 and the value of n $=$ 0.5, 1, and 1.5. It is found that the value of P increases from a minimum at the inner wall to a maximum at the outer wall for all values of the parameter n. Further, it is realized that increase in the value of Herschel–Bulkley numbers $Y_{h}$ , reduces the pressure drop values P. This is because of the fact that the pressure will tend to be lower for thick viscous fluids. Moreover, it is observed that the pressure does not vary so much with respect to the radial coordinate in the region near the outer wall.

The present results are compared with available results in literature for various particular cases and are found to be in agreement. When the Herschel–Bulkley number $Y_{h} = 0$, our results match with the results corresponded to power-law fluids given by [4]. In the case of non-rotating cylinders, the results of axial velocity components in our analysis are matching with that of the results of [14].

Fig. 17

Pressure Drop for N $=$ 0.3, n $=$ 0.5, $\Delta R=0.1, \Delta Z=0.02$ and Rt $=$ 20

Fig. 18

Pressure Drop for N $=$ 0.3, n $=$ 1, $\Delta R=0.1, \Delta Z=0.02$ and Rt $=$ 20

Fig. 19

Pressure Drop for N $=$ 0.3, n $=$ 1.5, $\Delta R=0.1, \Delta Z=0.02$ and Rt $=$ 20

Fig. 20

Pressure Drop for N $=$ 0.8, n $=$ 0.5, $\Delta R=0.05, \Delta Z=0.03$ and Rt $=$ 10

Fig. 21

Pressure Drop for N $=$ 0.8, n $=$ 1, $\Delta R=0.05, \Delta Z=0.03$ and Rt $=$ 10

Fig. 22

Pressure Drop for N $=$ 0.8, n $=$ 1.5, $\Delta R=0.05, \Delta Z=0.03$ and Rt $=$ 10

Conclusions

Numerical results for the entrance region flow in concentric annuli with rotating inner wall for Herschel–Bulkley fluids were presented. The effects of the parameters n, N and $Y_{h}$ on the pressure drop, the velocity profiles are studied. Numerical calculations have been performed for all admissible values of Herschel–Bulkley number $Y_{h}$, flow index n and aspect ratio N. The velocity distribution and pressure distribution along radial direction R have been presented geometrically. From this study, the following can be concluded.

• 1. Tangential velocity decrease from the inner wall to outer wall of the annulus and the tangential velocity is high for thick viscous fluids.

• 2. Increasing the flow index n, the axial velocity component U increases at all values of Herschel–Bulkley numbers $Y_{h}$ and the velocity profile develops faster as n increases.

• 3. Radial velocity is found to be dependent only on the axial coordinate.

• 4. Pressure increases from a minimum at the inner wall to a maximum at the outer wall for all values of the flow index n and pressure does not vary so much with respect to the radial coordinate in the region near the outer wall.