1 Introduction

Manufacturing is an important contributor to the economies of countries around the world, both developed and developing (Szirmai, 2011). Although there has been a recent debate about whether the industrial sector is still an important component of economic growth, the facts show that the dominance of the trade or service sector has shifted in many countries. The debate over whether manufacturing should continue to be the primary focus of industrial policy in developing countries is currently a matter of significant contention. Indeed, the lack of agreement reflects our weak understanding of the importance of the manufacturing sector, particularly for middle-income economies. In contrast to the predictions that arise from a particular theory, the well-documented patterns of structural change in different industries are generally accepted as empirical reality. Thus, it remains controversial whether a developing country today must be fully industrialized to become prosperous. Contemporary literature emphasizing the sectoral uniqueness of economic development also differs markedly from popular ideas that view growth as sector-neutral. Although several papers have attempted to highlight the importance of manufacturing in economic development (Su & Yao, 2016), Haraguchi et al. (2017) argue that manufacturing may continue to play a critical role in developing country economies. In this case, we could argue that the premature deindustrialization is not due to changes in the development characteristics of manufacturing that may have reduced its contribution to economic development, but rather to the inability of some countries to develop their manufacturing sector relative to others.

In the trajectory towards advancement, developing nations require a robust industrial sector to catalyse fostering income growth. The efficacy of the industrial sector constitutes a pivotal determinant of a nation's economic advancement. Notably, the average production growth in Indonesia's industrial sector between 2007 and 2019 stood at 4.02 percent, a figure that falls short when compared to the performance of low-income countries, which attained a growth rate of 5.28 percent, and middle-income countries, which achieved a more substantial rate of 6.09 percent (Global Economic Monitor, 2023). Furthermore, at the regional level, Indonesia, despite being the largest economy in Southeast Asia, is placed fifth in industrial performance according to the Competitive Industrial Performance (CIP) Index, after Singapore, Malaysia, Thailand, and Vietnam (UNIDO, 2020). On the other hand, Indonesia, as one of the fourth largest countries in terms of population, is still very dependent on the industrial sector to absorb labor. According to Badan Pusat Statistics (BPS), by 2022, more than 14 percent of the labor force in the manufacturing sector, or about 19,171 million workers. Figure 1 illustrates the shifts in the composition of the manufacturing workforce in Indonesia as compared to various key economic sectors. The manufacturing sector holds the third position among the sectors with the highest employment rates, following the agricultural and trade sectors. The trends indicate an economic transition from the traditional agriculture sector to the modern sector, as evidenced by the growing proportion of the workforce engaged in non-agricultural activities.

Fig. 1
figure 1

Source: Badan Pusat Statistik, Author’s Calculation

Annual trend of employment distribution among key economic sectors.

Full size image

BPS observed that an economic transition period commenced in the early 1990s, with the industrial sector emerging as the leader and the primary driving force of the national economy. Figure 2 illustrates the prevailing dominance of the manufacturing sector, which is projected to continue contributing approximately 18 percent to Indonesia's GDP until the year 2022. This is, of course, an important testament to the Indonesian economy that the industrial sector is still one of the driving forces of the economy.

Fig. 2
figure 2

Source: Badan Pusat Statistik, Author’s Calculation

Quarterly trend of GDP composition among key economic sectors.

Full size image

The growth of the industrial sector is one of the hopes for Indonesian workers to get decent jobs and income, so manufacturing companies need a good environment to develop in Indonesia. Industrial enterprises in Indonesia are engaged in various manufacturing sectors, which consist of micro, small, medium, and large enterprises. Micro industry with 1–4 employees, small industry with 5–19 employees, medium industry with 20–99 employees, and large industry with 100 or more employees. BPS noted that in 2022, the number of micro and small enterprises was 4.2 million enterprises, while medium and large industries were more than 30 thousand enterprises, and the number of these enterprises fluctuated quite a bit each year, as shown in Fig. 3 in panel (a) for medium and large enterprises and micro and small enterprises in panel (b). However, this trend in numbers does not reflect the problems in the industry market, i.e., entry and exit or survival of the industry. Of course, high turnover can be a problem because a company is expected to perform well not only in terms of numbers but also in terms of assets, profits, and employment. Therefore, studies on this topic are important.

Fig. 3
figure 3

Source: Badan Pusat Statistik, Author’s Calculation. Panel (a) is the trend of medium and large manufacturing firms, and Panel (b) shows the micro and small-size manufacturing firms. There is no data record in 2016 for micro and small firms

Trend of manufacturing enterprises number.

Full size image

The issue of industrial sector growth is of great importance to Indonesia, and one aspect that has received little attention from academia is the survival of firms in Indonesia. The availability of longitudinal data for firms in the industrial sector is not widespread, especially for a large number of small and micro firms; however, a survey of large and medium industries conducted by the government covers all large and medium firms, so it is possible to conduct a survival analysis of firms with large and medium sizes.

The ability of firms to enter and survive in the market depends on several factors, such as market structure, factor productivity, e.g., human capital, and financial access. The entry and survival patterns of firms, the number and size of new firms entering the market, the duration of their survival, and their market power over time are key determinants for understanding the competitive dynamics in the market. New entrants bring new products to the market and expand them into existing markets, putting competitive pressure on incumbent firms (Esteve-Pérez and Castillejo, 2006). The gradual changes of firms in the market, from creation to demise, can have a significant impact on the economy. Enterprise creation could contribute to the creation of more jobs, the development of new products and technologies, the transformation of market structures, the development of the supply chain, and the reduction of social exclusion. However, the failure of productive enterprises can lead to a waste of social, financial, and material resources.

This study investigates the determinants, especially efficiency, market competition, and other key determinants of manufacturing firm survival in Indonesia. Not only looking at the factors that influence manufacturing companies in surviving operations in Indonesia but also looking at what causes them to enter and leave the market. This study is concerned with performance factors, especially technical efficiency, market structure, macroeconomic conditions, and company characteristics. We employ firm-level panel data from Indonesia’s large and medium enterprises survey from 1995 to 2015. The contributions of this study are twofold. Firstly, the research employs the Ackerberg–Caves–Frazer (ACF) method to compute technical efficiency, mitigating endogeneity issues in estimating the production function as the foundation for efficiency score calculation. To our knowledge, this study represents the inaugural use of the ACF technique in investigating the association between efficiency and firm survival. Previous studies relied on diverse methodologies, including the utilization of innovation proxies (Buddelmeyer et al., 2006), Data Envelopment Analysis (DEA) by Dimara et al. (2008), certain financial health indicators (Manello & Calabrese, 2017), and conventional stochastic frontier approximation (Tsionas & Papadogonas, 2006). Secondly, beyond examining the impact of efficiency on firm survival, the study explores its effects on both firm exit and entry. This exploration aims to ascertain the consistency of estimation outcomes at both the firm and aggregate levels (Two-digit ISIC), as well as the consistency of the influence of efficiency on firm survival, exit, and entry.

The estimation was carried out in two stages, namely calculating efficiency using a stochastic frontier analysis model based on the translog production function, both time-invariant and time-varying. In addition, the efficiency score calculation is also based on the ACF model estimation to overcome the endogeneity problem in the estimation of the production function. The second stage is estimating the influence of technical efficiency and other control factors on firm survival using the Cox proportional hazard model, and this process is carried out in an analysis at the individual company level. Cox (1972, 1975) uses the hazard function to investigate the relationship between the likelihood of an event occurring and several regressors. The next estimation strategy is to estimate, in a panel structure with cross-sectional entities, the number of companies entering, exiting, and surviving per 2-digit ISIC sector. The analysis of regressors is developed without specifying a hazard function under the condition of "hazard proportionality," which states that the proportion of two types of hazards remains constant over time. The inter-relationship among survival ability, entering and exiting the markets, efficiency, market power, other characteristics of the firms, and macroeconomic performance is included in the area to be discussed in this study. There are not many publications about the survival of companies in Indonesia. One publication that is focused on survival in Indonesia was written by Brucal and Mathews (2021), who looked at the survival of medium and large firms after a flood disaster occurred at the district level.

The rest of the chapter is organized as follows. Section 2 summarizes existing literature related to the survival analysis of firms and their determinants with an emphasis especially those related to the determinant factors that will be analyzed in this study. Section 3 discusses the sources, structure, observations, and basic treatment performed. Besides that, analysis techniques and modeling strategies are also the main topics discussed in this section. Section 4 shows empirical results and discusses some of their interpretation and consequences. Section 5 provides concluding remarks, limitations, and recommendations for future research.

2 Literature review

There is a growing body of literature on business survival analysis, and some of it provides general factors, while others address specific issues. This section provides previous literature discussing the effect of efficiency and some key determinants of firm survival.

2.1 Efficiency and firm survival

This study focuses on the issue of the relationship between efficiency and firm survival; however, we also include control variables that adequately represent the determinants of firm survival. The relationship between efficiency and firm survival has been empirically tested in several previous studies. Jitsutthiphakorn (2021), which measures productivity by calculating total factor productivity, while Muzi et al. (2023) use labor productivity; however, Buddelmeyer et al. (2006) indirectly observed technical efficiency using two sets of innovation variables; Esteve-Pérez and Man ez-Castillejo (2006) take productivity and competition (price cost margins) into account in their firm survival study. While Tsionas and Papadogonas (2006) calculated technical efficiency as a measure of efficiency and looked at the influence of technical efficiency on firm exit, On the other hand, Manello and Calabrese (2017) used a non-parametric data envelopment analysis (DEA) approach to calculate efficiency scores. More productive firms survive in a well-performing market with fair competition, while less productive firms exit. A dynamic like this allows for the continuous reallocation of resources to their highest value. In the highly competitive business environment, existing firms are under pressure to improve their efficiency, often through innovative activity. In the fields of microeconomics and industrial organization, the connection between firm survival and productivity has been theoretically developed as a standard. Firms in standard frameworks act with the goal of profit maximization and are constrained by a budget function. Exits from the market occur when profits fall below the variable cost threshold in its most basic form.

2.2 Control variables

2.2.1 Competition and firm survival

In industrial organization literature, market competition is an essential factor in determining the company's performance in a market. The higher the level of competition, the more companies are required to be productive. A high concentration of industries may permit new entrant firms to operate on a suboptimal scale, providing some space for survival initial period after entering the markets. However, highly concentrated industries may have a higher potential for incumbent collusion and, as a result, more aggressive behavior toward new entrants. At empirical evidence, competition is measured by some indicators, e.g. number of competing firms, market share/concentration, and price cost margin. In the case of firm survival study, some papers e.g. Audretsch and Mahmood (1995), Lopez et al. (2017) employ price cost margin, whereas Audretsch (1991), and Garcia and Puente (2006) use market concentration, Kato (2009) uses industry density and size with quadratic relationship, and Jeong et al. (2016) indicate competition by number of competitors. They find that market structure increases the ability of firms to survive. The research on how competition impacts firm survival is mixed. Some studies find that competition reduces firm survival, while others find the opposite effect or no significant effect. Two studies found that competition decreases firm survival. Suarez (1995) found that firms in industries with dominant designs, indicating intense competition, had lower survival. Similarly, Utterback (1993) argued that firms founded during periods of high competition will have higher failure rates. In contrast, other studies found that competition increases firm survival. Børing (2015) found that product-innovative firms, which likely face high competition, had higher acquisition rates, indicating greater survival. Naidoo (2010) found that Chinese manufacturing SMEs with competitive advantages, developed through marketing innovation in response to competition, had greater perceived survival likelihood. Some studies found no significant effect of competition on firm survival. Januszewski (2002) found no effect of competition on productivity growth for German firms. Guadalupe (2008) found that while competition caused firms to flatten their hierarchies, it did not impact firm survival. The effect of competition also depends on firm characteristics. Naidoo (2010) and Guadalupe (2008) found that the positive impact of competition on survival was enhanced by strong corporate governance and organizational restructuring. In summary, while some studies find that competition reduces firm survival, the overall research is mixed. The effect of competition seems to depend on factors like firm and industry characteristics, governance, and the ability to restructure in response to competition.

2.2.2 Foreign, domestic investment, and ownership

The effects of foreign direct investment (FDI) also depend on a firm's experience and timing of entry. Early entrants gain higher market shares but lower survival rates, as Murray et al. (2012) show in a study of foreign firms in China. However, Shaver et al. (1997) find that firms with more experience investing in a host country and firms entering industries with a larger existing foreign presence have higher survival rates. This suggests experience and following other foreign investors can help firms overcome the disadvantages of being early movers. The type of FDI also matters. Chen et al. (2000) show that "expansionary" FDI seeking to exploit competitive advantages boosts firm growth and survival, while "defensive" FDI seeking cheap labor only boosts survival. Exporting, which often accompanies FDI, has similarly complex effects. Dzhumashev et al. (2016) find that while exporting initially increases the hazard of firm failure in the short term, in the long run, exporters benefit more from productivity gains and have lower failure rates. In summary, while foreign investment can threaten firm survival by increasing competition, it also frequently boosts survival by providing knowledge and market access. The net effect depends on a firm's experience, timing, industry conditions, and FDI motivations. With the right strategies and circumstances, FDI can ultimately strengthen rather than weaken a firm's viability. Qu and Harris (2018) show that financial assistance and the strength of political links have a greater likelihood of survival. On the other hand, Kubo and Phan (2019) show that government ownership has a nonlinear impact on company performance depending on the type of partnership. This non-linearity is also confirmed by Nguyen et al. (2022) who show that there is a threshold where increasing government ownership beyond a certain point will hurt company performance.

2.2.3 Openness

Trade openness is a means for companies to obtain better and cheaper resources or a wider market. However, problems arise for the company if it is unable to overcome the problems from the risks of international trade. This related empirical study confirms that ambiguity exists. International market activity raises the risk of volatility, which could have either positive or negative effects on the business, leaving the overall outcome unclear (Buch et al., 2009). According to Esteve-Pérez and Man̬ez-Castillejo (2006), a company's chances of surviving are decreased when it exports a lot. Wagner (2013) finds that exports will influence firm survival as long as there is two-way trade, or, in other words, the company also imports. This was added by Gibson and Graciano (2011): importing companies get two benefits at once, namely the relative price and the embodied technology of the input.

2.2.4 Capacity utilization

Several studies show the effect of capacity utilization on firm survival. Lecraw (1978) found that capacity underutilization in firms was negatively correlated with firm survival. Firms that operated at lower capacity utilization rates had lower projected profits and perceived higher risks, leading to lower survival rates. Lieberman (1989) supported this and finds that higher capacity utilization was positively associated with firm survival in chemical industries. Firms that expanded capacity in line with demand growth and had lower variability were more likely to survive. Ray (2021) took a cost-based approach, finding that firms operating at less than full capacity had higher average costs and lower survival rates. To minimize costs and ensure survival, firms needed to increase output and capacity utilization. Nikiforos (2012) argued that the desired rate of capacity utilization for cost-minimizing firms is endogenous. As returns to scale decrease with higher production, firms have an incentive to increase capacity utilization, leading to higher survival rates. In addition, Chatzoudes et al. (2022) supported this, finding financial constraints reduced short- and long-term survival, especially during economic crises. Performance drivers like capacity utilization and access to finance were key to the firm's survival.

2.2.5 Change inventory (inventory)

Basu and Wang (2011) argue that there was a negative relationship between inventory changes and firm performance. Additionally, this relationship is slightly mitigated for businesses that are typically low-carrying organizations as well as those in the wholesale and retail sectors. According to their research, there are significant mediators of the relationship between inventory fluctuations and business performance, including macroeconomic and industry-specific conditions. Bao (2004) suggests that the informativeness of change in inventory positively affects firm valuation. On the other hand, Lin et al. (2022) explore the impact of inventory productivity on venture survival and find a converse U-curve relationship. Additionally, financial constraints moderate the effect of inventory productivity on survival. Elsayed and Wahba (2016) proposethat inventory performance depends on the firm's life cycle stage, with firms in the expansion and revival stages exhibiting better inventory performance compared to firms in the inception or maturity stages.

2.2.6 Location (Java)

Choosing a production location and market is very important for the company's survival. Locations that provide infrastructure facilities and attractive market trends for companies provide advantages in production operations and the distribution of production results. This is supported by several studies. Manzato et al. (2011) found that variables such as accessibility to infrastructure supply, regional effects, demographic and economic aspects, and rent prices significantly affect firm survival rates. Shu (2018) focused on traded industries and found that regional concentrations of related industrial firms (localization) can moderate the effects of founder team industry and start-up experience on firm survival. Stearns et al. (1995) specifically argue that new businesses located in urban, suburban, or rural areas can have a significant impact on performance outcomes. Urban areas may have more competitors, but they also have a wealth of different resources. Although they may be less diverse, rural areas can help companies fill gaps in the market in the absence of competition. Bagley (2019) contends that taking into account a firm's geographic location within an industrial cluster, there may be a nonlinear relationship. He indicates a link that is inversely U-shaped. Furthermore, new enterprises benefit at extremely short distances from the cluster centroid. Any benefits from co-location are lost at intermediate distances, which in this case encompass the densest part of the cluster, possibly as a result of competition effects. As distance increases, this negative externality disappears.

2.2.7 Size

Company size and its impact on company performance or survival are theoretically ambiguous. In many industries, larger firms tend to have a survival advantage over smaller ones. This is often attributed to their greater access to resources, economies of scale, and established customer bases. Larger firms may have more diversified product lines, geographic reach, and financial stability, which can help them weather economic downturns and industry fluctuations more effectively. Small firms, while more vulnerable to economic shocks and competition, can exhibit resilience due to their agility and ability to adapt quickly. Niche markets, specialized expertise, and innovative solutions can enable small firms to carve out unique positions in the market, allowing them to survive and thrive. The papers present mixed findings on the relationship between firm size and firm survival. Palestrini (2015) explores the survival bias in the firm size distribution. Agarwal and Gort (1999) argues that the relationship between firm size and survival depends on the stage of the industry's life cycle. Some studies use some proxies for firm size such as assets by Agarwal and Audretsch, (2001), sales and assets (Dzhumashev et al., 2016), and number of employees (Bosio et al., 2020; Cefis & Marsili, 2005; Fernandez et al., 2021).

2.2.8 Macroeconomic variables

In addition to performance and market factors, macroeconomic factors must also be seen as important factors in determining whether a company should operate in a market. Macroeconomic conditions, workforce quality, and good economic policies will make companies choose to continue operating in a market. Holmes et al. (2010) identified firm survival by including macroeconomic variables such as interest rates and sectoral economic growth as drivers. Audretsch et al. (1997) also did the same thing with sectoral growth variables. Macroeconomic conditions can affect the company both from the input and output market sides. From the input side, companies that are oriented to the domestic market as their output market certainly hope for demand-side strength from the economy to absorb their production, while from the input side, such as energy prices that may represent capital utilization (Ghosal, 2003), policies, quality, and quantity of labor (Acs et al., 2007), can provide a boost to production. However, according to Bartoloni et al. (2020), complex events like recessions produce highly erratic and unstable corporate conditions. Production efficiency has a limited impact on a company's ability to survive such situations. Instead, it depends on one's aptitude for handling such complexity. They discovered that companies using talents and competencies to navigate environmental challenges more often are less likely to exit during a downturn compared to those that do not.

3 Methodology

3.1 Data

The data used in this study were collected from a survey of large and medium-scale manufacturing industries conducted by BPS. The survey is conducted annually and covers all large and medium-listed companies. This study uses a survey period from 1995 to 2015. In one census year, there were around 20,000 companies registered and surveyed. The results of the compilation of all observations amounted to 461,764. Each company has an identity code and a 5-digit ISIC (International Standard Industrial Classification) code, which indicates the global standard for categorizing productive activities. This study uses companies that existed in the last year of observation as existing companies, both those that have just entered the industry and those that have existed before. In addition to micro survey data, this research also uses macro data as an indicator of economic conditions, especially at the national level or at the location where the company operates. Both micro survey data and macro data are all from BPS, and World Development Indicators are from the World Bank. The company's data in the survey will simulate possible observations indicates in the selection of the age period that is the benchmark in the survival period. The cleaning of general survey data is carried out to see whether the responsiveness of the respondents is sufficient for some of the basic information needed for analysis. This study conducts a cleaning of company respondents who do not answer basic questions such as total cost or total energy required for production because we view that this information must be present in the production process, and we consider that responses not answered are considered unobserved.

3.2 Econometric model specification

3.2.1 Modeling of efficiency

The variable indicated is efficiency, which is calculated using stochastic frontier analysis (SFA) based on the production function to calculate the efficiency score. Refer to Coelli et al. (1998) and Tesema (2022). The production function is used to measure the technical efficiency (TE) score, where technical efficiency is estimated using the production function, and the technical efficiency score is calculated using the ratio of the predicted value of the production function to the actual production value data. The production function is estimated using the standard frontier model with a linear log form for both inputs and outputs. There are four inputs included in the model: the number of workers, total energy consumption including gasoline, diesel, gas, lubricant, coal, and electricity, fixed capital such as buildings, machinery, land, and vehicles, and raw materials. While allocative efficiency is calculated based on the estimation of the cost model function on output, input prices include energy prices, labor prices, capital prices, and raw material prices, which are calculated with the unit value of each input per unit amount of consumption and total expenditure for these inputs.

Raw material inputs that do not have an input price per unit are proxied using the producer price index. In general, the production function can be estimated with the following Eqs. (1) and (2):

$$ \ln \left( {y_{it} } \right) = {\text{exp}}(x_{it} \beta + V_{it} - U_{it} ) $$
(1)

where \(y_{it}\) represents the value of output for firm i in the t period, and \(x_{it}\) represents a (1 × K) vector with the values are functions of inputs consisting of labor, materials, energy, and capital (buildings, vehicles, machinery, lands, and other assets), and other explanatory variables for firm i in the t period, while β is a (K × 1) vector of unobserved coefficients to be measured. In addition, \(V_{it}\) is assumed to be error disturbance and distributed independently and identically and possess normal distribution with zero mean and unobserved variance, \(\sigma_v^2\), and \(U_{it}\) are non-negative, unobservable random variables connected to technical production inefficiencies, meaning that the observed output is not as high as it could be given the technology and input levels used. Based on the specifications of the stochastic production frontier model described in Eq. 1, the technical efficiency value can be formulated as in Eq. 2

$$ TE_{it} = {\text{exp}}( - U_{it} ) $$
(2)

where \(TE_{it}\) is the technical efficiency for i firm at t period. Coelli et al. (1998) argue that the stochastic frontier function has various forms, and the most common is the Cobb–Douglas form, which is from the simplest form to the most complex form, namely translog. Although the translog frees the production function from these constraints, it does so at the expense of having a form that is more challenging to handle analytically and susceptible to degrees of freedom, sufficient observation, and collinearity issues. Since the translog function is a flexible functional form. Although the Cobb–Douglas model is simple, it has limitations in terms of the elasticity of production inputs, which are constant, including the production scale of each observation entity. In addition, the elasticity of the substitution function is also 1. The basic difference between the Cobb–Douglas and translog model specifications is that the simple Cobb-Douglass model only includes production input variables without including interaction variables between variables in the estimation model as shown by Eqs. 3 and 4 as follows:

$$ lny_{it} = \alpha_0 + \mathop \sum \limits_{m = 1}^n \beta_m lnx_{it} + V_{it} - U_{it} $$
(3)
$$ lny_{it} = \alpha_0 + \mathop \sum \limits_{m = 1}^n \beta_m lnx_{it} + \frac{1}{2}\mathop \sum \limits_{m = 1}^n \beta_{mm} lnx_{it}^2 + \mathop \sum \limits_{m = 1}^n \mathop \sum \limits_{l \ne m}^n \beta_{lm} lnx_{it} + V_{it} - U_{it} $$
(4)

If we compare the two equations, it can be seen that Eq. 3 only contains the linear coefficient input variables without including derivative variables such as interactions and quadratic forms of production input variables. However, the translog production function is superior to the Cobb–Douglas function in approximating unknown production functions (Kymn & Hisnanick, 2001; Shih et al., 1977). The translog relaxes strong assumptions of the Cobb–Douglas like homotheticity, homogeneity and separability (Kymn & Hisnanick, 2001; Tzouvelekas, 2000). By not imposing these restrictions, the translog allows for variable returns to scale and non-neutral technical change (Kim, 1992; Tzouvelekas, 2000). Several studies found the translog specification preferable to the Cobb–Douglas. Tzouvelekas (2000) and Kymn and Hisnanick (2001) could not reject the translog in favor of the Cobb–Douglas. Heyer et al. (2004) also found the translog superior when accounting for factor utilization. However, Konishi and Nishiyama (2002) could not reject the translog for Japanese manufacturing. The translog’s flexibility allows it to account for complex production structures with multiple factors (Binswanger, 1974; Kymn & Hisnanick, 2001). The translog can be estimated with panel data to gain efficiency, as shown by Tzouvelekas (2000). It can also incorporate technical and allocative inefficiency, as Kumbhakar (1989) demonstrated. It can provide a superior fit to data and account for complex production structures and inefficiency. Though it faces issues with zero values, solutions have been developed to facilitate its use.

Stage 1 of the analysis method begins with estimating a stochastic frontier model based on the production function. Several approaches of estimation can be employed including standard stochastic frontier analysis models on panel data with time-invariant (TI) or time-varying decay (TVD) models based on maximum likelihood estimation technique. There is an ongoing debate in the literature on whether to use TI or TVD inefficiency models in panel data stochastic frontier analysis. Some papers argue for TI models, citing their simplicity and ability to control for unobserved heterogeneity (Greene, 2001; Paul & Shankar, 2020). However, others argue that time-varying models are more realistic, as inefficiency is unlikely to remain constant over long time periods (Colombi, 2013; Colombi et al., 2011; Peyrache & Rambaldi, 2012). Time-invariant proponents point out that their models can adequately control for unobserved heterogeneity by using random effects (Paul & Shankar, 2020), fixed effects (Greene, 2001), or latent class specifications (Greene, 2001). For example, Paul and Shankar (2020) propose a random effects model that allows for time-invariant inefficiency and unobserved heterogeneity. Through Monte Carlo simulations and an empirical example, Paul and Shankar (2020) show this model can perform well even in small samples. On the other hand, advocates of time-varying models argue that inefficiency is unlikely to remain static over time. Peyrache and Rambaldi (2012) propose a state-space model that allows for time-varying inefficiency and temporal variation in unobserved heterogeneity. Colombi (2013) proposes using the closed skew normal distribution to model time-invariant and time-varying inefficiency in panel data. The choice ultimately comes down to a trade-off between parsimony and flexibility in modeling temporal variation.

In addition, we use the Ackerberg–Caves–Frazer (ACF) method proposed by Ackerberg et al. (2015) to overcome the endogeneity problem in the estimation of the production function. Manjón and Manez (2016) argue that because the error term of the model typically contains output determinants that are observed by the firm but not by the analyst (firm's productivity or efficiency), inputs are likely to be endogenous variables if firms choose the level of inputs demanded in the production process optimally (that is, as the solution of a dynamic profit maximization problem). This indicates that estimations produced by conventional estimation techniques like ordinary least squares (OLS) are inconsistent. Additionally, more complex techniques like the fixed-effects estimator or instrumental variables within-groups estimator do not appear to be very effective (Griliches & Mairesse, 1995). The technique promoted by Levinsohn and Petrin (2003), according to Ackerberg, Caves, and Frazer (2015), may have identification problems. The method demonstrates that the labor input might not fluctuate independently of the nonparametric function that is being estimated using the low-order polynomial unless extra assumptions are made about the processes that generate the data. Moreover, Ackerberg, Caves, and Frazer (2015) suggest an estimation procedure that borrows elements from both the two-stage Olley and Pakes (1996) and Levinsohn and Petrin (2003) approaches but predicts all the input parameters in the second stage. This avoids the functional problem of dependence. By considering the advantages of the ACF method, we carried out a final analysis based on the efficiency values calculated using the ACF approach, and efficiency estimation using the standard stochastic frontier approach with the TVD and TI models only as comparisons.

3.2.2 Modeling of firm survival

The second stage of this study investigates the impact of technical efficiency on firm survival, employing two distinct approaches: one at the firm level and another at the 2-digit ISIC level, both structured as panels as outlined in Sect. 3.1. This exploration aims to assess the consistency of results across both individual firms and the aggregate level. Additionally, the categorization of observations into survives, exit, and entry groups enhance the comprehensiveness and coherence of depicting how technical efficiency influences a company's survival. The firm-level analysis adopts the Proportional Hazard Model approach, while the 2-digit ISIC analysis utilizes Poisson regression. Subsequent sections elaborate further on the methodology employed.

Muzi et al. (2023) argue that there is a possibility of bidirectional causality (reverse causality) between efficiency/productivity and firm survival where companies that can gradually survive are also able to learn to become more efficient and one way that can be used to overcome this is to use a lag variable. Therefore, the firm survival estimation in this study uses the first lag of technical efficiency as the concern variable for this study.

3.2.2.1 Firm level evidence

Two approaches are often used to look at factors that influence firm survival, namely the logit approach and the hazard model approach. This binary approach is used by many firm survival studies, including those by Audretsch (1991), Audretsch and Mahmood (1995), Banbury and Mitchell (1995), Lopez et al. (2017), Cefis and Marsili (2012), and Fernandes and Paunov (2015). However, several works of literature discuss binary models for survival analysis, raising several concerns. Binary models are not always applied or interpreted appropriately, and predictive inference from these models can be inaccurate (Henderson, 1995). Rychnovsk (2018) found that survival models outperformed logistic regression in predicting the probability of default. Koletsi and Pandis (2017) note that Cox regression, a popular survival analysis method, provides hazard ratios and confidence intervals, allowing for the adjustment of covariates. Nevertheless, logistic regression can still be useful for survival analysis when the proportional hazards assumption does not hold (Lim et al., 2010; MacKenzie, 2002). The use of logistic regression for analyzing firm survival is a popular but problematic approach, as evidenced by these papers. A key issue is that logistic regression cannot properly account for duration dependence—the tendency of hazard rates to initially increase, peak, and then decrease over a firm's lifetime (Gupta et al., 1999; Holmes et al., 2010; Kaniovski & Peneder, 2008; Mahmood, 2000). Alternative approaches like hazard models are better suited for this (Audretsch, 1995; Kaniovski & Peneder, 2008; Gupta, 1999; Mahmood, 2000; Holmes et al., 2010).

This study focuses on the use of Cox proportional hazard models. I estimate factors determining surviving firms during the period 1996–2015 by estimating the survival time of the companies using the Proportional Hazard Model, Cox Regression. Building a model of firm exit (survival) using standard estimation techniques such as Ordinary Least Square (OLS) introduces a sampling bias because some firms are more likely than others to remain in business (Lopez et al., 2017). According to Clayton and Hills (1993), due to the common form of the contribution to the partial log-likelihood, it has been demonstrated that the Cox model may be fitted using a Poisson GLM (Generalized Linear Model) by dividing follow-up time into as many periods as there are events. Since the sample period ends before most of the firms exit the market, this creates an additional problem. As a result, a censored data problem emerges, and we require alternative methods to address it. The use of information on survivor firms is a problem when performing survival analysis. To perform event history analysis, a common approach employs the proportional hazard model. This analysis allows us to look at what happens before an event occurs; in this case, the event is the firm exit. The specification of the survival function, describing the likelihood of firms' survival until a certain time has elapsed, is a critical process in event history analysis. Cox proposed the proportional hazards model with explanatory variables first (1972, 1975). The Cox model's logic is straightforward and elegant. The hazard factor for the ith firm can be written in the following Eq. 5:

$$ h_t = h_0 \left( t \right)exp\left( {\beta ^{\prime}x} \right) $$
(5)

where h0(t) is the general hazard function and \(\beta ^{\prime}x\) is the covariates and regression coefficients. In addition, the hazard ratio of the two hazards can be written as follows:

$$ \frac{h_i \left( t \right)}{{h_0 \left( t \right)}} = exp\left( {\beta ^{\prime}\left( {x_i - x_j } \right)} \right) $$
(6)

Equation 5 is the standard Cox hazard model, whereas Eq. 6 is the Weibull model, which is the ratio of two hazards, which demonstrates that the ratio remains constant over time. Even though both the Weibull and Cox models are members of the proportional hazard family of models, there is one significant difference between the Cox model and the proportional hazard models discussed (Box-Steffensmeier and Jones, 2004). Cox regression models lack an intercept term because the baseline hazard rate is not specified. To demonstrate this, consider the Cox model in scalar form as follows:

$$ h_i \left( t \right) = exp(\beta_1 x1_i + \beta_2 x2_i + ... + \beta_k xk_i )h_0 (t) $$
(7)

In the form of log ratio hazard model, we rewrite Eq. (6) into:

$$ log\left\{ {\frac{h_i (t)}{{h_0 (t)}}} \right\} = \beta_1 x1_i + \beta_2 x2_i + ... + \beta_k xk_i $$
(8)

Cox (1972, 1975) developed a nonparametric method called partial likelihood to estimate the parameters in Eq. (8). The parameter values are estimated using maximum partial likelihood estimation, which differs from MLE, as written in Eq. 9, in several ways that will be discussed as follows:

$$ logL = \mathop \sum \limits_{j = 1}^D \left[ { \sum \limits_{i\epsilon D_j } x_j \beta - d_j log\left\{ { \sum \limits_{k\epsilon R_j } exp(x_k \beta )} \right\}} \right] $$
(9)

where j shows the ordered failure times \(t_{(j)}\), j = 1, 2, …, D; Dj is the collection of \(d_j\) observations which fail at \(t_{(j)}\); \(d_j\) denotes the number of failures at \(t_{(j)}\); and \(R_j\) is the bundle of observations k which are at risk of failure at time \(t_{(j)}\) (that is, all k such that \(t_{0k} < t_{(j)}\) \(\le t_k\)). The Peto–Breslow approximation is used to handle ties in this logL formula for unweighted data.

Cox regression is the technique of comparing subjects who fail to subject who are at risk of failing; the latter set is referred to colloquially as a risk pool. When there are linked failure times, we must decide how to compute the risk pools for these linked observations. Assume that two observations fail in quick succession. The first observation is not included in the risk pool in the calculation involving the second observation because failure has already occurred. If the two observations have the same failure time, we must decide how to calculate the risk pool for the second observation and the order in which the two observations should be calculated. There are, at least, four approaches to handling the tied failure on the Cox regression in this study, which are Breslow, Efron, exact marginal likelihood, and exact partial likelihood.

3.2.2.2 Aggregate level evidence

The third analysis method used is aggregate level estimation for firm survival, firm entry, and firm exit. The data used is 2-digit ISIC aggregate data, which is built from the microdata used in the previous estimation. This is done to find out two things: first, whether the relationship between efficiency and survival is consistent with aggregate data, and second, how company efficiency influences not only company survival but also companies leaving or entering Indonesia. The estimation technique used is Poisson regression with a population averaged (PA) model. Poisson regression is specifically designed for count data, where the outcome variable represents the number of occurrences of an event within a fixed unit of time or space. Endogenous regressors and panel data are problems that the Poisson model is considerably better able to handle (Cameron, 2013). Gujarati (2004) argues that it is well-suited to situations where the outcome variable follows a Poisson distribution, which is often the case for count data. The probability distribution is Poisson probability distributions are particularly suitable for counting data. The general estimation model for the probability distribution function (PDF) of the Poisson distribution is given by Eq. 10 below:

$$ Y_i = \frac{{\mu^Y e^{ - \mu } }}{Y!} + \mu_i $$
(10)

If the likelihood that the variable Y has non-zero integer values is denoted by f(Y), and where Y! (refer to the Y factorial), Y in the estimates in this section is the number of companies in the 1998 cohort that survived until 2015, the number of companies that exited (exit), and the number of companies that entered Indonesia each year (entry). The efficiency variable used is the average of company efficiency in each year and every 2 digits of ISIC. Meanwhile, some of the control variables used are adjusted for the aggregate level. Variables in the form of categories are added up, such as investment status (domestic or foreign), location (Java), size, and inventory. On the other hand, the variables openness, PCM, HHI, percentage of ownership, and capacity are calculated as an average per 2 digits of ISIC.

3.3 Variable description

This section discusses variable descriptions in more detail. Table 1 summarizes the technical description of the variables:

Table 1 Variable description
Full size table

4 Results and discussion

4.1 Estimation of stochastic frontier model

We begin this section by analysing the results of estimating the production function with a stochastic frontier approach based on the trans logarithm model, as summarized in Table 2. The model is estimated under the assumption that time is invariant.

Table 2 Estimation of production function
Full size table

The estimation results show that the input coefficient is positive, which means that an increase in input increases output. The test results of the number of coefficients of both the TI and TVD models are close to 1, but after the constant return to scale test, it turns out that both models show rejection of the hypothesis that the estimation results are constant return to scale with a value of more than 1. The TVD and TI models show 1.36, and 1.28, while the ACF is 1.43, so it shows more of an increasing return to scale pattern at the 1 percent level. Those three models are quite consistent in terms of the character of the production estimation results, including the coefficients of the most dominant input variables and those with the least influence on output. Labor is the most dominant variable, followed by energy, materials, and capital. The results of the Sargan-Hansen test show a value of 1.42, which means that there is no rejection of the moment conditions used to specify the model.

Figure 4 shows that there is a positive trend in the average TE every year. The three measurements from the TVD, TI, and ACF models show efficiency values that tend to increase. The TE value of the TVD model shows relatively faster growth than other models, while the ACF model has a moderate value between TVD and TI. From the average value of the entire period, the TE values of the TVD, TI, and ACF models are 0.34, 0.15, and 0.23 respectively. Meanwhile, based on the average per sector of 2-digit ISIC, as shown in Fig. 5, the manufactured drink firms’ sector (No. 11) has the highest efficiency values of 0.85 and 0.36, and 0.3 for the TVD, TI, and ACF models, respectively. Meanwhile, the lowest efficiency value is owned by the Machinery and Equipment Repair and Installation sector (No. 33), with values of 0.22, 0.13, and 0.21 for the TVD, TI, and ACF models, respectively. This performance picture is supported by studies from the World Bank (2012) and the Asian Development Bank (2019) which show that the food and beverages sector still dominates the performance of the industrial sector in general in Indonesia.

Fig. 4
figure 4

Source: Author’s calculation

Annual average trend of technical efficiency score.

Full size image
Fig. 5
figure 5

Source: Author’s calculation

Two digits ISIC average of technical efficiency score.

Full size image

4.2 Estimation of firm survival

The descriptive statistical tabulation results for each variable are summarized in Tables 3 and 4 provides a correlation table between independent variables.

Table 3 Descriptive statistics of variables (survival model).
Full size table
Table 4 Correlation of firm survival determinants at firm level.
Full size table

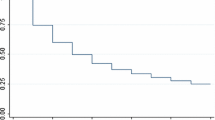
Figure 6 shows the survival pattern based on Kaplan–Meier while Fig. 7 shows the survival time pattern from the results of the Cox Proportional Hazard Model.

Fig. 6
figure 6

Kaplan–Meier survival estimate

Full size image
Fig. 7
figure 7

Cox proportional hazard model estimation (ACF efficiency with time varying model)

Full size image

The same number, 13, is displayed as the median survival value in both the Kaplan–Meier and Cox proportional hazards curves. However, the underlying function explains why the two have different patterns. The survival probabilities are determined using the Kaplan–Meier method, which divides the total number of people at risk by the number of survivors. The collective survival experience of a community is revealed by this curve. However, the Cox Proportional Hazard Model goes beyond survival analysis by accounting for the impact of factors on survival. It is assumed that the baseline hazard function varies with time and that the hazard rate is a linear combination of variables (Andrade, 2023). The Cox Proportional Hazards model is used to represent the relationship between covariates and the hazard rate, whereas the Kaplan–Meier estimator is used to estimate survival probability and cope with censored data. These two techniques are frequently combined in survival analysis to provide a thorough comprehension of time-to-event data. The first descriptive analysis employs the Kaplan–Meier estimator, whereas more detailed statistical modeling and hypothesis testing employ the Cox model (Nieto and Coresh, 1996).

Table 4 summarizes the correlations between variables. Cases of multicollinearity are rarely observed in survival studies. Based on this table, it can be seen that those that have a high correlation are between macro variables, especially growth, growthvar, inflationvar, and inflation whose correlation coefficient is above 0.9. Liverani et al. (2021) argue that in survival studies strong correlations between the explanatory variables can lead to unstable or erroneous estimates of the regression coefficients, as well as incorrect, non-significant p-values, inflated standard errors, and deflated partial t-tests. This assertion is further supported by Xue et al. (2007). Unfortunately, there is no consensus on how much correlation is considered to damage the estimation results. On the other hand, Gujarati (2004) argues that multicollinearity is a linear regression assumption, where if an exact linear relationship occurs it will violate the regression assumption. Exact linear means that the correlation coefficient is 1 between the variables. It is demonstrated that the OLS (Ordinary Least Square) estimators maintain their BLUE (Best Linear Unbiased Estimator) characteristics even in situations when multicollinearity is extremely strong, such as in the case of near multicollinearity (Gujarati, 2004).

The Cox Proportional Hazard model is estimated for each efficiency score generated by the models' TI, TVD, and ACF, and each model is estimated using robust and time-varying techniques summarized in Table 5. To improve the estimation, the results of the robust estimation are tested with a proportional hazard to see if the value of the hazard ratio is constant over time. Several variables are shown to meet the assumptions of the hazard model, including foreign, PCM, HHI, and stock, with probabilities of 0.25, 0.29, 0.24, and 0.89, respectively, while other variables are significant at the 1 percent level, as shown in Table 6. Under this condition, a survival model can be estimated using the time-varying covariates method as recommended by Zhang et al. (2018), and Wang et al. (2018). We use the time-varying method as the basis for our analysis and provide a robust method for comparison only. Apart from that, the efficiency calculation model with ACF is the model that we use as the basis of our analysis, and as a comparison, we also provide the results of the survival model estimation with the TE variable produced by the method TI and TVD.

Table 5 Firm survival estimation (Cox proportional hazard model)
Full size table
Table 6 Test of proportional-hazards assumption
Full size table

The coefficient TE appears to be negative in all models and significant at the 1 percent level, implying that the more efficient the firm is, the lower the risk and survival. The effect of efficiency calculated with the TI and TVD models on firm survival is higher than the effect of efficiency calculated with the ACF. The endogeneity treatment of the ACF model on the estimated effect of efficiency on firm survival makes a fairly large difference. The coefficient TE in the ACF model with a TVC estimate of 0.16, reduces risk or increases survival. This is consistent with the theoretical expectation that efficient firms are able to advance in the market, and this result is also confirmed by previous studies such as Dimara et al. (2008) and Tsionas and Papadogonas (2006). Income can also be considered a measure of productivity or efficiency, as done by Bosio et al. (2020), using income or profit to represent efficiency or productivity and see its impact on firm survival. In this study, income shows negative significance, which means that increasing company income has the impact of reducing hazards or increasing the company's survival time.

The impact of domestic and foreign investment variables on company characteristics is consistent across all models, revealing a shared influence. In all instances, these variables exhibit a negative effect on the hazard ratio or an increase in survival time. Notably, a higher proportion of foreign capital ownership within a company significantly diminishes the hazard, indicating prolonged survival time, as evidenced by the foreign variable. Both domestic and foreign investment statuses demonstrate a heightened probability of survival compared to the average. In the context of manufacturing companies in Indonesia, there exist three investment statuses: domestic, foreign, and non-facility. Presently, the majority of manufacturing companies in Indonesia, accounting for 76.16 percent, fall under the non-facility category. Domestic and foreign investments constitute 15.76 percent and 8.08 percent, respectively. Additionally, non-facility companies exhibit a lower average efficiency value (0.34) compared to domestic (0.40) and foreign (0.46) companies, as well as a lower average total firm value (0.36). Moreover, its median survival time is 12 years, while domestic and foreign investment has a median survival time of 18 and 17 years. This is supported by the findings of Kokko and Thang (2014) who found that both domestic and foreign companies have heterogeneity in survival, especially in the horizontal and upstream sectors.

The percentage of central government ownership also shows a negative influence on the hazard ratio, meaning that the greater the central government's ownership, the greater the chances of survival. The government's role in making strategic decisions may be more necessary in the initial conditions of company operations or companies that are experiencing a decline in performance. Meanwhile, government interference in company decisions, when the company is growing well, can trigger acts of corruption that causes cost and investment inefficiencies and end in company bankruptcy (Ghazali et al., 2022). Foreign Ownership (FO) has a negative effect on the hazard ratio, which means that an increase in the percentage of foreign capital ownership in the company increases the survival of the company. This is in line with previous studies such as those from Bernard and Sjöholm (2003) and Baldwin and Yan (2011). On the one hand, foreign investment can boost firm survival by providing knowledge spillovers and linkages to help new ventures (Burke et al., 2008). However, this effect depends on industry dynamics: FDI has a net negative effect on firm survival in dynamic, rapidly changing industries but a net positive effect in static, stable industries. Foreign ownership has a contribution to make in determining the survival of the company. The FO parameter shows a negative value, which means that multinational companies have a lower hazard ratio than other types of ownership, which means that multinational companies have a higher survival time than other types of ownership. Indonesia is still a good place for investors. Apart from absorbing labor, technology transfer is a clear benefit for the domestic economy. On the other hand, government ownership of the company has a negative impact on the company's survival. The influence of ownership varies greatly in literature studies, depending on political conditions and bureaucracy, which can lead to inefficient resource allocation, unwise investments, and a lack of long-term strategic planning, all of which can negatively impact the firm's survival.

Meanwhile, market structure factors are represented by price–cost-margin (PCM) and the Herfindahl Hirschman Index. Only HHI has a significant positive effect on the hazard ratio, meaning that the less competition, the less firm survival which means that the more monopolized the market, the more the company is unable to survive in it. Based on these findings, manufacturing companies in Indonesia hope that a good competitive climate, and healthy competition between companies in the market can improve company performance. Competition can drive firms to become more innovative and productive. When firms need to outperform their rivals, they often invest in research and development, leading to the creation of new and improved products and services, but at a certain point if it creates a price war and bad competition will hurt the company. A competitive market can force companies to innovate in production, marketing, or even financial strategies to improve their performance and enable them to survive the competition, but companies that are unable to do this will end up leaving the market. The impact of competition on firm performance is not solely positive or negative and depends on the firm's ability to adapt, differentiate itself, and effectively respond to competitive pressures. Firms that can balance the challenges and opportunities presented by competition are more likely to thrive in competitive markets. Additionally, government regulations and industry-specific factors can also influence how competition affects firms. The findings of this study are consistent with several other studies such as those from Garcia and Puente (2006), Burke and Hanley (2009), and Brito and Brito (2014). Nevertheless, Brito and Brito (2014) show that there is a heterogeneity effect between industries in responding to competition in the market, while Burke and Hanley (2009) reveal that the heterogeneity of firm response to market competition depends on the dynamics of entry and exit firms in markets where firms that can survive in the market if the entry and exit levels are high.

On the other hand, the negative coefficient shown by openness means that openness reduces the hazard ratio. Trade openness can provide firms with access to larger and more diverse markets. This can be particularly beneficial for firms that produce goods or services with a global demand. Increased market access can lead to higher sales and revenue, which can enhance a firm's survival prospects. Apart from the market side, the company's ability to survive through openness can also be achieved by supplying inputs at relatively cheaper prices, so that the company has an input price advantage. The results of this study are supported by a study from Kao and Lin (2022) which shows that companies that trade in both exports of production products and imports of raw materials have a higher chance of survival.

The production capacity used by the company has a negative impact on the hazard ratio, which means that the higher the production capacity used, the greater the survivor time. Capacity utilization refers to the extent to which a company is using its production capacity to meet its production targets. When a firm operates at a high level of capacity utilization, it can spread its fixed costs (e.g., machinery and facilities) over a larger volume of production. This can lead to lower average costs per unit, making the firm more competitive and financially stable. On the other hand, inventory does not play a role in determining the company's survival.

The location variable (Java) also shows a negative and significant influence on the hazard ratio, which shows that manufacturing companies located on the island of Java are better able to survive than companies located on other islands. Java, which is the center of economic activities, contributes, according to BPS, 56.47 percent to the total gross domestic product (GDP) of Indonesia, even though it covers only 6.75 percent of the total area of Indonesia and is inhabited by 56 percent of Indonesia's population. Many industries decide to operate on the island of Java, including micro, small, medium, and large industries, which account for 80 percent of companies. Stearns et al. (1995) argue that location has an important role in company performance where more advanced locations, such as cities, have a carrying capacity for companies to live longer, and this is consistent with the findings of our study where the island of Java is the national capital and, with infrastructure facilities and human resources, is the center for the economic life of the population. A densely populated location as a market for industrial output and infrastructure that is spread evenly may still be the goal of most firms in Java to survive.

Macroeconomic variables have a significant role in determining the survival of companies in Indonesia. Inflation and inflation variability have a positive impact on the hazard ratio, while economic growth has a negative impact on the hazard ratio, and growth variability has the opposite or positive impact on growth. This means that price stability and economic growth increase the survival rate of manufacturing companies. Apart from that, HDI as an indicator of human resource quality has a negative contribution to the hazard ratio or increases the company's survival time. Increasing the quality of the workforce provides companies with the opportunity to obtain quality workers, thereby increasing the company's productivity and survival. On the other hand, good human quality is a good contribution to the market for high-tech products for the company. Furthermore, lending rates have a positive impact on the hazard ratio, which means higher lending rates reduce the possibility of film survival. Lending rates as the main capital costs for companies are a burden for companies to invest or expand production scale.

4.3 Determinant of firm survival, entry, and exit (aggregate two digits ISIC)

This section provides additional analysis with aggregate data at the 2-digit ISIC level. Table 7 provides summary statistics for the determinant variables of companies that survive, enter, and exit. Because there was a change in the ISIC code numbering in 1998, observations at the aggregate level were carried out from 1998 to 2015.

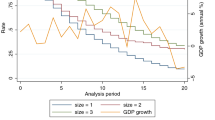
Table 7 Descriptive statistics of aggregate level.
Full size table

Apart from that, this section also provides additional analysis of factors that influence company entry, survival, and exit. Estimation is carried out using the Poisson regression with a population-averaged model. The results of the Poisson regression estimation are summarized in Table 8. Equation 8 was estimated three times by changing the outcome variables for survival, exit, and entry. It can be seen in the table that the efficiency variable significantly influences companies that survive, enter, and exit, where efficiency has a positive influence on companies that survive, has a positive influence on the number of companies entering, and has a negative influence on the number of companies leaving the Indonesian market. It means that the more efficient the company, the greater the possibility of surviving in Indonesia, encouraging companies to enter and preventing companies from leaving the market.

Table 8 Panel 2 digits ISIC poisson regression model results (population averaged model)
Full size table

The estimation at the aggregate level shows some differences and consistency with the firm-level results. The estimation results at the aggregate level show that TE has a positive effect on the number of companies that survive, the higher the average efficiency, the more companies will gradually survive. On the other hand, the average company efficiency positively influences the number of companies entering Indonesia and vice versa, the higher the average efficiency, the lower the number of companies leaving. In addition, company revenues, as expected, also show an influence on increasing the number of surviving companies and entering and reducing exiting companies. A company's high income increases the attraction of other companies to enter to seek their fortunes in the same market and reduces the possibility of companies leaving the market. Another variable that has a positive effect on the increasing number of companies entering is Domestic and Foreign investment which also has a positive effect on the number of companies that are able to survive in Indonesia. The more companies with domestic and foreign investment status, the more companies will be able to survive. Apart from that, in terms of their influence on the number of companies entering and leaving, both variables have a positive impact on the number of companies entering and a negative impact on companies leaving. The large number of companies with domestic status and foreign companies provides a positive signal for other companies to enter Indonesia and reduces the number of companies leaving. Openness also shows a positive effect on increasing the number of companies that survive and enter, and reducing the number of companies that leave. Access to international markets provides its own advantages, both production markets and competitive markets for input prices which may be more reasonable for the company's production cost structure.

In contrast, market structure influences fewer businesses to come and survive while increasing the number of businesses to go. The variables PCM and HHI demonstrate this. Strong competition may lead to the development of entry barriers, which will make it more challenging for new businesses to enter the market. There are frequently high entry barriers where there is fierce rivalry. These obstacles may consist of expensive initial startup costs, scale efficiencies that current rivals have, strong customer brand loyalty, and legal or regulatory constraints. It could be difficult for a fledgling business to get beyond these obstacles. Price wars, which are a common result of fierce competition, can reduce profit margins. This could work against newcomers, particularly if they don't have the economies of scale that more established rivals would have.

Consistent with the results at the firm level, average production capacity increases the number of surviving firms and new firms entering and conversely reduces the number of exiting firms. A company may benefit from economies of scale when it is running at or close to capacity. This indicates that when output rises, the average cost per unit of production falls. A company's ability to compete in a new market might be strengthened by lower average costs, particularly if the company can reach comparable levels of capacity utilization. Moreover, a high-capacity utilization rate may indicate a high level of interest in the company's goods or services. This encouraging signal might draw in new lenders, partners, or investors, which would make it simpler for the business to get the funding and assistance it needs to enter a new market.

In contrast to the results at the firm level, which show no significance, the estimation results at the aggregate level show strong significance of inventory. Inventory changes increase the number of companies that survive and enter and also increase the number of companies that leave. Effective inventory control is necessary to maximize working capital. An excessive amount of inventory takes up money that could be invested in expansion prospects, paid off debt, or utilized to solve operational issues. Conversely, keeping too little inventory might result in stock-outs, which can harm sales and customer satisfaction. The total cost structure of a company is influenced by the costs associated with holding inventory, such as storage, insurance, and obsolescence risk. Effective inventory management contributes to cost containment. A company that has an expensive structure because of poor inventory management may find it difficult to stay competitive, which could eventually threaten its future.

In the realm of macroeconomic factors, variables associated with uncertainty, namely inflationvar and growthvar, have a discernible impact on the dynamics of corporate survival, entry, and exit within the market. Manufacturing enterprises, particularly in Indonesia, express a distinct preference for a stable economic environment to bolster their ongoing operations. Notably, inflation plays a dual role by not only diminishing the number of surviving and entering firms but also amplifying the count of exiting firms. Conversely, economic growth emerges as a pivotal factor, contributing to an upswing in the survival and entry rates while concurrently mitigating the exit frequency. Recognized as a catalyst for market expansion, economic growth creates an advantageous climate for manufacturing entities. Delving into the financial landscape, lending rates exhibit a negative correlation with the survival and entry of companies, concurrently escalating the departure of firms from the market. Elevated lending rates continue to pose a challenge for companies, particularly those reliant on financial backing from local banks in Indonesia for investment and production expansion. Simultaneously, the quality of human resources, as measured by the Human Development Index (HDI), demonstrates a positive correlation with the number of surviving firms. However, it is noteworthy that while HDI does not function as a decisive factor influencing firms to enter the market, it significantly contributes to reducing the number of firms exiting.

However, several things need to be considered when looking at the results of both. The difference between aggregate and microdata is a real difference in distribution. Because we are looking at several components of the data, the data's nature itself may generate discrepancies in results. Aggregating data can lead to aggregation bias, where important variations within subgroups or individuals are lost. For example, if data on individual incomes and aggregated to compute average income by region, we may miss important disparities within each region that could be significant at the microdata level. Microdata often reveals individual-level heterogeneity that aggregate-level data might obscure. Individual characteristics and behaviors may vary significantly within a given group, and these variations can be important for understanding relationships between variables. Even though many differences may occur in the data-generating process into aggregate data to become count data in Poisson regression, Carstensen (2019) proves that whatever can be done by the Cox regression model can also be applied with Poisson regression, especially using split data. By converting to Poisson modeling, there is no loss but rather a significant increase in capability. The Cox model is significantly more computationally efficient and makes it simpler to create a survival curve using common software, which is important for most clinical investigations. The too-intricate modeling of survival curves has a downside in that it may cause small humps and notches on an estimated curve to be misinterpreted. The capabilities in the typical Cox analysis programs restrict how the desired interactions can be modelled when stratification or time-dependent variables are included and divert the user from understanding that alternative interactions between covariates may be of relevance. Another study from Selmer (1990) also found results that were close between Poisson and Cox, while Loomis et al. (2005), by estimating ungrouped data, provided results that were equivalent to the results of estimating Cox Proportional Hazard and Poisson Regression. Loomis et al. (2005) argue that using simulated data, Poisson regression analyses of ungrouped person-time data yield results equivalent to those obtained via proportional hazards regression: the results of both methods gave unbiased estimates of the ‘‘true’’ association specified for the simulation. Analyses of empirical data confirm that grouped and ungrouped analyses provide identical results when the same models are specified. However, bias may arise when exposure–response trends are estimated via Poisson regression analyses in which exposure scores, such as category means or midpoints, are assigned to grouped data.

5 Conclusion

This study aims to identify the factors that determine firm survival, exit, and entry using survey data from large and medium manufacturing companies in Indonesia. The focus of this study is the influence of a company's technical efficiency as a performance indicator. Technical efficiency is calculated using several approaches, namely stochastic frontier with a translog model, both time-invariant and time-varying, as well as the ACF (Ackerberg–Caves–Frazer) method, which treats endogeneity in the estimation of the production function in order to produce unbiased efficiency values. Several groups of control variables were identified in this study, including firm performance indicators such as income and capacity utilization; the second group of variables is the market structure represented by the Herfindahl–Hirschman Index (HHI) variable; and price cost margin (PCM). The third group of variables are variable characteristics, which include ownership, investment status, openness, location, and size. The fourth group is macroeconomic condition variables, which include inflation, economic growth, inflation variability, and growth variability as a proxy for risk. Another macro variable is the lending rate.

The Cox proportional hazard model estimation results show that technical efficiency reduces the hazard ratio or increases company survival for all models used. This confirms that the company's ability to achieve efficient production is an important factor in supporting the company's ability to survive. Apart from that, the aggregate data and Poisson regression models show that company efficiency increases the number of companies that survive during the observation period and increases the number of companies that enter. On the other hand, efficiency has a negative effect on the number of companies leaving the market; in other words, the more efficient the company, the smaller the possibility of the number of companies leaving the market. Although there are differences in data structure at the micro and aggregate levels that have methodological consequences, the corresponding results of the two estimation techniques, both the Cox proportional hazard model and Poisson, are supported by several previous applied statistics studies that show that the Poisson and proportional hazard models are equivalent.