Introduction

“It would be fair to say that studies conducted across the Western world have consistently found that a majority of prospective (and in-service) primary teachers have beliefs about mathematics that are narrow, formal and rigid” (Grootenboer, 2008, p. 479). For this reason, the investigation of ways to change and develop primary mathematics teachers’ beliefs remains an ongoing pursuit in mathematics education research (e.g., Maasepp & Bobis, 2014; Smith et al., 2012). These discussions are based on acknowledging teachers’ beliefs about mathematics as critical elements of mathematics competence (Voss et al., 2011) that shape teachers´ professional practices (Calderhead, 1996). Prior beliefs, developed during elementary and secondary school, are further shaped during university education (Fives & Buehl, 2012; Thompson, 1992) and are thereby influenced by university teachers (Geisler & Rolka, 2020; Grootenboer, 2003; Shilling-Traina & Stylianides, 2013).

In this paper, we focus on beliefs of prospective elementary teachers about mathematics, in particular on whether they are static or dynamic beliefs. Static beliefs represent an individual’s assumption that mathematics is a fixed construct with predetermined formulas and formal specifications. In contrast, individuals with dynamic beliefs see mathematics as an exploratory discipline in which individuals solve problems (Ernest, 1989; Grigutsch et al., 1998). Regarding teachers, empirical findings point to the presence of static beliefs about mathematics already at the outset of their university education (Grootenboer, 2003; Smith et al., 2012). If those beliefs do not alter during university studies, elementary teachers will remain inhibited from even attempting inquiry-based and experimental teaching throughout their professional life (Müller et al., 2007; White et al., 2006). Moreover, it has been reported in the past that university mathematics shows a static picture of mathematics (Grigutsch et al., 1998). Consequently, our study addresses two aspects: firstly, to determine how current university mathematics teaching influences students’ beliefs about mathematics and, secondly, whether our teaching approach that emphasises inquiry-based tasks in elementary mathematics teacher education can foster the development of dynamic beliefs and thereby change future elementary mathematics education (Stipek et al., 2001; Stylianides & Stylianides, 2011). In this regard, our study seeks to re-examine existing results. Since an inquiry-based approach to mathematics teacher education was found to influence prospective teachers’ beliefs (Laursen et al., 2014, 2016), this study seeks to replicate existing results in a different educational system. On one hand, this study can be described as a conceptual replication study (Cai et al., 2018), because we investigated an inquiry-based approach in a different learning environment. On the other hand, this study aims to specifically focus on prospective mathematics teachers’ beliefs about the nature of mathematics (Ernest, 1989; Grigutsch et al., 1998) and to focus on large groups of prospective elementary teachers for whom mathematics is a compulsory but not necessarily welcome subject. Therefore, we think that our study includes aspects that have not been investigated in the past. With the specific focus on prospective elementary teachers who are obliged to study mathematics as a major subject when enrolling in the teacher training programme, our study takes up a new facet in the research area of teachers’ beliefs. Finally, the focus of our research is not on additional measures to develop prospective mathematics teachers’ beliefs (e.g., Smith et al., 2012), but to develop these beliefs in a regular mathematics course of the first semester, where a large group of prospective elementary teachers are enrolled.

In this context, we looked at regular mathematics courses at two universities during students’ first semester. At the first university, which was our experimental group, the mathematics courses for prospective elementary teachers followed a teaching approach with inquiry-based tasks. At the second university, a classic and primarily lecture-based approach to subject-specific mathematics was used as a control group. At both universities, we measured prospective teachers´ beliefs about mathematics in a pre-post-test design. We examine the various constructs, current research, and research issues in more detail below.

Theoretical Framework

Beliefs

In recent decades, much research has focused on teachers’ beliefs (Fives et al., 2015; Phillip, 2007; Thompson, 1992). Historically, various definitions of the construct of beliefs with different aspects and emphases have been put forward. For this paper, we explore beliefs about the nature of mathematics (cf. Ernest, 1989; Thompson, 1992) that could be understood as the basis for receiving mathematical information and for acting mathematically (Phillip, 2007; Törner, 2003). Grigutsch et al. (1998) use the term ‘mathematical world views’ for specific belief clusters that they divide into static beliefs (schema and formalism view) and dynamic beliefs (process and application view):

  • The schema view denotes beliefs about mathematics as a collection of procedures that solve firmly defined tasks. In this view, learning mathematics include rote learning of definitions, rules, and formulas.

  • The formalism view denotes beliefs about mathematics as based on exact thinking, formulation, and proofs.

  • The process view denotes beliefs about mathematics as an activity characterised by thinking about problems and by gaining knowledge through the process of problem solving.

  • The application view denotes beliefs about the practical use of mathematics for society and in normal life.

Development of Beliefs

Beliefs about mathematics start to develop when children enter school, and the process continues throughout successive school years (Phillip, 2007; Stone, 2009; Thompson, 1992). By the time high school graduates enter university, they exhibit rather static beliefs (Grootenboer, 2008; Lannin & Chval, 2013; Maasepp & Bobis, 2014; Smith et al., 2012). This tendency is even more pronounced among students who have not chosen mathematics voluntarily and have been obliged to study mathematics (Törner & Grigutsch, 1994) This is often the case for students who enrol in an elementary teacher education programme. Thus, Schuck and Grootenboer (2004, p. 5) claim that students who enter teacher education mostly hold beliefs that negatively influence their later teaching of mathematics by preventing “them from teaching mathematics in ways that empower children."

University coursework for prospective elementary teachers is critically important because it is the only systematic experience they will have after high school that could impact their static beliefs about mathematics (Fives & Buehl, 2012; Grootenboer, 2003; Liljedahl et al., 2012). At the same time, research suggests that a strong impulse or triggering experience is necessary to prompt development from static to dynamic beliefs (Liljedahl et al., 2012). While additional methodology courses for prospective elementary mathematics teachers could change their beliefs (Smith et al, 2012), Cardetti and Truxaw (2014) suggest that stronger links between mathematics and teaching methods have a greater influence on the development of dynamic beliefs about mathematics.

Coursework that engages prospective teachers in actual problem solving (often in small groups), and which motivates reflective analysis, tends to significantly improve dynamic beliefs (Liljedahl et al., 2019; Maasepp & Bobis, 2014: Roscoe & Sriraman, 2011; Shilling-Traina & Stylianides, 2013). In this vein, Liljedahl et al. (2019) have argued that a reduction of static beliefs is only possible if dynamic beliefs are developed in their stead.

Effects of Beliefs

A long-held tenet concerning human nature is that beliefs influence people’s behaviour. For example, beliefs can impact people’s cognitive engagement (Ravindran et al., 2005) and act as filters for the reception and interpretation of new information (Fives & Buehl, 2012). Concerning teacher training, prospective teachers’ beliefs have an impact not only on their early university learning, but also throughout their entire university education (Fives & Buehl, 2012) and continue to influence their future careers as teachers. We also know that teachers’ beliefs impact their lesson planning and their behaviour in the classroom (Eichler & Erens, 2015; Levin et al., 2013). Some even argue that teachers’ beliefs are the essential foundation for teaching mathematics (Levin, 2015; Skott, 2015). The effect is extensive as teachers’ beliefs also impact their own students, whose beliefs are themselves formed by their teachers (Eichler, 2011; Phillip, 2007; Staub & Stern, 2002). This relationship will be problematic if it leads to undesirable consequences. For example, Pehkonen and Törner (1999) argue that static beliefs about mathematics are one of the most fundamental causes of teaching mathematics in a teacher-centred way, wherein the teacher provides mathematics as an entirely developed body of knowledge without any attempt to engage students in developing meaning through their own mathematical reasoning. White et al. (2006) have reported a similar relationship referring to elementary teachers’ beliefs and their teaching approach. The research clearly shows that teachers with static beliefs about mathematics are responsible for classes where students are less challenged and receive little support for active learning (Dubberke et al., 2008; Stipek et al., 2001). In contrast, teachers with dynamic beliefs tend to produce mathematics lessons through problem-solving tasks that facilitate their students’ active learning (Staub & Stern, 2002; Voss et al., 2011).

The research literature summarised here suggests critical connections between teachers’ beliefs and their teaching practices, and an equally important connection between their teaching practices and their students’ learning. Within the broad aim of improving teacher education programmes at university, we have attempted to assess the impact of an inquiry-based course designed to strengthen teachers’ dynamic beliefs. We further investigate whether our teaching approach can positively influence beliefs of prospective elementary teachers about the nature of mathematics, considering large university groups with approximately 200 students.

Research Questions

The study was designed to answer the following research questions on the beliefs of prospective elementary teachers:

RQ1:How do prospective elementary teachers’ beliefs about mathematics change during the first semester?

RQ2:Does the development of beliefs about mathematics during the first semester differ in prospective elementary teachers according to the predominant teaching approach adopted in their university course experiences?

Methods

Teaching Approaches

This study investigates the development of beliefs in the context of two contrasting teaching approaches implemented in elementary mathematics courses at two German universities. Both courses had very similar arithmetic and geometry content and were mandatory in the first semester of the elementary teacher training programme. Both courses also followed the same schedule: a 14-week semester, a two-hour lecture (large enrolment numbers with more than 150 participants) and one-hour discussion section (small enrolment numbers with several groups of 20–40 participants) per week. The approach to teaching mathematics differed: one course followed an inquiry-based teaching approach, the other a classical teaching approach. Our target group with the inquiry-based teaching approach constituted the treatment group in our quasi-experimental design.

The Teaching Approach with Inquiry-based Tasks

In our study, a specific teaching approach was designed, combining inquiry-based tasks with methodological elements of dialogic learning (Gallin & Ruf, 1998). The inquiry-based tasks were designed to emphasise the active process of engaging in mathematics. Such tasks encourage prospective elementary teachers to experiment with mathematics and reinvent for themselves important mathematical meanings. The methodological approach of dialogic learning includes three phases. First, the Think-phase is exemplified by the individual’s deep engagement in an inquiry-based task on a new topic, which in our study was introduced at the end of the following large enrolment lecture class (two hours per week). Second, the Pair-phase is characterised by small group activity, which took place during course discussion sessions (one hour per week). In this phase, a tutor assisted prospective elementary teachers in sharing and discussing their individual responses to the mathematical problem(s) that they had independently worked on. During the second phase, the tutor gave feedback on ideas, supported solution processes, and asked questions, but did not present a sample solution. Third, the Share-phase was attended by everyone and involved group action to close the dialogic process. In this phase, the course lecturer tackled the discoveries and solutions presented by prospective elementary teachers in their discussion sections for the purpose of developing the regular mathematical content by systematically classifying and generalising students’ contributions.

In our study, the inquiry-based tasks were implemented in the following manner: first, students were presented with concrete examples that came from an elementary school textbook to highlight the meaningfulness of the university mathematics (first pillar of inquiry-based mathematics education of Laursen & Rasmussen, 2019); second, they were prompted to discover patterns in the given examples, to search for more examples and describe their patterns, and to formulate a theorem reflecting the mathematical patterns; and third, they were asked to develop a proof of the emerging theorem. As an example, students were introduced to the wheat and chessboard problem in which a king had to repay a man who helped him solve a problem. The king began by paying the man a single grain of wheat for the first square of the chessboard and doubling the amount for each subsequent square. Thus, the man received 2 × 1 grains of wheat for the second square, 2 x (2 × 1) grains of wheat for the third square, and so on. Students were asked to figure out the number of grains of wheat for several squares. The example illustrates how inquiry-based tasks in elementary textbooks can be used for both elementary students (at a basic level using partial sums and powers of 2) and their prospective teachers (formulating relevant theorems and possible proofs for the partial sums formula to powers of k, where k is an arbitrary natural number). Finally, prospective elementary teachers at the target university documented their inquiry process and reflections by responding to specific prompts (cf. Eichler et al., 2022) in a portfolio.

The Classical Teaching Approach

The control group in this study was taught with a teaching approach that corresponds to a classic university mathematics lecture, in which learning is mainly receptive. The topics in this course were basic elements of arithmetic, number theory, and algebra.

In the lecture, mathematical content and example tasks were introduced formally on the board. The approach to a new topic was application-oriented through examples from daily life and historical anecdotes. For each topic, there were one or more lectures in which the mathematical content, proofs, or sample assignments were documented on the board. The content of these lectures formed the basis for weekly tasks that the prospective elementary teachers must independently work on and turn in. After working on tasks, prospective elementary teachers could participate in a one-hour discussion meeting where the correct task solutions are presented by assistants.

Weekly homework exercises focused on solving procedural tasks with the aim of practising mathematical techniques and proving mathematical theorems. To gain access to the final exam, students needed to achieve a specific pass score for homework exercises.

Instruments

Prospective elementary teachers’ beliefs about mathematics were measured with the scales published by Grigutsch et al. (1998), which refer to four dimensions: schema view, process view, formalism view, and application view. Statements within the item pools were classified by a four-point Likert scale, ranging from 0 (I do not agree) to 3 (I completely agree). The reliability of the sub-scales for the four aforementioned views in the mathematical world view of prospective elementary teachers can be found in Table 1 (computations based on our study data). The complete questionnaire is available in an open repository (https://osf.io/cxh3v/).

Table 1 Reliability of the mathematical world view sub-scales
Full size table

Despite the adoption of the scales from other studies, they do not furnish satisfactory reliability in the case of the formalism view in the pre-test. Removing items of the scale resulted in a lower coefficient, which means that no single item is responsible for that value. Maybe students were not completely informed about the formalism of university mathematics at the beginning of the semester and, therefore answer the items inconsistently. For this reason, we analyse results referring to the formalism view as an exploratory addition to the other analyses.

Study Design

The study follows a quasi-experimental, pre- and post-test design. Data were collected at both universities through a questionnaire administered before the winter term 2019/2020 and shortly before its end 14 weeks later. Filling out the questionnaires was voluntary and took place during a lecture (response rate > 90%).

Data Preparation and Data Analysis

The questionnaires were marked by an anonymous code that allowed pre- and post-test matching without identifying specific students. Based on this code, we were able to match 335 pre- and post-questionnaires; questionnaires with incorrect codes could not be matched and were excluded. Additionally, 31 data sets were excluded from the analysis due to missing values. In total, the data set comprised 304 prospective elementary teachers; 165 at university 1 (treatment group) and 139 at university 2 (control group).

We used the propensity score matching procedure with nearest-neighbour matching and a 1:1 matching to make the groups comparable (see Randolph et al., 2014). For the matching process, we used three criteria: secondary school grade in mathematics (PZeug), participation in a mathematical pre-course offered by the university (VK_M), and the student’s response to the question of whether they would have chosen mathematics if it had not been a compulsory part of the elementary teacher training programme (M_frei).

Mathematical performance in the form of the mathematics school grade could influence how students engage with university mathematics, regardless of the teaching approach. In addition, pre-existing organisational differences across the universities may influence the student groups. For example, many students who want to take as little mathematics as possible might be more likely to enrol at university 2 because they have to study less mathematics there than at university 1. Since differences in students' exposure to mathematics could influence the comparative results, we decided to use matching to examine equal groups based on the variables.

Figure 1 shows that the groups differ only slightly in their mathematics school grade (PZeug) and the decision to study mathematics (M_frei) before the matching. Additionally, Fig. 1 shows a larger difference of the groups in the case of pre-course participation (VK_M) before the matching. After the matching, there was no difference between the groups regarding the three criteria. This result can be seen by the fact that the absolute standardised mean difference of the three criteria is off-scale in Fig. 1 and, therefore, not shown in the figure.

Fig. 1
figure 1

Mean differences of the three matching criteria in both groups

Full size image

Based on the three criteria mentioned above, we matched N = 106 pairs of prospective elementary teachers with similar features, based on the pre-test data. After matching, the data set includes 106 of 165 students at university 1 and 106 of 139 students at university 2 (the remaining participants were excluded from the analysis).

For data analyses, we computed the mean value of each scale by summing the responses of the items. A mixed ANOVA with repeated measures was used to compare the two groups of prospective elementary teachers (using within-factor time and between-factor university). We used Cohen´s d and eta squared to evaluate the effects. We interpret a Cohen´s d value from 0.2 to 0.5 as a small effect, between 0.5 and 0.8 as a medium effect, and anything above as a large effect. A partial eta squared of 0.01 is a small effect, 0.06 is a medium effect and above 0.14 a large effect.

Results

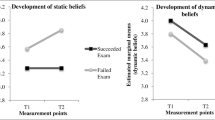
Figure 2 shows the means for both groups for each of the four scales: schema view, process view, formalism view, and application view (minimum 0 and maximum 3).

Fig. 2
figure 2

Overview of development of beliefs

Full size image

We found small changes in the static beliefs of prospective elementary teachers at the target university. For example, their schema view significantly decreased over the first semester (t(105) = -2.122, p = 0.036; Cohen’s d = 0.21) with a small effect, whereas the formalism view did not change during the semester (t(105) = 0.369, p = 0.713, Cohen’s d = 0.04). Thus, it can be said that prospective elementary teachers’ schema view decreased over the first semester in the target group, whereas their formalism view did not alter. Furthermore, we found changes in the dynamic beliefs of prospective elementary teachers at the target university. Their application view increased significantly (t(105) = 2.158, p = 0.033; Cohen’s d = 0.21), with a small effect. We found no changes in prospective elementary teachers’ process view (t(105) = 1.782, p = 0.078, Cohen’s d = 0.17) in the target university, although the results are close to the statistically chosen limits.

For the prospective elementary teachers in the control group, we found changes in their static beliefs during the first semester. The schema view of the control group decreased significantly (t(105) = -4.507 p < 0.001; Cohen’s d = 0.44), but the formalism view did not change (t(105) = 0.369, p = 0.713, Cohen’s d = 0.05). Moreover, we found changes in dynamic beliefs. The application view increased significantly (t(105) = 2.915, p = 0.004; Cohen’s d = 0.28) with a small effect. We found no changes regarding the process view (t(105) = -1.896, p = 0.061; Cohen’s d = 0.18), although the results are close to the statistically chosen limits.

Variance analysis with repeated measures showed no interaction effect regarding prospective elementary teachers’ schema view (F(1.210) = 3.449, p = 0.065, \({\eta }_{\text{p}}^{2}\) = 0.016), but the effect size indicates a small effect. Also Fig. 2 shows that the slopes of the two lines seem to be very different, which is why there is an indicator for a different development. For the formalism view (F(1.210) = 0.484, p = 0.487, \({\eta }_{\text{p}}^{2}\) = 0.002), and application view (F(1.210) = 0.141, p = 0.708, \({\eta }_{\text{p}}^{2}\) = 0.001), we found no interaction effect. Accordingly, there is no statistical evidence for a different development in the two groups. In contrast, a small interaction effect occurred in the process view (F(1.210) = 6.735, p = 0.010, \({\eta }_{\text{p}}^{2}\) = 0.031). Therefore, we assumed that the beliefs of the university students about process view in both courses developed differently, so the teaching approaches might have different effects.

Discussion

Our first research question addressed changes in beliefs about mathematics in prospective elementary teachers during the first semester. Regarding this question, our results suggest that such changes are possible. In the category of static beliefs, we observed a significant decrease in ratings of the schema view during the first semester of teacher education. Both university courses led to a mitigation of prospective elementary teachers’ schema view. Consequently, after the semester, students in both groups are less convinced that mathematics is a collection of procedures that solve firmly defined tasks. In contrast, we did not find changes in the formalism view in prospective elementary teachers during the first semester of teacher education. This suggests that students’ beliefs about the nature of mathematics /as a subject that consists of exact thinking, formulation, and proofs) do not change in the first semester. Since both courses were characterised by formal mathematics, we had expected a different pattern in the formalism view. Thus, there exists the possibility that the current university mathematics does not influence beliefs about the formalism view. However, we must note the low reliability of the formalism scale. In our opinion, the low reliability is not caused by an incomprehensible item, because this was statistically verified. Instead, we assume that the students were not able to assess the formalism of university mathematics in the pre-test due to their lack of experience with university mathematics courses, and therefore they answered the items inconsistently. An argument for this conjecture is the acceptable reliability in the post-test with the same items of the scale. Whatever reasons exist for the low reliability in the pre-test of the formalism scale, interpretation of the results should be made cautiously. In summary, our findings may contradict a historical artifact of university mathematics courses, which tend to convey static beliefs about mathematics (Grigutsch et al., 1998). Due to the negative effects of static beliefs for teachers (Dubberke et al., 2008; Pehkonen & Törner, 1999; Stipek et al., 2001; White et al., 2006), our findings may be considered a positive development of teacher education. It is possible that university teacher education presents a different picture of mathematics.

In the category of dynamic beliefs, our results revealed an increase in rankings of the application view for both groups of prospective elementary teachers. These results suggest that students in both groups developed higher beliefs about the practical use of mathematics for society and normal life during the first semester. Such changes are positive in the context of elementary teacher education, since empirical findings have shown that the application view has a positive impact on teaching (Müller et al., 2007; Staub & Stern, 2002; Voss et al., 2011). Again, the results suggest an evolving mathematics teacher education.

Regarding the process view, different patterns occurred as shown in Fig. 2. While it seems that the process view increased in the treatment group, the control group was characterised by a decrease. However, the statistical analysis does not show a development in both groups, whereas the results are nearly at the limits. Yet, when comparing both groups, it becomes apparent that there could be different developments. The beliefs about mathematics as an activity characterised by thinking about problems and by gaining knowledge through the process of problem solving thus developed in different directions in the two groups. For this reason, it can be noted that prospective elementary teachers’ process views can change over the first semester. In the context of the positive effects of dynamic beliefs for future teaching (Staub & Stern, 2002; Voss et al., 2011), teacher education can influence the process view during the first semester.

Our second research question addressed the development of beliefs dependent on the teaching approach. In the category of static beliefs, we found no differences regarding development of the schema view or the formalism view. Accordingly, the data showed no evidence that the static beliefs of prospective elementary teachers developed differently in either course. These results are surprising because the structure and content of the courses differed somewhat, and the focus on problem solving was more salient in the treatment group. Accordingly, our results suggest that prospective elementary teachers’ static beliefs can change even without explicit reference to problem-solving (Smith et al., 2012; White et al., 2006). It is also possible that our results could indicate that inquiry-based approaches have less impact in large-number university courses, maybe due to a lack of feedback. This argument is supported by the fact that the results of the schema view are very close to the limits we set in this work. Therefore, it can be discussed whether the control group decreased their beliefs about the schema view over the first semester more than the treatment group. Comparing these results with the results of Liljedahl et al. (2019), we postulate that an inquiry-based teaching approach can also develop beliefs about the nature of mathematics and may even offer greater potential for development.

Furthermore, we found that differences in development occurred in the category of dynamic beliefs. Whereas our results did not reveal any change in the application view, we found different patterns for the two groups regarding the process view. The treatment group with inquiry-based coursework showed an average increase, whereas the control group (classical university coursework) exhibited a decrease during the semester. In addition, our results show an interaction effect for both groups over the first semester. For this reason, a different development in both groups can be assumed. We interpret this result as an effect of the explicit problem-solving orientation in the inquiry-based course. Due to the positive effects of dynamic beliefs on teachers’ behaviour (Bender et al., 1999; Müller et al., 2007; Staub & Stern, 2002; Voss et al., 2011), we assume that this result can lead to appropriate changes in mathematics coursework for prospective elementary teachers at university. Finally, our results are in line with previously reported research that has shown that problem-solving experiences positively influence the beliefs of prospective mathematics teachers (Liljedahl et al., 2019; Maasepp & Bobis, 2014; Shilling-Traina & Stylianides, 2013). Moreover, the results further show that an inquiry-based learning approach focusing on the meaningfulness of university mathematics (Laursen & Rasmussen, 2019) can have a positive impact on prospective elementary teachers’ beliefs about the nature of mathematics in large-number university courses.

Overall, we found a decline in static and a rise in dynamic beliefs in the treatment group. This pattern confirms the hypothesis that dynamic and static beliefs reflect opposite ideas (Grigutsch et al., 1998), and corresponds with the findings of Liljedahl et al. (2019). Those authors thought that discarding static beliefs would only be possible if dynamic beliefs were developed in their stead. But our control group partly contradicts this expectation. In our study, the schema view consistently decreased in the control group, while the process view also decreased, even though less dramatically. Therefore, it is impossible to definitively state whether the beliefs of the prospective elementary teachers have evolved from static to dynamic status, even though this absent inverse development has been shown in other studies (e.g., Weygandt & Oldenburg, 2015). In this regard, it would be interesting to investigate whether, in a classic university course, an exchange occurs between beliefs representing the schema view with those representing the formalism view.

In conclusion, our study provides insights into the development of prospective elementary teachers’ beliefs about mathematics in the first semester of teacher education. Our results provide evidence that various beliefs changed during the first semester. Even though these results only indicate small effects, they show that beliefs can be changed through a brief intervention. The long-term effect of a one-semester intervention has yet to be examined. Due to the specific structure of our study, it is not possible to provide reasons for these changes. Although our findings suggest that the beliefs about mathematics, especially regarding the process view, can be influenced by an inquiry-based teaching approach, we cannot state that this approach triggered these changes. Within the groups, several aspects still differed: for instance, the lecturers, the tutors, and the sequence of mathematical content. To conclusively confirm that the different development is based on the teaching approach, further research is needed.

Another aspect that should be considered is the use of propensity-score matching. Through the procedure, we produced comparable groups based on the matching variables. However, it remains unclear whether there are other such variables that influence the experiment. Especially in the teaching context, it could be assumed that there be some other factors which have an influence. For this reason, it is true that we can speak of an increased comparability of the two groups studied in a quasi-experimental study with natural groups. However, a random division of the two groups (as an important basic requirement of an experiment) cannot be achieved with this matching process. Therefore, an influence of the procedure on the results cannot be excluded.