A novel three-stage multi-population evolutionary algorithm for constrained multi-objective optimization problems

Abstract

Lots of real-world optimization problems are inherently constrained multi-objective optimization problems (CMOPs), but the existing constrained multi-objective optimization evolutionary algorithms (CMOEAs) often fail to balance convergence and diversity effectively. Therefore, a novel constrained multi-objective optimization evolutionary algorithm based on three-stage multi-population coevolution (CMOEA-TMC) for complex CMOPs is proposed. CMOEA-TMC contains two populations, called mainPop and helpPop, which evolve with and without consideration of constraints, respectively. The proposed algorithm divides the search process into three stages. In the first stage, fast convergence is achieved by transforming the original multi-objective problems into multiple single-objective problems. Coarse-grained parallel evolution of subpopulations in mainPop and guidance information provided by helpPop can facilitate mainPop to quickly approach the Pareto front. In the second stage, the objective function of mainPop changes to the original problem. Coevolution of mainPop and helpPop by sharing offsprings can produce solutions with better diversity. In the third stage, the mining of the global optimal solutions is performed, discarding helpPop to save computational resources. For CMOEA-TMC, the combination of parallel evolution, coevolution, and staging strategy makes it easier for mainPop to converge and maintain good diversity. Experimental results on 33 benchmark CMOPs and a real-world boiler combustion optimization case show that CMOEA-TMC is more competitive than the other five advanced CMOEAs.

Introduction

In real-world applications, many optimization problems contain several conflicting objectives and multiple complicated constraints, such as the robot gripper optimization problem [26], the optimal scheduling in microgrids [15], the green coal production problem [5], and the structure optimization of a blended-wing-body underwater glider [22], etc. They can be defined as constrained multi-objective optimization problems (CMOPs) and expressed as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \hspace{5.0pt}&{}\mathbf {F(x)} = (f_1(\textbf{x}),f_2(\textbf{x}),\ldots , f_M(\textbf{x}))^\textrm{T}\in \mathbb {F}\\ \;\text {s.t.}\, &{}\textbf{x}\in \mathbb {S}\\ &{}g_i(\textbf{x})\le 0,\quad i=1,\ldots ,p\\ &{}h_i(\textbf{x})=0,\quad i=p+1,\ldots ,q, \end{array}\right. } \end{aligned}$$

(1)

where $\textbf{x}=(x_1,\ldots ,x_D )^\textrm{T}$ is a D-dimensional decision vector in the decision space $\mathbb {S}$, $\mathbf {F(x)}$ represents M objective functions that need to be optimized simultaneously, $\mathbb {F}$ is the objective space, p is the number of inequality constraints, $g_i (\textbf{x})$ represents the ith inequality constraints, $(q-p)$ is the number of equality constraints, and $h_i (\textbf{x})$ represents the $(i-p)$th equality constraints. The degree of constraint violation of $\textbf{x}$ at the ith constraint is calculated as

$$\begin{aligned} CV_i(\textbf{x})= {\left\{ \begin{array}{ll} max(0,g_i(\textbf{x})),&{}\textrm{if}\hspace{5.0pt}i\le p\\ max(0,|h_i(\textbf{x})-\eta |),&{}\textrm{otherwise} \end{array}\right. } ,\quad i=1,2,\ldots ,q,\nonumber \\ \end{aligned}$$

(2)

where $\eta$ is a sufficiently small positive value (e.g., $\eta =10^{-4}$) for relaxing the equality constraints to inequality constraints. The overall constraint violation value of $\textbf{x}$ is calculated as

$$\begin{aligned} \textrm{CV}(\textbf{x})=\sum \limits _{i=1}^{q}\textrm{CV}_i(\textbf{x}), \end{aligned}$$

(3)

then $\textbf{x}$ is feasible if $\textrm{CV}(\textbf{x})=0$; otherwise, it is infeasible. Suppose two feasible decision vectors $\textbf{x}_u$ and $\textbf{x}_v$, if any $f_i(\textbf{x}_u)\le f_i(\textbf{x}_v)$, and there is at least one dimension $f_i(\textbf{x}_u) <f_i(\textbf{x}_v)$, then $\textbf{x}_u$ is said to Pareto-dominate $\textbf{x}_v$, denoted as $\textbf{x}_u\prec \textbf{x}_v$.

A feasible solution is called Pareto-optimal when no other feasible solution dominates it. The set of all Pareto-optimal solutions in the search space is the Pareto set (PS). The image of all Pareto-optimal solutions in the objective space is the Pareto front (PF).

Compared with unconstrained MOPs, CMOPs are more challenging and have received more attention in recent years. The critical to solve CMOPs is to effectively balance feasibility, convergence, and diversity [19]. As a result, a number of novel algorithms have recently emerged. A common feature of such algorithms is the transformation of the original CMOPs to make better use of the potential information in the search space and to avoid the difficulties encountered in solving the original CMOPs directly [19]. Some scientists are motivated to solve CMOPs using multi-stage evolution methods. They tend to promote different performance at different stages of the algorithm, generally achieving fast convergence before considering feasibility and diversity, proposing algorithms, such as ToP [20], PPS [13], and CMOEA-MS [31]. Some scientists try to preserve infeasible solutions in the search process and extract useful genetic information from the infeasible ones to generate more diversified solutions. Along this line of research, many CMOEAs with multi-population cooperation methods have been proposed; for example, C-TAEA [18], CCMO [30], and Bico [21].

However, these algorithms also have certain drawbacks. It is difficult to design an effective transformation technique to guarantee the equivalence with the original problem. [14, 19] If the problem transformation mechanism is not reasonable, the algorithm performance will degrade dramatically due to the deviation of the transformed problem from the original one. The specific indication in multi-stage algorithms it that it may cause populations stuck in local optimums, especially when feasible regions are narrow or poorly distributed in the search space. In the case of multi-population algorithms, it is that too much attention to the transformed problem may lead to the waste of computational resources and poor feasibility when the PF of the transformed problem differs significantly from that of the original problem.

In this paper, to fully and efficiently explore the solution space and to better balance convergence and diversity, we combine multi-stage strategy and multi-population strategy, and propose a novel constrained multi-objective optimization evolutionary algorithm based on three-stage multi-population coevolution (CMOEA-TMC). The main contributions of CMOEA-TMC are listed as follows:

• 1. To address the problem that the single population is prone to fall into the local optimum, we propose a multi-population method that includes both parallel evolution and coevolution. (1) The main population, called mainPop, is divided into several subpopulations that evolve using the coarse-grained parallel algorithm to speed up convergence and perform global searches and (2) the helper population, called helpPop, is to better maintain diversity by providing information of infeasible solutions with mainPop during offspring generation and cross-evolution.

• 2. A novel three-stage strategy is designed to improve search efficiency and ensure solution feasibility. In the first stage, it focuses on fast convergence and global search by dividing subpopulations. In the second stage, it focuses on the independent evolution of subpopulations, which can maintain the diversity of solution sets. In the third stage, extreme value mining is performed to find global optimal solutions.

• 3. A novel algorithm named CMOEA-TMC is proposed. The combination of multi-population and multi-stage strategies allows the transformed problem to be as consistent as possible with the original ones and results in better overall performance of the algorithm. Systematic experiments on three sets of benchmark functions and a real-world case demonstrate the effectiveness of CMOEA-TMC.

The rest of this article is organized as follows. The section “Related work” overviews the state-of-the-art evolutionary approaches developed for CMOPs. The section “The proposed algorithms: CMOEA-TMC” describes the details of CMOEA-TMC. Afterward, in the section “Experimental research”, we compare CMOEA-TMC with five advanced CMOEAs on 33 benchmark problems and a real-world boiler combustion optimization problem, showing the competitiveness of CMOEA-TMC. Finally, the section “ Conclusion” concludes this article.

Related work

In the early days, scientists first focus on multi-objective optimization problems (MOPs) without constraints. The optimization algorithms for MOPs can be classified into two categories: traditional algorithms and intelligent algorithms [10]. Traditional algorithms include the weighting method, the constraint method, and the linear programming method [10]. For example, the weighting method refers to assigning appropriate weighting factors to the different objectives in a multi-objective problem according to their importance, and then summed up as a new objective function. Traditional algorithms always transform a multi-objective problem into a single-objective problem, in which only one solution can be obtained in each optimization, resulting in poor diversity [3]. Intelligent algorithms mainly refer to evolutionary algorithms (EAs), which iterate in the unit of population and can handle large, complex search spaces. These methods produce a set of solutions in a single run and are better suited to multi-objective optimization needs [4]. Considering the high robustness and broad applicability of EAs, it has been recognized as an efficient approach to solving MOPs [32]. Over the past 2 decades, many EAs, such as genetic algorithm (GA) [6], differential evolution (DE) [27], and particle swarm optimization (PSO), [11] have been applied, and multi-objective evolutionary algorithms (MOEAs) have performed well in solving various MOPs. Many scientists have studied MOEAs and made some improvements, such as domination-based EA [9, 36], decomposition-based EA [16, 37], indicator-based EA [35, 39], etc.

Over the last 2 decades, many constraint handling techniques (CHTs) have been proposed for constrained problems. They are constrained dominance principle (CDP) [9], penalty function methods [34], and $\varepsilon$-constrained methods [28]. Of these, CDP is the most widely used one because of its efficiency and simplicity. These CHTs are usually utilized to solve single-objective optimization problems and can be used to solve CMOPs by extension or modification. For example, Deb et al. [9] proposed the famous NSGA-II-CDP, which incorporates CDP into NSGA-II for environment selection. Fan et al. [12] proposed an angle-based CDP algorithm (MOEA/D-ACDP), which takes advantage of classical Pareto to compare infeasible solutions within a given angle. However, these methods still have some limitations, because they use relatively simple constraint information. They also have difficulty in achieving good results when dealing with types of problems, such as low feasible domains, strong constraints, and discontinuous PF. Therefore, there is a need to propose improved algorithms that are more applicable to CMOPs.

In recent years, to solve CMOPs more efficiently, many researchers try to transform CMOPs into other problems, such as multi-stage optimization problems or collaborative optimization problems. This can assist the population to discover some potential information during the evolutionary process and to converge better.

Multi-stage optimization generally involves dividing the optimization process into multiple stages, with different CHTs or different objects being optimized in different stages. Back in 2013, Miyakawa et al. [25] proposed a new CMOEA based on a two-stage non-dominated solution ranking. In the first stage, the degree of constraint violation for each constraint is considered as an objective function, and the whole population is classified into several fronts by non-dominated ranking based on the constraint violation values. In the second stage, each obtained front is reclassified by an undominated ranking based on the objective function value, and the parent population is selected from it. Miyakawa et al. claimed that feasible solutions with better objective functions can be found using this two-stage non-dominated ranking. Liu and Wang [20] proposed a two-stage framework called ToP for dealing with CMOPs with complex constraints. ToP is divided into two stages, the uniqueness of which is its first stage, where the CMOP is transformed into a constrained single-objective optimization problem using a weighted summation method. CDP is used to deal with the constraints, aiming at finding promising feasible regions and fast convergence, while the second stage is solved using common CMOEAs, such as NSGA-II and CMOEA/D. Fan et al. [13] embed the push–pull search (PPS) framework into CMOEA/D. PPS is also divided into two stages: in the push stage, only the objective function is considered for the search to approximate the unconstrained PF; in the pull stage, an improved CMOEA is used to pull the infeasible individuals obtained in the push stage to the feasible non-dominated regions. Tian et al. [31] devised a two-stage evolutionary algorithm, called CMOEA-MS, in which one stage helps the population to reach the feasible regions and the other stage allows the population to spread along the feasible boundaries. Furthermore, according to the status of the population, the algorithm can adaptively switch between the two stages.

Coevolution refers to the evolutionary technology in which multiple objects carry out the collaborative search through certain mechanisms and strategies, such as multi-population, multi-algorithm, and multi-strategy integrated evolution. When applied to CMOPs, multi-population and multi-constraint processing is mostly used. Li et al. [18] proposed a two-archive evolutionary algorithm (C-TAEA). It maintains two archives simultaneously: (1) a convergence-oriented archive (CA), which optimizes constraints and objectives, and (2) a diversity-oriented archive (DA), which optimizes only objectives. The two populations cooperate with each other in the mating selection and environmental selection. CCMO [30] is a coevolutionary algorithm that simultaneously computes two objective problems, the original problem and the helper problem. Typically, the original problem in CCMO is solved by population 1. The helper problem is defined as the original problem with constraints removed and is solved by population 2. Coevolution is achieved by sharing offspring between the two populations. Liu et al. [21] designed a novel bidirectional coevolutionary algorithm using both the main population and archive population. Specifically, the main population maintains the feasibility of the solution set and moves from the feasible side to the PF, while the archive population uses the angle information to maintain the diversity of the solution set and approach the PF from the infeasible side.

In view of the effectiveness of multi-stage algorithms and coevolutionary algorithms in dealing with CMOPs, some optimization algorithms that combine the two strategies have been produced recently. Fan et al. [14] improved CCMO by proposing a two-stage coevolutionary constrained multi-objective optimization evolutionary algorithm (TSC-CMOEA), which switches to the second stage when the rate of population change is too small during coevolution, discarding the helper problem and keeping only the main population evolving, thus saving computational resources and enhancing the convergence of the population. Ming et al. [24] proposed a new method with dual stages and dual populations, called DD-CMOEA. Specifically, the dual populations are mainPop and auxPop, which evolve with and without considering constraints, respectively. The dual stages are exploration and exploitation, focusing on extensive search for solutions with good objective values in the exploration stage and convergence to the true PF in the exploitation stage.

The proposed algorithms: CMOEA-TMC

Main framework of CMOEA-TMC

To overcome the current CMOEAs’ difficulty in effectively balancing feasibility, convergence, and diversity, this paper proposed a novel algorithm—CMOEA-TMC. As outlined in Fig. 1, the proposed CMOEA-TMC has three stages: fast convergence stage, diversity maintenance stage, and extremum mining stage. It is worth noting that the proposed algorithm contains two archives: the main population (called mainPop) and the help population (called helpPop). mainPop is used to search for the constrained PF throughout the process, and helpPop searches for the unconstrained PF in the first and second stages.

Fig. 1

The framework of CMOEA-TMC

Algorithm 1

Procedure of $CMOEA-TMC$

Algorithm 1 gives the pseudocode of CMOEA-TMC. In the first stage, the algorithm transforms the CMOP into multiple single-objective problems by setting different weight vectors, so as to achieve task partitioning of the complex problem. The detailed transformation process is described in the section “The first stage: fast convergence”. mainPop is also divided into multiple subpopulations and evolves using the coarse-grained parallel algorithm which has strong global search capability and achieves fast convergence. In addition, the guidance information provided by helpPop to mainPop ensures that the population can maintain good diversity. In the second stage, mainPop changes to use the original CMOP as the objective function, which is beneficial to obtaining more high-quality feasible solutions. Meanwhile, the subpopulations in mainPop maintain independent evolution, so that all candidate solutions obtained in the first stage continue to converge to more promising feasible domains, maintaining the diversity of the solution set. In the third stage, the individuals of all subpopulations in mainPop are aggregated together to optimize for the global optimal solution. And, helpPop no longer provides additional information, as we consider it more important to focus on the constrained PF in this stage. These three stages are further explained in the sections “The first stage: fast convergence”–“The third stage: extremum mining”.

It is worth emphasizing that to compare the performance of different solutions, CDP is applied to the environment selection. The definition of CDP is as follows. Given two decision vectors $\textbf{x}_u$ and $\textbf{x}_v$, $\textbf{x}_u$ is said to constraint-dominate $\textbf{x}_v$ if one of the following conditions is satisfied:

• (1) both $\textbf{x}_u$ and $\textbf{x}_v$ are infeasible, and $\textrm{CV}(\textbf{x}_u)\le \textrm{CV}(\textbf{x}_v)$;

• (2) $\textbf{x}_u$ is feasible, yet $\textbf{x}_v$ is infeasible;

• (3) both $\textbf{x}_u$ and $\textbf{x}_v$ are feasible, and $\textbf{x}_u\prec \textbf{x}_v$.

In general, CDP can motivate the population to approach or enter the feasible region promptly, because feasible solutions are always selected before infeasible solutions in environmental selection.

The first stage: fast convergence

Considering the fact that CMOEAs need to balance multiple objective functions, the convergence speed is inevitably slow, which presents a major challenge for solving CMOPs with a wide objective space. Therefore, this paper considers transforming a CMOP into multiple constrained single-objective optimization problems by weighted summation, and solves it using the coarse-grained parallel evolutionary algorithm, that is, a subpopulation in mainPop focuses on one of the single-objective problems. Handling with a single-objective optimization problem with constraints is much easier than handling with a multi-objective optimization problem with constraints. Although each subpopulation can only approach some local solutions in the PF of the original problem, the global search ability and convergence performance of the population are significantly improved. Setting appropriate weight vectors and ending conditions can keep the algorithm with good convergence and diversity, and provide high-quality initial solutions for subsequent optimization.

Thus, a CMOP with M objective functions is transformed into $(M+1)$ constrained single-objective optimization problems

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \hspace{5.0pt}&{}{\left\{ \begin{array}{ll} f^{'}_k(\textbf{x})=\frac{f_1(\textbf{x})+\cdots +(\omega +1)f_k(\textbf{x})+\cdots +f_M(\textbf{x})}{M+\omega }, &{}k=1,\ldots ,M\\ f^{'}_k(\textbf{x})=\frac{f_1(\textbf{x})+\cdots +f_M(\textbf{x})}{M}, &{}k=M+1 \end{array}\right. }\\ \;\text {s.t.}\, &{}\textbf{x}\in \mathbb {S}\\ &{}g_i(\textbf{x})\le 0,\quad i=1,\ldots ,p\\ &{}h_i(\textbf{x})=0,\quad i=p+1,\ldots ,q, \end{array}\right. } \end{aligned}$$

(4)

where $\omega$ is set to 2 based on the sensitivity analysis in the section “Sensitivity analysis of parameters in CMOEA-TMC”. Since we only change the objective function and keep the constraints unchanged, Eqs. (1) and (4) share the same feasible regions.

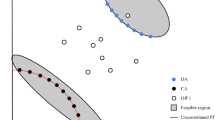
The benefits of multi-population strategy are explained below. As shown in Fig. 2, candidate solutions of single population are likely to be distributed in the center of the true PF, which leads it to potentially ignore solutions at the edges of the PF. As shown in Fig. 2, candidate solutions of multi-population may be evenly distributed across different locations of the true PF, which makes the expansion of the population distribution easier.

Fig. 2

Extending the distribution of mainPop using different population settings

Next, the implementation details of the first stage are explained in two parts: (1) update procedure and (2) switching condition.

(1) Update procedure In the first stage, for mainPop, we need it to converge quickly to the true PF, so differential evolution (DE) is considered as the search engine. The pseudocode is presented in Algorithm 2.

Algorithm 2

Evolution of subpopulation of mainPop in the first stage

We employ three popular generation strategies to generate offspring:

• (a) DE/current-to-rand/1:

  $$\begin{aligned} \textbf{u}_i = \textbf{x}_i+F*(\textbf{x}_{r1}-\textbf{x}_i)+F*(\textbf{x}_{r2}-\textbf{x}_{r3}). \end{aligned}$$

  (5)

• (b) DE/rand-to-best/1/bin:

  $$\begin{aligned}&\textbf{v}_i = \textbf{x}_{r1}+F*(\textbf{x}_{\textrm{best}}-\textbf{x}_{r1}) +F*(\textbf{x}_{r2}-\textbf{x}_{r3}) \end{aligned}$$

  (6)
  $$\begin{aligned}&\textbf{u}_{i,j} = {\left\{ \begin{array}{ll} \textbf{v}_{i,j}&{} \text {if} \;\textrm{rand}_j<\textrm{CR}\;\textrm{or}\;j=j_{\textrm{rand}} \\ \textbf{x}_{i,j}&{} \textrm{else}. \end{array}\right. } \end{aligned}$$

  (7)

• (c) DE/current-to-best/1:

  $$\begin{aligned} \textbf{u}_i = \textbf{x}_i+F*(\textbf{x}^{\textrm{help}}_{\textrm{best}}-\textbf{x}_i)+F*(\textbf{x}_{r1}-\textbf{x}_{r2}), \end{aligned}$$

  (8)

where $\textbf{v}_i$ is the ith mutant vector, $\textbf{u}_i$ is the ith trial vector, $r_1$, $r_2$, and $r_3$ are three mutually distinct integers chosen at random from [1, N], $\textbf{x}_{\textrm{best}}$ denotes the individual with the smallest objective function value in the current subpopulation, $\textbf{x}^{\textrm{help}}_{\textrm{best}}$ denotes the best individual of helpPop, $\textrm{rand}_j$ is a random number in [0, 1], $j_{\textrm{rand}}$ is a random integer in [1, D], F is the scaling factor, and CR is the crossover control parameter. In addition, as suggested by [20] and [33], F and CR are randomly chosen from the scaling factor pool (i.e., $Fpool =[0.6,0.8,1.0]$) and the crossover control parameter pool (i.e., $CRpool=[0.1,0.2,1.0]$), respectively.

In DE/current-to-rand/1, $\textbf{x}_i$ learns information from other randomly selected individuals, which facilitates the expansion of the global search. In DE/rand-to-best/1/bin, information about the best individual in the current subpopulation is used. Note that $\textbf{x}_{\textrm{best}}$ in Eq. (6) is determined based on the transformed objective function $f^{'}_k$. Before the population enters the feasible region, $\textbf{x}_{\textrm{best}}$ is similar to the randomly selected individual. After the population enters the feasible region, the population can be guided toward the optimal solution by $\textbf{x}_{\textrm{best}}$. In DE/current-to-best/1, information about the optimal individual in helpPop is used. In general, helpPop converges more quickly to the unconstrained PF, and if there is an infeasible region between $\textbf{x}^{\textrm{help}}_{\textrm{best}}$ and mainPop, mainPop has the opportunity to cross the infeasible region and be led to a more convergent feasible region. Overall, these three variants make good use of information about local and global optimum, allowing the evolution of populations to better balance convergence and diversity.

For helpPop, we use the GA operator for optimization and environmental selection based on the fitness evaluation strategy proposed in SPEA2 [41].

(2) Switching condition If we perform a large number of fitness evaluations in the first stage, all individuals in mainPop are likely to converge to the optimal solution of the transformed single-objective problems, which would result in the lack of diversity. To obtain high-quality feasible solutions that are close to the PF of the original CMOP but maintain good diversity, we have designed the following three conditions to ensure that the evolution of subpopulation can be terminated early.

• (a) Feasibility condition: Following the suggestion in [20], the feasibility proportion of the current subpopulation is larger than 1/3.

• (b) Convergence condition: Suppose that $f_{\textrm{max},j}$ and $f_{\textrm{min},j}$ represent the maximum and minimum values of the jth objective function among all feasible solutions found in the current subpopulation, respectively. Then, the jth objective function of each individual is normalized as

  $$\begin{aligned} \overline{f_j}(i) = \frac{f_j-f_{\textrm{min},j}}{f_{\textrm{max},j}-f_{\textrm{min},j}}. \end{aligned}$$

  (9)

  Subsequently, we add up all the normalized objective function values

  $$\begin{aligned} \overline{f^{'}}(i) = \sum \limits _{j=1}^{M}\overline{f^{'}_j}(i). \end{aligned}$$

  (10)

  Finally, we rank the feasible solutions from smallest to largest according to $\overline{f^{'}}(i)$. The convergence index ($\delta _{\textrm{con}}$) is defined as the maximum difference of $\overline{f^{'}}(i)$ among the first 1/2 feasible solutions

  $$\begin{aligned} \delta _{\textrm{con}} = \overline{f^{'}}(\textrm{median})-\overline{f^{'}}(1). \end{aligned}$$

  (11)

  If $\delta _{\textrm{con}}$ is less than 0.2, the convergence condition is regarded to be satisfied.

• (c) Diversity condition: Suppose that $f_{\textrm{median},j}$ and $f_{\textrm{min},j}$ represent the median and minimum values of the jth objective function among all feasible solutions found in the current subpopulation during evolution, respectively. The diversity index $\delta _{\textrm{div}}$ is defined as

  $$\begin{aligned} \delta _{\textrm{div}} = \min \left( \frac{f_{\textrm{median},j}-f_{\textrm{min},j}}{f_{\textrm{min},j}+1e^{-5}}\right) . \end{aligned}$$

  (12)

  If $\delta _{\textrm{div}}$ is less than 0.1, the diversity condition is regarded to be satisfied.

The purpose of the feasibility condition is to ensure that some feasible individuals have been obtained. The convergence condition indicates that some feasible solutions gradually converge to a small region, and the diversity condition indicates that some feasible solutions are relatively dispersed, rather than having converged to a small point. Therefore, for each subpopulation in mainPop, the first stage should terminate when the feasibility condition is satisfied and the convergence or diversity condition is met, thus ensuring convergence of the feasible solution and preventing loss of diversity.

When all subpopulations satisfy the above switching condition, the first stage of CMOEA-TMC ends and the second stage starts.

The second stage: diversity maintenance

Although we have found promising feasible solutions in the first stage, the performance of the population still needs to be improved. On the one hand, since we only use part of the feasible solutions in subpopulations of mainPop to measure the termination conditions in the first stage, it is possible that some individuals are far from the Pareto-optimal solution. On the other hand, due to the lack of an explicit diversity maintenance mechanism in single-objective optimization, the population is slightly less diverse across the PF. As shown in Fig. 3, the set of candidate solutions in Pop(2) is far away from the constrained PF, and some solutions in Pop(2) are dominated by solution A in Pop(1) and solution B in Pop(3). Without diversity maintenance, these solutions may enter the region where Pop(1) or Pop(3) is located, as circled in Fig. 3. We expect the diversity and convergence of mainPop to be further enhanced in the second stage, with a distribution as shown in Fig. 3 in the ideal state.

Fig. 3

Comparison of population distribution without and with diversity maintenance

Therefore, in this stage, we consider using the original CMOP to further optimize for the high-quality candidate solutions generated based on the first stage, to obtain a series of feasible solutions that are well distributed and converge well. Drawing on the ideas of CCMO [30], the coevolution of mainPop and helpPop is carried out in a weak cooperation by sharing the offsprings, to enable them have the opportunity to jump out of the infeasible region and evolve toward the global PF. The pseudocode for the second stage is presented in Algorithm 3.

Algorithm 3

Evolution of mainPop and helpPop in the second stage

In addition, we also set a switching condition for the second stage. When the number of function evaluations reaches 60% of the set maxFE, the second stage of CMOEA-TMC ends and the third stage starts.

The third stage: extremum mining

After the second stage, we have obtained a series of well-distributed and convergent feasible solutions, but the independent evolution of multiple subpopulations has led to the possibility of some dominant solutions among the generated feasible solutions. Therefore, in the third stage, all subpopulations of mainPop are combined and compete together for extremum mining. It is worth mentioning that because the helper problem can no longer support mainPop well, we discard helpPop in the third stage to save the computational resources.

Dynamic $\eta$ strategy for equation constraints

For equation constraints in CMOPs, we introduce a very small positive value eta to relax equation constraints to inequality constraints. The value of $\eta$ has a large impact on the convergence of the algorithm. If $\eta$ takes a larger value, the convergence is usually better, but it also leads to a large difference between the optimized solution and the true solution. if $\eta$ takes a small value, some infeasible solutions that are partially close to the feasible region may be discarded, because the equation constraints are not satisfied, thus affecting the convergence. Therefore, a dynamic $\eta$ strategy is used, with $\eta$ taking a slightly larger value in the early evolution, relaxing the stringency of the constraints on equations in the expectation of finding more promising solution sets, and gradually decreasing to an accepted value in the late evolution.

The specific dynamic adjustment formula for $\eta$ is as

$$\begin{aligned} \eta = {\left\{ \begin{array}{ll} 0.001-(\textrm{log}_{\frac{1}{5}\textrm{maxFE}}\textrm{FE})\\ \times (0.001-0.0001), &{}\textrm{FE}\le \frac{1}{5}\textrm{maxFE} \\ 0.0001, &{}\textrm{FE}>\frac{1}{5}\textrm{maxFE}, \end{array}\right. } \end{aligned}$$

(13)

where FE represents the current number of function evaluations and maxFE represents the maximum number of function evaluations set by the user.

Effectiveness analysis of CMOEA-TMC

To analyze the effectiveness and mechanism of CMOEA-TMC, we show the early, middle, and last population distribution of CMOEA-TMC on 2-objective MW11 in Fig. 4. The gray surfaces denote the feasible regions of the problem, and the black and red lines denote the unconstrained PF and constrained PF, respectively.

Fig. 4

Populations in the early, middle, and last generations of ToP, CCMO, and CMOEA-TMC on 2-objective MW11

Table 1 Parameter settings of the test sets

As shown in the first column of Fig. 4, the population of ToP converges quickly but can only converge to a single feasible region in the early generations and cannot spread to the other feasible regions at last. For MW11 which has three small feasible regions, ToP with only one population has a lack of diversity maintenance. CMOEA-TMC and CCMO behave similarly in the early generations. They both have two populations, one considering constraints and the other not considering constraints. However, helpPop of CMOEA-TMC converges faster in the early stage, which greatly helps mainPop to perform global search and thus maintain diversity. Population2 of CCMO converges slower than Population1, which may lead to the inability to provide useful information to Population1 during coevolution, and therefore, offsprings are mainly generated based on Population1.

In the middle generation, CMOEA-TMC evolves independently in three small feasible regions while generating offsprings located in infeasible regions. This indicates that mainPop and helpPop collaborate effectively and that CMOEA-TMC has the opportunity to spread across infeasible regions into feasible ones in the presence of dispersed feasible regions. In contrast, although CCMO also carries out cooperation between the two populations, the offsprings are mainly generated based on Population1, and thus, it has difficulty in accessing the previously missed feasible regions.

Throughout the evolutionary process, CMOEA-TMC explores the search space more fully. Finally, CMOEA-TMC obtains well-diversified final solutions and shows its strong performance.

Computational complexity of CMOEA-TMC

For CMOEA-TMC, there are three stages: the first stage is DE evolution of subpopulations, the second stage is GA evolution of subpopulations, and the third stage is overall GA evolution. Let us denote the subpopulation size, the number of subpopulations, the population size, the number of objectives, and the dimension of decision vectors by N, $M+1$, Q, M, and D, where $Q=N\times (M+1)$.

(1) Time complexity In the first stage, for each subpopulation, the time complexities of evolutionary variation, crossover, and environmental selection are O(ND), O(N), and O(N), respectively. Thus, the overall time complexity is $(M+1)\times (O(ND)+O(N)+O(N))=O(MND)$. In the second stage, for each subpopulation, the time complexities of mating selection, genetic operators, and environmental selection are O(N), O(ND), and $O(MN^2)$, respectively. In general, $O(MN^2)>O(ND)$, so the overall time complexity is $(M+1)\times O(MN^2)=O(M^2 N^2)$. In the third stage, the entire population Q undergoes GA evolution. The time complexities of mating selection, genetic operators, and environmental selection are O(Q), O(QD), and $O(MQ^2)$, respectively, where $O(MQ^2)$ is usually the largest. Thus, the time complexity of the third stage is $O(MQ^2)=O(M^3 N^2)$.

In summary, the time complexity of three stages of CMOEA-TMC is O(MND), $O(M^2 N^2)$, and $O(M^3 N^2)$, respectively. Some comparison algorithms that use GA operators, such as CCMO and C-TAEA, usually have a time complexity of $O(M^3 N^2)$, so the proposed algorithm has an advantage in the first and second stages and can result in a smaller time cost.

(2) Space complexity The memory consumption of CMOEAs is concentrated in the storage of the parent and offspring populations. CMOEA-TMC needs to store mainpop and offspring population, each of which takes up O(DQ) space. In the first stage, the transformed single-objective problem is used for performance comparison, so the space used to store the objective values and constraint violation values is O(Q) and O(Q), respectively. In the second and third stages, the space used for storing the objective values and constraint violation values is O(MQ) and O(Q), respectively. Considering the different stages together, the overall space complexity of CMOEA-TMC is ${O(DQ) + O(MQ) + O(Q)}$. The space complexity and the population size are closely correlated, because the different algorithms mainly store the parent and offspring population information in each iteration. When the population size is fixed, the differences in space complexity among different algorithms are small. For CMOEA-TMC, no additional storage content is introduced, so its space complexity is approximate to that of the comparison algorithms.

Experimental research

Test sets and parameters setting

To systematically evaluate the performance of CMOEA-TMC, three benchmark problem test suites are employed to compare CMOEA-TMC with other four CMOEAs. Test suites are DOC, MW, and CF. To be specific, DOC is a recently proposed test suite that contains both decision and objective constraints, and it also contains both inequality and equality constraints. MW is also a recently proposed test suite that covers various features, such as small feasible regions, high dimensional decision space, and so on. As a classic test suit, the CF test suit has nonlinear, discontinuous PF. The detailed description of these three test suits can be found in their original paper [20, 23, 38]. Table 1 shows parameter settings of the test sets used.

For CMOEA-TMC, we set $\omega$, $\delta _{\textrm{con}}$, and $\delta _{\textrm{div}}$ to 2, 0.2, and 0.1 based on parameter sensitivity experiments in the section “Sensitivity analysis of parameters in CMOEA-TMC”, and these values showed the best performance. For performance comparison, we consider five advanced CMOEAs, which are ToP, PPS, CCMO, RVEA, and C-TAEA. The parameters of all the compared algorithms are set as suggested in their original papers [2, 13, 18, 20, 30]. For the ToP framework, it is embedded with the constrained NSGA-II where the first phase ends when the feasibility proportion $P_\textrm{f}$ is larger than 1/3 and the difference $\delta$ is less than 0.2. For the PPS framework, it is embedded with the constrained MOEA/D, where the parameter settings are $\alpha =0.95$, $\tau =0.1$, $\textrm{cp}=2$, and $l=20$. Among these algorithms, ToP, PPS, and CCMO use DE to generate offspring solutions, while C-TAEA and RVEA employs the simulated binary crossover [7] and polynomial mutation [8] for generating offspring solutions. Besides, all the experiments in this paper were conducted on the PlatEMO proposed in [29].

Table 2 Mean and standard deviation of the IGD values obtained by TOP, PPS, CCMO, C-TAEA, RVEA, and CMOEA-TMC for 30 independent runs on the DOC test suite

Performance indicators

To measure the performance of different algorithms, two widely used metrics were employed in our experiments, which can measure both convergence and diversity.

• (1) Inverted Generational Distance (IGD) [1]: Assume that P is the set of feasible solutions obtained from a CMOEA, and $P^*$ is the set of points uniformly sampled along the real PF, IGD is defined as

  $$\begin{aligned} \textrm{IGD}(P,P^*) = \frac{1}{|P^* |}\sum \limits _{z^*\in P^*}\textrm{distance}(z^*,P), \end{aligned}$$

  (14)

  where $\textrm{distance}(z^*,P)$ is the Euclidean distance between $z^*$ and the nearest point in P, and $|P^* |$ is the total number of points in P. It can be seen that calculating IGD needs to know the real PF, and the smaller the IGD value, the better the performance of a CMOEA.

• (2) Hypervolume (HV) [40]: HV measures the volume enclosed by P and a specified reference point in the objective space, and it is defined as

  $$\begin{aligned} \textrm{HV}(P) = \textrm{VOL}\left( \bigcup \limits _{x\in S}[f_1(x),z_{1}^r]\times \cdots \times [f_M(x),z_{M}^r]\right) ,\nonumber \\ \end{aligned}$$

  (15)

  where VOL indicates the Lebesgue measure, and $z^r=(z_{1}^r,\ldots ,z_{M}^r )^\textrm{T}$ is a user-defined reference point. In this paper, the reference point is set to 1.1 times the lowest point of the PF, so that it can be dominated by all the feasible solutions in PF. It is worth noting that the larger the HV value, the better the performance of a CMOEA.

Experimental results of DOC problems

On the DOC problem test set, Table 2 shows the average and standard deviation of the IGD values for 30 independent runs of ToP, PPS, CCMO, C-TAEA, RVEA, and CMOEA-TMC on the DOC problem test set. Table 3 shows the average and standard deviation of the HV values. In those two tables, Wilcoxon’s rank-sum two-sided comparison [17] at the 0.05 significance level is performed to test the statistical significance of the experimental results between two algorithms. The two-sided Wilcoxon rank-sum test tests the null hypothesis that the data from two samples are continuously distributed samples with equal medians, against the alternative that they are not. For convenience, “+”, “-”, and “$\approx$” denote that a peer CMOEA performs better than, worse than, and similar to CMOEA-TMC, respectively. NaN indicates that the algorithm failed to find feasible solutions.

As can be seen from Tables 2 and 3, CMOEA-TMC clearly outperforms the other four compared algorithms on the DOC test set, achieving the best results on eight of the nine test problems, followed by CCMO, which achieves one best result on DOC7. It is found that DOC7 contains fewer constraints, and the helper population in CCMO can play a greater role. The DOC test set contains decision space constraints and objective space constraints, and the initial distribution of the objective function is more divergent, so it is more complex and difficult to solve. CMOEA-TMC shows better convergence and diversity on this series of problems, suggesting that the algorithm’s three-stage strategy and multiple subpopulations’ coevolutionary design are effective.

Table 3 Mean and standard deviation of the HV values obtained by TOP, PPS, CCMO, C-TAEA, RVEA, and CMOEA-TMC for 30 independent runs on the DOC test suite

Fig. 5

True PF and final solutions achieved by each algorithm on DOC1, DOC6, and DOC8

Figure 5 plots the performance of the six MOEAs on the three test problems DOC1, DOC6, and DOC8, where DOC1 and DOC6 are two-objective problems with continuous and discontinuous feasible domains, respectively, and DOC8 is a three-objective problem with a discontinuous feasible domain. In Fig. 5, the red line represents the true PF and the blue points are the final solutions obtained by the algorithm. It is clear that CMOEA-TMC exhibits the better convergence in all three problems, while the other CMOEAs still retain a large number of individuals far from the true PF. The fast convergence rate of CMOEA-TMC is mainly attributed to the single-objective evolution in the first stage and the coevolution with helpPop, which makes it easier for mainPop to skip the infeasible region and converge quickly. For DOC6 and DOC8 with discontinuous feasible regions, CMOEA-TMC shows better diversity than other CMOEAs, which is attributed to the strategy of independent parallel evolution of multiple subpopulations.

Meanwhile, to verify the effectiveness of the dynamic $\eta$ strategy, the static $\eta$ strategy and the dynamic $\eta$ strategy run 30 times independently for the three problems of DOC3, DOC5, and DOC7 with equation constraints, respectively. The mean and standard deviation of the obtained IGD values are calculated, and the final results using the static $\eta$ strategy and the dynamic $\eta$ strategy are presented in Table 4. The bolded data in Table 4 indicate the solution with the smaller IGD value obtained under the same algorithm for the same test problem with equation constraints, in both cases with static $\eta$ strategy and the dynamic $\eta$ strategy. It can be seen that IGD values of compared algorithm decreased with the dynamic $\eta$ strategy, except for the case where no feasible solution is obtained resulting in an NaN IGD value. After performing the two-sided Wilcoxon rank-sum test on the data, the IGD values of the static $\eta$ strategy are usually worse than or similar to the IGD values of the dynamic $\eta$ strategy, which means that the convergence and diversity of algorithms are improved after adopting the dynamic $\eta$ strategy.

Based on the above analysis, we can see that the novel multiple subpopulation parallel evolution method and three-stage strategy of CMOEA-TMC have good results on the DOC test set, and that the proposed dynamic $\eta$ adjustment strategy for equation constraints has some generality and can improve the performance of CMOEA for CMOPs with equation constraints.

Experimental results of MW and CF problems

To further verify the validity of CMOEA-TMC, we used MW and CF test suites for performance testing. Table 5 shows the average and standard deviation of the IGD values for 30 independent runs of ToP, PPS, CCMO, C-TAEA, RVEA, and CMOEA-TMC on the MW and CF test problem sets, and the HV results are presented in Table 6.

As shown in Tables 5 and 6, CMOEA-TMC achieves the best results on 11 problems with 6 for C-TAEA, 4 for PPS, 2 for RVEA, and 1 for CCMO. For the MW test set, CMOEA-TMC and C-TAEA perform better, probably because most of the MW functions have scattered and narrow feasible domains, so algorithms that are more concerned with diversity have better results. CMOEA-TMC maintains the uniform distribution of solution sets around the objective space through parallel evolution of subpopulations, and C-TAEA uses a diversity-oriented weighted vector method to keep the diversity in each direction, both of them focusing more on the maintenance of diversity in different directions. For the CF test set, the algorithms with DE operators (PPS and CMOEA-TMC) outperform other methods, because the CF functions have low-dimensional decision variables and discrete feasible regions, and DE may help to maintain good diversity.

Table 4 Mean and standard deviation of the IGD values before and after 30 independent runs of adding dynamic $\eta$ strategy on the DOC3, DOC5, and DOC7

Figure 6 plots the performance of the six CMOEAs on the three test problems MW5, MW12, and CF6. The red points are the true PF, the blue points are the final solutions obtained by each algorithm, and the gray areas represent the feasible regions in the target space. For MW5 with discontinuous and small feasible regions, CMOEA-TMC shows better diversity performance than other CMOEAs. For MW12 with feasible regions separated by infeasible regions, CMOEA-TMC crosses the local optimum and evolves toward the true PF, shows better convergence performance than other CMOEAs. For CF6 with true PF in segments, CMOEA-TMC can fully explore the target space and exhibits powerful performance.

Therefore, it can be concluded that the proposed CMOEA-TMC has better overall performance than compared CMOEAs when solving the benchmark CMOP, being able to better balance convergence and diversity, precisely due to the coevolution method and the three-stage algorithm design.

Sensitivity analysis of parameters in CMOEA-TMC

In CMOEA-TMC, there are three parameters (i.e., $\omega$, $\delta _{\textrm{con}}$ and $\delta _{\textrm{div}}$) that have an impact on the performance of the algorithm. $\omega$ determines the weight of different objective functions when converting a multi-objective problem into a single-objective problem. A large value of $\omega$ may cause subpopulations to fall into local optimum, while a small value of $\omega$ may cause overlapping search areas. $\delta _{\textrm{con}}$ and $\delta _{\textrm{div}}$ determine when to switch from the first stage to the second stage. A small value of $\delta _{\textrm{con}}$ or $\delta _{\textrm{div}}$ may result in the feasible solutions clustering in a very small region. However, with a large value of $\delta _{\textrm{con}}$ or $\delta _{\textrm{div}}$, the solution set may be far from the true PF when the first stage ends. Therefore, we conducted the sensitivity analysis of above three parameters.

We tested the performance on six test instances: DOC1, DOC6, DOC8, MW5, MW12, and CF6. Their PFs have different characteristics and therefore can provide insight on various aspects. We chose five different $\omega$ values: 1/2, 1, 2, 3, 4; four different $\delta _{\textrm{con}}$ values: 0.1, 0.2, 0.3, 0.4; and four different $\delta _{\textrm{div}}$ values: 0.05, 0.1, 0.15, 0.2. The average IGD values of the algorithm over ten independent runs were used as the evaluation criterion. The test results are shown in Figs. 7 and 8.

Fig. 6

True PF and final solutions achieved by each algorithm on MW5, MW12, and CF6

Table 5 Mean and standard deviation of the IGD values obtained by TOP, PPS, CCMO, C-TAEA, RVEA, and CMOEA-TMC for 30 independent runs on the MW and CF test suites

Table 6 Mean and standard deviation of the HV values obtained by TOP, PPS, CCMO, C-TAEA, RVEA, and CMOEA-TMC for 30 independent runs on the MW and CF test suites

Fig. 7

Average IGD values provided by CMOEA-TMC with different $\omega$ on DOC1, DOC6, DOC8, MW5, MW12, and CF6

Fig. 8

Average IGD values provided by CMOEA-TMC with different combinations of $\delta _{\textrm{con}}$ and $\delta _{\textrm{div}}$ on DOC1, DOC6, DOC8, MW5, MW12, and CF6

We can observe that, overall, CMOEA-TMC exhibits better performance with $\omega =2$, $\delta _{\textrm{con}}=0.2$ and $\delta _{\textrm{div}}=0.1$. Therefore, in this paper, $\omega$ is set to 2, $\delta _{\textrm{con}}$ is set to 0.2 and $\delta _{\textrm{div}}$ is set to 0.1.

Experiments on computing performance

To verify the computing performance of CMOEA-TMC, the average computation time of five comparative algorithms was counted. All experiments were performed on the computer with an i7-10510U CPU, on the PlatEMO built in MATLAB R2021b. Table 7 shows the average computation time spent by each algorithm running on the test problems in each test suit.

As shown in Table 7, for DOC and MW test suits, CMOEA-TMC has the shortest computation time except for RVEA. For CF test suite, the average computation time of CMOEA-TMC is slightly larger than that of ToP and RVEA, but much smaller than the other three algorithms. Therefore, the proposed CMOEA-TMC is computationally efficient.

Experimental results of real-world boiler combustion optimization problem

After testing CMOEA-TMC’s performance in solving a series of benchmark problems, this subsection examines the performance of CMOEA-TMC and four comparison CMOEAs on a real-world boiler combustion optimization problem.

Table 7 Mean time consumption (in seconds) of CMOEA-TMC and the peer CMOEAs on DOC, MW, and CF test suits

Power plant boilers have generated a lot of valuable historical data over many years of operation, which can be used to model the relationship between operating variables and performance indicators. The model can be optimized under specific constraints and the optimization results can provide guidance for adjustments to the boiler combustion process, thus improving the thermal efficiency and reducing the generation of pollutants.

In our experiment, the gradient boosted decision tree (GBDT) is used to model the operational data generated during boiler combustion. The inputs to the model are 19 non-adjustable operational variables and 16 adjustable operational variables, corresponding to variables, such as coal feed and damper opening in boiler combustion. The outputs of the model are four max–min normalized performance indicators corresponding to the outlet temperatures of air preheaters A and B and the $\textrm{NO}_x$ content of the inlet flue A and B. For the training process of GBDT, we used 5466 offline historical samples with the training data set of $5466\times 19$. Adequate historical data ensure the accuracy of GBDT, and an additional sample is used to test the performance of CMOEAs. The training and testing process is performed offline.

Table 8 Mean and standard deviation of the HV values obtained by TOP, PPS, CCMO, C-TAEA, RVEA, and CMOEA-TMC for ten independent runs on boiler combustion optimization

Fig. 9

Final solutions achieved by compared algorithm on real-world boiler combustion optimization problem

The demand of the power plant is to reduce these four performance indicators as much as possible to improve the coal combustion efficiency. By analyzing the historical data, it was found that the dampers opening corresponding to the 2nd, 4th, 9th, 12th, 14th, and 16th operating variables fluctuated very little, so the constraint was set to limit their optimization range to within 1% above and below the current sample value. The boiler combustion optimization model is as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \hspace{5.0pt}&{}{\left\{ \begin{array}{ll} f_1=\textrm{GBDT}_{1}(\textbf{v},\textbf{x})\\ f_2=\textrm{GBDT}_{2}(\textbf{v},\textbf{x})\\ f_3=\textrm{GBDT}_{3}(\textbf{v},\textbf{x})\\ f_4=\textrm{GBDT}_{4}(\textbf{v},\textbf{x})\\ \end{array}\right. }\\ \;\text {s.t.}\, &{}\textbf{x}\in \mathbb {S}\\ &{}g_i(\textbf{x})\le 0,\quad i=2,4,9,12,16,\\ \end{array}\right. } \end{aligned}$$

(16)

where $\textbf{v}$ is the non-adjustable operational variables, and $\textbf{x}$ is the adjustable operational variables.

Table 8 lists the HV values obtained for the six compared CMOEAs, where each CMOEA was run ten times independently. The population size was set to 100, maxFE was set to 10,000, and the reference point for calculating HV was set to [1,1,1,1]. From Table 8, it can be seen that CMOEA-TMC shows better overall performance than other CMOEAs in boiler combustion optimization, obtaining the best HV value. Figure 9 shows the results of some compared algorithms on this real-world problem, where four objective functions are reverse normalized to their actual values. The solutions obtained by CMOEA-TMC converge better and have smaller objective function values, which is more evident for the objective functions $f_2$ and $f_4$. Therefore, it can be concluded that the usefulness of CMOEA-TMC is also demonstrated in the real-world problem.

Conclusion

In this paper, a novel algorithm named CMOEA-TMC is proposed for solving complex CMOPs. The combination of parallel evolution, coevolution, and staging strategies better balances the feasibility, convergence, and diversity of solution sets. In the first stage, the subpopulations in mainPop evolve independently to achieve fast convergence. When the subpopulations all converge to a small region, the algorithm switches to the second stage, which enhances the collaboration between mainPop and helpPop to maintain population diversity and promote convergence. When the number of function evaluations reaches 60% of the set maximum, the algorithm switches to the third stage to find the global optimal non-dominated solutions.

The broad effectiveness of CMOEA-TMC is verified by applying on the DOC, MW, and CF test suites as well as a real-world problem in comparison with five advanced algorithms, namely ToP, PPS, CCMO, RVEA, and C-TAEA. Experimental results comparing with two-stage algorithms ToP and PPS show that the proposed three-stage strategy can help obtain solutions with better convergence. Experimental results comparing with multi-population algorithms CCMO and C-TAEA show that parallel evolution strategy and coevolution strategy proposed in this paper can well avoid populations from falling into local optimums. For CMOPs with complex constraints, such as the DOC test suit, the performance indicators of the proposed algorithm are significantly better than that of other algorithms, and the computation time is shorter. Therefore, CMOEA-TMC has good performance in CMOPs and can be applied to real-world problems. In addition, since good experimental results were obtained on the various test problems, the same population size specifications can be used for the new test problems. For test problems with more than three objectives, a larger number of population size and iterations are likely to be required, because more solutions are needed to cover the entire PF. As the efficiency of the offspring generation improves, the proposed algorithm will also have promising applications in many-objective optimization problems.