Introduction

Recently, unmanned aerial vehicles (UAVs) have gradually played an increasingly critical role in civil fields (such as earthquake relief and vegetation protection) and military fields (such as urban penetration and attacking enemy targets) [1]. Path planning, as one of the most fundamental and important problems in autonomous UAV flight, has been widely studied [2]. In recent decades, many path-planning algorithms have been proposed, which can be roughly divided into nature-inspired methods, grid-based methods, and sampling-based methods. Nature-inspired algorithms include artificial potential field (APF) methods [3], the interfered fluid dynamical system (IFDS) method [4] and intelligent algorithms. Among them, the APF and IFDS have the advantages of simple calculation and strong real-time performance, but the planned path can easily fall into a local minimum. Intelligent algorithms such as a genetic algorithm [5] can obtain the global optimal solution by iteration, but the calculation is more complicated in high-dimensional spaces. Heuristic search methods include the A* algorithm [6], anytime repairing A* (ARA) algorithm [7], sparse A* algorithm [8] and D* algorithm [9]. Although such algorithms can ensure that the optimal solution can be found if it exists, their search time increases sharply with increasing problem scale and spatial dimension. Sampling-based methods such as rapidly exploring random trees (RRT) [10] and probabilistic roadmaps (PRM) [11] usually sacrifice the optimal solution at grid search resolution for the ability to quickly find satisfactory solutions in high-dimensional complex state space and large-scale problems.

This paper focuses on solving the real-time path-planning and optimization problem of UAVs in complex dynamic environments with moving threats. Because of the influence of moving threats, planning needs to be constantly revised following the update of environmental information [12]. Therefore, the path-planning algorithm must have high planning and optimization efficiency and low storage requirements. Efficient planning and optimization calculations ensure that a UAV can generate the optimal path suitable for flight in real time, and low storage can effectively improve the scale of the UAV planning space. Because RRT and its derived algorithms [13, 14] build a tree structure through random sampling to quickly expand the search space, these algorithms still have very low computational complexity and high planning efficiency in high-dimensional environments. Therefore, these algorithms have good prospects in addressing UAV path planning in complex environments with moving threats. Note that most of the early works on RRT algorithms mainly focus on finding the feasible solutions, leaving a great possibility for improving the execution time and path optimization [15].

To deal with the path-planning problem in dynamic environments with moving threats, many improved RRT algorithms have been proposed, which are based on two different ideas. One idea is that algorithms will update the environment information and replan the path immediately after detecting changes in the environment, which requires the algorithms to have faster response speed, higher planning and optimization efficiency. Another idea is that algorithms actively avoid threats by predicting the trajectory of dynamic threats and planning collision-free paths. The algorithms with this idea can reduce the update frequency so that more time can be used to optimize the planning path to deal with the dynamic environment. Recently, many scholars have studied these two categories of RRT algorithms for dynamic environment path planning. The DRRT [16] algorithm uses tree pruning to update the plan. It takes the target position as the root of the tree to extend the tree, which simplifies the extension process. Bryant proposed an online RRT* algorithm [17] that ensures that new targets are always added to the spanning tree through online replanning. RRTX [18] uses a fast rewiring operation to repair damaged branches to rebuild the tree structure after detecting changes in the environment. These three algorithms mainly consider the information of moving threats from the current time to the next step of planning, meaning that path replanning is needed whenever the environment changes. Although the above algorithms optimize the replanning process to improve computing efficiency and ensure real-time performance, they still need a high replanning update frequency to address the movement of threats. In contrast to the above three replanning algorithms, the time constraint is considered by an algorithm based on the partial path-planning method [19]. This kind of algorithm adds the nodes without collision with the known threat trajectory to the tree and parallels the path planning by executing the UAV. Influenced by the partial path-planning method, a time-based RRT algorithm named Risk-RRT is proposed in [20]. Risk-RRT predicts the movement of a threat through a Gaussian process. Then, RRT is used to plan part of the path and control the robot to advance a certain distance along the planned path. Note that because Risk-RRT uses the traditional RRT as the underlying planner, the algorithm can quickly obtain feasible paths even though it cannot obtain optimized paths. Therefore, to improve the quality of the planned path, Zhang proposed the Risk-RRT* algorithm [21]. Risk-RRT* improves the underlying planner-based RRT to RRT*. The rewiring process of RRT* can optimize the tree structure to improve the planning path optimality. However, the rewiring process of RRT* will change the tree structure. Since Risk-RRT* is a time-based RRT* algorithm, the change in tree structure means that each affected node in the tree needs to update the information, including the parent and child node, timestamp and depth of the node. This process often brings many additional calculations, which reduces the percentage of time devoted to the path optimization process within the limited planning time and then affects the quality of the planned path.

This analysis shows that the above algorithms still have space and a possibility to be improved.

  1. (1)

    The flight environment of UAVs is usually a large three-dimensional (3D) space with many moving threats, and the moving frequency of threats is also high. Adopting replanning algorithms requires maintaining a high planning update frequency, which is difficult to achieve.

  2. (2)

    In a large 3D space, if the random sampling method is used to search the whole planning space, many useless sampling nodes may be generated. This result will make the planning inefficient and increase the planning time.

  3. (3)

    The longer a UAV performs a mission in a battlefield environment, the greater is the probability of being detected and attacked by the enemy. This circumstance necessitates improving the efficiency and quality of the planned path so that the UAV can quickly complete its task on the battlefield and reduce this probability. Therefore, combined with the above motivations, this paper will focus on further improving the partial planning algorithm based on time RRT. The algorithm can improve the efficiency of feasible path planning and quickly optimize the path based on avoiding additional computational consumption to ensure rapid planning efficiency and high path quality in the online dynamic path planning of UAVs with moving threats.

Therefore, in this paper, we propose the HPO-RRT* algorithm to solve the real-time path-planning problem of UAVs in a 3D dynamic environment. Figure 1 shows the basic framework of the algorithm, which adopts a hierarchical architecture. The HPO-RRT* algorithm can quickly plan a path suitable for UAV flight and ensure the optimization of the planned path. First, the HPO-RRT* algorithm uses the UAV perception system to update the world information and predict the moving threats before each plan. Then, an improved time-based RRT* algorithm is used in the path planner to obtain the heuristic path: the sampling bias method based on the APF function is used to guide the sampling towards the target position and avoid threats, the process of selecting the optimal parent node for the new node in RRT* is introduced, and lazy collision checking is adopted to reduce the running time of the algorithm while satisfying the avoidance of dynamic threats. Thus, a partial heuristic path can be quickly obtained. Finally, a low-cost path optimizer is used to quickly optimize the path generated by the path planner to ensure the homotopy optimality of the final planned path.

Fig. 1
figure 1

Basic framework of HPO-RRT*

Full size image

Our work mainly includes the following innovations:

  1. (1)

    A hierarchical planning framework suitable for real-time fast path planning in a UAV dynamic environment is designed (Fig. 1), which comprises a UAV perception system, a path planner based on the improved time-based RRT* and a low-cost path optimizer, to improve the planning efficiency and ensure path optimization.

  2. (2)

    In the bottom planner, a bias sampling method based on the APF function is used to guide the generation of sampling nodes, which can improve the sampling efficiency and reduce the planning time.

  3. (3)

    In the path planner, the process of neighbourhood optimal parent node selection and lazy collision checking is applied to the tree expansion, which improves the planning efficiency and obtains a path optimized as much as possible.

  4. (4)

    A low-cost path optimizer is designed to quickly optimize the path generated by the path planner without changing the tree structure.

  5. (5)

    The probability completeness and homotopy optimality of the HPO-RRT* algorithm are discussed and proven.

This paper is organized as follows. The following section describes the related work. “Problem formulation” describes the problems related to path planning in a dynamic environment. “HPO-RRT* algorithm” introduces the HPO-RRT* algorithm in detail in three aspects: the overall framework of HPO-RRT* (“Overall framework”), tree structure optimization and heuristic path planning (“Path planner”), and the low-cost heuristic path optimization method (“Low-cost path optimizer”). The analysis and proof of the probability completeness and homotopy optimality of HPO-RRT* are introduced in “Analysis”. In “The results of simulation experiments”, the simulation experiments are reported. In “Conclusions and future work”, we draw conclusions and discuss future work.

Related works

In this section, we first introduce the sampling strategy and related works to improve the RRT convergence speed. Then, Risk-RRT is taken as a typical example to describe the relevant basic knowledge of time-based RRT.

Sampling strategy

As a single-query path-planning method based on sampling, the RRT algorithm has been widely studied in the past three decades because of its high computational efficiency and strong scalability. However, RRT has the problem of slow convergence. Therefore, how to quickly converge has become a research focus.

The results show that changing the sampling strategy can effectively increase the convergence speed of the algorithm. Most RRT-like algorithms use an unbiased and uniform sampling strategy to explore the configuration space, which is pointless and greatly increases computational consumption, resulting in slower convergence speed. Therefore, an importance sampling strategy is proposed, which can extract samples from the preset distribution or configuration space. This method effectively increases the convergence speed [22]. Using prior information to guide local sampling is a strategy based on importance sampling. This strategy uses the planned path as a priori information to guide sampling around it, such as informed RRT* [23] and its batch sample iteration improved algorithm BIT* [24]. In addition, the ellipsoid heuristic sampling strategy is also adopted in [25, 26] to increase the convergence speed. Compared with the prior information-guided sampling strategy, direct bias sampling avoids the uniform sampling process when exploring feasible paths and usually brings a higher convergence speed. This strategy biases random samples to favorable areas through specific methods, such as Theta*-RRT*, to explore the configuration space. Using the APF method as a bias sampling strategy is a good choice. The attractive potential field of the APF is used to guide random sampling towards the target position bias in [27, 28]. Pharpatara [29] introduced a rotating potential field to the traditional APF to guide offset sampling with direction information. This paper also adopts the offset sampling method based on the APF function to increase the convergence speed. In contrast to [28], we combine attractive and repulsive potential fields to guide random sampling to further improve the sampling efficiency.

Time-based RRT

The difference between time-based RRT and classical RRT mainly lies in the representation of nodes in the tree. The tree node of classical RRT only records the location information of the node, while node \(x\) of time-based RRT can be defined as a structure containing six kinds of information, i.e. \(x:\left( {x_{{{{coor}}}} ,x_{{{{parent}}}} ,x_{{{{sons}}}} ,n,t,P_{{{{collisioncheck}}}} \left( t \right)} \right).\)

(1) \(x_{{{{coor}}}}\) represents the position information of \(x\) and is represented in \(O - xyz\). (2) \(x_{{{{parent}}}}\) represents the parent node of \(x\). Note that \(x_{{{{parent}}}}\) is also represented by a structure like \(x\). (3)\(x_{{{{sons}}}}\) represents any child node of \(x\), similar to \(x_{{{{parent}}}}\). (4) \(n\) indicates the depth of \(x\), that is, it needs to pass through \(n\) nodes from the root node to the \(x\). (5) \(t\) represents the timestamp of \(x\), which can be calculated by depth, i.e. \(t = t_{0} + n\Delta t\), where \(t_{0}\) is the timestamp of the root node and \(\Delta t\) is the time increment required for the UAV to pass through the adjacent nodes. (6) \(P_{{{{collisioncheck}}}} \left( t \right)\) is the collision risk probability between the node and the obstacles in the environment at time \(t\). In the Risk-RRT algorithm, \(P_{{{{collisioncheck}}}} \left( t \right)\) is defined as [20]:

$$ \begin{gathered} \left\{ \begin{gathered} P_{{{{collisioncheck}}}} \left( t \right) = P_{{{{static}}}} + (1 - P_{{{{static}}}} )P_{{{{moving}}}} (t) \hfill \\ P_{{{{moving}}}} (t) = 1 - \prod\limits_{k}^{K} {\left( {1 - P_{{{{moving}}}} \left( {p_{k} \left( t \right)} \right)} \right)} \hfill \\ \end{gathered} \right., \end{gathered} $$
(1)

where \(P_{{{{static}}}}\) represents the collision risk probability of the static threat, \(P_{{{{moving}}}} \left( t \right)\) represents the collision risk probability obtained for the moving threat at time \(t\), and \(P_{{{{moving}}}} \left( {p_{k} \left( t \right)} \right)\) represents the collision risk probability between the \(k{\text{-th}}\) moving obstacle and the node at time \(t\).

Time-based RRT is also an incremental algorithm similar to RRT, i.e. the tree structure continues to expand with increasing sampling nodes. In contrast to RRT, in the tree structure of time-based RRT, tree nodes with high collision risk or timestamps smaller than the current root node will be deleted.

Problem formulation

In this section, we define the path-planning problems in a dynamic environment with moving threats that will be solved in this paper and the notation used to describe them.

The planning environment is abstracted as a configuration space \(X \subseteq {\mathbb{R}}^{d}\). Let \(X_{{{{obs}}}} \subseteq X\) be the threat space composed of static threat \(X_{{{{sta}}}}\) and moving threat \(X_{{{{mov}}}}\), i.e. \(X_{{{{sta}}}} ,X_{{{{mov}}}} \in X_{{{{obs}}}}\). The obstacle-free space is defined as \(X_{{{{free}}}} = X\backslash X_{{{{obs}}}}\). In a dynamic environment, the configuration space is time varying, so the above two spaces are represented as \(X_{{{{obs}}}} \left( t \right)\) and \(X_{{{{free}}}} \left( t \right)\). \(x_{{{{init}}}} ,X_{{{{goal}}}}\) are the initial position and the target area, respectively. In this paper, \(X_{{{{goal}}}} = \left\{ {x \in X_{{{{free}}}} |\rho \left( {x,x_{{{{goal}}}} } \right) \le r_{{{{goal}}}} } \right\}\) is defined in the dynamic environment to detect whether the goal is reached, where \(\rho \left( {x_{1} ,x_{2} } \right)\) represents the Euclidean distance between \(x_{1}\) and \(x_{2}\). A ball with centre \(x \in X\) and radius \(r \in {\mathbb{R}}_{ > 0}\) is denoted as \(\mathfrak{B}_{x,r}\). The APF function is \(U:{\mathbb{R}}^{d} \to {\mathbb{R}}\), where the attractive and repulsive potential fields are \({U}_{{{{att}}}}\) and \(U_{{{{rep}}}}\), respectively. The potential field forces generated by these fields are \({\textbf{F}}_{{{{att}}}}\) and \({\textbf{F}}_{{{{rep}}}}\).

The following paragraphs describe some problems in path planning in a dynamic environment.

In contrast to the static environment, obstacles in a dynamic environment change their positions over time. Therefore, for the dynamic path-planning algorithm, time measurement must be introduced into the nodes so that the collision detector can use the time component to check the feasibility of the planned path. The dynamic environment proposed in this paper is described in Problem 1.

Problem 1

(Dynamic environment). If threats change location over time, the environment is called dynamic, i.e.

$$ \Delta X_{{{{obs}}}} = \bigcup\limits_{i = 0}^{I} {f_{i} \left( {x,t_{i} } \right)} . $$
(2)

The feasibility of the path is described in Problem 2.

Problem 2

(Feasible path planning). In the configuration space \(X\) containing \(X_{{{{obs}}}} \left( t \right)\) and \(X_{{{{free}}}} \left( t \right)\), given \(x_{{{{init}}}}\) and \(X_{{{{goal}}}} \left( {x_{{{{goal}}}} ,t} \right)\), a collision-free path \(\sigma :\left[ {0,T} \right] \to X_{{{{free}}}}\) can be planned, where \(\sigma \left( 0 \right) = x_{{{{init}}}}\), \(\sigma \left( T \right) \in X_{{{{goal}}}} \left( {x_{{{{goal}}}} ,T} \right)\).

Let \(\sum {}\) be the set of all feasible paths in obstacle-free space. The cost function \(c\left( \sigma \right) \in {\mathbb{R}}_{ > 0}\) represents the generation value of each feasible path \(\sigma\). Then, the optimal path-planning problem is described by Problem 3.

Problem 3

(Optimal path planning). Assuming that there is a solution set \(\sum {}\) for Problem 2, the path in which the cost function \(c\left( \sigma \right)\) is the smallest is the solution \(\sigma^{*}\) of the optimal path planning, i.e.

$$ \sigma^{*} = \mathop {\arg \min }\limits_{{\sigma \in \sum {} }} c\left( \sigma \right). $$
(3)

In UAV path planning, constraints are placed on the maximum steering angle \(\phi_{\max }\) and the maximum climbing/diving angle \(\gamma_{\max }\) [30]. Assume that the coordinates of any path node are \(\left( {x_{i} ,y_{i} ,z_{i} } \right)\). The constraints on \(\phi_{\max }\) and \(\gamma_{\max }\) are calculated as follows:

$$ \left\{ \begin{gathered} \phi_{i} = \arccos \left( {\frac{{{\textbf{a}}_{i}^{T} {\textbf{a}}_{i + 1} }}{{\left\| {{\textbf{a}}_{i} } \right\|_{2} \left\| {{\textbf{a}}_{i + 1} } \right\|_{2} }}} \right) \le \phi_{\max } \hfill \\ |\gamma_{i} | = \left| {\arctan \left( {\frac{{z_{i} - z_{i + 1} }}{{\left\| {{\textbf{a}}_{i} } \right\|_{2} }}} \right)} \right| \le \gamma_{\max } \hfill \\ \end{gathered} \right. $$
(4)

where the vector \({\textbf{a}}_{i}\) is \(\left[ {x_{i} - x_{i - 1} ,y_{i} - y_{i - 1} } \right]^{T}\).

Therefore, in this paper, the cost function between two points \(x_{1}\) and \(x_{2}\) in the configuration space is defined as follows:

$$ f_{c} \left( {x_{1} ,x_{2} } \right) = \left\{ { \, \begin{array}{*{20}l} {\rho \left( {x_{1} ,x_{2} } \right)} \hfill & {\phi \le \phi_{\max } ,|\gamma | \le \gamma_{\max } } \hfill \\ { + \infty } \hfill & {{\text{otherwise}}} \hfill \\ \end{array} \, } \right., $$
(5)

where \(\phi\) and \(\gamma\) are the steering angle and climbing/diving angle of the UAV flying along the planned path, respectively, which can be calculated through the geometric relationship between the two adjacent path segments. If these angles exceed their limits, it is considered that the planned path cannot meet the needs of the UAV, so the cost function is set to infinity. Thus, the cost function of the planned path can be expressed as:

$$ c\left( \sigma \right) = \sum\limits_{t = 1}^{T - 1} {f_{c} \left( {\sigma \left( t \right),\sigma \left( {t + 1} \right)} \right)} . $$
(6)

HPO-RRT* algorithm

In this section, we introduce the HPO-RRT* algorithm proposed in this paper in detail.

Overall framework

To address the path-planning problem of UAVs in dynamic environments with moving threats, the algorithm must be able to solve dynamic problems quickly. However, only obtaining the feasible path is not an optimal choice: the algorithm should also be able to quickly obtain the optimal solution. Note that many time-based RRT* algorithms need to prune the tree structure when optimizing the path, which inevitably results in more wasted branches and additional calculations of time-based nodes in the correction tree.

Therefore, the HPO-RRT* algorithm is proposed in this paper to satisfy the efficiency of real-time path planning and the superiority of paths in the dynamic environment of UAVs. The algorithm adopts a hierarchical framework for path planning and optimization. First, the UAV perception system is used for threat prediction and world information updates. Then, an improved time-based RRT* algorithm is used as the path planner. Finally, a low-cost path optimizer is used to optimize the path obtained by the planner. The pseudocode of the algorithm is shown in Algorithm 1, including one main cycle and five main processes.

  1. (1)

    Initialization (lines 1–3). This process initiates the HPO-RRT* algorithm. \(\sigma_{{{{opt}}}}\) is treated as an empty set. Similarly, the root node of tree \(T\) is set to \(x_{{{{init}}}}\), and the current positions \(x_{{{{cur}}}}\) of the UAV and time are initialized.

  2. (2)

    Termination condition (line 4). After detecting that \(x_{{{{cur}}}}\) has reached the target area \(X_{{{{goal}}}}\), the program is immediately terminated. Otherwise, continue running the program until \(x_{{{{cur}}}}\) arrives at \(X_{{{{goal}}}}\).

  3. (3)

    UAV perception system (lines 8–15). During any execution, the UAV will fly a certain distance according to the planned path, and then the planner will update the final state \(x_{{{{cur}}}}\) of the drone in this execution to the root of the new tree \(T_{{_{{{{new}}}} }}^{*}\). Next, nodes with timestamps less than \(x_{{{{cur}}}}\) in the tree and their descendants need to be deleted. Then, taking zero as the initial depth of \(x_{{{{cur}}}}\), the trajectory of the threat in the future time \(N_{l} \Delta t\) is predicted through the navigation system, where \(N_{l}\) is the maximum depth. Because of the movement of threats and UAVs, all information of maps, trees, UAVs and moving threats must be updated. This process is basically the same as that of Risk-RRT [20] except that the perception system is expanded from 2 to 3D. This paper mainly focuses on improving path planning and optimization, so the description of the perception process refers to [20].

  4. (4)

    Path planner (lines 16–20). The existing time-based RRT algorithm usually uses RRT as the bottom planner [15, 31]. Obviously, the planned path is not optimal, and a feasible path may not be obtainable within the time interval. In this paper, we use an improved time-based RRT* as the path planner. First, the bias sampling method based on the APF function is used to guide sampling node \({{x}}_{{{{apfrand}}}}\) towards the target region and away from the obstacle. Then, the time-based RRT* process of selecting the optimal parent node in the neighbourhood of the new node is introduced to optimize the tree structure, and the rewiring process in time-based RRT* is removed to avoid damage to the tree structure. Meanwhile, the tree structure is extended in combination with the lazy collision checking process. Finally, the heuristic path is obtained through the tree structure.

  5. (5)

    Path optimizer (line 21). Because all the nodes in the tree have time parameters and the time is irreversible, using the rewiring process in the tree structure to optimize the path will lead to the disorder of node timestamps in the tree, and repairing the tree structure will consume considerable extra time. Therefore, this paper designs a low-cost path optimizer that directly optimizes the heuristic path without changing the tree structure to obtain the optimal path \(\sigma_{{{{opt}}}}\).

figure a

Path planner

Bias sampling based on the APF function

In the traditional RRT algorithm, the sampling nodes are randomly selected in the collision-free configuration space, and then the extended nodes generate a search tree to the target area. Although this method can ensure the completeness of probability, in the three-dimensional space of UAV flight, the search efficiency is low because of the large random sampling space. In addition, HPO-RRT* is a planning algorithm based on time constraints. The path-planning time of the UAV will be limited to a fixed time interval, so the time of path planning is relatively short. Random sampling is inefficient and may be unable to plan a feasible path. Therefore, to plan the path efficiently, this paper proposes a bias sampling method based on APF functions, which makes the sampling nodes expand towards the target region and away from the threat to plan the path efficiently in a limited time.

The APF constructs the attractive potential field of the target position and the repulsive potential field of the threat. The resultant force \({\textbf{F}}_{{{{apf}}}}\) generated by these two potential fields guides the UAV to move towards the target point. In this paper, the following functions are used to define the attractive \(U_{{{{att}}}}\) and the repulsive \(U_{{{{rep}}}}\) potential fields, as well as their corresponding force vectors \({\textbf{F}}_{{{{att}}}}\) and \({\textbf{F}}_{{{{rep}}}}\), respectively. \({U}_{{{{att}}}}\) and \({\textbf{F}}_{{{{att}}}}\) are:

$${U}_{{{{att}}}} (x) = \frac{1}{2}{k}_{{{{att}}}} \rho^{2} (x,x_{g} ), $$
(7)
$$ {\textbf{F}}_{{{{att}}}} (x) = - \nabla ({U}_{{{{att}}}} ) = - k_{{{{att}}}} \rho (x,x_{g} )\frac{{\partial \rho (x,x_{g} )}}{\partial x}, $$
(8)

\(U_{{{{rep}}}}\) and \({\textbf{F}}_{{{{rep}}}}\) are

$$ U_{{{{rep}}}} (x) = \left\{ {\begin{array}{*{20}l} {\frac{1}{2}k_{{{{rep}}}} \left( {\frac{1}{{\rho (x,x_{{{{obs}}}} )}} - \frac{1}{{\rho_{o} }}} \right)^{2} } \hfill & {\rho (x,x_{{{{obs}}}} ) \le \rho_{o} } \hfill \\ 0 \hfill & {\rho (x,x_{{{{obs}}}} ) > \rho_{o} } \hfill \\ \end{array} } \right., $$
(9)
$$ {\textbf{F}}_{{{{rep}}}} (x) = \left\{ {\begin{array}{*{20}l} {k_{{{{rep}}}} \left( {\frac{1}{{\rho (x,x_{{{{obs}}}} )}} - \frac{1}{{\rho_{o} }}} \right)\frac{1}{{\rho (x,x_{{{{obs}}}} )^{2} }}\frac{{\partial \rho (x,x_{{{{obs}}}} )}}{\partial x}} \hfill & {\rho (x,x_{{{{obs}}}} ) \le \rho_{o} } \hfill \\ 0 \hfill & {\rho (x,x_{{{{obs}}}} ) > \rho_{o} } \hfill \\ \end{array} } \right., $$
(10)

where \(\rho_{o}\) is the maximum impact distance of the threat, and \(x_{{{{obs}}}}\) is the location of the threat.

According to Eqs. (7) and (9), the calculation of random sampling through APF bias is described as follows:

$$ {\textbf{F}}_{{{{att\_bias}}}} = - k_{{{{att}}}} \rho (x_{{{{rand}}}} ,x_{{{{goal}}}} ), $$
(11)
$$ {\textbf{F}}_{{{{rep}}\_{{bias}}}} = k_{{{{rep}}}} \left( {\frac{1}{{\rho (x_{{{{rand}}}} ,x_{{{{obs}}}} )}} - \frac{1}{{\rho_{o} }}} \right)\frac{1}{{\rho (x_{{{{rand}}}} ,x_{{{{obs}}}} )^{2} }}, $$
(12)
$$ {\textbf{F}}_{{{{apf}}\_{{bias}}}} = {\textbf{F}}_{{{{att}}\_{{bias}}}} + {\textbf{F}}_{{{{rep}}\_{{bias}}}} . $$
(13)

Then, the bias sampling node can be described as:

$$ {{x}}_{{{{apfrand}}}} = {{x}}_{{{{rand}}}} + k_{{{{bias}}}} \frac{{{\textbf{F}}_{{{{apf}}\_{{bias}}}} }}{{\left| {{\textbf{F}}_{{{{apf}}\_{{bias}}}} } \right|}}, $$
(14)

where \(k_{bias} \in {\mathbb{R}}_{ > 0}\) is the bias step.

Note that path planning using the APF function has disadvantages, such as inaccessible targets and easily falling into local minima. However, in this paper, the APF function is only used to bias the random sampling, not to find the path. At the same time, each sampling is an independent random event. Therefore, the shortcomings of the APF function can be effectively avoided.

In this paper, we further improve the approach described in [28]. Qureshi and Ayaz [28] calculate the influence of the attractive potential field on \(x_{{{{rand}}}}\) and determine whether to reserve bias sampling nodes by determining whether the distance between \(x_{{{{rand}}}}\) and \(x_{{{{obs}}}}\) is within the range of \(\rho_{o}\). Through the strategy of [28], the random sampling nodes outside the influence range of the repulsive potential field can be biased towards the goal, thereby improving the sampling efficiency. However, if the nodes are in the influence range of the repulsive potential field, they will be discarded. At this time, new nodes will be randomly sampled again to bias. Note that if the random sampling node within the influence range of the repulsive potential field can also be biased, repeated random sampling and collision check of this node will be avoided, thus further improving the sampling efficiency. Therefore, this paper introduces biased sampling of the repulsive potential field to retain all random sampling and expand the expansion space of the tree as much as possible. The pseudocode of the APF bias sampling is shown in Algorithm 2.

figure b

First, the \({\textbf{sample}} \_{\textbf{random}}\) function is used for random sampling in collision-free space \(X_{{{{free}}}}\). Second, the attractive force \({\textbf{F}}_{{{{att}}}}\) of \(x_{{{{goal}}}}\) to \(x_{{{{rand}}}}\) and the repulsive force \({\textbf{F}}_{{{{rep}}}}\) of \(x_{{{{obs}}}}\) to \(x_{rand}\) are calculated. Third, the resultant force \({\textbf{F}}_{{{{apf}}}}\) is calculated and then used to bias \(x_{{{{rand}}}}\) to \({{x}}_{{{{apfrand}}}}\). The final bias sample node \({{x}}_{{{{apfrand}}}}\) is obtained.

The expansion of the time-based tree

Similar to RRT*, time-based Risk-RRT* can also optimize the tree structure through the rewiring process to obtain asymptotically optimal partial planned paths when addressing path-planning problems with moving threats. However, because of the irreversibility of time, the rewiring process of Risk-RRT* will destroy the time-based tree structure. The time spent repairing the tree structure increases exponentially with the size of the tree, reducing the planning efficiency. In addition, in the sampling-based path-planning algorithm, collision checking is very time-consuming. Because the planning time using HPO-RRT* is a fixed short time interval, the planning efficiency is particularly important. Therefore, in this paper, the neighbouring parent selection process of Risk-RRT* is retained in the process of expanding the tree to optimize the tree structure, while the rewiring process is eliminated to ensure the efficiency of the path planner. Although this approach will sacrifice the optimality of the path, the path can be quickly optimized by a low-cost path optimizer that is more efficient than the rewiring process. At the same time, to expedite collision checking, a method of lazy collision checking is proposed in this paper, which improves the computational efficiency by ensuring that the planned path is collision free.

In the HPO-RRT* algorithm, the expansion of nodes is closely related to time. Each forward expansion of a node in the tree indicates that the execution time of the UAV increases by the time step \(\Delta t\). Therefore, any node \({{x}}_{i} \in T.V\) in the tree needs to record its timestamp, i.e. \({{x}}_{i} :\left( {x_{i}^{*} ,t + N_{i} \Delta t} \right)\), where \(x_{i}^{*}\) is the position coordinate of \({{x}}_{i}\), \(t\) is the start time of this extension process, and \(N_{i}\) is the number of time steps required to extend from the root node \(x_{{{{root}}}}\) of the current spanning tree to \(x_{i}\).

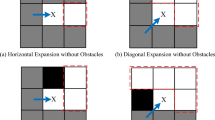
Note that the \({\textbf{Extend}}\) process is improved by using time-based RRT* as the basic planner. It only includes the process of selecting the optimal parent node in the neighbourhood of the new node \({{x}}_{{{{new}}}}\) and omits the rewiring process. This approach is used because only after selecting the optimal parent node of \({{x}}_{{{{new}}}}\), \({{x}}_{{{{new}}}}\) will be added to the time-based tree structure to obtain the timestamp. However, the time-based tree needs to update the timestamp of the node and all its descendants when rewiring the node and conducting collision checking again, which greatly increases the calculation time. A simple but typical example is shown in Fig. 2. In Fig. 2a, after adding \({{x}}_{{{{new}}}}\) to the time-based tree, the rewiring process will be executed in the neighbourhood of \({{x}}_{{{{new}}}}\). Obviously, the cost from \({{x}}_{0}\) through \({{x}}_{{{{new}}}}\) to \({{x}}_{8}\) is less than the cost from \({{x}}_{0}\) to \({{x}}_{8}\) in the original tree. If rewiring is performed, i.e. the new parent node of \({{x}}_{8}\) is \({{x}}_{{{{new}}}}\) (called \({{x}}_{2}^{^{\prime}}\) in (b)), the time-based tree will be updated to the structure shown in Fig. 2b. At this time, the timestamps of \({{x}}_{8}\), \({{x}}_{9}\), \({{x}}_{10}\) and \({{x}}_{11}\) are affected by rewiring and need to be updated to the timestamps of \({{x}}_{3}^{^{\prime}}\), \({{x}}_{4}^{^{\prime}}\), \({{x}}_{5}^{^{\prime}}\) and \({{x}}_{6}^{^{\prime}}\), respectively. In addition, because of the change in the timestamp, the collision checking of these update nodes must be reperformed to ensure that the nodes will not collide with the moving threats under the new timestamp. If collision checking cannot be passed, all branches formed by this node and all its child nodes need to be deleted. This process brings many additional computing costs. Therefore, in the HPO-RRT* algorithm, we delete the rewiring process of the time-based RRT* to reduce the computational consumption and meet the requirements of efficient and fast tree structure expansion within a fixed time interval. In addition, we keep the process of \({{x}}_{{{{new}}}}\) reselecting the new parent node. This process is retained because it is a forwards expansion process, which will only affect the relevant parameters of the new node\({{x}}_{{{{new}}}}\). Therefore, it will not bring additional computing consumption. Moreover, it can optimize the tree structure to a certain extent.

Fig. 2
figure 2

Rewiring process of the time-based tree

Full size image

The planning space in this paper contains static and moving threats. For static threats, the position remains fixed at each time step. However, the coordinates of moving obstacles change with time. During the planning of the current time interval, the UAV can only refer to the threat prediction trajectory before the current planning to expand the tree by \(N_{l}\) time steps \(\Delta t\) (Algorithm 1, line 12). However, as the predicted threat trajectory may not be accurate enough, the path obtained in this partial planning may become infeasible because of the new prediction of the threat trajectory in the next planning. An intuitive idea is to set \(N_{l}\) very small to improve the accuracy of obstacle prediction and reduce the number of potentially invalid and repeated collision checking calls to improve the calculation efficiency. However, this approach makes the expansion range of the tree in each cycle very small, which is not suitable for the large-scale 3D planning space of UAVs. Therefore, to ensure a certain extension range of the forwards tree and reduce the computational loss, this paper proposes a method of lazy collision checking, which delays the collision checking process until it must be called. Figure 3 illustrates lazy collision checking. This method defines a new extended time depth \(N_{c} < N_{l}\). In \(N_{c} \Delta t\), all extended branches perform collision checking. The step length of each UAV execution is also set in \(N_{c} \Delta t\). However, collision checking will not be performed in the time depth from \(N_{c} \Delta t\) to \(N_{l} \Delta t\). Because of the parallel planning and execution, the planning of the next time interval will start with a new root node, and the time depth for collision checking will continue to expand backwards. Therefore, all nodes on the final expansion tree will complete collision detection. Note that \(N_{c}\) greatly influences the performance of HPO-RRT*, so the calculation complexity and planning depth should be fully weighed.

Fig. 3
figure 3

Illustration of lazy collision checking

Full size image
figure c

The pseudocode of the \({\textbf{Extend}}\) process is shown in Algorithm 3. After the \({\textbf{SampleAPF}}\) process returns the biased sample \({{x}}_{{{{apfrand}}}}\), the forward expansion process begins. Similar to the time-based RRT*, the process of expanding the new node \({{x}}_{{{{new}}}}^{*}\) is realized by the \({\textbf{Nearest}}\), \({\textbf{Steer}}\) and \({\textbf{Near}}\) functions. In the expansion process of \({{x}}_{{{{new}}}}\), only its position is considered temporarily (i.e. let \({{x}}_{{{{new}}}}\) be \({{ x}}_{{{{new}}}}^{*}\)). First, the \({\textbf{Nearest}}\) function returns the closest node \(x_{{{{nearest}}}}^{*}\) between \({{x}}_{{{{apfrand}}}}\) and the tree node set \(T.V\), and then \({\textbf{Steer}}\) generates a new node on \({{x}}_{{{{new}}}}^{*}\). Next, the algorithm searches the neighbourhood formed by the sphere \(\mathfrak{B}_{{x_{{{{new}}}}^{*} ,r}}\) whose centre is \({{x}}_{{{{new}}}}^{*}\) and radius is \(r\) (where \(r = \gamma \left( {\frac{\log n}{n}} \right)^{1/d}\)[32]) to obtain the node set \({{X}}_{{{{near}}}}\) whose distance from \({{x}}_{{{{new}}}}^{*}\) in \(\mathfrak{B}_{{x_{new}^{*} ,r}}\) is less than \(r\). After connecting \({{x}}_{{{{new}}}}^{*}\) to \({{X}}_{near}\), the timestamp \( \, t_{{{{new}}}}\) of \({{x}}_{{{{new}}}}\) is arranged from small to large to form a potential parent node set \({{X}}_{{{{parent}}}}\). First, the algorithm judges whether \( \, t_{new}\) is within the time depth \(N_{c} \Delta t\). If this criterion is met, the algorithm performs collision detection to select the optimal parent node of \({{x}}_{{{{new}}}}\); if \( \, t_{new} \in \left( {N_{c} \Delta t,N_{l} \Delta t} \right]\), it directly selects without collision detection. If \( \, t_{new} > N_{l} \Delta t\), \({{x}}_{{{{new}}}}\) exceeds the maximum time depth limit of this planning. Finally, \({{x}}_{{{{new}}}}\) and its edge formed with the optimal parent node \({{x}}_{{{{parent}}}}\) are added to the tree \(T\).

Planning path finding

Because the growth of the tree can only occur in the fixed planning time of a single cycle, and the maximum time depth of the node is limited to \(N_{l} \Delta t\), for the 3D large-scale space \({{X}}_{{{{goal}}}}\) in which the UAV flies, it is almost impossible to generate an expansion tree in which the node falls in the target area SD after only one or several cycles. Therefore, this paper introduces a cost function composed of the true distance cost and the estimated distance cost to find the heuristic partial path in the single planning spanning tree, namely, the \({\textbf{HeuristicPathFinding}}\) process.

In a planning interval, tree expansion is limited by the maximum expansion depth \(N_{l}\). That is, in the nodes of tree \(T_{{{{new}}}}\), the maximum extension time depth is \(N_{l} \Delta t\). Based on this limitation, the node set of the true path cost can be defined as \(X_{l}\), including \(n_{l}\) nodes \(x_{l}\) with a time depth of \(N_{l} \Delta t\), i.e. \(X_{l} : = \left\{ {(x_{l,1}^{*} ,N_{l} \Delta t),...(x_{l,i}^{*} ,N_{l} \Delta t),...,\left( {x_{{l,n_{l} }}^{*} ,N_{l} \Delta t} \right)} \right\}\). The set of true costs of all paths that can reach \(x_{l,i}\) in the current tree is defined as \(g\left( {X_{l} } \right)\). The set of estimated costs from any node in \(X_{l}\) to the target region \(X_{goal}\) is defined as \(h\left( {X_{l} } \right)\). Then, the cost \(f\left( {X_{l} } \right)\) of the path is:

$$ f\left( {X_{l} } \right) = g\left( {X_{l} } \right) + h\left( {X_{l} } \right). $$
(15)

We aim to find the node \(x_{l,i}\) that can minimize \(f\left( {X_{l} } \right)\), i.e.

$$ x_{l,\min } = \mathop {\arg \min }\limits_{{x_{l,\min } \in X_{l} }} f\left( {X_{l} } \right). $$
(16)

For the time-based tree, the exact value of \(g\left( {X_{l} } \right)\) can be obtained by calculating the path length, while \(h\left( {X_{l} } \right)\) can only be estimated. Therefore, an acceptable estimation cost calculation method should be selected so that the real cost of reaching \(x_{{{{goal}}}}\) is not overestimated. The following formula is used for calculating the estimated cost \(h\left( {x_{l,i} } \right)\) of any node \(x_{l,i}\):

$$ h\left( {x_{l,i} } \right)_{{x_{l,i} \in X_{l} }} = k_{l} \rho \left( {x_{l,i} ,x_{{{{goal}}}} } \right), $$
(17)

where \(k_{l}\) is the heuristic parameter.

figure d

On the basis of the above calculation, we ensure that in each partial planning, we can find a heuristic partial path towards the target from the current time-based tree. Algorithm 4 gives the pseudocode of the \({\textbf{HeuristicPathFinding}}\) process. First, the algorithm finds all nodes with time depth \(t_{l}\) in tree \(T_{{{{new}}}}\) and forms a set \({{X}}_{l}\). Then, the node \({{x}}_{i,\min }\) that minimizes the estimation cost is found by \(f\left( {X_{l} } \right)\). Finally, the heuristic path \(\sigma_{heu}\) generated by the planner is found by \({{x}}_{i,\min }\).

Low-cost path optimizer

The path planner using the HPO-RRT* algorithm efficiently generates heuristic paths without guaranteeing the optimality of the paths. Although the time-based Risk-RRT* algorithm can obtain the optimal path, as an online path-planning algorithm used to address moving threats, it takes a long time in the optimization process and sometimes cannot optimize the path well in a short planning time. Qi et al. [33] uses RRT* to find the initial path and then uses the ant colony (ACO) algorithm to reoptimize the path. This hierarchical optimization is interesting, but the ACO algorithm brings high computational complexity. The Bellman–Ford (BF) algorithm [34], as an algorithm for solving the shortest path, provides a method for searching the shortest path in a weighted graph. Therefore, inspired by [33, 34], combined with the requirements of online dynamic path planning, this paper proposes a low-cost fast path optimization method. This method directly optimizes the heuristic path \(\sigma_{{{{heu}}}}\) generated by the path planner without changing the tree structure. Therefore, additional complex calculations are not needed to optimize the path more quickly and effectively.

The BF algorithm estimates the distance from any node to a specified node by relaxing the trigonometric inequality constraint of the connection between nodes in the weighted graph. In the path optimization process of HPO-RRT*, we use this algorithm to offset the path points to optimize the heuristic path. As shown in Fig. 4, the blue path is the heuristic path \(\sigma_{{{{heu}}}}\) that has not been optimized, and the green translucent path is the path \(\sigma^{*}\) that has been optimized once. In the cycle, bias optimization is performed on the nodes in \(\sigma_{{{{heu}}}}\) (excluding the initial point and the target point) in turn. After all the path nodes are optimized once, path B is obtained. Obviously, \({{cost}}\left( {\sigma^{*} } \right) < {{cost}}\left( {\sigma_{{{{heu}}}} } \right)\).

Fig. 4
figure 4

Bias optimization

Full size image

To clearly illustrate the optimization process, the offset to a is taken as an example. For the three nodes \(x_{1} ,x_{2} \, \;{\text{and}}\; \, x_{3}\) in the tree, the path cost from \(x_{1}\) directly to \(x_{3}\) is minimal. However, if \(x_{1}\) and \(x_{3}\) are directly connected (that is, connected by the orange dotted line), the timestamps of \(x_{3}\) and all its descendants need to be updated, resulting in many extra computations. In addition, if \({\mathbb{X}}_{obs}\) exists nearby, such as the handling of node \(x_{4}\), the directly connected edge \(\left( {x_{3} ,x_{5} } \right)\) will collide with the threat, causing the optimization path to fail. Therefore, we try to optimize the path by biasing the position of node \(x_{2}\) towards edge \(\left( {x_{1} ,x_{3} } \right)\). The specific method is to find the midnode \(x_{2}^{mid}\) of edge \(\left( {x_{1} ,x_{3} } \right)\). Then, move \(x_{2}\) along the vector \(\overrightarrow {{x_{2} x_{2}^{mid} }}\) by a step \(\lambda_{{{{opt}}}}\) to obtain the optimized node. For any node \(x_{i}\) in the path, the optimization step \(\lambda_{{{{opt}}}}\) is calculated as follows:

$$ \lambda_{{{{opt}}}} = k_{{{{opt}}}} \left( {\frac{{\left( {x_{i - 1} + x_{i + 1} } \right)/2 - x_{i} }}{{\rho \left( {\left( {x_{i - 1} + x_{i + 1} } \right)/2,x_{i} } \right)}}} \right), $$
(18)

where \(k_{opt} \in {\mathbb{R}}_{ > 0}\) a is the bias factor. Then, the optimized node \(x_{i}\) of any node \(x_{{{{new}}}}\) in the path can be expressed as:

$$ x_{{{{new}}}} = x_{i} + \lambda_{{{{opt}}}} . $$
(19)
figure e

Algorithm 5 gives the pseudocode of the \({\textbf{Low-costOptimizer}}\) process. Define a function to determine whether the optimization process is completed and assign it as false at the beginning of the algorithm. The function \({\textbf{CollisionCheck}}\left( {{{x}}_{i - 1} ,{{x}}_{new} ,{{x}}_{i + 1} } \right)\) means collision checking for the path segment from \({{x}}_{i - 1}\) through \({{x}}_{new}\) to \({{x}}_{i + 1}\). If the result is true, then \(\left( {{{x}}_{i - 1} ,{{x}}_{new} ,{{x}}_{i + 1} } \right)\) is a collision-free path segment. The function \({\textbf{MaxAngleCheck}}\left( {{{x}}_{i - 1} ,{{x}}_{new} ,{{x}}_{i + 1} } \right)\) indicates the UAV maximum angle constraint detection for the path segment \(\left( {{{x}}_{i - 1} ,{{x}}_{new} ,{{x}}_{i + 1} } \right)\). Note that line 18 compares the cost between the path before the current cycle and the optimized path to complete the current cycle. If the cost difference between the two paths before and after optimization is less than the threshold \(\varepsilon\), where \(\varepsilon \in {\mathbb{R}}\), then the path is hardly changed in the optimization process. When this result is obtained, the improvement of path quality in the optimization process is no longer obvious, i.e. the optimal path is essentially determined. Therefore, assign \({\textbf{FinishOptimization}}\) to true.

In any optimization cycle, first, the initial position is added to the optimization path \(\sigma_{{{{opt}}}}\). Next, the nodes in heuristic path \(\sigma_{{{{heu}}}}\) are biased optimized. If the optimized path meets the constraints of collision detection and UAV maximum angle, then the optimized path of this cycle planning is feasible. Finally, if the generated path can improve the path quality, start the next cycle with this path as the path to be optimized. The termination conditions of the optimization process shown in Algorithm 5 include the following criteria: (1) the process is terminated when collision detection or the maximum angle constraint of the UAV cannot be met; (2) in the same cycle, if the costs of the optimized path \(\sigma_{{{{opt}}}}\) and the nonoptimized path \(\sigma^{*}\) differ by less than \(\varepsilon\), the process terminates.

Obviously, throughout the optimization process, the original tree structure is unchanged, and the timestamps of all nodes are unmodified. We can obtain a better path \(\sigma_{{{{opt}}}}\) than heuristic path \(\sigma_{{{{heu}}}}\) by performing bias optimization on the nodes of the heuristic path. Despite additional computations, the computational cost of our method is negligible relative to methods that optimize tree structures to optimize paths.

Analysis

In this section, we analyse the probability completeness and homotopy optimality of HPO-RRT*.

Probabilistic completeness

Probabilistic completeness is mainly used to analyse the ability of algorithms to find feasible solutions. The HPO-RRT* algorithm finds the path in a single plan through the path planner and then optimizes the path directly generated by the path planner. Therefore, the probabilistic completeness analysis of HPO-RRT* only needs to consider some paths obtained through the path planner in a single plan.

Let \(V_{n}^{ALG}\) represent the set of tree nodes generated by algorithm \(ALG\) after iteration \(n\). Definition 1 gives the definition of probabilistic completeness.

Definition 1

(Probabilistic completeness). Given the initial node \(x_{{{{init}}}}\) and the goal region \(X_{{{{goal}}}}\), if algorithm \(ALG\) can find the feasible path from \(x_{{{{init}}}}\) to \(x_{{{{goal}}}} \in X_{{{{goal}}}}\) for any path-planning problem with a feasible solution, i.e.

$$ \mathop {\lim \, \inf }\limits_{n \to \infty } \parallel \left( {V_{n}^{ALG} \cap P_{{{{goal}}}} \ne \emptyset } \right) = 1, $$
(20)

then the algorithm is considered probability complete.

The RRT algorithm has been proven to be probability complete. HPO-RRT* covers all the key processes of RRT in the bottom planner. Similar to RRT, HPO-RRT* has probabilistic completeness, which is described in Theorem 1.

Theorem 1

(Probabilistic completeness of HPO-RRT*). Given a path-planning problem, if there is a feasible solution, then,

$$ \mathop {\lim \, }\limits_{n \to \infty } \parallel \left( {V_{n}^{PTL - RRT*} \cap P_{{{{goal}}}} \ne \emptyset } \right) = 1. $$
(21)

Proof of Theorem 1. The proof of Theorem 1 is based on the following three arguments.

  1. (1)

    As shown in Algorithm 1, the vertex set \(V^{PTL - RRT*}\) of the random tree \(T\) generated by HPO-RRT* includes node \(x_{{{{init}}}}\), and \(V_{0}^{PTL - RRT*} = x_{{{{init}}}}\), which is the same as RRT.

  2. (2)

    Similar to RRT, the tree generated by HPO-RRT* is connected. In other words, any random sampling node can be connected to the tree.

  3. (3)

    HPO-RRT* only plans the path within a fixed time interval of each cycle, and the time depth limits its expansion range. However, for any cycle \(i\), HPO-RRT* is the same as the RRT algorithm and has probability completeness. That is, in cycle \(i\), when sample \(n_{i}\) tends to infinity, the probability of HPO-RRT* finding a path from the current planning starting point (also the subtarget point of the last cycle planning, i.e. \(x_{{{{subgoal}},i - 1}}\)) to the subgoal node \(x_{{{{subgoal}},i}}\) is one, i.e.

    $$ \mathop {\lim \, }\limits_{{n_{i} \to \infty }} \parallel_{i} \left( {V_{{n_{i} }}^{PTL - RRT*} \cap x_{{{{subgoal}},i}} \ne \emptyset } \right) = 1. $$
    (22)

When the number of cycles is infinite, the subgoal node \(x_{{{{subgoal}},i}}\) can surely fall into the goal region \(X_{{{{goal}}}}\), and all partial paths are connected. Therefore, the probability that HPO-RRT* finds a path from \(x_{{{{init}}}}\) to \(X_{{{{goal}}}}\) can be expressed as:

$$ \mathop {\lim }\limits_{{n_{i} \to \infty ,i = 1,...N}} \parallel \left( {V_{n}^{PTL - RRT*} \cap X_{{{{goal}}}} \ne \emptyset } \right) = \prod\limits_{i = 0}^{N} {\mathop {\lim \, }\limits_{{n_{i} \to \infty }} \parallel_{i} } = 1. $$
(23)

Thus, Theorem 1 is proved.

Homotopy optimality

The asymptotic optimality of RRT* and many of its derivative algorithms has been proven. This section proves that HPO-RRT* has similar properties to these algorithms, which is called homotopy optimality.

Note that HPO-RRT* performs partial path planning within a fixed time interval of each planning. Therefore, the path that ensures the homotopy optimality of HPO-RRT* is obtained by optimizing the heuristic path in a fixed time interval planning, rather than the entire path from the initial position to the goal region. The relevant definitions of homotopy optimality and the proof process are as follows.

Definition 2

(Homotopy class of feasible paths [35]). For two arbitrary paths \(\sigma_{1}\) and \(\sigma_{2}\) with a fixed initial node and goal node, if one path can be continuously deformed into the other without intersecting any threat, then \(\sigma_{1}\) and \(\sigma_{2}\) are considered to belong to the same homotopy class \(\left[ \sigma \right]\).

When multiple paths belong to the same homotopy class \(\left[ \sigma \right]\), there must be a homotopy optimal path \(\sigma_{{{{opt}}}}^{*}\), which is the least costly path in \(\left[ \sigma \right]\). Thus, Lemma 1 is given as follows.

Lemma 1

(Homotopy optimality of \(\sigma_{{{{opt}}}}\)). Given that the homotopy class containing heuristic path \(\sigma_{{{{heu}}}}\) is \(\left\{ {\left[ \sigma \right]_{{{\text{PTL}} - {\text{RRT}}*}} \left| {\sigma_{{{{heu}}}} \in \left[ \sigma \right]_{{{\text{PTL}} - {\text{RRT}}*}} } \right.} \right\}\), the optimization path \(\sigma_{opt}\) returned by the path optimizer of HPO-RRT* is the homotopy optimal path of the homotopy class, which is the path with the lowest cost.

Proof of Lemma 1. In process \({\text{re-optimization}}\), we use a low-cost path optimization algorithm to quickly optimize heuristic path \(\sigma_{{{{heu}}}}\). When the path meets the termination conditions of the process, an optimized path \(\sigma_{{{{opt}}}}\) is generated. Therefore, the proof of Lemma 1 can be divided into three arguments according to the conditions of path termination optimization.

  1. (1)

    After the optimization process, the path cost is almost unchanged, i.e. \(\Delta {{cost}} < \varepsilon\). As we analysed in “Low-cost path optimizer”, if \(\Delta {{cost}} < \varepsilon\), then the path has reached optimality, so the generated path \(\sigma_{{{{opt}}}}\) is the homotopy optimal path in the homotopy class.

  2. (2)

    When the return value of \({{CollisionCheck}}\) is false, path \(\sigma_{{{{opt}}}}\) is obtained. First, we assume that the termination condition is triggered because edge cannot pass \({{CollisionCheck}}\). As shown in Fig. 5a, there are two kinds of optimized path (i.e. \(\sigma_{{{{opt}}}}\) is the blue path and \(\sigma_{opt}^{^{\prime}}\) is the green path). Suppose the \(\sigma_{opt}^{^{\prime}}\) whose cost is \({{cost}}\left( {\sigma_{opt}^{^{\prime}} } \right) < {{cost}}\left( {\sigma_{opt} } \right)\) and \({{cost}}\left( {\sigma_{opt} } \right) - {{cost}}\left( {\sigma_{opt}^{^{\prime}} } \right) > \varepsilon\), that is, \(\sigma_{opt}^{^{\prime}}\) must be closer to edge \(\left( {x_{1} ,x_{4} } \right)\) than \(\sigma_{{{{opt}}}}\). However, \(\sigma_{opt}^{^{\prime}}\) cannot pass the collision checking, and \(\sigma_{opt}^{^{\prime}}\) will collide with obstacles. This causes the \({{CollisionCheck}}\) procedure returns a false value. Then, process \({\text{re-optimization}}\) stops and returns the optimized path \(\sigma_{{{{opt}}}}\) before the start of the current cycle as the optimal path. Therefore, no path costs less than \(\sigma_{{{{opt}}}}\). Then, \(\sigma_{{{{opt}}}}\) can be claimed to be homotopy optimal in the homotopy class.

  3. (3)

    When the return value of \({{MaxAngleCheck}}\) is false, path \(\sigma_{{{{opt}}}}\) is obtained. First, we assume that the termination condition is triggered because edge cannot pass \({{MaxAngleCheck}}\). Similar to Proof 2), Fig. 5b shows two kinds of optimized path (i.e.\(\sigma_{opt}\) is the blue path and \(\sigma_{opt}^{^{\prime}}\) is the green path). The edge \(\left( {x_{0} ,x_{1} } \right)\) is the last segment of the optimized path obtained from the previous cycle planning It is assumed that there is a path \(\sigma_{opt}^{^{\prime}}\), and \({{cost}}\left( {\sigma_{opt}^{^{\prime}} } \right) < {{cost}}\left( {\sigma_{opt} } \right)\). Then, \(\sigma_{opt}^{^{\prime}}\) must be closer to edge \(\left( {x_{1} ,x_{4} } \right)\) than \(\sigma_{opt}\). However, the steering angle of \(\sigma_{opt}^{^{\prime}}\) is \(\phi^{^{\prime}}\), which is larger than the steering angle \(\phi_{\max }\)(i.e. the maximum steering of UAV) of \(\sigma_{{{{opt}}}}\). If the angle \(\phi^{^{\prime}}\) does not meet the UAV angle constraint, \({{MaxAngleCheck}}\) returns false. Obviously, \(\phi^{^{\prime}}\) does not meet the constraint. Then,\(\sigma_{opt}^{^{\prime}}\) is infeasible, and \({\text{re-optimization}}\) returns to path \(\sigma_{{{{opt}}}}\). Therefore, no path costs less than \(\sigma_{{{{opt}}}}\). It can be proven that \(\sigma_{{{{opt}}}}\) is homotopy optimal. Based on the above three arguments, \(\sigma_{{{{opt}}}}\) is proven to be the homotopy optimal path in the homotopy class containing \(\sigma_{heu}\).

Fig. 5
figure 5

Bias optimization

Full size image

The results of simulation experiments

In this section, we give the simulation experiments of the proposed algorithm. The main purpose is to verify the feasibility and advantages of the algorithm in a UAV flight environment. Therefore, “Simulation setup” shows various threats in the considered UAV flight dynamic environment and the settings of some basic parameters to make the results as close to the real battlefield environment as possible to increase the reliability.

Simulation setup

Dynamic environment design

Constructing a battlefield environment is a prerequisite for path planning. The closer the construction of the battlefield environment is to reality, the better the verified path-planning algorithm will be implemented on UAVs. Therefore, to verify the feasibility and advantages of the HPO-RRT* algorithm in a battlefield environment, this paper simulates the real dynamic environment, including real terrain, radar, air defence missiles, anti-aircraft guns and a tower, as the configuration space for UAV path planning. We have already introduced the modelling and calculation of these threats in our previous work [36]. Since this paper mainly focuses on the planning of the HPO-RRT* algorithm, the modelling of threats will not be further described.

Based on the five threats in the above-mentioned real battlefield, this paper designs two 3D dynamic environments, including a threat with known moving trajectories and a random moving threat, to test the performance of the proposed algorithm and compare HPO-RRT* with related algorithms. The terrain threat in the two scenarios uses a unified elevation map. The two scenarios contain static or moving radar, missiles and anti-aircraft artillery threats.

Experiment Scenario 1 Dynamic flight scenario with known moving trajectory threats.

The environment size is 400*400*60 \({\rm m}^{3}\). Radar 1, Missile 1 and Anti-aircraft gun 1 are moving threats, which start to move from their initial positions. The speed and moving time period are shown in Table 1. The remaining threats are static. When the moving threats touch the boundary of the configuration environment, they will rebound and then move in the opposite direction. There is no interaction between different moving threats.

Table 1 Parameters of the moving threats in Scenario 1
Full size table

Experiment Scenario 2 Dynamic flight scenario containing multiple random moving threats

The size of the environment is 400*400*60 \({\text{m}}^{3}\). The initial position of the terrain threat and the other three threats is the same as that of experimental Scenario 1. In Scenario 2, moving threats are randomly selected from all radars, air defence missiles and anti-aircraft guns in the environment. {1, 3, 5, 6} threats can be selected to move at the same time. The movement speed is randomly selected from {1, 3, 5, 7} \({\text{m}}/{\text{s}}^{2}\).The start time of the movement is any time during the planning period, and the time period of each movement is 3 s. All threats except those moving remain stationary. When the moving threats touch the boundary of the configuration environment, they rebound in the opposite direction and then continue to move. There is no interaction between different moving threats.

Basic parameter design

During the preparation of simulation experiments, the performance of the UAV, the location of threats in the environment, and the relevant basic parameters of the HPO-RRT* algorithm must be set. Table 2 shows the specific parameter names and values.

Table 2 Simulation experiment parameters
Full size table

Simulation experiments

In this section, the HPO-RRT* algorithm is applied to the two dynamic scenarios with moving threats designed in “Simulation setup” to verify its feasibility, optimization, efficiency and success rate of the HPO-RRT* algorithm in the dynamic environment of UAV flight. Additionally, to further verify the performance of the HPO-RRT* algorithm, we compared it with three dynamic planning or replanning algorithms derived from RRT, including RRTX, Risk-RRT and Risk-RRT*. In the two sets of scenarios, these algorithms are run many times to reduce the randomness of sampling-based algorithms. We evaluate the performance of each algorithm by taking the navigation time, planning path length and planning success rate as metrics.

Experiment Scenario 1 Figure 6 shows the UAV paths planned by the four algorithms in Scenario 1, and Table 3 shows some performance data in the experiment in Fig. 6. In general, compared with the other three algorithms, the path planned by HPO-RRT* is shorter and smoother. Moreover, in each partial planning, HPO-RRT* can quickly plan a longer path, so the planning efficiency and expansion range of this algorithm are also the best. In addition, HPO-RRT* has the shortest planning and execution time, stable performance, and a high success rate.

Fig. 6
figure 6

Experiment Scenario 1. Planned path diagram of different algorithms at different times, in which the blue line represents RRTX; the green line represents Risk-RRT; the yellow line represents Risk-RRT *; and HPO-RRT* is indicated by a red line. The grey translucent threat is the initial position of the three moving threats. a, c and e show path 3D diagrams at \(t = 10s,20s,27.8s\), respectively; b, d and f show the contour top views of the above time path

Full size image
Table 3 Length and navigation time of planned paths with the algorithms in Fig. 6
Full size table

RRTX is a replanning algorithm. Compared with similar algorithms, RRTX has faster information transmission speed and response speed and has better performance in the problem of path replanning in addressing moving threats. Although the tree structure needs to be pruned in RRTX path planning, which greatly reduces the corresponding speed and planning efficiency of the algorithm, Fig. 6 shows that RRTX can still maintain a good response speed and planning efficiency. In addition, when the tree structure is small at the initial stage of planning, the planned path quality is basically the same as that of the HPO-RRT* algorithm. However, when the sampling increases and the tree structure becomes larger, RRTX takes a long time to prune the tree structure, thus reducing the time to optimize the path. Thus, the quality of the paths planned by RRTX begins to lag behind that of HPO-RRT*. The path planned by RRTX becomes less smooth, and the angle loss increases when the UAV flies along this path. Risk-RRT, Risk-RRT* and HPO-RRT* are time-based RRT algorithms. In other words, little time needs to be spent in tree structure pruning during planning, so they have a fast response speed. However, Risk-RRT is an algorithm whose path planner is time-based RRT, thus using Risk-RRT for planning will generally only obtain one feasible path. Furthermore, the optimality and planning efficiency of the planned path cannot be guaranteed. Therefore, we can see that the paths and navigation times obtained by Risk-RRT and HPO-RRT* are considerably different. Compared with Risk-RRT, the quality of the planned path of Risk-RRT* has been improved to some extent. Risk-RRT* is an algorithm that needs to rewire the tree structure to optimize the path, but Fig. 6 shows that the improvement of the path quality is not large. This result is obtained because part of the planning time is short, and the time allocated to the reconnection process is limited. However, Risk-RRT* requires a large number of rewiring calculations to optimize the path, so it cannot optimize the path better in a limited time. Similar to RRTX, Risk-RRT* has good algorithm performance in the early stage due to its small tree structure. However, with increasing sampling, its performance gradually lags behind that of HPO-RRT*. It can be seen that HPO-RRT* always performs well in planning. HPO-RRT* uses APF bias sampling in the path planner to improve the quality and efficiency of sampling. At the same time, in the expansion of the tree, the lazy collision checking method is used to reduce the computational cost and expand the expansion range of the tree. After obtaining the heuristic path, HPO-RRT* uses the low-cost path optimizer to directly optimize the heuristic path to quickly obtain the optimized path. This optimization method does not change the structure of the time tree; that is, no additional calculation loss occurs in the optimization process. Therefore, compared with the other three algorithms, HPO-RRT* has the smallest navigation time, the shortest planned path and the highest smoothness.

Furthermore, in Scenario 1, each algorithm is repeated 50 times. We use the planned path length, navigation time and success rate to evaluate the performance of each algorithm. Figures 7, 8 and 9 compare the results. We find that the HPO-RRT* algorithm has good stability and algorithm performance. In the length comparison of 50 experiments, HPO-RRT* can use the low-cost path optimizer to fully and quickly optimize the path during planning so that the length of the planned path is always the shortest and the length variance is very small. Additionally, because HPO-RRT* maintains high planning efficiency, the navigation time can be quickly stabilized. Moreover, for the above reasons, the success rate of the algorithm is high. In other words, HPO-RRT* has good performance and stability when addressing UAV path planning in a dynamic environment with known moving threat trajectories.

Fig. 7
figure 7

Planned path length of 50 experiments of four algorithms

Full size image
Fig. 8
figure 8

Navigation time of 50 experiments of four algorithms

Full size image
Fig. 9
figure 9

Success rate

Full size image

Experiment Scenario 2 Experiment Scenario 2 focuses on the success rate and optimization of path-planning algorithms in a more complex dynamic environment. The algorithm performance is tested by setting the number and speed of moving threats in the UAV flight environment to a random generation state. Figure 10 and Table 4 show the performance of the four algorithms in one case with threats of random movement. Furthermore, for each combination of random threat number and speed in Scenario 2, each algorithm is tested in 6 trials. Therefore, for each algorithm, we conducted a total of 96 experiments on 16 combinations of random threats. We use the planned path length, navigation time and success rate to evaluate the performance of each algorithm. The performance of the algorithms is shown in Figs. 11 and 12. In general, compared with Scenario 1, the performance of the four algorithms declines in Scenario 2. This decline occurs because the four algorithms need to address more complex moving threats. However, compared with the other three algorithms, HPO-RRT* has the shortest and smoothest planned path length. The navigation time is also the shortest, and the success rate is also guaranteed. Therefore, the efficiency, effectiveness and stability of HPO-RRT* are demonstrated.

Fig. 10
figure 10

Experiment Scenario 2. Planned path diagram of different algorithms at different times, in which the blue line represents RRTX; the green line represents Risk-RRT; the yellow line represents Risk-RRT*; and HPO-RRT* is indicated by a red line. The grey translucent threat is the initial position of the three moving threats. a, c and e show the path 3D diagrams when t = 15 s, 30 s, 38.4 s, respectively; and b, d and f show the contour top views of the above time path

Full size image
Table 4 Length and navigation time of planned paths with the algorithms in Fig. 9
Full size table
Fig. 11
figure 11

Relationship between the success rate, average path length and obstacle speed and number

Full size image
Fig. 12
figure 12

Comparison of the mean and variance of the navigation time

Full size image

Figure 10 and Table 4 clearly show that the planning path quality of the HPO-RRT* algorithm remains superlative among the four algorithms. Because Risk-RRT has relatively low planning efficiency and no path optimization process, its planning path and navigation time are relatively poor. In more complex dynamic environments, Risk-RRT* does not have sufficient reconnection time, resulting in less obvious improvement of path quality. Under its ability of rapid replanning and optimization, RRTX can obtain a faster navigation time and higher-quality paths than Risk-RRT and Risk-RRT*. With its efficient planner and optimizer, HPO-RRT* also maintains a high-quality planning path and has the shortest response time in a dynamic environment with random moving threats.

Furthermore, to verify the performance quality of HPO-RRT* more comprehensively, 96 simulations were conducted on 16 combined random moving threats. Figures 11 and 12 show the results. In the combination of a few moving threats and slow moving speed, the four algorithms easily plan the path, and all find the path with basically the same success rate, with the path length of HPO-RRT* being the shortest. However, with an increase in the number and speed of threats, the success rate of the algorithms declines. In addition, it can be seen that HPO-RRT* guarantees almost the same success rate as RRTX, while the success rates of Risk-RRT and Risk-RRT * decrease significantly. Although HPO-RRT* as a time-based RRT algorithm has been proven to be inferior to the replanning algorithm (RRTX) in addressing path-planning problems in highly dynamic environments (i.e. environments with fast-moving threats and more moving threats), HPO-RRT* can maintain good adaptability to dynamic environments with its high-quality sampling and efficient expansion, and the performance loss of this algorithm is low. In terms of path quality, HPO-RRT* maintains certain advantages in various combinations of random moving threats, which depend on the low-cost path optimizer of HPO-RRT* to quickly and fully complete path optimization at any time. Meanwhile, HPO-RRT* has the shortest and most stable navigation time with the good performance of the efficient path planner and the low-cost path optimizer in its hierarchical planning architecture. In other words, HPO-RRT* can adapt to more complex dynamic environments and has good performance and stability.

Conclusions and future work

In this paper, a time-based RRT named HPO-RRT* is proposed to solve the real-time path-planning problem of UAVs in a dynamic environment. This algorithm adopts a hierarchical framework including the UAV perception system, path planner and path optimizer, which can optimize the path while improving efficiency. In the path planner, an improved time-based RRT* algorithm is used to obtain heuristic paths. The algorithm of the path planner improves the sampling process, tree expansion process and collision checking process to avoid additional calculation loss and improve planning efficiency. In the low-cost path optimizer, to avoid numerous calculations caused by the optimization tree structure, the heuristic path is directly optimized to quickly and efficiently obtain a homotopy optimal path. Simulations and comparisons show that the proposed algorithm has better performance.

In future work, we will conduct outdoor experimental verification on the independently developed quad-rotor platform to confirm the application value of the algorithm. In addition, we expect to extend HPO-RRT* to the formation and cooperation of UAVs in future work. An intuitive prospect is to use a formation framework to complete the cooperative path planning of UAVs. Of course, a better prospect is to bring HPO-RRT* into the full autonomous cooperative architecture.