Reinforcement-learning-based parameter adaptation method for particle swarm optimization

Abstract

Particle swarm optimization (PSO) is a well-known optimization algorithm that shows good performances in solving different optimization problems. However, the PSO usually suffers from slow convergence. In this article, a reinforcement-learning-based parameter adaptation method (RLAM) is developed to enhance the PSO convergence by designing a network to control the coefficients of the PSO. Moreover, based on the RLAM, a new reinforcement-learning-based PSO (RLPSO) algorithm is designed. To investigate the performance of the RLAM and RLPSO, experiments on 28 CEC 2013 benchmark functions were carried out to compare with other adaptation methods and PSO variants. The reported computational results showed that the proposed RLAM is efficient and effective and that the proposed RLPSO is superior to several state-of-the-art PSO variants.

Introduction

In recent years, the research community has witnessed an explosion of literature in the area of swarm and evolutionary computation [1]. Hundreds of novel optimization algorithms have been reported over the years and applied successfully in many applications, e.g., system reliability optimization [2], DNA sequence compression [3], systems of boundary value problems [4], solving mathematical equations [5, 6], object-level video advertising [7], and wireless networks [8]. Particle swarm optimization (PSO), which was first proposed in 1995 by Kennedy and Eberhart [9], is one of the most famous swarm-based optimization algorithms. Due to its simplicity and high performance, a multitude of enhancements have been presented on PSO during the last few decades, which can be simply categorized into three types: parameter selection, topology, and hybridization with other algorithms [10].

When solving different optimization problems, appropriate parameters need to be configured for PSO and its variants. The performance of PSO heavily depends on the parameter settings, which shows the importance of setting the parameter values. However, it is very difficult for humans to conduct a laborious preprocessing phase for the detection of promising parameter values and design the strategy to monitor the running state of PSO and then adjust the running parameters [11].

Fig. 1

Adaptation schemes

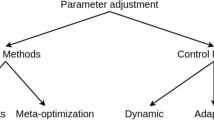
The current parameter setting algorithms are mainly divided into two categories: parameter tuning and parameter control. The classifications are shown in Fig. 1. Parameter tuning is relatively simple to implement, but because all its designs are determined before the optimization algorithm runs, it loses some adaptability to the problem when running. In contrast, parameter control will monitor the operation of the optimization algorithm to control the operation of the algorithm. Furthermore, the types of parameter control have been clearly defined, distinguishing deterministic, adaptive, or self-adaptive methods. Only adaptive methods are informed as they receive feedback from the EA run and assign values based on that feedback [12].

Thus, this paper focuses on adaptive methods.

Common parameter adaptation methods include control based on history, control based on test experiments, control based on fuzzy logic, and control based on reinforcement learning. In the existing adaptive methods, almost all the control rules need to be learned when the algorithm is running. Although fuzzy logic has pre-configured rules, it also needs to be manually configured item by item, which makes the current adaptation algorithms inefficient. In addition, these adaptation algorithms are usually designed for a certain optimization algorithm and cannot be applied to various optimization algorithms. However, in the image domain [13] and natural language processing domain [14], the pre-training models are very mature, which greatly improves the performance of subsequent tasks. This inspired us to use reinforcement learning to improve the particle swarm performance through pre-training. Using the adaptation method based on RL will bring the following benefits: 1. There is no need to manually design rules and tune parameters, which greatly reduces the burden on users. Although the parameters in RL are also very important, experiments have shown that using the same set of parameters achieves good results for different algorithms and test functions. Therefore, in the actual use process, it is not necessary to adjust the parameters in RL. 2. By learning from past experience, the application of the algorithm is more extensive, and the effect is better.

In this paper, we propose a reinforcement-learning-based parameter adaptation method (RLAM) by embedding a deep deterministic policy gradient (DDPG) [15] into the process of PSO. In the proposed method, there are two neural networks: the actor network and the action-value network. The actor network is trained to help the particles in the PSO choose their best parameters according to their states. The action-value network is trained to evaluate the performance of the actor network and provide gradients for the training of the actor network. The input of the actor network includes three parts: the percentage of iterations, the percentage of no-improvement iterations, and the diversity of the swarm. All the particles will be divided into several groups, and each group has their own action generated by the actor network. Typically, the action controls w, c1, and c2 in the PSO, but it has the ability to control any parameters if needed. A reward function is needed to train the two networks. The design is very simple and targeted at encouraging the PSO to obtain a better solution in every iteration. The whole process of training and utilizing the two networks is described in “Deep deterministic policy gradient”.

To evaluate the performance of the method proposed in this paper, three sets of experiments were designed: 1. Six particle swarm algorithm variants were selected, and their performances combined with the RLAM were compared with their original performances. 2. The RLAM was combined with the original PSO and compared with other adaptation methods. 3. A new reinforcement-learning-based PSO (RLPSO) was designed based on this method, and its performance was compared with five particle swarm variants and several advanced algorithms proposed in recent years. These experiments verified the effectiveness of the RLAM.

Main contributions of this paper

• 1. The reinforcement learning algorithm (DDPG algorithm) is introduced into the adaptation process, which greatly improves the parameter adaptation ability.

• 2. The concept of pre-training is introduced into the adaptation process so that the particle swarm algorithm can not only adapt the parameters based the current situation but also through past experience, which improves the intelligence level of the algorithm.

• 3. Based on the above improvements, a adaptive particle swarm optimization algorithm based on reinforcement learning (RLPSO) is proposed, which greatly improves the performance of the PSO.

Structure of paper

The rest of this paper is organized as follows. The definitions of the PSO and DDPG are presented in “Background information”. Related work on parameter setting is introduced in “Related work”. The implementation of the proposed RLAM and RLPSO algorithms is described in “Proposed Algorithm”. Experimental studies are presented in “Experiments”. Conclusions summarizing the contributions of this paper are presented in “Conclusions”.

Background information

Particle swarm optimization

Particle swarm optimization is the representation of swarm behaviors in some ecological systems, such as birds flying and bees foraging [16]. In the classic PSO, the movement of a particle is influenced by its own previous best position and the best position of the best particle in the swarm. To describe the state of the particles, the velocity $V_{i}$ and position $X_{i}$ of the $i^{th}$ particle are defined as follows:

$$\begin{aligned} V_{i}= & {} \left( v_{i}^{1}, v_{i}^{2}, \ldots , v_{i}^{D}\right) , i=1,2, \ldots , N\\ X_{i}= & {} \left( x_{i}^{1}, x_{i}^{2}, \ldots , x_{i}^{D}\right) , i=1,2, \ldots , N \end{aligned}$$

where D represents the dimension of the search space, and N represents the number of particles. As the search progresses, the two movement vectors are updated as follows:

$$\begin{aligned} V_{i}(t+1)= & {} w V_{i}(t)+c1*r1\left( p{ Best }_{i}-X_{i}(t)\right) \\{} & {} +c2*r2\left( g{ Best }-X_{i}(t)\right) \\ X_{i}(t+1)= & {} X_{i}(t)+V_{i}(t+1) \end{aligned}$$

where w is the inertia weight, c1 is the cognitive acceleration coefficient, c2 is the social acceleration coefficient, r1 and r2 are uniformly distributed random numbers within [0, 1], $V_{i}(t)$ denotes the velocity of the $i^{th}$ particle in the $t^{th}$ generation, $p{ Best }_{i}$ is the personal best position for the $i^{th}$ particle, and g Best is the best position in the swarm.

Reinforcement learning and deep deterministic policy gradient

This subsection introduces the DDPG and RL briefly. Further details can be found elsewhere [15].

Reinforcement learning

Reinforcement learning (RL) is a kind of machine learning. Its purpose is to guide the agent to perform optimal actions in the environment to maximize the cumulative reward. The agent will interact with the environment in discrete timesteps. At each timestep t, the agent receives an observation $s_t \in S$, takes an action $a_t \in A$, and receives a scalar reward $r_t(s_t, a_t)$. S is the state space, and A is the action space. The agent’s behavior is controlled by a policy $\pi :S \rightarrow A$, which maps each observation to an action.

Deep deterministic policy gradient

In the DDPG, there are four neural networks designed to obtain the best policy $\pi$: the actor network $\mu (s_t\vert \theta ^{\mu })$, target actor network $\mu ^{\prime }(s_t\vert \theta ^{\mu ^{\prime }})$, action-value network $Q(s_t,a_t\vert \theta ^{Q})$, and target action-value network $Q^{\prime }(s_t,a_t\vert \theta ^{Q^{\prime }})$. $\mu$ and $\mu ^{\prime }$ are used to choose the action based on the state, Q and $Q^{\prime }$ are used to evaluate the action chosen by the actor network. $\theta ^{\mu }$, $\theta ^{\mu ^{\prime }}$, $\theta ^{Q}$, and $\theta ^{Q^{\prime }}$ are the neural network weights of these neural networks. Initially, $\theta ^{\mu ^{\prime }}$ is a copy of $\theta ^{\mu }$ and $\theta ^{Q^{\prime }}$ is a copy of $\theta ^{Q}$. During training, the weights of these target networks are updated as follows:

$$\begin{aligned} \begin{aligned} \theta ^{Q^{\prime }}&\leftarrow \tau \theta ^{Q} + (1-\tau )\theta ^{Q^{\prime }} \\ \theta ^{\mu ^{\prime }}&\leftarrow \tau \theta ^{\mu } + (1-\tau )\theta ^{\mu ^{\prime }} \end{aligned} \end{aligned}$$

(1)

where $\tau \ll 1$.

To train the action-value network, we need to minimize the loss function:

$$\begin{aligned} L\left( \theta ^{Q}\right)= & {} \left( r\left( s_{t}, a_{t}\right) +\gamma Q^{\prime }\left( s_{t+1}, a_{t+1} \mid \theta ^{Q^{\prime }}\right) \right. \nonumber \\{} & {} \left. -Q\left( s_{t}, a_{t} \mid \theta ^{Q}\right) \right) ^{2} \end{aligned}$$

(2)

Then, the action-value network is used to train the actor network with the policy gradient

$$\begin{aligned} \begin{aligned} \nabla _{\theta ^{\mu }} J =\left. \left. \nabla _{a} Q\left( s, a \mid \theta ^{Q}\right) \right| _{s=s_{t}, a=\mu \left( s_{t}\right) } \nabla _{\theta _{\mu }} \mu \left( s \mid \theta ^{\mu }\right) \right| _{s=s_{t}} \end{aligned} \end{aligned}$$

(3)

The data flow of the training process is shown in Fig. 2. In this figure, critic is the action-value network.

Fig. 2

Training process of deep deterministic policy gradient (DDPG)

Comprehensive learning particle swarm optimizer (CLPSO)

In PSO, all particles are attracted by their own historical optima and the optima of all particles. The global optimum may be inside a local minimum, which will cause the particle swarm to prematurely converge to the wrong location. To solve this problem, we introduce the mechanism of the comprehensive learning particle swarm optimizer (CLPSO) in RLPSO, which allows particles to randomly learn the dimensions of different particles. Therefore, this section will introduce the CLPSO.

More details on the CLPSO can be found elsewhere [17]. The velocity updating equation used by the CLPSO is as follows:

$$\begin{aligned} v_i^d(t+1) = wv_i^d(t) + c * r * (pbest_{f_i(d)}^d - x_i^d(t)), \end{aligned}$$

(4)

where $f_i(d)=[f_i(1),f_i(2),\ldots ,f_i(D)]$ defines which particle’s pbest the $i^{th}$ particle should follow. The $d^{th}$ dimension of the $i^{th}$ particle should follow the ${f_i(d)}^{th}$ particle’s pbest in the $d^{th}$ dimension. r is a random number between 0 and 1. w and c are coefficients.

To determine $f_i(d)$, every particle has its own learning parameter $Pc_i$. The $Pc_i$ value for each particle is calculated by the following equation:

$$\begin{aligned} Pc_i = a + b * \frac{\left( exp\left( \frac{10(i-1)}{ps-1}\right) -1\right) }{exp(10)-1}, \end{aligned}$$

(5)

where ps is the population size, $a = 0.05$, and $b = 0.45$. When a particle updates its velocity for one dimension, a random value in [0, 1] is generated and compared with $Pc_i$. If the random value is larger than $Pc_i$, the particle of this dimension will follow its own pbest. Otherwise, it will follow another particle’s pbest for that dimension. CLPSO employs a tournament selection to choose a target particle. Furthermore, to avoid wasting function evaluations in the wrong direction, CLPSO defines a certain number of evaluations as the refreshing gap m. During the period in which a particle follows a target particle, the number of times the particle ceases to improve is recorded as $flag_{clpso}$. If $flag_{clpso}$ is bigger than m, the particle will obtain its new target particle by employing a tournament selection again.

Related work

When solving different optimization problems, appropriate parameters need to be configured for PSO and its variants. The performance of PSO heavily depends on the parameter setting, which shows the importance of setting the parameter values. The classifications are shown in Fig. 1. We will briefly review them next.

Parameter tuning

There are many parameters that need to be configured in the particle swarm algorithm, and these parameters are related to the quality of the final optimization result. Therefore, the parameters can be tested in groups, the parameter groups can be tested on all the test problems, and the parameter group with the best effect can be selected.

Since the end of last century, a number of automatic parameter tuning approaches have been put forward, such as Design of experiments [18], F-Race [19], ParamILS [20], REVAC [21], and SPO [22]. SMAC [23] and TPE [24] are the most commonly used methods in this field.

Determined parameter control

Determined parameter control refers to the adaptive methods whose parameters are determined before the actual optimization problem is solved, which can be mainly divided into two categories based on the optimization progress of the optimization problem: linear parameter variation and nonlinear parameter variation.

Linear strategies

Initially, all the parameters in the particle swarm algorithm were set to fixed values [9], but researchers have found that this method is not efficient, and it is difficult to balance the relationship between exploration and exploitation. Therefore, linear strategies have been proposed. A linear strategy means that algorithms pre-specify a linear expression during the running process and determine some of the current running parameters based on the running state.

In the paper [25], the researchers proposed a linearly reduced w parameter, which improved the fine-tune capability of the PSO in the later stage. The value of w decreased linearly from an initial value wmax to wmin. The specific formula for this change is as follows:

$$\begin{aligned} \omega (t)=\frac{t_{\max }-t}{t_{\max }}\left( \omega _{\max }-\omega _{\min }\right) +\omega _{\min } \end{aligned}$$

Then, in the paper [26], the researchers proposed a linear variation operation for three parameters. In addition to the linear decrease of w, c1 was increased linearly and c2 was decreased linearly. These parameters were preset with their maximum and minimum values. This method makes the PSO algorithm more inclined to search near the optimal value that it found in the early stage, which improves the particle’s exploration ability and improves its fine-tuning ability in the later stage, allowing it to quickly converge to the global optimal value. The formulas for the changes of c1 and c2 are shown as follows, and the change of w is consistent with the above formula:

$$\begin{aligned} \begin{aligned} c1&=\left( c1_{f}-c1_{i}\right) \frac{\text { iter }}{\text { MAXITR }}+c1_{i} \\ c2&=\left( c2_{f}-c2_{i}\right) \frac{\text { iter }}{\text { MAXITR }}+c2_{i} \end{aligned} \end{aligned}$$

(6)

In the paper [27], the researchers constructed a linearly growing w, which could also achieve a better performance in some of the problems given in the paper. The equation is as follows:

$$\begin{aligned} \omega (t)=0.5 \times \frac{t}{t_{\max }}+0.4 \end{aligned}$$

Considering that both the linear growth and decline of w have advantages in some problems, in the paper [28], the researchers constructed a w that linearly increased first and then linearly decreased. The specific changes are expressed as follows:

$$\begin{aligned} \omega (t)=\left\{ \begin{array}{cc} 1 \times \frac{t}{t_{\max }}+0.4, &{} 0 \le \frac{t}{t_{\max }} \le 0.5 \\ -1 \times \frac{t}{t_{\max }}+1.4, &{} 0.5<\frac{t}{t_{\max }} \le 1 \end{array}\right. \end{aligned}$$

In addition to the above-mentioned linear adjustment according to the running progress of the algorithm, there were also studies in which the parameters were linearly adjusted based on some other parameters.

For example, in the paper [29], the researchers adjusted the w value based on the average distance between particles. The specific adjustment method is as follows:

$$\begin{aligned} \omega (t)=\frac{\omega _{\max }-\omega _{\min }}{D_{\max }-D_{\min }} \times D(t)+\frac{D_{\max } \omega _{\min }-D_{\min } \omega _{\max }}{D_{\max }-D_{\min }} \end{aligned}$$

where D(t) denotes the average distance between particles, and $\omega _{\max }$ and $\omega _{\min }$ are predefined.

Nonlinear strategies

Inspired by the various linear strategies, many researchers have turned their attention to nonlinear strategies. These methods make parameter changes more flexible and closer to the needs of the problem.

In the paper [30], the author proposed the use of the E index to update w, which improves the convergence speed of the algorithm on some problems. In the paper [31], the author used a quadratic function to update the parameters. The test results showed that this method outperformed the linear transformation algorithm in most continuous optimization problems. In the paper [32], the author combined the sigmoid function into a linear transformation, allowing the algorithm to quickly converge in the search process. In the papers [33] and [34], the authors applied a chaotic model (logistic map) to the parameter transformation, which gave the algorithm a stronger search ability. Similarly, in the paper [35], the author set the parameters to random numbers and also obtained good results.

Adaptation parameter controlling

Adaptation parameter controlling are techniques for the dynamic adaptation of the algorithm’s parameters during its execution. They are typically based on performance feedback from the algorithm on the considered problem instance.

History based

The approaches proposed in some papers divide the whole running process into many small processes, using different parameters or strategies in each small process and judging whether the parameters or strategies are good enough based on the performance of the algorithm at the end of the small stage. The strategies or parameters that are good enough will be chosen more in subsequent runs. In the paper [36], the author built a parameter memory. In each run, all the running particles were assigned different parameter groups, and the parameters used by some particles with better performances after the small-stage run was completed were saved in the parameter memory. The parameters chosen by subsequent particles tended to be close to the average of the parameter memory. In the paper [37], the author designed five particle swarm operation strategies based on some excellent particle swarm variant algorithms in the past and kept a record of the success rate for each strategy. In the initial state, all the success rates were set to 50%, and then in each small process, a strategy was randomly selected for execution based on the weight of the past success rate. Based on the number of particles promoted, the memory of the success rate was updated. In the paper [38], the author improved the original EPSO, updated the designed strategy, divided the particle swarm into multiple subgroups, and evaluated the strategy separately, which further improved the performance of the algorithm.

Small test period based

This approach divides the entire optimization process into multiple sub-processes and divides each sub-process into two parts. One part is used to test the performance of the parameters or strategies, and the number of evaluations is generally less than 10%. The other part is the normal optimization process. In the paper [39], the author divided the parameters into many parameter groups based on the grid. In each performance test process, the population was divided into multiple subgroups, and the parameter groups around the grid of the previous process were tested. After running several iterations, the parameter group with the best effect was selected as the parameter group to be used. In the paper [40], the author divided the test sub-process into two processes. In the first process, the adjacent points of the current selection point were evaluated, and the probability of success was calculated. Then, in the second process, the direction with the highest probability of success was selected as the exploration direction, multiple steps in this direction were explored, and finally, the best parameter group in the second step was selected as the parameter configuration for the next operation. This method further improved the performance.

Fuzzy rules

In the paper [41], the author presented a new method for dynamic parameter adaptation in the PSO, where an improvement to the convergence and diversity of the swarm in the PSO using interval type-2 fuzzy logic was proposed. The experimental results were compared with the original PSO, which showed that the proposed approach improved the performance of the PSO. In the paper [42], the author presented work to improve the convergence and diversity of the swarm in the PSO using type-1 fuzzy logic applied it to classification problems.

Table 1 Reinforcement-learning-based adaptive methods

Reinforcement learning based

At present, most optimization algorithms based on reinforcement learning are based on Q-learning for adaptive control parameters and strategies. In the paper [43], the author combined a variety of topological structures, using the diversity of the particle swarm and the topological structure of the previous step as the state, and selected the topological structure with the largest Q value from the Q table as the topology to be used in the next optimization step. In the paper [44], the author used the Q-learning algorithm. Enter the state with how far from the optimal value and the ranking of the particle evaluation value among all particles. Different parameter groups were used as adaptation targets. The reward was determined based on whether the entire optimization problem grew, the current optimization progress, and the currently selected action. In the paper [45], the author used the Q-learning algorithm. The strategy selected in the previous step was the state input. The output actions controlled different strategies, such as jumping or fine-tuning. Finally, the reward was determined based on whether the whole optimization problem grew. In the paper [46], the author used the Q-learning algorithm. The particle position was taken as the state input. The output action controlled the prediction speeds of different particle strategies. Finally, the reward was determined based on the increase or decrease of the particle evaluation value. In the paper [47], the author used the Q-learning algorithm with the serial number of each particle, the particle position as the state input, and the output action to control two different strategies, and finally, the reward was determined according to whether the entire optimization problem grew. In the paper [48], the author adopted the algorithm of the policy gradient, which took the particle position pbest as the state input and the output action controls c1 and c2 and finally determined the reward based on the growth rate of the entire optimization problem.

A summary of these papers is shown in Table 1, which describes the method used in the paper, the state input, the action output, the reward input, and whether each particle was controlled separately. In this table, Q represents Q-Learning and PG represents Policy Gradient.

Section summary and motivation

First, current algorithms are not smart enough. If a human solves an optimization problem, he optimizes based on past experience and the current operating state. The current parameter tuning methods do not do this. They all adjust the policy during operation without using past experience. For the same type of problem, such as path planning, the algorithm proposed in this article can be trained in advance through various test problems. After that, the algorithm will remember the experience of this training. As a result, the convergence accuracy on new problems will be improved. The existing parameter adaptive method cannot be trained in advance and can only collect experience while operating.

Second, the current reinforcement learning methods introduced in parameter tuning methods all suffer from some performance issues. The currently used reinforcement learning method is mainly Q-learning, and another researcher used Policy Gradient.

Since Q-learning can only choose from a limited number of actions (usually four actions in past papers), this leads to the necessity of artificially mapping a high-dimensional continuous action space with a limited number of actions. This results in a huge drop in the variety of actions.

Policy Gradient (PG) can be used in continuous action space, but because its training process requires action probability, it must output a probability distribution and then determine the action by sampling. This approach makes the output actions random and reduces the performance of the reinforcement learning network.

DDPG absorbs the benefits of PG’s support for continuous motion. At the same time, an evaluation network is designed, which makes the action probability no longer needed in the training process and solves the problem of performance degradation caused by randomness.

Third, how to avoid the introduction of new parameters that require manual configuration and reduce the difficulty of algorithm configuration is also a question worthy of consideration.

Proposed Algorithm

In this section, an efficient parameter adaptation method is proposed. A variant of the particle swarm algorithm based on the above algorithm will be introduced later.

Parameter adaptation based on deep deterministic policy gradient (DDPG)

In this section, we first introduce the input and output of the actor network applied to the particle swarm algorithm. Next, we describe how the reward function scores based on changes in state. Then, the approach used to train the particle swarm algorithm is introduced. The process to run it with the trained network will be described later. Finally, the proposed new particle swarm algorithm is introduced.

State of particle swarm optimization (PSO, input of actor network)

The running state designed in this paper is divided into three parts: the current iteration progress, the current particle diversity, and the current duration of the particle no longer growing. In order for the neural network to work optimally, all operating states will eventually be mapped to the interval of [$-1,1$] and finally input to the neural network.

The iteration input is considered as a percentage of the iterations during the execution of the PSO, and the values for this input are in the range of 0 to 1. At the start of the algorithm, the iteration is considered to be at 0%, and the percentage is increased until it reaches 100% at the end of the execution. The values are obtained as follows:

$$\begin{aligned} Iteration = Fe\_num / Fe\_max \end{aligned}$$

(7)

where $Fe\_num$ is the number of function evaluations that have been performed, and $Fe\_max$ is the maximum number of function evaluation executions set when the algorithm is run.

The diversity input is defined by the following equation, in which the degree of the dispersion of the swarm is calculated:

$$\begin{aligned} {\text {Diversity}}(t)=\frac{1}{D} \sum _{i=1}^{D} \sqrt{\sum _{j=1}^{N}\left[ x_{i j}(t)-\overline{x_{j}}(t)\right] } \end{aligned}$$

(8)

where $x_{ij}(t)$ is the $j^{th}$ position of the $i^{th}$ particle in iteration t, $\overline{x_{j}}(t)$ is the $j^{th}$ average position of all the particles in iteration t. With lower diversity, the particles are closer together, and with higher diversity, the particles are more separated. The diversity equation can be taken as the average of the Euclidean distances between each particle and the best particle.

The stagnant growth duration input is used to indicate whether the current particle swarm is running efficiently. It is defined as follows:

$$\begin{aligned}{} & {} Iteration_{no-improvement} \nonumber \\{} & {} \quad = (Fe\_num-Fe\_num_{last-improve}) / Fe\_max \end{aligned}$$

(9)

where $Fe\_num_{last-improve}$ represents the number of evaluations at the last global optimal update.

Since the state distribution space is very different when optimizing different objective functions, unified normalization will cause some states to be too large or too small. To solve this problem and make it easier for the network to obtain information from the state, the state needs to be transformed. We believe that the transformation needs to meet the following requirements:

• 1. Make small changes significant.

• 2. The range needs to be mapped to the range of −1 to 1.

• 3. Information cannot be lost.

Based on the above requirements and inspired by previous work [49], we designed the following transformations.

The input is originally x, which can represent the Iteration, Diversity, or $Iteration_{no-improvement}$. The output is as follows:

$$\begin{aligned} state_i = sin(x*2^{i}) \end{aligned}$$

(10)

where $state_i$ is the $i^{th}$ parameter value newly generated from x. In this paper, i takes values of 0, 1, 2, 3, and 4. An x will eventually generate five new parameters.

For example, if $Iteration = x1$, $Diversity=x2$ and $Iteration_{no-improvement}=x3$, the new generated parameters will be as follows:

$$\begin{aligned} \begin{aligned}&sin(x1*2^{0}),sin(x1*2^{1}),sin(x1*2^{2}),\\&\quad sin(x1*2^{3}),sin(x1*2^{4}), \\&sin(x2*2^{0}),sin(x2*2^{1}),sin(x2*2^{2}),\\&\quad sin(x2*2^{3}),sin(x3*2^{4}), \\&sin(x3*2^{0}),sin(x3*2^{1}),sin(x3*2^{2}),\\&\quad sin(x3*2^{3}),sin(x3*2^{4}), \\ \end{aligned} \end{aligned}$$

The reason for this operation is that some of the above parameters are very small, and their changes are even smaller, which will cause the actor network to fail to capture their changes and fail to perform effective action output.

Fig. 3

Example of transform function

Part of the function image is shown in Fig. 3. The case where y is greater than 0 is regarded as 1, and the case where y is less than 0 is regarded as zero. These numbers are combined as shown in the lower part of the figure. These values are equivalent to the range of 7 to 0 in binary form. That is, the above transformation is similar to binarizing the original value. However, using binary values would waste computer memory when using floats. Instead, we use their float continuous counterparts—sinusoidal functions. In this way, the above requirements are met.

Fig. 4

Example of output of actor network

Action of PSO (output of actor network)

The actions designed in this paper are used to control the operating parameters in the PSO, such as w, c1, and c2. The parameters to be controlled can be set as required. The action output by the actor network does not control the above parameters of each particle separately but divides the particles into five subgroups, and it generates five sets of parameters to control the different groups.

We determine the corresponding subgroup based on the index of the particle. For example, if the index of the particle is 7, then the corresponding subgroup will be 7%5 = 2, i.e., subgroup 2. The indices of the subgroups are 0, 1, 2, 3, and 4. This method ensures that the numbers of individuals in every subgroup are similar.

For the traditional PSO algorithm, the obtained action vector $a_t$ is 20-dimensional, divided into five groups, each of which is aimed at a subgroup. For a subgroup, the action vector is four-dimensional: a[0] to a[3]. The w, c1, and c2 required for each round of the optimization algorithm are generated based on a[0] to a[3] as follows:

$$\begin{aligned} \begin{aligned}&w = a[0] * 0.8 + 0.1 \\&scale = 1 / (a[1] +a[2] + 0.00001) * a[3] * 8 \\&c1 = scale * a[1] \\&c2 = scale * a[2] \\ \end{aligned} \end{aligned}$$

(11)

where scale is a parameter that helps normalize c1 and c2, which is optional.

An example can be seen in Fig. 4. In this figure, the output represents action vector $a_t$, the action converter represents Eq. 11, and Action Group i (i can be 1 2 3 4 5) represents a[0] to a[3].

For some PSO variants, since the parameters were studied when developing the algorithm, the original parameter set is already quite good. To take advantage of the performance of the original parameter set, the new w, c1, c2 are configured according to the following formulas:

$$\begin{aligned} \begin{aligned} w&= a[0] * 0.5 + w_{origin} \\ c1&= a[1] * 0.5 + c1_{origin} \\ c2&= a[2] * 0.5 + c2_{origin} \\ \end{aligned} \end{aligned}$$

(12)

where $w_{origin}$, $c1_{origin}$, and $c2_{origin}$ represent the original parameters of the algorithm. In all subsequent experiments, each algorithm will choose one of the action parameter configuration methods for experimentation. If there are more parameters in the algorithm that need to be configured, the number of output parameters can be increased and configured like c1 or w.

Reward function

A reward function is used to calculate the reward after an action is executed. Its target is to encourage the PSO to obtain a better gBest. Therefore, the reward function is designed as follows:

$$\begin{aligned} r(t) = {\left\{ \begin{array}{ll} 1,&{}\quad gBest(t+1)<gBest(t)\\ -1 ,&{}\quad gBest(t+1)=gBest(t) \end{array}\right. } \end{aligned}$$

(13)

where gBest(t) is the best solution in the $t^{th}$ iteration.

Training

This section introduces the training process for the traditional PSO algorithm. Other particle swarm variants use basically the same process.

In the training process, each iteration of the particle swarm algorithm is equivalent to the agent performing an action in the environment, that is, an epoch of training. The particle swarm completes the optimization of an objective function, which is equivalent to the interaction between the agent and the environment, that is, an episode of training.

The training process is as follows. First, the actor network and the action-value network are randomly initialized, and the target actor network and the target action-value network are copied. A replay buffer R is then initialized in the second step to save the running state, actions, and rewards. The third step initializes the environment, including the initialization of the PSO and the initialization of the objective function to be optimized. The fourth step is to obtain the running state parameters from the particle swarm. The fifth step is to input the running state $s_t$ into the actor network, obtain the action $a_t$, and add a certain amount of random noise (the noise is used to help the network explore the policy space and will be removed after training). The random noise is normally distributed, with 0 as the mean and 0.5 as the variance. The formula is as follows:

$$\begin{aligned} a_t=Actor(s_t)+{\mathcal {N}}(0,0.5). \end{aligned}$$

(14)

The sixth step converts the resulting actions into the required w, c1, and c2 using Eq. 11. The seventh step is to perform an iteration of the PSO using the above parameters to obtain a new reward $r_{t+1}$ and a new state $s_{t+1}$. The eighth step saves the state, actions, and rewards to buffer R. The ninth step is to randomly select a batch of experiences from buffer R. The weights of the action-value network are updated by minimizing the loss function (Eq. 3). The weights of the actor network are updated (Eq. 2). The tenth step is to update the weights of the target action-value network and the target actor network according to Eq. 3. If the particle swarm has not finished iterating yet, then t is increased by 1, and the process returns to step 4. If the training is not completed, the process returns to step 3. The pseudocode is presented in Algorithm 1.

If the objective function used in training directly adopts the function to be optimized later, the effect will be better. If training is performed with a set of test functions, it can work on all the objective functions, but not as well as the first method. After training, a trained action network model is obtained for subsequent runs.

Running

In the running process, compared to the training process, many steps are removed, and the overall process is very simple. The operation process of the traditional particle swarm algorithm is introduced below. The implementation process of other particle swarm variant algorithms is basically the same as this process.

Fig. 5

Running process of particle swarm optimization (PSO) with reinforcement-learning-based parameter adaptation method (RLAM)

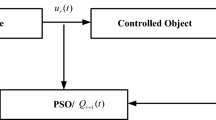
The flow chart of the PSO algorithm combined with RLAM is shown in Fig. 5. In addition to the original process of PSO, the new content is that before the particle velocity is updated, the running state of the particle swarm will be calculated, and a new parameter group will be generated to guide the particle update.

Network structure

This section introduces the network structures of the actor network and the action-value network in detail. Since the action-value network is only used in the pre-training process and the actor network needs to be used in the actual operation, to prevent excessive computation during the optimization process, a smaller actor network and a larger action-value network are designed. The schematic diagrams of the two networks are shown in Figs. 6 and 7.

Fig. 6

Network structure of actor network

Fig. 7

Network structure of action-value network

The action-value network adopts a design with a six-layer, fully connected network, and the activation function between the networks is a Leaky ReLU. The actor network adopts a design with a four-layer fully connected network, and the activation function between the networks is also a Leaky ReLU. In the last layer, to map the action to the required range of $-1$ to 1, a layer with the tanh activation function is added.

Reinforcement-learning-based PSO (RLPSO)

To better reflect the parameter adaptation ability of the RLAM, a new RLPSO algorithm based on the RLAM is designed. The speed update equation of this algorithm is as follows:

$$\begin{aligned} {v}_i^d(t+1)= & {} w * {v}_i^d(t)+ c1 * r1 * (pBest_{f_i(d)}^d - x_i^d(t)) \nonumber \\{} & {} +c2 * r2 * (gBest_i^d - x_i^d(t)) \nonumber \\{} & {} + c3 * r3 * (pBest_i^d - x_i^d(t)) \end{aligned}$$

(15)

where $f_i(d)$ and the reason it is used in RLPSO were introduced in “Comprehensive learning particle swarm optimizer (CLPSO)”, pBest is the particle’s own best experience, and gBest is the best experience in this swarm. w, c1, c2, c3, and $c_{mutation}$ are coefficients generated by the actor network based on the current running state. w, c1, c2, and c3 have been introduced in “Action of PSO (output of actor network)”. $c_{mutation}$ is an additional parameter that is generated in the same way as w. r1, r2, and r3 are all uniformly distributed random numbers between 0 and 1.

To prevent particles from being trapped in local optima, there is a mutation stage after the velocity updating. During this stage, first, a random number r4 between 0 and 1 is generated, and then r4 is compared with $c_{mutation} * 0.01 * flag_{clpso}$. If r4 is less than it, the mutation is performed, and the particle position is reinitialized in the solution space.

At the end of one period, particles move according to their velocities, and then particles’ fitness and historical best experience are updated. The pseudocode is presented in Algorithm 2.

Table 2 All test functions and their optimal values in CEC 2013

Table 3 Improvement of PSO variants after combining with RLAM

Experiments

To verify the performance of the proposed algorithm, three sets of experiments were conducted. In the first experiment, the RLAM was fused with various PSO variants, and the obtained results were compared with the original PSO variants. The second experiment compared the performance of the RLAM with other adaptation methods based on the classical particle swarm algorithm. Finally, the RLPSO designed based on the RLAM was compared with other current state-of-the-art algorithms in the third experiment.

In the experiments discussed below, to test the algorithm performance more comprehensively, we selected the CEC 2013 test set [50] for testing. The test set included 28 test functions that could simulate a wide variety of optimization problems. The test functions of CEC 2013 are shown in Table 2.

The domain of all the functions was $-100$ to 100. Due to the relatively large overall testing volume, in all runs, the end condition for all algorithms was to complete 10,000 evaluations.

For all algorithms that use RLAM, if not specified, the test and training sets are the functions being tested. For example, if there are multiple functions to be tested, they will be trained separately based on these functions and then tested separately.

The proposed algorithm was implemented using Python 3.9 on the 64-bit Ubuntu 16.04.7 LTS operating system. Experiments were conducted on a server with an Intel Xeon Silver 4116 2.1-GHz CPU and 128 GB of RAM. The source code used in experiments can be downloaded from this link: https://github.com/Firesuiry/RLAM-OPENSOURSE.

Improvement of PSO variants after combining with reinforcement-learning-based parameter adaptation method (RLAM)

In this experiment, we compared the performances of several PSO variants incorporating the RLAM with the original version.

• Comprehensive learning PSO (CLPSO) [17].

• Fitness-distance-ratio-based PSO (FDR-PSO) [51].

• Self-organizing hierarchical PSO with time-varying acceleration coefficients (HPSO-TVAC) [26].

• Distance-based locally informed PSO (LIPS) [52].

• Static heterogeneous swarm optimization (SHPSO) [53].

• Particle swarm optimization [54].

The combination of the PSO and the RLAM was as described above. For each problem, each algorithm was run 50 times, the test dimension was 30, and the final result is shown in Table 3.

Fig. 8

Heatmap of improvement

In Table 3, the improvement was calculated as follows:

$$\begin{aligned}{} & {} improve \nonumber \\{} & {} \quad {=}\,\, (gBest_{origin}{-}gBest_{train})/(gBest_{origin}\nonumber \\{} & {} \qquad -benchmark_{best}) \end{aligned}$$

(16)

where improve is the percentage of improvement, which is the data shown in the table, $gBest_{origin}$ is the optimal value obtained by the original version of the PSO variant, and $gBest_{train}$ is the optimal value obtained by the RLAM version of the PSO variant. Each row represents the result for a different evaluation function. $benchmark_{best}$ represents the optimal value of the current test function.

To show the improvement more intuitively, Fig. 8 shows the heatmap of the improvement of various PSO algorithms after adding the RLAM.

From Table 3 and Fig. 8, we can see that almost all the algorithms had significant improvements after incorporating the RLAM on all the test functions. The average improvement ranged from 13% to 29.2%, and the overall average improvement was 19.2%.

For the unimodal functions (F01–F05), PSO combined with RLAM obtained a high average increase. For the multimodal functions (F06–F20), the average improvement was significantly lower than that of the unimodal functions. The improvement was the lowest among the composition functions (F21–F28). In general, the magnitude of the improvement was inversely related to the complexity of the function.

We also notice that the improvement varied quite a lot, even within the same class of test functions. To further study the influencing factors of the improvement, we tested several hypotheses and carried out experimental verification.

First, we believe that the original performance of the algorithm will affect the improvement. If the algorithm itself is already very good, then its improvement will be small. In contrast, if the algorithm itself is poor, it is more likely to see a larger improvement.

Table 4 Pairwise comparison between PSO and PSO with RLAM on 30D problems

Table 5 Pairwise comparison between PSO and PSO with RLAM on 100D problems

Fig. 9

Parameter changes with diversity

In addition, we believe that the sensitivity of the algorithm to the parameters will affect the improvement. If the algorithm is not sensitive to the parameters, no matter how you adjust it, there will be no change.

Finally, we believe that the probability of gBest updating at each iteration during the algorithm run affects the magnitude of the improvement. At each iteration in the training process, the reward is 1 if gBest is updated and $-1$ otherwise. If there are few rewards in the algorithm run, the network may not learn anything during the learning process.

We designed the following features to reflect the sensitivity of the algorithm to parameters and the update probability of gBest: For each algorithm and test function combination, we traversed all parameters that could be adjusted by training (such as w, c1, and c2), with 11 preset values from 0, 0.1 to 0.9, 1. For each preset parameter, the algorithm ran 10 times on the test function with fixed parameters to obtain the average optimal value. The standard deviation of these 11 average optimal values was calculated. If it was larger, the algorithm was more sensitive to parameters. In the above experimental process, the percentage of iterations with updated gBest in the run of each algorithm and test function combination to the total number of iterations was recorded. For example, if the algorithm ran 10 steps in one run and gBest improved in three steps, then the probability of gBest improvement was 0.3.

Finally, we calculated the Spearman correlation coefficient between the optimal value obtained by the original algorithm, the parameter sensitivity of the algorithm and the update probability of gBest and the improvement with RLAM respectively. The results are shown in Table 6.

It can be seen that with the confidence level of $\alpha = 0.05$, the algorithm sensitivity, the average best update probability, and the original optimal value were positively correlated with the improvement.

To further investigate why the partial improvement was less than 0, we studied the parameters of the worst performing LIPS in function 19 as a function of the diversity, and the results are shown in the Fig. 9. The parameters of LIPS converged to the edge of the parameter definition domain as the diversity changed, indicating that the network had not learned useful knowledge, and the parameters of the PSO in function 1 changed significantly with the diversity. Based on this, we believe that the reason that the improvement was less than 0 was that the reinforcement learning failed to learn enough from experience in the past runs, which may have been caused by the performance limitations of the algorithm itself. In addition, the gBest update probability of LIPS on function 19 was 9%, and it ranked 119th in all 168 sets of data, which was lower than the overall average (32%). This also partially caused the reinforcement learning to fail to effectively learn from experience.

To provide a more comprehensive statistical analysis, non-parametric statistical tests were carried out. Table 4 presents the results of the pairwise comparison on a 30D problem, showing the number of cases in which the improvement was positive and negative as well as the p-values from the Wilcoxon test [43, 55]. We normalized the results on every function to be in [0, 1] based on the best and worst results obtained by all the algorithms [56]. As shown in the table, out of all six tested PSO methods, there were two algorithms for which the performance improved for all test functions after being combined with the RLAM. The performance of the worst of the other algorithms decreased in four of the 28 test functions. Overall, of the 168 combinations of test algorithms and test functions, the performance decreased for a total of 11 cases, and it improved in the other cases. Thus, the proportion of cases for which the RLAM was effective was 93.5%. To further test the effectiveness of the algorithm, we also ran the above experiments in 100 dimensions, and the results are shown in Table 5. In general, according to the results of the Wilcoxon test, all PSO variants with RLAM were better than their origin versions, with a level of significance $\alpha = 0.05$.

Table 6 Spearman correlation of optimal value, parameter sensitivity and gBest update probability with improvement

Table 7 Experimental results when the training and test sets were different

Table 8 Convergence accuracy comparison between RLAM and other adaptation methods

Fig. 10

Comparison between RLAM and other adaptation methods

To verify the generalization performance of RLAM, we used different training and test sets to test RLAM on the classic PSO algorithm. For different test functions, the functions in CEC2013 other than the function to be tested were used as the training set during training. For example, if the test set was function F1, then the training sets were F2, F3... F28. If the test set was function F2, then the training sets were F1, F3,...,F28. A total of 28 training processes were performed, and tests were carried out on 28 CEC2013 test functions. This experiment was performed on 30D problems. The other conditions and calculations were the same as in the previous experiments.

As can be seen in Table 7, the average improvement rate was 22.3%, and 27 of the 28 test functions were improved. The effect was slightly worse than that for the previous data, but with the confidence level of significance $\alpha = 0.05$, the results for the classic PSO with RLAM using different training and test sets was better than those of the corresponding original versions. The original PSO algorithm was improved, which showed that RLAM could still achieve significant results when the test and training sets were different.

Thus, we can conclude that the effect of RLAM was highly significant.

Comparison with other adaptation methods

To test the pros and cons of the RLAM with other adaptation methods, the RLAM was compared with four other adaptation methods. The other four algorithms were as follows:

• an adaptation algorithm based on type-1 fuzzy logic(TF1PSO) [57].

• an adaptation algorithm based on type-2 fuzzy logic(TF2PSO) [41].

• an adaptation algorithm based on the success rate history(SuccessHistoryPSO) [58].

• an adaptation algorithm based on Q-learning (QLPSO) [11].

In the result, the PSO with the RLAM was labeled as PSOtrain. Wilcoxon’s signed rank test (+, –, = in Table 8) at the 0.05 significance level was employed to compare the performances of the algorithms.

The best results obtained by the PSO with the RLAM and the PSO with other adaptation methods are listed in Table 8, and the best results are shown in bold. Some of the results were the same for several algorithms. Only one of the cases marked in bold was due to insufficient numerical resolution, and finer results would show differences between these algorithms. The fuzzy-logic-based adaptation performed the worst. The type-1-fuzzy-logic-based adaptation was the best for F7, whereas the type-2-fuzzy-logic-based adaptation was not the best in any cases. The adaptation based on successful history was the best for F16 and F23, while the adaptation based on reinforcement learning performed the best in the test. Of these, the adaptation based on Q-learning was the best for F4, F5, F18, F20, F25, and F26, and the RLAM was the best for a total of 19 other functions.

Figure 11 describes the ranking of these algorithms for multiple comparisons. From Fig. 10, we can see that the RLAM had the lightest overall color and the highest average ranking on the entire function test set. The adaptation based on Q-learning also worked well, but it performed the worst for six test functions: F14, F15, F16, F22, F23, and F27. The effects of the other algorithms were not much different. Of these, the adaptation algorithm based on type-1 fuzzy logic ranked better overall, with almost no worst results, indicating that its robustness was better.

Table 9 Pairwise comparison between PSO with RLAM and other adaptation methods on 30D problems

Table 10 Pairwise comparison between PSO with RLAM and other adaptation methods on 100D problems

Table 11 Comparison between RLPSO and other PSO variants

Table 12 Pairwise comparison between RLPSO and state-of-the-art PSO algorithms on 30D problems

Table 13 Pairwise comparison between RLPSO and state-of-the-art PSO algorithms on 100D problems

Table 9,10 shows the pairwise comparisons between the PSOs with other adaptation methods on 30D and 100D problems. According to the Sign test in [55], it is clear that the PSO with the RLAM was significantly better than the FT1PSO, FT2PSO, success-history-PSO, and QLPSO with a level of significance $\alpha = 0.05$. Overall, the RLAM exhibited excellent performances on all the test functions compared to other adaptation methods.

Comparison of RLPSO with other state-of-the-art PSO variants

Since most of the current state-of-the-art particle swarm algorithms combine many other optimization methods, adaptation parameters alone cannot provide a sufficient comparison. To test the strength of the RLAM applied in particle swarm optimization, here we compare the performance of the RLPSO based on the RLAM and some other particle swarm optimization algorithms. The algorithms compared include some of the widely used particle swarm algorithms: CLPSO [17], FDR-PSO [51], LIPS [52], PSO [9], and SHPSO [53], as well as several state-of-the-art variants of the PSO, including the EPSO [37], AWPSO [59], and PPPSO [60]. All the algorithms were executed 50 times for each problem and the results shown are the averages. Wilcoxon’s signed rank test (+, –, = in Table 11) at the 0.05 significance level was employed to compare the performances of the algorithms.

The best results obtained by the RLPSO and other PSO variants are listed in Table 11, and the best results are also shown in bold. The RLPSO was the best in 18 of the 28 test functions, far exceeding several other PSO algorithms. The SHPSO was the best for two functions, the AWPSO was the best for five functions, the PPPSO was the best for two functions, and the EPSO was the best for one function.

Figure 11 shows the specific ranking of each algorithm on different test problems. The RLPSO ranked very high on almost all problems, reflecting the excellent performance of the RLPSO. To show the stability of the proposed algorithm, convergence curves are shown in Fig. 12. Tables 12 and 13 show pairwise comparisons of the RLPSO results. According to the Sign test in [55], it is clear that RLPSO was significantly better than other PSOs with a level of significance of $\alpha = 0.05$.

In general, the RLPSO exhibited outstanding performances compared to many other particle swarm algorithms, which showed that the RLAM method can provide an excellent particle swarm variant algorithm after a certain amount of design, and the results highlighted the power of the RLAM.

Fig. 11

Comparison between RLPSO and other PSO algorithms

Fig. 12

Convergence curves between RLPSO and other PSO variants

Conclusions

In this paper, a reinforcement-learning-based parameter adaptation method (RLAM) and an RLAM-based RLPSO are proposed. In the RLAM, through each generation, the optimal coefficients are generated by the actor network, where the actor network is trained before running. It can be trained using the target function or using test functions. A combination of iterations, non-improving iterations, and diversity is used to reflect the state. The reward is calculated based on the change of the best result after an update. In the RLPSO, in addition to the RLAM, the CLPSO and mutation mechanisms are also added to the algorithm.

Furthermore, comprehensive experiments were carried out to compare the new algorithm with other adaptation methods, investigate the effects of the RLAM with different PSO variants, and compare the RLPSO with other state-of-the-art PSO variants. The proposed method was incorporated into multiple PSO variants and tested on the CEC 2013 test set, and almost all the PSO variants had improved final optimization accuracies. This result showed that the RLAM was beneficial and harmless in almost all the problems and all the optimization algorithms considered. It solves the problem that manual parameter adjustment is too cumbersome and burdensome.

The algorithm proposed in this paper was also compared with other adaptation methods, including adaptive particle swarm optimization based on Q-learning, adaptive particle swarm optimization based on fuzzy logic, and adaptive particle swarm optimization based on the success rate history. Based on the final results, the adaptive algorithm proposed in this paper significantly outperformed other adaptive algorithms.

Since most of the current state-of-the-art particle swarm algorithms combine many other methods, adaptation parameters alone cannot make a good comparison. Therefore, the RLPSO based on the RLAM was designed, which combined the CLPSO and some mutation and grouping operations. The final algorithm was compared with a variety of top particle swarm algorithms on the CEC 2013 test set, and the proposed algorithm was at the leading level.

In the future, based on the RLAM, the selection of states, the control of actions, and the applicability of other optimization algorithms will be further studied to further improve the optimization performance. We will focus on how to use this algorithm on binary optimization problems.