Introduction

In the actual decision-making process, the decision maker (DM) is usually required to offer their preference values over a set of alternatives. Preference relation is a useful tool to express the DMs’ preferences, which has been widely used in decision making and has gotten much attention over the past decades. Many types of preference relations have been proposed, such as fuzzy preference relation (FPR) [1,2,3], multiplicative preference relation [4, 5], linguistic preference relation [6, 7], interval-valued preference relation [8], intuitionistic preference relation [9,10,11]. Fuzzy sets are widely used [12], but they can only use one preference value to express the DM’s preference. In order to solve this problem, Torra [13] defined the hesitant fuzzy set (HFS) which employs several values to express the membership degree of the alternative, and now has been widely investigated recently [14, 15]. Based on the concept of HFS and FPR, Xia and Xu [16] defined hesitant fuzzy preference relation (HFPR).

Consistency plays an essential role in decision making, which guarantees the information provided by the DMs is rational [17,18,19]. In HFPR, each hesitant fuzzy element (HFE) has a set of preference values that denote the hesitant degree to which one alternative is preferred over another alternative. If two HFEs have different number of values, two opposite normalization principles are proposed: (1) α-normalization [20], which removes some of the elements in the long length of the HFEs and, (2) β-normalization [21, 22], which adds some elements into the short length of the HFEs. Zhu [23] proposed α-normalization and β-normalization for HFPRs. Subsequently, an FPR with a high consistency level was obtained using the α-normalization and regression method, which was used as the consistency level of the HFPR. Zhu et al. [22] first used α-normalization and β-normalization methods. Then, they used a distance measure to measure the consistency of the HFPR, i.e., the distance between the original HFPR and the HFPR that achieved acceptable consistency. Xu et al. [24] proposed an estimation measure normalization method to measure consistency based on additive consistency. Zhang et al. [21] used the β-normalization method to convert all the HFSs in the original HFPR into the same length, then measured the consistency through the distance and proposed an automatic iterative algorithm to improve the consistency.

Consensus is a significant problem that has been investigated widely in recent years. Currently, the consensus reaching process (CRP) includes interactive CRPs [24,25,26,27,28] and automatic CRPs [29, 30]. Gathering preferences, computing the agreement level, consensus control, and feedback generation are the primary aspects of the iteration-based CRP [31]. In gathering preferences, the ordered weighted average (OWA) operator and the induce ordered weighted average (IOWA) operator are widely used to aggregate preference relations into a collective one. Chen et al. [32] proposed an improved OWA operator generation algorithm and applied it to multicriteria decision-making. Jin et al. [33] proposed some standard and general forms of the IOWA operator, which takes the OWA weight vector as the inductive information. In the CRP, consensus checking and improvement process are two important processes. When DMs make decisions on the same issue, one needs to check whether their opinions are satisfied the requirements. The moderator will guide the experts to change their preferences, and finally achieve the consensus. Chen et al. [34] used the large-scale group decision-making method and k-means clustering method as well as the consensus reaching process to determine the final satisfaction level and ranking of passenger demands. Xu et al. [24] proposed an interaction mechanism and automatic mechanisms to achieve the predetermined consistency and consensus through a normalization approach based on additive consistency. He and Xu [35] proposed a consensus model implemented by a selection process and a consensus improvement process. Li et al. [36] proposed a consensus measure based on extracting priority weight vectors and constructing a model to reach the predetermined consensus. Xu et al. [37] proposed a group decision making (GDM) model that dynamically and automatically adjusts the weight of decision makers and uses an iterative consensus algorithm to improve the group consensus degree. The condition of the algorithm to stop is that both the individual consistency index and the group consensus index are controlled within the threshold. Wu and Xu [38] proposed a reciprocal preference relation-based consensus support model for GDM, designed a consistency adjustment process to make inconsistent reciprocal preference relations into acceptable consistency, and used an interactive method to achieve the consensus reaching process. Zhang et al. [39] developed a model to improve the consistency index, but it did not consider the consensus problem.

Based on the above literature review, there are still some limitations:

  1. (1)

    In [20,21,22,23,24,25], these papers use α-normalization, β-normalization, or other normalization methods to calculate the consistency and consensus of HFPRs. These methods make the number of elements in the HFS is same. However, it is ignored that the normalization method will distort the original information of DMs or cause information deficiency, making the decision result inaccurate.

  2. (2)

    In the study of consistency and consensus under HFPRs, some scholars only considered consistency but ignored consensus; some scholars considered to adjust the consensus index based on dynamic expert contributions in GDM without considering the consistency index. The consensus achieved by such adjustment may not be accurate enough because it ignores the validity of preference information provided by individuals. Some literature investigated both consistency and consensus, but it is not clear in the article whether the final individual consistency reaches an acceptable level. They ignored the consistency index in the process of consensus adjustment, and it may happen that the consistency index decreased or appeared to have unacceptable consistency when consensus was reached.

To overcome these limitations, this paper uses a non-normalization method to study the consistency and consensus of HFPR, and then proposes two algorithms to improve consistency and consensus based on this. Specifically, the main work of the paper is in twofold:

  1. (1)

    Worst consistency index (WCI) is used to measure the consistency degree of an HFPR. This paper uses 0–1 linear programming model [40, 41] to obtain the WCI of an HFPR. An iterative algorithm is proposed to improve the WCI. In each iteration, only one pair of preference values which is farthest from the consistent FPR is revised. In this way, the original information of DMs can be preserved as much as possible.

  2. (2)

    As different HFEs have different values, and it is hard to aggregate individual HFPRs into a group HFPR. In order to solve this problem, the envelope of an HFPR is proposed, a new IOWA operator is presented, which is called envelope HFPR-IOWA (EHFPR-IOWA) and the CRP is then carried out. It indicates that the CRP can be achieved and it can preserve the DMs’ original information as much as possible.

The rest of the paper is organized as follows. Section “Preliminaries” introduces some basic knowledge related to HFPRs. Section “Individual consistency of HFPRs” introduces the definition of WCI, and presents a 0–1 programming model to obtain WCI. Then, an algorithm is proposed to improve the WCI. A CPR algorithm is devised to help the DMs to reach the consensus. In section “An illustrative example and comparative analysis”, some numerical examples and comparative analysis are provided to illustrate the effectiveness of the proposed models. Finally, some conclusions are drawn in section “Conclusion”.

Preliminaries

For the sake of completeness, some basic concepts are reviewed.

FPRs

FPRs are the most common tools to express DMs’ preferences over alternatives and widely used in decision-making. The definition of FPRs can be represented as follows.

Definition 1

([42]). Let \(X = \{ x_{1} ,x_{2} ,...,x_{n} \}\) be a finite set of alternatives. An FPR on X is represented by a matrix, \(R = (r_{ij} )_{n \times n} \subset X \times X\) in which \(r_{ij} = \mu (x_{i} ,x_{j} ):X \times X \to\) \([0,1]\) with R assumed to be reciprocal in the following sense

$$ r_{ij} + r_{ji} = 1, \, i,j = 1,2,...,n. $$

\(r_{ij}\) represents the degree of the preference or intensity of the alternative \(x_{i}\) over \(x_{j}\): \(r_{ij}\) = 1/2 indicates that \(x_{i}\) and \(x_{j}\) is indifferent, \(r_{ij}\) = 1 indicates that \(x_{i}\) is absolutely preferred to \(x_{j}\), and \(r_{ij}\) > 1/2 indicates that \(x_{i}\) is preferred to \(x_{j}\). DMs only need to provide preferences for the upper triangular positions, the rest elements can be obtained from the reciprocal property.

Definition 2

([3, 42]). An FPR \(R = (r_{ij} )_{n \times n}\) is additively consistent if the following additive transitivity is satisfied:

$$ r_{ij} + r_{jk} - r_{ik} - 0.5 = 0, \, i,j,k = 1,2,...,n. $$
(1)

It shows that for a consistent reciprocal preference relation, the distance of any two rows is a constant. Summing both sides of \(r_{ij} = r_{ik} - r_{jk} + r_{kk}\) for all k ∈ N, it is derived as

$$ \begin{aligned} r_{ij} &= \frac{1}{n}\sum\limits_{k = 1}^{n} {(r_{ik} - r_{jk} + r_{kk} )} \hfill \\ & \quad = \frac{1}{n}\sum\limits_{k = 1}^{n} {r_{ik} - \frac{1}{n}\sum\limits_{k = 1}^{n} {r_{jk} } + 0.5}\\ & \quad = \frac{1}{n}\sum\limits_{k = 1}^{n} {(r_{ik} + r_{kj} )} - 0.5, \, \forall k \in N. \hfill \\ \end{aligned} $$
(2)

If R is a consistent reciprocal FPR, Eqs. (1) and (2) are equivalent. For any reciprocal FPR \(R = (r_{ij} )_{n \times n}\), one can use Eq. (2) to construct a consistent FPR \(A = (a_{ij} )_{n \times n}\), where

$$ a_{ij} = \frac{1}{n}\sum\limits_{k = 1}^{n} {(r_{ik} + r_{kj} )} - 0.5,\;i,j = 1,2,...,n. $$
(3)

It means that A is an additively consistent FPR. If R is not a consistent reciprocal FPR, some elements \(a_{ij}\) maybe out of the scope [0,1], but in [− q, 1 + q] where q > 0. In such a case, Herrera-Viedma et al. [3] proposed a method to transform matrix \(A = (a_{ij} )_{n \times n}\) into another matrix \(A^{\prime} = (a^{\prime}_{ij} )_{n \times n}\) where

$$ a^{\prime}_{ij} = \frac{{a_{ij} + q}}{1 + 2q},\;i,j = 1,2,...,n. $$

\(A^{\prime}\) is an FPR with additive consistency, \(a^{\prime} \in [0,1]\).

Based on Definition 2, Wu et al. [43] defined the additive CI of an FPR R as follows.

Definition 3

([43]). Let \(R = (r_{ij} )_{n \times n} \subset X \times X\) be an FPR, then the CI(R) is

$$ CI(R) = 1 - \frac{4}{n(n - 1)(n - 2)}\sum\limits_{i = 1}^{n - 2} {\sum\limits_{j = i + 1}^{n - 1} {\sum\limits_{k = j + 1}^{n} {|r_{ij} + r_{jk} - r_{ik} - 0.5|} } } . $$
(4)

Obviously, the higher the value CI(R) is, the more the consistent R is. If CI(R) = 1, then R is perfectly consistent. However, the initial preferences do not guarantee the perfect consistency which is expressed by the DM, a threshold \(\overline{CI}\) is set beforehand. If the current consistency level is lower than the threshold \(\overline{CI}\), i.e., \(CI(R) < \overline{CI}\), the DM needs to revise their preferences. If \(CI(R) \ge \overline{CI}\), the acceptable consistency is achieved and the decision result given by the DM is reasonable.

HFSs and HFPRs

Due to the complexity of the decision problems and the lack of expertise of DMs, they may hesitate in decision-making process, and give several preference values. To address this situation, Torra [13] introduced the concept of HFSs.

Definition 4

([13]). Let X be a fixed set, an HFS on X is in terms of a function h that when applied to X returns a subset of [0,1].

To be easily understood, Xia and Xu [44] expressed the HFS by a mathematical symbol

$$ E = \{ < x,h_{E} (x)|x \in X\} , $$

where \(h_{E} (x)\) is a set of values in [0,1], which denotes the possible membership degrees of the element \(x \in X\) to the set E. For convenience, \(h_{E} (x)\) is called a hesitant fuzzy element (HFE).

Xia and Xu [16] combined HFS with FPR and defined the HFPR. Later, Xu et al. [24] revised their definition that the elements do not need to be sorted in ascending or descending order.

Definition 5

([24]). Let \(X = \{ x_{1} ,x_{2} ,...,x_{n} \}\) be a fixed set, then an HFPR H on X is presented by a matrix \(H = (h_{ij} )_{n \times n} \subset X \times X\) where \(h_{ij} = \{ h_{ij}^{s} |s = 1,2,...,\# h_{ij} \}\) (\(\# h_{ij}\) is the number of elements in \(h_{ij}\)) is an HFE indicating all the possible preference degree(s) of the alternative \(x_{i}\) over\({\text{x}}_{\text{j}}\). Moreover, \(h_{ij}\) should satisfy the following conditions:

$$ \left\{ \begin{gathered} h_{ij}^{s} + h_{ji}^{s} = 1, \, i,j = 1,2,...,n; \, s = 1,2,...,\# h_{ij} \hfill \\ h_{ii} = \{ 0.5\} , \, i,j = 1,2,...,n \hfill \\ \# h_{ij} = \# h_{ji} , \, i,j = 1,2,...,n \hfill \\ \end{gathered} \right., $$

where \(h_{ij}^{s}\) and \(h_{ji}^{s}\) is the sth elements in \(h_{ij}\) and \(h_{ji}\), respectively.

In the process of decision-making, DMs are not sure about a determined value; they are hesitant in several values. The concept of hesitancy degree is defined as follows.

Definition 6

([45]). Let h be a HFS on \(X = \{ x_{1} ,x_{2} ,...,x_{n} \}\), and for any \(x_{i} \in X\), \(l(h(x_{i} ))\) be the length of \(h(x_{i} )\). Denote.

$$ Hd(h(x_{i} )) = 1 - \frac{1}{{l(h(x_{i} ))}}, $$
(5)
$$ Hd(H) = \frac{1}{n(n - 1)}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {Hd(h_{ij} )} } , $$
(6)

\(Hd(h(x_{i} ))\) is called the hesitancy degree of \(h(x_{i} )\), and Hd(H) the hesitancy degree of H, respectively. The larger the value of Hd(H), the more hesitant the DM.If Hd(H) = 1, it indicates that the DM is hesitant completely and difficult to determine the value of membership.

Definition 7

([46]). Let \(h_{i}\) (i = 1, 2, …, n) be a collection of HFS, and let \(h^{ + } = \mathop {\max }\limits_{{h_{i} \in h}} \left( {\{ h_{i} \} } \right)\), \(h^{ - } = \mathop {\min }\limits_{{h_{i} \in h}} \left( {\{ h_{i} \} } \right)\) and \(env(h) = [h^{ - } ,h^{ + } ]\). Then h+, \(h^{ - }\) and env(h) are, respectively, called the lower bound, the upper bound and the envelope of h.

Example 1.

Let \(h = \{ 0.2,03,0.4,0.5,0.6\}\) be an HFS, its envelope is \(h^{ - } = \min \{ 0.2,0.3,0.4,0.5,0.6\} = 0.2\), \(h^{ + } = \max \{ 0.2,0.3,0.4,0.5,0.6\} = 0.6\), \(env(h) =\)\([0.2,0.6]\).

Definition 8

([47]). Let \(h_{1} = [h_{1}^{ - } ,h_{1}^{ + } ]\) and \(h_{2} = [h_{2}^{ - } ,h_{2}^{ + } ]\), then the degree of possibility of \(h_{1} \ge h_{2}\) is formulated by

$$ p(h_{1} \ge h_{2} ) = \max \left\{ {1 - \max \left( {\frac{{h_{2}^{ + } - h_{1}^{ - } }}{{h_{1}^{ + } - h_{1}^{ - } + h_{2}^{ + } - h_{2}^{ - } }},0} \right),0} \right\}, $$
(7)

and construct a FPR \(P = (p_{ij} )_{n \times n}\) where \(p_{ij} = p(h_{1} \ge h_{2} )\), \(p_{ij} > 0\), \(p_{ij} + p_{ji} = 1\), \(p_{ii} = 0.5\), i, j = 1, 2, …, n.

IOWA aggregation operator

Let \(X = \{ x_{1,} ,...,x_{n} \}\) be a finite set of n alternatives and \(E = \{ e_{1} ,...,e_{m} \}\) be a set of m DMs. \(H_{v} = (h_{ij,v} )_{n \times n}\) is an HFPR matrix given by DM \(e_{v} \in E\), \(v = 1,2,...,m\), where \(h_{ij,v}^{{}}\) represents \(e_{v}\)’s preference degree of the alternative \(x_{i}\) over \(x_{j}\).

Yager [48] proposed a procedure to evaluate the overall satisfaction of quantifier Q important (\(u_{v}\)) criteria (or experts) (\(e_{v}\)) by the alternative \(x_{j}\). In this procedure, once the satisfaction values to be aggregated have been ordered, the weighting vector associated with an OWA operator using a linguistic quantifier Q are calculated by the following expression

$$ w_{i} = Q\left( {\frac{{\sum\nolimits_{v = 1}^{i} {u_{\sigma (v)} } }}{T}} \right) - Q\left( {\frac{{\sum\nolimits_{v = 1}^{i - 1} {u_{\sigma (v)} } }}{T}} \right), $$
(8)

being \(T = \sum\nolimits_{v = 1}^{i} {u_{\sigma (v)} }\) the total sum of importance, and σ the permutation used to produce the ordering of the values to be aggregated. In our case, the consistency levels of the HFPRs are used to derive the “importance” values associated with the experts.

The IOWA operator was introduced by Yager and Filev [49] as an extension of the OWA operator to allow for a varied sequencing of the aggregated values.

Definition 9

([49]). An IOWA operator of dimension n is a function \(\Phi w:(R \times R)^{n} \to R\), to which a set of weights is associated, \(W = (w_{1} ,...,w_{m} )^{T}\) with \(w_{i} \in [0,1]\), \(\sum\nolimits_{i} {w_{i} = 1}\), and it is defined to aggregate the set of second arguments of a list of n two-tuples \(\{ < u_{1} ,p_{1} > ,..., < u_{n} ,p_{n} > \}\), the expression is as follows:

$$ \Phi_{W} ( < u_{1} ,p_{1} > ,..., < u_{n} ,p_{n} > ) = \sum\limits_{i = 1}^{n} {w_{i} \cdot p_{\sigma (i)} } , $$
(9)

being σ a permutation of \(\{ 1,2,...,n\}\) such that \(u_{\sigma (i)} \ge u_{\sigma (i + 1)}\),\(\forall \, i = 1,...,n - 1\), i.e., \(< u_{\sigma (i)} ,p_{\sigma (i)} >\) is the two-tuple with \(u_{\sigma (i)}\), the ith highest value in the set \(\{ u_{1} ,...,u_{n} \}\).

In the above definition, the reordering of the set of values to be aggregated \(\{ p_{1} ,...,p_{n} \}\) is induced by the reordering of the set of values \(\{ u_{1} ,...,u_{n} \}\) associated with them, which is based upon their magnitude. Due to this use of the set of values \(\{ u_{1} ,...,u_{n} \}\), Yager called them the values of an order inducing variable and \(\{ p_{1} ,...,p_{n} \}\) the values of the argument variable [48,49,50,51].

Yager [48] considers the parameterized family of regular increasing monotone quantifiers

$$ Q(z) = z^{a} , \, a \ge 0. $$
(10)

In general, when a fuzzy quantifier Q is used to compute the weight of IOWA operator.

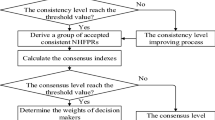
Individual consistency of HFPRs

In this section, WCI of an HFPR is introduced, and a method is proposed to obtain a matrix which has the WCI in HFPR. Then, an iterative algorithm is used to adjust this matrix to reach the predefined threshold.

Worst consistency of HFPRs

For an HFPR H, all the set of possible FPRs \(\Omega\) can be represented as:

$$ \Omega_{H} = \{ B^{q} = (b_{ij}^{q} )_{n \times n} |b_{ij}^{q} \in h_{ij} , \, b_{ij}^{q} + b_{ji}^{q} = 1, \, i,j = 1,2,...,n,q = 1,...,l\} . $$

Clearly, \(\# h_{ij}\) is the number of elements in \(h_{ij}\), where \(1 \le i < j \le n\), then there will be \(\prod\nolimits_{i = 1}^{n - 1} {\prod\nolimits_{j = i + 1}^{n} {\# h_{ij} } }\) possible FPRs in \(\Omega_{H}\). For convenience, let \(l = \prod\nolimits_{i = 1}^{n - 1} {\prod\nolimits_{j = i + 1}^{n} {\# h_{ij} } }\) and let all the possible FPRs be denoted by \(B^{q} = (b_{ij}^{q} )_{n \times n}\) \((q = 1,2,...,l)\).

First, the definition of the WCI of an HFPR is as follows:

Definition 10

([39]). Let H be an HFPR and \(\Omega_{H}\) is the collection of all the possible FPRs associated with H, then the WCI of HFPR is

$$ \begin{aligned}&WCI(H) = \mathop {\min }\limits_{{B \in \Omega_{H} }} CI(B) = \mathop {\min }\limits_{{B \in \Omega_{H} }} \\ &\quad\quad 1 - \frac{4}{n(n - 1)(n - 2)}\sum\limits_{i = 1}^{n - 2} {\sum\limits_{j = i + 1}^{n - 1} {\sum\limits_{k = j + 1}^{n} {|b_{ij} + b_{jk} - b_{ik} - 0.5|} } } , \end{aligned}$$
(11)

WCI(H) is determined by the FPR with the CI in \(\Omega_{H}\). It also provides the lower bound of the consistency level for an HFPR H. In addition, the larger the value WCI(H) is, the more the consistent H.

In the actual decision-making process, due to the difference in the knowledge background and technical ability of the DMs, the decision-making result of the DMs is not the optimal solution. Therefore, based on Definition 6, Zhang et al. [39] provided a method to calculate the WCI(H) as follows:

$$ \begin{aligned} & \min \, J_{1} = 1\\ & \quad - \frac{4}{n(n - 1)(n - 2)}\sum\limits_{i = 1}^{n - 2} {\sum\limits_{j = i + 1}^{n - 1} {\sum\limits_{k = j + 1}^{n} {|b_{ij} + b_{jk} - b_{ik} - 0.5|} } } \hfill \\ & \quad s.t.\left\{ \begin{gathered} b_{ij} = \sum\limits_{s = 1}^{{\# h_{ij} }} {\mu_{ij}^{s} h_{ij}^{s} } , \, i,j \in N, \, i < j \hfill \\ \sum\limits_{s = 1}^{{\# h_{ij} }} {\mu_{ij}^{s} } = 1, \, i,j \in N, \, i < j \hfill \\ \mu_{ij}^{s} = 0 \vee 1, \, i,j \in N, \, i < j \hfill \\ b_{ij} ,h_{ij}^{s} \in [0,1], \, {for} \, i < j. \hfill \\ \end{gathered} \right. \hfill \\ \end{aligned} $$
(12)

By introducing variables \(g_{ijk} =\)\(b_{ij} + b_{jk} - b_{ik} - 0.5\), \(|g_{ijk} | = f_{ijk}\), model (12) can be equivalently transformed into the following model:

$$ \begin{gathered} \min J_{1} = 1 - \frac{4}{{n(n - 1)(n - 2)}}\sum\limits_{{i = 1}}^{{n - 2}} {\sum\limits_{{j = i + 1}}^{{n - 1}} {\sum\limits_{{k = j + 1}}^{n} {f_{{ijk}} } } } \hfill \\ s.t.\left\{ \begin{gathered} b_{{ij}} = \sum\limits_{{s = 1}}^{{\# h_{{ij}} }} {\mu _{{ij}}^{s} h_{{ij}}^{s} } ,\quad i,j \in N,i < j \hfill \\ \sum\limits_{{s = 1}}^{{\# h_{{ij}} }} {\mu _{{ij}}^{s} } = 1,\quad i,j \in N,i < j \hfill \\ \mu _{{ij}}^{s} = 0 \vee 1,i,j \in N,\quad i < j \hfill \\ g_{{ijk}} = b_{{ij}} + b_{{jk}} - b_{{ik}} - 0.5,\quad \forall i < j < k \hfill \\ g_{{ijk}} \le f_{{ijk}} ,\quad \forall i < j < k \hfill \\ - g_{{ijk}} \le f_{{ijk}} , \forall i < j < k \hfill \\ b_{{ij}} ,h_{{ij}}^{s} \in [0,1],\quad for i < j. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$
(13)

Example 2.

Let H be an HFPR, which is shown as follows:

$$ H = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.3,0.5\} } & {\{ 0.7\} } & {\{ 0.7,0.8\} } \\ {\{ 0.7,0.5\} } & {\{ 0.5\} } & {\{ 0.2,0.3,0.4\} } & {\{ 0.5,0.6\} } \\ {\{ 0.3\} } & {\{ 0.8,0.7,0.6\} } & {\{ 0.5\} } & {\{ 0.7,0.8,0.9\} } \\ {\{ 0.3,0.2\} } & {\{ 0.5,0.4\} } & {\{ 0.3,0.2,0.1\} } & {\{ 0.5\} } \\ \end{array} } \right]. $$

Based on \(l = \prod\nolimits_{i = 1}^{n - 1} {\prod\nolimits_{j = i + 1}^{n} {\# h_{ij} } }\), one can see that there are 72 possible FPRs in the original HFPR \(H = (h_{ij} )_{4 \times 4}\). Solving model (13), one can obtain six matrices can obtain that having the same consistency index WCI(H) = 0.7333, where

$$ \begin{aligned} & B^{1} = \left[ {\begin{array}{*{20}l} {0.5} & {0.3} & {0.7} & {0.7} \\ {0.7} & {0.5} & {0.2} & {0.5} \\ {0.3} & {0.8} & {0.5} & {0.9} \\ {0.3} & {0.5} & {0.1} & {0.5} \\ \end{array} } \right],\;B^{2} = \left[ {\begin{array}{*{20}l} {0.5} & {0.3} & {0.7} & {0.7} \\ {0.7} & {0.5} & {0.3} & {0.5} \\ {0.3} & {0.7} & {0.5} & {0.9} \\ {0.3} & {0.5} & {0.1} & {0.5} \\ \end{array} } \right],\\ B^{3} &= \left[ {\begin{array}{*{20}l} {0.5} & {0.3} & {0.7} & {0.7} \\ {0.7} & {0.5} & {0.4} & {0.5} \\ {0.3} & {0.6} & {0.5} & {0.9} \\ {0.3} & {0.5} & {0.1} & {0.5} \\ \end{array} } \right], \hfill \\ B^{4} &= \left[ {\begin{array}{*{20}l} {0.5} & {0.3} & {0.7} & {0.8} \\ {0.7} & {0.5} & {0.2} & {0.5} \\ {0.3} & {0.8} & {0.5} & {0.9} \\ {0.2} & {0.5} & {0.1} & {0.5} \\ \end{array} } \right],\;B^{5} = \left[ {\begin{array}{*{20}l} {0.5} & {0.3} & {0.7} & {0.8} \\ {0.7} & {0.5} & {0.3} & {0.5} \\ {0.3} & {0.7} & {0.5} & {0.9} \\ {0.2} & {0.5} & {0.1} & {0.5} \\ \end{array} } \right],\\ B^{6} &= \left[ {\begin{array}{*{20}l} {0.5} & {0.3} & {0.7} & {0.8} \\ {0.7} & {0.5} & {0.4} & {0.5} \\ {0.3} & {0.6} & {0.5} & {0.9} \\ {0.2} & {0.5} & {0.1} & {0.5} \\ \end{array} } \right]. \hfill \\ \end{aligned} $$

Definition 11: Let \(H = (h_{ij} )_{n \times n}\) be an HFPR and let \(\overline{WCI} \, (\overline{WCI} \ge 0)\) be the consistency threshold, if \(WCI(H) \le \overline{WCI}\), H called an acceptably consistent HFPR.

Obviously, when the WCI of a given HFPR \(H = (h_{ij} )_{n \times n}\) is acceptable, then all FPRs \(B = (b_{ij} )_{n \times n}\) belonging to the HFPR are acceptably consistent, where \(b_{ij} \in h_{ij}\). Controlling the worst consistency level of the original HFPR can ensure the rationality of the results since all FPRs of the original HFPR have been considered. Therefore, this paper believes that the consistency of an HFPR is acceptable only when its WCI meets the predefined consistency level.

Improving the WCI of HFPRs

This section details how to improve the WCI of an HFPR. When the WCI of HFPR does not reach the predetermined threshold, experts need to revise their preferences or consider constructing a new preference relation.

First, one can get a FPR B which has the WCI of the HFPR. If the WCI(H) is smaller than the predefined threshold \(\overline{WCI}\), one should adjust matrix B to achieve the predetermined threshold. Then one put the modified FPR into the original HFPR, and recalculate the WCI. To keep the original information as much as possible, only one pair of elements is revised every time in the adjustment process for the preference relations.

The WCI improving process for HFPRs is detailed in Algorithm 1.

figure a

Examples for consistency improvement

Example 3.

(Continued from Example 2) To demonstrate Algorithm 1, Example 1 is still used for analysis.

Setting \(\overline{WCI} = 0.9\), the consistency adjustment parameter of β = 0.6.

Algorithm 1 is used to examine and improve the WCI of H.

Round 1. The WCI based on model (13) is used, and one have WCI(H(1)) = 0.7333 and six FPR matrices which have the same WCI, denoted as \(B^{(1)t}\)

$$\begin{aligned}B^{(1)1} & = \left[ {\begin{array}{*{20}l} {0.5} &{0.3} &{0.7} &{0.7} \\ {0.7} &{0.5} &{0.2} &{0.5} \\ {0.3} &{0.8} &{0.5} &{0.9} \\ {0.3} &{0.5} &{0.1} &{0.5} \\ \end{array} } \right],\\ B^{(1)2} & = \left[ {\begin{array}{*{20}l} {0.5} &{0.3} &{0.7} &{0.7} \\ {0.7} &{0.5} &{0.3} &{0.5} \\ {0.3} &{0.7} &{0.5} &{0.9} \\ {0.3} &{0.5} &{0.1} &{0.5} \\ \end{array} } \right],\\ B^{(1)3} & = \left[ {\begin{array}{*{20}l} {0.5} &{0.3} &{0.7} &{0.7} \\ {0.7} &{0.5} &{0.4} &{0.5} \\ {0.3} &{0.6} &{0.5} &{0.9} \\ {0.3} &{0.5} &{0.1} &{0.5} \\ \end{array} } \right],\\ B^{(1)4} & = \left[ {\begin{array}{*{20}l} {0.5} &{0.3} &{0.7} &{0.8} \\ {0.7} &{0.5} &{0.2} &{0.5} \\ {0.3} &{0.8} &{0.5} &{0.9} \\ {0.2} &{0.5} &{0.1} &{0.5} \\ \end{array} } \right],\\ B^{(1)5} & = \left[ {\begin{array}{*{20}l} {0.5} &{0.3} &{0.7} &{0.8} \\ {0.7} &{0.5} &{0.3} &{0.5} \\ {0.3} &{0.7} &{0.5} &{0.9} \\ {0.2} &{0.5} &{0.1} &{0.5} \\ \end{array} } \right],\\ B^{(1)6} & = \left[ {\begin{array}{*{20}l} {0.5} &{0.3} &{0.7} &{0.8} \\ {0.7} &{0.5} &{0.4} &{0.5} \\ {0.3} &{0.6} &{0.5} &{0.9} \\ {0.2} &{0.5} &{0.1} &{0.5} \\ \end{array} } \right].\end{aligned}$$

As \(WCI(H^{(1)} ) < \overline{WCI}\), the consistent FPR \(\tilde{B}^{(1)1}\) is calculated by Eq. (3). Then Step 4 in Algorithm 1 is applied, from which the deviation matrix \(\theta_{1}^{(1)1}\) is obtained;

$$ \tilde{B}^{(1)1} = \left[ {\begin{array}{*{20}l} {0.5} & {0.575} & {0.425} & {0.7} \\ {0.425} & {0.5} & {0.35} & {0.625} \\ {0.575} & {0.65} & {0.5} & {0.775} \\ {0.3} & {0.375} & {0.225} & {0.5} \\ \end{array} } \right],\;\theta_{1}^{(1)1} = \left[ {\begin{array}{*{20}l} 0 & {0.275} & {0.275} & 0 \\ {0.275} & 0 & {0.15} & {0.125} \\ {0.275} & {0.15} & 0 & {0.125} \\ 0 & {0.125} & {0.125} & 0 \\ \end{array} } \right]. $$

As \((i_{\tau } ,j_{\tau } ) = (1,2)\) and \(b_{ij,f + 1}^{(p)t} = \beta b_{ij,f}^{(p)t} + (1 - \beta )\tilde{b}_{ij,f}^{(p)t} = b_{12,1 + 1}^{(1)1} = 0.6b_{12,1}^{(1)1} + (1 - 0.6)\tilde{b}_{12,1}^{(1)1}\)\(= 0.41\). After 7 iterations, the modified element at position (1,2) should be 0.5711, position (1, 3) should be 0.4655. And the modified matrix \(H^{(2)}\) is

$$ H^{(2)} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.5,{0.5711} \} } & {\{ {0.4655} \} } & {\{ 0.7,0.8\} } \\ {\{ 0.5,0.4289\} } & {\{ 0.5\} } & {\{ 0.2,0.3,0.4\} } & {\{ 0.5,0.6\} } \\ {\{ 0.5345\} } & {\{ 0.8,0.7,0.6\} } & {\{ 0.5\} } & {\{ 0.7,0.8,0.9\} } \\ {\{ 0.3,0.2\} } & {\{ 0.5,0.4\} } & {\{ 0.3,0.2,0.1\} } & {\{ 0.5\} } \\ \end{array} } \right]. $$

Due to \(WCI(H^{(2)} ) = 0.8667 < 0.9\), a second round is needed.

Round 2. Based on model (13), \(WCI(H^{(2)} ) = 0.8667\) and two FPRs which have the same WCI, denoted as \(B^{(2)t}\). The adjusted FPR \(B^{(2)1}\), corresponding consistent FPR \(\tilde{B}^{(2)1}\) and deviation matrix \(\theta_{1}^{(2)1}\) are as follows:

$$ \begin{gathered} B^{(2)1} = \left[ {\begin{array}{*{20}l} {0.5} & {0.5} & {0.4655} & {0.8} \\ {0.5} & {0.5} & {0.2} & {0.5} \\ {0.5345} & {0.8} & {0.5} & {0.7} \\ {0.2} & {0.5} & {0.3} & {0.5} \\ \end{array} } \right],\\ \tilde{B}^{(2)1} = \left[ {\begin{array}{*{20}l} {0.5} & {0.6414} & {0.4328} & {0.6914} \\ {0.3586} & {0.5} & {0.2914} & {0.55} \\ {0.5673} & {0.7086} & {0.5} & {0.7586} \\ {0.3086} & {0.45} & {0.2414} & {0.5} \\ \end{array} } \right], \hfill \\ \theta_{1}^{(2)1} = \left[ {\begin{array}{*{20}l} 0 & {0.1414} & {0.0327} & {0.1086} \\ {0.1414} & 0 & {0.0914} & {0.05} \\ {0.0327} & {0.0914} & 0 & {0.0586} \\ {0.1086} & {0.05} & {0.0586} & 0 \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

Obviously, \((i_{\tau } ,j_{\tau } ) = (1,2)\) and \(b_{ij,f + 1}^{(p)t} = \beta b_{ij,f}^{(p)t} + (1 - \beta )\tilde{b}_{ij,f}^{(p)t} = b_{12,1 + 1}^{(2)1} = 0.6b_{12,1}^{(2)1}\)\(+ (1 - 0.6)\tilde{b}_{12,1}^{(2)1} = 0.4435\). After 2 iterations, the modified element at position (1,2) should be 0.6018. And the modified \(H^{(3)}\) is:

$$ H^{(3)} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ {0.5711} ,{0.6018} \} } & {\{ {0.4655} \} } & {\{ 0.7,0.8\} } \\ {\{ 0.4289,0.3982\} } & {\{ 0.5\} } & {\{ 0.2,0.3,0.4\} } & {\{ 0.5,0.6\} } \\ {\{ 0.5345\} } & {\{ 0.8,0.7,0.6\} } & {\{ 0.5\} } & {\{ 0.7,0.8,0.9\} } \\ {\{ 0.3,0.2\} } & {\{ 0.5,0.4\} } & {\{ 0.3,0.2,0.1\} } & {\{ 0.5\} } \\ \end{array} } \right]. $$

Due to \(WCI(H^{(3)} ) = 0.8904 < 0.9\), a third round is needed.

Round 3. Based on model (13), \(WCI(H^{(3)} ) = 0.8904\) and two FPRs which have the same WCI, denoted as \(B^{(3)t}\). The adjusted FPR \(B^{(3)1}\), corresponding consistent FPR \(\tilde{B}^{(3)1}\) and deviation matrix \(\theta_{1}^{(3)1}\) are:

$$ \begin{gathered} B^{(3)1} = \left[ {\begin{array}{*{20}l} {0.5} & {0.5711} & {0.4655} & {0.8} \\ {0.4289} & {0.5} & {0.2} & {0.5} \\ {0.5345} & {0.8} & {0.5} & {0.7} \\ {0.2} & {0.5} & {0.3} & {0.5} \\ \end{array} } \right],\\ \tilde{B}^{(3)1} = \left[ {\begin{array}{*{20}l} {0.5} & {0.6769} & {0.4505} & {0.7901} \\ {0.3231} & {0.5} & {0.2736} & {0.5322} \\ {0.5495} & {0.7264} & {0.5} & {0.7586} \\ {0.2909} & {0.4678} & {0.2414} & {0.5} \\ \end{array} } \right], \hfill \\ \theta_{1}^{(3)1} = \left[ {\begin{array}{*{20}l} 0 & {0.1058} & {0.015} & {0.0909} \\ {0.1058} & 0 & {0.0736} & {0.0322} \\ {0.0150} & {0.0736} & 0 & {0.0586} \\ {0.0909} & {0.0322} & {0.0586} & 0 \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

From \(\theta_{1}^{(3)1}\), \((i_{\tau } ,j_{\tau } ) = (1,2)\) and \(b_{ij,f + 1}^{(p)t} = \beta b_{ij,f}^{(p)t} + (1 - \beta )\tilde{b}_{ij,f}^{(p)t} = b_{12,1 + 1}^{(2)1} = 0.6b_{12,1}^{(2)1}\)\(+ (1 - 0.6)\tilde{b}_{12,1}^{(2)1} = 0.6134\). After 1 iteration, the modified element at position (1, 2) should be 0.6134. And the modified matrix, \(H^{(4)}\) is:

$$ H^{(4)} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ {0.6018} ,{0.6134} \} } & {\{ {0.4655} \} } & {\{ 0.7,0.8\} } \\ {\{ 0.3866,0.3982\} } & {\{ 0.5\} } & {\{ 0.2,0.3,0.4\} } & {\{ 0.5,0.6\} } \\ {\{ 0.5345\} } & {\{ 0.8,0.7,0.6\} } & {\{ 0.5\} } & {\{ 0.7,0.8,0.9\} } \\ {\{ 0.3,0.2\} } & {\{ 0.5,0.4\} } & {\{ 0.3,0.2,0.1\} } & {\{ 0.5\} } \\ \end{array} } \right]. $$

Because \(WCI(H^{(4)} ) = 0.9 \ge 0.9\), Algorithm 1 is terminated and one have \(\tilde{H} = H^{(4)}\), only three elements in the upper triangular part of H are modified.

Calculate the hesitancy index of H by Eqs. (5)–(6), \(Hd(H)\) = 17/72, \(Hd(\tilde{H})\) = 17/72.

Zhang et al. [21] introduced a consistency improvement algorithm for HFPR. Using Algorithm 2 in Zhang et al. [21] to improve the consistency index, the adjusted HFPR \(\tilde{H}_{2}\) is

$$ \tilde{H}_{2} = \left[ {\begin{array}{*{20}l} \begin{gathered} \{ 0.5\} \hfill \\ \{ 0.425,0.365,0.3875\} \hfill \\ \{ 0.5025,0.435,0.435\} \hfill \\ \{ 0.345,0.2,0.1775\} \hfill \\ \end{gathered} & \begin{gathered} \{ \underline{{0.5475}} ,\underline{{0.635}} ,\underline{{0.6125}} \} \hfill \\ \{ 0.5\} \hfill \\ \{ 0.62,0.61,0.5775\} \hfill \\ \{ 0.4325,0.355,0.31\} \hfill \\ \end{gathered} \\ \end{array} } \right.\left. {\begin{array}{*{20}l} \begin{gathered} \{ \underline{{0.4975}} ,\underline{{0.565}} ,\underline{{0.565}} \} \hfill \\ \{ \underline{{0.38}} ,\underline{{0.39}} ,\underline{{0.4225}} \} \hfill \\ \{ 0.5\} \hfill \\ \{ 0.3225,0.245,0.2125\} \hfill \\ \end{gathered} & \begin{gathered} \{ \underline{{0.655}} ,0.8,\underline{{0.8225}} \} \hfill \\ \{ \underline{{0.5675}} ,\underline{{0.645}} ,\underline{{0.69}} \} \hfill \\ \{ \underline{{0.6775}} ,\underline{{0.755}} ,\underline{{0.7875}} \} \hfill \\ \{ 0.5\} \hfill \\ \end{gathered} \\ \end{array} } \right]. $$

Table 1 illustrates the results between the proposed algorithm and Zhang et al. [21]’s method. Only 3 elements of the adjusted preference relation obtained using the proposed algorithm are changed. However, for the model in Zhang et al. [21], all of the elements are revised, it is hard for the DM to adjust all of their preferences. Further, the hesitancy degree about H and the adjusted matrix \(\tilde{H}\) using the proposed algorithm are preserved. When the algorithm in Zhang et al. [21]. is applied to adjust the HFPR H, the hesitancy degree is very large. As we can see, the HFPR obtained by this paper’s method can preserve the original opinions of DMs as much as possible.

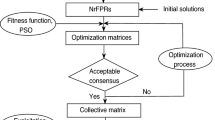
Table 1 The WCI, #H and Hd values of the proposed method and Zhang et al. [21]’s Method of Example 3
Full size table

Consensus building for HFPRs

In this section, the concept of EHFPRs is introduced, the measuring method of consensus index among group members is introduced, and then an algorithm of how to achieve group consensus is proposed.

Group consensus measure

Based on Definition 7, the concept of EHFPR is defined as follows:

Definition 12.

Let \(H = (h_{ij} )_{n \times n}\) be an HFPR, let \(G = (g_{ij} )_{n \times n} = ([g_{ij}^{ - } ,g_{ij}^{ + } ])_{n \times n}\) be an EHFPR, where \(g_{ij}^{ - }\) is the smallest value in \(h_{ij}\), and \(g_{ij}^{ + }\) is the largest term in \(h_{ij}\).

The distance between the EHFPRs can be defined as.

Definition 13.

Let \(G_{1} = (g_{ij,1} )_{n \times n} = [g_{ij,1}^{ - } ,g_{ij,1}^{ + } ]\) and \(G_{2} = (g_{ij,2} )_{n \times n} = [g_{ij,2}^{ - } ,g_{ij,2}^{ + } ]\) be two EHFPRs, the distance between G1 and G2 is defined as.

$$ d(G_{1} ,G_{2} ) = \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {||g_{ij,1} - g_{ij,2} ||} } = \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {(|g_{ij,1}^{ - } - g_{ij,2}^{ - } | + |g_{ij,1}^{ + } - g_{ij,2}^{ + } |)} } . $$
(15)

In consensus measure, two types are commonly used: one is the distance between the individual preference relation and the collective preference relation, the other are the distances among all the DMs. The first type of consensus measure is adopted in this paper. In this study, the EHFPR-IOWA operator is proposed to aggregate the individual HFPRs.

Based on Definition 9, the EHFPR-IOWA operator is defined as:

Definition 14.

Let \(E = \{ e_{1} ,e_{2} ,...,e_{m} \}\) be a set of DMs, and \(H_{v} = (h_{ij,v} )_{n \times n}\), \(v = 1,2,...,m\) be the HFPRs provided by the DMs on a set of alternatives \(X = \{ x_{1} ,x_{2} ,...,x_{n} \}\). The EHFPR-IOWA operator of dimension m, \(\Phi_{w}^{EHFPR}\) is an EHFPR-IOWA operator whose set of order inducing values is the set of worst consistency index values, \(\{ WCI_{1} ,WCI_{2} ,...,WCI_{m} \}\), associated with the set of DMs. Therefore, the collective HFPR is obtained as follows:

$$ H_{ij}^{c} = \Phi_{Q}^{EHFPR} ( < WCI_{1} ,h_{ij,1} > ,..., < WCI_{m} ,h_{ij,m} > ), $$
(16)

where Q is the fuzzy quantifier used to implement the fuzzy majority concept, and Eq. (8) is used to compute the weighting vector of the \(\Phi_{W}^{EHFPR}\).

Based on Eq. (16), one can obtain the collective preference relation. The group consensus is defined as:

Definition 15.

Let \(G_{v}\) (\(v = 1,2,...,m\)) be m EHFPRs provided by m individuals, where \(G_{v} = (g_{ij,v} )_{n \times n} = [g_{ij,v}^{ - } ,g_{ij,v}^{ + } ]\), \(v = 1,2,...,m\). Suppose \(G_{c} = (g_{ij,c} )_{n \times n} =\)\([g_{ij,c}^{ - } ,g_{ij,c}^{ + } ]\) is the group EHFPR aggregated by the EHFPR-IOWA operator. Then, the group consensus index (GCI) for Gv is.

$$ GCI(G_{v} ) = 1 - d(G_{ij,v} ,G_{ij,c} ) = 1 - \frac{1}{2n(n - 1)}\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {(|g_{ij,v}^{ - } - g_{ij,c}^{ - } | + |g_{ij,v}^{ + } - g_{ij,c}^{ + } |)} } . $$
(17)

If \(GCI(G_{v} ) = 1\), then the vth expert has perfect consensus with the group preference. Otherwise, the higher the value of \(GCI(G_{v} )\), the closer that expert is to the group.

If

$$ \mathop {\min }\limits_{v} GCI(G_{v} ) \ge \overline{GCI} , $$
(18)

then, all the DMs reach the consensus.

In fact, the predefined consensus threshold \(\overline{GCI}\) indicates the deviation degree between the individual preference relation and the group preference relation. In addition, this paper believes that the consensus is acceptable only when its GCI meets the predefined consensus threshold.

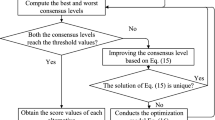
Consensus reaching process

In the GDM process, consensus process is essentially that consensus models need to be applied to assist the experts reach consensus. It means that most individuals are willing to revise their original preference values. By Definition 12, one can identify whose consensus level is not achieved.

In the following, an iterative procedure is proposed to achieve the consensus. This procedure stops until all the HFPRs reach an acceptable predefined consensus level or the maximum number of iterations is reached.

The detail of this consensus method is shown in Algorithm 2.

figure b
figure c

An illustrative example and comparative analysis

In this section, some examples are given to demonstrate the effectiveness of the proposed method.

An illustrative example

Supply Chain Management (SCM) is important for an industry. To reduce supply chain risk, maximize revenue, optimize business processes, and accomplish other goals, it is important to construct and SCM. It is a crucial issue to determine suitable supplies in SCM. The following example considers to select potential suppliers for a solar company with four potential suppliers (Zhang et al. [21]). Four managers were invited to provide their preference values for these four potential suppliers, and the four HFPRs Hv, v = 1, 2, 3, 4 are:

$$ \begin{gathered} H_{1} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.3\} } & {\{ 0.5,0,7\} } & {\{ 0.4\} } \\ {\{ 0.7\} } & {\{ 0.5\} } & {\{ 0.7,0.9\} } & {\{ 0.8\} } \\ {\{ 0.5,0.3\} } & {\{ 0.3,0.1\} } & {\{ 0.5\} } & {\{ 0.6,0.7\} } \\ {\{ 0.6\} } & {\{ 0.2\} } & {\{ 0.4,0.3\} } & {\{ 0.5\} } \\ \end{array} } \right], \hfill \\ H_{2} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.3,0.5\} } & {\{ 0.1,0.2\} } & {\{ 0.6\} } \\ {\{ 0.7,0.5\} } & {\{ 0.5\} } & {\{ 0.7,0.8\} } & {\{ 0.1,0.3,0.5\} } \\ {\{ 0.9,0.8\} } & {\{ 0.3,0.2\} } & {\{ 0.5\} } & {\{ 0.5,0.6,0.7\} } \\ {\{ 0.4\} } & {\{ 0.9,0.7,0.5\} } & {\{ 0.5,0.4,0.3\} } & {\{ 0.5\} } \\ \end{array} } \right], \hfill \\ H_{3} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.3,0.5\} } & {\{ 0.7\} } & {\{ 0.7,0.8\} } \\ {\{ 0.7,0.5\} } & {\{ 0.5\} } & {\{ 0.2,0.3,0.4\} } & {\{ 0.5,0.6\} } \\ {\{ 0.3\} } & {\{ 0.8,0.7,0.6\} } & {\{ 0.5\} } & {\{ 0.7,0.8,0.9\} } \\ {\{ 0.3,0.2\} } & {\{ 0.5,0.4\} } & {\{ 0.3,0.2,0.1\} } & {\{ 0.5\} } \\ \end{array} } \right], \hfill \\ H_{4} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.4,0.5,0.6\} } & {\{ 0.3,0.4\} } & {\{ 0.5,0.7\} } \\ {\{ 0.6,0.5\} } & {\{ 0.5\} } & {\{ 0.3\} } & {\{ 0.6,0.7,0.8\} } \\ {\{ 0.7,0.6\} } & {\{ 0.7\} } & {\{ 0.5\} } & {\{ 0.8,0.9\} } \\ {\{ 0.5,0.3\} } & {\{ 0.4,0.3,0.2\} } & {\{ 0.2,0.1\} } & {\{ 0.5\} } \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

Without loss of generality, let \(\overline{WCI} = 0.9\), \(\overline{GCL} = 0.9\), \(\varsigma = 0.6\).

Step 1. Let \(f = 0\), \(H_{v(f)} = (h_{ij,v(f)}^{{}} )_{n \times n} = (h_{ij,v}^{{}} )_{n \times n}\), v = 1, 2, …, m.

Step 2. Using model (13), the WCI of the four HFPRs are WCI(H1) = 0.8333, WCI(H2) = 0.6, WCI(H3) = 0.7333, WCI(H4) = 0.8677.

The WCI of the four individual HFPRs are unsatisfactory. Let the consistency adjustment parameter \(\beta = 0.6\), Algorithm 1 is applied to improve the consistency of these HFPRs, and the improved HFPRs are:

$$ \begin{gathered} \tilde{H}_{1} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.2280\} } & {\{ 0.5,0,5790\} } & {\{ 0.4\} } \\ {\{ 0.7720\} } & {\{ 0.5\} } & {\{ 0.7,0.9\} } & {\{ 0.8\} } \\ {\{ 0.5,0.4210\} } & {\{ 0.3,0.1\} } & {\{ 0.5\} } & {\{ 0.5536,0.56\} } \\ {\{ 0.6\} } & {\{ 0.2\} } & {\{ 0.4464,0.44\} } & {\{ 0.5\} } \\ \end{array} } \right], \hfill \\ \tilde{H}_{2} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.3,0.5\} } & {\{ 0.4689\} } & {\{ 0.6\} } \\ {\{ 0.7,0.5\} } & {\{ 0.5\} } & {\{ 0.6873,0.7\} } & {\{ 0.6362,0.6532,0.6952\} } \\ {\{ 0.5311\} } & {\{ 0.3103,0.3\} } & {\{ 0.5\} } & {\{ 0.5,0.6,0.7\} } \\ {\{ 0.4\} } & {\{ 0.3638,0.3468,0.3048\} } & {\{ 0.5,0.4,0.3\} } & {\{ 0.5\} } \\ \end{array} } \right], \hfill \\ \tilde{H}_{3} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.6018,0.6134\} } & {\{ 0.4655\} } & {\{ 0.7,0.8\} } \\ {\{ 0.4692,0.3886\} } & {\{ 0.5\} } & {\{ 0.2,0.3,0.4\} } & {\{ 0.5,0.6\} } \\ {\{ 0.5345\} } & {\{ 0.8,0.7,0.6\} } & {\{ 0.5\} } & {\{ 0.7,0.8,0.9\} } \\ {\{ 0.3,0.2\} } & {\{ 0.5,0.4\} } & {\{ 0.3,0.2,0.1\} } & {\{ 0.5\} } \\ \end{array} } \right], \hfill \\ \tilde{H}_{4} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.4,0.5,0.6\} } & {\{ 0.3,0.3280\} } & {\{ 0.5,0.7\} } \\ {\{ 0.6,0.5\} } & {\{ 0.5\} } & {\{ 0.3\} } & {\{ 0.6,0.6664,0.7\} } \\ {\{ 0.7,0.6720\} } & {\{ 0.7\} } & {\{ 0.5\} } & {\{ 0.8,0.9\} } \\ {\{ 0.5,0.3\} } & {\{ 0.4,0.3336,0.3\} } & {\{ 0.2,0.1\} } & {\{ 0.5\} } \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

The WCI for adjusted HFPRs are \(WCI(\tilde{H}_{1}^{{}} )\) = 0.9040, \(WCI(\tilde{H}_{2}^{{}} )\) = 0.9, \(WCI(\tilde{H}_{3}^{{}} )\) = 0.9, \(WCI(\tilde{H}_{4}^{{}} )\) = 0.9.

Based on the concept of envelope in Definition 9, one can obtain the EHFPRs \(\tilde{G}_{v} ,v = 1,2,...,m\) from HFPRs:

$$ \begin{gathered} \tilde{G}_{1} = \left[ {\begin{array}{*{20}l} {[0.5,0.5]} & {[0.228,0.228]} & {[0.5,0.579]} & {[0.4,0.4]} \\ {[0.7720,0.7720]} & {[0.5,0.5]} & {[0.7,0.9]} & {[0.8,0.8]} \\ {[0.421,0.5]} & {[0.1,0.3]} & {[0.5,0.5]} & {[0.5536,0.56]} \\ {[0.6,0.6]} & {[0.2,0.2]} & {[0.44,0.4464]} & {[0.5,0.5]} \\ \end{array} } \right], \hfill \\ \tilde{G}_{2} = \left[ {\begin{array}{*{20}l} {[0.5]} & {[0.3,0.5]} & {[0.4689,0.4689]} & {[0.6,0.6]} \\ {[0.5,0.7]} & {[0.5,0.5]} & {[0.6873,0.7]} & {[0.6362,0.6952]} \\ {[0.5311,0.5311]} & {[0.3,0.3103]} & {[0.5,0.5]} & {[0.5,0.7]} \\ {[0.4,0.4]} & {[0.3048,0.3638]} & {[0.3,0.5} & {[0.5,0.5]} \\ \end{array} } \right], \hfill \\ \tilde{G}_{3} = \left[ {\begin{array}{*{20}l} {[0.5,0.5]} & {[0.6018,0.6134]} & {[0.4655,0.4655]} & {[0.7,0.8]} \\ {[0.3886,0.4692]} & {[0.5,0.5]} & {[0.2,0.4]} & {[0.5,0.6]} \\ {[0.5345,0.5345]} & {[0.6,0.8]} & {[0.5,0.5]} & {[0.7,0.9]} \\ {[0.2,0.3]} & {[0.4,0.5]} & {[0.1,0.3]} & {[0.5,0.5]} \\ \end{array} } \right], \hfill \\ \tilde{G}_{4} = \left[ {\begin{array}{*{20}l} {[0.5,0.5]} & {[0.4,0.6]} & {[0.3,0.328]} & {[0.5436,0.7]} \\ {[0.5,0.6]} & {[0.5,0.5]} & {[0.3,0.3]} & {[0.6,0.708]} \\ {[0.672,0.7]} & {[0.7,0.7]} & {[0.5,0.5]} & {[0.8,0.9]} \\ {[0.3,0.4564]} & {[0.292,0.4]} & {[0.1,0.2]} & {[0.5,0.5]} \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

Step 3. The group preference relation is obtained by the EHFPR-IOWA operator. In this paper, \(Q(z) = z^{1/2}\) is used to represent fuzzy linguistic quantifier “most of”.

The detailed calculation steps are:

For example, the process of obtaining the group preference relationship \(H_{12,c}\) is:

WCI1 = 0.904, WCI2 = 0.9, WCI3 = 0.9, WCI4 = 0.9.

\(\tilde{g}_{12,1}^{ - } = 0.228\),\(\tilde{g}_{12,2}^{ - } = 0.3\), \(\tilde{g}_{12,3}^{ - } = 0.6018\), \(\tilde{g}_{12,4}^{ - } = 0.4\).

\(\sigma (1)\) = 1, \(\sigma (2)\) = 2, \(\sigma (3)\) = 3, \(\sigma (4)\) = 4.

\(T = WCI_{1} + WCI_{2} + WCI_{3} + WCI_{4}\) = 3.6040.

Q(0) = 0, \(Q\left( {\frac{{WCI_{4} }}{T}} \right) = 0.5008\), \(Q\left( {\frac{{WCI_{4} + WCI_{3} }}{T}} \right) = 0.7075\),\(Q\left( {\frac{{WCI_{2} + WCI_{3} + WCI_{4} }}{T}} \right) = 0.8662\), \(Q\left( {\frac{{WCI_{1} + WCI_{2} + WCI_{3} + WCI_{4} }}{T}} \right) = Q(1) = 1\).

w1 = 0.5008, w2 = 0.2067, w3 = 0.1587, w4 = 0.1338.

$$ g_{12,c}^{ - } = w_{1} \cdot \tilde{g}_{12,1}^{ - } + w_{2} \cdot \tilde{g}_{12,2}^{ - } + w_{3} \cdot \tilde{g}_{12,3}^{ - } + w_{4} \cdot \tilde{g}_{12,4}^{ - } $$

 = 0.5008·0.2280 + 0.2067·0.3 + 0.1587·0.6018 + 0.1338·0.4

 = 0.3252.

Other values can be obtained in a similar way, and the group consensus matrix is:

$$ G_{c} = \left[ {\begin{array}{*{20}l} {[0.5,0.5]} & {[0.3252,0.3952]} & {[0.4613,0.5046]} & {[0.5082,0.5450]} \\ {[0.6048,0.6748]} & {[0.5,0.5]} & {[0.5846,0.6990]} & {[0.6918,0.7343]} \\ {[0.4954,0.5387]} & {[0.301,0.4148]} & {[0.5,0.5]} & {[0.5987,0.6884]} \\ {[0.455,0.4918]} & {[0.2657,0.3082]} & {[0.3116,0.4012]} & {[0.5,0.5]} \\ \end{array} } \right]. $$

Step 4. Then using Eq.(17) to calculate the GCI, one obtain:\(GCI(\tilde{G}_{1} )\) = 0.8033, \(GCI(\tilde{G}_{2} )\) = 0.9125, \(GCI(\tilde{G}_{3} )\) = 0.8900, \(GCI(\tilde{G}_{4} )\) = 0.9226. As \(GCI(\tilde{G}_{1} )\) = 0.8033 < 0.9, \(GCI(\tilde{G}_{3} )\) = 0.8900 < 0.9, go to Step 5.

Step 5. Find the position of the element with the largest distance from the expert preference matrix to the group matrix and adjust it, one have:

$$ \theta_{1(f)}^{{}} = \left[ {\begin{array}{*{20}l} {[0,0]} & {[0.1476,0.2812]} & {[0.0959,0.1586]} & {[0.1437,0.2356]} \\ {[0.1476,0.2812]} & {[0,0]} & {[0.2073,0.2859]} & {[0.0894,0.1663]} \\ {[0.0959,0.1586]} & {[0.2073,0.2859]} & {[0,0]} & {[0.1348,0.2381]} \\ {[0.1437,0.2356]} & {[0.0894,0.1663]} & {[0.1348,0.2381]} & {[0,0]} \\ \end{array} } \right]. $$

Find the position of elements \(\theta_{{i_{\tau } j_{\tau } ,v(f)}}^{{}}\), where \(\theta_{{i_{\tau } j_{\tau } ,v(f)}}^{{}} = \max \{ \theta_{{i_{\tau } j_{\tau } ,v(f)}}^{ + } , \, \theta_{{i_{\tau } j_{\tau } ,v(f)}}^{ - } \}\). For \(\tilde{G}_{1(1)}\), since, \(\theta_{23,1(1)}^{{}} = \max \{ \theta_{23,1(1)}^{ - } ,\theta_{23,1(1)}^{ + } \}\)\(= \max \{ 0.2073,0.2859\} = 0.2859\) = \(\theta_{23,1(1)}^{ + }\). By Eq. (20), one have:

\(\tilde{g}_{23,1(2)}^{ + } = 0.6\tilde{g}_{23,1(1)}^{ + } + (1 - 0.6)g_{23,c(1)}^{ + }\) = 0.6⋅0.7863 + 0.4⋅0.5004 = 0.6719.

Similarly, other values can be obtained.

Step 6. Output the modified preference relations and group preference relation:

$$ \begin{gathered} \overline{G}_{1} = \left[ {\begin{array}{*{20}l} {[0.5,0.5]} & {[0.2870,0.4078]} & {[0.5,0.5156]} & {[0.5,0.5507]} \\ {[0.6797,0.772]} & {[0.5,0.5]} & {[0.5276,0.5869]} & {[0.7335,0.8]} \\ {[0.4844,0.5]} & {[0.413,0.4724]} & {[0.5]} & {[0.5536,0.7124]} \\ {[0.4493,0.5]} & {[0.2,0.2665]} & {[0.2876,0.4463]} & {[0.5,0.5]} \\ \end{array} } \right], \hfill \\ \overline{G}_{2} = \left[ {\begin{array}{*{20}l} {[0.5,0.5]} & {[0.3,0.5]} & {[0.4689\} } & {[0.6,0.6]} \\ {[0.5,0.7]} & {[0.5,0.5]} & {[0.6897,0.7]} & {[0.626,0.6532]} \\ {[0.5311,0.5311]} & {[0.3,0.3103]} & {[0.5,0.5]} & {[0.5,0.7]} \\ {[0.4,0.4]} & {[0.3468,0.374]} & {[0.3,0.5]} & {[0.5,0.5]} \\ \end{array} } \right], \hfill \\ \overline{G}_{3} = \left[ {\begin{array}{*{20}l} {[0.5,0.5]} & {[0.5113,0.6134]} & {[0.4655,0.4655]} & {[0.7,0.7342]} \\ {[0.3866,0.4887]} & {[0.5,0.5]} & {[0.3,0.4]} & {[0.5,0.6]} \\ {[0.5345,0.5345]} & {[0.6,0.7]} & {[0.5,0.5]} & {[0.7,0.9]} \\ {[0.2658,0.3]} & {[0.4,0.5]} & {[0.1,0.3]} & {[0.5,0.5]} \\ \end{array} } \right], \hfill \\ \overline{G}_{4} = \left[ {\begin{array}{*{20}l} {[0.5,0.5]} & {[0.4,0.6]} & {[0.3,0.328]} & {[0.5436,0.7]} \\ {[0.5,0.6]} & {[0.5,0.5]} & {[0.3,0.3]} & {[0.6,0.708]} \\ {[0.672,0.7]} & {[0.7,0.7]} & {[0.5,0.5]} & {[0.8,0.9]} \\ {[0.3,0.4564]} & {[0.292,0.4]} & {[0.1,0.2]} & {[0.5,0.5]} \\ \end{array} } \right], \hfill \\ \overline{G}_{c} = \left[ {\begin{array}{*{20}l} {[0.5,0.5]} & {[0.3755,0.5092]} & {[0.4041,0.4204]} & {[0.5436,0.6354]} \\ {[0.4908,0.6244]} & {[0.5,0.5]} & {[0.4307,0.5006]} & {[0.6338,0.7106]} \\ {[0.5796,0.5959]} & {[0.4996,0.5692]} & {[0.5,0.5]} & {[0.6883,0.7981]} \\ {[0.3644,0.4563]} & {[0.2894,0.3663]} & {[0.2019,0.3116]} & {[0.5,0.5]} \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

The consensus levels for the updated preference relations are \(GCI(\overline{H}_{1} )\) = 0.9082 \(GCI(\overline{H}_{2} )\) = 0.9085, \(GCI(\overline{H}_{3} )\) = 0.9001, \(GCI(\overline{H}_{4} )\) = 0.9225. The WCI of these adjustment matrices are \(WCI(\overline{H}_{1} )\) = 0.9040, \(WCI(\overline{H}_{2} ) = 0.9\), \(WCI(\overline{H}_{3} )\) = 0.9,\(WCI(\overline{H}_{4} )\) = 0.9119.

As we can see, the consensus has been reached. Then the alternatives can be ranked with the following steps.

Step 7. Based on AA operator, one can obtain the overall preference degree \(g_{i,c}\) (i = 1,2,3,4) of the alternative \(x_{i}\) (i = 1,2,3,4):

\(g_{1,c} = [0.4558,0.5162]\), \(g_{2,c} = [0.5136,0.5839]\), \(g_{3,c} = [0.5669,0.6158]\),

\(g_{4,c} = [0.3389,0.4085]\).

Step 8. Based on Eq. (7), and construct a FPR \(P = (p_{ij} )_{n \times n}\).

\(P = \left[ {\begin{array}{*{20}l} \begin{gathered} 0.5 \hfill \\ 0.9812 \hfill \\ 1 \hfill \\ 0 \hfill \\ \end{gathered} & \begin{gathered} 0.0188 \hfill \\ 0.5 \hfill \\ 0.857 \hfill \\ 0 \hfill \\ \end{gathered} \\ \end{array} \, \begin{array}{*{20}l} \begin{gathered} 0 \hfill \\ 0.143 \hfill \\ 0.5 \hfill \\ 0 \hfill \\ \end{gathered} & \begin{gathered} 1 \hfill \\ 1 \hfill \\ 1 \hfill \\ 0.5 \hfill \\ \end{gathered} \\ \end{array} } \right]\).

Step 9. Summing all elements in each line of the matrix P, i.e., \(p_{i} = \sum\nolimits_{j = 1}^{n} {p_{ij} }\), i = 1, 2, …, n: p1 = 1.5188, p2 = 2.6242, p3 = 4.357, p4 = 0.5, then one has \(p_{3} > p_{2} > p_{1} > p_{4}\). Therefore, the ranking of the alternatives is: \(x_{3} \succ x_{2} \succ x_{1} \succ x_{4}\), and the optimal alternative is \(x_{3}\).

Comparisons and discussions

Zhang et al. [21] introduced a decision support model for GDM to achieve the group consensus. To demonstrate the validity of the proposed method, a comparative study with Zhang et al. [21] method is conducted in this subsection.

Zhang et al. [21] used β-normalization to achieve the consensus, let the consistency threshold \(\overline{CI} = 0.9\), the consensus threshold \(\overline{GCI} = 0.9\), the consistency adjustment parameter λ = 0.6, and the consensus adjustment parameter θ = 0.6. Furthermore, in Zhang et al. [21]’s Algorithm 4, the DMs’ weights are given in advance as \(w = (0.1,0.5,0.3,0.1)^{T}\). If Algorithm 4 in Zhang et al. [18] is applied, then the normalized HFPRs are:

$$ \begin{gathered} H_{1} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.3,0.3,0.3\} } & {\{ 0.5,0,7,0.7\} } & {\{ 0.4,0.4,0.4\} } \\ {\{ 0.7,0.7,0.7\} } & {\{ 0.5\} } & {\{ 0.7,0.9,0.9\} } & {\{ 0.8,0.8,0.8\} } \\ {\{ 0.5,0.3,0.3\} } & {\{ 0.3,0.1,0.1\} } & {\{ 0.5\} } & {\{ 0.6,0.7,0.7\} } \\ {\{ 0.6,0.6,0.6\} } & {\{ 0.2,0.2,0.2\} } & {\{ 0.4,0.3,0.3\} } & {\{ 0.5\} } \\ \end{array} } \right], \hfill \\ H_{2} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.3,0.35,0.5\} } & {\{ 0.1,0.125,0.2\} } & {\{ 0.6,0.6,0.6\} } \\ {\{ 0.7,0.65,0.5\} } & {\{ 0.5\} } & {\{ 0.7,0.725,0.8\} } & {\{ 0.1,0.3,0.5\} } \\ {\{ 0.9,0.875,0.8\} } & {\{ 0.3,0.275,0.2\} } & {\{ 0.5\} } & {\{ 0.5,0.6,0.7\} } \\ {\{ 0.4,0.4,0.4\} } & {\{ 0.9,0.7,0.5\} } & {\{ 0.5,0.4,0.3\} } & {\{ 0.5\} } \\ \end{array} } \right], \hfill \\ H_{3} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.3,0.5,0.5\} } & {\{ 0.7,0.7,0.7\} } & {\{ 0.7,0.8,0.8\} } \\ {\{ 0.7,0.5,0.5\} } & {\{ 0.5\} } & {\{ 0.2,0.3,0.4\} } & {\{ 0.5,0.6,0.6\} } \\ {\{ 0.3,0.3,0.3\} } & {\{ 0.8,0.7,0.6\} } & {\{ 0.5\} } & {\{ 0.7,0.8,0.9\} } \\ {\{ 0.3,0.2,0.2\} } & {\{ 0.5,0.4,0.4\} } & {\{ 0.3,0.2,0.1\} } & {\{ 0.5\} } \\ \end{array} } \right], \hfill \\ H_{4} = \left[ {\begin{array}{*{20}l} {\{ 0.5\} } & {\{ 0.4,0.5,0.6\} } & {\{ 0.3,0.4,0.4\} } & {\{ 0.5,0.7,0.7\} } \\ {\{ 0.6,0.5,0.5\} } & {\{ 0.5\} } & {\{ 0.3,0.3,0.3\} } & {\{ 0.6,0.7,0.8\} } \\ {\{ 0.7,0.6,0.6\} } & {\{ 0.7,0.7,0.7\} } & {\{ 0.5\} } & {\{ 0.8,0.9,0.9\} } \\ {\{ 0.5,0.3,0.3\} } & {\{ 0.4,0.3336,0.3\} } & {\{ 0.2,0.1,0.1\} } & {\{ 0.5\} } \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

Using Zhang et al. [21]’s Algorithm 4, after two iterations, the adjusted HFPRs are:

$$ \begin{gathered} \tilde{H}_{1} = \left[ {\begin{array}{*{20}l} \begin{gathered} \{ 0.5\} \hfill \\ \{ 0.666,0.653,0.65\} \hfill \\ \{ 0.56,0.5478,0.456\} \hfill \\ \{ 0.556,0.5122,0.478\} \hfill \\ \end{gathered} & \begin{gathered} \{ 0.34,0.3470,0.35\} \hfill \\ \{ 0.5\} \hfill \\ \{ 0.4,0.3948,0.3060\} \hfill \\ \{ 0.324,2872,0.256\} \hfill \\ \end{gathered} \\ \end{array} } \right. \hfill \\ \, \left. {\begin{array}{*{20}l} \begin{gathered} \{ 0.44,0.4523,0.544\} \hfill \\ \{ 0.6,0.6052,0.694\} \hfill \\ \{ 0.5\} \hfill \\ \{ 0.424,0.3925,0.342\} \hfill \\ \end{gathered} & \begin{gathered} \{ 0.444,0.4878,0.522\} \hfill \\ \{ 0.676,0.7127,0.744\} \hfill \\ \{ 0.576,0.6075,0.658\} \hfill \\ \{ 0.5\} \hfill \\ \end{gathered} \\ \end{array} } \right], \hfill \\ \end{gathered} $$
$$ \begin{gathered} \tilde{H}_{2} = \left[ {\begin{array}{*{20}l} \begin{gathered} \{ 0.5\} \hfill \\ \{ 0.652,0.65,0.58\} \hfill \\ \{ 0.756,0.743,0.672\} \hfill \\ \{ 0.592,0.532,0.448\} \hfill \\ \end{gathered} & \begin{gathered} \{ 0.348,0.35,0.42\} \hfill \\ \{ 0.5\} \hfill \\ \{ 0.46,0.431,0.376\} \hfill \\ \{ 0.692,0.544,0.404\} \hfill \\ \end{gathered} \\ \end{array} } \right. \hfill \\ \, \left. { \, \begin{array}{*{20}l} \begin{gathered} \{ 0.244,0.257,0.328\} \hfill \\ \{ 0.54,0.569,0.624\} \hfill \\ \{ 0.5\} \hfill \\ \{ 0.516,0.424,0.348\} \hfill \\ \end{gathered} & \begin{gathered} \{ 0.408,0.468,0.552\} \hfill \\ \{ 0.3080,0.456,0.596\} \hfill \\ \{ 0.484,0.576,0.652\} \hfill \\ \{ 0.5\} \hfill \\ \end{gathered} \\ \end{array} } \right], \hfill \\ \end{gathered} $$
$$ \begin{gathered} \tilde{H}_{3} = \left[ {\begin{array}{*{20}l} \begin{gathered} \{ 0.5\} \hfill \\ \{ 0.582,0.485,0.488\} \hfill \\ \{ 0.482,0.4518,0.432\} \hfill \\ \{ 0.412,0.2962,0.256\} \hfill \\ \end{gathered} & \begin{gathered} \{ 0.4180,0.515,0.5120\} \hfill \\ \{ 0.5\} \hfill \\ \{ 0.652,0.6108,0.552\} \hfill \\ \{ 0.474,0.3832,0.34\} \hfill \\ \end{gathered} \\ \end{array} } \right. \hfill \\ \, \left. {\begin{array}{*{20}l} \begin{gathered} \{ 0.5180,0.5483,0.568\} \hfill \\ \{ 0.348,0.3892,0.448\} \hfill \\ \{ 0.5\} \hfill \\ \{ 0.358,0.2725,0.216\} \hfill \\ \end{gathered} & \begin{gathered} \{ 0.588,0.7038,0.744\} \hfill \\ \{ 0.526,0.6167,0.66\} \hfill \\ \{ 0.632,0.7175,0.784\} \hfill \\ \{ 0.5\} \hfill \\ \end{gathered} \\ \end{array} } \right], \hfill \\ \end{gathered} $$
$$ \begin{gathered} \tilde{H}_{4} = \left[ {\begin{array}{*{20}l} \begin{gathered} \{ 0.5\} \hfill \\ \{ 0.558,0.506,0.488\} \hfill \\ \{ 0.668,0.6258,0.591\} \hfill \\ \{ 0.49,0.3412,0.277\} \hfill \\ \end{gathered} & \begin{gathered} \{ 0.442,0.494,0.512\} \hfill \\ \{ 0.5\} \hfill \\ \{ 0.61,0.6198,0.603\} \hfill \\ \{ 0.432,0.3352,0.289\} \hfill \\ \end{gathered} \\ \end{array} } \right. \hfill \\ \left. { \, \begin{array}{*{20}l} \begin{gathered} \{ 0.332,0.3743,0.409\} \hfill \\ \{ 0.39,0.3802,0.3970\} \hfill \\ \{ 0.5\} \hfill \\ \{ 0.322,0.2155,0.186\} \hfill \\ \end{gathered} & \begin{gathered} \{ 0.51,0.6588,0.723\} \hfill \\ \{ 0.568,0.6647,0.711\} \hfill \\ \{ 0.678,0.7845,0.814\} \hfill \\ \{ 0.5\} \hfill \\ \end{gathered} \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

Based on Zhang et al. [21]’s Algorithm 4, all the values in these HFPRs are changed. This means that the DM’s original information are distorted greatly.

Some comparative analyses with some of the related methods are also conducted.

  1. (1)

    In (Zhang et al. [21]), the β-normalization method is used and it requires that the elements in the HFPRs have the same length; however, the normalized HFPRs were different from the original HFPRs when the new values are added to the original elements. Further, the β-normalization based approach only considered some of the possible FPRs. The approach in Xu et al. [37] does not consider the individual consistency. Generally, the consistency of an HFPR demonstrates the inherent logic of the preferences in the HFPR; therefore, if the individual consistency level is unacceptable, the group decision derived by aggregating the individual preferences may be not reliable.

  2. (2)

    Zhu and Xu [52] used α-normalization to reduce the individual HFPR to FPR, and used the highest consistency level in FPR as the consistency of HFPR. However, it does not consider the adjustment process of consistency and used α-standardization, resulting in missing decision information for DM.

  3. (3)

    Zhang et al. [39] applied average consistency and best consistency indexes in their consistency control, they randomly generated some HFPRs and used mixed 0–1 linear programming model to improve the consistency index. But the consensus is not considered.

  4. (4)

    In this paper, both the consistency and consensus are considered. However, the methods in (Zhang et al. [39], Xu et al. [37]) only consider one of the consistency and consensus, these may cause decision result not accurate. In Zhang et al. [39]’s method, the weight of each expert is given in advance, and the contribution of the expert in the decision-making process is not considered. In Xu et al. [37]’s method, expert weights are dynamically adjusted in the process of achieving consensus, but consistency is not considered.

A brief comparison is provided in Table 2. In Table 2, ‘Consistency control’ meant that all individuals consistency levels still met the predefined consistency levels after the consensus process.

Table 2 A comparison of various consistency and consensus methods
Full size table

To summarize, Algorithm 1 considers all the possible FPRs associated with HFPRs without adding or deleting any values, and the WCI is introduced to guarantee that all possible FPRs are acceptably consistent. Then, Algorithm 2 is proposed to improve the consensus of the HFPRs.

Conclusion

Consistency and consensus play an important role in HFPRs. In this paper, two algorithms are proposed to improve the consistency and consensus. The main contributions of the paper are:

  1. (1)

    A non-standardized approach is used to adjust the consistency and consensus process of HFPR.

  2. (2)

    An iterative algorithm for adjusting the WCI of individual HFPRs is proposed. To maintain more original information, only the elements with the largest deviation values in the consistency matrix are adjusted in each iteration.

  3. (3)

    An iterative algorithm for group consensus of HFPR is proposed. When achieve group consensus the WCI keeping unchanged or improved. This avoids inaccurate decision results caused by preference relations provided by individuals who do not satisfy the consistency.

Some problems still need to be investigated, including the effects of different adjustment parameters on the inconsistency and consensus adjustment processes are not considered; the consistency and consensus thresholds in HFPR are artificially determined. In the future, we will focus on the impact of different adjustment parameters on the adjustment process of inconsistency and achieving group consensus adjustment and search for a more intelligent method to determine the thresholds.