Abstract
The computational bottleneck in distributed optimization methods, which is based on projected gradient descent, is due to the computation of a full gradient vector and projection step. This is a particular problem for large datasets. To reduce the computational complexity of existing methods, we combine the randomized block-coordinate descent and the Frank–Wolfe techniques, and then propose a distributed randomized block-coordinate projection-free algorithm over networks, where each agent randomly chooses a subset of the coordinates of its gradient vector and the projection step is eschewed in favor of a much simpler linear optimization step. Moreover, the convergence performance of the proposed algorithm is also theoretically analyzed. Specifically, we rigorously prove that the proposed algorithm can converge to optimal point at rate of \({\mathcal {O}}(1/t)\) under convexity and \({\mathcal {O}}(1/t^2)\) under strong convexity, respectively. Here, t is the number of iterations. Furthermore, the proposed algorithm can converge to a stationary point, where the “Frank-Wolfe” gap is equal to zero, at a rate \({\mathcal {O}}(1/\sqrt{t})\) under non-convexity. To evaluate the computational benefit of the proposed algorithm, we use the proposed algorithm to solve the multiclass classification problems by simulation experiments on two datasets, i.e., aloi and news20. The results shows that the proposed algorithm is faster than the existing distributed optimization algorithms due to its lower computation per iteration. Furthermore, the results also show that well-connected graphs or smaller graphs leads to faster convergence rate, which can confirm the theoretical results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In this paper, we focus on constrained optimization problems over networks consisting of multiple agents, where the global objective function is a sum of local functions of all agents. These optimization problems have recently received great attentions and has arisen in many applications such as resource allocation [1,2,3], large-scale machine learning [4, 5], distributed spectrum sensing in cognitive radio networks [6], estimation in sensor networks [7, 8], coordination in multi-agent systems [9, 10], and power system control [11, 12]. Thus, the design of an optimization algorithm is necessary to solve such problems. Besides, we assume that each agent only knows its own objective function and can exchange information with its neighbors over networks. For this reason, efficient distributed optimization algorithms are necessitated using local communication and local computation over networks.
The seminal work concerning this problems was introduced in [13] (see also [14, 15]). Recently, Nedić et al. [16] proposed a distributed subgradient algorithm, which performs consensus step and descent step. Duchi et al. [17] proposed a distributed dual average method using a similar idea. Moreover, variants of the distributed subgradient algorithm can be also found in [18,19,20,21,22,23,24]. However, the projection step becomes prohibitive when dealing with massive data sets for solving the constrained optimization problem. To reduce the computational bottleneck of the projection step, the Frank–Wolfe algorithm (a.k.a. conditional gradient decent) was proposed in [25]. In the Frank–Wolfe algorithm, the projection step is eschewed by a more efficient linear optimization step. Recently, Frank–Wolfe algorithms have received much attention due to its versatility and simplicity [26]. Furthermore, variants of Frank–Wolfe methods can be found in [27,28,29,30]. In addition, a decentralized Frank–Wolfe algorithm over networks was presented in [31]. However, the full gradient vectors are employed at each iteration in the above methods.
Despite this progress, the computation of the full gradient vectors is a computational bottleneck for high-dimensional vectors. Therefore, the variants of Frank–Wolfe methods, which use the full gradient vectors to update the decision vectors, can be prohibitive for tackling high-dimensional data. Furthermore, the computation of the appropriate oracle can be prohibitive for high-dimensional data in each Frank–Wolfe iteration. For this reason, Lacoste-Julien et al. [32] presented a block-coordinate Frank–Wolfe method. Moreover, the variants of the work were prevailed in [33,34,35], which have been applied in many fields. Despite their success, nevertheless, the computation models of these algorithms belong to the centralized framework.
We have recently witnessed the rise of big data, which is high dimensional. Moreover, these data are sat over different networked machines. Therefore, distributed variants of block-coordinate Frank–Wolfe algorithms are desirable and necessary for tackling unprecedented dimensional optimization problems [36]. For this reason, we expect that the desired algorithm can greatly reduce the computational complexity by avoiding some expensive operations such as the computation of full gradient and projection operation at each iteration. Very recently, Zhang et al. [37] proposed a distributed algorithm for maximizing the submodular function by leveraging randomized block-coordinate and Frank–Wolfe methods, in which each local objective function needs to satisfy the diminishing returns property. Nonetheless, the objective function may not satisfy this property in some applications. For example, the loss function may be convex in multi-task learning and may be non-convex in deep learning. However, the distributed block-coordinate Frank–Wolfe variant over networks for convex or non-convex functions is barely known. Furthermore, the design and analysis of the variant remained hitherto an open problem.
To fill this gap, we propose a novel distributed randomized block-coordinate projection-free algorithm over networks. In the proposed algorithm, each agent randomly chooses a subset of the entries of gradient vector and moves along the gradient direction at each iteration, the projection step is replaced by the Frank–Wolfe step. Therefore, the computational burden is reduced for solving huge-scale constrained optimization problems. Furthermore, the proposed algorithm also suits the case that the structure of information is incomplete. For instance, the data are spread among the agents of the network. In addition, the convergence rate of our algorithm is theoretically analyzed for huge-scale constrained convex and non-convex optimization problems, respectively.
The main contributions of this paper are as follows:
-
1)
We propose a distributed randomized block-coordinate projection-free algorithm over networks, where local communication and computation are adopted. The algorithm uses the block-coordinate descent and the Frank–Wolfe techniques to reduce the computational cost of the entire gradient vector and the projection step, respectively.
-
2)
We theoretically analyze the convergence rate of our algorithm. The rate of \({\mathcal {O}}(1/t)\) and \({\mathcal {O}}(1/t^2)\) are derived under convexity and strong convexity, respectively.
-
3)
We also derive the rate of \({\mathcal {O}}(1/\sqrt{t})\) under non-convexity, where t is the number of iterations.
-
4)
We conduct simulation experiments on aloi and news20 datasets to evaluate the performance of our algorithm and confirm the theoretical results.
The remainder of the paper is organized as follows: in “Related work”, we review some related works. In “Problem formulation, algorithms design, and assumptions”, we first formulate the optimization problem; our algorithm is presented and the standard assumptions are also provided. In “Main results”, we describe the main results of the work. In “Convergence analysis”, we analyze the convergence properties of the proposed algorithm and prove the main results in detail. The performance of our designed algorithm is evaluated in “Experiments”. The conclusion of the paper is summarized in “Conclusion”.
Notation: We use boldface to denote the vector with suitable dimension. Scalars are denoted by normal font. We use \({\mathbb {R}}\) to denote the set of real numbers. Moreover, the symbol \({\mathbb {R}}^d\) denotes the set of real vectors with dimension d. The notation \({\mathbb {R}}^{d\times d}\) denotes the real matrix of size \(d\times d\). The notation \(\Vert \cdot \Vert \) denotes the standard Euclidean norm. The transpose operation of a vector \({\mathbf {x}}\) and a matrix A are designated as \({\mathbf {x}}^{\top }\) and \(A^{\top }\), respectively. The notation \(\langle {\mathbf {x}}, {\mathbf {y}}\rangle \) denotes the inner product of vectors \({\mathbf {x}}\) and \({\mathbf {y}}\). The identity matrix with suitable size is designated as I. The vector, in which all entries are 1, is designated as \(\mathbbm {1}\). Moreover, the expectation of a random variable X is designated as \({\mathbb {E}}[X]\). The main notations of this paper are summarized in Table 1.
Related work
Distributed optimization over networks is a challenging problem, where each agent only utilizes its local information. The framework of distributed computation models was developed in the seminal work [13], see also [14, 15]. In this framework, the goal is to minimize a common (smooth) function by communication. In contrast, a distributed subgradient descent method was presented in [16]. The objective is to minimize the sum of local functions by local communication and local computation. Its variants were developed in [17,18,19,20,21,22,23]. Furthermore, Chen et al. [24] developed distributed subgradient algorithm for weakly convex functions. To achieve fast convergence, accelerated distributed gradient descent algorithms were presented in [38,39,40,41,42]. Meanwhile, the distributed primal-dual algorithms were also developed in [43]. Moreover, Newton’s algorithms were developed in [44, 45], and quasi-Newton methods were provided in [46]. In addition, decentralized ADMM methods are considered in [47] and [48].
However, the projections is prohibitively expensive for massive data sets. Thus, the Frank–Wolfe method, which was presented in [25], is an efficient methods for solving large-scale optimization problems. In the Frank–Wolfe method, the projection step is replaced by a very efficient linear optimization step. The primal-dual convergence rate was analyzed in detail for Frank–Wolfe-type methods [26]. Furthermore, variants of Frank–Wolfe methods was found in [26,27,28,29,30]. In addition, Wai et al. [31] proposed a decentralized Frank–Wolfe algorithm over networks. Nevertheless, these methods need to compute the full gradient at each iteration.
For high-dimensional data, however, the computations of the entire gradient are prohibitive. To reduce the computational burden, coordinate-descent methods were studied in [49], where a subset of the entries of the gradient vector is updated at each iteration. Thus, the main difference among coordinate descent algorithms is the criteria of choosing the coordinate of the gradient vector. In these methods, the maximal and the cyclic coordinate search was often used [49]. Nevertheless, the convergence is difficult to prove for the cyclic coordinate search [50], and the convergence rate is trivial for the maximal coordinate search [49]. In addition, Nesterov studied random coordinate descent method in [50], where the choice of the coordinate was random. In [51], the authors extended the method to composite functions. Furthermore, the parallel coordinate descent methods were also well studied in [52, 53]. In [54], the authors proposed a random block-coordinate gradient projection algorithms. Wang et al. [55] studied coordinate-descent diffusion learning over networks. Notarnicola et al. [56] proposed a blockwise gradient tracking method for distributed optimization. Besides, coordinate primal-dual variants for distributed optimization were also investigated in [57, 58].
Further, a block Frank–Wolfe method by combining the coordinate descent method and the Frank–Wolfe technique was proposed in [32] and extensions of the work were prevailed in [33,34,35, 37]. To the best of our knowledge, distributed block-coordinate Frank–Wolfe variants over networks for convex or non-convex functions have rarely been investigated. For this reason, this paper focuses on the design and analysis of these variants. The comparison of different algorithms is summarized in Table 2.
Problem formulation, algorithms design, and assumptions
Let \({\mathcal {G}}=\left( {\mathcal {V}},{\mathcal {E}}\right) \) denote a network, where \({\mathcal {V}}=\left\{ 1,2,\ldots ,n\right\} \) denotes the set of agents and \({\mathcal {E}}\subset {\mathcal {V}}\times {\mathcal {V}}\) designates the edge set. The notation \(\left( i,j\right) \in {\mathcal {E}}\) designates an edge, where agent i can send information to agent j, \(i,j=1,\ldots ,n\). We use the notation \({\mathcal {N}}_i\) to designate the neighborhood of agent i. The constrained optimization problem of this paper is formulated as follows:
where \(f_i: {\mathcal {X}}\mapsto {\mathbb {R}}\) refers to the cost function of agent i for all \(i\in {\mathcal {V}}\), and \({\mathcal {X}}\subseteq {\mathbb {R}}^d\) denotes a constraint set.
Moreover, this paper assumes that the dimensionality d of the vector \({\mathbf {x}}\) is large. To solve the problem (1), distributed gradient descent (DGD) methods are proposed in recent years. For tackling the high-dimensional data, however, the computation of the full gradient is expensive and becomes a bottleneck. Furthermore, the projection step is also expensive and may become prohibitive in many computationally intensive applications. To alleviate this computational challenge, we propose a distributed randomized block-coordinate Frank–Wolfe algorithm to solve problem (1) for high-dimensional data.
In this paper, we assume that the communication pattern among agents is defined by a n-by-n weighted matrix, \(A:=\left[ a_{ij}\right] ^{n\times n}\). Moreover, suppose that
Assumption 1
For all \(i,j\in {\mathcal {V}}\), we have
-
1)
When \(\left( i,j\right) \in {\mathcal {E}}\), then \(a_{ij}>0\); \(a_{ij}=0\) otherwise. Furthermore, \(a_{ii}>0\) for all \(i\in {\mathcal {V}}\).
-
2)
The matrix A is doubly stochastic, i.e., \(\sum \nolimits _{i=1}^na_{ij}=1\) and \(\sum \nolimits _{j=1}^na_{ij}=1\) for all \(i,j\in {\mathcal {V}}\).

To reduce the computational bottleneck, each agent at each iteration randomly chooses a subset of the gradient vector. Therefore, the proposed algorithm is summarized in Algorithm 1. First, each agent i, \(i=1,\ldots ,n\), performs a consensus step, i.e.,
Second, each agent i performs the following aggregating step:
where \(Q_i\left( t\right) \in {\mathbb {R}}^{d\times d}\) denotes a diagonal matrix. Moreover, the definition of the diagonal matrix is presented as follows:
where \(\left\{ q_{i,t}\left( k\right) \right\} \) is a Bernoulli random variable sequence, \(k=1,\ldots ,d\). Furthermore, \(\text {Prob}\left( q_{i,t}\left( k\right) =1\right) :=p_i\), \(\text {Prob}\left( q_{i,t}\left( k\right) =0\right) :=1-p_i\), where we assume \(0<p_i\le 1\).
Finally, each agent i performs the following Frank–Wolfe step, i.e.,
and
where \(\gamma _t\in \left( 0,1\right] \) denotes a step size. Furthermore, we have the initial conditions \({\mathbf {s}}_i\left( 0\right) =\nabla f_i\left( {\mathbf {z}}_i\left( 0\right) \right) \), \(Q_i\left( 0\right) =I_d\).
By the definition of \(q_{i,t}\left( k\right) \), we know that the k-th entry of the gradient vector is missing when \(q_{i,t}\left( k\right) =0\), thus the k-th entry of \({\mathbf {s}}_i\left( t\right) \) in Eq. (3) is updated without using the gradient information. Furthermore, the update can randomly vary over time and across agents. In addition, we use the more efficient linear optimization step to eschew projection.
In this paper, each agent sends information to its neighbors over network \({\mathcal {G}}\). To ensure the dissemination of the information from all agents, we formalize the following assumption, which is a standard assumption in [60].
Assumption 2
Suppose that the network \({\mathcal {G}}\) is strongly connected.
From Assumption 2, we have \(|\lambda _2 \left( A\right) |<1\), where \(\lambda _2\left( \cdot \right) \) denotes the second largest eigenvalue of a matrix. Furthermore, for any \(x\in {\mathbb {R}}^n\), from linear algebra, we obtain
where \({\bar{x}}=\left( 1/n\right) \mathbbm {1}^{\top }x\). From Eq. (7), we can see that the average \({\bar{x}}\) is computed at a linear rate by average consensus.
Next, we introduce the smallest integer \(t_{0,\theta }\) such that
Therefore, following from Eq. (8), we obtain
Besides, the following assumptions are also provided.
Assumption 3
The set \({\mathcal {X}}\) is bounded and convex. Moreover, the optimal set \({\mathcal {X}}^{*}\) is nonempty.
Moreover, we define the diameter of \({\mathcal {X}}\) as follows:
Assumption 4
For any \({\mathbf {x}},{\mathbf {y}}\in {\mathcal {X}}\) and \(i\in {\mathcal {V}}\), there exist positive constants \(\beta \) and L such that
and
Then, \(f_i\) is \(\beta \)-smooth and L-Lipschitz.
From the Lipschitz condition, we have \(\left\| \nabla f_i\left( {\mathbf {x}}\right) \right\| \le L\) for any \({\mathbf {x}}\in {\mathcal {X}}\). Furthermore, the relation (10) is equivalent to \(\left\| \nabla f_i\left( {\mathbf {y}}\right) -\nabla f_i\left( {\mathbf {x}}\right) \right\| \le \beta \left\| {\mathbf {y}}-{\mathbf {x}}\right\| \) for all \(i\in {\mathcal {V}}\).
In addition, a function \(f_i\) is \(\mu \)-strongly convex if the function \(f_i\) satisfies the following condition: for \(\mu >0\),
holds for any \({\mathbf {x}}, {\mathbf {y}}\in {\mathcal {X}}\). Moreover, by the definition of the function f, we also know that f is \(\mu \)-strongly convex. Besides, we also introduce the following parameter:
where \({\mathcal {B}}_{{\mathcal {X}}}\) designates the boundary set of \({\mathcal {X}}\). From Eq. (12), the solution \({\mathbf {x}}^{*}\) belongs to the interior of \({\mathcal {X}}\) if \(\alpha >0\).
Let \({\mathcal {F}}_t\) denote the filtration of \(\{{\mathbf {x}}_i(t)\}\) generated by our algorithm described in Eqs. (2)–(6) up to time t at all agents. Assumption 5 is adopted on the random variables \(q_{i,t}\left( k\right) \).
Assumption 5
The random variables \(q_{i,t}\left( k\right) \) and \(q_{j,t}\left( l\right) \) are mutually independent for all i, j, k, l. Furthermore, the random variables \(\left\{ q_{i,t}\left( k\right) \right\} \) are independent of \({\mathcal {F}}_{t-1}\) for all \(i\in {\mathcal {V}}\).
Main results
To find the optimal solution of the problem (1), the optimal set is defined as
where \(f^{*}:=\min _{{\mathbf {x}}\in {\mathcal {X}}}f\left( {\mathbf {x}}\right) \). Besides, we introduce a variable, which is given by
The first result shows the rate of convergence for convex cost functions.
Theorem 1
Let Assumptions 1–5 hold. For \(i\in \left\{ 1,\ldots ,n\right\} \), the function \(f_i\) is convex and let \(p_i=1/2\). Furthermore, \(\gamma _t=2/t\) for \(t\ge 1\). Then, we have
where \(C_1:=t_{0,\theta }D\sqrt{n}\), \(C'_2:=\sqrt{2}n\beta \left( D+2C_1\right) \left( t_{0,\theta }\right) ^{\theta }\) with \(\theta \in \left( 0,1\right) \). Furthermore, assume that \(\alpha >0\) and all cost functions \(f_i\) are \(\mu \)-strongly convex. Then, for \(t\ge 2\), we have
where \(\zeta \) is a constant and is greater than 1.
The detailed proof is provided in “Convergence analysis”. By Theorem 1, we can see that the rate of convergence is \({\mathcal {O}}(1/t)\) when the cost functions \(f_i\) are convex. Furthermore, the rate of convergence is \({\mathcal {O}}(1/t^2)\) under strong convexity.
When each function \(f_i\) is possibly non-convex, we will derive the convergence rate. To this end, we first introduce the “Frank-Wolfe” gap of f at \(\overline{{\mathbf {x}}}\left( t\right) \),
From Eq. (15), we have \(\Gamma \left( t\right) \ge 0\). Moreover, \(\overline{{\mathbf {x}}}(t)\) is a stationary point when \(\Gamma (t)=0\) to the problem (1). The second result shows the rate of convergence for non-convex cost functions.
Theorem 2
Let Assumptions 1–5 hold. Suppose that each function \(f_i\) is possibly non-convex and T is an even number. Moreover, \(\gamma _t=1/t^\theta \) with \(0<\theta <1\). Then, for all \(T\ge 6\) and \(t\ge t_{0,\theta }\), if \(\theta \in \left[ 1/2,1\right) \), we have
where \(p_{\max }=\max _{i\in {\mathcal {V}}}p_i\), \(p_{\min }=\min _{i\in {\mathcal {V}}}p_i\), and \(C_2=\left( t_{0,\theta }\right) ^{\theta }2n\sqrt{p_{\max }}\beta \left( D+2C_1\right) \). If \(\theta \in \left( 0,1/2\right) \), we have
The detailed proof is provided in “Convergence analysis”. By Theorem 2, if the cost functions \(f_i\) are potentially non-convex, we can see that the quickest rate of convergence is \({\mathcal {O}}(1/\sqrt{T})\) when \(\theta =1/2\).
Convergence analysis
In this section, we will analyze the convergence rate. To this end, we define some variables as
Besides, we also obtain some equalities as follows:
Lemma 1
For any \(t\ge 0\), we have
-
(a)
\({\overline{\mathbf {s}}}\left( t+1\right) ={\mathbf {g}}\left( t+1\right) \);
-
(b)
\({\overline{\mathbf {x}}}\left( t+1\right) =\left( 1-\gamma _t\right) {\overline{\mathbf {x}}}\left( t\right) +\gamma _t{\overline{\mathbf {v}}}\left( t\right) .\)
Proof
(a) By Eq. (18), using Eq. (3) and the double stochasticity of A, we obtain
By recursively applying Eq. (21), we obtain
From the initial conditions \({\mathbf {s}}_i\left( 0\right) =\nabla f_i\left( {\mathbf {z}}_i\left( 0\right) \right) \) and \(Q_i\left( 0\right) =I_d\), we have
Therefore, part (a) is proved completely. (b) Using the double stochasticity of A, we obtain
Therefore, we finish the proof of part (b). \(\square \)
We now derive some important results, which are used in the convergence analysis.
Lemma 2
Let Assumption 1 hold. We assume that \(\gamma _t=1/t^{\theta }\) for \(\theta \in \left( 0,1\right] \). For \(i\in {\mathcal {V}}\) and \(t\ge t_{0,\theta }\), we get
where \(C_1=t_{0,\theta }D\sqrt{n}\).
Proof
We first have the following relation:
where we have used the property of the Euclidean norm to obtain the last inequality. Moreover, if the following inequality holds:
where \(C_1=t_{0,\theta }D\sqrt{n}\), then the result is obtained by using Eq. (24). Therefore, we next prove that Eq. (25) holds. To this end, we use induction to prove the above inequality. Because the constraint set \({\mathcal {X}}\) is convex, then \({\mathbf {z}}_i(t), \overline{{\mathbf {x}}}(t)\in {\mathcal {X}}\). Moreover, the set \({\mathcal {X}}\) is bounded by the diameter D, thus, Eq. (25) holds for \(t=1\) to \(t=t_{0,\theta }\). Further, suppose Eq. (25) holds for \(t\ge t_{0,\theta }\). Since \({\mathbf {x}}_i\left( t+1\right) =(1-t^{-\theta }){\mathbf {z}}_i\left( t\right) +t^{-\theta }{\mathbf {v}}_i\left( t\right) \), we have
where we have used Eq. (7) to obtain the last inequality. Furthermore, using the Cauchy–Schwarz inequality, we also obtain
where the second inequality holds due to the boundedness of \({\mathcal {X}}\); the third inequality is from the inequality \(\sum \nolimits _{i=1}^n\vert x_i\vert \le \sqrt{n}\sqrt{\sum \nolimits _{i=1}^nx_i^2}\); in the fourth and last inequalities we have used the induction hypothesis. Besides, \(\phi \left( x\right) :=\left( x/\left( x+1\right) \right) ^\theta \) is a monotonically increasing function of x. Thus, combining Eqs. (8), (26), and (27), we have
Using Eq. (28), we get
Therefore, the induction step is finished. The result is proved completely. \(\square \)
By Lemma 2, we have \(\lim _{t\rightarrow \infty }\left\| {\mathbf {z}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| =0\).
Lemma 3
If Assumption 1 holds and \(\gamma _t=1/t^{\theta }\) for \(\theta \in \left( 0,1\right) \), then, we obtain for \(i\in {\mathcal {V}}\) and \(t\ge t_{0,\theta }\)
where \(C_2=\left( t_{0,\theta }\right) ^{\theta }2n\sqrt{p_{\max }}\beta \left( D+2C_1\right) \).
Proof
From the property of the norm, we first have the following inequality:
where the first inequality is obtained using the inequality \({\mathbb {E}}\left[ \left\| {\mathbf {w}}\right\| \right] \le \sqrt{{\mathbb {E}}[\Vert {\mathbf {w}}\Vert ^2]}\) for any vector \({\mathbf {w}}\in {\mathbb {R}}^d\), we have also used the properties of the norm to obtain the last inequality. Therefore, if the following inequality holds:
then the result of this lemma is obtained using Eq. (30). To prove Eq. (31), a variable is defined as
Plugging Eq. (32) into Eq. (3) implies that
In addition, we have employed induction to derive Eq. (31). Following from Lemma 2 and the boundedness of gradients, we can know that Eq. (31) holds for \(t=1\) to \(t=t_{0,\theta }\). Then, we assume that Eq. (31) holds up to \(t\ge t_{0,\theta }\). According to the definition of \({\mathbf {S}}_i\left( t\right) \) and Eq. (33), we have
where in the first inequality we have used the conclusion of part (a) in Lemma 1 and Eq. (7). Furthermore, we introduce a variable, i.e.,
Therefore, the term \(\sum \nolimits _{i=1}^n\left\| {\mathbf {S}}_i\left( t\right) +\Delta _i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2\) can be bounded using the Cauchy–Schwarz inequality, i.e.,
Further, the term \(\left\| \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right\| \) can be bounded as follows:
where the last inequality is due to the inequality \((a-b)^2\le 2(a^2+b^2)\) for \(a,b\in {\mathbb {R}}^d\). In addition, by using the smoothness of \(f_i\) and Eq. (32), we also obtain
where the first inequality is derived by the definition of the matrix \(Q_i(t)\) and using the smoothness of \(f_i\); the second inequality is derived using the inequality \((\sum \nolimits _{i=1}^na_i)^2\le n\sum \nolimits _{i=1}^na_i^2\) and the fact that \(a_{ij}^2\le a_{ij}\) due to \(0\le a_{ij}\le 1\) for all \(i,j\in {\mathcal {V}}\); the third inequality is deduced using Eq. (6) and the triangle inequality; using Lemma 2 and the boundedness of \({\mathcal {X}}\) yields the fourth inequality; the last equality follows from Assumption 1.
Taking conditional expectation on both sides of Eq. (36), then applying Eq. (37), we obtain
where \(p_{\max }=\max _{i\in {\mathcal {V}}}p_i\). Taking conditional expectation on both sides of Eq. (35), and then using Eq. (38), the Cauchy–Schwarz inequality, and the definition of \(C_2\), we have
where the following inequality:
is used to derive the third inequality. Taking conditional expectation on both sides of Eq. (34) and then using Eq. (39), we deduce
Furthermore, by Eq. (8), we have for \(t\ge t_{0,\theta }\)
Plugging Eq. (41) into Eq. (40), we obtain
which implies that
Till now, we complete the induction step. Thus, Lemma 3 is proved completely. \(\square \)
Now, we start to prove Theorem 1 using Lemmata 1–3.
Proof of Theorem 1
Since each function \(f_i\) is \(\beta \)-smooth, the function f is also \(\beta \)-smooth. Thus, using Lemma 1 and the boundedness of \({\mathcal {X}}\), we have
Furthermore, we also obtain that for \(i=1,\ldots ,n\) and \({\mathbf {v}}\in {\mathcal {X}}\)
where the first equality holds by adding and subtracting \({\mathbf {S}}_i\left( t\right) \); using \({\mathbf {v}}_i\left( t\right) \in \arg \min _{{\mathbf {v}}\in {\mathcal {X}}}\left\langle {\mathbf {v}},{\mathbf {S}}_i\left( t\right) \right\rangle \) implies that the first inequality holds; the last inequality is derived by adding and subtracting \( \frac{1}{n}\sum \nolimits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) )\) and using the fact that \({\mathcal {X}}\) is bounded. By taking expectation with respect to the random variables \(Q_i(t)\) on Eq. (45) and using Assumption 5, we obtain
To estimate Eq. (46), we need to estimate the term
By adding and subtracting \({\mathbf {g}}\left( t\right) \), using the triangle inequality, we get
Using Eq. (19) yields
where the second inequality is obtained since all functions \(f_i\) are \(\beta \)-smooth; the last inequality is due to Lemma 2. Combining Eqs. (29), (46), (47), and (48) yields
Moreover, letting \({\mathbf {v}}=\tilde{{\mathbf {v}}}\left( t\right) \in \arg \min _{{\mathbf {v}}\in {\mathcal {X}}}\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}\right\rangle \) in Eq. (49) and using \(p_i=1/2\) for all \(i\in {\mathcal {V}}\), we further obtain
Taking expectation conditional with respect to \({\mathcal {F}}_{t}\) and using Eq. (49), we deduce
Subtracting \(f\left( {\mathbf {x}}^*\right) \) from both sides of Eq. (51) yields
where the last inequality is derived using \(\Big \langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \tilde{{\mathbf {v}}}\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \Big \rangle \le 0\).
(a) Using \(\tilde{{\mathbf {v}}}\left( t\right) \in \arg \min _{{\mathbf {v}}\in {\mathcal {X}}}\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}\right\rangle \) and the convexity of f, we deduce
Letting \(h(t):=f(\overline{{\mathbf {x}}}(t))-f({\mathbf {x}}^{*})\), and then substituting Eq. (53) into Eq. (52), implies that
where the last inequality is derived using \(f\left( \overline{{\mathbf {x}}}\left( t\right) \right) -f\left( {\mathbf {x}}^*\right) \ge 0\). Assume that \({\mathbb {E}}\left[ h\left( t\right) \mid {\mathcal {F}}_{t-1}\right] \le \kappa /t\) for \(t\ge 2\). Since \(\gamma _t=2/t\) for \(t\ge 2\), from Eq. (54), we obtain
where using the relation \(1/t-1/\left( t+1\right) \le 1/t^2\) yields the second inequality; the last inequality is due to the definition of \(\kappa \), and specifically
The induction step is completed and then the part (a) of Theorem 1 is proved.
(b) Because of the strong convexity of f and \(\alpha >0\), employing Lemma 6 in [59] yields
Substituting Eq. (56) into Eq. (52) implies that
When \(\sqrt{h\left( t\right) }-\gamma _t\sqrt{2\mu \alpha ^2}\le 0\), from Eq. (57), we obtain
where the last inequality is derived using the relation
for \(M\ge 1\). In addition, since
where \(\zeta \) is a constant such that \(\zeta > 1\). Thus, we obtain
Therefore, we conclude
When \(\sqrt{h\left( t\right) }-\gamma _t\sqrt{2\mu \alpha ^2}>0\), by using Eqs. (57) and (59), we obtain
where using \(1/t^2-1/\left( t+1\right) ^2\le 2/t^3\) yields the first inequality. Moreover, we define
Because \(\varphi \left( t\right) =1/t\) is monotone decreasing and tends to 0 as \(t\rightarrow \infty \). Moreover, \(\zeta >1\) and thus, the parameter \(t'\) exists. For any \(t>t'\), Eq. (61) is less than or equal to 0. Therefore, we obtain
For \(t\le t'\), we have
namely,
Furthermore, let \(\zeta =2\) and using the result of part (a) in Theorem 1, we have
In addition, the inequality \({\mathbb {E}}\left[ h\left( t\right) \mid {\mathcal {F}}_{t-1}\right] \le \kappa /t\) holds for all \(t\ge 2\). Therefore, we obtain part (b). \(\square \)
We next prove Theorem 2.
Proof of Theorem 2
Using Eq. (15) and the fact
we deduce
Furthermore, \(\Gamma \left( t\right) \ge 0\). Because of the smoothness of f with \(\beta \), then
Using Lemma 1 yields
Employing the triangle inequality implies that
where the last inequality is derived since \({\mathbf {z}}_i\left( t\right) \), \({\mathbf {v}}_i\left( t\right) \in {\mathcal {X}}\). Thus, Eq. (67) is bounded, i.e.,
Using Eq. (70) implies that
By summing both sides of Eq. (71) over , we obtain
In addition, since \(\gamma _t\ge 0\) and \(\Gamma \left( t\right) \ge 0\), then
Using the expression \(\gamma _t=t^{-\theta }\), for \(T\ge 6\) and \(\theta \in \left( 0,1\right) \), we get
When \(\theta \ge 1/2\), we deduce that
Plugging Eq. (75) into Eq. (72) implies that
where the last inequality holds because f is L-Lipschitz. Combining Eqs. (73) and (76), we have
where
When \(\theta <1/2\), we also have
Plugging Eq. (78) into Eq. (72) and using the Lipschitz condition of f, we deduce that
where the last inequality is due to \(T^{1-2\theta }\le 1\) for all \(\theta <1/2\). Combining Eqs. (73), (74), and (79), we have
where
Therefore, the results of Theorem 2 is obtained.
Experiments
The proposed algorithm is used to solve a multiclass classification problem with different loss functions and a structural SVM problem for evaluating the performance of our designed algorithm, respectively. In addition, the experiments are run in Windows 10 equipped with 1080Ti GPU and 64 GB memory. Moreover, we implement the experiment program in MATLAB 2018a.
Multiclass classification
We first introduce the multiclass classification problems: The notation \({\mathcal {S}}=\left\{ 1,\ldots ,\varrho \right\} \) designates the set of classes, each agent \(i\in \left\{ 1,\ldots ,n\right\} \) has access to a data example \({\mathbf {d}}_i\left( t\right) \in {\mathbb {R}}^d\), which denotes a class in \({\mathcal {S}}\), and needs to obtain a decision matrix \(X_i\left( t\right) =\left[ {\mathbf {x}}_1^{\top };\ldots ;{\mathbf {x}}_{\varrho }^{\top }\right] \in {\mathbb {R}}^{\varrho \times d}\). Furthermore, the class label is predicted by \(\arg \max _{h\in {\mathcal {S}}}{\mathbf {x}}_h^{\top }{\mathbf {d}}_i\left( t\right) \). The local loss function of each agent i is defined as follows:
where \(y_i\left( t\right) \) designates the true class label. Moreover, the constraint set \({\mathcal {X}}=\{X\in {\mathbb {R}}^{\varrho \times d}\mid \left\| X\right\| _{*}\le \delta \}\), where \(\Vert \cdot \Vert _{*}\) is the Frobenius norm of a matrix and \(\delta \) is a positive constant.
In our experiments, we employ some datasets to test the performance of the designed algorithm. For this reason, two relatively large multiclass datasets are chosen from the LIBSVM DataFootnote 1. Table 3 presents the summary of these datasets. Besides, the parameters are set by the theories suggest. For this reason, the step-size is set to be 2/t in these experiments.
Experimental results
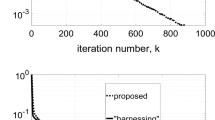
To demonstrate the performance advantage of our algorithm, we first compare the proposed algorithm with DeFW [31], EXTRA [39], and DGD [40] on different datasets with \(n=64\). As depicted in Fig. 1, the convergence speed of our algorithm is faster than DeFW, EXTRA, and DGD on two datasets news20 and aloi. At each iteration, the computational cost of the proposed algorithm is lower than DeFW, EXTRA, and DGD, the number of iterations in our designed algorithm is increased for a running time. Therefore, the convergence speed is accelerated correspondingly.
To investigate the impact of the number of nodes on the performance of our algorithm, we run the proposed algorithm on complete graphs with different nodes. As depicted in Fig. 2, the larger size of graph leads to the slower convergence rate. Furthermore, the convergence performance of our algorithm is comparable to the centralized gradient descent algorithm.
To evaluate the impact of network topologies on the performance of our algorithm, we run the proposed algorithm on a complete graph, a random graph (Watts–Strogatz), and a cycle graph, respectively. Moreover, the number of nodes in these graphs are set to be \(n=64\). The results are depicted in Fig. 3. We find that the complete graph can lead to slightly faster convergence than the random graph and the cycle graph. In other words, the better connectivity leads to the faster convergence rate in the proposed algorithm.
Conclusion
This paper has presented a distributed randomized block-coordinate Frank–Wolfe algorithm over networks for solving high-dimensional constrained optimization problems. Furthermore, detailed analyses of the convergence rate for our proposed algorithm are provided. Specifically, using a diminishing step-size, our algorithm converges at a rate of \({\mathcal {O}}(1/t)\) for convex objective functions; for the strongly convex objective functions, the convergence rate is \({\mathcal {O}}(1/t^2)\) when the optimal solution is an interior point of the constraint set. Moreover, our algorithm converges to a stationary point at a rate of \({\mathcal {O}}(1/\sqrt{t})\) under non-convexity by employing a diminishing step-size. Finally, the theoretical results have been confirmed by experiments. The results have shown that our algorithm is faster than the existing distributed algorithms. In the future work, we will devise and analyze of distributed adaptive block-coordinate Frank–Wolfe algorithms with momentum for training rapidly distributed deep neural networks.
Data availability
The data that support the findings of this study are news20 and aloi which are available from http://www.csie.ntu.edu.tw/cjlin/libsvm.
References
Xiao L, Boyd S (2006) Optimal scaling of a gradient method for distributed resource allocation. J Opt Theory Appl 129(3):469–488
Beck A, Nedić A, Ozdaglar A, Teboulle M (2014) An \(O\left(1/k\right)\) gradient method for network resource allocation problems. IEEE Trans Control Netw Syst 1(1):64–73
Wei E, Ozdaglar A, Jadbabaie A (2013) A distributed newton method for network utility maximization-I: Algorithm. IEEE Trans Autom Control 58(9):2162–2175
Bekkerman JLR, Bilenko M (2011) Scaling up machine learning: parallel and distributed approaches. Cambridge Univ. Press, Cambridge, U.K
Nedić A, Olshevsky A, Uribe C (2017) Fast convergence rates for distributed non-bayesian learning. IEEE Trans Autom Control 62(11):5538–5553
Bazerque J, Giannakis G (2010) Distributed spectrum sensing for cognitive radio networks by exploiting sparsity. IEEE Trans Signal Process 58(3):1847–1862
Lesser V, Ortiz C, Tambe M (2003) Distributed sensor networks: a multiagent perspective. Kluwer Academic Publishers, Norwell, MA
Rabbat M, Nowak R (2004) “Distributed optimization in sensor networks,’’in Proc. ACM IPSN, Berkeley, CA, USA, Apr. 26–27:20–27
Ishii H, Tempo R, Bai E (2012) A web aggregation approach for distributed randomized pagerank algorithms. IEEE Trans Autom Control 57(11):2703–2717
Necoara I (2013) Random coordinate descent algorithms for multi-agent convex optimization over networks. IEEE Trans Autom Control 58(8):2001–2012
Gan L, Topcu U, Low S (2013) Optimal decentralized protocol for electric vehicle charging. IEEE Trans Power Syst 28(2):940–951
S. Ram, V. Veeravalli, and A. Nedić, “Distributed non-autonomous power control through distributed convex optimization,”in Proc. IEEE INFOCOM, 2009, pp. 3001-3005
J. N. Tsitsiklis, “Problems in decentralized decision making and computation,”Ph. D. dissertation, Dept. Elect. Eng. Comp. Sci., Massachusetts Institute of Technology, Cambridge, 1984
Tsitsiklis JN, Bertsekas DP, Athans M (1986) Distributed asynchronous deterministic and stochastic gradient optimization algorithms. IEEE Trans Autom Control 31(9):803–812
Bertsekas DP, Tsitsiklis JN (1997) Parallel and distributed computation: numerical methods. Athena Scientific, Belmont, MA
Nedić A, Ozdaglar A (2009) Distributed subgradient methods for multi-agent optimization. IEEE Trans Autom Control 54(1):48–61
Duchi JC, Agarwal A, Wainwright MJ (2012) Dual average for distributed optimization: Convergence analysis and network scaling. IEEE Trans Autom Control 57(3):592–606
Nedić A, Ozdaglar A, Parrilo A (2010) Constraint consensus and optimization in multi-agent networks. IEEE Trans Autom Control 55(4):922–938
He X, Yu J, Huang T, Li C, Li C (2020) Average quasi-consensus algorithm for distributed constrained optimization: impulsive communication framework. IEEE Trans Cybern 50(1):351–360
Li H, Lü Q, Huang T (2019) Distributed projection subgradient algorithm over time-varying general unbalanced directed graphs. IEEE Trans Autom Control 64(3):1309–1316
X. Wen and S. Qin, “A projection-based continuous-time algorithm for distributed optimization over multi-agent systems,”Complex Intell. Syst., 2021
Chen G, Yang Q, Song Y, Lewis FL (2022) Fixed-time projection algorithm for distributed constrained optimization on time-varying digraphs. IEEE Trans Autom Control 67(1):390–397
Alaviani SS, Elia N (2021) Distributed convex optimization with state-dependent (social) interactions and time-varying topologies. IEEE Trans Signal Process 69:2611–2624
Chen S, Garcia A, Shahrampour S (2022) On distributed nonconvex optimization: projected subgradient method for weakly convex problems in networks. IEEE Trans Autom Control 67(2):662–675
Frank M, Wolfe P (1956) An algorithm for quadratic programming. Naval Res Logist Quart 3(1–2):95–110
M. Jaggi, “Revisiting Frank-Wolfe: Projection-free sparse convex optimization,”in Proc. Int. Conf. Mach. Learn., 2013, pp. 427-435
Harchaoui Z, Juditsky A, Nemirovski A (2015) Conditional gradient algorithms for norm-regularized smooth convex optimization. Math Program 152(1–2):75–112
Garber D, Hazan E (2016) A linearly convergent variant of the conditional gradient algorithm under strong convexity, with applications to online and stochastic optimization. SIAM J Opt 26(3):1493–1528
E. Hazan and H. Luo, “Variance-reduced and projection-free stochastic optimization,”in Proc. Int. Conf. Mach. Learn., 2016, pp. 1263-1271
Li B, Coutiño M, Giannakis GB, Leus G (2021) A momentum-guided frank-wolfe algorithm. IEEE Trans Signal Process 69:3597–3611
Wai H-T, Lafond J, Scaglione A, Moulines E (2017) Decentralized Frank-Wolfe algorithm for convex and non-convex problems. IEEE Trans Autom Control 62(11):5522–5537
S. Lacoste-Julien, M. Jaggi, M. Schmidt, and P. Pletscher, “Block-coordinate Frank-Wolfe optimization for structural SVMs,”in Proc. Int. Conf. Mach. Learn., 2013, pp. 53-61
A. Osokin, J.-B. Alayrac, I. Lukasewitz, P. K. Dokania, and S. Lacoste-Julien, Minding the gaps for block Frank-Wolfe optimization of structured SVMs. Proc Int Conf Mach Learn, 2016, pp. 593-602
Y. Wang, V. Sadhanala, W. Dai, W. Neiswanger, S. Sra, and E. P. Xing, Parallel and distributed block-coordinate Frank-Wolfe algorithms, In: Proc. Int. Conf. Mach. Learn., 2016, pp. 1548-1557
Zhang L, Wang G, Romero D, Giannakis GB (2017) Randomized block Frank-Wolfe for convergent large-scale learning. IEEE Trans Signal Process 65(24):6448–6461
Boyd S, Parikh N, Chu E, Peleato B, Eckstein J (2011) Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn 3(1):1–122
M. Zhang, Y. Zhou, Q. Ge, R. Zheng, and Q. Wu, Decentralized randomized block-coordinate Frank-Wolfe algorithms for submodular maximization over networks, IEEE Trans Syst Man Cybern Syst, early access, 2021
Jakovetić D, Xavier J, Moura JMF (2014) Fast distributed gradient methods. IEEE Trans Autom Control 59(5):1131–1146
Shi W, Ling Q, Wu G, Yin W (2015) Extra: an exact first-order algorithm for decentralized consensus optimization. SIAM J Opt 25(2):944–966
Qu G, Li N (2018) Harnessing smoothness to accelerate distributed optimization. IEEE Trans Control Netw Syst 5(3):1245–1260
Nedić A, Olshevsky A, Shi W (2017) Achieving geometric convergence for distributed optimization over time-varying graphs. J Opt SIAM 27(4):2597–2633
Xi C, Xin R, Khan UA (2018) ADD-OPT: Accelerated distributed directed optimization. Autom Control IEEE Trans 63(5):1329–1339
Mansoori F, Wei E (2021) FlexPD: a flexible framework of first-order primal-dual algorithms for distributed optimization. IEEE Trans Signal Process 69:3500–3512
Mokhtari A, Ling Q, Ribeiro A (2017) Network newton distributed optimization methods. IEEE Trans Signal Process 65(1):146–161
Bajović D, Jakovetić D, Krejić N, Jerinkić NK (2017) Newton-like method with diagonal correction for distributed optimization. SIAM J Opt 27(2):1171–1203
Eisen M, Mokhtari A, Ribeiro A (2017) Decentralized quasi-Newton methods. IEEE Trans Signal Process 65(10):2613–2628
Mota JFC, Xavier JMF, Aguiar PMQ, Püschel M (2013) D-ADMM: a communication-efficient distributed algorithm for separable optimization. IEEE Trans Signal Process 61(10):2718–2723
Shi W, Ling Q, Yuan K, Wu G, Yin W (2014) On the linear convergence of the admm in decentralized consensus optimization. IEEE Trans Signal Process 62(7):1750–1761
Bertsekas DP (1999) Nonlinear Programming, 2nd edn. Athena Scientific, Belmout, MA, USA
Nesterov Y (2012) Efficiency of coordinate descent methods on huge-scale optimization problems. SIAM J Opt 22(2):341–362
Richtárik P, Takáč M (2014) Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function. Math Program 144(1–2):1–38
Richtárik P, Takáč M (2016) Parallel coordinate descent methods for big data optimization. Math Program 156(1–2):433–484
I. Necoara, “Distributed and parallel random coordinate descent methods for huge convex programming over networks,”in Proc. IEEE Conf. Decis. Control, 2015, pp. 425-430
C. Singh, A. Nedć, and R. Srikant, “Random block-coordinate gradient projection algorithms,”in Proc. IEEE Conf. Decis. Control, 2014, pp. 185-190
Wang C, Zhang Y, Ying B, Sayed AH (2018) Coordinate-descent diffusion learning by network agents. IEEE Trans Signal Process. 66(2):352–367
Notarnicola I, Sun Y, Scutari G, Notarstefano G (2021) Distributed big-data optimization via blockwise gradient tracking. IEEE Trans Autom Control 66(5):2045–2060
Bianchi P, Hachem W, Lutzeler F (2016) A coordinate descent primal-dual algorithm and application to distributed asynchronous optimization. IEEE Trans Autom Control 61(10):2947–2957
Latafat P, Freris NM, Patrinos P (2019) A new randomized block-coordinate primal-dual proximal algorithm for distributed optimization. IEEE Trans Autom Control 64(10):4050–4065
J. Lafond, H.-T. Wai, and E. Moulines, “On the online Frank-Wolfe algorithms for convex and non-convex optimizations,”arXiv preprint arXiv: 1510.01171v2, Aug. 2015
A. Makhdoumi and A. Ozdaglar, “Graph balancing for distributed subgradient methods over directed graphs,”in Proc. IEEE Conf. Decis. Control, 2015, pp. 1364-1371
Funding
This work was supported in part by the National Natural Science Foundation of China (NSFC) under Grants No. 61976243, No. 72002133, and No. 61971458, and in part by the Leading talents of science and technology in the Central Plain of China under Grants No. 224200510004, and in part by the Scientific and Technological Innovation Team of Colleges and Universities in Henan Province under Grants No. 20IRTSTHN018, in part by the Ministry of Education of China Science Foundation under Grant No. 19YJC630174. and in part by the Key Technologies R & D Program of Henan Province under Grants No. 212102210083, and in part by the Luoyang Major Scientific and Technological Innovation Projects under Grants No. 2101017A.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declared no potential conflicts of interest with respect to the research, authorship, and publication of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhu, J., Wang, X., Zhang, M. et al. A distributed gradient algorithm based on randomized block-coordinate and projection-free over networks. Complex Intell. Syst. 9, 267–283 (2023). https://doi.org/10.1007/s40747-022-00785-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-022-00785-8