Abstract
In this paper, the definition of probability, conditional probability and likelihood function are generalized to the intuitionistic fuzzy observations. We focus on different estimation approaches of two-parameter Weibull (TW) distribution based on the intuitionistic fuzzy lifetime data including, maximum likelihood (ML) and Bayesian estimation methodology. The ML estimation of the parameters and reliability function of TW distribution is provided using the Newton–Raphson (NR) and Expectation–Maximization (EM) algorithms. The Bayesian estimates are provided via Tierney and Kadane’s approximation. In the Bayesian estimation approach, for the shape and scale parameters, the Gamma and inverse-Gamma priors are considered, respectively. Finally, a simulated data set is analyzed for illustrative purposes to show the applicability of the proposed estimation methods. The Monte Carlo simulations are performed to find the more efficient estimator in the intuitionistic fuzzy environment. The performances of the ML and Bayesian estimates of the parameters and reliability function are compared based on the mean biased (MB) and mean squared errors (MSE) criteria.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In classical researches, the available data are considered as crisp values/numbers. However, in real-world situations, some data are associated with an underlying imprecision due to inexactitude in the measuring process (human errors or machine errors), vagueness of the involved concepts or a certain degree of ignorance about the real values. Hence, the fuzzy set theory naturally provides an appropriate tool in modeling the imprecise data called fuzzy number (FN), and it is more efficient than considering only a single value or category. Garg [16] considered several linear and non-linear forms of fuzzy numbers with four different membership functions. Based on the findings, Cauchy FNs provide the preferential fit for the system data than triangular, normal and Gamma models based on the minimum level of the uncertainties in the form of the support spread at any confidence level.
In some cases, the number of failures or the lifetimes of items cannot be measured precisely, so they will be regarded as fuzzy random variables. The fuzzy random variable makes the combination of randomness and fuzziness more persuasive since the uncertainty and imprecision are modeled respectively by probability theory and fuzzy set theory. The pioneer researches in the field of the fuzzy random variable were executed by Kwakernaak [20] and Puri and Ralescu [29], afterward several types of investigation were motivated by the concept of fuzzy random variables and notions in classical probability are extended to the fuzzy environment. Among different researchers, we cite Liu et al. [21] (bivariate random fuzzy exponential distribution), Pak et al. [25] (fuzzy Weibull) and Shafiq et al. [30] (fuzzy lognormal).
The Bayesian estimation approach is of the main appealing in different sciences. Sindhu et al. [33] discussed the Bayesian estimation of a mixture Gumbel models and their industrial application for process monitoring in a new format of control chart. They evaluated the proposed chart by both data sets of failure times of windshields of aircraft and failure times of the air conditioning system of an airplane. The Bayesian inference of the mixture of two components of half-normal distribution based on both informative and non-informative priors are proposed by Sindhu et al. [34]. The posterior risks of the Bayesian estimators are compared to explore the effect of prior belief and loss functions. Recently, Sindhu et al. [31] concentrated on the Bayesian estimation of the shape parameter of the mixture of Topp-Leone with the non-informative priors under the censored data. They evaluated the survival times for 30 light bulbs in months and Bayesian estimates of the parameters under different loss functions.
Several estimation approaches are extended in fuzzy sets included the ML (NR and EM algorithms), uniformly minimum variance unbiased (UMVU) and Bayesian estimation methods. Denoeux [9] showed that the EM algorithm can be adapted to the fuzzy data called fuzzy EM (FEM). The proposed FEM method is utilized for the normal mean and variance estimation from a fuzzy sample, multiple regression analysis with crisp inputs and fuzzy outputs, and univariate finite normal mixture estimation from fuzzy data. Akbari and Khanjari Sadegh [1] generalized the two types of UMVU and Bayesian estimators to the fuzzy random variables based on Yao-Wu singed distance and \(\hbox {L}_2\)-metric. As a special case, they concentrated on the fuzzy random sample and triangular membership function. Parchami [28] reported the ML estimates of the parameters of exponential distribution based on fuzzy observations through the EM Algorithm.
In lifetime analysis, the reliability function plays a principal role, which indicates how many parts are still in use after a certain running time and have not yet failed. Since the fuzzy set theory was introduced by Zadeh [37], several investigators expanded the fuzzy set theory to reliability analysis [24]. The fuzzy reliability analysis of different distributions are considered in previous literature, such as exponential [36], Rayleigh [26, 27], Lomax [2] and Fréchet [22].
Fuentes-Huerta et al. [14] proposed a fuzzy maximum entropy approach to determine the maximum entropy reliability function considering the uncertainty and the maintenance staff knowledge. The combination of objective functions is simultaneously optimized in the Multi-objective optimization method. Garg [17] determined the interactive bi-objective reliability-cost of a series–parallel system under the fuzzy environment. They consider the fuzzy membership functions to handle the dissident character of different objectives. Niwas and Garg [23] focused on the reliability analysis of an industrial system under the failure-free warranty policy, with the negative exponential failure rate.
Based on Zadeh’s fuzzy set, several fuzzy set extensions for various objectives have been presented [4, 10, 11]. Among these extensions, the concept of intuitionistic fuzzy sets (IFS)s, introduced by Atanassov [3], has attracted more attention in practical problems, which makes descriptions of the objective world more realistic, practical and accurate. In the fuzzy set, the membership and non-membership grades of an object are complementary. But during deciding the degree of membership of an object, there is a degree of hesitation between the membership and non-membership. This feature is considered in IFS by defining a maximum value of one for the sum of the membership and non-membership values of an object. Based on the IFS, the intuitionistic fuzzy numbers (IFN)s as a generalization of FNs was proposed by Burillo et al. [5], applying in real-life problems. Thus, it is necessary to generalize the classical estimation methods from crisp numbers to IFNs. Garg [15] provided a new definition of membership function under IFS and focused on the fuzzy system reliability analysis to construct the membership and non-membership functions with different types of intuitionistic fuzzy failure rates (IFFR). The proposed approach is used in the fuzzy reliability analysis of series, parallel, and series–parallel systems using different types of IFFRs.
One of the classic distributions to fit lifetime data is the Weibull distribution, which demonstrates some prominent properties. Several modifications of the Weibull distribution are considered by the authors. The TW distribution with the shape and scale parameters has been extensively used in reliability and survival analysis, particularly in crisp data issues [13]. The probability density function (pdf), cumulative probability and reliability functions of the TW distribution are defined respectively as
where \(\varvec{\theta }=(\gamma ,\beta )\in {\mathbb {R}}^+\times {\mathbb {R}}^+\) is the vector of the unknown shape and scale parameters.
Consequently, the likelihood function of TW distribution based on the samples \((X_1,\ldots ,X_n)\) is obtained as below
The parameters of the Weibull distribution as well as the failure probability, based on crisp values, can be calculated using some proposed methods. Husniah et al. [19] proposed a multi-period lease contract for remanufactured products using Weibull distribution. Dahbi et al. [8] considered the analysis of wind power using the Weibull density function. Recently, Sindhu and Atangana [32] considered the reliability analysis of the exponentiated inverse Weibull distribution with the application of a surface-mounted electrolytic capacitor lifespan under an accelerated life testing, which influences average time to failure.
Despite several investigations on the estimation of the parameters of the Weibull distribution using fuzzy data, but the ML and Bayesian estimators of the Weibull parameters have not been discussed based on the IFNs data. The lifetime data might be imprecise and are represented in the form of IFNs, hence it is necessary to generalize crips estimation methods to IFNs. Due to the exigency of the estimation methods in IFN environments, we extend the classical ML (via NR and EM algorithms) and Bayesian estimation methods of crisp values of both parameters and reliability function of the TW distribution to the case of the IFNs. The estimation procedures are compared via the simulation study based on the MB and MSE factors.
Basic definition of the FN and IFS
In this section, we review some concepts of FN, fuzzy set theory and IFS, with two special classes of IFS, included the triangular intuitionistic fuzzy numbers (TIFNs) and trapezoidal intuitionistic fuzzy numbers (TrIFNs). We also develop some statistical semantics to the IFS, such as intuitionistic fuzzy probability, intuitionistic fuzzy conditional density, intuitionistic fuzzy likelihood and intuitionistic fuzzy conditional expectation.
Consider an experiment characterized by a probability space \(({\mathbb {R}}^n,{\mathfrak {A}},{\mathcal {P}})\), where \({\mathfrak {A}}\) is a \(\sigma \)-field of the Borel sets in \({\mathbb {R}}^n\) and \({\mathcal {P}}\) is probability measure over \({\mathbb {R}}^n\). The probability of any \(A\in {\mathfrak {A}}\) is defined as
Zadeh [37] extended the probability (1) to the fuzzy environment. In order to model imprecise data, a generalization of crisp numbers is necessary. The FN is a fuzzy subset \(({\tilde{x}})\), which is characterized by the membership function \(\mu _{{\widetilde{x}}}\), and satisfies the following constraints [39]
-
(i)
\(\mu _{{\widetilde{x}}}:{\mathbb {R}}\rightarrow [0,1]\) is Borel-measurable;
-
(ii)
\(\exists \, x_0\in {\mathbb {R}}\), such that \(\mu _{{\widetilde{x}}}(x_0)=1\).
-
(iii)
The \(\alpha \)-cuts are defined as \({\widetilde{x}}_\alpha =\{t\in {\mathbb {R}}\mid \mu _{{\widetilde{x}}}(t)\ge \alpha \}\) in a closed interval, for \(0<\alpha \le 1\).
Based on the definition of FN, a crisp number can be treated as a special case of the FN. Indeed, for a crisp real observation \(m\in {\mathbb {R}}\), its corresponding membership function is \(\mu _m(t)=1\), for \(t=m\) and \(\mu _m(t)=0\), for \(t\not =m\).
Regarding the concept of fuzzy sets, the notion of probability was extended to fuzzy events as follows [38].
Definition 1
(Zadeh [38]). Let \(({\mathbb {R}}^n,{\mathfrak {A}},{\mathcal {P}})\) be a probability space and consider the fuzzy observation \({\widetilde{x}}\), which is characterized as the observed FN value of a random experiment on the proposed probability space. So, the probability of occurring \({\tilde{x}}\) is defined as
Definition 2
(Atanassov [3]). Let \({\mathbb {X}}\) be a non-empty universal set. An IFS A in \({\mathbb {X}}\) is defined as an element of the form \(A=\{\langle x,\mu _A (x),\nu _A (x)\rangle \mid x\in {\mathbb {X}}\}\), where the functions \(\mu _A:{\mathbb {X}}\rightarrow [0,1]\) and \(\nu _A:{\mathbb {X}}\rightarrow [0,1]\) denote the degree of membership and non-membership of x in A, respectively, and \(0\le \mu _A(x)+\nu _A(x)\le 1\) for each \(x\in {\mathbb {X}}\).
In this paper, we assume \({\mathbb {X}}={\mathbb {R}}\), and the class of all IFSs is denoted as \(\mathcal {IF}({\mathbb {R}})\).
Definition 3
(Burillo et al. [5]). The IFN A in \({\mathbb {R}}\) is defined as \(A=\{\langle x,\mu _A (x),\nu _A (x)\rangle \vert x\in {\mathbb {R}}\}\) where the membership function \(\mu _A:{\mathbb {X}}\rightarrow [0,1]\) and the non-membership function \(\nu _A:{\mathbb {X}}\rightarrow [0,1]\) are defined as
where \(a_1\le a\le b\le c\le d\le d_1\) and \(0\le \mu _A(x)+\nu _A(x)\le 1\), for each \(x\in {\mathbb {R}}\). The left and right basic functions \(f^l(\cdot )\), \(f^r(\cdot )\), \(g^l(\cdot )\) and \(g^r(\cdot )\) are continues monotone membership and non-membership functions respectively, where \(f^l(\cdot )\), \(g^r(\cdot )\) are increasing and \(g^l(\cdot )\), \(f^r(\cdot )\) are decreasing functions.
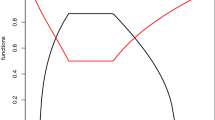
Two common TIFNs and TrIFNs classes of IFSs have received great attention in applications. The TIFN has the following membership and non-membership functions
where the values \(w_A\) and \(u_A\) represent maximum membership degree and minimum non-membership degree, such that \(w_A\in [0,1]\) and \(u_A\in [0,1]\), where \(0\le u_A+w_A \le 1\).
Figure 1 shows the membership and non-membership functions of a TIFN for the case \(a=d\), \(c=f\).
Intuitionistic fuzzy probability
In the following, we define some renovated notions of probability to the IFSs, which will be employed in the estimation discussion based on intuitionistic fuzzy observations.
Definition 4
Consider the probability space \(({\mathbb {R}}^n,{\mathfrak {A}},{\mathcal {P}})\), the probability of an intuitionistic fuzzy observation \({\widetilde{x}}\) in \({\mathbb {R}}^n\), which is the observed value of a random experiment as IFS is defined by
Consider the continuous random variable X with the pdf \(f_{\varvec{\theta }}(x)\), parameterized with \(\varvec{\theta }\). We introduce the conditional density of X given the intuitionistic fuzzy observation \({\widetilde{x}}\), called intuitionistic fuzzy conditional density, as follows
which satisfies the probability axioms,
-
(i)
\(f_{\varvec{\theta }}(x \vert {\widetilde{x}}) \ge 0\),
-
(ii)
\(\int _{\mathbb {R}} f_{\varvec{\theta }}(x \vert {\widetilde{x}}) dx =1\).
Subsequently, the likelihood function of \(\varvec{\theta }\) given IFS \({\widetilde{x}}\) is defined as below
Consider the independent identically distributed (i.i.d) random vector with the realization \(\widetilde{{\mathbf {x}}}=({\widetilde{x}}_1,\ldots ,{\widetilde{x}}_n)\), and the joint membership \(\mu _{\widetilde{{\mathbf {x}}}}(\cdot )\) and the corresponding non-membership functions \(\nu _{\widetilde{{\mathbf {x}}}}(\cdot )\) are satisfied in the following relation
Therefore, the intuitionistic fuzzy likelihood function (3) is written as follows
Indeed, we assume that \({\mathbf {X}}=(X_1,\ldots ,X_n)\) be a random variable of size n taken from a population with pdf \(f_{\varvec{\theta }}(x)\), and \(\widetilde{{\mathbf {x}}}=({\widetilde{x}}_1,\ldots ,{\widetilde{x}}_n)\) is the observed value of the sample. So, \({\widetilde{x}}_i\) is the intuitionistic fuzzy observed value of \(X_i\) with the membership function \(\mu _{{\widetilde{x}}_i}(x)\) and non-membership function \(\nu _{{\widetilde{x}}_i}(x)\) for \(i=1,\ldots ,n\). The intuitionistic fuzzy likelihood function is the product of the probability function based on the IFS \({\widetilde{x}}\) as follows
Corollary 1
The conditional probability of an IFS \({\widetilde{x}}^c\) to the probability of an IFS \({\widetilde{x}}\) is provided as
where the membership and non-membership functions of the subscription of two IFSs \({\widetilde{x}}\cap {\widetilde{x}}^c\) hold in the following equation
Corollary 2
Based on the conditional pdf, the expectation of the random variable X given the intuitionistic fuzzy observation \({\widetilde{x}}\) is defined as below
The estimation based on intuitionistic fuzzy observations
Based on n intuitionistic fuzzy observations \({\widetilde{x}}_1, \ldots , {\widetilde{x}}_n\), parameters of a distribution can be estimated intuitively by different estimation methods.
Here, we provide the parameters and reliability function estimation of the TW distribution by the ML and Bayesian estimation methods.
Let \(X_i\), \(i=1,\ldots ,n\), be the random variable distributed as (2), with the vector of parameters \(\varvec{\theta }\), and \({\widetilde{x}}_1,\ldots ,{\widetilde{x}}_n\) be observed imprecisely from the TW distribution. The intuitionistic fuzzy likelihood function is provided as
Thus, the intuitionistic fuzzy log-likelihood function is represented as
Therefore, the ML estimation of the vector \(\varvec{\theta }\) is obtained based on the root of the following score functions
Or equivalently,
where
The first derivatives of the TW distribution, with respect to each parameter, are computed as below
As can be seen, the ML estimates of the TW distribution cannot be obtained analytically, so some numerical methods are required to find the roots of (4). If \(\widehat{\varvec{\theta }}=({\widehat{\gamma }},{\widehat{\beta }})\) be the numerical solutions of (4), so they should satisfy in the regular conditions as below
where
We consider both NR and EM algorithms to compute the ML estimates of the vector \(\varvec{\theta }\).
NR Algorithm based on intuitionistic fuzzy observations
The NR Algorithm is a direct approach for estimating the relevant parameters in a likelihood function, which finds the root of score functions through an iterative procedure. Consider the initial values \(\varvec{\theta }^0=(\gamma ^0, \beta ^0)\), then at the \((h+1)^{th}\) step of the iteration, the updated parameters are obtained as
The iteration process continues until the convergency is reached, in the other word, for specified \(\varepsilon >0\), the process is repeated until \(\Vert \varvec{\theta }^{h+1}-\varvec{\theta }^h\Vert _2<\varepsilon \), where \(\Vert \cdot \Vert _2\) is the Euclidian norm. The initial values of the parameters are selected based on the ordinary ML estimates of the parameters of TW distribution. It is worth mention the NR algorithm is executed by the “nlm” command in statistical software “R”, which uses the NR algorithm as default. The ML estimate of \(\varvec{\theta }\) via NR algorithm is denoted by \(\widehat{\varvec{\theta }}_{NR}=({\widehat{\gamma }}_{NR},{\widehat{\beta }}_{NR})\).
EM algorithm based on intuitionistic fuzzy observations
The EM algorithm is a prevalent estimation strategy to compute the ML estimates iteratively, which is used in a variety of incomplete-data contents. Some superiorities of the EM algorithm than NR are facility in run, computational stability with appropriate convergence rate and potential asymptotic behavior of estimates. The EM algorithm is a feasible estimation method in fuzzy data, since the observed intuitionistic fuzzy data \(\widetilde{{\mathbf {x}}}\) can be regarded as an incomplete specification of a complete data vector \(\widetilde{{\mathbf {x}}}\).
In the following, the EM algorithm is investigated to determine the ML estimates of \(\varvec{\theta }=(\gamma ,\beta )\), containing the following iterative process.
-
1.
Consider the initial values of \(\varvec{\theta }\), as \(\varvec{\theta }^0=(\gamma ^0,\beta ^0)\), and set \(h=0\).
-
2.
In the \((h+1){th}\) iteration, the following expectations are computed
$$\begin{aligned} E_{1i}= & {} E_{\varvec{\theta }} \left( \log \left( \frac{X}{\beta }\right) \vert X \in {\widetilde{x}}_i\right) \nonumber \\= & {} \int _{\mathbb {R}} \log \left( \frac{x}{\beta }\right) f_{\varvec{\theta }} (x\vert x\in {\widetilde{x}}_i) dx\nonumber \\= & {} \int _{\mathbb {R}} \log \left( \frac{x}{\beta }\right) \nonumber \\&\quad \times \frac{\frac{1-\nu _{{\widetilde{x}}_i}(x)+\mu _{{\widetilde{x}}_i}(x)}{2} f_{\varvec{\theta }}(x)}{\int _{\mathbb {R}} \frac{1-\nu _{{\widetilde{x}}_i}(x)+\mu _{{\widetilde{x}}_i}(x)}{2}f_{\varvec{\theta }}(x) dx}\mid _{\varvec{\theta }=\varvec{\theta }^h} dx, \nonumber \\ E_{2i} = & {} E_{\varvec{\theta }} \left( \left( \frac{X}{\beta }\right) ^{\gamma }\log \left( \frac{X}{\beta }\right) \vert X \in {\widetilde{x}}_i\right) \end{aligned}$$(5)$$\begin{aligned}= & {} \int _{\mathbb {R}} \left( \frac{x}{\beta }\right) ^{\gamma }\log \left( \frac{x}{\beta }\right) f_{\varvec{\theta }} (x\vert x\in {\widetilde{x}}_i) dx \qquad \nonumber \\= & {} \int _{\mathbb {R}} \left( \frac{x}{\beta }\right) ^{\gamma }\log \left( \frac{x}{\beta }\right) \nonumber \\&\quad \times \frac{\frac{1-\nu _{{\widetilde{x}}_i}(x)+\mu _{{\widetilde{x}}_i}(x)}{2} f_{\varvec{\theta }}(x)}{\int _{\mathbb {R}} \frac{1-\nu _{{\widetilde{x}}_i}(x)+\mu _{{\widetilde{x}}_i}(x)}{2}f_{\varvec{\theta }}(x) dx}\vert _{\varvec{\theta }=\varvec{\theta }^h} dx,\nonumber \\ E_{3i}= & {} E_{\varvec{\theta }} \left( \frac{X^{\gamma }}{\beta ^{\gamma +1}}\vert X \in {\widetilde{x}}_i\right) \end{aligned}$$(6)$$\begin{aligned}= & {} \int _{\mathbb {R}} \frac{x^{\gamma }}{\beta ^{\gamma +1}} f_{\varvec{\theta }} (x\vert x\in {\widetilde{x}}_i) dx \nonumber \\= & {} \int _{\mathbb {R}} \frac{x^{\gamma }}{\beta ^{\gamma +1}} \nonumber \\&\quad \times \frac{\frac{1-\nu _{{\widetilde{x}}_i}(x)+\mu _{{\widetilde{x}}_i}(x)}{2} f_{\varvec{\theta }}(x)}{\int _{\mathbb {R}} \frac{1-\nu _{{\widetilde{x}}_i}(x)+\mu _{{\widetilde{x}}_i}(x)}{2}f_{\varvec{\theta }}(x) dx}\vert _{\varvec{\theta }=\varvec{\theta }^h} dx. \end{aligned}$$(7) -
3.
Based on the expectations (5)–(6), the values \(\widehat{\varvec{\theta }}^{h+1}=({\widehat{\gamma }}^{h+1},{\widehat{\beta }}^{h+1})\) are achieved, respectively as follows
$$\begin{aligned} {\widehat{\gamma }}^{h+1}\leftarrow & {} \frac{n}{-\sum _{i=1}^{n}E_{1i}+\sum _{i=1}^{n}E_{2i}},\\ {\widehat{\beta }}^{h+1}\leftarrow & {} \frac{n}{\sum _{i=1}^{n}E_{3i}}. \end{aligned}$$ -
4.
The process is iterated until it reaches convergence, the same as the NR algorithm. If the convergency is reached, then the current \(\widehat{\varvec{\theta }}^{h+1}=({\widehat{\gamma }}^{h+1},{\widehat{\beta }}^{h+1})\) are the ML estimates of \(\varvec{\theta }=(\gamma ,\beta )\) via EM algorithm, otherwise set \(h=h+1\) and go to step 2.
The ML estimate of \(\varvec{\theta }\) via EM algorithm is refereed as \(\widehat{\varvec{\theta }}_{EM}=({\widehat{\gamma }}_{EM},{\widehat{\beta }}_{EM})\).
Corollary 3
The ML estimation of the intuitionistic fuzzy reliability of TW distribution, defined as \(R_{\varvec{\theta }}(x)=\exp (-(\frac{x}{\beta })^\gamma )\), is concluded by the invariant properties of the ML estimates. Therefore, the ML estimates (by NR and EM algorithm) of \(R_{\varvec{\theta }}(x)\) is represented as follows
Bayesian estimation based on intuitionistic fuzzy observations
In recent decades, the Bayesian inference has received a great deal of attention which is a potential alternative to the classical statistic perspectives. In this section, we consider the independent Gamma and inverse-Gamma priors for shape and scale parameters, respectively. Hence, the joint prior of the \(\varvec{\theta }\) is represented as
where \( a_1,a_2,b_1,b_2 \) are hyperparameters. The posterior likelihood function of \(\varvec{\theta }\) given intuitionistic fuzzy observations \(\widetilde{{\mathbf {X}}}=\widetilde{{\mathbf {x}}}\) is indicated as
Thus, the intuitionistic fuzzy log-posterior likelihood function is written as
Finally, under the squared error loss function, the Bayesian estimate of any function of \(\varvec{\theta }\), say \(g(\varvec{\theta })\), is
where \(Q(\varvec{\theta })=\log \Big (\pi (\varvec{\theta }){\mathcal {L}}(\varvec{\theta }\vert \widetilde{{\mathbf {x}}})\Big )\). The posterior expectation (8) cannot be obtained analytically, hence we apply Tierney and Kadane’s approximation to derive the Bayesian estimates of parameters [35].
Consider the notation \(H(\varvec{\theta })=\frac{Q(\varvec{\theta })}{n}\) and \(H^{*}(\varvec{\theta })=\log (g(\varvec{\theta }))+H(\varvec{\theta })\), the Bayesian estimates of \( g(\varvec{\theta })\) are represented as
where \(\overline{\varvec{\theta }}\) and \(\overline{\varvec{\theta }}^{*}\) maximize \(H(\varvec{\theta })\) and \(H^{*}(\varvec{\theta })\), respectively, \( \Sigma \) and \( \Sigma ^{*} \) are the negatives of the inverse Hessians of \(H(\varvec{\theta })\) and \(H^{*}(\varvec{\theta })\) at maximum points of the corresponding functions. Therefore, \( \det \Sigma =(H_{11}H_{22}-H_{12}^2)^{-1} \) and \(\det \Sigma ^{*}=(H^{*}_{11}H^{*}_{22}-H_{12}^{*2})^{-1} \), where \(H_{ij},\, H^{*}_{ij},\,i,j=1,2\) denote the derivatives of \(H(\varvec{\theta })\) and \(H^{*}(\varvec{\theta })\), with respect to \(\gamma \) and \(\beta \). By set \(g(\varvec{\theta })=\gamma \) and \(g(\varvec{\theta })=\beta \), the Bayesian estimates of each parameter are obtained, directly. Due to the tedious calculation of derivative functions, they are eliminated from the paper.
The maximization of the functions \(H(\varvec{\theta })\) and \(H^{*}(\varvec{\theta })\) are computed numerically by the “nlm” command and the Hessians matrices are obtained by the “hessian” command at the package “numDeriv” in software “R”. So, \(\Sigma \) and \( \Sigma ^{*} \) are easily computed by the negative of inverse of related Hessians.
Corollary 4
The Bayesian estimate of the intuitionistic fuzzy reliability of TW distribution is obtained by taking \(g(\varvec{\theta })=R_{\varvec{\theta }}(\cdot )\) in the Bayesian estimation method. By applying Tierney and Kadane’s approximation, the Bayesian estimation of the reliability function is computed with the updated notation \(H^{*}(\varvec{\theta })=-\left( \frac{x}{\beta }\right) ^\gamma +H(\varvec{\theta })\) and the corresponding Hessian matrix.
Numerical examples
In this section, some numerical examples of the ML and Bayesian estimates are reported for comparison purposes.
Intuitionistic fuzzy data generation
In this section, the proposed estimation methods are applied on a simulated of IFSs, to compare the performances of estimation approaches. The random samples are generated by employing the intuitionistic fuzzy representation method. There are several families of fuzzy representations in the literature [6, 7, 18], we extend the family of interesting fuzzy representation proposed in [18] to IFS. Each representation transforms crisp data (real-valued random variable) into IFSs (associated intuitionistic fuzzy random variable (IFRV)) by mapping \({\widetilde{\gamma }}:{\mathbb {R}} \rightarrow \mathcal {IF}({\mathbb {R}})\) whose membership and non-membership functions are given by
such that
-
(i)
\(x_1,\ldots ,x_n\) is an i.i.d crisp random sample from distribution \(f_{\varvec{\theta }}(\cdot )\);
-
(ii)
\(a_i\) and \(b_i\) are selected randomly, such that \(a_i\le x_i \le b_i\), for each \(i=1,\ldots ,n\);
-
(iii)
\(w_i\in [0,1]\) and \(u_i\in [0,1]\) are selected randomly such that \(0\le w_i+u_i\le 1\), for each \(i=1,\ldots ,n\);
-
(iv)
\(h_L(\cdot ):{\mathbb {R}}\rightarrow [0,1]\) and \(h_R(\cdot ):{\mathbb {R}}\rightarrow [0,1]\).
Remark 1
The generated IFS covers TIFN as a special case, when set \(h_L(\cdot )=h_R(\cdot )=1\) in (9).
In all generated data sets used in this paper, the generated IFSs are considered as TIFNs. Consider the probability space \((\Omega , {\mathcal {A}}, P)\), and let \(X: \Omega \rightarrow {\mathbb {R}}\) be a random variable associated with \((\Omega , {\mathcal {A}}, P)\). The \(\mathcal {IF}({\mathbb {R}})\)-valued IFRV \({{\tilde{\gamma }}}_X: \Omega \rightarrow \mathcal {IF}({\mathbb {R}})\) will be called the \(\gamma \)-IFRV representation of the random variable X.
Optimal solutions
In this section, we generate the dataset \((x_1,\ldots ,x_n)\) form the TW distribution with parameters \(\varvec{\theta }=(\gamma ,\beta )=(5,10)\), with sample size \(n=30\). The data set is reported in Table 1, which is derived by the mechanism given in Sect. 4.1. Then, by \({\widetilde{\gamma }}\) intuitionistic fuzzy representation in (9), the crisp values of \((x_1,\ldots ,x_n)\) are transformed to the IFNs. Now by employing the NR and EM algorithms, the estimated values of the parameter \(\varvec{\theta }=(\gamma ,\beta )=(5,10)\) are obtained as
In this paper, the initial values of the parameters \(\gamma \) and \(\beta \) in the NR and EM algorithms are chosen as the ML estimates of 1000 samples from crisp TW distribution, which will be modified in each iteration of algorithms.
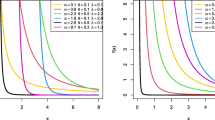
A contour plot is a graphical tool to represent a 3-dimensional surface by depicting constant z slices, called contours, on a 2-dimensional format. The location of point \(\widehat{\varvec{\theta }}_{NR}\) on the contour plot depicts the location of the values that minimized the proposed function.
The contour plot of the likelihood function of the intuitionistic fuzzy data is depicted in Fig. 2, which shows the location of the solution in NR algorithm. In Fig. 2, the parameters \( \gamma \) and \( \beta \) are respectively represented in the x-axis and y-axis, where the z-axis is the values of the intuitionistic fuzzy log-likelihood function. The minimum values of the intuitionistic fuzzy log-likelihood function are represented by red dash-line based on the NR algorithm.
We further calculate the Bayesian estimates of the unknown parameters, by using Tierney and Kadane’s approximation method. In order to obtain the values of hyperparameters \((a_1,a_2,b_1,b_2)\) of informative priors, we first generate 1000 samples from the complete TW distribution and corresponding to each sample, we derive the maximum likelihood estimates of the parameters and then compare the mean and variance of these samples with the mean and variance of the considered priors [12]. Then, we consider informative priors of \(\gamma \sim \Gamma (a_1,b_1)\) and \(\beta \sim \text {I}\Gamma (a_2,b_2)\) for the parameters. The Bayesian estimates of \(\varvec{\theta }=(\gamma ,\beta )=(5,10)\) based on the proposed approximation method is
Simulation study
In the following, a simulation study is provided to compare the performance of the proposed estimation methods based on 1000 iteration samples. Some numerical properties of the estimated parameters will be applied to investigate the performance of the estimation methods, such as MB and MSE.
The MB and MSE criteria for the estimated parameters over the simulated iteration loop are defined as follows
Comparison results
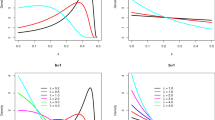
Table 2 consists of the MB and MSE values of the ML and Bayesian estimates over the simulated intuitionistic fuzzy observations. The positive values of MB show the overestimation, and negative values denote the underestimation of each estimation method. Based on the findings, the estimation methods in the intuitionistic fuzzy environment are convergent to the actual values of the parameters, and by increasing the sample size, the MSE values are gradually decreased. Moreover, the Bayesian estimation approach are more convenient than NR and EM, regarding the minimum values of MB and MSE.
Table 3 reports the estimated results for the reliability function by EM, NR and Bayesian estimation methods for different values of \(x=5,8,10\).
An estimation method is recommended based on the MB and MSE in the comparison outcomes. The results of Table 3 confirmed the convergence of the estimation methods. Also, the Bayesian estimation of the reliability function has preponderance than the classical ML method with respect to the MB and MSE values.
Conclusion remarks
In this paper, the probability notions are extended to the IFS and based on the TW lifetime distribution, the parameters, as well as the reliability function, are estimated. We focus on the generalization of the fuzzy, [25], to the intuitionistic fuzzy environment, which can be considered as a special case of IFN. Based on the IFS, the classical ML (NR and EM algorithms) and Bayesian estimation approaches are discussed. The Bayesian estimation is obtained through Tierney and Kadane’s approximation, under the informative priors and square error loss function. Based on the simulation findings for different combinations of parameters and sample size, all estimates are convergent to their actual values, and by increasing the sample size, the imprecise is increased due to decreasing MSE values. Moreover, in the intuitionistic fuzzy environment, the Bayesian estimation of the parameters and reliability function have prominent features that provide less of MSE and MB measures. The NR and EM algorithms exhibited almost analogous features with negligible less MSE values for NR than EM algorithm.
References
Akbari M, Khanjari Sadegh M (2012) Estimators based on fuzzy random variables and their mathematical properties. Iran J Fuzzy Syst 9(1):79–95
Al-Noor NH (2019) On the fuzzy reliability estimation for Lomax distribution. AIP Conf Proc 2183(1):110002
Atanassov K (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96
Baloui Jamkhaneh E, Nadarajah S (2015) A new generalized intuitionistic fuzzy set. Hacettepe J Math Stat 44(6):1537–1551
Burillo P, Bustince H, Mohedano V (1994) Some definition of intuitionistic fuzzy number, fuzzy based expert systems. Fuzzy Bulgarian Enthusiasts, Sofia
Colubi A, González-Rodríguez G (2007) Triangular fuzzification of random variables and power of distribution tests: empirical discussion. Comput Stat Data Anal 51(9):4742–4750
Colubi A, González-Rodríguez G, Lubiano MA, Montenegro M (2006) Exploratory analysis of random variables based on fuzzification. In: Lawry J, Miranda E, Bugarin A, Li S, Gil MA, Grzegorzewski P, Hryniewicz O (eds) Soft methods for integrated uncertainty modelling. Springer, Berlin, pp 95–102
Dahbi M, Benatiallah A, Sellam M (2013) The analysis of wind power potential in Sahara site of Algeria-an estimation using the ‘Weibull’ density function. Energy Procedia 36:179–188
Denoeux T (2011) Maximum likelihood estimation from fuzzy data using the EM algorithm. Fuzzy Sets Syst 183(1):72–91
Deschrijver G, Kerre EE (2003) On the relationship between extensions of fuzzy set theory. Fuzzy Sets Syst 133(2):227–235
Deschrijver G, Kerre EE (2007) On the position of intuitionistic fuzzy set theory in the framework of theories modelling imprecision. Inf Sci 177(8):1860–1866
Dey S, Singh S, Tripathi YM, Asgharzadeh A (2016) Estimation and prediction for a progressively censored generalized inverted exponential distribution. Stat Methodol 32:185–202
Dodson B (2006) The Weibull analysis handbook, 2nd edn. ASQ Quality Press
Fuentes-Huerta MA, González-González DS, Cantú-Sifuentes M, Praga-Alejo RJ (2021) Fuzzy reliability centered maintenance considering personnel experience and only censored data. Comput Indust Eng 107440(c):107
Garg H (2016) A novel approach for analyzing the reliability of series-parallel system using credibility theory and different types of intuitionistic fuzzy numbers. J Braz Soc Mech Sci Eng 38(3):1021–1035
Garg H (2018) Analysis of an industrial system under uncertain environment by using different types of fuzzy numbers. Int J Syst Assur Eng Manag 9(2):525–538
Garg H (2021) Bi-objective reliability-cost interactive optimization model for series-parallel system. Int J Math Eng Manag Sci 6(5):1331–1344. https://doi.org/10.33889/IJMEMS.2021.6.5.080
González-Rodríguez G, Colubi A, Gil MA (2006) A fuzzy representation of random variables: an operational tool in exploratory analysis and hypothesis testing. Comput Stat Data Anal 51(1):163–176
Husniah H, Pasaribu US, Iskandar BP (2021) Multi-period lease contract for remanufactured products. Alex Eng J 60(2):2279–2289
Kwakernaak H (1978) Fuzzy random variables I: definitions and theorems. Inf Sci 15(1):1-29
Liu Y, Tang W, Li X (2011) Random fuzzy shock models and bivariate random fuzzy exponential distribution. Appl Math Model 35(5):2408–2418
Neamah MW, Ali BK (2020) Fuzzy reliability estimation for Frechet distribution by using simulation. Period Eng Nat Sci 8(2):632–646
Niwas R, Garg H (2018) An approach for analyzing the reliability and profit of an industrial system based on the cost free warranty policy. J Braz Soc Mech Sci Eng 40(5):265. https://doi.org/10.1007/s40430-018-1167-8
Onisawa T, Kacprzyk J (1995) Reliability and safety analyses under fuzziness. Physica-Verlag, Heidelberg
Pak A, Parham G, Saraj M (2013) Inference for the Weibull distribution based on fuzzy data. Revista Colombiana de Estadística 36:337–356
Pak A, Parham G, Saraj M (2014) Reliability estimation in Rayleigh distribution based on fuzzy lifetime data. Int J Syst Assur Eng Manag 5(4):487–494
Pak A, Parham G, Saraj M (2014) Inference for the Rayleigh distribution based on progressive type-II fuzzy censored data. J Mod Appl Stat Methods 13(1):287–304
Parchami A (2018) Estimation of the exponential distribution parameter using the EM Algorithm based on fuzzy observations. Iran J Fuzzy Syst 15:123–137
Puri ML, Ralescu DA (1986) Fuzzy random variables. J Math Anal Appl 114(2):409–422
Shafiq M, Atif M, Alamgir C (2016) On the estimation of three parameters lognormal distribution based on fuzzy life time data. Sains-Malaysiana 45(11):1773–1777
Sindhu TN, Hussain Z, Aslam M (2019) On the Bayesian analysis of censored mixture of two Topp-Leone distribution. Sri Lankan J Appl Stat 19(1):13–30
Sindhu TN, Atangana A (2021) Reliability analysis incorporating exponentiated inverse Weibull distribution and inverse power law. Qual Reliab Eng Int 37(6):2399–2422
Sindhu TN, Riaz M, Aslam M, Ahmed Z (2015) Bayes estimation of Gumbel mixture models with industrial applications. Trans Inst Meas Control 38(2):201–214
Sindhu TN, Khan HM, Hussain Z, Al-Zahrani B (2018) Bayesian inference from the mixture of half-normal distributions under censoring. J Natl Sci Found 46(4):587–600
Tierney L, Kadane JB (1986) Accurate approximations for posterior moments and marginal densities. J Am Stat Assoc 81(393):82–86
Wu HC (2006) Fuzzy Bayesian system reliability assessment based on exponential distribution. Appl Math Model 30(6):509–530
Zadeh L (1965) Fuzzy sets. Inf Control 8(3):338–353
Zadeh L (1968) Probability measures of fuzzy events. J Math Anal Appl 23(2):421–427
Zimmermann HJ (2001) Fuzzy set theory and its applications, 4th edn. Kluwer Nihoff, Boston
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Conflict of interest On behalf of all the authors, the corresponding author states that there are no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The “R” codes of the Figs. 1 and 2 and Tables 1, 2 and 3.






Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Roohanizadeh, Z., Baloui Jamkhaneh, E. & Deiri, E. Parameters and reliability estimation for the weibull distribution based on intuitionistic fuzzy lifetime data. Complex Intell. Syst. 8, 4881–4896 (2022). https://doi.org/10.1007/s40747-022-00720-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-022-00720-x