Particle swarm optimization algorithm for the optimization of rescue task allocation with uncertain time constraints

Abstract

This paper focuses on the problem of robot rescue task allocation, in which multiple robots and a global optimal algorithm are employed to plan the rescue task allocation. Accordingly, a modified particle swarm optimization (PSO) algorithm, referred to as task allocation PSO (TAPSO), is proposed. Candidate assignment solutions are represented as particles and evolved using an evolutionary process. The proposed TAPSO method is characterized by a flexible assignment decoding scheme to avoid the generation of unfeasible assignments. The maximum number of successful tasks (survivors) is considered as the fitness evaluation criterion under a scenario where the survivors’ survival time is uncertain. To improve the solution, a global best solution update strategy, which updates the global best solution depends on different phases so as to balance the exploration and exploitation, is proposed. TAPSO is tested on different scenarios and compared with other counterpart algorithms to verify its efficiency.

Introduction

The development of the global economy has financially benefited many countries in the world, but also initiated numerous environmental issues. One of its biggest side effects could be the raise of disasters that critically damage human’s life, properties, and production [1]. Many disasters have natural causes, for instance: earthquakes, hurricanes, and floods. Many others are human-caused, or non-natural, disasters such as explosions, nuclear incidents, and building collapses. Sometimes, the disasters occurred in a very abrupt and erratic way, sometimes led to massive havoc, whilst their sources and causes were unforeseeable. Therefore, the post-catastrophe support and rescue are equally important as the disaster prediction and warning process. Autonomous and intelligent assistive systems have been prevalent in carrying on supportive missions in many hostile environments after disasters [2,3,4]. Non-human agents such as robots are increasingly exploited in such situations, especially in working in toxic and hazardous zones. Improving robots’ effectiveness and efficiency in rescuing becomes an interesting research area.

The research scopes and ideas in robot rescue are diverse, two of the topics most focused on could be: rescue structure design, and motion model and control [5]. The first one considers the big picture by designing an overall structure for robots to perform a series of rescuing tasks [5,6,7,8], for example: walking, driving, or delivering medical equipment and food. The second group focuses on the details of each task and aims at improving the robots’ speed, accuracy, and stability [9,10,11]. Significant studies in the latter one have been published, in which several robot control algorithms were proposed, for instance: simultaneous localization and mapping (SLAM) [12], particle filter (PF) [13], Kalman filter (KF) [13, 14], proportional integral derivative (PID) controller [15, 16], and sliding mode [17]. Those algorithms are considered the backbone of robot rescue performance theory these days.

Although the above methods can obtain valuable results in many simulated situations when the time factor is neglected, they are unable to address some practical issues. In simulated cases, the key questions for designing rescue and controlling robots would be and “How to pass stability through an uneven terrain?”, “How can the robots smoothly follow the setting rescue route?”, “How to rise the robot system’s reliability and survivability effectively by multi-sensor information fusion” When the survival time is tight, for example when some seriously injured people are trapped in a place after a chemical fire accident, there would be more complicated questions such as “What is the rescue route?”, “How can the survival time be estimated?”, “What is the priority order of tasks?” and “How can the rescue route be altered if some task time values are changed?”, these problems can be treated as a task allocation problems. Very limited evidence can be found in the literature that rigorously assesses the time factor in robot rescue. Some of our previous researches show positive outcomes in handling complex rescue routes in real-world situations with an assumption that survival time values are stable [18, 19]. Still, estimating the survival time in destructive locations remains a challenging issue.

It is noticed that the changing rate of survival time is not uniform under the condition of emergency rescue but presents as an exponential function with respect to time [20]. Different physical qualities and environments make the survival time uncertain while considering that it only generates minor differences in the survival time value, the value can be treated as an interval without loss of generality. That important evaluation suggested that the change of survival time can be modelled by establishing an interval function of survival time changing over time. With few related studies, and considering that rescue after a disaster is a key issue for security and emergency management, research on the rescue problem with uncertain deadlines is essential.

Based on the above analysis, the rescue task allocation problem—how to rescue survivors within an uncertain and limited survival time—is studied in this paper. Rescue task allocation actually is a nondeterministic polynomial hard (NP-hard) problem, its solving method is much complex, one common-used way to solve it is intelligent optimization algorithms, such as particle swarm optimization (PSO) algorithm, genetic algorithm (GA) and so on.

In light of PSO algorithm is simple to implement, has fewer tuning parameters and fast convergence speed, and can obtain the global optimal or suboptimal solution of the problem as well [19]. Moreover, the PSO algorithm and its variants require fewer evolutionary populations than other swarm intelligence algorithms. Considering the numerous advantages of PSO algorithm, PSO algorithm is employed to solve this problem.

This paper proposes an innovative robot rescue task allocation algorithm that robust in real-world situations when survival time is limited and uncertain. Inheriting the advantages of PSO algorithm, that algorithm establishes a mathematical model for task allocation variable, thus named TAPSO (task allocation PSO). TAPSO tackles this task allocation problem by taking the number of successful survivors (tasks) as an objective function. Moreover, TAPSO improves the particle decode method in the original PSO algorithm to define the rescue route, also upgrades the global best update method by estimating the differences in different evolutionary phases between it and local best solutions.

The organization of the rest of this paper is as follows: The next section reviews some researches on robot rescue task allocation topic. Section 3 defines the particular problems that need to be solved before converting them into a mathematical domain; followed by a demonstration of the TAPSO algorithm in Sect. 4. Section 5 provides the simulation results and analysis, whilst the conclusion and future work are presented in the final section.

Related work

A wide variety of approaches have been reported for solving the problem of rescue task allocation and achieved meaningful results. Traditional methods of addressing task allocation problems include behavior-based algorithms [21], market-based algorithms [22], linear planning methods [23], and intelligent optimization algorithms [24,25,26]. Technically, the behavior-based algorithm has the advantages of real-time, fault-tolerance, and robustness, but unable to obtain the global optimal solutions. Moreover, market-based algorithms are suitable for solving the task allocation problem in small- and medium-sized heterogeneous distributed collaborative robots, whilst the optimal global solution is not always be computed in reasonable time; unfortunately, it is resource-consuming—once communication is interrupted, its performance drops significantly. Linear planning methods apply matrix operations for presenting robots’ information and batch computing for a robot route, while the numbers of robots and tasks are considerable, the computing expense grows exponentially. Further, other hybrid linear planning methods [27,28,29] can find the optimal solution but are inefficient when the scale of the problem is large. Intelligent algorithms primarily employ GA, PSO, and other algorithms to solve the problem, several empirical reports suggested that this type of algorithms could be an answer for the perplexing issues of low convergence speed and easily converge at a local optimal solution [24,25,26].

Based on the communication topologies of robots, existing methods of task allocation can be classified into two categories: centralized and distributed. The centralized algorithm has a manager reacting like a server to assign tasks to each robot, and it can achieve the optimal solution; however, the performance of a centralized system deteriorates when the number of tasks is large, the computational load becomes heavy; therefore, a centralized algorithm is suitable for solving such task allocation problems where it is easy to obtain information about the environment and tasks for a relatively small scale. In contrast, the distributed algorithm has no manager; a few robots cannot communicate directly with each other, and the task allocation scheme is determined by the cooperation of robots that can communicate with each other. The distributed method can effectively improve the shortages of the centralized controller with heavy loads and poor fault tolerance; however, the communication cost of the distributed robot system is high, and the algorithm easily falls into the local optimum owing to the lack of global information. The following relevant literature offers supporting evidence.

In [30], Whitbrook et al. modified the performance impact (PI) task-allocation algorithm with ε-greedy and softmax auction selection methods to explore assignments with less rescue time; furthermore, in [31] the researchers presented a new algorithm based on the work in [30] to solve the problem of being trapped into the local minima and a static structure. To maximize the number of task allocations in a multi-robot system under strict time constraints, Turner et al. [32] proposed an effective algorithm to improve the solutions’ performance. However, they primarily focus on the application of market-based algorithms rather than generating global optimal solutions. Robot rescue task allocation is an optimization problem in reality, an optimal allocation strategy can help rescue effectively.

Different from market-based algorithm, PSO, an centralized algorithm, can offer the global optimal solution, and it has been implemented to the field of task allocation, for example, Yu [33] presented an improved particle swarm optimization (IPSO) algorithm to improve the efficiency of resource scheduling, and this IPSO algorithm can overcome the problem of premature; Nethravathis et al. [34] proposed a permutation optimization strategy based on PSO algorithm to solve the resource sharing among device-to-device communication problem; Lin et al. [35] illustrated a new group method to divide rescue tasks into groups according to their distances, and employed an improved PSO algorithm to assign the grouped tasks to robots, results indicated that the proposed method can increase the success rate of rescue; Singh et al. [36] presented a novel PSO algorithm for solving multi-objective flexible job-shop scheduling problem with the goal of finding approximations of the optimal solutions, and its results verified its effectiveness. From the above studies, PSO-based algorithms are effective to gain the optimal solutions, However, they are centralized algorithms, the global information is needed to present the optimal solution.

At present, Unmanned Aerial Vehicle (UAV) detection technology is a relatively mature method [37], accordingly, in this paper, the environmental information after a disaster is assumed to be known in advance. Because of the noise and other communication interference issues, the information is uncertain, and the interval is reasonable as a representation of the data. Further, the data obtained from the environment after a disaster are the survival time of each survivor, which are critical constraints for the robots to perform the rescue mission, as a result, the survival time is treated as an uncertain constraint. Hence, the problem of rescue task allocation with uncertain constraints is considered in this paper.

Description and modeling

Problem description

In this paper, uncertainty refers to the situation where the tasks’ survival time can only be estimated from the detected data, which we consider an interval based on the experience—a constraint when the robots provide emergency support to the survivors.

The ultimate target of the rescue task allocation is maximizing the number of survivors rescued (successful tasks). This paper focuses on solving the problem of uncertainty survival time constraints. For simplicity, the following assumptions are made:

• 1. Robots: all robots are identical. Their batteries are sufficient and their communication is maintained during the rescue process. A robot uses an equal amount of time on completing a rescue mission, once it reaches a survivor’s location.

• 2. Survivors: their survivor times are different but their locations are known in advance and remain unchanged during the rescue process. Each survivor can only be rescued by one robot.

• 3. Rescue route: a robot takes a rescue route in which it can rescue several survivors before returning to its initial position. The rescue routes of the two robots are not overlapped.

• 4. If a robot can reach a survivor before his survival time ends, a successful task is recorded. Otherwise, it is a failed task.

Accordingly, the task allocation problem in this study can be described as follows: After a disaster, the location and survival time of each survivor is acknowledged, each robot needs to construct a route to accomplish the rescue process. Under the time constraints (limited survival time), the robot should maximize the number of overall successful tasks, so that the successfully rescued survivors are maximum.

Problem modeling

Given that N tasks are allocated to M robots, the related notations are used in this research, which are listed in Table 1.

Table 1 The notations in this paper

To formulate the problem mathematically, a set of M rescued routes are represented by ${\text{rs}}_{1} \;{\text{rs}}_{2} \; \cdots \;{\text{rs}}_{i} \; \cdots \;{\text{rs}}_{M}$, where ${\text{rs}}_{i} = ({\text{rs}}_{i1} ,{\text{rs}}_{i2} , \cdots ,{\text{rs}}_{ij} , \cdots ,{\text{rs}}_{{i\left\lceil {N/M} \right\rceil }} )$, and the route formed by all robots’ rescue routes is ${\text{RS = [rs}}_{1} \;{\text{rs}}_{2} \; \cdots \;{\text{rs}}_{i} \; \cdots \;{\text{rs}}_{M} ]^{T}$.

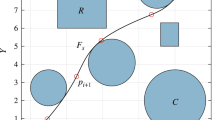
As depicted in Fig. 1, there are 13 survivors and 3 robots in an environment after a disaster, and their rescue route is represented as.

Fig. 1

Rescue environment with 13 survivors and 3 robots

${\text{RS}} = \left[ \begin{gathered} \hfill {\text{rs}}_{1} \\ \hfill {\text{rs}}_{2} \\ \hfill {\text{rs}}_{3} \\ \end{gathered} \right] = \left[ \begin{gathered} 2,6,10,0,0 \hfill \\ 7,4,12,3,9 \hfill \\ 1,11,5,8,13 \hfill \\ \end{gathered} \right]$, where the first robot executes the rescue in the sequential order of $T_{2} \to T_{6} \to T_{10}$, the second robot’s sequential order is $T_{7} \to T_{4} \to T_{12} \to T_{3} \to T_{9}$, and the last route for the third robot is $T_{1} \to T_{11} \to T_{5} \to T_{8} \to T_{13}$, where 0 in RS is to complete the matrix. The routes for all the three robots are depicted in Fig. 1, where the arrows illustrate the direction that robots are heading.

Accordingly, the survivor’s initial survival time is denoted as $\sigma_{0j} = \left[ {\sigma_{j} - \alpha ,\sigma_{j} + \alpha } \right]$. Survival time changes over time [20], when time $t_{ij}$ elapses, the survival time of task $T_{j}$ when the i-th robot $R_{i}$ reaching it, $\sigma_{ij}$, can be represented as follows:

$$ \sigma _{{ij}} = \left[ {\sigma _{{ij}}^{ - } ,\sigma _{{ij}}^{ + } } \right] = \left[ {(\sigma _{i} - \alpha )e^{{ - \gamma t_{{ij}} }} ,(\sigma _{i} + \alpha )e^{{ - \gamma t_{{ij}} }} } \right] $$

(1)

where $\gamma$ is a real number between 0 and 1, based on the result in reference [20]; in this paper $\gamma { = 0}{\text{.037}}$,$t_{ij} = {\text{dis}}_{ij} {/}v_{r}$, $dis_{ij}$ is the total distance that robot $R_{i}$ goes from its initial position to task $T_{j}$.

Each robot performs its respective tasks, and the merit is estimated by the number of successful tasks. Accordingly, each robot needs to construct an optimal route to gain the maximal number of successful tasks (successfully rescued survivors) under the time constraints.

Therefore, the objective in this paper is to maximize the number of successful tasks, under the previous assumptions and notations, the mathematical model is constructed as follows:

$$ {\text{Max}}[F^{ - } (y_{ij} ),F^{ + } (y_{ij} )] $$

(2)

s.t.

$$ \sum\limits_{i = 1}^{M} {y_{0i} = 1,\;\;i = 1,2, \ldots ,N} $$

(3)

$$ \begin{gathered} \sum\limits_{j = 1}^{M} {y_{ij}^{ + } \le 1,\;i = 1,2, \ldots ,N} \hfill \\ \sum\limits_{j = 1}^{M} {y_{ij}^{-\!\!-} \le 1,\;i = 1,2, \ldots ,N} \hfill \\ \end{gathered} $$

(4)

$$ \bigcap {{\text{rs}}_{i} } = \emptyset ,\;i = 1,2, \ldots ,M $$

(5)

$$ y_{ij}^{ + } ,y_{ij}^{ - } \in \{ \;0,\;1\;\} ,\;i,j = 1,2, \ldots ,N,i \ne j $$

(6)

$$ {\text{SN}}_{i} \le N,\;i = 1,2, \ldots ,M $$

(7)

where

$$ \begin{gathered} \begin{array}{*{20}c} {F^{ - } (y_{ij}^{ - } ) = \sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{{SN_{i} }} {y_{ij}^{ - } } } } \\ {F^{ + } (y_{ij}^{ + } ) = \sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{{SN_{i} }} {y_{ij}^{ + } } } } \\ \end{array} ,\begin{array}{*{20}c} {y_{ij}^{ - } {\text{ = sgn(}}\max (0,\sigma_{ij}^{ - } - \Delta ))} \\ {y_{ij}^{ + } {\text{ = sgn(}}\max (0,\sigma_{ij}^{ + } - \Delta ))} \\ \end{array} ,\;{\text{and }}{\text{sgn}} (x) = \left\{ \begin{gathered} \;\,1, \;\, x > 0 \hfill \\ \;0, \;\, x = 0 \hfill \\ - 1, \;\, x < 0 \hfill \\ \end{gathered} \right.. \hfill \\ , \hfill \\ . \hfill \\ \hfill \\ \hfill \\ \end{gathered} $$

Equation (2) maximizes the number of successful tasks. Constraint (3) restricts each robot starting from the initial position, which is a necessity-node for each robot. Constraint (4) ensures that each survivor can be rescued no more than once. Constraint (5) illustrates that the rescue route of any robot cannot be in conflict with another. Constraint (6) limits the rescue result to 0 or 1, where 0 represents failure and 1 is success. Constraint (7) guarantees that the rescued task number is smaller than the original task number.

The mathematical model of the problem is a model with an interval function. In the next section, PSO is employed to optimize this model to generate an optimal or suboptimal rescue assignment to satisfy (2) ~ (8). Significantly, there may exist more than one rescue routes with the same value of the objective function.

The proposed algorithm

The proposed algorithm, TAPSO, is presented in Algorithm 1, where the maximal iteration number is regarded as the stopping criterion. The proposed algorithm consists of three stages. In the first stage, the particles are generated randomly, and a decoding method is presented to estimate the particles, referring to lines 1–4. In the second stage, l_best and g_best are updated to balance the exploitation and exploration, as listed in lines 5–9. Finally, the particles are evolved by updating the formulae of velocity and position in lines 10–13. The algorithm will be elaborated in the following sections.

Furthermore, several improvements are made, primarily with the particle decode method and g_best update strategy. The highlighted lines are the work will be performed in this paper.

The main difference between the canonical PSO and TAPSO is the interval fitness, where the particles’ fitness values are intervals; thus, comparing with exact values, it is more difficult to distinguish which one is better. Moreover, it has an impact on the result of task allocation, so the comparison method between two intervals is essential and difficult. Once the superior particle is chosen, PSO can proceed based on the steps in Algorithm 1.

Canonical PSO

PSO algorithm is inspired by a flock of birds seeking food. It treats each solution of the optimization problem as a bird that flies at a certain velocity in the search space, and its velocity is adjusted dynamically [38,39,40]. The bird is abstracted as a particle without weight and volume, and the location of the i-th particle in all the n dimensions is represented as $X_{i} = (x_{i1} ,x_{i2} , \cdots ,x_{in} )$. Its velocity is represented as $V_{i} = (v_{i1} ,v_{i2} , \cdots ,v_{in} )$, which is the distance to be traveled by the particle from its current position. Each particle owns a fitness value determined by the objective function that needs to be optimized, and a record of one particle’s best location so far is stored, l_best, denoted as $P_{i} = (p_{i1} ,p_{i2} , \cdots ,p_{in} )$. All particles also know their global best location, g_best, denoted as $P_{g} = (p_{g1} ,p_{g2} , \cdots ,p_{gn} )$. The particles determine their further movements based on the experiences of their companions and themselves. Taking the canonical PSO (CPSO) algorithm [40] with inertia weight as an example, the updated formulae of a particle’s velocity and location are as follows:

$$ v_{ij} (t + 1) = wv_{ij} (t) + c_{1} r_{1} (p_{ij} (t) - x_{ij} (t))\;{ + }c_{2} r_{2} (p_{gj} (t) - x_{ij} (t)) $$

(8)

$$ x_{ij} (t + 1) = x_{ij} (t) + v_{ij} (t + 1) $$

(9)

where $w$ is the inertia weight, a user-specified parameter. A large inertia weight influences the particles toward global exploration by searching new areas, whereas a small inertia weight influences the particles toward detailed exploitation in the current search areas. $c_{1}$ and $c_{2}$ are positive constants called acceleration coefficients. Suitable inertia weight and acceleration coefficients can provide a balance between exploration and exploitation. $r_{1}$ and $r_{2}$ are random numbers within the range of [0,1].

Formula (8) is used to update the particle’s velocity based on its previous velocity and the distances between its current position and l_best along with g_best. The particle then flies toward a new position based on Formula (9).

To be applicable to the problem to be solved, a variant PSO, TAPSO, is employed to gain the optimal assignment of rescue task allocation. The details of TAPSO will be elaborated in the following subsections.

Decode method

In TAPSO, one particle represents one solution, which can be decoded as the assigned tasks of all robots, denoted as matrix RS.

As set forth, the rescue route is combined by a series of integers; hence, the particles are coded in integers, and the dimension of the particles is set to N.

Caution should be exercised in this decode process to avoid an infeasible solution. Accordingly, a reference rescue sequence $S_{R}$ is set in this paper, denoted as $S_{R} = (s_{{R{1}}} ,s_{{R{2}}} ,s_{{R{3}}} , \cdots ,s_{Rj} , \cdots ,s_{RN} )$,$S_{R}$ is a sequence of all N tasks without overlap. Assume a particle can be represented as $X_{i} = (x_{i1} ,x_{i2} , \cdots ,x_{ij} , \cdots ,x_{iN} )$, $1 \le i \le N_{p}$, where $N_{p}$ is the number of the particles in the swarm, and the dimension of each robot’s rescue sequence is set to $\left\lceil {N/M} \right\rceil$ so as to assign the tasks averagely to each robot. After decode, we can gain the rescue sequence of the i-th particle,$RS_{i}$, denoted as follows:

$$ {\text{RS}}_{i} = \left[ \begin{gathered} {\text{rs}}_{1}^{i} \hfill \\ {\text{rs}}_{2}^{i} \hfill \\ \cdots \hfill \\ {\text{rs}}_{M}^{i} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {\text{rs}}_{11}^{i} ,{\kern 1pt} \;{\text{rs}}_{12}^{i} , \cdots ,{\kern 1pt} \;{\text{rs}}_{1j}^{i} , \cdots ,\;{\text{rs}}_{{1\left\lceil {N/M} \right\rceil }}^{i} \\ {\text{rs}}_{21}^{i} ,{\kern 1pt} \;{\text{rs}}_{22}^{i} , \cdots ,{\kern 1pt} \;{\text{rs}}_{2j}^{i} , \cdots ,\;{\text{rs}}_{{2\left\lceil {N/M} \right\rceil }}^{i} \\ \quad \quad \quad \quad \quad \quad \;\; \cdots \\ {\text{rs}}_{M1}^{i} ,{\kern 1pt} \;{\text{rs}}_{M2}^{i} , \cdots ,{\kern 1pt} \;{\text{rs}}_{Mj}^{i} , \cdots ,\;{\text{rs}}_{{M\left\lceil {N/M} \right\rceil }}^{i} \\ \end{gathered} \right] $$

Taking Fig. 1 for example, there are 3 robots and 13 tasks, so, N = 13, M = 3,$\left\lceil {N/M} \right\rceil { = }5$. Therefore, assume the i-th particle can be represented as $X_{i} = (x_{i1} ,x_{i2} , \cdots ,x_{ij} , \cdots ,x_{iN} )$${ = (}5,13,22,16,77,9,22,45,68,4,3,12,83{)}$, correspondingly, assume its rescue sequence is:

${\text{RS}}_{i} = \left[ \begin{gathered} rs_{1}^{i} \hfill \\ rs_{2}^{i} \hfill \\ rs_{3}^{i} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} 2,\quad 6,\quad 10,\quad 0,\quad 0 \hfill \\ 7,\quad 4,\quad 12,\quad 3,\quad 9 \hfill \\ 1,\quad 11,\quad 5,\quad 8,\quad 13 \hfill \\ \end{gathered} \right]$.

Then two questions arise: How to decode a particle into a solution of different size? and How to guarantee the rescue sequence contains all tasks and have no overlap tasks among all robots?

Once overlap occurs, which means one task is rescued more than once, and it will create an unfeasible solution. Accordingly, the following decode method is designed to avoid this situation and satisfy the above requirements, which is as illustrated in Algorithm 2.

First, one dimension in particle i, denoted as $x_{ij}$, is selected to perform the mod and add operations; therefore, the obtained result should be an integer number between 1 and N. Next, the task corresponding to the gained integer number is selected and deleted from the reference rescue sequence $S_{R}$, listed in lines 2–4. Thus, we can obtain a sequence of integers by repeating the previous operations N times.

The number of elements in $S_{R}$ is N, they are all N tasks without overlap, the dimension of the particle is N as well. When performing the above decode steps one time, one task can be selected and then deleted from the $S_{R}$, the delete operation guarantee that the decode sequence has no overlap. When performing the above operations N time, all survivors can be selected and deleted from the $S_{R}$, as a result, the number of the tasks in $S_{R}$ decreases one compared with the previous operation. Therefore, when repeat N times, it can guarantee that all N tasks can be selected without overlap, there is hence the decode method can avoid the occurrence of unfeasible solutions, which can meet the requirement in this paper.

From the above operations, a sequence of N integers is gained, further, tasks need to assign to each robot, to assign averagely, the maximum number of tasks assigned to each robot is set to $\left\lceil {N/M} \right\rceil$. Firstly, the distances between the first task and all M robots are calculated, the task is then assigned to the robot with the shortest distance. Next, for the second task, we calculate the distance between it and the remaining (M-1) robots except for the selected one, the robot with the shortest distance is assigned to the task. Repeating the previous procedure M times, we can obtain a rescue sequence. For the remaining tasks, the same operations and a new round are performed, and then we can obtain the rescue routes, as listed in lines 8–13. Figure 2 depicts the assignment procedure for each robot. Overall, the rescue sequence for each robot is gained.

Fig. 2

The assignment procedure for each robot

Position and velocity update method

The particle is decoded as a series of integers, a ceil function is performed on the original position update formula to guarantee the updated position is an integer. Therefore, the particle’s position and velocity update formulae in this paper are listed as follows:

$$\begin{aligned} v_{ij} (t + 1) & = wv_{ij} (t) + c_{1} r_{1} (p_{ij} (t) - x_{ij} (t))\;\\& \quad + c_{2} r_{2} (p_{gj} (t) - x_{ij} (t)) \end{aligned}$$

(11)

$$ x_{ij} (t + 1) = \left\lceil {x_{ij} (t) + v_{ij} (t + 1)} \right\rceil $$

(12)

where ⌈ ⌉ indicates the ceil function.

Comparison between particles

In this paper, l_best and g_best are updated by comparing the fitness values between them and other particles. Because all fitness values are in the form of intervals, how to select the optimal one is essential.

Consequently, the comparison between the two intervals is given in this subsection. To select the optimal one, several criteria are determined; two common-used criteria definitions—the midpoint and distance of an interval—are given. For an interval [a^—, a⁺], its midpoint and distance are $(a^{ - } + a^{ + } )/2$ and $|a^{ + } - a^{ - } |$, respectively.

The principle of intervals comparison is that the larger the midpoint of an interval and the smaller the interval distance, the better the interval is. In this TAPSO algorithm, the particle with a larger midpoint and smaller distance will be elected as the candidates of l_best or g_best. The midpoint relates to the interval’s two bounds: the larger the better—it represents more successful tasks. The interval distance represents the difference between the upper and lower bounds, where a smaller value represents a smaller difference, and the rescued number is significantly more precise.

Assume two particles, $X_{i}$ and $X_{j}$, whose fitness is $[F_{i}^{ - } ,F_{i}^{ + } ]$ and $[F_{j}^{ - } ,F_{j}^{ + } ]$, respectively. The following formula is used to find the better one:

$$ f_{{{\text{max}}}} (X_{i} ,X_{j} ) = \left\{ \begin{gathered} X_{i} ,\left(\frac{{F_{i}^{ - } + F_{i}^{ + } }}{2} > \frac{{F_{j}^{ - } + F_{j}^{ + } }}{2}\right)\quad {\text{or}} \hfill \\ \quad \;\left(\frac{{F_{i}^{ - } + F_{i}^{ + } }}{2} = \frac{{F_{j}^{ - } + F_{j}^{ + } }}{2}\;{\text{and}}\;F_{i}^{ + } - F_{i}^{ - } < F_{j}^{ + } - F_{j}^{ - } \right) \hfill \\ X_{j} ,{\text{otherwirse}} \hfill \\ \end{gathered} \right. $$

(13)

Based on Formula (13), one can well perceive that A is better than B in Fig. 3a; in Fig. 3b, A is better; in Fig. 3c, B is better than A; in Fig. 3d, A is better than B.

Fig. 3

Four cases

l _best and g _best update strategies

During the search, g_best spreads information to particles, guides them to fly, and guarantees the particles find the optimal solution. g_best plays a significant role in the search process; consequently, the selection of g_best is particularly important, as discussed in this section.

Since g_best is selected from l_best, before update g_best, l_best should be determined in advance. If the current particle’s fitness is larger than or equal to l_best, then l_best updates to the current particle, and saves it in a set called the l_best set, which is used to update g_best later. Otherwise, l_best remains unchanged.

g_best is selected from the l_best set, but due to the particular nature of the problem, there may exist two situations while updating g_best: (1) only one l_best l_best in the set; (2) more than one l_best in the set. For these different cases, g_best update method is different and given as follows:

• 1. Only one l_best in the set

  If there is only one l_best in the set, compare it with the current g_best. If its fitness value is larger than or equal to g_best g_best, then, g_best updates to l_best; otherwise g_best stays the same.

• 2. More than one l_best in the set

There may exist three different cases:

Case 1: all l_best s in the set have different fitness values but are smaller than g_best.

In this case, g_best stays the same.

Case 2: all l_best s in the set have different fitness values.

In this case, g_best updates to the l_best with the largest fitness value.

Case 3: more than one l_best l_best have the same fitness, and their fitness values are larger than or equal to g_best.

In this case, l_best s may have different rescue sequences, so how to select one from many l_best s with the same fitness value is a problem that needs to be solved. To guarantee the swarm’s diversity and convergence, g_best updates dynamically.

At the initial stage of the search process, l_best which is equal to or larger than g_best, and having the greatest difference with g_best, is selected as the new g_best to guarantee the diversity of the swarm. In the later phase, the particle that is equal to or larger than g_best, but having the least difference with g_best, is selected as the new g_best to guarantee the swarm’s convergence. This ensures the swarm’s diversity and guarantees the algorithm’s convergence. This update method balances exploitation and exploration more effectively.

The difference between the two particles is defined and estimated by the method presented in Algorithm 3.

Assume the fitness value of l_best is equal to or larger than g_best, in which case g_best should update. g_best is denoted as $g_{{{\text{best}}}} = (p_{g1} ,p_{g2} , \cdots ,p_{gl} , \cdots ,p_{gN} )$. First, select a l_best from the l_best set, denoted as $lbest_{k} = (p_{k1} ,p_{k2} , \cdots ,p_{kj} , \cdots ,p_{iN} )$. After decoding, the rescue route of the current g_best, $S_{{{\text{gbest}}}}$, and one l_best, ${\text{RS}}_{{l{\text{best}}_{k} }}$, are

$$ S_{{g{\text{best}}}} = \left[ \begin{gathered} {\text{rs}}_{11}^{g} ,{\text{rs}}_{12}^{g} , \cdots ,{\text{rs}}_{13}^{g} , \cdots ,{\text{rs}}_{{1\left\lceil {N/M} \right\rceil }}^{g} \\ {\text{rs}}_{21}^{g} ,{\text{rs}}_{22}^{g} , \cdots ,{\text{rs}}_{23}^{g} , \cdots ,{\text{rs}}_{{2\left\lceil {N/M} \right\rceil }}^{g} \\ \cdots \\ \cdots \quad \quad \;\;{\text{rs}}_{ij}^{g} \quad \quad \cdots \\ \cdots \\ {\text{rs}}_{M1}^{g} ,{\text{rs}}_{M2}^{g} , \cdots ,{\text{rs}}_{M3}^{g} , \cdots ,{\text{rs}}_{{M\left\lceil {N/M} \right\rceil }}^{g} \\ \end{gathered} \right] $$

and ${\text{RS}}_{{l{\text{best}}_{k} }} = \left[ \begin{gathered} {\text{rs}}_{11}^{lk} ,{\kern 1pt} \;{\text{rs}}_{12}^{lk} , \cdots ,{\kern 1pt} \;{\text{rs}}_{1j}^{lk} , \cdots ,\;{\text{rs}}_{{1\left\lceil {N/M} \right\rceil }}^{lk} \\ {\text{rs}}_{21}^{lk} ,{\kern 1pt} \;{\text{rs}}_{22}^{lk} , \cdots ,{\kern 1pt} \;{\text{rs}}_{2j}^{lk} , \cdots ,\;{\text{rs}}_{{2\left\lceil {N/M} \right\rceil }}^{lk} \\ \cdots \\ \cdots \quad {\text{rs}}_{pq}^{lk} \quad \cdots \\ \cdots \\ {\text{rs}}_{M1}^{lk} ,{\kern 1pt} \;{\text{rs}}_{M2}^{lk} , \cdots ,{\kern 1pt} \;{\text{rs}}_{Mj}^{lk} , \cdots ,\;{\text{rs}}_{{M\left\lceil {N/M} \right\rceil }}^{lk} \\ \end{gathered} \right]$,respectively. Based on these, the difference between $S_{{g{\text{best}}}}$ and ${\text{RS}}_{{l{\text{best}}_{k} }}$ can be calculated. The particle having the greatest or least difference with g_best is selected as the new g_best based on the algorithm’s running phase, listed in lines 8–13.

The difference calculating method is described as follows: the indexes of the same tasks in both $lbest_{k}$ and g_best are found, and the deviation between the two indexes is calculated. Assuming ${\text{rs}}_{pq}^{lk} = {\text{rs}}_{ij}^{g}$, their index difference (one task’s deviation value), off, is presented as follows:

$$ {\text{index}}({\text{rs}}_{ij}^{g} ) - {\text{index}}({\text{rs}}_{pq}^{lk} ) $$

(14)

where ${\text{index}}({\text{rs}}_{ij}^{g} )$ is the index of ${\text{rs}}_{ij}^{g}$ in $S_{{g{\text{best}}}}$, and ${\text{index}}({\text{rs}}_{pq}^{lk} )$ is the index of ${\text{rs}}_{pq}^{lk}$ in ${\text{RS}}_{{l{\text{best}}_{k} }}$.

Consequently, based on formula (14), the difference between $lbest_{k}$ and g_best is calculated by formula (15):

$$ {\text{offs}} = \sum\limits_{{}}^{N} {|{\text{index}}({\text{rs}}_{ij}^{g} ) - {\text{index}}({\text{rs}}_{pq}^{lk} )|} $$

(15)

Hence, the particle with the maximum or minimum value of offs is selected as g_best based on the algorithm’s running phase, listed in lines 14–15.

The index definition is set as formula (16) shown, from which, any two particles’ difference can be calculated. The difference between formula (16) and normal matrix lays on the additional labels below each element, which are used to mark the sequence number for each element, where $a_{ij}$ denotes the jth task of robot i, $(i - 1)\left\lceil {N/M} \right\rceil + j$ is the sequence number of $a_{ij}$, i.e., ${\text{index}}(a_{ij} )$. Therefore, the sequence number in formula (16) is designed to calculate offs in formula (15).

$$ \left[ \begin{gathered} \quad \underbrace {{a_{11} }}_{1},\;\,\quad \;\quad \;\underbrace {{a_{12} }}_{2},\quad \quad \;\quad \underbrace {{a_{13} }}_{3},\quad \cdots ,\quad \;\underbrace {{a_{{1(\left\lceil {N/M} \right\rceil - 1)}} }}_{{\left\lceil {N/M} \right\rceil - 1}},\;\quad \underbrace {{a_{{1\left\lceil {N/M} \right\rceil }} }}_{{\left\lceil {N/M} \right\rceil }} \hfill \\ \quad \underbrace {{a_{21} }}_{{\left\lceil {N/M} \right\rceil + 1}},\quad \;\underbrace {{a_{22} }}_{{\left\lceil {N/M} \right\rceil + 2}},\quad \underbrace {{a_{23} }}_{{\left\lceil {N/M} \right\rceil + 3}},\quad \cdots ,\quad \underbrace {{a_{{2(\left\lceil {N/M} \right\rceil - 1)}} }}_{{2\left\lceil {N/M} \right\rceil - 1}},\;\quad \underbrace {{a_{{2\left\lceil {N/M} \right\rceil }} }}_{{2\left\lceil {N/M} \right\rceil }} \hfill \\ \quad \quad \quad \quad \; \cdots \quad \quad \quad \underbrace {{a_{ij} }}_{{(i - 1)\left\lceil {N/M} \right\rceil + j}}\quad \quad \quad \cdots \hfill \\ \underbrace {{a_{M1} }}_{{(M - 1)\left\lceil {N/M} \right\rceil + 1}},\underbrace {{a_{M2} }}_{{(M - 1)\left\lceil {N/M} \right\rceil + 2}},\underbrace {{a_{M3} }}_{{(M - 1)\left\lceil {N/M} \right\rceil + 3}}, \cdots ,\underbrace {{a_{{M(\left\lceil {N/M} \right\rceil - 1)}} }}_{{M\left\lceil {N/M} \right\rceil - 1}},\underbrace {{a_{{M\left\lceil {N/M} \right\rceil }} }}_{{M\left\lceil {N/M} \right\rceil }} \hfill \\ \end{gathered} \right] $$

(16)

To better illustrate the process of calculating offs, an example is given as following: suppose $l{\text{best}}_{k}$ and g_best are decodes as $S_{{g{\text{best}}}} = \left[ \begin{gathered} 1,2,3 \\ 4,5,0 \\ \end{gathered} \right]$ and $RS_{{l{\text{best}}_{k} }} = \left[ \begin{gathered} 5,2,0 \\ 4,1,3 \\ \end{gathered} \right]$, offs can be gained by formula (16), hence, $S_{{g{\text{best}}}} = \left[ \begin{gathered} \underbrace {1}_{1},\underbrace {2}_{2},\underbrace {3}_{3} \\ \underbrace {4}_{4},\underbrace {5}_{5},\underbrace {0}_{6} \\ \end{gathered} \right]$ and $RS_{{l{\text{best}}_{k} }} = \left[ \begin{gathered} \underbrace {5}_{1},\underbrace {2}_{2},\underbrace {0}_{3} \\ \underbrace {4}_{4},\underbrace {1}_{5},\underbrace {3}_{6} \\ \end{gathered} \right]$. Firstly, start from task 1, find its indexes in $S_{{g{\text{best}}}}$ and $RS_{{l{\text{best}}_{k} }}$, they are 1 and 5, respectively, and its off is ${|5 - 1| = 4}$; then, task 2, the indexes are 2 and 2, respectively and its off is 0; task 3′s off is $|3 - 6| = 3$; after that, task 4′s off is ${|4 - 4| = 0}$; finally, it’s task 5, and its off is $|5 - 1| = 4$; as a result, ${\text{offs}} = 4 + 0 + 3 + 0 + 4 = 11$.

There are three phases when running the algorithm: prophase, metaphase, and anaphase. The greatest and least differences at the prophase and anaphase can be selected to complete the g_best update, respectively. For the metaphase of the algorithm, the g_best update method is the same as the traditional update method, listed in lines 16–17.

Local search method

In this paper, local search methods are adopted to speed up the convergence to improve the solution’s superiority. Several classic local search methods could apply to the problem of task allocation in [41,42,43]. To find the best solutions and guarantee the algorithm against being trapped in the local optimum, the following local search method is used to improve this approach.

First, randomly select two elements in g_best, $p_{gl}$ and $p_{gk}$, and add a random number to each element;$p_{gl}$ becomes $p_{gl} \cdot (1 + {\text{rand}})$ and $p_{gk}$ becomes $p_{gk} \cdot (1 + {\text{rand}})$. Second, calculate the fitness of the newly generated particles, and once the fitness is larger than g_best, g_best updates to the new one; otherwise, exchange some portions of the two particles depicted in Fig. 4. Then, calculate the fitness of the new particle; if its fitness is better, g_best updates to the new one; otherwise, g_best remains the same. Repeat the above operations until reaching the stopping iterations.

Fig. 4

Exchange operation

Simulations

Parameter setting

To verify the proposed method, several scenarios are presented in this section, and different methods were used to compare with the proposed method. All the methods were run in Matlab R2013a, and parameters were set the same as [44]: population size of 100, evolutionary generation of 400, and $\gamma { = 0}{\text{.037}}$. In all experiments, the world x and y coordinates ranged from -5000 m to 5000 m; the initial survival time was 2000s; the threshold was 100 s; the velocity of the robot was 3.0 m/s.

In this section, 10 different scenarios were generated in different 2-Dimensional planes for 5 trails: 50 cases were tackled to determine the reference sequence. Furthermore, 18 difference cases were generated in different trails to determine the three phases. The contributions of the g_best update method were illustrated by 63 different cases.

Three comparison methods were used to verify the method in this paper. One method is the canonical PSO algorithm (CPSO); other strategies are the same with TAPSO. The second method is the Genetic Algorithm (GA), using the same strategies as TAPSO; the crossover and mutation probability were 0.80 and 0.10. The last comparison method is the consensus-based bundle auction (CBBA), which is based on a market auction strategy [45].

All of the following simulation results are based on 20 independent runs, with the best results highlighted in bold.

Selection of results under different scenarios

The reference rescue sequence,$S_{R}$, influences the decode result; thus, generating $S_{R}$ is essential to exploring a good solution.

In this paper, four different methods of generating $S_{R}$ are presented: random generation method, generated by the order from small to large, generated by survival time from small to large, and generated by distance from near to far. Assume there are N tasks, for the first method, $S_{R}$ is an integer array generated randomly within [1, N], and each integer can only appear once; for the second method, $S_{R} = (1,2,3, \cdots ,N)$, and the other two methods are generated based on the N tasks’ survival time and distance from each task to the robots (in this paper, initial points are same for all robots).

Based on four different generation methods, we executed our TAPSO algorithm respectively, and the results are listed in Table 2.

Table 2 Results and running time for different reference sequences

Table 2 reports that, in different rescue environments, the random generation method performed best, and 57% of cases were better than the other three methods except for the scenarios in which all the four methods obtained the same results. Furthermore, the CPU running time was relatively shorter than the other three methods, where 86% of cases obtained results in the shortest CPU running time. Survival time is the most important factor that affects the rescue results, however, among the 50 different cases, $S_{R}$ generated by survival time only beat its rivals 2 times, and its CPU running time performed best only 4 times. Although $S_{R}$ generation methods based on order and distance ranked in the middle, their CPU running time performed best 2 times, and the best results account for 24% and 22% of all cases, respectively. The random generation method for $S_{R}$ had the highest performance, as a result, in the following simulation, it was used to determine $S_{R}$.

Determining different running phases for TAPSO

In this paper, the search process is divided into three phases: prophase, metaphase, and anaphase. However, what were the corresponding periods?

In this paper, 18 different cases are given to select the three phases, as listed in Table 3. Moreover, eight different scenarios are presented, and the corresponding results are illustrated in Fig. 5.

Table 3 Results and running time for different periods

Fig. 5

Comparison results for different phase settings

In Table 3, the percentage indicates how much each phase accounted for the maximum iterations, and Fig. 5 lists the comparison results for each scenario. For case 9, its lower and upper values of the total number of successful tasks are the largest at the range of [260 272]. Also, the number of best results for case 9 is the largest. Because we are most interested in Case 9, so, prophase, metaphase, and anaphase are set as 30%, 40%, and 30% of the maximum iterations.

The contribution of the g _best update method

To estimate the contribution of the g_best update method, we compare the proposed method with the method that uses the common g_best update method in this section. Seven different scenarios, each with nine different cases, were used to verify the contribution of the g_best update method in TAPSO. Comparison results are listed in Table 4 and Fig. 6.

Table 4 Results and running time for different g_best update methods

Fig. 6

Result differences between the proposed and common g_best update methods for seven different trials

Table 4 reports that TAPSO always out-performed the common g_best update method in terms of the total number of successful tasks in 63 different cases. When the numbers of tasks are greater, the CPU running time of TAPSO made little difference from the common update method; in most instances, the CPU running time of TAPSO is even slightly shorter than the common method, since the new g_best update method can increase the convergence speed. For example, for all 9 cases when 4 robots rescued 56 tasks, the results for the two methods were [186 194] and [179 187], respectively. Their difference was 7; in the rescue situation, one more rescued survivor is of great value, not to mention 7. Furthermore, their difference in CPU running time was 0.06 s, which is extremely small compared with the entire rescue process.

Figure 6 illustrates the differences in results between TAPSO and the common g_best update method for 63 different cases, where the numbers denote the difference between two intervals of the two methods, the blue rectangle is the difference between the lower bounds of two intervals, and the orange rectangle is the difference between the upper bounds. Further, 0 represents two intervals being the same, and the larger of the difference represents the superior of the proposed methods. From Fig. 6, 46% (29 cases) of the solutions were improved from the use of the g_best update method in this paper, while 6.35% of the solutions did not outperform its counterpart, and 46% of the solutions were the same as the common method, especially in some relatively simple scenarios. For example, 30 robots rescued 60 tasks, and 8 cases out of 9 have the same results as the common method. For several complex scenarios, TAPSO performs better. From Table 4 and Fig. 6, we can assert that TAPSO handles certain complex scenarios better, and CPU running time makes little difference for the common g_best update method.

Comparisons with other methods

For the previous scenarios, the tasks can be assigned to the robot averagely. To better verify the proposed method, more complex scenarios should be considered. Furthermore, CPSO, GA and CBBA were employed as the comparison algorithms. For comparability, the parameters are the same for all algorithms, with simulation results listed in Table 5.

Table 5 Comparison results with methods in some more complex scenarios

Based on Table 5, even though the tasks were not assigned equally to each robot, TAPSO still performed the best; CBBA was always the fastest to obtain the results in terms of CPU running time, which is important for rescue, and GA required the longest time to solve the problem, but without obtaining any best result.

We can conclude that all methods except CBBA are relative computationally expensive. Despite this, TAPSO has the highest performance and can be used to solve the task allocation problem effectively. It is slightly time-consuming; however, it is still acceptable.

Conclusion

This study introduced TAPSO, an upgraded version of the well-known algorithm PSO, to address the robot rescue task allocation in uncertain time constraints problem. The principle ideas of the algorithm are establishing an objective function of the maximal number of successful tasks based on the change of the survival time; and building a mathematical model of task allocation. On the other hand, TAPSO improves the decode method and the global best solution update strategy in the original PSO thus increases the effectiveness of the robot's performance in complex scenes.

Several experiments have been conducted in various scenarios where TAPSO was benchmarked against three methods CPSO, GA and CBBA. Among the algorithms, TAPSO was outstanding in identifying optimal solutions. For some non-optimal solutions, CPSO and CBBA show shorter CPU running time than TAPSO, but the differences are minor and do not really affect the overall rescue strategies.

Although TAPSO demonstrated effectiveness and efficiency in handling task allocation with uncertainty time condition, the uncertainty of the robot’s velocity was not considered. In this paper, the velocity was declared as a constant, but it could be a variable. In many real-world scenarios, the velocity of moving robots might vary due to the complexity of the terrain and the accuracy of the detection of survivors’ locations. Like evaluating the allocated time, evaluating a robot’s velocity in different conditions remains a non-trivial work.

In the future, we attempt to address that uncertain velocity issue by integrating another function for the velocity changing over time. For rescuing in extremely complex environments, a modified approach powered by a distributed system will be investigated. Also, some latest technologies in AI and Machine Learning such as Transfer Learning and Reinforcement Learning will be considered to encounter some circumstances when the data about the locations and the survivors are incorrect or insufficient to train the robots.