An interval fuzzy number-based fuzzy collaborative forecasting approach for DRAM yield forecasting

Abstract

Most existing fuzzy collaborative forecasting (FCF) methods adopt type-1 fuzzy numbers to represent fuzzy forecasts. FCF methods based on interval-valued fuzzy numbers (IFNs) are not widely used. However, the inner and outer sections of an IFN-based fuzzy forecast provide meaning information that serves different managerial purposes, which is a desirable feature for a FCF method. This study proposed an IFN-based FCF approach. Unlike existing IFN-based fuzzy association rules or fuzzy inference systems, the IFN-based FCF approach ensures that all actual values fall within the corresponding fuzzy forecasts. In addition, the IFN-based FCF approach optimizes the forecasting precision and accuracy with the outer and inner sections of the aggregation result, respectively. Based on the experimental results, the proposed FCF-II approach surpassed existing methods in forecasting the yield of a dynamic random access memory product.

Introduction

Forecasting is a task that involves a lot of uncertainty and subjective judgments. Fuzzy collaborative forecasting (FCF) methods apply fuzzy logic to model uncertainty and incorporate experts’ subjective judgments. Therefore, FCF methods have great potential for forecasting tasks [9, 26]. Fuzzy association rules [3, 24, 35] and fuzzy inference systems (FISs) [28, 32, 51, 52] are conventional FCF methods that use multiple fuzzy rules from various points of view. However, existing applications of fuzzy association rules and FISs to forecasting have the following problems.

• 1. Most conventional fuzzy association rules and FISs cannot ensure that all actual values are included in the corresponding fuzzy forecasts.

• 2. Most existing fuzzy association rules and FISs fuzzify the target variable to consider uncertainty. However, it will be more effective to fuzzify parameters instead.

• 3. To include actual values in the corresponding fuzzy forecasts, most existing fuzzy association rules and FISs add the same allowance to all forecasts, which is inflexible and imprecise.

To overcome these difficulties, several FCF methods fuzzify parameters to guarantee that actual values are included in the corresponding fuzzy forecasts [6, 8, 34, 53]. In this study, an interval fuzzy number (IFN)-based FCF approach is proposed.

The motives for this study are explained as follows.

• 1. Owing to the existence of extreme cases, fuzzy forecasts generated using an existing FCF method are not sufficiently precise.

• 2. Fuzzy forecasts generated using existing FCF methods are usually type-1 fuzzy numbers [7, 12, 23]. Compared with type-1 fuzzy numbers, IFNs can better consider uncertainty [22]. However, FCF methods that generate IFN-based fuzzy forecasts are not widely used.

• 3. Most existing FCF methods apply fuzzy intersection (FI) to aggregate fuzzy forecasts and defuzzify the aggregation result using a back propagation network (BPN). Whether the same mechanism is applicable to IFN-based fuzzy forecasts should be investigated.

However, we cannot achieve the purpose by simply replacing type-1 fuzzy parameters with IFN-based fuzzy parameters. In an FCF method, experts’ fuzzy forecasts are usually aggregated using fuzzy intersection (FI), which narrows the range of a fuzzy forecast, thereby enhancing forecasting precision [10]. A prerequisite for this is that all actual values are contained in the corresponding fuzzy forecasts [9]. Obviously, the outer section of an IFN-based fuzzy forecast meets this requirement, while the inner section does not, which is problematic if IFN-based fuzzy forecasts by several experts are to be aggregated. To address this issue, in the proposed methodology, the inner and outer sections of experts’ fuzzy forecasts are aggregated and defuzzified separately, thereby providing meaningful information that serves different managerial purposes.

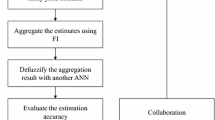
In the proposed IFN-based FCF approach, experts apply various fuzzy forecasting methods to generate diversified IFN-based fuzzy forecasts. To this end, a mixed binary nonlinear programming (MBNLP) problem is solved. Subsequently, FI is applied to aggregate all experts’ IFN-based fuzzy forecasts. Specifically, the inner and outer sections of IFN-based fuzzy forecasts are aggregated separately. Finally, two BPNs are constructed to defuzzify the aggregation results of the inner and outer sections, respectively. The originality of the proposed methodology resides in the following:

• Owing to the existence of extreme cases, a fuzzy yield forecast generated using an existing FCF method usually has a wide range. In contrast, the proposed methodology is able to narrow the range of a fuzzy yield forecast by excluding extreme cases.

• In existing FCF methods, experts’ fuzzy yield forecasts are usually aggregated into a single value. In contrast, the proposed methodology aggregates the inner and upper sections of experts’ fuzzy yield forecasts into two values for optimizing forecast precision and accuracy, respectively.

The contributions of this study include

• the development of a FCF method based on IFNs for collaborative yield forecasting,

• the further improvement of forecasting precision by excluding extreme cases, and

• two systematic mechanisms for aggregating the inner and upper sections of experts’ fuzzy yield forecasts, respectively.

The remainder of this paper is organized as follows. Section 2 discusses relevant previous studies. Section 3 introduces the proposed IFN-based FCF approach. Section 4 details the application of the IFN-based FCF approach to forecast the yield of a dynamic random access memory (DRAM) product. Finally, Sect. 5 concludes this study and provides some directions for future research.

Literature review

Fuzzy association rules and FISs are prevalent FCF methods. Fuzzy association rules are an important topic in data mining, and have been applied to pattern recognition and forecasting [3, 24, 35]. In extracting fuzzy association rules, the average satisfaction levels are compared. As a result, a fuzzy association rule may not be applicable to some historical data. A number of methods for extracting fuzzy association rules based on IFNs have been proposed [14, 36]. For example, Zarandi et al. [54] established an expert system based on IFN-based fuzzy association rules for forecasting stock prices. In an IFN-based fuzzy association rule, the lower membership function of each premise was derived by shifting the location of the upper membership function. Therefore, the lower and upper membership functions of each premise had an identical shape. Antonelli et al. [1] applied IFN-based fuzzy association rules to the classification of financial time series. Each premise in a fuzzy association rule was represented with an IFN with lower membership function positioned in the middle of the upper membership function. As a result, only the upper membership function of a premise needed to be considered in satisfying the support and confidence. Obviously, in most existing IFN-based fuzzy association rules, the lower and upper membership functions of a premise are heavily dependent.

Soto et al. [41] constructed an adaptive network-based FIS (ANFIS) to forecast a time series, in which both type-1 and type-2 fuzzy numbers were adopted. Both stochastic models and fuzzy sets are effective means of tackling uncertainty. From this point of view, Zhou et al. [57] incorporated IFNs into a Markov chain for a multi-stage interactive group decision-making task. Muhuri et al. [29] proposed an IFN-based multiobjective reliability redundancy allocation model. The model was converted into a crisp problem and solved using the nondominated sorting genetic algorithm II. Tian and Cao [43] proposed a fuzzy mixed integer programming model for a multimodal transportation problem, in which both transportation time and demand were estimated with IFNs. Soto et al. [42] constructed a fuzzy neural network ensemble to forecast a time series. Parameters in the fuzzy neural networks were given in interval type-2 fuzzy numbers, for which genetic algorithms and particle swarm optimization (PSO) algorithms were applied to optimize the membership functions. Wang et al. [48] applied the extended fuzzy-preference relation for IFNs to rank the priorities of factors critical to the cruise industry in Shanghai. The approach was similar to the hybrid of fuzzy extent analysis (FEA) and the technique for order preference by similarity to ideal solution (TOPSIS). In Wang [50], the weights of criteria for a quality function deployment (QFD) process were given in IFNs. Based on IFN-based weights, fuzzy weighted average (FWA) was applied to compare the performances of product designs. Efe [19] evaluated the quality of an educational institution website using fuzzy TOPSIS, in which all parameters were given in or approximated with IFNs. Compared with FWA, fuzzy TOPSIS was more sensitive to changes in the distances between an alternative and two reference points.

FISs have been widely applied to system control and forecasting. For example, Ying and Pan [52] constructed an ANFIS to forecast the regional electricity load in Taiwan. Lohani et al. [28] established a modified Takagi, Sugeno, and Kang (TSK) FIS to forecast the possibility of a flood in terms of hourly rainfall and river flow. Osório et al. [32] constructed an ANFIS to forecast wind power, in which mutual information, wavelet transformation, and evolutionary particle swarm optimization were applied to choose relevant features, preprocess the inputs, and tune the ANFIS configuration, respectively. Yang et al. [51] established a FIS to forecast several time series. The membership functions of premises in fuzzy inference rules were dynamic. In addition, a constant allowance was added to each forecast to consider uncertainty, which was imprecise. In the view of Sahin et al. [37, 38], the model of the forecasting error could be used to establish the lower and upper bounds, based on which fuzzy linguistic terms for forecasts were defined. Carvalho and Costa [4] proposed a fuzzy time series method, in which the range of a time series was divided into a number of fuzzy intervals. Then, the relationships between successive fuzzy intervals, rather than those between original values, were fitted as rules. To aggregate the consequences of rules, the weight of a rule was set to the maximal satisfaction level in fitting historical data. However, in this way, it was impossible to guarantee that all actual values were included in in the corresponding aggregation results.

When experts’ fuzzy forecasts may not contain actual values, a less risky way to aggregate experts’ fuzzy forecasts is to apply the fuzzy union operator (or s-norm), which is a prevalent treatment in FIS studies [25, 39, 49]. However, the range of possible values was widened.

Proposed methodology

Before introducing the details of the proposed methodology, some concepts of IFNs are described as follows.

Preliminary

First of all, the definition of an IFN is given.

Definition 1

(Interval fuzzy number, IFN) An IFN $\tilde{A}$ is a subset of real numbers R, which can be defined as a set of ordered pairs $\tilde{A}$ = {(x, $\mu_{{\tilde{A}}} (x)$)| x ∈ R}, where $\mu_{{\tilde{A}}} (x)$: R → [0, 1] is the interval-valued membership function of $\tilde{A}$ [18].

An IFN $\tilde{A}$ has two membership functions, namely the lower membership function (LMF) [$\mu_{{\tilde{A}_{l} }} (x)$] and upper membership function (UMF) [$\mu_{{\tilde{A}_{u} }} (x)$], such that $\mu_{{\tilde{A}}} (x) = [\mu_{{\tilde{A}_{l} }} (x),\;\mu_{{\tilde{A}_{u} }} (x)]$. An IFN is a special case of type-II fuzzy sets [2].

Definition 2

The inner support, outer support, and core of an IFN $\tilde{A}$ are defined respectively as

$$ i{\text{supp}}_{{\tilde{A}}} \, = \,\{ x\; \in \;{\mathbf{R}}|\mu_{{\tilde{A}_{l} }} (x)|\; > \,0\} $$

(1)

$$ o{\text{supp}}_{{\tilde{A}}} \, = \,\{ x\; \in \;{\mathbf{R}}|\;\mu_{{\tilde{A}_{u} }} (x)\;|\, > \,0\} $$

(2)

$$ {\text{core}}_{{\tilde{A}}} = \{ x \in {\mathbf{R}}|\mu_{{\tilde{A}_{l} }} (x) = \mu_{{\tilde{A}_{u} }} (x) = 1\} $$

(3)

Definition 3

(Interval-valued triangular fuzzy number, ITFN) When the LMF and UMF of an IFN $\tilde{A}$ are triangular functions, the IFN is called an interval-valued triangular fuzzy number (ITFN) with the following membership functions:

$$ \mu_{{\tilde{A}_{l} }} (x) = \left\{ {\begin{array}{*{20}l} {\frac{{x - A_{l1} }}{{A_{2} - A_{l1} }}} & {\text{if}} & {A_{l1} \leq sx < A_{2} } \\ {\frac{{A_{l3} - x}}{{A_{l3} - A_{2} }}} & {\text{if}} & {A_{2} \leq sx < A_{l3} } \\ 0 & {\text{otherwise}} & \\ \end{array} } \right. $$

(4)

$$ \mu_{{\tilde{A}_{u} }} (x) = \left\{ {\begin{array}{*{20}l} {\frac{{x - A_{u1} }}{{A_{2} - A_{u1} }}} & {\text{if}} & {A_{u1} \leq sx < A_{2} } \\ {\frac{{A_{u3} - x}}{{A_{u3} - A_{2} }}} & {\text{if}} & {A_{2} \leq sx < A_{u3} } \\ 0 & {\text{otherwise}} & \\ \end{array} } \right. $$

(5)

$\tilde{A}$ can be denoted as (($A_{l1} ,\;A_{2} ,\;A_{l3}$), ($A_{u1} ,\;A_{2} ,\;A_{u3}$)) or ($A_{u1} ,\;A_{l1} ,\;A_{2} ,\;A_{l3} ,\;A_{u3}$).

Definition 4

(α cut of an interval fuzzy number) The α cut of an interval fuzzy number $\tilde{A}$ is

$$ A(\alpha ) = [[A_{u}^{L} (\alpha ),\;A_{l}^{L} (\alpha )],\;[A_{l}^{R} (\alpha ),\;A_{u}^{R} (\alpha )]) $$

(6)

Definition 5

(Fuzzy intersection of two fuzzy numbers) The FI of two fuzzy numbers $\tilde{A}$ and $\tilde{B}$ is a fuzzy number given by

$$ \widetilde{FI}(\tilde{A},\;\tilde{B}) = \tilde{A} \cap \tilde{B} $$

(7)

The membership function of $\widetilde{FI}$ can be derived by applying the minimum t-norm as

$$ \mu_{{\widetilde{FI}}} (x) = \hbox{min} (\mu_{{\tilde{A}}} (x),\;\mu_{{\tilde{B}}} (x)) $$

(8)

In the proposed methodology, the FI of experts’ IFN-based fuzzy forecasts is obtained, for which the following theorems are helpful.

Theorem 1

(α cut of the fuzzy intersection of fuzzy numbers) The α cut of the FI of two fuzzy numbers $\tilde{A}$ and $\tilde{B}$ can be derived from those of the two fuzzy numbers as [5]

$$ \begin{aligned} {\text{FI}}(\alpha ) & = [{\text{FI}}^{L} (\alpha ),\;{\text{FI}}^{R} (\alpha )] \\ & = [\hbox{max} (A^{L} (\alpha ),\;B^{L} (\alpha )),\;\hbox{min} (A^{R} (\alpha ),\;B^{R} (\alpha ))] \\ \end{aligned} $$

(9)

Theorem 2

(Fuzzy intersection of two interval fuzzy numbers) The FI of two IFNs $\tilde{A}$ and $\tilde{B}$ is an IFN given by

$$ \widetilde{FI}(\tilde{A},\;\tilde{B}) = \tilde{A} \cap \tilde{B} $$

(10)

with the following membership function

$$ \mu_{{\widetilde{FI}}} (x) = [\hbox{min} (\mu_{{\tilde{A}_{l} }} (x),\;\mu_{{\tilde{B}_{l} }} (x)),\;\hbox{min} (\mu_{{\tilde{A}_{u} }} (x),\;\mu_{{\tilde{B}_{u} }} (x))] $$

(11)

Proof

According to the arithmetic for interval numbers:

$$ \begin{aligned} \mu_{{\widetilde{FI}}} (x) & = \hbox{min} (\mu_{{\tilde{A}}} (x),\;\mu_{{\tilde{B}}} (x)) \\ & = \hbox{min} ([\mu_{{\tilde{A}_{l} }} (x),\;\mu_{{\tilde{A}_{u} }} (x)],\;[\mu_{{\tilde{B}_{l} }} (x),\;\mu_{{\tilde{B}_{u} }} (x)]) \\ & = [\hbox{min} (\mu_{{\tilde{A}_{l} }} (x),\;\mu_{{\tilde{B}_{l} }} (x)),\;\hbox{min} (\mu_{{\tilde{A}_{u} }} (x),\;\mu_{{\tilde{B}_{u} }} (x))] \\ \end{aligned} $$

(12)

Theorem 2 is proved.

Theorem 3

(α cut of the fuzzy intersection of interval fuzzy numbers) The α cut of the FI of two IFNs $\tilde{A}$ and $\tilde{B}$ can be derived as:

$$ \begin{aligned} FI(\alpha ) = & [[{\text{max}}(A_{u}^{L} (\alpha ),\;B_{u}^{L} (\alpha )),\;{\text{max}}(A_{l}^{L} (\alpha ),\;B_{l}^{L} (\alpha ))], \\ & [{\text{min}}(A_{l}^{R} (\alpha ),\;B_{l}^{R} (\alpha )),\;{\text{min}}(A_{u}^{R} (\alpha ),\;B_{u}^{R} (\alpha ))]] \\ \end{aligned} $$

(13)

Proof

According to Theorem 2,

$$ \begin{aligned} FI(\alpha ) & = [FI^{L} (\alpha ),\;FI^{R} (\alpha )] \\ & = [\hbox{max} (A^{L} (\alpha ),\;B^{L} (\alpha )),\;\hbox{min} (A^{R} (\alpha ),\;B^{R} (\alpha ))] \\ & = [\hbox{max} ([A_{u}^{L} (\alpha ),\;A_{l}^{L} (\alpha )],\;[B_{u}^{L} (\alpha ),\;B_{l}^{L} (\alpha )]),\;\hbox{min} ([A_{l}^{R} (\alpha ),\;A_{u}^{R} (\alpha )],\;[B_{l}^{R} (\alpha ),\;B_{u}^{R} (\alpha )])] \\ & = [[\hbox{max} (A_{u}^{L} (\alpha ),\;B_{u}^{L} (\alpha )),\;\hbox{max} (A_{l}^{L} (\alpha ),\;B_{l}^{L} (\alpha ))],\;[\hbox{min} (A_{l}^{R} (\alpha ),\;B_{l}^{R} (\alpha )),\;\hbox{min} (A_{u}^{R} (\alpha ),\;B_{u}^{R} (\alpha ))]] \\ \end{aligned} $$

(14)

Theorem 3 is proved.

Procedure for implementing the proposed methodology

The procedure for implementing the proposed methodology comprises the following steps:

Step 1 Each expert applies an IFN-based fuzzy forecasting method to generate a fuzzy yield forecast.

Step 2 Apply the FI operator to aggregate the inner and outer sections of experts’ IFN-based fuzzy yield forecasts.

Step 3 Construct BPNs to defuzzify the aggregation results.

Step 4 Evaluate the forecasting performance.

Step 5 If the forecasting performance is satisfactory, then proceed to Step 8; otherwise, proceed to Step 6.

Step 6 Experts modify their IFN-based fuzzy yield forecasts.

Step 7 Each expert returns to Step 2.

Step 8 End.

IFN-based fuzzy forecasting method

In the proposed methodology, each expert applies the following IFN-based fuzzy forecasting method to generate a fuzzy forecast $\tilde{y}_{j}$ to forecast y by considering decision variables $\{ x_{i} \}$:

$$ \tilde{y}_{j} = \tilde{a}_{0} ( + )\sum\limits_{i = 1}^{m} {\tilde{a}_{i} x_{ji} } $$

(15)

where (+) denotes fuzzy addition. However, the values of fuzzy parameters in the IFN-based fuzzy forecasting method assigned by different experts are not the same. As a result, experts’ fuzzy forecasts are different and need to be aggregated.

To derive the values of IFN-based fuzzy parameters in (15), Chen and Wang [13] optimized the following MBNLP model.

(MBNLP model)

$$ \begin{aligned} {\text{Min}}\;\;Z_{1} = & \sum\limits_{{j = 1}}^{n} {(a_{{0u3}} + \sum\limits_{{i = 1}}^{m} {a_{{iu3}} x_{{ji}} } - a_{{0u1}} - \sum\limits_{{i = 1}}^{m} {a_{{iu1}} x_{{ji}} } } + \\ & a_{{0l3}} + \sum\limits_{{i = 1}}^{m} {a_{{il3}} x_{{ji}} } - a_{{0l1}} - \sum\limits_{{i = 1}}^{m} {a_{{il1}} x_{{ji}} } ) \\ \end{aligned} $$

(16)

subject to

$$ y_{j} \ge a_{0u1} + \sum\limits_{i = 1}^{m} {a_{iu1} x_{ji} } ;j\, = \, 1\,\sim \,n $$

(17)

$$ y_{j} \le a_{0u3} + \sum\limits_{i = 1}^{m} {a_{iu3} x_{ji} } ;j\, = \, 1\,\sim \,n $$

(18)

$$ \frac{{\sum\nolimits_{j = 1}^{n} {X_{j1} X_{j2} } }}{n} \ge (1 - p) $$

(19)

$$ y_{j} \ge X_{j1} \left( {a_{0l1} + \sum\limits_{i = 1}^{m} {a_{il1} x_{ji} } } \right);j\, = \, 1\,\sim \,n $$

(20)

$$ y_{j} \le X_{j2} \left( {a_{0l3} + \sum\limits_{i = 1}^{m} {a_{il3} x_{ji} } } \right);j\, = \, 1\,\sim \,n $$

(21)

$$ X_{j1} ,\;X_{j2} \in \{ 0,\;1\} ;j\, = \, 1\,\sim \,n $$

(22)

$$ a_{0u1} \le a_{0l1} \le a_{02} \le a_{0l3} \le a_{0u3} $$

(23)

$$ a_{iu1} \le a_{il1} \le a_{i2} \le a_{il3} \le a_{iu3} ;i\, = \, 1\,\sim \,m $$

(24)

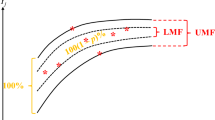
The objective function (16) minimizes the sum of the widths of IFN-based fuzzy forecasts by considering both LMF and UMF. Constraints (17) and (18) ensure that all actual values fall within the corresponding upper fuzzy forecasts. In contrast, only 100(1–p)% of actual values fall within the corresponding lower fuzzy forecasts, according to Constraint (19), which is illustrated in Fig. 1. In Constraints (20) and (21), $X_{j1}$ and $X_{j 2}$ are two state variables. When $X_{j1} \, = \, 1$, an actual value is higher than the lower bound of the lower fuzzy forecast; when $X_{j2} \, = \, 1$, an actual value is lower than the upper bound of the lower fuzzy forecast. Constraints (23) and (24) define the sequences of the endpoints of ITFNs.

Fig. 1

Inclusion intervals

To generate diversified fuzzy forecasts, objective function (16) is modified as

$$ \begin{aligned} {\text{Min}}\;\;Z_{2} = & w_{1} \sum\limits_{{j = 1}}^{n} {\left( {a_{{0u3}} + \sum\limits_{{i = 1}}^{m} {a_{{iu3}} x_{{ji}} } - a_{{0u1}} - \sum\limits_{{i = 1}}^{m} {a_{{iu1}} x_{{ji}} } } \right)^{o} } \\ & + w_{2} \sum\limits_{{j = 1}}^{n} {\left( {a_{{0l3}} + \sum\limits_{{i = 1}}^{m} {a_{{il3}} x_{{ji}} } - a_{{0l1}} - \sum\limits_{{i = 1}}^{m} {a_{{il1}} x_{{ji}} } } \right)^{o} } \\ \end{aligned} $$

(25)

where $w_{1}$ and $w_{2}$ are weights assigned to the sum of upper ranges and the sum of lower ranges, respectively. $w_{1} + w_{2} = 1$. The value of o reflects the sensitivity of an expert to the uncertainty of a fuzzy forecast: from small (not sensitive) to large (very sensitive) [46]. If o is a large value, it becomes difficult to solve the MBNLP problem [47]. For this reason, Chen and Wang [12] advised to choose the value of o from (0, 4].

In the proposed methodology, experts assign different values to o, p, $w_{1}$, and $w_{2}$ to generate diversified fuzzy forecasts. The values of parameters assigned by expert k are denoted with o(k), p(k), $w_{1} (k)$, and $w_{2} (k)$. The fuzzy forecast by expert k is indicated with $\tilde{y}_{j} (k)$.

FI for aggregating experts’ fuzzy forecasts

FI is applied to aggregate experts’ fuzzy forecasts [10, 27]:

$$ \widetilde{FI}(\{ \tilde{y}_{j} (k)\} ) = \mathop \cap \limits_{j} \tilde{y}_{j} (k) $$

(26)

According to Theorem 2,

$$ \mu_{{\widetilde{FI}}} (x) = [\mathop {\hbox{min} }\limits_{k} (\mu_{{\tilde{y}_{jl} (k)}} (x)),\;\mathop {\hbox{min} }\limits_{k} (\mu_{{\tilde{y}_{ju} (k)}} (x))] $$

(27)

An example, showing two experts’ IFN-based fuzzy forecasts, is given in Fig. 2. The FI results is illustrated in Fig. 3.

Fig. 2

An illustrative example

Fig. 3

FI result

From Figs. 2 and 3, the following phenomena can be observed:

• 1. Both the lower and upper membership functions of the FI result are polygonal functions.

• 2. The lower and upper membership functions of the FI result can be of different shapes, which is the distinct nature of the proposed methodology from existing methods.

• 3. The outer supports of all experts’ fuzzy forecasts include an actual value. The outer support of the FI result also includes the actual value, at least for the training (or learned) data.

• 4. It is highly possible that the inner supports of all experts’ fuzzy forecasts include an actual value. It is also possible for the inner support of the FI result to include the actual value. However, the possibility declines as more experts’ fuzzy forecasts are aggregated.

BPNs for defuzzifying the aggregation results

Two BPNs are constructed to defuzzify the aggregation results with the following configuration:

• 1. Input: inputs to the first BPN include each corner’s value and membership of the lower membership function. Inputs to the second BPN are those of the upper membership function.

• 2. A single hidden layer: the number of nodes in the hidden layer is the same as that of inputs.

• 3. Output: the output from the first BPN is the most possible forecast. The output from the second BPN is the forecast that considers extreme cases.

• 4. Training algorithm: the gradient descent (GD) algorithm is applied to train the BPNs to avoid overfitting [45].

• 5. Convergence criteria: the training process stops when the sum of squared error (SSE) falls below a pre-specified threshold,

$$ {\text{SSE}} = \sum\limits_{j = 1}^{n} {(y_{j} - o_{j} )^{2} } $$

(28)

or a maximal number of epochs have been run.

Application to a real case

The proposed methodology has been applied to forecast the yield of a DRAM product to evaluate its effectiveness. The case, including the yield data of the DRAM product within ten periods, was first investigated by Chen and Wang [11]. The yield data were decomposed into two parts: data of the first six periods for building the models, and the remaining data for evaluating forecasting performance.

Three experts applied the fuzzy forecasting method to forecast the yield of the DRAM product. The parametric values assigned by experts are summarized in Table 1. The MBNLP problems were coded in Lingo and solved using a branch-and-bound algorithm on a PC with i7-7700 CPU 3.6 GHz and 8 GB RAM. The execution time was less than 3 s. Experts’ forecasting results are shown in Fig. 4.

Table 1 The settings of parametric values by experts

Fig. 4

Experts’ forecasting results

FI was applied to aggregate experts’ fuzzy forecasts. Taking period 10 as an example, the FI result is illustrated in Fig. 5. The aggregation results at all periods are summarized in Fig. 6. Most actual values in test data fell within the inner and outer supports of the aggregation results. Since an inner support was much narrower than the outer support, the range of possible values by considering the inner support was more precise.

Fig. 5

FI result at period 7

Fig. 6

Aggregation results at all periods

Subsequently, the aggregation results were defuzzified using two BPNs. For this purpose, first, the corners of the aggregation result at each period were found out for the inner and outer sections, respectively. The results are summarized in Tables 2 and 3. The inner section of the aggregation result had at most three corners, while the outer section had at most four corners. As a result, the numbers of inputs to the two BPN defuzzifiers were set to six and eight, respectively. The number of nodes in the hidden layer was the same with that of inputs.

Table 2 Corners of the inner section of the aggregation result at each period

Table 3 Corners of the outer section of the aggregation result at each period

BPNs were trained using the GD algorithm to prevent overfitting. The convergence criteria were established as follows:

• 1. SSE < 10⁻⁴;

• 2. 500 epochs have been run.

The BPN defuzzifiers were implemented using the neural network toolbox of MATLAB 2017 on a PC with i7-7700 CPU 3.6 GHz and 8 GB RAM. The execution time was less than 1 s. The defuzzification results are shown in Figs. 7 and 8. A comparison of the defuzzification results using the two BPNs is provided in Fig. 9.

Fig. 7

Defuzzification result for the inner section of the aggregation result

Fig. 8

Defuzzification result for the outer section of the aggregation result

Fig. 9

Comparison of the defuzzification results by the two BPNs

The forecasting accuracy of the proposed methodology to test data was evaluated in terms of mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean-squared error (RMSE):

$$ {\text{MAE}} = \frac{{\sum\nolimits_{j = 1}^{n} {|y_{j} - \hat{y}_{j} |} }}{n}, $$

(29)

$$ {\text{MAPE}} = \frac{{\sum\nolimits_{j = 1}^{n} {\frac{{|y_{j} - \hat{y}_{j} |}}{{y_{j} }}} }}{n} \cdot 100\% , $$

(30)

$$ {\text{RMSE}} = \sqrt {\frac{{\sum\nolimits_{j = 1}^{n} {(y_{j} - \hat{y}_{j} )^{2} } }}{n}} . $$

(31)

Table 4 summarizes the results.

Table 4 Forecasting accuracy achieved using the proposed methodology (for test data)

For comparison, experts’ IFN-based fuzzy yield forecasts were defuzzified using an extension of the center-of-gravity (COG) method [15]:

$$ D(\tilde{y}_{j} ) = \frac{{y_{jl1} + y_{jl2} + y_{jl3} + y_{ju1} + y_{ju2} + y_{ju3} }}{6} $$

(32)

Then, forecasting performance without collaboration was evaluated for each expert. The results are summarized in Table 5.

Table 5 Experts’ forecasting performances without collaboration

According to the experimental results,

• 1. Obviously, forecasting performance was improved better after experts collaborated.

• 2. The most significant advantage of the proposed methodology over experts’ original fuzzy forecasts was in reducing MAE, which was up to 57% on average.

• 3. It was noteworthy that after defuzzification the result might exceed the range of the inner section.

• 4. The outer section of the aggregation result had more corners, which increased the degree of freedom in defuzzifying the aggregation result, thereby contributing to higher forecasting accuracy.

• 5. By contrast, the inner section of the aggregation result effectively narrowed the range of possible values and enhanced forecasting precision by up to 62%.

• 6. Table 6 shows the results from a paired t test to evaluate whether the advantage of the proposed methodology over existing methods was significant, with

Table 6 Paired t test results for improved forecasting accuracy

• H₀: The forecasting accuracy of the proposed methodology in terms of absolute error is the same as that of the existing method;

• H₁: The forecasting accuracy of the proposed methodology in terms of absolute error is more effective than that of the existing method.

Forecasting accuracy using the proposed methodology was significantly improved (at the 95% level) when compared with existing methods.

• 7. To elaborate the effectiveness of the proposed methodology, it was applied to another case containing the yield data of another DRAM product within fifteen periods. The yield data of the first ten periods were used to build the model, while the remaining was reserved for evaluating forecasting performance. In this case, three experts fulfilled the yield forecasting task collaboratively. Firstly, experts’ fuzzy yield forecasts are shown in Fig. 10. Subsequently, FI was applied to aggregate experts’ fuzzy yield forecasts. The results are summarized in Fig. 11. After defuzzifying the aggregation results using two BPNs, the representative yield forecasts were obtained, as shown in Fig. 12. Then, the forecasting performance using the proposed methodology was evaluated. The results are provided in Table 7. Obviously, the proposed methodology achieved high forecasting accuracy.

Fig. 10

Fuzzy yield forecasts by the experts

Fig. 11

Aggregation results

Fig. 12

Defuzzification results

Table 7 Forecasting performance using the proposed methodology

Conclusions

An IFN-based FCF approach was proposed in this study. In the proposed methodology, each expert solves a MBNLP problem to generate IFN-based fuzzy forecasts. Subsequently, FI is applied to aggregate the inner and outer sections of IFN-based fuzzy forecasts. Finally, two BPNs are constructed to defuzzify the aggregation results. Unlike existing IFN-based fuzzy association rules or FISs, the IFN-based FCF approach guarantees that all actual values fall within the corresponding fuzzy forecasts. In addition, compared with existing FCF methods, the IFN-based FCF approach improves forecasting precision and accuracy by considering the inner and outer sections of the aggregation result, respectively.

After applying the IFN-based FCF approach to forecast the yield of a DRAM product, the following conclusions are made:

• 1. The experimental results confirmed the effectiveness of experts’ collaboration in improving forecasting performance.

• 2. The inner and outer sections of the aggregation result could be considered in improving the forecasting precision and accuracy, respectively.

• 3. A compromise way was, therefore, to estimate the range of possible values by considering the inner section of the aggregation result, and to derive the most possible value based on the outer section.

In this study, experts solved the same MBNLP problem, but with different parametric values, to generate IFN-based fuzzy forecasts. In future studies, different MBNLP problems can be formulated to further diversify IFN-based fuzzy forecasts. In addition, FCF methods based on interval-valued intuitionistic fuzzy numbers [31, 44], hesitant interval-valued fuzzy numbers [55], and interval-valued pythagorean fuzzy numbers [20, 33] can be proposed as well. Further, an advanced algorithm needs to be designed to further enhance the efficiency of solving the MBNLP problem [e.g., PSO algorithms [16, 30, 40], ant colony optimization (ACO) algorithms [17, 21, 56].