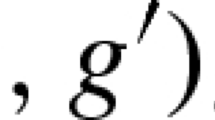Twisted Neumann–Zagier matrices

Abstract

The Neumann–Zagier matrices of an ideal triangulation are integer matrices with symplectic properties whose entries encode the number of tetrahedra that wind around each edge of the triangulation. They can be used as input data for the construction of a number of quantum invariants that include the loop invariants, the 3D-index and state-integrals. We define a twisted version of Neumann–Zagier matrices, describe their symplectic properties, and show how to compute them from the combinatorics of an ideal triangulation. As a sample application, we use them to define a twisted version of the 1-loop invariant (a topological invariant) which determines the 1-loop invariant of the cyclic covers of a hyperbolic knot complement, and conjecturally is equal to the adjoint twisted Alexander polynomial.

1 Introduction

1.1 Motivation

Ideal triangulations of 3-manifolds with torus boundary components were introduced by Thurston [26] as a convenient way to describe and effectively compute [2] complete hyperbolic structures on 3-manifolds. To do so, one assigns a complex number different from 0 or 1 to each tetrahedron and a polynomial equation around each edge of the triangulation. These so-called gluing equations have special shape that can be described by two matrices $\textbf{A}$ and $\textbf{B}$ (with rows and columns indexed by the edges and by the tetrahedra, respectively) whose entries describe the number of times (but not the order by which) tetrahedra wind around an edge. One of the main discoveries of Neumann–Zagier is that the matrix $(\textbf{A} | \textbf{B})$ becomes, after some minor modifications, the upper part of a symplectic matrix with integer entries [22]. The symplectic property of the NZ matrices and of the corresponding gluing equations define a linear symplectic structure on a vector space whose quantization leads to a plethora of quantum invariants that include the loop invariants of Dimofte and the first author [6, 8], the 3D-index in both the original formulation of Dimofte-Gaiotto-Gukov [9, 10] as well as the state-integral formulation of Kashaev and the first author [13] and Kashaev–Luo–Vartanov state-integral [1, 20]. All of those invariants are defined using the NZ matrices of a suitable ideal triangulation, and their topological invariance follows by proving that they are unchanged under Pachner 2–3 moves.

Our original motivation was to study the behavior of the loop invariants of [6] under cyclic covers. Since the latter are defined in terms of NZ data of an ideal triangulation, we were led to study the behavior of the NZ matrices under cyclic covers. By elementary topology, each tetrahedron of an ideal triangulation lifts to n tetrahedra in the n-fold cyclic cover, and lifting all the way to the infinite cyclic cover leads to the notion of NZ matrices which we can call equivariant or twisted (as is common in algebraic and geometric topology) or t-deformed (as is common in physics). We will use the term “twisted”, and keep in mind that the variable t below encodes topological information of cyclic covers.

Said differently, as the triangulation of the cyclic cover unfolds, so do its edges and the tetrahedra that wind around them. This is the content of the twisted NZ matrices. How can this elementary idea be non-trivial or interesting?

It turns out that the twisted NZ matrices have twisted symplectic properties which come from topology and using them one can give twisted versions of the above mentioned invariants, i.e., of the loop invariants [6, 8], the 3D-index in [9, 10] and [13] and KLV state-integral [1, 20]. A key property of such a twisted invariant is that it determines the corresponding (untwisted) invariant of all cyclic covers. For example, the twisted 1-loop invariant of a knot complement defined below satisfies this property.

Our goal is to define the twisted NZ matrices, describe their properties and show how to compute them in terms of the methods developed by SnapPy [2]. Having done so, we can use the twisted NZ matrices to define a twisted version of the 1-loop invariant, prove its topological invariance and conjecture that it equals to the adjoint twisted Alexander polynomial. It is interesting to note that the twisted 1-loop invariant depends only on the combinatorics of the NZ matrices of the infinite cyclic cover (which is abelian information), whereas the adjoint twisted Alexander polynomial depends on the complete hyperbolic structure given as a representation of the fundamental group.

The twisted NZ matrices introduced in this paper have further applications aside from the topological 1-loop polynomial invariants studied in the present paper. In the sequel paper [16], we use the twisted NZ matrices to study the behavior of the higher-loop invariants of [6] under cyclic coverings. The latter were recently shown to be topological invariants of cusped hyperbolic 3-manifolds [14]. A further application of twisted NZ matrices was given in our joint work [17] where we introduced a super-version of them to define 1-loop torsion polynomials for all representations of $\mathfrak {sl}_2(\mathbb {C})$ that we conjectured to be equal to their corresponding twisted Alexander polynomials. This conjecture was recently proven for all fibered 3-manifolds [15].

1.2 Torsion and its twisted version

Before discussing twisting matters further, let us recall a key motivating example. A basic invariant of a compact 3-manifold is the order of the torsion of its first homology. The behavior of this invariant for all cyclic covers of a knot complement is determined by a single Laurent polynomial, the Alexander polynomial. Explicitly, we have

$$\begin{aligned} \left| \textrm{tor}(H_1(M^{(n)};\mathbb {Z}))\right| = \prod _{\omega ^n=1} \Delta _K(\omega ) \end{aligned}$$

(1)

where $\Delta _K(t) \in \mathbb {Z}[t^{\pm 1}]$ is the Alexander polynomial of a knot $K \subset S^3$, $M^{(n)}$ is the n-fold cyclic cover of $M=S^3\setminus K$, and the left-hand side is the order of the torsion part of $H_1(M^{(n)};\mathbb {Z})$. This classical result connecting the torsion of the first homology to the Alexander polynomial (see, e.g., [12, (6.3), p.417]) is deeply rooted in the idea that the Alexander polynomial is the torsion of the infinite cyclic cover of M twisted by the abelianization map $\alpha :\pi _1(M) \rightarrow H_1(M;\mathbb {Z})=\mathbb {Z}$. In other words, we have

(2)

This idea has been extended in several directions. Among them, one can define the torsion of a 3-manifold using interesting representations of its fundamental group. For example, when M is a cusped hyperbolic 3-manifold, one can define a torsion using a (lifted) geometric $\textrm{SL}_2(\mathbb {C})$-representation $\rho$ of the fundamental group of its complement, or a symmetric power thereof. There are some technical difficulties that one must overcome, stemming from the fact that sometimes the corresponding chain complexes are not acyclic, hence the torsion depends on a choice of peripheral curves, as well as normalization issues, since the torsion is usually well defined up to a sign. These issues have been addressed in detail by [5, 11, 23]. Among the several torsion nvariants, we will be interested in the adjoint (Reidemeister) torsion $\tau _\gamma (M)$ of a one-cusped hyperbolic 3-manifold (such as a knot complement) using the adjoint representation $\textrm{Ad}_\rho =\text {Sym}^2(\rho ): \pi _1(M) \rightarrow \textrm{SL}_3(\mathbb {C})$, where $\gamma$ is a fixed peripheral curve. The adjoint torsion $\tau _\gamma (M) \in F^\times /\pm$ is a nonzero element of the trace field F of M, well defined up to a sign [23]. Just as in the case of the Alexander polynomial, there is a version of the adjoint twisted Alexander polynomial $\tau (M,\alpha ,t) \in F[t^{\pm 1}]/(\pm t^\mathbb {Z})$ (abbreviated by $\tau (M,t)$ when $\alpha$ is clear) defined in [5, 11, 27] using an epimorphism $\alpha : \pi _1(M) \rightarrow \mathbb {Z}$. Here, the ambiguity is given by multiplication by an element of $\pm t^\mathbb {Z}:=\{\pm t^r \, | \, r \in \mathbb {Z}\}$.

Two key properties of the adjoint twisted Alexander polynomial are the behavior under finite cyclic covers [11]

$$\begin{aligned} \tau (M^{(n)},t^n)=\prod _{\omega ^n=1}\tau (M,\omega \, t) \end{aligned}$$

(3)

and the relation with the adjoint torsion [28], namely

$$\begin{aligned} \tau (M,1)=0, \qquad \left. \frac{d}{dt}\right| _{t=1} \tau (M,t) = \tau _\lambda (M) \end{aligned}$$

(4)

where $\lambda$ is the canonical longitude, i.e., the peripheral curve satisfying $\alpha (\lambda )=0$.

1.3 Neumann–Zagier matrices and their twisted version

Having already discussed the torsion and twisted torsion, we now recall some basic facts from ideal triangulations of 3-manifolds and their gluing equations, following [22, 26]. Let M be an oriented hyperbolic 3-manifold with a torus boundary component (often called a one-cusped hyperbolic 3-manifold) equipped with an ideal triangulation ${\mathcal {T}}$. An Euler characteristic argument shows that the number N of tetrahedra in ${\mathcal {T}}$ is equal to the number of edges. We order the edges $e_i$ and the tetrahedra $\Delta _j$ of ${\mathcal {T}}$ for $1 \le i,j \le N$. A quad type of a tetrahedron is a pair of opposite edges; hence each tetrahedron has three quad types. We fix an orientation and a quad type of each tetrahedron $\Delta _j$ so that each edge of $\Delta _j$ admits a shape parameter among

$$\begin{aligned} z_j, \ z'_j=\frac{1}{1-z_j},\ \text {or } z''_j=1- \frac{1}{z_j} \in \mathbb {C}\setminus \{0,1\} \end{aligned}$$

with opposite edges having same parameters (see Fig. 1). We denote by $\square$ the three pairs of opposite edges of a tetrahedron, so that the edges of $\square$ are assigned the edge parameter $z^\square$.

Fig. 1

An ideal tetrahedron

A complete hyperbolic structure of M can be described by a special solution of the gluing equations. The latter describe the holonomy of the hyperbolic structure around each edge $e_i$ of ${\mathcal {T}}$, and have the (logarithmic) form

$$\begin{aligned} \sum _{j=1}^N \left( \textbf{G}_{ij} \log z_j +\textbf{G}'_{ij} \log z'_j +\textbf{G}''_{ij} \log z''_j\right) = 2\pi \sqrt{-1}. \end{aligned}$$

(5)

Here $\textbf{G}$, $\textbf{G}'$ and $\textbf{G}''$ are the gluing equation matrices whose rows and columns are indexed by the edges and by the tetrahedra of ${\mathcal {T}}$, respectively, such that the (i, j)-entry of $\textbf{G}^\square$ is the number of edges of $\Delta _j$ with parameter $z^\square _j$ is incident to the edge $e_i$ in ${\mathcal {T}}$. It will be convenient to introduce $\zeta$-variables

$$\begin{aligned} \zeta = \frac{d \log z}{dz}=\frac{1}{z}, \quad \zeta ' = \frac{d \log z'}{dz}=\frac{1}{1-z},\quad \zeta '' = \frac{d \log z''}{dz}=\frac{1}{z(z-1)} \end{aligned}$$

(6)

following [25]. Note that the three shape parameters in each tetrahedron satisfy the relation $z z' z''=-1$, and this implies the linear relation $\zeta +\zeta '+\zeta ''=0$. Thus one can eliminate the variable $\zeta '$ from any expression given in terms of $\zeta , \zeta '$, and $\zeta ''$, arriving at the Neumann–Zagier matrices

$$\begin{aligned} \textbf{A}:=\textbf{G}-\textbf{G}', \qquad \textbf{B}:=\textbf{G}''-\textbf{G}'. \end{aligned}$$

(7)

Note that

$$\begin{aligned} \textbf{G}\, \textrm{diag}(\zeta ) +\textbf{G}' \, \textrm{diag}(\zeta ') + \textbf{G}'' \, \textrm{diag}(\zeta '') = \textbf{A} \, \textrm{diag}(\zeta ) + \textbf{B} \, \textrm{diag}(\zeta '') \end{aligned}$$

(8)

where $\textrm{diag}(\zeta ^\square )$ denotes the diagonal matrix with diagonal entries $\zeta ^\square _1,\ldots ,\zeta ^\square _N$.

The NZ matrices have remarkable properties discovered in [22] which is a starting point for the quantization of the gluing equations and for passing from hyperbolic geometry to quantum topology. The symplectic property of the NZ matrices implies that

$$\begin{aligned} \textbf{A} \textbf{B}^T = \textbf{B} \textbf{A}^T. \end{aligned}$$

(9)

There are two enhancements of the gluing equations and of their corresponding matrices. The first is obtained by looking at the cusp, i.e., the peripheral (also called boundary) torus of the 3-manifold. By a peripheral curve, we mean an oriented, homotopically non-trivial, simple closed curve in the peripheral torus of M. A peripheral curve $\gamma$ gives a triple $(\textbf{C}_\gamma ,\textbf{C}'_\gamma ,\textbf{C}''_\gamma )$ of row vectors in $\mathbb {Z}^N$ that describe the completeness equation as

$$\begin{aligned} \sum _{j=1}^N \left( \textbf{C}_{\gamma j}\log z_j +\textbf{C}'_{\gamma j} \log z'_j +\textbf{C}''_{\gamma j} \log z''_j\right) = 0. \end{aligned}$$

(10)

Fixing a peripheral curve $\gamma$, let $\textbf{G}_\gamma ^\square$ denote the matrix obtained from $\textbf{G}^\square$ by replacing the last row by $\textbf{C}^\square _\gamma$, and likewise for $\textbf{A}_\gamma$ and $\textbf{B}_\gamma$.

The second enhancement is a combinatorial flattening of ${\mathcal {T}}$, that is a triple $(f,f',f'')$ of column vectors in $\mathbb {Z}^N$ such that

$$\begin{aligned} \textbf{G} f+\textbf{G}' f' + \textbf{G}'' f''&=(2,\ldots ,2)^T, \end{aligned}$$

(11)

$$\begin{aligned} f+ f' + f''&=(1,\ldots ,1)^T, \end{aligned}$$

(12)

$$\begin{aligned} \textbf{C}_\gamma f+\textbf{C}'_\gamma f' + \textbf{C}''_\gamma f''&=0 \end{aligned}$$

(13)

for any peripheral curve $\gamma$. This term was introduced in [6, Sec.4.4] as a necessary ingredient to define the 1-loop invariant (and there, it was called a combinatorial flattening compatible with any peripheral curve). Every ideal triangulation has combinatorial flattenings [21, Thm.4.5].

This concludes our discussion of the NZ matrices. We now introduce a twisted version of the NZ matrices of an ideal triangulation ${\mathcal {T}}$ of a 3-manifold M as above. We will fix an epimorphism $\alpha : \pi _1(M) \rightarrow \mathbb {Z}$ and a peripheral curve $\mu$ satisfying $\alpha (\mu )=1$. For instance, if M is a knot complement in $S^3$, then $\alpha$ is the abelianization map and $\mu$ is a meridian of the knot. Let $\widetilde{M}$ and $M^{(n)}$ denote the cyclic covers of M corresponding to $\alpha ^{-1}(0)$ and $\alpha ^{-1}(n \mathbb {Z})$, respectively. The ideal triangulation $\widetilde{\mathcal {T}}$ of the infinite cyclic cover $\widetilde{M}$ induced from ${\mathcal {T}}$ is equipped with an action of the deck transformation group $\mathbb {Z}$ (generated by the $\mu$-action), and induces an ideal triangulation ${\mathcal {T}}^{(n)}$ of the n-fold cyclic cover $M^{(n)}$.

We choose lifts $\widetilde{e}_i$ and $\widetilde{\Delta }_j$ of $e_i$ and $\Delta _j$ to $\widetilde{\mathcal {T}}$, respectively, and for $k \in \mathbb {Z}$ let $\textbf{G}_k^\square$ be the $N \times N$ matrix whose (i, j)-entry is the number of edges of $\mu ^k \cdot \widetilde{\Delta }_j$ with parameter $z_j^\square$ is incident to the edge $\widetilde{e}_i$ in $\widetilde{\mathcal {T}}$. Note that $\textbf{G}_k^\square$ is a zero matrix for all but finitely many k, as there are finitely many tetrahedra around $\widetilde{e}_i$. We define the twisted gluing equation matrices $\textbf{G}^\square (t)$ of ${\mathcal {T}}$ by

$$\begin{aligned} \textbf{G}^\square (t):= \sum _{k \in \mathbb {Z}} \textbf{G}^\square _k\, t^k \end{aligned}$$

(14)

and the twisted Neumann–Zagier matrices by

$$\begin{aligned} \textbf{A}(t):=\textbf{G}(t)-\textbf{G}'(t), \qquad \textbf{B}(t):=\textbf{G}''(t)-\textbf{G}'(t). \end{aligned}$$

(15)

(More generally, if $\textbf{X}(t)$ is a matrix with entries in $\mathbb {Z}[t^{\pm 1}]$, we denote by $\textbf{X}_k$ the coefficient of $t^k$ in $\textbf{X}(t)$.) Note that the rows and columns of these matrices are indexed by the edges and tetrahedra of ${\mathcal {T}}$, respectively, and that their entries are in the ring $\mathbb {Z}[t^{\pm 1}]$. Since the above matrices are well defined after fixing lifts of each edge and tetrahedron of ${\mathcal {T}}$, a different choice of lifts changes $\textbf{G}^\square (t)$, $\textbf{A}(t)$ and $\textbf{B}(t)$ by multiplication from the left or right by the same diagonal matrix $\textrm{diag}(t^{c_1},t^{c_2},\dots ,t^{c_N})$ for integers $c_1,c_2,\dots ,c_N$. This ambiguity propagates to any invariant constructed using these matrices.

A first property of the twisted NZ matrices $\textbf{A}(t)$ and $\textbf{B}(t)$ is that they determine the NZ matrices $\textbf{A}^{(n)}$ and $\textbf{B}^{(n)}$ of the cyclic covers ${\mathcal {T}}^{(n)}$ of ${\mathcal {T}}$, and moreover they do so via block circulant matrices, i.e., square matrices such that each row is obtained by its predecessor by a cyclic shift. We refer to [4] and [24] for details on the properties of block circulant matrices.

Theorem 1.1

We have

$$\begin{aligned} \textbf{X}^{(n)} = \begin{pmatrix} \sum _{r \equiv 0} \textbf{X}_r &{} \sum _{r \equiv 1} \textbf{X}_r &{} \cdots &{} \sum _{r \equiv n-1} \textbf{X}_r\\ \sum _{r \equiv n-1} \textbf{X}_r &{} \sum _{r \equiv 0} \textbf{X}_r &{} \cdots &{} \sum _{r \equiv n-2} \textbf{X}_r\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \sum _{r \equiv 1} \textbf{X}_r &{} \sum _{r \equiv 2} \textbf{X}_r &{} \cdots &{} \sum _{r \equiv 0} \textbf{X}_r \end{pmatrix} \end{aligned}$$

(16)

for $\textbf{X}=\textbf{G}^\square$, $\textbf{A}$ or $\textbf{B}$.

The twisted NZ matrices satisfy a twisted version of the symplectic property of Equation (9).

Theorem 1.2

We have

$$\begin{aligned} \textbf{A}(t) \textbf{B}(1/t)^T = \textbf{B}(t) \textbf{A}(1/t)^T. \end{aligned}$$

(17)

In other words, $\textbf{A}(t) \textbf{B}(1/t)^T$ is symmetric under tranposition followed by $t \mapsto 1/t$. In particular, $\textbf{A}(\omega ) \textbf{B}(\omega )^*$ is Hermitian for $\omega \in \mathbb {C}$ with $|\omega |=1$ and so is $\textbf{B}(\omega )^{-1}\textbf{A}(\omega )$ if $\textbf{B}(\omega )$ is non-singular. Here $X^*$ is the complex conjugate of the transpose of a matrix X. Note that given any ideal triangulation, we can choose quads so that $\textbf{B}$ (hence also $\textbf{B}(t)$, since $\textbf{B}(1)=\textbf{B}$) is invertible; see [6, App.A].

Remark 1.3

One can check that Equation (17) (or equivalently, its restriction to n-th roots of unity t) is equivalent to that $\textbf{A}^{(n)} (\textbf{B}^{(n)})^T = \textbf{B}^{(n)} (\textbf{A}^{(n)})^T$ for all $n \ge 1$.

We now come to a conjectural property of the twisted NZ matrices, which we have checked in numerous examples.

Conjecture 1.4

The Laurent polynomials $\det (\textbf{A}(t))$ and $\det (\textbf{B}(t))$ are palindromic, i.e., satisfy $p(t)=\varepsilon t^r p(1/t)$ for some $\varepsilon = \pm 1$ and an integer r.

We next discuss the behavior of the twisted NZ matrices under a 2–3 Pachner move relating an ideal triangulation ${\mathcal {T}}$ with N tetrahedra to another one $\overline{{\mathcal {T}}}$ with $N+1$ tetrahedra. Recall that such a move is determined by two tetrahedra with a common face in ${\mathcal {T}}$, which become three tetrahedra with a common edge in $\overline{{\mathcal {T}}}$ as shown in Fig. 2 below. Let us write the twisted NZ matrices $\textbf{A}(t)$ and $\textbf{B}(t)$ of the triangulation ${\mathcal {T}}$ schematically in columns as

$$\begin{aligned} \textbf{A}(t) = (a_1,\;a_2,\;a_i),\quad \textbf{B}(t) = (b_1,\;b_2,\;b_i), \end{aligned}$$

(18)

with $a_i$ meaning $(a_3,a_4,...,a_N)$ and similarly for $b_i$. Let $\overline{\textbf{A}}(t)$ and $\overline{\textbf{B}}(t)$ denote the corresponding twisted NZ matrices of $\overline{{\mathcal {T}}}$.

Theorem 1.5

With the above notation, there exists a lower triangular matrix P with 1’s on the diagonal such that

$$\begin{aligned} P \, \overline{\textbf{A}}(t) = \begin{pmatrix} -1 &{} -1 &{} -1 &{} 0 \\ b_1+b_2 &{} a_1 &{} a_2 &{} a_i \end{pmatrix},\qquad P \, \overline{\textbf{B}}(t) = \begin{pmatrix} -1 &{} -1 &{} -1 &{} 0 \\ 0 &{} a_2+b_1 &{} a_1+b_2 &{} b_i \end{pmatrix}. \end{aligned}$$

(19)

This corrects the omission of P in [6, Eqn.(3.27)], which does not affect the validity of the proofs in [6].

1.4 The 1-loop invariant and its twisted version

The adjoint Reidemeister torsion has a conjectural description in terms of the 1-loop invariant of [6]. The latter depends on the NZ matrices of an ideal triangulation, its shapes, their flattenings and a peripheral curve $\gamma$. With the notation of Sect. 1.3, the 1-loop invariant is defined by

$$\begin{aligned} \begin{aligned} \tau ^\textrm{CS}_\gamma ({\mathcal {T}})&:= \frac{\det \left( \textbf{A}_\gamma \, \textrm{diag}(\zeta ) + \textbf{B}_\gamma \, \textrm{diag}(\zeta '') \right) }{ 2\prod _{j=1}^N\zeta _j^{f_j} \zeta _j'^{f_j'} \zeta _j''^{f_j''}} \\&\,\,= \frac{\det \left( \textbf{G}_\gamma \, \textrm{diag}(\zeta ) +\textbf{G}_\gamma ' \, \textrm{diag}(\zeta ')+\textbf{G}_\gamma '' \, \textrm{diag}(\zeta '') \right) }{ 2\prod _{j=1}^N\zeta _j^{f_j} \zeta _j'^{f_j'} \zeta _j''^{f_j''}} \in F/ (\pm 1) \end{aligned} \end{aligned}$$

(20)

where the last equality follows from Equation (8). In [6], it is conjectured that the 1-loop invariant $\tau ^\textrm{CS}_\gamma ({\mathcal {T}})$ is equal to the adjoint torsion $\tau _\gamma (M)$ with respect to $\gamma$

$$\begin{aligned} \tau ^\textrm{CS}_\gamma ({\mathcal {T}}) {\mathop {=}\limits ^{?}} \tau _\gamma (M) \in F^\times / (\pm 1). \end{aligned}$$

(21)

Given the above conjecture and the discussion of Sect. 1.2, it is natural to predict the existence of a twisted version of the 1-loop invariant, defined in terms of the twisted NZ matrices. With the notation of Sect. 1.3, we define the twisted 1-loop invariant by

$$\begin{aligned} \tau ^\textrm{CS}({\mathcal {T}},t):= & {} \frac{\det \left( \textbf{A}(t) \, \textrm{diag}(\zeta ) + \textbf{B}(t) \, \textrm{diag}(\zeta '') \right) }{ \prod _{j=1}^N\zeta _j^{f_j} \zeta _j'^{f_j'} \zeta _j''^{f_j''}} \nonumber \\:= & {} \frac{\det \left( \textbf{G}(t)\, \textrm{diag}(\zeta )+\textbf{G}'(t) \, \textrm{diag}(\zeta ')+\textbf{G}''(t) \, \textrm{diag}(\zeta '') \right) }{ \prod _{j=1}^N\zeta _j^{f_j} \zeta _j'^{f_j'} \zeta _j''^{f_j''}} \in F[t^{\pm 1}]/ (\pm t^\mathbb {Z})\nonumber \\ \end{aligned}$$

(22)

where the second equality follows from the fact (analogous to Equation (8))

$$\begin{aligned} \textbf{G}(t)\, \textrm{diag}(\zeta ) +\textbf{G}'(t) \, \textrm{diag}(\zeta ') + \textbf{G}''(t) \, \textrm{diag}(\zeta '') = \textbf{A}(t) \, \textrm{diag}(\zeta ) + \textbf{B}(t) \, \textrm{diag}(\zeta ''). \end{aligned}$$

(23)

An elementary observation is that $\tau ^\textrm{CS}({\mathcal {T}},t)$ is well defined up to multiplication by an element in $\pm t^\mathbb {Z}$. Indeed, the computation in [6, Sec.3.5] shows that up to sign, the twisted 1-loop invariant is independent of the choice of a combinatorial flattening. It is also manifestly independent of the choice of a quad type of $\Delta _j$, as the definition (22) is symmetric with respect to $\zeta ,\zeta ',$ and $\zeta ''$. Finally, a different choice of lifts of the edges and tetrahedra of ${\mathcal {T}}$ results to left or right multiplication of all of the matrices $\textbf{G}^\square (t)$ by the same diagonal matrix $\textrm{diag}(t^{c_1},t^{c_2},\dots ,t^{c_N})$ for integers $c_1,c_2,\dots ,c_N$, hence the observation follows.

By the very definition of $\tau ^\textrm{CS}({\mathcal {T}},t)$, it leads to a twisted version of Conjecture (21), namely

$$\begin{aligned} \tau ^\textrm{CS}({\mathcal {T}},t) {\mathop {=}\limits ^{?}} \tau (M,t) \in F[t^{\pm 1}]/ (\pm t^\mathbb {Z}). \end{aligned}$$

(24)

We now list some properties of the twisted 1-loop invariant. The first concerns the topological invariance.

Theorem 1.6

$\tau ^\textrm{CS}({\mathcal {T}},t)$ is invariant under Pachner 2–3 moves between ideal triangulations that support the geometric representation.

Combining the above theorem with Proposition 1.7 of [6], we conclude that the twisted 1-loop invariant defines a topological invariant of one-cusped hyperbolic 3-manifolds.

The next two theorems concern the properties (3) and (4) of the adjoint twisted Alexander polynomial.

Theorem 1.7

For all $n \ge 1$, we have

$$\begin{aligned} \tau ^{\textrm{CS}}({\mathcal {T}}^{(n)},t^n)=\prod _{\omega ^n=1}\tau ^{\textrm{CS}}({\mathcal {T}},\omega \, t). \end{aligned}$$

(25)

Theorem 1.8

We have $\tau ^\textrm{CS}({\mathcal {T}},1)=0$ and $\left. \frac{d}{dt}\right| _{t=1} \tau ^{\textrm{CS}}({\mathcal {T}},t) = \tau _\lambda ^{\textrm{CS}}({\mathcal {T}})$ where $\lambda$ is the peripheral curve satisfying $\alpha (\lambda )=0$.

A corollary of the above theorems is a relation between the twisted 1-loop invariant and the 1-loop invariant of [6] for cyclic covers, namely

$$\begin{aligned} \frac{\tau ^\textrm{CS}_\mu ({\mathcal {T}}^{(n)})}{\tau ^\textrm{CS}_\mu ({\mathcal {T}})} = \prod _{ \begin{array}{c} \omega ^n=1 \\ \omega \ne 1 \end{array}} \tau ^\textrm{CS}({\mathcal {T}},\omega ). \end{aligned}$$

(26)

The next result concerns the symmetries of the twisted 1-loop invariant. Conjecture 1.4 implies a symmetry of the twisted 1-loop invariant which is known to hold for the adjoint twisted Alexander polynomial [18, 19], namely $\tau (M,t)=\tau (M,1/t)$.

Corollary 1.9

(assuming Conjecture 1.4) We have

$$\begin{aligned} \tau ^\textrm{CS}({\mathcal {T}},t) = \tau ^\textrm{CS}({\mathcal {T}},1/t) \in F[t^{\pm 1}]/(\pm t^\mathbb {Z}). \end{aligned}$$

(27)

We end our discussion on the twisted 1-loop invariant with a remark which suggests that the t-deformation variable is independent from the variable $\mathfrak {m}$ which is an eigenvalue of the meridian of an $\textrm{SL}_2(\mathbb {C})$-representation of $\pi _1(M)$.

Remark 1.10

By varying the representation, the adjoint Reidemeister torsion can be extended to a rational function on the geometric component $X_M$ of the $\textrm{SL}_2(\mathbb {C})$-character variety of a knot complement M [7], and consequently to a rational function of the geometric component of the A-polynomial curve. The same holds for the 1-loop invariant; see [6, Sec.4]. Likewise, we can extend the twisted 1-loop invariant to a twisted rational function on the geometric component of the character variety, i.e., to an element of the ring $C(X_M)[t^{\pm 1}]/(\pm t^\mathbb {Z})$, where $C(X_M)$ is the field of rational functions on $X_M$. Then, $\mathfrak {m} \in C(X_M)$ is a variable independent of t.

2 Proofs: twisted NZ matrices

In this section, we give proofs of the properties of the twisted NZ matrices, namely the relation to the NZ matrices of cyclic covers (Theorem 1.1), the symplectic properties (Theorem 1.2), and the behavior under 2–3 Pachner moves (Theorem 1.5).

Proof of Theorem 1.1

It is clear that ${\mathcal {T}}^{(n)}$ has nN tetrahedra, as ${\mathcal {T}}$ has N tetrahedra $\Delta _j$, $j=1,\ldots ,N$. Fixing a lift $\widetilde{\Delta }_j$ of each $\Delta _j$ to the infinite cyclic cover, we choose lifts of the tetrahedra of ${\mathcal {T}}^{(n)}$ by $\mu ^k \cdot \widetilde{\Delta }_j$ for $k=0, \ldots , n-1$. Similarly, we choose lifts of the edges of ${\mathcal {T}}^{(n)}$. Then it is clear from the construction of the n-fold cyclic cover that

$$\begin{aligned} \textbf{G}^{(n)\square }_k = \begin{pmatrix} \textbf{G}^\square _{nk} &{} \textbf{G}^\square _{nk+1}&{} \cdots &{} \textbf{G}^\square _{nk+n-1}\\ \textbf{G}^\square _{nk-1} &{} \textbf{G}^\square _{nk} &{} \cdots &{} \textbf{G}^\square _{nk+n-2}\\ \quad \vdots &{} \quad \vdots &{} \ddots &{} \quad \vdots \\ \textbf{G}^\square _{nk-n+1} &{} \textbf{G}^\square _{nk-n+2} &{} \cdots &{} \textbf{G}^\square _{nk} \end{pmatrix} \end{aligned}$$

(28)

for all $k \in \mathbb {Z}$, which implies

$$\begin{aligned} \textbf{G}^{(n)\square } = \begin{pmatrix} \sum _{r \equiv 0} \textbf{G}^\square _r &{} \sum _{r \equiv 1} \textbf{G}^\square _r &{} \cdots &{} \sum _{r \equiv n-1} \textbf{G}^\square _r\\ \sum _{r \equiv n-1} \textbf{G}^\square _r &{} \sum _{r \equiv 0} \textbf{G}^\square _r &{} \cdots &{} \sum _{r \equiv n-2} \textbf{G}^\square _r\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \sum _{r \equiv 1} \textbf{G}^\square _r &{} \sum _{r \equiv 2} \textbf{G}^\square _r &{} \cdots &{} \sum _{r \equiv 0} \textbf{G}^\square _r \end{pmatrix} \end{aligned}$$

(29)

This completes the proof of Theorem 1.1. $\square$

Proof of Theorem 1.2

Following Neumann [21], we consider the $\mathbb {Z}[t^{\pm 1}]$-module V generated by variables $Z_j,Z'_j,Z''_j$ subject to linear relations $Z_j+Z'_j+Z''_j=0$ for $1 \le j \le N$. We define a symplectic form on V as

$$\begin{aligned} \langle Z_i, Z''_j \rangle = \langle Z'_i, Z_j \rangle = \langle Z''_i, Z'_j \rangle = \delta _{ij} \end{aligned}$$

(30)

and

$$\begin{aligned} \langle c Z_ j, Z''_j \rangle = \langle Z_ j, \bar{c} Z''_j \rangle = c, \quad c \in \mathbb {Z}[t^{\pm 1}] \end{aligned}$$

where $\delta _{ij}$ is the Kronecker delta and $\bar{\ }: \mathbb {Z}[t^{\pm 1}]\rightarrow \mathbb {Z}[t^{\pm 1}]$ is the involution induced from the inversion $t \mapsto t^{-1}$. Note that $\langle Z''_i, Z_j \rangle = \langle Z''_i, -Z'_j - Z''_j\rangle = -\delta _{ij}$ and similarly, $\langle Z_i,Z'_j\rangle = \langle Z'_i,Z''_j \rangle = - \delta _{ij}$.

We associate an element $E_i \in V$ to each edge $e_i$ of ${\mathcal {T}}$ as

$$\begin{aligned} E_i = \sum _{j=1}^N \left( \textbf{G}(t)_{ij}Z_j+ \textbf{G}'(t)_{ij}Z'_j +\textbf{G}''(t)_{ij}Z''_j \right) . \end{aligned}$$

(31)

In what follows, we use the same argument given in the proof of [3, Thm.3.6] to show that

$$\begin{aligned} \langle E_a, E_b \rangle =0 \quad \text {for all } 1 \le a,b \le N. \end{aligned}$$

(32)

Considering the linear expansion of $\langle E_a,E_b \rangle$ using the equation (31), we have a non-trivial term when the edges $e_a$ and $e_b$ appear in some $\Delta _j$ with different shape parameters. Without loss of generality, suppose that $e_a$ and $e_b$ have parameters $Z_j$ and $Z''_j$, respectively. It is clear that $\widetilde{\Delta }_j$ contains $\mu ^\alpha \cdot \widetilde{e}_a$ and $\mu ^\beta \cdot \widetilde{e}_b$ for some $\alpha$ and $\beta \in \mathbb {Z}$. Equivalently, $\mu ^{-\alpha } \cdot \widetilde{\Delta }_j$ and $\mu ^{-\beta } \cdot \widetilde{\Delta }_j$ are attached to $\widetilde{e}_a$ and $\widetilde{e}_b$, respectively. We thus get a non-trivial term

$$\begin{aligned} \langle t^{-\alpha } Z_j, t^{-\beta } Z''_j \rangle = t^{\beta -\alpha } \end{aligned}$$

(33)

in the linear expansion from the triple $(\widetilde{\Delta }_j, \mu ^\alpha \cdot \widetilde{e}_a, \mu ^\beta \cdot \widetilde{e}_b)$. On the other hand, considering the face-pairing of the face of $\Delta _j$ containing $e_a$ and $e_b$, there is another tetrahedron $\Delta _{i}$ (possibly $i=j$), which also contains both $e_a$ and $e_b$. It follows that $\widetilde{\Delta }_i$ contains $\mu ^{\alpha +\gamma } \cdot \widetilde{e}_a$ and $\mu ^{\beta +\gamma } \cdot \widetilde{e}_b$ for some $\gamma \in \mathbb {Z}$. From this triple $(\widetilde{\Delta }_i, \mu ^{\alpha +\gamma } \cdot \widetilde{e}_a, \mu ^{\beta +\gamma } \cdot \widetilde{e}_b)$, we get another non-trivial term $-t^{(\beta +\gamma )-(\alpha +\gamma )}=-t^{\beta -\alpha }$ which we can pair with the term (33) to cancel out. Note that we have the minus sign here, since the face-pairing is orientation-reversing: the shape parameters of $e_a$ and $e_b$ for $\Delta _i$ are either $(Z_i,Z'_i)$, $(Z'_i,Z''_i)$, or $(Z''_i,Z_i)$. In this way, every non-trivial term that appears in the expansion of $\langle E_a,E_b\rangle$ is paired to cancel out. This proves the equation (32). We then directly obtain the desired equation (17), since we have

$$\begin{aligned} \langle E_a, E_b \rangle&= \sum _{j=1}^N \Big \langle \textbf{G}(t)_{aj} Z_j+\textbf{G}'(t)_{aj} Z'_j+\textbf{G}''(t)_{aj} Z''_j, \textbf{G}(t)_{bj} Z_j+\textbf{G}'(t)_{bj} Z'_j+\textbf{G}''(t)_{bj} Z''_j\Big \rangle \\&=\sum _{j=1}^N \Big (\textbf{G}(t)_{aj} \big (\textbf{G}''(1/t)_{bj} -\textbf{G}'(1/t)_{bj}\big ) \\&\quad +\textbf{G}'(t)_{aj} \big (\textbf{G}(1/t)_{bj} -\mathbf {G''}(1/t)_{bj}\big )+\textbf{G}''(t)_{aj} \big (\textbf{G}'(1/t)_{bj}-\textbf{G}(1/t)_{bj}\big ) \Big ) \\&=\sum _{j=1}^N \Big ( \big (\textbf{G}(t)_{aj}-\textbf{G}'(t)_{aj}\big ) \big (\textbf{G}''(1/t)_{bj}-\textbf{G}'(1/t)_{bj}\big )\\&\quad -\big (\textbf{G}''(t)_{aj}-\textbf{G}'(t)_{aj}\big ) \big (\textbf{G}(1/t)_{bj}-\textbf{G}'(1/t)_{bj}\big ) \Big ) \\&= \sum _{j=1}^N \Big (\textbf{A}(t)_{aj} \textbf{B}(1/t)_{bj} - \textbf{B}(t)_{aj} \textbf{A}(1/t)_{bj} \Big ) \, . \end{aligned}$$

$\square$

Proof of Theorem 1.5

Recall that a 2–3 Pachner move on ${\mathcal {T}}$ is determined by two tetrahedra $\Delta _\alpha$ and $\Delta _\beta$ with a common face in ${\mathcal {T}}$. Dividing the bipyramid $\Delta _\alpha \cup \Delta _\beta$ into three tetrahedra $\Delta _a, \Delta _b,$ and $\Delta _c$ as in Fig. 2, we obtain a new ideal triangulation $\overline{{\mathcal {T}}}$ with one additional edge $e_0$. We choose lifts of the five tetrahedra $\Delta _\alpha$, $\Delta _\beta$, $\Delta _a$, $\Delta _b$, $\Delta _c$ and the edge $e_0$ (to the infinite cyclic cover) such that $\widetilde{\Delta }_\alpha \cup \widetilde{\Delta }_\beta$ and $\widetilde{\Delta }_a \cup \widetilde{\Delta }_b \cup \widetilde{\Delta }_c$ are the same bipyramid containing $\widetilde{e}_0$. Note that the (twisted) gluing equation of $e_0$ is

$$\begin{aligned} \log z'_a + \log z'_b + \log z'_c = 2 \pi \sqrt{-1}. \end{aligned}$$

(34)

Fig. 2

2-3 Pachner move

There are nine edges on the bipyramid whose gluing equations are affected by the Pachner move: three at the triangle of the base pyramid and six others on the bipyramid but not on its base. The six edges give

$$\begin{aligned} \log z_\alpha= & {} \log z_b + \log z_c'' \quad \log z_\alpha ' =\log z_a''+\log z_c \quad \log z_\alpha '' =\log z_a+\log z_b'' \nonumber \\ \log z_\beta= & {} \log z_b''+\log z_c \quad \log z_\beta ' = \log z_a'' +\log z_b \quad \log z_\beta '' = \log z_a+ \log z_c'', \end{aligned}$$

(35)

and the three edges give

$$\begin{aligned} \begin{aligned} \log z_\alpha + \log z_\beta&=\log z'_a&\log z'_\alpha + \log z''_\beta&=\log z'_b&\log z''_\alpha + \log z'_\beta =\log z'_c. \end{aligned} \end{aligned}$$

(36)

The relations (36) are obtained from the relations (35) up to the gluing equation (34) of $e_0$ and the relation $\log z + \log z' + \log z''= \pi \sqrt{-1}$. For instance,

$$\begin{aligned} \log z_\alpha + \log z_\beta&= \log z_b + \log z''_c + \log z''_b +\log z_c \\&= 2 \pi \sqrt{-1} - \log z'_b - \log z'_c \\&= \log z'_a . \end{aligned}$$

Therefore, we can obtain the twisted gluing equation matrices $\overline{\textbf{G}}^\square (t)$ for $\overline{{\mathcal {T}}}$ from the twisted gluing equation matrices for $\overline{{\mathcal {T}}}$ by substituting $\log z_\alpha ^\square$ and $\log z_\beta ^\square$ in terms of the right hand side of equation (35) and the substitution is correct up to the gluing equation of $e_0$ and the relation $\log z + \log z' + \log z''= \pi \sqrt{-1}$. In matrix form, this implies that for some lower triangular matrix $Q=\begin{pmatrix} 1 &{} 0 \\ * &{} I_N \end{pmatrix}$ and an integer matrix C, we have

$$\begin{aligned} \begin{pmatrix} \overline{\textbf{G}}(t)_{a}&\overline{\textbf{G}}(t)_{b}&\overline{\textbf{G}}(t)_{c} \end{pmatrix}= & {} Q\begin{pmatrix} 0&{} 0 &{} 0\\ \textbf{G}''(t)_{\alpha } + \textbf{G}''(t)_{\beta } &{} \textbf{G}(t)_{ \alpha } + \textbf{G}'(t)_{\beta }&{} \textbf{G}'(t)_{\alpha } + \textbf{G}(t)_{\beta } \end{pmatrix} + C, \nonumber \\ \begin{pmatrix} \overline{\textbf{G}}'(t)_{a}&\overline{\textbf{G}}'(t)_{b}&\overline{\textbf{G}}'(t)_{c} \end{pmatrix}= & {} Q\begin{pmatrix} 1&{} 1 &{} 1\\ \textbf{0} &{} \textbf{0}&{} \textbf{0} \end{pmatrix} + C, \nonumber \\ \begin{pmatrix} \overline{\textbf{G}}''(t)_{a}&\overline{\textbf{G}}''(t)_{b}&\overline{\textbf{G}}''(t)_{c} \end{pmatrix}= & {} Q \begin{pmatrix} 0&{} 0 &{} 0\\ \textbf{G}'(t)_{\alpha } + \textbf{G}'(t)_{ \beta } &{} \textbf{G}''(t)_{ \alpha } + \textbf{G}(t)_{ \beta }&{} \textbf{G}(t)_{\alpha } + \textbf{G}''(t)_{\beta } \end{pmatrix} + C.\nonumber \\ \end{aligned}$$

(37)

Here $I_N$ is the identity matrix of size N and $X_{j}$ is the j-th column of a matrix X. Multiplying $P=\begin{pmatrix} 1 &{} 0 \\ \textbf{G}'(t)_{\alpha } + \textbf{G}'(t)_{\beta } &{} I_N \end{pmatrix} Q^{-1}$ on both sides of Equation (37), we obtain

$$\begin{aligned} \begin{aligned} P\begin{pmatrix} \overline{\textbf{G}}(t)_{a}&\overline{\textbf{G}}(t)_{b}&\overline{\textbf{G}}(t)_{c} \end{pmatrix}&= \begin{pmatrix} 0&{} 0 &{} 0\\ \textbf{G}''(t)_{\alpha } + \textbf{G}''(t)_{\beta } &{} \textbf{G}(t)_{ \alpha } + \textbf{G}'(t)_{\beta }&{} \textbf{G}'(t)_{\alpha } + \textbf{G}(t)_{\beta } \end{pmatrix} + PC, \\ P \begin{pmatrix} \overline{\textbf{G}}'(t)_{a}&\overline{\textbf{G}}'(t)_{b}&\overline{\textbf{G}}'(t)_{c} \end{pmatrix}&=\begin{pmatrix} 1&{} 1 &{} 1\\ \textbf{G}'(t)_{ \alpha } + \textbf{G}'(t)_{\beta } &{} \textbf{G}'(t)_{ \alpha } + \textbf{G}'(t)_{\beta } &{} \textbf{G}'(t)_{ \alpha } + \textbf{G}'(t)_{\beta } \end{pmatrix}+ PC, \\ P \begin{pmatrix} \overline{\textbf{G}}''(t)_{a}&\overline{\textbf{G}}''(t)_{b}&\overline{\textbf{G}}''(t)_{c} \end{pmatrix}&= \begin{pmatrix} 0&{} 0 &{} 0\\ \textbf{G}'(t)_{\alpha } + \textbf{G}'(t)_{\beta } &{} \textbf{G}''(t)_{\alpha } + \textbf{G}(t)_{\beta }&{} \textbf{G}(t)_{\alpha } + \textbf{G}''(t)_{\beta } \end{pmatrix} + PC \,. \end{aligned} \end{aligned}$$

(38)

It follows that

$$\begin{aligned} \begin{aligned} P\begin{pmatrix} \overline{\textbf{A}}(t)_{a}&\overline{\textbf{A}}(t)_{b}&\overline{\textbf{A}}(t)_{c} \end{pmatrix}&= \begin{pmatrix} -1&{} -1 &{} -1\\ \textbf{B}(t)_{ \alpha } + \textbf{B}(t)_{\beta } &{} \textbf{A}(t)_{ \alpha } &{} \textbf{A}(t)_{\beta } \end{pmatrix}, \\ P \begin{pmatrix} \overline{\textbf{B}}(t)_{a}&\overline{\textbf{B}}(t)_{b}&\overline{\textbf{B}}(t)_{c} \end{pmatrix}&= \begin{pmatrix} -1&{} -1 &{} -1\\ \textbf{0} &{} \textbf{A}(t)_{ \beta }+ \textbf{B}(t)_{ \alpha } &{} \textbf{A}(t)_{ \alpha } + \textbf{B}(t)_{\beta } \end{pmatrix}, \end{aligned} \end{aligned}$$

where P is a lower triangular matrix with 1’s on the diagonal. $\square$

3 Examples

In this section, we explain how to compute the twisted NZ matrices of an ideal triangulation using the methods of SnapPy. As is customary, we do so by the example of the simplest hyperbolic $4_1$ knot, and later by the $6_3$ knot.

3.1 The knot $4_1$

The knot complement M of the knot $4_1$ decomposes into two ideal tetrahedra $\Delta _1$ and $\Delta _2$. Using the default triangulation of SnapPy for $4_1$ with isometry signature cPcbbbiht_BaCB, the gluing equations are

$$\begin{aligned} e_1&: z_1^2 z_1' z_2^2 z_2'=1, \\ e_2&: z_1' (z_1'')^2 z_2' (z_2'')^2=1 \,, \end{aligned}$$

the corresponding gluing equation matrices are

$$\begin{aligned} \textbf{G} = \begin{pmatrix} 2 &{} 2 \\ 0 &{} 0 \end{pmatrix}, \qquad \textbf{G}' = \begin{pmatrix} 1 &{} 1 \\ 1 &{} 1 \end{pmatrix}, \qquad \textbf{G}'' = \begin{pmatrix} 0 &{} 0 \\ 2 &{} 2 \end{pmatrix} , \end{aligned}$$

and the NZ matrices are

$$\begin{aligned} \textbf{A}= \begin{pmatrix} 1 &{} 1\\ -1 &{} -1 \end{pmatrix}, \qquad \textbf{B}= \begin{pmatrix} -1 &{} - 1 \\ 1 &{} 1 \end{pmatrix} \end{aligned}$$

with

$$\begin{aligned} \textbf{A} \textbf{B}^T = \begin{pmatrix} -2 &{} 2 \\ 2 &{} -2 \end{pmatrix} \end{aligned}$$

symmetric. We can read the above information by looking at the triangulated cusp shown in Fig. 3.

Fig. 3

The triangulation of the peripheral torus of $4_1$

To describe the ideal triangulation $\widetilde{\mathcal {T}}$ of the infinite cyclic cover $\widetilde{M}$ of M, we consider the triangulation of the peripheral torus induced from ${\mathcal {T}}=\{\Delta _1,\Delta _2\}$ (see Fig. 3) together with its lift to the universal cover, the Euclidean plane $\mathbb {E}^2$. Note that each triangle of $\mathbb {E}^2$ with corner $z_j$ has a label $j \in \{1,2\}$ of the corresponding tetrahedron.

We now describe a second labeling of each triangle of $\mathbb {E}^2$ by an integer, obtained by choosing a cocycle representative of the abelianization map $\alpha : \pi _1(M) \twoheadrightarrow \mathbb {Z}$. This construction is standard and is appears in unpublished work of Goerner and also in Zickert [29, Sec.3.5]. Let G denote the dual dual 1-skeleton of the triangulation of $\mathbb {E}^2$ (see Fig. 4). Each vertex and edge of G correspond to a tetrahedron and face-pairing of ${\mathcal {T}}$, respectively, and that the edges of G are oriented from $\Delta _0$ to $\Delta _1$. Since the face-pairings generate the fundamental group $\pi _1(M)$, one can assign an integer $\alpha (p_i)$ to each face-pairing $p_i$ corresponding to the abelianization map $\alpha : \pi _1(M) \twoheadrightarrow \mathbb {Z}$. Since in our case there are two tetrahedra, we have four face-pairings, thus four integers $\alpha (p_1),\ldots ,\alpha (p_4)$ that are required to satisfy

$$\begin{aligned} \begin{aligned} \alpha (p_2)-\alpha (p_4)&=1&\alpha (p_1)-\alpha (p_4)&=1,\\ \alpha (p_1)-\alpha (p_3)&=1&\alpha (p_2)-\alpha (p_3)&=1. \end{aligned} \end{aligned}$$

(39)

Note that these equations are directly obtained from Fig. 4 with the $\mu$-action described in Fig. 3.

Fig. 4

Face-pairings

Fig. 5

The dual 1-complex of $\mathbb {E}^2$, where the labeling $\alpha (v)_j$ of a vertex v indicates that v is labeled by the j-th tetrahedron

Since $\mathbb {E}^2$ is a contractible space, we can assign an integer $\alpha (v)$ to each vertex v of G such that $\alpha (v_2)-\alpha (v_1)=\alpha ([v_1,v_2])$, where $[v_1,v_2]$ is an oriented edge of G from $v_1$ to $v_2$. Explicitly, the general solution of the linear equations (39) is given by

$$\begin{aligned} (\alpha (p_1), \alpha (p_2), \alpha (p_3), \alpha (p_4))=(a,a,a-1,a-1) \qquad (a \in \mathbb {Z}). \end{aligned}$$

(40)

It follows from the construction that if a vertex v corresponds to $\Delta _j$ in ${\mathcal {T}}$, then it corresponds to $\mu ^{\alpha (v)} \cdot \widetilde{\Delta }_j$ in $\widetilde{\mathcal {T}}$. Choosing $(\alpha (p_1),\alpha (p_2),\alpha (p_3),\alpha (p_4))=(0,0,-1,-1)$ and $\alpha (v)$ and $\widetilde{e}_i$ as in Fig. 4, we obtain the table

where the (i, k)-entry is the product of shape parameters contributed from $\mu ^k \cdot \widetilde{\Delta }_1$ and $\mu ^k \cdot \widetilde{\Delta }_2$ to $\widetilde{e}_i$ (the empty entries are 1). The gluing equation around $\widetilde{e}_i$ is the product of the entries of the corresponding row in the above table, i.e., the product over the vertices of polygons around each edge $\widetilde{e}_i$ in Fig. 4. Hence, we have

$$\begin{aligned}{} & {} \textbf{G}(t) = \begin{pmatrix} 2 t &{} 2t \\ 0 &{} 0 \end{pmatrix}, \qquad \textbf{G}'(t) = \begin{pmatrix} t^2 &{} 1 \\ t &{} t^2 \end{pmatrix}, \qquad \textbf{G}''(t) = \begin{pmatrix} 0 &{} 0 \\ 2t^2 &{} 2t \end{pmatrix}, \end{aligned}$$

(41)

$$\begin{aligned}{} & {} \textbf{A}(t) = \begin{pmatrix} - t^2 + 2 t &{} 2t -1\\ -t &{} -t^2 \end{pmatrix}, \qquad \textbf{B}(t) = \begin{pmatrix} -t^2 &{} - 1 \\ 2t^2-t &{} -t^2+2t \end{pmatrix} , \end{aligned}$$

(42)

giving that

$$\begin{aligned} \textbf{A}(t)\textbf{B}(1/t)^T = \begin{pmatrix} -2t+2-2 t^{-1} &{} t + t^{-2} \\ t^{2} + t^{-1} &{} -2t+2-2 t^{-1} \end{pmatrix} , \end{aligned}$$

which specializes to the matrix $\textbf{A} \textbf{B}^T$ when $t=1$.

3.2 The knot $6_3$

The default SnapPy triangulation of the knot $6_3$ with isometry signature gLLPQccdefffhggaacv_aBBb has six tetrahedra $\Delta _1,\ldots ,\Delta _6$ with the peripheral torus shown in Fig. 6.

Fig. 6

The triangulation of the peripheral torus of $6_3$

The gluing equations of the six edges are

$$\begin{aligned} e_1&: z_1 z_2 z_3 z_4 z_6 =1,\\ e_2&: z'_1 z_2' (z''_2)^2 z'_4 (z''_4)^2 z'_6=1,\\ e_3&: z''_1 z'_2 z'_3 z'_5 z''_6 =1, \\ e_4&: z''_1 z'_3 z'_4 z'_5 z''_6 =1, \\ e_5&: z'_1 z_3 (z''_3)^2 z_5 (z''_5)^2 z'_6 = 1, \\ e_6&: z_1 z_2 z_4 z_5 z_6 =1 \end{aligned}$$

and the corresponding gluing equation matrices are

$$\begin{aligned} \textbf{G} = \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 \\ 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1 \end{pmatrix}, \qquad \textbf{G}' = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 1 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 \\ 0 &{} 1 &{} 1 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix}, \qquad \textbf{G}'' = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 2 &{} 0 &{} 2 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 2 &{} 0 &{} 2 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix}. \end{aligned}$$

(43)

The NZ matrices are

$$\begin{aligned} \textbf{A}= \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 &{} 0 &{} 1 \\ -1 &{} -1 &{} 0 &{} -1 &{} 0 &{} -1 \\ 0 &{} -1 &{} -1 &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} -1 &{} -1 &{} -1 &{} 0 \\ -1 &{} 0 &{} 1 &{} 0 &{} 1 &{} -1 \\ 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1 \end{pmatrix}, \qquad \textbf{B}= \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -1 &{} 1 &{} 0 &{} 1 &{} 0 &{} -1 \\ 1 &{} -1 &{} -1 &{} 0 &{} -1 &{} 1 \\ 1 &{} 0 &{} -1 &{} -1 &{} -1 &{} 1 \\ -1 &{} 0 &{} 2 &{} 0 &{} 2 &{} -1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix}, \end{aligned}$$

with

$$\begin{aligned} \textbf{A} \textbf{B}^T = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 &{} -1 &{} 2 &{} 0 \\ 0 &{} -1 &{} 3 &{} 2 &{} -4 &{} 0 \\ 0 &{} -1 &{} 2 &{} 3 &{} -4 &{} 0 \\ 0 &{} 2 &{} -4 &{} -4 &{} 6 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} \end{aligned}$$

symmetric. As in Sect. 3.1, we assign an integer to (each oriented edge and) each vertex of the dual complex according to the abelianization map $\alpha : \pi _1(M)\twoheadrightarrow \mathbb {Z}$. See Fig. 7.

Fig. 7

The dual 1-skeleton of $\mathbb {E}^2$

Choosing a lift $\widetilde{e}_i$ of $e_i$ as in Fig. 7, we have the table

where the (i, k)-entry is the product of shape parameters contributed from $\mu ^k \cdot \widetilde{\Delta }_1, \ldots , \mu ^k \cdot \widetilde{\Delta }_6$ to $\widetilde{e}_i$. Hence, we have

$$\begin{aligned} \textbf{G}(t)&= \begin{pmatrix} t&{} t^2 &{} t &{} 1 &{} 0 &{} t \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} t &{} 0 &{} t &{} 0 \\ t^2 &{} t^2 &{} 0 &{} t^2 &{} t^2 &{} t^2 \end{pmatrix}, \textbf{G}'(t) = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 1 &{} t^2 &{} 0 &{} t &{} 0 &{} t^3 \\ 0 &{} t&{} t &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} t^2 &{} t^2 &{} t^3 &{} 0 \\ t^2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix},\nonumber \\&\textbf{G}''(t) = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} t+t^3 &{} 0 &{} 1+t^2 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} t \\ t^2&{} 0 &{} 0 &{} 0 &{} 0 &{} t^3 \\ 0 &{} 0 &{} 1+t^2 &{} 0 &{} 1+t^2 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} \end{aligned}$$

(44)

and

$$\begin{aligned} \textbf{A}(t)&= \begin{pmatrix} t&{} t^2 &{} t &{} 1 &{} 0 &{} t \\ -1 &{} -t^2 &{} 0 &{} -t &{} 0 &{} -t^3 \\ 0 &{} -t &{} -t &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} -t^2 &{} -t^2 &{} -t^3 &{} 0 \\ -t^2 &{} 0 &{} t &{} 0 &{} t &{} -1 \\ t^2 &{} t^2 &{} 0 &{} t^2 &{} t^2 &{} t^2 \end{pmatrix}, \qquad \nonumber \\&\textbf{B}(t) = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -1 &{} t-t^2+t^3 &{} 0 &{} 1-t+t^2 &{} 0 &{} -t^3 \\ 1 &{} -t &{} -t &{} 0 &{} -1 &{} t \\ t^2&{} 0 &{} -t^2 &{} -t^2 &{} -t^3 &{} t^3 \\ -t^2 &{} 0 &{} 1+t^2 &{} 0 &{} 1+t^2 &{} -1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix}, \end{aligned}$$

(45)

giving that

$$\begin{aligned}{} & {} \textbf{A}(t)\textbf{B}(1/t)^T =\\{} & {} \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -2t+4-2 t^{-1} &{} -t^2+t- 1 &{} -1+t^{-1}- t^{-2} &{} t^{3}+t^{-2} &{} 0 \\ 0 &{} -1+t^{-1}- t^{-2} &{} 3 &{} t^{-1}+ t^{-3} &{} -t-1 -t^{-1}-t^{-2} &{} 0 \\ 0 &{} -t^2+t-1 &{} t^3 + t &{} 3 &{} -t^{3}-t^{2} -t^{-1}-1 &{} 0 \\ 0 &{} t^{2}+t^{-3} &{} -t^{2}-t^{1} -1-t^{-1} &{} -1-t^{-1} -t^{-2}-t^{-3} &{} 2t+2+2 t^{-1}&{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} \end{aligned}$$

which specializes to matrix $\textbf{A} \textbf{B}^T$ when $t=1$.

4 Proofs: twisted 1-loop invariant

In this section, we give proofs of the properties of the twisted 1-loop invariant.

Proof Theorem 1.6

We will use the notation of Theorem 1.5 which relates the NZ matrices of two triangulations ${\mathcal {T}}$ and $\overline{{\mathcal {T}}}$ obtained by a 2–3 Pachner move shown in Fig. 2. Recall that a 2–3 Pachner move on ${\mathcal {T}}$ is determined by two tetrahedra $\Delta _\alpha$ and $\Delta _\beta$ with a common face in ${\mathcal {T}}$. Dividing the bipyramid $\Delta _\alpha \cup \Delta _\beta$ into three tetrahedra $\Delta _a, \Delta _b,$ and $\Delta _c$ as in Fig. 2, we obtain a new ideal triangulation $\overline{{\mathcal {T}}}$ with one additional edge $e_0$. Note that one can read off relations of shape parameters between ${\mathcal {T}}$ and $\overline{{\mathcal {T}}}$ directly from Fig. 2:

$$\begin{aligned} z'_a= z_\alpha z_\beta , \ z'_b=\frac{1-1/z_\beta }{1-z_\alpha },\, z'_c = \frac{1-1/z_\alpha }{1-z_\beta } \text { and } z_\alpha = \frac{1-1/z'_b}{1-z'_c}, \, z_\beta = \frac{1-1/z'_c}{1-z'_b} \end{aligned}$$

(46)

with the gluing equation $z'_a z'_b z'_c=1$ for the edge $e_0$.

We first consider the flattening part of the definition (22). A combinatorial flattening of $\overline{{\mathcal {T}}}$ satisfies the equation $f'_a+f'_b+f'_c=2$ (coming from the edge $e_0$) and determines one of ${\mathcal {T}}$ by

$$\begin{aligned} \begin{aligned} f_\alpha&=f_b+f''_c,&f'_\alpha&= f''_a+ f_c&f''_\alpha&=f_a+f''_b,\\ f_\beta&=f''_b+f_c,&f'_\beta&= f''_a + f_b,&f''_\beta&=f_a+f''_c. \end{aligned} \end{aligned}$$

(47)

Then a straightforward computation shows that

$$\begin{aligned} \prod _\square \zeta ^{\square f^\square _a}_a \zeta _b^{\square f^\square _b} \zeta ^{\square f^\square _c}_c = \pm \frac{z_\alpha (1-z_\alpha )z_\beta (1-z_\beta )}{1-z_\alpha z_\beta } \prod _\square \zeta ^{\square f^\square _\alpha }_\alpha \zeta ^{\square f^\square _\beta }_\beta . \end{aligned}$$

(48)

Moreover, combining Equation (37) with (46), one checks that

$$\begin{aligned}&\begin{pmatrix} \displaystyle \sum _\square \overline{\textbf{G}}^\square (t)_{a}\zeta ^\square _a&\displaystyle \sum _\square \overline{\textbf{G}}^\square (t)_{b}\zeta ^\square _b&\displaystyle \sum _\square \overline{\textbf{G}}^\square (t)_{c}\zeta ^\square _c \end{pmatrix} \begin{pmatrix} \frac{1}{z_\alpha z_\beta } &{} \frac{1}{z_\alpha z_\beta }-1 &{} \frac{1}{z_\alpha z_\beta }-1 \\ 0 &{} \frac{z_\beta (1-z_\alpha )(1-z_\alpha z_\beta )}{1-z_\beta } &{} 0 \\ 0 &{} 0 &{} \frac{z_\alpha (1-z_\beta )(1-z_\alpha z_\beta )}{1-z_\alpha } \end{pmatrix}\\&\quad = Q \begin{pmatrix} 1&{} 0 &{} 0 \\ *&{} \displaystyle \sum _\square \textbf{G}^\square (t)_{\alpha } \zeta ^\square _\alpha &{} \displaystyle \sum _\square \textbf{G}^\square (t)_{\beta }\zeta ^\square _\beta \end{pmatrix} \begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} z_\alpha z_\beta (1-z_\alpha ) &{} z_\alpha (1-z_\alpha ) \\ 0 &{} z_\beta (1-z_\beta ) &{} z_\alpha z_\beta (1-z_\beta ) \end{pmatrix}\,, \end{aligned}$$

where the determinant of the $3 \times 3$ matrix in the left (resp., right) hand side is $(1-z_\alpha z_\beta )^2$ (resp., $z_\alpha (z_\alpha -1) z_\beta (z_\beta -1) (1-z_\alpha z_\beta ))$. Combining this fact with the equation (48) and the fact that $\det Q=1$, we conclude that $\tau ^{\textrm{CS}}(\overline{{\mathcal {T}}},t) = \pm \tau ^{\textrm{CS}}({\mathcal {T}},t)$. $\square$

Proof of Theorem 1.7

Using Equation (28) and the fact that a combinatorial flattening of ${\mathcal {T}}^{(n)}$ is simply given by n copies of that of ${\mathcal {T}}$, it follows that

$$\begin{aligned} \tau ^\textrm{CS}({\mathcal {T}}^{(n)},t^n)&= \det \left( \displaystyle \sum _{k \in \mathbb {Z}} \left( \sum _\square \textbf{G}_k^{(n)\square }\, \textrm{diag}(\zeta ^\square ,\ldots ,\zeta ^\square )\right) t^{nk}\right) \cdot \left( \prod _{j=1}^N\zeta _j^{f_j} \zeta _j'^{f_j'} \zeta _j''^{f_j''}\right) ^{-n} \end{aligned}$$

(49)

$$\begin{aligned}&=\det \begin{pmatrix} W_0 &{} W_1&{} \cdots &{} W_{n-2}&{} W_{n-1} \\ t^{n} W_{n-1} &{} W_0&{} \cdots &{} W_{n-3}&{} W_{n-2} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ t^{n} W_2 &{} t^n W_3&{} \cdots &{}W_0&{} W_1 \\ t^{n} W_1 &{} t^n W_2&{} \cdots &{}t^n W_{n-1}&{} W_0 \end{pmatrix} \cdot \left( \prod _{j=1}^N\zeta _j^{f_j} \zeta _j'^{f_j'} \zeta _j''^{f_j''}\right) ^{-n} \end{aligned}$$

(50)

where $W_r = \sum _{k \in \mathbb {Z}} \sum _\square \textbf{G}_{nk+r}^{\square } \, \textrm{diag} (\zeta ^\square )\,t^{nk}$ for $0 \le r \le n-1$.

The block matrix in the equation (50) is called a factor block circulant matrix where the factor is $\textrm{diag}(t^n,\ldots , t^n)$. It is known that a factor block circulant matrix admits a block-diagonalization in terms of the representer $P(z)= W_0+W_1 z +\cdots + W_{n-1}z^{n-1}$:

$$\begin{aligned} \begin{pmatrix} W_0 &{} W_1&{} \cdots &{} W_{n-2} &{} W_{n-1} \\ t^{n} W_{n-1} &{} W_0&{} \cdots &{} W_{n-3} &{} W_{n-2} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ t^{n} W_2 &{} t^n W_3&{} \cdots &{}W_0&{} W_1 \\ t^{n} W_1 &{} t^n W_2&{} \cdots &{} t^n W_{n-1} &{}W_0 \end{pmatrix} = V \begin{pmatrix} P(t) &{} &{} &{} &{} \\ &{} P(\omega \, t) &{} &{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} &{} P(\omega ^{n-1} \, t) \end{pmatrix} V^{-1} \end{aligned}$$

(51)

where $\omega$ is a primitive n-th root of unity and V is a block Vandermonde matrix

$$\begin{aligned} V= \begin{pmatrix} I &{} I &{}\cdots &{} I \\ H_0 &{}H_1 &{}\cdots &{} H_{n-1} \\ H_0^2 &{}H_1^2 &{}\cdots &{} H_{n-1}^2 \\ \vdots &{} \vdots &{} &{} \vdots \\ H_0^{n-1} &{}H_1^{n-1} &{}\cdots &{} H_{n-1}^{n-1}\\ \end{pmatrix}, \quad H_i = \omega ^{i} \, \textrm{diag}(t,\ldots ,t). \end{aligned}$$

(52)

We refer to [24] for details. In particular, we have

$$\begin{aligned} \det \begin{pmatrix} W_0 &{} W_1&{} \cdots &{} W_{n-2} &{} W_{n-1} \\ t^{n} W_{n-1} &{} W_0&{} \cdots &{} W_{n-3} &{} W_{n-2} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ t^{n} W_2 &{} t^n W_3&{} \cdots &{}W_0&{} W_1 \\ t^{n} W_1 &{} t^n W_2&{} \cdots &{} t^n W_{n-1} &{}W_0 \end{pmatrix} =\prod _{\omega ^n=1} \det P(\omega \, t) \end{aligned}$$

(53)

where, by definition,

$$\begin{aligned} P(\omega \, t)&= \sum _{r=0}^{n-1} W_r (\omega \, t)^r \\&=\sum _{r=0}^{n-1} \left( \sum _{k \in \mathbb {Z}} \sum _\square \textbf{G}_{nk+r}^{\square } \textrm{diag} (\zeta ^\square ) (\omega t)^{nk}\right) (\omega t)^{r} \\&=\sum _{r=0}^{n-1} \sum _{k \in \mathbb {Z}} \left( \sum _\square \textbf{G}_{nk+r}^{\square } \textrm{diag} (\zeta ^\square ) \right) t^{nk+r} \omega ^{nk+r} \\&=\sum _{k \in \mathbb {Z}} \left( \sum _\square \textbf{G}_{k}^{\square } \textrm{diag} (\zeta ^\square )\right) (\omega \, t)^{k} \qquad (\text {since} \,\, \omega ^n=1). \end{aligned}$$

Combining the above calculations, we obtain

$$\begin{aligned} \tau ^{\textrm{CS}}({\mathcal {T}}^{(n)},t^n) = \prod _{\omega ^n=1} \frac{\det \left( \sum _{k\in \mathbb {Z}} \sum _\square \textbf{G}_{k}^{\square }\, \textrm{diag} (\zeta ^\square )\,(\omega \, t)^{k}\right) }{ \prod _{j=1}^N\zeta _j^{f_j} \zeta _j'^{f_j'} \zeta _j''^{f_j''}} = \prod _{\omega ^n=1} \tau ^{\textrm{CS}}({\mathcal {T}}, \omega \, t). \end{aligned}$$

(54)

$\square$

Proof of Theorem 1.8

Let $R(t) = \sum _{\square } \textbf{G}^\square (t)\, \textrm{diag}(\zeta ^\square )$ and $R_i(t)$ denote its i-th row. Since the sum of all rows of $\textbf{G}^\square (1) = \textbf{G}^\square$ is $(2,\ldots ,2)$ and $\zeta _j + \zeta '_j+ \zeta ''_j =0$, the sum $R_1(1)+\cdots +R_N(1)$ is a zero vector. It follows that $\det R(1)=0$ and thus $\tau ^{\textrm{CS}}({\mathcal {T}},1)=0$.

Since the determinant is a multilinear map, we have

$$\begin{aligned} \left. \frac{\partial }{\partial t} \right| _{t=1} \det R(t) = \sum _{i=1}^{N} \det \begin{pmatrix} R_1(1) \\ \vdots \\ \left. \frac{\partial }{\partial t}\right| _{t=1} R_i(t) \\ \vdots \\ R_N(1) \end{pmatrix}. \end{aligned}$$

(55)

For $i \ne N$, we exchange the i-th row $\left. \frac{\partial }{\partial t} \right| _{t=1} R_i(t)$ with the N-th row $R_N(1)$ and replace $R_N(1)$ by $-R_1(1)-\cdots -R_{N-1}(1)$. Then after some elementary row operations, we obtain

$$\begin{aligned} \left. \frac{\partial }{\partial t} \right| _{t=1} \det R(t) =\sum _{i=1}^N \det \begin{pmatrix} R_1(1) \\ \vdots \\ R_{N-1}(1) \\ \left. \frac{\partial }{\partial t}\right| _{t=1} R_i(t) \end{pmatrix} = \det \begin{pmatrix} R_1(1) \\ \vdots \\ R_{N-1}(1) \\ \left. \frac{\partial }{\partial t}\right| _{t=1} \sum _{i=1}^N R_i(t) \end{pmatrix}. \end{aligned}$$

(56)

Comparing the definitions of equation (20) and (22), it suffices to show that $\left. \frac{\partial }{\partial t}\right| _{t=1} \sum _{i=1}^N R_i(t)$ agrees with $\frac{1}{2}\sum _\square \textbf{C}_\lambda ^\square \textrm{diag}(\zeta ^\square )$ up to linear combination of $R_1(1),\ldots , R_{N}(1)$.

Let $\widetilde{\Sigma }$ be the pre-image of the peripheral torus $\Sigma$ under the covering map $\widetilde{M} \rightarrow M$. Note that ${\mathcal {T}}$ induces a triangulation of $\widetilde{\Sigma }$ where vertices and triangles of $\widetilde{\Sigma }$ correspond to edges and tetrahedra of $\widetilde{\mathcal {T}}$, respectively. For each triangle $\Delta$ of $\widetilde{\Sigma }$ corresponding to the tetrahedron $\mu ^k \cdot \widetilde{\Delta }_j$, we assign a corner parameter $t^k \log z^\square _j$ to each corner of $\Delta$ according to the quad type of $\Delta _j$. Then the sum $r_i(t)$ of corner parameters around a vertex of $\widetilde{\Sigma }$ corresponding to the edge $\widetilde{e}_i$ is

$$\begin{aligned} r_i(t)=\sum _{j=1}^N \sum _\square (\textbf{G}^\square (t))_{ij} \log z_j^\square . \end{aligned}$$

(57)

It follows that (see Equation (6))

$$\begin{aligned} R_i(t) = \begin{pmatrix} \frac{\partial }{\partial z_1} r_i(t)&\cdots&\frac{\partial }{\partial z_N} r_i(t) \end{pmatrix}. \end{aligned}$$

(58)

We choose any lift $\widetilde{\lambda }$ of $\lambda$ to $\widetilde{\Sigma }$. Since $\alpha (\lambda )=0$, $\widetilde{\lambda }$ is still a loop in $\widetilde{\Sigma }$. Up to homotopy, we may assume that $\widetilde{\lambda }$ is an edge-path in $\widetilde{\Sigma }$ so that the surface S bounded by $\widetilde{\lambda }$ and $\mu \cdot \widetilde{\lambda }$ is triangulated. Here we view S as a closed cylinder whose boundary is consisted of $\widetilde{\lambda }$ and $\mu \cdot \widetilde{\lambda }$. Let $c_\lambda (t)$ (resp., $\check{c}_\lambda (t)$) be the sum of corner parameters in S that are adjacent (resp., not adjacent) to $\widetilde{\lambda }$. By definition, the equation $c_\lambda (1)=0$ represents the completeness equation of $\lambda$. Hence,

$$\begin{aligned} \sum _\square \textbf{C}_\lambda ^\square \textrm{diag}(\zeta ^\square ) = \begin{pmatrix} \frac{\partial }{\partial z_1} c_\lambda (1)&\cdots&\frac{\partial }{\partial z_N} c_\lambda (1) \end{pmatrix}. \end{aligned}$$

(59)

Also, since S consists of triangles and $\zeta _j + \zeta '_j +\zeta ''_j=0$ for all j, we have

$$\begin{aligned} \frac{\partial }{\partial z_j} (c_\lambda (t)+\check{c}_\lambda (t))=0. \end{aligned}$$

(60)

On the other hand, $t c_\lambda (t)$ is the sum of corner parameters adjacent to $\mu \cdot \widetilde{\lambda }$ and not in S. It follows that the sum of corner parameters around vertices in $S {\setminus } \widetilde{\lambda }$ is given by $tc_\lambda (t)+\check{c}_\lambda (t)$. Since $S {\setminus } \widetilde{\lambda }$ is a fundamental domain of $\Sigma$, exactly two vertices in $S \setminus \widetilde{\lambda }$ correspond to a lift of $e_i$ for each $1 \le i \le N$. It follows that

$$\begin{aligned} t c_\lambda (t)+\check{c}_\lambda (t)= \sum _{i=1}^N (t^{a_i}+t^{b_i}) \, r_i(t). \end{aligned}$$

(61)

for some $a_i$ and $b_i \in \mathbb {Z}$ and thus

$$\begin{aligned} \left. \frac{\partial }{\partial t} \right| _{t=1} (t c_\lambda (t)+\check{c}_\lambda (t)) = \sum _{i=1}^N (a_i+b_i) r_i(1) +2 \left. \frac{\partial }{\partial t} \right| _{t=1} \sum _{i=1}^Nr_i(t) . \end{aligned}$$

(62)

Taking the partial derivative with respect to $z_j$, we obtain

$$\begin{aligned} \left. \frac{\partial }{\partial t} \right| _{t=1} \frac{\partial }{\partial z_j} \sum _{i=1}^Nr_i(t)&= \frac{1}{2} \frac{\partial }{\partial z_j} \left. \frac{\partial }{\partial t} \right| _{t=1} (t c_\lambda (t)+\check{c}_\lambda (t)) - \frac{1}{2} \sum _{i=1}^N (a_i+b_i) \frac{\partial }{\partial z_j}r_i(1) \end{aligned}$$

(63)

$$\begin{aligned}&=\frac{1}{2} \frac{\partial }{\partial z_j} c_\lambda (1) - \frac{1}{2} \sum _{i=1}^N (a_i+b_i) \frac{\partial }{\partial z_j}r_i(1) \,, \end{aligned}$$

(64)

where the second equation is followed from the equation (60) with the fact $t c_\lambda (t)+\check{c}_\lambda (t)=(t-1)c_\lambda (t) + c_\lambda (t)+\check{c}_\lambda (t)$. Combining the equations (58), (59), and (64), we obtain the desired result that $\left. \frac{\partial }{\partial t}\right| _{t=1} \sum _{i=1}^N R_i(t)$ agrees with $\frac{1}{2}\sum _\square \textbf{C}_\lambda ^\square \textrm{diag}(\zeta ^\square )$ up to linear combination of $R_1(1),\ldots , R_{N}(1)$:

$$\begin{aligned} \left. \frac{\partial }{\partial t} \right| _{t=1} \sum _{i=1}^N R_i(t) = \frac{1}{2}\sum _\square \textbf{C}_\lambda ^\square \textrm{diag}(\zeta ^\square ) + \frac{1}{2} \sum _{i=1}^N (a_i+b_i) R_i(1). \end{aligned}$$

(65)

$\square$

Remark 4.1

Rewriting Equation (65) in terms of NZ matrices, we have

$$\begin{aligned} \textbf{X}_\lambda = \begin{pmatrix} x_1(1) \\ \vdots \\ x_{N-1}(1) \\ 2\left. \frac{d}{dt} \right| _{t=1} (x_1(t) + \cdots + x_N(t)) \end{pmatrix} \end{aligned}$$

for $\textbf{X} = \textbf{A}$ and $\textbf{B}$ where $x_1(t),\ldots , x_N(t)$ are the rows of $\textbf{X}(t)$.

Proof of Corollary 1.9

The statement is equivalent to

$$\begin{aligned} \det \left( \textbf{A}(t)\, \textrm{diag}(\zeta ) + \textbf{B}(t)\, \textrm{diag}(\zeta '') \right) = \varepsilon t^r \det \left( \textbf{A}(1/t)\, \textrm{diag}(\zeta ) + \textbf{B}(1/t)\, \textrm{diag}(\zeta '') \right) \end{aligned}$$

(66)

for some $\varepsilon = \pm 1$ and some integer r and some choice of quads of ${\mathcal {T}}$. We make such a choice such that $\textbf{B}$ is non-singular. This is always possible; see [6, App.A]. Then, $\det \textbf{B}(t) \ne 0$, since $\textbf{B}(1)=\textbf{B}$. Conjecture 1.4 implies that $\det \textbf{B}(t)=\varepsilon t^r \det \textbf{B}(1/t) \ne 0$. This, combined with Theorem 1.2 gives

$$\begin{aligned}&\det \left( \textbf{A}(t) \,\textrm{diag}(\zeta ) + \textbf{B}(t)\, \textrm{diag}(\zeta '') \right) \\&\quad = \det \textbf{B}(t) \det \left( \textbf{B}(t)^{-1} \textbf{A}(t) + \textrm{diag}(\zeta ''/\zeta )\right) \det (\textrm{diag}(\zeta )) \\&\quad =\varepsilon t^r\det \textbf{B}(1/t) \det \left( \textbf{B}(1/t)^{-1} \textbf{A}(1/t) + \textrm{diag}(\zeta ''/\zeta )\right) \det (\textrm{diag}(\zeta )) \\&\quad =\varepsilon t^r\det \left( \textbf{A}(1/t)\, \textrm{diag}(\zeta ) + \textbf{B}(1/t)\, \textrm{diag}(\zeta '') \right) \end{aligned}$$

Note that Theorem 1.2 implies that $\textbf{B}(t)^{-1} \textbf{A}(t)= (\textbf{B}(1/t)^{-1} \textbf{A}(1/t))^T$ which is used in the second equality above. $\square$

We end this section by giving a proof of Equation (26). Taking the derivative of Equation (25) at $t=1$ and then simplifying the result by Theorem 1.8, we obtain

$$\begin{aligned} \frac{\tau ^\textrm{CS}_\lambda ({\mathcal {T}}^{(n)})}{\tau ^\textrm{CS}_\lambda ({\mathcal {T}})} = \frac{1}{n} \prod _{ \begin{array}{c} \omega ^n=1 \\ \omega \ne 1 \end{array}} \tau ^\textrm{CS}({\mathcal {T}},w) \end{aligned}$$

(67)

which is equivalent to Equation (26) due to Theorem 4.1 of [23] (explicitly, the ratio $\tau _\lambda ^{\textrm{CS}}({\mathcal {T}})/\tau _\mu ^{\textrm{CS}}({\mathcal {T}})$ is the cusp shape of M and $\tau _\lambda ^{\textrm{CS}}({\mathcal {T}}^{(n)})/\tau _\mu ^{\textrm{CS}}({\mathcal {T}}^{(n)})$ is n times of that).

5 Examples, continued

In this section, which is a continuation of Sect. 3, we compute the twisted 1-loop invariant of an ideal triangulation using the methods of SnapPy.

5.1 The knot $4_1$

In Sect. 3.1, we already gave the twisted NZ matrices of the $4_1$ knot. Using the same notation, we now give the remaining data, namely the shapes of the complete hyperbolic structure and flattenings, which are needed to compute the twisted 1-loop invariant.

The solution for the complete structure is $z_1=z_2=\frac{1+\sqrt{-3}}{2}$. Equations (41) and (42) give

$$\begin{aligned} \textbf{G}(t)\, \textrm{diag}(\zeta ) + \textbf{G}'(t)\, \textrm{diag}(\zeta ') + \textbf{G}''(t)\, \textrm{diag}(\zeta '') = \begin{pmatrix} 2\zeta _1 t + \zeta _1' t^2 &{} \zeta _2' + 2 \zeta _2 t\\ \zeta _1' t+ 2 \zeta _1'' t^2 &{} 2 \zeta _2'' t + \zeta _2' t^2 \end{pmatrix}. \end{aligned}$$

(68)

One easily checks that $(f_1,f_2)=(0,0)$, $(f'_1,f'_2)=(1,1)$, and $(f''_1,f''_2)=(0,0)$ are a combinatorial flattening of ${\mathcal {T}}$. Therefore, the twisted 1-loop invariant of ${\mathcal {T}}$ is given by

$$\begin{aligned} \tau ^{\textrm{CS}}({\mathcal {T}},t)&= \pm \frac{\det \begin{pmatrix} 2\zeta _1 t + \zeta _1' t^2 &{} \zeta _2' + 2 \zeta _2 t\\ \zeta _1' t+ 2 \zeta _1'' t^2 &{} 2 \zeta _2'' t + \zeta _2' t^2 \end{pmatrix} }{\zeta '_1 \zeta '_2} \end{aligned}$$

(69)

$$\begin{aligned}&= \pm t(t-1) \left( t^2- \frac{z_1 z_2+2z_1 +2z_2-4}{z_1z_2}\, t +1\right) . \end{aligned}$$

(70)

Substituting the solution for the complete structure into the above, we obtain

$$\begin{aligned} \tau ^{\textrm{CS}}({\mathcal {T}},t)=\pm t(t-1)(t^2-5t+1) \end{aligned}$$

well defined up to multiplication by a monomial $\pm t^r$ for some integer r, hence

$$\begin{aligned} \tau _\lambda ^{\textrm{CS}}({\mathcal {T}})=\pm 3 \,. \end{aligned}$$

5.2 The knot $6_3$

In this section, we give the geometric solution and the flattenings of the triangulation of the $6_3$ knot to compute its twisted 1-loop invariant, following the notation of Sect. 3.2.

The trace field of the $6_3$ knot is the number field of type [0, 3] and discriminant $-11 \cdot 31^2$ given by $F=\mathbb {Q}[\xi ]$ where $\xi \approx 1.073 - 0.558 \sqrt{-1}$ satisfies $\xi ^6 - \xi ^5 - \xi ^4 + 2 \xi ^3 - \xi + 1=0$. The solution for the complete structure is given exactly

$$\begin{aligned} (z_1, z_2, z_3, z_4, z_5, z_6) =(-\xi ^2 + \xi , -\xi ^2 + 1, -\xi ^3 + \xi ,-\xi ^2 + 1, -\xi ^3 + \xi ,-\xi ^2 + \xi )\nonumber \\ \end{aligned}$$

(71)

and approximately by

$$\begin{aligned}&z_1 \approx 0.23279 + 0.64139 \, i, z_2\approx 0.15884 + 1.20014 \, i, z_3 \approx 0.84116 + 1.20014 \, i, \\&z_4 \approx 0.15884 + 1.20014 \, i, z_5 \approx 0.84116+ 1.20014 \, i, z_6 \approx 0.23279 + 0.64139 \, i. \end{aligned}$$

It is easy to check that $(f_1,\ldots ,f_6)=(0,1,0,1,0,0)$, $(f'_1,\ldots ,f'_6)=(1,0,1,0,1,1)$, and $(f''_1,\ldots ,f''_6)=(0,0,0,0,0,0)$ is a combinatorial flattening of ${\mathcal {T}}$. Equations (44) and (45) give that

$$\begin{aligned}&\tau ^{\textrm{CS}}({\mathcal {T}},t) =\frac{\det \left( \textbf{G}(t)\, \textrm{diag}(\zeta ) + \textbf{G}'(t)\, \textrm{diag}(\zeta ') + \textbf{G}''(t)\, \textrm{diag}(\zeta '')\right) }{\zeta '_1 \zeta _2 \zeta _3' \zeta _4 \zeta '_5 \zeta '_6}\\&\quad = \frac{\det \begin{pmatrix} \zeta _1 t &{} \zeta _2 t^2 &{} \zeta _3 t &{} \zeta _4 &{} 0 &{} \zeta _6 t\\ \zeta _1' &{} \zeta _2'' t + \zeta _2' t^2 + \zeta _2''t^3 &{} 0 &{} \zeta _4''+\zeta _4' t + \zeta _4''t^2 &{} 0 &{} \zeta _6' t^3 \\ \zeta _1'' &{} \zeta _2' t &{} \zeta _3't &{} 0 &{} \zeta _5' &{} \zeta _6'' t \\ \zeta _1'' t^2 &{} 0 &{} \zeta _3' t^2 &{} \zeta _4' t^2 &{} \zeta _5' t^3 &{} \zeta _6'' t^3 \\ \zeta _1' t^2 &{} 0 &{} \zeta _3'' + \zeta _3 t + \zeta _3''t^2 &{} 0 &{} \zeta _5'' +\zeta _5 t + \zeta _5'' t^2 &{} \zeta _6'\\ \zeta _1 t^2 &{} \zeta _2 t^2 &{} 0&{} \zeta _4 t^2 &{} \zeta _5 t^2 &{} \zeta _6 t^2 \end{pmatrix} }{\zeta '_1 \zeta _2 \zeta _3' \zeta _4 \zeta '_5 \zeta '_6}\\ \end{aligned}$$

Substituting the solution for the complete structure into the above, we obtain

$$\begin{aligned} \tau ^{\textrm{CS}}({\mathcal {T}},t) =&\, (t-1) t^8 \big (44 - 15 \xi - 15 \xi ^2 + 34 \xi ^3 - 19 \xi ^5 \\&+(t+t^{-1})(-31 + 7 \xi + 7 \xi ^2 - 10 \xi ^3 + 3 \xi ^5) \\&+(t^2+t^{-2})(15 - 3 \xi - 3 \xi ^2 + 2 \xi ^3 + \xi ^5) -5(t^3+t^{-3}) + (t^4+t^{-4})\big ) \\ \approx&\, t^4 (-1.000 + 6.000 t - 12.805 t^2 + 33.472 t^3 - 85.242 t^4\\&+ 85.242 t^5 - 33.472 t^6 + 12.805 t^7 -6.000 t^8 + 1.000 t^9) . \end{aligned}$$

up to multiplication by a monomial $\pm t^r$ for some integer r, hence

$$\begin{aligned} \tau _\lambda ^{\textrm{CS}}({\mathcal {T}})=\pm (4 - 7 \xi - 7 \xi ^2 + 18 \xi ^3 - 11 \xi ^5) \approx \pm 15.8506\,. \end{aligned}$$