Toward a design methodology for particle dampers by analyzing their energy dissipation

Abstract

Particle dampers show a huge potential to reduce undesired vibrations in technical applications even under harsh environmental conditions. However, their energy dissipation depends on many effects on the micro- and macroscopic scale, which are not fully understood yet. This paper aims toward the development of design rules for particle dampers by looking at both scales. This shall shorten the design process for future applications. The energy dissipation and loss factor of different configurations are analyzed via the complex power for a large excitation range. Comparisons to discrete element simulations show a good qualitative agreement. These simulations give an insight into the process in the damper. For monodisperse systems, a direct correlation of the loss factor to the motion modes of the rheology behavior is shown. For well-known excitation conditions, simple design rules are derived. First investigations into polydisperse settings are made, showing a potential for a more robust damping behavior.

1 Introduction

Particle dampers show a huge potential for the vibration suppression of mechanical systems. They are very simple and robust design elements. As a container for the granular matter, either a box or a hole in the vibrating structure is used. Vibrational energy is transferred through the container onto the particles. Inelastic collisions and frictional effects inside the granular matter result in an energy dissipation and thus reduce the structural vibrations.

As a derivative of classical impact dampers, particle dampers show the same robust properties against harsh environmental conditions [23, 34]. In many cases they add only little mass to the system [16] and can be applied to a wide frequency range [4]. As a passive damping device, they additionally lead to inherently stable systems.

So far, particle dampers were successfully used in first different technical applications, e.g., for a rotary printing equipment [35], a Space Shuttle Main Engine liquid oxygen inlet tee [22], an oscillatory saw [14], or to spacecraft cantilever beam type appendages [33]. Although particle dampers show a huge potential, they are only little used in other technical applications. The major reason for this is their highly nonlinear behavior and the variety of influence parameters.

To obtain a better understanding of the complex mechanisms inside particle dampers, the discrete element method (DEM) is receiving more and more attention. The DEM has been developed by Cundall and Strack [5] for the simulation of granular systems consisting of discs and spheres. Nowadays, arbitrary particle shapes can be simulated [17, 20] but still spherical particles are mostly used due to efficiency reasons. The particle dynamics are mainly influenced by the particle interactions. Therefore, various contact models have been developed. These penalty laws can be but do not need to be based on physical laws [25].

To analyze the damping properties of particle dampers, their energy dissipation can be directly analyzed, i.e., without an underlying vibrating structure. Then, the energy dissipation and the loss factor are calculated using the complex power method, which was introduced for particle dampers by Yang [37]. Similar studies have also been performed by [7, 27, 36]. Also, Masmoudi [19] performed an extensive study including the effect of the dynamical particle mass. Indeed, in all cases the excitation range concerning the frequency and acceleration is relatively small. By Saluena [29] the motion modes of the rheology behavior of vibrating granular material are analyzed and compared to the loss factor. There, three different regimes are determined, namely the solid-, convective, and gas-like ones. By Zhang [39] this classification is refined into seven different motion modes to solid-like, local fluidization, global fluidization, convection, Leidenfrost effect, bouncing bed, and buoyancy convection. Also, Yin [38] studied those regimes and found a correlation to the loss factor. In all cases, no parameter analysis is performed and only a small excitation range is analyzed again. By Bannerman [3] and Sack [28] the bouncing bed motion mode was studied under zero gravity and the effecting parameters are determined. A simple formula for an optimized damper under this condition is derived just based on the gap clearance.

The insights of these results are combined in this paper and are applied to a large excitation range. Thus, a better understanding is obtained to develop a design methodology for particle dampers in the future. The DEM model is validated by experiments. In the DEM different motion modes are observed. Also, it is analyzed whether the formula of Bannerman and Sack [3, 28] for the bouncing bed motion mode can be applied under the condition of gravity. Then, different gap clearances are studied. These results are also extended to different particle radii, container shapes, sizes, and rotations. The simulation is also used to investigate the influence of the micro-mechanical behavior. At last, an outlook on the benefits of polydisperse systems is given.

This paper is organized in the following way: In Sect. 2 the theory to the complex power method and the motion modes is introduced. In Sect. 3 the experimental and numerical setups are explained. The results and obtained insights are then presented in Sect. 4. Finally, the conclusion is given in Sect. 5.

2 Characterization methods

Throughout this paper, the granular matter is subjected to an horizontal harmonic vibration by the container of form

$$\begin{aligned} x = X \sin (\varOmega t), \end{aligned}$$

(1)

with amplitude X and angular frequency $\varOmega = 2 \pi f$. The corresponding container velocity and acceleration follow as ${\dot{x}} = X \varOmega \cos (\varOmega t)$ and ${\ddot{x}} = -X \varOmega ^2 \sin (\varOmega t)$. Often, the dimensionless excitation intensity $\varGamma$ is used

$$\begin{aligned} \varGamma = \frac{X \varOmega ^2}{g}, \end{aligned}$$

(2)

with g as gravity constant. For such a vibration, different rheological behaviors of the granular material can be observed. These rheological behaviors can be divided into eight different motion modes. These motion modes describe the dynamics of the particle system. As the system exhibits different dynamics, also the amount of energy dissipation varies. This can be analyzed by using the complex power. The motion modes and complex power are described in the following.

2.1 Motion modes

Saluena [29] studied the motion modes of a horizontal vibrating granular material. Three different regimes are determined, namely the solid-, convective, and gas-like regimes. By Eshuis et al. [8] and Ansari et al. [2] additionally, the Leidenfrost effect, bouncing bed, and undulation states are reported for vertical vibrated granular matter. Zhang [39] classified his vertical vibrated granular matter into seven different motion modes, namely solid-like, local fluidization, global fluidization, convection, Leidenfrost effect, bouncing bed, and buoyancy convection. This classification of Zhang is also used by Yin [38]. To distinguish the different modes, animations, phase diagrams, and experimental observations can be used. Indeed, this task is not always trivial and unambiguous as the transition between the motion modes is smooth.

In this paper, five different motion modes are observed in the simulation of the particle dampers and shown in Fig. 1. In the upper picture, the absolute velocity of the granular matter is shown. In the lower one, the relative velocity of the granular matter to the container is pictured. All phase diagrams are taken at a container position of $x=0$, i.e., at the center of the stroke and the maximum container velocity.

The solid-like state, see Fig. 1a, is characterized by almost no relative motion between the particles and the container. This causes the granular matter just to look like one added block, staying at the container base and moving with the same velocity as the container. Here, this mode is considered as long as only one particle layer is showing some relative motion. It is reported by Eshuis et al. [8] and Ansari et al. [2] that this state occurs at low excitation intensities up to $\varGamma \approx 1$.

For excitation intensities $\varGamma > 1$, the granular systems come first in a state of local fluidization, see Fig. 1b. Particles located at the top surface become fluidized, i.e., irregular relative motion between the particles, while particles at the bottom still behave like a solid.

If the excitation intensity is further increased, the whole particle system becomes fluidized, called global fluidization, as shown in Fig. 1c. The transition from solid, to local fluidization to global fluidization is also called solid–fluid transition by Saluena [29].

It is reported that from this state, the particle system can migrate in different motion modes, like bouncing bed, convection, or Leidenfrost effect [38]. However, the Leidenfrost effect has only been observed for vertical vibrations. For the investigated particle dampers, only the bouncing bed motion mode is observed, see Fig. 1d. This means the particles move like a single body, but in contrast to the solid-like state, they do not stay on the container base but are distributed along the plane perpendicular to the container excitation.

In this research we also observed a motion mode we called decoupled, which is shown in Fig. 1e. This motion mode also migrates from the global fluidization. It is characterized by a very small absolute particle velocity compared to the velocity of the container. Thus, the granular matter appears to be decoupled. This can especially be observed at the relative velocity, as this one is pointing against the container motion.

Fig. 1

Different motion modes with the absolute particle velocity (top) and their relative velocity to the container (bottom) at $x=0$. The colors show the magnitude of the in-plane particle velocity normed by the container velocity ${\dot{X}}$ from low (blue) to high (red)

2.2 Complex power

In order to calculate the energy dissipation inside a vibrating granular matter, the complex power P is used. This concept was first applied to particle dampers by Yang [37]. Here, it is used as well in the experiments as in the simulations. For a given harmonic excitation, the complex power P is calculated by

$$\begin{aligned} P = \frac{1}{2} F V^{*}. \end{aligned}$$

(3)

Hereby, F denotes the fast Fourier transform (FFT) of the excitation signal and $V^{*}$ the conjugate FFT of the container velocity signal. The dissipated power $P_{\mathrm{diss}}$ and the maximum power stored in a cycle $P_{\mathrm{max}}$ follow from the complex power as

$$\begin{aligned} P_{\mathrm{diss}}&= \text {Real}(P) = \frac{1}{2} |F| |V| \cos (\phi _{\mathrm{F}} - \phi _{\mathrm{V}}), \end{aligned}$$

(4)

$$\begin{aligned} P_{\mathrm{max}}&= \text {Imag}(P) = \frac{1}{2} |F| |V| \sin (\phi _{\mathrm{F}} - \phi _{\mathrm{V}}). \end{aligned}$$

(5)

The phase angles of the force and velocity signals are denoted by $\phi _{\mathrm{F}}$ and $\phi _{\mathrm{V}}$, respectively. Dividing the dissipated power by the excitation frequency $\varOmega$, one obtains the dissipated energy per radian $E_{\mathrm{diss}}$ and the dissipated energy per cycle $\widetilde{E}_{\mathrm{diss}}$

$$\begin{aligned} E_{\mathrm{diss}}&= \frac{P_{\mathrm{diss}}}{\varOmega }, \end{aligned}$$

(6)

$$\begin{aligned} \widetilde{E}_{\mathrm{diss}}&= 2 \pi E_{\mathrm{diss}}. \end{aligned}$$

(7)

Following [37] the loss factor $\eta$ is defined as the ratio of the dissipated power to the maximum power stored in a cycle as

$$\begin{aligned} \eta = \frac{P_{\mathrm{diss}}}{P_{\mathrm{max}}} = \frac{E_{\mathrm{diss}}}{E_{\mathrm{max}}}. \end{aligned}$$

(8)

However, this classical definition of the loss factor is indeed not meaningful for application to particle dampers, due to the scaling with the maximum energy stored in a cycle. Therefore, here instead we adopted the approach of [19]. The reduced loss factor $\eta ^*$ is calculated by a scaling of the dissipated energy with the kinetic energy of the particle system using the mass of the particle bed $m_{\mathrm{bed}}$ to

$$\begin{aligned} \eta ^* = \frac{E_{\mathrm{diss}}}{\frac{1}{2} m_{\mathrm{bed}} V^2}. \end{aligned}$$

(9)

As a consequence, the reduced loss factor is independent of the container and particle mass and enables the comparison of different particle settings.

Another important quantity is the effective particle mass $m_{\mathrm{eff}}$. The effective particle mass describes how much mass of the particle bed $m_{\mathrm{bed}}$ is felt by the container, i.e., how much the mass of the granular matter is coupled to the container movement. It can be calculated by the effective moving mass $M_{\mathrm{eff}}$, which consists of the container mass $m_{\mathrm{con}}$ and the effective particle mass $m_{\mathrm{eff}}$ as $M_{\mathrm{eff}} = m_{\mathrm{con}} + m_{\mathrm{eff}}$ [30]. The effective moving mass is determined by dividing the FFT of the excitation signal F by the FFT of the acceleration signal A to

$$\begin{aligned} M_{\mathrm{eff}} = \frac{F}{A} = \frac{F}{V \varOmega }. \end{aligned}$$

(10)

3 Experimental and numerical setup

The experimental and numerical setups are developed, to analyze the motion modes and the resulting reduced loss factors of different particle settings. In both setups, a particle damper is subjected to a horizontal vibration over a large excitation range. An experimental and a numerical setting is used as this enables the analysis of various different settings. The experimental one is especially suited for large or polydisperse systems. The numerical setup is based on the discrete element method. With it, insights about the complex particle dynamics can be obtained, as, for instance, about the motion modes. Also, the micro-mechanical behavior or different container geometries can be analyzed.

3.1 Experimental setup

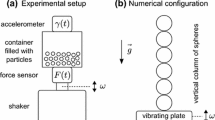
The experimental analysis is performed with the system shown in Fig. 2.

Fig. 2

Schematic representation (left) and picture (right) of the testbed

The particle container is realized as a cubical aluminum box with an inner edge length of 4 cm and a mass of $m_{\mathrm{con}} = 165\hbox { g}$. The container is excited by a controlled harmonic force via a shaker. The excitation force is controlled in such a way that the frequency and acceleration magnitude of the container stays constant. The force sensor, the accelerometers, and the control system are from BrÜel & Kjaer. Two accelerometers are used: the first for the controller and the second to trigger the measurement. While the container is excited by the LDS V455 shaker, its acceleration is controlled via the LDS Comet system. Due to the impacting particles on the container walls, the acceleration signal is very noisy. In order to use this acceleration signal in the control of the excitation, this accelerometer is additionally equipped with a mechanical low-pass filter. It consists of a plastic tube with a Young’s modulus of 86 N/mm$^2$. This filter element is designed in a way that its eigenfrequency is at 2.5 kHz. Hence, single particle impacts on the container walls are filtered efficiently, as their contact frequency is normally significantly above 5 kHz. Simultaneously, frequencies up to the excitation range of 1 kHz are only little influenced.

The velocity of the particle container is measured via a laser vibrometer (LV), the PSV-500, from Polytec. The data acquisition of the velocity and force signals are accomplished by the front end of the PSV-500 with a sampling frequency of 40 kHz. The second accelerometer, seen in Fig. 2, is not equipped with a filter as it is only used for triggering the measurement. The feasible measurement range of the system is between 40 Hz and 1 kHz and between $\varGamma = 1$ and $\varGamma = 40$. The measurement range is divided into a logarithmic grid of 108 points. Nine frequencies and twelve acceleration values are used, and each combination is measured for a duration of 2.5 s.

The setup is designed in a stiff way such that bending due to the assembly and container weight are negligible. Thus, only very little vibration in vertical (transvers) direction is observed.

3.2 Discrete element method

The discrete element method (DEM) is a discrete simulation method for granular materials. Every particle is considered as an unconstrained moving body only influenced by applied forces. The dynamics are described by Newton’s and Euler’s equation of motion for every particle [25]. For spherical particles, this reads

$$\begin{aligned} m_i {\ddot{{\varvec{x}}}} _i = {{\varvec{F}}} _i, \quad {{\varvec{I}}} _i {\dot{{\varvec{\omega }}}} _i = {{\varvec{M}}} _i \quad (i = 1, ..., N_{\mathrm{p}}), \end{aligned}$$

(11)

with ${\ddot{{\varvec{x}}}} _i$ and ${\dot{{\varvec{\omega }}}} _i$ being the translational and rotational accelerations. The particle mass is denoted by $m_i$ and its diagonal inertia tensor by ${{\varvec{I}}} _i$, whereby all three entries of ${{\varvec{I}}} _i$ are identical. The applied forces and moments are ${{\varvec{F}}} _i$ and ${{\varvec{M}}} _i$, and $N_{\mathrm{p}}$ is the total number of particles. Equation 11 is in general a coupled nonlinear differential equation with $6N_{\mathrm{p}}$ degrees of freedom for 3D simulations. Particle systems often contain a large number of particles (up to thousands or millions). During the time integration, all existing contacts need to be detected and resolved in every time step. Therefore, efficient detection algorithms and contact laws are needed. Also, the choice of an appropriate time integration scheme is crucial [9]. In this research, the algorithms presented in [21] are used and only shortly introduced.

3.2.1 Contact forces

In DEM simulations, particle–particle and particle–wall contacts occur. The contact partners are treated as rigid, thus only touching in a single point, as shown in Fig. 3. In continuous contact modeling, the contact partners i and j are allowed to overlap, and virtually connected by unilateral springs and dampers. Hereby, the corresponding contact forces occur which counteract the overlap ${{\delta }}$.

Fig. 3

Contact states of two spheres

In the simulations here, the formula of Gonthier [13] for the normal contact force is used. It is based on the contact law of Hertz [15] using physical parameters, namely the particle radius $r_{i/j}$, the Young’s modulus $E_{i/j}$ and the Poisson’s ratio $\nu _{i/j}$, and follows

$$\begin{aligned} F_{\mathrm {N}} = k \delta ^{3/2} \left( 1 + \frac{\bar{d}}{e} \frac{{\dot{{\delta }}}}{{\dot{{\delta }}} _{\mathrm{a}}} \right) . \end{aligned}$$

(12)

Hereby, the contact stiffness and the material parameters are given as

$$\begin{aligned} k&= \frac{4}{3 \pi (h_i + h_j)} \sqrt{\frac{r_i r_j}{r_i + r_j}}, \end{aligned}$$

(13)

$$\begin{aligned} h_{i/j}&= \frac{1 - \nu _{i/j}^2}{\pi E_{i/j}}. \end{aligned}$$

(14)

The penetration velocity and the initial penetration velocity in normal direction are denoted as ${\dot{{\delta }}}$ and ${\dot{{\delta }}} _{\mathrm{a}}$ respectively. The coefficient of restitution e ($0< e < 1$) controls the amount of energy dissipation during the contact. The nonlinear parameter $\bar{d}$ is only dependent on e and can be solved offline [13].

For spherical particles, the tangential forces result only from sticking and sliding friction, whereas the resistance of the surface is described by the coefficient of friction $\mu$. For highly dynamical systems the sticking friction can be neglected [9]. When only sliding friction is considered, a smoothing hyperbolic tangent function can be used, to avoid jumps in the friction forces at zero velocity, see [1]. Then, the sliding friction force reads

$$\begin{aligned} {{\varvec{F}}} _{\mathrm {R}} = -\mu |F_{\mathrm {N}}| {{\varvec{t}}} \tanh (\tau |{{\varvec{v}}} _{\mathrm {P}}^{\mathrm{t}}|) , \end{aligned}$$

(15)

with ${{\varvec{v}}} _{\mathrm {P}}^{\mathrm{t}}$ being the relative, tangential velocity at the boundary point P and $\tau$ is the smoothing parameter. The tangential direction is denoted by ${{\varvec{t}}}$. The resulting torques on the particles are only depending on the friction forces, as the normal forces are always pointing toward the center of mass of the spherical particles. For comparison also sticking friction is implemented, see [6]. However, in the simulation, this model is much more time-consuming and did not change the amount of dissipated energy of the particle dampers.

3.2.2 Contact detection and time integration

Another very important component of the DEM is the contact detection. All existing contacts have to be determined in every time step. A variety of algorithms have been developed for this task, such as sort-based, cell-based, or tree-based ones, decreasing the complexity to an optimum of $\mathcal {O}(N_{\mathrm{p}})$. In the program, the verlet list in combination with the link cell algorithm is used [25].

Also, the time integrator has a big influence on the simulation speed and the overall stability. As the contact detection and evaluation of the contact forces are most time-consuming in DEM simulations, the numerical effort for the time integrator itself is often negligible. But, its choice has a big influence on the number of evaluations of the equation of motion. In this research, good results with the fifth-order gear predictor–corrector algorithm [11] have been achieved.

3.2.3 Velocity-dependent coefficient of restitution

In DEM simulations often a constant coefficient of restitution (COR) is used. Indeed, this is in reality not the case, as the COR can depend on a variety of influence parameters, like the temperature or impact velocity. These influence parameters are mainly associated with the energy dissipation effect of the material. For the metals (S235 and Al6060) used in this work, the energy dissipation comes mainly from plastic deformations in the contact zone. Thus, the impact velocity has a big influence on the COR. There exist different investigations on the COR, as, for instance, in [12, 26, 32]. In this work, the finite element approach and material data from [32] are used to determine the COR. Metals often behave elastic–viscoplastic. This means that the plastic flow also depends on the strain rate. For the material description, the Perzyna model [24] is applied. This model relates the dynamic yield stress $\sigma _{\mathrm{d}}$ by a factor $\beta$ with the quasi-static yield stress $\sigma _{\mathrm{y}}$ and the effective plastic strain rate ${{\dot{\varepsilon }}}$ by

$$\begin{aligned} \sigma _{\mathrm{d}} = \beta \sigma _{\mathrm{y}} \quad {\text {with}}\quad \beta = 1 + \left( \frac{{{\dot{\varepsilon }}}}{\gamma } \right) ^m. \end{aligned}$$

(16)

The material viscosity parameter is denoted by $\gamma$, and the strain-rate hardening parameter by m. Both parameters are obtained in [32] from split Hopkinson pressure bar tests.

In Fig. 4 the quasi-static yield stress for S235 and Al6060 is shown. In Table 1 the corresponding material data and Perzyna coefficients are listed.

Fig. 4

Quasi-static stress–strain curves

Table 1 Material parameters obtained by the split Hopkinson pressure bar test [32]

Finite element simulations of two impacting particles are performed to determine the COR. A schematic representation of the sphere–sphere model is shown in Fig. 5 (left). An augmentation of the contact zone is shown in the lower part of the picture, to give an impression of the different mesh sizes. In the FE simulations, the spheres have an initial radius of 5 mm. The model can be scaled for different sphere sizes. Each sphere consists of 6093 axis symmetric 2D elements, in Abaqus called CAX4R. The element size varies between 0.5 mm till 0.015 mm. Both spheres are assigned with half the impact velocity with opposed signs.

Fig. 5

Left: Schematic representation of the FEM model of two impacting spheres. Right: Velocity-dependent COR for a sphere–sphere and sphere–wall contact for a sphere with 5 mm radius

The COR is evaluated by the normal velocities of the spheres before (0) and after (1) the collision of the sphere I and II, reading

$$\begin{aligned} e = \frac{v_{\mathrm{I}}^1 - v_{\mathrm{II}}^1}{v_{\mathrm{I}}^0 - v_{\mathrm{II}}^0}. \end{aligned}$$

(17)

The velocities before impact are prior known. The velocities after impact are evaluated at the center points of the spheres. The mean value of the last 200 time steps is taken, as the velocity is oscillating a little bit due to mechanical vibrations of the spheres, which are induced through the collision. If instead of a sphere–sphere contact a sphere–wall contact is simulated, one sphere is replaced by a wall. The wall is modeled as a cylinder with its diameter and length being the diameter of the sphere. The contour of the cylinder is completely clamped. In the later DEM simulations, often steel spheres of 5 mm radius are used. The container is made of aluminum. For these settings, the COR is shown in Fig. 5 (right). A high dependency on the impact velocity is observed. For both settings the COR is close to one for small impact velocities. When the impact velocity increases, the COR starts to decrease rapidly. For high velocities, the COR drops below 0.5.

3.3 Model verification

At first, the experimental and numerical setups are validated and compared. To check the experimental measurement system, the empty particle container is analyzed. As only minor damping effects exist, arising from the material damping and air resistance, the energy dissipation is very small. The mean value of the reduced loss factor is about 0.01.

In the next step, particles are filled in the container. Unhardened, steel balls, which are used in the hardened form for ball bearings, are utilized. These have a high degree of roundness and accurate material parameters are available for the later simulation purposes. For the first comparison, 58 particles with a radius of 5 mm are used. The maximum particle number to fit in the container is 65. The total weight of the particles is 240 g.

In order to compare the numerical with the experimental results, the measured frequencies and acceleration values are applied to the DEM simulation. The measured frequencies fit very well with the desired values. However, the measured acceleration values are up to 15 % off. This is mainly at high frequencies the case and caused through the transmissibility of the low-pass filter in the experiments.

For the simulation, the movement of the container is applied as given in Eq. (1). Using the computed particle–wall forces on the container, the complex power is determined. Each excitation grid point is simulated for 25 periods, whereas the first five periods are cut off to remove the irregular movement of the particles introduced by the initial conditions. The material parameters of Table 1 are used. The main adjustment parameters are the force laws and their influence variables. As normal force the formula of Gonthier [Eq. (12)] is chosen, whereby a constant COR as well as the velocity-dependent COR from Fig. 5 is utilized. Indeed, not the same materials for the particles are used in the experiment (V2A) as in the FEM simulation (S235), but their characteristics are very similar. For the friction force the three cases, e.g., no friction, sliding friction [Eq. (15)], and sticking friction [6], are analyzed.

The best result between experiment and simulation is achieved with the velocity-dependent COR and sliding friction which is pictured in Fig. 6 with the absolute values (top) and relative difference (bottom). The friction coefficient is set to $\mu = 0.1$ as it is the typical value found for steel in literature. These settings are used in all the following simulations if not specified differently. The relative mean difference of the energy dissipation is 0.36 for this setting. As seen in Fig. 6, there is a little discrepancy between both curves on the whole measurement range with no clear tendency to higher or lower values. This shows that the simulations meet the qualitative characteristics of the energy dissipation very well, with some quantitative differences in its magnitude. This result is also observed for other particle number and radii. At this point, it should be pointed out that using the velocity-dependent COR and the typical value for the coefficient of friction of steel means that no tuning at all was performed. This is remarkable as the excitation range in terms of the frequency and acceleration is over almost two decades. However, besides the quantitative discrepancies the simulations are very useful to give qualitative insights on the complex dynamics inside the damper.

Fig. 6

Comparison of experimental and numerical result for the energy dissipation of 58 steel particles of 5 mm radius. Top: Absolute values. Bottom: relative difference

If instead a constant COR is used, the relative mean difference is 0.44, and the best COR has to be found by excessive tuning. By neglecting friction the relative mean difference becomes 0.43. Taking the sticking friction algorithm, the relative mean difference is also 0.36, but the simulation time is much higher as with the sliding friction algorithm. The value of the friction coefficient seems to be of minor importance.

4 Experimental and numerical insights

To gain insights into the complex behavior of particle dampers and to analyze their damping efficiency, the numerical and the experimental setups are used. This section is further divided into monodisperse and polydisperse systems.

4.1 Monodisperse systems

At first, the rheology behavior of a monodisperse system is analyzed using the DEM simulation. As the particle dynamics are highly nonlinear, it is at first kind of arbitrary which particle setup is analyzed. Here, 550 steel particles of 2.5 mm radius are taken. The maximum particle number to fit in the container is 573. With this setting, there are about seven to eight particle layers in the container and the qualitative observations are also applicable to other particle settings.

In Fig. 7 the reduced loss factor and the motion modes for this setting are shown.

Fig. 7

Reduced loss factor (top) and motion modes (bottom) of 550 steel particles of 2.5 mm radius

Different motion modes can be observed, depending on both the frequency and acceleration of the container excitation. The solid-like state is only once seen at the lowest frequency and acceleration intensity (40 Hz, $\varGamma =1$). The solid-like state, see also Fig. 1a, is classified by almost no relative motion between the particles and the container. This results in a low energy dissipation and causes the reduced loss factor to be low ($\eta ^*=0.22$). In addition, the effective particle mass [Eq. (10)] is relative high with $m_{\mathrm{eff}} = 0.88 m_{\mathrm{bed}}$.

From the solid-like mode the system goes into the local fluidization mode, see also Fig. 1b, which is seen only for low acceleration intensities and low to medium frequencies ($f=40$–250 Hz, $\varGamma \le 2$). As still most of the particles behave like a solid and only the top layers show some relative motion, the reduced loss factor is still low ($\eta ^*=0.2$–0.35).

From the local fluidization mode, the system turns into the global fluidization mode, see also Fig. 1c. This mode is seen on a large area of the contour plot with low to medium reduced loss factor values ($\eta ^*=0.2$–0.5). The medium reduced loss factor values occur at the transition from the local to the global fluidization mode. This is the case at acceleration intensities of $\varGamma \approx 3$ with a slight decrease to higher frequencies. This behavior can be explained with the transition to global fluidization. There is a lot of relative motion between the particles, but the total kinetic energy is still comparatively low. This results in the medium reduced loss factor values. When from this point the acceleration intensity is further increased, the amount of relative motion is not increasing as much as the total amount of kinetic energy, resulting in a reduction of the reduced loss factor. It should be noted at this point that in the equivalent experiment in this regime reduced loss factor values up to $\eta ^* \approx 1$ are achieved.

The bouncing bed and decoupled motion mode, see Fig. 1d, e, develop from the global fluidization mode at high acceleration intensities ($\varGamma \ge 10$). The decoupled mode occurs at the medium to high frequencies ($f>150\,\hbox {Hz}$) and is characterized by a very small reduced loss factor ($\eta ^*=0.05-0.15$). This is reasonable as a decoupling of the particle mass from the container means that not much energy is transferred onto the particles anymore which could dissipate. This decoupling is also seen at the effective particle mass which reduces down to $m_{\mathrm{eff}} = 0.45 m_{\mathrm{bed}}$.

The bouncing bed mode instead appears at the low frequencies ($f<100 \,\hbox {Hz}$). The reduced loss factor range is very large and goes from $\eta ^*=0.13$ to $\eta ^*=0.87$. In this mode, the particles form a packed layer, but they do have a relative motion compared to the container. It is noticeable that the contour lines of the reduced loss factor in this mode agree very well with a constant container stroke, as indicated in Fig. 7. The energy dissipation caused in this motion mode is thus somehow very sensitive to the container stroke. In Bannerman [3] and Sack [28] a formula is derived to calculate the stroke of the maximum reduced loss factor. Indeed, their formula is derived and proven under the assumption of zero gravity. Also, their used frequencies are below 5 Hz. The predicted particle movement in this motion mode is shown in Fig. 8.

Fig. 8

Particle movement for the bouncing bed motion mode at maximum energy dissipation

They assume that the particle bed forms a packed layer on one container side, which is driven by the container. The particle bed leaves the container wall at the end of the inward container stroke, i.e., at position $x = 0$ and velocity ${\dot{x}} = X \varOmega$. Maximizing now the relative impact velocity between the particle bed and the opposite container wall at the next impact should maximize the energy dissipation. This is achieved if the particle bed hits the container on its next inward stroke at its maximum velocity, i.e., at $x = 0$ and $\varOmega t_{\mathrm{i}} = \pi$, with $t_{\mathrm{i}}$ being the impact time point. It is assumed that the particle bed adopts instantaneous the container wall velocity. The instantaneous velocity adoption of the particles implies a perfectly inelastic collision with the container wall. For a justification, see [3, 31]. Finally, they obtain that the optimal stroke is just depending on the clearance h. This is the distance between the packed particle bed and the opposite container wall, as indicated in Fig. 8.

The optimal stroke is achieved to

$$\begin{aligned} X_{\mathrm{opt}} = \frac{h}{\pi }. \end{aligned}$$

(18)

In this state, the dissipated energy per cycle follows

$$\begin{aligned} \widetilde{E}_{\mathrm{diss}}^{\mathrm{max}} = 4 m_{\mathrm{bed}} {\dot{X}} _{\mathrm{opt}}^2. \end{aligned}$$

(19)

If the container stroke is higher than the optimal stroke, i.e., an impact time point with $\varOmega t_{\mathrm{i}} < \pi$, the energy dissipation is obtained by

$$\begin{aligned} \widetilde{E}_{\mathrm{diss}} = \frac{1}{4} \widetilde{E}_{\mathrm{diss}}^{\mathrm{max}} \left( 1 - \cos {(\varOmega t_{\mathrm{i}})} \right) ^2. \end{aligned}$$

(20)

For lower strokes, i.e., an impact time point with $\varOmega t_{\mathrm{i}} > \pi$, the particle bed begins to spread irregularly, resulting in a low energy dissipation. The calculation of the clearance is indeed not trivial, as a particle system never forms a flat top surface. This leads especially for big particles and high filling ratios to inaccurate results. Possibilities are to take the distance from the highest particle or the medium distance from the top layer. However, here the question arises which particle belongs to the top layer and both methods are only applicable to simulations. We instead introduce the relative clearance as

$$\begin{aligned} \kappa = \frac{h}{L} \approx 1 - \frac{N_{\mathrm{P}}}{N_{\mathrm{P,max}}}, \end{aligned}$$

(21)

with L being the length of the container in excitation direction. The number of particles and the maximum number of particles to fit in the container are denoted by $N_{\mathrm{P}}$ and $N_{\mathrm{P,max}}$. Thus, the clearance can be calculated just using the filling ratio of the container. For the current setting, the optimal container stroke is pictured in Fig. 7. Indeed, the obtained value via the DEM simulation ($X_{\mathrm{opt}}=0.76\hbox { mm}$) is a little bit off the one by the analytical formula Eq. (18) ($X_{\mathrm{opt}}=0.51\hbox { mm}$). Also, the dissipated energy is only reaching about 80 % of the theoretical value by Eq. (19).

The difference of the optimal stroke obtained by the DEM simulation and the analytical formula is caused by the comparable large particle radius and the high filling ratio of 0.96. The particle radius is with a value of 2.5 mm on the same scale as the optimal clearance of 2.4 mm. Thus, less than one complete particle layer is free in the container. For these high filling ratios, Eq. (21) is inaccurate. This is because even for the maximum particle number still some free space remains in the container. The energy dissipation of Eq. (21) is not reached as the discretization of the excitation points is too coarse and the assumption of zero gravity is not fulfilled.

Nevertheless, it is remarkable that Eq. (18) is a good approximation for the optimal clearance, although a completely different setting and excitation range as in [3, 28] is used. In the following, it is analyzed if and how the just presented statements also hold true for other particle systems.

4.1.1 Particle size and number

In this section, the particle number and particle size are varied using experiments. By this, their influence on the motion modes is obtained and also the analytical formula for the optimal stroke Eq. (18) is analyzed again. In Fig. 9 the reduced loss factor for 40, 58, and 62 steel particles of 5 mm radius is shown. Hereby, the maximum particle number which would fit in the container is 65.

Fig. 9

Reduced loss factor of 40 (top), 58 (middle), and 62 (bottom) steel particles with 5 mm radius

All three plots show a similar contour, but their values are shifted. As Eq. (18) predicts, the optimum reduced loss factor of the bouncing bed modes shifts to lower strokes for a higher particle number. In Table 2 the optimal strokes obtained by the analytical formula and the determined values from the measurements are listed.

Table 2 Optimal strokes obtained from the analytical formula [Eq. (18)] and determined from the experiment (Fig. 9)

For the 40 particles the optimum does not lie in the measurement range and can thus not be determined. The value for the 58 particles is about a factor two off and for the 62 particles about a factor three. This can be explained by the fact that with a higher particle number the approximation of Eq. (21) gets more inaccurate. The same is true for bigger particles. The error of the 2.5 mm radius particles shown in Fig. 7 is much lower. Although some quantitative discrepancies between the experimental results and the analytical formula exist, the Eq. (18) is a good first approximation for the optimal stroke.

The other important regime is at the transition from local to global fluidization mode. Here, medium reduced loss factor values of about 0.5 are achieved for all particle settings at an acceleration of $\varGamma \approx 3$. Only for high frequencies ($f>$500 Hz), a higher particle number seems to be advantageous with reduced loss factor values even higher as one. We assume that this is due to an increased number of particle layers.

Next, the influence of the particle radius is analyzed by keeping the particle mass at a constant value of 240 g but varying the particle radius. In addition to the steel spheres of 2.5 mm and 5 mm radius, also a steel powder with a radius of 200 µm-400 µm is used. The reduced loss factors are shown in Fig. 10. Again, very similar contours are achieved. The biggest differences occur at the transition from the local to the global fluidization mode. Especially for the high frequencies, the smaller particles yield to higher reduced loss factors on a big excitation range. This is reasonable, as the mass of the smaller particles is less and thus less energy is necessary to introduce relative motion between them. Also, the number of particle layers is much higher. The bouncing bed state is indeed only little affected. All three settings lead here to a high reduced loss factor at a similar container stroke. In Table 3 the optimal strokes obtained by the analytical formula [Eq. (18)] and the determined values from the measurements are listed. For the smaller particle radii, the optimal stroke slightly increases and the difference between analytical formula and experiments gets less. Although the same particle mass is used the optimal stroke is changing, as with a smaller particle radius a higher particle mass fits into the container. The result also proves the above statement that with a smaller particle radius the approximation of Eq. (21) gets better.

Fig. 10

Reduced loss factors of steel particle systems with the same mass of 240 g but different particle radii

At last, it is analyzed whether the observations of Fig. 9 and Fig. 10 can be combined. We test how the reduced loss factor behaves for a small particle radius and different filling ratios. Therefore, three settings of 240 g, 285 g, and 305 g of steel powder are tested experimentally, with 310 g providing approximately the maximum filling ratio. The result is shown in Fig. 11.

Similar to Fig. 9, the settings with the higher filling ratios lead to a lower optimal stroke in the bouncing bed case. The value of the reduced loss factor at the optimal stroke is only little influenced. The reduced loss factor for the transition from the local to the global fluidization mode is, in contrast to Fig. 9, only little affected. All three settings lead here to high values on a big excitation range, with slightly higher reduced loss factor values for a higher filling ratio. This proves the above statement that an increased number of particle layers is advantageous. The result also implies that the clearance does not influence this regime.

4.1.2 Particle material

Three different particle materials are tested experimentally to analyze their influence on the reduced loss factor. Steel (V2A), tungsten, and polypropylene (PP) are used. The material parameters are summarized in Table 4.

Tungsten has about twice the density, stiffens, and tensile strength of steel. The density and tensile strength of polypropylene are about one decade lower than those of steel, and its stiffness is about two decades lower. This means that especially the PP exhibits a completely different material behavior. For the comparison 58 particles of 5 mm radius are used. The obtained reduced loss factors are shown in Fig. 12.

Although completely different materials are used, the quantitative differences are only small between the reduced loss factor curves. The same qualitative form from Fig. 7 can be observed. This means that the reduced loss factor is only weakly coupled to the particle material. This also implies that the energy dissipation of the damper is depending linearly on the density of the particle material. This is due to our definition of the reduced loss factor [Eq. (9)]. As a result, the particle material can be used for tuning the damper for the desired energy dissipation.

Table 3 Optimal strokes obtained from the analytical formula [Eq. (18)] and determined from the experiment (Fig. 10)

Fig. 11

Reduced loss factor of 240 g (top), 285 g (middle), and 305 g (bottom) steel powder

Table 4 Material parameters of tested particles

Fig. 12

Reduced loss factor of 58 particles with 5 mm radius for steel (top), tungsten (middle), and plastic (bottom)

4.1.3 Container shape

In this section, the influence of the container shape and orientation is analyzed using DEM simulations.

Cuboid Within the simulation the cubical particle container is changed to a cuboid with the same volume but the edge length are changed from 4 cm to 2, 4, and 8 cm, respectively, as shown in Fig. 13.

Fig. 13

Different cuboids used for analyzation with the edge length given as [width,height,depth] in cm

In this way, three different cuboids are received with two in-plane excitation possibilities each, resulting in six possible configurations. We simulated each configuration with 58 steel particles of 5 mm radius. The results are pictured in Fig. 14 and compared to the result of the cubical particle container. For better readability, the graphs are sorted by the edge length of the cubical particle container in excitation direction, i.e., in short ($L = 2\, \hbox {cm}$), medium ($L = 4\, \hbox {cm}$), and long ($L = 8\, \hbox {cm}$).

Fig. 14

Reduced loss factor of 58 steel particles with 5 mm radius for different cuboid particle containers

Note that the short edge length of the container is only 2 cm. Thus, only two particles fit next to each other for that edge, being a very extreme scenario. As a consequence, the following results should not be overinterpreted. Within the bouncing bed mode, big differences occur in the reduced loss factor in its magnitude as well as in the optimal stroke for all settings. The change of the optimal stroke is meaningful as the length of the container in excitation direction is changing and thus also the clearance, as seen in Eq. (21). It is interesting that especially the excitation along the short edge, see Fig. 14a, is leading to the highest reduced loss factors. This is in contrast to [31], where it is stated that for vertical vibrations at least three particle layers are necessary to obtain a high energy dissipation. Settings b) and c), excited along the medium and long container edge, even show lower reduced loss factors as the cube. Also, the optimal strokes do not fit to Eq. (18). Thus, these settings should be avoided. The fluidization modes are also affected. The cuboid II) is showing the least reduced loss factor values. As this cuboid has the biggest base area, only two particle layers exist. The cuboid III)$-z$ instead leads to the highest values. Both results prove the above statement that a sufficient number of particle layers are needed and more layers are advantageous. However, the cuboid III)$-x$ shows no improved behavior. This implies that also a sufficient number of particles in excitation direction are necessary to exhibit the fluidization mode efficiently.

Horizontal container layers Next, the influence of horizontal layers inside the cubical container are analyzed by DEM simulations. The cubical container is divided into four horizontal layers in the next step. In this way, only one particle layer is within a container layer. The corresponding result for 56 steel particles of 5 mm radius is shown in Fig. 15. The bouncing bed mode is hardly influenced. With container layers slightly higher values are achieved in the bouncing bed mode, as probably the gravitational acceleration has less influence. Big differences occur in the local and global fluidization area ($1<\varGamma < 5$). With layers they do not exist at all and very little reduced loss factors are obtained. This is feasible, as the fluidization modes are characterized by a movement between particle layers that do not exist here. The usage of horizontal layers could thus be useful for large containers operated in the bouncing bed mode.

Fig. 15

Reduced loss factor of 56 steel particles with 5 mm radius for the cubical particle container with layers (top) and without layers (bottom)

Orientation The influence of the container orientation is tested with three different configurations. For setting I), the cubical container is rotated by $45^{\circ }$ around the $x-$axis (excitation direction). For setting II), the container is rotated by $45^{\circ }$ around the $y-$axis, such that one container edge is pointing in excitation direction. For configuration III), the cube is rotated such that one of its corners is pointing in excitation direction. In Fig. 16 the results are shown for 58 steel particles of 5 mm radius. With all three orientations, the results are very similar to the standard configuration. Only the fluidization modes might be a little bit affected. As in this example very extreme container orientations are used, for technical applications little orientation inaccuracies should not be of importance.

Fig. 16

Reduced loss factor of 58 steel particles with 5 mm radius for different container orientations

Cylinder In the next step, a new container is manufactured as shown in Fig. 17 to analyze whether it is possible to adjust the clearance to a desired value for a given particle setting.

Fig. 17

Cylindrical particle container

The new container is a cylinder made of aluminum with an inner radius of 2 cm and an adjustable height of $5 \pm 0.5\hbox { cm}$. To realize the adjustable height, the container and the cap of the container are equipped with a fine thread. To prevent the cap from moving during the experiments, it is fixed by four screws. Therefore, the container has multiple stud holes around its circumference on the top. With this setting, it is possible to accurately tune the clearance of the particle bed. We tested a clearance of 4 mm with 312 g of steel powder. The cylinder is excited along its center line. The reduced loss factor is shown in Fig. 18 and exhibits the same characteristics as already mentioned for Fig. 7. Nevertheless, the optimal stroke of the bouncing bed mode obtained from the experiment is with a value of about 1.5 mm close to the calculated one via Eq. (18) of 1.27 mm. This shows that an accurate adjustment of the clearance is possible. Also, this proves again that the formula of Bannerman [3], e.g., Eq. (18), is also leading to acceptable results under the condition of gravity and friction.

Fig. 18

Reduced loss factor of cylinder filled with 312 g steel powder with 4 mm clearance

4.1.4 Microscopic effects

In Section 4.1.2 it was found experimentally that the reduced loss factor is almost independent of the used particle materials. Using the DEM, we now investigate in the effect of single material properties and analyze their effect on the reduced loss factor independent of each other and possibly for a bigger range of values.

Density In the following the influence of the density is investigated. Therefore, 58 steel spheres with radius 5 mm are used as baseline simulation. Then, the density of the spheres is changed from 7800 kg/$\mathrm{m}^3$ to 900 kg/$\mathrm{m}^3$ and 19250 kg/$\mathrm{m}^3$, respectively. These are the densities of our other particles used in the experiments (see Table 4) and are already very extreme values. All other parameters are kept constant. The result is shown in Fig. 19, and only minor differences can be observed. This proves the independence of the reduced loss factor on the density.

Fig. 19

Reduced loss factor of 58 steel particles of 5 mm radius for different densities

Young’s modulus Similar to the experiment, we found almost no dependency of the reduced loss factor on the Young’s modulus for the considered excitation range. Only if extreme low Young’s modulus values are chosen a difference can be observed. Therefore, 58 steel spheres with radius 5 mm are used as baseline simulation. Then, the Young’s modulus of the spheres is changed from 210 GPa to 1.1 MPa and 1000 GPa, respectively. These are the values of silicone and diamond. All other parameters are kept constant. The results are pictured in Fig. 20. For $E=1000\,\hbox {GPa}$ the result is showing almost no difference. For $E=1.1\,\hbox {MPa}$, we observed a shift of the bouncing bed state too much higher container strokes. This happens as the Young’s modulus is only affecting the contact forces [Eq. (12)] and thus the penetration and contact time of the contact partners. For very low Young’s modulus values the effective clearance gets bigger, as the penetration of the container wall by the particles has to be taken into consideration. The fluidization modes are only seen for low excitation frequencies ($f < 100\,\hbox {Hz}$). This might be due to the fact that for the high frequencies the particles stick together due to their high penetration. First experimental tests have shown that for a container material of PP (see Table 4) but steel particles the clearance is not affected but a considerable noise reduction is achieved. This could be a great advantage for technical applications.

Fig. 20

Reduced loss factor of 58 steel particles of 5 mm radius for different Young’s moduli

Contact parameters About the influence of the contact parameters, namely the coefficient of restitution and friction partially opposite statements exist, see, for instance, [3, 18, 36]. The main reasons are probably different areas of application and the values of the chosen coefficients. Nowadays, it is also reported that the magnitude of the coefficients might be of minor importance for the energy dissipation [10].

To obtain insights about the influence of the contact coefficients for our excitation conditions and range, we analyzed the energy dissipation of 58 steel particles of 5 mm radius using the DEM simulation. The ratio of the energy dissipation of normal contacts to frictional contacts is shown in Fig. 21.

Fig. 21

Ratio of dissipated energy of normal contacts to frictional contacts for 58 steel particles of 5 mm radius with $\mu = 0.1$ and the COR from Fig. 5

There exist three major regions. First, the energy dissipation is dominated by the normal contacts. Second is by friction or third is on the same scale. For low accelerations ($\varGamma < 4$), the dissipation is dominated by friction by a factor up to two. When the acceleration is increased, the dissipation becomes dominated by the normal contacts up to a factor of three for low frequencies ($f <500\,\hbox {Hz}$). In the area between both dissipation effects are on a similar scale.

When the coefficients are changed ($0.5< e< 0.99, 0.1< \mu < 0.5$), the contour of the reduced loss factor is only little influenced, as shown in Fig. 22 for four different settings. The corresponding ratios of the energy dissipation are shown in Fig. 23. The first setting is the standard setting with the COR obtained by FEM simulations, see Fig. 5, and $\mu = 0.1$, as discussed in section 3.3.

The second setting is simulated with an COR of $e = 0.5$, which is a rather low value already. The optimal stroke of the bouncing bed mode is shifted a little bit to higher strokes. The energy dissipation is completely dominated by the normal impacts.

The third setting is simulated with an COR of $e = 0.99$. Although the optimal stroke of the bouncing bed mode is not influenced, a high reduced loss factor value is observed on a much bigger excitation area. These high reduced loss factor values occur all below the optimal stroke of the bouncing bed mode. This implies a contact time with $\varOmega t_{\mathrm{i}} > \pi$ and leads for the other settings to a scattering of the particle bed. For the third setting instead, the particle bed remains packed, as observed from animations and the particle trajectories. Further analyzations are indeed not the scope of this paper. The energy dissipation is dominated by friction. Although the bigger excitation range is a nice attribute, to realize such a high COR in real applications might be not possible.

The fourth setting is simulated with a friction coefficient of $\mu = 0.5$ and the velocity-dependent COR from Fig. 5. The bouncing bed mode stays unchanged, but for the transition from the local to the global fluidization mode slightly higher values are achieved. The energy dissipation is dominated by friction again.

This leads to the conclusion that even if the ratio of normal to frictional losses might completely change due to the chosen contact coefficients, the total amount of dissipated energy is rather independent of the coefficient of restitution and friction for monodisperse systems. The little effect of the contact parameters on the bouncing bed mode might be explained by the inelastic collision of the particle bed with the container wall as shown in Fig. 8 and explained in [3, 31]. During this inelastic collision, multiple particle collisions occur and lead to an instantaneous velocity adaption of the particle bed with the container wall. This process is rather unaffected by the contact parameters. For the transition from the local to the global fluidization mode, we assume a similar explanation. This motion mode is characterized that in the whole particle bed relative motion between the particles is observed. As the energy dissipation per contact reduces, the number of contacts is increasing, thus leading to a similar energy dissipation.

Fig. 22

Reduced loss factor of 58 steel particles of 5 mm radius for different contact parameters

Fig. 23

Ratio of dissipated energy of normal contacts to frictional contacts for 58 steel particles of 5 mm radius for different contact parameters

4.1.5 Gravity

So far, the excitation occurred perpendicular to gravity. Next, the influence of an excitation against gravity and under zero gravity is analyzed. In Fig. 24 the reduced loss factor is shown for 58 steel particles of 5 mm radius for these two excitation conditions and compared to a horizontal excitation. For both settings, the optimal stroke of the bouncing bed mode is shifted to slightly higher values, as the effective clearance is increasing. This happens as the particles better distribute along the container wall in the corresponding excitation directions. For the vertical excitation with $\varGamma = 1$ and $f < 350\,\hbox {Hz}$, the reduced loss factor reduces dramatically. This happens, as no relative motion between the particles occurs. By assuming zero gravity the fluidization modes ($\varGamma \le 5$) are not visible at all anymore, as the relative motion between the particle layers is reduced a lot. This results in very low reduced loss factors in this area.

Fig. 24

Reduced loss factor of 58 steel particles of 5 mm radius excited in horizontal direction (top), vertical direction (middle), and under zero gravity (bottom)

4.2 Polydisperse systems

For monodisperse systems the bouncing bed mode and the transition from the local to the global fluidization mode can be used for an efficient dimensioning of particle dampers. Nevertheless, for the bouncing bed mode the excitation conditions have to be accurately known. High reduced loss factor values are achieved even at high accelerations. The fluidization modes can also lead to high reduced loss factor values but are only seen for comparable low accelerations.

The idea is to fill the gaps between big particles with particle powder to combine the benefits of both motion modes and to achieve thus an improved damping behavior. We tested experimentally 464 steel particles of 2.5 mm radius with and without 117 g of steel powder with a particle radius of 200 µm-400 µm. The obtained reduced loss factors are shown in Fig. 25. In the upper picture, the setting without additional steel powder is shown, i.e., the monodisperse system, and in the lower picture with additional steel powder, i.e., the polydisperse system.

Fig. 25

Reduced loss factor for of 464 steel particles of 2.5 mm radius. Top: Monodisperse system. Bottom: Polydisperse system filled up with 117 g steel powder

The resulting reduced loss factors show completely different contours. For the polydisperse system, only small reduced loss factors are achieved in the bouncing bed area. Instead, the polydisperse system is showing a high reduced loss factor for high frequencies ($f >500\,\hbox {Hz}$) up to $\varGamma = 15$. This area is also visible for pure steel powder, see, for instance, Fig. 18, but is not as large. The polydisperse system also shows an increased reduced loss factor at medium frequencies ($f = 70\,\hbox {Hz}$ till 250 Hz) and high accelerations ($\varGamma > 10$). It seems like the maximum value of the reduced loss factor occurs at a constant frequency of $f \approx 100\,\hbox {Hz}$. This would be advantageous for technical applications as it enables a damper design for a specific eigenfrequency of an underlying structure as the damper is robust against the excitation intensity.

Polydisperse systems might yield a segregation according to size as time elapses. However, in the experiment this was not observed so far. This might be due to the fact that the particle box was almost completely filled up with the bigger particles. Only the gaps between the bigger particles were filled with the particle powder. Thus, there might not enough space in the particle container for a complete segregation.

As simulations of the steel powder are very burdensome, it is hard to judge about the exact dynamic processes inside the polydisperse damper. Nevertheless, polydisperse systems show a high potential to damp medium frequencies efficiently on a robust level and this at a low cost basis. The deeper understanding of the dynamical processes inside the damper will be the aim of future research.

5 Conclusion

In this paper, the reduced loss factor of monodisperse as well as polydisperse particle dampers is analyzed using simulations and experiments. The obtained insights into the highly nonlinear behavior of particle dampers are a first step to enable an efficient dimensioning of particle dampers for an underlying structure. The analyzed particle container is driven at a grid of frequencies and accelerations in the range of 40 Hz till 1000 Hz and 10 m/$\mathrm{s^2}$ till 400 m/$\mathrm{s^2}$. Using the complex power method, the energy dissipation is obtained. The reduced loss factor, a scaling of the dissipated energy by the kinetic energy of the particles, is used to judge the efficiency of the damper and to compare the systems, independent of the container and particle mass.

For monodisperse systems multiple different motion modes are observed. Particularly, the bouncing bed mode and the transition from local to global fluidization lead to high reduced loss factor values. The transition from local to global fluidization occurs normally at accelerations of $\approx$30 m/$\mathrm{s^2}$ and is thus only suited for very special application. High filling ratios of the particle container and a small particle size are advantageous. This mode is not observed if not a sufficient number of particle layers exist or in the absence of gravity.

The bouncing bed state depends mainly on the clearance between the particle bed and the opposite container wall. The clearance is a function of the filling ratio and the container size. The clearance controls at which container stroke the maximum reduced loss factor occurs. The particle radius and material are of major importance. By a smaller particle radius, the estimation of the optimal container stroke gets more accurate. With the particle material, the amount of dissipated energy can be controlled. The material stiffness, the contact parameters, and the gravitation are of less effect on the reduced loss factor. The big drawback of the bouncing bed mode is that the excitation conditions have to be accurately known and for high frequencies the container stroke and thus the necessary clearance get very small.

For polydisperse systems, consisting of two different particle types with a magnitude difference in the radius, completely different results are achieved. Besides the high frequency area, also the medium frequency area (70 Hz till 250 Hz) is damped efficiently. The high reduced loss factor values occur at constant excitation frequency, making it interesting for technical applications.