1 Introduction

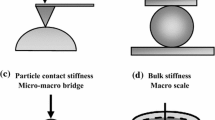
The mechanical behaviour of granular materials originates from force transmission at inter-particle contacts [18]. The use of discrete numerical modelling approaches enables the calculation of forces acting on individual particles, which is a non-trivial task in experimental approaches. Since its introduction by Cundall and Strack [3], DEM has been widely used for the modelling of particle interactions within an assembly. In most of the works reported so far, spheres or assemblies of spheres are used to represent particulate shape in order to facilitate contact calculations and speed up the simulations. However, particulate solids commonly have complex shapes, asperities and diverse chemical and mineralogical compositions and structures.

The importance of grain shape in force transmission has been highlighted in a number of studies (e.g. [1, 20, 25]) and several attempts have been made to include grain shape in DEM simulations (e.g. [4, 14]). Regarding asperities, it has experimentally been observed that the nano-scale surface roughness of particles influences the bulk material properties [23, 24, 27, 28]. However, there have been few attempts to include particle surface roughness in DEM. The works so far can be categorised into two groups: direct geometry refinement, and contact model enhancement [1, 12, 23, 31, 32]. In the former case, direct inclusion of roughness in DEM modelling has been carried out by assuming that asperities are small spheres, which are bonded to the main particles. This methodology is computationally expensive and restricted to surface roughness with a spherical shape [12, 31]. For the latter, development of normal force–displacement relationships for rough surfaces has been conducted by Cavarretta et al. [1], Otsubo et al. [23], and Zhao and Feng [32] using the statistical approach of Greenwood and Tripp [10]. In these models, a particle-scale roughness index proposed by Greenwood et al. [11] has been used. Cavarretta et al. [1] have subdivided the deformation progression of rough particles into asperity-dominant contact, transitional and Hertzian contact. They identified a threshold force and displacement, where the contact response transits from the so-called ‘initial plasticity’ to a Hertzian response. They used single particle compression tests to confirm the applicability of Hertz analysis for the last stage of deformation when the normal force exceeds the threshold. The initial stage of the indentation on rough surfaces was reported to be plastic, and the displacement was modelled using the hardness and elastic modulus of the material as input parameters. Initial plastic displacement was measured macroscopically and the hardness was the macroscopic hardness of the material with no means of considering asperities. The effect of loading on displacement of individual asperities could not be explored, since there was no means of reflecting shape of micro-asperities in the contact mechanics calculations. Therefore, the model has been further developed by Otsubo et al. [23] in which the threshold force and displacement are based on the assumptions of Greenwood and Tripp [10].

Deterministic contact mechanics gives the flexibility of considering complex surface characteristics in contact calculations. In tribology, there have been extensive efforts in investigating the effect of roughness on contact mechanics, covering both experimental and modelling aspects. In this study, an attempt is made to develop a force–displacement relationship for rough surfaces by coupling boundary element method (BEM) and DEM modelling. The contact behaviour of rough particles is analysed by BEM and the force–displacement relationship for rough surfaces is obtained and used in DEM calculation. The surface roughness and mechanical properties of glass ballotini (as used by previous researchers, e.g. [23]) are inputted in BEM and the output is represented by a customised contact model in DEM simulations. Details of BEM and DEM simulations are described below.

2 Contact mechanics modelling

2.1 Boundary element method (BEM)

The normal force–displacement relationship for the contact of rough particles is modelled using an in-house contact mechanics code developed by Ghanbarzadeh et al. [7, 8]. When two rough surfaces are in contact, individual asperities will bear the load and the area of contact is different from nominal Hertzian one. In order to calculate the discontinuous patchy real contact area and the contact pressure, the energy of the interface should be minimised [16]. The deformation of the interfaces \( \bar{u}_{z} ({\text{x,}}\;{\text{y}}) \) is then calculated using Boussinesq–Cerruti theory:

$$ \bar{u}_{z} = K*p_{d} = \mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{ - \infty }^{ + \infty } K\left( {x - \xi ,y - \eta } \right) p\left( {\xi ,\eta } \right) d\xi d\eta $$
(1)

\( p\left( {\xi ,\eta } \right) \) is the applied load, K is the convolution kernel and is calculated using half-space approximation:

$$ K\left( {x - \xi ,y - \eta } \right) = \frac{1}{{\pi E^{*} }}\frac{1}{{\sqrt {\left( {x - \xi } \right)^{2} + \left( {y - \eta } \right)^{2} } }} $$
(2)

where \( E^{*} \) is the equivalent elastic modulus of both materials (\( \frac{1}{{E^{*} }} = \frac{{\left( {1 - \nu_{1}^{2} } \right)}}{{E_{1} }} + \frac{{\left( {1 - \nu_{2}^{2} } \right)}}{{E_{2} }} \)). Here, \( \nu_{1} \),\( \nu_{2} \),\( E_{1} \) and \( E_{2} \) are Poisson’s ratio and elastic modulus of materials 1 and 2 respectively.

By movement of the rigid body in the normal direction, the interference (i) between the contacting surfaces can be obtained (Fig. 1). For the nodes experiencing contact, the elastic deformation must be equal to the body interference and the pressure is generated at the asperity. The summation of the contact forces arising from local nodes must also be equal to the applied load. Therefore, the set of equations for the contact of rough surfaces are as follows:

$$ \left\{ {\begin{array}{*{20}l} {r = \left( {Z_{2} \left( {x,y} \right) - Z_{1} \left( {x,y} \right)} \right) + \bar{u}_{z} \left( {{\text{x}},{\text{y}}} \right)} \hfill & {\forall x,y \in A_{c} } \hfill \\ {p\left( {x,y} \right) > 0} \hfill & {\forall x,y \in A_{c} } \hfill \\ {p\left( {x,y} \right) < H} \hfill & {} \hfill \\ {\mathop \sum \limits_{i,j = 1}^{i,j = N} p_{i,j} = F_{N} } \hfill & {} \hfill \\ \end{array} } \right\} $$
(3)

In Eq. 2, r is the rigid body movement of two rough surfaces in the normal direction, Z2 and Z1 are the surface profiles of the two rough particles, \( F_{N} \) is the total applied load in the normal direction, H is the hardness of the softer material in contact, \( A_{c} \) is the area of contact and N is the total number of nodes in the domain of study. In the current contact mechanics model, an elastic-perfectly plastic approach is incorporated. Hardness of the softer material is set to be the threshold for the plastic flow and the pressure does not exceed this value. This approach is widely used in other works in order to simulate elastic–plastic contact deformation [30]. More details of the approach can be found in Sahlin et al. [26] and Ghanbarzadeh et al. [7, 8].

Fig. 1
figure 1

Schematic of the contact of rough surfaces

Full size image

2.2 Rough surface generation and analysis

Digitised rough surfaces are necessary inputs of the contact mechanics simulation. They are generated using the method introduced by Hu and Tonder [15], using 2-D digital filters and autocorrelation functions. Fast Fourier Transforms are used for numerical efficiency. An autocorrelation function defines the shape of the asperities. There are several parameters that can be used to characterise the topography of the surfaces, such as Root Mean Square (RMS) roughness, skewness, kurtosis etc. Incorporation of all these surface parameters in a digitised surface needs careful characterisation of the real surfaces for extracting the desired parameters as input to the surface generation models [2]. Therefore, for simplicity only RMS roughness of the surfaces is used in the numerical simulations as input parameter and the results of all different cases are compared with the smooth case. An example of the surfaces used in the numerical simulation is shown in Fig. 2. The upper surface is set to be perfectly smooth and rigid and the lower surface has the composite surface roughness (S*q) of both particles in contact. The S*q is defined by Eq. 4. The contact in this condition is known to be equivalent to the real system of two rough particles.

Fig. 2
figure 2

Numerical model used in this study

Full size image
$$ S_{q}^{*} = \sqrt {S_{q1}^{2} + S_{q2}^{2} } $$
(4)

where Sq1 and Sq2 are the RMS roughness values of particles 1 and 2, respectively.

2.3 Normal force–displacement relationship

In order to obtain the normal force–displacement curves, the upper particle (upper surface) is moved in the normal direction. The normal force (\( F_{N} \)) is then calculated from the contact mechanics code solving the set of Eq. 2. Movement of the upper surface is adjusted by changing the value of r in Eq. 2. The deformation of the particles is simulated with step-wise increase in the value of r and the corresponding normal force is recorded. The results of normal force–displacement are compared with the Hertzian deformation for the case of entirely smooth particles (Sq = 0 µm) in order to test the accuracy of the numerical model prior to any simulations of rough surfaces and the results are plotted in Fig. 3.

Fig. 3
figure 3

Comparison between purely elastic BEM numerical model and the analytical Hertzian solution for two smooth particles in contact (E1 = E2 = 70 GPa)

Full size image

Simulations are carried out for RMS roughness (Sq) values of 0.1, 0.2, 0.5 and 1 µm. Firstly, the simulations for pure elastic contacts are conducted. The results are plotted in Fig. 4, and suggest that an increase in the Sq of the roughness of the surface shifts the normal force–displacement curve to the right as expected. For rougher surfaces, the highest asperity peaks carry the load and more compression is needed for achieving higher normal loads.

Fig. 4
figure 4

Normal force–displacement for pure elastic contact of rough surfaces (arrow shows the increase in the Sq value, E1 = E2 = 70 GPa)

Full size image

In contact of rough compressive surfaces, plastic deformation of the highest asperities readily occurs, if contact pressure exceeds the yield value, considering that the contact area is small. Thus pure elastic contact deformation of rough surfaces may not represent the correct stress fields. For this reason, the elastic-perfectly plastic deformation is used in this work and the results for different Sq values are reported in Fig. 5. A small difference prevails as compared to the pure elastic simulations of Fig. 4. The difference increases as the surfaces become rougher due to plastic deformation.

Fig. 5
figure 5

Normal force–displacement for elastic-perfectly plastic contact of rough surfaces (scattered points are elastic–plastic simulations and lines are pure elastic, E1 = E2 = 70 GPa and H = 6 GPa)

Full size image

3 Modelling of bulk compression

In a number of research and industrial application fields such as chemical and process engineering [13], civil engineering [22], and agricultural engineering [21], the behaviour of bulk particulate materials subjected to compression is of great interest.

In geotechnical engineering, soil-footing interactions or shallow footing is one of longest-dated topics with permanent relevance to practice [29]. This topic has received increasing attention in recent years, in particular for the design of offshore structures (e.g. [9, 17]). Previous DEM modelling reported by Gabrieli et al. [6] and Fu et al. [5] highlights the importance of the coefficient of friction on structural stiffness. However, there is no report on the role of surface roughness. Here, the effect of particle surface roughness on the bulk deformation mechanism of shallow footing is investigated using a BEM-DEM approach.

EDEM software package (DEM-Solutions, Edinburgh, UK) is used for DEM simulation. For contact deformation, an Application Programme Interface (API) is used employing standard C++ scripting. The direct implementation of BEM algorithm in DEM requires calculation of contact forces at each time step, so it is computationally very expensive. Therefore, an alternative approach is adopted in which a relationship between force and displacement is first developed and implemented taking account of the effect of roughness on particle dynamics. In this study, the Hertz model has been modified to account for elastic–plastic deformation of roughness.

3.1 Customised contact model

Based on Hertz anslysis [16], Eq. 5 provides a relationship between normal force (FN) and displacement (δ) for two smooth identical spheres in contact.

$$ F_{N} = \frac{4}{3}E^{*} \cdot R^{{\left( {\frac{1}{2}} \right)}} \cdot \delta^{{\left( {\frac{3}{2}} \right)}} $$
(5)

where E* is the effective contact Young’s modulus given by \( E^{*} = \, E/\left( {1 - \nu^{2} } \right) \) and R is the reduced radius (\( \frac{1}{R} = \frac{1}{{R_{1} }} + \frac{1}{{R_{2} }}) \), E is the elastic modulus and ν is Poisson’s ratio of the rough surface.

As reported in the literature and seen in the previous section, the rough surfaces show Hertzian response after a threshold normal force value [10]. For a given normal displacement, the normal load is lower for a rough particle than a smooth one. This difference in load (between smooth and rough cases) increases by increasing the normal displacement and becomes constant after the threshold force value. This trend can be represented by adding an error function to the normal force–displacement relationship (Eq. 6). As the value of surface roughness changes due to compression, a non-dimensional parameter, \( \frac{\delta }{{S_{q}^{*} }} \), is used in the error function. Greenwood and Tripp [10] proposed the following relationship to approximate the threshold normal contact force, \( F_{N} = S_{q}^{*} E^{*} \sqrt {2R^{*} S_{q}^{*} } \). In Eq. 6, two constants α and β are introduced into the model, where their values are obtained by comparing with BEM calculation. In this approach, the effect of roughness on normal load can be implemented with high efficiency. The modified normal force–displacement relationship is as follows:

$$ F_{N} = \frac{4}{3}E^{*} \cdot \sqrt {R^{*} } \cdot \delta^{{\left( {\frac{3}{2}} \right)}} - \beta S_{q}^{*} E^{*} \sqrt {R^{*} S_{q}^{*} } erf\left( {\alpha \frac{\delta }{{S_{q}^{*} }}} \right)\quad FN \ge 0 $$
(6)

The prediction of Eq. 6 for different values of Sq is compared with the BEM results in Fig. 6a. The values of α and β are listed in legend of Fig. 6a for four roughness values with the coefficient of determination R2 = 99%. Figure 6b shows the effect of α when all other variables are constant. It can be seen, α controls the so called ‘initial plasticity’. Figure 6c presents the effect of β on force–displacement relationship. β can change the slope of the force–displacement curve. This model is implemented in EDEM and is verified in the next section.

Fig. 6
figure 6

a Comparison between the prediction of BEM (black lines and markers) and Eq. 6 (red line and markers); b sensitivity of the prediction to α value when β is constant and equal to 20 for the case of Sq = 0.5; c sensitivity of the prediction to β value when α is constant and equal to 0.076 for the case of Sq = 0.5. (Color figure online)

Full size image

3.2 Numerical simulation of penetration of a rigid footing into a granular bed

Following Nadimi et al. [19], a box with internal dimension of 300 mm × 160 mm × 100 mm is used as shown in Fig. 7. 1.7 million particles are pluviated under gravity into half of the box and allowed to settle. Using symmetry reduces the computational expense. The particle size distribution consists of 20% of 0.78 mm diameter, 50% of 1.3 mm, and 30% of 2.1 mm particles following the experimental data of Nadimi et al. [19]. A rigid footing with the thickness of 10 mm, the width of 40 mm and the length of 160 mm is placed on the particles bed to represent plane strain condition. Regarding boundary effects, experimental and finite element simulations reported by Nadimi et al. [19] show that zone of maximum deformation is within the boundary of the model. The footing is pressed into the bed for a total displacement of 4 mm at quasi-static condition (0.001 mm/s). The physical and mechanical properties of particles are reported in the Table 1. In total, nine simulations are run with particle roughness values, i.e. Sq = 0, 0.5 and 1 µm and coefficient of friction values of φ = 0.3, 0.5 and 0.9.

Fig. 7
figure 7

The layout of the model showing the plane of symmetry

Full size image
Table 1 Particle properties in the simulation
Full size table

3.3 Results

In this study, the normal stiffness has only been modified for rough particles. The effect of roughness on tangential stiffness is more complicated and yet to be developed. Therefore, to investigate the effect of inter-particle friction on bulk behaviour, Fig. 8a–c show the stress–displacement curves when the coefficient of friction is varied and particle roughness is kept constant. There is a general agreement between all the three Figures that the increase in coefficient of friction significantly increases the stiffness of the bed.

Fig. 8
figure 8

Stress–displacement curve of footing on bed of particles with constant Sq and varying coefficient of friction (a–c), and varying Sq and constant coefficient of friction (d)

Full size image

Figure 8d presents the macroscopic stress–displacement curves when the coefficient of friction is constant (φ = 0.9) and particle roughness is varied. The capacity of the bed increases with increase in particle surface roughness. For a given set of condition, there exists a threshold, in most cases, above which the stress no longer increases further. This is due to particle rearrangement, i.e. sliding and rolling, in the shear band formed. This threshold is controlled by particle surface roughness and inter-particle friction (Fig. 8).

In order to compare the deformation mechanism of the particulate bed for different roughness values, a 20 mm thick slice in the middle of the bed is selected to avoid the boundary effects as shown in Fig. 9a. The magnitudes of the total force experienced by particles are compared in Fig. 9b, c for the cases of Sq = 0 and Sq = 1 µm, respectively. It can be seen that for rough particles the load is more localised/less distributed than smooth particles over the sheared volume. The velocity magnitudes of the particles at a given time, loading stage, are shown in Fig. 9d, e. The active zone of deformation can be clearly seen, where differences prevail between smooth and rough particles.

Fig. 9
figure 9

Deformation process beneath the footing, a selected layer of particles for the comparison, b total force magnitude on particles for Sq = 1 µm, c total force on particles for Sq = 0 µm, d velocity of particles for Sq = 1 µm, e velocity of particles for Sq = 0 µm (φ = 0.5)

Full size image

The normal contact force and associated magnitude together with contact deformation are illustrated in Fig. 10. This is obtained by drawing the contact vectors between particles and colouring them according to their magnitude of force or overlap. Normal force legend is limited to the range from 1 to 50 mN and normal overlap legend is limited to 2 to 10 µm for the sake of comparison. The effect of particle roughness on contact deformation can be clearly seen in these figures. Figure 10b shows contact deformation of smooth particles. By increasing the particle roughness, more particles experience large contact deformation and more wide spread (Fig. 10d, f). In contrast to the trend observed in normal contact deformation, the tangential slip or overlap is reduced by increasing the particle roughness (Fig. 11b, d, f). This shows that the smoother particles slide easier on each other. The tangential force network does not show any notable differences for the three surface roughness values (Fig. 11a, c, e). This is considered to result from not taking into account the influence of interlocking on tangential traction, a case to be considered in the next step.

Fig. 10
figure 10

Normal contact force network and contact deformation for particles with surface roughness of a, b Sq = 0; c, d Sq = 0.5; e, f Sq = 1 µm (φ = 0.5)

Full size image
Fig. 11
figure 11

Tangential force network and contact slip for particles with surface roughness of a, b Sq = 0; c, d; Sq = 0.5; e, f Sq = 1 µm (φ = 0.5)

Full size image

Figure 12 shows the effect of particle roughness on the evolution of the coordination number. Rough particles have a larger average coordination number than smooth particles during the compression. Furthermore, the coordination number decreases on penetration for the smooth case due to dilation around the footing zone. It can be concluded that an increase in the bearing capacity of the footing for the rough particles is related to the larger number of inter-particle contacts around the footing.

Fig. 12
figure 12

Evolution of coordination number for three different surface roughness (φ = 0.5)

Full size image

4 Conclusions

A novel approach for accounting elasto-plastic deformation of rough surface is presented by coupling BEM derived contact behaviour and DEM modelling for predicting bulk compression behaviour of a penetrating footing. In this framework, the effect of surface roughness of a particle on its contact interaction is quantified. A general contact model is proposed by considering the surface roughness in normal contact deformation behaviour. The model is implemented in EDEM commercial software to simulate the bulk behaviour. The developed model is employed to investigate the effect of particle roughness on bulk compression mechanism. In micromechanical investigations, it is shown that the spatial distribution of contact deformation increases in the normal direction, whilst in contrast the tangential slip reduces when increasing the particle surface roughness. The bed capacity increases for rough particles. This is attributed to a larger number of contacts present around the footing as it penetrates into the bed of rough particles. The proposed BEM-DEM framework can be employed for any material of interest with different surface roughness undergoing elasto-plastic deformation.