An efficient and stabilised SPH method for large strain metal plastic deformations

Abstract

Due to its simplicity and robustness, smooth particle hydrodynamics (SPH) has been widely used in the modelling of solid and fluid mechanics problems. Through the years, various formulations and stabilisation techniques have been adopted to enhance it. Recently, the authors developed JST–SPH, a mixed formulation based on the SPH method. Originally devised for modelling (nearly) incompressible hyperelasticity, the JST–SPH formulation is mixed in the sense that linear momentum and a number of strain definitions, instead of the displacements, act as main unknowns of the problem. The resulting governing system of conservation laws conveniently enables the application of the Jameson–Schmidt–Turkel (JST) artificial dissipation term, commonly employed in computational fluid dynamics, to solid mechanics. Coupled with meshless SPH discretisation, this novel scheme eliminates the shortcomings encountered when implementing fast dynamics explicit codes using traditional mesh-based methods. This paper focuses on the applicability of the JST–SPH mixed formulation to the simulation of high-rate, large metal elastic–plastic deformations. Three applications—including the simulation of an industry-relevant metal forming process—are examined under different loading conditions, in order to demonstrate the reliability of the method. Results compare favourably with both data from the previous literature, and simulations performed with a commercial finite elements package. Most noticeably, these results demonstrate that the total Lagrangian framework of JST–SPH, fundamental to reduce the computational effort associated with the scheme, retains its accuracy in the presence of large distortions. Moreover, an algorithmic flow chart is included at the end of this document, to facilitate the computer implementation of the scheme.

1 Introduction

Displacement-based explicit dynamic codes, implemented using low-order finite element methods, are commonly used for advanced numerical simulations in aerospace, automotive, biomedical, defence and manufacturing applications. However, difficulties arise in modelling high-speed impacts or large material deformations, often leading to simulation failure. In these scenarios, most computational codes prefer to employ the 8-noded underintegrated hexahedral element to model solid components [5]. Nonetheless, for many practical applications (e. g. crashworthiness, ballistics and metal forming), the extremely large deformations still result in severe mesh distortions. These lead to irregular and entangled elements, unless some form of adaptive remeshing is employed.

In addition, difficulties currently encountered by the widely employed, displacement-based, low-order finite element analysis include lower order of convergence for relevant field variables; excessive element distortion under large deformations, requiring periodic remeshing; locking behaviour in bending scenarios; non-physical pressure instabilities, and high-frequency noise due to Newmark-type time integrators.

Recent developments in computational methods for fast solid dynamics [1, 2, 7,8,9, 18, 19, 21, 23,24,25] recommend the representation of motion and deformation of a given body via a system of first-order, mixed formulation conservation laws. The partial differential equations (PDEs) that form this system do not present the displacement as the main unknown to be evaluated, instead yielding a set of other relevant quantities (i. e. velocity, deformation gradient, its cofactor matrix and scalar Jacobian), depending on the number of conservation equations being considered. This choice of the field variables will be driven on the one hand, by the need to reproduce certain features of material behaviour (e. g. near or full incompressibility) while ensuring polyconvexity of the strain energy function and, on the other hand, by the computational efficiency of the resulting scheme.

Mixed conservation laws have already been proven [1, 21, 25] to achieve second order of accuracy for stresses and strains. The two-field mixed formulation, composed of linear momentum $\vec {p}$ and deformation gradient ${{\mathbf {\mathsf{{F}}}}}$, was later augmented by including a governing equation to conserve the Jacobian J of the deformation gradient [18]. This enabled the scheme to effectively solve nearly and fully incompressible materials. Further enhancement of this $\{\vec {p}, {{\mathbf {\mathsf{{F}}}}}, J \}$ framework has also been recently reported in [7, 19] for modelling compressible, nearly incompressible and fully incompressible materials governed by a polyconvex constitutive law. In particular, this requires the presence of the matrix of co-factors of the deformation gradient ${{\mathbf {\mathsf{{F}}}}}$ (denoted here by ${{\mathbf {\mathsf{{H}}}}}$), leading to an extended system of field variables. The $\{ \vec {p}, {{\mathbf {\mathsf{{F}}}}}, {{\mathbf {\mathsf{{H}}}}}, J \}$ system can be reformulated to an alternative description in terms of entropy conjugates, as in [7, 19], due to the existence of a generalised convex entropy function. This readily facilitates the proof of existence of associated real wave speeds, which in turn establishes existence and uniqueness of real solutions.

A novel computational framework was devised to improve the numerical simulation behaviour during large material distortions, and to address the other numerical issues (e. g. locking, spurious oscillations) highlighted earlier. In a total Lagrangian perspective, the proposed methodology combines the use of smooth particle hydrodynamics (SPH), a meshless spatial discretisation technique, with an explicit, two-stage, total variation diminishing (TVD) Runge–Kutta temporal scheme.

To date, the application of mixed formulation has been largely focused on nearly incompressible hyperelasticity [1, 2, 21, 25], where many of the aforementioned shortcomings are encountered while using linear finite element methods. The work presented in this paper aims to investigate the feasibility of using the developed mixed formulation technique in the field of metal plasticity, by exploring some applications involving large material deformations. These will include a high-velocity impact scenario, where material is subjected to a non-uniform deformation and thus develops a large geometric discontinuity; a constrained boundary problem under heavy distortion, and the simulation of severe plastic deformation in a metallurgical process of industrial relevance.

This paper is organised as follows: a description of the mixed hyperbolic system of governing partial differential equations is presented in Sect. 2, while the adopted SPH discretisation methodology, that incorporates a stabilisation procedure based on a Jameson–Schmidt–Turkel (JST) artificial dissipation term, widely used in the field of computational fluid dynamics (CFD), will be detailed in Sect. 3. Numerical applications in metal plasticity are presented in Sect. 4, along with an assessment of the accuracy and stability of the methodology. These numerical examples are mainly chosen to demonstrate the potential and the accuracy of the developed computational strategy. Concluding remarks are then presented in Sect. 5. Finally, for the purpose of completeness, a brief outline of the chosen elasto-plastic constitutive model, including relevant computational procedures for evaluating the material deformation, is provided in “Appendix A”.

2 Conservation laws

In this paper, a vector will be expressed with the notation $\vec {a}$, and a tensor with ${{\mathbf {\mathsf{{A}}}}}$. The material and spatial coordinates are denoted by $\vec {X}$ and $\vec {x}$, respectively. The gradient operator that refers to initial spatial coordinates will be denoted by $\vec {\nabla }_0$. The symbol $\pmb {\varvec{\times }}$ represents the tensorial cross product, a key operation utilised in obtaining a concise mathematical representation of the proposed methodology. This notation was introduced in a series of papers devoted to the development of mixed formulation techniques [7,8,9, 19]. More details on the properties of the tensorial cross product can be found in the cited references.

The system of conservation laws describing the motion and deformation processes in terms of field variables $\vec {p}$, ${{\mathbf {\mathsf{{F}}}}}$, ${{\mathbf {\mathsf{{H}}}}}$, J can be written as:

$$\begin{aligned}&\frac{\partial \vec {p}}{\partial t} - \vec {\nabla }_0 \cdot {{\mathbf {\mathsf{{P}}}}}({{\mathbf {\mathsf{{F}}}}},{{\mathbf {\mathsf{{H}}}}},J) = \rho \vec {b} \end{aligned}$$

(2.1a)

$$\begin{aligned}&\frac{\partial {{\mathbf {\mathsf{{F}}}}}}{\partial t} - \frac{1}{\rho } \vec {\nabla }_0 \vec {p} = {{\mathbf {\mathsf{{0}}}}} \end{aligned}$$

(2.1b)

$$\begin{aligned}&\frac{\partial {{\mathbf {\mathsf{{H}}}}}}{\partial t} - \frac{1}{\rho } \vec {\nabla }_0 \times \left( \vec {p} \pmb {\varvec{\times }}{{\mathbf {\mathsf{{F}}}}} \right) = {{\mathbf {\mathsf{{0}}}}} \end{aligned}$$

(2.1c)

$$\begin{aligned}&\frac{\partial J}{\partial t} - \frac{1}{\rho } \vec {\nabla }_0 \cdot \left( {{\mathbf {\mathsf{{H}}}}}^\mathrm{T} \vec {p} \right) = 0 \end{aligned}$$

(2.1d)

In Eq. (2.1a), $\rho$ and $\vec {b}$, respectively, represent the material density and the body force per unit mass. System (2.1) is solved for $\vec {p}$, ${{\mathbf {\mathsf{{F}}}}}$, ${{\mathbf {\mathsf{{H}}}}}$, J with respect to time t. It is a set of hyperbolic PDEs similar in structure to those widely used in CFD [42]. This similarity enables one to employ well-established artificial dissipation numerical techniques from CFD to improve the computational stability of Eqs. (2.1a) and (2.1d) [1, 23, 24]. It is worth noting that, in the presence of non-smooth solutions, the above system (2.1) of local conservation laws must be accompanied by suitable jump conditions, as described in [42].

The notation adopted, along with a pictorial representation of the main measures of deformation used in (2.1), is illustrated in Fig. 1.

Fig. 1

Finite deformation process on a body $\varvec{\mathcal {B}}$ in the continuum. Shown are measures of fibre, area, and volume strain—${{\mathbf {\mathsf{{F}}}}}$, ${{\mathbf {\mathsf{{H}}}}}$, J—that define the process from the initial configuration $\varvec{\mathcal {B}}_0$, to $\varvec{\mathcal {B}} (t)$ at time t

It is evident from the expressions (2.1b) and (2.1c), respectively, for the ${{\mathbf {\mathsf{{F}}}}}$ and ${{\mathbf {\mathsf{{H}}}}}$ conservation variables, that, for both physical (required compatibility of strains, [8]) and mathematical (ensure convexity, [17]) reasons, two sets of involutions need to be satisfied by the solution of (2.1):

$$\begin{aligned}&\vec {\nabla }_0 \times {{\mathbf {\mathsf{{F}}}}} = {{\mathbf {\mathsf{{0}}}}} \end{aligned}$$

(2.2a)

$$\begin{aligned}&\vec {\nabla }_0 \cdot {{\mathbf {\mathsf{{H}}}}} = \vec {0} \end{aligned}$$

(2.2b)

In the above equations, the components of the material curl of ${{\mathbf {\mathsf{{F}}}}}$ in (2.2a), and of the material divergence of ${{\mathbf {\mathsf{{H}}}}}$ in (2.2b), can be expanded with the help of the Levi–Civita permutation symbol $\mathcal {E}_{ijk}$¹ as, respectively,

$$\begin{aligned} \left( \vec {\nabla }_0 \times {{\mathbf {\mathsf{{F}}}}} \right) _{ij}= & {} \sum _{k=1}^{3} \sum _{l=1}^{3} \mathcal {E}_{jkl} \frac{\partial F_{il}}{\partial x_k} \quad \text {and} \\ \left( \vec {\nabla }_0 \cdot {{\mathbf {\mathsf{{H}}}}} \right) _i= & {} \sum _{k=1}^3 \frac{\partial H_{ik}}{\partial x_k} \quad \text {for} \quad i,j = 1,2,3. \end{aligned}$$

Using the involutions described in (2.2), Eqs. (2.1c) and (2.1d) can be further simplified into [25]:

$$\begin{aligned}&\frac{\partial {{\mathbf {\mathsf{{H}}}}}}{\partial t} - {{\mathbf {\mathsf{{F}}}}} \pmb {\varvec{\times }}\vec {\nabla }_0 \left( \frac{\vec {p}}{\rho } \right) = {{\mathbf {\mathsf{{0}}}}} \end{aligned}$$

(2.3a)

$$\begin{aligned}&\frac{\partial J}{\partial t} - {{\mathbf {\mathsf{{H}}}}} : \vec {\nabla }_0 \left( \frac{\vec {p}}{\rho } \right) = 0 \end{aligned}$$

(2.3b)

In the place of the full set of conservation variables, denoted here by $\varvec{\mathcal {U}} = \{ \vec {p}, {{\mathbf {\mathsf{{F}}}}}, {{\mathbf {\mathsf{{H}}}}}, J\}$, reduced systems based on $\{ \vec {p}, {{\mathbf {\mathsf{{F}}}}}, J\}$, or only $\{ \vec {p}, {{\mathbf {\mathsf{{F}}}}} \}$ formulations have been adopted in the past. The robustness of these reduced systems has been positively ascertained by testing them against a thorough variety of numerical regimes and external conditions [1, 18, 24].

However, the complete $\{ \vec {p}, {{\mathbf {\mathsf{{F}}}}}, {{\mathbf {\mathsf{{H}}}}}, J \}$ mixed system of conservation laws (2.1) can be provided with mathematical—instead of merely empirical—proof of existence and stability of physically relevant solutions. Such a proof may be obtained by verifying the hyperbolicity of the system, i. e. whether $\varvec{\mathcal {U}}$ can be expressed in wave-like form [18, 27]:

$$\begin{aligned} \varvec{\mathcal {U}} = f \left( \vec {X} \cdot \vec {Z} - \lambda _i t \right) \vec {R}_i \quad i=1,2,3 \end{aligned}$$

(2.4)

In (2.4), $\vec {Z}$ is a chosen direction, $\lambda _i$ is the wave velocity and an eigenvalue of the system matrix, and $\vec {R}_i$ is the wave profile and the eigenvector of the system matrix corresponding to $\lambda _i$. As can be seen from (2.4), in order to prove the hyperbolicity of the system, its own matrix should present real and distinct eigenvalues, and eigenvectors orthogonal to each other. Only then the hyperbolicity of a system of conservation laws can be guaranteed by specifically choosing an elastic potential function $\varPsi$, for description of the material in use, able to satisfy certain convexity conditions. This would ensure the existence of minimum values of $\varPsi$, for the solution of the variational problem associated with an elastic system [27].

The most stringent convexity condition is the notion of polyconvexity [3, 27]. More precisely, the polyconvexity condition states that the potential strain function $\varPsi \left( {{\mathbf {\mathsf{{F}}}}}, {{\mathbf {\mathsf{{H}}}}}, J \right)$ has to be convex in the function space formed by the components of ${{\mathbf {\mathsf{{F}}}}}$ and ${{\mathbf {\mathsf{{H}}}}}$, and by J [3, 8]. This also ensures a one-to-one mapping between the stress ${{\mathbf {\mathsf{{P}}}}}$ and strain measures $\{ {{\mathbf {\mathsf{{F}}}}}, {{\mathbf {\mathsf{{H}}}}}, J \}$ [3, 16, 27, 31].

3 Discretisation

The governing systems of Eqs. (2.1) and (2.3) can be discretised by the SPH numerical scheme incorporating JST stabilisation components (JST–SPH) [21, 25].

The JST–SPH methodology consists of three key features:

• spatial discretisation with the SPH scheme;

• a JST-based numerical dissipation tool, adopted from CFD, to improve the accuracy and the stabilisation of the overall discretisation procedure;

• an explicit, two-stage total variation diminishing Runge–Kutta time integrator scheme to follow the time evolution of the solutions during dynamic simulations.

The above main features of the proposed methodology will be briefly elaborated in the following sections.

3.1 The SPH method

Being a meshfree technique, SPH can be effectively employed in the simulation of high-velocity impacts and high strain-rate deformations [10, 15, 20, 26, 28, 29, 34, 39, 40]. In fact, beyond the yield point, SPH discretisation becomes attractive because large distortions make standard Lagrangian finite elements analyses difficult to pursue, without resorting to remeshing techniques that increase the computational cost [5, 38]. This subsection briefly outlines the background for the SPH method and details the total Lagrangian SPH discretisation of the governing system of equations. The adoption of a total Lagrangian SPH formulation allows to avoid numerical tensile instabilities [4, 11, 33, 40]. However, it was proven in [32] that for simulations involving material discontinuities (such as cracks and fragmentation), stabler results are achieved when switching to Eulerian kernels over the discontinuity regions while retaining Lagrangian kernels elsewhere.

In a discretised domain, the SPH interpolation of a function variable $\phi (\vec {x})$ at any arbitrary point $\vec {x}$, denoted here by $\langle \phi (\vec {x}) \rangle$, can be approximated by:

$$\begin{aligned} \langle \phi (\vec {x}) \rangle \approx \sum _b V_b \; \phi (\vec {x}_b) \; W(\vec {x}_b - \vec {x}, h) \end{aligned}$$

(3.1)

where $V_b$ is the fractional volume assigned to a neighbouring particle in $\vec {x}_b$, h is the smoothing length, and $W(\vec {x}_b - \vec {x}, h)$ is usually a polynomial function with compact support $\mathcal {D}$ of radius 2h (that is, W vanishes for $\Vert \vec {x}_b - \vec {x} \Vert \ge 2h$). Although studies introducing adaptivity via a variable radius of support h exist in the particle methods literature (see [35]), here h and consequently $\mathcal {D}$ and V for in-field particles are kept constant for simplicity.

For accurate interpolation of any given function, the polynomial kernel should satisfy the following reproducibility conditions:

$$\begin{aligned}&\int _{\mathcal {D}} W(\vec {r}, h) \, \hbox {d} \vec {r} = 1 ; \end{aligned}$$

(3.2a)

$$\begin{aligned}&\lim _{ h \rightarrow 0} W(\vec {r}, h) \rightarrow \delta (\vec {r}) \end{aligned}$$

(3.2b)

In (3.2), $\vec {r} = \vec {x}_b - \vec {x}$, and $\delta (\vec {r})$ represents the Dirac delta function centred at 0. The first derivative of a given function $\phi$ can be discretised in terms of SPH interpolation as

$$\begin{aligned} \vec {\nabla } \phi (\vec {x}) = \sum _b V_b \; \phi (\vec {x}_b) \; \vec {\nabla } W (\vec {r}, h) \end{aligned}$$

(3.3)

Several different types of kernel functions have been employed as SPH interpolators. In the present work, to maintain the continuity for spatial derivatives of kernel function up to the fourth order, the following quintic spline polynomial is adopted as the kernel function:

$$\begin{aligned}&W(\vec {r},h) = \frac{\alpha }{h^{d}} {\left\{ \begin{array}{ll} \left( 2 - r_h \right) ^5 - 16 \left( 1 - r_h \right) ^5 &{}\quad \text {if }\quad r_h \le 1 \\ \left( 2 - r_h \right) ^5 &{} \quad \text {if }\quad 1 < r_h \le 2 , \quad r_h = \frac{\Vert \vec {r} \Vert }{h}\\ 0 &{} \quad \text {if } \quad r_h > 2 \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.4)

In (3.4), d is the number of spatial dimensions of the problem, and $\alpha$ is a normalising constant that depends on d as,

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha = \frac{1}{32 \pi } &{}\quad \text {if } d = 2\\ \alpha = \frac{7}{40 \pi } &{}\quad \text {if } d = 3 \end{array}\right. } \end{aligned}$$

(3.5)

It is widely known that the fundamental discretised form of SPH interpolation in (3.1) suffers from poor accuracies at and in the vicinity of the domain boundaries. More precisely, (3.1) does not completely satisfy the partition of unity condition at or near the boundaries, due to the truncation of kernel functions. To improve the accuracy of the SPH interpolation near boundaries, and to exactly preserve momentum, corrections must be introduced on both the kernel and the gradient of the kernel [10,11,12]. In the present work, the accuracies of the kernel and the gradient of kernel are improved by using correction methods proposed in [12]. The corrected SPH kernel $\tilde{W} \left( \vec {r}, h \right)$ and the corrected gradient of kernel $\vec {\tilde{\nabla }}_0 W (\vec {r}, h)$ defined in [12] exactly fulfil first-order completeness, that is, they allow the SPH representation to exactly reproduce linear fields.

The corrected SPH interpolation of a given function $\vec {f} (\vec {X})$ will thus be expressed as,

$$\begin{aligned} \vec {\nabla }_0 \vec {f} (\vec {X}_a) = \sum _{b \in \varLambda _a^b} V_b (\vec {f}_b - \vec {f}_a) \otimes \vec {\tilde{\nabla }}_0 W_b (\vec {X}_a). \end{aligned}$$

(3.6)

In (3.6), $\varLambda _a^b$ identifies the set of neighbours b of a particle a, at which the gradient is evaluated. The mixed $\{ \vec {p}, {{\mathbf {\mathsf{{F}}}}}, {{\mathbf {\mathsf{{H}}}}}, J \}$ system described by Eqs. (2.1) and (2.3) can now be discretised in space using the corrected SPH interpolation as described above.

Further, to obtain the discretised form of (2.1a), the weak statement for the linear momentum evolution [10,11,12, 43] can be obtained by employing work–conjugate pairs [7, 19]. With the help of integration by parts, this yields

$$\begin{aligned} \int _{V} \delta \vec {v} \cdot \frac{\partial \vec {p}}{\partial t} \hbox {d}V = \int _V \delta \vec {v} \cdot \rho \vec {b} \hbox {d}V + \int _{\partial V} \delta \vec {v} \cdot \vec {t} \hbox {d}A - \int _V {{\mathbf {\mathsf{{P}}}}} : \vec {\nabla }_0 \delta \vec {v} \, \hbox {d}V \end{aligned}$$

(3.7)

In (3.7), virtual velocities are denoted by $\delta \vec {v}$. By using particle discretisation on the domain V, the above expression (3.7) is approximated to:

$$\begin{aligned}&\sum _{a=1}^N V_a \delta \vec {v}_a \cdot \frac{\hbox {d} \vec {p}_a}{\hbox {d} t} = \sum _{a=1}^N V_a \delta \vec {v}_a \cdot \rho \vec {b}_a \nonumber \\&\quad +\sum _{a=1}^N A_a \delta \vec {v}_a \cdot \vec {t}_a - \sum _{a=1}^N V_a {{\mathbf {\mathsf{{P}}}}}_a : \vec {\nabla }_0 \delta \vec {v}_a \end{aligned}$$

(3.8)

In (3.8), $A_a$ and $\vec {t}_a$ are, respectively, associated area and traction force assigned to particles a located at or near the domain boundary. The density is assumed to be homogeneous throughout the domain. Equation (3.8) can now be expressed in terms of SPH discretisation as

$$\begin{aligned} \frac{\partial \vec {p}_a}{\partial t}= & {} \rho \vec {b}_a + \frac{A_a}{V_a} \vec {t}_a \nonumber \\&- \sum _{b \in \varLambda ^b_a} V_b \left[ {{\mathbf {\mathsf{{P}}}}}_b \, \vec {\tilde{\nabla }}_0 W_a (\vec {X}_b) - {{\mathbf {\mathsf{{P}}}}}_a \, \vec {\tilde{\nabla }}_0 W_b (\vec {X}_a) \right] \end{aligned}$$

(3.9)

The last term on the right-hand side of Eq. (3.9) represents the resultant internal force $\vec {T}_a$ acting on particle a:

$$\begin{aligned} \vec {T}_a = \sum _{b \in \varLambda _a} V_b \left[ {{\mathbf {\mathsf{{P}}}}}_b \vec {\tilde{\nabla }}_0 W_a (\vec {X}_b) - {{\mathbf {\mathsf{{P}}}}}_a \vec {\tilde{\nabla }}_0 W_b (\vec {X}_a) \right] \end{aligned}$$

(3.10)

Conservation laws given by Eqs. (2.3) and (2.1d), respectively, for strain measures ${{\mathbf {\mathsf{{F}}}}},\, {{\mathbf {\mathsf{{H}}}}}$, and J, can also be discretised in a similar manner to what has been done for (3.9), with the linear momentum $\vec {p}$ evaluated through SPH:

$$\begin{aligned}&\frac{\partial {{\mathbf {\mathsf{{F}}}}}_a}{\partial t} = \frac{1}{\rho } \sum _{b \in \varLambda ^b_a} V_b \left( \vec {p}_b - \vec {p}_a \right) \otimes \vec {\tilde{\nabla }}_0 W_b (\vec {X}_a) \end{aligned}$$

(3.11a)

$$\begin{aligned}&\frac{\partial {{\mathbf {\mathsf{{H}}}}}_a}{\partial t} = {{\mathbf {\mathsf{{F}}}}}_a \varvec{\times } \frac{1}{\rho } \sum _{b \in \varLambda ^b_a} V_b \left( \vec {p}_b - \vec {p}_a \right) \otimes \vec {\tilde{\nabla }}_0 W_b (\vec {X}_a) \end{aligned}$$

(3.11b)

$$\begin{aligned}&\frac{\partial J_a}{\partial t} = {{\mathbf {\mathsf{{H}}}}}_a : \frac{1}{\rho } \sum _{b \in \varLambda ^b_a} V_b \left( \vec {p}_b - \vec {p}_a \right) \otimes \vec {\tilde{\nabla }}_0 W_b (\vec {X}_a) \end{aligned}$$

(3.11c)

Depending on the chosen materials, the above semi-discrete formulation (3.9)–(3.11) may still suffer from accumulated numerical instabilities over a long span of time response. Therefore, it is necessary to address any such instability via suitable computational procedures.

3.2 JST artificial dissipation

In the context of SPH, various artificial dissipation techniques have been used in the past [28,29,30] to alleviate the aforementioned numerical instabilities. Alternatively, SPH can be stabilised by introducing stress points in the formulation (see [33]). In this case, however, a background mesh would be needed for the computation and assignment of fractional volumes. In the present work, an adapted nodally conservative JST stabilisation term $\varvec{\mathcal {D}}^\mathrm{JST}(\varvec{\mathcal {U}}_a)$ will be incorporated into (3.9), mirroring CFD techniques. The hyperbolic nature of the first-order conservation laws in system (2.1), reflecting that of the Euler equations in fluid dynamics, makes it possible to introduce the JST term as a dissipative component [1].

The nodally conservative JST stabilisation is additively decomposed into a second-order (harmonic) operator $\varvec{\mathcal {D}}_2(\varvec{\mathcal {U}}_a)$ and a fourth-order (biharmonic) operator $\varvec{\mathcal {D}}_4(\varvec{\mathcal {U}}_a)$ as:

$$\begin{aligned} \varvec{\mathcal {D}}^\mathrm{JST}(\varvec{\mathcal {U}}_a) = \varvec{\mathcal {D}}_2(\varvec{\mathcal {U}}_a) + \varvec{\mathcal {D}}_4(\varvec{\mathcal {U}}_a) \end{aligned}$$

(3.12)

where

$$\begin{aligned}&\varvec{\mathcal {D}}_{2}(\varvec{\mathcal {U}}_a) = \kappa ^{(2)} c_p \, \Delta x_{\text {min}} \sum _{b \in \varLambda ^b_a} V_b \left( \varvec{\mathcal {U}}_b - \varvec{\mathcal {U}}_a \right) \tilde{\nabla }^2_0 W_b(\vec {X}_a) \end{aligned}$$

(3.13a)

$$\begin{aligned}&\varvec{\mathcal {D}}_{4}(\varvec{\mathcal {U}}_a) = - \kappa ^{(4)} c_p \, \Delta x_{\text {min}}^3 \sum _{b \in \varLambda ^b_a} V_b \nonumber \\&\quad \left( \frac{\varvec{\mathcal {D}}_{2}(\varvec{\mathcal {U}}_b) - \varvec{\mathcal {D}}_{2}(\varvec{\mathcal {U}}_a)}{\kappa ^{(2)} c_p \, \Delta x_{\text {min}}} \right) \tilde{\nabla }^2_0 W_b(\vec {X}_a) \end{aligned}$$

(3.13b)

In (3.13), $c_p$ is the pressure wave speed, $\Delta x_\mathrm{min}$ is the particle spacing, $\kappa ^{(2)}$ and $\kappa ^{(4)}$ are user-defined parameters, while the $\tilde{\nabla }^2_0$ symbol represents a corrected Laplacian operator, applied to kernel W as detailed in [10].

3.3 Semi-discrete governing equations

Out of the four unknowns in the vector of state $\varvec{\mathcal {U}}$, only $\vec {p}$ and J will see JST dissipation terms appear in their respective conservation laws (3.9) and (3.11c). $\varvec{\mathcal {D}}^\mathrm{JST} ({{\mathbf {\mathsf{{F}}}}}) = \varvec{\mathcal {D}}^\mathrm{JST} ({{\mathbf {\mathsf{{H}}}}}) = {{\mathbf {\mathsf{{0}}}}}$ are imposed in order to respect conditions (2.2), set to ensure these strain measures preserve compatibility with the domain motions. This is because ${{\mathbf {\mathsf{{F}}}}}$ and ${{\mathbf {\mathsf{{H}}}}}$ are now main independent variables of the problem, and are not associated with displacements $\vec {x}$. In the context of the standard displacement-based method, it is worth recalling that ${{\mathbf {\mathsf{{F}}}}}$ is directly computed from $\vec {x}$, which acts as main independent variable of the problem.

In the light of the above, the spatial semi-discretisation yielded by the JST–SPH methodology reads as:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial \vec {p}_a}{\partial t} = \frac{A_a}{V_a} \vec {t}_a + \rho \vec {b}_a\\&\quad - \sum _{b \in \varLambda _a} V_b \left[ {{\mathbf {\mathsf{{P}}}}}_b \, \vec {\tilde{\nabla }}_0 W_a (\vec {X}_b) - {{\mathbf {\mathsf{{P}}}}}_a \, \vec {\tilde{\nabla }}_0 W_b (\vec {X}_a) \right] + \varvec{\mathcal {D}}^\mathrm{JST} (\vec {p}_a) \\&\frac{\partial {{\mathbf {\mathsf{{F}}}}}_a}{\partial t} = \sum _{b \in \varLambda _a} \frac{V_b}{\rho } (\vec {p}_b - \vec {p}_a) \otimes \vec {\tilde{\nabla }}_0 W_b (\vec {X}_a) \\&\frac{\partial {{\mathbf {\mathsf{{H}}}}}_a}{\partial t} = {{\mathbf {\mathsf{{F}}}}}_a \varvec{\times } \sum _{b \in \varLambda _a} \frac{V_b}{\rho } (\vec {p}_b - \vec {p}_a) \otimes \vec {\tilde{\nabla }}_0 W_b (\vec {X}_a)\\&\frac{\partial J_a}{\partial t} = {{\mathbf {\mathsf{{H}}}}}_a : \sum _{b \in \varLambda _a} \frac{V_b}{\rho } (\vec {p}_b - \vec {p}_a) \otimes \vec {\tilde{\nabla }}_0 W_b (\vec {X}_a) + \mathcal {D}^\mathrm{JST} (J_a) \end{aligned} \right. \end{aligned}$$

(3.14)

Due to the incompatibility between strains and displacements introduced by the adoption of the mixed $\{ \vec {p}, {{\mathbf {\mathsf{{F}}}}}, {{\mathbf {\mathsf{{H}}}}}, J\}$ formulation, discussed above, the conservation of angular momentum will not in general be satisfied by the discretised system of Eq. (3.14). In addition, the conservation of linear momentum may also not be respected, due to the lack of radial symmetry introduced by kernel and gradient corrections that are applied on particles located at, or in the vicinity, of domain boundaries.

With the aim to preserve the linear and angular momenta, the internal forces $\vec {T}$ and the JST dissipation terms $\varvec{\mathcal {D}}^\mathrm{JST}$ have to be amended, in order to enforce the following conditions:

$$\begin{aligned} \left\{ \begin{array}{ll} \sum \limits _{a=1}^N V_a \vec {T}_a = \vec {0}; &{}\quad \sum \limits _{a=1}^N V_a \vec {x}_a \times \vec {T}_a = \vec {0}; \\ \sum \limits _{a=1}^N V_a \varvec{\mathcal {D}}^\mathrm{JST} (\vec {p}_a) = \vec {0} ;&{}\quad \sum \limits _{a=1}^N V_a \vec {x}_a \times \varvec{\mathcal {D}}^\mathrm{JST} (\vec {p}_a) = \vec {0};\\ \sum \limits _{a=1}^N V_a \mathcal {D}^\mathrm{JST} (J_a) = 0&{} \end{array} \right. \end{aligned}$$

(3.15)

To impose conditions (3.15), a procedure based on the method of Lagrangian multipliers has been implemented (see [25] for more details).

3.4 Two-stage TVD Runge–Kutta temporal integration

To obtain a fully discretised system, that is able to describe the time evolution of the solution, the set of particle equations (3.14) has to be now explicitly integrated between chosen time intervals.

The solution will update from current time step $t^n$ to next step $t^{n+1}$, until the end of the simulation. An explicit, two-stage TVD Runge–Kutta integrator scheme will be used for the purpose of time integration as follows:

$$\begin{aligned}&\varvec{\mathcal {U}}^{*}_{a} = \varvec{\mathcal {U}}^{n}_{a} + \Delta t \, \varvec{\mathcal {R}}_{a} \left( \varvec{\mathcal {U}}^n_a \,, t^n \right) \end{aligned}$$

(3.16a)

$$\begin{aligned}&\varvec{\mathcal {U}}^{**}_{a} = \varvec{\mathcal {U}}^{*}_{a} + \Delta t \, \varvec{\mathcal {R}}_{a} \left( \varvec{\mathcal {U}}^*_a \,, t^{n+1}\right) \end{aligned}$$

(3.16b)

$$\begin{aligned}&\varvec{\mathcal {U}}^{n+1}_{a} = \frac{\varvec{\mathcal {U}}^{n}_{a} + \varvec{\mathcal {U}}^{**}_{a}}{2} \end{aligned}$$

(3.16c)

The size of the time step, $\Delta t$, in (3.16) is obtained using the Courant–Friedrichs–Lewy (CFL) condition [42]:

$$\begin{aligned} \Delta t = \alpha _{cfl} \, \frac{h_l}{\max (c_p)_{a}} \quad a = 1,\dots ,N \end{aligned}$$

(3.17)

In (3.17), $h_l$ is the characteristic length of the problem, here chosen to be equal to the initial distance between two particles, and $\alpha _{cfl}$ is a user-defined constant assuming values between 0 and 1. The lower the value of $\alpha _{cfl}$, the better the accuracy of the simulation.

The TVD Runge–Kutta scheme as defined in (3.16) has the advantage of being able to control the amount of spurious energy introduced by the explicit time integration, while allowing it to retain its qualities of speed and simplicity, especially when compared to implicit time-stepping methods.

Current particles positions, $\vec {x}_a$ for $a=1,\dots ,N\,$, are obtained monolithically from the two-stage Runge–Kutta process (3.16), given $\varvec{\mathcal {U}} = \vec {x}$ and $\varvec{\mathcal {R}} (\varvec{\mathcal {U}}) = \dfrac{\vec {p}}{\rho }$.

4 Applications

In this section, the proposed JST–SPH algorithm will be used to perform three numerical examples. The first amongst these will be the classic Taylor bar test for high-speed-impact plasticity effects: a three-dimensional cylindrical metal bar that impacts a horizontal wall at a high velocity. In the second example, the performance of the method is assessed by examining the elasto-plastic compression of a constrained rectangular body. The last example involves the simulation of the equal channel angular extrusion (ECAE) cold metal forming process, where a workpiece is forced to pass through two 90° turns inside an extrusion die. The localised distortions caused by the substantial shear stresses experienced by the workpiece at these 90° turns should constitute an ideal test for assessing the capability of the developed methodology under large strain, high-velocity conditions.

4.1 Taylor bar high-speed impact

A common benchmark test for plastic deformation at high speed is the Taylor bar impact problem [41], illustrated in Fig. 2.

Fig. 2

Taylor bar problem. Initial configuration

Fig. 3

Taylor bar problem. The pictures show the cross-sectional shape of the bar, and the plastic strain contour plot at various instants in the simulation

Fig. 4

Taylor bar problem. The pictures show the cross-sectional shape of the bar, and the von Mises stress contour plot at various instants in the simulation

Elastic behaviour is governed by the material energy function presented in Eq. (A.1). Equation (A.1) is coupled with the plastic yield model described in “Appendix A”, using the linear isotropic hardening law presented in (A.14). The material is assumed to be copper, with the following properties: Young’s modulus $E = 117$ GPa, Poisson ratio $\nu = 0.35$, yield stress $\sigma ^{Y}_{0} = 0.4$ GPa, hardening modulus $H = 0.1$ GPa and density $\rho = 8930$$\text {kg}/\text {m}^3$. The bar has initial height $h_0 = 32$ mm and radius $r_0 = 3.2$ mm, and is discretised by a set of 4131 particles arranged in a regular pattern. The impact is supposed frictionless and takes place at an initial speed of the bar of $\textit{v}_{0z} = -227\,\text {m}/\text {s}$ in the z direction, normal to the rigid wall. Due to the extensive plastic dissipation, the JST stabilising term is set to a very low value.

Figure 3 presents results of the Taylor bar simulation performed by JST–SPH. As observed in experimental results [44], in Fig. 3 the plastic front appears closer to the bottom wall at the early stages of the simulation (red contour regions). It then slowly moves towards the top of the bar, as more kinetic energy dissipates into plastic strain.

To investigate the stress distribution across the bar, the von Mises equivalent stress is plotted in Fig. 4. A gradual increase in the plastic stress flow over time can be clearly observed.

In Table 1, the radius of the bottom face at time $t = 80$ µs is compared to the results of identical tests performed using different numerical methodologies [1]. It can be noted that the mixed formulation techniques, being locking-free, avoid excessive rigid response of the structure often demonstrated by low-order finite elements, displacement-based analyses.

Table 1 Taylor bar problem. Radius of bottom face at time $t = 80$ µs, obtained from different numerical methods

Fig. 5

Taylor bar problem. Total values, summed over all particles, of the internal energy (blue line), plastic dissipation (yellow line) and JST artificial dissipation (red line) over simulation time. (Color figure online)

Plots of the total internal energy and of energy dissipation associated with plastic deformation and JST artificial dissipation are reported in Fig. 5.

The equations used to evaluate the total internal energy $U_{\text {int}}$, the total plastic dissipation $W_{(p)}$ and the artificial JST dissipation $W_\mathrm{(JST)}$ at each time step are given as follows:

$$\begin{aligned} {U_{\text {int}}}&= {\sum _{a=1}^N \frac{\Delta t}{\rho } \Vert {\vec {p}}_a \left( {\vec {X}}, t \right) \Vert \cdot \Vert {\vec {T}}_a \Vert } \end{aligned}$$

(4.1a)

$$\begin{aligned} {W_{(p)}}&= {\sum _{a=1}^N J \Vert \varvec{\sigma }_a \Vert \cdot \Delta \epsilon _{(p) a}} \end{aligned}$$

(4.1b)

$$\begin{aligned} {W_\mathrm{(JST)}}&= {\sum _{a=1}^N \frac{\Delta t}{\rho } \varvec{\mathcal {D}}^\mathrm{JST}_a \left( {\vec {p}}_a \right) } \end{aligned}$$

(4.1c)

It is shown in Fig. 5 that artificial dissipation introduced by the JST algorithm constitutes a negligible quantity.

4.2 Highly constrained problem with moving discontinuity

An example of the use of JST–SPH in a highly constrained setting is presented in [21, 25] for a fully elastic, nearly incompressible material. The effects of plasticity will be studied in this similar example, where a bidimensional rectangular block with dimensions $1 \, \text {m} \, \times \, 0.5 \, \text {m}$ is considered under the assumption of plane strain. The material is copper, with properties chosen to be the same as those in the Taylor bar example in Sect. 4.1.

An external velocity $\vec {v} = \left( 0, -10 \right) ^\mathrm{T} \, \text {m}/\text {s}$ is applied throughout the simulation on the top side of the block, as shown in Fig. 6. Roller boundary conditions are applied to its left, right and bottom edges.

Fig. 6

Constrained block under external velocity load

The rectangular block is discretised by 231 regular particles. Additional numerical parameters used in the simulation are CFL number $\alpha _{cfl} = 0.3$ and JST coefficient $\kappa ^{(2)} = 0$ and $\kappa ^{(4)} = \dfrac{1}{1024}$.

Fig. 7

Constrained block problem. Comparison between JST–SPH (top row) and finite elements results obtained using Abaqus/Explicit (bottom row). Configurations shown at subsequent instants during the deformation history; the plastic strain profile is shown through the colour scale

These specific values of $\kappa ^{(2)}$ and $\kappa ^{(4)}$ were chosen in order to provide the simulation with a small amount of JST numerical dissipation, useful to suppress any spurious pressure oscillations at the initial stages of the process.

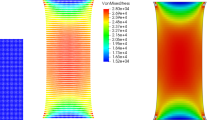
The purpose of this example is to demonstrate the capability of the total Lagrangian framework of the JST–SPH method, in the presence of high, localised distortions. The evolution of the von Mises equivalent plastic strain $\epsilon _{(p)}$ during the analysis is shown in the top row of Fig. 7. For comparison, the same simulation has been run using a commercial finite element method package, without any remeshing, and the results are presented in the bottom row of Fig. 7.

Results obtained by using increasing numbers of particles in the simulation are presented in Fig. 8.

Fig. 8

Constrained block problem. Comparison between JST–SPH (top row) analyses obtained using different particles resolutions at time $t = 15 \, \text {ms}$ into the simulation. Contour plot of plastic strain profile shown

It is observed from Figs. 7 and 8 that the basic finite element method is not able to handle the excessive distortions, whereas the JST–SPH method is able to simulate severe material deformation without exhibiting any numerical instability.

Plots of the total internal energy and of energy dissipation associated with plastic deformation and JST artificial dissipation are reported in Fig. 9. Energy quantities have been calculated using (4.1). It is shown in Fig. 9 that artificial dissipation introduced by the JST algorithm is a negligible quantity. Roller constraints imposed at the boundaries of the block are at the origin of irregularities appearing in the internal energy plot [calculated as in (4.1a)].

4.3 Simulation of the equal channel angular extrusion (ECAE) process

Numerous metallurgical techniques exploit the mechanics of plastic deformation to attain smaller grain size, and consequently better material properties, for metals and alloys. Amongst them, ECAE [36, 37] can offer high levels of shear strain for relatively low levels of external pressure, making it an ideal material processing technique for mass production. In the present setting, the ECAE process will be simulated in a channel with two 90° turns, analogous to the set-up analysed in [36] using a commercial finite element software. This example will demonstrate the robustness of the JST–SPH numerical scheme under a demanding dynamical process, where the material is subjected to continuous large deformation.

Fig. 9

Constrained block problem. Total values, summed over all particles, of the internal energy (blue line), plastic dissipation (yellow line) and JST artificial dissipation (red line) over the simulation time. (Color figure online)

The analysis is performed in plane strain conditions, and the material is made of commercially pure aluminium (Al1100, $E = 69$ GPa, $\nu = 0.33$, $\rho = 2800~\text {kg}/\text {m}^3$, width $l = 8$ mm). The walls of the die are assumed rigid. Its right-angled corners are rounded, with 1.5 mm and 1 mm external and internal fillet radii. The initial set-up of the experiment is presented in Fig. 10.

Fig. 10

ECAE simulation, initial set-up

Fig. 11

Pressure p at various stages of the ECAE process. Top row, JST–SPH results. Bottom row, finite elements commercial solver Abaqus/Explicit, linear elements

Fig. 12

Equivalent plastic strain (peeq) $\epsilon _{(p)}$ at various stages of the ECAE process. Top row, JST–SPH results. Bottom row, finite elements commercial solver Abaqus/Explicit, linear elements

The simulations are performed with a regular mesh of 400 particles. Contact between workpiece and die is assumed to be lubricated, and considered frictionless during the simulation. For the purpose of simplicity, a contact algorithm based on a reflective, bouncing back procedure [22] is adopted to simulate the interaction between the die walls and the particles representing billet material.

Given that large plastic deformations are expected, it is useful to introduce numerical dissipation at the early stages of the simulation, to prevent pressure instabilities that may arise when the billet initially comes into contact with the bottom wall of the channel. To facilitate this, for each particle, the JST term $k^{(4)}$ was defined as function of the equivalent plastic strain $\epsilon _{(p)}$, to ensure that $k^{(4)}$ linearly decreases, as plastic dissipation gradually sets in. This is achieved by adopting the following formula:

$$\begin{aligned} {\left\{ \begin{array}{ll} k^{(4)} = \frac{1}{64} - 2 \left( \frac{1}{64} - \frac{1}{4096} \right) \epsilon _{(p)} &{} \quad \text {if } \; \epsilon _{(p)} \le 0.5\\ k^{(4)} = \frac{1}{4096} &{}\quad \text {if } \; \epsilon _{(p)} > 0.5 \end{array}\right. } \end{aligned}$$

(4.2)

The plastic yield stress of the billet material is assumed to follow the nonlinear hardening law given by:

$$\begin{aligned} \sigma ^Y (\epsilon _{(p)}) = A (0.02 + \epsilon _{(p)})^{0.27} \quad \text {where} \quad A = 159 \times 10^6 \end{aligned}$$

(4.3)

Equation 4.3 is solved for $\epsilon _{(p)}$ numerically by using the Newton–Raphson method.

Fig. 13

JST–SPH ECAE. Total values, summed over all particles, of the internal energy (blue line), plastic dissipation (yellow line) and JST artificial dissipation (red line) over the simulation time. The evolution of these quantities discloses information on various stages of the process. (Color figure online)

Figures 11 and 12, respectively, depict the distributions of pressure and plastic strains during the deformation process of the billet, at various instants in time. For the purpose of comparison, Figs. 11 and 12 also present the corresponding pressure and plastic strain distributions obtained with a commercial finite element software (Abaqus/Explicit) using linear quadrilateral elements.

It can be noted that the results from the JST–SPH method correlate well with those obtained with the finite element method. Results from Figs. 11 and 12 are also consistent with observations reported in [36]. It is evident from the figures that the particle distribution in the vicinity of sharp corners of the channel is not smooth at the later stages of the simulation. This uneven distribution of the particles can be attributed to boundary effects. The plastic strain contour illustrated in Fig. 12 compares well with results reported in [36]. Further, it is clearly evident that the plastic strain distribution increases significantly as the billet material passes through each bend of the channel in the die. This feature is what is mainly exploited in the ECAE process to achieve the desired level of plastic strain in the workpiece.

Investigation of the energy patterns throughout the simulation confirms that plastic deformation is the main mechanism of energy dissipation, being on average two orders of magnitude larger than the energy dissipation introduced by activating the JST stabilisation term. Figure 13 compares the energies associated with plastic deformation, JST artificial dissipation, and the total internal energy of the bar during the simulation of the entire ECAE process. Energy quantities in Fig. 13 were calculated using (4.1).

As shown in Fig. 13, the values of total internal energy and of total plastic dissipation follow specific trends that can be linked to the motion of the billet inside the channel of the die. For example, a peak value for both energies was observed around $0.00142 \, \text {s}$, corresponding to the instant in which the billet comes into contact with the bottom wall of the middle (horizontal) part of the channel. Following that, the energy values begin to decline steeply during the expansion of the billet material in the mid-channel. A similar, but less pronounced energy pattern can be observed once the bar reaches, and then begins to flow into the second channel, with a peak value attained around $0.035 \, \text {s}$. Moreover, it transpires from Fig. 13 that the energy values are highly oscillatory when the billet initially passes through the angular sections of the channel. However, the frequency and the intensity of these oscillations gradually decrease, as the material moves away from the angular sections.

In addition, Fig. 13 shows the gradual decrease in energy dissipation associated with the JST term at the onset of plastic deformation. This effect follows from the definition of the JST terms in (4.2), and further demonstrates that higher artificial dissipation values are only required at the very early stages of the simulation, that is, before any plastic deformation takes place.

In order to verify the accuracy of the simulation, a convergence study was performed by varying the number of particles in the discretised domain.

The quantity under analysis is the amount of plastic strain at $0.035 \, \text {s}$, both in local (the maximum equivalent plastic strain $\max \epsilon _{(p)}$ amongst particles) and in global (the plastic dissipation developed in the single time step leading to instant $0.035 \, \text {s}$) terms. Apart from the mesh of 400 particles used so far, alternative meshes with 88, 216 and 640 particles were employed. The results of the convergence analysis are presented in Fig. 14. It can be noted from the figure that the chosen parameters monotonically converge with increasing particle density.

Fig. 14

JST–SPH ECAE. Convergence plot of local maximum plastic strain $\epsilon _{(p)}$ (in blue, left y-axis) and total dissipation $W_{(p)}$ due to plasticity (in red, right y-axis) at the time step entering $0.035 \, \text {s}$ in simulation time. (Color figure online)

The mesh with 640 particles has also been utilised for closer comparison of the degree of similarity between the JST–SPH ECAE test conducted here with the analysis found in [36]. For this purpose, the strain contour in the direction normal to the billet movement has been investigated towards the end of the test, at simulation time $t = 0.04 \, \text {s}$. The two locations selected are “Section 1” positioned at the centre of the middle channel, and “Section 2” at $5 \, \text {mm}$ from the second corner of the die. The above locations are consistent with those of the results reported in [36].

Ten equally spaced target positions have been chosen across the two sections of interest. Local values of the plastic strain $\epsilon _{(p)}$ have been computed using SPH interpolated values over neighbouring particles. Results are presented in Fig. 15. Comparison of Fig. 15 with results reported in [36] reveals that plastic strain patterns of the two tests match closely along Section 2, the main difference being that the JST–SPH analysis predictably presents a smoother curve. The same can be observed for Section 1, for which there is qualitative agreement with results from [36], except for the points near the upper wall, where results obtained with JST–SPH yield larger plastic strain. This discrepancy can be attributed to the fact that these points lie in the vicinity of the upper wall, and closer to the first bend. As can be noted in Fig. 12, also the accuracy of the plastic strain at these points is affected by the same boundary effects.

Fig. 15

JST–SPH ECAE. Plastic strain $\epsilon _{(p)}$ distribution across the billet sections labelled in colour at margin, at $t = 0.04 \, \text {s}$. Compare to Fig. 5 in [36]

Parametric analyses reported in [36] provided an opportunity for further verification of the validity of the results.

In [36], geometrical properties of the die are modified in order to investigate the possibility of enhancing ECAE metallurgical performances. One of these parameters was the length of the middle channel of the die. In [36], it was noted that interesting deformed shapes develop, when the middle channel is shortened from 24 to 16 mm. The upper part of second bend has a large unfilled area, while the billet experiences more stress due to bending than due to shear. This effect is particularly severe around the inner region of the billet in the vicinity of the bottom part of the second bend. Both of these phenomena could be identified in an analogous simulation performed with JST–SPH, as presented in Fig. 16 at time $t = 0.027 \, \text {s}$. Results obtained with the finite elements commercial solver Abaqus/Explicit, using linear quadrilateral elements, are also shown in Fig. 16.

It is evident from the numerical examples that the JST–SPH scheme eliminates the excessive element distortions usually associated with mesh-based methods during the simulation of large plastic strains. In addition, the total Lagrangian framework adopted here provides an efficient modelling tool to gain better understanding of the physics underlying large material deformations.

An algorithmic diagram, illustrating the JST–SPH solution procedure for simulating elasto-plastic material deformations, is presented next.

Fig. 16

On the left, contour plot obtained with JST–SPH of the equivalent plastic strain $\epsilon _{(p)}$ distribution over a modified version of the die, with a shortened middle channel length, at time $t = 0.027 \, \text {s}$. On the right, analogous result obtained on Abaqus/Explicit, with linear quadrilateral finite elements and no remeshing

5 Conclusions

This paper has focused on the application of JST–SPH mixed formulation in metal plasticity. This methodology has proved to be a valid tool for computing plastic deformations under dynamic regimes. It has been shown that there is good agreement between results reported in the previous section and data for the same tests found in the literature. The Taylor bar impact case provides an ideal application for JST–SPH, since SPH performs particularly well in high-velocity, large deformation settings. On the other hand, the ECAE test confirmed the robustness of JST–SPH: the total Lagrangian framework was able to withstand high local gradients of stresses, strains and displacements, while the presence of a constant loading in time did not lead to any kind of instability. This robustness was further evidenced in the constrained block simulation, where it can be seen that JST–SPH is able to achieve accurate results while preserving the initial connectivity under very large distortions. The same outcome cannot be obtained with standard mesh-based methods, without remeshing. It was noted, in the case of the ECAE simulation, that the results in the vicinity of the boundaries were slightly affected by sharp corners. These boundary effects can be easily eliminated by using more sophisticated boundary treatments. This will be one of the focal points in future publications.

Appendix A: Rate-independent plastic constitutive relations

In the following, a stretch-based, elastic energy function will be defined as [14]:

$$\begin{aligned} \varPsi (\lambda _1, \lambda _2, \lambda _3, J)= & {} \mu [(\ln \lambda _1)^2 + (\ln \lambda _2)^2 + (\ln \lambda _3)^2]\nonumber \\&+ \frac{\lambda }{2} (\ln J)^2 \end{aligned}$$

(A.1)

where $\mu$ and $\lambda$ are the Lamé constants, and $\lambda _1$, $\lambda _2$, $\lambda _3$ are the principal stretches, such that the right Cauchy–Green deformation tensor, ${{\mathbf {\mathsf{{C}}}}}$ [14], can be expressed as:

$$\begin{aligned} {{\mathbf {\mathsf{{C}}}}} = \sum _{a=1}^3 \lambda ^2_a \, \vec {N}_a \otimes \vec {N}_a \end{aligned}$$

(A.2)

In (A.2), $\vec {N}_a$, $a = 1,2,3$, are the principal directions in the reference frame.

From (A.1), it is possible to calculate the first Piola–Kirchhoff stress tensor ${{\mathbf {\mathsf{{P}}}}}$ for a polyconvex material in the elastic realm and, in so doing, to close the system of conservation laws (2.1) [7, 8, 19]:

$$\begin{aligned} {{\mathbf {\mathsf{{P}}}}} \left( {{\mathbf {\mathsf{{F}}}}}, {{\mathbf {\mathsf{{H}}}}}, J \right) = {\varvec{\Sigma }}_{{{\mathbf {\mathsf{{F}}}}}} + {\varvec{\Sigma }}_{{{\mathbf {\mathsf{{H}}}}}} \pmb {\varvec{\times }}{{\mathbf {\mathsf{{F}}}}} + \Sigma _J {{\mathbf {\mathsf{{H}}}}} \end{aligned}$$

(A.3)

In (A.3), ${\varvec{\Sigma }}_{{{\mathbf {\mathsf{{F}}}}}}$, ${\varvec{\Sigma }}_{{{\mathbf {\mathsf{{H}}}}}}$ and $\Sigma _J$ are the entropy conjugates of strain variables ${{\mathbf {\mathsf{{F}}}}}$, ${{\mathbf {\mathsf{{H}}}}}$ and J. More detailed definitions of entropy conjugates can be found in [7, 19].

Equation (A.3) provides solutions while in the elastic regime. However, once the deformation state progresses beyond the yield point and acquires a plastic component, the first Piola–Kirchhoff stress tensor ${{\mathbf {\mathsf{{P}}}}}$ will be hereby computed as a function of the Cauchy stress ${\varvec{\sigma }}$ in the current configuration, following [14]:

$$\begin{aligned} {{\mathbf {\mathsf{{P}}}}} = J {\varvec{\sigma }} {{\mathbf {\mathsf{{F}}}}}^{-T} \end{aligned}$$

(A.4)

The stress tensor ${\varvec{\sigma }}$ in (A.4) can be expressed in spatial principal directions $\vec {n}_a$, $a=1,2,3$ as

$$\begin{aligned} {\varvec{\sigma }} = \sum _{a=1}^{3} \sigma _{a} \, \vec {n}_a \otimes \vec {n}_a \end{aligned}$$

(A.5)

where $\sigma _{a}$ is given by

$$\begin{aligned} \sigma _{a} = \kappa \frac{\ln J}{J} + 2 \frac{\mu }{J} \left( \ln \lambda _{(e)a} - \frac{1}{3} \ln J \right) \quad a = 1,2,3 \end{aligned}$$

(A.6)

Fig. 17

A typical von Mises-defined yield surface in plain stress and in the presence of isotropic hardening. Radial return mapping also shown

In (A.6), the bulk modulus $\kappa$ for the material was introduced. Operating in principal directions holds the distinct advantage of making quantities computed in the current section automatically frame invariant.

The elastic principal stretches $\lambda _{(e)a}$ for $a=1,2,3$ in (A.6), and the principal directions $\vec {n}_a$, $a=1,2,3$ in (A.5) are obtained as the eigenvalues and eigenvectors of the elastic part ${{\mathbf {\mathsf{{b}}}}}_{(e)}$ of the left Cauchy–Green deformation tensor ${{\mathbf {\mathsf{{b}}}}}$, as

$$\begin{aligned} {{\mathbf {\mathsf{{b}}}}}_{(e)} = \sum _{a=1}^{3} \lambda _{(e)a}^2 \, \vec {n}_a \otimes \vec {n}_a \end{aligned}$$

(A.7)

The plastic part of the deformation enters the algorithm just described through the preliminary evaluation of ${{\mathbf {\mathsf{{b}}}}}_{(e)}$, obtained using the plastic part of the right Cauchy–Green strain tensor in (A.2), ${{\mathbf {\mathsf{{C}}}}}_{(p)}$, at the beginning of each time step:

$$\begin{aligned} {{\mathbf {\mathsf{{b}}}}}_{(e)} = {{\mathbf {\mathsf{{F}}}}} {{\mathbf {\mathsf{{C}}}}}^{-1}_{(p)} {{\mathbf {\mathsf{{F}}}}}^\mathrm{T} \end{aligned}$$

(A.8)

Given the deviatoric component ${\varvec{\sigma }}_{\mathrm{dev}}$ of the stress tensor ${\varvec{\sigma }}$ found in (A.5), and its principal components $\sigma _{\mathrm{dev},a}$, $a=1,2,3$:

$$\begin{aligned}&{\varvec{\sigma }}_{\mathrm{dev}} = {\varvec{\sigma }} - \kappa \frac{\ln J}{J} {{\mathbf {\mathsf{{I}}}}} {;} \nonumber \\&\quad \sigma _{\mathrm{dev},a} = 2 \frac{\mu }{J} \left( \ln \lambda _{(e)a} - \frac{1}{3} \ln J \right) \quad a = 1,2,3 \end{aligned}$$

(A.9)

the plastic domain is entered when the equivalent stress $\sigma _\mathrm{eq} = \sqrt{\dfrac{3}{2} \left( {\varvec{\sigma }}_{\mathrm{dev}} : {\varvec{\sigma }}_{\mathrm{dev}} \right) }$ is past the yield point, as determined by the von Mises yielding criterion:

$$\begin{aligned} \sigma _\mathrm{eq} - \sigma ^{Y} \le 0 \end{aligned}$$

(A.10)

In (A.10), $\sigma ^{Y} = \sigma ^Y ( \epsilon _{(p)} )$ is the yield stress, that in general will be a function of the history of accumulated plastic deformation during the process, through a material hardening rule.

In case condition (A.10) does not hold, plastic deformation develops, $\epsilon _{(p)} > 0$, and the yield surface is updated through a radial return mapping procedure, whereby the normal to the yield surface $\vec {m} = \left( m_1, m_2, m_3 \right)$ is expressed by

$$\begin{aligned} m_a = \frac{\sigma _{\mathrm{dev},a}}{\sqrt{{\varvec{\sigma }}_{\mathrm{dev}}:{\varvec{\sigma }}_{\mathrm{dev}}}} \quad a=1,2,3 \end{aligned}$$

(A.11)

and the principal components of the deviatoric stress tensor $\sigma _{\mathrm{dev},a}$ are updated as [14]

$$\begin{aligned} \sigma _{\mathrm{dev},a}^\mathrm{upd} = \sigma _{\mathrm{dev},a} - 2 \mu \, \Delta \epsilon _{(p)} \, m_a \quad a=1,2,3 \end{aligned}$$

(A.12)

The resulting increment in equivalent plastic strain $\Delta \epsilon _{(p)}$ will be computed as the strain amount necessary to keep the updated equivalent plastic stress $\sigma _\mathrm{eq}^\mathrm{upd} = \sqrt{\dfrac{3}{2} \left( {\varvec{\sigma }}_{\mathrm{dev}}^\mathrm{upd} : {\varvec{\sigma }}_{\mathrm{dev}}^\mathrm{upd} \right) }$ on the yield surface:

$$\begin{aligned} \sigma _\mathrm{eq}^\mathrm{upd} (\Delta \epsilon _{(p)}) - \sigma ^{Y} (\epsilon _{(p)}, \Delta \epsilon _{(p)}) = 0 \end{aligned}$$

(A.13)

In the case of the classic hardening rule that linearly depends on $\Delta \epsilon _{(p)}$, i. e.

$$\begin{aligned} \sigma ^{Y} = \sigma ^Y_0 + H \left( \epsilon _{(p)} + \Delta \epsilon _{(p)} \right) \end{aligned}$$

(A.14)

where $\sigma ^Y_0$ is the initial yield stress value, and H is the hardening modulus, $\Delta \epsilon _{(p)}$ can be explicitly obtained as

$$\begin{aligned} \Delta \epsilon _{(p)} = \frac{\sigma _\mathrm{eq} - \sigma ^{Y} \left( \epsilon _{(p)} \right) }{3 \mu + H} \end{aligned}$$

(A.15)

If instead a more complicated dependency of the type $\sigma ^Y = \sigma ^Y (\Delta \epsilon _{(p)})$ is in place, then $\Delta \epsilon _{(p)}$ has to be extracted numerically.

Once $\Delta \epsilon _{(p)}$ is known, the elastic principal stretches $\lambda _{(e)a}$ can be corrected to take the plastic dissipation into account

$$\begin{aligned} \lambda ^\mathrm{upd}_{(e)a} = \lambda _{(e)a} e^{- \Delta \epsilon _{(p)} \, m_a} \quad a=1,2,3 \end{aligned}$$

(A.16)

and the updated Cauchy stress components in principal directions $\sigma ^\mathrm{upd}_{\mathrm{dev},a}$ from (A.12) are returned as

$$\begin{aligned} \sigma ^\mathrm{upd}_{\mathrm{dev},a} = 2 \frac{\mu }{J} \left( \ln \lambda _{(e)a} - \frac{1}{3} \ln J \right) \left( 1 - \frac{2 \mu \Delta \epsilon _{(p)}}{\sqrt{{\varvec{\sigma }}_{\mathrm{dev}}:{\varvec{\sigma }}_{\mathrm{dev}}}} \right) \end{aligned}$$

(A.17)

Equation (A.16) allows updating the elastic deformation tensor ${{\mathbf {\mathsf{{b}}}}}^\mathrm{upd}_{(e)}$ accordingly:

$$\begin{aligned} {{\mathbf {\mathsf{{b}}}}}^\mathrm{upd}_{(e)} = \sum _{a=1}^{3} \left( \lambda _{(e)a} \right) ^2 \vec {n}_a \otimes \vec {n}_a \end{aligned}$$

(A.18)

Equation (A.18) exploits the known fact that plastic dissipation does not alter principal directions $\vec {n}_a$, $a=1,2,3$. What is left in order to complete the algorithm is then to substitute in Eq. (A.5) $\sigma _{a}$ with $\sigma ^\mathrm{upd}_{\mathrm{dev},a}$ obtained from (A.17), and to add the dilatation pressure term $\kappa \dfrac{\ln J}{J}$. The plastic deformation state is also updated as

$$\begin{aligned} {{\mathbf {\mathsf{{C}}}}}^{-1}_{(p)}&= {{\mathbf {\mathsf{{F}}}}}^{-1} {{\mathbf {\mathsf{{b}}}}}_{(e)} {{\mathbf {\mathsf{{F}}}}}^{-T} \end{aligned}$$

(A.19a)

$$\begin{aligned} \epsilon ^\mathrm{upd}_{(p)}&= \epsilon _{(p)} + \Delta \epsilon _{(p)} \end{aligned}$$

(A.19b)

The von Mises plastic algorithm described in this section is depicted in Fig. 17 in the case of isotropic hardening.