Comparison of elements and state-variable transfer methods for quasi-incompressible material behaviour in the particle finite element method

Abstract

The Particle Finite Element Method (PFEM) is attractive for the simulation of large deformation problems, e.g. in free-surface fluid flows, fluid–structure interaction and in solid mechanics for geotechnical engineering and production processes. During cutting, forming or melting of metal, quasi-incompressible material behaviour is often considered. To circumvent the associated volumetric locking in finite element simulations, different approaches have been proposed in the literature and a stabilised low-order mixed formulation (P1P1) is state-of-the-art. The present paper compares the established mixed formulation with a higher order pure displacement element (TRI6) under 2d plane strain conditions. The TRI6 element requires specialized handling, involving the deletion and re-addition of edge-mid-nodes during triangulation remeshing. The robustness of both element formulations is analysed along with different state-variable transfer schemes, which are not yet widely discussed in the literature. The influence of the stabilisation factor in the P1P1 element formulation is investigated, and an equation linking this factor to the Poisson ratio for hyperelastic materials is proposed.

1 Introduction

The Particle Finite Element Method (PFEM) is well suited for large deformation problems and shape changes of solid bodies. In solid mechanics, PFEM has for example been applied in geomechanics, see [6, 15, 23], in metal cutting, see [8, 24, 26], and for simulating flowing hot molten metal, [1, 14]. In perspective, PFEM also appears to be suitable for the modelling and simulation of material deposition in an additive manufacturing process such as Direct Energy Deposition with a Laser Beam. In the PFEM, linear elements are a natural choice, however these elements restrict the usage in cases of quasi-incompressible material behaviour.

In solid mechanics PFEM literature, mainly three approaches are established for dealing with quasi-incompressible material behaviour:

• First-order mixed triangular elements (P1P1) of displacement-pressure ($\varvec{u}$-p) or displacement-volume-dilatation ($\varvec{u}$-$\phi$) type, see [1, 6, 8, 15, 23, 26]. The $\varvec{u}$-p formulation is reported in [8] to produce slightly better stress distributions than the $\varvec{u}$-$\phi$ formulation, whereas [23] reports the $\varvec{u}$-$\phi$ formulation to perform slightly better in the scatter-free representation of Lode-angles than the $\varvec{u}$-p formulation. A three-field formulation $\varvec{u}$-$\phi$-p is also tested, but the third field is not necessary according to [23]. As the $\varvec{u}$-$\phi$ formulation does not restrict the material model formulation to a volumetric-isochoric split, this formulation is chosen in the present paper.

• First-order pure displacement triangular elements with strain smoothing onto the nodes and nodal integration, see [29], usually referred to as smoothed PFEM, i.e. SPFEM. An edge-based smoothing version with Gauss-integration has also been proposed, see [18]. The smoothing prevents the element-wise calculation of the global tangent stiffness matrix contributions, which considerably complicates the finite element implementation for implicit time integration. SPFEM is therefore especially suited for explicit time integration, where no tangent stiffness matrix is needed. Furthermore, [25] combined an edge-based smoothing with a first order mixed $\varvec{u}$-p formulation.

• Second-first-order mixed triangular elements of displacement-stress ($\varvec{u}$-$\varvec{\sigma }$) type, where the edge-mid-nodes are neglected in remeshing, see e.g. [28] and [30]. The large number of unknowns is therein treated in a variational setting with a so-called second-order cone programming solver.

Although it has been shown in the context of standard FEM that a second-order pure displacement triangular element (TRI6) already performs considerably better than first-order displacement elements and close to more advanced element technologies, see [10], this option has so far not been reported in the PFEM-literature to the authors’ knowledge. In the present paper, a TRI6 element is applied in PFEM and compared to the stabilised mixed P1P1 element of $\varvec{u}$-$\phi$-type under 2d plane strain conditions. Amongst the state-of-the-art formulations the P1P1 element can still straightforwardly be implemented in standard FEM-algorithms and is therefore preferred to the other mentioned formulations. The restriction to 2d plane strain represents a simplification that excludes the consideration of advanced remeshing methods necessary in 3d PFEM simulations. For example, mesh-smoothing is essential in 3d to address specially distorted tetrahedra, commonly referred to as slivers, cf. [8, 22].

The frequent remeshing in the PFEM requires a transfer of state-variables. One option is the mapping of the previous stress tensor which is then additively combined with the new stress increment in a strain-rate based hypoelastic material model, see e.g. [14]. However, the present paper follows the strict deformation based approach used in [23] and [8], which allows for the application of hyperelasticity-type constitutive relations. Thereby, details on the mapping of previous deformation, especially in the context of $\varvec{u}$-$\phi$ formulations, are elaborated.

The transfer of state-variables has a large influence on the stability and accuracy of the PFEM. In the present work, this transfer is done directly rather than via the node points. This contradicts the classic particle-based spirit of PFEM and the early state-of-the-art of a L2-projection of the variables onto the node points, see e.g. [24, 27]. However, copying state-variables directly between old and new quadrature points has become the state-of-the-art in PFEM since it avoids unnecessary variable smoothing in unchanged mesh regions, see [6, 26]. Thereby, the information of the closest previous quadrature point is copied, so that this method is abbreviated as closest point mapping (CPM) in the following. Especially for coarse meshes and large spatial changes of state-variables, the CPM introduces a considerable error in the transfer. To improve the transfer quality, the interpolation of state-variables from three of the previous quadrature points has been proposed in [17] and used in [30]. In [17], two such schemes are proposed: the arbitrary linear interpolation method interpolates from the three nearest quadrature points in the reference mesh, whereas the unique element method uses the previous element which contains the new quadrature point and interpolates or extrapolates from the quadrature points of this unique element. The unique element method makes use of the high smoothness of the variables within one element which yielded the best results in [17]. However, in the present paper the arbitrary linear interpolation method is applied in a straightforward implementation by using a background-triangulation of all previous quadrature points where it is only necessary to interpolate by standard shape functions. The method is abbreviated as background triangle mapping (BTM). Furthermore, the interpolation in the BTM mapping can furthermore be improved by transfer operators suggested in [5] which preserve incompressible deformation states in linear operations such as interpolation. Since it involves a spectral decomposition it will be evaluated as to whether the effort is justified for the numerical examples.

The repeated remeshing applied in the PFEM maintains the node points and recreates the connectivities and the outer shape of the bodies. A constrained Delaunay triangulation of the points is followed by an $\alpha$-shape detection as it is nowadays well established, see e.g. [7]. In some references, e.g. [27], the shape detection is performed prior to the Delaunay triangulation. However, this sequencing results in higher computational costs.

The present paper compares both element-formulations for quasi-incompressible material behaviour in a deformation based updated Lagrangian formulation. Moreover, a comparative analysis of different variable transfer schemes is conducted. While the general concept of the discussed element types and state-variable transfer methods is extendable to 3d, the present paper is restricted to 2d plane strain conditions for conceptual simplicity. The model is yet restricted to a purely mechanical formulation in order to provide insight into the selection of a set of methods to be applied in thermo-mechanical simulations, e.g. in the context of additive manufacturing processes.

2 Updated Lagrangian finite element formulation

The PFEM is an incremental remeshing technique where the considered particles, respectively nodes, are retained throughout the simulation. Therefore, the exact referential coordinates of the points are known, whereas a new element mesh is generated on the deformed, respectively spatial, coordinates. When the element-nodes in a strongly deformed configuration are newly connected, these nodes probably do not form an appropriate element in the reference configuration. Consequently, a total Lagrangian formulation is not possible but a formulation in the current configuration, cf. [8], or an updated Lagrangian formulation, cf. [20], is necessary. Here, the updated Lagrangian formulation has the advantage of keeping integration space and shape function gradients constant until the next remeshing. In contrast to a stress-incremental hypoelastic formulation, a deformation based hyperelastic model is applied in this work. Therefore the deformation history has to be known after remeshing.

The continuum mechanical basis is formulated in an incremental setting which is visualised in Fig. 1. The considered total time span is subdivided in discrete time steps $\varDelta t$ to describe the points $t_0,\dots , t_n, t_{n+1}$ in time. The total displacement $\varvec{u}=\varvec{u}_{n+1}$ is separated into the displacement history $\varvec{u}_n$ and the displacement increment $\varDelta \varvec{u}$, such that

$$\begin{aligned} \varvec{u} = \varvec{u}_n + \varDelta \varvec{u} \end{aligned}$$

(1)

Fig. 1

Configurations in updated Lagrangian formulation

Three configurations are mainly focussed on, namely the reference configuration $\mathcal {B}_{0}$ with placements $\varvec{X}$, the previous configuration $\mathcal {B}_{n}$ with placements $\varvec{X}_n= \varvec{X} + \varvec{u}_n$, which represents the last remeshing state, and the current configuration ${\mathcal {B}_t}$ with placements $\varvec{x} = \varvec{X} + \varvec{u}$. Accordingly, the deformation gradient is multiplicatively decomposed into

$$\begin{aligned} \varvec{F} = \frac{\partial \varvec{x}}{\partial \varvec{X}_n}\cdot \frac{\partial \varvec{X}_n}{\partial \varvec{X}} =\varDelta \varvec{F} \cdot \varvec{F}_n \end{aligned}$$

(2)

Due to previous remeshings, the previous deformation gradient $\varvec{F}_n$ can not be calculated in a total Lagrangian sense. Instead, the total deformation gradient (2) is stored as $\varvec{F}_{\! n}$ at the end of a time step and treated similarly to a state-variable.

The previous domain $\mathcal {B}_{n}$ is subdivided into $n_{el}$ finite elements. The displacement field and spatial gradients are approximated via $n_\textrm{en}$ nodal values $\varvec{u}^{eA}$ per element e and shape functions $N^A$ as

$$\begin{aligned} \varvec{u}^e = \sum \limits _{A=1}^{n_\textrm{en}}\varvec{u}^{eA}\,N^A, ~~ \frac{\partial \varDelta \varvec{u}}{\partial \varvec{X}_n} = \sum \limits _{A=1}^{n_\textrm{en}}\varDelta \varvec{u}^{eA}\otimes \frac{\partial N^A}{\partial \varvec{X}_n} \end{aligned}$$

(3)

The weak form of the balance of linear momentum, see e.g. [16], formulated in the previous configuration results in

$$\begin{aligned} \textbf{r}= {{{{\textbf {{\textsf {A}}}}}}}_{e=1}^{n_\textrm{el}}\Big [ \varvec{M}^{eAB}\cdot \ddot{\varvec{u}}^B + \varvec{f}^{eA}_\textrm{int} - \varvec{f}^{eA}_\textrm{vol} - \varvec{f}^{eA}_\textrm{sur} \Big ] = \varvec{0} \end{aligned}$$

(4)

including assembly with respect to all $n_\textrm{el}$ elements e and node combinations A and B, with

$$\begin{aligned} \varvec{M}^{eAB}&= \int \limits _{\mathcal {B}_{n}^{e}} \rho _0\;N^A\,\varvec{I}\,N^B \;J_n^{-1 }\,\textrm{d}V_n\end{aligned}$$

(5)

$$\begin{aligned} \varvec{f}^{eA}_\textrm{int}&= \int \limits _{\mathcal {B}_{n}^{e}} \varvec{P} \cdot \varvec{F}_n^\textrm{t}\cdot \nabla _{\!\varvec{X}_n}{N^A} \; J_n^{-1 }\,\textrm{d}V_n\end{aligned}$$

(6)

$$\begin{aligned} \varvec{f}^{eA}_\textrm{vol}&= \int \limits _{\mathcal {B}_{n}^{e}} \rho _0\,N^A\,\varvec{b} \; J_n^{-1 }\,\textrm{d}V_n\end{aligned}$$

(7)

$$\begin{aligned} \varvec{f}^{eA}_\textrm{sur}&= \int \limits _{\partial \mathcal {B}_{n}^{e\varvec{t}} } N^A\;\varvec{P}\cdot \varvec{F}_n^\textrm{t}\cdot \varvec{N}_n \; J_n^{-1 }\,\textrm{d}A_n\end{aligned}$$

(8)

Here, $\ddot{\varvec{u}}^B$ is the second time derivative of the displacement of node B, i.e. the acceleration, $\rho _0$ is the referential mass density, $\varvec{P}$ is the Piola stress tensor, $\varvec{b}$ is the body force vector and $\partial \mathcal {B}_{n}^{e\varvec{t}}$ is the Neumann-boundary with prescribed tractions and surface normal vector $\varvec{N}_n$ in the previous configuration. Moreover, $\varvec{I}$ denotes the second order identity tensor. For the push forward from the referential to the previous configuration, ${J_n=\det (\varvec{F}_{\! n})>0}$ is used for the volume transformation, $\varvec{F}_{\! n}$ is used for gradient transformations and ${{\text {cof}}(\varvec{F}_{\! n})=J_n\,\varvec{F}_{\! n}^{-\textrm{t}}}$ is used for area transformations according to

$$\begin{aligned} \textrm{d}V&= J_n^{-1} \,\textrm{d}V_n \end{aligned}$$

(9)

$$\begin{aligned} \nabla _{\!\varvec{X}}(\bullet )&=\nabla _{\!\varvec{X}_n}(\bullet )\cdot \varvec{F}_{\! n} \end{aligned}$$

(10)

$$\begin{aligned} \textrm{d}\varvec{A}&= J_n^{-1 }\,\varvec{F}_n^\textrm{t}\cdot \varvec{N}_n\,\textrm{d} A_n \end{aligned}$$

(11)

The contributions of element e and node A and B of the internal forces $\varvec{f}^{eA}_\textrm{int}$, the volume forces $\varvec{f}^{eA}_\textrm{vol}$, the surface forces $\varvec{f}^{eA}_\textrm{sur}$ and the mass matrix $\varvec{M}^{eAB}$ are assembled to global vectors and matrices and form the residual $\textbf{r}$ in (4), which is nonlinear in the global list of unknown displacements $\textbf{u}$ and solved numerically with a Newton–Raphson scheme.

The acceleration in (4) is approximated with an implicit Euler backward scheme, i.e.

$$\begin{aligned} \ddot{\varvec{u}}\approx \frac{\dot{\varvec{u}}-\dot{\varvec{u}}_n}{\varDelta t}= \frac{\varvec{u}-\varvec{u}_n}{\varDelta t^2}-\frac{\dot{\varvec{u}}_n}{\varDelta t}\end{aligned}$$

(12)

where the vectors $\varvec{u}_n$ and $\dot{\varvec{u}}_n$ are extracted from global lists $\textbf{u}_n$ and $\dot{\textbf{u}}_n$ which are stored from the last time step.

The linearisation of $\varvec{r}$ in (4) for the Newton scheme then reads

$$\begin{aligned} \textbf{J} = \frac{\textrm{d}\textbf{r}}{\textrm{d}\textbf{u}} =&{{{{\textbf {{\textsf {A}}}}}}}_{e=1}^{n_\textrm{el}}\Bigg [ \frac{1}{\varDelta t^2} {\varvec{M}^{eAB}} +\varvec{K}^{eAB} \Bigg ] \end{aligned}$$

(13)

with

$$\begin{aligned} \varvec{K}^{eAB}= \int \limits _{\mathcal {B}_{n}^{e}} \nabla _{\!\varvec{X}_n}{N^A}\cdot \varvec{F}_n \circ \frac{\partial \varvec{P}}{\partial \varvec{F}} \cdot \varvec{F}_n^\textrm{t}\cdot \nabla _{\!\varvec{X}_n}{N^B} \; J_n^{-1 }\,\textrm{d}V_n\end{aligned}$$

(14)

and the multiplication symbol $\circ$ defined as

$$\begin{aligned} \left[ \varvec{T}\circ \varvec{{{{{\textbf {{\textsf {A}}}}}}}}\right] _{ijkl} = T_{jm}\,{{{{\textbf {{\textsf {A}}}}}}}_{imkl} \end{aligned}$$

(15)

Remark: Although the updated Lagrangian formulation is of incremental nature, the global unknown can be the total displacement list $\textbf{u}$. The constant offset $\textbf{u}_n$ according to (1) connects $\textbf{u}$ and $\varDelta \textbf{u}$, such that both, i.e. $\textbf{u}$ and $\varDelta \textbf{u}$ can be used as solution variable. If PFEM is implemented in a displacement based framework, usually the total displacement $\textbf{u}$ is used as unknown, and only the element formulation has to be changed along with the remeshing methods described in the next section.

3 PFEM—particle finite element method

In PFEM simulations, the cloud of points which represents the body under consideration is frequently remeshed and the shape of the boundary is redefined. In other remeshing schemes, the boundaries are preserved and the points are regenerated. Within the PFEM, the preservation of the points has the advantage of more straightforward state-variable transfer schemes. The redefinition of the boundary makes PFEM flexible for boundary changes, especially as the remeshing is usually performed for every time step to track possible shape changes. Although this is not the focus of the present paper, applications of PFEM often include shape changes due to large deformations.

3.1 Mesh and boundary generation

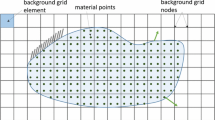
The converged global displacement list of the last time step $\textbf{ u}_n$ defines the placements $\textbf{X}_n = \textbf{X} + \textbf{u}_n$ of the new previous configuration, which is used for the mesh generation. The discretisation is performed by a Delaunay triangulation of the points, originally introduced by [11]. Figure 2a shows the triangulation, whereby the algorithm includes the boundary polygon of the previous mesh, here by applying a constrained Delaunay triangulation. This prevents undesired mesh distortion in the surface region. The Delaunay triangulation discretises the convex hull of the body. To remove all elements outside the actual shape of the body, the $\alpha$-shape method introduced by [12] is applied in a modified version, which has become standard in PFEM, see [7, 13]. Thereby, the $\alpha$-shape detection is based on a preceding Delaunay triangulation which already enforces that each triangle circumcircle contains no further points. Testing the circumcircles for emptiness by verifying that they do not contain any other vertices, which was a component of the original $\alpha$-shape method, is therefore obsolete.

Fig. 2

Constrained Delaunay triangulation and $\alpha$-shape detection of the point cloud representing the body

In summary, all elements of the constrained Delaunay triangulation are subjected to the $\alpha$-test

$$\begin{aligned} r_{\alpha }=\alpha \,l_\textrm{char}<r_{\text {circum}\,T}\quad \Rightarrow \quad \text {reject } T \end{aligned}$$

(16)

i.e. when the test radius $r_\alpha$ fits into the circumcircle radius $r_{\text {circum}\,T}$ of a triangle T, the element is not considered to be part of the body. As test radius, a characteristic mesh size $l_\textrm{char}$ is used and multiplied by the $\alpha$ value. For homogeneous mesh densities, a constant $l_\textrm{char}$ can be used, e.g. $l_\textrm{char}=l_\textrm{min}$, the minimal particle distance in the cloud, see [27]. For inhomogeneous mesh-densities, [7] proposed a local characteristic length $l_{\textrm{char}}^\textrm{loc}$. The average point distance of the node-point p to its $n_\textrm{nb}$ neighbour nodes is calculated in the previous mesh as

$$\begin{aligned} d_\textrm{avg}^p=\sum _{i=1}^{n_\textrm{nb}} \frac{\Vert \,\varvec{X}_{n,i}-\varvec{X}_{n,p}\,\Vert }{n_\textrm{nb}} \end{aligned}$$

(17)

with $\Vert \bullet \Vert =\sqrt{\bullet \cdot \bullet }$. For each triangle in the new mesh, the average point-distances $d_\textrm{avg}^p$ are further averaged over the three element nodes via

$$\begin{aligned} l_{\textrm{char}}^\textrm{loc}= \frac{1}{3}\sum _{p=1}^{3} d_\textrm{avg}^p \end{aligned}$$

(18)

This value is used in the $\alpha$-test (16) for the respective triangle. Thereby, it is important to use the previous mesh for the calculation of $d_\textrm{avg}^p$. The newly generated mesh may still contain potentially very large, distorted triangles as shown in Fig. 2a, which are subsequently removed by the $\alpha$-shape algorithm. Including these elements in the calculation of $d_\textrm{avg}^p$ would artificially increase the averaged point distance, resulting in inaccuracies in the $\alpha$-shape detection.

A resulting mesh after application of the $\alpha$-shape method is shown in Fig. 2b. All edges that appear only once in the connectivity define the boundary polygon which needs to be stored for the constrained Delaunay triangulation of the next remeshing.

3.2 Transfer of state-variables

Two options are considered here for the transfer of the state variables—a direct copying of the variables from the closest quadrature point in the old mesh (CPM), see [17, 26], and an interpolation from three old quadrature points in a background triangle mesh (BTM) as also used in [30] and [17]. Both schemes only change the history data if the global position of a quadrature point changes. Where the previous and new quadrature points occupy the same spatial position, the copying operation does, in general, not alter an equilibrium state. Due to the very frequent remeshing within PFEM, the connectivities and quadrature point positions often undergo localised adjustments within small areas of the mesh. Hence these schemes prevent unnecessary smoothing which can be seen in the standard least-square mapping approach which has been used in early PFEM publications, e.g. [24, 27].

3.2.1 Closest point mapping (CPM)

For the direct transfer of state-variables between meshes, a background triangulation connecting the old integration points is used. Triangulations simplify the search of a nearest neighbour¹. The method is illustrated in Fig. 3a. Due to a simple copy, nonlinear properties of the mapped deformation gradient, such as the determinant, are preserved which is important for incompressible deformation states.

3.2.2 Background triangulation mapping (BTM)

By analogy with the CPM, the BTM is constructed based on a background triangulation of the old integration points. In the BTM, interpolation from the three quadrature points of the enclosing background triangle is employed when the new quadrature point does not coincide with an existing old quadrature point, as illustrated in Fig. 3b. Such algorithm preserves beneficial properties of the CPM, i.e. smoothing of variables is not activated in regions where the mesh does not change. In regions experiencing mesh changes, interpolation is intended to reduce transfer errors compared to the CPM, particularly for coarser discretisations.

The BTM coincides with the algorithm denoted arbitrary Lagrangian interpolation in [17], whereas the denomination BTM refers to the use of a background triangulation, here a Delaunay triangulation. In [30] a slightly different version, also suggested in [17], is applied in PFEM, where the data is mapped from the quadrature points of one unique old element. This element contains the new quadrature point. This motivates the denomination of the algorithm as unique element method. In the present paper only the interpolation from the three quadrature points of the background triangle, independent of the corresponding old element, is considered.

Fig. 3

Illustration of mapping methods for a typical edge-flip connectivity change when the mesh is reconstructed for the same point positions after deformation. Both considered elements, TRI6 and P1P1,  need three quadrature points per element

The interpolation is based on linear shape functions $N^A$, where

$$\begin{aligned} \textbf{s}_q = \sum \limits _{A=1}^{3}\, \textbf{s}_A\,N^A(\varvec{\xi }_q) \end{aligned}$$

(19)

interpolates background-point state-variables $\varvec{s}_A$ to new quadrature point state-variables $\varvec{s}_q$. Here, the points of the background mesh A are the old quadrature points. The new quadrature point q therefore lies within this triangle. For the interpolation (19) the natural coordinates $\varvec{\xi }_q$ are calculated from rearranging

$$\begin{aligned} \varvec{X}_{n,q} = \sum \limits _{A=1}^{3}\, \varvec{X}_{n,A}\,N^A(\varvec{\xi }_q)\end{aligned}$$

(20)

Since all physical coordinates of old quadrature points $\varvec{X}_{n,A}$ and of the new quadrature point $\varvec{X}_{n,q}$ are known, the solution for $\varvec{\xi }_q$ can be derived analytically for specific shape functions. At the boundary of the body, the background triangulation may contain rather distorted triangles, which leads to poor interpolation weights. Furthermore, a new quadrature point can lie outside of any background triangle. In both cases, the data of the closest old quadrature point is copied instead of using an interpolation. As a quality threshold for the background triangles, the radius ratio

$$\begin{aligned} \frac{r_{\text {in}\,T}}{r_{\text {circum}\,T}}<0.005 \end{aligned}$$

(21)

of insphere radius $r_{\text {in}\,T}$ to circumsphere radius $r_{\text {circum}\,T}$ is used, as introduced by [9], see also [19] for further information on element quality measures. The algorithmic treatment of the BTM is further illustrated in Fig. 4 for a linear triangular mesh along with the respective interpolation weights.

Fig. 4

Illustration of BTM for linear triangles with one quadrature point. Left new quadrature point receives interpolated values with weights from shape functions. Right new quadrature point receives data from closest quadrature point since background triangle is too distorted at the boundary. For coinciding quadrature points, the data is copied without smoothing

The interpolation of variables from nearby points is a linear averaging operation. Nonlinear operations, such as the determinant, are in general not preserved by these interpolations. This aspect is critical for almost incompressible deformation states. An algorithm introduced by [5] uses the logarithm of the polar decomposition $\varvec{F}= \varvec{R} \cdot \varvec{U}$ to preserve isochoric deformation states. The basic idea is to formulate $\det (\varvec{F})$ in eigenstretches $\lambda _ {1,2,3}$, i.e.

$$\begin{aligned} \det (\varvec{F}) = \det (\varvec{R} \cdot \varvec{U})=\det (\varvec{R})\,\det (\varvec{U})=\prod \limits _{i=1}^3 \lambda _i \end{aligned}$$

(22)

and, thereafter, application of the logarithm operation. The determinant then transforms to the sum of eigenstretches, namely

$$\begin{aligned} \log (\det (\varvec{F})) =\log \left( \prod \limits _{i=1}^3 \lambda _i \right) =\sum \limits _{i=1}^3 \log (\lambda _i)={\text {tr}}(\log (\varvec{U})) \end{aligned}$$

(23)

The resulting sum is a linear operator which is preserved within the linear interpolation. The following steps are necessary for this procedure

• Polar decomposition of $\varvec{F} = \varvec{R}\cdot \varvec{U}$, calculation of $\log (\varvec{U})$ and $\log (\varvec{R})$

• Interpolation of $\log (\varvec{U})$ and $\log (\varvec{R})$ from three old quadrature points to the considered new quadrature point

• Additional spectral decomposition of the interpolated $\log (\varvec{U})$ in order to calculate $\varvec{U}$, application of the Rodrigues formula to calculate $\varvec{R}$ from $\log (\varvec{R})$, composition of $\varvec{F} = \varvec{R}\cdot \varvec{U}$

For details the reader is referred to [5]. This algorithm adds considerable numerical cost to the state-variable transfer, since the number of mapped variables doubles for each deformation tensor and the transfer also involves spectral decompositions. However, applying this formulation within the BTM requires decomposition only in regions where connectivity changes occur.

As a computationally cheaper option, a multiplicative decomposition of $\varvec{F}$ into $\varvec{F}^\textrm{vol}$ and $\varvec{F}^\textrm{iso}$ before the interpolation is also considered as an alternative.

4 PFEM—Element technology

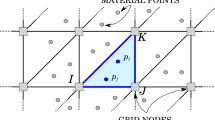
For the application of PFEM in the context of quasi-incompressible material behaviour, the two compared element types are illustrated in Fig. 5

Fig. 5

Illustration of P1P1 element with 9 degrees of freedom and TRI6 element with 12 degrees of freedom in 2d. To avoid introducing additional errors from numerical integration of non-constant integrands, three quadrature points are selected for both elements

4.1 Quadratic TRI6 triangular elements

The TRI6 element depicted in Fig. 5 is a standard triangular displacement element with biquadratic shape functions. However, in the context of PFEM remeshing, some particularities occur. The TRI6 formulation shares some methodologies with the only mentioned higher order element used in PFEM, i.e. the mixed second order displacement first order stress element, cf. [28, 30]. These references mention the edge-mid-nodes being neglected during remeshing – further details will be complemented in the following. PFEM is a remeshing method that preserves nodal points. When considering a point cloud which includes the edge-mid-nodes of the TRI6 element, no standard remeshing algorithm can directly fit a new TRI6 element into the existing point configuration. Instead, the remeshing algorithm typically constructs a linear triangular element first and then introduces edge-mid-nodes. These edge-mid-nodes serve their purpose of improving the element behaviour within a single calculation step and are subsequently erased and regenerated during the remeshing process. It is important to consider the following details:

• Additional nodes during the Finite Element solution make a double book-keeping necessary for implementation, i.e. one data structure for the cloud of real particles and one data structure for the mesh with all corner- and mid-nodes and their degrees of freedom, placements etc.

• Before remeshing, nodal data is stored in the cloud data-structure and the edge-mid-nodes are erased. Element data has to be kept for the state-variable mapping.

• After remeshing and variable mapping, cloud-data is interpolated onto the new edge-mid-nodes which are placed on the straight line between corner-nodes. During the subsequent time step iteration, the element edges can be curved and thus represent the quasi-incompressible deformation better than a linear triangular element.

• Boundary conditions need to be enforced at the edge-mid-nodes located between corner-nodes where boundary conditions are specified. For example, on a Dirichlet boundary, if boundary conditions are not enforced, the edge-mid-nodes may protrude from the surface. Neglecting to apply boundary conditions on the edge-mid-nodes on a Neumann boundary significantly reduces the robustness of the calculation. A pragmatic solution is the application of linear constraints to fix the edge-mid-nodes m to the geometrical midpoint between two corner-nodes $c_1$ and $c_2$ according to

  $$\begin{aligned} \varvec{u}_m = \frac{\varvec{u}_{c_1} + \varvec{u}_{c_2}}{2} \end{aligned}$$

  (24)

  for all boundary edges with prescribed boundary conditions.

4.2 Mixed stabilised P1P1 element formulation

The use of stabilised low-order mixed elements is well established throughout the PFEM literature, e.g. [1, 6, 8, 15, 23, 25, 26]. The P1P1 element depicted in Fig. 5 does not require the handling of additional edge-mid-nodes as the TRI6 element, making it more straightforward to implement in the PFEM remeshing strategy. However, an additional global balance equation needs to be solved by analogy with other multiphysics FE implementations of coupled problems. Furthermore, a stabilisation technique is required because both fields are approximated with low-order shape functions, which can lead to violation of the LBB stability conditions. The Polynomial Pressure Projection method introduced by [2] is frequently applied in the context of PFEM, as detailed in [8, 25], and will be adapted here. An overview of stabilisation techniques can be found in [31], while [1] presents the application of an alternative method within the context of PFEM.

In the present paper, the $\varvec{u}$-$\phi$ formulation is adopted which uses the volume dilatation $\phi$ as a primary global variable, which is coupled to the local quantity $J=\det (\varvec{F})$ via an additional balance equation. Based on [23] the referential weak form of the system of two balance equations reads

$$\begin{aligned} \mathcal {W}_{\varvec{u}}=&\int \limits _{\mathcal {B}_{0} } \nabla _{\!\varvec{X}}\delta \varvec{u} :\widetilde{\varvec{P}}\,\textrm{d}V + w_\textrm{sur}+ w_\textrm{vol}+w_\textrm{dyn}= 0 \end{aligned}$$

(25)

$$\begin{aligned} \mathcal {W}_{\phi }=&\int \limits _{\mathcal {B}_{0} } \delta \phi \,[\phi -J]\,\textrm{d}V = 0 \end{aligned}$$

(26)

with the test functions $\delta \varvec{u}$ and $\delta \phi$. In comparison to the stationarity conditions of a Hu-Washizu three-field functional for incompressibility, see [4], the pressure-condition is neglected. Furthermore, the test function $\delta p$ from the dilatation condition in [4] is replaced with $\delta \phi$ yielding a dimensionless format of the constraint-equation (26). In this section, the referential format is chosen for simplicity and the push forward transformation to the previous configuration $\mathcal {B}_{n}$ is based on (9), (10) and (11). In contrast to the standard balance of linear momentum (4), a modified Piola stress tensor $\widetilde{\varvec{P}}(\widetilde{\varvec{F}})$ is used, with the definition of the modified deformation gradient as

$$\begin{aligned} \widetilde{\varvec{F}}= \left[ \frac{\phi }{J}\right] ^{{1}/{3}}\,\varvec{F}= \phi ^{1/3}\,\varvec{F}^\textrm{iso}\end{aligned}$$

(27)

whereby $\varvec{F}^\textrm{iso}=J^{-{1}/{3}}\,\varvec{F}$ is the isochoric part of the deformation gradient. The volumetric part $\varvec{F}^\textrm{vol}=J^{1/3}\,\varvec{I}$ is replaced by the global volume dilatation variable, i.e. $\widetilde{\varvec{F}}^\textrm{vol}=\phi ^{1/3}\,\varvec{I}$. In an updated Lagrangian setting according to (2) a decomposition into history $\varvec{F}_{\! n}$ and increment $\varDelta \varvec{F}$ of the deformation gradient is made. This yields the modified deformation gradient to take the representation

$$\begin{aligned} \widetilde{\varvec{F}}= \left[ \frac{\phi }{\det (\varDelta \varvec{F}\cdot \widetilde{\varvec{F}}_{\!n})}\right] ^{1/3}\,\varDelta \varvec{F}\cdot \widetilde{\varvec{F}}_{\!n}\end{aligned}$$

(28)

The use of $\widetilde{\varvec{F}}_{\!n}$ as the history variable is motivated by its spatial smoothness, which contributes to improved solution convergence. On the point-level, both $\varvec{F}_{\! n}$ and $\widetilde{\varvec{F}}_{\!n}$ yield identical isochoric parts, as demonstrated by

$$\begin{aligned} \widetilde{\varvec{F}}_{\!n}^\textrm{iso}=\frac{\widetilde{\varvec{F}}_{\!n}}{\det (\widetilde{\varvec{F}}_{\!n})^{1/3}}=\frac{\phi ^{1/3}\,\varvec{F}_{\! n}^\textrm{iso}}{\phi ^{1/3}}=\varvec{F}_{\! n}^\textrm{iso} \end{aligned}$$

(29)

However, significant spatial oscillations are exhibited by $\varvec{F}$ making it unsuitable as history variable. These spatial oscillations stem from $\varvec{F}^\textrm{vol}= J^{1/3}\,\varvec{I}$, which is no longer used in the element formulation. In contrast, the distribution of $\widetilde{\varvec{F}}$ is much smoother than the distribution of $\varvec{F}$ and aligns better with the nodal field of $\phi$, leading to a more robust implementation.

The P1P1 element does not satisfy the LBB stability conditions because both, the primary field $\varvec{u}$ and the constraint field $\phi$ are approximated using identical first-order shape functions. The LBB condition conceptually requires that the primary field $\varvec{u}$ exhibits a higher degree of continuity compared to the constraint field $\phi$ to ensure a well-defined coupled system of Eqs. (25)-(26), cf. [31]. In a linear triangular element, the displacement gradient and consequently the Piola stress in (25) are constant. Therefore, reducing the order of continuity for the constraint field $\phi$—a common approach used for other element formulations—is not applicable to satisfy the continuity requirements in this context. Hence, an extension of (26) is required to stabilise the formulation. Without this stabilisation, the mixed element formulation may exhibit apparent solution convergence during implementation, but volumetric locking and pressure oscillations still persist.

The Polynomial Pressure Projection, cf. [8, 25, 31], extends the constraint Eq. (26) to

$$\begin{aligned} \widetilde{\mathcal {W}}_{\phi }=\int \limits _{\mathcal {B}_{0} } \delta \phi \,[\phi -J] \,\textrm{d}V+\int \limits _{\mathcal {B}_{0} } \frac{\alpha _\textrm{s}^\phi }{G}\,\left[ \delta \phi \,\phi - \delta {\breve{\phi }}\, \breve{\phi }\right] \,\textrm{d}V= 0 \end{aligned}$$

(30)

Hereby, the shear modulus G is measured in Pascals (Pa). Similarly, the stabilisation factor $\alpha _\textrm{s}^\phi$ is assigned units of Pa to maintain the dimensionless nature of the constraint equation, as introduced in [23]. Moreover, $\breve{\phi }$ is a discontinuous projection of $\phi$. The motivation of this approach is an L2-projection of the C0 continuous $\phi$-field onto an elementwise constant and discontinuous field $\breve{\phi }$ in order to compensate for the interpolation mismatch. The L2 mapping reads

$$\begin{aligned} \int \limits _{\mathcal {B}_{0} } \frac{1}{2}\,\left[ \phi -\breve{\phi }\right] ^2 \,\textrm{d}V~\rightarrow ~ \text {Min} & \Rightarrow \quad \int \limits _{\mathcal {B}_{0} } \delta \breve{\phi } \,\left[ \phi -\breve{\phi }\right] \,\textrm{d}V=0 \end{aligned}$$

(31)

which is mentioned in [25, 31] to be solved element-wise for the unknown $\breve{\phi }$. However, the L2-mapping (31) can alternatively be directly inserted into (30) to condense $\breve{\phi }$ from the equations, cf. [8, 25, 31]. With identical linear shape functions $N^A$ for both fields the discretisations reads

$$\begin{aligned} \varvec{u}^e&= \sum \limits _{A=1}^3 \varvec{u}^{eA}\,N^A&\frac{\partial \varvec{u}}{\partial \varvec{X}}&= \sum \limits _{A=1}^3 \varvec{u}^{eA}\otimes \frac{\partial N^A}{\partial \varvec{X}}\end{aligned}$$

(32)

$$\begin{aligned} \phi ^e&= \sum \limits _{A=1}^3 \phi ^{eA}\,N^A&\breve{\phi }^e&= \sum \limits _{A=1}^3 \breve{\phi }^{eA}\,\breve{N}^A \end{aligned}$$

(33)

with the shape functions formulated in the natural coordinates $\xi _\bullet$ of the master-element as

$$\begin{aligned} N^1&= 1-\xi _1-\xi _2\,,&N^2&= \xi _1\,,&N^3&= \xi _2 \end{aligned}$$

(34)

$$\begin{aligned} \breve{N}^1&=1/3\,,&\breve{N}^2&=1/3\,,&\breve{N}^3&=1/3 \end{aligned}$$

(35)

The stabilisation term of the constraint equation (30) is discretised on element level as

$$\begin{aligned} \widetilde{\mathcal {W}}_{\phi \,\textrm{stab}}=\delta \phi ^A\,\int \limits _{\mathcal {B}_{0}^{e}} \frac{\alpha _\textrm{s}^\phi }{G}\,\left[ N^A N^B\,\phi ^B - \breve{N}^A \breve{N}^B \breve{\phi }^B \right] \,\textrm{d}V \end{aligned}$$

(36)

with nodes A and B, where the nodal test function values of the last term has been interchanged from $\delta \breve{\phi }^A$ to $\delta \phi ^A$ as mentioned in [31]. Now, the discretised form of the L2-Mapping (31) on element level results in

$$\begin{aligned} \delta \breve{\phi }^A \int \limits _{\mathcal {B}_{0}^{e}} \breve{N}^A N^B \,\textrm{d}V\,\phi ^B = \delta \breve{\phi }^A \int \limits _{\mathcal {B}_{0}^{e}} \breve{N}^A\breve{N}^B \,\textrm{d}V\,\breve{\phi }^B \end{aligned}$$

(37)

The direct solution of this mapping at the element level, as proposed in [25, 31], is not possible because the smoothing matrix, which results from the assembly process and precedes the solution vector $\breve{\varvec{\upphi }}^e$ of the element, becomes singular due to the shape functions (35). However, by inserting (37) into (36), the unknown discontinuous pressure variable $\breve{\phi }^B$ is condensed. The discretised residual force contributions take the representations

$$\begin{aligned}&\varvec{f}^{eA}_{\varvec{u}} = \int \limits _{\mathcal {B}_{0}^{e}} \widetilde{\varvec{P}}\cdot \nabla _{\!\varvec{X}}N^A\,\textrm{d}V- \int \limits _{\mathcal {B}_{0}^{e}} \rho _0\,N^A\,\varvec{b} \,\textrm{d}V \end{aligned}$$

(38)

$$\begin{aligned}&\,- \int \limits _{\partial \mathcal {B}_{0}^{e\varvec{t}}} N^A\;\varvec{t}_0 \,\textrm{d}A+ \int \limits _{\mathcal {B}_{0}^{e}} \rho _0\;N^A\,\varvec{I}\,N^B \,\textrm{d}V~\cdot \, \ddot{\varvec{u}}^B \nonumber \\&\varvec{f}^{eA}_{\phi }= -\int \limits _{\mathcal {B}_{0}^{e}} N^A\,J \,\textrm{d}V\nonumber \\&\,+\!\Bigg [ \int \limits _{\mathcal {B}_{0}^{e}} N^A N^B \,\textrm{d}V\!+\!\underbrace{\int \limits _{\mathcal {B}_{0}^{e}} \frac{\alpha _\textrm{s}^\phi }{G}\left[ N^A N^B \!-\! \breve{N}^A N^B \right] \,\textrm{d}V} _{\displaystyle {K^{eAB}_{\phi \phi \,\textrm{stab}}}} \!\Bigg ]\phi ^B \end{aligned}$$

(39)

In (38), $\widetilde{\varvec{P}}$ depends nonlinearly on $\phi$ according to (29), which is why the internal contribution and its linearisations are integrated with three quadrature points. The elemental stabilisation matrix $\varvec{K}^{e}_{\phi \phi \,\textrm{stab}}$ assembled from (39) consists of two mass-like matrices. The first is also integrated with three quadrature points because using only one quadrature points yields a zero matrix in the subtraction. In the references [8, 23, 25], the second mass-like contribution $\breve{N}^A N^B$ is given as $\breve{N}^A \breve{N}^B$ which does not fit into the above given derivation. In practice both matrices are identical due to identical constant $\breve{N}^A$ and the partition of unity property of $N^B$.

The linearisation of the residual contributions yields

$$\begin{aligned} \varvec{K}^{eAB}_{\varvec{u}\varvec{u}}&= \int \limits _{\mathcal {B}_{0}^{e}}\nabla _{\!\varvec{X}}N^A\circ \frac{\partial \widetilde{\varvec{P}}}{\partial \widetilde{\varvec{F}}} :\frac{\partial \widetilde{\varvec{F}}}{\partial \varvec{F}}\cdot \nabla _{\!\varvec{X}}{N^B} \,\textrm{d}V \end{aligned}$$

(40)

$$\begin{aligned} \varvec{K}^{eAB}_{\varvec{u}\phi }&= \int \limits _{\mathcal {B}_{0}^{e}}\nabla _{\!\varvec{X}}N^A\circ \frac{\partial \widetilde{\varvec{P}}}{\partial \widetilde{\varvec{F}}}:\varvec{F}\, \left[ \frac{1}{3} \,\frac{\phi ^{[{1}/{3}-1]}}{J^{1/3}}\right] \,N^B\,\textrm{d}V\end{aligned}$$

(41)

$$\begin{aligned} \varvec{K}^{eAB}_{\phi \varvec{u}}&= -\int \limits _{\mathcal {B}_{0}^{e}} N^A\,J\,\varvec{F}^{-\textrm{t}} \cdot \nabla _{\!\varvec{X}}N^B\,\textrm{d}V\end{aligned}$$

(42)

$$\begin{aligned} \varvec{K}^{eAB}_{\phi \phi }&= \int \limits _{\mathcal {B}_{0}^{e}} N^A N^B \,\textrm{d}V+\int \limits _{\mathcal {B}_{0}^{e}} \frac{\alpha _\textrm{s}^\phi }{G}\,\left[ N^A N^B - \breve{N}^A N^B \right] \,\textrm{d}V \end{aligned}$$

(43)

with the notation $\circ$ being introduced in (15) and the deriviative in (40) follows from (29) as

$$\begin{aligned} \frac{\partial \widetilde{\varvec{F}}}{\partial \varvec{F}}=\left[ \varvec{I} \,\overline{\otimes }\,\varvec{I} -\frac{1}{3}\,\varvec{F}\otimes \varvec{F}^{-\textrm{t}} \right] \,\left[ \frac{\phi }{J}\right] ^{1/3} \end{aligned}$$

(44)

wherein $\left[ \varvec{I} \,\overline{\otimes }\,\varvec{I}\right] _{ijkl}=\delta _{ik}\,\delta _{jl}$ and $\delta _{ij}$ denoting the Kronecker delta.

The stabilising contributions in (39) and (43) are governed by the stabilisation factor $\alpha _\textrm{s}^\phi$, which will be discussed further in the following paragraph. In [23], a different stabilisation parameter $\alpha _\textrm{s}^p$ is introduced for the $\varvec{u}$-p formulation compared to $\alpha _\textrm{s}^\phi$ for the $\varvec{u}$-$\phi$ formulation, and specific values for these factors are not provided. According to [8], an identical stabilisation factor $\alpha _\textrm{s}=1$ can be chosen for both formulations. However, to be precise, the units of the stabilisation factors differ between the two formulations. References [6, 26, 31] recommend $\alpha _\textrm{s}^p\approx 1$ as a stabilisation factor for the $\varvec{u}$-p formulation. The present paper proposes to use a stabilisation factor in the order of magnitude of the compression modulus, i.e. $\alpha _\textrm{s}^\phi =K$. This choice is motivated by a simplified relation between the pressure p and the volume dilatation $\phi$ for nearly incompressible hyperelastic materials, as discussed in [4]. Thereby, the pressure p can be derived from the volumetric Helmholtz free energy density $\psi ^\textrm{vol}$ as

$$\begin{aligned} \psi ^\textrm{vol}&= \frac{1}{2}\,K\,[J-1]^2 \end{aligned}$$

(45)

$$\begin{aligned} \Rightarrow \quad p&=\frac{\partial \psi ^\textrm{vol}}{\partial J}=K\,[J-1]\end{aligned}$$

(46)

which shows that J, and thus $\phi$, is related to the pressure p via K. Therefore, $\alpha _\textrm{s}^\phi =K$ should be suitable for the $\varvec{u}$-$\phi$ formulation, while references [6, 26, 31] recommend $\alpha _\textrm{s}^p\approx 1$ for the $\varvec{u}$-p formulation. Interestingly, this leads to

$$\begin{aligned} \frac{\alpha _\textrm{s}^\phi }{G}= \frac{K}{G} = \frac{2}{3}\frac{[1+\nu ]}{[1-2\,\nu ]} \end{aligned}$$

(47)

as a prefactor for the stabilisation term in (39). This can be interpreted as a dimensionless factor scaling the amount of stabilisation according to the incompressibility of the material. The function is visualised in Fig. 6 alongside a reduced prefactor of $K/[10\,G]$, both of which will be tested in the subsequent examples with respect to the influence on the solution quality and the stability of the element formulation.

Fig. 6

Ratio of compression modulus K and shear modulus G proposed as stabilisation prefactor

4.3 Material model

A compressible Neo-Hooke-type hyperelastic material model is used with the Helmholtz free energy density

$$\begin{aligned} \psi _0 = \frac{1}{2}\,\lambda \,\ln ^2(J) + \frac{1}{2}\,\mu \,\left[ \varvec{F}:\varvec{F}-3\right] - \mu \,\ln (J) \end{aligned}$$

(48)

and the Lame parameters $\lambda$ and $\mu$ which are related to the Young’s modulus E and the Poisson ratio $\nu$ via

$$\begin{aligned} \lambda = \frac{E\,\nu }{[1+\nu ][1-2\,\nu ]}\,, \quad \mu = \frac{E}{2\,[1+\nu ]} \end{aligned}$$

(49)

as well as to the compression modulus K and shear modulus G via

$$\begin{aligned} \lambda = K-\frac{2\,G}{3}\,, \quad \mu =G \end{aligned}$$

(50)

Resulting from a hyperelastic form, the Piola stresses $\varvec{P}$ are expressed as

$$\begin{aligned} \varvec{P} =\frac{\partial \psi _0}{\partial \varvec{F}}= \left[ \lambda \,\ln (J) - \mu \right] \,\varvec{F}^{-\textrm{t}} + \mu \,\varvec{F}\end{aligned}$$

(51)

5 Numerical examples

The performance of the element formulations and mappings is analysed in this section for 2d examples under plane strain conditions. A quasi-incompressible rubber block under compression is considered. The first example depicts a block strongly constrained in deformation by Dirichlet boundary conditions, with a Poisson ratio very close to 0.5. This example compares to literature results and investigates the influence of the stabilisation factor $\alpha _\textrm{s}^\phi$ for the P1P1 formulation, along with a short element comparison to the TRI6 element. A second example compares the element performance of the P1P1 and the TRI6 element and the influence of the transfer-methods on a less constrained block with reduced incompressibility and relaxed geometric constraints compared to the first example.

The abbreviations used in the parameter studies are

• TRI6: six-noded 2d quadratic triangular element

• P1P1: mixed three-noded 2d linear triangular element with additional node variable $\phi$, coupled to the local contribution $\det (\varvec{F})$

• CPM: closest point mapping – state-variables are copied from the closest quadrature point of the previous mesh

• BTM: background triangle mapping – state-variables are interpolated from a background triangulation of the old quadrature points. Direct data copy for coinciding points.

• ISO1 (for BTM) – $\varvec{F}^\textrm{vol}$ and $\varvec{F}^\textrm{iso}$ are interpolated separately to approximately preserve isochoric deformations

• ISO2 (for BTM) – $\log (\varvec{U})$ and $\log (\varvec{R})$ are interpolated to exactly preserve isochoric deformations

In case of the P1P1 element, the modified deformation gradient $\widetilde{\varvec{F}}_{\!n}$ is used as the history variable instead of the deformation gradient $\varvec{F}_{\! n}$ used in the TRI6 element. This also applies to the ISO1 and ISO2 decompositions.

5.1 Highly constrained rubber block under compression

The boundary-value problem depicted in Fig. 7a is used as first benchmark, taken from [3, 21], to analyse the influence of the stabilisation factor $\alpha _\textrm{s}^\phi$ and to find a suitable value for $\alpha _\textrm{s}^\phi$. A prescribed displacement of $u_\textrm{pre}=0.2$ mm on the left half of the top surface is applied. The load represents a frictionless rigid indenter inducing a stress singularity at the middle of the top surface. The material is described by the Neo-Hooke model from (48) with a compression modulus $K=10^5$ MPa and shear modulus $G=2$ MPa, i.e. Young’s modulus $E=5.99996$ MPa and Poisson ratio $\nu =0.49999$. Selecting a Poisson ratio close to the incompressible limit and enclosing the rubber blocks to both sides results in a quasi-incompressible deformation state. Simulating such behaviour is challenging within a finite element setting. A mesh grid is constructed with a resolution of $4\times 8$ element edges by defining a regular arrangement of nodes. However, to improve mesh quality during deformation, the node distribution is further improved. In alternating rows, nodes are shifted by half an edge-length relative to the underlying regular grid. Additionally, endpoints are inserted in these rows to maintain a good boundary description. This refined mesh configuration enhances the grid’s regularity, leading to significantly fewer unnecessary connectivity changes in the subsequent remeshing operations. The resulting mesh can be seen in Fig. 7b. Since the grid is mostly regular, a constant $l_\textrm{char}=0.2$ mm is used for the $\alpha$-shape method along with $\alpha =1.1$ for the $\alpha$-test, cf. (16). The displacement is applied linearly in 200 steps of $\varDelta u_\textrm{pre}=0.001$ mm. The CPM variable mapping is chosen for this study, because connectivity changes occur only for low stabilisation parameters $\alpha _\textrm{s}^\phi \le 100$ MPa and only for time, respectively load steps subsequent to $u_\textrm{pre}=0.168$ mm. Consequently, the choice of mapping has minimal impact on the results and conclusions drawn from this example.

Fig. 7

Highly constrained rubber block under compression with $\nu =0.49999$ and unit length $a=1$ mm, after [3]

The stabilisation factor $\alpha _\textrm{s}^\phi$ in the P1P1 formulation is analysed in Fig. 8 by comparing the related force-displacement curves. Increasing the factor leads to softer behaviour. The value for $\alpha _\textrm{s}^\phi =1$ MPa reported in [8] yields a very stiff behaviour along with slight deviations from the smooth curves starting at $u_\textrm{pre}=0.168$ mm when the connectivities start to change and variable mapping becomes influential. These connectivity changes only occur in this example for small stabilisation factors $\alpha _\textrm{s}^\phi \le 100$ MPa and the resulting non-smooth deformations. The oscillations of the related force-displacement diagrams, which can be seen in the detail view in Fig. 8, are a result of the transfer error of the CPM mapping. This can be seen in comparison with the FEM reference curve shown in the detail view of Fig. 8, where these oscillations do not occur. The choice of $\alpha _\textrm{s}^\phi =\{1, 2, 5, 10,100\}$ MPa does not show a significant influence and the related curves quasi coincide. Choosing higher factors $\alpha _\textrm{s}^\phi =\{10^3,10^4,10^5\}$ MPa leads to increasingly softer material behaviour. Hereby, $\alpha _\textrm{s}^\phi =10^4~\text {MPa}=K/10$ yields a final reaction force which is very similar to the results reported in [3, 21]. The references report final reaction force levels of approximately $F_\textrm{reac}=6.5$ N for different advanced finite element formulations. A comparison of pressure contour plots for $\alpha _\textrm{s}^\phi =1$ MPa and $\alpha _\textrm{s}^\phi =10^4$ MPa in Fig. 9 shows the importance of increasing the stabilisation factor to avoid locking and pressure oscillations for such extreme quasi-incompressibility. The results indicate that an appropriate stabilisation factor might be $\alpha _\textrm{s}^\phi =K/10$. This leads to a complete prefactor in the P1P1 formulation (39) of $\alpha _\textrm{s}^\phi /G=K/[10\,G]$ which is a function of $\nu$ as depicted in Fig. 6.

Fig. 8

Influence of $\alpha _\textrm{s}^\phi$ values in MPa on behaviour of P1P1 element with CPM mapping in PFEM. The reference FEM solution, visible in the detail view, shows that oscillations for small stabilisation values occur only when PFEM remeshing is used

Fig. 9

Influence of stabilisation factor for P1P1 element on pressure distribution and surface curvature of the bulge

To compare the results for $\alpha _\textrm{s}^\phi =K/10$ to the proposed TRI6 element, Fig. 10 shows a comparison of both element formulations. The results show a stiffer behaviour for the TRI6 element, until the PFEM simulation no longer converges at $u_\textrm{pre}=0.172$ mm. The last converged time step is indicated with the $\times$-symbol in Fig. 10. To enable a comparison nonetheless, Fig. 10 also shows a comparison of both element formulations with their FEM version without remeshing. In these two PFEM simulations, no connectivity changes occurred and hence, the CPM  preserves the state-variables perfectly and the simulation results are identical for the P1P1 element. However, the TRI6 PFEM-element bears another difference to its FEM counterpart apart from variable mapping, which is the resetting of the edge-mid-nodes to the straight edges between the corner-nodes. The resulting impact of the differing movability of the edge-mid-nodes is evident in the smoothness of the bulge curvature shown in Fig. 11. This yields a loss of robustness which leads to divergence of the Finite Element solver of the PFEM-TRI6 simulation, as indicated in Fig. 10. The FEM-TRI6 simulation converges without problems and shows an appropriate, but slightly stiffer behaviour compared to the P1P1 element. As the elements shall be applied in PFEM, the next section will show whether the TRI6 element is suitable for use in another test case.

Fig. 10

Comparison of P1P1 and TRI6  formulations and respective FEM formulations without remeshing. $\times$-symbol indicates last converged time step

Fig. 11

Influence of resetting the edge-mid-nodes in PFEM remeshing of the TRI6 element on the curvature of the bulge. Pressure plots at $u_\textrm{pre}=0.172$ mm with grey outlines from P1P1 simulation with $\alpha _\textrm{s}^\phi =K/10$ MPa as reference

5.2 Moderately constrained rubber block under compression

This section will investigate whether the choice of $\alpha _\textrm{s}^\phi =K/10$ also applies for less constrained boundary value problems and whether the element performance differences are similar to the previously analysed example. Furthermore, the influence of the variable mapping will be analysed for large deformations with significant connectivity changes which did not occur in the previous example. The influence of the mesh-density is also analysed. The following example is taken from [3] but reduced to 2d plane strain conditions. This indicates that the subsequent results are not quantitatively comparable with the reference, since the suppression of out-of-plane deformation increases the geometrical stiffness of the problem. The boundary value problem is illustrated in Fig. 12. The material parameters are adopted from [3] as bulk modulus $K=501$ MPa and shear modulus $G=3.2296$ MPa, which is equivalent to a Young’s modulus of $E=9.6482$ MPa and a Poisson ratio of $\nu =0.4968$. Moreover, boundary and incompressibility constraints are significantly weakened compared to the first example in Sect. 5.1. To be specific, the boundary on the right is considered as a free surface, a traction load is applied instead of prescribed displacements and a lower Poisson ratio is chosen. A time step size of $\varDelta t = 0.1$ ms was tested for a majority of the parameter variations, resulting in robust solution convergence with only small deviations from finer time step sizes in the solution fields. However, for a more detailed resolution of the displacement vs. time step diagrams, which are essential for the analysis, a very fine time step of $\varDelta t = 0.01$ ms is applied over 1000 steps. Smaller time steps result in more frequent remeshing and state-variable transfer, amplifying their effects. This emphasises the differences between the mapping methods, making the analysis simpler and clearer. The vertical traction load is defined in the reference configuration according to the Cauchy theorem as $\varvec{t}_0= \varvec{P}\cdot \varvec{N}$, representing a dead load. The magnitude of the traction load is linearly increased to the maximum of 30 MPa. Although the grid is regular at first, large deformations lead to significant stretching at the right edge of the traction load and compression on the left side. Therefore, the local characteristic length $l_\textrm{char}^\textrm{loc}$ from (18) is used for the $\alpha$-shape method along with $\alpha =2.5$ for the $\alpha$-test, cf. (16). The high value of $\alpha$ allows for the preservation of highly stretched elements within the mesh. Typically, under such conditions, the shape of the body would change—however, this example focuses specifically on bulk behaviour rather than on surface changes.

Fig. 12

Moderately constrained rubber block under compression from vertical traction $\varvec{t}_0$, with $\nu =0.4968$ and length $a=50$ mm – plane strain version of example considered in [3]

The vertical displacement $u_y^\textrm{mid}$ of the left-most node on the top surface is analysed, which corresponds to the midpoint considering symmetry boundary conditions at the left edge. The influence of the stabilisation factor $\alpha _\textrm{s}^\phi$ is observed to be less significant in this example compared to the first case in Sect. 5.1. Figure 13 illustrates the resulting midpoint vertical displacements $u_y^\textrm{mid}$ over time steps for a 32$\times$32 discretisation. The compression of the block leads in general to a stiffening behaviour which can be seen in the reduction of the displacement slope. The displacement vs. load step curves for different values of $\alpha _\textrm{s}^\phi$ are almost identical – a close-up view shows that the behaviour is slightly softer with increasing values of $\alpha _\textrm{s}^\phi$. However, for $\alpha _\textrm{s}^\phi =K=501$ MPa the connectivity-changes occurring in the remeshing tend to flip back and forth from one step to the next, leading to result deviations and finally to divergence of the solution algorithm. The displacement vs. time step curve in Fig. 13 for $\alpha _\textrm{s}^\phi =501$ MPa shows the resulting transfer error in minimal deviations from a smooth path, with slight oscillations evident along its length. In Fig. 14 the corresponding flipping of the mesh edges can be seen for a representative set of time steps. A study of the pressure fields reveals that $\alpha _\textrm{s}^\phi =1$ on the other hand is too small to suppress oscillations of the pressure field especially for small deformations at time step 10, see Fig. 15. Interestingly, deformation and pressure field are almost identical when comparing the last time step for $\alpha _\textrm{s}^\phi =1$ MPa and $\alpha _\textrm{s}^\phi =50.1$ MPa, which can be seen in Fig. 16. Mostly oscillation-free pressure fields throughout the load-path and no instabilities that occur for higher values support the conclusion of the previous example in Sect. 5.1 in proposing $\alpha _\textrm{s}^\phi =K/10$ as stabilisation factor for P1P1 elements of $\varvec{u}$-$\phi$ type.

Fig. 13

Influence of $\alpha _\textrm{s}^\phi$ on behaviour of P1P1 element with CPM mapping for moderate test. Increasing $\alpha _\textrm{s}^\phi$ yields slightly softer response, instabilities for $\alpha _\textrm{s}^\phi$=K=501, $\times$-symbol indicates last converged time step

Fig. 14

Section of the mesh close to the right edge of the nodal traction load area for representative time steps. Arrows show the nodal surface forces which represent the vertical traction load $\varvec{t}_0$. P1P1 Element with CPM and $\alpha _\textrm{s}^\phi =K=501$ MPa reveals back and forth flipping of the connectivities

Fig. 15

Comparison of pressure field for P1P1 element with CPM at time step 10 of 1001

Fig. 16

Comparison of deformation and pressure field for P1P1 element with CPM at last time step 1001 shows almost identical results for both factors

Fig. 17

Performance of both element types depending on meshsize and state-variable transfer schemes. The coarse mesh in subfigures a and b shows the advantage of the BTM-ISO2 mapping for better stability and the overall better performance of the P1P1 element. The TRI6 element shows similar performance as the P1P1 element in the fine discretisation in subfigures (c) and (d). The last converged time step is indicated with a $\times$-symbol for each time-series

After an appropriate stabilisation factor for the P1P1 element has been determined from the above analysis, the performance of the two element formulations, along with the influence of state-variable transfer methods and mesh size, will be investigated. Regarding mesh-size, increasing the mesh density leads to problems in this example due to the stress concentration at the right edge of the traction load. The finer mesh resolves this stress concentration instead of smoothing it. Therefore a comparison of mesh sizes is limited, e.g. a $64\times 64$ mesh did not deliver more insight but would have required advanced remeshing techniques such as point-insertion, which are not in the focus of the present paper, see e.g. [26]. However, the two mesh-sizes 16$\times$16 and 32$\times$32 delivered comprehensive results without the singularity influencing the comparison. Figure 17 shows the resulting displacements of the top surface’s midpoint $u_y^\textrm{mid}$ of a 16$\times$16 and a 32$\times$32 grid for all elements and state-variable transfer methods. The finer discretisation shows quite smooth curve profiles for most parameters as illustrated in Fig. 17c and d with some clear distinctions. To be specific, the CPM mapping produces more deviations from the smooth curve paths due to the variable mapping than the BTM mapping. For the fine discretisations, the treatment of the isochoric states with the ISO1 and ISO2 approach during BTM-interpolation yields almost identical curves. However, using no treatment of isochoric states (BTM-ISO0) leads to algorithmic divergence in the P1P1 formulation visible in Fig. 17d. Also for the coarse discretisation, a BTM mapping with a simple interpolation of the variables (BTM-ISO0) leads to early divergence of the solution algorithm and to large deviations from the solution path in both, the TRI6 formulation in Fig. 17a and the P1P1 formulation in Fig. 17b. Interpolating $\varvec{F}^\textrm{vol}$ and $\varvec{F}^\textrm{iso}$ separately (BTM-ISO1) leads to better convergence, although the TRI6 element still shows large deviations towards the end. The special interpolation scheme introduced in (23) (BTM-ISO2) yields a smooth curve progression superior to the CPM method and the BTM method with ISO0 or ISO1. Comparing the two element types, especially for the coarse discretisation a clear advantage in robustness is visible for the P1P1 element in the sense of a regularity in the progression of the result curve. Even with the best mapping (BTM-ISO2) the TRI6 element still shows deviations from a smooth curve. For the fine discretisation, the TRI6 element is clearly also suitable for use and yields similar results to the P1P1 element when using the BTM  transfer scheme.

5.3 Calculation times

From a theoretical perspective, the TRI6 element is expected to require more calculation time than the P1P1 element due to the presence of 12 elemental degrees of freedom (TRI6), compared to 9 (P1P1) within a 2d setting. In a practical test of the present implementation in Matlab conducted on identical computer hardware, the TRI6 element demonstrated a 90% increase in computation time for the 16$\times$16 mesh and a 40% increase for the 32$\times$32 mesh. The overhead associated with deleting and inserting edge-mid-nodes in the TRI6 formulation appears to diminish with finer discretisation, primarily attributing the longer calculation times to the difference in the number of degrees of freedom. For the different state-variable transfer methods, the overall time step calculation-time did not vary significantly. Especially for increased deformation, the simulations featuring the BTM-ISO1 or -ISO2 mappings tend to need less iteration steps in the global FEM solution which compensates for the higher numerical cost of the variable mapping.

6 Discussion

The present paper investigates the applicability of the TRI6 element for quasi-incompressible elasticity in the context of the Particle Finite Element Method under 2d plane strain conditions. The element was compared with the established P1P1 element in the less investigated but beneficial $\varvec{u}$-$\phi$ version, which does not necessitate a volumetric-isochoric split in the material model. Both element formulations were embedded into PFEM, which involves the frequent remeshing of the node points, a shape-detection, the transfer of state-variables and an updated Lagrangian FE-formulation. For the state-variable transfer, an improved algorithm using an interpolation from the previous quadrature points was investigated along with approaches to preserve the quasi-incompressible deformation states during interpolation. The element formulations were described with details for the handling of edge-mid-nodes in the TRI6 element and complemented the P1P1 literature with respect to the choice of the deformation history tensor and the stabilisation factor.

The following conclusions can be drawn from the investigations:

• The stabilisation factor for the P1P1 formulation is advised not be set to $\alpha _\textrm{s}^\phi =1$ MPa, as suggested in [8]. Instead, a value $\alpha _\textrm{s}^\phi =K/10$ MPa is recommended, which has demonstrated good agreement with literature reaction-force values, smooth progression of result curves during the simulation and avoiding pressure-oscillations. This recommendation is summarised in a simple equation for the stabilisation factor based on the Poisson ratio. Hereby, the results showed that an adjustment of the theoretically motivated equation is advisable, yielding

  $$\begin{aligned} \frac{\alpha _\textrm{s}^\phi }{G}= \frac{K}{10\,G} = \frac{2}{30}\frac{[1+\nu ]}{[1-2\,\nu ]} \end{aligned}$$

  (52)

  as the proposed prefactor for the stabisilation term in the P1P1 formulation, see (30). Therefore, the stabilisation can be automatically adjusted to the degree of quasi-incompressibility of the considered hyperelastic problem.

• For Poisson ratios very close to 0.5 along with high geometrical constraints in the boundary value problem under consideration, the P1P1 element clearly outperforms the TRI6 element when an appropriate stabilisation factor $\alpha _\textrm{s}^\phi$ is chosen.

• For less severe quasi-incompressibility and less geometrical constraints in the considered boundary value problem, both elements perform equally for a fine discretisation. For a coarser discretisation the P1P1 element again performs better.

• The state-variable transfer which is currently most established in the literature is the CPM mapping, cf. [6, 26]. The mapping results in severe oscillations of representative displacement vs. time step curves due to the repeated remeshing. Especially coarse discretisations benefit considerably from the more advanced transfer scheme BTM. Apart from [30], such algorithm has not yet been established in the PFEM literature. The results clearly show that the BTM is best combined with a special interpolation operation, where the scheme based on a polar decomposition (ISO2) performs very well, but also the separate interpolation of $\varvec{F}^\textrm{vol}$ and $\varvec{F}^\textrm{iso}$, denoted as ISO1, yields results superior to the established CPM mapping.

It has been shown that a TRI6 element is indeed applicable in PFEM simulations with quasi-incompressible deformation states. In view of the higher number of degrees of freedom in the TRI6 element compared to the P1P1 element leading to a higher computational cost, due to the more involved handling of variables in the TRI6 formulation, and especially due to the overall better performance of the P1P1 element, the already established P1P1 formulation is recommended. For this formulation implemented in a strict deformation based Updated-Lagrange PFEM formulation, the present paper adds important details on history variable handling and brings a rarely used advanced transfer method, the BTM mapping, into focus. Especially coupled with interpolation operators preserving the isochoric deformation states, the additional effort of the mapping pays out in a reduced number of iteration steps, better algorithmic convergence and smoother progression of solution-quantities during the simulation, especially for coarser meshes.

The adaption of PFEM to 3d simulations significantly increases the complexity of the geometric meshing and required re-meshing methods, cf. [8, 22]. Therefore, the application of PFEM in 3d simulations has not been addressed in the present paper. However, the element formulations and state-variable transfer methods discussed here are directly applicable to 3d simulations. Nevertheless, the conclusions drawn from this study should be validated through 3d simulations in future research.

For inelastic material models with more state-variables and high strain levels, future work shall investigate the optimal remeshing frequencies in order to find a compromise between the mapping errors and the resolution of material deformation and shape changes. Moreover, in future applications, e.g. the simulation of Direct Energy Deposition and the incompressible flow of molten metal, it will be necessary to reassess whether the P1P1 element continues to outperform the TRI6 element. The stabilisation factor for the P1P1 element needs to be readjusted to the problem because the proposed relation (52) is only valid for hyperelasticity. Here, the TRI6 element can be an alternative since it does not rely on a stabilisation factor. Furthermore, the TRI6 element can be an alternative when the P1P1 element is not applicable in a specific programming environment or software package.