The influence of AAR coupler features on estimation of in-train forces

Abstract

Inadequate management of large in-train forces transferred through coupler systems of a railway train leads to running and structural failures of vehicles. Understanding these phenomena and their mitigation requires accurate estimation of relative motions and in-train forces between vehicle bodies. Previous numerical studies have ignored inertia of coupling elements and the impacts between couplers. Thus, existing models underestimate the additional dynamic variations in in-train forces. Detailed multi-body dynamic models of two AAR (Association of American Railroads) coupler systems used in passenger and freight trains are developed, incorporating coupler inertia and various slacks. Due to the modeling and simulation complexities involved in a full train model, with such details of coupler system, actual longitudinal train dynamics is not studied. A system comprising only two coupling units, inter-connecting two consecutive vehicles, is modeled. Considered system has been fixed at one end and an excitation force is applied at the other end, to mimic a relative force transmission through combined coupler system. Simulation results obtained from this representative system show that, noticeable influence in in-train forces are expected due to the combined effect of inertia of couplers and intermittent impacts between couplers in the slack regime. Maximum amplitude of longitudinal reaction force, transferred from draft gear housing to vehicle body, is expected to be significantly higher than that predicted using existing models of coupler system. It is also observed that the couplers and knuckles are subjected to significant longitudinal and lateral contact forces, due to the intermittent impacts between couplers. Thus, accurate estimation of draft gear reaction force and impact forces between couplers are essential to design vehicle and coupler components, respectively.

1 Introduction

A railway coupling is a mechanism used to connect railroad vehicles (coaches/wagons) to form a train, with functional objectives of transmission and dissipation of in-train forces. Inadequate force management in coupler systems leads to longitudinal discomfort [1,2,3], running instability [4, 5], failures and disengagement of vehicles [6, 7]. Thus, accurate estimation of in-train forces is critical to assess structural and operational safety of vehicle elements or train as a whole. A rail vehicle coupler system typically includes inter-connection elements and energy-absorbing elements, often referred as couplers and draft gears, respectively.

This study is concerned with Association of American Railroads (AAR) standard, automatic coupler systems. AAR automatic coupler systems are globally, the most widely used coupling mechanisms for freight trains [8] till date. Couplers of AAR coupler systems require some slack (clearance) to facilitate automatic inter-connection through their integrated component called knuckle (Fig.  1b). While, slack is desirable for freight trains to control starting dynamics [9], it is disadvantageous in case of passenger trains, as it induces significant longitudinal jerks and running instability during acceleration/declaration [10]. Therefore, a very low slack design, “H” type, called tight-lock coupling [11] is being used in passenger trains in various countries, including India, due to heavy haul capacity and economic benefits of AAR couplers [12].

While, coupler connects vehicles and transmits in-train forces, draft gear provides stiffening and buffering actions against impacts and vibrations [13]. Thus, characteristics of coupler systems govern the dynamics of train, as whole [14, 15]; especially longitudinal train dynamics (LTD). LTD studies involve estimation of relative motions and in-train forces between vehicles [16]. Besides laboratory and field tests, numerical simulations are the backbone of railway research community, as these experiments involve high cost, large development time and most importantly the regulations. Therefore, most of the scientific studies on LTD are based on numerical simulations, which require accurate description of railroad vehicle elements. As dynamic in-train forces are transferred through and managed by coupler systems, their modeling is crucial for accurate prediction of relative motions and forces [17].

Early studies ignored couplers and mathematically modeled the coupling system as a linear spring-damper element [18, 19], directly connected between two vehicles, to represent equivalent draft gear characteristics, which shows substantially different hysteresis behavior than that of a draft gear. However, these models ignored coupler slack, which is an important aspect of railway coupling system. Later studies considered nonlinearity of the system by including coupler slack, for instance Ahmed et al. [20] used clearance dead-band along with linear spring-damper elements. A slightly better representation of draft gear hysteresis was developed in Ref. [21]. Although this model considers bilinear stiffness to characterize nonlinear stiffening of spring toward the end of loading stage, the simulated characteristics differ significantly from experimental characteristics. A better model [22] was proposed by adding additional cubic term of displacement for improved approximation of nonlinear stiffening. This model can simulate close value of peak force and energy absorption; however, overall force variation significantly deviates from the actual trend. Hsu et al. [23] developed an improved model, incorporating frictional hysteresis by replacing cubic term with a velocity dependent exponential function. It also incorporated preload of draft gear. No separate models were developed till then, for different draft gear types. With further advancements in modeling approaches, lately various advanced models relating to different draft gear types have been developed.

A major breakthrough in longitudinal dynamic simulations came with more sophisticated friction draft gear model, friction wedge model, developed by Cole [24]. In this analytical approach, draft gear characteristics can be completely defined through its well-known physical attributes: friction coefficients, wedge angles, spring stiffness, etc. Cole’s model [24] has been widely used in various railway dynamic studies [25,26,27]. An advanced model of double stage friction draft gear was given by Wu et al. [28], which assumes four working stages of the draft gear. This model has been extensively used in the studies of dynamics of trains in which double stage friction draft gear based coupler systems are used [29,30,31]. All these mathematical models can be implemented readily in numerical simulations; however, commercial MBD software widely use look-up table method [5, 32,33,34,35,36,37,38]. It requires a large set of experimental dynamic characteristics (force–deflection) at various loading rates and the approaches to solve discontinuity during transition velocity, to connect loading and unloading paths [39].

The hysteresis characteristics of friction draft gears can be accurately described through its well-defined physical attributes. However, precise description of damping mechanism of polymers is not well-established, hence, their hysteresis models are presently developed using experimental dynamic characteristics. Modern approaches of modeling polymer draft gears, in general, include look-up table [4, 32, 40,41,42,43] and polynomial fitting methods [44, 45]. The common approach to model polymer draft gear characteristics is, fitting experimental characteristics with higher-order polynomials [44, 45] and developing deflection and velocity dependent empirical relations.

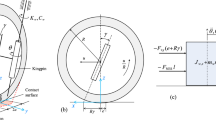
Figure 1a illustrates interconnection between two rail vehicles, by means of AAR coupler system and important components of the assembly. Details are presented for the general case, for instance, during curve negotiation. The close representation of equivalent elements for vibration model of coupler system is illustrated in Fig. 1b. Coupler interconnection is, however, a complex interaction involving various design slacks. Important features associated with coupler interconnection are presented in Fig. 2a. Also, draft gear action is highly nonlinear. A typical nonlinear dynamic characteristic of draft gears is presented in Fig. 2b. While main features of draft gear can be identified as masses, equivalent nonlinear stiffening and damping (Fig. 2b), those in coupler include masses, structural stiffness and slacks (Fig.  2a). Illustrated slack between buffing shoulders during fully stretched condition of knuckles, shown in Fig.  2a, has been referred to as knuckle slack in this study, while, the slack between coupler and knuckle contours is referred as contour slack. Total design slack is thus the sum of knuckle slacks and contour slack. Slack between faces of horn and wing of either side couplers is referred as lateral coupler slack.

Fig. 1

a Illustration of coupling between two vehicles and b schematic diagram of equivalent vibration elements

Fig. 2

a Enlarged view of coupler interaction and b typical force-deflection characteristics of a draft gear

Most recent mathematical models of draft gears incorporate nonlinear stiffening and damping with good accuracy [8, 39] (dynamic effects due to draft gear mass is ignored); however, coupler slack is the only feature of couplers, that is included in the form of a dead-zone. It is usually combined in the draft gear model itself, to represent a coupling unit. Some of the models also include structural stiffness of coupler and knuckle. Such a simplified model, shown in Fig.  3a, is widely used in LTD studies involving curve negotiation and emergency braking [4, 32] scenarios, while that shown in Fig.  3b is extensively used in simulations for vehicles running on tangent tracks [26, 38]. Couplers are combined and modeled as a massless link of twice the length of individual coupler, to estimate the coupler angle to compute tangential forces.

Fig. 3

Schematic diagrams of equivalent vibration elements of a conventional model for curve negotiation and emergency braking and b conventional model for perfect longitudinal motion on tangent tracks

Studies addressing effect of clearance on various mechanisms [46,47,48,49] show that actual acceleration or force transfer is considerably different than those considered without clearance. Noteworthy deviations in transmitting forces between connected bodies are caused by intermittent impacts and frictional rubbing during metal-metal contact; hence dynamic aspects of presence of clearance in a mechanism should not be overlooked. To the authors’ knowledge, no significant work is found, addressing actual dynamic interactions between couplers due to the slack and inertia except in Refs. [50,51,52,53]. Although Lu et al. [50] considered normal contact and frictional forces between coupler heads, inertia and structural stiffness characteristics are disregarded. Yao et al. [51] and Cole et al. [52] though mentioned the effect of coupler inertia; slack induced impacts and frictional transitions between couplers are not incorporated. The inertial effects of coupler contribute in interaction between coupler heads, giving rise to intermittent impacts and frictional rubbing actions [54]. Recently, Yadav et al. [53] developed a mathematical model of such a coupling system, incorporating masses of couplers. It has been shown that, there is significant difference in the estimation of in-train forces and jerks, with and without consideration of coupler masses. However, they did not accommodate relative rotation between couplers to estimate the lateral forces. Also, interaction between couplers and their respective knuckles are not modeled.

This study develops multi-body dynamic model of AAR automatic coupler systems, for numerical simulations to analyze the actual dynamics of coupling system. An attempt has been made in this study to address the implications of various slacks and inertial effects of couplers on longitudinal dynamics of rail vehicles. Multi-body dynamic models of two coupling types have been developed to incorporate rotational degree of freedom of the couplers for improved analysis of interactions between the contours of couplers and knuckles within slack regime. Knuckle clearance is also incorporated. It includes more details of a coupler system than the existing mathematical models and is able to capture the frictional transitions and the resulting lateral reaction.

Two types of AAR standard coupling systems have been analyzed. For convenience in discussions, following nomenclature is defined:

• Passenger car coupling: An H-type coupling, with very small slack, used in passenger trains

• Freight car coupling: An E-type coupling, with large slack, used in freight trains

Focus is on differences in dynamic behavior, predicted with and without consideration of couplers inertia. The effects of important design parameters are investigated for abovementioned couplings, and compared with those predicted using respective conventional coupling model, used in earlier studies. Particularly, the steep variations in draft gear reaction forces are analyzed, due to the intermittent impacts and friction actions, occurring in the vicinity of clearance zone. Detailed multi-body dynamic models of these couplings, incorporating inertial, geometrical and contact properties, are developed to investigate the expected dynamic behaviors of these coupler systems. Conventional mathematical models are not modeled mathematically, but they are replicated by manually assigning very small masses to the components of detailed models itself, discarding knuckles and locking together the two couplers.

2 Important features of AAR automatic couplers

An automatic coupler provides a three-dimensional mechanism to form inter-connection between rail vehicles, through its integrated component called knuckle. AAR standard automatic couplers are designated as types, “E”, “F” and “H”, based on different design (contour profiles and coupler heads) and permissible slack. AAR coupler systems can broadly, have four possible slacks: (a) contour slack, (b) knuckle slack, (c) yoke connection slack, and (d) draft gar slack. Yoke connection slack and draft gear slack arise due to wear and tear but contour and knuckle slacks are design intended slacks to deliver the desired actions. E-type couplers are characterized by highest slack, with typical design slack (contour + knuckle slack) up to 20 mm, followed by F-type couplers with design slack up to 10 mm. Both these couplers are primarily used in freight trains. In H-type couplers, popularly known as tight-lock couplers, used in passenger trains, a maximum design slack up to 3.2 mm is allowed.

Knuckle slack is provided on all AAR type couplers to avoid load transfer through knuckle pin, which is the weakest component of the assembly. Improved design and precisely machined mating surfaces of coupler and knuckle allow H-type couplers to form inter-connection utilizing knuckle slack itself, and ideally it does not require additional contour slack. The reason for avoiding excessive slack in passenger train couplers (H-type) is that slack induces longitudinal jerks and running instability during acceleration/declaration [10]. On the other hand, in freight train couplers (E and F type), additional slack in the form of contour slack is provided to control starting dynamics [9]. Moreover, excessive slack may lead to very high magnitude of jerks, sufficient to cause failure of vehicle and coupling components and may also cause train-parting. In addition, large slack can also induce additional lateral force, coupled with longitudinal in-train force. Hence, accurate analysis of influence of slacks is essential.

Various design slacks and resulting interactions of coupler components during operation are illustrated in Fig. 4. Top row of figures displays front sectional views and bottom row displays top views. Left side coupler and corresponding knuckle are omitted in front sectional views for clarity. Once, couplers are interconnected, knuckles are locked to prevent the knuckle rotation (clockwise for K2 and counter-clockwise for K1). However, a small amount of rotation of knuckles is possible in the opposite directions (counter-clockwise for K2 and clockwise for K1) because of available small slack d$_3$, as shown in Fig. 4d. Figure 4a illustrates a random position of couplers. It can be seen that the outer diameter of knuckle pin is provided with some tolerance (knuckle slack). Although, lock inhibits unlocking of knuckle, small translational movements (Fig. 4d) of knuckles are also possible within the cavity inside respective coupler heads, due to presence of slacks d$_1$ (omitted in Fig. 4d for clarity) and d$_2$. A small amount of slack between faces of horn of one coupler and the corresponding cavity (wing pocket) on other coupler (Fig. 1c), allows a very small amount of relative rotation between couplers. These horn and wing features are though present in H-type and F-type couplers, there are no wing pockets in E-type couplers, allowing comparatively larger rotation between couplers, constrained by the amount of contour slack. During buff mode, knuckle transfers the force by interacting with coupler on matching contour, called buffing shoulders (Fig. 4b) and through the faces of pin protector regions. In draft mode, it transfers the load through its pulling lug contacting the pulling lug on coupler (Fig. 4c) and through the faces of pin protector regions. Thus, coupler pin does not stake any buff or draft load in a defect-free coupler system and its only function of it is to assist knuckle to rotate during mating of couplers. In this study, only design slack (contour + knuckle) has been considered. Thus, numbers of interactions are possible within coupling regime: (i) interaction of buffing shoulder (in buff mode: Fig. 4b) or pulling lug (in draft mode: Fig. 4c) of a knuckle with its own coupler, along with pin protector (ii) interaction of knuckle head with opposite coupler head (in buff mode Fig. 4e) and (iii) interaction of knuckle nose with opposite knuckle nose (in draft mode: Fig. 4f).

Fig. 4

Illustration of positions of coupler components during ideal equilibrium: a front sectional view; b buff mode (front sectional view); c draft mode (front sectional view); d top view; e buff mode (top view); f draft mode (top view)

3 Multi-body dynamic models

The focus of this study is to address the influence of coupler’s features on estimation of in-train forces, rather analyzing full train dynamics. This work is thus restricted to modeling and analysis of coupler system only. Simulations are performed using MSC ADAMS platform, using fixed time-step with sample time of $1 \times 10^{-3}$ s.

3.1 Analysis approach and simplifications

In a real railway train, the centerlines of vehicles and the centerline of couplings do not exactly coincide, under running condition, even on tangent tracks. Thus, in real situation, the two ends of a coupling system are constrained by vehicle body connections and instantaneous operational conditions, such as braking, curve or grade negotiation. While, actual constraints on a coupler system are never perfect in the longitudinal direction, running of train on a tangent track has been considered in this study, along with the assumption that centerlines of two vehicles are perfectly aligned. Thus, the centerline, connecting the yoke pins of two couplers is perfectly along longitudinal direction. However, small rotation between couplers, around the yoke pins are allowed, constrained by the slack between faces of horn of one coupler and the corresponding cavity on other coupler (Fig. 2a), in case of H-type couplers and due to the absence of these features in E-type couplers.

An ideal LTD simulation model of complete train, under such assumptions, is presented in Fig. 5a. Combining all the forces acting on the vehicle (braking force $F_\text {b}$, combined resistance force $F_\text {r}$ and coupling force $F_\text {c}$), equivalent longitudinal forces on two adjacent vehicles can be simplified as $F_i(t)$ and $F_{i + 1}(t)$ (Fig. 5b). Subsequently, the system consisting two coupling units, as shown in Fig. 5c, is analyzed in this work using a relative longitudinal force, $F(t) = F_{i + 1}(t)-F_i(t)$, applied on the right end of the coupling system. Draft gear of left coupling unit is kept fixed, while that of right unit is kept free to translate. Reaction at the fixed draft gear is the equivalent force transmitted to its connected vehicle. Therefore, the analyzed results in this study, does not represent the actual dynamics that of a real railway train. However, these results reveal important dynamic influences of the features of AAR coupler systems and similar effects are expected in an actual train system.

Fig. 5

a LTD model of train, b forces acting between two vehicles and c representative forces on coupling system

The longitudinal force ($F(t) = F_0 \sin (\omega t)$) applied on free side draft gear is a harmonic force with a characteristic frequency. We focus on periodic excitations under normal running condition, and chose a typical longitudinal coupler force amplitude ($F_0$) of 400 kN [55,56,57,58]. Two explicit frequencies $\omega _1 = 0.5$ Hz and $\omega _2 = 5.0$ Hz are chosen from the important frequency range of coupler forces, ranging between 0 Hz to 5 Hz [30]. Considering combined mass of couplers and other moving components to be 700 kg and assuming a linear constant stiffness of draft gear as 10 MN/m [3], a quick calculation shows that the linear natural frequency (p) of the system is 19.02 Hz (when couplers are in contact). It can be said the coupler experiences quasi-static ($\omega _1 / p = 0.026$ ) to dynamic ($\omega _2 / p = 0.260$) excitations. This linear spring stiffness is just used to confer the regime of excitation frequency range (quasi-static to dynamic) that coupler system experiences due to the considered external excitation range. It is to be noted that this linear stiffness value is not used in MBD models, instead actual dynamic characteristics of draft gears is used, as presented in Sect. 3.2.2.

3.2 Dynamic models of coupler systems

Multi-body modeling allows inclusion of most of the intended features in detail. In accordance with stated simplifications in Sect. 2, coupling systems alone are modeled in MSC ADAMS multi-body dynamic platform. Three-dimensional CAD models of coupling assembly (except draft gears) are imported in ADAMS to capture important feature of couplers (Fig. 6). Due to sharing limitations of proprietary designs by manufacturing organizations, approximate three dimensional CAD models of couplers are developed with the help of visual details and loose measurements. A polymer based balanced draft gear is considered for passenger car coupling, while a rubber-spring based friction draft gear is considered for freight car coupling. Characteristics of draft gears are represented through nonlinear force (deflection and velocity dependent) elements, acting between yoke and draft gear housings. For the mentioned reasons, actual yoke and draft gear housing bodies are not modeled. Representative bodies with connection points for nonlinear force elements are created (highlighted in Fig. 6). Although, in the absence of detailed models and accurate characteristics of components, exact quantitative predictions cannot be made, these models provide remarkable qualitative description of dynamics of coupling systems.

Fig. 6

CAD model of a passenger car and b freight car coupling system

A single, detailed CAD model of passenger car coupling is developed and also extended to freight car coupling, by

• removing wing pockets,

• providing contour slacks, and

• manually assigning the appropriate masses to the various components and scaling the inertia values proportionally.

MBD models represent slightly modified versions of Figs. 1–3. A rigid connection is assumed between vehicles and draft gears and the structural stiffness of mounting frame and masses of draft gear components are ignored. Representative draft gear housing component is though required for the modeling of draft gear connection points, which has been assigned a small mass, manually. Figure 7a represents connection setup for detailed model of passenger car coupling and Fig. 7b, c represents corresponding equivalent vibration schematics. While other structural stiffness’s can be ignored in this limited study, the locking stiffness resulting from draft gear components, needs to be incorporated for accurate modeling of behavior of a friction draft gear [24, 59, 60]. Therefore, in case of freight car coupling, a linear spring element with stiffness equals half the locking stiffness has been incorporated in series with the left side draft gear, combining the locking stiffness (springs in series) of both the draft gears into one (Fig. 8). This stiffness is typically of the order of 100 MN/m [24, 59, 60], thus a linear stiffness of 50 MN/m is provided to the spring. Figure 8a represents connection setup for detailed model of freight car coupling and Fig. 8b, c represent corresponding equivalent vibration schematics. It is to be noted that in case of detailed model of freight car coupling, contact force CF$_6$ is absent due to the absence of wing and pocket features in E type couplers. To incorporate the locking stiffness, an additional transnational joint J$_0$ between left draft gear housing and an additional body is provided. Fixed joint J$_1$ is provided to the additional body with respect to ground. This additional body is required to provide the connection point for the spring element. Also, in this case, one more force element SF$_0$ is used in addition to the ones in the model of passenger car coupling.

Fig. 7

a Connections and forces setup in ADAMS View and b, c equivalent vibration schematics of detailed model for passenger car coupling

Fig. 8

a Connections and forces setup in ADAMS View and b, c equivalent vibration schematic of conventional model for freight car coupling

The same CAD models are also extended to represent conventional models, by choosing appropriate connections. For this purpose, knuckles are ignored, two couplers are locked together to make a single entity and bodies are provided with negligible masses (5% of their actual masses), denoted conventional models. Half slacks in the form of dead-zone are provided to the either side draft gear. Figure 9a represents connection setup for representative conventional model of passenger car coupling and Fig. 9b represents corresponding equivalent vibration schematics. Similar connection setup (Fig. 10) has also been extended for freight car coupling (except CF$_6$). Considered axis system is presented in Fig. 7a, where x represents longitudinal direction and y represents lateral direction. First letter of subscripts in various variables represents side (left or right) of component and second letter represents the name of component (e.g., c stands for coupler). List of various connections and forces between different components for all the cases are provided in Table 1. Adopting MSC ADAMS terminology, letter J denotes joint, SF denotes single component force element and CF denotes contact force element.

Fig. 9

a Connections and forces setup in ADAMS View and b equivalent vibration schematic of conventional model for passenger car coupling

Fig. 10

a Connections and forces setup in ADAMS View and b equivalent vibration schematic of conventional model for freight car coupling

Table 1 Connections and forces between different components of MBD models

Since, the contact type interaction is provided between a knuckle and its respective coupler; knuckle is free to move within slack regime. Again, since lock is modeled as integral part of coupler body, it prevents opening of knuckle; however, knuckle is free to rotate within permissible angle.

3.2.1 Joints

Joints $\text {J}_1$ and $\text {J}_7$ are fixed joints which constrain all 6 degrees of freedom, where $\text {J}_1$ is used to lock left draft gear housing in case of passenger car coupling while it locks additional body in freight car coupling, w.r.t. ground (fixed support). Joint $\text {J}_7$ locks together the two couplers to simulate the baseline case in both types of couplings. Joints $\text {J}_2$ and $\text {J}_5$ allow only translational motion to draft gear housing relative to yoke along X-axis. Joint $\text {J}_0$ provides translation to draft gear housing w.r.t additional body. Joints $\text {J}_3$ and $\text {J}_4$ allow rotation of couplers about Z-axis, w.r.t. yoke. Joint $\text {J}_6$ allows translation of right side draft gear housing with respect to ground.

3.2.2 Force elements

Spring force element $\text {SF}_0$ provides locking stiffness to the draft gear system in case of friction draft gear, with the stiffness value equals 50 MN/m. Excitation force element ($\text {SF}_3$) is a harmonic force with magnitude of 400 kN. Two explicit values of frequency, $\omega$ (= 0.5, 5.0 Hz) are chosen, as discussed in Sect. 3.1. Nonlinear force element ($\text {SF}_1$ or $\text {SF}_2$), representing draft gear force $F_\text {dg}(x, \dot{x}$), is a function of draft gear deflection (x) and velocity ($\dot{x}$). Dynamic characteristics of draft gears to model nonlinear force elements, were produced using mathematical models given in Refs. [45] and [24] using drop hammer test data of polymer based balanced draft gear and rubber-spring based friction draft gear (Fig. 11a, b), respectively.

As suggested in [45], polymer draft gear can be modeled through polynomial fitting method. This approach requires only dynamic loading and unloading curves using drop hammer test at certain frequency (usually at 10 Hz). Initially, sixth-order polynomial functions of displacement (x) are fitted on them and their mean or weighted mean is assumed to be the static characteristics of draft gear. Thus, the approximate static force component $F_\text {s}(x)$ can be estimated using Eq. (1), as [45]

$$\begin{aligned} F_\text {s}(x) = g_1 \sum \limits _{n=1}^k a_n x^n + g_2 \sum \limits _{n=1}^k b_n x^n \end{aligned},$$

(1)

where k is the degree of curve, and indices n = 1, 2, 3, 4 represent draft loading, draft unloading, buff loading and buff unloading, respectively. Polynomial coefficients $a_n$ and $b_n$ are determined by fitting polynomials on dynamic curves, and $g_1 + g_2 = 1$.

Differences between loading curves and their respective mean curves are then used to estimate the hysteresis components, termed as dynamic force components $F_\text {d}(x,\dot{x})$. These are fitted separately, as functions of both velocities and deflections (Equation (2)), given as [45]

$$\begin{aligned} F_\text {d}(x,\dot{x}) = \left[ F_3 + F_4 \left| \frac{x}{x_\text {max}}\right| ^p \left| \frac{\dot{x}}{\dot{x}_\text {max}}\right| ^q \right] \times \left[ 1-\exp \left( -\gamma _3 \left| \frac{\dot{x}}{\dot{x}_\text {max}}\right| ^r \right) \right] \end{aligned},$$

(2)

where $\dot{x}$ is the velocity, and parameters $F_3$, $F_4$, p, q, r and $\gamma _3$ are determined by fitting Eq. (2) on dynamic loading or unloading components, separately. $x_\text {max}$ and $\dot{x}_\text {max}$ are chosen as 0.2 m and 10 m/s, respectively, as suggested in Ref. [45]. Preload $F_3$ is assumed to be zero.

Reaction force of the draft gear, $F_\text {dg}$ is then defined as the sum of static component, $F_\text {s}$ and dynamic component, $F_\text {d}$, expressed as [45]

$$\begin{aligned} F_\text {dg}(x, \dot{x}) = F_\text {s}(x) + F_\text {d}(x, \dot{x}) \end{aligned}.$$

(3)

Despite close fitting of polynomials in general, it can overestimate or underestimate the curves, when there are insufficient data points [61]. Due to the limited data points, extracted manually from the graphs of drop hammer characteristics, provided by the local manufacturer, static characteristics for polymer draft gear is fitted with following exponential function (Eq. (4)) instead of using Eq. (1), on mean values obtained from dynamic curves. Exponential fitting provided a consistent trend, even with small number of experimental data points. Dynamic force component $F_\text {d}$ is modeled same as in [45].

$$\begin{aligned} F_\text {s}(x) = F_0 + F_1 \exp (\gamma _1 x)+ F_2 \exp (\gamma _2 x) \end{aligned},$$

(4)

where $F_0, F_1, F_2, \gamma _1$, and $\gamma _2$ are the tuning parameters.

Nonlinear characteristic of friction draft gears is, however, substantially different than polymer draft gears. A friction wedge model, given by Cole [24] is adopted in this study. In this analytical approach, hysteresis effect is defined through friction coefficients, wedge angles and spring stiffness. Draft gear force, $F_\text {dg}$ for a single stage friction draft gear (Eq. (5)) can be expressed as [24]

$$\begin{aligned} F_\text {dg}(x, \dot{x}) = \frac{f_\text {s} \tan (\theta )}{\tan (\theta ) \pm \mu } \end{aligned},$$

(5)

where $f_\text {s}$ is the equivalent spring force, $\theta$ is the wedge angle, $\mu$ is the velocity dependent coefficient of friction, ‘+’ corresponds to unloading case, and ‘−’ corresponds to loading case.

A simple velocity based classical Coulomb’s friction model with finite slope, mathematically described by Eq. (6), is used [61]:

$$\begin{aligned} \mu (\dot{x})= \left\{ \begin{array}{ll} u_\text {k} \ \text {sgn} (\dot{x}) &{} |\dot{x}| > \dot{x}_\text {tr}\\ \mu _\text {s} + \frac{|\dot{x}|}{\dot{x}_{\text {tr}}} (\mu _\text {k} - \mu _\text {s}) \ \text {sgn} (\dot{x}) &{} 0 < |\dot{x}| \le \dot{x}_\text {tr}\\ \mu _\text {s} \ \text {sgn} (\dot{x}) &{} |\dot{x}| =0 \end{array} \right. \end{aligned},$$

(6)

where $\mu _\text {k}$ is the dynamic friction coefficient, $\mu _\text {s}$ is the static friction coefficient, and $\dot{x}_\text {tr}$ is the friction transition velocity.

While in coil spring based friction draft gears, spring force is generally defined trough linear spring stiffness or bilinear stiffness, rubber spring force is described through nonlinear stiffness. In absence of exact static characteristics of rubber spring used in friction draft gear, the nonlinear stiffness of spring is modeled through multi-linear relationship, given by Eq. (7) by tuning the stiffness parameters using Eq. (5). Loading is defined in four stages while unloading is defined in two stages.

$$ \begin{aligned} f_\text {s} (x)= \left\{ \begin{array}{ll} (k_{\text {l}1} x + c_{\text {l}1}) \text {sgn} (x) &{} 0 \le |x|< x_{\text {l}1}, |\dot{x}| \ge 0\\ (k_{\text {l}2} x + c_{\text {l}2}) \text {sgn} (x) &{} x_{\text {l}1} \le |x|< x_{\text {l}2} ,|\dot{x}| \ge 0\\ (k_{\text {l}3} x + c_{\text {l}3}) \text {sgn} (x) &{} x_{\text {l}2} \le |x|< x_{\text {l}3} ,|\dot{x}| \ge 0\\ (k_{\text {l}4} x + c_{\text {l}4}) \text {sgn} (x) &{} x_{\text {l}3} \le |x|, |\dot{x}| \\ (k_{\text {u}1} x + c_{\text {u}1}) \text {sgn} (x) &{} 0 \le |x|< x_{\text {u}1} \,|\dot{x}|<0 \\ (k_{\text {u}2} x + c_{\text {u}2}) \text {sgn} (x) &{} x_{\text {u}1} \le |x|, |\dot{x}| <0 \end{array} \right. \end{aligned},$$

(7)

where k is the spring stiffness, c is the force intercept, first index of subscript (l or u) represents loading or unloading stage and second index represents linear segment number. List of various parameters to generate dynamic characteristic data of polymer and friction draft gears (Fig. 11a, b) are provided in Tables 2 and 3, respectively.

Table 2 Fitting parameters for polymer draft gear model

Table 3 Fitting parameters for friction draft gear model

ADAMS implementation requires three dimensional spline curves to be constructed using characteristics data. Numbers of force-deflection curves are generated at various loading rates and corresponding data has been used to construct spline curves. Three dimensional plots of dynamic characteristics of polymer based balanced draft gear and rubber-spring based friction draft gear, are presented in Fig. 11c and d, respectively. An important difference between two draft gears is that, in case of friction draft gear (Fig. 11b, d), force variation is much more steeper in the vicinity of zero velocity than polymer draft gear (Fig. 11a, c), due to the transition between static and dynamic friction.

Fig. 11

a Fitting of mathematical model (Eqs. (2)–(4)) on experimental data of polymer draft gear; b fitting of mathematical model (Eqs. (5)–(7)) on experimental data of friction draft gear; c three dimensional force–deflection characteristics of polymer draft gear; d three dimensional force–deflection characteristics of friction draft gear

3.2.3 Contacts

Table 4 presents contact forces (CF₁−CF₆) parameters. Contact force exponent and penetration depth are chosen according to the recommendations in Ref. [62], for steel-steel contact. A negligibly small damping coefficient (0.0001% of stiffness value) is chosen for realistic realization of metal to metal contact. Stiction transition velocity is taken to be 0.5% ($1 \times 10^{-2}$ m/s) of maximum relative lateral velocity between couplers (2 m/s, found from simulations). While, studies on estimation of friction coefficients between coupler and knuckle surfaces are not available, reference values are chosen from the studies on rail–wheel interface [63] and general tribological experiment on steel-on-steel contact [64], to approximate the friction coefficients. Stiffness of coupler components is taken to be $2 \times 10^9$ N/m.

Table 4 System parameters for MBD models

3.2.4 Masses

The known masses of various components are approximated by using “Geometry and Density” feature, through user input for density values. Inertia is automatically computed by MBD software, using geometries and assigned masses. Approximate masses of various components of MBD models are listed in Table 5.

Table 5 Masses of various components of MBD models (unit: kg)

3.2.5 Slacks

In both the couplings, each knuckle is provided with 1.5 mm slack, i.e., $d_\text {lk} = d_\text {rk}$ = 1.5 mm. Zero slack is provided between coupler and knuckle contours of passenger car coupling ($d_\text {lc} = d_\text {rc}$ = 0 mm), while contour slack of 12 mm is provided in freight car coupling ($d_\text {lc} = d_\text {rc}$ = 12 mm). Thus, in passenger car coupling, design slack on each coupler is 3 mm and in freight car coupling, it is 15 mm. Passenger car coupling is also provided with 2 mm of lateral coupler slack ($d_\text {uh} = d_\text {lh}$ = 2 mm).

4 Dynamics of coupler systems

Because of discontinuous features (slacks and dry friction) of AAR couplers, steep variations are expected in the in-train forces. Therefore, it is important to estimate the actual forces being transmitted through coupler system to the vehicles and components of coupler system.

4.1 Interaction between couplers

As described in the preceding sections, metal-to-metal impacts and resulting frictional transitions, induce additional dynamic forces. While these forces get partially dissipated by the draft gear before reaching to the vehicle bodies, coupler bodies and knuckles are directly subjected to them. Thus a clear assessment of extent of impact forces is critical for designing the coupler components.

Applied excitation force is of the form $-F_0 \sin (\omega \times {t})$, thus, simulation starts with buff mode. Buff and draft periods for one cycle are marked in Fig. 12a. Figures  12 and 13 present the variations of total longitudinal contact force with time, on left side coupler for five initial cycles of passenger and freight car couplings at a higher frequency (5.0 Hz) and lower frequency (0.5 Hz), respectively. Figure 12a presents the longitudinal contact forces on passenger car coupler and its maximum magnitude peaks reach up to about 1000 kN. Similarly, the longitudinal contact forces on freight car coupler reach up to about 1500 kN (Fig. 12b), except two outlier peaks near 0.22 s and 0.53 s, while applied excitation force magnitude is just 400 kN. However, at a lower frequency (0.5 Hz), the magnitudes (Fig. 13a, b) are a bit lower (about 800 kN for passenger car coupler and about 1200 kN for freight car coupler), yet considerably higher than the excitation force magnitude. It is to be noted that overall force variation is of the order of 1200 kN in freight car coupling; however, lots of peaks greater than 1200 kN are observed which can be attributed to the numerical solver error in calculation of friction force, near relative velocity approaching zero (Fig. 14). The overall lower magnitudes at lower excitation frequency in both the cases are due to the fact that near quasi-static excitation, impact velocities are significantly lower compared to the higher excitation frequency case (Fig. 14). Overall higher longitudinal contact forces at higher as well as lower frequency, in case of freight car coupling, compared to the passenger car can be attributed to the larger relative velocities achieved before impact (Fig. 14) due to the combined effect of larger slack and rotation. Thus, it can be said that under prescribed constraint conditions, passenger car couplers experience about 800–1000 kN of impact forces in longitudinal direction, while freight car couplers experience about 1200–1500 kN of longitudinal impact forces at longitudinal excitation force with magnitude of 400 kN, under the prominent range of excitation frequency.

Fig. 12

Longitudinal contact force on left coupler of a passenger car coupling and b freight car coupling, at a higher frequency (5.0 Hz)

Fig. 13

Longitudinal contact force on left coupler of a passenger car coupling and b freight car coupling, at a lower frequency (0.5 Hz)

Fig. 14

Longitudinal relative impact velocities between couplers of a passenger car coupling and b freight car coupling, at a higher frequency (5.0 Hz) and lower frequency (0.5 Hz)

Due to the curved contours, longitudinal and lateral contact forces do not contain absolute normal contact and tangential frictional forces, respectively, but also contain the components of each other. Figures 15 and 16 present lateral contact forces on left side coupler of passenger and freight car couplings, at a higher frequency (5.0 Hz) and lower frequency, respectively. Except one peak at around 0.28 s, the maximum lateral contact forces reach up to about 250 kN, in case of passenger car coupling, at higher frequency (Fig. 15a), while it is about 500 kN, in case of freight car coupling (Fig. 15b). Almost similar magnitude forces are seen at lower frequency also (Fig. 16). These lateral contact forces originate due to impacts between couplers, while the applied external force is purely along longitudinal direction. Although this magnitude is quiet low but it is comparable to that of applied longitudinal excitation force magnitude.

Fig. 15

Lateral contact force on left coupler of a passenger car coupling and b freight car coupling, at a higher frequency (5.0 Hz)

Fig. 16

Lateral contact force on left coupler of a passenger car coupling and b freight car coupling, at a lower frequency (0.5 Hz)

Coupler interaction analysis shows that couplers and knuckles are subjected to the longitudinal contact forces of almost 2–2.5 times the excitation force amplitude, in case of passenger car couplers. On the other hand, due to the larger clearance, freight car couplers and knuckles are subjected to the longitudinal contact forces of about 3–3.5 times the excitation force amplitude. Additionally, passenger and freight car couplers are also subjected to lateral contact forces of about 0.62 and 1.25 times the longitudinal excitation force amplitude, respectively. Such contact force estimations of full train models are thus important to design the coupler components.

4.2 Reaction from draft gear

Because of higher structural stiffness of coupler components, high frequency impact forces are present in the longitudinal force, being transmitted to the draft gear, as seen in Figs. 12 and  13. While, these impact forces get partially or fully dissipated by the draft gear, estimation of accurate reaction force from draft gear to the mounting connection elements and vehicle body is important for their structural design.

Figures 17 and 18 present the longitudinal reaction forces on fixed draft gear housing of passenger and freight car couplings, at a higher frequency (5.0 Hz) and lower frequency, respectively. Draft gear reaction forces computed using detailed model are compared with corresponding forces computed using conventional models and with corresponding contact forces. Due to the negligible masses assigned to various coupling elements and in the absence of impacts, quasi-static equilibrium leads to the draft gear reaction force, almost equals the excitation force, at both the frequencies, except the dead-band feature due to the slack (marked by arrow in Fig. 17a). It is seen that although impact forces are almost absorbed, some overshoots in draft gear forces during starting of both buff and draft mode are present for passenger car coupling, at higher frequency (Fig. 17a). In case of freight car couplers (Fig. 17b), apart from overshoot during contact occurrence, additional overshoots are also observed around maximum displacement condition due to the velocity reversal (Fig. 20b), caused by locking stiffness. Same is not the case with conventional model, which follows almost harmonic pattern with its magnitude about 400 kN. On the other hand, impact forces at lower excitation frequency (Fig. 18), are almost absorbed and the draft gear reaction forces follow almost same pattern as the conventional model. Thus, conventional models can closely estimate the in-train forces for quasi-static excitation frequency range but underestimate additional force components for the dynamic frequency ranges.

Fig. 17

Longitudinal reaction force on fixed draft gear housing of a passenger car coupling and b freight car coupling, at a higher frequency (5.0 Hz)

Fig. 18

Longitudinal reaction force on fixed draft gear housing of a passenger car coupling and b freight car coupling, at a lower frequency (0.5 Hz)

To identify the reason for the overshoots at higher frequency, deflection, and velocity patterns of left yoke, which are the deflection and velocity of draft gear, are analyzed. Figure 19a, b present the deflections and velocities of draft gear of passenger car coupling, at a higher excitation frequency (5.0 Hz) and lower excitation frequency (0.5 Hz), respectively. It can be seen that, for a lower excitation frequency (0.5 Hz), coupler inertia has no effect within quasi-static regime; displacement is almost harmonic and velocity is negligible. Figure 19a shows that, for a higher frequency (5.0 Hz) excitation, initially displacement reaches to its maximum value (about 48 mm) very fast and during this period, velocity kept on increasing rapidly, due to both, inertial effect and intermittent impacts. Consequently, draft gear force kept on increasing and produced an overshoot (Fig. 19a), reaching longitudinal force value up to about 1000 kN, evident in Fig. 20a. Thus, this overshoot is an additional component, due to inertial effects of couplers. This additional force is about 200 kN during buff loading and is about 600kN during draft loading, which are comparable to the applied excitation force magnitude (400 kN). Similar reasons can be sought for freight car coupler system also.

Fig. 19

Deflection and velocity states of draft gear for passenger coupling at a 5.0 Hz and b 0.5 Hz

Figure 20 presents force-deflection plots at both the excitation frequencies and also compares with corresponding drop hammer characteristics. It is observed in Fig. 17, that in passenger car coupling, overshoot is lower during buff mode than in draft mode. It is because of asymmetric stiffness in buff (softer) and draft (harder) modes (Fig. 20a). For the deflection about 50 mm, draft gear force reaches up to 1000 kN in draft mode and up to only 600 kN in buff mode (Fig. 20a), in the case of a higher frequency $\omega = 5.0$ Hz) . In freight car coupling, a rubber-spring based friction draft gear is used, in which same set of spring and friction wedges act in both the modes, consequently, the overshoot during buff mode is almost same as in draft mode. Draft gear force reaches up to 900 kN in both the modes for a deflection of about 50 mm (Fig. 20b). For lower frequency ($\omega = 0.5$ Hz) deflections are lower than 50 mm in both the cases and corresponding draft gear forces reached to the lower values. Another important observation is that draft gear forces are well inside the envelope of drop hammer characteristics. Also, it can be seen that different dynamic characteristics of draft gears lead to different levels of energy absorption and peak forces.

Fig. 20

Longitudinal reaction force on fixed draft gear housing-yoke deflection characteristics of a passenger car coupling and b freight car coupling

5 Conclusions

AAR coupler systems are complex three dimensional vibration systems, with design intended slack (clearance) and comparable components masses. A railway coupler system experiences a wide range of excitation frequency, from quasi-static to dynamic. Although, at lower excitation frequencies, inertial effects are negligible, but at higher excitation frequencies, inertia of coupling components, more importantly the masses of couplers have noticeable influence. Also, the slack in these couplers induces intermittent impacts and rubbing actions. Coupler masses have noticeable effect on longitudinal reaction of draft gear, transmitted to its connected vehicle. It induces significant overshoot, almost same magnitude as applied external force, under the assumed constraints in this study. Neglecting this additional component gives under-estimated in-train forces and may provide incorrect assessment of operational and structural safety of vehicles and components. This study demonstrates the importance of consideration of important features of coupler systems for design and operational assessment of rail vehicles. Such detailed models of coupler systems, coupled with full train can be used to determine the accurate forces for structural design of couplings and vehicles.