1 Introduction

The longitudinal train dynamics (LTD) studies motions of all types of rolling stock vehicles moving in the longitudinal track direction [1]. This branch of mechanics deals with the longitudinal movement of any train holistically and to a certain extent with relative longitudinal motions of train components. Within the LTD, both lateral and vertical movements of carriages, or locomotives, can be omitted.

In an overview article, Wu et al. [2] presented the historical approach to issues of LTD since 1831, when, for the first time, Mohawk and Hudson had observed the dynamic behavior of ‘slack’ actions, referred to as a series of train vehicle impacts (during state transitions of connections—from tension to compression—or vice versa). The authors [2] focused, mainly, on the issues of longitudinal train dynamics, which cover the following problems: numerical solvers, vehicle connection systems, air brake systems, wagon dumper systems, locomotives, resistance forces, gravitational components, vehicle in-train instabilities, and computing schemes.

For long heavy-haul trains besides the LTD, some meaningful progress has been accomplished in the carriage system dynamics and coupled dynamics of vehicle-track systems. However, there are still some difficulties during the simulation of longitudinal impulse interactions such, as changes in momentum of railway carriages on the elastic track structure [3].

Oprea [4] pointed out that studies on start-up dynamics of railway trains helped to ensure comfort for passengers and, also, running safety of trains.

Ansari et al. [5] comprehensively discussed the influences of stiffness and damping of couplers and load distribution pattern on the train longitudinal dynamic behaviors. They also determined the optimum placement of the second locomotive to obtain the lowest longitudinal forces.

In recent years, modeling and simulations as research methods of rail vehicle-track dynamics have been intensively developed. Sharma et al. [6] presented an overview of applications of rail vehicle-track dynamic modeling. They noted that relative motions between two adjacent carriages known as ‘slack actions’ had been caused due to looseness and horizontal displacements in spring and damper connections. According to them, a coupling ‘free slack’ is defined as the free movement allowed by the sum of clearances in wagon connections. They emphasized that these clearances occurred in the auto-coupler knuckles and draft gear assembly pins.

In railways, not only passive damping systems with non-linear stiffness characteristics are used, especially in the suspension, but also magnetorheological dampers integrated with the secondary vertical suspension system. Parameters of magnetorheological dampers are dependent on current, amplitude, and frequency of excitations, as described in Refs. [7, 8]. It naturally results in improved ride quality and passenger comfort in comparison to the existing passive system.

Sharma [9] modeled longitudinal train dynamics of the locomotive-hauled passenger train of Rajdhani Express based on experimental results and some data from the literature. He evaluated the performance of the rail vehicle in its five braking phases. He noticed that the maximum compressive coupler force of 1.49 MN occurred in the third quarter of the train.

The traction and braking actions can cause large longitudinal forces in inter-vehicle coupling systems, especially in long and heavy-haul trains. This paper focuses on electric multiple units (EMUs) with the distributed power, blended and (or) electronic braking, advanced slip controls, and permanently coupled carriages, for which LTD problems may seem not to be such an essential issue. In practice, things are not quite so effortless because quite large longitudinal forces may occur in EMUs by the improper use of the distributed power control [10]. The EMU requires no separate locomotive, as electric traction motors are incorporated within one or a number of its vehicles. The asynchrony of EMU vehicles’ traction or braking action may lead to large forces due to longitudinal vibrations. Such vibrations may ultimately lead to a failure of the coupler or even superstructure [11].

To the best of the author’s knowledge in the field of longitudinal train dynamics, the object of this work is to improve a method for reduction of the longitudinal coupler forces present during the traction and braking of the passenger train for outer suburban and long-distance configurations. This train should travel at high speeds and accelerate/brake quickly to increase average travel velocities and lower door-to-door trip time.

Depending on operator needs, there are several ways to reduce the maximum of coupler forces. The most preferred solution is a simple solution based on the assumption that all vehicles of a multiple-unit train (MUT) move at the same speed while maintaining simultaneously fixed intervals between individual carriages. This solution requires the application of a new method for distributed power. The MUTs have no locomotives, and their drive system consists of several self-propelled units in a fixed formation, thus providing that the traction is distributed along the train length. The new control system will supervise the distributed power to reduce the longitudinal coupler forces.

2 Functionality of advanced railway couplers

Different types of couplers have been used to connect adjoining carriages. Most used couplers allow a certain amount of slack to occur between wagons. In the case of heavy-haul trains, the slack presence helps the train start. In the heavy-haul train, its lack causes that the locomotive needs to pull the full load of the train at once, and hence the locomotive may not have sufficient power to start. However, in the high-speed train, the slack presence is unfavorable. It allows individual vehicles to move independently of each other, and thus they can end up traveling at different speeds to each other. If the speed difference is high enough between individual vehicles, then the forces acting in the coupler between adjoining carriages may be high enough to break it [12].

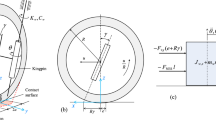
Advanced tight-lock inter-vehicle connections [13] installed on adjacent vehicles of a high-speed train provide running stability during acceleration or deceleration. They have insignificantly small slackness. The tight-lock railway connections themself represent coupler systems that consist of springs and dampers, as shown in Fig. 1, where \(k_{i\left( 1 \right)}\) and \(c_{i\left( 1 \right)}\) are stiffness and damping coefficients. Elements of these connection systems are parallel as they should share across the same absolute values of variables (such as relative displacements and velocities).

Fig. 1
figure 1

Adjacent vehicles of a high-speed train joined via the advanced inter-vehicle connection

Full size image

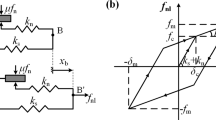
Let us notice that it is not easy to determine the nonlinear dynamic characteristic of the advanced coupler. As described in Fig. 2a, this characteristic can often be represented by the three-zone displacement model. Figure 2b shows the damping force characteristic of the longitudinal inter-vehicle damper. This damper reduces longitudinal impacts and also can improve the lateral stability and ride comfort of the train.

Fig. 2
figure 2

Characteristics of inter-vehicle connection components: a shows a relationship between spring force and displacement of the semi-permanent tight-lock coupler, whereas b demonstrates a damping force characteristic of the longitudinal inter-vehicle damper (in both cases, the sub-index i stands for the sequence number of the advanced inter-vehicle connection)

Full size image

For advanced inter-vehicle connections, active isolation of longitudinal vibration is proposed as a target solution. However, both characteristics of the semi-permanent tight-lock coupler and longitudinal inter-vehicle damper are nonlinear. Moreover, if the system is highly nonlinear over the full range of operation, its adaptive schemes associated with the control algorithm may show severe limitations. Therefore, stroke limitations defined by \(\left[ { - x_{{{\text{s}}_{1\left( i \right)} }} ,{ }x_{{{\text{s}}_{1\left( i \right)} }} } \right]\) for tight-lock couplers are adopted, as well as velocity-jump constraints set by \(\left[ { - \dot{x}_{{{\text{d}}_{1\left( i \right)} }} ,{ }\dot{x}_{{{\text{d}}_{1\left( i \right)} }} } \right]\) for longitudinal inter-vehicle dampers. Thus, due to automatic control, the coupler forces will have values within the range of their linear characteristics. In consequence, the coupler forces of this advanced connection system will not exceed the established admissible values.

Structural failure of railway couplers may cause accidents and even lead to catastrophic damages. Therefore, it is critical to ensure that the couplers are in healthy structural condition. The measurement of coupler-force values can be performed within the structural health monitoring (SHM) system for railway couplers [14]. This system consists of, among others, accelerometers, which determine coupler movements, and digital strain sensors, which measure deformation strains on coupler bodies.

3 Modeling of longitudinal dynamics of multiple-unit trains

A system of differential equations can describe the longitudinal dynamic behavior of the MUT. Assuming that there is no vertical or lateral movement of each train vehicle, the MUT model has a much simpler structure.

The EMUs can be divided into two broad categories [15]. The EMUs of the first category consist of independent vehicles, each of which rests on two bogies (see model A of Fig. 3). Such EMU vehicles, which do not share bogies, can be longer. However, they need more bogies and must be equipped with additional anti-overlap systems between the two adjacent vehicles to reduce the consequences of a railway accident. Each of the two adjacent vehicles of the second category EMUs shares at least one the same bogie (see model B of Fig. 3). The advantage of this category is that the EMU has a reduced number of bogies in the train. Besides, shared boogies assure reduction of their lateral oscillations, less rolling, and pitching at high speeds. On the other hand, it is necessary to use shorter vehicle bodies to meet the limit requirements concerning the smallest permissible radii of railway track curves.

Fig. 3
figure 3

LTD models of MUTs: a model A; b model B

Full size image

The LTD model of MUT is necessary to design control algorithms. This model allows testing different control strategies without the need to use a physically available EMU.

As shown in Fig. 3, \(x_{i}\) (\(i = 1, 2, 3\)) describe the position of vehicle centers. Model A consists of three vehicles with masses of \(m_{i}^{{\text{A}}}\) connected by stiffness and damping couplers. Note that \(k_{j\left( 1 \right)}^{{\text{A}}}\) and \(c_{j\left( 1 \right)}^{{\text{A}}}\) (\(j = 1, 2\)) are the stiffness and damping coefficients, respectively. \(F_{i}^{{\text{A}}}\) are the tractive forces. \(R_{i}^{{\text{A}}}\) are the forces, which resist the motion of each vehicle. Similarly, model B consists of three vehicles with masses of \(m_{i}^{{\text{B}}}\) and four bogies. \(m_{k}^{{\text{Q}}}\) (\(k = 1, 2, 3, 4\)) are masses of Jacob bogies and \(q_{k}\) are their coordinates.

Although various external loads act on each train carriage, only these loads, related solely to the longitudinal direction, are significant to model the LTD, as assumed here. When the train moves on along a straight line, the rolling resistance forces are independent of the train speed. They act on each carriage and occur as the results of wheel-rail friction and friction in bearings. These forces, however, are functions of various types of frictional resistance. Furthermore, for further analysis, certain forms of velocity-dependent rolling resistance forces are negligibly small except for those forces, which may occur due to track deflection. Without any cross-wind effect and in the open-air conditions, the total drag on the traveling train is usually calculated by the use of the following Davis’ formula [16, 17]:

$$F_{{\text{R}}} = a + bv + cv^{2} ,$$
(1)

where \(F_{{\text{R}}}\) is the train resistance (i.e., the total drag); \(a\), \(b\), and \(c\) are constants, which depend upon the type of train; and \(v\) is the train speed. Note that bearing and contact frictions vary with the weight of the train and the number of axles. The second term of this equation is proportional to train speed. This term expresses increased rolling resistance at high speed despite that it also includes some components of laminar airflow. The last corresponds in size to speed-squared and expresses the aerodynamic drag. As indicated in [18], the aerodynamic drag of MUT consists of separate drag forces with a different value for each carriage. Equation (1), therefore, has been converted to the form, which estimates the total drag force, \(R_{i}\), acting only on the \(i\)th carriage of the train:

$$R_{i} = A_{i} + B_{i} v + C_{i} v^{2} ,$$
(2)

where \(A_{i} \mathop = \limits^{{{\text{def}}}} \left( {\alpha_{i} + \beta_{i} \eta_{i} } \right)W_{i}\) and \(B_{i} \mathop = \limits^{{{\text{def}}}} \gamma_{i} W_{i}\), in which \(W_{i}\) (\(i = 1, 2, \ldots , p\)) is the weight of the ith carriage and p denotes the number of train carriages, \(\alpha_{i}\) is the rolling resistance coefficient assigned to the ith carriage, \(\beta_{i}\) is its bearing resistance coefficient, \(\gamma_{i}\) is its flange resistance (in the case of a curved track), and \(\eta_{i}\) denotes the axles’ number counted for the \(i\)th carriage; \(C_{i}\) is the aerodynamic resistance coefficient of the \(i\)th carriage. The sample coefficient values of Davis’s constants for some trains are given in Ref. [1].

4 Design of master control system to supervise MUT activities related to the LTD

The two-level control system for multiple-unit electric trains has a slightly complex structure. It consists of a master control level, which works similar to standard cruise control, and a lower control level, which compose of associated together slave negative feedback controllers for process variables to decrease the longitudinal coupler forces in the MUTs.

The master level of the control system is an innovative closed-loop negative feedback control system. This control system has an unconventional solution through the application of the arrangement of two parallel-connected PID controllers. These controllers have the possibility of weighing their output signals, as demonstrated in Fig. 4a.

Fig. 4
figure 4

Block diagram of the master controller for speed regulation built upon a parallel arrangement of two PID controllers, b bumpless transfer method, and c two nonlinear dynamic compensators connected in parallel

Full size image

As in the past, PID controllers are readily used in control applications due to their universality and simple structure [16, 17]. They are used not only in low-order systems but even in high-order systems owing to their advantageous properties. One of the disadvantages of these standardized controllers is that they, in some cases, cannot place all the poles as desired when controlling higher-order plant models. To deal with this problem, Persson and Ǻström introduced the dominant pole placement method, refer to [18]. For a structurally complex system, system delay is usually variable during the control process. Therefore, the hierarchical control system is structured as least complicated as possible element arrangement. The second PID controller with time-delay compensation is wherefore applied and, thus, reduces the time-delay effect in the closed control system with negative feedback. Besides, separate tuning rules for both PID controllers provide smooth control action when switching signals between their different working points. There is also a possibility of an online adaptation of the multipliers for their output-weighting. Due to this adaptation, the closed-loop response error disappears more rapidly than in the case of using only one single PID controller [19].

The controller output signal is the tractive force \(F_{1}\), driving the first bogie of MUT. The motor starting current and the wheel-rail adhesions during the startup process limit the maximum value for \(F_{1}\). Because any one of the processing signals cannot exceed its allowable physical limits, the saturation effects are taken into account in the master control system. As depicted in Fig. 4a, through the saturation function, the limiters of \(F_{1}\) are \(\pm F_{{{\text{max}}}}\). It is worth noting that slave negative feedback controllers establish other tractive forces. The saturation thresholds also apply to braking forces. Thus, it is possible to model the power transmission system without going into more details, how one, a few, or all of the electric motors of MUT can create torques applied to the wheels.

To include the process effects of the digital controller delay and the analog-to-digital (A/D) conversion, and the digital-to-analog (D/A) conversion, standard block diagrams for the continuous-time control systems need to be modified [20]. The master controller block diagram for speed regulation, shown in Fig. 4, consists of blocks of continuous-time transfer functions. At the second input to the master controller, the continuous-time transfer function denoted as A/D mimics the operation of the A/D converter. In the case under consideration, it is the second-order Butterworth filter, which is an analog low pass filter to prevent aliasing. The term, \(1/T\), is the filter cut off frequency. The cut off frequency has to be below one-half of the sampling frequency. The replacement block for the D/A converter in the form of a continuous-time transfer function emulates the conversion of the controller digital output signal back to an analog signal and performs a zero-order hold function. In Fig. 4a, the labeled ‘Delay’ block mimics the delay effects caused by the parallel system of two digital PID controllers. This block has the continuous-time transfer function with the constant parameter, \(k\). The value of \(k\) is the transfer function order for the parallel system of two digital PID controllers. This value is established in mathematical terms of the Z-transform. The block diagram of Fig. 4a is the starting point for building the master discrete controller for speed regulation. The PID continuous-time transfer functions of this master controller can be easily converted to discrete-time transfer functions (Z-transform transfer function).

The developed method of active vibration reduction in the railway couplers is to be a compromise solution between its implementation costs and its operational performance. An additional task for the two-level automatic control system is to keep force values of every railway coupler element within the linearized range limited by its thresholds. If the full range of non-linear characteristics of any railway connection is needed, the active vibration isolation system will be turned off, leaving only passive damping in operation. The assumption adopted in this way enables a significant simplification of the structure of the control system.

Even for linear plants, however, with actuator saturation, if, during the control design, the constraints on the actuator input are not accounted for, the results can sometimes give undesired effects [21]. A saturation link is often placed in the front of the PID controller integration branch to prevent windup. When the plant model represents a double integration processing, the saturation link is also placed in the PID controller proportional branch.

A modified PID controller with back-calculation and clamping, as well as a tracking mode, represents another built-in anti-windup method. This controller is used to prevent integration windup in the PID controller [22].

A technique related to the anti-windup methods is the so-called bumpless transfer method [21]. In the bumpless transfer method, a supervising system supervises multiple controllers designed for the same linearized control system and switches among them. Inputs of three controllers, \(C_{1}\), \(C_{2}\), and \(C_{3}\), are connected to the same output of the feedback summing point, as illustrated in Fig. 4b. These controllers are hot (i.e., all the time, they process the error). Switching between the controllers’ outputs occurs when the error magnitude achieves a specified threshold value, with some hysteresis to avoid frequent switching back and forth.

Besides, to reduce the windup and improve the transient response, the master controller can be built upon nonlinear dynamic compensators (\(C_{1}\) and \(C_{2}\)) with two parallel channels [22], as shown in Fig. 4c. Nonlinear nondynamic links are placed here in both channels. The first channel starts with a saturation link with a unity threshold (when the signal amplitude is less than 1), and the second, with a unity dead-zone (when the signal amplitude is higher than 1).

The first version of the master controller, shown in Fig. 4a, was selected for further considerations due to its least complex structure and satisfactory results obtained during the LTD computer simulations.

The master speed control system of the MUT to supervise the activities related to the LTD is represented by a block diagram shown in Fig. 5. This negative feedback control system allows to maintain a prescribed relationship of \(\dot{x}_{1}^{{\text{c}}}\) to \(\dot{x}_{1}\), where \(\dot{x}_{1}^{{\text{c}}}\) represents the desired speed of the first MUT vehicle called the ‘leader’ in the distribute power operation, and \(\dot{x}_{1}\) is the measured (i.e., actual) speed of this vehicle. The return signal \(\dot{x}_{1}\) goes into the summing point from the feedback path. In the summing point, the difference between \(\dot{x}_{1}^{{\text{c}}}\) and \(\dot{x}_{1}\) becomes the error speed.

Fig. 5
figure 5

Block diagram of the master control system to supervise MUT activities related to the LTD

Full size image

The master controller for speed regulation amplifies this error and produces the output signal transmitted to an actuator. In the considering case, the actuator is to be the traction motor of the first vehicle. When the traction motor powered by electrical energy receives a control signal, it responds by converting its driving torque into the wheel tractive force \(F_{1}\). The MUT has no locomotives, but power is distributed along this train by multiple traction motors. Slave control systems control the distribution of tractive forces, \(F_{i}\), driving other vehicles. The distribution of \(F_{i}\) depends on \(F_{1}\).

The block diagram of Fig. 5 has the subsystem block labeled ‘LTD model + Slave control systems.’ The role of this block is to encapsulate nested block diagrams for LTD equations and slave control systems.

The design of robust control systems involves choosing the controller structure and then adjusting the controller setting parameters to achieve acceptable performance in the presence of uncertainty. The controller structure should provide that the control system response can meet founded performance criteria. The first objective of the designing control system is that this system output should very accurately track the input desired speed, \(\dot{x}_{1}^{{\text{c}}}\). The second objective is maintaining the internal forces in the advanced inter-vehicle connections, \({\varvec{F}}^{{\text{s}}}\) and \({\varvec{F}}^{{\text{d}}}\), within the given range of permissible values. Note that \({\varvec{F}}^{{\text{s}}}\) is the vector of reduced spring forces in semi-permanent tight-lock couplers (or secondary suspensions), for which \(k_{i}\) are equivalent stiffnesses. \({\varvec{F}}^{{\text{d}}}\) is the vector of reduced damping forces in advanced inter-vehicle connections (or secondary suspensions) with equivalent damping coefficients \(c_{i}\). Another crucial goal of the control system design is minimizing the effect of disturbances on system output signals.

To explain why there are no adverse couplings between the master control system and slave control systems of this hierarchical control structure, let us consider the operation of simplified forms of both these control levels. Albeit not only frequency-domain but also time-domain performance measures can describe the closed-loop feedback control system performances, the description in frequency-domain terms will merely be considered.

The objective of any one of the negative-feedback controllers, which are represented by, widely used in the industry, PID controllers, is to respond to the error. However, the purpose of compensators, such as the lead, lag, and lag-lead compensators, is to change the original dynamics of the plant. In the considering case, an appropriate master-compensator should be interconnected with the LTD model to form the master nonlinear control-affine system to control the speed \(\dot{x}_{1}\).

The closed-loop master control system is based on the series compensation. For this compensation type, the controller, , is inserted into the forward path in series with the controlled system, , which describes the LTD model with slave control systems. Both and are state-dependent transfer functions of the complex variable \(s\), and the state vector . To guarantee the stable closed-loop control system, the design of the master controller is based on a pole-placement algorithm.

As shown in Fig. 5, the input signal to the block labeled ‘LTDM + SCSs’ is the tractive force \(F_{1}\). The actual output \(\dot{x}_{1}\) is feedback, compared with the reference input \(\dot{x}_{1}^{{\text{c}}}\) (i.e., the velocity command). The error, \(e = \dot{x}_{1}^{{\text{c}}} - \dot{x}_{1}\), at the summing point output is passed into the compensator, . The primary task of such a type of master control system is to keep the control variable \(\dot{x}_{1}\) to the desired value \(\dot{x}_{1}^{{\text{c}}}\), despite external disturbances d in some frequency range. Since the master-system (state-dependent) transfer function of the closed-loop system is the following form:

(3)

the output signal \(\dot{x}_{1}\) tracks the input signal \(\dot{x}_{1}^{{\text{c}}}\) accurately (i.e., \({ }\dot{x}_{1} \simeq \dot{x}_{1}^{{\text{c}}}\)) in the frequency range when and, therefore, is close to 1.

However, the master control system does not perform directly and alone tasks of active vibration damping, concerning the maintenance of zero values for the following process control variables:

  • \(\Delta x_{j}\)—the distance change between both ends of the selected inter-vehicle connection, which connects two carriages,

  • \(\Delta \dot{x}_{j}\)—the difference of velocities of both ends of the considering railway connection,

  • \(\int \Delta x_{j} {\text{d}}\tau\)—the integral over time (\(\tau\)) of the distance change between both ends of this connection.

The design of slave control systems enabling the realization of the active vibration damping in the MUT inter-vehicle connections is different from the master speed-control system design. In each slave control system, a slave controller in the form of an adjusting gain parameter , is placed in the feedback path. Therefore, such a control configuration is referred to as feedback compensation. The controlled system only consists of the LTD model. is the state-dependent transfer function inserted without anything else into the forward path (i.e., between the summing point and the take-off point). The input to the slave-system transfer function is the tractive force \(F_{1}\). The transfer function of the closed-loop system is given by

(4)

In this case, the output signal (i.e., one of the three process control variables, e.g., \(\Delta x_{j}\)) tracks the setpoint equal to zero in the frequency range when . The primary task of the slave control system is to control the tractive force of the ith drive unit, \(F_{i}\), in correlation to the tractive force of the ‘leader’ drive unit, \(F_{1}\).

5 Typical applications of train dynamics models together with the slave control structure selection to reduce coupler forces in the MUTs

EMU configurations can include various combinations of power carriages. The power carriages with motored bogies, like electric locomotives, are self-propelled and not used as passenger carriages in a locomotive-hauled train. Usually used connections between carriage bodies of MUT are couplers (i.e., mechanisms used to connect rolling stock in a train) or Jacobs’ bogies.

The posed task is to design a new hierarchical control system to bring the MUT smoothly up to speed 50 m/s, followed by braking to 0 m/s, utilizing an electric or hybrid traction system with the possibility of energy recovery. The command signal for the MUT speed is broken down into the following stages: (i) start-up (the MUT speed varies continuously from standstill to the cruising speed), (ii) cruising (the MUT speed is maintained constant at the cruising value), (iii) braking (the MUT speed is reduced from cruising to a standstill), and (iv) stop (the MUT speed is zero). The performance task requires establishing a method of MUT tractive effort control and then selecting the controller characteristics. The software package of Scilab, called Xcos, provides functionalities to determine control strategies for both open and closed control systems with negative feedback.

Numerical simulations carried out with the help of Scilab/Xcos toolbox for modeling and simulation of dynamic (continuous and discrete) systems mimic operations of the master control system of the MUT to supervise the activities related to the LTD.

5.1 Test simulations for the MUT with couplers used as connections between carriage bodies

Let us consider a train consisting of one electric locomotive and two individual passenger wagons, as shown in Fig. 3a (i.e., model A), with the following assumptions made: \(F_{1}^{{\text{A}}} \ne 0\), \(F_{2}^{{\text{A}}} = 0\), and \(F_{3}^{{\text{A}}} = 0\). Train model parameters are selected based on data from [23]. Note that in Figs. 6 and 7, the results of computer simulations for this example are labeled by Ex. 1. Figure 6a shows train acceleration to the line speed of 50 m/s at full power, motoring at the line speed, and then train braking at standard service rate. Figure 6b illustrates the dependence on the time of the tractive forces \(F_{i}^{{\text{A}}}\). Time courses of changes of the train speed \(\dot{x}_{1}\) and any one of the tractive forces \(F_{i}^{{\text{A}}}\) correspond to each other.

Fig. 6
figure 6

Numerical results based on the LTD for model A of the MUT: a train speed \(\dot{x}_{1}\) vs. time; b tractive forces \(F_{i}^{{\text{A}}}\) vs. time (in Ex. 1 and 2, passive vibration damping is only used; in Ex. 3 both passive and active vibration damping are used)

Full size image
Fig. 7
figure 7

Numerical results based on the LTD for model A of the MUT: a coupler spring forces \(F_{1}^{{{\text{s}}\left( {\text{A}} \right)}}\) and \(F_{2}^{{{\text{s}}\left( {\text{A}} \right)}}\) vs. time; b coupler damping forces \(F_{1}^{{{\text{d}}\left( {\text{A}} \right)}}\) and \(F_{2}^{{{\text{d}}\left( {\text{A}} \right)}}\) vs. time (in Ex. 1 and 2, passive vibration damping is only used; in Ex. 3 both passive and active vibration damping are used)

Full size image

Figure 7 shows variations of coupler forces in both advanced inter-vehicle connections. Changes in the coupler forces, \(F_{i}^{{{\text{s}}\left( {\text{A}} \right)}}\) and \(F_{i}^{{{\text{d}}\left( {\text{A}} \right)}}\) \(\left( {i = 1, 2} \right)\), as well as the train speed \(\dot{x}_{1}\), are also correlated. Both connections consist of the parallel connection systems of the spring connectors with the viscous dampers. They are placed between the 1st and 2nd carriages as well as between the 2nd and 3rd carriages.

The use of viscous dampers with the following damping coefficients, \(b_{1}^{{\text{A}}}\) and \(b_{2}^{{\text{A}}}\), provides passive damping of longitudinal vibrations. The passive vibration damping method based on energy dissipation can be very efficient in damping out high-frequency excitations. However, passive damping of dynamic forces in train couplers can be insufficient in the case of an uncorrelated traction distribution in the MUT, especially in the range of low-frequency vibrations. The active damping method ensures more effective damping of low-frequency vibrations. However, this method requires the application of additional actuators. The actuators generate second forces or controlled displacements to compensate for the effects of response on the action of external forces or kinematic excitations directly acting on components of the MUT. Unfortunately, this method requires an external power source, which should supply energy of quite considerable amounts. It is a crucial disadvantage of this method. Therefore, active vibration isolators are not used widely in practice. Bearing in mind that the cost reduction of the active damping usage, both actuators and the energy supply for them will be created by the distributed traction system with all vehicles (or bogies) motored, i.e., via the distribution of the traction or braking forces in the MUT.

To verify the correctness of actions of slave control systems enabling the realization of the active vibration damping in the MUT inter-vehicle connections and to check their ability to cooperate with the master control level without adverse couplings, ponder once again the MUT shown in Fig. 3a. \(F_{1}^{{\text{A}}} \ne 0\), \(F_{2}^{{\text{A}}} \ne 0\), and \(F_{3}^{{\text{A}}} \ne 0\), since all carriages of this train are self-propelled.

For the MUT with all vehicles motored, the slave control systems are based on the feedback compensation. Note that the loop of the negative-feedback slave control system, as illustrated in Fig. 8, is closed by the LTD model. Figure 8 shows that the block diagrams of the slave control systems are nested in the block diagram of the master control system, which is depicted in Fig. 5.

Fig. 8
figure 8

Essential part of the block diagram of the slave control systems enabling the realization of the active vibration damping in the MUT inter-vehicle connections (all MUT carriages are self-propelled)

Full size image

The computer simulations’ results are labeled by Ex. 2, when all MUT carriages are self-propelled (i.e., \(F_{1}^{{\text{A}}} \ne 0\), \(F_{2}^{{\text{A}}} \ne 0\), and \(F_{3}^{{\text{A}}} \ne 0\)), and the only passive vibration damping is used. In the case of the application of both passive and active vibration damping, they are designated by Ex. 3. For a value of the leader tractive force \(F_{1}\), determined by the master control system, the slave control systems gently adjust the appropriate distribution of the forces acting simultaneously as tractive and compensative, \(F_{2}^{{\text{A}}}\) and \(F_{3}^{{\text{A}}}\). Such adjustment makes it possible to significantly decrease close to zero the following longitudinal coupler forces: \(F_{1}^{{{\text{s}}\left( {\text{A}} \right)}}\), \(F_{2}^{{{\text{s}}\left( {\text{A}} \right)}}\), \(F_{1}^{{{\text{d}}\left( {\text{A}} \right)}}\), and \(F_{2}^{{{\text{d}}\left( {\text{A}} \right)}}\). When the MUT has all motored vehicles (even when passive vibration damping is only employed), the coupler forces are much smaller than in the case labeled as Ex. 1.

5.2 Active vibration damping in the MUT inter-vehicle connections under external disturbances

The control systems of the MUT are often subjected to unwanted external disturbance signals, for example, sudden gusts of wind tending to change LTD conditions, disturbances that emerge from the time variation of carriages’ masses, disruptions raised from braking with degraded adhesion, and those caused by the time variation of the track curvature, etc.

Let us investigate how the feedback of the active vibration damping system of the MUT (model A of Fig. 3a) provides support in mitigating the effect of these disturbances on the overall hierarchical control system response. For the MUT, the identical desired speed profile, shown in Fig. 6a, is assumed. All MUT carriages are self-propelled (i.e., \(F_{1}^{{\text{A}}} \ne 0\), \(F_{2}^{{\text{A}}} \ne 0\), and \(F_{3}^{{\text{A}}} \ne 0\)). The MUT is subjected to two types of external disturbances. The first of them is in the form of the variable in time total drag force acting on the 2nd vehicle, \(R_{2}\), and the second is in the form of step changes in the weight of the 2nd vehicle as illustrated in Fig. 9a.

Fig. 9
figure 9

Analysis of the slave control systems. a Time course of the variability of external disturbances acting on the second carriage of the MUT; b compensating action of tractive forces during active vibration damping

Full size image

During computer simulations, both active and passive vibration damping systems are used. The results of the numerical calculations are shown in Figs. 9, 10 and 11. In these figures, the outcomes influenced by disturbances in the form of the changing force \(R_{2}\) are marked by Ex. 4. The rest of them, which concern the operation of disturbances caused by the second vehicle weight with a variable value, are marked as Ex. 5. Figure 9b shows the compensating action of tractive forces \(F_{1}^{{\text{A}}}\), \(F_{2}^{A}\), and \(F_{3}^{{\text{A}}}\) during active vibration damping.

Fig. 10
figure 10

Response action of the passive and active vibration damping systems: a coupler spring forces \(F_{1}^{{{\text{s}}\left( {\text{A}} \right)}}\) and \(F_{2}^{{{\text{s}}\left( {\text{A}} \right)}}\) vs. time; b coupler damping forces \(F_{1}^{{{\text{d}}\left( {\text{A}} \right)}}\) and \(F_{2}^{{{\text{d}}\left( {\text{A}} \right)}}\) vs. time

Full size image
Fig. 11
figure 11

Response action of the active vibration damping systems: a coupler spring forces \(F_{1}^{{{\text{s}}\left( {\text{A}} \right)}}\) and \(F_{2}^{{{\text{s}}\left( {\text{A}} \right)}}\) vs. time; b coupler damping forces \(F_{1}^{{{\text{d}}\left( {\text{A}} \right)}}\) and \(F_{2}^{{{\text{d}}\left( {\text{A}} \right)}}\) vs. time

Full size image

For active vibration damping, the feedback action introduced in slave control systems makes the response of these systems relatively insensitive to external disturbances, as shown in Figs. 10 and 11. Figure 10 shows the passive vibration damping system cannot so effectively reduce external disturbances. During the impact of these disturbances on the MUT with only passive vibration damping, the coupler forces’ values are significant concerning those shown in Fig. 11 (and unnoticed in Fig. 10), which express the effective response action of the active vibration damping systems from Fig. 8.

For the MUTs with all self-propelled 10 + carriages, computer simulations of the action effectiveness for active vibration damping systems have also been carried out. The simulation results have shown that the values of the couplers forces are included in the following ranges: \(- 3\,{\text{N}} < F_{i}^{{{\text{s}}\left( {\text{A}} \right)}} < 3\,{\text{N}}\) and \(- 80\,{\text{N}} < F_{i}^{{{\text{d}}\left( {\text{A}} \right)}} < 80\,{\text{N}}\). It should be emphasized that the use of systems for active vibration damping allows substantially to eliminate the risk of such events as pitches of rail vehicle bodies and bogies due to coupler impact forces.

5.3 MUT operating in the push–pull configuration

EMU configurations can include various combinations of power carriages. The push–pull MUT (represented by model A of Fig. 3a) has the first and the third (in this case the last) motored vehicles. It means that the traction forces are as follows: \(F_{1}^{{\text{A}}} \ne 0\), \(F_{2}^{{\text{A}}} = 0\), and \(F_{3}^{{\text{A}}} \ne 0\). Figure 12a shows a course of velocity change over time of the MUT for the following successive stages: the acceleration to the set velocity of 50 m/s, the cruising at the constant speed, then the deceleration during braking. The simulation results for the push–pull MUT are summarized in Figs. 12 and 13. During these simulations, both active and passive vibration damping systems are used.

Fig. 12
figure 12

Simulation results based on the LTD for model A of the push–pull MUT: a train speed \(\dot{x}_{1}\) vs. time; b tractive forces \(F_{i}^{{\text{A}}}\) vs. time (in Ex. 6, passive vibration damping is only used)

Full size image
Fig. 13
figure 13

Simulation results based on the LTD for model A of the push–pull MUT: a coupler spring forces \(F_{1}^{{{\text{s}}\left( {\text{A}} \right)}}\) and \(F_{2}^{{{\text{s}}\left( {\text{A}} \right)}}\) vs. time; b coupler damping forces \(F_{1}^{{{\text{d}}\left( {\text{A}} \right)}}\) and \(F_{2}^{{{\text{d}}\left( {\text{A}} \right)}}\) vs. time (in Ex. 6, passive vibration damping is only used)

Full size image

In Fig. 12 and 13, the outcomes are marked by Ex. 6 when the passive vibration damping is only used. An attempt has been made to reduce the forces in the railway couplers using active vibration damping. The slave control systems based on the feedback compensation have been employed to achieve this goal. Note that the loop of the negative-feedback slave control system shown in Fig. 14 is based on differently defined inputs of reference signal than in the case of active vibration damping systems for all motored carriages of the MUT (as depicted in Fig. 8). It is caused by that the coupler between the 1st and 2nd carriages is stretched. In turn, the coupler between the 2nd and 3rd carriages is compressed. In such a case, only the respective equalization of the absolute values of the compressive and tensile forces is possible. And, this goal has been achieved according to results labeled by Ex. 7 of Fig. 13.

Fig. 14
figure 14

Essential part of the block diagram of the slave control systems enabling the realization of the active vibration damping in the push–pull MUT

Full size image

However, the values of the forces in the railway couplers remain too large. Therefore, for both tractive and braking forces, the allowable value set is limited by \(- 42.5\,{\text{kN}} \le F_{i}^{{{\text{s}}\left( {\text{A}} \right)}} \le 42.5 \;{\text{kN}}\) and \(- 42.5\,{\text{kN}} \le F_{i}^{{{\text{d}}\left( {\text{A}} \right)}} \le 42.5\; {\text{kN}}\). Due to the established limits, the hierarchical control system, which consists of two control levels, has reduced the tractive force, \(F_{1}\) (produced by the leader drive unit). The ability of MUT to accelerate and decelerate has also decreased. The outcomes labeled by Ex. 8 of such control are illustrated in Figs. 12 and 13.

5.4 Test simulations for the MUT with Jacobs’ bogies used as connections between carriages’ bodies

Let us consider a train shown in Fig. 3b (model B), which has two standard bogies situated on both its ends, of which only the first is with an electrically powered traction motor. The other two Jacobs’ bogies of the train connect the three carriage bodies. Therefore, \(F_{1}^{{\text{B}}} \ne 0\), \(F_{2}^{{\text{B}}} = 0\), \(F_{3}^{{\text{B}}} = 0\), and \(F_{4}^{{\text{B}}} = 0\). Train model parameters are also selected based on data from [23]. This example is labeled by Ex. 9, kept the same as the simulation scenario of the ride by the MUT (see Fig. 12a), for which Figs. 12 and 13 show the summary results of numerical calculations The label Ex. 10 is assigned to such simulations, during which all MUT bogies are self-propelled (i.e., \(F_{1}^{{\text{B}}} \ne 0\), \(F_{2}^{{\text{B}}} \ne 0\), \(F_{3}^{{\text{B}}} \ne 0\), and \(F_{4}^{{\text{B}}} \ne 0\)), and simultaneously the method of passive vibration damping is solely applied. When besides the passive vibration damping method, the active vibration damping method is employed, the simulation outcomes are designated by the label Ex. 11. It can be noticed that the active vibration damping method only slightly improves the evenness of the distribution of forces transmitted by springs and dampers of the bogies’ second suspensions compared to the passive vibration damping method. The active vibration damping method might be a bit more effective during acting external disturbances on the MUT (such, for instance, as combined excitations or wind gusts). In this case, the employed active vibration damping method is also based on slave control systems with the feedback compensation configuration (Figs. 15, 16).

Fig. 15
figure 15

Simulation results based on the LTD for model B of the MUT: a train speed \(\dot{x}_{1}\) vs. time; b tractive forces \(F_{i}^{{\text{B}}}\) vs. time (in Ex. 9 and 10, passive vibration damping is only used; in Ex. 11 both passive and active vibration damping are used)

Full size image
Fig. 16
figure 16

Simulation results based on the LTD for model A of the MUT: a secondary suspension spring forces \(F_{1}^{{{\text{s}}\left( {\text{B}} \right)}}\) and \(F_{2}^{{{\text{s}}\left( {\text{B}} \right)}}\) vs. time; b secondary suspension damping forces \(F_{1}^{{{\text{d}}\left( {\text{B}} \right)}}\) and \(F_{2}^{{{\text{d}}\left( {\text{B}} \right)}}\) vs. time (in Ex. 9 and 10, passive vibration damping is only used; in Ex. 11 both passive and active vibration damping are used)

Full size image

The loops of the negative-feedback slave control systems, shown in Fig. 17, are tailored to vibration damping in the MUT with Jacobs’ bogies used as connections between carriages’ bodies. This adaptation consists of choosing the appropriate reference input signals. The assumption is made that the coordinates, \(q_{j}\) (see Fig. 17), have zero initial values. The springs of the second suspensions are non-deformed at the initial time, typically denoted \(t = 0\). This assumption allows keeping the desired initial distances between the bogies with uniform deformation of the springs during the simulation ride.

Fig. 17
figure 17

Essential part of the block diagram of the slave control systems enabling the realization of the active vibration damping in the MUT with Jacobs’ bogies (all MUT bogies are self-propelled)

Full size image

6 Conclusions

The paper examines an original method for coupler force reduction in both distributed and concentrated traction systems [24]. The results show that the most efficient way for reducing coupler forces is the method based on active vibration damping applied in the distributed traction systems. The obtained substantial reduction of coupler forces, wherein, is not solely caused by active vibration damping but, most of all, properties of the distributed traction systems themselves. Nevertheless, by applying the original method for coupler force reduction in the MUTs composed of separate self-propelled carriages with couplers used as connections between carriage bodies, an even better result is achieved. Namely, the values of dynamic forces carried through railway couplings are closely reduced to zero. However, for load-bearing structures of the MUTs supported on all motored Jacobs’ bogies, the method of active vibration damping is not so very effective. As the traction and braking forces transmitted by Jacobs’ bogies are only slightly more evenly distributed. Therefore, their load-bearing structures can carry only slightly smaller stresses, which are a little more uniformly distributed in the longitudinal direction.

The innovative two-level control system is applied to reduce vibration amplitudes of dynamic forces in couplers of the MUTs. This developed control system consists of the master control level, which performs like standard cruise control, and the secondary control level implemented to reduce the dynamic vibrations in couplers. Between the higher and lower control levels of this system, there are no noticeable adverse couplings.

The correctness of the new hierarchical control system has been successfully validated for LTD problems of the MUT. This system has a simple structure that can be modified. Besides, this system allows considering combinations of diverse traction control models for the MUTs using computationally efficient numerical methods. These models are essential for the prevention of wheels from excessive slip (for traction) or sliding (for braking) [25, 26].

This system makes it possible to find compromise solutions for control issues, which represent, for instance, setting the compromise between the possibility of obtaining simultaneously the low overshoot and the close to zero value of the steady-state error. Most of all, it is also susceptible to modifications, which lead to the much better performance obtained with the adopted additional nonlinear feedforward action or by the possibility of self-tuning implementation [27]. The developed method of active damping of vibrations in railway couplers of MUTs does not require additional actuators for compensative forces. Through this, such an advanced vibration damping method seems to be not too costly to implement.