A study on controllability of fractional dynamical systems with distributed delays modeled by $\Omega$-Hilfer fractional derivatives

Abstract

This paper deals with the controllability of fractional dynamical systems with distributed delays modeled by $\Omega$-Hilfer fractional derivatives. Firstly, the $\Omega$-Hilfer fractional problem is defined and solution representation of x(t) with the help of Laplace transform, Mittag-leffler function is obtained. Furthermore, the controllability of linear system is achieved based on controllability Grammarian matrix and rank matrix criteria. Moreover, to study the nonlinear system, theorem of schauder’s fixed point of continuous function is satisfied. Then, both the system should be controllable for the $\Omega$-Hilfer fractional derivatives. Finally, two numerical examples are discussed to support the controllability Grammarian matrix results.

1 Introduction

Fractional differential equations have been in more consideration among researchers. In the last decade, the growing number of researchers give more importance and relevance in different topic in fractional differential equations. The fractional calculus as a branch of mathematical analysis is been used extensively in integro-differential equation. Ever since fractional calculus is established, there has been a lot of research on real-time applications of non-integer-order derivative. Fractional differential equation is explored more in various applications, such as biology, computer science, engineering, physics, chemistry, elctrochemistry, polymer rheology, control theory, etc., [1,2,3,4,5,6].

Recently, the controllability concepts are becoming more popular in fractional dynamical system and therefore the fundamental concept used in control theory are studied in the literature for the analysis of the dynamical system. The theory of controllability is studied in both finite and infinite spaces. In early 1960 [7] the fractional dynamical systems got a lot of attention among the researchers and they investigated more about control systems [8,9,10]. On the other hand, the controllability theory attracted and played an important roles in physics, engineering, control theory that have connection to optimal control and design control, etc. The dynamical systems was extensively studied in [11,12,13,14,15,16,17]. Invantaka stamova et.al investigated the fractional dynamical using fundamental theory and numerous applications of fractional-order equation and this application used in recent times.

1.1 Literature review

In recent times, time delays have been growing prominence in the engineering systems, such as biological, physical, chemical and engineering systems. Time delays have more application in real systems which can be referred from the articles mentioned [18,19,20,21,22], for example, biological, physical, chemical and their industry. Distributed delay system models have extensive range of applications in various fields [23,24,25]. Here, we consider the reachability and controllability of the fractional dynamical systems with control and distributed delay [26]

$$\begin{aligned} E^{c} D^{\delta } =&Ax(t) + Bu(t) + Cu(t-\tau ),t\ge 0\\ u(t) =&\psi (t),-r \le t \le 0\\ u(0) =&x_{0} \end{aligned}$$

where $D^{\delta }x(t)$ denotes an $\delta$ order Caputo fractional derivative and the fractional-order $0 < \delta \le 1$; E, A, B, C are the known constant matrices, $x \in R^{n}$ is the state variable and $u \in R^{m}$ is the control input; $\tau > 0$ is the time control delay then the $\psi (t)$ is the initial control function.

Hilfer introduced the concept of generalized R-L fractional derivatives that contain R-L and Caputo fractional derivatives as particular cases. In recent decade, Hilfer fractional derivative inspired by lot researchers and this generation utilizes the Hilfer work in delay or without delay and in many applied mathematics fields.

From the above discussion, controllability had been solved in different operator with various model in FDE. On the hand, Hilfer [27, 28] introduced new type for fractional derivative those are Riemann–Liouville and Caputo fractional derivative. In recent decade, the work has inspired by many researchers and they worked on this topic [29, 30]. In [31] the authors studied the controllability of Hilfer fractional derivative with damped dynamical systems and integro-differential equations and also investigated the numerical examples which validated the results. In recent years, Hilfer fractional derivative (HFD) have been applied in various concepts and examples are [32] studied with respect to the HFD in delay with non-dense domain and used in controllability results and finally graphical results obtained with examples. Amin Jajarmi. et.al, [33] studied the analysis and applications in $\Psi$-HFD used in initial value problem to bring the uniqueness solution to solve the simulation results in $\Psi$-HFD. In 2022 Vellappandi, et.al [34] developed the $\Psi$-HFD in reachability in fractional optimal problem in dynamical system and numerical results are solved using in predictor-corrector algorithm with theoretical solution. Recently, $\Psi$-HFD is studied in new type of derivative called tempered [35] $\Psi$-Hilfer fractional derivative and the results are studied for their uniqueness, stability, existence and well-posedeness with suitable examples. In 2007 Yang, M et. al investigated the Riemann–Liouville fractional derivative and using Hilfer fractional derivative in approximate controllability with non-local conditions [36]. In 2012, Furati, K.M. et.al discussed the existence, nonexistence, uniqueness involving Hilfer fractional derivatives [37,38,39]. In 2017, Mahmudov,N.I [40, 41] investigated some semi-linear in abstract equation and evolution equations in Hilbert spaces for the approximate and finite approximate controllability. In 2019 Wang, J.,et al [42] compared the approximate and finite approximate controllability of Hilfer fractional evolution hemivariational inequalities by fixed point theorem, where approximate in linear heat equation and finite approximate controllability of differential systems. In 2020 M.Vellappandi et.al discussed $\psi$-Hilfer pseudo-fractional derivatives using the reachability of fractional dynamical systems [43,44,45].

In applications point of view, control of fractional-order derivatives have been proposed in recent decade with many real-life examples. As an example, Pereira et.al [46] studied the genetic algorithm-based FOPID controller tuning provided better controllability for load disturbances and greater set-point tracking compared to conventional PI and Type II controllers in voltage and current modes and it demonstrated applicability for worst conditions, with a range of parameters deviation higher than the standard deviation of -20 typically applied in power electronics designs. A sensorless speed control strategy for a three-phase induction motor using an extended Kalman filter (EKF) and a fractional-order-based PID controller and this approach aims to reduce the ripples in torque generated by the motor and improve tracking speed was studied in [47]. Ajmera et.al [48] proposed the use of fuzzy logic to enhance the performance of the sliding mode controller and the gains of the sliding term and fractional PID term are tuned online by a fuzzy system, which helps avoid chattering and improve the system’s response against external load torque. Moreover, tepljakov et.al [49] aimed to address the advantages of fractional-order proportional-integral-derivative (FOPID) controllers compared to conventional integer-order (IO) PID controllers, the benefits of using FOPID controllers in real-time implementation, and the advantages of near-ideal fractional-order behavior in control practice. The paper also discusses FOPID controller tuning methods and how seeking globally optimal tuning parameter sets can benefit designers of industrial FOPID control. In [50], the authors introduces a fuzzy logic algorithm to realize the parameter self-tuning of the fractional-order proportional–integral–differential (PID) controller, which is selected as the position regulator of the servo motor. This approach combines the precision of fractional-order PID controller with the adaptability of fuzzy control and adds feed-forward to improve the response speed.

1.2 Research gap and motivation

To best of our knowledge, there is no investigation on this type of problems. The problem of $\Omega$-Hilfer fractional derivatives for controllability of fractional dynamical system with distributed delay which is of great advantages is used in theoretical problem and applications potential, is seldom studied by applying the Hilfer fractional method. In [51], authors studied the caputo derivative in controllability of fractional dynamical in distribute delay. From this motivation, we introduced distributed delay in $\Omega$-Hilfer fractional derivatives. Consider the linear $\Omega$-Hilfer fractional differential equation in the form

$$\begin{aligned} D^{\delta ,\beta ,\Omega } x(t)= & {} Ax(t) + Bu(t) \\{} & {} + \int ^{0}_{-h}\text {d}_{\eta }C(t,\eta )u(t-\eta ), t\epsilon [0,T] \\{} & {} I^{1-\gamma }x(0)= 0 \end{aligned}$$

and consider the nonlinear $\Omega$-Hilfer fractional differential equation represented by

$$\begin{aligned} D^{\delta ,\beta ,\Omega } x(t)= & {} Ax(t) + Bu(t) + \int ^{0}_{-h}\text {d}_{\eta }C(t,\eta )u(t-\eta )\\{} & {} +f(t,x(t),u(t)), t\epsilon [0,T] = J, 0< \delta < 1 \\{} & {} I^{1-\gamma }x(0)= 0 \end{aligned}$$

where $D^{\delta ,\beta ,\Omega }$ denotes the $\Omega$-Hilfer fractional derivative of order $0< \delta < 1$ and the type $0 \le \beta \le 1$, $\gamma = \delta + \beta (1-\delta )$, $I^{1-\gamma }$ is the is the RL fractional integral with respect to $1-\gamma$, where the state and control vector are $x \in R^{n}$ in A constant matrix and $u \in R^{m}$ in B constant matrices then n $\times$n and n$\times$m are the dimension of the matrix respectively and the third integral term is in the Lebesgue Stieltjes sense with respect to $\eta$. However, under this framework, we shall encounter some kind of difficulties which are:

• By constructing Laplace transform and Mittag-Leffler function in multiple parameter, how to analyze the controllability dynamics system of the proposed $\Omega$-Hilfer fractional problem and obtain the controllable criteria?

• In $\Omega$-Hilfer fractional problem with the effect of the distributed delay on the convergence rate within the given interval can be controlled?

1.3 Contribution and paper organization

By above questions we analyze this paper on controllability of fractional dynamical system with distributed delay via $\Omega$-Hilfer fractional derivatives. The main contribution of this work are listed as follows:

• Firstly, Hilfer fractional dynamical problem $D^{\delta ,\beta ,\Omega } x(t) =f(t)$ is solved based on Mittag-Leffler matrix function and use of Laplace transform to find the solution of x(t).

• Then the linear system of Hilfer fractional dynamical problem is solved using the controllability Gramian matrix and the rank matrix theorem.

• Lately, the nonlinear system of Hilfer fractional dynamical problem is proposed by Arzela–Ascoli theorem and Schawder fixed point theorem.

• Finally, two examples are obtained which validate our controllability Gramian matrix theorem.

The remainder of this article is organized as follows. In Sect. 2, some preliminaries on fractional calculus basic definition and solution representation are demonstrated. In Sect. 3, the discussion of the linear fractional dynamical system in controllability Grammarian matrix and rank matrix. In Sect. 4, the model of the nonlinear fractional dynamical system with theorem of continuous function are presented. In Sect. 5, an example is given to illustrate the theory.

Fig. 1

Work flow of controllability system

2 Preliminaries

Definition 1

The Riemann–Liouville$^{'}$s fractional integral of order $\delta > 0$ with function is defined by [52, 53]

$$\begin{aligned} I^{\delta ;\Omega }f(x) = \frac{1}{\Gamma (\delta )}\int ^{x}_{a} \Omega ^{'}(t)(\Omega (x) - \Omega (t)^{\delta - 1})f(t)\text {d}t. \end{aligned}$$

(1)

Definition 2

The Hilfer fractional derivative of order $\delta$ and type $0 \le \beta \le 1$, is defined by [52, 53]

$$\begin{aligned} D^{\delta ,\beta ;\Omega } f(x)= & {} I^{\beta (n -\delta );\Omega }_{a+} \left( \frac{1}{\Omega ^{'}(x)}\frac{d}{dx}\right) ^{n}\nonumber \\{} & {} \times I^{(1- \beta )(n -\delta );\Omega }_{a+} f(x). \end{aligned}$$

(2)

Definition 3

Let $\Omega$-R-L fractional integrals be a generator of $h: J \rightarrow [0,\infty ]$.

$$\begin{aligned} I^{\delta ;\Omega }_{a+}f(x)= & {} h^{-1} (I^{\delta ;\Omega }_{a+} g(f(x)))\nonumber \\{} & {} \times \int ^{x}_{a}\left[ h^{-1}\frac{\Omega ^{'}(t)(\Omega (x) - \Omega (t)^{\delta - 1})}{\Gamma (\delta )} f(t)\right] \text {d}t.\nonumber \\ \end{aligned}$$

(3)

Definition 4

Let $\Omega$-Hilfer fractional derivative be a generator of $h: [a,b] \rightarrow [0,\infty ]$.

$$\begin{aligned}{} & {} D^{\delta ,\beta ;\Omega }_{a+} f(x) =h^{-1} (D^{\delta ,\beta ;\Omega }_{a+} g(f(x))) \nonumber \\{} & {} \quad = I^{\beta (n -\delta );\Omega }_{a+} h^{-1}((\frac{D}{\Omega ^{'}(x)})^{n}) I^{1-\gamma ;\Omega }_{a+}f(x). \end{aligned}$$

(4)

Definition 5

Let the Mittag-Leffler function is defined by [52]

$$\begin{aligned} E_{\delta ,\beta }(z) = \sum \limits ^{\infty }_{m=0} \frac{z^{m}}{\Gamma (\delta k+ \beta )},\delta ,\beta > 0 \end{aligned}$$

Let K be a $n\times n$ matrix, such that

$$\begin{aligned} E_{\delta ,\beta }(z) = \sum \limits ^{\infty }_{m=0} \frac{K^{m}}{\Gamma (\delta k+ \beta )},\delta ,\beta > 0 \end{aligned}$$

Consider the following Hilfer fractional differential equation

$$\begin{aligned}&D^{\delta ,\beta ;\Omega }_{a+} x(t) = Ax(t)+f(t), t \epsilon [t_{0},t_{1}]\nonumber \\&I^{1-\gamma ;\Omega }_{t_{0}} x_{t_{0}} = x_{0} \end{aligned}$$

(5)

This implies

$$\begin{aligned} x(t)&= x_{0}(\Omega (t) -\Omega (t_{0}))^{\gamma -1})E_{\delta ,\gamma }(K(\Omega (t) -\Omega (s))^{\delta })\\&\quad + \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t) -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)\\&\quad \times (\Omega (t) -\Omega (s))^{\delta })f(s)\text {d}s. \end{aligned}$$

3 Linear systems

Consider the linear $\Omega$-Hilfer fractional equation with delay is represented by

$$\begin{aligned} D^{\delta ,\beta ;\Omega }_{a+} x(t)= & {} Ax(t) + B u(t) \nonumber \\{} & {} + \int ^{0}_{-h}\text {d}_{\eta }C(t,\eta )u(t-\eta ), t\epsilon [0,T] \end{aligned}$$

(6)

$$\begin{aligned} I^{1-\gamma ;\Omega }_{t_{0}} x(0)= 0 \end{aligned}$$

where $D^{\delta ,\beta ,\Omega }$ denotes the $\Omega$-Hilfer fractional derivative of order $0< \delta < 1$, $h>0$ and the type $0 \le \beta \le 1$, $\gamma = \delta + \beta (1-\delta )$, $I^{1-\gamma }$ is the is the RL fractional integral with respect to $1-\gamma$, where the state and control vector are $x \in R^{n}$ in A constant matrix and $u \in R^{m}$ in B constant matrices then n $\times$n and n$\times$m are the dimension of the matrix respectively and the third integral term is in the Lebesgue Stieltjes sense with respect to $\eta$.

.

$$\begin{aligned} x(t) =&h^{-1}\int ^{t}_{0} (\Omega ^{'}(s)(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\nonumber \\&\quad -\Omega (s))^{\delta }) B u(s)\text {d}s + h^{-1}\int ^{t}_{0} (\Omega ^{'}(s)(\Omega (t)\nonumber \\&\quad -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\nonumber \\&\quad -\Omega (s))^{\delta }) \Big [\int ^{0}_{-h}\text {d}_{\eta }C(t,\eta )u(t-\eta )\Big ]\text {d}s \end{aligned}$$

(7)

Definition 6

Let the linear system (6) is controllable on J. Let $x_{0}$ $\epsilon$ $R^{n}$ and there control u $\epsilon$ $L^{1}(0,T)$ and time T is satisfies.

Definition 7

Let the linear system (7) is controllable on J and then vector $x_{1}\epsilon R^{n}$ and the control u(t) defined on J then the system (7) satisfies x(T ) = x$_{1}$. The system (7) is given by: [54]

$$\begin{aligned} x(t)&= \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&\quad -\Omega (s))^{\delta }) B u(s)\text {d}s\\&\quad +\left[ \int ^{0}_{-h}\text {d}C_{\eta }[h^{-1} \int ^{t}_{0} (\Omega ^{'}(s)(\Omega (t)\right. \\&\quad \left. -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\right. \\&\quad \left. -\Omega (s))^{\delta })C(s,\eta )u(s-\eta )\right] \text {d}s \end{aligned}$$

$$\begin{aligned} x(t)&= \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&\quad -\Omega (s))^{\delta }) B u(s)\text {d}s\\&\quad +\int ^{0}_{-h}\text {d}C{\eta } \Big [\int ^{0}_{\eta } h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&\quad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&\quad -\Omega (s)-\eta )^{\delta })C(s-\eta ,\eta ) u_{0}(s)\text {d}s\Big ] \\&+ \int ^{0}_{-h}\text {d}C{\eta } \Big [\int ^{t+\eta }_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&\quad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s)-\eta )^{\delta })\\ {}&C(s-\eta ,\eta ) u(s)\text {d}s \Big ] \\ x(t)&= \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&\quad -\Omega (s))^{\delta }) B u(s)\text {d}s + \int ^{0}_{-h}dC{\eta } \Big [\int ^{0}_{\eta } h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&\quad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s)-\eta )^{\delta })\\ {}&\quad \times C(s-\eta ,\eta ) u_{0}(s)\text {d}s\Big ] + \int ^{t}_{0} \Big [\int ^{0}_{-h} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&\quad -\Omega (t)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&\quad -\Omega (s)-\eta )^{\delta }) d_{\eta }C_{t}(s-\eta ,\eta )\Big ] u(s)\text {d}s \end{aligned}$$

then

$$\begin{aligned} C_{t}(s,\eta ) = \left\{ \begin{array}{ll} C(s,\eta ),s \le t \\ 0, s > t \\ \end{array} \right. \end{aligned}$$

then $dC_{\eta }$ is the Lebesgue Stieltjes with the variable $\eta$.

Here, we introduce the notation

$$\begin{aligned} R(t,s)&= \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\nonumber \\&\quad -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s))^{\delta }) B u(s)\text {d}s\nonumber \\&\quad + \int ^{0}_{-h} h^{-1} (\Omega ^{'}(s)(\Omega (t)-\Omega (s)-\eta )^{\delta -1})\nonumber \\&\quad \times E_{\delta ,\delta }(h(K)(\Omega (t)\nonumber \\&\quad -\Omega (s)-\eta )^{\delta }) \text {d}_{\eta }C_{t}(s-\eta ,\eta ) \end{aligned}$$

(8)

we define the Gramian matrix

$$\begin{aligned} G(0,T) = \int ^{T}_{0} R(T,s)R^{*}(T,s)\text {d}s \end{aligned}$$

such that $*$ indicates the transpose matrix.

Theorem 1

Let the linear system (7) is relatively controllable on J iff the controllability Gramian

$$\begin{aligned} G = \int ^{T}_{0} R(T,s)R^{*}(T,s)\text {d}s \end{aligned}$$

is positive definite.

Proof

Let us define control function u(t),

$$\begin{aligned} u(t)&= R^{*}(T,t) G^{-1} (x_1 - \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&\quad -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s))^{\delta }) B u_0(s)\text {d}s\\ {}&\quad - \int ^{0}_{-h}dC{\eta } \Big [\int ^{0}_{\eta } h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&\quad -\Omega (t)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s)-\eta )^{\delta })\\ {}&C(s-\eta ,\eta ) u_{0}(s)ds\Big ]) \\ x(T)&= \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&\quad -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s))^{\delta }) B u(s)\text {d}s\\ {}&\quad + \int ^{0}_{-h}dC{\eta } \Big [\int ^{0}_{\eta } h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&\quad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (T)-\Omega (s)-\eta )^{\delta })\\ {}&\quad \times C(s-\eta ,\eta ) u_{0}(s)ds\Big ] \!+\! \int ^{T}_{O}\Big [\!\int ^{0}_{-h}\! h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&\quad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s)-\eta )^{\delta })\\&\quad \text {d}_{\eta }C_{t}(s-\eta ,\eta )\Big ]\Big [\int ^{0}_{-h} h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&\quad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s)-\eta )^{\delta })\\&\quad \times \text {d}_{\eta }C_{t}(s-\eta ,\eta )\Big ]^{*} G^{-1}((x^{-1}\! -\! \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&\quad -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s))^{\delta })\\&B u(s)\text {d}s \\ {}&- \int ^{0}_{-h}\text {d}C{\eta } \Big [\int ^{0}_{\eta } h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&\quad -\Omega (s)-\eta )^{\delta -1} E_{\delta ,\delta }(h(K)(\Omega (t)\\&\quad -\Omega (s)-\eta )^{\delta })\\ {}&C(s-\eta ,\eta ) u_{0}(s)ds\Big ])\text {d}\eta = x_{1} \end{aligned}$$

If G(0,t) it is not positive definite such that a nonzero exists in z.

$$\begin{aligned} z^{*}Gz = 0 \\ z^{*}\int ^{T}_{0}R(T, s)R^{*}(T, s)z\text {d}s = 0 \\ z^{*}R(T, s) = 0, on [0, T ] \end{aligned}$$

.

$$\begin{aligned} x(T)&= \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&\quad -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s))^{\delta }) B u(s)\text {d}s \\&\quad +\int ^{0}_{-h}\text {d}C{\eta } \Big [\int ^{0}_{\eta } h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&\quad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (T)-\Omega (s)-\eta )^{\delta })\\ {}&\quad \times C(s-\eta ,\eta ) u_{0}(s)\text {d}s\Big ] \\&\quad + \int ^{t}_{0}\Big [\int ^{0}_{-h} h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&\quad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (T)-\Omega (s)-\eta )^{\delta })\\ {}&\quad \times C(s-\eta ,\eta )\Big ] u(s)\text {d}s = 0 \end{aligned}$$

$$\begin{aligned} 0 =&z^{*}z+\int ^{T}_{0} y^{*} R(T , s) u(s)\text {d}s \\&\quad + z^{*} \int ^{0}_{-h}\text {d}C{\eta }\Big [\int ^{0}_{\eta } h^{-1}\\&\quad \times (\Omega ^{'}(s)(\Omega (T)-\Omega (s)-\eta )^{\delta -1})\\&\quad \times E_{\delta ,\delta }(h(K)(\Omega (T)-\Omega (s)-\eta )^{\delta } C(s-\eta ,\eta ) u_{0}\text {d}s\Big ] \end{aligned}$$

But the 2nd and 3rd term are zero leading to the conclusion $z^{*}z$ = 0. This is a contradiction to $z \ne 0$. Thus, G(0, T) is positive definite. $\square$

Theorem 2

Linear $\Omega$-Hilfer fractional dynamical system is controllable on J iff

$$\begin{aligned}{} & {} \!\!\text {rank}\ [Q,PQ,P^{2}Q,...,P^{n-1}Q,R,PR,P^{2}R,...,P^{n-1}R]\nonumber \\{} & {} \quad = n. \end{aligned}$$

(9)

From [19], then condition (11) is equal to the $\left\langle P\ Q,R \right\rangle$ = $R^{n}$

Proof

First, let us find the necessary part and it enclose two cases.

Case 1:Let us consider the time $T > \eta$ and the linear system (7) is relatively controllable for the initial state $x_{0} = 0$ and control $\Omega$ = 0 for any x $\epsilon R^{n}$. From Rf1 the control u(s) exists, then

$$\begin{aligned} x =&\int ^{0}_{t+\eta } [h^{-1}(\Omega ^{'}(s)(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)\\&-\Omega (s))^{\delta })B+\int ^{-h}_{0} \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)-(\Omega (s)\\&-\eta )^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-(\Omega (s)-\eta ))^{\delta })\\&\times C(\Omega (s)-\eta ,\eta )dC_{\eta }\Big ]u(s)\text {d}s\\ {}&+ \int ^{t+\eta }_{t} \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)\\&-\Omega (s))^{\delta })Bu(s)\Big ]\text {d}s. \end{aligned}$$

From above we imply $x \epsilon \left\langle P|Q,R\right\rangle$. Then, $R^{n} = \left\langle P|Q,R\right\rangle$ and (11) satisfies the condition.

Case 2:Let the proof is similar to case 1 and its omitted for $T \epsilon (0, \eta ]$ Let us prove the sufficient condition in 2 cases.

Case 1: Let the time $T > \eta$. Suppose that the linear system (7) such that $R^{n} = \left\langle P|Q,R\right\rangle$. For $\hat{x} \epsilon R^{n}$, initial states $x_{0}$ and initial control $\Omega$, assume

$$\begin{aligned} g =&\hat{x} - x_{0}(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-\Omega (s))^{\delta })\\ {}&- \int ^{0}_{t+\eta } \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)-\Omega (s))^{\delta -1})E_{\delta ,\delta }(K(\Omega (t)\\&-\Omega (s))^{\delta })\Big ]B + \int ^{-h}_{0} \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)-(\Omega (s)\\&\times -\eta )^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)\\&-(\Omega (s)-\eta ))^{\delta })\\&\times C(\Omega (s)-\eta ,\eta )\text {d}C_{\eta }\Big ]\text {d}s\Omega (0) \\ {}&- \int ^{t+\eta }_{t} \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)\\&-\Omega (s))^{\delta })\Big ]B\Omega (0)\text {d}s\\ {}&- \int ^{-h}_{0} \Big [\int ^{\eta }_{0}(h^{-1}\Omega ^{'}(s)(\Omega (t)\\&-(\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-(\Omega (s)-\eta ))^{\delta })\\&\times C(\Omega (s)-\eta ,\eta )\Omega (s)ds\Big ]\text {d}C_{\eta } \end{aligned}$$

For $g \epsilon R^{n}$ = $R^{n} = \left\langle P|Q,R\right\rangle$, using [19], we get $g \epsilon R(0, 0, 0)$ such that there exists the control $u^{*}(s) \epsilon L^{1}(0, T)$.

$$\begin{aligned} G=&\int ^{0}_{t+\eta } \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-\Omega (s))^{\delta })\Big ]B\\ {}&+ \int ^{-h}_{0} \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)\\&-(\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-(\Omega (s)-\eta ))^{\delta })\\ {}&\times C(\Omega (s)-\eta ,\eta )dC_{\eta }\Big ]u^{*}(s)\text {d}s \\ {}&+ \int ^{t+\eta }_{t} \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-\Omega (s))^{\delta })\Big ]Bu^{*}(s)\text {d}s. \end{aligned}$$

Let us $u(s) = u^{*}(s) + \Omega (0)$, then

$$\begin{aligned} \hat{x} =&x_{0}(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-\Omega (s))^{\delta })\\ {}&- \int ^{0}_{t+\eta } \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)\\&-\Omega (s))^{\delta })\Big ]B\\ {}&+ \int ^{-h}_{0} \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)\\&-(\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-(\Omega (s)-\eta ))^{\delta })\\ {}&C(\Omega (s)-\eta ,\eta )dC_{\eta }\Big ]u(s)\text {d}s\\ {}&+ \int ^{t+\eta }_{t} \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-\Omega (s))^{\delta })u(s)\Big ]B\text {d}s\\ {}&+ \int ^{-h}_{0} \Big [\int ^{\eta }_{0}(h^{-1}\Omega ^{'}(s)(\Omega (t)\\&-(\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-(\Omega (s)-\eta ))^{\delta })\\ {}&C(\Omega (s)-\eta ,\eta )\Omega (s)\text {d}s\Big ]\text {d}C_{\eta } \end{aligned}$$

$\Rightarrow$ the system (7) is controllable for $T > \eta$.

Case 2:Let the $T \epsilon (0, \eta ]$; suppose (11) such that $R^{n} = \left\langle P|Q,R\right\rangle$. For $x \epsilon R^{n}$, initial states $x_{0}$, let

$$\begin{aligned} G = \hat{x} - x_{0}(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-\Omega (s))^{\delta }) \end{aligned}$$

(10)

For $k \epsilon R^{n}$ = $\left\langle P|B,C\right\rangle$, using [19], we get $k \epsilon R(0, 0)$. Then, the control $u^{*}(s) \epsilon L^{1}(0, T)$ and the initial control $\Omega ^{*} \epsilon L^{1}(\eta , 0)$ there exists,

$$\begin{aligned} K =&\int ^{0}_{t} h^{-1}(\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-\Omega (s))^{\delta })Bu^{*}s\text {d}s\\ {}&+ \int ^{\eta }_{t+\eta } \Big [\int ^{-h}_{0}(h^{-1}\Omega ^{'}(s)(\Omega (t)\\&-(\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-(\Omega (s)-\eta ))^{\delta })\\ {}&C(\Omega (s)-\eta ,\eta )\text {d}C_{\eta }\Big ]\Omega ^{*}\text {d}s. \end{aligned}$$

Then, we have

$$\begin{aligned} \hat{x} =&x_{0}(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)\\&-\Omega (s))^{\delta })\\ {}&+ \int ^{0}_{t} \Big [h^{-1}(\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(K(\Omega (t)-\Omega (s))^{\delta })\Big ] Bu^{*}s\text {d}s\\ {}&+ \int ^{\eta }_{t+\eta } \Big [\int ^{-h}_{0}(h^{-1}\Omega ^{'}(s)(\Omega (t)\\&-(\Omega (s)-\eta )^{\delta -1})E_{\delta ,\delta }(K(\Omega (t)-(\Omega (s)-\eta ))^{\delta })\\ {}&C(\Omega (s)-\eta ,\eta )\text {d}C_{\eta }\Big ]\Omega ^{*}\text {d}s. \end{aligned}$$

then the system (7) is controllable. $\square$

4 Nonlinear systems

Consider the nonlinear $\Omega$-Hilfer fractional equation with delay is represented by

$$\begin{aligned} D^{\delta ,\beta ;\Omega }_{a+} x(t)= & {} Ax(t) + B u(t) + \int ^{0}_{-h}\text {d}_{\eta }C(t,\eta )u(t-\eta )\nonumber \\{} & {} +f(t,x(t),u(t)), t\epsilon [0,T] \nonumber \\= & {} J, 0< \delta < 1 \end{aligned}$$

(11)

$$\begin{aligned} I^{1-\gamma ;\Omega }_{t_{0}} x(0)= 0 \end{aligned}$$

where $0< \delta < 1$, $0< \beta < 1$, $\gamma$ = $\delta + \beta (1-\delta )$,then $x\epsilon$ $R^{n}$ and $u \epsilon$ $R^{m}$. Then

$$\begin{aligned} x(t) =&\int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&-\Omega (s))^{\delta }) B u(s)\text {d}s\\ {}&+ \int ^{0}_{t} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&-\Omega (t))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&-\Omega (s))^{\delta }) f(s,m(s),n(s))\text {d}s\\&+\int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&-\Omega (t))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&-\Omega (s))^{\delta }) [\int ^{0}_{-h}d_{\eta }C(t,\eta )u(t-\eta )]\text {d}s \end{aligned}$$

By Fubini theorem

$$\begin{aligned} =&\int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&-\Omega (s))^{\delta }) B u(s)\text {d}s \\ {}&+ \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&-\Omega (s))^{\delta })f(s,m(s),n(s))\text {d}s\\ {}&+\int ^{0}_{-h}\text {d}C{\eta } \Big [\int ^{0}_{\eta } h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&-\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (T)\\&-\Omega (s)-\eta )^{\delta }) \\ {}&C(s-\eta ,\eta ) u_{0}(s)\text {d}s\Big ]\\ {}&+ \int ^{t}_{0}\Big [\int ^{0}_{-h} h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&-\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (T)\\&-\Omega (s)-\eta )^{\delta })\\ {}&\text {d}_{\eta }C_{t}(s-\eta ,\eta )\Big ] u(s)\text {d}s \end{aligned}$$

Where

$$\begin{aligned} C_{t}(s,\eta ) = \left\{ \begin{array}{ll} C(s,\eta ),s \le t \\ 0, s > t \\ \end{array} \right. \end{aligned}$$

then $dC_{\eta }$ denotes the Lebesgue Stieltjes with the variable $\eta$. For our convenience, we introduce the constants

$$\begin{aligned}&\eta (y(0),x_{1},m,n) \\&\quad = x_{1} - \int ^{T}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&\qquad -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (T)\\&\qquad -\Omega (s))^{\delta })B u(s)\text {d}s\\ {}&- \int ^{T}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&\qquad -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (T)\\&\qquad -\Omega (s))^{\delta }) f(s,m(s),n(s))\text {d}s\\ {}&- \int ^{0}_{-h}dC{\eta } \Big [\int ^{0}_{\eta } h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&\qquad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (T)\\&\qquad -\Omega (s)-\eta )^{\delta })\\ {}&C(s-\eta ,\eta ) u_{0}(s)\text {d}s\Big ] \end{aligned}$$

Let us we define u(t) function

$$\begin{aligned} u(t) = R^{*}(T,t)G{-1}(\eta (y(0),x_{1},z,v)) \end{aligned}$$

Theorem 3

Suppose that the continuous function f and satisfies this condition

$$\begin{aligned} {\lim \limits _{|(x,u)|\rightarrow 0}} \frac{|f(t,x,u)|}{|x,u|} = 0 \end{aligned}$$

then the uniformly for t $\in$ $[t_{0},t_{}]$. Assume that linear $\Omega$ Hilfer system (7) is relatively controllable, then the nonlinear $\Omega$ Hilfer system (11) is globally relatively controllable on J.

Proof

Let us define the operator $\Omega :P\rightarrow P$

$$\begin{aligned} \Omega (m, n) = (x, u), \end{aligned}$$

where

$$\begin{aligned} u(t) =&R^{*}(T,t)G^{-1}(x_{1} - \int ^{T}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (T)-\Omega (s))^{\delta })B u(s)\text {d}s \\ {}&-\int ^{T}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&-\Omega (s))^{\delta }) f(s,m(s),n(s))\text {d}s)\\ {}&- \int ^{0}_{-h}dC{\eta } [\int ^{\eta }_{0}( h^{-1} (\Omega ^{'}(s)(\Omega (T)\\&-\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (T)\\&-\Omega (s)-\eta )^{\delta })\\ {}&C(s-\eta ,\eta ) u_{0}(s)ds) \\ x(t) =&\int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&-\Omega (s))^{\delta }) B u(s)\text {d}s\\ {}&+ \int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&-\Omega (s))^{\delta })f(s,m(s),n(s))ds\\ {}&+\int ^{0}_{-h}\text {d}C{\eta }\Big [\int ^{0}_{\eta } h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&-\Omega (s)-\eta )^{\delta }) \\ {}&C(s-\eta ,\eta ) u_{0}(s)\text {d}s\Big ]\\ {}&+\int ^{t}_{0} \Big [\int ^{0}_{-h} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\&-\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\&-\Omega (s)-\eta )^{\delta }) \\ {}&d_{\eta }C(s-\eta ,\eta )\Big ] u(s)\text {d}s \end{aligned}$$

consider the following notations are,

$$\begin{aligned}{} & {} a_{1} = ||\int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\{} & {} \quad -\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s))^{\delta })|| \\{} & {} a_{2} = ||\int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\\{} & {} \quad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)-\Omega (s)-\eta )^{\delta })|| \\{} & {} a_{3} = ||\int ^{0}_{\eta } h^{-1} (\Omega ^{'}(s)(\Omega (t)\\{} & {} \quad -\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\\{} & {} \quad -\Omega (s)-\eta )^{\delta }) C(s-\eta ,\eta ) u_{0}\text {d}s|| \\{} & {} a_{4} = sup||R^{*}(T,t)|| \\{} & {} d_{1} = ||4a_{4}|G^{-1}|[x_{1}+a_{3}]|| \\{} & {} d_{2} = ||4a_{3}|| \\{} & {} c_{1} = ||4a_{1} B|| \\{} & {} c_{2} = ||4a_{2}|| \\{} & {} sup|f| = sup{|f(s,m(s),n(s))|s \epsilon J} \end{aligned}$$

There exist

$$\begin{aligned}{} & {} u(t) \le ||R^{*}(T,t)|| |G^{-1}|[x_{1}+a_{3}] + a_{1}sup|f|ds \\{} & {} \le \Big [\frac{d_{1}}{4} + \frac{c_{1}}{4} sup|f|\Big ]ds \\{} & {} \le \Big [\frac{d}{4} + \frac{c}{4} sup|f|\Big ] \\{} & {} x(t) \le a_{3} + a_{1}u(s)ds + a_{2}sup|f|ds \\{} & {} \le \Big [\frac{d}{4} + \frac{c}{4} sup|f|ds + \frac{c}{4} sup|f|\Big ]ds \\{} & {} \le \Big [\frac{d}{2} + \frac{c}{2} sup|f|\Big ] \end{aligned}$$

By [55] the function f satisfies for each pair of positive constants c and d, there exists a positive constant z such that, if $\Vert q\Vert \le z$, then $c|f (t, q)| + d \le z$, for all $t \in J$. Therefore, if $\Vert m\Vert \le \frac{z}{2}$ and $\Vert n\Vert \le \frac{z}{2}$, then $\Vert m(s)\Vert + \Vert n(s)\Vert \le z$, for all $s \in J$ such that $d + c \sup \Vert f \Vert \le z$. Therefore, $\Vert u(s)\Vert \le \frac{z}{4a}$, for all $s \in J$, and hence $\Vert u\Vert \le \frac{z}{4a}$, which gives $\Vert x\Vert \le \frac{z}{2}$. Then we have proved, if $P(z) = {(m, n) \in P: \Vert m\Vert \in \frac{z}{2} and \Vert n\Vert \in \frac{z}{2}}$, then $\Omega$ maps P(z) into itself. Since f is continuous, it implies that the operator is continuous, and hence is completely continuous by the application of Arzela-Ascoli’s theorem. Because P(z) is closed, bounded and convex, the Schauder fixed point theorem guarantees that $\Omega$ has a fixed point $(m, n) \in P(z)$ such that $\Omega (m, n) = (m, n) \equiv (x, u)$. Hence x(t) is the solution of the system (11) and satisfy the $x(T ) = x_{1}$,then the control function u(t) steers the system (11) from initial complete state y(0) to $x_{1}$ on J. Hence, the system (11) is controllable on J. $\square$

5 Examples

Example 1

Consider the linear $\Omega$-Hilfer fractional equation as

$$\begin{aligned} D^{\frac{1}{2},\frac{1}{3},\Omega } x(t)= & {} \begin{bmatrix} 0 &{} 2\\ -1 &{} 0 \end{bmatrix} x(t) + \begin{bmatrix} 1\\ 1 \end{bmatrix} u(t)\nonumber \\{} & {} + \begin{bmatrix} e^{\eta }cos(t) &{} e^{\eta }sin(t) \\ -e^{\eta }sin(t) &{} e^{\eta }cos(t) \end{bmatrix} \end{aligned}$$

(12)

From above we have the matrix which are

$$\begin{aligned} A= & {} \begin{bmatrix} 0 &{} 2\\ -1 &{} 0 \end{bmatrix}, B = \begin{bmatrix} 1\\ 1 \end{bmatrix}, c(t,\eta )\nonumber \\= & {} \begin{bmatrix} e^{\eta }cos(t) &{} e^{\eta }sin(t) \\ -e^{\eta }sin(t) &{} e^{\eta }cos(t) \end{bmatrix} \end{aligned}$$

(13)

This shows that

$$\begin{aligned}{} & {} \begin{bmatrix} B&AB&C&AC\end{bmatrix}\\{} & {} \quad = \begin{bmatrix} 0 &{} 2 &{} e^{\eta }cos(t) &{} e^{\eta }sin(t) &{} -e^{\eta }sin(t) &{} e^{\eta }cos(t)\\ -1 &{} 0 &{} -e^{\eta }sin(t) &{} e^{\eta }cos(t) &{} e^{\eta }cos(t) &{} e^{\eta }sin(t)\\ \end{bmatrix} \end{aligned}$$

$$\begin{aligned} \text {rank}\begin{bmatrix} B&AB&C&AC\end{bmatrix} = 2 \end{aligned}$$

From Theorem 3.4, for all $T > 0$, the system (20) is controllable. Hence taking the unique control when $T \epsilon (0, 1]$. For $x_{0}$ and $x_{1}$ assume that there exist $\Omega _{1}(s) \epsilon L^{1}(\eta , 0)$, $u_{1} \epsilon L^{1}(0, T)$ and $\Omega _{2}(s) \epsilon L^{1}(\eta , 0)$, $u_{2} \epsilon L^{1}(0, T )$ such that

$$\begin{aligned} x_{1}=&x(T) = x_{0}(\Omega (T)-\Omega (s))^{\frac{1}{3}-1}) E_{\frac{1}{2},\frac{1}{3}}(A(\Omega (T)-\Omega (s))^{\frac{1}{2}})\\ {}&+ \int ^{0}_{T} [(\Omega ^{'}(s)(\Omega (T)-\Omega (s))^{\frac{1}{2}-1}) E_{\frac{1}{2},\frac{1}{2}}(A(\Omega (T)\\&-\Omega (s))^{\frac{1}{2}})Bu_{i}s\text {d}s\\ {}&+ \int ^{\eta }_{t+\eta } [\int ^{-1}_{0}(\Omega ^{'}(s)(\Omega (T)\\&-(\Omega (s)-\eta )^{\frac{1}{2}-1}) E_{\frac{1}{2},\frac{1}{2}}\\ {}&(A(\Omega (T)-(\Omega (s)-\eta ))^{\frac{1}{2}})C(\Omega (s)\\&-\eta ,\eta )dC_{\eta }]\Omega _{i}\text {d}s, i = 1,2 \end{aligned}$$

Then

$$\begin{aligned}&\int ^{0}_{T} [(\Omega ^{'}(s)(\Omega (T)-\Omega (s))^{\frac{1}{2}-1}) E_{\frac{1}{2},\frac{1}{2}}(A(\Omega (T)\\&\quad -\Omega (s))^{\frac{1}{2}})Bu_{1}s\text {d}s\\ {}&\quad + \int ^{\eta }_{t+\eta } [\int ^{-1}_{0}(\Omega ^{'}(s)(\Omega (T)\\&\quad -(\Omega (s)-\eta )^{\frac{1}{2}-1}) E_{\frac{1}{2},\frac{1}{2}}(A(\Omega (T)\\&\quad -(\Omega (s)-\eta ))^{\frac{1}{2}})\\ {}&\quad \times C(\Omega (s)-\eta ,\eta )\text {d}C_{\eta }]\Omega _{1}\text {d}s, \\ =&\int ^{0}_{T} [(\Omega ^{'}(s)(\Omega (T)\\&-\Omega (s))^{\frac{1}{2}-1}) E_{\frac{1}{2},\frac{1}{2}}(A(\Omega (T)\\&-\Omega (s))^{\frac{1}{2}})Bu_{2}s\text {d}s \\ {}&+ \int ^{\eta }_{t+\eta } [\int ^{-1}_{0}(\Omega ^{'}(s)(\Omega (T)\\&-(\Omega (s)-\eta )^{\frac{1}{2}-1}) E_{\frac{1}{2},\frac{1}{2}}(A(\Omega (T)\\&-(\Omega (s)-\eta ))^{\frac{1}{2}})\\ {}&\quad \times C(\Omega (s)-\eta ,\eta )\text {d}C_{\eta }]\Omega _{2}\text {d}s, \\&\int ^{0}_{T} [(\Omega ^{'}(s)(\Omega (T)-\Omega (s))^{\frac{1}{2}-1}) E_{\frac{1}{2},\frac{1}{2}}(A(\Omega (T)\\&-\Omega (s))^{\frac{1}{2}})B(u_{1}(s) - Bu_{2}(s))\text {d}s\\ =&\int ^{\eta }_{t+\eta } [\int ^{-1}_{0}(\Omega ^{'}(s)(\Omega (T)\\&-(\Omega (s)-\eta )^{\frac{1}{2}-1}) E_{\frac{1}{2},\frac{1}{2}}(A(\Omega (T)\\&-(\Omega (s)-\eta ))^{\frac{1}{2}})\\ {}&\quad \times C(\Omega (s)-\eta ,\eta )dC_{\eta }](\Omega _{2}(s) - \Omega _{1}(s))\text {d}s, \end{aligned}$$

we obtain

$$\begin{aligned} u_{1}(s) = u_{2}(s)\ and\ \Omega _{1}(s) = \Omega _{2}(s) \end{aligned}$$

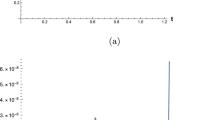
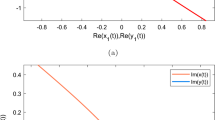
Then, the control is unique. Therefore, by the Theorem 1, the system is completely controllable. Using MATLAB, we complete the numerical solution x(t) in (12) in the interval [0,2].

Example 2

Let the nonlinear $\Omega$-Hilfer fractional equation as

$$\begin{aligned}{} & {} D^{0.8,0.9,\Omega } x(t) = \begin{bmatrix} 0 &{} 1\\ -1 &{} 0 \end{bmatrix} x(t) + \begin{bmatrix} 1\\ 1 \end{bmatrix} u(t) \nonumber \\{} & {} \quad + c(t,\eta ) \begin{bmatrix} e^{\eta }cos(t) &{} e^{\eta }sin(t) \\ -e^{\eta }sin(t) &{} e^{\eta }cos(t) \end{bmatrix} \nonumber \\{} & {} \quad +f(x(t),u(t)),t\epsilon [0,1] \end{aligned}$$

(14)

$$\begin{aligned} I^{1-\gamma ;\Omega }_{t_{0}}x(0) = 0. \end{aligned}$$

$$\begin{aligned}&A = \begin{bmatrix} 0 &{} 1\\ -1 &{} 0 \end{bmatrix}, B = \begin{bmatrix} 1\\ 1 \end{bmatrix}, c(t,\eta ) = \begin{bmatrix} e^{\eta }cos(t) &{} e^{\eta }sin(t) \\ -e^{\eta }sin(t) &{} e^{\eta }cos(t)\end{bmatrix},\nonumber \\&f(t,x(t)) = \begin{bmatrix}\frac{x_{1}}{1+x_{2}^{2}(t)}\\ \frac{x_{2}}{1+x_{2}^{1}(t)} \end{bmatrix} \end{aligned}$$

(15)

Let the mittag-leffler matrix function is h(K) = A is [54]

$$\begin{aligned}{} & {} E_{\frac{1}{4}}(At^{\frac{1}{4}}) = \begin{bmatrix} N_{1} &{} N_{2}\\ N_{3}&{} N_{4} \end{bmatrix} \end{aligned}$$

(16)

$$\begin{aligned}{} & {} E_{\frac{1}{4},\frac{1}{4}}(A(\Omega (T)-(\Omega (s)-\Omega (\eta )))^{\frac{1}{4}}) = \begin{bmatrix} M_{1} &{} M_{2}\\ M_{3}&{} M_{4} \end{bmatrix} \end{aligned}$$

(17)

Where

$$\begin{aligned}{} & {} M_{1} = {\sum ^{\infty }_{j=0}} \frac{(-1)^{j}(\Omega (T)-(\Omega (s)-\Omega (\eta )))^{2j\frac{1}{4}}}{\Gamma (2j+1)\frac{1}{4}} \\{} & {} M_{2} = {\sum ^{\infty }_{j=0}} \frac{(-1)^{j}(\Omega (T)-(\Omega (s)-\Omega (\eta )))^{(2j+1)\frac{1}{4}}}{\Gamma (j+1)2\frac{1}{4}} \\{} & {} M_{3} = {-\sum ^{\infty }_{j=0}} \frac{(-1)^{j}(\Omega (T)-(\Omega (s)-\Omega (\eta )))^{(2j+1)\frac{1}{4}}}{\Gamma (j+1)2\frac{1}{4}} \\{} & {} M_{4} = {\sum ^{\infty }_{j=0}} \frac{(-1)^{j}(\Omega (T)-(\Omega (s)-\Omega (\eta )))^{2j\frac{1}{4}}}{\Gamma (2j+1)\frac{1}{4}} \end{aligned}$$

$$\begin{aligned}{} & {} ((\Omega (T)-(\Omega (s)-\Omega (\eta )))^{\frac{1}{4}}-1)E_{\frac{1}{4},\frac{1}{4}}(A(\Omega (T)\nonumber \\{} & {} \quad -(\Omega (s)-\Omega (\eta )))^{\frac{1}{4}}) = \begin{bmatrix} cos_{\delta }(t) &{} sin_{\delta }(t)\\ -sin_{\delta }(t)&{} cos_{\delta }(t) \end{bmatrix} \end{aligned}$$

(18)

$$\begin{aligned} R(t,s) =&\int ^{t}_{0} h^{-1} (\Omega ^{'}(s)(\Omega (t)\nonumber \\&-\Omega (s))^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\nonumber \\&-\Omega (s))^{\delta }) B u(s)\text {d}s\nonumber \\ {}&+ \int ^{0}_{-h} h^{-1} (\Omega ^{'}(s)(\Omega (t)\nonumber \\&-\Omega (s)-\eta )^{\delta -1}) E_{\delta ,\delta }(h(K)(\Omega (t)\nonumber \\&-\Omega (s)-\eta )^{\delta }) \text {d}_{\eta }C_{t}(s-\eta ,\eta ) \end{aligned}$$

(19)

$$\begin{aligned} = \begin{bmatrix} U(s) &{} V(s)\\ -V(S) &{} U(s) \end{bmatrix} \end{aligned}$$

(20)

$$\begin{aligned}{} & {} U(s) = \int ^{0}_{-h} e^{\eta }\Big [cos_{\delta }(\Omega (T)-\Omega (s)-\Omega (\eta ))cos(\Omega (s)\\{} & {} \quad -\Omega (\eta ))-sin_{\delta }(\Omega (T)-\Omega (s)-\Omega (\eta ))\\{} & {} \quad sin(\Omega (s)-\Omega (\eta ))\Big ]\text {d}_{\eta }\\{} & {} V(s) = \int ^{0}_{-h} e^{\eta }\Big [sin_{\delta }(\Omega (T)-\Omega (s)-\Omega (\eta ))cos(\Omega (s)\\{} & {} \quad -\Omega (\eta ))-cos_{\delta }(\Omega (T)-\Omega (s)-\Omega (\eta ))\\{} & {} \quad sin(\Omega (s)-\Omega (\eta ))\Big ]\text {d}_{\eta } \end{aligned}$$

The reachability Gramian matrix is given by

$$\begin{aligned} G= & {} \int ^{T}_{0} R(T,s)R^{*}(T,s)\text {d}s \\= & {} \int ^{T}_{0} [U^{2}(s)+ V^{2}(s)]\begin{bmatrix} 1 &{} 0 \\ 0 &{} 1 \end{bmatrix}\text {d}s \end{aligned}$$

is positive definite, for some T > 0.

6 Conclusion

In this paper, we investigated the controllability criteria of $\Omega$-Hilfer fractional dynamical systems with delay in linear and nonlinear cases. By defining some assumption and using controllability Grammarian matrix, rank matrix and Schauder fixed point theorem, the proposed results satisfied both the linear and nonlinear systems. Finally, we analyzed two examples to validate to controllability of the fractional dynamical system. In future work, we will discuss the $\Omega$-Hilfer fractional dynamical systems in damped model with delay concept. Mainly, the damped model have variety of applications problem to justify fractional operator like Caputo and Hilfer.