Skip to main content

Advertisement

SpringerLink
Log in

Impact of habitat destruction and its subsequent regeneration on the dynamics of a Holling type II prey–predator interacting species system with prey refuge

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

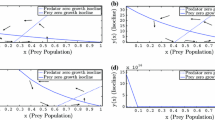
Here, we have studied the effects of habitat destruction and its regeneration effort on the dynamical behavior of prey–predator species system considering prey refuge with the help of mathematical model. In the formulation of the model, it is assumed that the habitat is destroyed due to anthropogenic activities, such as deforestation, overgrazing, mining, urbanization, intensive cultivation, and industrialization associated with human population growth and habitat destruction which have deleterious effects on the vital parameters of the prey–predator species system. We investigated how the dynamics of the prey and predator populations are influenced by changes in habitat destruction, control efforts, and subsequent regeneration of habitat. The stability analysis and bifurcation study of the mathematical model are carried out both analytically and numerically to understand the dynamical behavior of the system. With the help of numerical simulations and stability analysis, we analyze the environmental impact of habitat destruction, prey refuge, and habitat regeneration. It is observed from the stability analysis of the equilibrium points that the effects of habitat destruction will be apparent only when the level of habitat destruction becomes more than the critical value \(D_\textrm{c}\). Furthermore, a sensitivity analysis of the interior equilibrium point is also carried out by using normalized forward sensitivity method to investigate the impact of model parameters. It is shown that as the growth rate of human population increases, the amount (proportion) of destroyed habitat increases causing decrease in the equilibrium densities of prey and predator populations. It is observed that stable coexisting behavior is changed to coexisting oscillatory behavior by taking coefficient measuring decrease in the natural availability of refuge for prey on account of habitat destruction as a bifurcation parameter. It is derived from the analysis of the model that as the effort rate for regenerating destructed habitat per unit amount of habitat destroyed increases, then initially, the prey and predator population both starts increasing but as the effort rate increases further, then the predator population tends to extinction on account of complete restoration of refuge habitat. Hence, for the coexistence of both the populations of prey and predator, it is suggested that the regeneration effort need not be applied beyond a specific limit.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Data Availability

To perform numerical simulation we have assumed hypothetical parametric values which is available with in the article.

References

  1. Kauzeni AS (1995) A paradigm for community wildlife management: the case of protected areas of the serengeti region ecosystem. Research paper No. 37 (New Series). Dar es Salaam, Tanzania: Institute of Resource Assessment, University of Dar es Salaam

  2. Kideghesho JR (2001) Mitigating the loss of wildlife habitats in Tanzania: current and future strategies. Tanzan J For Nat Conserv 74:149–161

    Google Scholar 

  3. Kideghesho JR, Nyahongo JW, Hassan SN, Tarimo TC, Mbije NE (2006) Factors and ecological impacts of wildlife habitat destruction in the Serengeti ecosystem in Northern Tanzania. AJEAM-RAGEE 11:917–932

    Google Scholar 

  4. Mwalyosi RBB (1992) Land-use changes and resource degradation in South-West Masailand Tanzania. Environ Conserv 19(2):145–152

    Article  Google Scholar 

  5. Niebuhr BBS, Wosniack ME, Santos MC, Raposo EP, Viswanathan GM, da Luz MGE, Pie MR (2015) Survival in patchy landscapes: the interplay between dispersal, habitat loss and fragmentation. Sci Rep 5:11898. https://doi.org/10.1038/srep11898

    Article  Google Scholar 

  6. Kruess A, Tscharntke T (1994) Habitat fragmentation, species loss, and biological control. Science 264:1581–1584

    Article  Google Scholar 

  7. Schneider MF (2001) Habitat loss, fragmentation and predator impact: spatial implications for prey conservation. J Appl Ecol 38:720–735

    Article  Google Scholar 

  8. Misra AK, Tiwari PK (2015) A model for the effect of density of human population on the depletion of dissolved oxygen in a water body. Environ Dev Sustain 17:623–640

    Article  Google Scholar 

  9. Sarkar K, Khajanchi S, Mali PC (2022) A delayed eco-epidemiological model with weak Allee effect and disease in prey. Int J Bifurc Chaos 32(8):2250122

    Article  MathSciNet  Google Scholar 

  10. Sarkar K, Khajanchi S (2022) An eco-epidemiological model with the impact of fear. Chaos Interdiscip J Nonlinear Sci 32(8):083126

    Article  MathSciNet  Google Scholar 

  11. Misra OP, Chaturvedi D (2016) Fate of dissolved oxygen and survival of fish population in aquatic ecosystem with nutrient loading: a model. Model Earth Syst Environ. https://doi.org/10.1007/s40808-016-0168-9

    Article  Google Scholar 

  12. Khajanchi S (2014) Dynamic behavior of a Beddington-DeAngelis type stage structured predator-prey model. Appl Math Comput 244:344–360

    MathSciNet  Google Scholar 

  13. Biswas S, Ahmad B, Khajanchi S (2022) Exploring dynamical complexity of a cannibalistic eco-epidemiological model with multiple time delay. Math Methods Appl Sci 46(4):4184–4211

    Article  MathSciNet  Google Scholar 

  14. Sarkar K, Khajanchi S, Mali PC, Nieto JJ (2020) Rich dynamics of a predator-prey system with different kinds of functional responses. Complexity. https://doi.org/10.1155/2020/4285294

    Article  Google Scholar 

  15. Khajanchi S (2017) Modeling the dynamics of stage-structure predator–prey system with Monod-Haldane type response function. Appl Math Comput 302:122–143

    MathSciNet  Google Scholar 

  16. Sarkar K, Khajanchi S (2020) Impact of fear effect on the growth of prey in a predator-prey interaction model. Ecol Complex 42:100826

    Article  Google Scholar 

  17. Donelan SC, Grabowski JH, Trussell GC (2017) Refuge quality impacts the strength of nonconsumptive effects on prey. Ecology 98(2):403–411

    Article  Google Scholar 

  18. Abdulghafour AS, Naji RK (2018) The impact of refuge and harvesting on the dynaics of prey-predator system. Sci Int 30(2):315–323

    Google Scholar 

  19. Jana D (2014) Stabilizing effect of prey refuge and predator’s interference on the dynamics of prey with delayed growth and generalist predator with delayed gestation. Int J Ecol. https://doi.org/10.1155/2014/429086

    Article  Google Scholar 

  20. Molla H, Rahman MS, Sarwardi S (2018) Dynamics of a predator-prey model with Holling type II functional response incorporating a prey refuge depending on both the species. Int J Nonlinear Sci Numer Simul. https://doi.org/10.1515/ijnsns-2017-0224

    Article  Google Scholar 

  21. Chen L, Chen F, Chen L (2010) Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a constant prey refuge. Nonlinear Anal Real World Appl 11:246–252

    Article  MathSciNet  Google Scholar 

  22. Naji RK, Majeed SJ (2016) The dynamical analysis of a prey-predator model with a Refuge-Stage structure prey population. Int J Differ Equ. https://doi.org/10.1155/2016/2010464

    Article  MathSciNet  Google Scholar 

  23. Devi S (2013) Effects of prey refuge on a ratio-dependent predator–prey model with stage-structure of prey population. Appl Math Model 37:4337–4349

    Article  MathSciNet  Google Scholar 

  24. Kant S, Kumar V (2014) Delayed prey-predator system with habitat complexity and refuge. Int Conf Math Sci. https://doi.org/10.13140/2.1.3493.8884

    Article  Google Scholar 

  25. Khajanchi S, Banerjee S (2017) Role of constant prey refuge on stage structure predator-prey model with ratio dependent functional response. Appl Math Comput 314:193–198

    MathSciNet  Google Scholar 

  26. Kar TK (2005) Stability analysis of a prey-predator model incorporating a prey refuge. Commun Nonlinear Sci Numer Simul 10:681–691

    Article  MathSciNet  Google Scholar 

  27. Ma Z, Wang S, Li W, Li Z (2013) The effect of prey refuge in a patchy predator-prey system. Math Biosci 243:126–130

    Article  MathSciNet  Google Scholar 

  28. Kadhim ZJ, Majeed AA, Naji RK (2016) The bifurcation analysis of a stage structured prey food web model with refuge. Iraqi J Sci. Special Issue, Part A 139–155

  29. Ma Z, Wang S, Wang T, Tang H (2017) Stability analysis of prey-predator system with Holling type functional response and prey refuge. Adv Differ Equ. https://doi.org/10.1186/s13662-017-1301-4

    Article  MathSciNet  Google Scholar 

  30. Tilman D, May RM, Lehman CL, Nowak MA (1994) Habitat destruction and the extinction debt. Lett Nat 371:65–66

    Article  Google Scholar 

  31. Tilman D, Lehman CL, Yin C (1997) Habitat destruction, dispersal, and deterministic extinction in competitive communities. Am Nat 149(3):407–435

    Article  Google Scholar 

  32. dos Santos FS, Johst K, Huth A, Grimm V (2010) Interacting effects of habitat destruction and changing disturbance rates on biodiversity: who is going to survive? Ecol Model 221:2776–2783

    Article  Google Scholar 

  33. Liu H, Lin Z, Qi X, Zhang M, Yang H (2012) Interactive effects of habitat destruction and competition on exotic invasion. Eco Inform 9:69–75

    Article  Google Scholar 

  34. Stone L, Eilam E, Abelson A, Ilan M (1996) Modelling coral reef biodiversity and habitat destruction. Mar Ecol Prog Ser 134:299–302

    Article  Google Scholar 

  35. Misra OP, Kushwah P, Singh Sikarwar C (2013) Dynamical study of native and exotic competing populations: effects of habitat destruction. Ecol Complex 17:46–55

    Article  Google Scholar 

  36. Swihart RK, Feng Z, Slade NA, Mason DM, Gehring TM (2001) Effects of habitat destruction and resource supplementation in a predator–prey metapopulation model. J Theor Biol 210:287–303

    Article  Google Scholar 

  37. Strohm S, Tyson R (2009) The effect of habitat fragmentation on cyclic population dynamics: a numerical study. Bull Math Biol 71:1323–1348

    Article  MathSciNet  Google Scholar 

  38. Mullu D (2016) A Review on the effect of habitat fragmentation on ecosystem. J Nat Sci Res 6(15):1

    Google Scholar 

  39. Hale JK (1969) Ordinary differential equations. Wiley Interscience, New York

    Google Scholar 

  40. Birkoff G, Rota GC (1982) Ordinary differential equations. Ginn, Boston

    Google Scholar 

  41. Wang N, Zhao M, Hengguo Y, Dai C, Wang B, Wang P (2016) Bifurcation behavior analysis in a predator-prey model. Hindawi Publishing Corporation Discrete Dynamics in Nature and Society. 11. https://doi.org/10.1155/2016/3565316

  42. Chitnis N, James Hyman M, Jim Cushing M (2008) Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull Math Biol 70(5):1272–1296

    Article  MathSciNet  Google Scholar 

  43. Szwabin ski J, Pekalski A (2006) Effects of random habitat destruction in a predator-prey model. Phys A 360:59–70

  44. Ryall KL, Fahrig L (2005) Habitat Loss decreases predator-prey ratios in a pine-bark beetle system. Oikos 110:265–270

    Article  Google Scholar 

Download references

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Engineering Mathematics & Computing, Madhav Institute of Technology & Science, Gwalior, M.P., India

    Divya Chaturvedi

  2. School of Mathematics and Allied Sciences, Jiwaji University, Gwalior, M.P., India

    O. P. Misra

Authors
  1. Divya Chaturvedi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. P. Misra
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors certify that they have participated sufficiently in the work to take responsibility for the content, including participation in the concept, design, analysis, writing or revision of the manuscript. Furthermore, each author certifies that this material or similar material has not been published in any other journal. Both authors have contributed equally in the concept or formulation of problem, analysis or interpretation of data, and drafting the manuscript.

Corresponding author

Correspondence to Divya Chaturvedi.

Ethics declarations

Conflict of interest

There is no conflict of interest.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chaturvedi, D., Misra, O.P. Impact of habitat destruction and its subsequent regeneration on the dynamics of a Holling type II prey–predator interacting species system with prey refuge. Int. J. Dynam. Control 12, 1332–1345 (2024). https://doi.org/10.1007/s40435-023-01275-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-023-01275-6

Keywords

Search

Navigation