Skip to main content
SpringerLink
Log in

Deterministic and stochastic analysis of a two-prey–one-predator system with fear effect and switching behaviour in predation

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

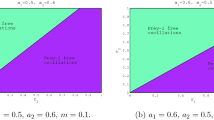
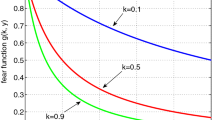
In this article, we have analysed a two-prey–one-predator system in which predator feeds on the more abundant prey species (switching in predation) and also the reproduction of both prey species is greatly reduced by the presence of predator (fear affect). The goal of this work is to investigate the dynamical characteristics of the system in both deterministic and stochastic environments. Well-posedness of the deterministic system has been justified by analysing the basic dynamical properties of that system. Stability conditions at various feasible equilibrium points are derived in terms of model parameters. The impact of parametric fluctuation has also been investigated on the model dynamics by using local bifurcation analysis. We also have studied the proposed model in a fluctuating environment by considering death rate of each species as stochastic parameter. Our mathematical findings have been justified and illustrated through numerical simulation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Data availability

The data used to support the findings of the study are available within the article.

References

  1. Cresswell W (2011) Predation in bird populations. J Ornithol 152:251–263

    Article  Google Scholar 

  2. Mondal S, Samanta GP (2021) Impact of fear on a predator-prey system with prey-dependent search rate in deterministic and stochastic environment. Nonlinear Dyn 104:2931–2959. https://doi.org/10.1007/s11071-021-06435-x

    Article  Google Scholar 

  3. Sahoo D, Samanta G, De la Sen M (2021) Impact of fear and habitat complexity in a predator-prey system with two different shaped functional responses: A comparative study. Discret Dyn Nat Soc 2021:6427864. https://doi.org/10.1155/2021/6427864

    Article  MathSciNet  MATH  Google Scholar 

  4. Saha S, Samanta GP (2020) A prey-predator system with disease in prey and cooperative hunting strategy in predator. J Phys A: Math Theor 53(48):485601

    Article  MathSciNet  MATH  Google Scholar 

  5. Malthus TR (1798) An essay on the principle of population as it affects the future improvement of society, with remarks on the speculations of Mr. Godwin, M. Condorcet, and other writers. The Lawbook Exchange Ltd

    Google Scholar 

  6. Verhulst PF (1838) Notice sur la loi que la population suit dans son accroissement. Corresp Math Phys 10(2):113–126. https://doi.org/10.1016/j.mbs.2012.11.007

    Article  Google Scholar 

  7. Lotka AJ (1925) Elements of physical biology. Williams and Wilkins company

  8. Volterra V (1927) Variazioni e fluttuazioni del numero d’individui in specie animali conviventi. Memoria della Reale Accademia Nazionale dei Lincei

  9. Rosenzweig ML, MacArthur RH (1963) Graphical representation and stability conditions of predator-prey interactions. Am Nat 97(895):209–223

    Article  Google Scholar 

  10. Creel S, Christianson D, Liley S, Winnie JA (2007) Predation risk affects reproductive physiology and demography of elk. Science 315(5814):960. https://doi.org/10.1126/science.1135918

    Article  Google Scholar 

  11. Das BK, Sahoo D, Samanta GP (2022) Impact of fear in a delay-induced predator-prey system with intraspecific competition within predator species. Math Comput Simul 191:134–156. https://doi.org/10.1016/j.matcom.2021.08.005

    Article  MathSciNet  MATH  Google Scholar 

  12. Mondal S, Samanta GP (2020) Dynamics of a delayed predator-prey interaction incorporating nonlinear prey refuge under the influence of fear effect and additional food. J Phys A: Math Theor 53(29):295601

    Article  MathSciNet  MATH  Google Scholar 

  13. Mondal S, Samanta GP, Nieto JJ (2021) Dynamics of a predator-prey population in the presence of resource subsidy under the influence of nonlinear prey refuge and fear effect. Complexity 2021:9963031. https://doi.org/10.1155/2021/9963031

    Article  Google Scholar 

  14. Sweitzer RA, Jenkins SH, Berger J (1997) Near-extinction of porcupines by mountain lions and consequences of ecosystem change in the great basin desert. Conserv Biol 11(6):1407–1417. https://doi.org/10.1046/j.1523-1739.1997.96138.x

    Article  Google Scholar 

  15. Cook DB, Hamilton WJ (1944) The ecological relationships of red fox food in eastern new york. Ecology 25(1):91–104. https://doi.org/10.2307/1930765

    Article  Google Scholar 

  16. Murdoch WW (1969) Switching in general predators: experiments on predator specificity and stability of prey populations. Ecol Monogr 39(4):335–354. https://doi.org/10.2307/1942352

    Article  Google Scholar 

  17. Tansky M (1978) Switching effect in prey-predator system. J Theor Biol 70(3):263–271. https://doi.org/10.1016/0022-5193(78)90376-4

    Article  MathSciNet  Google Scholar 

  18. Prajneshu, Holgate P (1987) A prey-predator model with switching effect. J Theoret Biol 125(1):61–66. https://doi.org/10.1016/S0022-5193(87)80179-0

    Article  MathSciNet  Google Scholar 

  19. Saha S, Samanta G (2021) Modelling of a two prey and one predator system with switching effect. Comput Math Biophys 9:90–113. https://doi.org/10.1515/cmb-2020-0120

    Article  MathSciNet  MATH  Google Scholar 

  20. Zanette LY, White AF, Allen MC, Clinchy M (2011) Perceived predation risk reduces the number of offspring songbirds produce per year. Science 334(6061):1398–1401. https://doi.org/10.1126/science.1210908

    Article  Google Scholar 

  21. Elliott KH, Betini GS, Norris DR (2017) Fear creates an allee effect: experimental evidence from seasonal populations. Proc R Soc B Biol Sc 284(1857):20170878. https://doi.org/10.1098/rspb.2017.0878

    Article  Google Scholar 

  22. Suraci JP, Clinchy M, Dill LM, Roberts D, Zanette LY (2016) Fear of large carnivores causes a trophic cascade. Nat Commun 7:10698. https://doi.org/10.1038/ncomms10698

    Article  Google Scholar 

  23. Wang X, Zanette L, Zou X (2016) Modelling the fear effect in predator-prey interactions. J Math Biol 73:1179–1204. https://doi.org/10.1007/s00285-016-0989-1

    Article  MathSciNet  MATH  Google Scholar 

  24. Das A, Samanta GP (2018) Modeling the fear effect on a stochastic prey-predator system with additional food for predator. J Phys A Math Theor 51(46):465601. https://doi.org/10.1088/1751-8121/aae4c6

    Article  MathSciNet  Google Scholar 

  25. Sahoo D, Samanta GP (2021) Impact of fear effect in a two prey-one predator system with switching behaviour in predation. Differ Equ Dyn Syst. https://doi.org/10.1007/s12591-021-00575-7

    Article  Google Scholar 

  26. Lande R (1993) Risks of population extinction from demographic and environmental stochasticity and random catastrophes. Am Nat 142(6):911–927

    Article  Google Scholar 

  27. May RM (1973) Stability in randomly fluctuating versus deterministic environments. Am Nat 107(957):621–650

    Article  Google Scholar 

  28. Xia Y, Yuan S (2020) Survival analysis of a stochastic predator-prey model with prey refuge and fear effect. J Biol Dyn 14(1):871–892. https://doi.org/10.1080/17513758.2020.1853832

    Article  MathSciNet  Google Scholar 

  29. Das A, Samanta GP (2018) Stochastic prey-predator model with additional food for predator. Physica A 512:121–141. https://doi.org/10.1016/j.physa.2018.08.138

    Article  MathSciNet  MATH  Google Scholar 

  30. Khan QJA, Balakrishnan E, Wake GC (2004) Analysis of a predator-prey system with predator switching. Bull Math Biol 66(1):109–123

    Article  MathSciNet  MATH  Google Scholar 

  31. Tiwari PK, Al Amri KAN, Samanta S, Khan QJA, Chattopadhyay J (2021) A systematic study of autonomous and nonautonomous predator–prey models with combined effects of fear, migration and switching. Nonlinear Dyn 103(2):2125–2162

  32. Samanta GP (1996) Influence of environmental noises on the gomatam model of interacting species. Ecol Model 91(1–3):283–291

    Article  Google Scholar 

  33. Samanta GP (1991) Stochastic analysis of a noisy oscillator. Appl Math Lett 4(2):61–63

    Article  MathSciNet  MATH  Google Scholar 

  34. Bera SP, Maiti A, Samanta GP (2016) Stochastic analysis of a prey-predator model with herd behaviour of prey. Nonlinear Anal Modell Control 21(3):345–361

    Article  MathSciNet  MATH  Google Scholar 

  35. Liu G, Qi H, Chang Z, Meng X (2020) Asymptotic stability of a stochastic may mutualism system. Comput Math Appl 79(3):735–745

    MathSciNet  MATH  Google Scholar 

  36. Hale JK (1977) Theory of functional differential equations. Springer, New York

    Book  MATH  Google Scholar 

  37. Perko L (2013) Differential equations and dynamical systems, vol 7. Springer Science & Business Media

    MATH  Google Scholar 

  38. Das A, Samanta GP (2020) A prey-predator model with refuge for prey and additional food for predator in a fluctuating environment. Physica A Stat Mech Appl. https://doi.org/10.1016/j.physa.2019.122844

    Article  MATH  Google Scholar 

  39. Mao X (2011) Stochastic differential equations and applications. WOODHEAD PUBLISHING, Oxford

    Google Scholar 

  40. Barbalat I (1959) Systems d’equations differentielles d’oscillations nonlinearies. Revue Roumaine des Mathematiques Pures et Appliquees 4(2):267–270

    MATH  Google Scholar 

  41. Ji C, Jiang D (2011) Dynamics of a stochastic density dependent predator-prey system with Beddington–Deangelis functional response. J Math Anal Appl 381:441–453. https://doi.org/10.1016/j.jmaa.2011.02.037

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the anonymous referees and Professor Jian-Qiao Sun (Editor-in-Chief) for their valuable comments and helpful suggestions, which have helped them to improve the presentation of this work significantly. The research of J.J. Nieto has been partially supported by the Agencia Estatal de Investigacion (AEI) of Spain, cofinanced by the European Fund for Regional Development (FEDER) corresponding to the 2014-2020 multiyear financial framework, project PID2020-113275GB-I00; and by Xunta de Galicia under grant ED431C 2019/02.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Engineering Science and Technology, Shibpur, Howrah, 711103, India

    Amartya Das, Debgopal Sahoo & Guruprasad Samanta

  2. Instituto de Matemáticas, Universidade de Santiago de Compostela, Santiago de Compostela, 15782, Spain

    Juan J. Nieto

Authors
  1. Amartya Das
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Debgopal Sahoo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guruprasad Samanta
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Juan J. Nieto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Debgopal Sahoo.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest regarding this work.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Das, A., Sahoo, D., Samanta, G. et al. Deterministic and stochastic analysis of a two-prey–one-predator system with fear effect and switching behaviour in predation. Int. J. Dynam. Control 11, 1076–1101 (2023). https://doi.org/10.1007/s40435-022-01028-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-022-01028-x

Keywords

Search

Navigation