1 Introduction

Nowadays, The SARS-Cov-2 pandemic pose a great threat to human health, which has introduced an evident research boom into biophysical and mathematical modeling of infection expansions. In order to develop control strategies to prevent disease epidemics and reduce the number of infections, many scholars have used mathematical models of reaction-diffusion equations to study the infection mechanisms of infectious diseases, for example in [1,2,3,4,5,6]. Moreover, reaction -diffusion mechanisms have been successfully applied to many patterning phenomena in predator-prey system [7,8,9,10,11,12].

It should be noted that most of the above models have continuous terms. But in practice, when an infectious disease occurs in the host population, some treatment measures need to be considered, which usually was described by some discontinuous (or non-smooth) control functions when constructing the mathematical model. Moreover, the discontinuous control strategy has been also extensively studied in many other resource management areas in real life. For instance, discontinuous harvesting on fishery was investigated in [13]. Li et al. [14] studied the the dynamic behaviour of a computer worm virus system with discontinuous control

strategy. In [15], Guo et al. considered the impact of discontinuous treatments to SIR epidemic system. Zhang and Zhao considered a predator-prey model with discontinuous harvesting policy with spatial diffusion in [16]. However, there are few results in the public literature on the effects of discontinuous treatments in SIR epidemic diffusive system. Recently, in [17], Li et al. studied the global dynamics of a diffusive SIR epidemic system with linear incidence rate and discontinuous term. Other relate work can be found in [18,19,20].

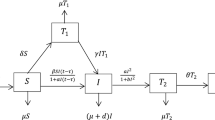
Inspired by [17] and the above discussions. In this article, we consider a diffusive SIR epidemic model with nonlinear saturated incidence rate and discontinuous treatments. First, we denote the densities of susceptible and infected individuals at position x and time t by S(x, t) and I(x, t), respectively. Besides, a saturated incidence rate function \(g(I)=\frac{\beta I}{1+mI}\) is considered, which was first proposed by Capasso and Serio in [21], subsequently, many scholars have done relevant research about this type of incidence rate (for example, [22,23,24]). Where \(m>0\) is the saturation coefficient, \(\beta >0\) is the rate of disease transmission. This incidence rate seems to be more realistic in some cases, as the number of effective contacts between infected and susceptible individuals may be saturated at high levels of infection due to congestion in infected individuals or protective measures in susceptible individuals. Therefore, we focus on the following epidemic reaction-diffusion model under Neumann boundary conditions

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial S}{\partial t}-d_{1}\triangle S=A-\frac{\beta SI}{1+mI}-\mu S,&{} x\in \Omega , t>0,\\ \displaystyle \frac{\partial I}{\partial t}-d_{2}\triangle I=\frac{\beta SI}{1+mI}-\mu _{1}I-\lambda h(I)I,&{} x\in \Omega , t>0,\\ \displaystyle \frac{\partial S(t,x)}{\partial n}=\frac{\partial I(t,x)}{\partial n}=0,&{} x\in \partial \Omega , t>0,\\ S(0,x)=S_{0}(x)\ge 0, I(0,x)=I_{0}(x)\ge 0, &{} x\in \Omega ,\\ \end{array} \right. \nonumber \\ \end{aligned}$$
(1.1)

where S(x, t), I(x, t) and m are described as before. \(\Omega \) is a bounded open set in \(R^{n}\), n is the outward unit normal vector of the boundary \(\partial \Omega \). The homogeneous Neumann boundary conditions indicate that the epidemic system is self-inclusion and zero population flux across the boundary. \(d_1 > 0\) and \(d_2 > 0\) are the diffusion rates of susceptible and infected individuals, respectively. And the positive number A is the recruitment rate of susceptible individuals. The positive coefficients \(\mu \) and \(\mu _{1}\) represents natural mortality and mortality caused by diseases, respectively. Function h(I) represents the treatment strategy which \(\lambda \) is positive coefficient. We give some properties of function h(I) as follows.

  1. (H1)

    h(I) is continuous except in a cluster of countable isolated points \({\rho _{k}}\), where \(h(\rho _{k}^+)\) and \(h(\rho _{k}^-)\) represents the right and left limits, respectively, with \(h(\rho _{k}^+)>h(\rho _{k}^-)\). Besides, h(I) has a finite discontinuous points in any compact interval \([0,+\infty )\).

  2. (H2)

    h(I) is monotonically non-decreasing in \([0,+\infty )\), \(\forall I \in [0, +\infty )\), \(0\le h(I)\le 1 \) and \(h(0) = h(0^{+}) = 0\).

Due to the function h(I) is not continuous, here, we applying differential inclusion theory instead of theories and methods in ordinary differential equations, So the system (1.1) can be written as the following differential inclusion

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial S}{\partial t}-d_{1}\triangle S=A-\frac{\beta SI}{1+mI}-\mu S,&{} x\in \Omega , t>0,\\ \displaystyle \frac{\partial I}{\partial t}-d_{2}\triangle I\in \frac{\beta SI}{1+mI}-\mu _{1}I-\lambda {\overline{co}}[h(I)]I,&{} x\in \Omega , t>0,\\ \displaystyle \frac{\partial S(t,x)}{\partial n}=\frac{\partial I(t,x)}{\partial n}=0,&{} x\in \partial \Omega , t>0,\\ S(0,x)=S_{0}(x)\ge 0, I(0,x)=I_{0}(x)\ge 0, &{} x\in \Omega ,\\ \end{array} \right. \nonumber \\ \end{aligned}$$
(1.2)

where \({\overline{co}}[h(I)]=[h(I^{-}), h(I^{+})]\), \(h(I^{-}), h(I^{+})\) represent the left and right limits of function h at I, respectively.

Remark 1.1

\({\overline{co}}[h(I)]\) is an interval with non-empty interior when h is discontinuous at I, while \({\overline{co}}[h(I)] = h(I)\) is a singleton if h is continuous at I.

When saturation coefficient \(m=0\), the nonlinear saturated incidence rate become the linear incidence rate, which is corresponding to the system in literature [17]. To the best of the authors’ knowledge, there are few analysis results about diffusive SIR epidemic model with saturated incidence rate and discontinuous term in the open literature. The aim of this paper is to investigate whether we can conclude some different dynamic behaviour of the system (1.1) owing to the saturated incidence rate, and whether saturation coefficient m will affects the global stability of the endemic equilibrium of system (1.1). The rest of this paper is arranged as follows. Firstly, we mainly investigate the existence and some properties of the solution of the diffusive epidemic system (1.1) in Sect. 2. Secondly, we discuss about the existence of the endemic equilibrium of the system in Sect. 3. Thirdly, by constructing different suitable Lyapunov functions, we prove the global asymptotic stability of the disease free equilibrium(DFE) and endemic equilibrium(EE) respectively in Sect. 4. Finally, we give a brief conclusion in Sect. 5.

2 The existence of solution

In this section, we are concerned with the existence and properties of the solution of the system (1.1). Firstly, we assume that the initial values S(x, 0), I(x, 0) of system (1.1) satisfy the following condition.

(H3) \(S(x,0), I(x,0)\in L^{\infty }\), \(S(x,0)>0\) and \(I(x,0)>0\) on \(\Omega \).

Lemma 2.1

Suppose that the assumptions (H1-H3) hold, then there exist two positive constants \(M_{1}\) and \(M_{2}\), which depend on \(A, \beta , m, \mu , \mu _{1},\lambda \) and initial values \(S_{0}, I_{0}\), such that every possible solution (S(x, t), I(x, t)) of system (1.1) satisfy

$$\begin{aligned} \begin{array}{lll} \displaystyle M_{1}\le S(x,t), I(x,t)\le M_{2}. \end{array} \end{aligned}$$
(2.1)

Proof

Firstly, to prove the boundedness of solutions \((S(x, t), I(x, t))\), we give the invariant rectangle \(\Sigma :=[{\mathcal {S}}_{1}, {\mathcal {S}}_{2}] \times [{\mathcal {I}}_{1}, {\mathcal {I}}_{2}]\), where

$$\begin{aligned} \begin{array}{lll} \displaystyle {\mathcal {S}}_{1}=\min \left\{ \frac{Am}{\beta +\mu m}, \frac{\mu _1}{\beta }, \min _{x\in \Omega }S_0(x) \right\} ;\\ {\mathcal {S}}_{2}=\max \left\{ \frac{A}{\mu }, \max _{x\in \Omega }S_0(x)\right\} ,\\ \displaystyle {\mathcal {I}}_{1}=\min \left\{ \frac{\beta {\mathcal {S}}_{1}-\mu _{1}}{m\mu _{1}}, \min _{x\in \Omega }I_0(x) \right\} ;\\ {\mathcal {I}}_{2}=\max \left\{ \frac{\beta {\mathcal {S}}_{2}}{m(\mu _{1}+\lambda )}, \max _{x\in \Omega }I_0(x) \right\} . \end{array} \end{aligned}$$
(2.2)

Obviously, \(S_0(x)\) and \(I_0(x)\) are closed for the rectangle \(\Sigma \). The vector field of the system (1.1) is given

$$\begin{aligned} \begin{array}{lll} \displaystyle \left( A-\frac{\beta SI}{1+mI}-\mu S, \frac{\beta SI}{1+mI}-\mu _{1}I-\lambda h(I)I \right) , \end{array} \end{aligned}$$
(2.3)

all points on the rectangle \(\Sigma \) point inside. Secondly, through the above analysis, we have the following conclusions:

  1. (i)

    On the left side of the first quadrant invariant rectangle with \(S={\mathcal {S}}_{1}\), \({\mathcal {I}}_{1}<I<{\mathcal {I}}_{2}\), by the definition of \({\mathcal {S}}_{1}\), it satisfies the following estimate:

    $$\begin{aligned}&\displaystyle A-\frac{\beta SI}{1+mI}-\mu S=A-\frac{\beta {\mathcal {S}}_{1}I}{1+mI}-\mu {\mathcal {S}}_{1}\nonumber \\&\quad >A-\frac{\beta {\mathcal {S}}_{1}}{m}-\mu {\mathcal {S}}_{1}\ge 0. \end{aligned}$$
    (2.4)
  2. (ii)

    On the right side of the the first quadrant invariant rectangle with \(S={\mathcal {S}}_{2}\), \({\mathcal {I}}_{1}<I<{\mathcal {I}}_{2}\), by the definition of \({\mathcal {S}}_{2}\), it satisfies the following estimate:

    $$\begin{aligned}&\displaystyle A-\frac{\beta SI}{1+mI}-\mu S=A-\frac{\beta {\mathcal {S}}_{2}I}{1+mI}-\mu {\mathcal {S}}_{2}\nonumber \\&\quad <A-\mu {\mathcal {S}}_{2}\le 0. \end{aligned}$$
    (2.5)
  3. (iii)

    On the bottom side of the the first quadrant invariant rectangle with \(I={\mathcal {I}}_{1}\), \({\mathcal {S}}_{1}<S<{\mathcal {S}}_{2}\), by the definition of \({\mathcal {I}}_{1}\), it satisfies the following estimate:

    $$\begin{aligned}&\displaystyle \frac{\beta SI}{1+mI}-\mu _{1}I-\lambda {\overline{co}}[h(I)]I=\frac{\beta S{\mathcal {I}}_{1}}{1+m{\mathcal {I}}_{1}}-\mu _{1}{\mathcal {I}}_{1}\nonumber \\&\quad >\frac{\beta {\mathcal {S}}_{1}{\mathcal {I}}_{1}}{1+m{\mathcal {I}}_{1}}-\mu _{1}{\mathcal {I}}_{1}\ge 0. \end{aligned}$$
    (2.6)
  4. (iv)

    On the left side of the the first quadrant invariant rectangle with \(I={\mathcal {I}}_{2}\), \({\mathcal {S}}_{1}<S<{\mathcal {S}}_{2}\), by the definition of \({\mathcal {I}}_{2}\), it satisfies the following estimate:

    $$\begin{aligned}&\displaystyle \frac{\beta SI}{1+mI}-\mu _{1}I-\lambda {\overline{co}}[h(I)]I=\frac{\beta S{\mathcal {I}}_{2}}{1+m{\mathcal {I}}_{2}}-\mu _{1}{\mathcal {I}}_{2} -\lambda {\mathcal {I}}_{2}\nonumber \\&\quad <\frac{\beta {\mathcal {S}}_{2}}{m}-\mu _{1}{\mathcal {I}}_{2}-\lambda {\mathcal {I}}_{2}\le 0. \end{aligned}$$
    (2.7)

Finally, by virtue of the definition on [20], in view of the above discussions, we can conclude that \(\Sigma :=[{\mathcal {S}}_{1}, {\mathcal {S}}_{2}] \times [{\mathcal {I}}_{1}, {\mathcal {I}}_{2}]\) is the invariant rectangle of the vector field (2.3). Thus, we can choose \(M_1 = \min \{{\mathcal {S}}_1, {\mathcal {I}}_1\}\) and \(M_2 = \max \{{\mathcal {S}}_{2}, {\mathcal {I}}_{2}\}\), which completes the proof. \(\square \)

Now, we give the following definition. Firstly, we denote

$$\begin{aligned}&\displaystyle \varphi _{1}(S,I)=A-\frac{\beta SI}{1+mI}-\mu S,\nonumber \\&\varphi _{2}(S,I)=\frac{\beta SI}{1+mI}-\mu _{1}I-\lambda {\overline{co}}[h(I)]I. \end{aligned}$$
(2.8)

Definition 2.1

(S, I) is the strong solution [or weak solution] of the differential inclusion (1.2), where S, \(I \in C([0, T]; H)\), and there exists \(\psi _{2}(S, I) \in L^1([0, T]; H), \psi _{2}(S, I) \in \varphi _{2}(S, I)\) almost everywhere in (0, T), and such that solution is a strong solution [or weak solution] over (0, T) to the system, which is given by

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{\partial S}{\partial t}-d_{1}\triangle S=\varphi _1(S,I),\\ \displaystyle \frac{\partial I}{\partial t}-d_{2}\triangle I=\psi _2(S,I). \end{array} \right. \end{aligned}$$
(2.9)

Obviously, we can obtain that the map \(\varphi _{1}(S, I)\) is bounded. By assumptions (H1), (H2) and (H3), with combining the above discussions, it is easy to know \(\varphi _{2}(S, I)\) is an upper semi-continuous bounded set-valued mapping with non-empty compact convex values.

Next, we denote

$$\begin{aligned} \begin{array}{lll} \displaystyle \Psi U=(d_{1}\triangle S,d_{2}\triangle I),U=(S,I)\in D(\Psi ),\\ \displaystyle D(\Psi )=\Bigg \{U=(S,I)\in H^2(\Omega )^2,\frac{\partial S(x,t)}{\partial n}=0,\\ \qquad \qquad \frac{\partial I(x,t)}{\partial n}=0\Bigg \}. \end{array} \end{aligned}$$

Let X be a real Banach space, \(U=(S,I)\) be the solution of system (1.1) with initial value \(U(0)=(S_0,I_0)>0\), and we defined \(\Psi :D(\Psi )\ni X\rightarrow X\) is the infinitesimal generator of a \(C_0\)-semigroup of linear contractions I(t). Furthermore, we defined \(\Psi :[0,T]\times X \rightarrow X\) be a function which measurable in t and Lipschitz continuous in X, uniformly with respect to \(t \in [0,T]\). Then we have the following conclusion:

  1. (i)

    If \(U_{0}\in X\), there exists a unique weak solution of system (2.9).

  2. (ii)

    If X is a Hilbert space, \(\Psi \) is a self-adjoint and dissipative on X with \(U(0)\in D(\Psi )\), and we can obtained

    $$\begin{aligned} \begin{array}{lll} \displaystyle U\in W^{1,2}([0,T];X)\cap L^2([0,T];D(\Psi )), \end{array} \end{aligned}$$
    (2.10)

    which shows that the weak solution of system (2.9) is actually a strong solution.

Theorem 2.1

Suppose that assumptions (H1),(H2) and (H3) hold, then system (1.1) has at least one strong solution.

Proof

By the Theorem 2.4 in [28], there exists a strong solution (S, I) of system(1.1) with \(t\in [0,T_0]\), where \(0<T_0<+\infty \). Thus, for system (1.1), there exists a maximum existence interval \([0,T_{max}]\). According to [29], if the condition \(T_{max} <+\infty \), then

$$\begin{aligned}&\max (\parallel S(x,t)\parallel _{L^{\infty }(\Omega )}+\parallel I(x,t)\parallel _{L^{\infty }(\Omega )})\nonumber \\&\quad =\infty \,\,in\,\,[L^{2}(\Omega )]^2,\,\,when\,\, t\rightarrow T_{max}. \end{aligned}$$
(2.11)

But by Lemma 2.1, where the invariant \(\Sigma \) is an \(L^{\infty }\) a priori bound for the solution (S, I) of the system (1.1), it is a contradiction which implies \(T_{max} =\infty \), i.e., so for all \((x, t) \in \Omega \times [0, +\infty )\), the solution of system (1.1) exists and bounded. Which completes the proof. \(\square \)

3 The existence of the equilibria

In this section, we are concerned about the existence of disease free equilibrium(DFE) and endemic equilibrium(EE) of the system (1.1). We using the analysis method in [17]. Firstly, when \(h(I)=0\), the DFE \(E_0(S_0^*,I_0^*)=(\frac{A}{\mu },0)\) always exists. Additionally, the EE \(E^*=(S^*,I^*)\) satisfies

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle 0=A-\frac{\beta SI}{1+mI}-\mu S,\\ \displaystyle 0\in \frac{\beta SI}{1+mI}-\mu _{1}I-\lambda {\overline{co}}[h(I)]I. \end{array} \right. \end{aligned}$$
(3.1)

Through a simple transformation, we define g(I) as follows

$$\begin{aligned} \begin{array}{lll} \displaystyle g(I):=\frac{1}{\lambda } \left[ \frac{A \beta }{(\beta +\mu m)I+\mu }-\mu _1\right] =[h(I^{-}), h(I^{+})].\\ \end{array}\nonumber \\ \end{aligned}$$
(3.2)

Lemma 3.1

The system (3.1) has a unique positive solution \({\bar{I}}\) satisfying \({\bar{I}}< \frac{A\beta -\mu \mu _1}{\mu _1(\beta +\mu m)}\) if \(A\beta >\mu \mu _1\) holds.

Proof

We are divided into the following three steps to prove.

  1. Step 1.

    We prove that system (3.1) exists a positive solution \({\bar{I}}\), when \(A \beta > \mu \mu _{1}\) holds, it means \(g(0)>0\), and we know the function g(I) is the monotonically decreasing of I and h(I) is non-decreasing of I. Obviously, \(g(I)\le 0\) if \(I\ge \frac{A\beta -\mu \mu _{1}}{\mu _{1}(\beta +\mu m)}\). Therefore, the set \(\left\{ I:g(I)\ge h(I^+), I>0 \right\} \) is bounded, then denote \({\bar{I}}=\sup \left\{ I:g(I)\ge h(I^+), I>0\right\} \). So, we can obtained that \(g({\bar{I}})\ge h({\bar{I}}^-)\) and \(0\le {\bar{I}}\le \frac{A\beta -\mu \mu _1}{\mu _{1}(\beta +\mu m)}\).

  2. Step 2.

    We prove \(g({\bar{I}})\in [h({\bar{I}}^-),h({\bar{I}}^+)]\). If not, \(g({\bar{I}})>h({\bar{I}}^+)=\lim _{I\rightarrow {\bar{I}}^+}h(I)\). Therefore, we can find a small constant number \(\epsilon \) such that \(g({\bar{I}}+\epsilon )>h({\bar{I}}+\epsilon )=h(({\bar{I}}+\epsilon )^+)\), which does not conform to the definition of \({\bar{I}}\). So, \(g({\bar{I}})\in [h({\bar{I}}^-),h({\bar{I}}^+)]\).

  3. Step 3.

    We prove that \({\bar{I}}\) is the unique positive solution of system (3.1). Let \(I_1={\bar{I}}\) is a solution of (3.1), and \(I_2\ne I_1\) is another positive solution of (3.1), then, there exists \(\gamma _1\in {\overline{co}}[h(I_1)]\) and \(\gamma _2\in {\overline{co}}[h(I_2)]\), so we have

    $$\begin{aligned}&\displaystyle \frac{A\beta }{(\beta +\mu m)I_1+\mu }-\mu _1=\lambda \gamma _1,\nonumber \\&\frac{A\beta }{(\beta +\mu m)I_2+\mu }-\mu _1=\lambda \gamma _2. \end{aligned}$$
    (3.3)

    From the monotonicity of h(I), it implies that \(H=\frac{\gamma _1-\gamma _2}{I_1-I_2}\ge 0\). However, after subtraction of the two equations of (3.3), we obtain

    $$\begin{aligned}&\displaystyle \gamma _1-\gamma _2=-\frac{A\beta (\beta +\mu m)}{\lambda [(\beta +\mu m)I_1+\mu ][(\beta +\mu m)I_2+\mu ]}\nonumber \\&\quad (I_1-I_2), \end{aligned}$$
    (3.4)

which is a contradiction. The proof of the lemma is completed. \(\square \)

A direct result of Lemma 3.1 is the following theorem of endemic equilibrium.

Theorem 3.1

Assume assumptions (H1-H3) hold and \(A \beta >\mu \mu _1+\mu \lambda \), then the system (1.1) has a unique endemic equilibrium \(E^*=(S^*,I^*)\), where \(I^*\)=\(\frac{A\beta -\mu (\mu _1+\lambda \gamma ^*)}{(\mu _1+\lambda \gamma ^*)(\beta +\mu m)}\) and \(S^*\)= \(\frac{A(1+mI^*)}{\beta I^*+\mu (1+mI^*)}\) with \(\gamma ^*\in {\overline{co}}[h(I)]\).

Remark 3.1

By differentiating the equilibrium density of infected individuals with respect to the saturation coefficient m, we get

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{{{\mathrm{d}}}I^*}{{\mathrm{d}}m}=-\frac{\mu [A\beta -\mu (\mu _1+\lambda \gamma ^*)]}{(\mu _1+\lambda \gamma ^*)(\beta +\mu m)^2}, \end{array} \end{aligned}$$
(3.5)

when \(A \beta >\mu \mu _1+\mu \lambda \) holds, \(I^*\) is decreasing with the saturation coefficient m, it means when \(m \rightarrow +\infty \), the infective individuals may cannot persist.

4 Global stability of DFE and EE

In this section, we discussed the global stability of disease free equilibrium and endemic equilibrium in the invariant rectangle \(\Sigma \), respectively. Firstly, the global stability of DFE \(E_0\) is discussed as follows.

Theorem 4.1

Suppose that \(A\beta \le \mu \mu _1\), then DFE \(E_0=(S_0^*,I_0^*)\) of system (1.1) is globally asymptotically stable.

Proof

We define

$$\begin{aligned} \begin{array}{lll} \displaystyle V_1(t)= \int _{\Omega }\left[ S-S_0^*-S_0^* \ln \frac{S}{S_0^*}+I\right] {\mathrm{d}}x. \end{array} \end{aligned}$$
(4.1)

Obviously, \(V_1(t)\) is a smooth function. Now, denote

$$\begin{aligned} G(S,I)=\begin{pmatrix} d_{1}\triangle S+A-\frac{\beta SI}{1+mI}-\mu S \\ d_{2}\triangle I+\frac{\beta SI}{1+mI}-\mu _{1}I-\lambda {\overline{co}}[h(I)]I \end{pmatrix}. \end{aligned}$$
(4.2)

From (H1) and (H2), it is easy to know that the map G is an upper semi-continuous set-valued map with non-empty compact convex value. For any \((w_1,w_2)\in G(S,I)\), there exist a function \(\gamma _{1}(t)\in {\overline{co}}[h(I)]\), we have

$$\begin{aligned} w=\begin{pmatrix} w_1\\ w_2 \end{pmatrix} =\begin{pmatrix} d_{1}\triangle S+A-\frac{\beta SI}{1+mI}-\mu S \\ d_{2}\triangle I+\frac{\beta SI}{1+mI}-\mu _{1}I-\lambda \gamma _1 I \end{pmatrix}. \end{aligned}$$
(4.3)

So from the above discussions, by calculating \(\nabla V(S,I)\cdot w\), we can obtain that

$$\begin{aligned} \begin{aligned} \displaystyle \frac{{\mathrm{d}}}{{\mathrm{d}}t}V_1(t)&=\displaystyle \int _{\Omega }\left[ \frac{{\mathrm{d}}}{{\mathrm{d}}t}\left( S-S_0^*-S_0^* \ln \frac{S}{S_0^*}+I\right) \right] {\mathrm{d}} x,\\ \displaystyle&=\displaystyle \int _{\Omega }\left[ \left( 1-\frac{A}{S\mu }\right) \left( d_{1}\triangle S+A-\frac{\beta SI}{1+mI}-\mu S\right) \right. \\&\quad \left. +\left( d_{2}\triangle I+\frac{\beta SI}{1+mI}-\mu _{1}I-\lambda \gamma _1 I\right) \right] {\mathrm{d}} x,\\ \displaystyle&=\displaystyle \int _{\Omega }\left[ \left( 1-\frac{A}{S\mu }\right) d_{1}\triangle S+d_{2}\triangle I\right] {\mathrm{d}} x\\ \displaystyle&+\displaystyle \int _{\Omega }\left[ \left( 1-\frac{A}{S\mu }\right) \left( A-\frac{\beta SI}{1+mI}-\mu S\right) \right. \\&\quad \left. +\left( \frac{\beta SI}{1+mI}-\mu _{1}I-\lambda \gamma _1 I\right) \right] {\mathrm{d}} x.\\ \end{aligned}\nonumber \\ \end{aligned}$$
(4.4)

Owing to the homogeneous Neumann boundary condition, we obtain

$$\begin{aligned} \begin{array}{lll} \begin{aligned} \displaystyle F_{1}&{}=\displaystyle \int _{\Omega }\left[ \left( 1-\frac{A}{S\mu }\right) d_{1}\triangle S+d_{2}\triangle I\right] {\mathrm{d}} x,\\ \displaystyle &{}=\displaystyle -\int _{\Omega }\frac{A}{\mu S^2}d_{1}|\nabla S|^{2} {\mathrm{d}} x \le 0. \end{aligned} \end{array} \end{aligned}$$
(4.5)

Furthermore, when \(A\beta \le \mu \mu _1\), we have

$$\begin{aligned} \begin{aligned} \displaystyle F_{2}&= \displaystyle \int _{\Omega }\left[ \left( 1-\frac{A}{S\mu }\right) \left( A-\frac{\beta SI}{1+mI}-\mu S\right) \right. \\&\quad \left. +\left( \frac{\beta SI}{1+mI}-\mu _{1}I-\lambda \gamma _1 I\right) \right] {\mathrm{d}} x ,\\ \displaystyle&= \displaystyle \int _{\Omega }\left[ \left( 2A-\mu S-\frac{A^2}{\mu S}\right) +\frac{A\beta I}{\mu (1+mI)}\right. \\&\quad \left. +\left( -\mu _{1}I-\lambda \gamma _1 I\right) \right] {\mathrm{d}} x,\\ \displaystyle&\le \displaystyle \int _{\Omega }\left[ \left( 2A-\mu S-\frac{A^2}{\mu S}\right) +(\frac{A\beta }{\mu }-\mu _{1})I\right] {\mathrm{d}} x,\\ \displaystyle&\le 0. \end{aligned} \end{aligned}$$
(4.6)

Therefore, we can obtain that

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{{\mathrm{d}}}{{\mathrm{d}}t}V_1(t)=F_{1}+F_{2}\le 0. \end{array} \end{aligned}$$
(4.7)

Thus, the disease free equilibrium \(E_0\) is stable, and when \((S,I)=(\frac{A}{\mu },0)\), \(\frac{{\mathrm{d}}}{{\mathrm{d}}t}V_1(t)=0\). So the singleton \(E_0\) is the maximum compact invariant set in \(\Gamma =\{(S,I)|\frac{{\mathrm{d}}}{{\mathrm{d}}t}V_1(t)|=0\}\). By the Lasalle invariance principle [31], \(E_0\) is globally asymptotically stable for system (1.1). The proof is completed. \(\square \)

Theorem 4.2

Suppose that \(4A(1+mI^*)> \beta m M_2I^{*^{2}}\) and \(A \beta >\mu \mu _1+\mu \lambda \) hold, then EE \(E^*=(S^*,I^*)\) of system (1.1) is globally asymptotically stable.

Proof

We define

$$\begin{aligned} \begin{array}{lll} \displaystyle V_2(t)=\int _{\Omega }\left[ S-S^*-S^* \ln \frac{S}{S^*}+I-I^*-I^* \ln \frac{I}{I^*}\right] {\mathrm{d}} x. \end{array}\nonumber \\ \end{aligned}$$
(4.8)

\(V_2(t)\) is a smooth function, based on assumptions (H1) and (H2), there exist a function \(\gamma _{2}\in {\overline{co}}[h(I)]\), we have

$$\begin{aligned} w=\begin{pmatrix} w_1\\ w_2 \end{pmatrix} =\begin{pmatrix} d_{1}\triangle S+A-\frac{\beta SI}{1+mI}-\mu S \\ d_{2}\triangle I+\frac{\beta SI}{1+mI}-\mu _{1}I-\lambda \gamma _{2} I \end{pmatrix}. \end{aligned}$$
(4.9)

By calculating \(\nabla V(S,I)\cdot w\), we can obtain

$$\begin{aligned} \begin{array}{lll} \begin{aligned} \displaystyle \frac{{\mathrm{d}}}{{\mathrm{d}}t}V_2(t)&{}=\displaystyle \int _{\Omega }\left[ \left( \frac{S-S^*}{S}\right) \frac{{\mathrm{d}}S}{{\mathrm{d}}t} +\left( \frac{I-I^*}{I}\right) \frac{{\mathrm{d}}I}{{\mathrm{d}}t}\right] {\mathrm{d}} x,\\ \displaystyle &{}=\displaystyle \int _{\Omega }\left( \frac{S-S^*}{S}d_{1}\triangle S+\frac{I-I^*}{I}d_{2}\triangle I\right) {\mathrm{d}} x\\ \displaystyle &{}+\displaystyle \int _{\Omega }\left[ \left( \frac{S-S^*}{S}\right) \left( A-\frac{\beta SI}{1+mI}-\mu S\right) \right. \\ &{}\quad \left. +\left( \frac{I-I^*}{I}\right) \left( \frac{\beta SI}{1+mI}-\mu _{1}I-\lambda \gamma _{2} I\right) \right] {\mathrm{d}} x.\\ \end{aligned} \end{array} \end{aligned}$$
(4.10)
Fig. 1
figure 1

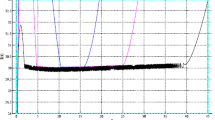
Dynamic behavior of system (1.1) for \(S(0,x)=I(0,x)=1, d_1=d_2=1, A=2, \beta =0.1, m=0.5, \mu =0.5, \mu _1=0.6, \lambda =0.2\)

Full size image
Fig. 2
figure 2

Dynamic behavior of system (1.1) for \(S(0,x)=I(0,x)=1, d_1=d_2=1, A=3, \beta =0.5, m=0.5, \mu =0.5, \mu _1=0.6, \lambda =0.2\)

Full size image

Owing to the homogeneous Neumann boundary condition, we can get

$$\begin{aligned}&\begin{array}{lll} \begin{aligned} \displaystyle F_{3}&{}=\displaystyle \int _{\Omega }\left( \frac{S-S^*}{S}d_{1}\triangle S+\frac{I-I^*}{I}d_{2}\triangle I\right) {\mathrm{d}} x,\\ \displaystyle &{}= -\displaystyle \int _{\Omega }\left[ \frac{S^*}{S^2}d_{1}|\nabla S|^{2} +\frac{I^*}{I^2}d_{2}|\nabla I|^{2}\right] {\mathrm{d}} x \le 0 . \end{aligned} \end{array} \end{aligned}$$
(4.11)
$$\begin{aligned}&\begin{aligned} \displaystyle F_{4}&=\displaystyle \int _{\Omega }\left[ \left( \frac{S-S^*}{S}\right) \left( A-\frac{\beta SI}{1+mI}-\mu S\right) \right. \\&\quad \left. +\left( \frac{I-I^*}{I}\right) \left( \frac{\beta SI}{1+mI}-\mu _{1}I-\lambda \gamma _{2} I\right) \right] {\mathrm{d}} x,\\ \displaystyle&=\displaystyle \int _{\Omega }\left[ \left( S-S^*\right) \left( \frac{A}{S}-\frac{A}{S^*} +\frac{\beta I^*}{1+mI^*}-\frac{\beta I}{1+mI}\right) \right. \\&\quad \left. +\left( I-I^*\right) \left( \frac{\beta S}{1+mI}-\frac{\beta S^*}{1+mI^*}\right) \right. \\&\quad \left. -\lambda \left( I-I^*\right) \left( \gamma _{2}-\gamma _{*}\right) \right] {\mathrm{d}} x,\\ \displaystyle&=\displaystyle \int _{\Omega }\left[ -\frac{A}{SS^*}\left( S-S^*\right) ^2+\frac{\beta mI^*\left( I-I^*\right) \left( S-S^*\right) }{(1+mI^*)(1+mI)}\right. \\&\quad \left. -\frac{\beta mS^*(I-I^*)^2}{(1+mI^*)(1+mI)}-\lambda (I-I^*)(\gamma _{2}-\gamma _{*})\right] {\mathrm{d}} x. \end{aligned} \end{aligned}$$
(4.12)

By the monotonicity of h(I), we have \(\lambda (I-I^*)(\gamma _{2}-\gamma _{*})\ge 0\). Therefore, if

$$\begin{aligned} \begin{array}{lll} \displaystyle &{}\displaystyle \left( \frac{\beta mI^*(I-I^*)}{(1+mI^*)(1+mI)}\right) ^2-\displaystyle \frac{4A\beta m(I-I^*)^2}{S(1{+}mI^*)(1{+}mI)}\\ \displaystyle &{}{=}\displaystyle \frac{\beta m(I{-}I^*)^2}{(1{+}mI^*)(1+mI)}\left( \frac{\beta mI^{*^{2}}}{(1{+}mI^*)(1+mI)}{-}\displaystyle \frac{4A}{S}\right) <0, \end{array}\nonumber \\ \end{aligned}$$
(4.13)

holds, then \(F_{4}\le 0\). By a simple calculation, if \(4A(1+mI^*)> \beta m M_2I^{*^{2}}\), then we can get

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{\beta mI^{*^{2}}}{(1+mI^*)(1+mI)}-\frac{4A}{S}&{}<\displaystyle \frac{\beta mI^{*^{2}}}{1+mI^*}-\frac{4A}{S},\\ \displaystyle &{}<\displaystyle \frac{\beta mI^{*^{2}}}{1+mI^*}-\frac{4A}{M_2}<0. \end{array} \end{aligned}$$
(4.14)

As a result, combined with (4.11), we have

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{{\mathrm{d}}}{{\mathrm{d}}t}V_2(t)=F_{3}+F_{4}\le 0. \end{array} \end{aligned}$$
(4.15)

Thus, the endemic equilibrium \(E^*\) is stable, and when \((S,I)=(S^*,I^*)\), \(\frac{{\mathrm{d}}}{{\mathrm{d}}t}V_2(t)=0\). So the singleton \(E^*\) is the maximum compact invariant set in \(\Gamma =\{(S,I)|\frac{{\mathrm{d}}}{{\mathrm{d}}t}V_2(t)|=0\}\). By the Lasalle invariance principle [31], \(E^*\) is globally asymptotically stable for system (1.1). The proof is completed. \(\square \)

5 Numerical simulation

In this section, we show numerical simulations regarding our model to illustrate and support the theoretical results of the previous sections. We illustrate the DFE is globally asymptotically stable if the basic regeneration number \(R_0\) is less than unity in Fig.1 corresponding to \(S(0,x)=I(0,x)=1, d_1=d_2=1, A=2, \beta =0.1, m=0.5, \mu =0.5, \mu _1=0.6, \lambda =0.2\). Then we obtain \(R_0=0.667<1\), which implies that DFE \(E_0=(4,0)\) is globally asymptotically stable by Theorem 4.1 where disease will extinct. And for Fig.2, we show that the EE is globally asymptotically stable, for \( h(I)=\left\{ \begin{array}{lll} 0,&{}I(t)<1\\ 0.8,&{}I(t)\ge 1 \end{array} \right. \), let \(S(0,x)=I(0,x)=1, d_1=d_2=1, A=3, \beta =0.5, m=0.5, \mu =0.5, \mu _1=0.6, \lambda =0.2\). Then we obtain \(A\beta >\mu \mu _1+\mu \lambda \), which implies the EE is globally asymptotically stable by Theorem 4.2 where disease spread in the human world.

6 Conclusion

In this paper, we investigate the dynamic of a diffusive SIR epidemic model under discontinuous treatments. Due to the discontinuous term, the existence of strong solution or weak solution of system(1.1) is proved under the framework of differential inclusion. Based on the differential inclusions theory, we analysis the existence of endemic equilibrium of the system (1.1). Moreover, by constructing different suitable Lyapunov functions, we investigate the global asymptotic stability of the disease free equilibrium(DFE) and the endemic equilibrium(EE), respectively.

Compared to literature [17], a different incidence rate \(g(I)=\frac{\beta I}{1+mI}\) is considered in the system (1.1). When saturated incidence rate \(m=0\), the nonlinear saturated incidence rate become the linear incidence rate, which is corresponding to the system in [17]. When saturated incidence rate \(m\rightarrow +\infty \), we conclude that the infective individuals cannot persist in Remark 3.1. This result seems to be consistent with realistic intuition : the more behavioral changes of susceptible individuals or the inhibition of crowding effect of infected individuals, the better disease control. When saturated incidence rate \(0<m<+\infty \), from Theorem 4.2, it is shown that saturated incidence rate m may affect the global stability of the endemic equilibrium. Furthermore, if linear incidence rate is considered and the discontinuous treatments term does not exist in the system(1.1), that is \(m=0\) and \(\lambda =0\), then from Theorem 4.1 and Theorem 4.2 we can easily define the basic reproduction number \(R_0=\frac{A\beta }{\mu \mu _1}\). When \(R_0<1\), the DFE is globally asymptotically stable, and when \(R_0>1\), the EE is globally asymptotically stable. However, in the system (1.1), due to nonlinear incidence rate and the discontinuous term, it follows from Fig.1, we can obtain that when \(R_0<1\), the DFE is also globally asymptotically stable, and when \(R_0>1+\frac{\lambda }{\mu _1}\), it follows from Fig.2, the EE is also globally asymptotically stable. But, when \(1< R_0<1+\frac{\lambda }{\mu _1}\), whether the endemic equilibrium is globally asymptotically stable is still unknown, which will be considered in our future work.