1 Introduction

Increased fatigue strength, fracture strength, corrosion resistance, and surface integrity guarantee the reliability of products made of Ti–6Al–4V titanium alloy during their life cycle [1]. Therefore, it is crucial to understand the effect of milling process conditions on the residual stresses (RS) state of the machined surface [2]. The influence of RS on product quality can be beneficial or detrimental, depending on their magnitude, pattern, and distribution. Sasahara [3] and Guo et al. [4] reported that compressive RS increases fatigue strength and corrosion resistance, while tensile RS decreases these properties.

A previous investigation showed the defect of smeared/adhered material on the machined surface in the finishing process (meso-machining) with a ball-end tool of components with complex geometry on the Ti–6Al–4V titanium alloy. The defect occurs when the position of the raw material concerning the direction of the tool feed and the value of the lead and tilt angles generates an up-milling machining strategy. The up-milling machining together with the inherent mechanical properties of the titanium alloy, specifically the mechanical resistance, low thermal conductivity and the modulus of elasticity [5], promote the defect of adhered material, an expression of the BUE BUL phenomenon [6]. Medical or aerospace industries do not accept components with this kind of defect. Also, the milling experiments using the down-milling strategy in the meso-machining on the Ti–6Al–4V alloy showed compressive residual stresses. An interplanar space \(d_0 = 1.71705\) Å perpendicular to the surface was found in a surface free of residual stress taken as a reference in the family of crystallographic planes \(\{ 1012\}\) of the alpha phase of the alloy, while in the meso-machined surface, the X-ray diffraction (XRD) essay showed an interplanar space \(d = 1.71952\) Å. The calculated strain was \(\varepsilon = 0.0014\,{\text{mm}}/{\text{mm}}\), and its increase corroborated the presence of compressive residual stresses on the machined surface accordingly with Fitzpatrick et al. [7].

On the other hand, Malekian et al. [8] state that when the tool cutting edge radius is comparable to the thickness of the conventional chip, machining models are not applicable. De Oliveira et al. [9] argue that when the ratio between chip thickness and cutting edge radius decreases, the processed material is subjected to elastoplastic deformation (ploughing) and not to a chip formation process, increasing the specific cutting force. In their experiments, they showed that in meso- and macro-machining, the specific cutting force depends only on the feed per tooth, while in micro-machining, it depends on both the feed per tooth and the depth of cut. Attanasio et al. [10] performed groove milling experiments with planar micro-end mills using depths of cut ap = 10 μm on the Ti–6Al–4V alloy. They found specific cutting force values higher than those in meso- and macro-machining operations.

Considering that the specific cutting force increases in the milling processes on a micrometric scale in the Ti–6Al–4V alloy, this research aims to establish if the multi-axis micro-machining process with a ball-end mill generates higher residual stresses on the surface than those on the meso-machining process.

2 Materials and methods

2.1 Chip formation process in ball-end milling

In the five-axis finishing process, with a ball-end tool, the geometry of the undeformed chip is in the shape of a curved wedge bounded by two spherical surfaces, as shown in Fig. 1. Its thickness varies from zero to a maximum determined by the feed per tooth \(f_z\) (up-milling). Depending on the directions of feed (F) and cross-feed (CF) vectors, the thickness could vary from a maximum (\(f_z\)) to zero (down-milling). The chip formation process could be represented by rotating the cutting edge around the tool axis and translating the tool in the F direction (Fig. 1). It depends on the helix angle of the cutting edge, the direction of rotation of the tool, and the lead \((\beta )\) and tilt \((\varphi )\) angles of the tool axis.

Fig. 1
figure 1

Lead and tilt angles, undeformed chip and chip formation process

Full size image

Eight positions of the cutting tool concerning the normal vector to the surface nP of the raw material are possible, as shown in Fig. 2. Tilting the tool axis in the F direction considers the \(\beta\) angle as positive and negative in the opposite case. Tilting the tool in the CF direction considers the \(\varphi\) angle positive [11]. The positive direction of the CF is towards the side of the uncut raw material. Additionally, the replication of these four positions depends on the location of the uncut raw material concerning the F direction, whether it is to the right or left of the tool [12]. A five-axis machining centre is necessary to obtain these eight positions.

Fig. 2
figure 2

Kinematics of the position of the cutting tool in the five-axis milling process [11]

Full size image

2.2 Representation of five-axis milling on a three-axis vertical machining centre

Setting up a flat surface on the X–Y table of a three-axis (3DOF) vertical machining centre (VMC) aligns the tool axis with the Z-axis of the machine, and this configuration would not allow to obtain the lead and tilt angles. Therefore, a machine with at least five-axis (5 DOF) is required. However, a technological and economically affordable alternative to reproduce any of the positions of 5 DOF machining, in a VMC with 3 DOF, consists in rotating the flat surface around the X-axis at an \(\omega\) angle and rotating the F vector at an \(\alpha\) angle, as shown in Fig. 3. The \(\omega\) and \(\alpha\) angles can be calculated as a function of \(\beta\) and \(\varphi\) angles using (1). The tool offset \(ap_z\) in the Z-axis direction is determined as a function of the \(\omega\) angle to remove a material layer of \(ap\) thickness. Figure 4 shows the kinematics of the eight possible combinations of lead and tilt angles in the process of five-axis milling, with a ball-end tool, of an inclined flat surface on a 3DOF machine. It also shows the starting point of the milling process and the F and CF vectors to obtain the desired values of the lead and tilt angles.

$$\omega = \cos^{ - 1} \left( {\frac{1}{{\sqrt {1 + (\tan \beta )^2 + (\tan \varphi )^2 } }}} \right)\,{\text{and}}\,\alpha = \tan^{ - 1} \left( {\frac{\tan \beta }{{\tan \varphi }}} \right)$$
(1)
Fig. 3
figure 3

Example of a five-axis milling process kinematics in a 3 DOF VMC

Full size image
Fig. 4
figure 4

Starting point, F and, CF vectors to reproduce the kinematics of the five-axis milling process in 3 DOF VMC. Strategies used in bold

Full size image

2.3 Experimental setup

When the axis of a ball-end mill aligns with the normal vector to the surface, it results in a null cutting speed at the central point of the tool, inhibiting the chip formation process and promoting elastic and plastic deformation. Tool tilting becomes essential to avoid this scenario. Employing CAD software, the lead and tilt angles were modified, verifying the orientation of the cutting edge relative to the undeformed chip. Figure 5 illustrates the kinematics of the machining strategies selected for the experimental tests. In (a), a down-milling strategy, with inclination angles tilt = 30° and lead = − 8°, positions the material to be removed to the right of F direction, resulting in the generation of the chip from the maximum to the minimum thickness. In (b), an up-milling strategy, with inclination angles tilt = 30° and lead = 8°, situates the material to be removed to the left of F direction, leading to the generation of the chip from the minimum to the maximum thickness (Fig. 1).

Fig. 5
figure 5

Kinematics of chip formation process. Down-milling on the left. Up-milling on the right

Full size image

The angles obtained for the down-milling strategy using (1) were \(\omega\) = 30.72° and \(\alpha\) = − 13.62°. For the up-milling strategy \(\omega\) = 30.72° and \(\alpha\) = 13.62°. For the experiment, the \(\omega\) angle was approximated to 30° and the \(\alpha\) angle to 14°. In both cases, the machining process was started from the lower right corner of the sample, reversing the F direction, following Fig. 4. A 500-\({\mu m}\) diameter cutting tool from ISCAR®, featuring a Physical Vapour Deposition (PVD) coating of Al–Ti–N, and an 8-mm-diameter tool from KENNAMETAL®, coated with a PVD multilayer consisting of Ti–N/Ti–Al–N, were employed in both scenarios, operating under dry conditions. PVD-coated carbide cutting tools stand as the foremost preference for the machining of titanium and titanium alloys, primarily due to their superior capacity to mitigate the detrimental effects of heat generation and wear during the machining process at medium cutting speeds [13].

Once the cutting strategies were selected, the value of the cutting parameters was determined (Table 1). To generate an equivalence of conditions between the processes of micro- and meso-machining, cross-feed, depth of cut, and feed per tooth were taken as a percentage of the tool diameter. The tool rotation speed was estimated considering a cutting speed of \(60\,{\text{m}}/{\text{min}}\), based on the effective cutting diameter that varies as a function of the \(\omega\) angle of inclination of the surface and the depth of cut \(ap\) (2).

$$D_{{\text{eff}}} = D\sin \left[ {\omega + \cos^{ - 1} \left( {\frac{D - 2ap}{D}} \right)} \right]$$
(2)
Table 1 Cutting parameters used in the experimental tests
Full size table

Figure 6 illustrates the setup carried out on the 3 DOF VMC and the Nakanishi® high-speed spindle adapted for micro-machining operations from 20,000 to 80,000 rpm. Also, it shows the micro-machining process with the down-milling cutting strategy. The \(\omega\) angle and the direction of the vectors F and CF determine it. Four samples were manufactured, two by micro-machining (down-milling and up-milling) and two by meso-machining (down-milling and up-milling). Finally, a parallelepiped sample was extracted from the workpiece using wire electrical discharge machining (WEDM), thus obtaining a geometry suitable for characterisation using XRD and scanning electron microscopy (SEM) techniques.

Fig. 6
figure 6

Experimental setup in a 3 DOF VMC for micro-milling using down-milling strategy

Full size image

2.4 Residual stress measurement on Ti–6Al–4V titanium alloy

Titanium and most titanium alloys crystallise at room temperature in the hexagonal close packing (HCP) crystal structure [14], called the \(\alpha\)-phase, with lattice parameters \(a = 2.9511\) Å and \(c = 4.6843\) Å. Above the \(\beta\)-transus temperature (882 °C), the dominant structure is body centred cubic (BCC), called the \(\beta\)-phase, with lattice parameter \(a = 3.32\) Å [15]. Figure 7 shows a visual representation of the two crystal structures mentioned with their most densely packed crystallographic planes. Alloying elements such as aluminium, oxygen, and nitrogen are \(\alpha\)-stabilisers; others, such as vanadium and molybdenum are \(\beta\)-stabilisers. If the titanium alloy contains \(\beta\)-stabilisers, a mixture of \(\alpha\)-phase plus \(\beta\)-phase will be present below the \(\beta\)-transus temperature; otherwise, only \(\alpha\)-phase will be present. At room temperature, the Ti–6Al–4V alloy is composed of between 50 and 90% by volume of \(\alpha\) phase, depending on the thermal treatment it has undergone, making it the dominant phase [16] and the one used in residual stress measurements. Three Miller indices \(\{ hkl\}\) identify the crystallographic planes in cubic crystalline structures, and four indices \(\{ hkil\}\) called Miller-Bravais the HCP crystal structure. The distance between two parallel crystallographic planes \(d_{\{ hkl\} }\) in the HCP structure is a function of the lattice parameters \((a,c)\) and the Miller–Bravais indices (3).

$$\frac{1}{{d_{hkl}^2 }} = \frac{4}{3}\frac{{\left( {h^2 + hk + k^2 } \right)}}{a^2 } + \frac{l^2 }{{c^2 }}$$
(3)
Fig. 7
figure 7

Left, \(\alpha\) phase (HCP). Right, \(\beta\) phase (BCC). For pure titanium

Full size image

When X-rays are incident on a surface, the crystallographic planes cause interference patterns by diffraction. The phenomenon occurs when two waves superimpose to form a resulting wave of greater, lesser or equal amplitude. Diffraction depends on the interplanar distance \(d\) and the wavelength \(\lambda\) of the incident X-rays. Rays scatter in different directions, but those scattered by atoms of parallel crystallographic planes \(k\) will be in phase. They will add to the contribution of the diffracted rays, increasing the intensity and producing peaks in the diffraction pattern, as shown in Fig. 8. Bragg's Law (4) governs this behaviour and is the principle of XRD theory.

$$k\lambda = 2d sin\theta$$
(4)
Fig. 8
figure 8

Diffraction pattern for the Ti–6Al–4V electropolished surface

Full size image

A perfect crystal structure would have sharp peaks at the 2θ angle of the crystallographic plane analysed [14]. During a machining process such as grinding, milling or turning, the plastic deformation of the material causes the crystalline structure to undergo three-dimensional and non-uniform changes. The peaks widen and undergo displacements at the 2θ angle. It is essential to clarify that deformations are not only caused by machining processes but also by thermal treatments, metallurgical processes and crystalline imperfections such as dislocations or interfacial defects. According to Bragg's Law (4), the variation of the \(2\theta\) angle is related to the variation of the interplanar distance \(d_{\left\{ {hkl} \right\}}\) since the wavelength \(\lambda\) is constant. For the above reason, if the interplanar distance of the crystallographic plane in a stress-free state \(d_0\) is known, it is possible to characterise the residual stresses state through deformation analysis.

An electropolished sample of the annealed Ti–6Al–4V titanium alloy was the reference surface free of residual stresses. The sample used as an anode had an area of \(163.4\,{\text{mm}}^2\). The material of the cathode was graphite. The electrolyte, taken from Piotrowski et al. [17], contained \(200\,{\text{cm}}^3\) of methanol, \(10\,{\text{cm}}^3\) of sulphuric acid, \(7\,{\text{cm}}^3\) of water, \(8\,{\text{g}}\) of aluminium chloride, and 5 g of zinc chloride. The electropolishing process was at 4.6 V at a constant current density of \(1000\,{\text{A}}/{\text{m}}^2\) for 20 min.

2.5 Residual stress tensor

According to Hooke's Law, the stress tensor \(\sigma_{ij}\) (5) has a linear relation with the strain tensor \(\varepsilon_{kl}\) through the elastic stiffness tensor \(c_{ijkl}\). The stress in the direction of any unit vector \(n\) (Fig. 9b) is estimated by (6). The strain \(\varepsilon_n\), in the direction of \(L_3\), is determined using (7), expressing the vector \(n\) as a function of the angles \(\phi\) and \(\psi\) (8) used in the XRD test [18]. Each of the components of the unit strain tensor influences the unit strain in the direction of the \(n\)-vector.

$$\sigma_{ij} = c_{ijkl} \cdot \varepsilon_{kl} \quad {\text{where}}:\,\sigma_{ij} = \left[ {\begin{array}{*{20}c} {\sigma_{11} } & {\sigma_{12} } & {\sigma_{13} } \\ {\sigma_{21} } & {\sigma_{22} } & {\sigma_{23} } \\ {\sigma_{31} } & {\sigma_{32} } & {\sigma_{33} } \\ \end{array} } \right] \,{\text{and}}\,\varepsilon_{kl} = \left[ {\begin{array}{*{20}c} {\varepsilon_{11} } & {\varepsilon_{12} } & {\varepsilon_{13} } \\ {\varepsilon_{21} } & {\varepsilon_{22} } & {\varepsilon_{23} } \\ {\varepsilon_{31} } & {\varepsilon_{32} } & {\varepsilon_{33} } \\ \end{array} } \right]$$
(5)
$$\sigma_n = \sigma_{ij} n_i n_j = \sigma_{11} n_1^2 + \sigma_{22} n_2^2 + \sigma_{33} n_3^2 + \sigma_{12} n_1 n_2 + \sigma_{13} n_1 n_3 + \sigma_{23} n_2 n_3$$
(6)
$$\begin{aligned} \varepsilon_n & = \varepsilon_{\phi \psi } = \varepsilon_{11} \cos^2 \phi \sin^2 \psi + \varepsilon_{22} \sin^2 \phi \sin^2 \psi + \varepsilon_{33} \cos^2 \psi \\ & \quad + \varepsilon_{12} \sin 2\phi \sin^2 \psi + \varepsilon_{13} \cos \phi \sin 2\psi + \varepsilon_{23} \sin \phi \cos 2\psi \\ \end{aligned}$$
(7)
$$n = \left( {\cos \phi \sin \psi ,\sin \phi \sin \psi ,\cos \psi } \right)$$
(8)
Fig. 9
figure 9

Left, sample setup in the XRD equipment. Right, \({{\text{sin}}}^{2}\psi\) method representation

Full size image

The deformation \(\varepsilon_n\) of a given crystallographic plane \((hkl)\) is obtained employing (9) if the interplanar distance in the \(n\)-direction (\(d_{\varphi \psi } )\) and the interplanar distance in a stress-free state \(d_0\) are known. Due to the anisotropy of the crystal structure of the \(\alpha\)-phase of the Ti–6Al–4V alloy, the elastic behaviour at the microscopic scale differs from the behaviour at the macroscopic scale; therefore, it is necessary to use the X-ray Elastic Constants (XEC) (\(1/2 \cdot s_{2\left( {hkl} \right)}\), \(s_{1(hkl)}\)), dependent on the analysed crystallographic plane (10), in order to obtain the residual stress tensor [5].

$$\varepsilon_n = \varepsilon_{\phi \psi } = \frac{{d_{\phi \psi } - d_0 }}{d_0 }$$
(9)
$$\begin{aligned} \varepsilon_{\phi \psi } & = 1/2 \cdot s_{2\left( {hkl} \right)} \left[ {\sigma_{11} \cos^2 \phi \sin^2 \psi + \sigma_{22} \sin^2 \phi \sin^2 \psi + \sigma_{33} \cos^2 \psi } \right] \\ & \quad + 1/2 \cdot s_{2(hkl)} \left[ {\sigma_{12} \sin 2\phi \sin^2 \psi + \sigma_{13} \cos \phi \sin 2\psi + \sigma_{23} \sin \phi \sin 2\psi } \right] \\ & \quad + s_{1(hkl)} \left[ {\sigma_{11} + \sigma_{22} + \sigma_{33} } \right] \\ \end{aligned}$$
(10)

2.6 Sample setup in the XRD equipment

The electropolished and the machined samples were placed in the XRD equipment, oriented to the laboratory coordinate system denoted by \(S_i \left( {i = 1, 2, 3} \right)\), as shown in Fig. 9. A PANalytical® X'Pert series equipment equipped with an X-ray generator tube with a copper anode, which produced \(K_{\alpha 1}\) and \(K_{\alpha 2}\) radiation with \(\lambda\) wavelengths of \(1.54060\) Å and \(1.54443\) Å, respectively, operating at \(45\,{\text{kV}}\) and \(40\,{\text{mA}}\), was used. The estimation of the residual stress tensor was carried out with the X'Pert Stress software from the same manufacturer of the equipment, in the peak presented at the 2θ = 141.63° angle (family of crystallographic planes \(21\overline{3}3\)), rotating the specimen around the \(S_3\)-axis, \(\phi\) = 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315° angles. At each \(\phi\) angle, six measurements of the interplanar distance were taken, using the \(\sin^2 \psi\) method, varying the \(\psi\) angle between 0° and 45° [18]. The interplanar distance free of RS \(d_{0\{ 21\overline{3}3\} } = 0.81552\) Å, taken as a reference, was obtained from the electropolished surface considering an elasticity modulus \(E = 114.76\,{\text{GPa}}\), a Poisson's ratio \(v = 0.3217\), and XEC \(S_1 = 0\) and \(1/(2S_2 ) = 11.89\).

2.7 Projection of the stress tensor on the machining coordinate system

Being (11) the stress tensor \(\sigma_{ij}\) defined in the \(S_i\) laboratory coordinate system of the XRD equipment, the representation of the principal stress tensor is expressed through transformation (12), where \(V\) is the matrix of eigenvectors of the tensor. To determine the stress in any direction \({{\varvec{n}}}\), for example, in the F or the CF direction, the Cauchy formula (13) is used. The machining coordinate system, defined by the vectors F and CF, is rotated by an \(\alpha\) angle around the \(S_3\) axis of the coordinate \(S_i\) system (Fig. 10).

$$\sigma_{ij} = \left[ {\begin{array}{*{20}c} {\sigma_{11} } & {\sigma_{12} } & {\sigma_{13} } \\ {\sigma_{21} } & {\sigma_{22} } & {\sigma_{23} } \\ {\sigma_{31} } & {\sigma_{32} } & {\sigma_{33} } \\ \end{array} } \right]$$
(11)
$$\sigma_P = V^{\prime} \sigma_{ij} V$$
(12)
$$\sigma_n = \sigma_{ij} n$$
(13)
Fig. 10
figure 10

Left, laboratory and machining coordinate systems. Right, residual stress tensor representation

Full size image

3 Results

3.1 The surface finish of the samples

Figure 11 shows that the down-milling machining strategy, both at the micro- and meso-levels, produces surfaces with a good surface finish. It is also appreciable that the up-milling strategy machining, at the micro- and meso-levels, creates a defect called smeared/adhered material on the surface [6].

Fig. 11
figure 11

Surface finish assessment of machined samples through SEM at a magnification of × 200

Full size image

3.2 The cutting edge of microtools

A new tool was used for machining each of the surfaces. No evident wear was observed in the 8-mm-diameter tools used in the down-milling and up-milling meso-machining strategies, nor in the 500-\({\mu m}\) tool used in the down-milling micro-machining when using the SEM characterisation technique. Specifically, Fig. 12 shows the 500-\({\mu m}\) tool used for up-milling micro-machining. The tool edge shows minor wear, approximately 3 \({\mu m}\), concerning the 25 \({\mu m}\) of the flank face. Also, the SEM shows the built-up edge (BUE BUL) phenomenon on the tool rake face, as reported by Parida et al. [19] when machining at \(40\,{\text{m}}/{\text{min}}\).

Fig. 12
figure 12

The 500-\(\mathrm{\mu m}\) tool used in up-milling micro-machining. Tool wear. BUE BUL phenomenon

Full size image

3.3 Residual stress state on electropolished surface

The XRD test of the electropolished surface provided the interplanar distances of the crystallographic plane families \(\{ 1012\}\) and \(\{ 1013\}\) (Fig. 8), which were substituted into (4). The lattice parameters, \(a = 2.9249\) Å and \(c = 4.6714\) Å, for the HCP crystal structure of the \(\alpha\)-phase of the Ti–6Al–4V titanium alloy, are obtained by solving the generated system of equations. These parameters vary from those of pure titanium, causing the interplanar distances and diffraction peaks to differ, as shown in Table 2.

Table 2 Interplanar space and \(2\theta\) angle comparison between Ti and Ti–6Al–4V alloy
Full size table

Table 2 also shows that slight variations of the interplanar space \(d\) generate more significant variations of the angle \(2\theta\) at high values of \(2\theta\), so it is recommended to perform the residual stress analysis at high values of the \(2\theta\) angle (2θ > 120°) [7]. The analysis performed on the electropolished specimen in the \(\{ 2133\}\) crystallographic plane resulted in the stress tensor and standard deviation shown in (14), with an interplanar distance \(d_{0\{ 21\overline{3}3\} } = 0.81552\) Å. Figure 13 shows the diffraction pattern for 2θ > 120°.

$$\sigma_{ij} = \left[ {\begin{array}{*{20}c} { - 1.6} & 0 & 0 \\ 0 & {1.2} & 0 \\ 0 & 0 & {1.6} \\ \end{array} } \right];\,\sigma_{ij} = \left[ {\begin{array}{*{20}c} {3.5} & 0 & 0 \\ 0 & {3.5} & 0 \\ 0 & 0 & {1.07} \\ \end{array} } \right]$$
(14)
Fig. 13
figure 13

Ti–6Al–4V electropolished surface diffraction pattern \((2\theta > 120^\circ )\)

Full size image

3.4 Residual stress state on machined surfaces

Figure 14 shows the F and CF directions for the down-milling and up-milling machining strategies, with respect to the coordinate system \(S_i\) of the XRD equipment. Table 3 shows the residual stress tensor in the laboratory coordinate system, the principal stress tensor, and the projection of the stress tensor obtained using (5), in the F and CF directions, for each of the machined samples.

Fig. 14
figure 14

F and CF vectors with respect to the reference coordinate system of the XRD machine

Full size image
Table 3 Residual stress tensor on machined surfaces
Full size table

4 Discussion

Regarding the multi-axis micro-machining process with a ball-end mill on the Ti–6Al–4V alloy, it was shown that, on a micrometric scale, the smeared/adhered material defect also occurs. The defect can be attributed to the high friction produced when the chip is formed from the minimum to the maximum thickness, characteristic of the up-milling machining strategy, in combination with the high tensile strength and low modulus of elasticity of the alloy [15]. Lizzu et al. also report adhered material on the surface in up-milling meso-machining on tilted surfaces with a ball-end mill. They attribute the defect to the difficulty of efficiently evacuating the chip in this type of strategy [20].

The formation of the BUE BUL phenomenon on the tool rake face in the up-milling micro-milling strategy is related to the defect of adhered material on the surface because the material detached from the tool rake face is redeposited on the machined surface, affecting the surface finish [21]. The absence of evident wear on the 8-mm-diameter tools, as well as the 500-\({\mu m}\) micro-tool used in down-milling micro-milling, is attributed to the small machined area of the sample \((7 \times 9\,{\text{mm}}^2 )\).

As reported by Changfeng et al. [22], it was found that in all the machined surfaces compressive stresses were generated (\(\sigma_{11}\), \(\sigma_{22}\)). The variation between up-milling and down-milling machining strategies changed the value of the residual stresses, but not their behaviour. The compressive stresses on the surface produced a reaction tensile stress perpendicular to the surface \(\left( {\sigma_{33} } \right)\), which is corroborated by verifying the increase in the interplanar distance \(d_{\left\{ {21\overline{3}3} \right\}}\) of the family of crystallographic planes parallel to the surface of the specimen when \(\psi = 0\). Rahul et al. [23] report compressive stresses in frontal micro-machining processes with a 1000-\({{\upmu m }}\) diameter tool on the Ti–6Al–4V titanium alloy of \(510\,{\text{MPa}}\) in the feed direction and \(350\,{\text{MPa}}\) in the cross-feed direction. They used a cutting speed \(V_c = 15.7\,{\text{m}}/\min\) a feed per tooth \(f_z = 4\,{\mu m}\), and a depth of cut \(a_p = 100\,{\mu m}\). The same behaviour of the residual stresses is evidenced in the present investigation but with lower values. The higher values reported by [20] could be attributable to the greater depth of cut used, which increases the compressive residual stresses, according to what was reported by Wimmer et al. [24]. Zhang et al. [25] argue that the increase in temperature, produced by using higher cutting speeds, results in a thermal effect that can reduce the value of compressive residual stresses. They also conclude that higher cutting forces generate higher residual stresses.

The compressive stresses, in the down-milling micro-milling strategy, both in the F and CF directions, were higher than those observed in the meso-milling process. This is attributed to the higher specific cutting force required in micro-milling processes. Attanasio et al. [10] performed groove milling experiments with a cylindrical mill \(\left( {D = 200\,{\mu m}} \right)\), with depths of cut \(ap = 10\,{\mu m}\) on the Ti–6Al–4V alloy. They determined values of the specific cutting force in the order of \(4500\,{\text{N}}/{\text{mm}}^2\), where the increase is evident, with respect to the meso- and macro-machining strategies, where the specific cutting force ranges from \(1300\,{\text{and}}\,1900\,{\text{N}}/{\text{mm}}^2\). On the other hand, Rahman et al. [26] report that chip formation mechanisms at a micrometric scale are associated with intense plastic deformation phenomena because the relationship between the tool edge radius and the depth of cut generates a negative rake angle. The higher compressive stresses in the F direction can be explained based on what was reported by Basso et al. [27] because in the down-milling machining strategy the chip formation process occurs by confining the material towards the generated surface where the gradient of the accumulated cutting energy is greater.

In the up-milling machining strategy, both at the micro- and meso-levels, higher compressive stresses were observed in the CF direction, with respect to those found in the F direction. This is attributed to the fact that the stresses measured on the surfaces are an average of the chip deformed and adhered on the surface and not to the average of the desired surface.

5 Conclusions

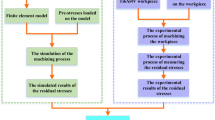
An experimental investigation to compare the residual stresses state in five-axis micro- and meso-milling processes with a ball-end mill on the Ti–6Al–4V titanium alloy was carried out. The main conclusions are as follows:

  • A methodology was proposed to emulate the possible positions of a ball-end mill in five-axis machining on a VMC with 3 DOF by simultaneously varying the lead and tilt angles, reducing research costs.

  • It is not recommended to use the up-milling machining strategy, which generates the chip from the minimum to maximum thickness due to the defect of adhered material on the surface caused by the BUE BUL phenomenon, both at the micro- and meso-milling level.

  • Compressive residual stresses were produced on the surface in the four cases studied. The down-milling machining strategy produced higher compressive stresses in the direction of feed than the ones produced in cross-feed. Compressive stresses in the feed direction and the cross-feed direction were higher in micro-milling.

  • The best surface finish, with higher compressive stresses on the surface, was obtained with the down-milling strategy, which, in the case of milling with a ball-end mill, corresponds to the strategy obtained by using negative lead angles, positive tilt angles, and the material to be removed located to the right of the tool feed direction F.

  • In up-milling machining, both at the micro- and meso-levels, higher compressive stresses were found in the direction of cross-feed. Presumably, the measurement result is the chip´s average redeposited on the surface and not the surface itself.