1 Introduction

The ships and platforms are usually equipped with HCS (Heave Compensation System). The technical solutions for HCS are different. In the paper the main idea of optimisation is: how to stabilise the raiser despite both vertical motion of the base and its horizontal motion caused by sea weaving. In all cases using the HCS, it means using moving vertically the upper end of the raiser. An important issue in the riser design is to stabilise the load despite the movements of the unit (platform or vessel) to which the riser’s upper end is connected. While compensation of the vertical movements caused by waves is relatively easy to implement, the horizontal motion compensation is much more difficult. To compensate vertical movement are often used solution that are combination of passive and active hydraulic systems [1,2,3,4]. The active heave compensation system based on linear control techniques, which have been mounted on drill-ship was object of paper [1]. A nonlinear controller was proposed for active compensator based on an electric hydraulic drive in [2]. In both papers the vertical movements caused by waving sea are compensated by AHC (Active Heave Compensation). In order to avoid a collision between two raisers, the [3] have been proposed control based on adjusting the top tension. Effective length of raisers is selected by the controller which is taking into account the forces of water environment impact. One the proposals of application of active compensation system is to minimalise of raiser angle deviation in connection with the well head and at the top joint. The paper [4] presents a mathematical model of the hydraulic system that allows to reduce of the upper and the lower raiser angle. The purpose of this study is to demonstrate that riser end’s vertical movements can mitigate the impact of the unit’s horizontal movements on bending moments at selected riser points. This may be important if some areas along the riser length need to be protected against overloads. A similar problem with regard to planar was considered in the study [5]. To formulate a riser dynamics model in this study, a modification was applied of the Rigid Finite Element Method (RFEM) presented in [6, 7] for planar systems, and in [8] for spatial systems. The subject of the analysis was the riser presented in [9], which features large deflections due to substantial horizontal distance between the positions of its upper and lower ends. The statics calculation results were compared with the result of the aforementioned study [9]. Also analysed was the impact of riser’s length and of the horizontal distance between its upper and lower ends directly affecting its curvature and natural vibration frequency. Calculations were also completed to demonstrate how the number of the elements into which a riser is divided affects the accuracy of vibration frequency results.

Fig. 1
figure 1

Analysed riser a bent, b straight M—bending moment, \(T_L \)—top tension force

Full size image

The nonlinear model of riser dynamics was used to formulate and solve the optimisation task. Harmonic motion was assumed in the horizontal plane with known amplitude and frequency. A spline function was sought that determines the riser end’s additional vertical displacements, which ensure that the bending moment at a selected point shall be the least different from its initial (static) value. At each optimisation step, the riser dynamics equations needed to be integrated. The calculations were performed for various amplitudes of the base’s horizontal movement.

An extensive discussion on the state of the art in modelling and on problems in total dynamic analysis of offshore systems is presented by Chakrabarti [10]. Although Starossek [11], Jain [12], Patel and Seyed [13] report many different modelling methods, the most popular methods used are the finite element methods [14, 15] and the lumped mass methods [16, 17]. Those methods are used in commercial packages such as Riflex and Orcaflex. The Flexible Segment Model (FSM) presented in [18, 19] is another similar approach. The RFEM used in this paper has been also successfully used for dynamic analysis of flexible systems containing beam-like links [20, 21], plates and shells [22, 23].

2 Riser dynamics model

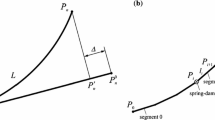
Figure 1 shows the analysed riser.

The riser was divided into rfe and sde as described in detail in [8, 24], into \(n+1\) rfes (numbered \(0\ldots n\)) and n sdes (numbered \(1\ldots n\)). The riser’s lower end was connected with a semi-rigid spherical joint to the sea bottom, and the upper end with an articulated ball joint to the base (platform or vessel). The movement of each rfe is described by the vector components:

$$\begin{aligned} q_i =\left[ {{\begin{array}{l} {x_i } \\ {y_i } \\ {z_i } \\ {\psi _i } \\ {\theta _i } \\ \end{array} }} \right] , \end{aligned}$$
(1)

where: \(x_i ,y_i ,z_i \)—coordinates of \(rfe_i \),

\(\psi _i ,\theta _i\)—Z, Y Euler angles (Fig. 2), determining the element’s orientation, with torsional deflection neglected.

Fig. 2
figure 2

Generalised rfe coordinates

Full size image

The equations of individual elements’ motion, derived from the Lagrange equations, employ the homogeneous transformation method [24, 25]. The Rigid Finite Element Method’s modification is described in [8], so the description of the mathematical model which follows is reduced to major determinations and relationships. In paper [8] each rfe has 6 degrees of freedom, while in the approach presented the torsional flexibility is omitted. The coordinates of the point defined in the local coordinate system \(\{i{\}}'\) combined with rfe i, may be expressed in the inertial system according to the following formula:

$$\begin{aligned} \mathbf{r}=\mathbf{B}_i \mathbf{r}^{\prime }, \end{aligned}$$
(2)

where: \({\mathbf{B}_i} = \left[ {\begin{array}{ll} {\mathbf{R}_i} &{} {\mathbf{r}_{i,0}}\\ 0 &{} 1 \\ \end{array}}\right] \)—homogeneous transformation matrix.

$$\begin{aligned}&{} \mathbf{R}_i =\left[ {{\begin{array}{lll} {c\psi _i } &{}\quad {-s\psi _i } &{}\quad 0 \\ {s\psi _i } &{}\quad {c\psi _i } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ \end{array} }} \right] \left[ {{\begin{array}{lll} {c\theta _i } &{}\quad 0 &{}\quad {s\theta _i } \\ 0 &{}\quad 1 &{}\quad 0 \\ {-s\theta _i } &{}\quad 0 &{}\quad {c\theta _i } \\ \end{array} }} \right] ,\\&\mathbf{r}_{i,0} =\left[ {{\begin{array}{l} {x_{i,0} } \\ {y_{i,0} } \\ {z_{i,0} } \\ \end{array} }} \right] , \end{aligned}$$

\(\mathbf{{r}'}_ =\left[ {{\begin{array}{llll} {{x}'} &{} {{y}'} &{} {{z}'} &{} 1 \\ \end{array} }} \right] ^{T}\)—coordinates of the point in the local system \(\{i\}'\),

\(\mathbf{r}_ =\left[ {{\begin{array}{llll} x &{} y &{} z &{} 1 \\ \end{array} }} \right] ^{T}\)—coordinates of the point in the global system \(\{\}\),

\(c\psi _i =\cos \psi _i ,s\psi _i =\sin \psi _{i,} c\theta _i =\cos \theta _i ,s\theta _i =\sin \theta _i .\) Elements of \(\mathbf{B}_i \) matrix are defined unequivocally by the components of the vector \(\mathbf{q}_i \) . The kinetic energy of rfe i can be defined with following dependence [24]:

$$\begin{aligned} E_i =\frac{1}{2}tr\{\dot{\mathbf{B}}_i {\mathbf{H}}_i \dot{\mathbf{B}}_i ^{T}\}, \end{aligned}$$
(3)

where: \(\mathbf{H}_i =\int _{mi} {\mathbf{r}_i^{\prime }\mathbf{r}_i^{\prime T}dm_i .} \)

The Lagrange operators from kinetic energy of rfe i may be presented as follows:

$$\begin{aligned} \varepsilon _{\mathrm{q}i} (E_i )=\frac{d\partial E_i }{dt\partial \dot{\mathbf{q}}}-\frac{\partial E_i }{\partial \mathbf{q}_i }=\mathbf{A}_i \ddot{\mathbf{q}}_{i}+\mathbf{h}_i ,, \end{aligned}$$
(4)

where: \(a_{i,jk} =\{\mathbf{B}_{i,j} \mathbf{H}_i \mathbf{B}_{i,k}^T \}j,k=1,\ldots ,m\),

$$\begin{aligned} h_{i,j} =\sum _{k=1}^m {\sum _{l=1}^m \{q_{i,k}q_{i,l}\} tr\{\mathbf{B}_{i,k} \mathbf{H}_i \mathbf{B}_{i,kl}^T \}j=1,\ldots ,m,} \end{aligned}$$

\(m=5\)-number of generalised coordinates describing movement of rfe i.

The high number of elements present in (4) is at the same time equal to nil. Therefore, in this paper, a similar method was used to that referred to in [9]: products and traces of matrices, referred to in (4), were calculated analytically.

Fig. 3
figure 3

Reaction forces

Full size image

In order to connect rfes in kinematic chain reflecting considered raiser, the constrain equation is formulated and reaction forces in points \(A_i \) are introduced in equations of motion. Following procedure described in [8], the generalised forces acting on ith rfe are as follows (Fig. 3):

$$\begin{aligned} \mathbf{Q}_0^{(\mathbf{F})}= & {} \mathbf{Q}_0^{(A_0 )} =-\bar{\mathbf{{D}}}_0^T \mathbf{F}_1 , \end{aligned}$$
(5.1)
$$\begin{aligned} \mathbf{Q}_i^{(\mathbf{F})}= & {} \mathbf{Q}_i^{(A_i )} +\mathbf{Q}_i^{(A_{i+1} )} =\bar{\mathbf{{D}}}^{T}{} \mathbf{F}_i\nonumber \\&-\bar{\mathbf{{D}}}_i^T \mathbf{F}_{i+1} ,\quad \hbox { for } i=1,\ldots , n. \end{aligned}$$
(5.2)

where: \(\mathbf{F}_i =\left[ {F_{i,x} ,F_{i,y} ,F_{i,z} } \right] ^{T}\) are expressed in inertial coordinate system \(\{\}\),

$$\begin{aligned} \left( {\bar{\mathbf{{D}}}_0 } \right) _{3x5}= & {} \left[ {{\begin{array}{lllll} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ \end{array} }} \right] ,\\ \left( {\bar{\mathbf{{D}}}_i } \right) _{3x5}= & {} \left[ {{\begin{array}{lllll} 1&{}\quad 0&{}\quad 0&{}\quad {-l_i s\psi _i c\theta _i }&{}\quad {-l_i s\psi _i c\theta _i } \\ 0&{}\quad 1&{}\quad 0&{}\quad {l_i c\psi _i c\theta _i }&{}\quad {l_i s\psi _i s\theta _i } \\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad {-c\theta _i } \\ \end{array} }} \right] . \end{aligned}$$

The constraint equations are involved in acceleration form:

$$\begin{aligned}&\bar{\mathbf{D}}_{i-1} {\ddot{\mathbf{q}}}_{i-1} -\bar{\mathbf{{D}}}_0 {\ddot{\mathbf{q}}}_i =\mathbf{G}_i , \quad i=1,2,\ldots ,n \end{aligned}$$
(6.1)
$$\begin{aligned}&\bar{\mathbf{{D}}}_n {\ddot{\mathbf{q}}}_n =\mathbf{G}_{n+1} \end{aligned}$$
(6.2)

where \(\left( {\mathbf{G}_i } \right) _{3x1} =\mathbf{G}_i \left( {q_0 ,\dot{q}_i } \right) , \left( {\mathbf{G}_{n+1} } \right) _{3x1} =\mathbf{G}_{n+1} \left( {q_n ,\dot{q}_n } \right) \) are presented in paper [8].

The potential energy of gravity forces of refs can be exposed in the form:

$$\begin{aligned} V_i^g =m_i gy_{c,i} \end{aligned}$$
(7)

where m is mass of ith rigid element, g is gravity acceleration,\(y_{c,i} \) is y coordinate of mass centre of i-th element.

From (7) it is obtained:

$$\begin{aligned} \frac{\partial V_i^g }{\partial \mathbf{q}_i }=m_i g\left[ {{\begin{array}{l} 0 \\ 1 \\ 0 \\ {a_i c\psi _i c\theta _i } \\ {-a_i s\psi _i s\theta _i } \\ \end{array} }} \right] . \end{aligned}$$
(8)

The elastic deformation energy \(\hbox {sde}i \) is defined by expression:

$$\begin{aligned} V_i^s =\frac{1}{2}c_i \alpha _i^2 , \end{aligned}$$
(9)

coefficients \(c_i \) were determined from:

$$\begin{aligned} c_i =\frac{E_r \cdot I_r }{\Delta L}, \end{aligned}$$
(10)

where: \(E_r\)—stiffness modulus of riser material, \(I_r\)—moment of inertia of riser cross section, \(\Delta L\)—length of the original element, the bendability of which is reflected by sdei. Since \(\alpha _i \) and angles \(\psi _i , \theta _i \) are interrelated according to:

$$\begin{aligned} \cos \alpha _i =\cos \theta _i \cos \psi _i , \end{aligned}$$
(11)

then:

$$\begin{aligned} \frac{\partial V_i^s }{\partial \psi _i }=c_i \alpha _i \frac{\cos \theta _i \sin \psi _i }{\sin \alpha _i }, \end{aligned}$$
(12.1)
$$\begin{aligned} \frac{\partial V_i^s }{\partial \theta _i }=c_i \alpha _i \frac{\sin \theta _i \cos \psi _i }{\sin \alpha _i }. \end{aligned}$$
(12.2)

Provided that the angles \(\psi _i \)and \(\theta _i \) are small, formulas (5) are reduced to well-known expressions:

$$\begin{aligned} \frac{\partial V_i^s }{\partial \psi _i }=c_i \psi _i , \end{aligned}$$
(13.1)
$$\begin{aligned} \frac{\partial V_i^s }{\partial \theta _i }=c_i \theta _i , \end{aligned}$$
(13.2)

The water environment impact forces can be introduced using Morison equations [26, 27]. The forces caused by flow inside the element are disregarded. Then into account are taken the following:

  • buoyancy force,

  • viscous resistance forces,

  • inertia force.

After calculations presented in details in paper [8], the equations of motion of the system considered can be written in the form:

$$\begin{aligned} \left\{ {\begin{array}{l} \mathbf{M}_0 \ddot{\mathbf{q}}_0 +\bar{{\mathbf{D}}}_0^T \mathbf{F}_1 =\mathbf{f}_0 \\ \vdots \\ \mathbf{M}_i \ddot{\mathbf{q}}_i -\bar{{\mathbf{D}}}^{T}{} \mathbf{F}_i +\bar{{\mathbf{D}}}_i^T \mathbf{F}_{i+1} =\mathbf{f}_i , \\ \vdots \\ \mathbf{M}_n \ddot{\mathbf{q}}_n -\bar{{\mathbf{D}}}_n^T \mathbf{F}_{n+1} =\mathbf{f}_n \\ \end{array}} \right. \end{aligned}$$
(14)

where: \(\mathbf{M}_i =\mathbf{A}_i -\mathbf{A}_{I,i} ,\)

$$\begin{aligned} \mathbf{f}_i =-\mathbf{h}_i -\frac{V_i^g }{\partial \mathbf{q}_i }+\frac{V^{s}}{\partial \mathbf{q}_i }+\mathbf{Q}_i^\mathrm{we} , \end{aligned}$$

\(\mathbf{A}_{I,i} \) is matrix of added water [8],

\(\mathbf{Q}_i^\mathrm{we} \) is vector of all generalised forces arising from water environment. In general matrix form the above equation can be written as:

$$\begin{aligned} \mathbf{M}\ddot{\mathbf{q}}-\mathbf{DR}=\mathbf{f} \end{aligned}$$
(15.1)
$$\begin{aligned} \mathbf{D}^{T}{\ddot{\mathbf{q}}}=\mathbf{G} \end{aligned}$$
(15.2)

where: \(\mathbf{M}_{5(n+1)x5(n+1)} =\mathrm{diag}\{\mathbf{M}_0 ,\mathbf{M}_1 ,\ldots ,\mathbf{M}_n \}\), \(\mathbf{M}_{i,5x5} =\mathbf{M}_i (\mathbf{q}_i )\)—mass matrix of element i with variable coefficients, \(\mathbf{q}_{5(n+1)} =\left[ {\mathbf{q}_0^T ,\mathbf{q}_1^T ,\ldots ,\mathbf{q}_n^T } \right] ^{T}\)—vector of generalised coordinates, \(\mathbf{R}_{3(n+1)} =\left[ {\mathbf{R}_1^T ,\ldots ,\mathbf{R}_1^T ,\mathbf{R}_{n+1}^T } \right] ^{T}\)—vector of constrain reactions in rfe connections, \(\mathbf{R}_i =\left[ {R_i^x ,R_i^y ,R_i^z } \right] ^{T}\)—reactions at point \(A_i \), \(\mathbf{D}_{5(n+1)x3(n+1)} =\mathbf{D}(\mathbf{q})\)—matrix of coefficients, \(\mathbf{f}_{5(n+1)} =\mathbf{f}(t,\mathbf{q},{\dot{\mathbf{q}}})\)—vector of loads and nonlinear relations, \(\mathbf{G}_{3(n+1)} =\mathbf{G}(t,\mathbf{q},{\dot{\mathbf{q}}})\)—vector of the right sides of constrain equations in the acceleration form.

The block-diagonal form of weight matrix \(\mathbf{M}\) enables easy determination of the inverse matrix \(\mathbf{M}^{-1}\). Equations (15) can thus be formulated as:

(a) set of linear algebraic equations:

$$\begin{aligned} (\mathbf{D}^{T}{} \mathbf{M}^{-1}{} \mathbf{D})\mathbf{R}=\mathbf{G}-(\mathbf{D}^{T}\mathbf{M}^{-1})\mathbf{f}, \end{aligned}$$
(16.1)

the solution of which enables determination of forces in sdes connection,

(b) generalised acceleration formulas:

$$\begin{aligned} {\ddot{\mathbf{q}}}=\mathbf{M}^{-1}{} \mathbf{f}+(\mathbf{M}^{-1}{} \mathbf{D})\mathbf{R}=\mathbf{F}(t,\mathbf{q},{\dot{\mathbf{q}}}). \end{aligned}$$
(16.2)

With vector \(\mathbf{R}\) known, the longitudinal and transverse forces may be determined in rfe connection with adjacent elements and the base in point \(A_{n+1}\).

The system motion equations were integrated by the Runge-Kutta IVth order method. To stabilise the constrain equations, the Baumgart method was applied.

3 Model validation, natural vibration frequency determination

Subject to numerical analysis was one of the risers presented in [9]. Listed in Table 1 are the riser’s geometric and material parameters and the parameters needed to determine the water impact forces.

Table 1 Riser parameters
Full size table

Table 2 shows how increasing the number of elements affects the minimum and maximum forces at point \(A_{n+1} \), and the maximum and minimum bending moments for \(s = 70\) m. These values were obtained assuming a forced movement of the base in the direction of axis x according to:

$$\begin{aligned} x_{A_{n+1} } =-a+a\cos \omega t \end{aligned}$$
(17)

where: \(a = 2\,\hbox {m},\, \omega =\frac{2\pi }{T_f },\, T_f = 12\) s.

Table 2 Impact of number n on calculation results
Full size table
Table 3 Impact of number n on frequency of riser’s natural vibrations
Full size table
Table 4 Impact of parameter H on frequency of riser’s natural vibrations
Full size table

The results shown in [9] were obtained by the finite difference method.

The difference between the values obtained in [9] and from the present model does not exceed 5% already at \(n = 60\).

The impact of number n on the results accuracy was also analysed for the riser’s natural vibration frequency calculation. The frequencies were calculated using the procedure described in [28]. With the assumption that:

$$\begin{aligned} \mathbf{q}=\mathbf{q}_0 +\Delta \mathbf{q}, \end{aligned}$$
(18)

and the approximation of the right side of (16.2) by:

$$\begin{aligned} \mathbf{F}=\frac{\partial \mathbf{F}}{\partial \mathbf{q}}\Delta \mathbf{q}+\mathbf{F}(\mathbf{q}_0 ), \end{aligned}$$
(19)

and with the assumption that

$$\begin{aligned} {\ddot{\mathbf{q}}}_0 =\mathbf{F}(\mathbf{q}_0 ), \end{aligned}$$
(20)

then after simple transformations the problem of eigenvalues and eigenvectors takes the form:

$$\begin{aligned} \left[ {-\mathbf{C}-\mathbf{\omega }^{2}{} \mathbf{I}} \right] \Delta \mathbf{q}=\mathbf{0} \end{aligned}$$
(21)

Gradients matrix C may be calculated by the finite difference method. In this study the central five-point differences were employed. Table 3 shows the impact of number n on \(\omega \) for a riser with the parameters from Table 1, for \(H=1800\) m.

Table 5 Frequencies of vertical riser’s natural vibration
Full size table
Fig. 4
figure 4

Forced horizontal movement of riser’s top end

Full size image
Fig. 5
figure 5

Bending moment \(M\left( {s,t} \right) \) for a \(s = 70\,\mathrm{m}\), b \(s = 170\,\mathrm{m}\)

Full size image

It is seen that already the differences between \(n = 160\) and \(n = 40\) do not exceed 1%. Table 4 shows the vibration frequencies of the same riser for different parameters of H. This parameter was so chosen, in order to eliminate the riser’s contact with the sea bottom (beyond point \(A_0\) ), which enabled elimination of the “sea bed interaction” problem.

The vibration frequencies of the vertical riser (without bending) from Fig. 1b are shown in Table 5.

Fig. 6
figure 6

Top tension force \(T_L\) for \(a = 3\hbox { m}\), \(a = 4\hbox { m}\) and \(a = 5\hbox { m}\)

Full size image
Fig. 7
figure 7

Riser positions at selected moments in time

Full size image
Fig. 8
figure 8

Optimisation procedure

Full size image
Fig. 9
figure 9

Courses of a bending moment \(M\left( {s,t} \right) \), b top tension \(T_L \left( t \right) \) before and after the optimisation, c function \(y_{A_{n+1} } \left( t \right) \)

Full size image
Fig. 10
figure 10

Courses of a bending moment \(M\left( {s,t} \right) \), b top tension \(T_L \left( t \right) \) before and after the optimisation, c function \(y_{A_{n+1} } \left( t \right) \)

Full size image
Fig. 11
figure 11

Courses of a bending moment \(M\left( {s,t} \right) \), b top tension \(T_L \left( t \right) \) before and after the optimisation, c function \(y_{A_{n+1} } \left( t \right) \)

Full size image
Fig. 12
figure 12

Courses of a bending moment \(M\left( {s,t} \right) \), b top tension \(T_L \left( t \right) \) before and after the optimisation, c function \(y_{A_{n+1} } \left( t \right) \)

Full size image
Fig. 13
figure 13

Courses of riser top end position a before optimisation, b after optimisation—O1, c after optimisation—O2

Full size image

Comparison of \(\omega \) from Tables 3 and  5 shows significant differences between them. The frequencies of the vertical riser’s vibration in planes XY and YZ are identical due to the circular cross section.

4 Dynamic optimisation task

It was assumed in the study that the movement of the riser’s upper end \(A_{n+1} \) takes the cyclic form with periodic time \(T_f = 12\) s and amplitudes \(a = 3\), 4 and 5 m. Figure 4 shows the motion forced in cycles 1 and 2. The deformation in the initial stage (\(t < 3\) s) is due to the assumption of uniform initial conditions for vector\(\left. {{\dot{\mathbf{q}}}} \right| _{t=0} \).

The bending moment course for \(a = 4\) m at points \(s = 70\,\hbox {m}\) and \(s = 170\) m is shown in Fig. 5. For \(s \approx 70\,\hbox {m}\) the bending moment is the largest. The top tension force course for the same s is given in Fig. 6.

Figure 7, alternatively, shows the riser’s positions at several selected moments in time during the forced motion’s first and second cycles.

The analysis of the above graphs shows that bending moments M and top tension forces \(T_L \) change by approx. 10% relative to the baseline.

Therefore, the dynamic optimisation task was formulated as:

Sought for is the function:

$$\begin{aligned} y_{A_{n+1} } =y_{A_{n+1} } \left( \mathbf{p} \right) =y_{A_{n+1} } \left( {p_1 ,p_2 ,\ldots ,p_{m-1} } \right) \nonumber \\ \end{aligned}$$
(22)

such as that functional

$$\begin{aligned} {\textit{case O1}}\quad \Omega= & {} \Omega \left( \mathbf{p} \right) =\left[ \frac{1}{T}\int _0^T \left[ M\left( {s,t} \right) -M^0 \left( s \right) \right] ^{ 2}\right] ^{\frac{1}{2}},\nonumber \\ \end{aligned}$$
(23.1)
$$\begin{aligned} {\textit{case O2}}\quad \Omega= & {} \Omega \left( \mathbf{p} \right) =\left[ {\frac{1}{T}\int _0^T {\left[ {T_L \left( t \right) -T_L^0 } \right] ^{ 2}} } \right] ^{\frac{1}{2}},\nonumber \\ \end{aligned}$$
(23.2)

reaches the minimum, under conditions:

$$\begin{aligned}&p_i^{\min } \le p_i \le p_i^{\max } i=1,\ldots ,m-1, \end{aligned}$$
(24.1)
$$\begin{aligned}&p_0 =y_{A_{n+1} } \left( 0 \right) =p_m =y_{A_{n+1} } \left( {T_S } \right) =0, \end{aligned}$$
(24.2)

where: \(p_i^{\min } ,p_i^{\max } -\) minimum and maximum permissible limits of parameters \(p_i \), \(p_i =y_{A_{i+1} } (t_i ), t_i -\) equidistant points in range \(\left\langle {0;T_S } \right\rangle \) for \(i=0,1,\ldots ,m.\)

The downhill simplex method [29] has been applied in order to solve the optimisation task. Optimisation procedure used for calculating the values of function \(y_{A_{n+1} } \left( \mathbf{p} \right) \) is shown in Fig. 8. This procedure has been used for both cases considering stabilisation of the bending moment and torsional force. The criterion for stopping the optimisation process is the maximum acceptable difference between the following values:

$$\begin{aligned} \varepsilon _M^{\max }= & {} \mathop {\max }\limits _{0<t<T} \left( {M\left( {s,t} \right) -M^0 \left( s \right) } \right) , \end{aligned}$$
(25.1)
$$\begin{aligned} \varepsilon _T^{\max }= & {} \mathop {\max }\limits _{0<t<T} \left( {T_L \left( t \right) -T_L^0 } \right) , \end{aligned}$$
(25.2)

or the number of optimisation steps \(j^{\max }\).

A characteristic feature of the nonlinear optimisation task so formulated is that for each combination of parameters \(p_1 \div p_{m-1} \) the system motion equations (23) needed to be integrated to calculate the value of functional \(\Omega \). Hence, the numerical effectiveness of the methods of riser discretisation and of system motion equations integration is so important. Assumed in the calculations, the results of which are shown hereinafter, was \(n = 40\). Under this assumption, one step of the optimisation procedure with integration step \(h=0.02\) s can be completed on a mid-range PC computer in 2 s or less.

5 Optimisation results

Numerical calculations involving the minimisation of functionals (23.1) and (23.2) were performed for amplitudes \(a = 3\), 4 and 5 m of the riser’s upper end horizontal displacement in XZ plane. Time interval \(\left\langle {0;T_S } \right\rangle \), where \(T_S =24\) s, was divided into \(m = 10\) sub-intervals, and parameters \(p_i =y_{A_{i+1} } (t_i )\), at the start and end of each sub-interval, were chosen considering conditions (24.1) and (24.2). Constraints \(p_i^{\min } \) and \(p_i^{\max } \) in the optimisation tasks were assumed to be \(\pm a/2\). Subsequent Figs. 9, 10, 11 and 12 show the resulting courses of bending moment \(M\left( {s,t} \right) \) at point \(s=70\) m, and of top tension force \(T_L \left( t \right) \) before and after the optimisation.

In all analysed cases the riser top end’s vertical displacements needed to stabilise the moments at the selected point, or the tension force, did not exceed 1.1 m. The choice of a better stabilisation requires direct comparison of the resulting courses. Compared below are the two ways considered to stabilise movement amplitude \(a=4\) m.

It may be found by analysing courses \(M\left( {s,t} \right) \) in Fig. 12a that the bending moment at point \(s=70\) m is better stabilised in case O1. The difference \(M^{\max } -M^{\min } \)for the results after optimisation in case O1 is 1.33 kN, and in case O2 is 5.4 kN, whereas the resulting \(T_L \left( t \right) \) courses differ only slightly (Fig. 12c). Similar findings were observed when analysing the other courses for amplitudes \(a=3\) and 5 m.

The riser’s top end positions before and after the optimisation is shown in Fig. 13.

In case O1, when the bending moment was stabilised at the indicated point in the two motion cycles, similar trajectories were obtained of the riser top end’s movement projected on XY and YZ planes. It is different when the riser’s tension force is stabilised, i.e. in case O2, when the resulting trajectories in the first and second cycles vary considerably.

Both the stabilisation methods herein reported have effect of the reduction of the bending moment and the tension force alike. Shown in Table 6 are the calculated differences between the maximum and minimum M and \(T_L \).

Table 6 Differences between maximum and minimum bending moment and top tension before and after optimisation
Full size table

In the first optimisation case (O1) differences \(M^{\max } -M^{\min } \)did not exceed 1.6 kN, which at the initial difference of approx. 34 kN, should be considered a very good result. Better results in the top tension minimising were obtained in case O1, where they were slightly better than in case O2. Difference \(T_L^{\max } -T_L^{\min } \)after the optimisation is on average higher by 5.2 kN in case O1 than in case O2.

6 Conclusions

The riser dynamics model formulated in this study features high numerical effectiveness. This makes it suitable for solving certain optimisation tasks. They consist in such a selection of riser top end’s vertical displacements that despite its periodic movement in the horizontal plane the stresses from bending moments at certain points are stabilised. It is also indicated how the distance riser’s top and bottom end effects its curvature and changes its natural vibration frequency. The optimisation results shown in this paper are fragmentary. But it is possible to carry out more calculations, which could provide a learning set for ANN (artificial neural network), as shown in [7]. Because AHC (active heave compensation) devices are used in the practice, the proposed algorithms could be implemented in practice.