1 Introduction

In the last decades, significant success has been showed by geophysics in oil and mineral ores exploration. Several techniques were proposed for the detection or/and mapping of hidden deposits and structures related to hydrocarbon accumulation. Of course, borehole geophysics is one of the most widely used of all geophysical tools. It used to obtain further in-depth (in situ) information that is crucial in better understanding of subsurface conditions via measuring, investigating, and analyzing the physical properties of the surrounding rocks by means of the drilled borehole. The most frequent and useful applied borehole geophysical methods are based on self-potential, electrical resistivity, sonic or acoustic velocity, temperature, natural and induced radioactivity. It is possible to figure out the drilled wells as an example by examining core samples but the gained information via this way would be incomplete even useless to define the nature of the drilled rocks and clarify or distinguish between the types of fluids presented in the rock formations if not complemented by certain new borehole logging techniques which represent a tremendous source of information (Serra 1984). Substantially, the measured data through these techniques are typically effective in characterizing geologic, fluid flow, fracture patterns, and structural properties especially with the continual refinement that have been launched to the equipment and the automated interpretation systems used for this purpose (Aguilera 1980; Bonter et al. 2019; Akbar 2021).

There has been a great development related to well-logging technology. The year 1980 marked the beginning of a qualitative leap in the interpretation and processing of wireline logging data collected from deep boreholes. Several computer-based inversion methods equipped with quality checking tools have been launched by petroleum companies for evaluating hydrocarbon formations such as Global system by Schlumberger (Mayer and Sibbit 1980), Ultra system by Gearhart (Alberty and Hashmy 1984), and Optima system by Baker Atlas (Ball et al. 1987). These computer-processed log interpretation systems provide more accurate and reliable estimation of petrophysical properties such as porosity, water saturation and matrix volumes compared to the conventional (quick look or deterministic) methods. Via the inversion methods, all the available data sets are combined in a joint inversion procedure to accurately derive the petrophysical parameters, while they are derived by using the conventional ones separately from each other by the analysis of a specific single well log. Inversion of well-logging data using these systems is conducted in a local way which means processing data acquired in a particular depth-point and providing an estimate for the petrophysical parameter only to that point in a set of separate inversion runs (Mayer and Sibbit 1980; Drahos 2005). Such local inverse problem can be solved by using linear optimization techniques (Marquardt 1963) with obtaining fast and satisfactory results in typical cases. Since the number of probe measurements to some extent exceeds that of the inversion unknowns to be determined in each depth-point, the problem represents a marginal over-determined inverse one along the borehole. It is a known fact that in the case of inversion of a small number of measurement data (and poor a priori information), the result is strongly affected by the measurement error (noise), thus we not always obtain a satisfactory result in terms of the accuracy and reliability of the local parameter estimation (Dobróka et al. 2016). It is possible to overcome this problem and obtain more accurate results by increasing the measured information from several well logs, but it also has known technological limitations and additional costs. Given that the truthful calculation of hydrocarbon reserves demands the most reliable estimations of the petrophysical parameters by reducing the harmful effect of data noise, a new method called interval inversion has been introduced for the analysis of open-hole logging data (Dobróka 1995; Dobróka and Szabó 2001).

By means of the interval inversion method, all data of a longer depth interval are processed in one joint inversion procedure. The petrophysical properties of the geologic formations (unknowns) are related to the measured data by setting depth-dependent response functions. A series expansion-based approach (Dobróka 1995) is suitable for discretizing the model parameters and approximating them not only in one point but in the entire processed depth-interval as well. By this formulation, the relative number of measured data compared to the series expansion coefficients which represent the unknowns of the inverse problem is increased. Hence, a high data to unknown parameter overdetermined ratio can be achieved which enhances the quality of the interpretation results (Dobróka and Szabó 2002, 2005). The method was further developed, and the so-called zone parameters are computed with the petrophysical parameters as a new inversion unknowns (Dobróka et al. 2007; Dobróka and Szabó 2011). Also, complex reservoirs were processed by the method, thus several rock matrix components which may be presented in volcanic or metamorphic can be determined (Dobróka et al. 2012). The application of the method also extended to evaluate organ-rich shale formations (Szabó and Dobróka 2020). In case of layer co-ordinates determination, the local inversion method gives an estimate only for the petrophysical parameters at a given depth point and does not contain information about the layer boundaries. In this case, the estimation of the rock interfaces is considered using another non-inversion procedure. Giving that, the entire measurement datasets collected from a greater depth interval contains information about the layer boundaries and since the interval inversion method processes the entire dataset in a joint inversion process to define the layer boundaries by developing an appropriate algorithm within the inversion (Dobróka et al. 2009; Dobróka and Szabó 2012, 2015).

In view of the great benefits of the interval inversion algorithm in determining the layer boundaries and petrophysical parameters, we further developed the 2D interval inversion approach which integrates dataset of several neighbouring deep wells to estimate lateral change of layer thickness together with the lateral and vertical variation of the petrophysical parameters. In this study, we apply Legendre polynomials as orthogonal set of basis functions instead of (non-orthogonal) power functions used in our earlier applications. Thus, 2D petrophysical models can be obtained in a more accurate and reliable way, and geometry of the layer boundary of the geologic structures can be figured if the specified wells are in the same range.

2 Inversion methodology

2.1 Forward problem and discretization scheme

In formulating the forward problem, the model vector of the petrophysical parameters is introduced as following

$${\mathbf{m}}\left( {x,z} \right) = \left[ {\emptyset \left( {x,z} \right), S_{x0} \left( {x,z} \right), S_{w} \left( {x,z} \right), V_{sh} \left( {x,z} \right)} \right]^{{\text{T}}} ,$$
(1)

where x and z represent the horizontal and vertical coordinates, \(\emptyset\) is porosity, \({S}_{x0}\) and \({S}_{w}\)—water saturation in invaded and uninvaded zones, respectively, and \({V}_{sh}\) is volume of shale. The volume of sand \({V}_{sd}\) is derived from the material balance equation as

$$\emptyset + V_{sh} + V_{sd} = 1.$$
(2)

The k-th observed data is calculated from the model parameters in Eq. (1) in a certain petrophysical relationship which is termed as response functions and connect the model parameters with the log measurements via

$$d_{k}^{{\left( {calc} \right)}} \left( {z,x} \right) = g_{k} \left( {m_{1} \left( {x,z} \right), \ldots \ldots ,m_{M} \left( {x,z} \right)} \right),$$
(3)

where \({{d}_{k}}^{\left(calc\right)}\left(z,x\right)\) indicates the k-th calculated data in depth z under horizontal distance x. A detailed survey of the response functions of (Alberty and Hashmy 1984) are given in the following equations

$$GR = \rho_{b}^{ - 1} \left( {V_{sh} GR_{sh} \rho_{sh} + V_{sd} GR_{sd} \rho_{sd} } \right) ,$$
(4)
$$K = \rho_{b}^{ - 1} (\emptyset s_{x0} k_{mf} { }\rho_{mf} + V_{sh} K_{sh} \rho_{sh} + V_{sd} K_{sd} \rho_{sd} ,$$
(5)
$$Th = \rho_{b}^{ - 1} (\emptyset s_{x0} Th_{mf} { }\rho_{mf} + V_{sh} Th_{sh} \rho_{sh} + V_{sd} Th_{sd} \rho_{sd} ,$$
(6)
$$U = \rho_{b}^{ - 1} (\emptyset s_{x0} U_{mf} { }\rho_{mf} + V_{sh} U_{sh} \rho_{sh} + V_{sd} U_{sd} \rho_{sd} ,$$
(7)
$$\emptyset_{N} = \emptyset (\emptyset_{N,mf} - \left( {1 - s_{x0} } \right)C_{cor} { } - { }2\emptyset \left( {1 - s_{x0} } \right)S_{hf} \left( {1 - 2.2\rho_{hc} } \right)\cdot[ {1 - \left( {1 - s_{x0} } \right)\left( {1 - 2.2\rho_{hc} } \right)} ] + V_{sh} \emptyset_{N,sh} + V_{sd} \emptyset_{N,sd} ,$$
(8)
$$\rho_{b} = \emptyset \left[ {\rho_{mf} - 1.07\left( {1 - s_{x0} } \right)\left( {\alpha_{0} - \rho_{mf} - 1.24\rho_{hc} } \right)} \right] + V_{sh} \rho_{sh} + V_{sd} \rho_{sd} ,$$
(9)
$$\Delta t = \emptyset \left[ {\Delta t_{{{\text{mf}}}} s_{x0} + \left( {1 - s_{x0} } \right)\Delta t_{ch} { }} \right] + V_{sh} \Delta t_{{{\text{sh}}}} + V_{sd} \Delta t_{sd} ,$$
(10)
$$\frac{1}{{R_{d} }} = \frac{{\emptyset^{2} S_{w}^{2} }}{{aR_{w} \left( {1 - v_{sh } } \right)}} + \frac{{v_{sh } s_{w} }}{{R_{sh} }} ,$$
(11)
$$\frac{1}{{R_{s} }} = \frac{{\emptyset^{2} S_{x0}^{2} }}{{aR_{w} \left( {1 - v_{sh } } \right)}} + \frac{{v_{sh } s_{x0} }}{{R_{sh} }} ,$$
(12)
$$P_{e} = \emptyset \left[ {s_{x0} Pe_{mf} + \left( {1 - s_{x0} } \right)Pe_{hc} } \right] + V_{sh} + V_{sd} + V_{c} { }Pe_{c} .$$
(13)

Equations (4)–(13) comprise the volumetric fractions of the rock’s solid and fluid constituents, and also the physical properties of mud filtrate (mf), hydrocarbon (hc), shale (sh), and sand (sd). The textural parameters which include cementation exponent (m), saturation exponent (n) and tortuosity factor (a) are treated as known constants. The denotations and actual values of zone parameters can be seen in Table 1. Core information and literatures can be utilized to determine the values of the zone parameters (Dobróka et al. 2016).

Table 1 Well log types and the zone parameters applied to 2D interval inversion
Full size table

A series expansion-based technique (Dobróka 1995) is utilized to discretize the petrophysical parameters for numerical computations

$$m_{i} \left( {x,z} \right) = \mathop \sum \limits_{q = 1}^{{Q_{i} }} \mathop \sum \limits_{l = 1}^{{L_{i} }} B_{ql}^{\left( i \right)} {\Psi }_{q - 1} \left( {x){\Psi }_{l - 1} (z} \right),$$
(14)

where \({m}_{i}\) denotes the i-th petrophysical parameter (i = 1,2,…,M), \({B}_{ql}\) is the ql-th expansion coefficient and \({\Psi }_{q}\left(x\right)\mathrm{ and }{\Psi }_{l}\left(\mathrm{z}\right)\) are the q-th and l-th basis functions depending on one of the two coordinates, respectively. Orthogonal Legendre polynomials are used to approximate the model parameters for obtaining more reliable solutions: \({\Psi }_{q-1}\left(x\right)={P}_{u}\left(x\right)={({2}^{u} u!)}^{-1}\frac{{d}^{u}}{{dz}^{u}}{({z}^{2}-1)}^{u}\), where u is the degree of polynomial. By applying Eq. (14) to expand the model parameters in Eq. (1) into series, the expansion coefficients represent the unknowns of the 2D inverse problem

$${\mathbf{B}} = \left[ {B_{1}^{\left( 1 \right)} , \ldots ,B_{Q}^{\left( 1 \right)} , B_{1}^{\left( 2 \right)} , \ldots ,B_{Q2}^{\left( 2 \right)} , B_{1}^{\left( M \right)} , \ldots ,B_{QM}^{\left( M \right)} } \right]^{{\text{T}}} .$$
(15)

Also, the k-th response function in Eq. (3) becomes

$$d_{k}^{{\left( {calc} \right)}} \left( {x,z} \right) = g_{k} \left( {B_{1}^{\left( 1 \right)} , \ldots ,B_{QM}^{M} } \right).$$
(16)

The solution of the inverse problem can be given by minimizing the L2-norm based objective function

$$E = \frac{1}{FPN}\mathop \sum \limits_{f = 1}^{F} \mathop \sum \limits_{p = 1}^{P} \mathop \sum \limits_{k = 1}^{N} \left( {\frac{{d_{fpk}^{{\left( {meas} \right)}} - d_{fpk}^{{\left( {calc} \right)}} }}{{d_{fpk}^{{\left( {meas} \right)}} }}} \right)^{2} = \min ,$$
(17)

where F denotes the number of boreholes, P is the number of depth points processed in the interval inversion procedure and N is the same number of probes applied in each well.

Not only the lateral variation of petrophysical properties, but that of the layer boundaries can also be described by the suggested discretization method. Similar to Eq. (14), the layer thickness functions can also be expanded into series using proper basis functions and the expansion coefficients can be treated as inversion unknowns. We discretize the thickness function of the r-th layer as

$$h_{r} \left( x \right) = \mathop \sum \limits_{t = 1}^{{T_{r} }} C_{t\;}^{\left( r \right)} \psi_{t-1\;}\left( x \right),$$
(18)

where Ct is the t-th expansion coefficient and \({\Psi }_{t}\left(\mathrm{x}\right)\) is the t-th univariate basis function depending on the lateral coordinate. When using Legendre polynomials, we scale the values of x coordinates to the range of [− 1,1], in which the polynomials are orthogonal. Thus, one can reduce the magnitude of the unknown series expansion coefficients and decrease the correlation between them to assure more reliable estimation. The use of bivariate series expansion can be avoided for some practical reasons. The depth of a given layer can be given by expansion coefficient C1, which equals to the depth coordinate of the (upper or lower) boundary of the homogenous (plane) layer. A condition that the layers could not intersect each other and the number of layers is constant during the inversion procedure should be met. This requirement meets when the initial values of C1 are properly set and their search domain is preliminary constrained. In 2D inversion, the initial layer boundary coordinates can be assumed as the same constant in each well. Practically, the expansion coefficients corresponding to the higher degree basis functions (t ≥ 2) are slightly changed to describe the thickness variation around the depth level given by C1. By using a differential genetic algorithm or other global optimization method, it is also possible to fix the search domain of expansion coefficients prior to inversion (Dobróka and Szabó 2012). The vector of inversion unknowns is formed by expanding vector B (Eq. (15)) by coefficients C. In case of having a great overdetermination ratio, the 2D interval inversion method solved by minimizing norm (17) may give an automated estimation for both the petrophysical properties and the layer boundary coordinates in a stable and accurate inversion procedure.

2.2 Global inversion algorithm

Unlike the linear optimization methods which could possibly bring the solution to a local minimum, global optimization seeks the absolute minimum of the objective function. Some of the most used global optimization methods in geophysics are Simulated Annealing (Metropolis et al. 1953), the Genetic Algorithm (Holland 1975) and Particle Swarm Optimization (Kennedy and Eberhart 1995). Simulated Annealing (SA) was originally developed to model the thermal equilibrium state of solids, which is analogously used in this study to search the global optimum of objective function (E) defined in Eq. (17).

The method depends on the modification of the model vector, in this case the i-th model parameter of the n-th iteration is modified properly as follow

$$m_{i}^{{\left( {n + 1} \right)}} = m_{i}^{\left( n \right)} \pm b,$$
(19)

where b is the amount of perturbation randomly changing in the domain of\(0\le b\le {b}_{max}\), while parameter \({b}_{max}\) is renewed according to \({b}_{max}={b}_{max}.\varepsilon\), where \(\varepsilon\) is a specified number from the interval of 0 and 1. During the random seeking, the energy function E is calculated and compared with the previous one in every iteration step (ΔE). The acceptance probability of the new model relies on the Metropolis criteria

$$p\left( {\Delta E,T} \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {if\;\;\Delta E \le 0} \hfill \\ {e^{ - \Delta E/T} ,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.,$$
(20)

where the model is always accepted when the value of energy function is lower in the new state than that of the previous one. If the energy of the new model increased, there is also some probability of acceptance depending on the values of energy E and control temperature T. If the criterion

$$\alpha \le p\left( {\Delta E} \right)$$
(21)

fulfills, the new model is accepted, else it is rejected (α is a random number generated with uniform probability from the interval of 0 and 1). This criterion assures the escape from the local minima of the objective function. It was approved that the global minimum is guaranteed when the schedule cooling of Geman and Geman (1984) is used

$$T\left( n \right) = \frac{{T_{0} }}{{{\text{ln}}\left( n \right)}} \left( {n > 1} \right),$$
(22)

where T0 is the initial temperature. The SA algorithm is very effective, but the logarithmic reduction of temperature in Eq. (22) is rather time consuming. Various attempts were made to shorten the CPU time. Ingber (1989) proposed a modified SA algorithm called Very Fast Simulated Re-Annealing (VFSR). Consider different ranges of variation for each model parameter

$$m_{i}^{min} =\, \le m_{i}^{\left( k \right)} \le m_{i}^{max} .$$
(23)

The perturbation of the i-th model parameter at iteration (n + 1) is as follows

$$m_{i}^{{\left( {n + 1} \right)}} = m_{i}^{n} + y_{i} \left( {m_{i}^{max} - m_{i}^{min} } \right),$$
(24)

where yi is a random number between − 1 and 1 generated from a specified non-uniform probability distribution function. The global optimum is guaranteed the i-th cooling schedule being as the following

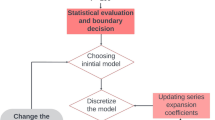
$$T_{i} \left( n \right) = T_{0,i} {\text{exp}}\left( { - c_{i} \sqrt[M]{k}} \right),$$
(25)

where T0,i is the initial temperature of the i-th model parameter, ci is the i-th control parameter, and M is the number of model parameters. A detailed flowchart of the inversion procedure can be seen in Fig. 1.

Fig. 1
figure 1

Flowchart illustrating the 2D interval inversion procedure using a hybrid (VFSA + DLSQ) optimization technique

Full size image

2.3 Quality of parameter estimation

After reaching the near vicinity of the optimum via the VFSR algorithm and for quality assurance on inversion results we switch the Damped Least Squares (DLSQ) method to perform linear optimization (Marquardt 1959). At the end of the procedure the estimation error can be computed by implementing discrete inverse theory (Menke 1984). In case of the linear methods, the connection between data covariance cov (d) and covariance matrix cov (m) model is

$$cov \left( {\mathbf{m}} \right) = {\varvec{G}}^{ - g} cov({\varvec{d}}^{{\left( {obs} \right)}} )\left( {{\varvec{G}}^{ - g} } \right)^{{\text{T}}} ,$$
(26)

where G−g denotes the general inverse matrix of the DLSQ method. The model covariance matrix is computed with the covariance matrix of series expansion coefficients and Legendre polynomials of different degrees as basis functions (Dobróka et al. 2016). If the dispersion of the data is known, the above formula can be used to determine the error of approximated parameters. The error of the i-th model parameter is estimated from the main diagonal of the covariance matrix

$$\sigma_{mi} = \left[ {cov \left( {\mathbf{m}} \right)_{ii} } \right] ^{1/2} .$$
(27)

The accuracy of the inversion outputs can also be measured by applying the correlation coefficient, which define the degree of linear dependence between the i-th and j-th model parameters

$$corr \left( {\mathbf{m}} \right)_{ij} = \frac{{corr \left( {\mathbf{m}} \right)_{ij} }}{{\left[ {corr \left( {\mathbf{m}} \right)_{ij} corr \left( {\mathbf{m}} \right)_{jj} } \right]^{1/2} }}.$$
(28)

If the correlation coefficient is close to ± 1, the model parameters have strong connection, indicating an unreliable solution. Reliable solution requires a model with weakly correlated parameters with absolute value of correlation coefficients less than 0.4. It is sometimes useful to characterize the correlation matrix by a single scalar, which is known as the mean spread

$$S = \left[ {\frac{1}{{M\left( {M - 1} \right)}}\mathop \sum \limits_{i = 1}^{M} \mathop \sum \limits_{j = 1}^{M} \left( {corr \left( {\mathbf{m}} \right)_{ij} - \delta_{ij} } \right)^{2} } \right]^{1/2} ,$$
(29)

where δ is the Kronecker-delta symbol (which is 1 if i = j, and 0 otherwise). Also, another index number which characterize the fitting between the measured and calculated can be computed on the resultant model. In percent relative data distance is

$$D_{d} = 100\left( E \right)^{1/2} .$$
(30)

In the case of synthetic model tests, another index that evaluates the goodness of model fit can be introduced. In percent the model distance is

$$D_{m} = \left[ {\frac{1}{LM}\mathop \sum \limits_{l = 1}^{L} \mathop \sum \limits_{i = 1}^{M} \left( {m_{li}^{\left( e \right)} - m_{li}^{\left( r \right)} } \right)^{2} } \right]^{1/2} \cdot 100,$$
(31)

where \({m}_{li}^{\left(e\right)}\) and \({m}_{li}^{\left(r\right)}\) denote the i-th estimated and exact known model parameters respectively in the l-th layer (L is the total number of layers).

3 Numerical results

To test the proposed inversion algorithm a two-layered structure made up of shale and hydrocarbon bearing sand was used (Fig. 2). To simulate real borehole measurements, the synthetic data are calculated in six wells (W-1, W-2,…,W-6) with dz = 0.1 m sampling interval. The interval length is 20 m, and 5 percentage Gaussian distributed noise is added to N = 12,060 data samples. The processed well logs are illustrated in Fig. 3. The target model of the inverse problem is provided in Table 2.

Fig. 2
figure 2

2D synthetic model showing the lithology, the target, the intial and the estimated layer boundaries

Full size image
Fig. 3
figure 3

Noisy synthetic well logs computed in wells W-1–W-6

Full size image
Table 2 Petrophysical parameters and layer boundary coordinates of the target model
Full size table

For our 2D inversion the model parameters (\(\emptyset\), Sx0 and Vsh) with the layer boundaries were discretized by using Legendre polynomials of degree 4 as basis functions. In this case, the number of unknowns (expansion coefficients) was Q = 35, delivering an overdetermination ratio of 344. The main component of rock matrix was quartz (Vsd), possibly will be obtained by the material balance equation out of inversion. Also, water saturation (SX0) in the disturbed zone was computed by the empirical formula SX0 = SW0.2, which is based on huge amount of observations of well log analysts in Miocene gas reservoirs of the Pannonian basin (the exponent of Sw may change between 1/2 and 1/5). One more important parameter inherent the calculation of hydrocarbon saturation (Shc) could be obtained by subtracting water saturation (SW) from unity in the uninvaded zone.

The initial model comprised first-gauss values of expansion coefficients of the petrophysical parameters and the layer boundary. Solving our 2D interval inversion was achieved by utilizing a hybrid VFSA + DLSQ optimization algorithm. The petrophysical parameters and layer boundaries were derived from 35 expansion coefficients which can be seen in Table 3. The development of convergence during inversion can be found in Fig. 4 showing that the procedure was stable and convergent. The optimum solution was obtained at Dd = 5.1% data misfit and Dm = 4.9% model distance. Estimates for petrophysical parameters were close to desired values with small estimation errors as shown in Table 4 and Figs. 5, 6, 7. Mean spread value was S = 0.32 which confirms the reliability of the solution. Also, accurate and reasonable values were obtained for petrophysical parameters derived from the inversion results as shown in Table 5.

Table 3 Petrophysical parameters and layer boundary coordinates estimated by 2D interval inversion (polynomial degree is n = 4)
Full size table
Fig. 4
figure 4

Development of convergence during 2D interval inversion (polynomials degree = 4), a data distance vs. iteration steps, b model distance vs. iteration steps curves

Full size image
Table 4 Estimated parmaeters by 2D interval inversion (degree of polynomials is 4)
Full size table
Fig. 5
figure 5

Results of 2D hybrid (VFSA + DLSQ) interval inversion in drill holes W1-W6: a target porosity distribution, b estimated porosity, c) estimation errors of porosity

Full size image
Fig. 6
figure 6

Results of 2D hybrid (VFSA + DLSQ) inversion in drill holes W1-W6: a target water saturation distribution, b estimated water saturation, c estimation error of water saturation values

Full size image
Fig. 7
figure 7

Results of 2D hybrid VFSA + DLSQ inversion in drill holes W1-W6: a Target shale content b estimated shale content c Estimated errors

Full size image
Table 5 Petrophysical parameters derived from the 2D inversion results (polynomial degree is n = 4)
Full size table

It must be mentioned that a realistic estimation for the accuracy of inversion results can only be given in the knowledge of the full data covariance matrix (in Eq. (26)). Since well logging operations lack the repetition of measurements, we do have only approximate information of the error of the observed quantities. Moreover, the unknown modeling error coming from the simplified Eqs. (4)–(13) is also added to the variance of input data. In the industry, generally the data are considered uncorrelated and of the same variance. In our methodology, it is allowed to incorporate the full covariance matrix of well logging parameters (if it is measured) to improve the reliability of error estimation. Earlier a significant increase of estimation accuracy was achieved for interval inversion results against local (depth by depth) inversion (Dobróka et al. 2016). The error intervals given in the present study is consistent with that results and the error values are for information purposes.

It is also worth to be noting that describing fine structures and sudden changes require more series coefficients which can be achieved by increasing the polynomials degree in Eq. (14). In our synthetic modeling by increasing the polynomials degree to 10, the number of unknowns to be estimated are increased up to 77, resulting in decrease of the overdetermined ratio, which may affect negatively the quality of inversion results. However, owing to a large number of inverted data, we could obtain reasonable results as seen in Table 6. The data and model distances are illustrated in Fig. 8, also the 2D cross-section of petrophysical parameters is shown in Fig. 9.

Table 6 Estimated parameters by 2D interval inversion (degree of polynomials is 10)
Full size table
Fig. 8
figure 8

Development of convergence during 2D interval inversion (degree of polynomials is 10). a Data distance vs. iteration step, b Model distance vs. iteration step

Full size image
Fig. 9
figure 9

Results of 2D inversion in drill holes W1–W6 with 10 polynomials degree: a porosity b water saturation c shale content

Full size image

4 Field results

It is reasonable to apply the proposed method to field data following successfully assessing it by synthetic tests. As a consequence, the 2D interval inversion approach was used to process in situ-well logging measurements obtained in four boreholes, W-1–W-4, located in an Egyptian hydrocarbon field (Fig. 10a). The investigated area namely Al Baraka oilfield which is considered the first discovering outside Egypt’s conventional producing fields. The concession is situated in the Komombo Basin, located 800 km south of Cairo and is characterized by multiple stacked sand reservoirs. The concession contains the producing Al Baraka oilfield, covering a development area of 50 km2. The major reservoir unit in the study area consists of mainly alternating sandstone and shale sequences known as Abu Ballas Formation and Six Hills Formation. The available data samples corresponding to given Gamma-ray (GR), Shallow- (Rs) and Deep (Rd) resistivity, neutron porosity (\(\emptyset\)N), and bulk density (ρb).

Fig. 10
figure 10

a Location map of the drilled wells in Komombo Basin, Egypt, b the convergence of the 2D inversion procedure shown by the data distance vs. number of iterations curve

Full size image

The maximum number of iterations for the inversion operation was chosen 5000. In the first layer, the initial values of the expansion coefficients for porosity, water saturation, and shale content are 0.25, 0.40, and 0.09, respectively. In the second, they are 0.16, 1.0, and 0.7, and in the third, they are 0.23, 0.4, and 0.08. Regarding to layer boundaries, H1(x) = 4 m and H2(x) = 12 m. The solution was observed at Dd = 6.5% relative data distance (Fig. 10b). The estimated model parameters and their errors are provided in Table 7, together with the calculated mean spread value which was R = 0.32. Further, 2D models of the results are illustrated in Fig. 11. It can be noticed that the investigated interval revealed two types of lithology, i.e., sand (hydrocarbon-bearing zones) and shale. The interpreted lithological results are well supported by the geological and stratigraphic settings of the investigated area which is a half-graben system filled with thick non-marine sediments deposited during Early Cretaceous (Hauterivian to Barremian) followed by marine deposition during Albian/Cenomanian (argillaceous sandstones and shales) and later shales and marine limestones during Late Cretaceous and early Tertiary (Dolson et al. 1999). Furthermore, the estimated petrophysical parameters utilizing 2D interval inversion showed a close agreement with the results of previous studies by using traditional analysis (Ali 2015; Othman et al. 2015; Senosy et al. 2020).

Table 7 Petrophysical parameters and layer boundary coordinates estimated by 2D interval inversion (polynomial degree is n = 10)
Full size table
Fig. 11
figure 11

Results of 2D inversion in drill holes W1–W4, Komombo Basin, Egypt: a porosity distribution, b water saturation distribution, c shale content distribution

Full size image

5 Conclusions

In the present study, we show a newly developed 2D interval inversion approach for evaluating 2D petrophysical models. The proposed method allows for the determination of lateral changes of layer boundaries as well as the lateral and vertical variation of petrophysical parameters along boreholes profile in stable and convergent procedure. Accordingly, two-dimensional models were created, the geometry of the geological structures and the morphology of hydrocarbon reservoirs were well defined as well. The feasibility of the modified method was verified on synthetic and Egyptian field data related to hydrocarbon bearing formations. With a high overdetermination ratio which considered the essential features of the interval inversion method, we successfully estimate the model parameters with minimal errors of a synthetic model built up of two-layers. Also, accurate results were obtained in case of multi-layers’ application of Egyptian field data. In light of that, the only criterion for making the method more effective and powerful is to keep the high overdetermined ratio. The developed method can be extended and applied to groundwater (or geothermal) reservoirs and unconventional hydrocarbon formations assuming 2D and/or 3D geological features.