Integrated workflow incorporating the Hurst exponent and interval inversion for evaluating groundwater formations

Abstract

A novel well-log-analysis approach is presented for an improved prediction of petrophysical properties in groundwater formations. Geophysical well logs are simultaneously processed for quantifying the lithology, storage capacity, and water flow parameters. A fully automated data processing workflow is proposed, the feasibility of which is assured by an appropriate starting model set by the joint application of factor analysis and the Hurst exponent, and a solution of a highly overdetermined inverse problem. The Hurst exponent is used for zone boundary detection, which assists the series expansion-based interval inversion method applied for estimation of the petrophysical parameters of clastic formations. The hydraulic conductivity as a well log is directly derived from the inversion results. The workflow is tested using both synthetic data contaminated with 5% Gaussian distributed noise and real data collected from a thermal water well in Baktalórántháza, eastern Hungary. At the test site, the Hurst exponent extracted from the wireline logs allows one to divide the processed interval into subzones around the Pleistocene-Miocene boundary. The observed wireline logs are inverted to estimate the volumetric parameters (porosity, shale content, water saturation, etc.) of the same zones. The predicted parameters, including hydraulic conductivity, reveal that Pleistocene sediments contain good aquifers with formation quality varying with depth. The shale volume and hydraulic conductivity logs show a proper match with the core data, which confirms the results of the comprehensive analysis. The suggested workflow is recommended for the evaluation of groundwater formations located in different depth domains, from unsaturated sediments to geothermal reservoirs.

Résumé

Une nouvelle approche d’analyse des diagraphies est présentée pour une meilleure prédiction des propriétés pétrophysiques dans les formations aquifères. Les diagraphies géophysiques sont traitées simultanément pour quantifier la lithologie, la capacité de stockage et les paramètres d’écoulement de l’eau. Un processus de traitement des données entièrement automatisé est proposé, sa faisabilité est assurée par un modèle de départ approprié défini par l’application conjointe de l’analyse factorielle et de l’exposant de Hurst, et par la résolution d’un problème inverse fortement surdéterminé. L’exposant de Hurst est utilisé pour la détection des limites de zones, ce qui facilite la méthode d’inversion d’intervalle basée sur l’expansion des séries, appliquée pour l’estimation des paramètres pétrophysiques des formations clastiques. La conductivité hydraulique en tant que diagraphie de puits est directement dérivée des résultats de l’inversion. Le plan de travail est testé en utilisant à la fois des données synthétiques contaminées par un bruit gaussien distribué à 5% et des données réelles recueillies dans un puits d’eau thermale à Baktalórántháza, dans la partie orientale de la Hongrie. Sur le site d’essai, l’exposant de Hurst extrait des diagraphies filaires permet de diviser l’intervalle traité en sous-zones autour de la limite Pléistocène-Miocène. Les diagraphies filaires observées sont inversées pour estimer les paramètres volumétriques (porosité, teneur en schiste, saturation en eau, etc.) des même zones. Les paramètres prédits, y compris la conductivité hydraulique, révèlent que les sédiments du Pléistocène contiennent de bons aquifères dont la qualité de la formation varie avec la profondeur. Les diagraphies du volume de schiste et de la conductivité hydraulique correspondent bien aux données des carottes, ce qui confirme les résultats de l’analyse globale. Le plan de travail proposé est recommandé pour l’évaluation des formations aquifères situées dans différents domaines de profondeur, des sédiments non saturés aux réservoirs géothermiques.

Resumen

Se presenta un novedoso método de análisis de registros de pozos para mejorar la predicción de las propiedades petrofísicas de las aguas subterráneas. Los registros geofísicos de pozos se procesan simultáneamente para cuantificar la litología, la capacidad de almacenamiento y los parámetros de flujo de agua. Se propone un flujo de procesamiento de datos totalmente automatizado, cuya viabilidad queda garantizada por un modelo inicial adecuado establecido mediante la aplicación conjunta del análisis factorial y el exponente de Hurst, y la solución de un problema inverso altamente sobredeterminado. El exponente de Hurst se utiliza para la detección de límites zonales, lo que ayuda al método de inversión de intervalos basado en la expansión de series que se aplica para la estimación de los parámetros petrofísicos de formaciones clásticas. La conductividad hidráulica como registro de pozo se deriva directamente de los resultados de la inversión. El flujo de análisis se prueba utilizando datos sintéticos contaminados con un 5% de ruido gaussiano distribuido y datos reales recogidos en un pozo de agua termal en Baktalórántháza, al este de Hungría. En el lugar de la prueba, el exponente de Hurst extraído de los registros realizados con cable permite dividir el intervalo procesado en subzonas en torno al límite Pleistoceno-Mioceno. Los registros observados se invierten para estimar los parámetros volumétricos (porosidad, contenido de arcilla, saturación de agua, etc.) de las mismas zonas. Los parámetros previstos, incluida la conductividad hidráulica, revelan que los sedimentos pleistocenos contienen buenos acuíferos con una calidad de formación que varía con la profundidad. Los registros de volumen de arcillas y conductividad hidráulica muestran una correspondencia adecuada con los datos de los testigos, lo que confirma los resultados del análisis completo. El flujo de tareas sugerido se recomienda para la evaluación de formaciones de aguas subterráneas situadas en diferentes dominios de profundidad, desde sedimentos no saturados hasta reservorios geotérmicos.

摘要

提出了一种新的测井分析方法, 以改进对地下水结构中岩石物性的预测。地球物理测井数据同时用于量化岩性、储存能力和水流参数。我们提出了一个全自动化的数据处理工作流程, 其可行性由因子分析和Hurst指数的联合应用建立了适当的初始模型, 并解决了高度超定的反问题。Hurst指数用于区域边界检测, 有助于基于级数展开的区间反演方法, 用于估算碎屑岩层的岩石物性参数。作为测井数据的水力导数可以直接从反演结果中获得。该工作流程经过了综合使用了5%高斯分布噪声影响数据和从匈牙利东部的Baktalórántháza热水井收集的真实数据进行测试。在测试现场, 从测井数据中提取的Hurst指数允许将处理的区间分成围绕更新世-中新世的子区域。观察到的电缆测井数据被反演以估算相同区的体积参数(孔隙度、页岩含量、水饱和度等)。预测的包括渗透系数等参数, 揭示了更新世沉积物含有质量随深度变化的良好含水层。页岩含量和渗透系数测井数据与核心数据表现出良好的匹配, 从而确认了综合分析的结果。推荐的工作流程适用于位于不同深度范围内从非饱和沉积物到地热储层的地下水结构评估。

Kivonat

A felszín alatti víztároló képződmények kőzetfizikai tulajdonságainak becslésére egy új fúrólyuk-geofizikai szelvényértelmezési eljárást mutatunk be. A szelvényeket egyidejűleg dolgozzuk fel a litológia, tárolókapacitás és az áramlási jellemzők meghatározása céljából. Egy teljesen automatizált adatfeldolgozási eljárást javaslunk, melynek alkalmazhatóságát a faktoranalízis és a Hurst-kitevő együttes alkalmazásával meghatározott kezdeti modell, valamint a nagymértékben túlhatározott inverz feladat megoldása biztosítja. A Hurst kitevőt a zónahatárok azonosítására használjuk, amely a törmelékes üledékek kőzetfizikai paramétereinek becslésére alkalmazott sorfejtéses intervalluminverziós módszert támogatja. A szivárgási tényező szelvényt közvetlenül az inverziós eredményekből származtatjuk. Az eljárást 5%-os Gauss-eloszlású zajjal terhelt szintetikus adatok, ill. a kelet-magyarországi Baktalórántházán mélyített termálvízkutató fúrásban mért szelvények felhasználásával vizsgáljuk. A mérési területen a fúrólyukszelvényekből számított Hurst kitevő lehetővé teszi a vizsgált mélységintervallum zónákra bontását és a pleisztocén-miocén határ azonosítását. A karotázs szelvények inverziójával becsülhetjük ezen zónákon belül a porozitást, agyagtartalmat, víztelítettséget, mint térfogatjellemző mennyiségeket. A becsült kőzetjellemzők és a szivárgási tényező értékek azt mutatják, hogy a pleisztocén üledékek jó víztartó rétegek. Az agyagtartalom és szivárgási tényező szelvények jó egyezést mutatnak laboratóriumi magadatokkal, mely megerősíti a szelvényértelmezés eredményét. A bemutatott eljárás a felszínközeli telítetlen üledékektől a geotermikus tározókig, különböző mélységi tartományokban elhelyezkedő víztároló képződmények értékelésére felhasználható.

Resumo

Uma nova abordagem de análise de perfil de poço é apresentada para uma melhor previsão de propriedades petrofísicas em formações de água subterrânea. Os registros geofísicos dos poços são processados simultaneamente para quantificar a litologia, a capacidade de armazenamento e os parâmetros de fluxo de água. É proposto um fluxo de trabalho de processamento de dados totalmente automatizado, cuja viabilidade é garantida por um modelo inicial adequado definido pela aplicação conjunta da análise fatorial e do expoente de Hurst, e uma solução de um problema inverso altamente sobredeterminado. O expoente de Hurst é utilizado para detecção de limites de zona, o que auxilia o método de inversão de intervalo baseado em expansão de séries aplicado para estimativa de parâmetros petrofísicos de formações clásticas. A condutividade hidráulica como perfil de poço é derivada diretamente dos resultados de inversão. O fluxo de trabalho é testado usando dados sintéticos contaminados com ruído distribuído gaussiano a 5% e dados reais coletados de um poço de água termal em Baktalórántháza, leste da Hungria. No local de teste, o expoente de Hurst extraído dos perfis wireline permite dividir o intervalo processado em subzonas em torno da fronteira Pleistoceno-Mioceno. Os perfis de perfilagem observados são invertidos para estimar os parâmetros volumétricos (porosidade, teor de xisto, saturação de água, etc.) das mesmas zonas. Os parâmetros previstos, incluindo a condutividade hidráulica, revelam que os sedimentos do Pleistoceno contêm bons aquíferos com qualidade de formação variando com a profundidade. Os registros de volume de xisto e condutividade hidráulica mostram uma correspondência adequada com os dados principais, o que confirma os resultados da análise abrangente. O fluxo de trabalho sugerido é recomendado para a avaliação de formações subterrâneas localizadas em diferentes domínios de profundidade, desde sedimentos não saturados até reservatórios geotérmicos.

Introduction

For several decades, borehole geophysical logs have served as one of the most reliable in situ information resources in the evaluation of geological formations. Well-log-analysis approaches, mostly adapted from the oil industry, are increasingly used in groundwater exploration and other hydrogeophysical investigations (Rubin and Hubbard 2006). Wireline logging methods can be classified according to the sensitivity of the recorded data to different rock characteristics. Well logging tools primarily sensitive to lithology may include the natural gamma-ray intensity, spontaneous potential, natural gamma-ray spectrometry, and borehole caliper and image logs, while porosity-sensitive measurements usually include the bulk density, neutron porosity, and acoustic travel-time logs (Serra 1986; Asquith and Krygowski 2006). Resistivity or induction log suites, including shallow, medium, and deep resistivity logs, are primarily used for water saturation estimation (Archie 1952). Open-hole logs are processed for providing basic information about the geometrical (e.g., layer boundaries, effective layer thicknesses, local dip direction, hole caliper etc.) and petrophysical parameters (e.g., porosity, shale content, water saturation, shale and sand volume etc.) of the rock formations. All of the aforementioned establish the identification of lithology, delineation and characterization of the groundwater aquifers, and the quantitative assessment of water reserves and quality (Csókás 1995). There are also several other geophysical or hydrodynamic parameters that are directly unmeasurable in boreholes. Some of them can be derived from the interpreted logs to give ample and continuous information along a borehole or between the wells. Although the hydraulic conductivity can be measured directly by a nuclear magnetic resonance instrument (Walsh et al. 2013), it is normally calculated using the observed logs, typically from the resistivity and porosity logs, and grain-size distribution curves available in the field (Szabó et al. 2015; Zhu et al. 2016).

The increasing demand for access to high quality observation data and interpreted parameters represents a great challenge for scientific research. Advanced measurement tools or arrays, and innovative inversion and machine learning algorithms, are required to be developed continuously so that they are applicable to complex geological situations (Cranganu et al. 2015; Kang et al. 2019; Szűcs et al. 2021). With respect to method development, this study offers a new alternative to hydrogeophysical data processing. From a historical viewpoint, there are two common theoretical or conceptual frameworks in well log analysis. Conventional approaches, such as the graphical cross-plot techniques or the deterministic methods involving a solution to an ill-posed algebraic problem, generally require several subsequent data processing steps. They basically derive one petrophysical parameter from a part of the observed logs, then in the next step, a new parameter is calculated from another well-log suit, or it is derived from the quantities estimated in the previous step (Sclumberger 1991). This workflow is relatively quick, but the main disadvantage of this concept is that it does not make efficient use of the common information contained in the entire dataset, and this approach is therefore unable to provide the desired estimation accuracy of the predicted parameters. Inverse modeling has become a vital technique to interpret well logging data, as such models can avoid the weaknesses of the aforementioned deterministic (and other single-log or quick-look) interpretation methods. In fact, inversion methods treat all model parameters as random variables and process all suitable well logs simultaneously in an automatic procedure to give an estimation of all petrophysical parameters with their accuracies (Alberty and Hashmy 1984; Ball et al. 1987). The uncertainty of the estimated model parameters can be given by applying the law of error propagation in a linearized inversion procedure (Menke 1984). In the quality check of the estimated model, crucial questions involve the accuracy of the input data and the reliability of the prior information which are used to constrain the solution of the inherently ambiguous inverse problem. In well log analysis, one of the pieces of information to be acquired early relates to the boundaries of the geological formations and subzones. Assuming a petrophysical model built up from homogeneous layers, the detection of layer boundaries is crucial for a reliable estimation of the volumetric parameters (porosity, shale volume, matrix composition etc.) of the rock units.

Multivariate statistical methods can be used for the processing of well logging datasets with the aim of clustering the data objects to find lithological similarities and patterns or reducing their dimensionality to interpret the data more easily. The added advantage of dimension reduction is that one can detect the most influential data types or extract unmeasurable information hidden in the measured dataset. Factor analysis transforms the observed variables into a smaller number of statistical quantities called ‘factors’ that practically represent a linear combination of the original (input) variables (Lawley and Maxwell 1962). Shaly formations have been evaluated as a part of previous groundwater studies (Szabó et al. 2014; Dennis and Lawrence 1984; Neasham 1977) and such studies have also included the estimation of hydraulic conductivity using near-surface geophysical data (Niwas and Celik 2012). In the study reported here, the fractal characteristics of the first factor’s scores have been investigated using analysis of the Hurst exponent, and the study makes use of it for detecting the location of layer boundaries. Several approaches have been previously proposed for facies recognition using fractal analysis. López and Aldana (2007) used wavelet-based fractal analysis and a waveform classifier for improved lithofacies classification. Li et al. (2018) explored the impact of fracture density on acoustic logging signals in carbonate reservoirs using advanced analysis techniques such as the Hilbert-Huang transform and principal component analysis (PCA). Their findings suggest that acoustic features in the frequency domain, particularly those related to the Hilbert spectrum and marginal spectrum, exhibit stronger correlations with fracture density compared to features in the time domain, paving the way for a new predictive model based on genetic algorithm-based support vector machine methods for accurately estimating fracture density in such reservoirs. The natural gamma ray and porosity logs were analyzed to identify depositional patterns and tendencies. It was found that the high fractal dimensions were associated with shales and the low ones correspond to the sands. Hernandez-Martinez et al. (2013) used a multifractal Hurst analysis for electrofacies identification and for revealing well-logging signal complexities. Li et al. (2021) proved that the study of the fractals of well logging data can be extended to fracture identification. They concluded that the degree of fracture development is correlated with an increase in the acoustic log and dual lateral differential fractal dimensions.

In the first phase of the proposed workflow, the Hurst exponent is applied to identify the lithology changes along a borehole and to support the inversion process with information on layer boundaries for a more reliable estimation of petrophysical parameters. In the next step, a special indirect interpretation method, the so-called interval inversion, is applied. Unlike the local inversion techniques used to invert the dataset collected by different probes at a given depth to predict the petrophysical properties only to the same depth (Alberty and Hashmy 1984; Ball et al. 1987), here, all the measured data of a greater depth interval are processed to estimate the petrophysical parameters of several layers in a joint inversion procedure. The narrow overdetermination (data-to-unknowns) ratio of the local inversion schemes makes the inversion process highly sensitive to data noise. In contrast, interval inversion is characterized by a high overdetermination rate, which allows a much more accurate estimation of the petrophysical parameters. The large data-to-unknowns ratio is assured by increasing the input data as well as reducing the number of unknowns, as this study describes the model parameters by a smaller number of series expansion coefficients. Several studies have proven the success of this inversion strategy, primarily in terms of reducing estimation errors (Dobróka et al. 2016). This study aims to develop an overarching framework to investigate the inhomogeneity inside each layer and detect an accurate location of the layer boundaries using the FA-Hurst exponent integration. Estimation of the scale- and depth-dependent Hurst exponent using the instantaneous slope, instead of average slope, gives the advantage of tracking the homogeneity of a subinterval by detecting the subinterval boundaries. Using this information, the interval inversion method is employed to estimate the petrophysical parameters in the automatically selected zones. Moreover, as part of the inversion procedure, the vertical variations of the model parameters within the layers were also determined by using a special series expansion technique. In the last phase, an additional algorithm assists in calculating a hydraulic conductivity log, which is derived from the inversion results. Csókás (1995) suggested an evaluation method based on the Kozeny-Carman equation, which calculates the hydraulic conductivity solely from well logs. As demonstrated, the Csókás method works well in high-porosity clastic water-bearing structures.

The integrated workflow described here yields two main improvements with respect to well log analysis. The first one involves application of the scale- and depth-dependent Hurst exponent in the study of lithological characteristics. Usually, the geometrical characteristics of the layers are predefined manually by the log analyst, but the workflow described here gives an automatic way to detect the layer boundaries by studying the fractal characteristics of the factor scores that properly correlate with the lithological information. The second innovation point is based on the concept of interval inversion developed at the Department of Geophysics (UM; Institute of Exploration Geosciences, Hungary), which can increase the numerical stability of the inversion procedure, also the optimal overdetermination ratio, and the accuracy of estimates. Volumetric parameters estimated by interval inversion provide an accurate input for hydraulic conductivity estimation. This method is an adaptation of the interval inversion method used in oilfield applications (Dobróka et al. 2009; Szabó and Dobróka 2020), and it can be recommended as a robust tool to evaluate groundwater formations. The proposed workflow is tested both on synthetic well logs and field data collected in East Hungary, and the estimation results are confirmed by core data.

Methods

Factor analysis of well logs

Factor analysis as a multivariate statistical approach can be applied to explore the hidden relations between the latent variables and those of the observed ones. These factors explain most of the total variance of the input dataset, while the dimensionality of the original problem is reduced. The results arising from the multivariate problem can be described by a few factors with minimum information loss. The statistical factors extracted from well logs are necessarily uncorrelated to each other, thus they contain independent information about the studied formation. The strength of partial correlations with the measured logs can be of different amounts. By studying these correlations, one can decide what input parameters significantly influence the derived factors. The most important advantage of this approach is that the different petrophysical parameters that are directly unmeasurable in the borehole can be related to some factors and derived from them based on these connections. Szabó and Dobróka (2013) showed that factor analysis may reveal interrelationships between the statistical factors extracted from the observed data and some important petrophysical characteristics that are valid in different geological environments. In their study, high correlation was found between the first statistical factor explaining a major part of the variance of the input dataset and the shale volume, associated with wells in Hungary and North America. In clastic formations, shale volume estimation is of high importance in characterizing the lithology and calculating the effective porosity of the aquifers.

The original data matrix D of size N × K is decomposed into the sum of two matrices

$$\textbf{D}=\textbf{F}{\textbf{L}}^{\mathrm{T}}+\textbf{E}$$

(1)

where F denotes the N × M matrix of factor scores, L is the K × M factor loading matrix and E is the N × K matrix of residuals (N is the number of observed depth points along the processed interval, K is the number of measured well log types, M is the number of extracted factors, T is the transpose operator). (Note that all nomenclature is also defined in the Appendix.) The factor scores form a well log representing the depth variation of a given factor, while the factor loadings (or weights) represent the correlation coefficients between the factors and the measured logs. Considering that the matrix of factor scores is orthogonal (FF^T = I, where I is the identity matrix), the correlation matrix of the standardized input variables is

$$\textbf{R}={\mathrm{N}}^{-1}{\textbf{D}}^{\mathrm{T}}\textbf{D}=\textbf{L}{\textbf{L}}^{\mathrm{T}}+\boldsymbol{\Psi}$$

(2)

where Ψ represents a diagonal matrix of error variances. The commonalities being the variance portions of common factors can be found in the main diagonal of the reduced correlation matrix LL^T. There are several ways of computing the factor loadings and scores such as with application of the spectral decomposition of the reduced correlation matrix, the maximum likelihood method, soft computing methods, etc. For instance, the maximum likelihood method uses the following objective function, expressing a weighted deviation between the measured data matrix and the matrix calculated by the common factors, to derive both the factor scores and loadings in one statistical procedure. Regarding the knowledge of factor loadings, Bartlett (1937) derived a linear solution, by which the factor scores can be calculated as follows

$${\textbf{F}}^{\mathrm{T}}={\left({\textbf{L}}^{\mathrm{T}}{\boldsymbol{\Psi}}^{-1}\textbf{L}\right)}^{-1}\ {\textbf{L}}^{\mathrm{T}}{\boldsymbol{\Psi}}^{-1}{\textbf{D}}^{\mathrm{T}}$$

(3)

The first column of matrix F includes the scores of the first factor, which form a well log found to be primarily sensitive to the lithology characteristics of hydrocarbon formations, i.e., shale content, in different oilfields (Szabó and Dobróka 2013) and in different groundwater-bearing formations (Szabó et al. 2014). In this study, it is assumed that the link between the first factor and shale volume can be consistently used also in clastic groundwater formations. The factor loadings are estimated using a quick noniterative method suggested by Jöreskog (2007)

$$\textbf{L}={\left(\textbf{diag}{\boldsymbol{\Sigma}}^{-1}\right)}^{-\frac{1}{2}}\Omega {\left(\boldsymbol{\Gamma} -\theta \textbf{I}\right)}^{-\frac{1}{2}}\textbf{U}$$

(4)

where Γ is the diagonal matrix of the first R number of eigenvalues of the sample covariance matrix Σ. The eigenvalues can be found in the columns of matrix Ω, and U denotes an arbitrarily chosen M-by-M orthogonal matrix, θ is the Jöreskog constant, which gives the optimal number of factors in the case of θ ≤ 1. The factor loadings of the first factor are studied to find the strength of correlation between the relevant factor and all types of well logs used in this study. In this manner, the most influential wireline log types can be found in estimating the shale volume. For easier interpretation, the extracted factors are rotated (i.e., orthogonally transform the factor loadings) to find the best correlation between the factors and petrophysical properties (i.e., shale volume) using the varimax algorithm suggested by Kaiser (1958). Supposing that the rotated first factor is a good shale indicator, it can be used to estimate the shale volume (e.g., out of inversion), or it can serve as input for the application of the rescaled range analysis (R/S) method to estimate the Hurst exponent.

Hurst analysis of well logs

The Hurst exponent is related to the rescaled range analysis (R/S) method presented by Hurst (1951), who was responsible for dam building along the Nile River in Africa. Hurst was inspired by the random process definition which was established by Einstein and mentioned in Milton and Okamoto (2018). The fluctuation of the water levels around the mean over years was observed, and Hurst tried to check if the fluctuation was random or had a hidden regular pattern. The proposed R/S technique can distinguish completely random time series from correlated ones. The investigation of fractal characteristics of well logs usually helps to extract information on pore structure, fluid content and textural properties of rocks hidden in the measured data. In this study, it is possible to examine the hydrogeophysical logs to make conclusions on the layer boundaries of groundwater formations and subzones by studying the Hurst exponent. As a specialty, the method used here applies a similar Hurst analysis, suggested by Hernandez-Martinez et al. (2013), not directly on the measured logs, but using the first factor log, in which the lithological information extracted jointly from all well logs is concentrated. An improved lithology identification mechanism was expected from this analysis, which can be beneficially used in the subsequent automated inversion algorithm in the developed workflow.

Consider vector d as representing one column of data matrix D in Eq. (1). The ith element of the data vector is d_i = d(z_i), which represents the ith datum of a given well log. Index i runs over 1,2,...,N, where N is the total number of observed data measured along a borehole. Let the original dataset be divided into S number of subsets of equal length L, where L ∈ {x ∈ Z | 0 ≤ x ≤ 1, | Nx is an integer}. Then one computes the datasets of the partial summations

$${x}_j=\sum_{k=1}^j\left({x}_k-{\overline{x}}_s\right)$$

(5)

where ${\overline{x}}_s$ is the mean of each subset of length L. The range of the dataset relative to the mean within each subseries x_j is calculated as R_s = max(x_j)–min(x_j), which is rescaled by the corresponding standard deviation σ_s giving R_s/σ_s = (R/S)_s. The rescaled range must be estimated over the S number of arbitrarily chosen subsets of length L with different sizes from which the average of these ranges is calculated. If the stochastic process is associated to the observed variable scales with a certain I∈(I_min, I_max) (some part of N), the average of the preceding ratios can be connected to I through a power law

$${\overline{\left(R/S\right)}}_s\cong {I}^H$$

(6)

where H is called the Hurst exponent, which reflects the fractal measure of the correlations that exist in the dataset. According to Mandelbrot and Wallis (1969), parameter H must always be greater than or equal to zero, and the value of H = 0.5 shows a white-noise process. High values of H indicate stronger autocorrelation in the dataset. In the case of H > 1.5, the stochastic nature of long-range autocorrelations is questionable, and their deterministic background is assumed.

This study employs both scale-dependent and scale-and-depth-dependent Hurst exponents to analyze the fractal characteristics of lithological formations. The Hurst exponent is determined at various points along the log-log relationship between the rescaled range (R/S) and the scale of subintervals. An innovative investigation using lithological representative factor analysis and rigorous statistical assessment is conducted to explore variations in fluctuation type and intensity. The Hurst exponent as a function of scale and depth H(I,z) is analyzed to identify the subintervals in the rock units, thereby giving a possibility to study the fractal characteristics of the first factor log. Based on test runs, the scale interval between I_min = 1 and I_max = 100 with an increment of 5 was chosen. The depth-dependent Hurst exponent serves to highlight the different patterns of the first factor. In addition to the Hurst exponent, further statistical calculations were proposed for a more accurate delineation of the subzone boundaries. The scale of different patterns can change during the analysis, which can affect the extraction of fractal characteristics. To take this into consideration, a Z-scoring quantity was introduced, as a function of scale and depth Z(I,z), which measures the deviation of the Hurst exponent from its mean at a specific depth. In accordance with the principle of superposition, the values of Z(I,z) are relatively close to each other at the same facies interval, while quite far away from each other in different facies. It was proposed to calculate the cumulative sum of the scores Z(I,z) and that of the mean of the Hurst exponent H(I,z), respectively, to better emphasize the boundary contrast between the different lithological units.

Interval inversion of well logs

The petrophysical model of groundwater formations includes such volumetric parameters as porosity, shale volume, and fractional volume of the matrix constituents. In fully saturated formations, the model simplifies as the water saturation of the flushed and uninvaded zones is constant (unity), respectively. The depth distribution of the petrophysical parameters (porosity, shale volume, fractional volume of rock matrix) along a series of layers are estimated conventionally by local inversion of the measured wireline logs, which means that the inverse problem must be solved for each depth independently from each other, where the local relation between the model and the data is normally expressed by

$${\textbf{d}}^{(c)}=\textbf{g}\left(\textbf{m}\right)$$

(7)

where g is a vector-vector (response) function used for calculating the theoretical data (d^(c)) in the given depth and m is the model vector estimated by inversion. In this study, the forward problem is solved by using the set of response functions described in section ‘Synthetic modeling test’. To extract the model parameters from Eq. (7), normally the weighted least squares method is used, which minimizes the overall distance between the measured and calculated data (e) normalized by the variances of each data type (Menke 1984)

$$E={\left\Vert {\textbf{e}}^{\mathrm{T}}\textbf{We}\right\Vert}_2^2+{\varepsilon}^2{\left\Vert \textbf{m}\right\Vert}_2^2$$

(8)

where W is the weight matrix including the data variances in its main diagonal, ε is the damping factor to numerically stabilize the ill-posed (linearized) inversion procedure (Levenberg 1944). In water prospecting, usually the number of observed data types is barely more than that of the unknowns, which leads to a marginally overdetermined inverse problem. The estimation accuracy is highly influenced by the data-to-unknowns ratio, which can be significantly increased by integrating the data of a greater depth interval and inverting them in a joint inversion procedure. Based on this idea, Dobróka et al. (2016) introduced the interval inversion method, which is used in this workflow to estimate the depth distribution of the volumetric parameters of water-bearing formations.

The interval inversion method developed at the Geophysical Department (UM) inverts the data of an arbitrarily chosen depth interval to predict the petrophysical parameters at the same interval. Extending the validity of Eq. (7) to a bigger depth range gives

$${d_k}^{(c)}(z)={g}_k\left({m}_1(z),{m}_2(z),\dots, {m}_P\left(\mathrm{z}\right)\right)$$

(9)

where d_k represents the kth measured log, K is the number of well log types, and P is the number of model parameters (k = 1,2,…,K, p = 1,2,…,P). The pth model parameter of the predefined interval can be discretized using a series of expansion techniques

$${m}_p(z)={\sum}_{q=1}^{Q_p}{B_q}^{(p)}{\Psi}_q(z)$$

(10)

where ${B}_q^{(p)}$ is the qth expansion coefficient, and Ψ_q(z) is the corresponding qth basis function (q = 1,2,…,Q_p). The latter is a known quantity and previously set before inversion—for instance, a model with homogeneous layers can be properly described by choosing the basis functions as a combination of unit step functions (Dobróka and Szabó 2012). This study uses the Legendre polynomials as basis functions to describe the variation of the model parameters within the layer (Dobróka et al. 2016). The aim of inversion is to estimate the unknown expansion coefficients in Eq. (10), for instance, when Legendre polynomials are used, the Q_p number of expansion coefficients must be estimated for each model parameter. (The total number of unknowns is Q = Q₁ + Q₂ + … + Q_P.) The advantage of using this discretization scheme is that the depth distribution of model parameters can be described by fewer unknowns than in local inversion, hence the overdetermination ratio and the accuracy of inversion estimation can be also increased. The high overdetermination allows one to include additional parameters as unknowns, and in this way, the interval inversion method can estimate the layer thicknesses (Dobróka et al. 2009; Dobróka and Szabó 2012). In this study, the layer boundary coordinates were fixed from the Hurst analysis. The inverse problem can be solved analogously by using Eq. (8) to give an estimation for the expansion coefficients

$$\textbf{B}=\left({\textbf{G}}^{\mathrm{T}}\textbf{WG}+{\varepsilon}^2\textbf{I}\right){\textbf{G}}^{\mathrm{T}}{\textbf{Wd}}^{(m)}$$

(11)

where G is the Jacobi matrix including the derivatives of calculated data with respect to the series expansion coefficients, and d^(m) is the measured data vector including all data of the entire processing interval. Once the expansion coefficients are given, one can substitute them into Eq. (10) to produce the depth distribution of the unknown petrophysical parameters.

The normalized root mean squared error was used to measure the fit between the measured and calculated data

$$\updelta ={\left[{N}^{-1}\sum\nolimits_{k=1}^N\left(\frac{{d_k}^{(m)}-{{d_k}^{(c)}}^2}{{d_k}^{(m)}}\right)\right]}^{\frac{1}{2}}$$

(12)

where 100δ gives the misfit in percent. There is another possibility to check the quality of the estimated parameters. Along with knowledge of the accuracy of the measured data, the uncertainty of the petrophysical properties can be predicted. The information of the former can be obtained from the calibration of well logging tools, user manuals or literature resources (e.g., Horváth 1973). When the wireline logs are measured with different accuracies and assumed to be correlated, the following relation exists between the data covariance matrix including the data variances in its main diagonal and the covariance matrix of the model parameters (Menke 1984)

$$\operatorname{cov}\textbf{m}={\textbf{G}}^{-\mathrm{g}}\operatorname{cov}{\textbf{d}}^{(m)}{\left({\textbf{G}}^{-\mathrm{g}}\right)}^{\mathrm{T}}$$

(13)

where G^–g is the generalized inverse matrix of the inversion method. In the inverse problem here, applying the error propagation law, the covm is derived from covB using Eq. (12), where the general inverse matrix is calculated using the basis functions introduced in Eq. (10) (Dobróka et al. 2016). The uncertainty of the lth petrophysical parameter can be calculated from the square root of the main diagonal elements of the model covariance matrix. This approach gives an error range for each petrophysical property in the function of depth. By using the model covariance matrix and the standard deviation of the relevant model parameters, one can calculate the correlation coefficient of the given pair of model parameters. The full correlation matrix informs about the strength of the correlation between the estimated petrophysical properties. To avoid the problem of ambiguity and to perform reliable inverse modeling, the model parameters with low correlation coefficients are favorable to be selected as the unknowns.

Theory of the Csókás method

Hydraulic conductivity (K_h), a key parameter in evaluating groundwater formations, expresses the ease with which a fluid can flow through the pore spaces of the formation. In this workflow, quantity K_h is derived from the volumetric parameters estimated by interval inversion (as described in section ‘Interval inversion of well logs’). The most widely used method for hydraulic conductivity estimation is based on the Kozeny-Carman model (Amaefule et al. 1993)

$${K}_{\mathrm{h}}=\frac{\rho_{\mathrm{w}}g}{\mu}\frac{d^2}{180}\frac{\varnothing^3}{{\left(1-\varnothing \right)}^2}$$

(14)

where ∅ (v/v) is formation porosity, ρ_w (g/cm³) and μ (Ns/m²) are the density of pore water and dynamic viscosity, respectively, d (cm) is the dominant grain diameter, and g (cm/s²) is the normal value of the gravity acceleration. The dominant grain size can be estimated from sieve analysis

$$d=\frac{d_{10}+{d}_{60}}{2}{\left(\frac{d_{10}}{d_{60}}\right)}^{\frac{1}{2}}$$

(15)

where d₁₀ (cm) and d₆₀ (cm) are the grain diameters read at 10 and 60% cumulative frequencies of the grain-size distribution curve. Csókás (1995) assumed a connection between the dominant grain size and resistivity formation factor (F*) originally suggested by Alger (1971). The latter is calculated as F* = R₀/R_w, where R₀ is the resistivity of the fully saturated formation and R_w is that of the pore water in the same formation (Archie 1952). By combining Alger’s empirical equation, Csókás further improved Eq. (10) to estimate the hydraulic conductivity (cm/s)

$${K}_{\mathrm{h}}=\mathrm{C}\frac{\varnothing^3}{{\left(1-\varnothing \right)}^4}\frac{{\left(\lg \frac{R_0}{R_{\mathrm{w}}}\right)}^2}{{\left(\frac{R_0}{R_{\mathrm{w}}}\varnothing \right)}^{1.2}}$$

(16)

where C is a site-specific constant. Equation (16) is valid in poorly sorted sediments with a formation factor of less than 10. The Csókás method developed at the Geophysical Department (UM) gives a continuous (in situ) estimate of hydraulic conductivity, transmissivity, critical flow velocity, specific surface of grains, and water yield, by using solely well logs. It is limited to the evaluation of unconsolidated groundwater formations (with small values of formation factor); however, it is based on relatively cheap well logging measurements to reduce the costs of rock sampling, pumping tests, and laboratory measurements.

The conducted workflow

This paper presents an integrated workflow used for the prediction of petrophysical properties in groundwater formations. The fully automated data processing workflow includes the subsequent application of factor analysis (section ‘Factor analysis of well logs’), Hurst analysis (section ‘Hurst analysis of well logs’), interval inversion (section ‘Interval inversion of well logs’), and the Csókás method (section ‘Theory of the Csókás method’). In the first step, the measured well logs are standardized before the application of factor analysis to satisfy Eq. (2). In the phase of factor analysis, the statistical factors are extracted from the scaled well logs by using Eqs. (3)–(4). Among the rotated factors, the first one is used, which serves as input for the subsequent Hurst analysis. The layer boundaries are identified by examining the vertical distribution of the Hurst exponent given in Eq. (6) along the investigated well, which serves as input for inverse modeling. Given the knowledge of the layer boundary coordinates, the interval inversion algorithm is applied to estimate the layer parameters such as porosity, shale volume and sand volume. The inversion method potentiates the calculation of the petrophysical property values either in homogeneous or inhomogeneous layers (with a proper series expansion scheme, even a combination of the two) by using Eqs. (10)–(11). In the last phase, the porosity and resistivity logs are used to derive the hydraulic conductivity for the investigated interval by Eq. (16). At the end of the workflow, in a quality check procedure, the estimation errors of the petrophysical parameters are calculated using Eq. (13) and the results compared with core data to confirm their accuracy and reliability.

For solving the well logging inverse problem there needs to be theoretical response equations, which are represented in a vectorial form in Eq. (7). To calculate the well log data in shaly sand formations, the following response functions suggested by Sclumberger (1991) are applied

$$\mathrm{SP}={V}_{\mathrm{sh}}\ {\mathrm{SP}}_{\mathrm{sh}}+{C}_{\mathrm{T}}\lg \frac{R_{\mathrm{mf}}}{R_{\mathrm{w}}}\left(1-{V}_{\mathrm{sh}}\right)$$

(17)

$$\mathrm{GR}={\rho_{\mathrm{b}}}^{-1}\left({V}_{\mathrm{sh}}\ {\mathrm{GR}}_{\mathrm{sh}}{\rho}_{\mathrm{sh}}+{V}_{\mathrm{sd}}{\mathrm{GR}}_{\mathrm{sd}}\ {\rho}_{\mathrm{sd}}\ \right)$$

(18)

$${\rho}_{\mathrm{b}}=\varnothing \left[\left({\rho}_{\mathrm{mf}}{S}_{\mathrm{x0}}\right)+{\rho}_{\mathrm{g}}\left(1-{S}_{\mathrm{x0}}\right)\right]+{V}_{\mathrm{sh}}{\rho}_{\mathrm{sh}}+{V}_{\mathrm{sd}}\ {\rho}_{\mathrm{sd}}$$

(19)

$${\varnothing}_{\mathrm{N}}=\varnothing \left[\left({\varnothing}_{\mathrm{N},\mathrm{mf}}{S}_{\mathrm{x0}}\right)+{\varnothing}_{\mathrm{N},\mathrm{g}}\left(1-{S}_{\mathrm{x0}}\right)\right]+{V}_{\mathrm{sh}}{\varnothing}_{\mathrm{N},\mathrm{sh}}++{V}_{\mathrm{sd}}{\varnothing}_{\mathrm{N},\mathrm{sd}}$$

(20)

$$\Delta t=\varnothing \left[\Delta {t}_{\mathrm{mf}}{S}_{\mathrm{x0}}+\left(1-{S}_{\mathrm{x0}}\right)\Delta {t}_{\mathrm{g}}\right]+{V}_{\mathrm{sh}}\Delta {t}_{\mathrm{sh}}+{V}_{\mathrm{sd}}\Delta {t}_{\mathrm{sd}}$$

(21)

$$\frac{1}{\sqrt{R_{\mathrm{d}}}}=\left[\frac{{V_{\mathrm{sh}}}^{\left(1-0.5{V}_{\mathrm{sh}}\right)}}{\sqrt{R_{\mathrm{sh}}}}+\frac{{\sqrt{\varnothing}}^{\mathrm{m}}}{\sqrt{{\mathrm{a}R}_{\mathrm{w}}}}\right]{\sqrt{S_{\mathrm{w}}}}^n$$

(22)

$$\frac{1}{\sqrt{R_{\mathrm{s}}}}=\left[\frac{{V_{\mathrm{s}\mathrm{h}}}^{\left(1-0.5{V}_{\mathrm{s}\mathrm{h}}\right)}}{\sqrt{R_{\mathrm{s}\mathrm{h}}}}+\frac{{\sqrt{\varnothing}}^{\mathrm{m}}}{\sqrt{{\mathrm{a}R}_{\mathrm{m}\mathrm{f}}}}\right]{\sqrt{S_{\mathrm{x}0}}}^n$$

(23)

where SP is the spontaneous potential, and C_T is the temperature correction factor. Porosity (∅), shale volume (V_sh) and sand volume (V_sd) represent the unknown model parameters. In formations fully saturated with water (water saturation both in the flushed and uninvaded zone is S_x0 = S_w = 1), there are only two unknowns at each depth, because the sand volume can be derived easily from the material balance equation V_sd = 1 – ∅ – V_sh. On the left side of Eqs. (18)–(23), one finds the simulated data as natural gamma-ray intensity (GR), bulk density (gamma-gamma) (ρ_b), neutron porosity (∅_N), sonic (P wave) travel-time (Δt), shallow resistivity (R_s) and deep resistivity (R_d). In addition to the volume characteristics, there are many other parameters on the right side of the Eqs. (17)–(23). These site-specific constants represent the physical properties of the fluid, shale and matrix components given in the water zone. The meaning and selected values of these zone parameters are given in Table 1. The physical and textural properties of larger zones and other constants of the response functions of measured logs must be known before the inversion procedure takes place. This site-specific information can be acquired from laboratory measurements, literature, and by a special inversion technique (Szabó 2018). In this study, it is assumed that the zone parameters are constant and focus on the preliminary estimation of layer boundary coordinates (layer thicknesses) using the new workflow to improve the inversion of hydrogeophysical logs. The list of zone parameters appearing in Eqs. (17)–(23) can be found in the Appendix.

Table 1 Selected values of zone parameters for calculating synthetic well logs in the modelled groundwater formation

In the inversion process, the wireline logs are recalculated using the Eqs. (18)–(23) iteratively, to reduce the misfit between the measured and calculated data. The interval inversion approach gives the depth distribution of porosity, shale content, and sand volume, which forms the basis of the prediction of hydraulic conductivity. The flowchart in Fig. 1 shows the statistical procedure for exploring the fractal characteristics of the first factor, which is integrated with interval inversion to predict the petrophysical parameters used as input for estimating the hydraulic conductivity by the Csókás method.

Fig. 1

The statistical workflow for hydraulic conductivity estimation using integration between the Hurst analysis and interval inversion

Results

Synthetic modeling test

The aim of the modeling experiments using simulated data is to test the performance of the suggested method from a numerical point of view. It is assumed that the response Eqs. (18)–(23) perfectly describe the relationship between the well logging data and the model parameters, i.e., they can predict the data without any error. By inverting the quasimeasured data, one can measure how accurately the inversion algorithm reconstructs the target (an exactly known) model. To simulate real borehole measurements using the known model parameters, it is necessary to add some amount of noise to the synthetic (noiseless) data, which are then inverted in the interval inversion process. The data distance is measured using Eq. (12), and graphically shows the fit between the well logs of the estimated and target model.

The proposed workflow is tested using synthetic data generated by Eqs. (18)–(23), assuming the known depth distributions of model parameters ∅, V_sh, and V_sd in four homogeneous layers fully saturated with water (S_x0 = S_w = 1). The layer boundaries of the shaly sandy beds are exactly known. The textural, shale and fluid parameters are chosen as constants in the probe response equations (see Table 1). The synthetic well-logging data contain readings from GR, ρ_b, ∅_N, Δt, R_s, and R_d logs over a 20-m (relative) depth interval sampled at 0.1 m distance (Fig. 2). Since there are four layers and three petrophysical quantities per layer, the number of unknowns (Q) is 12, while the total number of data (N) is 200. (In this case, the number of expansion coefficients equals that of the petrophysical quantities in Eq. 10). The number of unknowns was reduced to Q^* = 8 by deriving the sand volume from the material balance equation (section ‘The conducted workflow’); hence, the overdetermination ratio N/Q^* = 150. Compared to the local inversion, where two parameters are estimated from six data depth-by-depth (the data-to-unknows ratio is only 3), the relative increase of the overdetermination ratio is 50. The synthetic data were contaminated with 5% Gaussian distributed noise (the noiseless data were modified with random numbers generated from the Gaussian distribution, with zero mean and standard deviation σ_d = 0.05), which means that the deviation between the quasi-measured and the noiseless data is δ = 5%.

Fig. 2

Synthetic wireline logs contaminated with 5% Gaussian distributed noise (tracks 1–6) and the exactly known layer parameters (tracks 7–8) as input for testing the proposed well log analysis workflow

In the first step of the workflow, factor analysis is applied to synthetic data for dimensionality reduction and lithology identification. The factor loadings are calculated by Eq. (4) and then the factor logs are derived using Eq. (3). In each column of the factor loading matrix (L), the correlation relations between the relevant factor and each log can be studied. It is shown in Table 2 that the first factor correlates strongly with all observed variables (positively with GR, ∅_N, and Δt logs, and inversely with the resistivity logs) except the bulk density log, and it contains most of the total variance of the input variables (the first two factors explain more than 90% of the data variance, while the third one is considered as an error factor). The natural gamma ray, neutron porosity, acoustic and resistivity logs are very sensitive to the variation of the shale volume along the well; hence the first factor log works as a good lithology indicator.

Table 2 Rotated factor loadings derived by factor analysis of synthetic wireline logs

In the second step of the workflow, Hurst analysis is applied to the first factor log including a combined information of the lithological logs. The Hurst exponent is calculated using Eqs. (5)–(6) to identify the (known) layer boundaries. It can be seen in Fig. 3 that the Hurst exponent as a function of scale and depth H(I,z) correctly indicates the three rock interfaces at depths of 7, 10, and 15 m. The calculated mean of the Hurst-exponent, the cumulative sum of the mean, and the cumulative sum of scoring Z(I,z) also change at the exact known depth coordinates of the lithologic boundaries. The mean of the Hurst exponent at the layer boundaries is ~0.5, while it is lower than zero within each layer referring to the background noise. The last track of Fig. 3 also represents three anomalies of the scale I distribution at the same boundaries. The scale range is selected as between 10 and 70, based on preliminary program runs. This range is suggested for a high-resolution result, where the depth window for the depth-dependent Hurst exponent is 0.74 m. In Fig. 3, at the boundary’s location, there are anomalies of maximum 0.5 (check the colored legend). The shift of the anomalies of the contour plot is related to the difference in the depth window; therefore, the cumulative sum of the mean of the Hurst exponent is calculated for a more accurate estimation of the layer boundaries, which shows a line deflection at the depths of different boundaries. The result of the Hurst analysis can provide an estimation of the number of layer boundaries with an approximate prediction of their exact location.

Fig. 3

Result of Hurst analysis of the first factor log extracted by factor analysis of the synthetic well logs contaminated with 5% Gaussian distributed noise. Tracks 2–5 show the changes of the Hurst exponent and its related quantities at each layer boundary

In the third step of the workflow, the noisy synthetic well logs are inverted to estimate the porosity, shale volume and sand content of the formations. To describe the four-layered homogeneous model, a combination of unit step (Heaviside) functions is applied for series expansion. In Eq. (10), the basis function of the qth layer is chosen as Ψ_q(z) = u(z − Z_q–1) − u(z − Z_q). Since this basis function has a value of 1 within the qth layer and has a zero value otherwise, the qth expansion coefficient corresponds to the constant value of the given model parameter in the qth layer (q = 1,2,3,4). The depth coordinates of the layer boundaries are automatically given from the Hurst analysis: Z₀ = 0 (fixed), Z₁ = 7, Z₂ = 10, Z₃ = 15, and Z₄ = 20 m (fixed). In the interval inversion procedure, one estimates the series expansion coefficients using Eq. (11). The model parameters (porosity and shale volume) are derived by substituting the expansion coefficients into Eq. (10). The development of convergence is steady and fast, showing a stable inversion procedure, and the data misfit calculated by Eq. (12) decreases from 76 to 5% (Fig. 4).

Fig. 4

Development of convergence during the interval inversion of synthetic data contaminated by 5% Gaussian distributed noise

The inversion results can be found in Fig. 5. There is a proper fit between the quasi-measured well logs (black curves) and those calculated using the estimated (layer-wise constant) model parameters (dashed red lines). The last track of the figure shows the predicted (dashed red lines) and exactly known petrophysical parameters (black lines). The difference is very small and not visible on the logs; on average it is less than 0.001 v/v. This remarkable agreement between the target and estimated model is achieved because of the applied discretization scheme and a great amount of data-to-unknowns ratio. The feasibility of the interval inversion method in groundwater formations has been proven, and its field application is promising.

Fig. 5

Result of interval inversion of the synthetic well logs contaminated with 5% Gaussian distributed noise. Tracks 1–6 show the fit between the observed (black line) and calculated (red-dashed line) data and track 7 includes the known and estimated model parameter distributions, assuming a petrophysical model of homogeneous layers

Test using real data

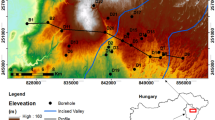
The suggested well log analysis workflow is applied to Cenozoic aquifers found in Baktalórántháza-1 well in Szabolcs-Szatmár-Bereg County in North-East Hungary. The drillhole penetrates clastic formations of Pleistocene and Miocene age fully saturated with water. In the exploration phase, surface geophysical measurements and well logging operations did not show hydrocarbon indications, but the borehole was found suitable for producing thermal water. Vertical electrical sounding measurements indicated Pleistocene sediments dominated by sands of various grain sizes in the upper 80–100 m interval of the subsurface region. Borehole geophysics gives more detailed information about the underlying rocks of the shaly sand sequence. Based on wireline logging data, one can locate a sequence consisting of sands ranging from 100 to 160 m, succeeded by a shaly interval, and a coarse-grained bed that is 5–15 m thick. The boundary of the Pleistocene and upper Miocene period was detected at the depth of 240 m. The Pannonian shaly complex mainly consists of clayey sand, gravel, clayey silt, clayey marl, and bituminous clay. The location map of Baktalórántháza-1 well can be found in Fig. 6.

Fig. 6

Map of Hungary, including the location of Baktalórántháza-1 well (red circle)

The observed dataset includes typical well logs and laboratory data measured on 97 rock samples taken quite frequently along the investigated interval. The interval of 100–450 m is processed, where the SP, GR, neutron-thermal neutron intensity (NN), gamma-gamma intensity (GG), and R_s data were available every 0.1 m along the well. The core data available are the hydraulic conductivity and shale volume derived from grain-size analysis done on the rock specimen. In the first step of the proposed workflow, the aforementioned logs were processed using factor analysis. Two factors were extracted from the borehole dataset; the factor loadings are listed in Table 3. The factor loading matrix shows that the lithology-sensitive logs such as SP and GR, and the saturation-sensitive R_s log, have the highest impact on the first factor. The second factor correlates to the gamma-gamma (GG) tool, which informs us about the porosity of the groundwater formations.

Table 3 Rotated factor loadings derived by factor analysis of well logs recorded in Baktalórántháza 1 well

In the second step of the workflow, the Hurst exponent is computed to quantify the degree of autocorrelation of the calculated first factor. The Hurst exponent lies between the range 0–1.5, and indicates the variability observed in the F₁ log. This variability is specifically characterized by the scale- and depth-dependent Hurst exponent denoted as H(I,z). The sampling window is chosen as 10 m, and the scale parameter ranges from 40 to 100 for the most resolved range. The calculated scale- and depth-dependent Hurst exponent ranges from 0 to 0.6 (Fig. 7). The Hurst exponent close to 0.5 is indicative of a random walk or Brownian series, in which there is no correlation between the measured points and future observations. The boundaries between the two intervals can be indicated as a Brownian interval, in other words, the boundary is not a sharp surface, this zone will have an unpredictable pattern. The Hurst exponent less than 0.5 refers to the antipersistent series, in which an increase is most likely to be followed by a decrease. In the case of the intervals that have Hurst exponent values higher than 0.5, it means that these intervals are persistent. In the persistent interval, an increase in the well log value will most likely be followed by another increase in the short term, also a decrease will be followed by another decrease. This result is very important for detecting the transgression and regression patterns within the major sequences. The separation between different zones depends on the variation of the mean values of function H(I,z). For a more reliable interpretation, the cumulative sum of the Z scores of this mean is also involved, along with the cumulative sum of the mean of the Hurst exponent. The results show that the boundaries between different zones have a pattern of a nearly fixed value of around H = 0.5, while the pattern could change within each layer. Five zones (zones 1–5) are extracted, where the boundaries are located at depths of 145, 210, 255, and 330 m, respectively. The depth of 255 m can be identified as the Pleistocene–Miocene boundary according to the wellsite geology report. The mean of the Hurst exponent shows a mirror image for the F₁ log, which could be used in the future as a facies identification technique.

Fig. 7

Results of the Hurst analysis of the first factor log (F₁) extracted by factor analysis of well logs measured in Baktalórántháza 1 well. Tracks 2–5 show the changes of the Hurst exponent and its related quantities at each identified lithological boundary

In the third step of the workflow, interval inversion of the borehole geophysical logs is performed by using those zone boundaries as the prior information that is predefined by Hurst analysis. The theoretical logs using these model parameters are generated using Eqs. (17)–(22), and their log constants are given by clustering the input data and preliminary geological information (Table 4). The initial model parameters of the five zones are set (Table 5) assuming a fully saturated formation. The initial model is constructed using the material balance equation, in which the sand volume is calculated from the previous two parameters (out of inversion). The theoretical logs using these model parameters are shown with the observed well logs in Fig. 8. The red curve shows the computed data in each predefined zone. In each zone, the petrophysical parameters are assumed to be unvarying during the inversion process, which assures a large overdetermination ratio. The result of the interval inversion of in-situ well logs is given also in Table 5.

Table 4 Selected values of zone parameters for calculating well logs in the interval inversion procedure

Table 5 Starting values of petrophysical parameters and those estimated by interval inversion assuming five homogeneous zones in Baktalórántháza 1 well

Fig. 8

Observed wireline logs (black curve) and the calculated logs (red curve) using the initial model obtained from Hurst analysis assuming five homogeneous zones along the processing interval

To describe the depth variation of the petrophysical parameters within the five zones in more detail, a series expansion is applied using an orthogonal set of polynomials, which allows for estimation of the petrophysical parameters of the inhomogeneous layers in the given zone. In Eq. (10), the basis function of the qth zone is given as Ψ_q(z) = P_q–1(z), where P_q–1 is the qth degree Legendre polynomial. The 40th degree Legendre polynomials are used for each model parameter, with Q = 402 unknowns against N = 3,470 data. The data-to-unknowns ratio of the interval inversion is 8.6, which is higher than the local inversion, which is just 5/2. The convergence plot in Fig. 9 confirms the stability of the inversion procedure. The data misfit calculated by Eq. (12) decreases from 24 to 7% in a convergent inversion procedure.

Fig. 9

Development of convergence during the interval inversion of borehole logging data measured in Baktalórántháza-1 well

The inversion result is shown in Fig. 10, where the predicted parameters show a decrease in the porosity percentage from the top of the logs, and an increase in the shale content in the deeper zones. The misfit between the calculated and measured wireline logs naturally originated in the effect of data noise, and in the polynomial approximation of the series expansion-based interval inversion methods (thin layers cannot be detected due to resolution limitations). Moreover, the tool response functions are approximate equations carrying modeling errors, the extent of which are not known exactly. The zone parameters are set arbitrarily in Eqs. (17)–(23), which may cause further uncertainties in the data misfit and the estimation error of the inverted petrophysical parameters. The accuracy of porosity and shale volume is calculated by Eq. (13), where the standard deviation values of observed well logs are chosen as typical values: σ_d(SP) = 0.0484, σ_d(GR) = 0.0484, σ_d(GG) = 0.005, σ_d(NN) = 0.002, σ_d(R_s) = 0.05. The confidence intervals of the estimated model parameters are given in Fig. 11. It is demonstrated that the shale volume can be estimated very accurately (within 0.01 v/v) and porosity can also be reliably predicted (0.01–0.03 v/v). The reliability of shale volume estimation is confirmed by laboratory measurements. In the last track of the figure, a strong correlation can be seen between the shale volume log and core data in each zone.

Fig. 10

Results of interval inversion of borehole logging data measured in Baktalórántháza 1 well. Tracks 1–5 show the fit between the observed (black line) and calculated (red–dashed line) data, and track 6 includes the estimated model parameter distributions, assuming a petrophysical model of five inhomogeneous zones

Fig. 11

The porosity and shale-content logs estimated by interval inversion of well logs observed in Baktalórántháza 1 well. Black lines demonstrate the estimated petrophysical parameter, while the red lines show their error bounds derived from the model covariance matrix. Track 3 shows the validation of the predicted shale volume log with core measured shale volume data

In the last step of the workflow, the vertical distribution of hydraulic conductivity along the well is estimated using the Csókás method. The porosity log estimated by inversion and the observed resistivity log are used as input for applying Eq. (16). On the other hand, the characteristic grain size values of Eq. (15) are determined from the grain size distribution curves given at depth levels where rock samples were taken. The hydraulic conductivity is calculated then by using Eq. (14). It can be seen in Fig. 12 that there is a proper agreement between the shale volume and hydraulic conductivity logs and their values coming from laboratory measurements. The validation of the estimated logs by core data confirms the feasibility of the proposed workflow in the groundwater-bearing formations in Hungary.

Fig. 12

Shale volume (track 1) and hydraulic conductivity (track 2) logs estimated by interval inversion of well logs (solid lines), characteristic grain sizes (tracks 3–5), and the core measured values of these parameters (red circles) in the Baktalórántháza 1 well

Discussion

The proposed well-log-analysis workflow consists of three phases. The first phase aims to identify the boundaries of layers or lithological units. The boundaries detection step starts with dimensionality reduction of the well logging data set using factor analysis. The factors are estimated as a linear combination of the observed variables. This groundwater study has confirmed earlier observations by the authors that the first factor is highly influenced by those log types that are most sensitive to lithology. An advantage of factor analysis is that the lithological and other petrophysical information hidden in the raw dataset can be concentrated into a few factors and extracted from the factors directly in a fast procedure. In the second phase, the Hurst exponent analysis is applied to the first factor, which allows a more reliable estimation for the layer boundaries than can be given by a single analysis of any lithological logs—for instance, natural gamma-ray or the spontaneous potential log can be sometimes noisy because of environmental and physical effects. The first factor combines the information of several logs sensitive to lithology variations, which can result in an increase in the accuracy of layer boundary prediction.

The scale- and depth-dependent Hurst exponent seems to be an effective tool in the identification of formation boundaries. The contour plot (Figs. 3 and 7) including the change of the Hurst exponent with different scales gives an additional possibility to better identify the lithological contrasts. The obtained values of the Hurst exponent (≤0.5–0.6) show that at the boundaries the well-logging data can be described under random walk or Brownian motion, which means unpredictable patterns, neither mean-reverting nor trending. The feasibility tests using synthetic data recognized the four layers and their boundaries even when processing noisy data. In the real borehole environment, a more complex formation was investigated, including higher-conductivity sand and gravels of the Pleistocene layer and dominantly impermeable shaly formations of the Miocene interval. Along the 350-m logged interval, the combined application of the factor and Hurst analyses identified five bigger zones. By discussing the same concept used in noisy synthetic data investigation, the scale- and depth-dependent Hurst exponent tends to form a closed anomaly at the zone boundaries, with an average of around H = 0.5. The boundary between the Pleistocene and Miocene sediments is located at the depth of 240 m. This study shows the division of the Pleistocene formations into three zones, linked to the change in the grain sizes of the aquifers (sand and gravel beds), as well as the shale content variation, within the sequence.

The interval inversion of well logs provides the basic volumetric parameters of groundwater formations (porosity, shale volume, matrix volume). The great amount of overdetermination allows one to incorporate more unknowns, such as fractional volumes of other mineral types, water, and other fluid saturations. In this study, a simple model including only two parameters (porosity and shale volume) is used to estimate the depth distribution of effective porosity, which is an important input for assessing the storage capacity and permeability or hydraulic conductivity of the formations. The depth function of volumetric parameters can be expanded into series in different ways, and it is demonstrated that the inversion of well logs works properly both for homogenous layers and inhomogeneous ones, too. In the latter case, Legendre polynomials are used as basis functions to describe the variation of petrophysical properties within the zones. It requires even more unknowns (series expansion coefficients) to be estimated, which may cause the slight reduction of estimation accuracy. Dobróka et al. (2016) suggests giving an optimal number of expansion coefficients at the minimum correlation between the unknowns. This technique, based on testing the intercorrelations between the model parameters, leads to a reliable inversion result; of course, a trade-off must be made between the increase of the vertical resolution of groundwater parameters and the reduction of their estimation error. The two goals cannot be achieved at the same time; however, by choosing the number of expansion coefficients and the type of basis functions, even more complicated structures can be described with much fewer unknowns than in the case of traditional local inversion. This can bring a significant improvement in terms of a more stable and accurate solution of the inversion procedure, i.e., more effective suppression of the noise of the input data. The confidence intervals in Fig. 10 are proportional to the accuracy of the input logs. In case of a higher level of data noise, the inversion procedure provides a result with greater uncertainty according to the law of error propagation. Local (depth-by-depth) inversion may be greatly affected by outliers, but the interval inversion is only moderately affected by them, where the dataset of a larger interval is jointly inverted, and the deconvolution has a favorable smoothing and noise-reduction effect.

To effectively use the Csókás method, there needs to be a sequence of strata with resistivity formation factor F ≤ 10. In the Baktalórántháza 1 well, in the given loose fully saturated sediments, this criterion is met. Using this technique, the depth variation of hydraulic conductivity (or permeability) was estimated, which shows a decreasing trend in the Miocene sediments as the shale percentage increases, while the shallow Pleistocene sediments show an increase in the hydraulic conductivity. The Csókás hydraulic conductivity shows that the Pleistocene deposits, which are mainly composed of sands, represent a good aquifer while the Miocene part, which includes a higher amount of shale, represents an aquitard. The dominating grain-size curve shows a continuous trend in the deeper sequence’s grain size while presenting a fluctuating pattern with an overall increasing tendency. The accuracy and reliability of the estimation results that can be obtained by the proposed workflow highly depend on the uncertainty of the input data. There is a limitation in the data accuracy caused by instrumental and environmental noises. The inversion unknowns are sometimes highly correlated to each other, which may increase the risk of getting an unstable inversion process from a numerical point of view and an ambiguous solution. The latter can be effectively treated by involving reliable a priori (laboratory, geological, geophysical etc.) information on the investigated groundwater formation. In setting the degree of polynomials, a very high number of coefficients assures a proper vertical resolution; however, at the same time it decreases the overdetermination ratio and estimation accuracy. To get reliable information on the petrophysical properties of groundwater formations, a trade-off must be taken between the data-to-unknowns ratio (number of expansion coefficients) and the required estimation accuracy. The setting of zone parameters is also of importance to get a proper fit between the observations and predictions. Because of the high overdetermination of the inverse problem, it is possible to estimate some zone parameters to be estimated by interval inversion, which requires detailed parameter sensitivity studies to select the suitable zone parameters before inversion. The application of Hurst analysis to well logs also involves some other limitations. This algorithm was tested using data contaminated with Gaussian noise, and further investigations are to be done for noise following non-Gaussian statistics. On the other hand, the estimation of the Hurst exponent from the R/S method needs an optimal number of data points, which can be reached in the case of borehole logging datasets; as the number of data points increases, the more the hidden pattern is discovered.

Conclusions

A fully automated (multistep) data processing method is shown, which is based on the joint application of all suitable borehole geophysical logs recorded in groundwater wells. The conducted workflow consists of a series of innovative interpretation techniques that are used simultaneously to improve the evaluation of groundwater formations. One can effectively use the proposed method to detect the geometrical and petrophysical properties of water-bearing layers based on the following:

• 1. Factor analysis is applicable to dimensional reduction and to transforming the observed logs into a small number of statistical variables, with the first factor demonstrating a substantial lithological effect that can be used as a shale volume estimator.

• 2. The Hurst exponent is presented as an effective rock-typing tool. Estimation of the Hurst exponent may reduce the effect of noise in individual logs and enhance the boundary estimation using a scale- and depth-dependent Hurst exponent. Compared to its previous borehole geophysical applications, a new result is that the Hurst method is not based directly on the raw data, but rather on the statistical quantities extracted from them by factor analysis. With the factor analysis, one can concentrate the information into some factors and reveal the hidden information about the lithology. Emphasis is placed on analysis of the scaling interval, which is very important for achieving better vertical resolution.

• 3. The interval inversion method can predict the most important volumetric parameters to an arbitrarily chosen depth interval, instead of solving a set of local inverse problems along the borehole. Porosity, mineral fractions, and fluid saturations were estimated through interval inversion of well logs, the results of which were quality-checked by error analysis and core data validation. The interval inversion method allows a more accurate and reliable estimation of petrophysical properties than local inversion methods (Dobróka et al. 2016), which is an innovative tool in the identification of water reservoirs and the estimation of water storage capacity.

• 4. Applying the Csókás method, one can calculate the changes in hydraulic conductivity continuously along a borehole or between water wells over a bigger region. In this manner, hydraulic conductivity estimation can be improved if the local relation between the dominant grain size and resistivity formation factor is determined. The site-specific constant in the Csókás formula should be estimated by these regression relations. By making a product from the zone boundary coordinates and hydraulic conductivity values, transmissivity calculations can be made for further hydrogeological studies.

In the future, analysis of the Hurst exponent can be used for solving broader hydrogeological problems beyond well logs, e.g., river discharge patterns or groundwater fluctuations. Furthermore, the proposed algorithm can be extended to investigate the geometrical and petrophysical parameters in the case of multidimensional inverse problems. Moreover, the proposed algorithm can be used for investigating complex hydrogeological reservoirs, such as fractured carbonate or volcanic aquifers, and can provide crucial insights into water reserves and flow patterns, aiding in effective groundwater management strategies. Finally, as the geometrical information can be extracted from the fractal study, more unknowns can be involved in the inverse problem, such as the zone parameters of the tool response equations. The proposed workflow may assist in the improved assessment of other types of groundwater systems, providing a reliable and quality-checked information for hydrogeophysicists and hydrogeologists.

Appendix

Nomenclature

a:

Tortuosity factor

B :

Series expansion coefficient

C :

Site-specific constant of Csókás method

cov:

Covariance matrix

C _T :

Temperature factor used for calculation of SP (mV)

d :

Vector of standardized well logging data

D :

Standardized data matrix as input for factor analysis

d :

Dominant grain size

d ₁₀ :

Grain diameter at 10% cumulative frequency

d ₆₀ :

Grain diameter at 60% cumulative frequency

e :

Vector of data prediction errors (interval inversion)

E :

Matrix of residuals (factor analysis)

F :

Matrix of factor scores

F* :

Formation resistivity factor

G :

Jacobi matrix

G ^-g :

Generalized inverse matrix

GG_mf:

Gamma-gamma intensity of mud filtrate (cpm)

GG_sd:

Gamma-gamma intensity of sand (cpm)

GG_sh:

Gamma-gamma intensity of shale (cpm)

GR:

Natural gamma-ray intensity log (API)

GR_sd:

Natural gamma-ray intensity of sand (API)

GR_sh:

Natural gamma-ray intensity of shale (API)

H :

Hurst exponent

K_h:

Hydraulic conductivity

L :

Matrix of factor loadings

L :

Length of subset

m:

Cementation exponent

M :

Number of statistical factors

n:

Saturation exponent

N :

Number of investigated depths along a borehole

NN_mf:

Neutron-neutron intensity of mud filtrate (cpm)

NN_sd:

Neutron-neutron intensity of sand (cpm)

NN_sh:

Neutron-neutron intensity of shale (cpm)

R :

Correlation matrix of standardized data

R :

Range of the dataset relative to the mean of the dataset

R ₀ :

Resistivity of the fully saturated formation

R _d :

Resistivity measured by deep penetration tool (ohmm)

R _mf :

Resistivity of mud filtrate (ohmm)

R _s :

Resistivity measured by shallow-penetration tool (ohmm)

R _sh :

Resistivity of shale (ohmm)

R _w :

Resistivity of pore water (ohmm)

S :

Number of arbitrarily chosen subsets

SP:

Spontaneous potential log (mV)

SP_sh:

Spontaneous potential of shale (mV)

S _w :

Water saturation in uninvaded zone (v∕v)

S _x0 :

Water saturation in invaded or flushed zone (v∕v)

V _sd :

Volume fraction of sand (v∕v)

V _sh :

Volume fraction of shale (v∕v)

W :

Matrix of weighting coefficients

Γ :

Matrix of eigenvalues of sample covariance matrix

Δt:

Acoustic interval time log (μs/ft)

Δt_mf:

Acoustic interval time of mud filtrate (μs∕ft)

Δt_sd:

Acoustic interval time of sand (μs∕ft)

Δt_sh:

Acoustic interval time of shale (μs∕ft)

ε :

Damping (regularization) factor

ρ _b :

Bulk density log (g∕cm³)

_mf :

Density of mud filtrate (g∕cm³)

ρ _sd :

Density of sand (g∕cm³)

ρ _sh :

Density of shale (g∕cm³)

Σ :

Covariance matrix of standardized data

Ψ :

Basis function (interval inversion)

θ :

Jöreskog’s constant

Ψ :

Matrix of specific variances (factor analysis)

δ :

Relative data distance (dimensionless)

Ω :

Matrix of eigenvectors of sample covariance matrix

Ф :

Shale-free (effective) porosity (v∕v)

Ф _N :

Neutron porosity (v∕v)

Ф _N,mf :

Neutron porosity of mud filtrate (v∕v)

Ф _N,sd :

Neutron porosity of sand (v∕v)

Ф _N,sh :

Neutron porosity of shale (v∕v)