On the periodic motions of a one-degree-of-freedom oscillator

Abstract

We present a mechanical model for an oscillator with one degree of freedom under the influence of a flowing medium. Under fairly general conditions we show that the ensuing differential equation has at most two limit cycles and we give examples where exactly two limit cycles will occur. The implications of this result are that it is possible for a system of this kind to exhibit galloping even when the so-called Den Hartog criterion of local instability is not satisfied.

1 Introduction

The study in this paper has two different objectives: on one hand the mechanical interpretation of a one-dimensional mathematical model, on the other hand the global mathematical analysis of periodic solutions to a planar system of autonomous ordinary differential equations.

From a mechanical and practical perspective we study the behaviour of an elastic structure in a flowing medium, in particular the occurrence of so-called galloping under different conditions of a symmetrical object. The main goal is to investigate what the role of the Den Hartog criterion is for the possibility of galloping. Traditionally it is assumed that galloping can occur if the stationary position of the object is unstable, i.e. if the Den Hartog criterion is satisfied, see [1, 2]. However, we will argue that if the criterion does not hold true and the stationary position is (locally) stable, galloping may still occur, according to our global analysis of the differential equation that describes the dynamics of the oscillator. The model we consider is a one-degree-of-freedom oscillator, where the wind and motion of the structure are normal, i.e. perpendicular to each other, see Haaker and van der Burg [3]. According to [4] a misinterpretation of the Den Hartog criterion also occurred in one-degree-of-freedom galloping not necessarily normal to the wind direction [5] and in the case of two-degree-of-freedom oscillations [6].

From a mathematical point of view the study is relevant because it contains a proof that the upper bound of limit cycles is equal to two for a planar system of nonlinear autonomous ODEs (ordinary differential equations). Most practical applications where limit cycles can occur (the famous example of this type is the van der Pol equation) typically have no or at most one limit cycle. Results where a strict upper bound of more than one limit cycle is realized can sometimes follow from bifurcation analysis, e.g. small-amplitude limit cycles created in an Andronov-Hopf bifurcation, global bifurcation near Hamiltonian systems or singularly perturbed systems, see De Maesschalck and Dumortier [7]. In this paper the strict upper bound of two limit cycles is not obtained from such a perturbation analysis but by using a theorem of Rychkov concerning an upper bound of limit cycles in systems with an antisymmetric component. An example of a one-degree-of-freedom oscillator with more than one limit cycle, is also reported by Liu et al. [8], but there the result is derived from perturbation analysis.

Obtaining an upper bound of two limit cycles for a Liénard system is related to the $16^{th}$ Hilbert problem which asks for an upper bound of limit cycles in so-called polynomial systems. Even though the system in our paper is not polynomial, the relation follows from the fact that a quadratic system can be transformed to Liénard systems, so results in these systems may help in the investigation of quadratic systems.

2 The model

Elastic structures with non-circular cross sections in flowing media can experience fluid forces that change with the orientation towards the flow. If the structure oscillates, then the orientation, i.e. the direction of the relative flow velocity experienced by the structure, changes. Also as a result, the fluid forces oscillate and may either decrease or increase the oscillation of the structure. In the latter case the structure is said to be aerodynamically unstable, and large amplitude oscillations, known as galloping, may occur.

Haaker and van der Burgh [3] proposed a model to study a one-degree-of-freedom aeroelastic oscillator. To obtain model equations a quasi-steady approach is used. The fluid forces are completely determined by the instantaneous relative flow velocity that the structure experiences. On this basis the fluid forces in the dynamic state are modeled by known stationary forces experienced by the structure when subjected to a relative flow resulting from the uniform flow and the flow induced by the motion of the structure. For the quasi-steady theory to be applicable the frequency associated with vortex-shedding should be well above the structure’s natural frequency [9].

The stationary fluid forces can be measured in wind tunnel experiments and are usually expressed in the form of dimensionless coefficients depending on the angle of attack $\alpha$ [9], i.e. the angle between the flow velocity and some reference axis of the structure such as the symmetry axis. Generally, the fluid forces are decomposed in a drag force $F_D$ in the flow direction and a lift force $F_L$ perpendicular to the flow direction. The resulting dimensionless coefficients are $C_D(\alpha )$ and $C_L(\alpha )$, respectively, the drag and lift coefficient.

Haaker and van der Burgh have studied a one-degree-of-freedom aeroelastic oscillator, a mass-spring system put in a uniform wind field with flow velocity U, which is restricted to oscillate in a vertical z direction perpendicular to U, see Fig. 1.

Fig. 1

A one-degree-of-freedom mass-spring system

The angle between U and the symmetry axis, denoted with $\alpha _s$, is called the static angle of attack. This $\alpha _s$ is a system parameter and does not vary in the dynamic state. Notice that the angle of attack $\alpha$ in the dynamic situation depends on ${\dot{z}}$, the velocity of the mass. It is shown in [3] that this oscillator can be modeled by a second order ordinary differential equation:

$$\begin{aligned} \ddot{z}+2\beta {\dot{z}}+z=K\sqrt{1+{\dot{z}}^2}(-C_D(\alpha ){\dot{z}}-C_L(\alpha ) ), \end{aligned}$$

(1)

with $\alpha =\alpha _s+\arctan ({\dot{z}})$, where z is the ratio of the relative deflection and reduced velocity, $\beta$ the dimensionless damping coefficient and K a dimensionless positive constant.

3 Conditions on the involved functions

An interesting question is whether Eq. (1) has periodic solutions; in particular whether it is possible to determine the conditions on the parameters and aerodynamic coefficients such that periodic solutions occur. In a physical interpretation stable periodic solutions are identified with the phenomenon of galloping or flutter.

By applying the transformation $x = -{\dot{z}}, y = z$, Eq. (1) can be written as a so-called Liénard system:

$$\begin{aligned} \frac{dx}{dt} = y - F(x), \frac{dy}{dt} = -x, \end{aligned}$$

(2)

where

$$\begin{aligned} F(x)=K\sqrt{1+x^2}(C_D(\alpha )x-C_L(\alpha ))+2\beta x, \end{aligned}$$

(3)

and

$$\begin{aligned} \alpha =\alpha _s-\arctan (x). \end{aligned}$$

(4)

There exists an extensive literature on periodic solutions of Liénard systems, see for instance the books by Ye Yanqian et al. [10] and by Zhang Zhifen et al. [11]. Most results concern the non-existence, existence and uniqueness of limit cycles of system (2).

It was assumed in [3] that the drag- and lift coefficient curves can be locally approximated by

$$\begin{aligned} \begin{aligned} C_D(\alpha )&=C_{D0},\\ C_L(\alpha )&=C_{L1}\alpha +C_{L3}\alpha ^3, \end{aligned} \end{aligned}$$

(5)

where $C_{D0}, C_{L1}$ and $C_{L3}$ are real parameters satisfying

$$\begin{aligned} C_{D0} > 0, \hspace{5pt} C_{L1} < 0, \hspace{10pt} C_{L3} \ge 0. \end{aligned}$$

(6)

In the remainder of this paper we will only consider the symmetrical case $\alpha _s=0$, i.e. the case where in the static situation the static angle of attack is such that the lift force is absent.

The corresponding Liénard function F(x) for the case $\alpha _s=0$ becomes:

$$\begin{aligned} F(x)=K\sqrt{1+x^2}(C_{D0}x+C_{L1}\arctan (x) + C_{L3}\arctan (x)^3) +2\beta x. \end{aligned}$$

(7)

For this case the following result was shown in [3]:

Theorem 1

Consider system (2) with $\alpha _s=0$ where Eq. (5) hold. If

$$\begin{aligned}{} & {} C_{D0}+C_{L1}+\frac{2\beta }{K}<0 \end{aligned}$$

(8)

$$\begin{aligned}{} & {} C_{D0}>0, \end{aligned}$$

(9)

then system (2) has exactly one closed orbit, a stable limit cycle.

In this theorem the first condition $C_{D0}+C_{L1}+\frac{2\beta }{K}<0$ is the so-called Den Hartog criterion ensuring that the stationary solution is unstable. It is the aim of this paper to study the number of closed orbits of system (2) under more general conditions. In particular we will consider the system with $\alpha _s=0$ where we do not impose a condition on the stability of the equilibrium solution, i.e. we also include the case where the equilibrium is locally asymptotically stable. The latter corresponds to the situation where the Den Hartog criterion is not satisfied. Note that the condition $C_{D0}>0$ is always assumed to hold, as it relates to a positive drag.

Moreover we allow more general conditions on the lift coefficient $C_L(\alpha )$ than the restricted parametrized form expressed through Eq. (5). The conditions which we impose on Eq. (3) are the following:

Definition 1

The following conditions will be imposed on the functions in Eq. (3):

• (i) $\alpha _s=0,$

• (ii) $C_D(\alpha )=C_{D0}>0,$

• (iii) $C_L(\alpha )=-C_L(-\alpha ),$

• (iv) $\frac{d}{d\alpha }[\frac{1}{\alpha }(C_L(\alpha )+\frac{d^2 C_L(\alpha )}{d\alpha ^2})]<0,$

where it is assumed that $C_L(\alpha )$ is $C^3[-\frac{\pi }{2},\frac{\pi }{2}]$.

Note that the special choice for the drag and lift coefficients in [3] is contained in the more general structure of Definition 1. The conditions (ii) and (iii) impose a general structure on the behaviour of the oscillator. The conditions (iii) and (iv) are needed to establish the upper bound on the number of limit cycles in the Liénard system.

4 Properties of the Liénard functions

The conditions in Definition 1 imply that the structure of the function F(x) in Eq. (3) (with $\alpha _s=0$) has restrictions.

For the further study of limit cycles we need to consider derivatives of this function as well. The critical function f(x), defined to be the derivative of F(x) in Eq. (3) with respect to x, is given by:

$$\begin{aligned} f(x)=F'(x)=\frac{K }{\sqrt{1+x^2}}\left( (1+2x^2)C_{D0} -x C_L(\alpha )+\frac{dC_L(\alpha )}{d\alpha }\right) + 2\beta . \end{aligned}$$

(10)

Its derivative can be simplified into the following form:

$$\begin{aligned} f'(x)=\frac{K }{(1+x^2)^{3/2}}\left( x(3+2x^2)C_{D0} - C_L(\alpha )-\frac{d^2 C_L(\alpha )}{d\alpha ^2} \right) . \end{aligned}$$

(11)

Proposition 2

Under conditions (i) and (ii) in Definition 1 the functions F(x), f(x), $f'(x)$ in Eq. (3) satisfy:

$$\begin{aligned}{} & {} \lim _{x \rightarrow \infty } F(x)= \infty , \\{} & {} \lim _{x \rightarrow \infty } f(x)= \infty , \\{} & {} \lim _{x \rightarrow \infty } f'(x)= S_0>0. \end{aligned}$$

Proof

To prove this proposition the critical observation is that in F(x) the drag term dominates over the other terms. This is due to the fact that the function $\alpha =-\arctan (x)$ is bounded for large x. The damping term $2 \beta x$ is an order of magnitude lower for large x and therefore essentially $F(x) \sim K\sqrt{1+x^2}C_{D0} x$ for large x and the statements in the proposition follow. $\square$

The main implication of this proposition is that the functions will be positive for large x. This will restrict the configurations of the zeroes of these functions. Condition (iv) in Definition 1 ensures a further critical restriction on the functions:

Proposition 3

The function $f'(x)$ has at most one positive zero $x^*$ under conditions (i), (ii) and (iv) in Definition 1.

Proof

We rewrite the function $f'(x)$ in Eq. (11) as a product of two factors:

$$\begin{aligned} f'(x)=\frac{-K \alpha }{(1+x^2)^{3/2}}\left( \frac{(x(3+2x^2)C_{D0}}{-\alpha } +\left( \frac{ C_L(\alpha )+\frac{d^2 C_L(\alpha )}{d\alpha ^2}}{\alpha } \right) \right) \equiv \frac{-K \alpha }{(1+x^2)^{3/2}} H(x),\nonumber \\ \end{aligned}$$

(12)

where $\alpha =-\arctan (x)$.

The first factor $\frac{-K \alpha }{(1+x^2)^{3/2}}$ is easily seen to be positive.

We will prove that the second factor H(x) is monotonically increasing for $x \ge 0$, establishing that $f'(x)$ has at most one positive zero.

From the condition (iv) in Definition 1 we know that

$$\begin{aligned} \frac{d \left( \frac{C_L(\alpha )+\frac{d^2 C_L(\alpha )}{d\alpha ^2}}{\alpha }\right) }{dx} = -\frac{1}{1+x^2}\frac{d \ }{d\alpha }\left[ \frac{C_L(\alpha )+\frac{d^2 C_L(\alpha )}{d\alpha ^2}}{\alpha }\right] >0. \end{aligned}$$

Therefore, in order to prove that the derivative of H(x) is positive we only need to prove that the first term $H_1(x)$ of H(x) has a positive derivative, where

$$\begin{aligned} H_1(x)=\frac{(3x + 2x^3)C_{D0}}{\arctan (x)}. \end{aligned}$$

Differentiation gives

$$\begin{aligned} H_1'(x)=\frac{(6x^2+3)(x^2+1)\arctan (x)-x(2x^2+3)}{(x^2+1)\arctan ^2(x)}, \end{aligned}$$

(13)

from which we obtain

$$\begin{aligned} \lim _{x\downarrow 0}H_1'(x) = 0. \end{aligned}$$

(14)

We define $H_1'(x)=\frac{B(x)}{\arctan ^2(x)}$ with

$$\begin{aligned} B(x)=(6x^2+3)\arctan (x)-\frac{x(2x^2+3)}{x^2+1}, \end{aligned}$$

(15)

and hence

$$\begin{aligned} B(0)=0. \end{aligned}$$

(16)

Finally, differentiation of Eq. (15) yields

$$\begin{aligned} B'(x)= {}{{2\,x\,\left( 6\,x^4\,\arctan (x)+12\,x^2\,\arctan (x)+6\,\arctan (x)+2\,x^3+3\,x\right) }\over {\left( x^2+1\right) ^2}}{}. \end{aligned}$$

(17)

Therefore, for $x > 0$ it holds that $B'(x) > 0$ and as a result of Eq. (16) it follows that also $B(x) > 0$ for $x > 0$. This implies, through Eq. (14) that also $H'(x) > 0$ for $x > 0$. Since $H'(x)>0$, we know from Eq. (12) that $f'(x)$ has at most one positive zero. $\square$

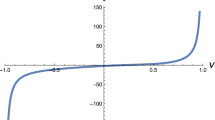
As an example, Fig. 2 shows the functions f(x) and $f'(x)$ for $x \ge 0$ for the choice of parameters $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -18.3\alpha + \alpha ^3, \beta =1$.

Fig. 2

The functions f(x) and $f'(x)$ for $x \ge 0$ for the parameters $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -18.3\alpha + \alpha ^3, \beta =1$

The consequences of this proposition are that the configurations of f(x) are limited in the following way:

Proposition 4

Under the conditions (i), (iii) and (iv) in Definition 1 the functions defined in Eqs. (3) and (10) satisfy:

• (A) $f(0) \ge 0$, $f(x)>0$ for $x > 0$,

• (B) $f(0) \le 0$, $f(x)<0$ for $0 \le x< x_{f}$, $f(x_{f})=0$, $f(x)>0$, for $x>x_{f}$

• (C) $f(0)>0$, $f(x)>0$ for $0 \le x< x_{f_1}$, $f(x_{f_1})=0$, $f(x)<0$ for $x_{f_1}<x<x_{f_2}$, $f(x_{f_2})=0$, $f(x)>0$ for $x>x_{f_2}$. Moreover, on the interval $x>x_{f_2}$ $f'(x)>0$.

Proof

From Proposition 3 we know that f(x) can have at most two positive zeroes. The three cases A, B and C in the lemma correspond to no zero, one zero and two zeroes respectively.

In case A we necessarily have that the function is positive because from Proposition 2 we know that the function is positive for large x.

In case B there is a unique positive zero $x_{f}$ and according to Proposition 2 the function is positive (negative) for $x>x_{f}$ ($0<x<x_{f}$). Note that this is the only case of the three where f(0) cannot be positive.

In case C there are two positive zeroes $x_{f_1}<x_{f_2}$. Since Proposition 2 states that the function is positive for large x, we get the signs of the function as indicated in the lemma. Moreover, necessarily $f(0)>0$. The last statement that on the interval $x>x_{f_2}$ $f'(x)>0$ follows from the fact that $f'(x)$ has a unique zero $x^*$ such that $x^*<x_{f_2}$ and $f'(x)>0$ for $x>x^*$ according to Proposition 2. $\square$

This proposition is the fundamental result for proving an upper bound of the number of limit cycles of system (2) under the conditions of Definition 1. We will see in the next section that the cases A, B and C correspond to the cases with no limit cycles, exactly one limit cycle and at most two limit cycles respectively.

5 The number of limit cycles for the Liénard system (2)

According to Proposition 4 there are three cases to consider for the structure of the function $f(x)=F'(x)$ in system (2) under the conditions of Definition 1. The next three sections contain the details of the limit cycle configurations in those cases.

To find an upper bound on the number of limit cycles we need information about the functions of system (2) for $x<0$ as well. For this we need to impose the previously unused condition (iii) in Definition 1 which imposes a symmetry on the functions F(x) and f(x):

Proposition 5

Under condition (iii) in Definition 1 the function F(x) in Eq. (3) is anti-symmetrical, i.e. $F(x)=-F(-x)$, and f(x) is symmetrical, i.e. $f(x)=f(-x)$.

All the statements in the previous sections were about the behaviour for the functions for $x>0$ and they translate directly into statements about $x<0$ through these symmetries.

An important property of the system which will hold in all three cases of Proposition 4 is the boundedness of system (2):

Proposition 6

System (2) with the conditions defined in Definition 1 is bounded.

Proof

The proof follows by application of Dragilev’s Theorem, see [10, Theorem 5.1]. According to this theorem, the Liénard system (2) is bounded if the following condition holds: there are constant $M > 0$ and $C > D$ such that

$$\begin{aligned} \begin{aligned} F(x) \ge C, x > M,\\ F(x) \le D, x < -M. \end{aligned} \end{aligned}$$

(18)

From Proposition 2 and condition (iii) in Definition 1 it follows that there exists an $x_A>0$ such that $F(x)>F(x_A)>0$ for $x>A$ ($x<A$). Because F(x) is anti-symmetrical it follows that our system satisfies the condition of Dragilev’s Theorem, with $M = x_A$ and $C = -D = F(x_A)$. In fact, the implication is that there is a closed curve at which the vector field of system (2) is either flowing inwards or tangent. This boundary curve shows that all solutions eventually flow inward into the region bounded by this closed curve. $\square$

Notice that in this case we do not need the additional condition (iv) in Definition 1.

5.1 Case A of Proposition 4

In Case A the function f(x) is positive for all x because of Proposition 5. According to the Bendixson theorem, there cannot be limit cycles in such a case because $-f(x)$ corresponds to the divergence of the vector field associated with system (2). Using the boundedness of the solutions according to Proposition 6, we obtain:

Proposition 7

For Case A in Proposition 4 system (2) with the conditions satisfying Definition 1 has no limit cycles. The singularity at $x=0$ is globally asymptotically stable.

Figure 3  shows an example of the phase portrait of system (2) for Case A.

Fig. 3

Case A: phase portrait of syetem (2) for the parameters $K=0.1, C_D(\alpha )\!=\!0.5, C_L(\alpha )= -15\alpha + \alpha ^3, \beta =1$

5.2 Case B

In Case B the function f(x) has two zeroes $-x_{f}$ and $x_{f}$ because of the symmetry in f(x). For such symmetrical Liénard systems with two zeroes it is well-known that the system can have at most one limit cycle:

Proposition 8

For Case B in Proposition 4 system (2) with the conditions defined in Definition 1 has exactly one limit cycle, which is hyperbolic and stable.

Proof

This is a well-known theorem for anti-symmetrical Liénard systems, see for instance [11, 12], but we provide a new simple proof using a so-called Cherkas-Dulac function. In [13] it was shown that if there exists a function B(x, y) such that div(B(x, y)P(x, y), B(x, y)Q(x, y)) has fixed sign in a region $\Omega$, then there is at most limit cycle in $\Omega$ for the system $\frac{dx}{dt}=P(x,y), \ \frac{dy}{dt}=P(x,y)$ and it is hyperbolic.

We choose the function $B(x,y)=\frac{1}{(x^2+(y-F(x))^2-{x_{f}}^2)^{\frac{1}{2}}}$ where $x_{f}$ is the unique positive zero of f(x). Note that the function B(x, y) is singular on the oval $\Gamma$ defined by $C(x,y) = x^2+(y-F(x))^2-{x_{f}}^2=0$. The oval $\Gamma$ is situated in the strip $|x |\le x_f$, see Fig. 4.

Fig. 4

Case (B): the oval $\Gamma$ for the parameters $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -22\alpha + \alpha ^3, \beta =1$

Furthermore, trajectories of system (2) always cross the oval $\Gamma$ from the interior to the exterior because $\frac{C(x,y)}{dt}=-2f(x)(y-F(x))^2$ which is $\le 0$ on the oval. For the chosen function B(x, y) we get

$$\begin{aligned} div(BP,BQ) =-\frac{(x^2-{x_{f}}^2)f(x)}{(x^2+(y-F(x))^2-{x_{f}}^2)^{\frac{3}{2}}} \end{aligned}$$

(19)

which has fixed sign because f(x) vanishes exactly at the zeroes of $x^2-x_{f}^2$. The existence of the stable limit cycle follows from the fact that the system is bounded according to Proposition 6 and the flow of the vector field on the oval $\Gamma$. Note that by Bendixson’s theorem, limit cycles need to intersect the line $x=-x_f$ and $x=x_f$. Application of the Poincaré-Bendixson theorem proves the existence of at least one stable limit cycle which we have just proved to be unique and hyperbolic. $\square$

Figure 5  shows an example of the phase portrait of system (2) for Case B. The stable limit cycle is drawn in green, dotted style.

Fig. 5

Case B: phase portrait of system (2) for the parameters $K\!=\!0.1, C_D(\alpha )\!=\!0.5, C_L(\alpha )= -22\alpha + \alpha ^3, \beta =1$

5.3 Case C

In Case C the function f(x) has four zeroes $-x_{f_2}$, $-x_{f_1}$ $x_{f_1}$, $x_{f_2}$ because of the symmetry in f(x). Moreover $f'(x)>0$ for $x>x_{f_2}$. To prove an upper bound for the number of of limit cycles we will use a theorem by Rychkov which ascertains that Liénard systems of the form (2) have at most two limit cycles if certain conditions are satisfied.

Theorem 9

Suppose that when $x \in (-d,d)$ the following conditions hold

• (1) $f(-x) = f(x)$,

• (2) for $x>0$ f(x) has only zeros $\alpha _1$ and $\alpha _2$, $0< \alpha _1< \alpha _2 < d$,

• (3) $F(\alpha _1) > 0$ and $F(\alpha _2) < 0$,

• (4) f(x) monotonically increases for $x \in (\alpha _2,d)$. Then system (2) has at most two limit cycles in the strip $|x |< d$.

This theorem can be applied to conclude that in Case C at most two limit cycles occur:

Proposition 10

For Case C in Proposition 4 system (2) with the conditions defined in Definition 1 has at most two limit cycles. If they exist, the inner limit cycle is unstable and the outer limit cycle is stable.

Proof

It is clear that in Case C conditions (1), (2), (4) of Theorem 9 are trivially satisfied, with $\alpha _1 = x_{f_1}$ and $\alpha _2 = x_{f_2}$. To show that condition (3) is satisfied we can use the fact that $F(0) = 0$, $f(0) >0$ and $f(x)>0$ on the interval $0<x<\alpha _1$ which means that $F(\alpha _1)>0$. If $F(\alpha _2)$ were to be equal to or larger than 0, then $F(x)\ge 0$ for all x. However, in such a case no limit cycles can occur. This can be seen by considering the family of closed orbits given by the level curves of

$$\begin{aligned} M(x,y)=x^2 + y^2 \end{aligned}$$

(20)

and evaluating system (2) along these curves, which gives

$$\begin{aligned} \left( \frac{dM}{dt}\right) _{(2)} = -2xF(x) \end{aligned}$$

(21)

Therefore if F(x) does not change sign for $x>0$ there can be no limit cycles. It follows that for the existence of limit cycles necessarily $F(\alpha _2)<0$. The resulting graph for F(x) is depicted in Fig. 6, for the parameter choice $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -18.3\alpha + \alpha ^3, \beta =1$.

Fig. 6

The function F(x) for parameter values $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -18.3\alpha + \alpha ^3, \beta =1$

In this case the singularity at the origin is stable, because $f(0)>0$. It means that for two nested hyperbolic limit cycles surrounding the origin, the inner cycle necessarily must be unstable and the outer cycle stable.

$\square$

It should be noted that the application of the Cherkas-Dulac function of the previous section shows that in the strip $-x_{f_2}<x<x_{f_2}$ at most one limit cycle can lie and it will be unstable and hyperbolic if it exists. From this it follows that if there are two limit cycles, at least one of them has to cross the lines $x=-x_{f_2}$ and $x=x_{f_2}$. In particular it means that if two limit cycles collapse onto a semi-stable limit cycles under the variation of a parameter (in particular the parameter $\beta$ in F(x), because it corresponds to a rotated vector field parameter in the vector field defined by system (2)), then the semi-stable limit cycle will have to cross the two lines $x=-x_{f_2}$ and $x=x_{f_2}$.

6 Main result

The previous sections showed results for upper bounds on the number of limit cycles in the different cases for the function f(x) as described in Proposition 4. In this section we will interpret the results in terms of the physical parameters, in particular in terms of the parameters determining the Den Hartog criterion.

The Den Hartog criterion is meant to identify the case where the equilibrium solution (the origin in the phase plane of system (2)) is unstable. In general under such a condition there will be (at least one) stable limit cycle causing the occurrence of the phenomenon of galloping where all solutions, regardless of the initial conditions, eventually will approach a global periodic solution.

Therefore we first identify the condition determining the stability of the equilibrium point. It is easily seen that this stability is determined by the sign of the divergence of the vector field of system (2), i.e. the sign of f(0), as long as it is not equal to zero. Therefore we get:

Proposition 11

System (2) with the conditions satisfying Definition 1 has an unstable (stable) equilibrium point $(x=0,z=0)$ if $V_0<0$ ($V_0>0$), where $V_0=K(C_{D0}+\frac{dC_L(\alpha )}{d\alpha }|_{\alpha =0})+2 \beta$.

Here $V_0$ is the quantity used in the Den Hartog criterion: if $V_0<0$, then the equilibrium is unstable, corresponding to the instability requirement of the equilibrium causing galloping. As we will argue below, this is not the only situation in which galloping will occur though.

In the case when $V_0=0$, the equilibrium point is a weak focus. In this case the origin is either stable or unstable. Cases A and B of Proposition 4 cover $f(0)=0$ and according to the results of the previous section there will be no (one) limit cycle for Case A) ( Case B) ).

We summarize the three propositions in the following main theorem where the number of limit cycles is expressed in terms of the stability of the equilibrium point:

Theorem 12

Consider system (2) with $\alpha _s=0$ where

$$\begin{aligned}{} & {} C_D(\alpha )=C_{D0}>0, \\{} & {} C_L(\alpha )=-C_L(-\alpha ), \\{} & {} \frac{d}{d\alpha }\left[ \frac{1}{\alpha }\left( C_L(\alpha )+\frac{d^2 C_L(\alpha )}{d\alpha ^2}\right) \right] <0. \end{aligned}$$

If the origin is unstable, then system (2) has exactly one hyperbolic stable limit cycle.

If the origin is stable, then system (2) has at most two limit cycles.

Proof

If $f(0)<0$, then Case B in Proposition 4 holds true. according to the corresponding Proposition 8, there exists a unique hyperbolic limit cycle.

If $f(0)>0$, then Cases A and C in Proposition 4 hold true. According to the corresponding Propositions 7 and 10, there does not exist a limit cycle (Case A) or there are at most two limit cycles (Case C).

If $f(0)=0$, then either the origin is a stable or an unstable weak focus. The origin cannot be a center because of the inflow of the vector field for large x, see Lemma 6. From the boundedness of the system it follows that there is an even number (including 0) of limit cycles if the origin is stable and an odd number if it is unstable. Since Propositions 7, 8 and 10 established that the number of limit cycles is 0, exactly 1, and at most 2 in Cases A, B and C of Proposition 4, respectively, it follows that the origin must be stable in Case A and unstable in Case B when $f(0)=0$. $\square$

7 Exactly two limit cycles

So far we have only proved that at most two limit cycles can occur. We will now show that it is possible that exactly two limit cycles occur. This could be proved using a Andronov-Hopf bifurcation from an unstable weak focus which is surrounded by a unique stable limit cycle. However, we prefer to show the existence of two limit cycles using a direct global method.

In order to find an explicit example with two limit cycles, we will use the following lemma by Zhifen et al [11]:

Proposition 13

Consider system (2) on the strip $x \in (-d,d)$ where the function $f(x) \equiv \frac{dF(x)}{dx}$ is even. Assume the following conditions hold:

• (1) F(x) has exactly two simple positive zeroes $a_1$ and $a_2$ with $0< a_1< a_2 < d$.

• (2) For $x \in (0,a_1)$ it holds that $F(x) > 0$.

• (3) There exists a $b_1 > a_1$ such that $a_1+b_1 < a_2$ and $F(x) \le -F(x+b_1)$ for $x \in [0,a_1]$.

• (4) There exists a $b_2 > a_2$ such that $a_2+b_2 < d$ and $-F(x+b_2) \le F(x)$ for $x \in [a_1,a_2]$. Then system (2) has at least two limit cycles, with one limit cycle passing through each of the intervals $(a_1,a_1+b_1)$ and $(a_2,a_2+b_2)$.

We will now show that the system corresponding to the function F(x) depicted in Fig. 6 satisfies the conditions of Proposition 13. For this example we choose $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -18.3\alpha + \alpha ^3, \beta =1$.

First, we establish numerically that the positive zeroes of F(x) satisfy $a_1 \approx 2$ and $a_2 \approx 6.75$. Now we choose $b_1=a_1+1$ and $b_2=a_2 - a_1 +1$. If follows that $a_1+b_1=2a_1 + 1 < a_2$ and $a_2+ b_2 =2a_2-a_1+1 < d$ for a sufficiently large d. The conditions $F(x) \le -F(x+b_1)$ for $x \in [0,a_1]$ and $-F(x+b_2) \le F(x)$ for $x \in [a_1,a_2]$, are also satisfied upon a visual inspection of F(x), see Fig. 7.

Fig. 7

The functions F(x) and $-F(x)$ for parameter values $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -18.3\alpha + \alpha ^3, \beta =1$

Finally, Fig. 8  shows the resulting phase portrait for system (2) for the parameter choice corresponding to Fig. 7. The outer limit cycle, which is stable, is depicted as a green, dotted curve, while the inner, unstable limit cycle, is depicted as a red dashed curve.

Fig. 8

Phase portrait for system (2) for parameter values $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -18.3\alpha + \alpha ^3, \beta =1$

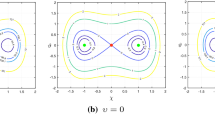
Figure 9, which depicts the phase portrait of system (2) for $x \ge 0$ for the same choice of parameters as before, clearly shows that the inner most limit cycle intersects the x-interval $[a_1,a_1+b_1] = [a_1,2a_1+1]$ while the outer most limit cycle intersects the x-interval $[a_2,a2+b_2] = [a_2,2a_2-a_1+1]$.

Fig. 9

Phase portrait for system (2) for $x \ge 0$ for the parameter values $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -18.3\alpha + \alpha ^3, \beta =1$

It is easy to verify that the parameter $\beta$ rotates the vector field (2). As a result, if we decrease $\beta$ then the inner most limit cycle in Fig. 8 will get smaller and eventually disappear in a Andronov-Hopf bifurcation when $C_{D0}+C_{L1}+\frac{2\beta }{K}=0$. The outer most limit cycle will grow larger for decreasing $\beta$. For increasing $\beta$ the two limit cycles will move closer to each other. Figure 10  shows the phase portrait for system (2) where $\beta$ has increased to 1.023. It is clear that the two limit cycles almost coincide.

Fig. 10

Phase portrait for system (2) for the parameter values $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -18.3\alpha + \alpha ^3, \beta =1.023$

Figure 11  shows the phase portrait for system (2) where $\beta$ has further increased to 1.03. By now the two limit cycles have disappeared through the occurrence of a semi-stable limit cycle.

Fig. 11

Phase portrait for system (2) for the parameter values $K=0.1, C_D(\alpha )=0.5, C_L(\alpha )= -18.3\alpha + \alpha ^3, \beta =1.03$

8 Conclusions

In this paper we showed that for a general one-degree-of-freedom oscillator under the influence of flowing media at most two limit cycles can occur and that situations with exactly two limit cycles do occur. The result that a unique stable limit cycle exists for an unstable equilibrium is not surprising and confirms previously reported results on galloping, i.e. when the Den Hartog criterion is satisfied. The novelty of our results is that there exist parameter values for which a stable equilibrium can be surrounded by two limit cycles, of which the inner cycle is unstable.

The interpretation for the oscillator is that for initial values inside the unstable limit cycle all solutions will tend to the equilibrium but that for initial values outside the unstable limit cycle the solutions will approach the bigger stable limit cycle when $t \rightarrow \infty$, in particular this implies the occurrence of galloping in the presence of a stable equilibrium.

It should be pointed out that the damping coefficients $\beta$ in system (2) is a rotated vector field parameter. It means that when it becomes large enough the two limit cycles will disappear in a semi-stable limit cycle for a critical value of $\beta$ and no limit cycles exist for $\beta$ values larger than this critical value. The fact that eventually no limit cycles will exist, is due to the fact that when $\beta$ is chosen large enough, the function F(x) will be positive for all $x>0$ implying, as we saw in the proof of the main Theorem 12, the non-existence of limit cycles.

What remains to be done in future research is to try to get results for the case $\alpha _s \ne 0$, which will be very difficult because to our knowledge no applicable theorems exist to prove an upper bound of two limit cycles. For the case of an unstable equilibrium better results could be achieved by applying an appropriate uniqueness theorem for Liénard systems.

Other improvements on the model could be to change the type of oscillator as was proposed in [3].