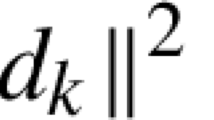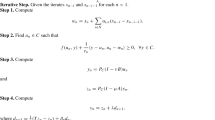Modified Newton–CAPRESB method for solving a class of systems of nonlinear equations with complex symmetric Jacobian matrices

Abstract

In this paper, we contemplate addressing nonlinear problems involving complex symmetric Jacobian matrices. Firstly, we establish a parameter-free method called modified Newton–CAPRESB (MN–CAPRESB) method by harnessing the modified Newton method as the outer iteration and the CAPRESB (Chebyshev accelerated preconditioned square block) method as the inner iteration. Secondly, the local and semilocal convergence theorems of MN–CAPRESB method are proved under some conditions. Eventually, the numerical experiments of two kinds of complex nonlinear equations are presented to validate the feasibility of MN–CAPRESB method compared to other existing iteration methods.

1 Introduction

In many fields of physics and engineering, we often encounter nonlinear problems. Examples of such systems can be seen in Ortega and Rheinboldt (2000), Rheinboldt (1998) and references therein.

We contemplate addressing the large and sparse nonlinear system:

$$\begin{aligned} F(x) = 0. \end{aligned}$$

(1)

Here,

$$\begin{aligned} F: {\mathbb {D}} \subset {\mathbb {C}}^n \rightarrow {\mathbb {C}}^n \end{aligned}$$

represents a continuously differentiable function.

We assume that the Jacobian matrix $F'(x)$ has the following form:

$$\begin{aligned} F'(x) = W(x) + iT(x), \end{aligned}$$

(2)

where $i = \sqrt{-1}$ and matrices $W(x),T(x)\in {\mathbb {R}}^{n\times n}$ are symmetric positive definite (SPD) and symmetric positive semidefinite (SPSD), respectively.

For solving Eq. (1), many researchers have devoted themselves to proposing numerous methods (Ortega and Rheinboldt 2000; Rheinboldt 1998; King 1973). The Newton method is considered as a efficient and widely used iterative method for addressing nonlinear problems. The inexact Newton method (Dembo et al. 1982) outperforms the Newton method. It could be formulated as follows:

$$\begin{aligned} F'(x_k)m_k = -F(x_k) + r_k, \text { with } x_{k+1} := x_k + m_k. \end{aligned}$$

Here, $x_0 \in {\mathbb {D}}$ stands for the provided initial vector, while $r_k$ denotes a residual acquired during the inner iteration process. The modified Newton method (Darvishi and Barati 2007) was established to reduce the computational load in Newton method, which has the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_k = x_k - F'(x_k)^{-1} F(x_k), \\ x_{k+1} = y_k - F'(x_k)^{-1} F(y_k). \end{array}\right. } \end{aligned}$$

Among the above methods, we can observe that tackling linear equations is an integral part in these methods. So we review the methods for addressing complex linear equation

$$\begin{aligned} A{\tilde{f}} = b, \quad A \in {\mathbb {C}}^{n\times n}, \quad {\tilde{f}}, b \in {\mathbb {C}}^n, \end{aligned}$$

(3)

where $A=W+iT$ and the matrices $W,T\in {\mathbb {R}}^{n\times n}$ are SPD and SPSD, respectively. In 2003, the Hermitian and skew-Hermitian splitting (HSS) method was constructed by Bai et al., which was based on the specific structure of A (Bai et al. 2003). The modified HSS (MHSS) (Bai et al. 2010) and preconditioned MHSS (PMHSS) (Bai et al. 2011) methods have also been established for enhancing the HSS method. Moreover, Hezari et al. established a single-step iterative method known as the SCSP method in Hezari et al. (2016). Subsequently, other researchers have extended and improved upon this method, leading to the development of more effective iteration methods (Zheng et al. 2017; Salkuyeh and Siahkolaei 2018). Furthermore, Wang et al. presented a novel iteration method combining real and imaginary parts (CRI) (Wang et al. 2017). Since then, a number of researchers have devoted their efforts to developing efficient iteration methods (Xiao and Wang 2018; Huang 2021; Shirilord and Dehghan 2022) to solve Eq. (3).

Additionally, it can be confirmed that Eq. (3) is equivalent to the following equation:

$$\begin{aligned} {\mathcal {A}}f \equiv \begin{bmatrix} W &{}\quad -T \\ T &{}\quad W \end{bmatrix} \begin{bmatrix} z^{(1)} \\ z^{(2)} \end{bmatrix} = \begin{bmatrix} p \\ q \end{bmatrix} \equiv c. \end{aligned}$$

(4)

Here, ${\tilde{f}} = z^{(1)} + iz^{(2)}$ and $b = p + iq$. To address Eq. (4), a block PMHSS iteration method (Bai et al. 2013) and the DSS real-valued iteration method (Zhang et al. 2019) were proposed, which can be seen as the variants of PMHSS method (Bai et al. 2011) and DSS method (Zheng et al. 2017). In recent years, several iteration methods akin to the generalized successive overrelaxation (GSOR) approach have also been developed (Salkuyeh et al. 2015; Hezari et al. 2015; Edalatpour et al. 2015; Liang and Zhang 2016). Moreover, Axelsson et al. presented the preconditioned square block (PRESB) preconditioner in Axelsson et al. (2014):

$$\begin{aligned} {\mathcal {P}}_{\textrm{PRESB}} = \begin{bmatrix} W &{}\quad -T \\ T &{}\quad \alpha ^2 W + 2\alpha T \end{bmatrix}, \end{aligned}$$

where $\alpha$ is a real positive parameter.

The previously mentioned methods are effective in solving linear systems, but require the selection of a positive parameter or even two parameters, which can be time-consuming during practical implementation. For addressing this issue, a number of researchers provided theoretical optimal parameters in their methods (Bai et al. 2003, 2010, 2011; Hezari et al. 2016; Zheng et al. 2017) while the process of computing optimal parameters often involves the calculation of the eigenvalues of matrices, costing relatively much time. To avoid selecting parameters, Liang and Zhang (2021) proposed a parameter-free method called the Chebyshev accelerated PRESB (CAPRESB) method. They took advantage of the fact that the eigenvalues of ${\mathcal {P}}_{\textrm{PRESB}}^{-1}{\mathcal {A}}$ are located in the interval [0.5, 1] when $\alpha = 1$, making the PRESB method comparably efficient without the parameter selection.

By incorporating the Newton method with the HSS method, Bai et al. established the Newton–HSS method to address complex nonlinear systems in Bai and Guo (2010) and it was improved by Wu et al. who established the modified Newton–HSS method (Wu and Chen 2013). Examples of such methods can be seen in Zhang et al. (2021, 2022), Yu and Wu (2022), Xiao et al. (2021), Dai et al. (2018), Feng and Wu (2021). In this paper, drawing inspiration from these ideas, we establish a parameter-free method called MN–CAPRESB method by incorporating the modified Newton method with CAPRESB method.

Throughout the full paper, we utilize the notation $\Vert \cdot \Vert$ to represent the Euclidean norm of a vector or a matrix. If there is no specific explanation, the matrices $W,T\in {\mathbb {R}}^{n\times n}$ are SPD and SPSD, respectively. Moreover, $\Re (\cdot )$ and $\Im (\cdot )$ are used to represent the real and complex components of the corresponding number, respectively.

The structure of the paper is outlined as follows. In Sect. 2, we present the MN–CAPRESB method. In Sects. 3 and 4, the local and semilocal convergence theorems of our approach are demonstrated under proper conditions, respectively. In Sect. 5, we provide numerical results to illustrate the benefits of our approach compared to the MN–MHSS (Yang and Wu 2012), MN–PMHSS (Zhong et al. 2015), MN–SSTS (Yu and Wu 2022) and MN–PSBTS (Zhang et al. 2022) methods. Eventually, we provide a concise conclusion in Sect. 6.

2 MN–CAPRESB method

First of all, we review the CAPRESB method (Liang and Zhang 2021). For simplicity of notation, we denote

$$\begin{aligned} {\mathcal {P}} = \begin{bmatrix} W &{}\quad -T \\ T &{}\quad W + 2T \end{bmatrix}. \end{aligned}$$

${\mathcal {P}}$ is the special case of ${\mathcal {P}}_{\textrm{PRESB}}$ when $\alpha = 1$. The details of CAPRESB method can be described as follows:

$$\begin{aligned} {\mathcal {P}}u_0 = r_0, \quad f_1 = f_0 + \frac{\tau _0}{2}u_0 \end{aligned}$$

(5)

and

$$\begin{aligned} {\mathcal {P}}u_k = r_k, \quad f_{k+1} = \zeta _k f_k + (1-\zeta _k)f_{k-1} + \tau _k u_k, \quad k = 1,2,\ldots , \end{aligned}$$

(6)

where $r_k = c-{\mathcal {A}}f_k$, $\tau _k$ and $\zeta _k$ are positive acceleration parameters with

$$\begin{aligned} \tau _0 = \frac{4}{{\tilde{\lambda }}_{\max }+{\tilde{\lambda }}_{\min }} \end{aligned}$$

and

$$\begin{aligned} \tau _k=\left( \frac{{\tilde{\lambda }}_{\max }+{\tilde{\lambda }}_{\min }}{2}-\left( \frac{{\tilde{\lambda }}_{\max }-{\tilde{\lambda }}_{\min }}{4}\right) ^2\tau _{k-1}\right) ^{-1},\quad \zeta _k=\frac{{\tilde{\lambda }}_{\max }+{\tilde{\lambda }}_{\min }}{2}\tau _k, \quad k=1,2,\ldots \end{aligned}$$

with ${\tilde{\lambda }}_{\max }=1$ and ${\tilde{\lambda }}_{\min }=0.5$. The iteration formulas (5)-(6) are categorized to the Chebyshev acceleration method (Golub and Varga 1961). Moreover, for the CAPRESB method, we can obtain the Algorithms 1 and 2 in Liang and Zhang (2021).

Algorithm 1

Liang and Zhang (2021) Computation of u from ${\mathcal {P}}u=r$ with $u= [u^{{(1)}^T}, u^{{(2)}^T}]^T$ and $r=[r^{{(1)}^T}, r^{{(2)}^T}]^T$

Algorithm 2

Liang and Zhang (2021) CAPRESB iteration method for (4)

From Algorithms 1 and 2, we know that the CAPRESB method involves two linear systems about $W+T$ at each iteration step, which can be accurately solved through sparse Cholesky factorization or approximately through a preconditioned conjugate gradient (PCG) approach.

Actually, another parameter-free method called CADSS method was also proposed in Liang and Zhang (2021), which accelerates the double-step scale splitting real-valued method (Zhang et al. 2019) with Chebyshev accelerated iteration method. Similarly, we can also establish MN–CADSS method. However, at each step of CADSS method it involves four linear systems to be solved. Based on it, we think that the CAPRESB method outperforms the CADSS method. Hence, we only establish the modified Newton–CAPRESB method.

Now, we summarize the convergence characteristics of the CAPRESB method in Liang and Zhang (2021). From Axelsson (1996), the iterative error $e_k = f_k - f_*$ satisfies

$$\begin{aligned} e_k = Q_k({\mathcal {P}}^{-1}{\mathcal {A}})e_0 \quad \text {with} \quad Q_k(z) = \frac{T_k\left( \frac{{\tilde{\lambda }}_{\max }+{\tilde{\lambda }}_{\min }-2z}{{\tilde{\lambda }}_{\max }-{\tilde{\lambda }}_{\min }}\right) }{T_k\left( \frac{{\tilde{\lambda }}_{\max }+{\tilde{\lambda }}_{\min }}{{\tilde{\lambda }}_{\max }-{\tilde{\lambda }}_{\min }}\right) },\quad k = 0,1,2,\ldots , \end{aligned}$$

(7)

where $f_*$ represents the exact solution of (4) and

$$\begin{aligned} T_k(z) = \frac{1}{2}\left[ \left( z+\sqrt{z^2-1}\right) ^k + \left( z-\sqrt{z^2-1}\right) ^k\right] ,\quad -\infty< z < +\infty , \end{aligned}$$

which conforms to the subsequent recurrence equations:

$$\begin{aligned} T_0(z) = 1,\quad T_1(z) = z \quad \text {and} \quad T_{k+1}(z) = 2zT_k(z) - T_{k-1}(z),\quad k = 1,2,\ldots . \end{aligned}$$

Consequently, we have

$$\begin{aligned} \max \limits _{\lambda _{\min } \le \lambda \le \lambda _{\max }} |Q_k(\lambda )| \le \max \limits _{{\tilde{\lambda }}_{\min } \le \lambda \le {\tilde{\lambda }}_{\max }} |Q_k(\lambda )| = \frac{1}{|T_k\left( \frac{{\tilde{\lambda }}_{\max }+{\tilde{\lambda }}_{\min }}{{\tilde{\lambda }}_{\max }-{\tilde{\lambda }}_{\min }}\right) |} \le 2\left( \frac{\sqrt{2}-1}{\sqrt{2}+1}\right) ^k, \end{aligned}$$

(8)

where $\lambda _{\max }$ and $\lambda _{\min }$ represent the largest and smallest eigenvalues of the matrix ${\mathcal {P}}^{-1}{\mathcal {A}}$, respectively, satisfying

$$\begin{aligned} {\tilde{\lambda }}_{\min } \le \lambda _{\min } \le \lambda _{\max } \le {\tilde{\lambda }}_{\max }. \end{aligned}$$

If ${\mathcal {P}}^{-1}{\mathcal {A}}$ is symmetric, it is straightforward to derive the convergence characteristics according to Eqs. (7) and (8). Moreover, the authors in Liang and Zhang (2021) have proved that ${\mathcal {P}}^{-1}{\mathcal {A}}$ can be diagonalized, which contributes to the convergence characteristics of the CAPRESB method. Now, we summarize the convergence characteristics of the CAPRESB method in Liang and Zhang (2021).

Theorem 2.1

We denote $e_k = f_k - f_*$ and ${\tilde{e}}_k = {\tilde{f}}_k-{\tilde{f}}_*$, $k=0,1,\ldots$. Here, $f_k = \begin{bmatrix} z^{(1)}_k \\ z^{(2)}_k \end{bmatrix}$, $f_* = \begin{bmatrix} z^{(1)}_* \\ z^{(2)}_* \end{bmatrix}$, ${\tilde{f}}_k = z^{(1)}_k + iz^{(2)}_k$, ${\tilde{f}}_* = z^{(1)}_* + iz^{(2)}_*$, and $f_*$ and ${\tilde{f}}_*$ are the exact solutions of (4) and (3), respectively. Then we have

$$\begin{aligned} \Vert e_k\Vert \le \sqrt{\kappa _2(H)}\kappa _{\mu }\theta ^{k}\Vert e_0\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert {\tilde{e}}_k\Vert \le \sqrt{\kappa _2(H)}\kappa _{\mu }\theta ^{k}\Vert {\tilde{e}}_0\Vert , \end{aligned}$$

$k=0,1,\ldots$, where $H=W+T$, $\kappa _2(H) = \Vert H\Vert \Vert H^{-1}\Vert$, $\kappa _{\mu } = 2+\mu _{\max }^2+\mu _{\max }\sqrt{4+\mu _{\max }^{2}}$, $\theta =\frac{\sqrt{2}-1}{\sqrt{2}+1}$, and $\mu _{\max }$ represents the largest eigenvalue of the matrix $W^{-1}T$.

Proof

From Theorem 3.1 in Liang and Zhang (2021), we know that there exist inverse matrix ${\tilde{X}}$ and diagonal matrix D such that

$$\begin{aligned} {\mathcal {P}}^{-1}{\mathcal {A}} = {\tilde{X}}D{\tilde{X}}^{-1}, \end{aligned}$$

where $\kappa _2({\tilde{X}}) \le \frac{\sqrt{\kappa _2(H)}\kappa _{\mu }}{2}$. According to the Eqs. (7) and (8), we can obtain

$$\begin{aligned} \Vert e_k\Vert&= \Vert Q_k({\mathcal {P}}^{-1}{\mathcal {A}})e_0\Vert = \Vert Q_k({\tilde{X}}D{\tilde{X}}^{-1})e_0\Vert \\&= \Vert {\tilde{X}}Q_k(D){\tilde{X}}^{-1}e_0\Vert \le \Vert {\tilde{X}}\Vert \Vert Q_k(D)\Vert \Vert {\tilde{X}}^{-1}\Vert \Vert e_0\Vert \\&= \kappa _2({\tilde{X}}) \Vert Q_k(D)\Vert \Vert e_0\Vert \le \sqrt{\kappa _2(H)}\kappa _{\mu }\theta ^{k}\Vert e_0\Vert , \end{aligned}$$

$k=0,1,\ldots$. It is trivial to see $\Vert {\tilde{e}}_k\Vert = \Vert e_k\Vert$ and $\Vert {\tilde{e}}_*\Vert = \Vert e_*\Vert$. Hence, the other formula holds. $\square$

Moreover, we propose the following theorem to further describe the convergence characteristics.

Theorem 2.2

In accordance with the conditions stated in Theorem 2.1, we can hold

$$\begin{aligned} \Vert e_k\Vert \le \sqrt{M}\left( 2+M^2+M\sqrt{4+M^{2}}\right) \theta ^{k}\Vert e_0\Vert \end{aligned}$$

(9)

and

$$\begin{aligned} \Vert {\tilde{e}}_k\Vert \le \sqrt{M}\left( 2+M^2+M\sqrt{4+M^{2}}\right) \theta ^{k}\Vert {\tilde{e}}_0\Vert , \end{aligned}$$

(10)

$k=0,1,\ldots$, where $M = \Vert W^{-1}\Vert (\Vert W\Vert +\Vert T\Vert )$ and $\theta =\frac{\sqrt{2}-1}{\sqrt{2}+1}$.

Proof

Actually, we can obtain

$$\begin{aligned} \kappa _2(H) \le \frac{\lambda _{\max }(W)+\lambda _{\max }(T)}{\lambda _{\min }(W)} = M \end{aligned}$$

and

$$\begin{aligned} \mu _{\max } \le \Vert W^{-1}\Vert \Vert T\Vert \le M. \end{aligned}$$

Hence, from Theorem 2.1, it holds that

$$\begin{aligned} \Vert e_k\Vert \le \sqrt{\kappa _2(H)}\kappa _{\mu }\theta ^{k}\Vert e_0\Vert \le \sqrt{M}\left( 2+M^2+M\sqrt{4+M^{2}}\right) \theta ^{k}\Vert e_0\Vert , \end{aligned}$$

$k=0,1,\ldots$. Moreover, it is straightforward to know the other formula holds. $\square$

The CAPRESB method is converged when $W,T\in {\mathbb {R}}^{n\times n}$ are both SPSD and null(W) $\cap$ null(T) = 0, where null(A) denotes the null space of A (Liang and Zhang 2021). We restrict W to be SPD to better estimate $\kappa _2(H)$ and $\mu _{\max }$ as Theorem 2.2 shows.

Then, we propose the MN–CAPRESB method, which implies that we utilize CAPRESB method for the following equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} F'(x_k)d_k = -F(x_k),\quad y_k = x_k + d_k, \\ F'(x_k)h_k = -F(y_k),\quad x_{k+1} = y_k + h_k. \end{array}\right. } \end{aligned}$$

(11)

Actually, the MN–CAPRESB method for addressing Eq. (1) can be derived as demonstrated in Algorithm 3. We make the following markings to better illustrate the algorithm. ${\mathcal {P}}(x)$ and ${\mathcal {A}}(x)$ denote the special case of ${\mathcal {P}}$ and ${\mathcal {A}}$ when $W = W(x)$ and $T = T(x)$, respectively. Moreover, $c(x) \equiv \begin{bmatrix} \Re {(-F(x))}\\ \Im {(-F(x))} \end{bmatrix}$.

Algorithm 3

MN–CAPRESB method

3 Local convergence theorem of the MN–CAPRESB method

Suppose that $x_* \in {\mathbb {N}}_0 \subseteq {\mathbb {D}}$ with $F(x_*) = 0$, and ${\mathbb {N}}(x_*, r)$ represents an open ball centered at $x_*$ with radius r.

Assumption 3.1

For any $x \in {\mathbb {N}}(x_*, r) \subset {\mathbb {N}}_0$, we assume that the formulas below are satisfied.

(THE BOUNDED CONDITION) There exist numbers $\beta , \gamma > 0$ such that

$$\begin{aligned} \max \{\Vert W(x_*)\Vert , \Vert T(x_*)\Vert \} \le \beta , \quad \max \{\Vert W(x_*)^{-1}\Vert , \Vert F'(x_*)^{-1}\Vert \} \le \gamma . \end{aligned}$$

(THE LIPSCHITZ CONDITION) There exist numbers $L_w, L_t \ge 0$ such that

$$\begin{aligned} \Vert W(x) - W(x_*)\Vert \le L_w\Vert x - x_*\Vert , \quad \Vert T(x) - T(x_*)\Vert \le L_t\Vert x - x_*\Vert . \end{aligned}$$

Lemma 3.1

Under the condition that $r \in (0, \frac{1}{\gamma L})$ and subject to Assumption 3.1, $W(x)^{-1}$ and $F'(x)^{-1}$ exist for all $x \in {\mathbb {N}}(x_*, r) \subset {\mathbb {N}}_0$. Additionally, the formulas below are satisfied for any $x, z \in {\mathbb {N}}(x_*, r)$ with $L:= L_w + L_t$:

$$\begin{aligned}&\Vert F'(x) - F'(x_*)\Vert \le L \Vert x - x_*\Vert , \\&\max \{\Vert W(x)^{-1}\Vert ,\Vert F'(x)^{-1}\Vert \} \le \frac{\gamma }{1-\gamma L\Vert x - x_*\Vert }, \\&\Vert F(z)\Vert \le \frac{L}{2}\Vert z - x_*\Vert ^2 + 2\beta \Vert z - x_*\Vert , \\&\Vert z - x_* - F'(x)^{-1}F(z)\Vert \le \frac{\gamma }{1 - \gamma L\Vert x - x_*\Vert } \left( \frac{L}{2} \Vert z - x_*\Vert + L\Vert x - x_*\Vert \right) \Vert z - x_*\Vert . \end{aligned}$$

Proof

The proof closely resembles that of Lemma 3.3 in Xie et al. (2020), so we omit it here. $\square$

Lemma 3.2

In accordance with the conditions stated in Lemma 3.1, let $r \in (0, r_0)$, $r_0:= \min \{r_1, r_2\}$ and $u:= \min \{l_*, m_*\}$, where

$$\begin{aligned} r_1&=\frac{\beta }{L(1+3\gamma \beta )},\\ r_2&= \frac{2(1-2\tau \beta \gamma \theta ^{u})}{(5+\tau )\gamma L}, \end{aligned}$$

$l_* = \liminf _{k \rightarrow \infty } l_k$ and $m_* = \liminf _{k \rightarrow \infty } m_k$. Moreover, the number u is subjected to

$$\begin{aligned} u > \left\lfloor -\frac{\ln (2\tau \beta \gamma )}{\ln \theta }\right\rfloor , \end{aligned}$$

where the notation $\lfloor \cdot \rfloor$ represents the smallest integer at least as much as the corresponding real number. Additionally, we set

$$\begin{aligned} g(t;v) = \frac{\gamma }{1-\gamma Lt}\left[ \left( \frac{3+\tau }{2}\right) Lt+2\tau \beta \theta ^{v}\right] . \end{aligned}$$

Subsequently, for all $x_k \in {\mathbb {N}}(x_*,r) \subset {\mathbb {N}}_0$, we have

$$\begin{aligned} \Vert d_{k,l_k}-d_k\Vert \le \tau \theta ^{u}\Vert d_k\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert h_{k,m_k}-h_k\Vert \le \tau \theta ^{u}\Vert h_k\Vert . \end{aligned}$$

Here, $d_{k,l_k}$ and $h_{k,m_k}$ are obtained by Algorithm 3, $d_k = -F'(x_k)^{-1}F(x_k)$ and $h_k = -F'(x_k)^{-1}F(y_k)$. Moreover, $\theta =\frac{\sqrt{2}-1}{\sqrt{2}+1}$ and $\tau =\sqrt{{\tilde{M}}}\left( 2+{\tilde{M}}^2+{\tilde{M}}\sqrt{4+{\tilde{M}}^{2}}\right)$ with ${\tilde{M}}=3\gamma \beta$. When $t \in (0, r)$ and $v>u$, we can obtain that

$$\begin{aligned} g(t;v)< g(r_0;u) < 1. \end{aligned}$$

Proof

Firstly, since $r<\frac{1}{\gamma L}$, for all $x_k \in {\mathbb {N}}(x_*,r)$, it holds that

$$\begin{aligned} \Vert W(x_k)\Vert \le \Vert W(x_k)-W(x_*)\Vert +\Vert W(x_*)\Vert \le L_w\Vert x_k-x_*\Vert +\beta \end{aligned}$$

and

$$\begin{aligned} \Vert T(x_k)\Vert \le \Vert T(x_k)-T(x_*)\Vert +\Vert T(x_*)\Vert \le L_t\Vert x_k-x_*\Vert +\beta . \end{aligned}$$

Moreover, in accordance with Lemma 3.1, since $r<r_1$,

$$\begin{aligned} \Vert W(x_k)^{-1}\Vert (\Vert W(x_k)\Vert +\Vert T(x_k)\Vert )\le \frac{\gamma (L\Vert x_k-x_*\Vert +2\beta )}{1-\gamma L\Vert x_k-x_*\Vert }\le 3\gamma \beta . \end{aligned}$$

According to the formula (10) in Theorem 2.2, we have

$$\begin{aligned} \Vert d_{k,l_k}-d_k\Vert&\le \sqrt{M_k}\left( 2+M_k^2+M_k\sqrt{4+M_k^{2}}\right) \theta ^{l_k}\Vert d_{k,0} - d_k\Vert \\&\le \tau \theta ^{l_k}\Vert d_k\Vert \le \tau \theta ^{u}\Vert d_k\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert h_{k,m_k}-h_k\Vert&\le \sqrt{M_k}\left( 2+M_k^2+M_k\sqrt{4+M_k^{2}}\right) \theta ^{m_k}\Vert h_{k,0} - h_k\Vert \\&\le \tau \theta ^{m_k}\Vert h_k\Vert \le \tau \theta ^{u}\Vert h_k\Vert , \end{aligned}$$

where $M_k = \Vert W(x_k)^{-1}\Vert (\Vert W(x_k)\Vert +\Vert T(x_k)\Vert )$. Furthermore, since $0< t < r$, $r<r_2$ and $v>u$, we have

$$\begin{aligned} g(t;v) = \frac{\gamma }{1-\gamma Lt}\left[ \left( \frac{3+\tau }{2}\right) Lt+2\tau \beta \theta ^{v}\right]< g(r_0;u)<1. \end{aligned}$$

$\square$

Theorem 3.1

In accordance with the conditions stated in Lemmas 3.1 and 3.2, for all $x_0 \in {\mathbb {N}}(x_*, r)$ and any positive integers sequences $\{l_k\}_{k=0}^\infty , \{m_k\}_{k=0}^\infty$, the sequence $\{x_k\}_{k=0}^\infty$ generated by the Algorithm 3 converges to $x_*$. Furthermore, it holds that

$$\begin{aligned} \limsup _{k\rightarrow \infty } \Vert x_k - x_*\Vert ^{\frac{1}{k}} \le g(r_0; u)^2. \end{aligned}$$

Proof

Firstly, according to Lemmas 3.1, 3.2 and formula (11), if $x_k \in {\mathbb {N}}(x_*,r) \subset {\mathbb {N}}_0$, we can obviously obtain

$$\begin{aligned} \Vert y_k - x_*\Vert&= \Vert x_k - x_* + d_{k,l_k}\Vert \\&\le \Vert x_k-x_*-F'(x_k)^{-1}F(x_k)\Vert +\Vert d_{k,l_k}-d_k\Vert \\&\le \frac{\gamma }{1 - \gamma L\Vert x_k-x_*\Vert }\frac{3L}{2} \Vert x_k - x_*\Vert ^2\\&\quad +\frac{\gamma \tau \theta ^{l_k}}{1 - \gamma L\Vert x_k-x_*\Vert }\left( \frac{L}{2}\Vert x_k - x_*\Vert ^2 +2\beta \Vert x_k-x_*\Vert \right) \\&=\frac{\gamma }{1 - \gamma L\Vert x_k-x_*\Vert }\left( \frac{3+\tau \theta ^{l_k}}{2}L\Vert x_k-x_*\Vert +2\tau \beta \theta ^{l_k}\right) \Vert x_k-x_*\Vert \\&\le \frac{\gamma }{1 - \gamma L\Vert x_k-x_*\Vert }\left( \frac{3+\tau }{2}L\Vert x_k-x_*\Vert +2\tau \beta \theta ^{l_k}\right) \Vert x_k-x_*\Vert \\&= g(\Vert x_k - x_*\Vert ; l_k) \Vert x_k - x_*\Vert \\&\le g(r_0; u) \Vert x_k - x_*\Vert \\&\le \Vert x_k - x_*\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert x_{k+1} - x_*\Vert&= \Vert y_k - x_* + h_{k,m_k}\Vert \\&\le \Vert y_k-x_*-F'(x_k)^{-1}F(y_k)\Vert +\Vert h_{k,m_k}-h_k\Vert \\&\le \frac{\gamma }{1 - \gamma L\Vert x_k-x_*\Vert }\left( \frac{L}{2}\Vert y_k-x_*\Vert +L\Vert x_k-x_*\Vert \right) \Vert y_k-x_*\Vert \\&\quad +\frac{\gamma \tau \theta ^{m_k}}{1 - \gamma L\Vert x_k-x_*\Vert }\left( \frac{L}{2}\Vert y_k-x_*\Vert ^2+2\beta \Vert y_k-x_*\Vert \right) \\&=\frac{\gamma }{1 - \gamma L\Vert x_k-x_*\Vert }\bigg (\frac{1+\tau \theta ^{m_k}}{2}L\Vert y_k-x_*\Vert \\&\quad +L\Vert x_k-x_*\Vert +2\tau \beta \theta ^{m_k}\bigg )\Vert y_k-x_*\Vert \\&\le \frac{\gamma g(\Vert x_k-x_*\Vert ;l_k)}{1 - \gamma L\Vert x_k-x_*\Vert }\bigg (\frac{1+\tau \theta ^{m_k}}{2}Lg(\Vert x_k-x_*\Vert ;l_k)\Vert x_k-x_*\Vert \\&\quad +L\Vert x_k-x_*\Vert +2\tau \beta \theta ^{m_k}\bigg )\Vert x_k-x_*\Vert \\&\le \frac{\gamma g(\Vert x_k-x_*\Vert ;l_k)}{1 - \gamma L\Vert x_k-x_*\Vert }\left( \frac{3+\tau \theta ^{m_k}}{2}L\Vert x_k-x_*\Vert +2\tau \beta \theta ^{m_k}\right) \Vert x_k-x_*\Vert \\&\le g(\Vert x_k-x_*\Vert ;l_k)g(\Vert x_k-x_*\Vert ;m_k)\Vert x_k-x_*\Vert \\&\le g(\Vert x_k-x_*\Vert ;u)^2\Vert x_k-x_*\Vert \\&\le g(r_0;u)^2\Vert x_k-x_*\Vert \\&\le \Vert x_k-x_*\Vert . \end{aligned}$$

Based on the above formulas, we can use mathematical induction to prove that $\{x_k\}_{k=0}^\infty \subset {\mathbb {N}}(x_*, r)$ converges to $x_*$. Actually, we have $\Vert x_0 - x_*\Vert < r$. Moreover, it holds

$$\begin{aligned} \Vert x_1 - x_*\Vert {\le } g(\Vert x_0 - x_*\Vert ; u)^2\Vert x_0 - x_*\Vert {\le } \Vert x_0 - x_*\Vert < r. \end{aligned}$$

Therefore, we have $\Vert x_1 - x_*\Vert < r$. Furthermore, assume that $x_n \in {\mathbb {N}}(x_*,r)$, then it holds that

$$\begin{aligned} \Vert x_{n+1} - x_*\Vert&{\le } g(\Vert x_n - x_*\Vert ; u)^2\Vert x_n - x_*\Vert \\&{\le } g(r_0; u)^{(2n+2)}\Vert x_0 - x_*\Vert < r, \end{aligned}$$

which implies that $x_{n+1} \in {\mathbb {N}}(x_*,r)$ and

$$\begin{aligned} \limsup _{k\rightarrow \infty } \Vert x_k - x_*\Vert ^{\frac{1}{k}} \le g(r_0; u)^2. \end{aligned}$$

Additionally, when $n \rightarrow \infty$, we get $x_{n+1} \rightarrow x_*$. $\square$

4 Semilocal convergence theorem of MN–CAPRESB method

Assumption 4.1

Let $x_0\in {\mathbb {C}}^n$ and assume that the formulas below are satisfied.

(THE BOUNDED CONDITION) There exist positive numbers $\beta , \gamma$ and $\delta$ such that

$$\begin{aligned} \max \{\Vert W(x_0)\Vert ,\Vert T(x_0)\Vert \}\le \beta ,\quad \max \{\Vert W(x_0)^{-1}\Vert ,\Vert F'(x_0)^{-1}\Vert \}\le \gamma ,\quad \Vert F(x_0)\Vert \le \delta . \end{aligned}$$

(THE LIPSCHITZ CONDITION) There exist numbers $L_w, L_t \ge 0$ such that for any $x,z\in {\mathbb {N}}(x_0,r)\subset {\mathbb {N}}_0$,

$$\begin{aligned} \Vert W(x) - W(z)\Vert \le L_w\Vert x - z\Vert ,\quad \Vert T(x) - T(z)\Vert \le L_t\Vert x - z\Vert . \end{aligned}$$

Lemma 4.1

Subject to Assumption 4.1, for all $x, z \in {\mathbb {N}}(x_0, r)$, if $r \in (0, \frac{1}{\gamma L})$, we have $W(x)^{-1}$ and $F'(x)^{-1}$ exist. Additionally, we can obtain the following inequalities with $L:= L_w+L_t:$

$$\begin{aligned}&\Vert F'(x) - F'(z)\Vert \le L \Vert x - z\Vert , \\&\Vert F'(x)\Vert \le L \Vert x - x_0\Vert + 2\beta , \\&\Vert F(x) - F(z) - F'(z)(x - z)\Vert \le \frac{L}{2} \Vert x - z\Vert ^2, \\&\max \{\Vert W(x)^{-1}\Vert ,\Vert F'(x)^{-1}\Vert \} \le \frac{\gamma }{1-\gamma L\Vert x - x_0\Vert }. \end{aligned}$$

Proof

The proof resembles the Lemma 3 of Zhang et al. (2021); therefore, we omit it here. $\square$

Let we denote

$$\begin{aligned} a:=L\gamma (1+\eta ),\quad b:=1-\eta ,\quad c:=2\gamma \delta , \quad \text {where}\quad \eta :=\max _k\{\max \{\eta _k, {\tilde{\eta }}_k\}\}<1. \end{aligned}$$

The sequences of iteration $\{t_k\}$ and $\{s_k\}$ are subject to the formulas below:

$$\begin{aligned} {\left\{ \begin{array}{ll} t_0=0,\\ s_k=t_k-\dfrac{g(t_k)}{h(t_k)},\\ t_{k+1}=s_k-\dfrac{g(s_k)}{h(t_k)}. \end{array}\right. } \end{aligned}$$

(14)

Here,

$$\begin{aligned} {\left\{ \begin{array}{ll} g(x)=\frac{1}{2}ax^2-bx+c,\\ h(x)=ax-1. \end{array}\right. } \end{aligned}$$

We have the following property about the two sequences.

Lemma 4.2

Suppose that the numbers are subject to

$$\begin{aligned} \gamma ^2 \delta L \le \frac{(1 - \eta )^2}{4(1 + \eta )}. \end{aligned}$$

Then the sequences $\{t_k\}$ and $\{s_k\}$ of (14) converge to $t_*$ with $t_* =\frac{b-\sqrt{b^2-2ac}}{a}$. Furthermore,

$$\begin{aligned}&0 \le t_k< s_k< t_{k+1}< t_*,\\&t_{k+1} - s_k < s_k - t_k. \end{aligned}$$

Proof

The proof can be seen in Lemma 4.2 and Lemma 4.3 of Wu and Chen (2013). $\square$

Theorem 4.1

In accordance with the conditions stated in Lemmas 4.1 and 4.2, define $r:= \min \{r_1, r_2\}$ and $u:= \min \{l_*, m_*\}$, where

$$\begin{aligned} r_1= & {} \frac{\beta }{L(1+3\gamma \beta )},\\ r_2= & {} \frac{b-\sqrt{b^2-2ac}}{a}, \end{aligned}$$

$l_* = \liminf _{k\rightarrow \infty } l_k$ and $m_* = \liminf _{k\rightarrow \infty } m_k$. Moreover, the number u is subject to

$$\begin{aligned} u > \left\lfloor \frac{\ln \frac{\eta }{\tau }}{\ln \theta } \right\rfloor , \end{aligned}$$

where $\tau$ and $\theta$ are same in Lemma 3.2. Then the sequence $\{x_k\}_{k=0}^\infty$ generated by the Algorithm 3 converges to $x_*$.

Proof

In fact, for any $x_k \in {\mathbb {N}}(x_*,r)$, analysis resembling that of Lemma 3.2 indicates

$$\begin{aligned} \Vert d_{k,l_k}-d_k\Vert \le \tau \theta ^{l_k}\Vert d_k\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert h_{k,m_k}-h_k\Vert \le \tau \theta ^{m_k}\Vert h_k\Vert . \end{aligned}$$

We use mathematical induction to prove the following formulas:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert x_k - x_0\Vert \le t_k - t_0, \\ \Vert F(x_k)\Vert \le \frac{1-\gamma L t_k}{(1+\eta )\gamma }(s_k - t_k), \\ \Vert y_k - x_k\Vert \le s_k - t_k, \\ \Vert F(y_k)\Vert \le \frac{1-\gamma L t_k}{(1+\eta )\gamma }(t_{k+1} - s_k), \\ \Vert x_{k+1} - y_k\Vert \le t_{k+1} - s_k. \\ \end{array}\right. } \end{aligned}$$

(15)

According to Lemmas 4.1, 4.2 and formula (12), we can obtain

$$\begin{aligned} \Vert x_0 - x_0\Vert&= 0 \le t_0 - t_0, \\ \Vert F(x_0)\Vert&\le \delta \le \frac{2\gamma \delta }{\gamma (1+\eta )} = \frac{1-\gamma L t_0}{(1+\eta )\gamma }(s_0-t_0), \\ \Vert y_0 - x_0\Vert&= \Vert d_{0,l_0}\Vert \le \Vert d_{0,l_0}-d_0\Vert +\Vert d_0\Vert \\&\le (1+\tau \theta ^{l_0})\Vert d_0\Vert \le (1+\tau \theta ^{l_0})\gamma \delta \le 2\gamma \delta = s_0-t_0, \\ \Vert F(y_0)\Vert&\le \Vert F(y_0)-F(x_0)-F'(x_0)(y_0-x_0)\Vert +\Vert F(x_0)+F'(x_0)(y_0-x_0)\Vert \\&\le \frac{L}{2}\Vert y_0-x_0\Vert ^2 + \eta \Vert F(x_0)\Vert \le \frac{L}{2}s_0^2 + \eta \delta \le \frac{1-\gamma L t_0}{(1+\eta )\gamma }(t_1 - s_0), \\ \Vert x_1 - y_0\Vert&\le \Vert h_{0,m_0}\Vert \le \Vert h_{0,m_0}-h_0\Vert +\Vert h_0\Vert \\&\le (1+\tau \theta ^{m_0})\Vert h_0\Vert = (1+\tau \theta ^{m_0})\Vert F'(x_0)^{-1}F(y_0)\Vert < (1+\eta )\gamma \Vert F(y_0)\Vert \le t_1-s_0. \end{aligned}$$

Hence, when $k=0$, the inequalities (15) are true. Now, assume that when $n \le k-1$, the inequalities (15) hold. We consider the case $n=k$. For the first inequality in (15), we can obtain

$$\begin{aligned} \Vert x_k - x_0\Vert&\le \Vert x_k - y_{k-1}\Vert + \Vert y_{k-1} - x_{k-1}\Vert + \Vert x_{k-1} - x_0\Vert \le t_k - t_0. \end{aligned}$$

Since $x_{k-1},y_{k-1}\in {\mathbb {N}}(x_0,r)$ and due to the inequalities(13) as well as formulas in Lemma 4.1, it holds that

$$\begin{aligned} (1 + \eta )\gamma \Vert F(x_k)\Vert&\le (1 + \eta )\gamma \Vert F(x_k) - F(y_{k-1}) - F'(y_{k-1})(x_k - y_{k-1})\Vert \\&\quad + (1 + \eta )\gamma \Vert (F'(y_{k-1})-F'(x_{k-1}))(x_k-y_{k-1})\Vert \\&\quad + (1 + \eta )\gamma \Vert F(y_{k-1}) + F'(x_{k-1})(x_k - y_{k-1})\Vert \\&\le \frac{(1 + \eta ) \gamma L}{2}\Vert x_k - y_{k-1}\Vert ^2 + (1 + \eta ) \gamma L\Vert y_{k-1}-x_{k-1}\Vert \Vert x_k-y_{k-1}\Vert \\&\quad +\eta (1 + \eta )\gamma \Vert F(y_{k-1})\Vert \\&\le \frac{a}{2}(t_k^2-s_{k-1}^2) - at_{k-1}(t_k-s_{k-1}) +\eta (1 - \gamma L t_{k-1})(t_k - s_{k-1})\\&= g(t_k) - g(s_{k-1}) + b(t_k - s_{k-1}) - at_{k-1}(t_k-s_{k-1})\\&\quad + \eta (1 - \gamma L t_{k-1})(t_k - s_{k-1}) \\&= g(t_k) - \frac{h(t_{k-1}) + 1 - at_{k-1}-\eta \gamma Lt_{k-1}}{h(t_{k-1})}g(s_{k-1})\\&= g(t_k) + \frac{\eta \gamma L t_{k-1}}{h(t_{k-1})}g(s_{k-1})\\&< g(t_k) = -h(t_k)(s_k - t_k) < (1 - \gamma Lt_k)(s_k - t_k). \end{aligned}$$

Therefore, it holds that

$$\begin{aligned} \Vert F(x_k)\Vert \le \frac{(1 - \gamma Lt_k)}{(1 + \eta )\gamma }(s_k - t_k) \end{aligned}$$

and then

$$\begin{aligned} \Vert y_k - x_k\Vert&\le (1 + \tau \theta ^{l_k})\Vert F'(x_k)^{-1}\Vert \Vert F(x_k)\Vert \\&\le (1 + \eta )\frac{\gamma }{1 - \gamma Lt_k}\Vert F(x_k)\Vert \\&\le s_k - t_k. \end{aligned}$$

Also, by the inequality (12), we can obtain

$$\begin{aligned} (1 + \eta )\gamma \Vert F(y_k)\Vert&\le (1 + \eta )\gamma \Vert F(y_k) - F(x_k) - F'(x_k)(y_k - x_k)\Vert \\&\quad + (1 + \eta )\gamma \Vert F(x_k) + F'(x_k)(y_k - x_k)\Vert \\&\le \frac{(1 + \eta ) \gamma L}{2}\Vert y_k - x_k\Vert ^2 +\eta (1 + \eta )\gamma \Vert F(x_k)\Vert \\&\le \frac{(1 + \eta ) \gamma L}{2}(s_k - t_k)^2 +\eta (1 - \gamma L t_k)(s_k - t_k)\\&= g(s_k) - g(t_k) + b(s_k - t_k) - at_k(s_k-t_k)\\&\quad + \eta (1 - \gamma L t_k)(s_k - t_k)\\&= g(s_k) - g(t_k) - (1 - at_k-\eta \gamma L t_k)\frac{g(t_k)}{h(t_k)} \\&= g(s_k) - \frac{h(t_k) + 1 - at_k-\eta \gamma Lt_k}{h(t_k)}g(t_k)\\&= g(s_k) + \frac{\eta \gamma L t_k}{h(t_k)}g(t_k)\\&< g(s_k) = -h(t_k)(t_{k+1} - s_k) < (1 - \gamma Lt_k)(t_{k+1} - s_k). \end{aligned}$$

It follows that

$$\begin{aligned} \Vert F(y_k)\Vert \le \frac{(1 - \gamma Lt_k)}{(1 + \eta )\gamma }(t_{k+1} - s_k) \end{aligned}$$

and then

$$\begin{aligned} \Vert x_{k+1} - y_k\Vert&\le (1 + \tau \theta ^{m_k})\Vert F'(x_k)^{-1}\Vert \Vert F(y_k)\Vert \\&\le (1 + \eta )\frac{\gamma }{1 - \gamma Lt_k}\Vert F(y_k)\Vert \\&\le t_{k+1} - s_k. \end{aligned}$$

Consequently, for any k, the formulas (15) are true. Since $\{t_k\}$ and $\{s_k\}$ converge to $t_*$, $\{x_k\}$ and $\{y_k\}$ also converge, to say $x_*$. Additionally, according to Eq. (7) and

$$\begin{aligned} y_k = x_k + d_{k,l_k},\quad k = 0,1,\ldots , \end{aligned}$$

we have

$$\begin{aligned} \liminf _{k\rightarrow \infty } \begin{bmatrix} \Re (d_{k,l_k})\\ \Im (d_{k,l_k}) \end{bmatrix}&= \liminf _{k\rightarrow \infty } (I-Q_{l_k}({\mathcal {P}}(x_k)^{-1}{\mathcal {A}}(x_k)))\begin{bmatrix} \Re (d_k)\\ \Im (d_k) \end{bmatrix}\\&= (I-Q_{l_*}({\mathcal {P}}(x_*)^{-1}{\mathcal {A}}(x_*))) \begin{bmatrix} \Re (F'(x_*)^{-1}F(x_*))\\ \Im (F'(x_*)^{-1}F(x_*)) \end{bmatrix} = 0. \end{aligned}$$

In addition, since the eigenvalues of $Q_{l_*}({\mathcal {P}}(x_*)^{-1}{\mathcal {A}}(x_*))$ are located in $(-1,1)$ according to Eq. (8), we have $F(x_*)=0$. $\square$

5 Numerical examples

In this part, we display two nonlinear problems to show the robustness of the MN–CAPRESB method. We compare our method to the MN–MHSS (Yang and Wu 2012), MN–PMHSS (Zhong et al. 2015), MN–SSTS (Yu and Wu 2022) and MN–PSBTS (Zhang et al. 2022) methods. In practical implementation, selecting parameters can be a complex headache. When conducting the experiments, for MN–MHSS and MN–PMHSS methods, to avoid this repetitive and tedious process, we adopt the same experimental ideas as Xie et al. (2020) to directly use the selected parameters, which are determined experimentally by minimizing the respective iteration steps and errors in relation to the precise solution. We use the following termination condition in the outer iteration:

$$\begin{aligned} \frac{\Vert F(x_k)\Vert }{\Vert F(x_0)\Vert } \le 10^{-6}. \end{aligned}$$

Moreover, we use Outer IT and Inner IT to represent the number of outer and inner iterations, respectively, and we denote the elapsed CPU time in seconds as “CPU time”. The experimental results draw a conclusion that MN–CAPRESB method achieves better results than both MN–MHSS and MN–PMHSS methods without the process of selecting a parameter and exhibits strong competitiveness by virtue of its inherent lack of dependence on parameter selection compared to the MN–SSTS and MN–PSBTS methods.

Example 1

(Yang and Wu 2012) We examine the subsequent nonlinear equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} v_t - ( \alpha _1 + i\beta _1 )( v_{x_1x_1} + v_{x_2x_2} ) + \rho v = -( \alpha _2 + i\beta _2 )v^{\frac{4}{3}}, &{}\quad \text {in }(0,1]\times \Omega , \\ v(0,x_1,x_2) = v_0(x_1,x_2), &{}\quad \text {in }\Omega , \\ v(t,x_1,x_2) = 0, &{}\quad \text {in }(0,1]\times \partial \Omega , \end{array}\right. } \end{aligned}$$

where $\Omega =[0,1]\times [0,1]$, the coefficients $\alpha _1=\beta _1=1$, $\alpha _2=\beta _2=1$ and $\rho > 0$.

For discretizing this system, we can utilize a similar methodology in Yang and Wu (2012) and get the following equation:

$$\begin{aligned} F(x) = Mx + (\alpha _2+i\beta _2)h\Delta t\psi (x) = 0 \end{aligned}$$

with

$$\begin{aligned}&M = h(1+\rho \Delta t)I_{n} + (\alpha _1+i\beta _1)\frac{\Delta t}{h}(I_N\otimes B_N + B_N\otimes I_N), \\&\psi (x) = \left( x_1^{\frac{4}{3}},x_2^{\frac{4}{3}},\ldots ,x_n^{\frac{4}{3}}\right) ^T, \end{aligned}$$

where $B_N = \text {tridiag}(-1,2,-1)$ and $n = N^2$.

During the experiments, the initial vector $x_0=[1,1,\ldots ,1]^T$ and the inner tolerance $\eta _k$ and $\tilde{\eta _k}$ of linear systems have the same value $\eta$.

Tables 1 and 2 present the parameters $\alpha$ used in experiments for the MN–MHSS and MN–PMHSS methods, respectively. These optimal parameters are determined based on extensive experiments in Xie et al. (2020). Moreover, Tables 3 and 4 show the two parameters used in the experiments for the MN–SSTS and MN–PSBTS methods. It is worth emphasizing that the main advantage of the MN–CAPRESB method is its parameter-free nature, contributing to the effectiveness and convenience of the MN–CAPRESB method in practical implementation.

In Tables 5, 6, 7, 8 and 9, we display the experimental results regarding these five approaches associated with the problem size $N = 2^5$ with inner tolerance $\eta = 0.1, 0.2, 0.4$, as well as for $N = 2^6$ and $N = 2^7$ with the same inner tolerance value $\eta = 0.4$, respectively. Additionally, the parameter $\rho = 1, 10, 200$, respectively. From these tables, we know that the MN–CAPRESB method almost obtains extraordinary results regarding errors, CPU time, and inner and outer iterations compared to the MN–MHSS and MN–PMHSS methods. By comparing the results of different parameter values, we can observe that the MN–CAPRESB method consistently performs well across different values of $\rho$, $\eta$ and N, demonstrating lower errors and fewer iterations compared to the MN–MHSS and MN–PMHSS methods. Additionally, MN–CAPRESB demonstrates heightened competitiveness due to its inherent parameter-free nature in comparison with the MN–SSTS and MN–PSBTS methods. Therefore, the MN–CAPRESB method can be considered as an effective method.

Indeed, from Tables 5, 6 and 7, it is evident that the residuals of the MN–CAPRESB method exhibit identical values despite having the same scales N and parameters $\rho$, but varying inner tolerances $\eta$. As the inner tolerance increases, the numbers of outer iterations steps for MN–MHSS and MN–PMHSS methods significantly increase, which leads to longer runtime, while the MN–CAPRESB method remains constant. Thus, the MN–CAPRESB method is robust and efficient. On the other hand, as the scale of the problem increases, the MN–CAPRESB method has become increasingly advantageous in terms of time compared to the MN–MHSS and MN–PMHSS methods, which has more obvious advantages when dealing with large-scale problems. From Table 9, when $N=2^7$, the MN–CAPRESB method almost takes half and one-third of the time compared to the MN–PMHSS and MN–MHSS methods, respectively. While the MN–CAPRESB method may not yield as strong results as the MN–SSTS and MN–PSBTS methods, its inherent lack of parameter selection confers a competitive edge.

Table 1 The optimal values $\alpha$ in the MN–MHSS method in Example 1 (Xie et al. 2020)

Table 2 The optimal values $\alpha$ in the MN–PMHSS method in Example 1 (Xie et al. 2020)

Table 3 The optimal values in the MN–SSTS and MN–PSBTS methods with $N=2^5$ in Example 1

Table 4 The optimal values in the MN–SSTS and MN–PSBTS methods with $\eta = 0.4$ in Example 1

Table 5 Comparison results for $\eta = 0.1$ and $N = 2^5$ in Example 1

Table 6 Comparison results for $\eta = 0.2$ and $N = 2^5$ in Example 1

Table 7 Comparison results for $\eta = 0.4$ and $N = 2^5$ in Example 1

Table 8 Comparison results for $\eta = 0.4$ and $N = 2^6$ in Example 1

Table 9 Comparison results for $\eta = 0.4$ and $N = 2^7$ in Example 1

Example 2

(Xie et al. 2020) Considering the complex nonlinear Helmholtz system:

$$\begin{aligned} -\Delta u + \sigma _1 u + i\sigma _2 u = -e^u, \end{aligned}$$

with $\sigma _1$ and $\sigma _2$ being both real coefficient functions. We can wield finite differences to discretize the problem, which contributes to the following nonlinear equation:

$$\begin{aligned} F(x) = Kx + \phi (x) = 0, \end{aligned}$$

where

$$\begin{aligned} K = (M + \sigma _1 I) + i\sigma _2 I \end{aligned}$$

and

$$\begin{aligned} \phi (x) = (e^{x_1}, e^{x_2}, \ldots , e^{x_n})^T \end{aligned}$$

with

$$\begin{aligned} M = I\otimes C_N + C_N\otimes I \quad \text {and} \quad C_N = \frac{1}{h^2}\text {tridiag}(-1, 2, -1). \end{aligned}$$

During our experiments, we take values of parameters $\sigma _1=100$ and $\sigma _2=1000$. Tables 10 and 11 show the parameters used in experiments. In addition, the initial guess $x_0 = [0,0,\ldots ,0]^T$, the inner tolerance $\eta = 0.1, 0.2, 0.4$ as well as the problem size $N=30, 60, 90$, respectively. Also, we use above five iteration methods to solve this nonlinear problem. We can know that MN–PMHSS method is almost as efficient as MN–MHSS method while MN–CAPRESB method outperforms them upon Tables 12, 13 and 14. Actually, MN–CAPRESB method almost takes half of the time and one-third of inner iteration steps compared to MN–MHSS and MN–PMHSS methods. Moreover, MN–CAPRESB method is competitive with MN–SSTS and MN–PSBTS methods from cpu, outer and inner iterations. Consequently, we yield the conclusion that MN–CAPRESB method outperforms MN–MHSS and MN–PMHSS methods and stands as a viable competitor to MN–SSTS and MN–PSBTS methods.

Table 10 The optimal values $\alpha$ in the MN-MHSS and MN-PMHSS methods in Example 2 (Xie et al. 2020)

Table 11 The optimal values in the MN–SSTS and MN–PSBTS methods in Example 2

Table 12 Comparison results for $N = 30$ in Example 2

Table 13 Comparison results for $N = 60$ in Example 2

Table 14 Comparison results for $N = 90$ in Example 2

6 Conclusion

In this paper, we establish a parameter-free method called the MN–CAPRESB method for addressing nonlinear complex equations by harnessing the modified Newton method as the outer iteration and the CAPRESB (Chebyshev accelerated preconditioned square block) method as the inner iteration. The local and semilocal convergence theorems of our approach are proved. Moreover, to validate the superiority and robustness of the MN–CAPRESB method, we conduct some experiments on two kinds of nonlinear examples compared to other existing iteration methods. Unlike some existing methods, the MN–CAPRESB method can avoid selecting one parameter or even two parameters. However, our research is not exhaustive. We may harness other efficient outer iteration method to accelerate our method, which may be a interesting topic to further explore.