New q-rung orthopair fuzzy Aczel–Alsina weighted geometric operators under group-based generalized parameters in multi-criteria decision-making problems

Abstract

The concept of q-rung orthopair fuzzy set (q-ROF) defined as generalization of intuitionistic fuzzy set (IFS) and Pythagorean fuzzy set (PyFS) has more flexible structure according to several clusters. Therefore, it is a benefit tool to obtain various results for different values of q. The basic benefit of generalized concepts is to rate level of truth and falsity and reduce to error margin. Thus, while the final decision is decided by experts, the most accuracy finding is to present. Aczel–Alsina t-norm (AA-TN) and t-conorm (AA-TCN) structures were defined by Aczel and Alsina in 1982. The both concepts include parameters changing according to prefer, decision, and request of experts. In this paper, q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator (q-ROFAAWG) is produced and also ordered and hybrid concepts (q-ROFAAOWG, q-ROFAAHWG) are obtained using Aczel–Alsina operators (AAOs). Hence, this operator is expanded to generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator (Gq-ROFAAWG), ordered and hybrid concepts (Gq-ROFAAOWG, Gq-ROFAAHWG) using single parameter. Finally, group-based generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator (GGq-ROFAAWG), ordered and hybrid concepts (GGq-ROFAAOWG, GGq-ROFAAHWG) are proposed and their properties are worked. Moreover, an algorithm-based multi-criteria decision-making is given and applied over a numerical example to illustrate the effective of the proposed method. The results are evaluated for different values of parameters. In addition to, comparative analysis is developed to show the superiority of proposed approach than existing methods.

1 Introduction

Decision-making is one of the most effective structures used in daily life. Owing to authority of symbolizing decision-making process, multi-criterion decision-making (MCDM) models often have been used to define real decision-making problems, see Ozlu (2023, 2022a), etc.. Due to the limitations of human intelligence and the complex nature of MCDM problems, it can be difficult for decision-makers (DMs) to identify the accurate alternatives. Therefore, it is natural that incorrect values assigned for the alternatives containing very strong uncertainty and fuzzy. To date, many clusters have been defined like fuzzy set (FS) (Zadeh 1965), intuitionistic fuzzy set (IFS) (Atanassov 1986) that is defined as $\langle \mu (x),\nu (x)\rangle$ where $0\le \mu (x)+\nu (x)\le 1$ for $\mu (x)$ and $\nu (x)$ are membership and non-membership degrees, respectively, Pythagorean fuzzy set (PyFS) (Yager 2014) is defined as $\langle \mu (x),\nu (x)\rangle$ where $0\le \mu (x)^2+\nu (x)^2\le 1$ for $\mu (x)$ and $\nu (x)$ are membership and non-membership degrees, respectively, and q-rung orthopair fuzzy set (q-ROFS) (Yager 2016) is proposed as $0\le \mu (x)^q+\nu (x)^q\le 1$ for $(q\ge 1)$ and indeterminate is revealed with $\pi (x)=(\mu (x)^q+\nu (x)^q-\mu (x)^q\nu (x)^q)^{(\frac{1}{q})}$ for $\mu (x)$ and $\nu (x)$ are membership and non-membership degrees, respectively. It is open that this concept is a generalization of IFS and PyFS. The basis drawback of PyFS and IFS is that they are not sufficient to overcome with some situations. For example, an expert provides an ordered pair as $\langle 0.8, 0.9\rangle$, but this modeling cannot be represented with PyFS or IFS, because of $0.8 + 0.9\ge 1$ or $0.8^2 + 0.9^2\ge 1$. The q-ROF can easily cope with this situation where the above sets are useless. Then, this cluster has been started to be worked under different disciplines; Liu and Wang (2018b) proposed some aggregation operators over q-rung orthopair fuzzy sets; Liu and Liu (2018a) defined Bonferroni mean operators based on q-ROF; Hamy mean operators over q-rung orthopair fuzzy sets were worked by Wang et al. (2019a). In addition to, Wei et al. (2019) introduced to Maclaurin symmetric mean operators and surveyed applications over potential evaluation of emerging technology. Akram et al. (2021a, 2021b) revealed to a hybrid decision-making method based on q-rung orthopair fuzzy soft information and q-Rung orthopair fuzzy graphs under Hamacher operators, respectively. Moreover, Riaz et al. (2020a) proposed some q-rung orthopair fuzzy hybrid aggregation operators and TOPSIS method for multi-attribute decision-making. Some works for q-ROF can be surveyed in Joshi et al. (2018) and Wang et al. (2019b), Liu and Liu (2019), Riaz et al. (2020b) and Ozlu (2022b).

Generalized structures have more advantages according to structures calculated with single value. For example;

• 1. The comparative analysis is given in their own;

• 2. Generalized structures host more clusters into their structures;

• 3. Different results can be obtained according to prefer, request, or offer of decision-makers.

AA-TN and AA T-CN with condition having a parameter $\lambda \in [0,\infty )$ were defined by Aczel and Alsina (1982). Several authors have had more works owing to variableness parameters about this subject. The different forms of AA-TN have been proposed in Generator of Parametric T-norms (Babu and Ahmed 2017). Senapati et al. (2022a, 2022b) presented to AA-aggregation operators under intuitionistic and interval-valued intuitionistic fuzzy environment and tested over MCDM. Moreover, Senepati (2022(c)) has obtained a new level of AA family by combining AA-aggregation operators and picture fuzzy sets. Then, Hussain et al. (2022a) proposed to Aczel–Alsina aggregation operators on T-spherical fuzzy (TSF) information and gave an application over TSF and Hussain et al. (2022b) developed novel Aczel–Alsina operators for PyFS with application in multi-attribute decision-making. However, owing to the presence of noisy channels over time, the presentation of decision-making matrices as a single matrix, or the creation of a single matrix with different operations complicated to choose the ideal alternative, generalized approaches have been carried to group generalizations. The group generalized logic is that while decision matrix is being created, each expert can add his/her own opinion to the decision matrix obtained according to decision-maker’s priority, separately. Thus, two different matrices and weight vectors are revealed and these matrices are converted to generalized assessment matrix by combining two matrices. The several works have been made about this subject; see Riaz et al. (2020b), Hayat et al. (2018), Garg and Arora (2018) and Hussain et al. (2021).

It has been followed that several papers penned under q-ROF accept that the experts are completely familiar with the handled object. However, in daily life, we can encounter with complex situations. For instance, information provided by a sick person for treatment may not always guide the expert/senior correctly. In this statement, it can cause either the patient faces with very serious problems or the process of disease prolongs. However, if the expert decides to exchange information with a different senior, the patient will be saved from the wrong treatment and the treatment period will be shorter. To deal with these cases, generalized concepts are important, because the results are obtained for several values. This will inform about what decision to get. In this paper, q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator (q-ROFAAWG) is presented and it has been determined as a step to reach more general concepts called generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator (Gq-ROFAAWG) and group-based generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator (GGq-ROFAAWG). The obtained GGq-ROFAAWG is to host multiple parameters in its own structure. Thus, acquired results are provided as more objective. Also, thanks to this concept, the decision-makers’ own ideas have been added to the decision matrices. Thus, subjective results can be eliminated. AA- TN and AA-TCN structures introduced by Aczel and Alsina indicate stronger impact owing to variableness parameters than other TN and T-CN applications. The proposed operators have presented more general structure according to other concepts. Thus, different results, rankings have been obtained with changing of parameter. The contributions of paper can be ordered as follows:

• Q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator (q-ROFAAWG), q-rung orthopair fuzzy Aczel–Alsina weighted ordered geometric operator (q-ROFAAOWG), and q-rung orthopair fuzzy Aczel–Alsina weighted Hybrid geometric operator (q-ROFAAHWG) have been presented;

• Generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator (Gq-ROFAAWG), generalized q-rung orthopair fuzzy Aczel–Alsina weighted ordered geometric operator (Gq-ROFAAOWG), and generalized q-rung orthopair fuzzy Aczel–Alsina weighted Hybrid geometric operator (Gq-ROFAAHWG) have been proposed;

• Group-based generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric (GGq-ROFAAWG) operator, group-based generalized q-rung orthopair fuzzy Aczel–Alsina ordered weighted geometric (GGq-ROFAAOWG) operator, and group-based generalized q-rung orthopair fuzzy Aczel–Alsina hybrid weighted geometric (GGq-ROFAAHWG) operator have been revealed;

• An application has been given over investment of a company;

• The comparison analyses have been proposed with the various papers.

The remaining of paper is organized as follows: Section 2 includes the basic definitions and propositions of AA-TN and AA-TCN, q-ROF; in Sect. 3, we present to q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator, ordered and hybrid concepts and put forward the basic operations; Sect. 4 introduces generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator, ordered and hybrid instructions and some properties; Sect. 5 includes to group-based generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator, ordered and hybrid concepts; Sect. 6 proposes a numerical example; Sect. 7 presents comparative analysis.

2 Preliminary

In this section, we recall some basic notions of AA-TN and AA-TCN structures and the q-rung orthopair fuzzy set.

Definition 1

(Zadeh 1965) Let E be a universe. A fuzzy set X over E is a mapping defined as follows:

$$\begin{aligned} X=\{(\mu _X(x)/x): x\in E\} \end{aligned}$$

where $\mu _X:E\rightarrow [0.1]$.

Here, $\mu _X$ called membership function of X, and the value $\mu _X(x)$ is called the grade of membership of $x\in E$. The value represents the degree of x belonging to the fuzzy set X.

Definition 2

(Yager 2016) Let X be a reference set. A q-rung orthopair fuzzy set $\Im$ is defined as follows:

$$\begin{aligned} \Im =\Big \langle \Big (x,\mu _{\Im }(x),\nu _{\Im }(x)\Big ):x\in X \Big \rangle , \end{aligned}$$

for $h_{\Im }(x)=\{\langle \mu _{\Im }(x),\nu _{\Im }(x)\rangle :(\mu _{\Im }(x))^q+(\nu _{\Im }(x))^q\le 1\}$ in here we call cluster of pairs $h_{\Im }=h_{\Im }(x)$ as q-rung orthopair fuzzy set (q-ROHFS) and is indicated $h_{\Im }=\{(\mu ,\nu ):(\mu )^q+(\nu )^q\le 1\}$ for $q\ge 1$.

Definition 3

(Yager 2016) Let ${\Im }=\{(\mu ,\nu )\}$ be q-ROHFe. In this statement, score function and accuracy function of ${\Im }$ are defined, respectively, as follows:

$$\begin{aligned}{} & {} S({\Im })=\sum ((\mu )^q-(\nu )^q)\\{} & {} A({\Im })=\sum ((\mu )^q+(\nu )^q). \end{aligned}$$

Aczel–Alsina t-norm (TN) and t-conorm (TCN) were proposed by Aczel and Alsina in 1982 as follows.

Definition 4

(Aczel and Alsina 1982) Aczel–Alsina TN is defined as follows:

$T_\Im ^\lambda (a,b)=\left\{ \begin{array}{ll} T_D(a,b), &{} \texttt { if } \lambda =0 \\ \min (a,b), &{} \texttt { if } \lambda =\infty \\ e^{-((-ln(a))^\lambda +(-ln(b))^\lambda ))^\frac{1}{\lambda }}\\ \textrm{otherwise}\\ \end{array} \right.$

and

Aczel–Alsina TCN is defined as follows:

$T_\Im ^\lambda (a,b)=\left\{ \begin{array}{ll} T_D(a,b), &{} \texttt { if } \lambda =0 \\ \min (a,b), &{} \texttt { if } \lambda =\infty \\ 1-e^{-((-ln(1-a))^\lambda +(-ln(1-b))^\lambda ))^\frac{1}{\lambda }}\\ \textrm{otherwise},\\ \end{array} \right.$

where $\lambda \in [0,\infty )$.

3 Q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator

The concept of q-Rung Orthopair fuzzy set (q-ROFS) was defined by Yager (2016). In this section, this concept is applied for Aczel–Alsina Operators.

Definition 5

Let ${\Im _1}=\{(\eta _1,\upsilon _1)\}$ and ${\Im _2}=\{(\eta _2,\upsilon _2)\}$ accept two q-ROFSs and some basic properties based on Aczel–Alsina are proposed for $q\ge 1$ and $\lambda \ge 1$ as follows:

• 1. $\Im _1\oplus \Im _2=\Bigg \langle \root q \of {1-e^{-\Big (\sum _{j=1}^2(-\ln (1-\eta _j^q))^\lambda \Big )^\frac{1}{\lambda }}}, e^{-\Big (\sum _{j=1}^2(-\ln (\upsilon _j))^\lambda \Big )^\frac{1}{\lambda }}\Bigg \rangle ,$

• 2. $\Im _1\otimes \Im _2=\Bigg \langle e^{-\Big (\sum _{j=1}^2(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^2(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle ,$

• 3. $\hbar \Im _1=\Bigg \langle \root q \of {1-e^{-\Big (\hbar (-\ln (1-\eta _1^q))^\lambda \Big )^\frac{1}{\lambda }}}, e^{-\Big (\hbar (-\ln (\upsilon _1))^\lambda \Big )^\frac{1}{\lambda }}\Bigg \rangle ,$

• 4. $\Im ^\hbar _1=\Bigg \langle e^{-\Big (\hbar (-\ln (\eta _1))^\lambda \Big )^\frac{1}{\lambda }},\root q \of {1-e^{-\Big (\hbar (-\ln (1-\upsilon _1^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle .$

Definition 6

Let ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ be collection of q-ROFSs for $(j=1,2,\ldots ,n)$ and propose q-rung orthopair fuzzy Aczel–Alsina weighted geometric (q-ROFAAWG) operator for $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ as follows:

• 1. $\mathrm{q-ROFAAWG}:\Phi ^n\rightarrow \Phi$ is a mapping called as q-rung orthopair fuzzy Aczel–Alsina weighted geometric (q-ROFAAWG) operator for $q\ge 1$ and $\lambda \ge 1$, $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ is defined as follows:

  $$\begin{aligned}{} & {} \mathrm{q-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n)=w_1\Im _1\otimes w_2\Im _2\otimes \cdots \otimes w_n\Im _n\\{} & {} \quad = \Bigg \langle e^{-\Big (\sum _{j=1}^nw_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle ; \end{aligned}$$

• 2. $\mathrm{q-ROFAAOWG}:\Phi ^n\rightarrow \Phi$ is a mapping called as q-rung orthopair fuzzy Aczel–Alsina ordered weighted geometric (q-ROFAAOWG) operator for $q\ge 1$, $\lambda \ge 1$ and $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ is defined as follows:

  $$\begin{aligned}{} & {} \mathrm{q-ROFAAOWG}(\Im _1,\Im _2,\ldots ,\Im _n)=w_1\Im _{\sigma (1)}\otimes w_2\Im _{\sigma (2)}\otimes \cdots \otimes w_n\Im _{\sigma (n)}\\{} & {} \quad = \Bigg \langle e^{-\Big (\sum _{j=1}^nw_j(-\ln (\eta _{\sigma (j)}))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(-\ln (1-\upsilon _{\sigma (j)}^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle ; \end{aligned}$$

  where $\sigma (1),\sigma (2),\ldots ,\sigma (j)$ is a permutation of $j=1,2,\ldots ,n$ and also $\Im _{\sigma (j-1)}\ge \Im _{\sigma (j)}$.

• 3. $\mathrm{q-ROFAAHWG}:\Phi ^n\rightarrow \Phi$ is a mapping called as q-rung orthopair fuzzy Aczel–Alsina Hybrid weighted geometric (q-ROFAAHWG) operator for $q\ge 1$, $\lambda \ge 1$ and $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ is defined as follows:

  $$\begin{aligned}{} & {} \mathrm{q-ROFAAHWA}(\Im _1,\Im _2,\ldots ,\Im _n)=\varpi _1\check{\Im }_{\sigma (1)}\otimes \varpi _2\check{\Im }_{\sigma (2)}\otimes \cdots \otimes \varpi _n\check{\Im }_{\sigma (n)}\\{} & {} \quad = \Bigg \langle e^{-\Big (\sum _{j=1}^n\varpi _j(-\ln (\check{\eta }_{\sigma (j)}))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^n\varpi _j(-\ln (1-\check{\upsilon }_{\sigma (j)}^q))^\lambda \Big )^\frac{1}{\lambda }}} \Bigg \rangle , \end{aligned}$$

  where $\sigma (1),\sigma (2),\ldots ,\sigma (j)$ is a permutation of $j=1,2,\ldots ,n$ and also $\Im _{\sigma (j-1)}\ge \Im _{\sigma (j)}$ for $\varpi =(\varpi _1,\varpi _2,\ldots ,\varpi _n)$ associated vector, such that $\sum _{j=1}^n \varpi _j=1$ and from here $\check{\Im _j}=k \varpi _j\Im _j$ for $(j=1,2,\ldots ,n)$ where k is a balancing coefficient.

3.1 Characteristic properties of q-ROFAAWG

In this section, we define some characteristic properties of q-ROFAAWG.

Theorem 1

Let be as collection of q-ROFs ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ for $(j=1,2,\ldots ,n)$ and $q\ge 1$, $\lambda \ge 1$. If the value is aggregated, it is still a q-ROFS and

$$\begin{aligned}{} & {} \mathrm{q-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n)=w_1\Im _1\otimes w_2\Im _2\otimes \cdots \otimes w_n\Im _n\\{} & {} \quad = \Bigg \langle e^{-\Big (\sum _{j=1}^nw_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}} \Bigg \rangle . \end{aligned}$$

Proof

We can prove with through induction method to above equation. For $n=2$

$$\begin{aligned}{} & {} w_1\Im _1\otimes w_2\Im _2= \Bigg \langle e^{-\Big (w_1(-\ln (\eta _1))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (w_1(-\ln (1-\upsilon _1^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \otimes \\{} & {} \quad \Bigg \langle e^{-\Big (w_2(-\ln (\eta _2))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (w_2(-\ln (1-\upsilon _2^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{j=1}^2w_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^2w_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle . \end{aligned}$$

Thus, it provides for $n=k$ as follows:

$$\begin{aligned}{} & {} \mathrm{q-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _k)=\Bigg \langle e^{-\Big (\sum _{j=1}^kw_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }},\\{} & {} \quad \root q \of {1-e^{-\Big (\sum _{j=1}^kw_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle , \end{aligned}$$

and for $n=k+1$

$$\begin{aligned}{} & {} \displaystyle {\bigotimes _ {j=1}^{k+1} w_j(\Im _{j}})=\displaystyle {\bigotimes _ {j=1}^{k} w_j(\Im _{j})\otimes w_{k+1}(\Im _{k+1})=}\\{} & {} \quad \Bigg \langle e^{-\Big (\sum _{j=1}^kw_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^kw_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \otimes \\{} & {} \quad \Bigg \langle e^{-\Big (w_{k+1}(-\ln (\eta _{k+1}))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (w_{k+1}(-\ln (1-\upsilon _{k+1}^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad = \Bigg \langle e^{-\Big (\sum _{j=1}^{k+1}w_{j}(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^{k+1}w_{j}(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle . \end{aligned}$$

It holds for $n=k+1$, so provides for all n. $\square$

Theorem 2

(idempotency) Let accept collection of q-ROFs that ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ $(j=1,2,\ldots ,n)$ and $q\ge 1$, $\lambda \ge 1$. Let be $\Im _{j}=\Im$. Thus, $\mathrm{q-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n)=\Im$.

Proof

First, let write $\mathrm{q-ROFAAWG}$ operator

$$\begin{aligned}{} & {} \mathrm{q-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n)=w_1\Im _1\otimes w_2\Im _2\otimes \cdots \otimes w_n\Im _n\\{} & {} \quad = \Bigg \langle e^{-\Big (\sum _{j=1}^nw_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle , \end{aligned}$$

since $\sum _{j=1}^n w_j=1$

$$\begin{aligned}{} & {} =\Bigg \langle e^{-\Big ((-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big ((-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad =\Bigg \langle e^{(\ln (\eta ))}, \root q \of {1-e^{\ln (1-\upsilon ^q)}}\Bigg \rangle \end{aligned}$$

for $e^{ln(x)}=x$,

$=\langle \eta ,\upsilon \rangle$

and from here $\mathrm{q-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n)=\Im$. $\square$

Theorem 3

(monotonicity) Let accept two q-ROFs that ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ and ${\Im ^*_j}=\{(\eta ^*_j,\upsilon ^*_j)\}$ for $(j=1,2,\ldots ,n)$, $q\ge 1$ and $\lambda \ge 1$. If ${\Im _j}\le {\Im ^*_j}$, $\mathrm{q-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n)\le \mathrm{q-ROFAAWG}(\Im ^*_1,\Im ^*_2,\ldots ,\Im ^*_n)$.

Proof

It is open that ${\Im _j}\le {\Im ^*_j}$ for $(j=1,2,\ldots ,n)$ and from here $\displaystyle {\otimes _{j=1}^{n} w_j(\Im _{j})}\le \displaystyle {\otimes _{j=1}^{n} w_j(\Im ^*_{j})}$, and thus, $\mathrm{q-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n){\le } \mathrm{q-ROFAAWG}(\Im ^*_1,\Im ^*_2,\ldots ,\Im ^*_n)$.

$\square$

Theorem 4

(Boundedness) Let accept collection of q-ROFs that ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ and, $\Im _j^+$ and $\Im ^-_j$ maximum and minimum elements for $(j=1,2,\ldots ,n)$, $q\ge 1$ and $\lambda \ge 1$. Thus,

$\Im ^-_j\le \mathrm{q-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n) \le \Im _j^+.$

Proof

We accept that $\Im _j^+=\max \{\Im _j\}=\{(\eta _j^+,\upsilon _j^+)\}$ and $\Im _j^-=\min \{\Im _j\}=\{(\eta _j^-,\upsilon _j^-)\}$. Thus, $\eta _j^+=\max \{\eta _j\}$, $\upsilon _j^+=\min \{\upsilon _j\}$ and $\eta _j^-=\min \{\eta _j\}$, $\upsilon _j^-=\max \{\upsilon _j\}$ from here

$e^{-\Big (\sum _{j=1}^nw_j(-\ln (\eta ^-_j))^\lambda \Big )^\frac{1}{\lambda }}\le e^{-\Big (\sum _{j=1}^nw_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}\le e^{-\Big (\sum _{j=1}^nw_j(-\ln (\eta ^+_j))^\lambda \Big )^\frac{1}{\lambda }}$;

similarly

$$\begin{aligned}{} & {} \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(-\ln (1-{\upsilon _j^-}^q))^\lambda \Big )^\frac{1}{\lambda }}}\le \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(-\ln (1-{\upsilon _j}^q))^\lambda \Big )^\frac{1}{\lambda }}}\\{} & {} \quad \le \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(-\ln (1-{\upsilon _j^+}^q))^\lambda \Big )^\frac{1}{\lambda }}}; \end{aligned}$$

the proof is completed. $\square$

4 Generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator

Definition 7

Let ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ be collection of q-ROFSs for $(j=1,2,\ldots ,n)$ and accept a generalized parameter $\tau =(\eta _\tau ,\upsilon _\tau )$. Thus, we define generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric (Gq-ROFAAWG) operator for $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ as follows:

• 1. $\mathrm{Gq-ROFAAWG}:\Phi ^n\rightarrow \Phi$ is a mapping called as generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric (Gq-ROFAAWG) operator for $q\ge 1$, $\lambda \ge 1$; $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ is defined as follows:

  $$\begin{aligned}{} & {} \mathrm{Gq-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n)=\tau \otimes \Big (\otimes _{j=1}^nw_j\Im _j\Big )\\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{j=1}^nw_j(\eta _\tau (-\ln (\eta _j))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(\upsilon _\tau (-\ln (1-\upsilon _j^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle ; \end{aligned}$$

• 2. $\mathrm{Gq-ROFAAOWG}:\Phi ^n\rightarrow \Phi$ is a mapping called as generalized q-rung orthopair fuzzy Aczel–Alsina ordered weighted geometric (Gq-ROFAAOWG) operator for $q\ge 1$ and $\lambda \ge 1$; $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ is defined as follows:

  $$\begin{aligned}{} & {} \mathrm{Gq-ROFAAOWG}(\Im _1,\Im _2,\ldots ,\Im _n)=\tau \otimes \Big (\otimes _{j=1}^nw_j\Im _j\Big )\\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{j=1}^nw_j(\eta _\tau (-\ln (\eta _{\sigma (j)}))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(\upsilon _\tau (-\ln (1-\upsilon _{\sigma (j)}^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle ; \end{aligned}$$

  where $\sigma (1),\sigma (2),\ldots ,\sigma (j)$ is a permutation of $j=1,2,\ldots ,n$ and also $\Im _{\sigma (j-1)}\ge \Im _{\sigma (j)}$.

• 3. $Gq-ROFAAHWG:\Phi ^n\rightarrow \Phi$ is a mapping called as generalized q-rung orthopair fuzzy Aczel–Alsina hybrid weighted geometric (Gq-ROFAAHWG) operator for $q\ge 1$ and $\lambda \ge 1$; $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ is defined as follows:

  $$\begin{aligned}{} & {} \mathrm{Gq-ROFAAHWG}(\Im _1,\Im _2,\ldots ,\Im _n)=\tau \otimes \Big (\otimes _{j=1}^n\varpi _j\check{\Im }_{\sigma (j)}\Big )\\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{j=1}^n\varpi _j(\eta _\tau (-\ln (\check{\eta }_{\sigma (j)}))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^n\varpi _j(\upsilon _\tau (-\ln (1-\check{\upsilon }_{\sigma (j)}^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle , \end{aligned}$$

where $\sigma (1),\sigma (2),\ldots ,\sigma (j)$ is a permutation of $j=1,2,\ldots ,n$ and also $\Im _{\sigma (j-1)}\ge \Im _{\sigma (j)}$ for $\varpi =(\varpi _1,\varpi _2,\ldots ,\varpi _n)$ associated vector, such that $\sum _{j=1}^n \varpi _j=1$ and from here $\check{\Im _j}=n \varpi _j\Im _j$ for $(j=1,2,\ldots ,n)$ where n is a balancing coefficient.

4.1 Characteristic properties of Gq-ROFAAWG

In this section, we give some characteristic properties of Gq-ROFAAWG.

Theorem 5

Let ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ be collection of q-ROFSs and a generalized parameter $\tau =(\eta _\tau ,\upsilon _\tau )$ for $(j=1,2,\ldots ,n)$ and define generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric (Gq-ROFAAWG) operator for $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ where $q\ge 1$ and $\lambda \ge 1$ as follows:

$$\begin{aligned}{} & {} \mathrm{Gq-ROFAAWA}(\Im _1,\Im _2,\ldots ,\Im _n)=\tau \otimes \Big (\otimes _{j=1}^nw_j\Im _j\Big )\\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{j=1}^nw_j(\eta _\tau (-\ln (\eta _j))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(\upsilon _\tau (-\ln (1-\upsilon _j^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle . \end{aligned}$$

Proof

We can prove with helping to induction method to above equation. For $n=2$

$$\begin{aligned}{} & {} w_1\Im _1\otimes w_2\Im _2= \Bigg \langle e^{-\Big (w_1(\eta _\tau (-\ln (\eta _1))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (w_1(\upsilon _\tau (-\ln (1-\upsilon _1^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad \otimes \Bigg \langle e^{-\Big (w_2(\eta _\tau (-\ln (\eta _2))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (w_2(\upsilon _\tau (-\ln (1-\upsilon _2^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{j=1}^2w_j(\eta _\tau (-\ln (\eta _j))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^2w_j(\upsilon _\tau (-\ln (1-\upsilon _j^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle . \end{aligned}$$

For $n=k$ as follows:

$$\begin{aligned}{} & {} \mathrm{Gq-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _k)=\tau \otimes \Big (\otimes _{j=1}^kw_j\Im _j\Big )\\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{j=1}^kw_j(\eta _\tau (-\ln (\eta _j))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^kw_j(\upsilon _\tau (-\ln (1-\upsilon _j^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle , \end{aligned}$$

and for $n=k+1$

$$\begin{aligned}{} & {} \displaystyle {\bigotimes _ {j=1}^{k+1} \tau (w_j\Im _{j}})=\displaystyle {\bigotimes _ {j=1}^{k} \tau (w_j\Im _{j})\otimes \tau (w_{k+1}\Im _{k+1})}\\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{j=1}^kw_j(\eta _\tau (-\ln (\eta _j))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^kw_j(\upsilon _\tau (-\ln (1-\upsilon _j^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad \otimes \Bigg \langle e^{-\Big (w_{k+1}(\eta _\tau (-\ln (\eta _{k+1}))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (w_{k+1}(\upsilon _\tau (-\ln (1-\upsilon _{k+1}^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{j=1}^{k+1}w_j(\eta _\tau (-\ln (\eta _j))^\lambda )\Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^{k+1}w_j(\upsilon _\tau (-\ln (1-\upsilon _j^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle . \end{aligned}$$

It holds for $n=k+1$, so provides for all n. $\square$

Theorem 6

(Idempotency) Let accept collection of q-ROFs that ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ and a generalized parameter $\tau =(\eta _\tau ,\upsilon _\tau )$ $(j=1,2,\ldots ,n)$. In this statement, if $\Im _{j}=\Im$, $\mathrm{Gq-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n)=\Im$ where $q\ge 1$ and $\lambda \ge 1$.

Proof

The proof can be made as similar to proof of Theorem 2.

$\square$

Theorem 7

(Monotonicity) Let determine two q-ROFs that ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ and also a generalized parameter $\tau =(\eta _\tau ,\upsilon _\tau )$ ${\Im ^*_j}=\{(\eta ^*_j,\upsilon ^*_j)\}$ where $(j=1,2,\ldots ,n)$, $q\ge 1$ and $\lambda \ge 1$. If ${\Im _j}\le {\Im ^*_j}$, $\mathrm{Gq-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n)\le \mathrm{Gq-ROFAAWG}(\Im ^*_1,\Im ^*_2,\ldots ,\Im ^*_n)$ where $q\ge 1$ and $\lambda \ge 1$.

Proof

It is clear from proof of Theorem 3. $\square$

Theorem 8

(Boundedness) Let define collection of q-ROFs that ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ and, $\Im _j^+$ and $\Im ^-_j$ maximum and minimum elements for $(j=1,2,\ldots ,n)$. Thus,

$\Im ^-_j\le \mathrm{Gq-ROFAAWG}(\Im _1,\Im _2,\ldots ,\Im _n) \le \Im _j^+$ where $q\ge 1$ and $\lambda \ge 1$.

Proof

It is open from proof of Theorem 4.

$\square$

Now, let define some special cases of Gq-ROFAAWG as follows:

$\bullet$ If $q=1$ and $\tau _k=(0,0)$, Gq-ROFAAWG is reduced to Intuitionistic Aczel–Alsina Geometric operator (IAAG).

$\bullet$ If $q=2$ and $\tau _k=(0,0)$, Gq-ROFAAWG is reduced to Pythagorean Aczel–Alsina Geometric operator (PyAAG).

Similarly, Gq-ROFAAHWG and Gq-ROFAAOWG operators can be induced to Hybrid and Ordered structures of IAAG and PyAAG.

5 Group-based generalized Q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator

In this section, we convert the proposed Gq-ROFAAWG operators by using together with several generalized parameters and provide to decide more accurate using their own expertise of multiple decision-makers. These operators are that group-based generalized Q-rung orthopair fuzzy Aczel–Alsina weighted geometric (GGq-ROFAAWG) operator, group-based generalized Q-rung orthopair fuzzy Aczel–Alsina ordered weighted geometric (GGq-ROFAAOWG) operator, and group-based generalized Q-rung orthopair fuzzy Aczel- Alsina hybrid weighted geometric (GGq-ROFAAHWG) operator.

Definition 8

Let ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ be collection of q-ROFSs for $(j=1,2,\ldots ,n)$ and define to set of generalized parameters $\tau _\iota =(\eta _{\tau _\iota },\upsilon _{\tau _\iota })$ for $(\iota =1,2,\ldots ,p)$. Thus, we define group-based generalized Q-rung orthopair fuzzy Aczel–Alsina weighted geometric (GGq-ROFAAWG) operator for $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ where $q\ge 1$ and $\lambda \ge 1$ and associated weight vector $\hat{w}_\iota \in [0,1]$ and $\sum _{\iota =1}^p \hat{w}_\iota =1$ as follows:

$$\begin{aligned}{} & {} \mathrm{GGq-ROFAAWG}((\tau _1,\tau _2,\ldots ,\tau _p),\langle \Im _1,\Im _2,\ldots ,\Im _n\rangle )\\{} & {} \quad =\Big (\otimes _{\iota =1}^p\hat{w}_\iota \tau _\iota \Big )\otimes \Big (\otimes _{j=1}^nw_j\Im _j\Big )\\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad \otimes \Bigg \langle e^{-\Big (\sum _{j=1}^nw_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda +\sum _{j=1}^nw_j(-\ln (\eta _j))^\lambda )\Big )^\frac{1}{\lambda }},\\{} & {} \quad \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda +\sum _{j=1}^nw_j(-\ln (1-\upsilon _j^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle . \end{aligned}$$

Theorem 9

Let ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ be collection of q-ROFSs for $(j=1,2,\ldots ,n)$ and think to set of generalized parameters $\tau _\iota =(\eta _{\tau _\iota },\upsilon _{\tau _\iota })$ for $(\iota =1,2,\ldots ,p)$. Thus, we define group-based generalized Q-rung orthopair fuzzy Aczel–Alsina weighted geometric (GGq-ROFAAWG) operator for $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ and associated weight vector $\hat{w}_\iota \in [0,1]$, and $\sum _{\iota =1}^p \hat{w}_\iota =1$ for $q\ge 1$ and $\lambda \ge 1$ as follows:

$$\begin{aligned}{} & {} \mathrm{GGq-ROFAAWG}((\tau _1,\tau _2,\ldots ,\tau _p),\langle \Im _1,\Im _2,\ldots ,\Im _n\rangle )= \Big (\otimes _{\iota =1}^p\hat{w}_\iota \tau _\iota \Big )\otimes \Big (\otimes _{j=1}^nw_j\Im _j\Big )\\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda +\sum _{j=1}^nw_j(-\ln (\eta _j))^\lambda )\Big )^\frac{1}{\lambda }},\\{} & {} \qquad \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda +\sum _{j=1}^nw_j(-\ln (1-\upsilon _j^q))^\lambda )\Big )^\frac{1}{\lambda }}} \Bigg \rangle . \end{aligned}$$

Proof

Let utilize for proof mathematical induction formulae as follows:

For $n=2$:

$$\begin{aligned}{} & {} \Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad \otimes \Bigg \langle e^{-\Big (\sum _{j=1}^2w_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^2w_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle , \end{aligned}$$

and from here

$$\begin{aligned}{} & {} \Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda +\sum _{j=1}^2w_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }},\\{} & {} \qquad \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda +\sum _{j=1}^2w_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle . \end{aligned}$$

It is open that it holds for $n=2$.

Let accept for $n=\zeta$

$$\begin{aligned}{} & {} \Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda +\sum _{j=1}^\zeta w_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }},\\{} & {} \quad \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\eta _{\tau _\iota }^q))^\lambda +\sum _{j=1}^\zeta w_j(-\ln (1-\eta _j^q))^\lambda \Big )^\frac{1}{\lambda }}} \Bigg \rangle . \end{aligned}$$

The result holds for $n=\zeta +1$ as follows:

$$\begin{aligned}{} & {} \Bigg (\displaystyle {\otimes _ {\iota =1}^{p} \hat{w}_j(\tau _{\iota }})\Bigg )\otimes \Bigg (\Big (\otimes _ {j=1}^{\zeta } w_j(\Im _{j})\Big )\otimes w_{\zeta +1}(\Im _{\zeta +1})\Bigg )\\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad \otimes \Bigg ( \Bigg \langle e^{-\Big (\sum _{j=1}^\zeta w_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }},\root q \of {1-e^{-\Big (\sum _{j=1}^\zeta w_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad \otimes \Bigg \langle e^{-\Big ( w_{\zeta +1}(-\ln (\eta _{\zeta +1}))^\lambda \Big )^\frac{1}{\lambda }},\root q \of {1-e^{-\Big ( w_{\zeta +1}(-\ln (1-\upsilon _{\zeta +1}^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \Bigg ) \\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \otimes \\{} & {} \quad \Bigg ( \Bigg \langle e^{-\Big (\sum _{j=1}^{\zeta +1} w_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }},\root q \of {1-e^{-\Big (\sum _{j=1}^{\zeta +1} w_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \Bigg ), \end{aligned}$$

and from here

$$\begin{aligned}{} & {} \Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda +\sum _{j=1}^{\zeta +1}w_j(-\ln (\eta _j))^\lambda \Big )^\frac{1}{\lambda }},\\{} & {} \quad \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda +\sum _{j=1}^{\zeta +1}w_j(-\ln (1-\upsilon _j^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle . \end{aligned}$$

Thus, proof is completed. The monotoncity, idempotent, and boundedness are open from above proofs.

$\square$

Example 1

Let determine set of experts as $\{\mathfrak {D}_1,\mathfrak {D}_2\}$ and weight vector as $w=(0.3,0.7)$ where $\mathfrak {D}_1=\langle 0.6,0.5\rangle$, $\mathfrak {D}_2=\langle 0.4,0.4\rangle$. Also, we define three alternatives and associated weight vector as follows; $\Im _1=\langle 0.5,0.6\rangle$, $\Im _2=\langle 0.8,0.8\rangle$, $\Im _3=\langle 0.2,0.2\rangle$ and $\hat{w}=(0.3,0.3,0.4)$, respectively. For $q=3$ and $\lambda =4$; GGq-ROFAAWA can be calculated as follows:

$$\begin{aligned}{} & {} \mathrm{GGq-ROFAAWG}((\mathfrak {D}_1,\mathfrak {D}_2),\langle \Im _1,\Im _2,\Im _3\rangle )\\{} & {} \quad =\Bigg \langle e^{-\kappa ^\frac{1}{4}}, \root 3 \of {1-e^{-z^\frac{1}{4}}} \Bigg \rangle \\{} & {} \quad = \langle 0.0177,0.1627\rangle , \end{aligned}$$

where $\kappa =\Big ((0.3(-\ln (0.6))^4)+(0.7(-\ln (0.4))^4)+(0.3(-\ln (0.5))^4)+(0.3(-\ln (0.8))^4)+(0.4(-\ln (0.2))^4)\Big )$,

$z=\Big ((0.3(-\ln (1-0.5^3))^4)+(0.7(-\ln (1-0.4^3))^4)+(0.3(-\ln (1-0.6^3))^4)+(0.3(-\ln (1-0.8^3))^4)+(0.4(-\ln (1-0.2^3))^4)\Big ).$

Definition 9

Let ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ be collection of q-ROFSs for $(j=1,2,\ldots ,n)$ and think to set of generalized parameters $\tau _\iota =(\eta _{\tau _\iota },\upsilon _{\tau _\iota })$ for $(\iota =1,2,\ldots ,p)$. Therefore, we define group-based generalized Q-rung orthopair fuzzy Aczel–Alsina ordered weighted geometric(GGq-ROFAAOWG) operator for $w_j \in [0,1]$ and $\sum _{j=1}^n w_j=1$ and associated weight vector $\hat{w}_\iota \in [0,1]$ and $\sum _{\iota =1}^p \hat{w}_\iota =1$ where $q\ge 1$ and $\lambda \ge 1$ as follows:

$$\begin{aligned}{} & {} GGq-ROFAAOWG((\tau _1,\tau _2,\ldots ,\tau _p),\langle \Im _1,\Im _2,\ldots ,\Im _n\rangle )\\{} & {} \quad = \Big (\otimes _{\iota =1}^p\hat{w}_\iota \tau _\iota \Big )\otimes \Big (\otimes _{j=1}^nw_j\Im _j\Big ) \\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad \otimes \Bigg \langle e^{-\Big (\sum _{j=1}^nw_j(-\ln (\eta _{\sigma (j)}))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^nw_j(-\ln (1-\upsilon _{\sigma (j)}^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda +\sum _{j=1}^nw_j(-\ln (\eta _{\sigma (j)}))^\lambda )\Big )^\frac{1}{\lambda }},\\{} & {} \quad \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda +\sum _{j=1}^nw_j(-\ln (1-\upsilon _{\sigma (j)}^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle , \end{aligned}$$

where $\sigma (1),\sigma (2),\ldots ,\sigma (j)$ is a permutation of $j=1,2,\ldots ,n$ and also $\Im _{\sigma (j-1)}\ge \Im _{\sigma (j)}$.

Example 2

Let determine set of experts as $\{\mathfrak {D}_1,\mathfrak {D}_2\}$ and weight vector as $w=(0.3,0.7)$ where $\mathfrak {D}_1=\langle 0.6,0.5\rangle$, $\mathfrak {D}_2=\langle 0.4,0.4\rangle$. Also, we define three alternatives and associated weight vector as follows; $\Im _1=\langle 0.5,0.6\rangle$, $\Im _2=\langle 0.8,0.8\rangle$, $\Im _3=\langle 0.2,0.1\rangle$ and $\hat{w}=(0.3,0.3,0.4)$, respectively. For $q=3$ and $\lambda =4$, GGq-ROFAAOWG can be calculated as below;

$s(\Im _1)=0.091$, $s(\Im _2)=0$ and $s(\Im _3)=0.007$; in this statement $\Im _2<\Im _3<\Im _1$

$$\begin{aligned}{} & {} \mathrm{GGq-ROFAAOWG}((\mathfrak {D}_1,\mathfrak {D}_2),\langle \Im _1,\Im _2,\Im _3\rangle )\\{} & {} \quad =\Bigg \langle e^{-\kappa ^\frac{1}{4}}, \root 3 \of {1-e^{-z^\frac{1}{4}}} \Bigg \rangle \\{} & {} \quad = \langle 0.0055,0.1736\rangle , \end{aligned}$$

where

$$\begin{aligned} \kappa= & {} \Big ((0.3(-\ln (0.6))^4)+(0.7(-\ln (0.4))^4)\\{} & {} +(0.3(-\ln (0.5))^4)+(0.4(-\ln (0.8))^4)+(0.3(-\ln (0.1))^4)\Big )\\ z= & {} \Big ((0.3(-\ln (1-0.5^3))^4)+(0.7(-\ln (1-0.4^3))^4)\\{} & {} +\,(0.3(-\ln (1-0.6^3))^4)+(0.4(-\ln (1-0.8^3))^4)+(0.3(-\ln (1-0.2^3))^4)\Big ). \end{aligned}$$

Definition 10

Let ${\Im _j}=\{(\eta _j,\upsilon _j)\}$ be collection of q-ROFSs for $(j=1,2,\ldots ,n)$ and think to set of generalized parameters $\tau _\iota =(\eta _{\tau _\iota },\upsilon _{\tau _\iota })$ for $(\iota =1,2,\ldots ,p)$. Therefore, we define group-based generalized Q-rung orthopair fuzzy Aczel–Alsina hybrid weighted geometric(GGq-ROFAAHWG) operator for $w_j \in [0,1]$, $q\ge 1$, $\lambda \ge 1$ and $\sum _{j=1}^n w_j=1$ and associated weight vector $\hat{w}_\iota \in [0,1]$ and $\sum _{\iota =1}^p \hat{w}_\iota =1$ as follows:

$$\begin{aligned}{} & {} \mathrm{GGq-ROFAAHWG}((\tau _1,\tau _2,\ldots ,\tau _p),\langle \Im _1,\Im _2,\ldots ,\Im _n\rangle )\\{} & {} \quad = \Big (\otimes _{\iota =1}^p\hat{w}_\iota \tau _\iota \Big )\otimes \Big (\otimes _{j=1}^n\varpi _j\check{\Im _j}\Big )\\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad \otimes \Bigg \langle e^{-\Big (\sum _{j=1}^n\varpi _j(-\ln (\check{\eta }_{\sigma (j)}))^\lambda \Big )^\frac{1}{\lambda }}, \root q \of {1-e^{-\Big (\sum _{j=1}^n\varpi _j(-\ln (1-\check{\upsilon }_{\sigma (j)}^q))^\lambda \Big )^\frac{1}{\lambda }}}\Bigg \rangle \\{} & {} \quad =\Bigg \langle e^{-\Big (\sum _{\iota =1}^p(\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda +\sum _{j=1}^n\varpi _j(-\ln (\check{\upsilon }_{\sigma (j)}))^\lambda )\Big )^\frac{1}{\lambda }},\\{} & {} \quad \root q \of {1-e^{-\Big (\sum _{\iota =1}^p(\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda +\sum _{j=1}^n\varpi _j(-\ln (1-\check{\eta }_{\sigma (j)}^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle , \end{aligned}$$

where $\sigma (1),\sigma (2),\ldots ,\sigma (j)$ is a permutation of $j=1,2,\ldots ,n$ and also $\Im _{\sigma (j-1)}\ge \Im _{\sigma (j)}$ for $\varpi =(\varpi _1,\varpi _2,\ldots ,\varpi _n)$ aggregation-associated vector, such that $\sum _{j=1}^n \varpi _j=1$ and from here $\check{\Im _j}=n \varpi _j\Im _j$ for $(j=1,2,\ldots ,n)$ where n is a balancing coefficient.

Example 3

Let determine set of decision-makers $\{\mathfrak {D}_1,\mathfrak {D}_2\}$ and weight vector as $w=(0.3,0.7)$ where $\mathfrak {D}_1=\langle 0.3,0.2\rangle$, $\mathfrak {D}_2=\langle 0.2,0.3\rangle$. Also, we determine three alternatives and associated weight vector as follows; $\Im _1=\langle 0.5,0.8\rangle$, $\Im _2=\langle 0.9,0.4\rangle$, $\Im _3=\langle 0.2,0.5\rangle$ and $\hat{w}=(0.2,0.3,0.5)$ and ${\varpi }=(0.4,0.3,0.3)$ respectively. For $q=3$ and $\lambda =4$; GGq-ROFAAHWG can be calculated as follows.

For GGq-ROFAAHWG, first, we evaluate to both q-ROFs according to score function as follows:

$\check{\Im _1}=3\times 0.2\times \langle 0.5,0.8\rangle =\langle 0.0384,0.5547\rangle$ and $\check{\Im _2}=3\times 0.3\times \langle 0.9,0.4\rangle =\langle 0.3455,0.0687\rangle$

$\check{\Im _3}=3\times 0.5\times \langle 0.2,0.5\rangle =\langle 0.0029,0.1001\rangle$, and thus, we can obtain to follow ordering by utilizing score function, $s(\check{\Im _1})<s(\check{\Im _3})<s(\check{\Im _2})$ from here:

$$\begin{aligned}{} & {} \mathrm{GGq-ROFAAHWG}((\mathfrak {D}_1,\mathfrak {D}_2),\langle \check{\Im }_1,\check{\Im }_2,\check{\Im }_3\rangle )\\{} & {} \quad = \Bigg \langle e^{-\kappa ^\frac{1}{4}}, \root 3 \of {1-e^{-z^\frac{1}{4}}}\Bigg \rangle \\{} & {} \quad = \langle 0.0007,0.0114\rangle , \end{aligned}$$

where

$$\begin{aligned} \kappa= & {} \Big ((0.3(-\ln (0.3))^4)+(0.7(-\ln (0.2))^4)+(0.3(-\ln (0.0384))^4)\\{} & {} +(0.4(-\ln (0.3455))^4)+(0.3(-\ln (0.0029))^4)\Big ),\\ z= & {} \Big ((0.3(-\ln (1-0.2^3))^4)+(0.7(-\ln (1-0.3^3))^4)+(0.3(-\ln (1-0.5547^3))^4)\\{} & {} +(0.4(-\ln (1-0.0687^3))^4)+(0.3(-\ln (1-0.1001^3))^4)\Big ). \end{aligned}$$

Now, we survey some special cases of GGq-ROFAAWG.

$\bullet$ If $q=1$ and $\tau _\iota =(0,0)$, GGq-ROFAAWG is reduced to intuitionistic Aczel–Alsina geometric operator (IAAG).

$\bullet$ If $q=2$ and $\tau _\iota =(0,0)$, GGq-ROFAAWG is reduced to Pythagorean Aczel–Alsina geometric operator (PyAAG).

6 An application of MCDM based on GGq-ROFAAWG

In this section, the proposed GGq-ROFAAWG is given into an algorithm and applied over an MCDM problem with m alternatives and n criterions. Let accept as a set of alternatives that $\textbf{a}=\{\textbf{a}_1,\textbf{a}_2,\ldots ,\textbf{a}_m\}$ and also $\mathcal {C}=\{\mathcal {C}_1,\mathcal {C}_2,\ldots ,\mathcal {C}_n\}$ as a set of criterions and determine a weight vector of criterions $w_j=(w_1,w_2,\ldots ,w_n)$ where $w_j>0, j=1,2,\ldots ,n$ and $\sum _{j=1}^nw_j=1$. The decision-makers determine to decision-making matrix, such that $\mathfrak {D}_{ij}=\langle \eta _{ij},\upsilon _{ij}\rangle$ where $\eta _{ij}$, $\upsilon _{ij}$ is membership value and non-membership value, respectively, with condition that $0\le (\eta _{ij})^q+(\upsilon _{ij})^q\le 1$ for $q\ge 1$.

To interpret more accurate the obtained information, let define set of decision-makers as $\mathfrak {D}=\{\mathfrak {D}_1,\mathfrak {D}_2,\ldots ,\mathfrak {D}_k\}$, such that their prefers or ideas are presented by q-ROFs and indicated $\mathfrak {D}_\phi =\langle \eta _{\mathfrak {D}_\phi }, \upsilon _{\mathfrak {D}_\phi }\rangle$ where $\phi =(1,2,\ldots ,k)$ and as weight vector $\check{w}_k>0, k=1,2,\ldots ,\phi$ and $\sum _{k=1}^\phi \check{w}_k=1$.

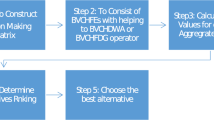
Then, the following steps have been defined for algorithm (Fig. 1).

Fig. 1

Flowcard of proposed MCDM method

7 Numerical example

A company wants to invest and therefore surveys some alternatives. Thus, ceo of company determines four decision-makers and requests to evaluate some alternatives under different criteria and experts consist of five alternatives and five criteria as follows;

(1) ${\textbf{a}_1}$, car factory; (2) ${\textbf{a}_2}$, food factory; (3) ${\textbf{a}_3}$, an airport factory; (4) ${\textbf{a}_4}$, wind power panel manufacturing factory; (5) ${\textbf{a}_5}$, computer production factory. The government desires to be assessed under five criteria, such that

(1) ${\mathcal {C}}_1$: labor, (2) ${\mathcal {C}}_2$: experience, (3) ${\mathcal {C}}_3$: cost, (4) ${\mathcal {C}}_4$: proximity to raw material, (5) ${\mathcal {C}}_5$: cultural fit.

The experts define weights of criteria by $w_1 = 0.2, w_2 = 0.5, w_3 = 0.1,w_4 = 0.1,w_5 = 0.1$ for $q=3$ and $\lambda =4$ respectively. The priority desires determined by the experts $\{\mathfrak {D}_1,\mathfrak {D}_2,\mathfrak {D}_3,\mathfrak {D}_4\}$ in order to create more accurate results with the obtained information are presented in Table 2 and weight vector $\check{w}=(0.3,0.2,0.1,0.4)$ are determined, such that $\check{w}_j\in [0,1]$ and $\sum _{j=1}^4 \check{w_j}=1.$

Step 1: The decision-makers determine alternatives for each of criteria over qROF-assessment matrix into Table 1 as follows:

Table 1 Algorithm

Table 2 qROF-assessment matrix $[\varrho ]_{5\times 5}$

Step 2: Define evaluation matrix of experts using generalized parameter and taking into account preferences and priorities as follows:

Step 3: Define a new generalized assessment matrix as indicated into Table 3 by collecting together Tables 1 and 2 as follows.

Table 3 Generalized parameter matrix defined by decision-makers $[\varsigma ]_{5\times 4}$

Step 4: Obtain aggregated values using GGq-ROFAAWA based on data in Table 4 for $q=3$ and $\lambda =4$

$$\begin{aligned}{} & {} \mathrm{GGq-ROFAAWG}((\tau _1,\tau _2,\ldots ,\tau _p),\langle \Im _1,\Im _2,\ldots ,\Im _n\rangle )\\{} & {} \quad \Bigg \langle e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (\eta _{\tau _\iota }))^\lambda +\sum _{j=1}^nw_j(-\ln (\eta _j))^\lambda )\Big )^\frac{1}{\lambda }},\\{} & {} \quad \root q \of {1-e^{-\Big (\sum _{\iota =1}^p\hat{w}_\iota (-\ln (1-\upsilon _{\tau _\iota }^q))^\lambda +\sum _{j=1}^nw_j(-\ln (1-\upsilon _j^q))^\lambda )\Big )^\frac{1}{\lambda }}}\Bigg \rangle . \end{aligned}$$

Table 4 Group-based generalized Q-rung orthopair assessment matrix $\chi _{5\times 9}$

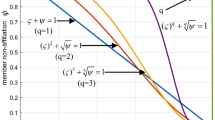
Step 5: The obtained values are as follows: $\pi _1=\langle 0.1564,0.2458\rangle$, $\pi _2=\langle 0.4359,0.0721\rangle$, $\pi _3=\langle 0.2703,0.3003\rangle$, $\pi _4=\langle 0.2634,0.4122\rangle$, $\pi _5=\langle 0.2071,0.0770\rangle$, and from here, score values of $\pi _i$ are obtained that $s(\pi _1)=-0.0110$, $s(\pi _2)=0.0824$, $s(\pi _3)=-0.0073$, $s(\pi _4)=-0.0517$ and $s(\pi _5)=0.0084$. Thus, rankings are provided; $\textbf{a}_2>\textbf{a}_5>\textbf{a}_3>\textbf{a}_1>\textbf{a}_4$. If we accept as $q=3$ and $\lambda =2$, the aggregated values are revealed, such that $\pi _1=\langle 0.1793,0.4283\rangle$, $\pi _2=\langle 0.3826,0.2468\rangle$, $\pi _3=\langle 0.2899,0.4820\rangle$, $\pi _4=\langle 0.3308,0.4363\rangle$, $\pi _5=\langle 0.2459,0.2608\rangle$, and if score values, $s(\pi _1)=-0.0728$, $s(\pi _2)=0.0409$, $s(\pi _3)=-0.0876$, $s(\pi _4)=-0.0468$ and $s(\pi _5)=-0.0028.$

Step 6: The orderings are that $\textbf{a}_2>\textbf{a}_5>\textbf{a}_4>\textbf{a}_1>\textbf{a}_3$. If we swap with q and $\lambda$ parameters, such that $q=4,5,6,7,8,10,15,20$ and $\lambda =3,5,6,10,15,17,25,50$, the score values and rankings are given in Tables 4 and 5.

Table 5 Ranking alternatives according to score values under GGq-ROFAAWG for $(\lambda =4)$

If the results are surveyed according to orderings of Alternatives, alternative $\textbf{a}_2$ is the most desirable and the most undesirable alternative is $\textbf{a}_4$ for different q values. Now, let us keep the q values constant and change the $\lambda$ values (Fig. 2).

As seen from score values, the best alternative is same for all $\lambda$ and q values. The proposed operator is reality, objective, and effective (Fig. 3).

8 Comparative and discussion

1. First, we give some comparisons by reducing an expert number of decision-makers and the obtained comparison is made within itself and the effect of decision-makers is understood on the rankings for above example, see Fig. 4. As seen from results, the best alternative focuses for all of the cases that is ${\textbf {a}}_2$ and ${\textbf {a}}_3$. When the above results are surveyed, it is open that ideal alternative is ${\textbf {a}}_2$ (Table 6).

2. We compare to different methods with our method in here, if we solve with our method to example of cutting tool of CNC machines in paper of Riaz et al. (2020a) and Liu et al. (2018), the results are within Table 7 as follows.

From Table 7, it is understood that there is an agreement about the best alternative among the presented operator and other operators. $\textbf{a}_4$ is the most desirable choice into all of the operators and if $\textbf{a}_1$, is the most undesirable result. It is open that the proposed operator has more advantages than compared operators such as adding extra $\lambda$ parameter, directly reflecting the ideas of the decision-makers as well as the common decision, while creating the decision-making matrix (Fig. 5).

3. If we solve with GGq-ROFAAWG the example about the disease of Pneumonia proposed using decision matrix presented by Hussain et al. (2021), the obtained score values that, $s(\pi _1)=0.1375$, $s(\pi _2)=0.2901$, $s(\pi _3)=0.2171$, $s(\pi _4)=0.1559$. If the ranking is $\textbf{a}_2>\textbf{a}_3>\textbf{a}_4>\textbf{a}_1$. The defined operator is reality, objective, and flexible. Moreover, the proposed operators have more advantages than operators presented by Hussain et al. (2021) because of reason to be used a variable. Our operators have two variables and increasing the number of variables will increase the flexible ratio (Fig. 6).

4. In this comparison, the proposed operator is analyzed with paper of Riaz et al. (2020b). Table 8 indicates the results obtained with our method. When the score values are surveyed, ideal alternative is same with GGQROFWG, GGQROFOWG, and GGQROFHWG as understood from Table 8. Moreover, the proposed operators have more advantages than operators presented by Riaz et al. (2020b) because of reason to be used a variable. Our operators have two variables and increasing the number of variables will increase the flexible ratio (Fig. 7).

5. If this comparison, the proposed operator is tested with paper of Qiyas et al. (2023). In here, if we solve example defined over hospital selection using the proposed operator, Table 9 indicates the results obtained with our method. When the score values are surveyed, ranking of alternative is same with q-rung orthopair fuzzy dombi weighted averaging operator (q-ROFDOWA) and q-rung orthopair fuzzy dombi weighted geometric operator (q-ROFDOWG) as understood from Table 9. Moreover, the proposed method has more advantages than method presented by Qiyas et al. (2023) because of the decision-making matrix (DMM) is obtained with decision-makers’ joint decision, but in our method, ideas of experts are reflected into DMM, separately. Thus, error margin is eliminated (Fig. 8).

9 Conclusion

Generalized concepts are widely used today, because they sort within themselves, contain many clusters, and can change according to the request and preference of decision-maker. In this manuscript, we developed q-rung orthopair fuzzy Aczel–Alsina weighted geometric(q-ROFAAWG) operator by utilizing q-Rung Orthopair fuzzy sets (q-ROFs) and T-norm and T-conorm of Aczel–Alsina and also ordered and hybrid concepts (q-ROFAAOWG, q-ROFAAHWG). Then, some properties of q-ROFAAWG as monotonicity, idempotency, and boundedness were surveyed to provided or not. Then, flexibility structure of q-ROFAAWA was developed and Generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric Gq-ROFAAWG and ordered and hybrid structures Gq-ROFAAOWG and Gq-ROFAAHWG were produced by operating with single parameter. In addition, structure of group-based parameters produced as different from other MCDM problems was applied and decision-makers were allowed to intervene in the decision-making matrix one by one. Thus, the possibility of error was minimized. Therefore, we defined group-based generalized q-rung orthopair fuzzy Aczel–Alsina weighted geometric operator (GGq-ROFAAWG) and ordered and hybrid concepts (GGq-ROFAAOWA, GGq-ROFAAHWA). The proposed GGq-ROFAAWG has some advantages as follows:

Fig. 2

The graphical representation of alternatives for different q values

Fig. 3

The graphical representation of alternatives for different $\lambda$ values

Fig. 4

The rankings obtained with a single expert

Table 6 Ranking alternatives according to score values under GGq-ROFAAWG for $(q=3)$

Table 7 Comparative analyses according to score values under GGq-ROFAAWG for $(q=3)$ and $(\lambda =4)$

Fig. 5

The comparison analyses with papers of Riaz et al. (2020a) and Liu et al. (2018)

Fig. 6

The comparison analyses with paper of Hussain et al. (2021)

Table 8 Comparative analyses according to score values under GGq-ROFAAWG for $(q=3)$ and $(\lambda =4)$

Fig. 7

The comparison analyses with paper of Riaz et al. (2020b)

Table 9 Comparative analyses according to score values under GGq-ROFAAWG for $(q=3)$ and $(\lambda =4)$

Fig. 8

The comparison analyses with paper of Qiyas et al. (2023)

• 1. The use of two different variables, q and $\lambda$, increases the flexibility of the concept.

• 2. GGq-ROFAAWG includes a lot of generalized parameter set, while most generalizations involve a single parameter.

• 3. Thanks to the generalized parameters, in our method, the experts are able to intervene directly in the decision matrix.

However, the presented method has some limitations like each q value may not be quite for the proposed constructions. For example; $q=2$ does not work for $\langle 0.8,0.9\rangle$ because of $0.8^2+0.9^2>1$. In this statement, decision-makers’ opinions can be wanted to be changed or value q can be increased. Moreover, logarithmic functions may not yield result for every value or similar results may be obtained like chosen as $\langle 0,0\rangle$ by experts. In addition to, we introduce an algorithm and a numerical example indicating flexibility of our method. Our results have a big agreement in their own for different values of $\lambda$ and q and the given comparative analyzes explain that our method is flexible, reality, and inclusive.

In future, we plan to combine the operators and cluster using the methods like TOPSIS, TODIM ELECTRE, etc.. In addition, we work to justify whether this algorithm can be applied to large-scale data set.