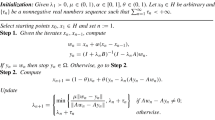Abstract
The main purpose of this paper is to propose and study a two-step inertial anchored version of the forward–reflected–backward splitting algorithm of Malitsky and Tam in a real Hilbert space. Our proposed algorithm converges strongly to a zero of the sum of a set-valued maximal monotone operator and a single-valued monotone Lipschitz continuous operator. It involves only one forward evaluation of the single-valued operator and one backward evaluation of the set-valued operator at each iteration; a feature that is absent in many other available strongly convergent splitting methods in the literature. Finally, we perform numerical experiments involving image restoration problem and compare our algorithm with known related strongly convergent splitting algorithms in the literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \({\mathcal {H}}\) be a real Hilbert space, and let \(A:{\mathcal {H}}\rightarrow 2^{{\mathcal {H}}}\) and \(B:{\mathcal {H}}\rightarrow {{\mathcal {H}}}\) be two monotone operators. The problem of finding a zero of the sum of A and B also known as the monotone inclusion problem is defined as
We denote the solution set of this problem by \((A+B)^{-1}(0)\).
The monotone inclusion is an important problem in optimization as well as in signal processing, image recovery, and machine learning. For instance, consider the minimization problem:
where \(f:{\mathcal {H}}\rightarrow (-\infty ,~+\infty ]\) is proper convex and lower semicontinuous, and \(g:{\mathcal {H}}\rightarrow {\mathbb {R}}\) is convex and continuously differentiable. The solutions to (1.2) are solutions to the problem:
where \(\partial f\) denotes the subdifferential of f and \(\nabla g\) is the gradient of g. Thus, the minimization problem of the sum of two convex functions is a special case of the monotone inclusion problem (1.1). Problems of the form (1.1) are often solved by splitting algorithms which involve evaluating A and B separately by means of a forward evaluation of B and a backward evaluation of A rather than their sum (\(A+B\)). These algorithms have undergone tremendous study which has been motivated by the desire to devise faster, computationally inexpensive and much more applicable methods. Among these splitting algorithms is the following forward–backward splitting algorithm (Lions and Mercier 1979; Passty 1979):
where \(I_{{\mathcal {H}}}\) is the identity operator on \({\mathcal {H}}\) and \(\lambda \) is a positive constant. This algorithm involves only one forward evaluation of B and one backward evaluation of A per iteration, and it is known to converge weakly to a solution of the inclusion problem (1.1) when B is \(L^{-1}\)-cocoercive (which is strict), \(\lambda \in (0, 2L^{-1})\), A is maximal monotone and \((A+B)^{-1}(0)\) is nonempty. Strongly convergent variants of Algorithm (1.3) have been studied under the strict cocoercive assumption on B in Takahashi et al. (2010); Wang and Wang (2018).
The strict cocoercive assumption on B in Algorithm (1.3) (and its strong convergent variants) was removed in Tseng (2000), where the author proposed the following forward–backward–forward splitting algorithm (also known as Tseng’s splitting method):
The main advantage of this algorithm is that it converges weakly to a solution of (1.1) under the much more weaker assumption that B is monotone and L-Lipschitz continuous, \(\lambda \in (0, L^{-1})\), A is maximal monotone and \((A+B)^{-1}(0)\ne \emptyset \). However, its main disadvantage is that it involves two forward evaluations of B, and this might affect the efficiency of the algorithm especially when this algorithm is applied to optimization arising from large-scale problems and optimal control theory, where computations of pertinent operators are often very expensive (see (Lions 1971)). Strongly convergent variants of Algorithm (1.4) were studied in Gibali and Thong (2018); Thong and Cholamjiak (2019), and they also have the disadvantage of requiring two forward evaluations of B.
This disadvantage was recently overcome by Malitsky and Tam (2020); they proposed the following forward–reflected–backward splitting algorithm:
The main advantage of Algorithm (1.5) is that it requires only one forward evaluation of B even when B is monotone and Lipschitz continuous. The reflexive Banach space variant of Algorithm (1.5) was studied in Izuchukwu et al. (2022), and when B is linear, Algorithm (1.5) has the same structure as the reflected–forward–backward splitting algorithm proposed and studied in Cevher and Vũ (2021). However, due to the computational structure of Algorithm (1.5) (unlike Algorithm (1.3) and Algorithm (1.4)), its strongly convergent variants are very rare in the literature despite that in infinite-dimensional spaces, strong convergence results are much more desirable than weak convergence results.
Recently, fast convergent algorithms for solving optimization problems have been of great interest to many researchers. On one hand, the anchored extrapolation step is known to be one of the most important ingredients for improving the convergence rate of optimization algorithms (see (Qi and Xu 2021; Yoon and Ryu 2021) for details). On the other hand, the inertial technique which is based upon a discrete analog of a second-order dissipative dynamical system is also known for its efficiency in improving the convergence speed of iterative algorithms. The one-step inertial extrapolation \(x_n+{\vartheta }(x_n-x_{n-1})\) is the most commonly used technique for this purpose. It originates from the heavy ball method of the second-order dynamical system for minimizing a smooth convex function:
where \(\gamma >0\) is a damping or friction parameter. Polyak (1964) was the first author to propose the heavy ball method, Alvarez and Attouch (2001) extended it to the setting of a general maximal monotone operator. In Bing and Cho (2021), the authors proposed the following one-step inertial viscosity-type forward–backward–forward splitting algorithm (Bing and Cho 2021, Algorithm 3.4):
where f is a contraction mapping and \(\vartheta _n\) is the inertial parameter. They proved that the sequence \(\{x_n\}\) generated by Algorithm (1.6) converges strongly to a solution of the monotone inclusion problem (1.1) (see also (Bing and Cho (2021), Theorem 3.3), a version of Algorithm (1.6) without the contraction mapping). In (Suparatulatorn and Chaichana (2022), Algorithm 1), Suparatulatorn and Chaichana proposed a one-step inertial parallel shrinking-type algorithm for solving a finite family of monotone inclusion problems. Also, in Alakoya et al. (2022); Liu et al. (2021); Tan et al. (2022); Taiwo and Mewomo (2022), the authors proposed and studied one-step inertial algorithms that tackle the particular case, where A is the normal cone of some nonempty, closed and convex set (i.e., one-step inertial algorithms that solve variational inequality problems).
However, it was discussed in (Poon and Liang 2019, Section 3) that one-step inertial term may fail to provide acceleration to ADMM. Let \(H_1, H_2 \subset {\mathbb {R}}^2\) be two subspaces such that \(H_1 \cap H_2 \ne \emptyset \). Consider the feasibility problem:
It was shown in [25, Section 4] that for problem (1.7), the two-step inertial fixed point iteration
where \(T:=\frac{1}{2}\Big (I+(2P_{H_1}-I)(2P_{H_2}-I)\Big )\), converges faster in terms of both the number of iterations and the CPU time, than the one-step inertial fixed point iteration
Furthermore, it was shown, using problem (1.7), that the sequences generated by the one-step inertial fixed point iteration (1.8) converge more slowly than those generated by its non-inertial version. This shows that the one-step inertial fixed point iteration (1.8) may fail to provide acceleration. But as discussed in (Liang 2016, Chapter 4), employing the multi-step inertial, like the two-step inertial term \(x_n+{\vartheta }(x_n-x_{n-1})+{\beta }(x_{n-1}-x_{n-2})\), \({\vartheta } > 0\), \({\beta }< 0\), could resolve the issue of not providing acceleration. Thus in Combettes and Glaudin (2017); Dong et al. (2019); Iyiola and Shehu (2022); Li et al. (2022); Polyak (1987), the authors recently studied multi-step inertial algorithms and showed that multi-step inertial terms (e.g., the two-step inertial term) enhances the speed of optimization algorithms.
In this paper, we investigate the strong convergence of a two-step inertial anchored variant of the forward-reflected-backward splitting algorithm (1.5). In other words, we propose a two-step inertial forward–reflected–anchored–backward splitting algorithm and prove that it converges strongly to a solution of Problem (1.1). The proposed algorithm involves only one forward evaluation of the monotone Lipschitz continuous operator B and one backward evaluation of the maximal monotone operator A at each iteration; a feature that is absent in many other available strongly convergent inertial splitting algorithms in the literature. Furthermore, we perform numerical experiments for problems emanating from image restoration, and these experiments confirm that our proposed algorithm is efficient and faster than other related strongly convergent splitting algorithms in the literature.
2 Preliminaries
The operator \(B: {\mathcal {H}}\rightarrow {\mathcal {H}}\) is called L-cocoercive (or inverse strongly monotone) if there exists \(L>0\) such that
and monotone if
The operator B is called L-Lipschitz continuous if there exists \(L>0\) such that
Let A be a set-valued operator \(A:{\mathcal {H}}\rightarrow 2^{{\mathcal {H}}}\), then A is said to be monotone if
The monotone operator A is called maximal if the graph \({\mathcal {G}}(A)\) of A, defined by
is not properly contained in the graph of any other monotone operator. In other words, A is called a maximal monotone operator if for \((x,{\widehat{x}})\in {\mathcal {H}}\times {\mathcal {H}}\), we have that \(\langle {\widehat{x}}-{\widehat{y}}, x-y\rangle \ge 0\) for all \((y,{\widehat{y}})\in {\mathcal {G}}(A)\) implies \({\widehat{x}}\in Ax\).
For a set-valued operator A, the resolvent associated with it is the mapping \(J_{\lambda }^{A}: {\mathcal {H}}\rightarrow 2^{{\mathcal {H}}}\) defined by
If A is maximal monotone and B is single-valued, then both \(J_{\lambda }^{A}\) and \(J_{\lambda }^{A}(I_{{\mathcal {H}}}-\lambda B)\) are single-valued and everywhere defined on \({\mathcal {H}}\). Furthermore, the resolvent \(J_{\lambda }^{A}\) is nonexpansive.
The following hold in a real Hilbert space \({\mathcal {H}}\):
and
Lemma 2.1
Saejung and Yotkaew (2012) Suppose that \(\{p_{n}\}\) is a sequence of nonnegative real numbers, \(\{\alpha _{n}\}\) is a sequence of real numbers in (0, 1) satisfying \(\sum _{n=1}^\infty \alpha _n=\infty \), and \(\{q_n\}\) is a sequence of real numbers such that
If \(\limsup \limits _{i\rightarrow \infty } q_{n_i}\le 0\) for each subsequence \(\{p_{n_i}\}\) of \(\{p_{n}\}\) satisfying \(\liminf \limits _{i\rightarrow \infty }\left( p_{n_i+1}-p_{n_i}\right) \ge 0\), then \(\lim \limits _{n\rightarrow \infty } p_n=0\).
Lemma 2.2
Lemaire (1997) Suppose that \(A:{\mathcal {H}}\rightarrow 2^{{\mathcal {H}}}\) is maximal monotone and \(B:{\mathcal {H}}\rightarrow {\mathcal {H}}\) is monotone Lipschitz continuous, then \((A+B):{\mathcal {H}}\rightarrow 2^{{\mathcal {H}}}\) is maximal monotone.
Lemma 2.3
Maingé (2007) Suppose that \(\{p_{n}\}\) and \(\{r_{n}\}\) are sequences of nonnegative real numbers such that
where \(\{\alpha _{n}\}\) is a sequence in (0, 1) and \(\{s_{n}\}\) is a real sequence. Let \(\sum _{n=1}^{\infty }r_{n}<\infty \) and \(s_{n}\le \alpha _{n}M\) for some \(M\ge 0\). Then, \(\{p_{n}\}\) is bounded.
3 Two-step inertial forward–reflected–anchored–backward splitting algorithm
In this section, we first propose and then study the convergence analysis of the following algorithm.
Algorithm 3.1
Let \(\lambda _0,\lambda _1>0\), \(\vartheta \in [0, 1)\), \(\beta \le 0\), \(\delta \in \Big (t,~\frac{1-2t}{2}\Big )\) with \(t\in (0, \frac{1}{4})\), and choose sequences \(\{\alpha _n\}\) in (0, 1) and \(\{e_n\}\) in \([0, \infty )\) such that \(\sum _{n=1}^{\infty } e_n< \infty \). For arbitrary \({\hat{v}}, x_{-1},x_0,x_1 \in {\mathcal {H}}\), let the sequence \(\{x_n\}\) be generated by
for all \(n\ge 1,\) where
Algorithm 3.1 is called a two-step inertial forward–reflected–anchored–backward splitting algorithms since it involves an anchor \({\hat{v}}\), an anchoring coefficient \(\alpha _n\), a two-step inertial term and the forward–reflected–backward splitting algorithm (1.5). This algorithm can also be viewed as a two-step inertial Halpern-type forward–reflected–backward method since it is based on the Halpern iteration. For more information on the convergence of Halpern-type methods for solving optimization problems, see, for example, Qi and Xu (2021); Yoon and Ryu (2021).
Assumption 3.2
-
(a)
A is maximal monotone,
-
(b)
B is monotone and Lipschitz continuous with constant \({L}>0\),
-
(c)
\((A+B)^{-1}(0)\) is nonempty,
-
(d)
\(\vartheta \) and \(\beta \) satisfy \(0\le \vartheta<\frac{1}{3}\left( 1-2(\frac{1}{2}-t)\right) , ~~\frac{1}{3+4\vartheta }\left( 3\vartheta -1+2(\frac{1}{2}-t)\right) <\beta \le 0.\)
Remark 3.3
By (3.1), \(\lim \nolimits _{n\rightarrow \infty }\lambda _n={\lambda }\), where \({\lambda }\in [\min \{\delta {L}^{-1}, \lambda _1\}, ~\lambda _1+e]\) with \(e=\sum _{n=1}^\infty e_n\) (see (Liu and Yang 2020)). If \(e_n=0\), then the step size \(\lambda _n\) in (3.1) is similar to the one in Bing and Cho (2021), which is derived from the paper (Yang and Liu 2019) for solving variational inequalities.
Lemma 3.4
Let \(\{x_n\}\) be generated by Algorithm 3.1 when Assumption 3.2 holds. If \(\lim \limits _{n\rightarrow \infty }\alpha _n=0\), then the sequence \(\{x_n\}\) is bounded.
Proof
Let \({\widehat{x}}\in (A+B)^{-1}(0)\) and \(u_n:=\alpha _n{\hat{v}}+(1-\alpha _n) v_n\), where \(v_n=x_n+\vartheta (x_n-x_{n-1})+\beta (x_{n-1}-x_{n-2})\). Then
and
Since A is monotone, we get from (3.2) and (3.3) that
This implies
where the last equation follows from (2.1).
Now, using the monotonicity of B, we get
Also, using (3.1), we have
Using Remark 3.3 and noting that \(\delta \in \Big (t,~\frac{1-2t}{2}\Big ),\) we see that \(\lim _{n\rightarrow \infty }\frac{\lambda _{n-1}}{\lambda _{n}}\delta =\delta <\frac{1}{2}-t\). Hence, there exists \(n_0\ge 1\) such that \(\frac{\lambda _{n-1}}{\lambda _{n}}\delta <\frac{1}{2}-t~\forall n\ge n_0\). Thus, we obtain that
Putting (3.5) and (3.6) in (3.4), we obtain
From (2.1), we get
Replacing \({\widehat{x}}\) by \(x_{n+1}\) in (3.8), we get
Now, subtracting (3.9) from (3.8), we obtain
Using (3.10) in (3.7), we obtain
From (2.2), we get
Also, from (2.1), we get
Now, observe that
Putting (3.14), (3.15) and (3.16) in (3.13), we obtain
Now, putting (3.12) and (3.17) in (3.11), we obtain
This implies that
Set \(c_1:=-\left( 2(\frac{1}{2}-t)+3\vartheta -1+(1+\vartheta )(|\beta |-\beta )\right) \), \(c_2:=1-3\vartheta -2(\frac{1}{2}-t)-2|\beta |-2\vartheta |\beta |+\beta +2\vartheta \beta \) and \(p_n:=\Vert x_n-{\widehat{x}}\Vert ^2-\vartheta \Vert x_{n-1}-{\widehat{x}}\Vert ^2-\beta \Vert x_{n-2}-{\widehat{x}}\Vert ^2 +2\lambda _{n-1}\langle Bx_n-Bx_{n-1},{\widehat{x}}-x_{n}\rangle +(1-|\beta |-\vartheta -\frac{1}{2}+t)\Vert x_n-x_{n-1}\Vert ^2+c_1\Vert x_{n-1}-x_{n-2}\Vert ^2\). Then, (3.18) becomes
Next, we show that \(c_1\), \(c_2\) are positive and \(p_n\) is nonnegative. From Assumption 3.2 (d), \(3\vartheta -1+2(\frac{1}{2}-t)<0\). Thus, \(\frac{1}{2+2\vartheta }\left( 3\vartheta -1+2(\frac{1}{2}-t)\right)<\frac{1}{3+4\vartheta }\left( 3\vartheta -1+2(\frac{1}{2}-t)\right) <\beta \), which implies that \(3\vartheta -1+2\left( \frac{1}{2}-t\right) -2\beta -2\vartheta \beta <0\).
Since \(|\beta |=-\beta \), we obtain
which implies that \(c_1>0\).
Now, using \(\frac{1}{3+4\vartheta }\left( 3\vartheta -1+2(\frac{1}{2}-t)\right) <\beta \), we obtain that \(1-3\vartheta -2(\frac{1}{2}-t)+3\beta +4\beta \vartheta >0.\) Since \(|\beta |=-\beta \), we get
Hence, \(c_2>0\).
On the other hand, since \(\beta \le 0\) and \(c_1>0\), we get for all \(n\ge n_0\), that
Since \(\vartheta <\frac{1}{3}\left( 1-2(\frac{1}{2}-t)\right) \), we get \(3\vartheta -1+2(\frac{1}{2}-t)<0\). This imply that \(1-3\vartheta -(\frac{1}{2}-t)>0\), and \( 3\vartheta -1+2(\frac{1}{2}-t)<\frac{1}{3+4\theta }(3\vartheta -1+2(\frac{1}{2}-t))<\beta \). Hence, \(-|\beta |-3\vartheta +1-2(\frac{1}{2}-t))>0\). Therefore, we get from (3.22) that \(p_n\ge 0\) for all \(n\ge n_0\). Using these facts in (3.19), we obtain that \(\{p_n\}\) is bounded. It then follows from (3.22) that the sequence \(\{x_n\}\) is indeed bounded, as claimed. \(\square \)
We now state and prove the convergence theorem of this paper.
Theorem 3.5
Let \(\{x_n\}\) be generated by Algorithm 3.1 when Assumption 3.2 holds. If \(\lim _{n\rightarrow \infty }\alpha _n=0\) and \(\sum _{n=1}^\infty \alpha _n=\infty \), then \(\{x_n\}\) converges strongly to \(P_{(A+B)^{-1}(0)}{\hat{v}}\).
Proof
Let \({\widehat{x}}=P_{(A+B)^{-1}(0)}{\hat{v}}\). Then by (2.1), we get
Again, using (2.1), we get
where \(M:=\sup \limits _{n\ge 1}\Vert x_{n+1}-{\hat{v}}\Vert \) which exists due to the boundedness of \(\{x_n\}\) proved in Lemma 3.4.
Now, using (3.23) and (3.24) in (3.7), we see that
Next, putting (3.12) and (3.17) in (3.25), we obtain
This implies that
That is,
where \(d_n=1-2\vartheta -2(\frac{1}{2}-t)+\beta +2\vartheta \beta -|\beta |-\beta ^2-\vartheta ^2+(1-\alpha _n)(\vartheta ^2-\vartheta -\vartheta |\beta |)+(1-\alpha _n)(\beta ^2-|\beta |-\vartheta |\beta |)\), \(t_n=\Vert x_n-{\widehat{x}}\Vert ^2-\vartheta \Vert x_{n-1}-{\widehat{x}}\Vert ^2-\beta \Vert x_{n-2}-{\widehat{x}}\Vert ^2 +2\lambda _{n-1}\langle Bx_n-Bx_{n-1},{\widehat{x}}-x_{n}\rangle +(1-|\beta |-\vartheta -\frac{1}{2}+t)\Vert x_n-x_{n-1}\Vert ^2+c_n\Vert x_{n-1}-x_{n-2}\Vert ^2\), \(c_n=-\left[ 2(\frac{1}{2}-t)+2\vartheta -\beta -\vartheta \beta -1+|\beta |+\vartheta ^2-(1-\alpha _n)(\vartheta ^2-\vartheta -\vartheta |\beta |)\right] \) and \(q_n=\alpha _n\Vert {\hat{v}}-{\widehat{x}}\Vert ^2+2(1-\alpha _n)\langle {\hat{v}}-{\widehat{x}}, v_n-{\widehat{x}}\rangle +2(1-\alpha _n)M \Vert x_{n+1}-v_n\Vert \).
From (3.20), we have \(1-3\vartheta -2(\frac{1}{2}-t)-|\beta |+\beta -\vartheta |\beta |+\vartheta \beta >0,\) which implies that
Thus, there exists \(n_1\ge n_0\) such that \(c_n>0\) for all \(n\ge n_1\). Also, from (3.21), we have \(1-3\vartheta -2\left( \frac{1}{2}-t\right) -2|\beta |+\beta -2|\beta |\vartheta +2\beta \vartheta >0\), which implies
There exists \(n_2\ge n_0\) such that \(d_n>0\) for all \(n\ge n_2\). Therefore,
Let \(\{t_{n_i}\}\) be a subsequence of \(\{t_n\}\) such that \(\liminf _{i\rightarrow \infty }\left( t_{n_i+1}-t_{n_i}\right) \ge 0\). Then, it follows from (3.26) that
Since \(\lim _{i\rightarrow \infty }(1-\alpha _{n_i})d_{n_i}>0\), we get
Thus,
Using (3.28) and (3.29), we obtain
Since \(\lim _{n\rightarrow \infty }\alpha _n=0\), we get
Using (3.30) and (3.31), we obtain
From (3.28) and the Lipschitz continuity of B, we find that
In the light of Lemma 3.4, we see that \(\{x_{n_i}\}\) is bounded. Thus, we can choose a subsequence \(\{x_{n_{i_j}}\}\) of \(\{x_{n_i}\}\) such that \(\{x_{n_{i_j}}\}\) converges weakly to some \(x^*\in {\mathcal {H}}\), and
Now, consider \((u, v)\in {\mathcal {G}}(A+B)\). Then \(\lambda _{n_{i_j}}(v-Bu)\in \lambda _{n_{i_j}}Au\). Using this, (3.3) and the monotonicity of A, we find that
Thus, using the monotonicity of B, we obtain
As \(j\rightarrow \infty \) in (3.35), we obtain, using (3.32) and (3.33), that \(\langle v, u-x^*\rangle \ge 0\). By Lemma 2.2, \(A+B\) is maximal monotone. Hence, we get that \(x^*\in (A+B)^{-1}(0)\).
Since \({\widehat{x}}=P_{(A+B)^{-1}(0)}{\hat{v}}\), it follows from (3.34) and the characterization of the metric projection that
Using (3.29), (3.30) and (3.36), we obtain that \(\limsup _{i\rightarrow \infty }q_{n_{i}}\le 0\). Thus, in view of the condition \(\sum _{n=1}^\infty \alpha _n=\infty \), Lemma 2.1 and (3.27), we see that \(\lim _{n\rightarrow \infty }t_n=0\). This together with (3.22) imply that \(\{x_n\}\) converges strongly to \({\widehat{x}}=P_{(A+B)^{-1}(0)}{\hat{v}}\), as asserted. \(\square \)
The step size defined in (3.1) makes it possible for Algorithm 3.1 to be applied in practice even when the Lipschitz constant L of B is not known. However, when this constant is known or can be calculated, we simply adopt the following variant of Algorithm 3.1:
Algorithm 3.6
Let \(\lambda \in \Big (0,~\frac{1}{2\,L}\Big )\), \(\vartheta \in [0, 1)\), \(\beta \le 0\), and choose the sequence \(\{\alpha _n\}\) in (0, 1). For arbitrary \({\hat{v}}, x_{-1}, x_0,x_1 \in {\mathcal {H}}\), let the sequence \(\{x_n\}\) be generated by
Remark 3.7
Using arguments similar to those in Lemma 3.4 and Theorem 3.5, we can establish that the sequence \(\{x_n\}\) generated by Algorithm 3.6 converges strongly to \(P_{(A+B)^{-1}(0)}{\hat{v}}\).
Remark 3.8
-
(a)
We obtained strong convergence results for Algorithm 3.1 without assuming that either A or B is strongly monotone (a condition that is quite restrictive). Rather, we modified the forward–reflected–backward splitting algorithm in Malitsky and Tam (2020) appropriately to obtain our strong convergent results.
-
(b)
Compared to Izuchukwu et al. (2023), we proved the strong convergence of Algorithm 3.1 using the double inertial technique.
Remark 3.9
A more careful examination of Algorithm 3.1 and it convergence analysis can help us to relax the Lipschitz continuity on B to uniform continuity (see, for example (Thong et al. (2023), page 1114). In a finite-dimensional space, B can even be continuous (see (Izuchukwu and Shehu 2021, Section 3)). However, as seen in these papers, this relaxation may be achieved with the cost of having strict restrictions on the stepsize \(\{\lambda _n\}\) (e.g., through some linesearch techniques). Therefore, we intend to investigate these restrictions in detail in a different project in the future.
4 Numerical illustrations
In this section, using test examples which originate from image restoration problem, as well as an academic example, we compare Algorithm 3.1 with other strongly convergent algorithms (Alakoya et al. 2022, Algorithm 3.2), (Bing and Cho (2021), Algorithm 3.3 and Algorithm 3.4) and (Tan et al. 2022, Algorithm 3.4).
Example 4.1
We consider the image restoration problem:
where \(\lambda >0\) (we take \(\lambda =1\)), \({\hat{x}}\in {\mathbb {R}}^m\) is the original image to be restored, \({\hat{c}}\in {\mathbb {R}}^N\) is the observed image and \({\mathcal {D}}: {\mathbb {R}}^m\rightarrow {\mathbb {R}}^N\) is the blurring operator. The quality of the restored image is measured by
where SNR means signal-to-noise ratio, and \(x^*\) is the recovered image.
For the implementation, we take \(x_0 = {\textbf {0}} \in {\mathbb {R}}^{m\times m}\) and \(x_{-1}=x_1 = {\textbf {1}} \in {\mathbb {R}}^{m\times N}\), and use the following image found in the MATLAB Image Processing Toolbox:
-
(a)
Tire Image of size \(205 \times 232\). To create the blurred and noisy image (observed image), we use the Gaussian blur of size \(9\times 9\) and standard deviation \(\sigma =4\).
-
(b)
Cameraman Image of size \(256 \times 256\). We use the Gaussian blur of size \(7\times 7\) and standard deviation \(\sigma =4\).
-
(c)
Medical Resonance Imaging (MRI) of size \(128 \times 128\). We use the Gaussian blur of size \(7\times 7\) and standard deviation \(\sigma =4\).
Example 4.2
Let \({\mathcal {H}}={\mathfrak {l}}_2({\mathbb {R}}):=\{x=(x_1, x_2,...,x_i,...),~~x_i \in {\mathbb {R}}:\sum \nolimits _{i=1}^{\infty }|x_i|^2<\infty \}\) and \(||x||_{\mathfrak {l}_2}:= \left( \sum \nolimits _{i=1}^\infty |x_i|^2 \right) ^{\frac{1}{2}} \; ~~\forall x \in \mathfrak {l}_2({\mathbb {R}}).\)
Define \(A,B:\mathfrak {l}_2\rightarrow \mathfrak {l}_2\) by
and
Then, A is maximal monotone and B is Lipschitz continuous and monotone with Lipschitz constant \({L}=1\).
The behavior of \(\text{ TOL}_n\) for Example 4.2 with \(\epsilon =10^{-7}\): Top Left: Case 1; Top Right: Case 2; Bottom left: Case 3; Bottom Right: Case 4
For the implementation, we take the starting points:
Case 1: \(x_0=(\frac{2}{3}, \frac{4}{9}, \frac{8}{27}, \cdots )\), \(x_{-1}=x_1= (\frac{2}{3}, \frac{4}{9}, \frac{8}{27}, \cdots ) \).
Case 2: \(x_0=(\frac{2}{3}, \frac{4}{9}, \frac{8}{27}, \cdots )\), \(x_{-1}=x_1= (\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \cdots )\).
Case 3: \(x_0=(1, \frac{1}{2}, \frac{1}{4}, \cdots )\), \(x_{-1}=x_1= (\frac{4}{5}, \frac{16}{25}, \frac{64}{125}, \cdots )\).
Case 4: \(x_0= (1, \frac{1}{4}, \frac{1}{9}, \cdots )\), \(x_{-1}=x_1= (\frac{3}{4}, \frac{9}{16}, \frac{27}{64}, \cdots ).\)
During the implementation, we make use of the following:
-
Algorithm 3.1: \(\lambda _0 = 0.1, \lambda _1 = 0.3, \delta =0.25, \alpha _n=\frac{0.005}{3n+25000}, e_n = \frac{16}{(n+1)^{1.1}}, t=0.2, \vartheta = 0.12, \beta =\{0, -0.01\}\).
-
Alakoya et al. (2022) (Alg. 3.2): \(\theta =0.12, \lambda _1=0.3,\mu =0.25,\alpha _n=\frac{0.005}{3n+25000}, \rho _n = \frac{16}{(n+1)^{1.1}}, \xi _n=\frac{1}{(2n+1)^4}, f(x)=\frac{1}{3}x\).
-
Bing and Cho (2021) (Alg. 3.3): \(\theta =0.12, \lambda _1=0.3,\mu =0.25,\alpha _n=\frac{0.005}{3n+25000}, \beta _n=0.5(1-\alpha _n), \epsilon _n=\frac{1}{(2n+1)^4}\).
-
Bing and Cho (2021) (Alg. 3.4): \(\theta =0.12, \lambda _1=0.3,\mu =0.25,\alpha _n=\frac{0.005}{3n+25000}, \epsilon _n=\frac{1}{(2n+1)^4}, f(x)=\frac{1}{3}x\).
-
Tan et al. (2022) (Alg. 3.4): \(\tau =0.12, \mu =0.25, \vartheta _1=0.3, \theta =1.5, \sigma _n=\frac{0.005}{3n+25000}, \varphi _n=0.5(1-\sigma _n), \epsilon _n=\frac{100}{(n+1)^2}, \xi _n=\frac{16}{(n+1)^{1.1}}\).
We then use the stopping criterion; \(\text{ TOL}_n:=0.5\Vert x_n - J^A(x_n - Bx_n)\Vert ^2<\epsilon \) for all algorithms, where \(\epsilon \) is the predetermined error.
All the computations are performed using Matlab 2016 (b) which is running on a personal computer with an Intel(R) Core(TM) i5-2600 CPU at 2.30GHz and 8.00 Gb-RAM.
In Tables 1 and 2, “Iter” and “CPU” mean the CPU time in seconds and the number of iterations, respectively.
Remark 4.3
Figures 1, 2, 3 can be seen clearly (or understood better) by looking at the graphs of “SNR” vs “Iteration number (n)”, and Table 1. Note that the larger the SNR, the better the quality of the restored image.
5 Conclusion
We have proposed a two-step inertial forward–reflected–anchored–backward splitting algorithm for solving the monotone inclusion problem (1.1) in a real Hilbert space. We have also proved that the sequence generated by this algorithm converges strongly to a solution of the monotone inclusion problem. This algorithm inherits the attractive features of the forward–reflected–backward splitting algorithm (1.5), namely it involves only one forward evaluation of B even when B is not required to be cocoercive. However, unlike the forward–reflected–backward splitting algorithm (1.5), our algorithm converges strongly. Numerical results show that the proposed algorithm is efficient and faster than other related strongly convergent splitting algorithms in the literature. We remark that our proposed algorithm involves a restrictive condition on \(\{e_n\}\); for example, the sequence \(\{\frac{1}{n}\}\) does not satisfy this condition. Therefore, we intend to relax the restriction on \(\{e_n\}\) in our ongoing projects.
Availability of supporting data
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
References
Alakoya TO, Mewomo OT, Shehu Y (2022) Strong convergence results for quasimonotone variational inequalities. Math Meth Oper Res 95:249–279
Alvarez F, Attouch H (2001) An Inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal 9:3–11
Bing T, Cho SY (2021) Strong convergence of inertial forward-backward methods for solving monotone inclusions. Appl Anal. https://doi.org/10.1080/00036811.2021.1892080
Cevher V, Vũ BC (2021) A reflected forward-backward splitting method for monotone inclusions involving Lipschitzian operators. Set-Valued Var Anal 29:163–174
Combettes PL, Glaudin LE (2017) Quasi-nonexpansive iterations on the affine hull of orbits: from Mann’s mean value algorithm to inertial methods. SIAM J Optim 27:2356–2380
Dong QL, Huang JZ, Li XH, Cho YJ, Rassias TM (2019) MiKM: multi-step inertial Krasnosel’skii-Mann algorithm and its applications. J Global Optim 73:801–824
Gibali A, Thong DV (2018) Tseng type methods for solving inclusion problems and its applications, Calcolo, 55. https://doi.org/10.1007/s10092-018-0292-1
Iyiola OS, Shehu Y (2022) Convergence results of two-step inertial proximal point algorithm. Appl Numer Math 182:57–75
Izuchukwu C, Shehu Y (2021) New inertial projection methods for solving multivalued variational inequality problems beyond monotonicity. Netw Spat Econ 21:291–323
Izuchukwu C, Reich S, Shehu Y, Taiwo A (2023) Strong convergence of forward-reflected-backward splitting methods for solving monotone inclusions with applications to image restoration and optimal control. J Sci Comput 94:1–31
Izuchukwu C, Reich S, Shehu Y (2022) Convergence of two simple methods for solving monotone inclusion problems in reflexive Banach spaces, Results Math., 77, https://doi.org/10.1007/s00025-022-01694-5
Lemaire B (1997) Which fixed point does the iteration method select? Recent advances in optimization. Spring Berlin, Germany 452:154–157
Liang J (2016) Convergence rates of first-order operator splitting methods. PhD thesis, Normandie Université; GREYC CNRS UMR 6072
Li X, Dong Q.L, Gibali A (2022) PMiCA - Parallel multi-step inertial contracting algorithm for solving common variational inclusions. J Nonlinear Funct Anal 2022
Lions JL (1971) Optimal control of systems governed by partial differential equations. Springer, Berlin
Lions PL, Mercier B (1979) Splitting algorithms for the sum of two nonlinear operators. SIAM J Numer Anal 16:964–979
Liu H, Yang J (2020) Weak convergence of iterative methods for solving quasimonotone variational inequalities. Comput Optim Appl 77(2):491–508
Liu L, Cho SY, Yao JC (2021) Convergence analysis of an inertial Tseng’s extragradient algorithm for solving pseudomonotone variational inequalities and applications. J Nonlinear Var Anal 5:627–644
Maingé PE (2007) Approximation methods for common fixed points of nonexpansive mappings in Hilbert spaces. J Math Anal Appl 325(1):469–479
Malitsky Y, Tam MK (2020) A forward-backward splitting method for monotone inclusions without cocoercivity. SIAM J Optim 30:1451–1472
Passty GB (1979) Ergodic convergence to a zero of the sum of monotone operators in Hilbert spaces. J Math Anal Appl 72:383–390
Polyak BT (1964) Some methods of speeding up the convergence of iterates methods. USSR Comput Math Phys 4(5):1–17
Polyak BT (1987) Introduction to Optimization. Optimization Software, Publications Division, New York
Poon C, Liang J (2019) Trajectory of alternating direction method of multipliers and adaptive acceleration. In Advances In Neural Information Processing Systems
Poon C, Liang J, Geometry of First-Order Methods and Adaptive Acceleration. arXiv:2003.03910
Qi H, Xu HK (2021) Convergence of Halpern’s iteration method with applications in optimization. Numer Funct Anal Optim. https://doi.org/10.1080/01630563.2021.2001826
Saejung S, Yotkaew P (2012) Approximation of zeros of inverse strongly monotone operators in Banach spaces. Nonlinear Anal 75:742–750
Suparatulatorn R, Chaichana K (2022) A strongly convergent algorithm for solving common variational inclusion with application to image recovery problems. Appl Numer Math 173:239–248
Taiwo A, Mewomo OT (2022) Inertial viscosity with alternative regularization for certain optimization and fixed point problems. J Appl Numer Optim 4:405–423
Takahashi S, Takahashi W, Toyoda M (2010) Strong convergence theorems for maximal monotone operators with nonlinear mappings in Hilbert spaces. J Optim Theory Appl 147:27–41
Tan B, Qin X, Yao JC (2022) Strong convergence of inertial projection and contraction methods for pseudomonotone variational inequalities with applications to optimal control problems. J Glob Optim 82:523–557
Thong DV, Cholamjiak P (2019) Strong convergence of a forward–backward splitting method with a new step size for solving monotone inclusions. Comput Appl Math38. https://doi.org/10.1007/s40314-019-0855-z
Thong DV, Reich S, Shehu Y, Iyiola OS (2023) Novel projection methods for solving variational inequality problems and applications. Numer Algorithms 93:1105–1135
Tseng P (2000) A modified forward-backward splitting method for maximal monotone mappings. SIAM J Control Optim 38:431–446
Wang Y, Wang F (2018) Strong convergence of the forward-backward splitting method with multiple parameters in Hilbert spaces. Optimization 67:493–505
Yang J, Liu H (2019) Strong convergence result for solving monotone variational inequalities in Hilbert space. Numer Algorithms 80:741–752
Yoon TH, Ryu EK (2021) Accelerated algorithms for smooth convex-concave minimax problems with \({\cal{O}}(1/k^2)\) rate on squared gradient norm, arXiv preprint arXiv:2102.07922
Acknowledgements
We thank the referees sincerely for their valuable comments and suggestions that help to improve our manuscript.
Funding
Open access funding provided by University of the Witwatersrand.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Ethical approval and consent to participate
All the authors gave the ethical approval and consent to participate in this article.
Consent for publication
All the authors gave consent for the publication of identifiable details to be published in the journal and article.
Additional information
Communicated by Justin Wan.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Izuchukwu, C., Aphane, M. & Aremu, K.O. Two-step inertial forward–reflected–anchored–backward splitting algorithm for solving monotone inclusion problems. Comp. Appl. Math. 42, 351 (2023). https://doi.org/10.1007/s40314-023-02485-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-023-02485-6
Keywords
- Forward–reflected–backward method
- Two-step inertial
- Halpern’s iteration
- Monotone inclusion
- Strong convergence