Spectral variational multi-scale method for parabolic problems: application to 1D transient advection-diffusion equations

Abstract

In this work, we introduce a variational multi-scale (VMS) method for the numerical approximation of parabolic problems, where sub-grid scales are approximated from the eigenpairs of associated elliptic operator. The abstract method is particularized to the one-dimensional advection-diffusion equations, for which the sub-grid components are exactly calculated in terms of a spectral expansion when the advection velocity is approximated by piecewise constant velocities on the grid elements.We prove error estimates that in particular imply that when Lagrange finite element discretisations in space are used, the spectral VMS method coincides with the exact solution of the implicit Euler semi-discretisation of the advection-diffusion problem at the Lagrange interpolation nodes. We also build a feasible method to solve the evolutive advection-diffusion problems by means of an offline/online strategy with reduced computational complexity.We perform some numerical tests in good agreement with the theoretical expectations, that show an improved accuracy with respect to several stabilised methods.

1 Introduction

The variational multi-scale is a general methodology to deal with the instabilities arising in the Galerkin discretisation of PDEs (partial differential equations) with terms of different derivation orders (see cf. Hughes 1995; Hughes and Stewart 1995; Hughes et al. 1998)).

The VMS formulation is based upon the formulation of the Galerkin method as two variational problems, one satisfied by the resolved scales and another satisfied by the sub-grid scales of the solution. To build a feasible VMS method, the sub-grid scales problem is approximately solved by some analytic or computational procedure. In particular, an element-wise diagonalisation of the PDE operator leads to the Adjoint Stabilised Method, as well as to the Orthogonal Sub-Scales (OSS) method, introduced by Codina in Codina (2000). Within these methods, the effect of the sub-grid scales is modelled by means of a dissipative interaction of operator terms acting on the resolved scales. The VMS methods have been successfully applied to many flow problems, and in particular to Large Eddy Simulation (LES) models of turbulent flows (cf. Hughes et al. 2000; John 2006; Chacón Rebollo and Lewandowski 2014).

The application of VMS method to evolution PDEs dates back to the 1990s, when the results from Hughes (1995) were extended to nonsymmetric linear evolution operators, see (Hughes and Stewart 1995). The papers (Harari 2004; Harari and Hauke 2007) deal with the spurious oscillations generated in the Galerkin method for parabolic problems due to very small time steps. The series of articles (Hauke and Doweidar 2005a, b, 2006) deal with transient Galerkin and SUPG methods, transient subgrid scale (SGS) stabilized methods and transient subgrid scale/gradient subgrid scale (SGS/GSGS), making a Fourier analysis for the one-dimensional advection-diffusion-reaction equation.

A stabilised finite element method for the transient Navier–Stokes equations based on the decomposition of the unknowns into resolvable and subgrid scales is considered in Codina (2002); Codina et al. (2007). Further, (Asensio et al. 2007) compares the Rothe method with the so-called Method of Lines, which consists on first, discretise in space by means of a stabilized finite element method, and then use a finite difference scheme to approximate the solution.

More recently, (Chacón Rebollo and Dia 2015) introduced the use of spectral techniques to model the sub-grid scales for 1D steady advection-diffusion equations. The basic observation is that the eigenpairs of the advection-diffusion operator may be calculated analytically on each grid element. A feasible VMS-spectral discretization is then built by truncation of this spectral expansion to a finite number of modes. An enhanced accuracy with respect to preceding VMS methods is achieved.

In Chacón Rebollo et al. (2020), the spectral VMS method is extended to 2D steady advection-diffusion problems. It is cast for low-order elements as a standard VMS method with specific stabilised coefficients, that are anisotropic in the sense that they depend on two grid Péclet numbers. To reduce the computing time, the stabilised coefficients are pre-computed at the nodes of a grid in an offline step, and then interpolated by a fast procedure in the online computation.

The present paper deals with the building of the spectral VMS numerical approximation to evolution advection-diffusion equations. We construct an abstract spectral VMS discretisation of parabolic equations, that is particularised to 1D advection-diffusion equations. The sub-grid components are exactly calculated in terms of spectral expansions when the driving velocity is approximated by piecewise constant velocities on the grid elements. We prove error estimates that in particular imply that when Lagrange finite element discretisations in space are used, the solution provided by the spectral VMS method coincides with the exact solution of the implicit Euler semi-discretisation at the Lagrange interpolation nodes. We also build a feasible method to solve the evolutive advection-diffusion problem by means of an offline/online strategy that pre-computes the action of the sub-grid scales on the resolved scales. This allows to dramatically reduce the computing times required by the method. We further perform some numerical tests for strongly advection dominated flows. The spectral VMS method is found to satisfy the discrete maximum principle, even for very small time steps. A remarkable increase of accuracy with respect to several stabilised methods is achieved.

The outline of the paper is as follows. In Sect. 2, we describe the abstract spectral VMS discretisation to linear parabolic problems, which is applied to transient advection-diffusion problems in Sect. 3. A feasible method is built in Sect. 4, based upon an offline/online strategy. We present in Sect. 5 our numerical results, and address some conclusions in Sect. 6.

2 Spectral VMS method

In this section, we build the spectral VMS discretisation to abstract linear parabolic equation.

Let $\Omega$ a bounded domain in $\mathbb {R}^d$ and $T>0$ a final time. Let us consider two separable Hilbert spaces on $\Omega$, X and H, so that $X \subset H$ with dense and continuous embedding. We denote $(\cdot ,\cdot )$ the scalar product in X; $X'$ and $H'$ are the dual topological spaces of X and H, respectively, and $\langle \cdot , \cdot \rangle$ is the duality pairing between $X'$ and X. We identify H with its topological dual $H'$ so that $X \subset H \equiv H' \subset X'$. Denote by $\mathcal{L}(X)$ the space of bilinear bounded forms on X and consider $b \in L^1(0,T; \mathcal{L}(X))$ uniformly bounded and X-elliptic with respect to $t\in (0,T)$.

Given the data $f \in L^2(0,T;X')$ and $u_0 \in H$, we consider the following variational parabolic problem:

$$\begin{aligned} \left\{ \begin{array}{l} \text{ Find } u \in L^2((0,T);X) \cap C^0([0,T];H) \text{ such } \text{ that, } \\ \displaystyle \frac{d}{dt}(u(t),v) \,+\, b(t;u(t),v) \,=\, \langle f(t),v\rangle \quad \forall \, v \in X, \quad \text{ in } \mathcal{D}'(0,T), \\ u(0) \,=\, u_0 \quad \text{ in } H. \end{array}\right. \end{aligned}$$

(1)

It is well known that this problem is well posed and, in particular, admits a unique solution (Dautray and Lions 1992). To discretize this problem, we proceed through the so-called Horizontal Method of Lines (Asensio et al. 2007; Bernardi et al. 2004; Harari and Hauke 2007). First, we discretise in time by the Backward Euler scheme and then we apply a steady spectral VMS method to the elliptic equations appearing at each time step.

Consider a uniform partition of the interval [0, T], $\{0=t_0<t_1<\ldots <t_N=T\}$, with time-step size $\Delta t=T/N$. The time discretization of problem (1) by the Backward Euler scheme gives the following family of stationary problems: given the initialization $u^0 \,=\, u_0$,

$$\begin{aligned} \left\{ \begin{array}{l} \text{ Find } u^{n+1}\in X \text{ such } \text{ that, } \\ \left( \displaystyle \frac{u^{n+1}-u^n}{\Delta t}, v\right) + b^{n+1}(u^{n+1},v) \,=\, \Delta t\, \langle f^{n+1},v \rangle \quad \forall \, v\in X, \\ \forall \, n=0,1, \ldots ,N-1, \end{array}\right. \end{aligned}$$

(2)

where $b^{n+1}$ and $f^{n+1}$ are some approximations of $b(t;\cdot ,\cdot )$ and f(t), respectively, at $t=t_{n+1}$.

To discretise in space problem (2), we assume that $\Omega$ is polygonal (when $d=2$) or polyhedric (when $d=3$), and consider a family of conforming and regular triangulations of $\overline{\Omega }$, $\{\mathcal{T}_{h}\}_{h>0}$, formed by simplicial elements, where the parameter h denotes the largest diameter of the elements of the triangulation $\mathcal{T}_{h}$. The VMS method is based on the decomposition,

$$\begin{aligned} X=X_h\oplus \tilde{X}, \end{aligned}$$

where $X_h$ is a continuous finite element sub-space of X constructed on the grid $\mathcal{T}_{h}$, and $\tilde{X}$ is a complementary, infinite-dimensional, sub-space of X. Notice that this is a multi-scale decomposition of the space X, being $X_h$ the large or resolved scale space and $\tilde{X}$ the small or sub-grid scale space. This decomposition defines two projection operators $P_h: X \mapsto X_h$ and $\tilde{P}: X \mapsto \tilde{X}$, by

$$\begin{aligned} P_h (v)= v_h ,\quad \tilde{P}(v)=\tilde{v}, \quad \forall \, v\in X, \end{aligned}$$

(3)

where $v_h$ and $\tilde{v}$ are the unique elements belonging to $X_h$ and $\tilde{X}$, respectively, such that $v= v_h + \tilde{v}$. Hence, one can decompose the solution of problem (2) as

$$\begin{aligned} u^{n+1}=u_{h}^{n+1}+\tilde{u}^{n+1}, \end{aligned}$$

where $u_{h}^{n+1}=P_h (u^{n+1})$ and $\tilde{u}^{n+1}=\tilde{P}(u^{n+1})$ satisfy the coupled problem,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \left( \frac{u^{n+1}_h-u^n_h}{\Delta t},v_h \right) + \left( \frac{\tilde{u}^{n+1}-\tilde{u}^n}{\Delta t}, v_h \right) + b^{n+1}(u^{n+1}_h,v_h) + b^{n+1}(\tilde{u}^{n+1},v_h) = \langle f^{n+1},v_h \rangle &{} (4.1) \\ \displaystyle \left( \frac{u^{n+1}_h-u^n_h}{\Delta t},\tilde{v} \right) + \left( \frac{\tilde{u}^{n+1}-\tilde{u}^n}{\Delta t}, \tilde{v} \right) + b^{n+1}(u^{n+1}_h,\tilde{v}) + b^{n+1}(\tilde{u}^{n+1},\tilde{v}) = \langle f^{n+1},\tilde{v} \rangle &{} (4.2) \\ \forall v_h \in X_h, \, \forall \tilde{v}\in \tilde{X}, \end{array}\right. \end{aligned}$$

for all $\, n=0,1, \ldots ,N-1$. The small scales component $\tilde{u}^{n+1}$ thus satisfies,

$$\begin{aligned} (\tilde{u}^{n+1}, \tilde{v}) + \Delta t \ b^{n+1}(\tilde{u}^{n+1},\tilde{v}) = \langle R^{n+1}(u_h^{n+1}),\tilde{v}\rangle \end{aligned}$$

(4)

where $\langle R^{n+1}(u_h^{n+1}),\tilde{v}\rangle$ is the residual of the large scales component, defined as,

$$\begin{aligned} \begin{array}{r} \langle R^{n+1}(u_{h}^{n+1}), \tilde{v}\rangle := (u^{n}_h+ \tilde{u}^{n},\tilde{v}) + \Delta t \ \langle f^{n+1},\tilde{v}\rangle - (u^{n+1}_h, \tilde{v}) - \Delta t \ b^{n+1}(u^{n+1}_h,\tilde{v}), \,\forall \, \tilde{v}\in \tilde{X}. \end{array} \end{aligned}$$

In condensed notation, this may be written as,

$$\begin{aligned} \tilde{u}^{n+1}=\Pi ^{n+1}(R^{n+1}(u_{h}^{n+1})), \end{aligned}$$

(5)

where

$$\begin{aligned} \begin{array}{cccl} \Pi ^{n+1}: &{} \tilde{X} &{} \rightarrow &{} \tilde{X} \\ &{} g &{} \mapsto &{} \Pi ^{n+1}(g) = \tilde{G} \end{array} \end{aligned}$$

is the static condensation operator on $\tilde{X}$ defined as,

$$\begin{aligned} ( \tilde{G} , \tilde{v}) +\Delta t \ b^{n+1}(\tilde{G},\tilde{v})=\langle g, \tilde{v}\rangle \quad \forall \, \tilde{v}\in \tilde{X}, \text{ for } \text{ any } g \in \tilde{X}'. \end{aligned}$$

Inserting expression (5) in the large scales equation (.1), leads to the condensed VMS formulation of problem (2):

$$\begin{aligned} \left\{ \begin{array}{l} \text{ Find } u_{h}^{n+1}\in X_h \text{ such } \text{ that } \\ (u^{n+1}_h, v_h) + \Delta t \, b^{n+1}(u^{n+1}_h,v_h) + (\Pi ^{n+1}(R^{n+1}(u_{h}^{n+1})), v_h)+\Delta t \,b^{n+1}(\Pi ^{n+1}(R^{n+1}(u_{h}^{n+1})), v_h) \\ \quad \quad =\Delta t\, \langle f^{n+1},v_h \rangle \,+\, (u^{n}_h+ \Pi ^n ( R^n ( u^n_h) ),v_h) \\ \forall \, v_h\in X_h,\,\,\forall \, n=0,1, \ldots ,N-1, \end{array}\right. \end{aligned}$$

(6)

with $u_h^0=P_h(u_0)$. This problem is an augmented Galerkin formulation, where the additional terms represent the effect of the small scales component of the solution $(\tilde{u}^{n+1})$ on the large scales component $(u_{h}^{n+1})$.

To build an approximation of the sub-grid scales, we use a spectral decomposition of the operator associated to the variational formulation on each grid element, at each discrete time. To apply this approximation to problem (6), the small scales space $\tilde{X}$ is approximated by the “bubble” sub-spaces,

$$\begin{aligned} \tilde{X}\simeq \tilde{X}_h = \bigoplus _{K\in \mathcal {T}_h}\tilde{X}_K, \quad \text{ with } \tilde{X}_K=\{\tilde{v}\in \tilde{X}, \text{ such } \text{ that } \text{ supp }(\tilde{v})\subset K\}. \end{aligned}$$

(7)

Hence, we approximate

$$\begin{aligned} \tilde{u}^{n+1}\simeq \tilde{u}^{n+1}_h = \sum _{K\in \mathcal {T}_h}\tilde{u}^{n+1}_K, \quad \text{ with } \tilde{u}^{n+1}_K \in \tilde{X}_K, \quad \forall \, n=0,1, \ldots ,N-1. \end{aligned}$$

(8)

Then, problem (4) is approximated by the following family of decoupled problems,

$$\begin{aligned} \begin{array}{l} (\tilde{u}_K^{n+1},\tilde{v}_K) + \Delta t \ b^{n+1}(\tilde{u}_K^{n+1},\tilde{v}_K)=\langle R^{n+1}(u_h^{n+1}),\tilde{v}_K\rangle , \quad \forall \, \tilde{v}_K\in \tilde{X}_K, \quad \forall \, K\in \mathcal {T}_h. \end{array} \end{aligned}$$

(9)

Let $\mathcal {L}^{n+1}: X \mapsto X'$ be the operator defined by

$$\begin{aligned} \langle \mathcal {L}^{n+1} w,v \rangle =b^{n+1}(w,v), \quad \forall \, w, v \in X, \end{aligned}$$

(10)

and let $\mathcal {L}^{n+1}_K$ be the restriction of this operator to $\tilde{X}_K$. Let us also consider the weighted $L^2$ space,

$$\begin{aligned} L^2_p(K)=\{w:K\rightarrow \mathbb {R} \text{ measurable } \text{ such } \text{ that } p|w|^2\in L^1(K)\}, \end{aligned}$$

where p is some measurable real function defined on K,  which is positive a.e. on K. This is a Hilbert space endowed with the inner product

$$\begin{aligned} (w,v)_p=\int _K p(x) w(x) v(x) dx. \end{aligned}$$

We denote by $\Vert \cdot \Vert _{p}$ the norm on $L^2_p(K)$ induced by this inner product.

Now, we can state the following result, which allows to compute the small scales on each grid element by means a spectral expansion.

Theorem 2.1

Let us assume that there exists a complete sub-set $\{\tilde{z}_j^{n,K}\}_{j\in \mathbb {N}}$ on $\tilde{X}_K$ formed by eigenfunctions of the operator $\mathcal {L}^{n}_K$, which is an orthonormal system in $L^2_{p^{n,K}}(K)$ for some weight function $p^{n,K}\in C^1(\bar{K}).$ Then,

$$\begin{aligned} \begin{array}{l} \tilde{u}_K^{n}=\displaystyle \sum _{j=1}^{\infty }\beta _j^{n,K} \, r^{n,K}_j \, \tilde{z}_j^{n,K}, \quad \forall \, n=1,\ldots ,N, \end{array} \end{aligned}$$

(11)

where $\beta _j^{n,K} = (\Lambda _j^{n,K})^{-1}$, with $\Lambda _j^{n,K}=1+\Delta t \, \lambda _j^{n,K}$ being $\lambda _j^{n,K}$ the eigenvalue of $\mathcal {L}^{n}_K$ associated to $\tilde{z}_j^{n,K}$, and

$$\begin{aligned} r^{n,K}_j = \langle R^{n}(u_h^{n}), p^{n,K}\,\tilde{z}_j^{n,K}\rangle . \end{aligned}$$

This is a rather straightforward application of Theorem 1 in Chacón Rebollo and Dia (2015), that we do not detail for brevity.

Once the eigenpairs $(\tilde{z}_j^{n+1,K},\lambda _j^{n+1,K})$ are known, the previous procedure allows us to directly compute $u_h^{n+1}$ from problem (6), approximating the sub-grid component $\tilde{u}^{n+1}$ by expressions (8) and (11). This gives the spectral VMS method to fully discretize problem (1). Namely,

$$\begin{aligned} \left\{ \begin{array}{l} \text{ Find } u_{h}^{n+1}\in X_h \text{ such } \text{ that } \\ (u^{n+1}_h, v_h) + \Delta t \, b^{n+1}(u^{n+1}_h,v_h) + (\tilde{u}^{n+1}_h, v_h) + \Delta t \, b^{n+1}(\tilde{u}^{n+1}_h ,v_h) \\ \qquad = \Delta t\, \langle f^{n+1},v_h \rangle + (u^{n}_h,v_h) + (\tilde{u}_h^{n}, v_h) \\ \forall \, v_h \in X_h, \quad \forall \, n=0,1,\ldots ,N-1, \end{array}\right. \end{aligned}$$

(12)

where,

$$\begin{aligned} \tilde{u}^{n+1}_h = \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \langle R^{n+1}_h(u_h^{n+1}), p^{n+1,K} \,\tilde{z}_j^{n+1,K}\rangle \, \tilde{z}_j^{n+1,K}, \quad \forall \, n=0, \ldots ,N-1, \end{aligned}$$

(13)

with

$$\begin{aligned} \begin{array}{r} \langle R_h^{n+1}(u_{h}^{n+1}), \tilde{v}\rangle := (u^{n}_h+ \tilde{u}_h^{n},\tilde{v}) + \Delta t \ \langle f^{n+1},\tilde{v}\rangle - (u^{n+1}_h, \tilde{v}) - \Delta t \ b^{n+1}(u^{n+1}_h,\tilde{v}), \,\forall \, \tilde{v}\in \tilde{X}. \end{array} \end{aligned}$$

$u_h^0 \,=\, P_h(u_0)$ and $\tilde{u}_h^0 \in \tilde{X}_h$ some approximation of $\tilde{u}^0$.

3 Application to transient advection-diffusion problems

In this section, we apply the abstract spectral VMS method introduced in the previous section to transient advection-diffusion equations, that we state with homogeneous boundary conditions,

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t u +\textbf{a}\cdot \nabla u-\mu \Delta u = f &{} \text{ in } \Omega \times (0,T), \\ u=0 &{} \text{ on } \partial \Omega \times (0,T), \\ u(0)=u_0 &{} \text{ on } \Omega , \end{array}\right. \end{aligned}$$

(14)

where $\textbf{a} \in L ^\infty (0,T;W^{1,\infty }(\Omega ))^d$ is the advection velocity field, $\mu >0$ is the diffusion coefficient, $f\in L^2((0,T);L^2(\Omega ))$ is the source term and $u_0\in L^2(\Omega )$ is the initial data. Different boundary conditions may be treated as well, as these also fit into the general spectral VMS method introduced in the previous section.

The weak formulation of problem (14) reads,

$$\begin{aligned} \left\{ \begin{array}{l} \text{ Find } u\in L^2((0,T);H^1_0(\Omega ))\cap C^0([0,T];L^2(\Omega )) \text{ such } \text{ that, } \\ \displaystyle \frac{d}{dt}(u(t),v) + (\textbf{a}\cdot \nabla u(t),v) + \mu (\nabla u(t),\nabla v)= \langle f(t),v\rangle \quad \forall \, v\in H_0^1(\Omega ), \\ u(0)=u_0. \end{array}\right. \end{aligned}$$

(15)

Problem (15) admits the abstract formulation (1) with $H=L^2(\Omega )$, $X=H^1_0(\Omega )$ and

$$\begin{aligned} b(w,v)=(\textbf{a}\cdot \nabla w,v)+\mu (\nabla w,\nabla v), \quad \forall \, w,v\in H^1_0(\Omega ). \end{aligned}$$

In practice, we replace the velocity field $\textbf{a}$ by $\textbf{a}_h$, the piecewise constant function defined a. e. on $\overline{\Omega }$ such that $\textbf{a}_h =\textbf{a}_K$ on the interior of each element $K\in \mathcal{T}_{h}$. Then, we apply the spectral VMS method to the approximated problem,

$$\begin{aligned} \left\{ \begin{array}{ll} \text{ Find } U^{n+1}\in H^1_0(\Omega ) \text{ such } \text{ that } \\ \begin{array}{r} \left( \displaystyle \frac{U^{n+1}-U^n}{\Delta t}, v\right) + (\textbf{a}_h^{n+1}\cdot \nabla U^{n+1},v) + \mu (\nabla U^{n+1},\nabla v)= \langle f^{n+1},v\rangle , \;\forall \, v\in H^1_0(\Omega ), \end{array} \\ \forall \, n=0,1, \ldots ,N-1, \end{array}\right. \end{aligned}$$

(16)

with $u^0=u_0$.

In this case, $\mathcal {L}^n w =\textbf{a}_h^n \cdot \nabla w - \mu \Delta w$ is the advection–diffusion operator. Proposition 1 in Chacón Rebollo and Dia (2015) proved that the eigenpairs $(\tilde{w}_j^{n,K}, \lambda _j^{n,K})$ of operator $\mathcal {L}^n_K$ can be obtained from the eigenpairs $(\tilde{W}_j^K, \sigma _j^K)$ of the Laplace operator in $H_0^1(K)$, in the following way:

$$\begin{aligned} \begin{array}{l} \tilde{w}_j^{n,K} = \psi ^{n,K} \, \tilde{W}_j^K, \quad \psi ^{n,K}(x)= \exp \left( \frac{1}{2\mu } \,\textbf{a}_K^n\cdot x \right) \\ \lambda _j^{n,K} = \mu \, \left( \sigma _j^K + \displaystyle \frac{|\textbf{a}_K^n|^2}{4\mu ^2} \right) , \quad \forall \, j\in \mathbb {N}. \end{array} \end{aligned}$$

(17)

Moreover, for the weight function

$$\begin{aligned} \displaystyle p^{n,K}(x)= (\psi ^{n,K})^{-2}= \exp \left( -\frac{1}{\mu }\,\textbf{a}_K\cdot x\right) \end{aligned}$$

(18)

the sequence

$$\begin{aligned} \tilde{z}_j^{n,K} = \displaystyle \frac{\tilde{w}_j^{n,K}}{\Vert \tilde{w}_j^{n,K}\Vert _{p^{n,K}}}, \quad \forall \, j\in \mathbb {N}, \end{aligned}$$

(19)

is a complete and orthonormal system in $L_{p^{n,K}}^2(K)$ (see Theorem 2 in Chacón Rebollo and Dia (2015)). Then, Theorem 2.1 holds and it is possible to apply the method (12) to problem (16).

3.1 One dimensional problems

The eigenpairs of the Laplace operator can be exactly computed for grid elements with simple geometrical forms, as it is the case of parallelepipeds. In the 1D case, the elements $K\in \mathcal{T}_{h}$ are closed intervals, $K=[a,b]$. The eigenpairs $(\tilde{W}_j^K, \sigma _j^K)$ are solutions of the problem

$$\begin{aligned} \left\{ \begin{array}{l} -\partial _{xx} \tilde{W}^K = \sigma ^K \, \tilde{W}^K \,\, \text{ in } K, \\ \tilde{W}^K(a)=\tilde{W}^K(b)=0. \end{array}\right. \end{aligned}$$

Solutions of this problem are

$$\begin{aligned} \tilde{W}_j^K = \sin \big ( \sqrt{\sigma _j^K} \, (x- a) \big ), \quad \sigma _j^K= \left( \frac{j\pi }{h_K} \right) ^2, \,\, \text{ with } h_K=b-a,\,\, \text{ for } \text{ any } j\in \mathbb {N}. \end{aligned}$$

As the function $p^{n,K}$ defined in (18) is unique up to a constant factor, to express the eigenpairs in terms of non-dimensional parameters, we replace $p^{n,K}$ by (we still denote it in the same way),

$$\begin{aligned} p^{n,K}(x)= \exp \left( -2\, P_{n,K}\, \frac{x-a}{h_K}\right) , \end{aligned}$$

(20)

where $P_{n,K}=\displaystyle \frac{|\textbf{a}_K^n|\,h_K}{2\mu }$ is the element Péclet number. Then, from expressions (17) and (19),

$$\begin{aligned} \tilde{z}_j^{n,K}=\sqrt{\frac{2}{h_K}} \exp \left( P_{n,K} \frac{x- a}{h_K}\right) \, \sin \left( j\pi \frac{x- a}{h_K}\right) , \quad \lambda _j^K= \mu \, \left( \frac{j\pi }{h_K} \right) ^2 + \displaystyle \frac{|\textbf{a}_K^n|^2}{4\mu }. \end{aligned}$$

(21)

It follows

$$\begin{aligned} \displaystyle \beta _j^{n,K} = \frac{1}{1+S_K(P_{n,K}^2+\pi ^2j^2)} \quad \text{ for } \text{ any } j\in \mathbb {N}, \end{aligned}$$

(22)

where $S_K=\displaystyle \frac{\Delta t\, \mu }{h_K^2}$ is a non-dimensional parameter that represents the relative strength of the time derivative and diffusion terms in the discrete equations, at element K.

3.2 Error analysis

We afford in this section the error analysis for the solution of the 1D evolutive convection-diffusion problem by the spectral VMS method (12).

Let $\{\alpha _i\}_{i=0}^I \in \bar{\Omega }$ be the Lagrange interpolation nodes of space $X_h$. Let $\omega _i=(\alpha _{i-1},\alpha _i)$, $i=1,\ldots , I$. Setting $\tilde{X}_i=H^1_0(\omega _i)$, it holds,

$$\begin{aligned} H^1_0(\Omega )= X_h \oplus \tilde{X},\quad \text{ with } \, \tilde{X}=\bigoplus _{i=1}^I \tilde{X}_i. \end{aligned}$$

Observe that this decomposition generalises (7) with $\tilde{X}_h=\tilde{X}$. Moreover, when operator in (10) is $\mathcal {L}^n w =\textbf{a}_h^n\cdot \nabla w - \mu \Delta w$, problem (4) can be exactly decoupled into the family of problems (9). In particular, if the projection operator $P_h$ in (3) is the Lagrange interpolate on $X_h$, then $U_h^n =P_h(U^n)$, $\tilde{U}_h^n= U^n- U_h^n \in \tilde{X}$ and consequently, $U_h^n \in X_h$ satisfies method (12).

Notice that thanks to the spectral expansion, the sub-grid scales contribution in method (12), when the advection velocity is element-wise constant, is exactly computed, and then, the discretisation error only is due to the time discretisation and the approximation of the advection velocity $\textbf{a}$, but not to the space discretisation.

Therefore, to analyze the discretisation error we compare the solution of problem (16) to the solution of the implicit Euler time semi-discretisation of problem (15),

$$\begin{aligned} \left\{ \begin{array}{l} \text{ Find } u^{n+1}\in H^1_0(\Omega ) \text{ such } \text{ that } \\ \left( \displaystyle \frac{u^{n+1}-u^n}{\Delta t}, v\right) + (\textbf{a}^{n+1}\partial _x u^{n+1},v) + \mu \,(\partial _x u^{n+1},\partial _x v)= \langle f^{n+1},v\rangle \quad \forall \, v\in H^1_0(\Omega ), \\ \forall \, n=0,1, \ldots ,N-1, \end{array}\right. \end{aligned}$$

(23)

with $u^0=u_0$.

We assume that $\textbf{a}_h$ restricted to each K is extended by continuity to $\partial K$. Given a sequence $b=\{b^n,\,n=1,\ldots , N\}$ of elements of a normed space Y, let us denote,

$$\begin{aligned} \Vert b\Vert _{l^p(Y)}=\left( \Delta t \,\sum _{n=1}^N \Vert b^n\Vert _Y^p \right) ^{1/p},\quad \Vert b\Vert _{l^\infty (Y)}=\max _{n=1,\ldots ,N} \Vert b^n\Vert _Y. \end{aligned}$$

We shall use the following discrete Gronwall’s lemma, whose proof is standard, and so we omit it.

Lemma 3.1

Let $\alpha _n$, $\beta _n$, $\gamma _n$, $n=1,2,\ldots$ be non-negative real numbers such that

$$\begin{aligned} (1-\sigma \,\Delta t) \,\alpha _{n+1} + \beta _{n+1} \le (1+\tau \,\Delta t) \,\alpha _n + \gamma _{n+1} \end{aligned}$$

for some $\sigma \ge 0$, $\tau \ge 0$. Assume that $\sigma \, \Delta t \le 1-\delta$ for some $\delta >0$. Then it holds

$$\begin{aligned} \alpha _n \le e^{\rho \,t_n}\,\alpha _0 + \frac{1}{\delta } \,\sum _{l=1}^n e^{\rho \, (t_n-t_l)}\, \gamma _l, \end{aligned}$$

and

$$\begin{aligned} \sum _{l=1}^n\beta _l \le \left( 1+\frac{\tau }{\sigma } +(\sigma +\tau )\,e^{\rho \, t_{n-1}}\,t_{n-1} \right) \,\alpha _0 +\frac{1}{\delta } \, \left( 1+ (\sigma +\tau )\,e^{\rho \, t_{n-1}}\,t_{n-1} \right) \sum _{l=1}^n\,\gamma _l, \end{aligned}$$

with $\displaystyle \rho =(\sigma +\tau )/\delta$.

Let $e=\{e^n,\,n=0,1,\ldots , N\} \subset H^1_0(\Omega )$ be the sequence of errors $e^n=u^n - U^n \in H^1_0(\Omega )$, where we recall that $U^n$ is the solution of the discrete problem (16), and denote $\delta _t e^{n+1}=\displaystyle \frac{e^{n+1}-e^n}{\Delta t}$. It holds the following result.

Proposition 3.2

Assume that $\textbf{a}\in L^\infty (\Omega \times (0,T))^d$, $f\in L^2(\Omega \times (0,T))$, $\displaystyle \Delta t \le (1-\varepsilon )\, \frac{\mu }{\Vert \textbf{a}\Vert _{L^\infty (\Omega \times (0,T))}^2}$ for some $\varepsilon \in (0,1)$ and $\Vert \textbf{a}_h\Vert _{L^\infty (\Omega \times (0,T))} \le D\, \Vert \textbf{a}\Vert _{L^\infty (\Omega \times (0,T))}$ for some constant $D>0$. Then,

$$\begin{aligned} \Vert \delta _t e\Vert _{l^2(L^2(\Omega ))}+ \mu \Vert e\Vert _{l^\infty (H^1_0(\Omega ))} \le C\, \Vert \textbf{a}_h -\textbf{a}\Vert _{l^2(L^\infty (\Omega ))}, \end{aligned}$$

(24)

for some constant $C>0$ independent of h, $\Delta t$ and $\mu$.

Proof

Let us subtract (16) from (23) with $v=v_h\in X_h$. This yields

$$\begin{aligned} \begin{array}{l} \left( \displaystyle \frac{e^{n+1}-e^n}{\Delta t}, v_h\right) + (\textbf{a}_h^{n+1}\partial _x e^{n+1},v_h) + \mu \,(\partial _x e^{n+1},\partial _x v_h)= ((\textbf{a}_h^{n+1}-\textbf{a}^{n+1})\partial _x u^{n+1},v_h) . \end{array} \end{aligned}$$

Setting $v_h = \delta _t e^{n+1}$, and using the identity $2(b,b-a)=\Vert b\Vert _{L^2(\Omega )}^2-\Vert a\Vert _{L^2(\Omega )}^2+\Vert b-a\Vert _{L^2(\Omega )}^2$ for any $a,\, b \in {L^2(\Omega )}^d$ yields

$$\begin{aligned} \Delta t \,\Vert \delta _t e^{n+1}\Vert ^2_{L^2(\Omega )} +\Delta t \, (\textbf{a}_h^{n+1}\partial _x e^{n+1},\delta _t e^{n+1})+ & {} \frac{\mu }{2}\, \left( \Vert \partial _x e^{n+1}\Vert ^2_{L^2(\Omega )}- \Vert \partial _x e^n\Vert ^2_{L^2(\Omega )} \right) \nonumber \\\le & {} \Delta t \,((\textbf{a}_h^{n+1}-\textbf{a}^{n+1})\partial _x u^{n+1},\delta _t e^{n+1}). \end{aligned}$$

(25)

It holds

$$\begin{aligned} |(\textbf{a}_h^{n+1}\,\partial _x e^{n+1},\delta _t e^{n+1})|\le & {} \Vert \textbf{a}_h^{n+1}\Vert _{L^\infty (\Omega )}\,\Vert \partial _x e^{n+1}\Vert _{L^2(\Omega )}\, \Vert \delta _t e^{n+1}\Vert _{L^2(\Omega )}\nonumber \\\le & {} \frac{1}{2} \Vert \delta _t e^{n+1}\Vert ^2_{L^2(\Omega )}+\frac{ \Vert \textbf{a}\Vert _{L^\infty (\Omega \times (0,T))}^2}{2}\,\Vert \partial _x e^{n+1}\Vert ^2_{L^2(\Omega )}. \end{aligned}$$

(26)

As $\textbf{a}\in L^\infty (\Omega \times (0,T))^d$, $f\in L^2(\Omega \times (0,T))$, then the $u^n$ are uniformly bounded in $L^\infty (0,T;H^1_0(\Omega ))$, due to the standard estimates for the implicit Euler method in strong norms. Then, for some constant $C>0$,

$$\begin{aligned} ((\textbf{a}_h^{n+1}-\textbf{a}^{n+1})\partial _x u^{n+1},\delta _t e^{n+1})\le & {} \Vert \textbf{a}_h^{n+1}-\textbf{a}^{n+1}\Vert _{L^\infty (\Omega )}\,\Vert \partial _x u^{n+1}\Vert _{L^2(\Omega )}\, \Vert \delta _t e^{n+1}\Vert _{L^2(\Omega )}\nonumber \\\le & {} C \, \Vert \textbf{a}_h^{n+1}-\textbf{a}^{n+1}\Vert _{L^\infty (\Omega )}^2 + \frac{1}{4}\, \Vert \delta _t e^{n+1}\Vert ^2_{L^2(\Omega )}. \end{aligned}$$

(27)

Hence, combining (26) and (27) with (25),

$$\begin{aligned} \frac{\Delta t}{4} \,\Vert \delta _t e^{n+1}\Vert ^2_{L^2(\Omega )} +\frac{\mu }{2}\, ( 1- \sigma \,\Delta t )\, \Vert \partial _x e^{n+1}\Vert ^2_{L^2(\Omega )}\le \frac{\mu }{2}\, \Vert \partial _x e^n\Vert ^2_{L^2(\Omega )} + C \, \Delta t\,\Vert \textbf{a}_h^{n+1}-\textbf{a}^{n+1}\Vert _{L^\infty (\Omega )}^2, \end{aligned}$$

with $\sigma =\displaystyle \frac{\Vert \textbf{a}\Vert _{l^\infty (L^\infty (\Omega ))}^2}{\mu }$. Applying the discrete Gronwall’s lemma 3.1, estimate (24) follows. $\square$

Corollary 3.3

Under the hypotheses of Proposition 3.2, it holds

$$\begin{aligned} \mu \,\Vert e^n\Vert _{l^\infty (L^\infty (\Omega ))}\le C\, \Vert \textbf{a}_h -\textbf{a}\Vert _{l^2(L^\infty (\Omega ))} \end{aligned}$$

(28)

for some constant $C>0$. Moreover, if $\textbf{a}$ is constant, then the solution $U_h^n$ of the spectral VMS method (12) coincides with the solution $u^n$ of the implicit Euler time semi-discretisation (23) at the Lagrange interpolation nodes of space $X_h$.

Proof

In one space dimension $H^1(\Omega )$ is continuously injected in $L^\infty (\Omega )$. Then estimate (28) follows from estimate (24).

If $\textbf{a}$ is constant obviously $U^n = u^n$ for all $n=0,1,\ldots , N$. As $U^n_h(\alpha _i) = U^n(\alpha _i)$ at the Lagrange interpolation nodes $\alpha _i$, $i=1,\ldots ,I$, then $U_h^n$ coincides with $u^n$ at these nodes. $\square$

4 Feasible method: offline/online strategy

Building the spectral VMS method using the formulation (12) requires quite large computing times, due to the summation of the spectral expansions that yield the coefficients of the matrices that appear in the algebraic expression of the method.

In order to reduce this time, we shall neglect the dependency of method (12) w.r.t. $\tilde{u}^{n-1}$.

Then, our current discretization of problem (1) is the following,

$$\begin{aligned} \left\{ \begin{array}{l} \text{ Find } u_{h}^{n+1}\in X_h \text{ such } \text{ that } \\ (u^{n+1}_h, v_h) + \Delta t \, b^{n+1}(u^{n+1}_h,v_h) + (\tilde{u}^{n+1}_h, v_h) + \Delta t \, b^{n+1}(\tilde{u}^{n+1}_h ,v_h) \\ \qquad = \Delta t\, \langle f^{n+1},v_h \rangle + (u^{n}_h,v_h) + (\tilde{u}_h^{n}, v_h) \\ \forall \, v_h \in X_h, \quad \forall \, n=0,1,\ldots ,N-1, \end{array}\right. \end{aligned}$$

(29)

where $\tilde{u}^{n+1}_h$ is given by (13), but $\tilde{u}^{n}_h$ is defined from an approximated residual:

$$\begin{aligned} \tilde{u}^{n}_h = \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n,K} \, \langle \hat{R}^n_h(u_h^{n}), p^{n,K} \,\tilde{z}_j^{n,K}\rangle \, \tilde{z}_j^{n,K} \end{aligned}$$

(30)

with

$$\begin{aligned} \langle \hat{R}^n_h({u}^n_h), \tilde{v} \rangle = ({u}^{n-1}_h,\tilde{v})+ \Delta t \, \langle f^n,\tilde{v}\rangle - ({u}^n_h,\tilde{v})-\Delta t\, b^n({u}^n_h,\tilde{v}),\quad \forall \tilde{v} \in \tilde{X}. \end{aligned}$$

Neglecting the dependency of method (12) w.r.t. $\tilde{u}^{n-1}$ allows to eliminate the recurrence in time of the sub-grid scales. Thanks to this fact, problem (29) is equivalent to a linear system (that we describe in detail in Appendix), whose coefficients only depend on non-dimensional parameters.

4.1 Application to 1D transient advection-diffusion problems

In this case the coefficients of the linear system equivalent to problem (29) only depend on two non-dimensional parameters, as we confirm below.

As we can see in Appendix, if $\left\{ \varphi _m\right\} _{m=1}^{L+1}$ is a basis of the space $X_h$ associated to a partition $\{ x_1< x_2< \cdots < x_{L+1}\}$ of $\Omega$, the solution $u_{h}^{n+1}$ of (29) can be written as

$$\begin{aligned} u_h^{n+1} = \displaystyle \sum _{m=1}^{L+1} u_m^{n+1}\varphi _m. \end{aligned}$$

Then, the unknown vector $\textbf{u}^{n+1}=(u_1^{n+1},u_2^{n+1},\ldots ,u_L^{n+1},u_{L+1}^{n+1})^t\in \mathbb {R}^{L+1}$ is the solution of the linear system

$$\begin{aligned} \textbf{A}^{n+1} \, \textbf{u}^{n+1} = \textbf{b}^{n+1}, \end{aligned}$$

(31)

where the matrix and second term are defined in (47) from matrices $A_i^{n+1}$ and $B_i^{n+1}$ given by (39)–(42) and (43)–(46).

We focus, for instance, on the coefficients of matrix $A^n_1$:

$$\begin{aligned} (A^n_1)_{lm}= \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n,K} (\varphi _m, p^{n,K} \tilde{z}_j^{n,K})(\tilde{z}_j^{n,K}, \varphi _l ). \end{aligned}$$

Let $K=[x_{l-1},x_l]\in \mathcal{T}_{h}$. From expressions (20) and (21), $p^{n,K}$ and $\tilde{z}_j^{n,K}$ depend on the element non-dimensional parameters $P_{n,K}$ and $S_K$ and the non-dimensional variable $\displaystyle \hat{x}=\frac{x-x_{l-1}}{h_K}$. The change of variable $\hat{x} \in [0,1] \mapsto x\in K$ from the reference element [0, 1] to element K in the integral expressions

$$\begin{aligned} (\varphi _m, p^{n,K} \tilde{z}_j^{n,K})=\int _K \varphi _m\, p^{n,K}(x) \tilde{z}_j^{n,K}(x) \, dx,\quad (\tilde{z}_j^{n,K}, \varphi _l ) = \int _K \tilde{z}_j^{n,K}(x)\, \varphi _l(x)\, dx \end{aligned}$$

readily proves that these expressions (up to a factor depending on h) can be written as functions of $S_K$ and $P_K$. Further, by (22) the coefficients $\beta _j^{n,K}$ also depend on $P_{n,K}$ and $S_K$. Then, for each $K\in \mathcal{T}_{h}$ the spectral expansion that determines the element contribution to coefficient $(A^n_1)_{lm}$, that is,

$$\begin{aligned} \sum _{j=1}^{\infty } \beta _j^{n,K} (\varphi _m, p^{n,K} \tilde{z}_j^{n,K})(\tilde{z}_j^{n,K}, \varphi _l ), \end{aligned}$$

is a function of $P_{n,K}$ and $S_K$, up to a factor depending on h. This also holds for the coefficients of all other matrices that defines the linear system (31), $A^n_i$ and $B^n_i$, as these are built from the basic values $(\varphi _m, p^{n,K} \tilde{z}_j^{n,K})$, $(\tilde{z}_j^{n,K}, \varphi _l )$, $b^n(\varphi _m, p^{n,K} \tilde{z}_j^{n,K})$ and $b^n(\tilde{z}_j^{n,K}, \varphi _l )$. We take advantage of this fact to compute these matrices in a fast way, by means of an offline/online computation strategy.

4.2 Offline stage

In the offline stage we compute the element contribution to the coefficients of all matrices appearing in system (31) as a function of the two parameters P and S, that take values at the nodes of a uniform grid, between minimum and maximum feasible values of these parameters. That is,

$$\begin{aligned} \left\{ (P_i,S_j)=( \Delta \, i , \Delta \,j ), \quad \forall \, i,j = 1,2,\ldots M \right\} , \quad \text{ with } \Delta >0. \end{aligned}$$

(32)

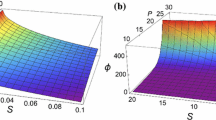
In order to set these values, we consider the piecewise affine finite element functions associated to a uniform partition of $\Omega$ with step h. In practical applications the advection dominates and P takes values larger than 1. Also, taking usual values of diffusion coefficient and $h \simeq \Delta t$ (that is, $C_1 \leqslant \Delta t/h \leqslant C_2$ for some constants $C_1, C_2>0$), S takes low positive values. Moreover, when we compute the spectral series that determines the coefficients of the system matrices as functions of P and S, we observe that these values are nearly constant as P and S approaches 20. For instance, we can see in Figs. 1, 2 and 3 how the spectral series for the diagonal coefficient of $A_3$ matrix tend to a constant value as P or S increase to 20. The behavior of coefficients in the remaining matrices is similar. Therefore, in numerical tests, we will consider a step $\Delta =0.02$ and $M=1000$ in (32).

Fig. 1

Values of the spectral series to compute the diagonal coefficient of matrix $A_3$ for each pair (P, S)

Fig. 2

Values of the spectral series to compute the diagonal coefficient of matrix $A_3$ for $(P,S) \in (0,20)\times (0,1)$

Fig. 3

Values of the spectral series to compute the diagonal coefficient of matrix $A_3$ for $(P,S) \in (0,1)\times (0,1)$

To do the computations in this stage, in order to avoid computational roundoff problems due to large velocities, we express the eigenfunctions of the advection-diffusion operator given in (19) in terms of the midpoint of the grid elements $\displaystyle x_{\frac{l,l+1}{2}} = \displaystyle \frac{x_l+x_{l+1}}{2}$. That is, we consider

$$\begin{aligned} \tilde{z}_j^K=\sqrt{\frac{2}{h_K}} \exp \left( \frac{|a_K|}{2\mu }(x- x_{\frac{l,l+1}{2}})\right) \sin \left( j\pi \frac{x-{x_{l}}}{h_K}\right) , \quad \text{ for } \text{ any } j\in \mathbb {N}. \end{aligned}$$

We further truncate the spectral series neglecting all the terms following to the first term that reaches an absolute value less than a prescribed threshold $\varepsilon$. Actually, we have taken $\varepsilon =10^{-10}$. In Fig. 4 we represent the number of these summands needed to reach a first term with absolute value smaller than this $\varepsilon$ for the series defining the diagonal coefficient of $A_3$ matrix. As we can see, more terms are needed as P increases and as S decreases to 0.

Fig. 4

Number of summands needed to reach a first term with absolute value lower than $\varepsilon =10^{-10}$ for the series defining the diagonal coefficient of matrix $A_3$, in terms of (P, S)

4.3 Online stage

In the online stage, for each grid element K we compute the contribution of this element to the coefficients of all matrices appearing in system (31). Then, we sum up over grid elements, to calculate these coefficients.

For that, we determine $P_K$ and $S_K$ and find the indices $i,\, j \in {1,\ldots , M}$ such that $(P_K,\, S_K)$ belongs to $[P_i , P_{i+1}] \times [S_j , S_{j+1}]$. In other case, if $P_k<\Delta$ we set $i=1$ and if $P_K >\Delta M$ we set $i=M-1$, and similarly for j in terms of $S_K$.

As we see above, each element contribution is a function of $P_K$ and $S_K$ that we denote $C(P_K,S_K)$ in a generic way. For instance, for matrix $A^n_1$,

$$\begin{aligned} C(P_K,S_K)= \sum _{j=1}^{\infty } \beta _j^{n,K} (\varphi _m, p^{n,K} \tilde{z}_j^{n,K})(\tilde{z}_j^{n,K}, \varphi _l ). \end{aligned}$$

Then, we compute $C(P_k,S_K)$ by the following second-order interpolation formula:

$$\begin{aligned} C(P_K,S_K) \simeq \sum _{k=1}^4 \frac{Q_k}{Q} \, C(\alpha _k), \end{aligned}$$

where the $\alpha _k$ are the four corners of the cell $[P_i , P_{i+1}] \times [S_j, S_{j+1}]$, $Q=\Delta ^2$ is its area and the $Q_k$ are the areas of the four rectangles in which the cell is split by $(P_k,S_K)$ (see Fig. 5).

Fig. 5

Splitting of interpolation cell for online computation of matrices coefficients

5 Numerical tests

In this section, we present the numerical results obtained with the spectral method to solve 1D advection-diffusion problems. Our purpose, on the one hand, is to confirm the theoretical results stated in Corollary 3.3 for the spectral VMS method and, on the other hand, test the accuracy of the spectral VMS and feasible spectral VMS methods for problems with strong advection-dominance, in particular by comparison with several stabilised methods.

5.1 Test 1: Accuracy of spectral VMS method for constant advection velocity

To test the property stated in Corollary 3.3, we consider the following advection-diffusion problem:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t u +a \, \partial _x u-\mu \, \partial ^2_{xx} u = 0 &{} \text{ in } (0,1)\times (0,T), \\ u(0,t)=\exp ((\mu -a)t),\quad u(1,t)=\exp (1+(\mu -a)t) &{} \text{ on } (0,T), \\ u(x,0)=\exp (x) &{} \text{ on } (0,1), \end{array}\right. \end{aligned}$$

(33)

whose exact solution is given by $\exp (x+(\mu -a)t).$

We set $T=0.1$, $a=1$ and $\mu =20$. We apply the spectral VMS method (12) to solve this problem with time step $\Delta t=0.01$ and piecewise affine finite element space on a uniform partition of interval (0, 1) with steps $h=0.05/(2^i)$ for $i=2,3,\ldots ,7$. We have truncated the spectral expansions that yield the small scales $\tilde{u}_h^n$ to 10 eigenfunctions. The errors in $l^\infty (L^2)$ and $l^2(H^1)$ norms computed at grid nodes are represented in Fig. 6. We observe that, indeed, the errors quite closely do not depend on the space step h.

Moreover, we have computed the convergence orders in time, obtaining very closely order 1 in $l^2(H^1)$ norm and order 2 in $l^\infty (L^2)$ norm, as could be expected.

Fig. 6

Test 1. $l^\infty (L^2)$ and $l^2(H^1)$ errors for the spectral VMS solution of problem (33)

In the following numerical experiments we consider the 1D problem (14) setting $\Omega =(0,1)$, with constant velocity field a, source term $f=0$ and the hat-shaped initial condition

$$\begin{aligned} u_0 = \left\{ \begin{array}{ll} 1 &{} \text {if } |x-0.45|\le 0.25 , \\ 0 &{} \text {otherwise.} \end{array} \right. \end{aligned}$$

(34)

We also set $X_h$ to be the piecewise affine finite element space constructed on a uniform partition of interval (0, 1) with step size h.

5.2 Test 2: Accuracy of spectral VMS method

Very large Péclet numbers

In this test we examine the accuracy of spectral VMS method for very high Péclet numbers. To do that, we set $a=1000$ and $\mu = 1$, and solve this problem by the spectral VMS method (12), truncating to 150 spectral basis functions the series (13) that yield the sub-grid components. The solution interacts with the boundary condition at $x=1$ in times of order 1/a (considering that the length of $\Omega$ is 1), that is, $10^{-3}$. We then set a time-step $\Delta t = 10^{-3}$. Moreover, we set $h=0.02$ that corresponds to $P=10$ and $S=2.5$. We present the results obtained in Fig. 7, where we represent the Galerkin solution (in red) on the left panels and the spectral solution (in cyan) on the right panels, both with the exact solution (in blue): in (a) the first 4 time-steps, in (b) time-steps from 5 to 7 and in c times-steps 8 and 9. By Corollary 3.3 the discrete solution coincides at the grid nodes with the exact solution of the implicit Euler semi-discretisation, the expected errors at grid nodes are of order $\Delta t=10^{-3}$. We can see that the spectral solution indeed is very close to the exact solution at grid nodes.

Fig. 7

Solution of problem (14) for $a=1000, \mu = 1, f=0$ and $u_0$ given by (34) with $\Delta t=10^{-3}$ and $h=0.02$ ($P = 10$, $S = 2.5$). The spectral VMS solution is compared to the exact solution and the Galerkin solution. The results for time-steps numbers 1 to 4, 5 to 7 and 8 to 9 are respectively represented in figures (a), (b) and (c)

As the discrete solution coincides at the grid nodes with the exact solution of the implicit Euler semi-discretisation and $u^0$ is exact, then $u^1_h$ should coincide with the exact solution at grid nodes. This can already be observed in Fig. 7 (a). We also test this result with different discretisation parameters. We actually set $\Delta t = 10^{-5}$ and $h=0.02$ that corresponds to $P=10$ and $S=0.025$. The solution in the first time-step is represented in Fig. 8 (a) and a zoom around $x=0.7$ in depicted in (b). Indeed the discrete solutions coincides with the exact one at grid nodes.

Fig. 8

Solution of problem (14) for $a=1000, \mu = 1, f=0$ and $u_0$ given by (34) with $\Delta t=10^{-5}$ and $h=0.02$ ($P=10$, $S=0.025$). The spectral VMS solution is compared to the exact solution and the Galerkin solution at first time step. Figures (a) and (b) respectively show these solutions in the whole domain and a zoom around $x=0.7$

Very small time steps

We test here the arising of spurious oscillations due to extra small time-steps. These spurious oscillations occur in the solutions provided by the Galerkin discretisation when $CFL <CFL_{bound} = P/(3(1-P))$ (see Harari and Hauke 2007). For that, we consider the same problem as in this section but with $a=20$, $h=0.01$ and the time-step $\Delta t$ is chosen such that $CFL/CFL_{bound}= 1/2$. We obtain the results shown in Fig. 9, where we have represented the first five time-steps. As one can see the spectral solution does not present any oscillation.

Fig. 9

Solution of problem (14) for $a=20, \mu = 1, f=0$ and $u_0$ given by (34) with $h=0.01$ and $\Delta t$ such that $CFL/CFL_{bound}= 1/2$ ($P=0.1$, $S=0.0926$). Red lines represent Galerkin solution and cyan lines represent spectral VMS solution in each step-time

5.3 Test 3: Accuracy of the feasible spectral VMS method. Comparison with other stabilised methods

We next proceed to compare the results obtained with the feasible spectral VMS method (29) with those obtained by several stabilised methods.

Stabilised methods add specific stabilising terms to the Galerkin discretisation, generating the following matrix scheme,

$$\begin{aligned} (M+\Delta t \, R^n + \Delta t \, a^2 \, \tau \, M_{s}) \, \textbf{u}^{n+1} = M \, \textbf{u}^n, \end{aligned}$$

where M and $R^n$ are, respectively, mass and stiffness matrices, while $M_{s}$ is a tridiagonal matrix defined by $({M_s})_{i,i} = \frac{2}{h}, \quad ({M_s})_{i+1,i}=({M_s})_{i,i+1} = -\frac{1}{h}$. Each stabilised method is determined by the stabilised coefficient $\tau$. In particular, we consider:

• 1. The optimal stabilisation coefficient for 1D steady advection-diffusion equation (Christie et al. 1976; John and Novo 2011),

  $$\begin{aligned} \tau _{1D} = \displaystyle \frac{\mu }{|a|^2} (P\coth (P)-1). \end{aligned}$$

  (35)

• 2. The stabilisation coefficient based on orthogonal sub-scales proposed by Codina in Codina (2000),

  $$\begin{aligned} \tau _{C}= \displaystyle \left( \left( 4 \frac{\mu }{h^2} \right) ^2 + \left( 2 \frac{|a|}{h} \right) ^2 \right) ^{-1/2}. \end{aligned}$$

  (36)

• 3. The stabilisation coefficient based on $L_2$ proposed by Hauke et al. (2008),

  $$\begin{aligned} \tau _H = \displaystyle \min \left\{ \frac{h}{\sqrt{3}|a|} , \frac{h^2}{24.24\mu } , \Delta t \right\} . \end{aligned}$$

  (37)

• 4. The stabilisation coefficient separating the diffusion-dominated from the convection-dominated regimes proposed by Franca in Chacón Rebollo et al. (2015),

  $$\begin{aligned} \tau _{F}= \displaystyle \frac{h}{|a|}\, \min \{P,\tilde{P}\}, \end{aligned}$$

  (38)

  where $\tilde{P}>0$ is a threshold separating the diffusion dominated ($P \le \tilde{P}$) to the advection dominated ($Pe > \tilde{P}$) regimes.

In Figs. 10, 11 and 12, we show the solutions of each method for different values of P and S, always for advection-dominated regime $P>1$. We also display the errors in $l^{\infty }(L^2)$ and $l^2(H^1)$ norms for the solutions of these problems in Tables 1, 2 and 3. As it can be observed in the three tables, spectral method reduces the error between 10 and 100 times compared to the stabilised methods, without presenting oscillations.

Fig. 10

Comparison of different stabilised methods to solve problem (14) when $P=3$, $S=25$ with $\Delta t=10^{-2}$ and $h=0.02$. Solutions in the three first time-steps

Table 1 $l^{\infty }(L^2)$ and $l^2(H^1)$ errors for the solutions represented in Fig. 10

Fig. 11

Comparison of different stabilised methods to solve problem (14) when $P=1$ and $S=5$ with $\Delta t=10^{-3}$ and $h=10^{-2}$. Solutions in the three first time-steps. Right: zoom around $x=0.7$

Table 2 $l^{\infty }(L^2)$ and $l^2(H^1)$ errors for the solutions represented in Fig. 11

Fig. 12

Comparison of different stabilised methods to solve problem (14) when $P=3.5$ and $S=100$ with $\Delta t = 10^{-2}$ and $h=10^{-2}$. Solutions in the three first time-steps. Right: zoom around $x=0.99$

Table 3 $l^{\infty }(L^2)$ and $l^2(H^1)$ errors for the solutions represented in Fig. 12

Next, we consider the same tests performed in Sect. 5.2, but applying the feasible spectral VMS method.

Firstly, we check the behaviour of the feasible spectral VMS method (29) for very large Péclet numbers. In Fig. 13 we represent the solution of same problem as in Fig. 7 obtained with this method. We show solutions in time-steps 1 to 4 in (a), times-steps 5 to 7 in (b) and time-steps 8 and 9 in (c). As we can observe, the spectral method is the closest to the reference solution without presenting any spurious oscillations.

Fig. 13

Solution of problem (14) for $a=1000, \mu = 1, f=0$ and $u_0$ given by (34) with $\Delta t=10^{-3}$ and $h=0.02$ ($P = 10$, $S = 2.5$). The feasible spectral VMS is compared with different stabilised methods. The results for time-steps numbers 1 to 4, 5 to 7 and 8 to 9 are respectively represented in figures (a), (b) and (c)

Secondly, Fig. 14 is the analogous to Fig. 8, but comparing the feasible spectral VMS with different stabilised methods. Although Hauke’s solution is closer to the exact solution than the spectral method, we can see on the right figure that this approximation does not satisfy the Maximun Principle.

Fig. 14

First time-step solution of problem (14) for $a=1000, \mu = 1, f=0$ and $u_0$ given by (34) with $\Delta t=10^{-5}$ and $h=0.02$ ($P=10$, $S=0.025$). The feasible spectral VMS is compared with different stabilised methods in the whole domain $\Omega =(0,1)$ in (a) and in a zoom around $x=0.7$ in (b)

Finally, we illustrate the fact that the feasible spectral VMS method is the only method among those studied that does not have oscillations for small time steps, when $CFL <CFL_{bound}$. In Fig. 15, we can see the first five time-steps solutions obtained with each method using a time-step that verifies $CFL/CFL_{bound} = 1/2$.

Fig. 15

Solution of problem (14) for $a=20, \mu = 1, f=0$ and $u_0$ given by (34) with $h=0.01$ and $\Delta t$ such that $CFL/CFL_{bound}= 1/2$ ($P=0.1$, $S=0.0926$). The feasible spectral VMS is compared with different stabilised methods

In the following subsection we compare the computing costs of the Spectral method with and without offline/online strategy with the other considered methods.

5.4 Computing cost

We are going compare the computing time required by the methods introduced in expressions (35)–(38) with the spectral method with and without offline/online strategy. We have implemented all considered methods with the Matlab application R2022b (9.13.0) in a Mac Mini Model M1 2020 computer.

First, let us note that the offline stage described in Subsection 4.1, which is performed once for all, has taken 3.15 hours. On the other hand, Table 4 shows the computing times (in seconds) required for each method to solve problem (14) when $P=3$, $S=25$ ($a=300, \mu =1, h=0.02,\Delta t=0.01$), $u_0$ given in (34) and $T=1$. In the case of the offline/online strategy, the time corresponds to the online stage.

Table 4 Computing time required by each method to solve problem (14) when $P=3$, $S=25$ ($a=300, \mu =1, h=0.02,\Delta t=0.01$) and $u_0$ given in (34) and $T=1$ in increasing times order

As we can see, Spectral method without offline/online strategy requires approximately two to three times the time required by the other considered methods. However, this disadvantage is solved when we use the offline-online strategy.

6 Conclusions

In this paper we have extended to parabolic problems the spectral VMS method developed in Chacón Rebollo and Dia (2015) for elliptic problems. We have constructed a feasible method to solve the evolutive advection-diffusion problem by means of an offline/online strategy that pre-computes the effect of the sub-grid scales on the resolved scales.

We have proved that when Lagrange finite element discretisations in space are used, the solution obtained by the fully spectral VMS method (12) coincides with the exact solution of the implicit Euler semi-discretisation of the advection-diffusion problem at the Lagrange interpolation nodes.

We have performed some numerical tests that have confirmed this property for very large Péclet numbers and very small time steps, by the fully spectral VMS method. Also some additional tests show an improved accuracy with respect to several stabilised methods for the feasible spectral VMS method (29), with moderate gains of computing times.

The methodology introduced here may be extended to multi-dimensional advection-diffusion equations, by parameterising the sub-grid scales in an offline step. This research is at present in progress.

Appendix: Matrix formulation of the scheme

Problem (29) is equivalent to a linear system with a particular structure that we describe next. If $\left\{ \varphi _m\right\} _{m=1}^{L+1}$ is a basis of the space $X_h$, the solution $u_{h}^{n+1}$ is obtained as

$$\begin{aligned} u_{h}^{n+1} = \displaystyle \sum _{m=1}^{L+1} u_m^{n+1}\varphi _m, \end{aligned}$$

where $\textbf{u}^{n+1}=(u_1^{n+1},\ldots ,u_{L+1}^{n+1})^t\in \mathbb {R}^{L+1}$ is the unknown vector. Taking $v_h=\varphi _l$, with $l=1\ldots L$, each term in (29) can be written in the following way:

$$\begin{aligned} (u^{n+1}_h, \varphi _l)= & {} \displaystyle \sum _{m=1}^L (\varphi _m,\varphi _l) \, u_m^{n+1} = \Big ( M \, \textbf{u}^{n+1} \Big )_l \\ b^{n+1}(u^{n+1}_h,\varphi _l)= & {} \displaystyle \sum _{m=1}^L b^{n+1}(\varphi _m,\varphi _l) \, u_m^{n+1} = \Big ( R^{n+1} \, \textbf{u}^{n+1} \Big )_l \\ (f^{n+1}, \varphi _l) = \Big ( \textbf{F}^{n+1} \Big )_l \end{aligned}$$

where

$(M)_{lm} =(\varphi _m,\varphi _l),$

$(R^{n+1})_{lm} =b^{n+1}(\varphi _m,\varphi _l),$

$$\begin{aligned} \begin{array}{l} (\tilde{u}^{n+1}_h, \varphi _l) = \displaystyle \sum _{m=1}^L \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (\varphi _m,p^{n+1,K} \tilde{z}_j^{n+1,K}) \, (\tilde{z}_j^{n+1,K},\varphi _l) \, u_m^{n} \\ \qquad \qquad \quad \qquad +\displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (\tilde{u}_h^n,p^{n+1,K} \tilde{z}_j^{n+1,K}) \, (\tilde{z}_j^{n+1,K},\varphi _l) \\ \qquad \qquad \quad \qquad + \, \Delta t \, \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (f^{n+1},p^{n+1,K} \tilde{z}_j^{n+1,K}) \, (\tilde{z}_j^{n+1,K},\varphi _l) \\ \qquad \qquad \quad \qquad -\displaystyle \sum _{m=1}^L \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (\varphi _m,p^{n+1,K} \tilde{z}_j^{n+1,K}) \, (\tilde{z}_j^{n+1,K},\varphi _l) \, u_m^{n+1} \\ \qquad \qquad \quad \qquad - \, \Delta t \, \displaystyle \sum _{m=1}^L \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, b^{n+1} (\varphi _m,p^{n+1,K} \tilde{z}_j^{n+1,K}) \, (\tilde{z}_j^{n+1,K},\varphi _l) \, u_m^{n+1} \\ \qquad \qquad \qquad =\Big ( A^{n+1}_1 \, \textbf{u}^{n} + \textbf{G}^{n+1}_1 + \Delta t \, \textbf{F}^{n+1}_1 -A^{n+1}_1 \, \textbf{u}^{n+1} - \Delta t \, A^{n+1}_2 \, \textbf{u}^{n+1} \Big )_l, \end{array} \end{aligned}$$

with

$$\begin{aligned}{} & {} (A^{n+1}_1)_{lm} = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (\varphi _m, p^{n+1,K} \tilde{z}_j^{n+1,K}) \,(\tilde{z}_j^{n+1,K}, \varphi _l ), \end{aligned}$$

(39)

$$\begin{aligned}{} & {} \quad (A^{n+1}_2)_{lm} = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, b^{n+1}(\varphi _m, p^{n+1,K} \tilde{z}_j^{n+1,K}) \, (\tilde{z}_j^{n+1,K}, \varphi _l ),\nonumber \\{} & {} \quad (\textbf{F}^{n+1}_1)_l = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \langle f^{n+1},p^{n+1,K} \tilde{z}_j^{n+1,K} \rangle \, (\tilde{z}_j^{n+1,K},\varphi _l), \nonumber \\{} & {} \quad (\textbf{G}^{n+1}_1)_l = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (\tilde{u}_h^n,p^{n+1,K} \tilde{z}_j^{n+1,K}) \, (\tilde{z}_j^{n+1,K},\varphi _l), \end{aligned}$$

(40)

and

$$\begin{aligned} b^{n+1}(\tilde{u}^{n+1}_h, v_h)= & {} \displaystyle \sum _{m=1}^L \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (\varphi _m,p^{n+1,K} \tilde{z}_j^{n+1,K}) \, b^{n+1}(\tilde{z}_j^{n+1,K},\varphi _l) \, u_m^{n} \\{} & {} + \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (\tilde{u}_h^n,p^{n+1,K} \tilde{z}_j^{n+1,K}) \, b^{n+1}(\tilde{z}_j^{n+1,K},\varphi _l) \\{} & {} + \, \Delta t \, \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (f^{n+1},p^{n+1,K} \tilde{z}_j^{n+1,K}) \, b^{n+1}(\tilde{z}_j^{n+1,K},\varphi _l) \\{} & {} -\displaystyle \sum _{m=1}^L \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (\varphi _m,p^{n+1,K} \tilde{z}_j^{n+1,K}) \, b^{n+1}(\tilde{z}_j^{n+1,K},\varphi _l) \, u_m^{n+1} \\{} & {} - \, \Delta t \, \displaystyle \sum _{m=1}^L \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, b^{n+1} (\varphi _m,p^{n+1,K} \tilde{z}_j^{n+1,K}) \, b^{n+1}(\tilde{z}_j^{n+1,K},\varphi _l) \, u_m^{n+1} \\= & {} \Big (A^{n+1}_3 \, \textbf{u}^{n} + \textbf{G}^{n+1}_2+ \Delta t \, \textbf{F}^{n+1}_2 - A^{n+1}_3 \, \textbf{u}^{n+1} - \Delta t \,A^{n+1}_4 \, \textbf{u}^{n+1} \Big )_l, \end{aligned}$$

where

$$\begin{aligned}{} & {} (A^{n+1}_3)_{lm} = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (\varphi _m, p^{n+1,K} \tilde{z}_j^{n+1,K}) \, b^{n+1}(\tilde{z}_j^{n+1,K}, \varphi _l ), \end{aligned}$$

(41)

$$\begin{aligned}{} & {} \quad (A^{n+1}_4)_{lm} =\displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, b^{n+1}(\varphi _m, p^{n+1,K} \tilde{z}_j^{n+1,K} \, b^{n+1}(\tilde{z}_j^{n+1,K}, \varphi _l ), \nonumber \\{} & {} \quad (\textbf{F}^{n+1}_2)_l = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \langle f^{n+1},p^{n+1,K} \tilde{z}_j^{n+1,K} \rangle \, b^{n+1}(\tilde{z}_j^{n+1,K},\varphi _l),\nonumber \\{} & {} \quad (\textbf{G}^{n+1}_2)_l = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, (\tilde{u}_h^n,p^{n+1,K} \tilde{z}_j^{n+1,K}) \, b^{n+1}(\tilde{z}_j^{n+1,K},\varphi _l). \end{aligned}$$

(42)

Taking in account the definition of $\tilde{u}_h^n$ in (30), the second terms $\textbf{G}^{n+1}_1$ and $\textbf{G}^{n+1}_2$ can be expressed in the following way:

$$\begin{aligned} \Big (\textbf{G}^{n+1}_1 \Big )_l= & {} \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \beta _j^{n,K} \, \langle \hat{R}^n_h({u}^n_h), p^{n,K} \, \tilde{z}_j^{n,K} \rangle (\tilde{z}_j^{n+1,K},\varphi _l \Big ) \\= & {} \Big ( B_1^{n+1} \, \textbf{u}^{n-1} + \Delta t \, \textbf{F}^{n+1}_3 - B_1^{n+1} \, \textbf{u}^{n} - \Delta t \, B_2^{n+1} \, \textbf{u}^{n} \Big )_l, \\ \Big (\textbf{G}^{n+1}_2 \Big )_l= & {} \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \beta _j^{n,K} \, \langle \hat{R}^n_h({u}^n_h), p^{n,K} \, \tilde{z}_j^{n,K} \rangle \, b^{n+1}(\tilde{z}_j^{n+1,K},\varphi _l \Big ) \\= & {} \Big ( B_3^{n+1} \, \textbf{u}^{n-1} + \Delta t \, \textbf{F}^{n+1}_4 - B_3^{n+1} \, \textbf{u}^{n} - \Delta t \, B_4^{n+1} \, \textbf{u}^{n} \Big )_l, \end{aligned}$$

where

$$\begin{aligned}{} & {} (B^{n+1}_1)_{lm} = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \beta _j^{n,K} \, (\varphi _m, p^{n,K} \tilde{z}_j^{n,K}) \,(\tilde{z}_j^{n+1,K}, \varphi _l ), \end{aligned}$$

(43)

$$\begin{aligned}{} & {} (B^{n+1}_2)_{lm} = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \beta _j^{n,K} \, b^n(\varphi _m, p^{n,K} \tilde{z}_j^{n,K}) \, (\tilde{z}_j^{n+1,K}, \varphi _l ), \end{aligned}$$

(44)

$$\begin{aligned}{} & {} (B^{n+1}_3)_{lm} = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \beta _j^{n,K} \, (\varphi _m, p^{n,K} \tilde{z}_j^{n,K}) \, b^{n+1} (\tilde{z}_j^{n+1,K}, \varphi _l ), \end{aligned}$$

(45)

$$\begin{aligned}{} & {} (B^{n+1}_4)_{lm} = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \beta _j^{n,K} \, b^n(\varphi _m, p^{n,K} \tilde{z}_j^{n,K}) \, b^{n+1} (\tilde{z}_j^{n+1,K}, \varphi _l ),\nonumber \\{} & {} (\textbf{F}^{n+1}_3)_l = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \beta _j^{n,K} \, \langle f^{n},p^{n,K} \tilde{z}_j^{n,K} \rangle \, (\tilde{z}_j^{n+1,K},\varphi _l),\nonumber \\{} & {} (\textbf{F}^{n+1}_4)_l = \displaystyle \sum _{K\in \mathcal {T}_h} \sum _{j=1}^{\infty } \beta _j^{n+1,K} \, \beta _j^{n,K} \, \langle f^{n},p^{n,K} \tilde{z}_j^{n,K} \rangle \, b^{n+1}(\tilde{z}_j^{n+1,K},\varphi _l). \end{aligned}$$

(46)

Here we are neglecting the interaction between different eigenfunctions in two consecutive time steps. Obviously, this occurs when the operator is time independent.

Thus, problem (29) is equivalent to the lineal system

$$\begin{aligned} \textbf{A}^{n+1} \, \textbf{u}^{n+1} = \textbf{b}^{n+1}, \end{aligned}$$

where $\textbf{A}^{n+1}\in \mathbb {R}^{(L+1)\times (L+1)}$ and $\textbf{b}^{n+1}\in \mathbb {R}^{(L+1)}$ are given by

$$\begin{aligned} \begin{array}{l} \textbf{A}^{n+1}= M + \Delta t \, R^{n+1} - \mathcal{A}^{n+1},\\ \textbf{b}^{n+1} = \Big ( M - (A^{n+1}_1 + \Delta t \, A^{n+1}_3) - (A^{n}_1 + \Delta t \, A^{n}_2) {+} \mathcal{B}^{n+1} \Big ) \textbf{u}^n\\ \qquad \qquad + \Big ( A^{n}_1 - B_1^{n+1} - \Delta t \, B_3^{n+1} \Big ) \, \textbf{u}^{n-1}\\ \qquad \qquad + \Delta t \, \textbf{F}^{n+1} - \Delta t \, \textbf{F}^{n+1}_1 - \Delta t^2 \, \textbf{F}^{n+1}_2 + \Delta t \, \textbf{F}^{n}_1 - \Delta t \, \textbf{F}^{n+1}_3 - \Delta t^2 \, \textbf{F}^{n+1}_4, \end{array} \end{aligned}$$

with

$$\begin{aligned} \mathcal{A}^{n+1}= & {} A^{n+1}_1 + \Delta t \, A^{n+1}_2 + \Delta t \, A^{n+1}_3 + \Delta t^2 \, A^{n+1}_4,\\ \mathcal{B}^{n+1}= & {} {B_1^{n+1} + \Delta t \, B_2^{n+1} + \Delta t \, B_3^{n+1} + \Delta t^2 \, B_4^{n+1}}. \end{aligned}$$

Here, M and $R^{n+1}$ are, respectively, the mass and stiffness matrices from the Galerkin formulation and $A_i^{n+1}$ and $B_i^{n+1}$ are the matrices that represent the effect of the small scales component of the solution on the large scales component.