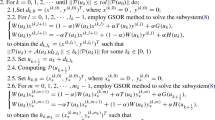Two new effective iteration methods for nonlinear systems with complex symmetric Jacobian matrices

Abstract

In this paper, we mainly discuss the iterative methods for solving nonlinear systems with complex symmetric Jacobian matrices. By applying an FPAE iteration (a fixed-point iteration adding asymptotical error) as the inner iteration of the Newton method and modified Newton method, we get the so–called Newton-FPAE method and modified Newton-FPAE method. The local and semi-local convergence properties under Lipschitz condition are analyzed. Finally, some numerical examples are given to expound the feasibility and validity of the two new methods by comparing them with some other iterative methods.

1 Introduction

Since in most areas of physics, mathematics and engineering, nonlinear systems are more common than linear systems, we usually need to solve nonlinear equations. Examples about nonlinear systems including Schrödinger equation (Sulem and Sulem 1999) and Ginzburg–Landau equation (Aranson and Kramer 2002).

Let $F: {\mathbb {D}}\subset {\mathbb {C}}^n \rightarrow {\mathbb {C}}^n$ be a continuously differentiable mapping defined on an open convex domain ${\mathbb {D}}$ in the n-dimensional complex space ${\mathbb {C}}^n$, here in this article we consider the large-scale sparse nonlinear equations:

$$\begin{aligned} F(x)=0. \end{aligned}$$

(1)

We assume Jacobian matrix $F'(x)$ to be large, sparse and complex symmetric, i.e.,

$$\begin{aligned} F'(x)=W(x)+iT(x), \end{aligned}$$

(2)

with W(x) and T(x) being both symmetric matrices. Moreover, W(x) is real positive definite and T(x) is real positive semi-definite matrices, respectively.

Some nonlinear equations can be solved analytically, but most of the nonlinear equations need to be solved numerically. Such nonlinear systems as (1) often arise in scientific computing and engineering areas. In this paper, we will focus on the iterative numerical solutions for such systems.

Perhaps the most natural idea for solving (1) is the Newton method,

$$\begin{aligned} x_{k+1} = x_{k} - F'(x_{k})^{-1}F(x_{k}), \quad k = 0,1,2,\dots , \end{aligned}$$

(3)

where $x_{0}$ is a given initial guess. Thus, it is equivalent to solving the Newton equation

$$\begin{aligned} F'(x_{k})s_{k} = - F(x_{k}),\ \text {with} \ x_{k+1} :=x_{k} + s_{k}. \end{aligned}$$

(4)

at the kth iteration.

One way is that we use linear iterative methods to solve Newton equation (4), especially when the scales of problems are large and sparse. In this sense the Newton method is inner-outer iterative method. For example, when GMRES method is used as an inner solver for Newton equation (4), the Newton-GMRES method (Bellavia et al. 2001) is obtained and widely used. Some similar efficient methods have been widely used such as Newton–Krylov subspace method (Brown and Saad 1994; Knoll and Keyes 2004), Newton-CG (CG means Conjugate Gradient) method (Sternberg and Hinze 2010) and so on.

Of course the choice of inner iteration methods plays an important role when we use them to solve Newton equations.

In the past few years, some HSS-based methods (HSS is the abbreviation for the Hermitian and skew-Hermitian splitting) have been proposed to solve large-scale sparse linear systems. In order to solve non-Hermitian positive definite linear systems, Bai et al. (2003) first introduced the HSS method. Some algorithms, such as preconditioned modified HSS (PMHSS) method (Bai et al. 2010, 2011) and single step HSS (SHSS) method (Li and Wu 2015), were proposed later to improve the HSS method. Because of the efficiency of these HSS-based methods, many scholars have done a lot of research in recent years, see Xiao and Wang (2018); Huang et al. (2018); Siahkolaei and Salkuyeh (2019); Zhang et al. (2019); Wang et al. (2017, 2018). By applying these methods as inner iterations of Newton methods, the corresponding Newton-HSS type methods can be obtained, such as Newton-HSS method (Bai and Guo 2010) and Newton-MHSS method (Yang and Wu 2012), which have been used and studied widely.

To promote the efficiency, one can also try to improve the outer iteration to get better iterative methods. For example the modified Newton method (Darvishi and Barati 2007):

$$\begin{aligned} \left\{ \begin{array}{l} y_k=x_k-{F'(x_k)}^{-1}F(x_k),\\ x_{k+1}=y_k-{F'(x_k)}^{-1}F(y_k),\;\; k=0, 1, 2, \dots . \end{array}\right. \end{aligned}$$

(5)

With just one more evaluation of F per step, the advantage of the modified Newton method is that it has at least R-order of convergence three, which is much better than the Newton method. Using HSS method as the inner iteration of modified Newton method, an effective method named modified Newton-HSS method (Wu and Chen 2013) which presents better properties than Newton-HSS method was obtained. Furthermore, the multi-step modified Newton-HSS method (Li and Guo 2017a, b), which includes the Newton-HSS method and the modified Newton-HSS method as special cases, outperforms the modified Newton-HSS method. To our knowledge, there have been a succession of theses showing the efficiency of such kind of Newton-HSS based methods, see Zhong et al. (2015); Chen and Wu (2018); Xie et al. (2019) for more examples.

In this paper, we aim to obtain effective iteration methods by applying an FPAE iteration (Xiao and Wang 2018) as the inner iteration of both the Newton method and modified Newton method. This paper is organized as the following. In Sect. 2, the FPAE iteration (a fixed-point iteration adding asymptotical error) is reviewed. In Sect. 3, the Newton-FPAE method is constructed. The local and semi-local convergence properties of the Newton-FPAE method under Lipschitz condition are analyzed in Sects. 4 and 5. Then in Sect. 6, the modified Newton-FPAE method is developed and its convergence properties are proposed. Some numerical examples are presented to show the computational efficiencies of Newton-FPAE method and modified Newton-FPAE method in Sect. 7. Finally, in Sect. 8, a brief conclusion is given.

2 A review: a fixed-point iteration adding the asymptotical error

In the paper Xiao and Wang (2018), in order to solve the complex symmetric linear system, Xiao and Wang proposed a fixed-point iteration adding the asymptotical error (FPAE). In this section, we firstly review the FPAE method.

For any symmetric positive definite matrix V and any $\alpha > 0$, the fact that $Vx = Vx - \alpha (Ax-b) = Vx - \alpha [(W + iT)x - b ]$ inspires us to construct the iterations

$$\begin{aligned} Vx_{k+1} = Vx_{k} - \alpha [(W + iT)x_{k} - b ]. \end{aligned}$$

(6)

That is

$$\begin{aligned} Vx_{k+1} = Vx_{k} - \alpha (Ax_{k} - b). \end{aligned}$$

We can rewrite Eq. (6) as the standard form

$$\begin{aligned} \begin{aligned} x_{k+1}&= M(\alpha ,V)x_{k} + N(\alpha ,V)b \\&= M(\alpha ,V)^{k+1}x_{0} + \sum _{i=0}^{k} M(\alpha ,V)^{i}N(\alpha ,V)b, \ \ k = 0,1,2,\dots , \end{aligned} \end{aligned}$$

(7)

where

$$\begin{aligned}&M(\alpha ,V) = I - \alpha V^{-1}W - i\alpha V^{-1}T, \\&N(\alpha ,V) = \alpha V^{-1}. \end{aligned}$$

Let

$$\begin{aligned} B(\alpha ,V) = \frac{1}{\alpha }V \ \text {and} \ C(\alpha ,V) = \frac{1}{\alpha }V-(W+iT), \end{aligned}$$

then we have

$$\begin{aligned} A = B(\alpha ,V) - C(\alpha ,V) \ \text {and}\ M(\alpha ,V) = B(\alpha ,V)^{-1}C(\alpha ,V). \end{aligned}$$

Thus, this splitting matrix $B(\alpha , V)$ can be utilized as a preconditioner for the complex matrix $A\in {\mathbb {C}}^{n\times n}$. We naturally hope to adjust $B(\alpha ,V)$ to get smaller spectral radius of the iterative matrix $M(\alpha ,V)$, so $B(\alpha ,V)$ can be called the FPAE preconditioner.

The convergence analysis of FPAE iteration (Xiao and Wang 2018) showed that the spectral radius of the iterative matrix satisfies:

$$\begin{aligned} \rho (M(\alpha , V)) \le \sqrt{\max \left\{ \left( 1-\alpha \lambda _{\min }^{V}\right) ^{2},\left( 1-\alpha \lambda _{\max }^{V}\right) ^{2}\right\} + \alpha ^2 \left( \sigma _{\max }^{V}\right) ^{2}} =: \delta ^{V}(\alpha ) , \end{aligned}$$

(8)

where

$$\begin{aligned} \lambda _{\min }^{V}&= \min _{\lambda _{j} \in {\text {sp}}\left( V^{-\frac{1}{2}} W V^{-\frac{1}{2}}\right) }\left\{ \lambda _{j}\right\} ,\ \lambda _{\max }^{V} = \max _{\lambda _{j} \in {\text {sp}}\left( V^{-\frac{1}{2}} W V^{-\frac{1}{2}}\right) }\left\{ \lambda _{j}\right\} ,\\ \sigma _{\min }^{V}&= \min _{\lambda _{j} \in {\text {sp}}\left( V^{-\frac{1}{2}} TV^{-\frac{1}{2}}\right) }\left\{ \lambda _{j}\right\} ,\ \sigma _{\max }^{V} = \max _{\lambda _{j} \in {\text {sp}}\left( V^{-\frac{1}{2}} TV^{-\frac{1}{2}}\right) }\left\{ \lambda _{j}\right\} . \end{aligned}$$

As long as the parameter $\alpha$ satisfies

$$\begin{aligned} 0< \alpha <\min \left\{ \frac{2 \lambda _{\min }^{V}}{\left( \lambda _{\min }^{V}\right) ^{2}+\left( \sigma _{\max }^{V}\right) ^{2}}, \ \frac{2 \lambda _{\max }^{V}}{\left( \lambda _{\max }^{V}\right) ^{2}+\left( \sigma _{\max }^{V}\right) ^{2}} \right\} , \end{aligned}$$

(9)

then $\delta ^{V}(\alpha )<1$, i.e. FPAE iteration converges to the exact solution.

In practical implementation, for the sake of convenience, $V=W$ is generally taken. Then the FPAE iteration reduces to

$$\begin{aligned} Wx_{k+1} = [(1-\alpha )W - i\alpha T]x_k + \alpha b. \end{aligned}$$

(10)

We can rewrite (10) as

$$\begin{aligned} x_{k+1} = M(\alpha )x_{k} + N(\alpha )b, \end{aligned}$$

where $M(\alpha ) = (1-\alpha )I - i\alpha W^{-1}T$ and $N(\alpha ) = \alpha W^{-1}$. Also we define

$$\begin{aligned} B(\alpha ) = \frac{1}{\alpha }W \ \text {and} \ C(\alpha ) = \frac{1-\alpha }{\alpha }W - iT, \end{aligned}$$

then it holds

$$\begin{aligned} A = B(\alpha ) - C(\alpha ) \ \text {and}\ M(\alpha ) = B(\alpha )^{-1}C(\alpha ). \end{aligned}$$

Then the spectral radius of iteration matrix $\rho (M(\alpha ))$ is bounded by $\delta (\alpha )$, that is,

$$\begin{aligned} \rho (M(\alpha )) \le \delta (\alpha ) := \sqrt{(1-\alpha )^2 + \alpha ^2\rho ^2(W^{-1}T)}. \end{aligned}$$

(11)

If $0<\alpha <\dfrac{2}{1+\rho ^2(W^{-1}T) },$ then $\delta (\alpha )<1\ i.e.$, the iteration converges. Moreover, the optimal parameter $\alpha _*$ which minimize the upper bound of spectral radius $\delta (\alpha )$ is given by $\alpha _* = \dfrac{1}{1 + \rho ^2( W^{-1}T )} \in (0,1)$ which leads to

$$\begin{aligned} \delta (\alpha _*) = \frac{\rho (W^{-1}T)}{ \sqrt{1+\rho ^2 (W^{-1}T)} }. \end{aligned}$$

3 The Newton-FPAE method

In this section, to solve nonlinear equations with complex symmetric Jacobian matrices, we introduce our Newton-FPAE method.

Applying the FPAE method as the inner iteration for the Newton method, then the Newton-FPAE method for solving nonlinear system (1) can be written as the following:

Algorithm 1

Newton-FPAE method

1. Given an initial guess $x_{0}$, a positive constant $\alpha$, and a positive integer sequence $\{l_{k}\}^{\infty }_{k=0}$.

2. For $k=0,1,2,\cdots ,$ until $\Vert F(x_{k})\Vert \le tol \Vert F(x_{0})\Vert$ do:

    2.1. Set $d_{k, 0} :=0$.

    2.2. For $l=0,1,2,\cdots ,l_{k}-1$, apply FPAE method to the linear system (4):

$$\begin{aligned} V(x_{k}) d_{k, l+1} = V(x_{k}) d_{k, l} - \alpha \left[ (W(x_{k})+i T(x_{k})) d_{k, l} + F(x_{k})\right] , \end{aligned}$$

and obtain $d_{k, l_{k}}$ such that

$$\begin{aligned} \Vert F(x_{k})+F'(x_{k})d_{k, l_{k}}\Vert \le \eta _{k}\Vert F(x_{k})\Vert \;\; \text {for some} \;\; \eta _{k} \in [0, 1). \end{aligned}$$

(12)

    2.3. Set

$$\begin{aligned} x_{k+1}=x_{k}+d_{k, l_{k}}. \end{aligned}$$

By straightforward derivation we can obtain the following uniform expressions of $d_{k,l_{k}}$ and $x_{k+1}$,

$$\begin{aligned} d_{k, l_{k}}&= -\sum _{i=0}^{l_{k}-1} M(\alpha ,V(x_{k});x_{k} )^{i} N(\alpha ,V(x_{k});x_{k}) F(x_{k}), \end{aligned}$$

(13)

$$\begin{aligned} x_{k+1}&= x_{k} -\sum _{i=0}^{l_{k}-1} M(\alpha ,V(x_{k});x_{k})^{i} N(\alpha ,V(x_{k});x_{k}) F(x_{k}) \nonumber \\&= x_{k} - \left( I - M(\alpha ,V(x_{k}); x_{k})^{l_{k}}\right) F'(x_{k})^{-1} F(x_{k}), \end{aligned}$$

(14)

where

$$\begin{aligned} M(\alpha , V(x); x)=I - \alpha V(x)^{-1}F'(x),\ \text {and} \ N(\alpha ,V(x);x) = \alpha V(x)^{-1}. \end{aligned}$$

Since the selection of V(x) affects the calculation and storage, in the practical implementation, $V(x)=W(x)$ is usually taken for convenience. Then we get

$$\begin{aligned} M(\alpha ; x) = I - \alpha W(x)^{-1}F'(x),\ N(\alpha ;x) = \alpha W(x)^{-1}. \end{aligned}$$

If we set

$$\begin{aligned} B(\alpha ;x) = \frac{1}{\alpha }W(x),\ C(\alpha ;x) = \frac{1}{\alpha }W(x)-F'(x), \end{aligned}$$

then

$$\begin{aligned} F'(x) = B(\alpha ;x)- C(\alpha ;x),\\ M(\alpha ; x) = B(\alpha ;x)^{-1}C(\alpha ;x). \end{aligned}$$

4 Local convergence property of the Newton-FPAE method

In this section, we prove the local convergence property of the Newton-FPAE method under Lipschitz condition. In the remainder of this article, $x_*$ is the solution of $F(x)=0$, $N(x_*,r)$ denotes an open ball centered at $x_*$ with radius $r>0$.

Lemma 1

(Perturbation Lemma) Ortega and Rheinboldt (1970) Let $M,N \in {\mathbb {C}}^{n \times n}$ and assume that M is nonsingular, with $\Vert M^{-1}\Vert \le \xi .$ If $\Vert M-N\Vert \le \delta$ and $\delta \xi < 1$, then N is also nonsingular, and

$$\begin{aligned} \Vert N^{-1}\Vert \le \frac{\xi }{1-\delta \xi }. \end{aligned}$$

The proof of Lemma 1 can be found in Ortega and Rheinboldt (1970).

Assumption 1

For any $x \in {\mathbb {N}}(x_*, r) \subset {\mathbb {N}}_0$, assume the following conditions hold

(A1) (The bounded condition) there exist positive constants $\beta$ and $\gamma$ such that

$$\begin{aligned} \max \Big \{ \Vert W(x_*)\Vert , \,\, \Vert T(x_*)\Vert \Big \} \le \beta \ \text {and} \ \Vert F'(x_*)^{-1}\Vert \le \gamma . \end{aligned}$$

(15)

(A2) (The Lipschitz condition) there exist nonnegative constants $L_1$ and $L_2$ such that

$$\begin{aligned} \Vert W(x)-W(x_*)\Vert \le L_1 \Vert x-x_*\Vert ,\\ \Vert T(x)-T(x_*)\Vert \le L_2 \Vert x-x_*\Vert . \end{aligned}$$

(16)

Lemma 2

Under Assumption 1, for any $x, y \in {\mathbb {N}}(x_*, r)$, if $r\in \left( 0, \frac{1}{\gamma L} \right)$, then $F'(x)^{-1}$ exists. And the following inequalities hold with $L := L_1+L_2$ for any $x, y \in {\mathbb {N}}(x_*, r)$:

$$\begin{aligned}&\Vert F'(x)- F'(x_*)\Vert \le L\Vert x-x_*\Vert ,\\&\Vert F'(x)^{-1}\Vert \le \frac{\gamma }{1-\gamma L\Vert x-x_*\Vert },\\&\Vert F(y)\Vert \le \frac{L}{2}\Vert y-x_*\Vert ^{2} + 2\beta \Vert y-x_*\Vert ,\\&\Vert y-x_*-F'(x)^{-1}F(y)\Vert \le \frac{\gamma }{1-\gamma L\Vert x-x_*\Vert }\bigg (\frac{L}{2}\Vert y-x_*\Vert +L\Vert x-x_*\Vert \bigg )\Vert y-x_*\Vert . \end{aligned}$$

Proof

For the proof of the first inequality

$$\begin{aligned} \Vert F'(x)- F'(x_*)\Vert&= \Vert W(x)+ iT(x) - W(x_*)- iT(x_*)\Vert \\&\le \Vert W(x)- W(x_*)\Vert + \Vert i(T(x) - T(x_*))\Vert \\&\le L_1 \Vert x-x_*\Vert + L_2 \Vert x-x_*\Vert = L\Vert x-x_*\Vert . \end{aligned}$$

From the condition of $r\in \left( 0, \frac{1}{\gamma L} \right)$, then $\gamma L\Vert x-x_*\Vert <1$. Then according to the bounded condition $\Vert F'(x_*)^{-1}\Vert \le \gamma$ and the above formula $\Vert F'(x)- F'(x_*)\Vert \le L\Vert x-x_*\Vert$, by Lemma 1, $F'(x)^{-1}$exists and

$$\begin{aligned} \Vert F'(x)^{-1}\Vert \le \frac{\gamma }{1-\gamma L\Vert x-x_*\Vert }. \end{aligned}$$

By

$$\begin{aligned}&\Vert F'(x_*)\Vert = \Vert W(x_*)+ iT(x_*) \Vert \le \Vert W(x_*) \Vert + \Vert iT(x_*) \Vert \le 2\beta ,\\&\quad F(y) = F(y) - F(x_*) - F'(x_*)(y-x_*) + F'(x_*)(y-x_*) \\&\quad = \int _{0}^{1} \bigg ( F'(x_* + t(y-x_*)) -F'(x_*) \bigg ) dt(y-x_*) + F'(x_*)(y-x_*) , \end{aligned}$$

then

$$\begin{aligned} \Vert F(y)\Vert&\le \left\| \int _{0}^{1} \bigg ( F'(x_* + t(y-x_*)) -F'(x_*) \bigg )dt(y-x_*) \right\| + \Vert F'(x_*)(y-x_*) \Vert \\&\le \Vert y-x_*\Vert \int _{0}^{1} \Vert ( F'(x_* + t(y-x_*)) -F'(x_*) ) \Vert dt + \Vert F'(x_*)(y-x_*) \Vert \\&\le \Vert y-x_*\Vert \int _{0}^{1} \Vert Lt(y-x_*)\Vert dt + \Vert F'(x_*)(y-x_*) \Vert \\&\le \frac{L}{2} \Vert y-x_* \Vert ^{2} + 2\beta \Vert y-x_*\Vert . \end{aligned}$$

As for the last inequality, since

$$\begin{aligned}&\ y-x_*-F'(x)^{-1}F(y) \\&\quad = -F'(x)^{-1} \bigg ( F(y) - F(x_*) -F'(x)(y-x_*) + F'(x)(y-x_*) - F'(x)(y-x_*) \bigg ) \\&\quad = -F'(x)^{-1} \int _{0}^{1} \bigg ( F'(x_*+ t(y-x_*) ) -F'(x_*) \bigg )\mathrm{d}t(y-x_*) \\&\quad \quad + F'(x)^{-1}\left( F'(x)-F'(x_*)\right) (y-x_*) , \end{aligned}$$

then

$$\begin{aligned}&\ \Vert y-x_*-F'(x)^{-1}F(y) \Vert \le \Vert -F'(x)^{-1}\Vert \\&\quad \cdot \bigg ( \int _{0}^{1} \Vert F'(x_*+t(y-x_*)) - F'(x_*) \Vert dt + \Vert F'(x)-F'(x_*)\Vert \bigg ) \cdot \Vert y-x_*\Vert \\&\quad \le \frac{\gamma }{1-\gamma L\Vert x-x_*\Vert } \bigg ( \frac{L}{2}\Vert y-x_*\Vert + L\Vert x-x_*\Vert \bigg ) \Vert y-x_*\Vert . \end{aligned}$$

This completes the proof of Lemma 2. $\square$

Theorem 1

Under the assumptions of Lemma 2, for $0< \alpha < \dfrac{2}{1+\rho ^2(W(x_*)^{-1}T(x_*))}$, suppose that $r\in (0, r_0)$ and define $r_0 :=min\{ r_1,r_2\}$, where

$$\begin{aligned} r_{1} = min\{ \frac{\tau \theta \alpha }{8 \gamma L_{1}+4 \alpha \gamma L}, \frac{\alpha }{4\gamma L_1} \},\ \ r_{2} = \frac{1-2 \beta \gamma [(\tau +1) \theta ]^{u}}{3 \gamma L} , \end{aligned}$$

with $u=\liminf _{k \rightarrow \infty } l_{k}$, and the constant u satisfies

$$\begin{aligned} u > \left\lfloor - \frac{\ln (2 \beta \gamma )}{\ln ((\tau +1) \theta )} \right\rfloor , \end{aligned}$$

where the symbol $\lfloor \cdot \rfloor$ is used to denote the smallest integer no less than the corresponding real number, $\tau \in \big (0, \frac{1-\theta }{\theta }\big )$ is a prescribed positive constant and

$$\begin{aligned} \theta :=\theta \left( \alpha ; x_{*}\right) =\Vert M(\alpha ; x_{*}) \Vert \le \sqrt{ (1-\alpha )^2 + \alpha ^2\rho ^2(W(x_*)^{-1}T(x_*))} =: \delta (\alpha ;x_*) <1. \end{aligned}$$

Then for $0< \alpha < \dfrac{2}{1+\rho ^2(W(x_*)^{-1}T(x_*))}$, any $x\in {\mathbb {N}}(x_*, r)$ and any sequences $\{l_{k}\}^{\infty }_{k=0}$ of positive integers, the iteration sequence $\{x_{k}\}^{\infty }_{k=0}$ generated by the Newton-FPAE method is well defined and converges to $x_*$. Moreover, it holds that

$$\begin{aligned} \limsup _{k\rightarrow \infty } \Vert x_k-x_*\Vert ^{\frac{1}{k}} \le g(r_0; u), \end{aligned}$$

here we use the notation

$$\begin{aligned} g(t ; v)=\frac{2 \gamma }{1-\gamma L t}\left( Lt + \beta [(\tau +1) \theta ]^{v}\right) , \text { for } t\in (0,r) \text { and } v>u. \end{aligned}$$

Proof

First, we try to give an estimate of the iterative matrix $M(\alpha ;x)$ of the inner solver: if $x\in {\mathbb {N}}(x_*,r)$, then

$$\begin{aligned} \Vert M(\alpha ;x) \Vert \le (\tau + 1)\theta < 1. \end{aligned}$$

By the bounded condition and the fact that $\Vert M(\alpha ;x_*)\Vert \le \delta (\alpha ;x_*) < 1,$

$$\begin{aligned} \Vert B(\alpha ; x_{*})^{-1}\Vert&= \Vert \left( I-M(\alpha ;x_{*})\right) F'(x_{*})^{-1} \Vert \\&\le \left( 1 + \Vert M(\alpha ;x_*)\Vert \right) \Vert F'(x_*)^{-1}\Vert \le 2\gamma . \end{aligned}$$

Then

$$\begin{aligned}&B(\alpha ; x)-B(\alpha ; x_{*}) = \frac{1}{\alpha }(W(x)-W(x_{*})), \\&\quad C(\alpha ; x)-C(\alpha ; x_{*}) = \frac{1}{\alpha }(W(x)-W(x_{*})) - (F'(x)-F'(x_{*})), \end{aligned}$$

by Lipschitz condition, we have

$$\begin{aligned}&\Vert B(\alpha ; x)-B(\alpha ; x_{*})\Vert \le \frac{1}{\alpha }\Vert W(x)-W(x_{*})\Vert \le \frac{L_{1}}{\alpha }\Vert x-x_{*}\Vert ,\\&\quad \Vert C(\alpha ; x)-C(\alpha ; x_{*})\Vert \le \frac{1}{\alpha }\Vert W(x)-W(x_{*})\Vert + \Vert F'(x)-F'(x_{*})\Vert \\&\quad \le (\frac{L_1}{\alpha } + L)\Vert x-x_*\Vert . \end{aligned}$$

Since $\Vert B(\alpha ; x_{*})^{-1}\Vert \le 2 \gamma$, by Lemma 1

$$\begin{aligned} \Vert B(\alpha ; x)^{-1}\Vert \le \frac{2 \gamma }{1-2 \gamma \frac{L_{1}}{\alpha } \Vert x-x_{*} \Vert } \le \frac{2 \alpha \gamma }{\alpha -2 \gamma L_{1}\Vert x-x_{*}\Vert }, \end{aligned}$$

and

$$\begin{aligned}&M(\alpha ; x)-M(\alpha ; x_{*}) = B(\alpha ; x)^{-1} C(\alpha ;x) - B(\alpha ; x_{*})^{-1} C(\alpha ; x_{*}) \\&\quad = B(\alpha ; x)^{-1} \bigg ( \big (C(\alpha ;x) - C(\alpha ;x_*)\big ) - \big (B(\alpha ;x) - B(\alpha ;x_*)\big )M(\alpha ; x) \bigg ), \end{aligned}$$

then

$$\begin{aligned}&\Vert M(\alpha ; x)-M(\alpha ; x_{*})\Vert = \Vert B(\alpha ; x)^{-1} C(\alpha ; x)-B(\alpha ; x_{*})^{-1} C(\alpha ; x_{*}) \Vert \\&\quad \le \Vert B(\alpha ; x)^{-1}\Vert \cdot \bigg [ \Vert C(\alpha ; x)-C (\alpha ; x_{*})\Vert + \Vert B(\alpha ; x)-B(\alpha ; x_{*})\Vert \cdot \Vert M( \alpha ; x_{*})\Vert \bigg ] \\&\quad \le \frac{2 \alpha \gamma }{\alpha -2 \gamma L_{1}\Vert x-x_{*}\Vert } \big (2 \cdot \frac{L_{1}}{\alpha }+L \big )\Vert x-x_{*}\Vert \\&\quad = \frac{(4 \gamma L_{1}+2 \alpha \gamma L)\Vert x-x_{*}\Vert }{\alpha -2 \gamma L_{1}\Vert x-x_{*}\Vert }. \end{aligned}$$

Since $\Vert x-x_*\Vert <r \le r_1 = min\{ \dfrac{\tau \theta \alpha }{8 \gamma L_{1}+4 \alpha \gamma L}, \dfrac{\alpha }{4\gamma L_1} \}$, then $\alpha - 2\gamma L_1\Vert x-x_*\Vert \ge \dfrac{1}{2} \alpha$, obviously

$$\begin{aligned} \frac{(4 \gamma L_{1}+2 \alpha \gamma L)\Vert x-x_{*}\Vert }{\alpha -2 \gamma L_{1}\Vert x-x_{*}\Vert } < \frac{(4 \gamma L_{1}+2 \alpha \gamma L) }{\frac{1}{2} \alpha } \cdot \frac{\tau \theta \alpha }{8 \gamma L_{1}+4 \alpha \gamma L} = \tau \theta . \end{aligned}$$

That is

$$\begin{aligned}&\Vert M(\alpha ;x)-M(\alpha ;x_*)\Vert \le \frac{(4 \gamma L_{1}+2 \alpha \gamma L)\Vert x-x_{*}\Vert }{\alpha -2 \gamma L_{1}\Vert x-x_{*}\Vert }< \tau \theta ,\\&\quad \Vert M(\alpha ; x)\Vert \le \Vert M(\alpha ; x)-M(\alpha ; x_*)\Vert + \Vert M(\alpha ; x_{*})\Vert <(\tau +1) \theta , \end{aligned}$$

this is the estimate of $\Vert M(\alpha ; x)\Vert .$

Since $t\in (0,r)$ and $r<r_2 = \frac{1-2 \beta \gamma [(\tau +1) \theta ]^{u}}{3 \gamma L}$, we get

$$\begin{aligned} g(t ; v)=\frac{2 \gamma }{1-\gamma Lt}\left( Lt+\beta [(\tau +1) \theta ]^{v}\right)<g(r_{0} ; u)<1. \end{aligned}$$

Then we prove a recursive relationship of $\Vert x_{k}-x_{*}\Vert$ :

$$\begin{aligned}&\Vert x_{k+1}-x_{*}\Vert = \Vert x_{k}-x_{*}-(I-M(\alpha ; x)^{l_{k}}) F'(x_{k})^{-1} F(x_{k})\Vert \\&\le \Vert x_{k}-x_{*}-F'(x_{k})^{-1} F(x_{k})\Vert + \Vert M(\alpha ;x)^{l_{k}}\Vert \cdot \Vert F'(x_{k})^{-1} F(x_{k})\Vert \\&\quad \le \frac{\gamma }{1-\gamma L\Vert x-x_{*}\Vert } \frac{3L}{2} \Vert x_{k}-x_{*}\Vert ^{2} + [(\tau +1) \theta ]^{l_{k}} \\&\quad \frac{\gamma }{1-\gamma L\Vert x-x_{*}\Vert } \left( \frac{L}{2}\Vert x_{k} -x_{*}\Vert ^{2}+2 \beta \Vert x_{k}-x_{*}\Vert \right) \\&\quad = \frac{(3+[(\tau +1) \theta ]^{l_{k}}) \gamma L}{2(1-\gamma L\Vert x-x_{*}\Vert )} \Vert x_{k}-x_{*} \Vert ^{2} + \frac{2 \beta \gamma [(\tau +1) \theta ]^{l_{k}} }{1-\gamma L\Vert x-x_{*}\Vert } \Vert x_{k}-x_{*}\Vert \\&\quad \le \frac{2 \gamma }{1-\gamma L\Vert x-x_{*}\Vert } \left( L\Vert x_{k}-x_{*}\Vert + \beta [(\tau +1) \theta ]^{l_{k}} \right) \cdot \Vert x_{k}-x_{*}\Vert \\&\quad = g\left( \Vert x_{k}-x_{*}\Vert ; l_{k}\right) \cdot \Vert x_{k}-x_{*}\Vert \\&\quad< g(r_{0} ; u) \Vert x_{k}-x_{*} \Vert <\Vert x_{k}-x_{*}\Vert . \end{aligned}$$

Now we can prove the convergence of $\{x_{k}\} \subset {\mathbb {N}}(x_{*}, r)$.

First, for $k=0$, since $\Vert x_{0}-x_{*}\Vert<r<r_{0}$, then

$$\begin{aligned} \Vert x_{k+1}-x_{*}\Vert< \Vert x_{k}-x_{*}\Vert< \cdots< \Vert x_{0}-x_{*}\Vert < r, \end{aligned}$$

$i.e. \ \{x_{k}\} \subset {\mathbb {N}}(x_{*}, r)$. since

$$\begin{aligned} \Vert x_{k+1}-x_{*}\Vert< g(r_{0};u) \Vert x_{k}-x_{*}\Vert <r, \end{aligned}$$

by mathematical induction, assuming for some $k=n$, $x_n \in {\mathbb {N}}(x_{*}, r)$, then

$$\begin{aligned} \Vert x_{n+1}-x_{*}\Vert< g(r_{0};u)\Vert x_{n}-x_{*}\Vert<\cdots< g(r_{0};u)^{n+1}\Vert x_{0}-x_{*}\Vert <r , \end{aligned}$$

which means $n\rightarrow \infty ,x_{n+1}\rightarrow x_*.$

This is the end of proof of Theorem 1. $\square$

5 Semi-local convergence property of the Newton-FPAE method

In this section, we study the semi-local convergence property of the Newton-FPAE method after giving some assumptions on F(x).

Assumption 2

For any $x_{0} \in {\mathbb {N}}_0$, assume the following conditions hold.

(A1) (The bounded condition) there exist positive constants $\beta$ and $\gamma$ such that

$$\begin{aligned} \max \Big \{ \Vert W(x_0)\Vert ,\ \Vert T(x_0)\Vert \Big \} \le \beta \ , \ \Vert F'(x_0)^{-1}\Vert \le \gamma \ {\text{ a }nd} \ \Vert F(x_0)\Vert \le \delta . \end{aligned}$$

(17)

(A2) (The Lipschitz condition) there exist nonnegative constants $L_1$ and $L_2$ such that for any $x, y \in {\mathbb {N}}(x_{0}, r) \subset {\mathbb {N}}_{0}$

$$\begin{aligned} \Vert W(x)-W(y)\Vert&\le L_1 \Vert x-y\Vert , \end{aligned}$$

(18)

$$\begin{aligned} \Vert T(x)-T(y)\Vert&\le L_2 \Vert x-y\Vert . \end{aligned}$$

(19)

Lemma 3

Under the condition of Assumption 2, for any $x, y \in {\mathbb {N}}(x_{0}, r)$, if $r\in \left( 0,\frac{1}{\gamma L}\right)$, and we denote $L:=L_1+L_2$, then $F'(x)^{-1}$ exists and:

$$\begin{aligned}&\Vert F'(x)-F'(y) \Vert \le L\Vert x-y\Vert , \\&\Vert F'(x)\Vert \le L\Vert x-x_0\Vert +2\beta ,\\&\Vert F(x)-F(y)-F'(y)(x-y) \Vert \le \frac{L}{2}\Vert x-y\Vert ^{2},\\&\Vert F'(x)^{-1} \Vert \le \frac{\gamma }{1-\gamma L \Vert x-x_{0}\Vert }. \end{aligned}$$

Proof

The proofs of the first and fourth formulas are similar to Lemma 2.2 and will not be repeated.

Since

$$\begin{aligned} \Vert F'(x_{0})\Vert = \Vert W(x_{0}) + i T(x_{0}) \Vert \le \Vert W(x_{0}) \Vert + \Vert i T(x_{0}) \Vert \le 2 \beta , \end{aligned}$$

then

$$\begin{aligned} \Vert F'(x)\Vert \le \Vert F'(x)-F'(x_{0})\Vert + \Vert F'(x_{0})\Vert \le L\Vert x-x_{0}\Vert +2\beta . \end{aligned}$$

And since

$$\begin{aligned} F(x)-F(y)-F'(y)(x-y) = \int _{0}^{1} \left( F'(y+t(x-y)) - F'(y)\right) \mathrm{d}t(x-y), \end{aligned}$$

then

$$\begin{aligned} \Vert F(x)-F(y)-F'(y)(x-y)\Vert&= \left\| \int _{0}^{1} \left( F'(y+t(x-y)) - F'(y)\right) \mathrm{d}t(x-y) \right\| \\&\le \frac{L}{2}\Vert x-y\Vert ^{2}. \end{aligned}$$

$\square$

We define the following functions:

$$\begin{aligned} g(t) = \frac{1}{2}at^2-bt+c, \ h(t) = at-1, \end{aligned}$$

where $a = L\gamma (1+\eta ), \ b = 1-\eta , \ c=2\gamma \delta$, and $\eta =\eta _k < 1$ is the termination condition of the inner iteration.

Set $t_0=0$, construct a sequence $\{t_{k}\}$ as follows:

$$\begin{aligned} t_{k+1} = t_{k} - \frac{g(t_{k})}{h(t_{k})}, \ k=0,1,2,\cdots . \end{aligned}$$

(20)

Lemma 4

Assume that the above constants satisfy

$$\begin{aligned} \gamma ^{2} \delta L \le \frac{(1-\eta )^{2}}{4(1+\eta )}. \end{aligned}$$

Then the sequence $\{t_k\}$ constructed by the above rules is monotonically increasing and converges to $t_* = \dfrac{b-\sqrt{b^2-2ac}}{a}$.

Proof

Since $g(t) = \frac{1}{2}at^2-bt+c$ is a quadratic function with a quadratic coefficient greater than 0, by direct computation it is easy to get the following results.

Set $t_{*} = \dfrac{b-\sqrt{b^2-2ac}}{a}$, then for $t\in [0,t_*]$, the following inequality holds:

$$\begin{aligned} g(t)\ge 0, \ g'(t)< 0, \ g''(t) > 0, \\ h(t)<g'(t)<0. \end{aligned}$$

Now we prove that for any k there is $t_{k}<t_{k+1}<t_{*}$ by mathematical induction. Suppose the above formula holds for $k-1$, i.e. $t_{k-1}<t_{k}<t_{*}$.

We set $t_{k+1} - t_{k} = -\dfrac{g(t_{k})}{h(t_{k})} = U(t_{k})$, then

$$\begin{aligned} U' = \frac{-g'h+gh'}{h^2} , \end{aligned}$$

for $t_k \in [0,t_*]$, $U'(t_k) < 0$, $U(t_k)>U(t_*)>0$, then $t_k < t_{k+1}$.

On the other hand, the function $t-\dfrac{g(t)}{h(t)}$ is monotonically decreasing on $[0,\dfrac{b}{a}]$ since

$$\begin{aligned} -\frac{g(t_k)}{h(t_k)} \le -\frac{g(t_k)}{g'(t_k)}, \end{aligned}$$

then $t_{k+1} \le t_*- \dfrac{g(t_*)}{g'(t_*)} = t_*$.

By mathematical induction, for any k, $t_k<t_{k+1}<t_{*}$, then the sequence $\{t_{k}\}$ is monotonically increasing and converges to $t_*$. $\square$

Theorem 2

Under the conditions of Assumption 2 and Lemma 4, we define $r:=\min (r_1,r_2)$, where

$$\begin{aligned} r_{1} = min\{ \frac{\tau \theta \alpha }{8 \gamma L_{1}+4 \alpha \gamma L}, \frac{\alpha }{4\gamma L_1} \} \ \text {and}\ r_{2}=\frac{b-\sqrt{b^{2}-2 a c}}{a}, \end{aligned}$$

and define $u=\liminf _{k \rightarrow \infty } l_{k},$ and the constant u satisfies

$$\begin{aligned} u>\left\lfloor -\frac{\ln \eta }{\ln \left( (\tau +1) \theta \right) } \right\rfloor , \end{aligned}$$

$\tau \in \left( 0,\frac{1-\theta }{\theta } \right)$ is a prescribed positive constant, $\lfloor \cdot \rfloor$ represents the smallest integer no less than the corresponding value, and

$$\begin{aligned} \theta :=\theta \left( \alpha ; x_{0}\right) =\Vert M(\alpha ; x_{0}) \Vert \le \sqrt{ (1-\alpha )^2 + \alpha ^2\rho ^2(W(x_0)^{-1}T(x_0))} =: \delta (\alpha ;x_0) <1. \end{aligned}$$

Then the iteration sequence $\{x_k\}$ generated by Newton-FPAE method converges to $x_*$, which satisfies $F(x_*) = 0$.

Proof

First, similar to the proof in Lemma 2, we obtain the estimate of $\Vert M(\alpha ;x)\Vert$, that for any $x \in {\mathbb {N}}(x_0,r)$,

$$\begin{aligned} \Vert M(\alpha ;x)\Vert \le (\tau +1)\theta < 1. \end{aligned}$$

We prove the following conclusions by mathematical induction:

$$\begin{aligned} \left\{ \begin{array}{lll} \Vert x_{k}-x_{0}\Vert \le t_{k}-t_{0}, \\ \Vert F(x_{k}) \Vert \le \dfrac{1-\gamma Lt_{k}}{\gamma (1+\eta )}(t_{k+1}-t_{k}), \\ \Vert x_{k+1}-x_{k}\Vert \le t_{k+1}-t_{k}. \end{array}\right. \end{aligned}$$

(21)

First, when $k=0$ :

$$\begin{aligned}&\Vert x_{0}-x_{0}\Vert =0 \le t_{0}-t_{0}, \\&\Vert F(x_{0}) \Vert \le \delta \le \frac{2 \gamma \delta }{\gamma (1+\eta )}=\frac{1-\gamma L t_{0}}{\gamma (1+\eta )}(t_{1}-t_{0}), \\&\Vert x_{1}-x_{0}\Vert = \Vert I-M(\alpha ; x_{0})^{l_{0}}\Vert \cdot \Vert F'(x_{0})^{-1} F(x_{0})\Vert \le (1 + \theta ^{l_{0}} )\gamma \delta < 2 \gamma \delta = t_{1}-t_{0}. \end{aligned}$$

Now we have proved that the formula (22) is true when $k=0$. Assuming that for any non-negative integer less than k the formula (22) is true, then we only need to prove that for k the formula (22) is true.

Since

$$\begin{aligned} \Vert x_{k}-x_{0}\Vert&\le \Vert x_{k}-x_{k-1}\Vert +\Vert x_{k-1}-x_{0}\Vert \\&\le t_{k} - t_{k-1}+t_{k-1}-t_{0} = t_{k} - t_{0}< t_{*} <r_{2} , \end{aligned}$$

and

$$\begin{aligned} (1+\eta ) \gamma \Vert F(x_{k})\Vert&\le (1+\eta )\gamma \Vert F(x_{k})- F(x_{k-1})-F'(x_{k-1})(x_{k}-x_{k-1})\Vert \\&\quad + (1+\eta ) \gamma \Vert F(x_{k-1})+F'(x_{k-1})(x_{k}-x_{k-1}) \Vert \\&\le \frac{(1+\eta ) \gamma L}{2}\Vert x_{k}-x_{k-1}\Vert ^{2} + (1+\eta ) \gamma \cdot \eta \Vert F(x_{k-1}) \Vert \\&\le \frac{(1+\eta ) \gamma L}{2}(t_{k}-t_{k-1})^{2} + \eta (1-\gamma L t_{k-1})(t_{k}-t_{k-1}) \\&= g(t_{k}) - g(t_{k-1}) + b(t_{k}-t_{k-1}) - at_{k-1}(t_{k}-t_{k-1}) \\&\quad + \eta (1-\gamma L t_{k-1})(t_{k}-t_{k-1}) \\&= g(t_{k}) - g(t_{k-1}) + (1-\gamma L t_{k-1}) \frac{g(t_{k-1})}{-h(t_{k-1})} \\&< g(t_{k}) = -h(t_{k})(t_{k+1}-t_{k}) < (1-\gamma L t_{k})(t_{k+1}-t_{k}) , \end{aligned}$$

then

$$\begin{aligned} \Vert F(x_{k}) \Vert \le \frac{(1-\gamma L t_{k})}{(1+\eta ) \gamma }(t_{k+1}-t_{k}), \end{aligned}$$

hence

$$\begin{aligned} \Vert x_{k+1}-x_{k}\Vert&\le \left\| I-M(\alpha ; x_{k})^{l_{k}} \right\| \cdot \left\| F'(x_{k})^{-1} F(x_{k}) \right\| \\&\le (1+\theta ^{l_{k}}) \Vert F'(x_{k})^{-1}\Vert \cdot \Vert F(x_{k})\Vert \\&\le (1+\eta ) \frac{\gamma }{1-\gamma L t_{k}} \Vert F(x_{k})\Vert \\&\le t_{k+1} - t_{k}. \end{aligned}$$

Therefore, the above formula holds for any non-negative integer k.

For the reason that sequence $\{ t_k\}$ converges to $t_*$, and

$$\begin{aligned} \Vert x_{k+1} - x_{0}\Vert&\le \Vert x_{k+1} - x_{k}\Vert + \Vert x_{k}-x_{0}\Vert \\&\le t_{k+1} - t_{0} < t_{*} = r_{2}, \end{aligned}$$

then the sequence $\{ x_k\}$ converges to $x_*$. For $\Vert M(\alpha ;x_{*})\Vert <1$ we have

$$\begin{aligned} F(x_{*}) = 0. \end{aligned}$$

The proof of Theorem 2 is completed. $\square$

6 Modified Newton-FPAE method

In this section, we apply the FPAE method again as the inner solver for the modified Newton method (5), then the modified Newton-FPAE method is introduced.

Algorithm 2

Modified Newton-FPAE method

1. Given an initial guess $x_{0}$, a nonnegative constant $\alpha$, and two positive integer sequences $\{l_{k}\}^{\infty }_{k=0}$, $\{m_{k}\}^{\infty }_{k=0}$.

2. For $k=0, 1, \cdots ,$ until $\Vert F(x_{k})\Vert \le tol \Vert F(x_{0})\Vert$ do:

    2.1. Set $d_{k, 0}=h_{k, 0} :=0$.

    2.2. For $l=0, 1, \cdots , l_{k}-1$, apply FPAE method to the first equation of (5):

$$\begin{aligned} V(x_{k}) d_{k, l+1} = V(x_{k}) d_{k, l} - \alpha \left[ (W(x_{k})+i T(x_{k})) d_{k, l} + F(x_{k})\right] , \end{aligned}$$

and obtain $d_{k, l_{k}}$ such that

$$\begin{aligned} \Vert F(x_{k})+F'(x_{k})d_{k, l_{k}}\Vert \le \eta _{k}\Vert F(x_{k})\Vert \ \text {for some} \ \eta _{k} \in [0, 1). \end{aligned}$$

(22)

    2.3. Set

$$\begin{aligned} y_{k} = x_{k}+d_{k, l_{k}}. \end{aligned}$$

    2.4. Compute $F(y_{k})$.

    2.5. For $m=0,1,2, \cdots , m_{k}-1$, apply FPAE method to the second equation of (5):

$$\begin{aligned} V(x_{k}) h_{k,m+1} = V(x_{k}) h_{k, m} - \alpha \left[ (W(x_{k})+i T(x_{k})) h_{k, m} + F(x_{k})\right] , \end{aligned}$$

and obtain $h_{k, m_{k}}$ such that

$$\begin{aligned} \Vert F(y_{k})+F'(x_{k})h_{k, m_{k}}\Vert \le {\tilde{\eta }}_{k}\Vert F(y_{k})\Vert \ \text { for some} \ {\tilde{\eta }}_{k} \in [0, 1). \end{aligned}$$

(23)

    2.6. Set

$$\begin{aligned} x_{k+1}=y_{k}+h_{k, m_{k}}. \end{aligned}$$

Similarly, in practice, $V(x)=W(x)$ is generally taken, then we get:

$$\begin{aligned} M(\alpha ;x) = I-\alpha W(x)^{-1}F'(x), \ N(\alpha ;x) = \alpha W(x)^{-1}, \end{aligned}$$

Set

$$\begin{aligned} B(\alpha ;x) = \frac{1}{\alpha }W(x), \ C(\alpha ;x) = \frac{1}{\alpha }W(x)-F'(x). \end{aligned}$$

then

$$\begin{aligned} M(\alpha ;x) = B(\alpha ;x)^{-1}C(\alpha ;x), \\ F'(x) = B(\alpha ;x)- C(\alpha ;x). \end{aligned}$$

The equivalent formula of the iteration:

$$\begin{aligned} y_{k}= & {} x_{k}-\sum _{i=0}^{l_{k}-1} M(\alpha ; x_{k})^{i} N(\alpha ; x_{k}) F(x_{k}), \nonumber \\= & {} x_{k}-\left( I-M(\alpha ; x_{k})^{l_{k}}\right) F'(x_{k})^{-1} F(x_{k}), \end{aligned}$$

(24)

$$\begin{aligned} x_{k+1}= & {} y_{k} - \left( I-M(\alpha ; x_{k})^{l_{k}}\right) F'(x_{k})^{-1} F(x_{k}). \end{aligned}$$

(25)

By similar demonstration of convergence properties of Newton-FPAE method, we can derive the following local convergence theorem and semi-local convergence theorem:

Theorem 3

(Local convergence of modified Newton-FPAE method under Lipschitz condition) Under the condition of Assumption 1, for $0< \alpha < \dfrac{2}{1+\rho ^2(W(x_*)^{-1}T(x_*))}$, any $x_0 \in {\mathbb {N}}(x_*,r)$ and any positive integer sequences $\{l_k\}$ and $\{m_k\}$, where $r\le r_0 :=\{r_1,r_2\}$, and

$$\begin{aligned} r_{1} = min\{ \frac{\tau \theta \alpha }{8 \gamma L_{1}+4 \alpha \gamma L}, \frac{\alpha }{4\gamma L_1}\}, \ \ r_{2}=\frac{1-2 \beta \gamma [(\tau +1) \theta ]^{u}}{3 \gamma L}, \end{aligned}$$

with

$$\begin{aligned} u = \min \{ l_*,m_* \}, \ l_{*}=\liminf _{k \rightarrow \infty } l_{k}, \ m_{*}=\liminf _{k \rightarrow \infty } m_{k}, \end{aligned}$$

and the constant u satisfies

$$\begin{aligned} u > \left\lfloor -\frac{\ln (2 \beta \gamma )}{\ln ((\tau +1) \theta )} \right\rfloor , \end{aligned}$$

where $\lfloor \cdot \rfloor$ represent for the smallest integer not less than the corresponding value, $\tau \in \left( 0,\frac{1-\theta }{\theta }\right)$ is a positive constant, and

$$\begin{aligned} \theta :=\theta \left( \alpha ; x_{*}\right) =\Vert M(\alpha ; x_{*}) \Vert \le \sqrt{ (1-\alpha )^2 + \alpha ^2\rho ^2(W(x_*)^{-1}T(x_*))} =: \delta (\alpha ;x_*) <1. \end{aligned}$$

We still use the notation

$$\begin{aligned} g(t;v) = \frac{2 \gamma }{1-\gamma L t}\left( L t+\beta [(\tau +1) \theta ]^{v}\right) , \end{aligned}$$

then the iteration sequence $\{x_k\}$ generated by modified Newton-FPAE method converges to $x_*$, and

$$\begin{aligned} \limsup _{k \rightarrow \infty } \Vert x_{k}-x_{*}\Vert ^{\frac{1}{k}} \le g(r_{0};u)^{2}. \end{aligned}$$

Proof

It is similar to the theorem 1 unless the recursive relationship of $\Vert x_{k}-x_{*}\Vert$.

$$\begin{aligned} \Vert y_{k}-x_{*}\Vert&= \Vert x_{k}-x_{*}-(I-M(\alpha ; x_k)^{l_{k}}) F'(x_{k})^{-1} F(x_{k})\Vert \\&\le \Vert x_{k}-x_{*}-F'(x_{k})^{-1} F(x_{k})\Vert + \Vert M(\alpha ;x_k)^{l_{k}}\Vert \cdot \Vert F'(x_{k})^{-1} F(x_{k})\Vert \\&\le \frac{\gamma }{1-\gamma L\Vert x_k-x_{*}\Vert } \frac{3L}{2} \Vert x_{k}-x_{*}\Vert ^{2} \\&\quad + [(\tau +1) \theta ]^{l_{k}} \frac{\gamma }{1-\gamma L\Vert x_k-x_{*}\Vert } \left( \frac{L}{2}\Vert x_{k}-x_{*}\Vert ^{2}+2 \beta \Vert x_{k}-x_{*}\Vert \right) \\&= \frac{(3+[(\tau +1) \theta ]^{l_{k}}) \gamma L}{2(1-\gamma L\Vert x_k-x_{*}\Vert )} \Vert x_{k}-x_{*} \Vert ^{2} + \frac{2 \beta \gamma [(\tau +1) \theta ]^{l_{k}} }{1-\gamma L\Vert x_k-x_{*}\Vert } \Vert x_{k}-x_{*}\Vert \\&\le \frac{2 \gamma }{1-\gamma L\Vert x_k-x_{*}\Vert } \left( L\Vert x_{k}-x_{*}\Vert + \beta [(\tau +1) \theta ]^{l_{k}} \right) \cdot \Vert x_{k}-x_{*}\Vert \\&= g\left( \Vert x_{k}-x_{*}\Vert ; l_{k}\right) \cdot \Vert x_{k}-x_{*}\Vert \\&< g(r_{0} ; u) \Vert x_{k}-x_{*} \Vert <\Vert x_{k}-x_{*}\Vert , \end{aligned}$$

$$\begin{aligned} \Vert x_{k+1}-x_{*}\Vert&= \Vert y_{k}-x_{*}-(I-M(\alpha ; x)^{m_{k}}) F'(x_{k})^{-1} F(x_{k})\Vert \\&\le \Vert y_{k}-x_{*}-F'(x_{k})^{-1} F(y_{k})\Vert + \Vert M(\alpha ;x)^{m_{k}}\Vert \cdot \Vert F'(x_{k})^{-1} F(y_{k})\Vert \\&\le \frac{\gamma }{1-\gamma L\Vert x_k-x_{*}\Vert } \big (\frac{L}{2} \Vert y_k-x_{*}\Vert + L\Vert x_k-x_*\Vert \big ) \Vert y_k-x_*\Vert \\&\quad + [(\tau +1) \theta ]^{m_{k}} \frac{\gamma }{1-\gamma L\Vert x_k-x_{*}\Vert } \left( \frac{L}{2}\Vert y_{k}-x_{*}\Vert ^{2}+2 \beta \Vert y_{k}-x_{*}\Vert \right) \\&\le \bigg (\frac{\gamma L}{1-\gamma L\Vert x_k-x_*\Vert } \bigg ( \frac{1+[(\tau +1)\theta ]^{m_k}}{2}\Vert y_k-x_*\Vert +\Vert x_k-x_*\Vert \bigg ) \\&\quad +\frac{2\beta \gamma [(\tau +1)\theta ]^{m_k}}{1-\gamma L\Vert x_k-x_*\Vert } \bigg )\Vert y_k-x_*\Vert \\&\le \frac{2\gamma g(\Vert x_k-x_*\Vert ;l_k)}{1-\gamma L\Vert x_k-x_*\Vert }\\&\left( \frac{1+g(\Vert x_k-x_*\Vert ;l_k)}{2} \cdot L\Vert x_k-x_*\Vert +\beta [(\tau +1)\theta ]^{m_k} \right) \Vert x_k-x_*\Vert \\&< \frac{2\gamma g(\Vert x_k-x_*\Vert ;l_k)}{1-\gamma L\Vert x_k-x_*\Vert } \left( L\Vert x_k-x_*\Vert +\beta [(\tau +1)\theta ]^{m_k} \right) \Vert x_k-x_*\Vert \\&= g(\Vert x_k-x_*\Vert ;l_k)g(\Vert x_k-x_*\Vert ;m_k)\Vert x_k-x_*\Vert \\&\le g(\Vert x_k-x_*\Vert ;u)^2\Vert x_k-x_*\Vert \\&< g(r_0;u)^2\Vert x_k-x_*\Vert <\Vert x_k-x_*\Vert . \end{aligned}$$

(26)

Then by the analogous derivation of Theorem 1, we conclude that $x_k$ converges to $x_*$, and

$$\begin{aligned} \limsup _{k \rightarrow \infty } \Vert x_{k}-x_{*}\Vert ^{\frac{1}{k}} \le g(r_{0};u)^{2}. \end{aligned}$$

$\square$

Theorem 4

(Semi-local convergence of modified Newton-FPAE method under Lipschitz condition) Under the condition of Assumption 2 and Lemma 4, for $0< \alpha <$$\dfrac{2}{1+\rho ^2(W(x_0)^{-1}T(x_0))}$ and any positive integer sequences $\{l_k\}$ and $\{m_k\}$. We define $r\le r_0 :=\{r_1,r_2\}$, where

$$\begin{aligned} r_{1} = min\{ \frac{\tau \theta \alpha }{8 \gamma L_{1}+4 \alpha \gamma L}, \frac{\alpha }{4\gamma L_1}\}, \ \ r_{2}=\frac{b-\sqrt{b^{2}-2 a c}}{a}, \end{aligned}$$

define

$$\begin{aligned} u = \min \{ l_*,m_* \}, \ l_{*}=\liminf _{k \rightarrow \infty } l_{k}, \ m_{*}=\liminf _{k \rightarrow \infty } m_{k}. \end{aligned}$$

and the constant u satisfies

$$\begin{aligned} u > \left\lfloor -\frac{\ln (2 \beta \gamma )}{\ln ((\tau +1) \theta )} \right\rfloor , \end{aligned}$$

where $\lfloor \cdot \rfloor$ denotes the smallest integer no less than the corresponding value, $\tau \in \left( 0,\frac{1-\theta }{\theta }\right)$ is a positive constant and

$$\begin{aligned} \theta :=\theta (\alpha ; x_{0}) = \Vert M(\alpha ; x_{0})\Vert \le \delta ^{V}(\alpha ; x_{0})<1, \end{aligned}$$

then the iteration sequence $\{x_k\}$ generated by modified Newton-FPAE method convergence to $x_*$, and satisfies

$$\begin{aligned} F(x_*) = 0. \end{aligned}$$

Proof

It is similar to the proof of theorem 2.

Define the sequences $\{t_k\},\{s_k\}$ with $t_0=0$ :

$$\begin{aligned} \left\{ \begin{array}{ll} s_k = t_k-\dfrac{g(t_k)}{h(t_k)}, \\ t_{k+1} = s_k-\dfrac{g(s_k)}{h(t_k)}. \end{array}\right. \end{aligned}$$

(27)

Then prove the following conclusion by the similar derivation of (22)

$$\begin{aligned} \left\{ \begin{array}{lllll} \Vert x_{k}-x_{0}\Vert \le t_{k}-t_{0}, \\ \Vert F(x_{k}) \Vert \le \dfrac{1-\gamma Lt_{k}}{\gamma (1+\eta )}(s_{k}-t_{k}), \\ \Vert y_k-x_k\Vert \le s_k-t_k, \\ \Vert F(y_k)\Vert \le \dfrac{1-\gamma Lt_k}{(1+\eta )\gamma }(t_{k+1}-s_k), \\ \Vert x_{k+1}-y_{k}\Vert \le t_{k+1}-s_{k}. \end{array}\right. \end{aligned}$$

(28)

The proof of the rest part is omitted. $\square$

7 Numerical examples

In this section, we show the validity of Newton-FPAE method and modified Newton-FPAE method by comparing them with some other existing methods. For example the Newton-PMHSS method (Zhong et al. 2015). Since the nonlinear HSS-like method in Bai and Yang (2009), the two-stage relaxation method in Bai (1997a) and Bai (1997b) can also solve the weekly nonlinear systems in our numerical examples, we compare our methods with these methods as well. In our experiments, we take $V(x) = W(x)$ as preconditioner of Newton-FPAE method, modified Newton-FPAE method and modified Newton-PMHSS method. The number of iteration steps (denoted as “IT”) and CPU running time (denoted as “CPU time”) are compared. One of the important issues is how to choose the parameters. In our experiment, we use the experimental optimal parameters $\alpha _*$ which minimize the corresponding iteration steps and errors. The numerical results were computed using MATLAB Version R2017b, on a laptop with Core AMD A8-7100 and 8.00 GB of RAM. The CPU running time is recorded by the command “tic-toc”.

Example 7.1 Consider the following nonlinear Helmholtz equation:

$$\begin{aligned} -\Delta u + \sigma _{1} u + i \sigma _{2} u=-e^{u}, \end{aligned}$$

(29)

where $\sigma _{1}$ and $\sigma _{2}$ are real coefficient. Here u satisfies the Dirichlet boundary condition in the rectangular region $D = [0, 1] \times [0, 1]$. By making the finite difference on the N $\times$ N grid with mesh size h=1/(N+1) to discretize the differential equation, complex nonlinear equations corresponding of the following form can be derived:

$$\begin{aligned} F(x)=Mx+\Phi (x)=0, \end{aligned}$$

(30)

where

$$\begin{aligned} M=(K+\sigma _{1} I) + i \sigma _{2}I, \\ \Phi (x)=(e^{x_{1}}, e^{x_{2}}, \cdots , e^{x_{n}} )^{T}, \end{aligned}$$

with

$$\begin{aligned} K=I \otimes B_{N}+B_{N} \otimes I, \end{aligned}$$

and

$$\begin{aligned} B_{N}=\frac{1}{h^{2}} {\text {tridiag}}(-1,2,-1) \in R^{N \times N}. \end{aligned}$$

In this numerical experiment, we take $\sigma _1=1,\sigma _2=10 .$ The initial guess is $x_0=\mathbf{0}$, with 0 being the zero vector, and the termination condition of the outer iteration is

$$\begin{aligned} \frac{\Vert F(x_{k})\Vert }{\Vert F(x_{0})\Vert } \le 10^{-6}. \end{aligned}$$

The prescribed tolerance $\eta _k$ and ${\tilde{\eta }}_k$ for controlling the accuracy of the inner iteration are both set to be $\eta$. Which means that the stopping criterions for the inner iterations of modified Newton-PMHSS (MN-PMHSS), modified Newton-FPAE (MN-FPAE), and Newton-FPAE methods are set to be

$$\begin{aligned} \frac{\Vert F'(x_k)d_{k,l_k}+F(x_k)\Vert _2}{\Vert F(x_k)\Vert _2} \le \eta . \end{aligned}$$

In this numerical experiment, we choose $\eta _{k}=\tilde{\eta _{k}}=\eta =0.1,0.2,0.4$. The size of the grids are $N=30,60,90,$ respectively.

Table 1 The experimental optimal values $\alpha _*$ for the three iterations in Example 7.1

The experimental optimal iteration parameters $\alpha _*$ for MN-PMHSS method, Newton-FPAE method and MN-FPAE method with different $\eta$ at $N=30, 60, 90$ are given in Table 1. And the experimental results of the three methods at $N=30, 60, 90$ are given in Tables 4, 5, 6, respectively. In these tables, “Outer IT” denotes the outer iteration steps, and the “Inner IT” denotes the total inner iteration steps.

Table 2 Numerical results for $N=30$ in Example 7.1

Table 3 Numerical results for $N=60$ in Example 7.1

Table 4 Numerical results for $N=90$ in Example 7.1

As can be seen from Tables 2, 3, and 4, Newton-FPAE method and MN-FPAE method have significant advantages in the number of iterations when solving this problem with respect to MN-PMHSS method. For example, the inner iteration steps of Newton-FPAE and MN-FPAE are about half of those of MN-PMHSS. The CPU time of Newton-FPAE is a little longer than MN-PMHSS, but the CPU time decrease to just a little more than half the time of Newton-FPAE and MN-PMHSS when MN-FPAE method is used.

Table 5 Numerical results for nonlinear HSS-like method in Example 7.1

Table 6 Numerical results for two-stage relaxation method in Example 7.1

The reason why inner iteration steps of Newton-FPAE method and MN-FPAE method are less than MN-PMHSS method is mainly because the inner iteration of the two methods is better. That is, FPAE iteration has a higher efficiency than PMHSS iteration. Since modified Newton method is superior than Newton method, the CPU time of Newton-FPAE is a little longger than MN-PMHSS. While when using MN-FPAE method, the CPU time reduced a lot. So we can conclude that modified Newton-FPAE method has much advantage in solving this example.

Table 5 shows the experimental optimal iteration parameters of nonlinear HSS-like method and its numerical results. Table 6 displays the numerical results of two-stage relaxation method with parameter $(\omega , \gamma ) = (1.0,1.0),\ (1.2,1.2),\ (1.5,1.5)$, respectively. For simplicity’s sake, here in the two-stage relaxation method we set $B = M, \ C = O,\ D = diag(B)$, L, U are the strictly lower, strictly upper triangular matrices of $(-B)$, and $s = 2$. It is obvious that our methods are superior in this example.

Example 7.2 Considering the following nonlinear system

$$\begin{aligned} \left\{ \begin{array}{ll} u_t-(\alpha _1+i \beta _1)(u_{xx}+u_{yy})+\varrho u=- (\alpha _2+i \beta _2) u^{\frac{4}{3}},\;\;\;\;\; \mathrm{in}\;\; (0, 1] \times \Omega ,\\ u(0,x, y)=u_0(x,y), \;\; \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \mathrm{in} \;\; \Omega ,\\ u(t,x,y)=0,\;\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \mathrm{on} \;\; (0, 1] \in \partial \Omega , \end{array}\right. \end{aligned}$$

where $\Omega =(0, 1)\times (0, 1)$, $\partial \Omega$ is the boundary of $\Omega$, and $\varrho$ is a positive constant used to measure the magnitudes of the reaction term. By applying the centered finite difference scheme on the equidistant discretization grid with the stepsize $\Delta t=h=\frac{1}{N+1}$, the system of nonlinear equations (1) is obtained with following form

$$\begin{aligned} F(u)= Mu+(\alpha _2+i \beta _2)h \Delta t \Psi (u) =0, \end{aligned}$$

(31)

where N is a prescribed positive integer,

$$\begin{aligned} M = h(1+\varrho \Delta t) I_n + (\alpha _1+i \beta _1) \frac{\Delta t}{h} (A_N \otimes I_N+I_N \otimes A_N), \\ \Psi (u) = (u^{\frac{4}{3}}_1, u^{\frac{4}{3}}_2, \cdots , u^{\frac{4}{3}}_n)^{T}, \end{aligned}$$

with $A_{N} = tridiag(-1, 2, -1)$. Here, $\otimes$ the Kronecker product symbol, and $n=N \times N$.

Then the Jacobian matrix is

$$\begin{aligned} F'(u)=M+\frac{4}{3}(\alpha _2+i \beta _2)h \Delta t diag(u^{\frac{1}{3}}_1, u^{\frac{1}{3}}_2, \cdots , u^{\frac{1}{3}}_n). \end{aligned}$$

Obviously, $u_* = 0$ is a solution of (31), so $F'(u_*) = M$, then the following inequality holds,

$$\begin{aligned} \Vert F'(u)-F'(u_*)\Vert \le \frac{4}{3}\sqrt{\alpha ^2+\beta ^2}h \Delta t \Vert u-u_*\Vert ^{\frac{1}{3}}. \end{aligned}$$

In actual computations, the coefficients are set to be $\alpha _1 = 1, \beta _1 = 0.1, \alpha _2 = 1, \beta _2 = 0.1$. The initial guess is $u_0 = 1$. The stopping criterion for the outer iteration is set to be

$$\begin{aligned} \frac{\Vert F(u_k)\Vert _2}{\Vert F(u_0)\Vert _2} \le 10^{-6}, \end{aligned}$$

and the stopping criterions for the inner iterations of MN-PMHSS, MN-FPAE, and Newton-FPAE methods are set to be

$$\begin{aligned} \frac{\Vert F'(u_k)d_{k,l_k}+F(u_k)\Vert _2}{\Vert F(u_k)\Vert _2} \le \eta = 0.1. \end{aligned}$$

Table 7 The experimental optimal values $\alpha _*$ in Example 7.2

The experimental optimal iteration parameters $\alpha _*$ for MN-PMHSS method, Newton-FPAE method and MN-FPAE method at $N=30, 60, 90$ are given in Table 7.

Tables 8, 9, 10 have shown the numerical results of MN-PMHSS method, Newton-FPAE method and MN-FPAE method. Here “Outer IT” denotes the outer iteration steps, and the “Inner IT” denotes the total inner iteration steps just like Example 7.1. Table 11 is about the optimal parameters of nonlinear HSS-like method and its numerical results. Table 12 shows the numerical results of two-stage relaxation method with parameter $(\omega , \gamma ) = (1.0,1.0),\ (1.2,1.2),\ (1.5,1.5)$, respectively. Here we take $B = M,\ C = O$, $D = diag(B)$, $s = 2$, and L, U are strictly upper triangular matrices of $(-B)$, respectively.

Table 8 Numerical results for $N=30$ in Example 7.2

Table 9 Numerical results for $N=60$ in Example 7.2

Table 10 Numerical results for $N=90$ in Example 7.2

Table 11 Numerical results for nonlinear-HSS like method in Example 7.2

Table 12 Numerical results for two-stage relaxation method with $N=30$ in Example 7.2

Table 13 Numerical results for two-stage relaxation method with $N=60$ in Example 7.2

Table 14 Numerical results for two-stage relaxation method with $N=90$ in Example 7.2

As can be seen from the above tables, in Example 7.2, our methods showed the similar advantages in Example 7.1 when compared with MN-PMHSS method and nonlinear HSS-like method. But when compared with the two-stage relaxation method, although the number of iteration are still much less than the two-stage relaxation method, sometimes it takes more CPU running time. That is mainly because that the computation in the two-stage relaxation method is faster when the command “sparse()” is used to store and compute huge-scale matrices in the iteration.

Example 7.3 Considering the nonlinear system ${F(x) = 0}$, where ${x=(x_1,x_2,...,x_n)^T}$ and $F = (F_1,F_2,...,F_n)^T$, with

$$\begin{aligned} {F_j(x)} = \left( (5+i)-(2+i)x_j\right) x_j - x_{j-1} - x_{j+1}+1,j=1,2,...,n, \end{aligned}$$

and $x_0= x_{n+1}=0.$

Then the Jacobian matrix of F(x) is

$$\begin{aligned} {F'(x)}= \left( \begin{array}{ccccc} (5+i)-(4+2i)x_{1} &{} -1 &{} \cdot \cdot \cdot &{} 0 &{} 0\\ -1 &{} (5+i)-(4+2i)x_{2} &{} \cdot \cdot \cdot &{} 0 &{} 0\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0 &{} 0 &{} \cdot \cdot \cdot &{} (5+i)-(4+2i)x_{n-1} &{} -1\\ 0 &{} 0 &{} \cdot \cdot \cdot &{} -1 &{}(5+i)-(4+2i)x_{n}\\ \end{array}\right) . \end{aligned}$$

We set the initial guess $x^{(0)}=(-1,...,-1)^T$. Now we solve this nonlinear equation by MN-PMHSS, Newton-FPAE method and MN-FPAE method. The stopping criterion for the outer iteration is set to be

$$\begin{aligned} \frac{\Vert F(x^{(k)})\Vert _2}{\Vert F(x^{(0)})\Vert _2} \le 10^{-12}, \end{aligned}$$

and the stoping criterion of the inner iteration is

$$\begin{aligned} \frac{\Vert F'(x^{(k)})d_{k,l_k}+F(x^{(k)})\Vert _2}{\Vert F(x^{(k)})\Vert _2} \le \eta . \end{aligned}$$

Here $x^{(k)}$ is the results after k-th iteration. We set the inner stop critierion $\eta _{k}=\tilde{\eta _{k}}=\eta =0.1,0.2,0.4$, the dimension of the problem $n = 500,1000,2000.$ Of course, the experimentally optimal parameters $\alpha$ are used in MN-PMHSS, Newton-FPAE and MN-FPAE methods. Table 15 shows the experimental optimal parameters.

Table 15 The experimental optimal values $\alpha _*$ for the three iterations in Example 7.3

Table 16 Numerical results for $n=500$ in Example 7.3

Table 17 Numerical results for $n=1000$ in Example 7.3

Table 18 Numerical results for $n=2000$ in Example 7.3

From Tables 16, 17, 18, we can see that the number of iterations in Newton-FPAE and MN-FPAE method are less than MN-PMHSS. And especially the modified Newton-FPAE takes less CPU running time, which is similar to the example 1.

Table 19 Numerical results for nonlinear HSS-like method in Example 7.3

Table 20 Numerical results for two-stage relaxation method in Example 7.3

But when compared with the nonlinear HSS-like method in Table 19 and the two-stage relaxation method in Table 20, they don’t take much advantages. In our opinion, the MN-FPAE method and Newton-FPAE method are very suitable for those problems whose Jacobian matrices’s image parts are not so big compared with real parts. But, if in practical computation Newton-FPAE method and MN-FPAE method are not superior than some other methods, we can use some preconditioner techniques or modified methods in the inner iteration to improve them. For example, see Section 3 of Xiao and Wang (2018), the PFPAE method.

8 Conclusions

Iterative methods for solving nonlinear systems are of great significance in practical applications. For nonlinear systems with complex symmetric Jacobian matrices, the most classical iterative scheme is the Newton method. In this paper, by applying an FPAE method as an inner iteration of the Newton method and modified Newton method, the corresponding Newton-FPAE method and the modified Newton-FPAE method are obtained, respectively. Local and semi-local convergence of the two iterative schemes under Lipschitz conditions are proved.

The numerical experiments show that the modified Newton-FPAE methods have obvious advantages over some other methods in terms of the number of iterations and CPU time. Our methods make some progress in the improving of efficiency when solving this kind of nonlinear systems. In practical use, we can also take some preconditioner techniques or modified methods in the inner iteration to improve the efficiency.