1 Introduction

The main idea of direct adaptive control (DAC) is to directly modify a set of the control law’s parameters to design a stable closed-loop system. A direct adaptive controller is established by combining both the control and adaptive laws. The adaptive law instantly estimates the parameters of the control law, which can be designed from the ideal case, where the system’s parameters are certain and well defined (Spooner et al., 2002; Ioannou & Sun, 1996, 1988). Several settings of approximator structures, such as neural networks and fuzzy systems, are discussed in Spooner et al. (2002). By adjusting their parameters, these structures serve as universal approximators to represent the controller of the system in the direct adaptive approach. This paper contributes to the control community by designing a new DAC based on fractional-order techniques.

Fractional adaptive control research activity is dramatically increasing because of its ability to simulate complex problems in many modern applications such as AI and machine learning. The authors in Liu et al. (2017) use the adaptive fuzzy backstepping control method to compensate for the uncertainty in a class of fractional-order nonlinear systems. The backstepping control technique can be further extended to apply to the fractional-order nonlinear systems. Fractional-order adaptation laws are obtained as a natural result of fractional-order derivative of Lyapunov function. In Yin and Chu (2010), adaptive synchronization of two chaotic system with unknown parameters modeled by a fractional-order differential equation was studied while in Lin and Lee (2011), adaptive fuzzy sliding mode control (SMC) is proposed to synchronize two time-delay chaotic fractional-order systems with uncertainties. The model reference adaptive control problem is applied to fractional-order linear and nonlinear systems and investigated in Wei et al. (2014), where the reference model adaptive control scheme is extended to fractional-order systems, while in Chen et al. (2016) indirect model reference adaptive control problem for fractional-order systems is studied. The estimation of adaptive parameter schemes for classes of linear fractional-order (FO) systems was presented in Rapaic and Pisano (2014). The work Shen and Lam (2016) has given for non-discrete-time positive FO delay systems and has provided the sufficient and necessary condition for stability. It has shown that the \(L_{\infty }\) gain of this system does not depend on the magnitude of delays and can be determined by the matrices of the system. In Lu and Chen (2010), the authors have introduced a necessary and sufficient condition for the strong asymptotic stability of systems modeled by FO derivative equations with the order between 0 and 1. They demonstrate the results in terms of linear matrix inequality (LMI). This paper has been commented on by the authors of Aguiar et al. (2015). They have proven that the conditions are sufficient but not necessary. Studying, analyzing or improving the performance of fractional-order control systems is a promising area of research. However, fractional-order systems are still insufficiently utilized in real-life applications.

Despite the fact that there are some systems’ components that have fractional properties which entail fractional phenomena (Li et al., 2009), the physical meaning of a fractional derivative is still not well understood (Podlubny, 2002). Moreover, most of the systems in the control literature are already modeled by integer-order differential equations. However, in many researches, fractional calculus, when used as a controller, exhibits advantages over its integer-order counterpart (Aburakhis & Ordóñez, 2018). The authors in Pan and Das (2012) have shown that the FO PID controller has better performance compared to the classical PID controller due to its additional degrees of freedom. In Sun and Ma (2017), the authors used fractional calculus to design a practical adaptive terminal SMC for tracking problem, and they have shown that fractional-order sliding mode control is more accurate and faster when compared with the conventional one. In Ibrahim (2013), fractional calculus has been used to generalize differential polynomial neural networks and the author suggests using this method for the modeling of complex systems. The results show that the fractional differential polynomial neural network satisfies a quicker approximation to the exact value compared to the classical method. The authors in Ullah et al. (2016) generalize the sliding mode control method by using fractional calculus derivatives. They propose to use a fuzzy logic system to reduce the discontinuous switching gain. Similarly, in Efe (2008), a fractional integration scheme has been discussed for fractional SMC. Based on former studies of fractional-order operators in the area of control engineering, there is significant evidence of the superiority of fractional-order compared to classical integer-order operators in terms of robustness and performance (Malek & Chen, 2016). However, the fractional-order adaptive laws for the above studies resulted from taking the fractional-order derivative of the error manifold. In the proposed method, we chose the integer-order derivative for the error manifold. This choice is more practical since the system we are controlling is already modeled using ordinary integer-order differential equations. While many past studies tried to use the fractional-order derivative of the adaptive law, they had to turn to the error manifold’s fractional-order derivative. In contrast, we reserve the fractional-order derivative’s long-term memory benefits solely for updating the controller’s parameters. In this way, we offer a clearer distinction and practicality in real-world applications.

In this paper, a novel version of fractional-order (FO) adaptive law for direct adaptive control is introduced, together with a rigorous proof of closed-loop stability. The new FO-DAC is based on Caputo derivative due to its advantages over the Riemann–Liouville derivative, which results from the integer derivative of the Riemann–Liouville definition. The Riemann–Liouville derivative of a constant is not zero and also has an initialization problem. When the Riemann–Liouville derivative is used, zero initial conditions are necessary to avoid singularity problems, but zero initial conditions cannot be used for the parameter error. The Caputo derivative avoids these two problems because its initial conditions take on the same form as for integer-order derivative (Podlubny, 1998; Xue & Bai, 2017), and the Caputo derivative of a constant is 0 (Monje et al., 2010; Diethelm, 2010). Physically, the Caputo derivative is much better understood and more suitable for real-world problems (Podlubny, 1998; Xue & Bai, 2017). The technique introduced in this paper is an improvement over existing methods because it uses an integer-order stable manifold with a FO adaptive law, which makes this approach implementable in practice. Since most control systems are already modeled using integer-order IO differential equations, the integer-order error manifold is more practical to consider. On the other hand, the FO derivative for the adaptation law significantly increases the design degrees of freedom (Monje et al., 2010). This advantage can enable the designer to enhance the controller’s performance beyond that of the approximator’s structure in classical adaptive control. Specifically, the fractional-order derivative provides an added degree of freedom, offering improved control energy and fast response. This is in contrast to classical adaptive control methods, which might primarily focus on optimizing the response speed through an increase in the controller’s learning rate. By leveraging the advantages of our method, designers can achieve better performance than with traditional approximator structures. While classical methods often boost response speed by increasing the controller’s learning rate, as referenced in Noriega and Wang (1998), our method provides comprehensive improvements to controller functionality.

The paper is formed as follows: Section 2 reviews some of the fundamental FO system concepts and also function approximation, and Sect. 3 describes the class of nonlinear systems under consideration. Section 4 first goes over DAC upon which the framework for the main result of the novel FO-DAC technique is based. Section 5 contains an illustrative example, and finally, Sect. 6 concludes the paper.

2 Preliminaries

Here, fractional-order systems are reviewed and linked to the paper’s ideas. Firstly, we introduce the Riemann–Liouville integral that is required to generalize the Lyapunov candidate function in Section 4.1. Secondly, we introduce the definitions of the Riemann–Liouville and Caputo derivatives. The Riemann–Liouville derivative is the resultant of from taking the integer-order derivative to the Lyapunov candidate function. However, this result needs to be aligned with the Caputo derivative. Therefore, we introduce a new lemma that generalizes the equality between the two definitions.

2.1 A Basic Guide to Fractional Calculus

A non-integer-order derivative operator is a generalization of the classical integer-order derivative operator. There are too many definitions for fractional-order derivative (Li, 2015; Monje et al., 2010), but the most frequently used definitions are the Riemann–Liouville definition,

$$\begin{aligned} D^\nu h(t)= \frac{1}{\Gamma (m-\nu )} \frac{\textrm{d}^m}{\textrm{d}t^m} \int _0^t (t-u )^{m-\nu -1}h(u ) \textrm{d}u, \end{aligned}$$
(1)

where \(\Gamma (\cdot )\) describes the Gamma function, and the Caputo definition,

$$\begin{aligned} D_*^\nu h(t)= \frac{1}{\Gamma (m-\nu )} \int _0^t (t-u )^{m-\nu -1}h^{(m)}(u ) \textrm{d}u, \end{aligned}$$
(2)

where \( m-1< \nu < m \), and \(m \in \mathbb {N_+}\). Both use the Riemann–Liouville fractional integral operator of order \(\nu \), which is defined as

$$\begin{aligned} I^{\nu } h(t) = \frac{1}{\Gamma (\nu )} \int _0^t (t-u )^{\nu -1}h(u ) \textrm{d}u, \end{aligned}$$
(3)

where \(t \in {\mathbb {R}}^+\), \(\nu \in {\mathbb {R}}^+\) and \(h:{\mathbb {R}} \rightarrow {\mathbb {R}}\) is an m-times continuously differentiable function (Podlubny, 1998; Diethelm, 2010; Monje et al., 2010). Till now there is not a clear enough understanding of the physical and geometric meaning of the fractional-order integration or differentiation (Podlubny, 2002). However, the general interpretation by Pan and Das (2012) is that the area under the curve, which can be imagined by the IO integration, varies as time proceeds while the integral keeps a memory all of the past values in FO integration. The most important property of this operator is

$$\begin{aligned} \lim _{\nu \rightarrow 0^+ }I^\nu h(\cdot )= h(\cdot ). \end{aligned}$$

The Caputo derivative operator (Diethelm, 2010; Li, 2015), which will be utilized in this paper, takes the integer-order differentiation of the function first, i.e., \(D_*^\nu h(t)= I^{m-\nu } D^{m} h(t)\), while the Riemann–Liouville is the opposite of it, \( D^\nu h(t)= D^m I^{m-\nu }h(t),\) where \( m = \lceil \nu \rceil \), and \(\lceil \cdot \rceil \) is the ceiling function. The largest difference between the two definitions is the derivative of a constant. It can be noticed from (1) and (2), the Caputo derivative of a constant is zero, unlike the Riemann–Liouville operator, which is stated in the following lemma.

Lemma 1

(Monje et al., 2010; Diethelm, 2010) The Caputo derivative of a constant is zero. For any constant \(c \in {\mathbb {R}},\)

$$\begin{aligned} D_*^\nu c=0. \end{aligned}$$

For this reason, the Caputo derivative can be used to model the rate of change. Also, one of the other features of the Caputo derivative is that the initial conditions of the Caputo-based fractional differential equations are in the form of integer derivatives, which is the same form as that of ordinary differential equations. This feature makes this derivative more amenable in practical situation. This paper will use the FO Caputo derivative to represent the FO adaptive law. However, the stability analysis requires the use of the Riemann–Liouville derivative, and its relationship to the Caputo derivative as it will be shown later in Sect. 4.1.

Lemma 2

(Diethelm, 2010) For t, \(\nu \), and m defined above, the relationship between Caputo and Riemann–Liouville operators is

$$\begin{aligned} D_*^\nu h(t) = D^\nu h(t) - \sum _{k=0}^{m-1}\frac{t^{k-\nu }}{\Gamma (k+1-\nu ) }h^{(k)}(0). \end{aligned}$$
(4)

The following Lemma generalizes the equality between the Caputo and Riemann–Liouville derivatives. It will be used directly in the stability proof.

Lemma 3

For \(t \in {\mathbb {R}}^+\), \(m, {\bar{m}} \in {\mathbb {N}}_+\) the Caputo and Riemann–Liouville derivatives of the continuously differentiable function \( f(t)=\left( h(t)-h(0)\right) ^{{\bar{m}}} \) are equal. That is,

$$\begin{aligned} D^\nu \left( h(t)-h(0)\right) ^{{\bar{m}}} =D_*^\nu \left( h(t)-h(0)\right) ^{{\bar{m}}}, \end{aligned}$$

if \({\bar{m}} \ge m \), where \(m-1< \nu < m,\) and \(h: {\mathbb {R}} \rightarrow {\mathbb {R}}\) is a continuously m-times differentiable function.

Proof

From Lemma 2, the Caputo derivative and Riemann–Liouville derivative are equal if the last term of (4) is equal to zero, which can be ensured if \(f(0), {\dot{f}}(0), \dots , f^{(m-1)}(0)\) are equal to zero. By letting

$$\begin{aligned} f(t)=\left( h(t)-h(0)\right) ^{{\bar{m}}}, \end{aligned}$$

where \({\bar{m}} \in {\mathbb {N}}_+\), the initial condition of f(t) and its derivatives up to the \(({\bar{m}}-1)^{th}\) one are also zero since the term in parenthesis is present in all high order terms. \(\square \)

Lemma 4

For \(t \in {\mathbb {R}}^+\), when \(\nu =1\) the Caputo derivative becomes the classical integer-order derivative,

$$\begin{aligned} D_*^1 h(t)=\frac{\textrm{d}}{\textrm{d}t}h(t). \end{aligned}$$

Proof

See Appendix A. \(\square \)

Recently, many researchers have delved into the stability of fractional-order systems. For example, the stability of LTI systems is discussed in Monje et al. (2010), while Li et al. (2009), Li et al. (2010) present a fractional Lyapunov direct method for fractional-order nonlinear dynamic systems. Despite the insights offered by these works, our research takes a different approach. One of the main contributions of our paper is addressing systems in the traditional integer-order differential equation format while employing fractional-order derivatives for the adaptation mechanism.

3 Class of Systems

Consider the normal form of an input–output feedback linearizable nonlinear system

$$\begin{aligned} \begin{aligned} {\dot{q}}&= \phi (q,z),\\ {\dot{z}}&= A_c z+b_c \left( f(q,z)+g(q,z) u\right) , \end{aligned} \end{aligned}$$
(5)

where \(q \in {\mathbb {R}}^d, z \in {\mathbb {R}}^{n_z}\), \(n_z+d=n\),

$$\begin{aligned} A_c = \begin{bmatrix} 0 &{} 1 &{} 0 &{}\dots &{}0\\ 0 &{} 0 &{} 1 &{}\dots &{}0\\ .\\ .\\ 0 &{} 0 &{} 0 &{}\dots &{}1\\ 0 &{} 0 &{} 0 &{}\dots &{}0\\ \end{bmatrix} \in {\mathbb {R}}^{n_z\times n_z} \end{aligned}$$

and \(b_c=[0,\dots , 0, 1]^\top \in {\mathbb {R}}^{n_z}\)(Khalil, 1996).

In this system, \( q \in {\mathbb {R}}^d \) represents the regulated output states, while \(z \in {\mathbb {R}}^{n_z} \) denotes the zero dynamics. Together, these state vectors describe the complete state of the system.

The functions f(q, z) and g(q, z) represent the nonlinearities of the system. While the exact forms of these functions might be unknown, they possess certain properties that are essential for our control approach, such as the lower bound or the upper bound.

Assumption 1

(Khalil, 1996) The system described in (5) is locally Lipschitz in \([q^\top , z^\top ]^\top \) and piece-wise continuous in t as per the control law \(u=v(t,z)\).

Assumption 1 guarantees the existence and uniqueness of the trajectory z(t) starting from the initial condition z(0) satisfying (5).

Assumption 2

The nonlinear system (5) is minimum phase.

Regulating the error between the output and the reference to zero is the most common control problem. This error and its derivative will be used to deduce the control law. The error manifold is defined as:

$$\begin{aligned} e = k_1(z_1-r)+...+k_{n_z -1}(z_{n_z -1}-{r}^{(n_z -2)})\nonumber \\ +(z_{n_z}-{r}^{(n_z -1)}), \end{aligned}$$
(6)

where r(t) is the reference signal, and its derivatives \({\dot{r}}, \dots , r^{(n_z)}\) are all assumed to be bounded and available, such as via the use of a reference model. The gains \(k_i\) are chosen so that the polynomial

$$\begin{aligned} s^{n_z}+k_{n_z-1}s^{n_z-1}+\dots +k_1 \end{aligned}$$

is Hurwitz. The first derivative of the error manifold is:

$$\begin{aligned} {\dot{e}} = \varkappa (t,z)+f(q,z)+g(q,z)u, \end{aligned}$$
(7)

where \(\varkappa (t,z)=k_1(z_2-{\dot{r}})+...+k_{n_z -1}(z_{n_z}-{r}^{(n_z -1)})-{r}^{(n_z)}.\)

4 Direct Adaptive Control (DAC)

This section is commenced by prefacing integer-order direct adaptive control for the reader’s convenience, and followed by the main contribution of the paper, which is a fractional-order direct adaptive control. The controller can be applied in practice to physical systems modeled by IO differential equations since only the update law of the controller’s parameters is FO.

The adaptive control technique is used to deal with the uncertainties in system (5). There are several schemes of DAC, minimum variance stochastic, self-tuning controllers, model reference adaptive control, Goh (1994), Tan et al. (2013); Mirkin and Gutman (2010). In this paper, adaptation is done to approximate an unknown stabilizing controller directly.

The DAC approach assumes that there exists an unknown ideal static controller that performs a tracking or regulation task, where the tracking task merely means regulating the error between the output and reference to zero. The ideal controller that drives the error system (6) to zero may be considered to be a feedback linearizing controller of the form

$$\begin{aligned} u^*_{FL}=\frac{-1}{g(q,z)}(f(q,z)+\varkappa +k e), \end{aligned}$$
(8)

where \(k>0\), and it can be represented within a compact set \(S\in {\mathbb {R}}^{n+n_z+1}\) as

$$\begin{aligned} u_{FL}^*={\mathcal {F}}({\mathcal {P}}^*,q,z,{\bar{r}}) +w(q,z,{\bar{r}}), \end{aligned}$$
(9)

where \({\mathcal {F}}(\cdot )\) is a universal approximator, \({\mathcal {P}}^*\in {\mathbb {R}}^p\) is an unknown ideal vector of parameters such that the representation error \(w(\cdot )\) is minimized over S and \({\bar{r}}=[r, {\dot{r}},..., r^{(n_z)}]^\top \) (Spooner et al., 2002).

Since \({\mathcal {P}}^*\) is unknown, we will instead use its estimate \(\hat{{\mathcal {P}}}(t)\) to be updated online. Therefore, the unknown controller will be estimated using

$$\begin{aligned} u_{FL}={\mathcal {F}}(q,z,\bar{r,}\hat{{\mathcal {P}}}), \end{aligned}$$
(10)

and \({\bar{r}}\) is defined above. The parameter error

$$\begin{aligned} \tilde{{\mathcal {P}}}=\hat{{\mathcal {P}}}-{\mathcal {P}}^* \end{aligned}$$
(11)

is considered as a new state vector that needs to be regulated to zero or at least be kept inside a compact invariant set.

The error e in (6) denotes the system error, quantifying the deviation of the system’s state z from the desired reference trajectory r(t). On the other hand, the term \(w(q,z,{\bar{r}})\) in (9) represents the representation error introduced when approximating the ideal controller using a universal approximator, where it captures the difference between the ideal and the estimated controller.

Since the DAC approach is based on approximating the controller itself, then the representation error w, which results from the approximator being of finite size p, will be compensated for using a stabilizing term, \(u_s\). Hence, the control law will be in the form

$$\begin{aligned} u = u_{FL}+u_s. \end{aligned}$$
(12)

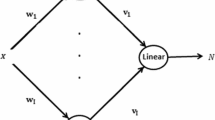
By using a linearly parametrized function approximator with universal approximation properties, such as fuzzy systems and neural networks (Spooner et al., 2002), we can express the relationship as given in (10). This becomes:

$$\begin{aligned} u_{FL}=\hat{{\mathcal {P}}}^\top \zeta (q,z,{\bar{r}}), \end{aligned}$$
(13)

where \( \zeta (q,z,{\bar{r}})\) is a vector of radial basis functions. Hence, the control law (12) is chosen as

$$\begin{aligned} u = \hat{{\mathcal {P}}}^\top \zeta (q,z,{\bar{r}}) + u_s. \end{aligned}$$
(14)

Thereby the derivative of the error manifold is

$$\begin{aligned} {\dot{e}}&= \varkappa (t,z)+f(q,z)+g(q,z)[\hat{{\mathcal {P}}}^\top \zeta (q,z,{\bar{r}}) + u_s],\nonumber \\&= \varkappa (t,z)+f(q,z)+g(q,z)[\hat{{\mathcal {P}}}^\top \zeta (q,z,{\bar{r}}) \nonumber \\&\quad -{{\mathcal {P}}^*}^\top \zeta (q,z,{\bar{r}})+ {{\mathcal {P}}^*}^\top \zeta (q,z,{\bar{r}})+ u_s],\nonumber \\&= \varkappa (t,z)+f(q,z)+g(q,z)[\tilde{{\mathcal {P}}}^{\top }\zeta (q,z,{\bar{r}})+u_s\nonumber \\&\quad -w(q,z,{\bar{r}})]-f(q,z)-\varkappa (t,z)-ke,\nonumber \\&=-ke+g(\tilde{{\mathcal {P}}}^{\top }\zeta (q,z,{\bar{r}})+u_s-w(q,z,{\bar{r}})), \end{aligned}$$
(15)

where \(\hat{{\mathcal {P}}}(t)\in {\mathbb {R}}^p\) is the on-line estimation of the constant but unknown \({{\mathcal {P}}}^{*}\in {\mathbb {R}}^p.\) Furthermore, there are some assumptions that should be considered.

Assumption 3

The function g: \({\mathbb {R}}^n \rightarrow {\mathbb {R}}\) is continuously differentiable (\(g \in C^1\)). Moreover, there exist constants \(L_{w}\), \(L_{g_z}\), \(g_0\), and \(g_1\), such that when \({\mathcal {P}}^*\) is used in (9),

$$\begin{aligned} \left\Vert w(q,z,{\bar{r}})\right\Vert \le L_{w}, ~~ \forall ~ [q^{ \top }, z^{ \top } ]^\top \in S, \end{aligned}$$
(16)

and

$$\begin{aligned} \left\Vert \frac{\partial g}{\partial z}\right\Vert \le L_{g_z}, ~~~~0< g_0 \le g(q,z) \le g_1, ~~ \forall ~ [q^{ \top }, z^{ \top } ]^\top \in S, \end{aligned}$$

with \(L_w\) and \(L_{g_z}\) the smallest bounds.

Assumption 4

The constants \(L_{w}\), \(L_{g_z}\), and \(g_0\) are known. However, Assumption 4 can be dispensed with by estimating these bounds online.

Theorem 1

(Spooner et al., 2002) Consider the system described in (5). Let Assumptions 1, 2, 3, 4 hold. The use of the adaptation law

$$\begin{aligned} \dot{\hat{{\mathcal {P}}}}(t)=-\gamma \zeta (q,z,{\bar{r}}) e, \end{aligned}$$
(17)

where \(\gamma \) is the leaning rate, to update the controller parameters (14), where

$$\begin{aligned} u_s=- \left( L_{w}+\frac{L_{g_z}}{2g_0^2}\vert e \vert \right) \text {sgn}(e) \end{aligned}$$
(18)

is the stabilizing term, guarantees that the error of the system (6) will be asymptotically stable and parameter’s error (11) will be bounded.

More details on stability analysis can be found in Spooner et al. (2002).

4.1 Fractional-Order Direct Adaptive Control (FO-DAC)

This section presents the main result and contribution of this paper. It first provides a rigorous stability analysis of the new FO-DAC scheme that uses an IO error manifold but a FO adaptation law with order \(0< \nu <1\). Then, it replaces the discontinuous stabilizing term with a continuous approximation and derives its impact on the closed-loop behavior. It is shown that traditional IO-DAC is a restrictive example of the general fractional-order direct adaptive control.

A fractional-order integral sliding surface was proposed in Aghababa (2014), while a fuzzy SMC with fractional-order dynamics of a class of second-order systems was derived in Ullah et al. (2016), where the uncertainty was assumed to be a part of the system. Conversely, this paper assumes that f(q, z), and g(q, z) are unknown, but instead of approximating them, a stabilizing controller is directly approximated. And as mentioned, the error manifold and its integer-order derivative are utilized, which is more suitable for a system that is already modeled by an integer-order differential equation.

Theorem 2

Consider the nonlinear control system (5) that satisfies Assumptions 1, 2, 3, and 4. Boundedness of all signals in the closed-loop system is achieved when using the FO adaptive law

$$\begin{aligned} D_*^\nu \hat{{\mathcal {P}}}= -\gamma \zeta (q,z,{\bar{r}}) e \end{aligned}$$
(19)

to update the parameters of the controller (14), with

$$\begin{aligned} u_s= - \left( {\hat{L}}_k+ L_{w}+\frac{L_{g_z}}{2g_0^2}\vert e\vert \right) \text {sgn}(e), \end{aligned}$$
(20)

where \({\hat{L}}_k\) is the estimated value of \(L_k=\underset{\hspace{-.09em}[\hspace{-.09em}q^{\hspace{-.09em} \top \hspace{-.09em}} \hspace{-.09em}\hspace{-.09em}, z^{\hspace{-.09em} \top }\hspace{-.09em},\hspace{-.09em}{\bar{r}}^\top ]^\top \hspace{-.09em}\hspace{-.09em} \in \hspace{-.09em}S}{\max }(\tilde{{\mathcal {P}}}_0^\top \zeta ),\) and updated using the following additional adaptation law

$$\begin{aligned} \dot{{\hat{L}}}_k=\gamma _k\vert e\vert . \end{aligned}$$
(21)

Moreover, e(t) converges to zero as \(t\rightarrow \infty \).

Proof

Consider the proposed Lyapunov candidate

$$\begin{aligned}{} & {} V_{FO} (e,\tilde{{\mathcal {P}}},{\tilde{L}}_k)=\frac{1}{2g}e^{2}\nonumber \\{} & {} \quad +\frac{1}{2 \gamma } I^{1-\nu }\left( \tilde{{\mathcal {P}}}(s )-\tilde{{\mathcal {P}}}(0)\right) ^{\top }\left( \tilde{{\mathcal {P}}}(s )-\tilde{{\mathcal {P}}}(0)\right) +\frac{1}{2\gamma _k}{\tilde{L}}_k^2,\nonumber \\ \end{aligned}$$
(22)

where the operator I is defined in (3) with \(1-\nu >0,\) \(\tilde{{\mathcal {P}}}(0)\) is an unknown constant vector, \({\tilde{L}}_k = {\hat{L}}_k -L_k\) and \(L_k\) is an unknown upper bound of \({\mathcal {P}}^\top (0) \zeta (q,z,{\bar{r}})\) and \({\hat{L}}_k\) is its estimation, and \(\gamma , \gamma _k>0\) are the adaptation gains. It can be noticed that, via a coordinate transformation, the proposed candidate can be shifted by the initial condition \(\tilde{{\mathcal {P}}}(0)\) to drive the equilibrium point to zero. Moreover, since \(1-\nu >0,\) the fractional order \(\nu \) in this paper is confined to the interval (0, 1). Considering Lemma 3, the integer-order derivative of \( I^{1-\nu }\left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) ^{\top }\left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) \) is the Riemann–Liouville derivative, which is equal to the Caputo derivative,

$$\begin{aligned}{} & {} D^\nu \left[ \left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) ^{\top }\left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) \right] =\nonumber \\{} & {} D_*^\nu \left[ \left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) ^{\top }\left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) \right] . \end{aligned}$$
(23)

By taking the first derivative of the Lyapunov candidate (22) and considering the derivative of the error manifold (15), it follows that

$$\begin{aligned}{} & {} {\dot{V}}_{FO} \le -\frac{k}{g_1} e^2 + \tilde{{\mathcal {P}}}^\top \zeta (z,{\bar{r}}) e+\frac{L_{g_z}}{2g_0^2}\vert e\vert ^2+L_{w}\vert e\vert + u_se \nonumber \\{} & {} + \frac{1}{2\gamma } D_*^\nu \left[ \left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) ^{\top }\left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) \right] +\frac{1}{\gamma _k}{\tilde{L}}_k\dot{{\hat{L}}}_k.\nonumber \\ \end{aligned}$$
(24)

Now, consider the following lemma.

Lemma 5

Let \(\Omega :{\mathbb {R}} \rightarrow {\mathbb {R}}^n \) be continuously differentiable function, then for \( t > 0,\)

$$\begin{aligned} D_*^\nu \Omega ^\top \Omega \le 2 \Omega ^\top D_*^\nu \Omega . \end{aligned}$$
(25)

Proof

See Appendix B. \(\square \)

Lemma 5 is used to show that

$$\begin{aligned}{} & {} D_*^\nu \left[ \left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) ^\top \left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) \right] \nonumber \\{} & {} \le 2 \left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) ^{\top } D_*^\nu \left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) , \end{aligned}$$
(26)

which can be substituted into (24), thus

$$\begin{aligned}{} & {} {\dot{V}}_{FO} {\le } -\frac{k}{g_1} e^2 {+} \tilde{{\mathcal {P}}}^\top \zeta (q,z,{\bar{r}}) e {+}\frac{L_{g_z}}{2g_0^2}\vert e\vert ^2+L_{w}\vert e\vert + u_se\nonumber \\{} & {} + \frac{1}{\gamma } \left( \tilde{{\mathcal {P}}}-\tilde{{\mathcal {P}}}_0\right) ^{\top } D_*^\nu \hat{{\mathcal {P}}}+\frac{1}{\gamma _k}{\tilde{L}}_k\dot{{\hat{L}}}_k, \end{aligned}$$
(27)

where \(\tilde{{\mathcal {P}}}_0 = \tilde{{\mathcal {P}}}(0)\) and \(D_*^\nu \left( \tilde{{\mathcal {P}}}-\tilde{{\mathcal {P}}}_0\right) =D_*^\nu \hat{{\mathcal {P}}}\) (Lemma 1). Then, using the fractional-order adaptive law (19), we obtain

$$\begin{aligned} {\dot{V}}_{FO}&\le -{\bar{k}} e^2 +\frac{L_{g_z}}{2g_0^2}\vert e\vert ^2+L_{w}\vert e\vert + u_se+ L_k\vert e\vert +\frac{1}{\gamma _k}{\tilde{L}}_k\dot{{\hat{L}}}_k \nonumber \\&= -{\bar{k}} e^2 +\frac{L_{g_z}}{2g_0^2}\vert e\vert ^2+L_{w}\vert e\vert + u_se+ {\hat{L}}_k\vert e\vert \nonumber \\&\quad -{\tilde{L}}_k\vert e\vert +\frac{1}{\gamma _k}{\tilde{L}}_k\dot{{\hat{L}}}_k, \end{aligned}$$
(28)

where \( {\bar{k}}=k/g_1\). Then, we choose stabilizing term as (20) and the additional adaptive law as (21). Therefore, (28) becomes

$$\begin{aligned} {\dot{V}}_{FO} \le -{\bar{k}} e^2, \end{aligned}$$
(29)

A negative semi-definite upper bound of \({\dot{V}}_{FO} \) is obtained, after applying the LaSalle–Yoshizawa theorem (Spooner et al., 2002) \( \begin{Vmatrix}^\top \end{Vmatrix} \), or \( \begin{Vmatrix}^\top \end{Vmatrix} \) (since \(\tilde{{\mathcal {P}}}_0\) is constant) is uniformly bounded, and the error e(t) is asymptotically stable \(\square \)

Remark 1

In general, the parameter vector \({\mathcal {P}}^*\), which can be represented as \({\mathcal {P}}^*=\hat{{\mathcal {P}}}(0)-\tilde{{\mathcal {P}}}(0)\), is a weight vector of the radial basis functions that is used to approximate the controller, or it can also be an unknown system parameter. However, in most physical systems, a priori knowledge could be obtainable. This knowledge can be exploited to establish a bounded and convex set \(\Omega \) such that \({\mathcal {P}}^* \in \Omega \), as well as \([q^{\top }, z^{\top }, {\bar{r}}^{\top }]^\top \in S \). If that is the case, the term \(\frac{1}{\gamma _k}{\tilde{L}}_k^2\) in Lyapunov candidate (22) can be removed, the stabilizing term becomes

$$\begin{aligned} u_s= - \left( L_k + L_{w}+\frac{L_{g_z}}{2g_0^2}\vert e\vert \right) \text {sgn}(e). \end{aligned}$$
(30)

Remark 2

Conversely of Remark 1, we may not have enough information about the system. In this case, we will estimate the bounds \(L_w\) and \(L_{g_z}\). That can be preformed in the same way of the estimation of \(L_k\). Then, two more extra adaptive laws will take place:

$$\begin{aligned} \dot{{\hat{L}}}_w&=\gamma _w \vert e\vert , \end{aligned}$$
(31)
$$\begin{aligned} \dot{{\hat{L}}}_w&=\gamma _{g_z} \frac{ \vert e\vert }{2g_0^2}, \end{aligned}$$
(32)

where \(\gamma _w\) and \(\gamma _{g_z}\) are positive gains. Therefore, the new stabilizing term will be

$$\begin{aligned} u_s= - \left( {\hat{L}}_k + {\hat{L}}_{w}+\frac{{\hat{L}}_{g_z}}{2g_0^2}\vert e\vert \right) \text {sgn}(e). \end{aligned}$$
(33)

However, the RHS of the adaptive laws (21), (31) and (32) is positive. This could be a problematic in the new stabilizing term (33). Therefore, some technique, for example \(\sigma \)-Modification, can be used to overcome this problem.

Remark 3

The proposed Lyapunov candidate (22) can be considered as a general form of the integer-order one introduced in Spooner et al. (2002), where

$$\begin{aligned}{} & {} \lim _{\nu \rightarrow 0}I^\nu \left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) ^{\top }\left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) \nonumber \\{} & {} =\left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) ^{\top }\left( \tilde{{\mathcal {P}}}(t)-\tilde{{\mathcal {P}}}(0)\right) , \end{aligned}$$
(34)

and

$$\begin{aligned} D_*^1\hat{{\mathcal {P}}}=\dot{\hat{{\mathcal {P}}}}. \end{aligned}$$
(35)

Remark 4

Fractional-order adaptation provides clear benefits when compared with integer-order adaptation: the fractional-order derivative effectively possesses memory, to a larger degree than the integer order derivative. The extent to which this additional memory is used can be chosen via the derivative order \(\nu \), which serves in practice as an additional degree of freedom that the control system designer can use to improve performance. Crucially, as our simulation example in Section 5 illustrates, the improvement in performance that FO adaptation provides (considering both tracking error and control energy) cannot be trivially obtained by simply increasing the adaptation gain in the IO case.

Remark 5

The results reached in the above paragraphs are proof of the stability of using the fractional-order DAC for the case where \(\nu \in (0,1)\). The generalization of the stability proof of FO-DAC of order \(\nu >1 \) is still an open problem, to our knowledge.

Fig. 1
figure 1

Block diagram denoting the B &B system

Full size image

4.1.1 Smoothing the Controller

High-frequency switching may occur due to the discontinuous stabilizing term (20). The unwanted chattering can cause problems in the Lipschitz condition, which can affect the uniqueness and existence of the solution. In practical applications, undesirable outcomes arise from both high-frequency switching and excessive gain in the control. For these reasons, the usage of the sgn function is not practical. Therefore, to suppress the undesired chattering, the sat function,

$$\begin{aligned} \text {sat}(\varkappa ) = {\left\{ \begin{array}{ll} 1, &{} \text { if } \varkappa > 1, \\ \varkappa , &{} \text { if } \mid \varkappa \mid \le 1, \\ -1, &{} \text { if }\varkappa < -1, \end{array}\right. } \end{aligned}$$
(36)

may be used instead of the sgn function in (20). Particularly, the sign function (\(\text {sgn}(e)\)) is replaced with the saturation function \(\left( \text {sat}(\frac{1}{\Upsilon }e)\right) \), where \(\Upsilon >0\) in (20). This change leads to different stability results, as shown next.

Before picking the stabilizing term, the derivative of (22) is

$$\begin{aligned} {\dot{V}}_{FO} \le -{\bar{k}} e^2 +\frac{L_{g_z}}{2g^2_0}\vert e\vert ^2+L_{w}\vert e\vert +u_s e+{\hat{L}}_k \vert e\vert . \end{aligned}$$
(37)

When \( \vert e\vert > \Upsilon \), \(\text {sat}(\frac{1}{\Upsilon }e)=\text {sgn}(e)\), then the inequality (29) is obtained. When \( \vert e\vert \le \Upsilon \), \(\text {sat}(e)=\frac{e}{\Upsilon }\) and

$$\begin{aligned} {\dot{V}}_{FO}\le ~ \varpi (e), \end{aligned}$$

where

$$\begin{aligned} v (e)&=\left( \!\! \left( L_{w}+{\hat{L}}_k \right) \!-\! \left( \! \frac{L_w}{\Upsilon }\!+\!\frac{{\hat{L}}_k}{\Upsilon }\!+\!{\bar{k}}\!-\!\frac{L_{g_z}}{2g_0^2}\!\right) \! \vert e\vert \right. \nonumber \\&\quad \left. {}-\frac{L_{g_z}}{2\Upsilon g_0^2 }\vert e\vert ^2 \right) \vert e\vert . \end{aligned}$$
(38)

Note that \( \varpi (e) \) equals zero at \( e=\lbrace \pm {\bar{\Upsilon }} \rbrace \), greater than zero when \(\vert e\vert < {\bar{\Upsilon }}, \)  and less than zero otherwise, where \({\bar{\Upsilon }}\) is the root of (38). Therefore, the set \( \Xi =\lbrace e \in {\mathbb {R}} ~:~\vert e\vert \le {\bar{\Upsilon }}\rbrace \) can be defined as a positively invariant set. Hence, \(\underset{t\rightarrow \infty }{\text {lim}}|e(t)|\le {\bar{\Upsilon }}\) since \(\lbrace e \in {\mathbb {R}}:\vert e\vert = {\bar{\Upsilon }}\rbrace \) is also invariant set. At the end, we obtain UUB. Notice that

$$\begin{aligned} {\bar{\Upsilon }}&= \frac{\Upsilon g_0^2 }{L_{g_z}} \left( \!-\! \left( \frac{L_w}{\Upsilon } +\frac{{\hat{L}}_k}{\Upsilon }+{\bar{k}}-\frac{L_{g_z}}{2g_0^2}\right) \right. \nonumber \\&\left. ~~+\!\sqrt{\!\!\left( \! \frac{L_w}{\Upsilon }\!+\!\frac{{\hat{L}}_k}{\Upsilon }\!+\!{\bar{k}}\!-\!\frac{L_{g_z}}{2g_0^2}\! \right) ^2\!\!+\frac{2L_{g_z}}{\Upsilon g_0^2 }\left( L_{w}+{\hat{L}}_k\right) } \right) , \end{aligned}$$
(39)

which can be suitably calibrated with the appropriate selection of gains to minimize the area of the convergence.

5 Numerical Example

In this section, the ball and beam example is solved using the proposed technique, which is also compared with traditional IO adaptive control.

5.1 Ball and Beam (B &B)

The ball and beam (B &B) control system is usually used as a benchmark to evaluate and investigate the performance of the controller structure, where its dynamics are an example of high nonlinearity and it is ultimately unstable even when the beam is near the horizontal.

The experiment involves several components, such as a rigid ball, cantilever beam, DC motor, and various sensors. The schematic diagram in Fig. 2 illustrates that the structure of the B &B system is created by attaching the beam to the motor, with a rigid rolling ball resting on the beam. The primary idea behind this setup is to utilize the motor’s torque to regulate the position of the ball on the beam. Furthermore, the study will be extended by introducing a disturbance to the input signal, with the aim of analyzing the system’s robustness and its ability to maintain stable control in the presence of external disturbances. This approach will provide insights into the system’s performance and its potential for real-world applications.

The system is composed of an inner loop and an outer loop as shown in Fig. 1.

Fig. 2
figure 2

The schematic diagram of the B &B system

Full size image

The state space equations of the inner loop are:

$$\begin{aligned} \begin{bmatrix} {\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3 \end{bmatrix} = \begin{bmatrix} 0&{}1&{}0\\ 0&{}0&{}1\\ 0&{}a_1&{}a_2 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}+\begin{bmatrix} 0\\ b_1\\ b_2 \end{bmatrix}u_i \end{aligned}$$
(40)
$$\begin{aligned} y_i = \begin{bmatrix} 1&0&0 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}, \end{aligned}$$
(41)

where the input of the inner loop is defined as \(u_i(t) = i(t)\), representing the input current used by the motor. The output of the inner loop is the angle of the beam, denoted by \(y_i(t) = \vartheta (t) = x_1\), with \(x_2\) representing the angular acceleration of the beam and \(x_3\) denoting the angular acceleration of the beam. The parameters \(b_1 = 280.12\), \(b_2 = -18577.14\), \(a_1 = -87885.84\), and \(a_2 = -1416.4\) are used in this context. The desired position of the ball is denoted by r. Additional details on this topic can be found in Ordonez et al. (1997). The Newton’s second law will be used to model the outer-loop system for small angle \(\vartheta \) (\(\sin \vartheta \approx \vartheta \)),

$$\begin{aligned} \begin{aligned} {\dot{x}}_4&= x_5,\\ {\dot{x}}_5&= f(x) +g(x) u_o, \end{aligned} \end{aligned}$$
(42)

where \(x_4\) is the ball position on the beam, \(x_5\) is the velocity of the ball on the beam, \( f(x)= a_4 \tan ^{-1}(100x_5) (e^{-10^4x_5^2}-1)\), and \( g(x)= a_3 = -514.96\). In the inner loop, the proportional integral derivative controller controls the position of the beam to the reference angle by actuating the motor. The input of the controller is the error \(\vartheta _e\), which is the difference between the beam angle \(\vartheta \) and the reference angle. By well-designing the inner-loop controller, its motion will be quicker compared to the outer one. Here, we choose a PID controller with gains \(k_p = 20,\) \(k_i = 10,\) and \(k_d=0.1\). The FO-DAC will be implemented for the outer-loop system (42), where we consider the ball position \(y_o=x_4\) to be the output of the system and the beam angle \(u_o = \vartheta =x_1\) is the system input. By referring to Assumption 3, there are \({\underline{g}}, {\overline{g}}\) such that \(-\infty < {\underline{g}}\le g\le {\overline{g}}\le 0 \), and \( \mid {\dot{g}}(x)\mid \le L_{g_x} <\infty .\) In this example, we will set \({\overline{g}} = -10\) and \(L_{g_x} = 0.001\). As mentioned the proposed technique will keep the error manifold in input–output form. The goal is to track the reference r by the output \(x_4\), and then, the tracking error is:

$$\begin{aligned} e =k_1(x_4-r)+x_5-{\dot{r}}. \end{aligned}$$
(43)

The reference will be specified to be a constant, \(r = 4\), which is measured from the left edge of the beam, hence,

$$\begin{aligned} {\dot{e}}=\varkappa +f(x)+g(x)u, \end{aligned}$$

where \(\varkappa =k_1x_5\). Note that in this case g is negative. The derivative of the error manifold is

Fig. 3
figure 3

The ball position on the beam \(y_o\) when using FO-DAC (\(\nu =0.6,0.8\) and 0.9) and IO-DAC w.r.t. time

Full size image
$$\begin{aligned} {\dot{e}}=-ke+g(\tilde{{\mathcal {P}}}^{\top }\zeta (x,{\bar{r}})+u_s-w(x,{\bar{r}})). \end{aligned}$$
(44)

Therefore, the control law is

$$\begin{aligned} u = \hat{{\mathcal {P}}}^\top \zeta (x,{\bar{e}})+u_s, \end{aligned}$$

where \({\bar{e}}=-\varkappa -k e\), the adaptation law is

$$\begin{aligned} D_*^\nu \hat{{\mathcal {P}}}=\gamma \zeta (x,{\bar{e}})e, \end{aligned}$$

and

$$\begin{aligned} \dot{{\hat{L}}}_k=\gamma _k\vert e\vert , \end{aligned}$$

where \(\gamma = 0.08,\) and \(\gamma _k= 0.001,\) and the stabilizing term is

$$\begin{aligned} u_s=-\left( {\hat{L}}_k+ L_w+\frac{L_{g_x}}{2{\overline{g}}^2}\vert e\vert \right) \text {sat}\left( \frac{1}{\Upsilon }e\right) , \end{aligned}$$

where the parameters \(\Upsilon =0.1\) and \(L_{w}=0.01\). Moreover, NNs are applied to approximate the controller with a radial basis function \(\varphi (s)=\exp (-\frac{s^2}{\gamma _s^2})\), where \(\gamma _s=1\). Four radial basis functions scaled by 0.25 are chosen for each input, \(x \in {\mathbb {R}}^2\) and \({\bar{e}}\in {\mathbb {R}}\), to implement the multilayer perceptron approximator with one hidden layer. Hence, \(p=3^4\) parameters. The Matlab Simulink toolbox is used to solve this example numerically, where the fractional-order integrator is implemented using FOMCON (Fractional Order Modeling and Control Toolbox). Figure 3 shows the output behavior \(y_o=x_4\) for \(\nu = 0.6, 0.8, 0.9\) and \(\nu = 1\) (IO). Table 1 presents the control energy and the mean-squared error for different orders of \(\nu \), including the integer-order case.

Table 1 Mean-squared error and control energy for different choices of order \(\nu \)
Full size table

There exists a trade-off between the mean-squared error (MSE) and the control energy, as demonstrated in Table 1. This relationship allows for effective management of the control energy; specifically, to achieve a certain acceptable error level, one can select an optimal value for mean-squared error, such as \(\nu =0.8\). By noticing Fig. 4, if one has flexibility with the steady-state error and control energy, then the low order \(\nu = 0.02\) can be chosen.

This example illustrates the advantages of using the FO-DAC technique. The additional degree of freedom provided by \(\nu \) yields flexibility in the trade-off between control energy and fast response.

Fig. 4
figure 4

Comparing the ball position on the beam \(y_o\) when using FO-DAC, \(\nu =0.02\) and 0.8, w.r.t. time

Full size image

Through a comparison of the input–output (IO) and feedback-output (FO) adaptive laws expressed as \(\dot{\hat{{\mathcal {P}}}} = \gamma f(\zeta ,e )\) and \(D^\nu \hat{{\mathcal {P}}} = \gamma f(\zeta ,e)\), respectively, with the same learning rate of \(\gamma \), it has been observed that the performance of FO-DAC, specifically for a value of \(\nu = 0.8\), surpasses that of IO-DAC. This is due to the additional parameter, \(\nu \), which activates the time factor \(t^{1-\nu }\), thereby enabling retention of all prior values. However, the optimal value of \(\nu \) that results in the best performance, is yet to be determined and is an ongoing research topic addressed in this paper.

To evaluate the robustness of our proposed control technique, we will add white noise to the input of our system. White noise added to the input in a real experiment can represent various disturbances and uncertainties, such as measurement noise, actuator noise, parameter uncertainty, and external disturbances. By testing our controller’s performance under such noisy and uncertain conditions, we can improve its robustness and effectiveness.

Fig. 5
figure 5

Ball position on the beam (\(y_o\)) over time, obtained using FO-DAC (\(\nu =0.6,0.8,\) and 0.9) and IO-DAC with noise present

Full size image

In conclusion, we simulated the system for a longer period of time (\(t=5\) sec) as shown in Fig. 5 and found that our proposed control technique is able to effectively deal with both the uncertainty of the model and the added noise. The results show that our adaptive law has the ability to accurately estimate the unknown parameters of the system and compensate for the effects of the added noise on the measured ball position. This demonstrates the robustness and effectiveness of our proposed control technique in dealing with noisy and uncertain conditions. Overall, our study provides a valuable contribution to the field of control systems and highlights the importance of developing robust and adaptive control techniques for real-world applications.

6 Conclusion

In this paper, we have introduced a new direct adaptive control method for a class of nonlinear input–output feedback linearizable systems that uses a fractional-order derivative to update the controller’s parameters. This technique is an improvement over existing methods in the literature because it keeps the integer-order derivative of the error manifold and uses a fractional-order adaptive law, which possesses longer-term memory compared with the integer-order adaptive law. This feature may also have the advantage of reducing the complication of having to use a large number of approximator parameters. The FO update law uses the Caputo derivative, as opposed to the Riemann–Liouville definition. The Caputo derivative is more suitable in practice because it represents the rate of change and allows conventional initial conditions to be incorporated in the modeling of the system by the differential equations. We show that the conventional integer-order direct adaptive law (\(\nu =1\)) is a special case of the fractional-order one (\(0<\nu <1\)). We present a simulation example to illustrate the performance improvement and extra flexibility provided by the FO adaptive law, as compared with the integer case. The results demonstrate the robustness and effectiveness of our adaptive law in accurately estimating the unknown parameters of the system and compensating for the effects of the added noise on the measured ball position. The proof of stability using the FO adaptive law to approximate the uncertainty is a paradigm shift in the field of adaptive control because, everything else being equal, more capability can be provided by changing the derivative order.