Epidemiological Control of COVID-19 Through the Theory of Variable Structure and Sliding Mode Systems

Abstract

This paper proposes a new mathematical model called SIRDQ considering control laws for the government actions in order to reduce the quarantine periods. The proposed control laws guarantee the regulation of the effective number of reproduction to a desired value, which is directly related to the propagation of the epidemic model. We consider two control strategies based on first-order sliding mode and super-twisting algorithm due to its robustness with respect to parametric uncertainties and disturbances, as found in epidemiological models. The stability analysis of the closed-loop system is rigorously presented. Simulations show that the employed control strategies assure better levels of isolation to be adopted.

1 Introduction

On December 31th, 2020, the World Health Organization (WHO) was informed of cases of pneumonia of unknown cause in the city of Wuhan, China. A new coronavirus, which belongs to a large family of virus that cause diseases ranging from the common cold to more serious illnesses, was identified as the cause by the Chinese authorities on January 7th, 2020, and was initially named “2019-nCoV” (WHO 2020).

With a high diffusion capacity and, consequently, a fast increase in the number of cases, the virus has been spread to most countries in the world. Therefore, on March 11th, 2020, WHO (2020) declared that the outbreak could be characterized as a pandemic.

Transmission is mainly individual-to-individual by means of respiratory droplets. SARS-CoV-2 infection pattern in humans is similar to that of other coronaviruses, such as severe acute respiratory syndrome coronavirus (SARS-CoV) and Middle East respiratory syndrome coronavirus (MERS-CoV) (Cavalcante and Abreu 2020).

In Brazil, COVID-19 spreading through the country and community transmission was declared nationwide on March 20th, 2020. In this context, the city of Rio de Janeiro is one of the largest urban centers and the first COVID-19 case was reported on March 6th 2020, just 11 days after the Brazilian first case (Cavalcante and Abreu 2020). Since then, the city of Rio de Janeiro has provided data on confirmed cases and deaths of SARS-CoV-2, with open access. These datasets are available considering confirmed, recovered and infected cases, per day as well as its moving average over the last 7 days.

Although we will not consider a particular study of case for any determined city, Figs. 1 and 2 help us to illustrate the typical real data of a metropolis, such as Rio de Janeiro, considering the period of spread of the epidemic from March 06th 2020 to April 19th 2021.

Fig. 1

Confirmed cases of COVID-19 in the city of Rio de Janeiro

Fig. 2

Confirmed deaths of COVID-19 in the city of Rio de Janeiro

In this pandemic scenario, the treatment of the disease and its prevention require social and medical resources that are often insufficient. The health systems only try to mitigate its consequences to avoid complications and fatal outcomes. This disease has shown a high infection and fatality rates (Pazos et al. 2020). In addition to the fear of infection, COVID-19 has caused a feeling of insecurity in all aspects of life, from the collective to the individual perspective, from the daily functioning of society to changes in individual-to-individual relationships (Faro et al. 2020). Although measures such as quarantine and social isolation are possible control variables in the event of a pandemic, its prolongation can be detrimental to the country’s economy and, furthermore, considerably impacts the mental health of the population.

As a result, studies on the dynamics and possible control strategies have great interest to the scientific community and to the society as a whole. For instance, Oro et al. (2020) study the modeling and forecast of the number of new daily cases of COVID-19, in the State of Paraná by using an Autoregressive Distributed Lag Model. Batistela et al. (2020) study the dynamics of the Covid-19 pandemic by proposing a Susceptible–Infected–Removed—Sick (SIRSi) compartmental model. The proposed model considers the possibility of unreported or asymptomatic cases, and differences in the immunity within a population. Gomes et al. (2020) proposes a computational model with intelligent machine learning for analysis of epidemiological data and real time forecasting the dynamic propagation behavior of COVID-19 in Brazil.

From control point of view, Pataro et al. (2021) investigate how to apply model predictive control (MPC) algorithms to plan appropriate social distancing policies that mitigate the pandemic effects by considering the states of Bahia and Santa Catarina (Brazil). Dias et al. (2021) proposes a control law to adjust the physical distancing level to guarantee the fastest way to finish the outbreak with the number of hospitalized individuals below the desired value. Furthermore, the use of nonlinear control techniques, specifically the sliding mode control (SMC), has been widely used in the literature in several applications (Oliveira et al. 2016; Roy and Roy 2020; Andrade et al. 2014) and also for the control of infectious diseases (Rohith and Devika 2020; Ibeas et al. 2013; Xiao et al. 2012).

The sliding mode is a control strategy able to drive and constrain the system output to the equilibrium in finite time. In closed-loop, the main advantage of this approach is its robustness with respect to matched disturbances and parametric uncertainties. On the other hand, the epidemiological systems are highly uncertain once their parameters hardly can be precisely obtained which makes the sliding mode control (SMC) as well as the super-twisting algorithm (STA) extremely suitable. In particular, STA preserves the proprieties above with a continuous and smooth control action, rather than the classical discontinuous SMC.

In the ideal first-order sliding mode, the sliding variable reaches and remains the equilibrium in finite time by using a switching scheme of infinite frequency (discontinuous control) (Utkin 2016). In practice, it is impossible to ensure such commutation which yields a high-frequency oscillation in the sliding variable during the steady-state. This behavior is called chattering. In order to alleviate the chattering, it is possible to employ the average version of the switching control signal, the average control, by using a linear filter whose time constant is sufficiently small to keep the slow-frequency component undistorted, but large enough to eliminate the high-frequency component. Therefore, the real sliding mode only ensures the convergence with residual errors. On the other hand, the super-twisting algorithm is a continuous sliding mode control approach able to guarantee the exact convergence in finite time precluding the chattering phenomenon. In the scenario of measurement noises, it is thus expected that STA is less sensitive than discontinuous SMC (Pérez-Ventura and Fridman 2019).

In order to analyze the COVID-19 outbreak dynamics, this paper proposes a new mathematical model called Susceptible, Infected, Recovered, Dead and Quarantined (SIRDQ) inspired by Kermack and McKendrick (1927) and Gaff and Schaefer (2009), and two control laws based on sliding mode control (SMC) (Utkin 1978, 1992) which are able to regulate the effective number of reproduction of the virus to theoretical desirable values. In the stability analysis, we consider parametric uncertainties and prove the robustness of the closed-loop systems by using Lyapunov’s stability theory.

This paper is organized as follows. The mathematical model SIRDQ and its analysis are discussed in Sect. 2. Section 3 presents both SMC designs to control the outbreak of COVID-19. The numerical simulations are carried out in Sect. 4. Finally, Sect. 5 presents conclusions.

2 Problem Statement

A decisive step in the modeling and dynamic analysis of epidemics was the introduction of the Susceptible, Infectious and Removed (SIR) compartmental approach. According to the authors themselves, Kermack and McKendrick (1927), the epidemiological dynamics can be explained as follows: one or more people Infected are introduced into a community of more or less Susceptible individuals to the disease in question. The disease spreads from infected to non-infected individuals through contact. Each infected person travels the course of the disease, being ultimately Removed from the number of the sick individuals, due to recovery or death.

The classic SIR model, as presented in Kermack and McKendrick (1927), is limited to the case where all members of the community are initially equally susceptible to the disease in a scenario where only the so-called “herd immunity” or “population immunity” is applicable. In other words, all members of the community can be contaminated and interventions are not considered in order to mitigate the consequences of the epidemiological outbreak, such as, for example, administration of drugs that reduce the number of deaths, vaccination that confers immunity to the population or social isolation that guarantees the non-dissemination of the disease agent.

The SIR model is a nonlinear dynamical system given by

$$\begin{aligned} \dot{S}(t)&=-\frac{\alpha }{N}S(t)I(t), \end{aligned}$$

(1)

$$\begin{aligned} \dot{I}(t)&=\frac{\alpha }{N}S(t)I(t)-\lambda I(t), \end{aligned}$$

(2)

$$\begin{aligned} \dot{R}(t)&=\lambda I(t), \end{aligned}$$

(3)

where the variable $t \in \mathbb {R^{+}}$ represents the time instant in days, $S(t) \in \mathbb {R}$, $I(t) \in \mathbb {R}$ and $R(t) \in \mathbb {R}$ are state variables representing, respectively, the numbers of Susceptible, Infected and Removed people, $\alpha >0$ is the constant rate of spread of the disease, $\lambda >0$ is the constant rate which individuals move from infected to removed status, and N is the total number of individuals.

Despite the widespread use of the SIR model (1)–(3), from the engineering point of view, its use is limited to the analysis and prediction of epidemiological behavior since measures such as vaccines and social isolation to reduce contagion and the duration of the outbreak are not contemplated. Even so, it is not difficult to find in the literature contributions that assume a small change in (1)–(3) by replacing the constant $\alpha$ by

$$\begin{aligned} \alpha (t)=\alpha _0-u(t), \end{aligned}$$

(4)

where $\alpha _{0}>0$ and $u(t)\in [0,1 ]$ represents the control signal. In this context, u(t) is faced as the government action (level of social isolation or vaccination of the population). As simple and tempting as this change may seem, there is a contradiction in this approach that makes the results questionable. More precisely, the behavior of the effective reproduction number $R_{0}$ (Adam 2020).

The basic reproduction number ($R_0$), also called the basic reproduction ratio or basic reproductive rate, is an epidemiological metric used to describe the contagiousness or transmissibility of infectious agents (Delamater et al. 2019). The basic reproduction number is defined as: the average number of secondary cases arising from an average primary case in an entirely susceptible population that essentially measures the maximum reproductive potential for an infectious disease (Diekmann and Heesterbeek 2000). On the other hand, mathematically, the effective reproduction number is defined as an instantaneous rate of change in cases compared to those removed individuals (Keeling and Grenfell 2000), i.e.,

$$\begin{aligned} R_{0}(t):=\frac{d(I(t)+R(t))}{dR(t)}=\frac{\dot{I}(t)+\dot{R}(t)}{\dot{R}(t)} . \end{aligned}$$

(5)

For example, for (1)–(3) one has the effective reproduction number given by

$$\begin{aligned} R_{0}(t)=\frac{\alpha }{\lambda }\frac{S(t)}{N} . \end{aligned}$$

(6)

In this way, it is possible to rewrite (1)–(3) such as

$$\begin{aligned} \dot{S}(t)&=-\lambda R_{0}(t)I(t), \end{aligned}$$

(7)

$$\begin{aligned} \dot{I}(t)&=\lambda R_{0}(t)I(t)-\lambda I(t), \end{aligned}$$

(8)

$$\begin{aligned} \dot{R}(t)&=\lambda I(t). \end{aligned}$$

(9)

Note that, if $\alpha$ is considered a variable parameter, as in (4), we have

$$\begin{aligned} R_{0}(t)=\frac{(\alpha _{0}-u(t))}{\lambda }\frac{S(t)}{N} . \end{aligned}$$

(10)

Therefore, assuming (4) and at the same time considering the effective number of reproduction ($R_{0}(t)$) as a constant is indeed a mistake from the point of view of control as well as from the point of view of identification-prediction based on the SIR model. Going through this discussion, if we assume that the contamination rate can be considered as (4), there is another problem, i.e., the lack of memory of the variable $R_{0}(t)$. The assumption of (4) is linked with the possibility of $R_{0}(t)$ varies infinitesimally from its maximum value ($\max \{R_{0}(t)\} =\frac{\alpha _{0}}{\lambda }$) to the minimum ($\min \{R_{0}(t)\} = 0$), in a reciprocal manner, which is not viable either.

Motivated by such limitations, and inspired by the contributions of Kermack and McKendrick (1927) and Gaff and Schaefer (2009), this paper considers a compartmental model of the type Susceptible, Infected, Recovered, Dead and

Quarantined (SIRDQ):

$$\begin{aligned} \dot{S}(t)&=-\frac{\alpha }{N} S(t)I(t)+\frac{\beta }{N}S(t)Q(t)-uS(t), \end{aligned}$$

(11)

$$\begin{aligned} \dot{I}(t)&=\frac{\alpha }{N} S(t)I(t)-\lambda _{1}I(t)-\lambda _{2}I(t), \end{aligned}$$

(12)

$$\begin{aligned} \dot{R}(t)&=\lambda _{1}I(t), \end{aligned}$$

(13)

$$\begin{aligned} \dot{D}(t)&=\lambda _{2}I(t), \end{aligned}$$

(14)

$$\begin{aligned} \dot{Q}(t)&=-\frac{\beta }{N}S(t)Q(t)+uS(t), \end{aligned}$$

(15)

where $S(t) \in \mathbb {R}$, $I(t) \in \mathbb {R}$, $R(t) \in \mathbb {R}$, $D(t) \in \mathbb {R}$ and $Q(t) \in \mathbb {R}$ are the state variables that represent, respectively, the numbers of Susceptible, Infected, Recovered, Dead and Quarantined individuals, $u \in [0, 1 ]$ consists of non-pharmaceutical government action (level of social isolation), while $\alpha > 0$ is the constant rate of disease spread, $\beta >0$ is the constant which people leave the quarantine, $\lambda _{1}> 0$ is the constant rate which subjects move from infected to recovered, $\lambda _{2}>0$ is the constant rate which individuals move from infected to dead, and

$$\begin{aligned} N = S(t)+I(t)+R(t)+D(t)+Q(t) \end{aligned}$$

(16)

represents the total number of individuals.

Note that (11)–(15) allows us to take into account important aspects left out of the SIR model. The SIRDQ model considers the government action u that forces social isolation, through quarantine, mitigating the consequences of the outbreak, infected, sequelae and deaths. At the same time, such a model includes the phenomenon of falling quarantine adhesion through the nonlinear term $\frac{\beta }{N} S (t) Q (t)$. In scenarios where pharmacological actions are not available or are still being tested, non-adherence to quarantine has a direct effect on the prolongation of the outbreak and the decline of the economy.

Finally, according to Keeling and Grenfell (2000), the effective reproduction number $R_{0}(t)$ of the SIRDQ model is defined by

$$\begin{aligned} R_{0}(t):=\frac{\dot{I}+\dot{R}+\dot{D}}{\dot{R}+\dot{D}}=\frac{\alpha }{\lambda _{1}+\lambda _{2}}\frac{S(t)}{N}, \end{aligned}$$

(17)

with time derivative satisfying

$$\begin{aligned} \dot{R}_{0}(t)=\frac{\alpha }{\lambda _{1}+\lambda _{2}}\left[ -\alpha \frac{S(t)}{N}\frac{I(t)}{N}+\beta \frac{S(t)}{N}\frac{Q(t)}{N}-u\frac{S(t)}{N}\right] . \end{aligned}$$

(18)

Considering that the potential of an epidemic is based on the magnitude of the value of $R_0(t)$. An outbreak is expected to continue if $R_0(t)>1$ and to extinguish if $R_0(t)<1$. Thus, in order to contain the epidemiological outbreak, the control objective is defined as the regulation of $R_{0}(t)$ to a reference value $R_{0} ^ {\text{ ref }} \in ]0.1 [$. In other words, we design u so that the regulation error

$$\begin{aligned} \tilde{R}_{0}(t):=R_{0}(t)-R_{0}^{\text {ref}}, \end{aligned}$$

(19)

with dynamics

$$\begin{aligned} \dot{\tilde{R}}_{0}(t)=\frac{\alpha }{\lambda _{1}+\lambda _{2}}\left[ -\alpha \frac{S(t)}{N}\frac{I(t)}{N}+\beta \frac{S(t)}{N}\frac{Q(t)}{N}-u\frac{S(t)}{N}\right] , \end{aligned}$$

(20)

it is taken to zero or a small neighborhood of zero. To achieve this goal, in the next section two control strategies based on sliding modes will be presented.

Throughout the paper, the following assumptions are considered:

• (A1) During the early stages of an epidemic, in a large population, the number of susceptible people can be considered constant, since any change is small compared to the total number of individuals N (Kermack and McKendrick 1927). Since the course of an epidemic is short compared with the life of an individual, the population may be considered as remaining constant. Then, in our approach, the total number of individuals N is a constant. On the other hand, in the early stages of an epidemic, the number of infected people introduced into a community of unaffected individuals is very small while the number of quarantined individuals or deaths are null. Therefore, number of susceptible individuals are approximately equal to the total number of individuals. For the purpose of analysis, the assumption (A1) for simplifying the dynamics of $\tilde{R}_{0}(t)$ given by (20) is used. The argument that the population is large enough so that the number of susceptible individuals is considered constant during the initial period of the epidemic ($S (t) /N \approx 1$) combined with the rapid response of SMC, with the justification that the control law has been used since the beginning of the outbreak, allow us to rewrite (20) as

  $$\begin{aligned} \dot{\tilde{R}}_{0}(t)=\frac{\alpha }{\lambda _{1}+\lambda _{2}}\left[ -\alpha \frac{I(t)}{N}+\beta \frac{Q(t)}{N}-u\right] . \end{aligned}$$

  (21)

  Of course, the assumption (A1) is restrictive, however, we understand that the control strategy using social isolation is effective only in the early stages of the epidemic (Al-Radhawi et al. 2021; Angulo et al. 2021; Sontag 2021). After this period, new control variables and pharmacological actions such as vaccination (Zhong et al. 2021) must be added to the model so that it makes sense. Furthermore, assumption (A1) simplifies the mathematical effort required in the demonstration of the main theorems.

• (A2) The parameters $\alpha$, $\beta$, $\lambda _{1}$ and $\lambda _{2}$ in (11)–(15) are uncertain; however, its positive lower-upper bounds are known, such that:

  $$\begin{aligned} \underline{\alpha }&< \alpha< \overline{\alpha } , \quad \underline{\beta }< \beta < \overline{\beta }, \end{aligned}$$

  (22)
  $$\begin{aligned} \underline{\lambda }_{1}&< \lambda _{1}< \overline{\lambda }_{1} \quad \text{ e } \quad \underline{\lambda }_{2}< \lambda _{2} < \overline{\lambda }_{2} . \end{aligned}$$

  (23)

  In general, the parameters of epidemiological systems are difficult to obtain accurately. A possible strategy for choosing the upper and lower bounds is to select similar diseases (more or less aggressive) as a basis or even the existing knowledge of other models elaborated in the literature. There is no theoretical limit value for choosing an upper/lower bounds, however, if the bounds are overestimated, the control effort will be overly large.

• (A3) The variable $R_{0}(t)$ in (17) is an output of the plant (11)–(15) that is available for feedback. Note that the assumption (A3) is plausible since, in practice, data are released and government actions are taken with sampling interval $h =1$ [day] (Aström and Wittenmark 1997). Thus, the basic number of reproduction in (17) can be extracted daily from the data using a recursive difference equation given by

  $$\begin{aligned} \hat{R}_{0}(t):=\frac{I(t)-I(t-1)+R(t)-R(t-1)+D(t)-D(t-1)}{R(t)-R(t-1)+D(t)-D(t-1)}, \end{aligned}$$

  (24)

  where $t \in \mathbb {N}$ represents the current day in question. The Eq. (17) as well as (24) of the manuscript represent the same phenomenon. Notice, from (17), one has

  $$\begin{aligned} R_{0}(t)=\dfrac{\dfrac{\text {d}I(t)}{\text {d}t}+\dfrac{\text {d}R(t)}{\text {d}t}+\dfrac{\text {d}D(t)}{\text {d}t}}{\dfrac{\text {d}R(t)}{\text {d}t}+\dfrac{\text {d}D(t)}{\text {d}t}}, \end{aligned}$$

  (25)

  whose derivatives terms can be approximated by using the backward Euler’s method such that

  $$\begin{aligned} \dfrac{\text {d}I(t)}{\text {d}t}&\approx \dfrac{I(t)-I(t-h)}{h} , \end{aligned}$$

  (26)
  $$\begin{aligned} \dfrac{\text {d}R(t)}{\text {d}t}&\approx \dfrac{R(t)-R(t-h)}{h} , \end{aligned}$$

  (27)
  $$\begin{aligned} \dfrac{\text {d}D(t)}{\text {d}t}&\approx \dfrac{D(t)-D(t-h)}{h} , \end{aligned}$$

  (28)

  with periodic sampling h. On the other hand, from Eq. (24), one obtains

  $$\begin{aligned} \hat{R}_{0}(t)&= \dfrac{\dfrac{I(t)-I(t-h)}{h}+\dfrac{R(t)-R(t-h)}{h}+\dfrac{D(t)-D(t-h)}{h}}{\dfrac{R(t)-R(t-h)}{h}+\dfrac{D(t)-D(t-h)}{h}} \end{aligned}$$

  (29)
  $$\begin{aligned}&\approx \dfrac{\dfrac{\text {d}I(t)}{\text {d}t}+\dfrac{\text {d}R(t)}{\text {d}t}+\dfrac{\text {d}D(t)}{\text {d}t}}{\dfrac{\text {d}R(t)}{\text {d}t}+\dfrac{\text {d}D(t)}{\text {d}t}} \end{aligned}$$

  (30)
  $$\begin{aligned}&=R_{0}(t). \end{aligned}$$

  (31)

  In a nutshell, from (29)–(31), $\hat{R}_{0}(t)\approx R_{0}(t)$. In our particular case, we have $h=1$ day. Furthermore, if $I(t) \rightarrow 0$ then $R_{0}(t)\approx \hat{R}_{0}(t) \rightarrow 0$.

3 Sliding Mode Control

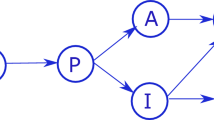
Sliding mode control theory is considered to be one of the main strategies for dealing with uncertain systems. In the following, we present two possible approaches based on first-order and second-order sliding modes such that the closed-loop system can represented by Fig. 3.

Fig. 3

Block diagram illustrating the closed-loop system

3.1 First-Order Sliding Mode

The classic sliding mode, also called first-order SMC, is able to drive the output of a given dynamic system to zero in finite time and keeping it in this situation in a precise and robust way through a control signal with high-frequency switching (Utkin 1992). Such switching behavior is sometimes an undesirable phenomenon and it is usual to use a low-pass filter in the design to achieve an appropriate smooth estimate of the ideal equivalent control (Utkin 1992).

The control law is governed by a variable structure system

$$\begin{aligned} u={\left\{ \begin{array}{ll} \ \ \overline{\alpha }+\overline{\beta }+\delta , \quad \text {if} \quad \tilde{R}_{0}(t)>0 \\ -\overline{\alpha }+\underline{\beta }-\delta , \quad \text {if} \quad \tilde{R}_{0}(t)<0 \end{array}\right. } , \end{aligned}$$

(32)

where $\delta >0$ is a sufficiently small constant that satisfies $\delta + \overline{\alpha }<\underline{\beta }$, used to ensure that the sliding surface $\tilde{R}_{0}(t) = 0$ is reached in finite time.

Theorem 1

Consider the epidemiological system SIRDQ (11)–(15) with dynamics of the effective reproduction number $R_{0}(t)$ given by (18), regulation error $\tilde{R}_{0}(t)$ in (19) and control law u in (32). If all the assumptions (A1)–(A3) are satisfied, then the sliding surface $\tilde{R}_{0}(t) = 0$ is reached in finite time.

Proof

Consider the following energy function

$$\begin{aligned} V=\tilde{R}_{0}^{2}(t), \end{aligned}$$

(33)

whose time derivative is given by

$$\begin{aligned} \dot{V}=2\tilde{R}_{0}(t)\dot{\tilde{R}}_{0}(t). \end{aligned}$$

(34)

Replacing (21) into (34), one has

$$\begin{aligned} \dot{V}=2\tilde{R}_{0}(t)\frac{\alpha }{\lambda _{1}+\lambda _{2}}\left[ -\alpha \frac{I(t)}{N}+\beta \frac{Q(t)}{N}-u\right] . \end{aligned}$$

(35)

If $\tilde{R}_{0}(t)>0$, plugging (32) into Eq. (35), the latter becomes

$$\begin{aligned} \dot{V}=2|\tilde{R}_{0}(t)|\frac{\alpha }{\lambda _{1}+\lambda _{2}}\left[ -\alpha \frac{I(t)}{N}+\beta \frac{Q(t)}{N}-\overline{\alpha }-\overline{\beta }-\delta \right] . \end{aligned}$$

(36)

From (16) it can be concluded that $\frac{I(t)}{N} <1$ and $\frac{Q (t)}{N}<1$. Therefore,

$$\begin{aligned} \dot{V}&<2|\tilde{R}_{0}(t)|\frac{\alpha }{\lambda _{1}+\lambda _{2}}\left[ \alpha +\beta -\overline{\alpha }-\overline{\beta }-\delta \right] . \end{aligned}$$

(37)

Applying the upper bounds (22) to (37) arrives to

$$\begin{aligned} \dot{V}&<-2\frac{\alpha \delta }{\lambda _{1}+\lambda _{2}}|\tilde{R}_{0}(t)|. \end{aligned}$$

(38)

If $\tilde{R}_{0}(t) <0$, replacing (32), Eq. (35) becomes

$$\begin{aligned} \dot{V}=-2|\tilde{R}_{0}(t)|\frac{\alpha }{\lambda _{1}+\lambda _{2}}\left[ -\alpha \frac{I(t)}{N}+\beta \frac{Q(t)}{N}+\overline{\alpha }-\underline{\beta }+\delta \right] . \end{aligned}$$

(39)

Applying the upper bounds (22) to (39), we arrive at

$$\begin{aligned} \dot{V}&<-2\frac{\alpha \delta }{\lambda _{1}+\lambda _{2}}|\tilde{R}_{0}(t)|. \end{aligned}$$

(40)

So, it is easy to verify that (40) is also satisfied, $\forall \tilde{R}_{0} (t) \in \mathbb {R} - \{0\}$. Note that, with (33), it is possible to rewrite the inequality (40) as

$$\begin{aligned} \dot{V}&<-2\frac{\alpha \delta }{\lambda _{1}+\lambda _{2}}\sqrt{V} \nonumber \\ \quad&<-2\frac{\underline{\alpha }\delta }{\underline{\lambda }_{1}+\underline{\lambda }_{2}}\sqrt{V}. \end{aligned}$$

(41)

Defining the auxiliary variable $\tilde{V}: = \sqrt{V}$, it is verified that differential equation $\dot{\tilde{V}} = \frac{1}{2} \frac{\dot{V}}{\sqrt{V}}$ is satisfied and

$$\begin{aligned} \dot{V}=2\dot{\tilde{V}}\sqrt{V}. \end{aligned}$$

(42)

Then, by replacing (42) on the left-hand side of the inequality (41), we arrive at

$$\begin{aligned} \dot{\tilde{V}}<-\frac{\underline{\alpha }\delta }{\underline{\lambda }_{1}+\underline{\lambda }_{2}}. \end{aligned}$$

(43)

Recalling the Comparison Lemma (Khalil 2002, p. 102), we conclude that an upper bound $\bar{V}$ to $\tilde{V}$ is ensured by the solution of the dynamic system

$$\begin{aligned} \dot{\bar{V}}=-\frac{\underline{\alpha }\delta }{\underline{\lambda }_{1}+\underline{\lambda }_{2}}, \end{aligned}$$

(44)

as long as the initial condition is chosen as $\bar{V}(0)=\tilde{V}(0)=|\tilde{R}_{0}(0)|$. The solution to this differential equation is

$$\begin{aligned} \bar{V}(t)&=\bar{V}(0)-\frac{\underline{\alpha }\delta }{\underline{\lambda }_{1}+\underline{\lambda }_{2}}t \nonumber \\ \quad&=|\tilde{R}_{0}(0)|-\frac{\underline{\alpha }\delta }{\underline{\lambda }_{1}+\underline{\lambda }_{2}}t, \end{aligned}$$

(45)

Hence, there is a finite time instant $t_{f}=\frac{(\underline{\lambda }_{1}+\underline{\lambda }_{2})|\tilde{R}_{0}(0)|}{\underline{\alpha }\delta }$ such that $\bar{V}(t_{f})=0$. Given that $\bar{V}(t)>\tilde{V}(t)=|\tilde{R}_{0}(t)|$, it can be shown that there is a finite time $t_{s} \in [0, t_{f}[$ such that the sliding mode occurs and the sliding surface $\tilde{R}_{0}(t)=0$ is reached. $\square$

3.2 Second-Order Sliding Mode—Super-Twisting

An alternative to alleviate chattering due to the discontinuous control signal is the Super-Twisting algorithm. The Super-Twisting is a second-order sliding mode controller that does not require derivatives of $\tilde{R}_{0}(t)$ for its implementation, guaranteeing all the main properties of the first-order sliding modes with the advantage of being naturally continuous (Gonzalez et al. 2012).

The super-twisting-based control law is

$$\begin{aligned} u= \bar{\beta }+\kappa _{1}|\tilde{R}_{0}(t)|^{\frac{1}{2}}\text {sgn}(\tilde{R}_{0}(t))+\kappa _{2}\int _{0}^{t}\text {sgn}(\tilde{R}_{0}(\gamma ))\hbox {d}\gamma , \end{aligned}$$

(46)

where $\bar{\beta }>\beta$, $\kappa _{1}$ and $\kappa _{2}$ are arbitrary positive constants in order to ensure the sliding surface $\tilde{R}_{0}(t) = 0$ is reached finite time.

Theorem 2

Consider the epidemiological system SIRDQ (11)–(15) with dynamics of the effective reproduction number $R_{0}(t)$ given by (18), regulation error $\tilde{R}_{0}(t)$ in (19) and control law u in (46). If all the assumptions (A1)–(A3) are satisfied, then the sliding surface $\tilde{R}_{0}(t) = 0$ is reached in finite time.

Proof

First, plugging (46) into (21), the closed-loop regulation error satisfies

$$\begin{aligned} \dot{\tilde{R}}_{0}(t)&=\frac{\alpha }{\lambda _{1}+\lambda _{2}}\left[ -\alpha \frac{I(t)}{N}+\beta \frac{Q(t)}{N}- \bar{\beta }+\right. \nonumber \\&\quad \left. -\kappa _{1}|\tilde{R}_{0}(t)|^{\frac{1}{2}}\text {sgn}(\tilde{R}_{0}(t))-\kappa _{2}\int _{0}^{t}\text {sgn}(\tilde{R}_{0}(\gamma ))\hbox {d}\gamma \right] , \end{aligned}$$

(47)

since $\frac{I(t)}{N} \in [0,1]$ and $\frac{Q(t)}{N} \in [0,1]$ along with (16) and $\bar{\beta }>\beta$ from assumption (A2). In addition, one has

$$\begin{aligned} \dot{\tilde{R}}_{0}(t)&\le \frac{\alpha }{\lambda _{1}+\lambda _{2}}\left[ -\alpha \frac{I(t)}{N}-(\bar{\beta }-\beta )+\right. \nonumber \\&\quad \left. -\kappa _{1}|\tilde{R}_{0}(t)|^{\frac{1}{2}}\text {sgn}(\tilde{R}_{0}(t))-\kappa _{2}\int _{0}^{t}\text {sgn}(\tilde{R}_{0}(\gamma ))\hbox {d}\gamma \right] \nonumber \\&\le -k_{1}|\tilde{R}_{0}(t)|^{\frac{1}{2}}\text {sgn}(\tilde{R}_{0}(t))-k_{2}\int _{0}^{t}\text {sgn}(\tilde{R}_{0}(\gamma ))\hbox {d}\gamma , \end{aligned}$$

(48)

where $k_{1}=\frac{\alpha \kappa _{1}}{\lambda _{1}+\lambda _{2}}$ and $k_{2}=\frac{\alpha \kappa _{2}}{\lambda _{1}+\lambda _{2}}$. Now, invoking the Comparison Lemma (Khalil 2002, Lemma 3.4), there exists an upper bound $\bar{R}_{0}(t)$ of $\tilde{R}_{0}(t)$ for all $t\ge 0$ given by the solution of the dynamic system

$$\begin{aligned} \dot{\bar{R}}_{0}(t)&=-k_{1}|\bar{R}_{0}(t)|^{\frac{1}{2}}\text {sgn}(\bar{R}_{0}(t))-k_{2}\int _{0}^{t}\text {sgn}(\bar{R}_{0}(\gamma ))\hbox {d}\gamma , \end{aligned}$$

(49)

since that $\bar{R}_{0}(0)=\tilde{R}_{0}(0)$.

By defining the state variables $x_{1}(t):=\bar{R}_{0}(t)$ and $x_{2}(t):=-k_{2}\int _{0}^{t}\text {sgn}(\bar{R}_{0}(\gamma ))\hbox {d}\gamma$, the dynamic in (49) can be represented in the state-space formulation as

$$\begin{aligned} \dot{x}_{1}(t)&=-k_{1}|x_{1}(t)|^{\frac{1}{2}}\text {sgn}(x_{1}(t))+x_{2}(t), \end{aligned}$$

(50)

$$\begin{aligned} \dot{x}_{2}(t)&=-k_{2}~\text {sgn}(x_{1}(t)) , \end{aligned}$$

(51)

and, finally, by choosing

$$\begin{aligned} \zeta (t)=\begin{bmatrix}\zeta _{1}(t)\\ \zeta _{2}(t)\end{bmatrix}=\begin{bmatrix}|x_{1}(t)|^{\frac{1}{2}}\text {sgn}(x_{1}(t))\\ x_{2}(t)\end{bmatrix} , \end{aligned}$$

(52)

one arrives to

$$\begin{aligned} \dot{\zeta }(t)&=\frac{1}{|\zeta _{1}(t)|}A\zeta (t), \quad A=\begin{bmatrix}-\frac{1}{2}k_{1} &{} \frac{1}{2} \\ -\frac{1}{2}k_{2} &{} 0 \end{bmatrix}, \end{aligned}$$

(53)

where A is a Hurwitz matrix for any positive constants $k_{1}>0$ and $k_{2}>0$ (Moreno and Osorio 2012). Once A is a Hurwitz matrix, given the positive defined matrix $Q=Q^{T}=\frac{k_{1}}{2}\begin{bmatrix} 2k_{2}+k_{1}^{2} &{} -k_{1} \\ -k_{1} &{} 1 \end{bmatrix}$, there exists a positive definite matrix $P=P^{T}=\frac{1}{2}\begin{bmatrix} 4k_{2}+k_{1}^{2} &{} -k_{1} \\ -k_{1} &{} 2 \end{bmatrix}$ which satisfy the algebraic Lyapunov equation

$$\begin{aligned} A^{T}P+PA=-Q. \end{aligned}$$

(54)

Now, consider the following candidate to Lyapunov equation

$$\begin{aligned} V(\zeta )=\zeta ^{T}(t)P\zeta (t), \end{aligned}$$

(55)

satisfying the inequality

$$\begin{aligned} \lambda _{\min }\{P\}\Vert \zeta (t)\Vert ^{2} \le V(\zeta ) \le \lambda _{\max }\{P\}\Vert \zeta (t)\Vert ^{2}. \end{aligned}$$

(56)

The time derivative of (55) along (53) is

$$\begin{aligned} \dot{V}(\zeta )=\dot{\zeta }^{T}(t)P\zeta (t)+\zeta ^{T}(t)P\dot{\zeta }(t). \end{aligned}$$

(57)

Plugging the right-hand side of (53) into (57), one gets

$$\begin{aligned} \dot{V}(\zeta )&=\frac{1}{|\zeta _{1}(t)|}\zeta ^{T}(t)A^{T}P\zeta (t)+\frac{1}{|\zeta _{1}(t)|}\zeta ^{T}(t)PA\zeta (t) \nonumber \\&=\frac{1}{|\zeta _{1}(t)|}\zeta ^{T}(t)(A^{T}P+PA)\zeta (t), \end{aligned}$$

(58)

and, by using the Algebraic Lyapunov Equation (54), one has

$$\begin{aligned} \dot{V}(\zeta )&=-\frac{1}{|\zeta _{1}(t)|}\zeta (t)^{T}Q\zeta (t). \end{aligned}$$

(59)

Therefore, its upper bound is given by

$$\begin{aligned} \dot{V}(\zeta )&\le -\frac{\lambda _{\min }\{Q\}}{|\zeta _{1}(t)|}\Vert \zeta (t)\Vert ^{2} \nonumber \\&\le -\frac{\lambda _{\min }\{Q\}}{\lambda _{\max }\{P\}}\frac{1}{|\zeta _{1}(t)|}V(\zeta ) \nonumber \\&=-\frac{\lambda _{\min }\{Q\}}{\lambda _{\max }\{P\}}\frac{1}{|\zeta _{1}(t)|}V^{\frac{1}{2}}(\zeta )V^{\frac{1}{2}}(\zeta ) . \end{aligned}$$

(60)

From the left-hand side of inequality (56), notice that

$$\begin{aligned} 0&\le V(\zeta )-\lambda _{\min }\{P\}\Vert \zeta (t)\Vert ^{2} \nonumber \\&= \lambda _{\min }\{P\}\left( \frac{1}{\lambda _{\min }\{P\}}V(\zeta )-\Vert \zeta (t)\Vert ^{2}\right) \nonumber \\&= \lambda _{\min }\{P\}\underbrace{\left( \frac{1}{\lambda _{\min }\{P\}^{\frac{1}{2}}}V^{\frac{1}{2}}(\zeta )+\Vert \zeta (t)\Vert \right) }_{>0} \nonumber \\&\quad \times \underbrace{\left( \frac{1}{\lambda _{\min }\{P\}^{\frac{1}{2}}}V^{\frac{1}{2}}(\zeta )-\Vert \zeta (t)\Vert \right) }_{\ge 0}, \end{aligned}$$

(61)

hence

$$\begin{aligned} \Vert \zeta (t)\Vert \le \frac{1}{\lambda _{\min }\{P\}^{\frac{1}{2}}}V^{\frac{1}{2}}(\zeta ). \end{aligned}$$

(62)

On the other hand, $\Vert \zeta (t)\Vert =\sqrt{\zeta _{1}^{2}(t)+\zeta _{2}^{2}(t)}$ and $|\zeta _{1}(t)| \le \Vert \zeta (t)\Vert$, then, by using (62), it results in

$$\begin{aligned} V^{\frac{1}{2}}(\zeta )\ge \lambda _{\min }\{P\}^{\frac{1}{2}}|\zeta _{1}(t)|. \end{aligned}$$

(63)

Finally, by using (63), an upper bound to (60) can be given by

$$\begin{aligned} \dot{V}(\zeta )&\le -\frac{\lambda _{\min }\{Q\}\lambda _{\min }\{P\}^{\frac{1}{2}}}{\lambda _{\max }\{P\}}V^{\frac{1}{2}}(\zeta ) , \end{aligned}$$

(64)

and one can conclude that $V(\zeta )>0$ with $\dot{V}(\zeta )<0$ such that $\zeta (t)$ converges to zero in finite time. Moreover, from the comparison principle (Khalil 2002, Lemma 3.4), the solution of

$$\begin{aligned} \dot{\bar{V}}(t)&=-\frac{\lambda _{\min }\{Q\}\lambda _{\min }\{P\}^{\frac{1}{2}}}{\lambda _{\max }\{P\}}\bar{V}^{\frac{1}{2}}(t) , ~~ \bar{V}(0)=V(t=0), \end{aligned}$$

(65)

leads to

$$\begin{aligned} \bar{V}(t)&=\left( V^{\frac{1}{2}}(t=0)-\frac{\lambda _{\min }\{Q\}\lambda _{\min }\{P\}^{\frac{1}{2}}}{2\lambda _{\max }\{P\}}t\right) ^{2}, \end{aligned}$$

(66)

where $\bar{V} (t)$ is an upper bound to V(t) for all $t\ge 0$ and, therefore, $\tilde{R}_{0}(t)$ converges to zero in finite time reaching this value at most in $t_{st}=\frac{2\lambda _{\max }\{P\}V^{\frac{1}{2}}(t=0)}{\lambda _{\min }\{Q\}\lambda _{\min }\{P\}^{\frac{1}{2}}}$. $\square$

4 Simulation

In this section, the simulation results obtained for the closed-loop system consisting of the plant (11)–(15), the output $R_{0}(t)$ in (17) with the first-order sliding mode control law (32) and super-twisting algorithm control law (46). The model parameters are $\alpha =$ 0.5464, $\beta = 0.4417, \lambda _ {1} = 0.1$ and $\lambda _ {2} = 0.032$. These constants are defined in (Bastos and Cajueiro 2020). The population of the city of Rio de Janeiro was chosen as an example and, therefore, $N = 6.718.903$ individuals according to the latest IBGE sense and based on data provided by the City Hall. The initial conditions are $I (0) = 4$, $R (0) = 0$, $D (0) = 0$, $Q (0) = 0$, such that $S (0) = N-I (0)-R(0)-D(0)-Q (0) = 6.718.899$ individuals. The reference value is $R_ {0} ^ {\text{ ref }} = 0.5$, and the first-order sliding mode controller constants are $\underline{\alpha } = 0.1$, $\overline{\alpha } = 0.6$, $\underline{\beta } = 0.08$, $\overline{\beta } = 0.5$ and $\delta = 0.002$, while the super-twisting algorithm parameters are $\kappa _{1}=0.25$ and $\kappa _{2}=0.025$.

4.1 Fist-Order Sliding Mode Control

Although the approach seems to be unrealistic due to the high-frequency switching of the control law u (isolation levels), it is possible to find a continuous signal that approximates the equivalent control $u_\mathrm{eq} (t)$ using the equivalent extended control (Utkin 1978). According to this theory, an approximation $u_\mathrm{av} (t)$ to $u_\mathrm{eq} (t)$ is obtained by filtering the sign u. In this context, the dynamics of $u_\mathrm{av} (t)$ is given by

$$\begin{aligned} \tau \dot{u}_\mathrm{av}(t)=-u_\mathrm{av}(t)+u, \end{aligned}$$

(67)

where $\tau \ge 0$ is a constant. The lower the value of $\tau$, the more $u_\mathrm{av}(t)$ approaches $u_\mathrm{eq} (t)$. Note that if $\tau = 0$, $u_\mathrm{av} (t) = u$.

Figure 4 shows the behavior of the closed-loop system for various values of $\tau$. The lower $\tau$, faster the control objective is achieved, see Fig. 4b. Assuming that it is desired to keep $R_{0}(t)$ close to 0.5 (Fig. 4c), all strategies converge toward an isolation of approximately 40%, see Fig. 4a. However, Fig. 4e, g make it clear that in order to avoid a high number of infected and dead individuals, it is essential, at the beginning of the epidemic, to adhere to a high level of isolation. The effective reproduction number $R_ {0} (t)$ is directly related to the number of susceptible individuals S(t) , see Eqs. (6), (10) and (17). Therefore, for a reduction in the level of transmission of the disease, if no vaccine is available, it is necessary that a large part of the population remains in quarantine, see Fig. 4d, h.

Fig. 4

Simulation results obtained for the closed-loop system when the control law is (32) and (67) with regulation error $\tilde{R}_{0}(t)=R_{0}(t)-R_{0}^{\text {ref}}$

Figure 5 shows the result obtained when the signal $R_ {0} (t)$ is not available and we use $\hat{R} _ {0} (t)$ in (24) for the construction of the regulation error, that is, the regulation error becomes $\tilde{R} _ {0} (t) = \hat{R} _ {0} (t) -R_ {0} ^ {\text{ ref }}$. The regulation error reaches a neighborhood of the origin, Fig. 5b, c, however, the lack of an accurate information significantly aggravates the epidemiological plot with an increase in the number of infected and dead individuals, see Fig. 5e, g.

Fig. 5

Simulation results obtained for the closed-loop system when the control law is (32) and (67) with regulation error $\tilde{R}_{0}(t)=\hat{R}_{0}(t)-R_{0}^{\text {ref}}$

4.2 Super-Twisting Algorithm

Figure 6 shows the closed-loop system by using the super-twisting control law (46). The smooth control effort shown in Fig. 6a can ensure the convergence of the variable $\tilde{R}_{0}(t)$ to zero, see Fig. 6b, such that output $R_{0}(t)$ achieves its desired value $R_{0}^\mathrm{{ref}}$ in finite time, see Fig. 6c. To avoid a high number of infected individuals and deaths, see Fig. 6e, f, g, it is essential, at the beginning of the epidemic, to adhere a high level of social isolation Q(t), see Fig. 6d, h. As mentioned before, the effective reproduction number $R_{0}(t)$ is directly related to the number of susceptible individuals S(t), see Eqs. (6), (10) and (17).

Fig. 6

Simulation results obtained for the closed-loop system when the control law is (46) with regulation error $\tilde{R}_{0}(t)=R_{0}(t)-R_{0}^{\text {ref}}$

Figure 7 shows the result obtained if the variable $R_ {0} (t)$ is unavailable, it is possible to estimate the regulation error as $\tilde{R} _ {0} (t) = \hat{R} _ {0} (t) -R_ {0} ^ {\text{ ref }}$. In this case, the error does not converge to zero but it reaches a neighborhood of the origin, see Fig. 7b, c. Of course, by using an estimate, there is an increase in the number of infected population and, consequently, deaths, see Fig. 7e, g.

Fig. 7

Simulation results obtained for the closed-loop system when the control law is (46) with regulation error $\tilde{R}_{0}(t)=\hat{R}_{0}(t)-R_{0}^{\text {ref}}$

4.3 Discussion

Due to the low level of testing, high level of spreading of contagious as well as the large number of asymptomatic individuals, by distinguishing susceptible individuals from the infected ones becomes an extremely difficult task. Therefore, in our approach, we use a quarantine to susceptible individuals because we cannot identify exactly the infected individuals.

In our model, all those people who cannot isolate themselves due to financial issues, illnesses or with inevitable familiar relationship are considered susceptible individuals. Moreover, our quarantine compartment contemplates the social isolation abandonment behavior, unfortunately and often promoted by public figures who insist on scientific denial and bet on conspiracy theories.

The basic reproduction number $R_{0}=R_{0}(0)$ is one of the most important quantities in epidemiology. By assuming that in the early stage of the outbreak the population is initially susceptible ($S(0) \approx N$), a pathogen can invade only if $R_{0}(0)>1$ (Keeling and Rohani 2008). The value of $R_{0}(0)$ depends on both the disease and the host population (Anderson and May 1982). Mathematically, we can calculate $R_{0}(0)$ as (17),

$$\begin{aligned} R_{0}(0)=\dfrac{\alpha }{\lambda _{1}+\lambda _{2}}\frac{S(0)}{N}\approx \dfrac{\alpha }{\lambda _{1}+\lambda _{2}}. \end{aligned}$$

(68)

In other words, the $R_{0}$ is obtained by multiplying the transmission rate $\alpha$ and the average infectious period $1/(\lambda _{1}+\lambda _{2})$. The constant $\alpha$ represents rate with which new cases are produced by an infectious individual when the entire population is susceptible. Therefore, the basic reproduction number $R_{0}=R_{0}(0)$ does not depend on the infected individuals while the effective reproduction number $R_{0}(t)$ is related to the number of susceptible individuals. In our quarantine framework, we can reduce the proportion of the effective reproduction number $R_{0}(t)$ and hence eradicate the disease since any infection that, on average, cannot successfully transmit to more than one new host is not going to spread (Lloyd-Smith et al. 2005).

Notice, if the control law put all susceptible individuals in quarantine, i.e., into a severe lockdown, the course of time the pandemic comes to an end. One of the main ideas of our control schemes is to avoid these cases of severe lockdowns and study how the pandemic’s effects can be alleviated by using non-pharmacological actions.

Although our manuscript does not address the aforementioned issues, delay compensation and robustness to disturbances (which may lead to resurgence peaks) and time-varying parametric uncertainties are topics well studied in the sliding mode control literature such that, in the future, our contribution can be expanded in these directions as well. On the other hand, recent contributions in these topics by using others control strategies can be found, for instance, in Castaños and Mondié (2021), Pataro et al. (2021) and Dias et al. (2021). Such references were included in the revised version of the manuscript.

5 Conclusion

Epidemics of infectious diseases such as COVID-19 have been recurrent throughout the history and can cause major problems for the affected population, such as saturation of the hospital network, economic crisis, etc. In this context, mathematical models can be valuable tools, as they are able to provide estimates for possible scenarios of the disease spread, helping to delimit borderline cases and intermediate situations that are plausible as well. In addition, dynamic models combined with modern control techniques allow for the development of efficient strategies for the introduction and relaxation of epidemic mitigation measures. Information like this is essential to help authorities make decisions about the allocation of limited resources in the event of an epidemic.

From the control point of view, this is a challenging problem, since the process is represented by a nonlinear model, faced with the complexity of the variable $R_{0}$, with uncertain parameters or even subject to time variations in some cases in the literature. In addition, it is faced with the complexity of the variable $R_{0}(t)$ which may vary according to the social dynamics of a population under a certain control policy (e.g., see Eq. (10)), that is, it does not capture the current status of an epidemic and can increase and decrease when the number of cases is low (Adam 2020). This paper proposed a new mathematical model SIRDQ that considered the governmental action through the quarantine in order to reduce the number of infected people and deaths. In addition, a first-order sliding mode control law and super-twisting algorithm have been proposed in order to regulate the effective reproduction number $R_0$ in values lower than the unit, leading mathematically to the extinction of the epidemic. The simulation results illustrate that the control strategies were proved to be potentially efficient in the process of regulating the $R_0$ and, consequently, resulting in better (lower) levels of isolation to be adopted by the population.