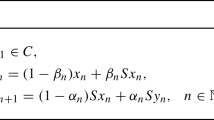1 Introduction

Let \(\mathcal {C}\) be a nonempty, closed and convex subset of a real Hilbert space \(\mathcal {H}.\) The variational inequality problem (VIP) is defined as follows: Find \(x\in \mathcal {C}\) such that

$$\begin{aligned} \langle Ax, y-x\rangle \ge 0, \hspace{0.1cm} \forall y\in \mathcal {C}, \end{aligned}$$
(1.1)

where \(A:\mathcal {H}\rightarrow \mathcal {H}\) is an operator. We denote by \(VI(\mathcal {C},A)\) the solution set of the problem (1.1).

Definition 1.1

Let \(A:\mathcal {H}\rightarrow \mathcal {H}\) be a mapping. Then, A is said to be

  1. (i)

    L-co-coercive (or L-inverse strongly monotone), if there exists a constant \(L>0\) such that

    $$\begin{aligned} \big <Ax-Ay,x-y\big >\ge L\Vert Ax-Ay\Vert ^2,~~ \forall x,y \in \mathcal {H}, \end{aligned}$$
  2. (ii)

    Monotone, if

    $$\begin{aligned}\big <Ax-Ay,x-y\big >\ge 0,~~ \forall x,y \in \mathcal { H}. \end{aligned}$$
  3. (iii)

    Pseudomonotone, if

    $$\langle Ay, x-y \rangle \ge 0 \implies ~\langle Ax,x-y \rangle \ge 0,~\forall x,y \in \mathcal {H},$$

Note that (i) \(\implies \) (ii) \(\implies \) (iii) but the converses are not always true.

A central problem in nonlinear analysis is the VIP, which was first introduced independently by Fichera [18] and Stampacchia [51]. It plays an important role in the study of several important concepts in pure and applied sciences such as mechanics, neccessary optimality conditions, operations research, systems of nonlinear equations, among others (see [19, 25, 62]). Many authors have analyzed and studied iterative algorithms for approximating the solution of the VIP (1.1) and other related optimization problems, (see [2, 10, 20, 27, 36, 41, 52, 56], and the references therein).

Under certain conditions, there are two common methods used in approximating the solution of the VIP (1.1). These methods are the projection method and the regularized method. To use these methods, a certain level of monotonicity is required for the cost operator. In this work, our main focus is on the projection method. Several authors have proposed and studied projection type algorithms for approximating the solutions of VIP (1.1) (see [1, 13, 14, 22, 30, 43, 60] and other references therein).

Tseng [57] introduced and studied Tseng’s extragradient method for approximating the solution of the VIP (1.1). The proposed method is defined as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=P_{\mathcal {C}}(x_n-\lambda Ax_n)\\ x_{n+1}=y_n-\lambda (Ay_n-Ax_n),~~\forall n\ge 0, \end{array}\right. }\end{aligned}$$

where A is monotone, L-Lipschitz continuous and \(\lambda \in \Big (0,\frac{2}{L}\Big ).\) The author obtained a weak convergence result under the assumption that \(VI(\mathcal {C},A)\ne \emptyset .\)

The equilibrium problem (EP) was introduced by Blum and Oettli [7] and they defined it as follows: Find \(x\in \mathcal {C}\) such that

$$\begin{aligned} \Phi (x,y)\ge 0, ~~\forall y\in \mathcal {C}, \end{aligned}$$
(1.2)

where \(\mathcal {C}\) is a nonempty, closed and convex subset of a real Hilbert space \(\mathcal {H}\) and \(\Phi :\mathcal {C}\times \mathcal {C}\rightarrow \mathbb {R}\) is a bifunction. A point \(x\in \mathcal {C}\) that solves this problem is called the equilibrium point. We denote the solution set of EP (1.2) by \(EP(\Phi ).\) The EP (1.2) has received a lot of attention from several authors due to its application to problems arising in the field of optimization, economics, physics, variational inequalities, among others (see, for example, [39, 42, 47, 53] and other references therein). Several authors have analyzed and proposed various iterative algorithms for approximating the solution of the EP and other related optimization problems, (see, for example, [24, 40, 46] and other references therein).

Let \(\mathcal {H}_1, \mathcal {H}_2\) and \(\mathcal {H}_3\) be real Hilbert spaces. Let \(\mathcal {C},\mathcal {Q}\) be nonempty, closed and convex subsets of \(\mathcal {H}_1\) and \(\mathcal {H}_2,\) respectively. Let \(\mathcal {F}_1:\mathcal {H}_1\rightarrow \mathcal {H}_3\) and \(\mathcal {F}_2:\mathcal {H}_2\rightarrow \mathcal {H}_3\) be bounded linear operators. The split equality problem (SEP) is defined as follows:

$$\begin{aligned} \text{ Find }~x\in \mathcal {C}~\text {and}~y\in \mathcal {Q}~\text {such that}~\mathcal {F}_1x=\mathcal {F}_2y. \end{aligned}$$
(1.3)

The SEP which was first proposed by Moudafi [37] allows asymmetric and partial relations between the variables x and y. It is used in numerous practical problems such as game theory, medical image reconstruction, partial differential equation, decomposition method, among others (see [29, 50]). We denote the solution set of (1.3) by

$$\Omega _{SEP}:=\left\{ (x,y)\in \mathcal {C}\times \mathcal {Q}\,|\,\mathcal {F}_1x=\mathcal {F}_2y\right\} .$$

Several authors have studied several effective methods for solving the SEP (see [50, 58] and other references therein).

If \(\mathcal {H}_2=\mathcal {H}_3\) and \(\mathcal {F}_2=I \) (I is the identity operator), (1.3) reduces to the split feasibility problem (SFP) proposed by Censor et al. [12] and defined as follows:

$$\begin{aligned} \text{ Find }~x\in \mathcal {C}~\text{ such } \text{ that }~\mathcal {F}_1x\in \mathcal {Q}, \end{aligned}$$

where \(\mathcal {F}_1:\mathcal {H}_1\rightarrow \mathcal {H}_2\) is a bounded linear operator. One of the most common method for solving (1.3) is the CQ projection method proposed and studied by Bryne et al. [9]. They defined it as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{n+1}=P_{\mathcal {C}}(x_n-\eta _n \mathcal {F}_1^*(\mathcal {F}_1x_n-\mathcal {F}_2y_n))\\ y_{n+1}=P_{\mathcal {Q}}(y_n+\eta _n\mathcal {F}_2^*(\mathcal {F}_1x_n-\mathcal {F}_2y_n)), \end{array}\right. } \end{aligned}$$
(1.4)

where \(\eta _n\in \Big (\epsilon , \frac{2}{\lambda _{\mathcal {F}_1}+\lambda _{\mathcal {F}_2}}-\epsilon \Big ),\) and \(\lambda _{\mathcal {F}_1}\) and \(\lambda _{\mathcal {F}_2}\) are the matrix operator norms \(\Vert \mathcal {F}_1\Vert \) and \(\Vert \mathcal {F}_2\Vert ,\) respectively. Note that the step size \(\eta _n\) in Algorithm (1.4) is dependent on the operator norms, which are difficult and sometimes impossible to compute. Several authors have studied several effective methods for solving SFP (see [50] and other references therein).

Another problem of interest in this study is the fixed point problem (FPP), which is formulated as follows:

$$\begin{aligned} \text{ Find } x\in \mathcal {H} \text{ such } \text{ that } {T}x=x, \end{aligned}$$

where \({T}:\mathcal {H}\rightarrow \mathcal {H}\) is a nonlinear mapping. We denote the set of fixed points of T by F(T). Several problems in sciences and engineering can be formulated as the problem of finding solutions of FPP of nonlinear mappings.

If \(\mathcal {C}\) and \(\mathcal {Q}\) are the sets of fixed points of some nonlinear operators, the SEP (1.3) becomes the split equality common fixed point problem (SECFPP) which is defined as

$$\begin{aligned} \text{ Find } ~x\in F({T}_1) ~\text{ and }~ y\in F({T}_2)~\text{ such } \text{ that } ~\mathcal {F}_1x=\mathcal {F}_2y, \end{aligned}$$
(1.5)

where \(F({T}_1)\ne \emptyset \) and \(F({T}_2)\ne \emptyset \) are the sets of fixed points of \({T}_1\) and \({T}_2,\) respectively, \({T}_1:\mathcal {H}_1\rightarrow \mathcal {H}_1\) and \({T}_2:\mathcal {H}_2\rightarrow \mathcal {H}_2\) are nonlinear mappings and \(\mathcal {F}_1:\mathcal {H}_1\rightarrow \mathcal {H}_3,~\mathcal {F}_2:\mathcal {H}_2\rightarrow \mathcal {H}_3\) are bounded linear operators.

If \(\mathcal {H}_2=\mathcal {H}_3\) and \(\mathcal {F}_2=I,\) then the SECFPP (1.5) reduces to the following split common fixed point problem (SCFPP) introduced by Censor et al. [11]

$$\begin{aligned} \text{ Find } x\in F({T}_1)~\text{ such } \text{ that }~\mathcal {F}_1x\in F({T}_2). \end{aligned}$$

Several authors have studied and proposed effective methods for solving SCFPP (see [49] and other references therein).

The SECFPP was first studied by Moudafi et al. [37]. They introduced the following simultaneous iterative method for solving the SECFPP

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{n+1}={T}_1(x_n-\eta _n\mathcal {F}_1^*(\mathcal {F}_1x_n-\mathcal {F}_2y_n))\\ y_{n+1}={T}_2(y_n+\eta _n\mathcal {F}_2^*(\mathcal {F}_1x_n-\mathcal {F}_2y_n)), \end{array}\right. } \end{aligned}$$
(1.6)

where \(\eta _n\in \Big (\epsilon , \frac{2}{\lambda _{\mathcal {F}_1}+\lambda _{\mathcal {F}_2}}-\epsilon \Big ), \lambda _{\mathcal {F}_1}\) and \(\lambda _{\mathcal {F}_2}\) are the spectral radius of \(\mathcal {F}_1^*\mathcal {F}_1\) and \(\mathcal {F}_2^*\mathcal {F}_2,\) respectively, and \({T}_1\) and \({T}_2\) are firmly quasi-nonexpansive mappings. We also observe that the step size of Algorithm (1.6) depends on the operator norms. Hence to implement Algorithm (1.6), one has to compute the operator norms of \(\mathcal {F}_1\) and \(\mathcal {F}_2\) which are difficult to compute. Several authors have studied and proposed modifications of Algorithm (1.6) for better implementation (see [36, 37, 64] and other references therein).

Recently, Lopéz et al. [32] studied and proposed a method for estimating the step size which does not require prior knowledge of the operator norms for solving the SFP. Dong et al. [17] and J. Zhao [63] also proposed new choices of step size which do not require prior knowledge of the operator norm for solving SECFPP.  Zhao [63] studied the SEP and presented the following step size which guarantees convergence of the iterative method without prior knowledge of the operator norm of \(\mathcal {F}_1\) and \(\mathcal {F}_2\)

$$\begin{aligned} \eta _n\in \Big (0,\frac{2\Vert \mathcal {F}_1x_n-\mathcal {F}_2y_n\Vert ^2}{\Vert \mathcal {F}_1^*(\mathcal {F}_1x_n-\mathcal {F}_2y_n)\Vert ^2+\Vert \mathcal {F}_2^*(\mathcal {F}_1x_n-\mathcal {F}_2y_n)\Vert ^2}\Big ). \end{aligned}$$

The main purpose of this work is to find a common element of split equalities of the VIP, EP and common fixed point of nonexpansive semigroups. Several algorithms have been proposed for approximating the common solution of VIP, EP and FPP due to the applications it has on mathematical models whose constraints can be expressed as VIP, EP and FPP. Particularly, finding common solution problems has application in signal processing, network resource allocation, image recovery, among others (see [26, 33, 34] and other references therein).

Recently, Latif and Eslamian [31] studied and introduced a new algorithm for finding a common element of split equalities of EP, monotone VIP with Lipschitz operator and fixed point problem of nonexpansive semigroups satisfying the uniformly asymptotically regularity (u.a.r) condition in Hilbert spaces. The authors obtained strong convergence result for the proposed algorithm. However, their proposed algorithm has certain drawbacks. For instance, their method requires computing two projections each per iteration onto \(\mathcal {C}\) and \(\mathcal {Q},\) which makes it computationally expensive to implement. Moreover, the associated cost operators for the VIP are required to be monotone and Lipschitz continuous and the step size of the algorithm depends on the Lipschitz constants of these operators. In addition, the authors needed to impose the uniformly asymptotically regularity condition on the nonexpansive semigroups to obtain their result. All of these drawbacks limit the scope of application of their proposed method.

The inertial technique has been employed by several authors to increase the convergence rate of iterative methods. Polyak [45] studied the convergence of the following inertial extrapolation algorithm

$$\begin{aligned} x_{n+1}=x_n+\alpha _1(x_n-x_{n-1})-\alpha _2Ax_n,\hspace{0.1cm}\forall n\ge 0, \end{aligned}$$

where \(\alpha _1\) and \(\alpha _2\) are two real numbers. Recently, there has been an increased interest in studying inertial type algorithm (see [2, 5, 6, 23, 28, 59] and other references therein).

Motivated by the above results in the literature and other related results in this direction, we propose and study an inertial Tseng’s extragradient algorithm for the SEP for finding a common element of solution of the EP, VIP and common fixed point of nonexpansive semigroups with the following features:

  1. (i)

    Different from other existing methods for finding a common element of the solution of the EP, VIP and fixed point problem of nonexpansive semigroups, our method only requires that the underlying operator for the VIP be pseudomonotone, uniformly continuous and without the weak sequential continuity condition often used in the literature. Also, we do not need to assume the u.a.r condition employed by authors in the literature to obtain our strong convergence result.

  2. (ii)

    Different from other existing methods in the literature for solving non-Lipschitz VIP, our method does not require any linesearch technique but rather uses an easily implementable self-adaptive step size technique that generates non-monotonic sequence of step sizes. Also, our method only requires one projection each per iteration onto the feasible sets \(\mathcal {C}\) and \(\mathcal {Q}.\)

  3. (iii)

    Our method employs the inertial extrapolation technique to increase the rate of convergence (see [4,5,6] and other references therein).

  4. (iv)

    The proof of our strong convergence result does not rely on the usual “two cases approach" widely used in many papers to prove strong convergence results.

Finally, we provide some numerical experiments for our proposed method in comparison with the related method in the literature to show the applicability of our proposed method.

The rest of the paper is organized as follows: In Section 2 we present some definitions and lemmas needed to obtain the strong convergence result. In Section 3, we present our proposed method and discuss some of its important features. In Section 4, the convergence of our method is investigated and in Section 5, we present some numerical experiments of our method in comparison with a related method in the literature. We conclude in Section 6.

2 Preliminaries

In this section, we recall some lemmas, results and definitions which will be required in subsequent sections to obtain our strong convergence result. Let \(\mathcal {H}\) be a real Hilbert space with inner product \(\langle \cdot ~ \cdot \rangle \), and associated norm \(||\cdot ||\) defined by \(||x||=\sqrt{\langle x, x\rangle },\) \(\forall x\in \mathcal {H}\). We denote the strong and weak convergence by “\(\rightarrow \)” and “\(\rightharpoonup \)”, respectively. Also, we denote the set of weak limits of \(\{x_n\}\) by \(w_{\omega }(x_n),\) that is

$$\begin{aligned} w_{\omega }(x_n):=\left\{ x\in \mathcal {H}\,:\,x_{n_j}\rightharpoonup x\text { for some subsequence } \{x_{n_j}\} \text { of } \{x_n\}\right\} . \end{aligned}$$

Definition 2.1

Let \(T:\mathcal {H}\rightarrow \mathcal {H}\) be a mapping. Then, T is said to be

  1. (i)

    L-Lipschitz continuous, if there exists a constant \(L>0\) such that

    $$\begin{aligned} \Vert Tx-Ty\Vert \le L\Vert x-y\Vert ,~~ \forall x,y\in \mathcal {H}; \end{aligned}$$

    if \(L\in [0,1),\) then T is called a contraction;

  2. (ii)

    Uniformly continuous, if for every \(\epsilon >0,\) there exists \(\delta =\delta (\epsilon )>0,\) such that

    $$\Vert Tx-Ty\Vert<\epsilon \quad \text {whenever}\quad \Vert x-y\Vert <\delta ,~~\forall x,y\in \mathcal {H};$$
  3. (iii)

    Sequentially weakly continuous, if for each sequence \(\{x_n\},\) we have \(x_n\rightharpoonup x\in \mathcal {H}\) implies that \(Tx_n\rightharpoonup Tx\in \mathcal {H};\)

  4. (iv)

    Nonexpansive if T is 1-Lipschitz continuous;

  5. (v)

    Firmly nonexpansive if

    $$\Vert Tx-Ty\Vert ^2\le \Vert x-y\Vert ^2-\Vert (I-T)x-(I-T)y\Vert ^2,~~\forall x,y\in \mathcal {H}.$$

More information on firmly nonexpansive mappings can be found, for example, in [21, Section 11]. Observe that uniform continuity is a weaker notion than Lipschitz continuity.

Definition 2.2

A one-parameter family mapping \(\mathcal {T}=\{T(s)\,:\,0\le s<+\infty \}\) from \(\mathcal {H}_1\) into itself is said to be a nonexpansive semigroup if it satisfies the following conditions:

  1. (i)

    \(T(0)x=x,\) \(\forall x\in \mathcal {H}_1;\)

  2. (ii)

    \(T(s+u)=T(s)T(u)\) for all \(s,u\ge 0;\)

  3. (iii)

    For each \(x\in \mathcal {H}_1,\) the mapping T(s)x is continuous;

  4. (iv)

    \(\Vert T(s)x-T(s)y\Vert \le \Vert x-y\Vert \) for all \(x,y\in \mathcal {H}_1\) and \(s\ge 0.\)

We denote the common fixed point set of the semigroup \(\mathcal {T}\) by \(F(\mathcal {T})=\{x\in \mathcal {C}\,:\,T(s)x=x,~\forall s\ge 0\}.\) It is well known that \(F(\mathcal {T})\) is closed and convex [8].

Lemma 2.3

[48, 55] Let \(\mathcal {C}\) be a nonempty bounded closed and convex subset of a real Hilbert space \(\mathcal {H}.\) Let \(\mathcal {T}=\{T(s)\,:\,s\ge 0\}\) from \(\mathcal {C}\) be a nonexpansive semigroup on \(\mathcal {C}\). Then for all \(h\ge 0,\)

$$\begin{aligned} \limsup \limits _{t \rightarrow \infty ,~x\in \mathcal {C}}\Big \Vert \frac{1}{t}\int _{0}^{t}T(s)x-T(h)\Big (\frac{1}{t}\int _{0}^{t}T(s)xdx\Big )\Big \Vert =0. \end{aligned}$$

Lemma 2.4

[55] Let \(\mathcal {C}\) be a nonempty bounded closed and convex subset of a real Hilbert space \(\mathcal {H}.\) Let \(\{x_n\}\) be a sequence and let \(\mathcal {T}=\{T(s)\,:\,s\ge 0\}\) from \(\mathcal {C}\) be a nonexpansive semigroup on \(\mathcal {C},\) if the following conditions are satisfied

  1. (i)

    \(x_n\rightharpoonup x;\)

  2. (ii)

    \(\limsup _{s \rightarrow \infty }\limsup _{n \rightarrow \infty }\Vert T(s)x_n-x_n\Vert =0,\)

then, \(x\in F(\mathcal {T}).\)

It is well known that if D is a convex subset of \(\mathcal {H},\) then \(T:D\rightarrow \mathcal {H}\) is uniformly continuous if and only if, for every \(\epsilon >0,\) there exists a constant \(M<+\infty \) such that

$$\begin{aligned} \Vert Tx-Ty\Vert \le M\Vert x-y\Vert + \epsilon ,~~ \forall x,y\in D. \end{aligned}$$
(2.1)

For the proof of (2.1), see [61, Theorem 1].

Lemma 2.5

[38] Let \(\mathcal {H}\) be a real Hilbert space, then the following assertions hold:

  1. (1)

    \(2\langle x, y \rangle =\Vert x\Vert ^2+\Vert y\Vert ^2-\Vert x-y\Vert ^2=\Vert x+y\Vert ^2-\Vert x\Vert ^2-\Vert y\Vert ^2,~\forall x,y \in \mathcal {H};\)

  2. (2)

    \(\Vert \alpha x+(1-\alpha )y\Vert ^2 = \alpha \Vert x\Vert ^2+(1-\alpha )\Vert y\Vert ^2-\alpha (1-\alpha )\Vert x-y\Vert ^2,~\forall x,y \in \mathcal {H},~ \alpha \in \mathbb {R};\)

  3. (3)

    \(\Vert x+y\Vert ^2 \le \Vert x\Vert ^2+2\langle y, x+y \rangle , ~\forall x,y \in \mathcal {H}\).

Lemma 2.6

[16] Assume that \(A:\mathcal {H} \rightarrow \mathcal {H} \) is a continuous and pseudomonotone operator. Then, x is a solution of (1.1) if and only if \(\langle Ay,y -x \rangle \ge 0,~ \forall y\in \mathcal {C}.\)

Lemma 2.7

[35] Let \(\mathcal {H}\) be a real Hilbert space and \(\mathcal {C}\) be a nonempty closed and convex subset of \(\mathcal {H}\). If the mapping \(h:[0,1] \rightarrow \mathcal {H}\) defined as \(h(t):=A(tx+(1-t)y)\) is continuous for all \(x,y \in \mathcal {C}\) (i.e. h is hemicontinuous), then \(M(A,\mathcal {C}):=\{x \in \mathcal {C}\,:\, \big <Ay,y-x \big > \ge 0,~ \forall y\in \mathcal {C}\}\subset VI(\mathcal {C}, A).\) Moreover, if A is pseudo-monotone, then \(VI(\mathcal {C}, A)\) is closed, convex and \(M(\mathcal {C}, A)=VI(\mathcal {C}, A)\).

Recall that for a nonempty, closed and convex subset \(\mathcal {C}\) of \(\mathcal {H}\), the metric projection denoted by \(P_\mathcal {C}\), is a map defined on \(\mathcal {H}\) onto \(\mathcal {C}\) which assigns to each \(x\in \mathcal {H}\), the unique point in \(\mathcal {C}\), denoted by \(P_\mathcal {C} x\) such that

$$||x-P_\mathcal {C}x||=\inf \{||x-y||\,:\,y\in \mathcal {C}\}.$$

Lemma 2.8

[21] Let \(\mathcal {C}\) be a closed and convex subset of a real Hilbert space \(\mathcal {H}\) and \(x,y\in \mathcal {H}.\) Then

  1. (i)

    \(\Vert P_{\mathcal {C}}x-P_{\mathcal {C}}y\Vert ^2\le \left\langle P_{\mathcal {C}}x-P_{\mathcal {C}}y,~x-y\right\rangle ;\)

  2. (ii)

    \(\Vert P_{\mathcal {C}}x-y\Vert ^2\le \Vert x-y\Vert ^2-\Vert x-P_{\mathcal {C}}x\Vert ^2.\)

Assumption 2.9

[7] Let \(\Phi :\mathcal {C}\times \mathcal {C}\rightarrow \mathbb {R}\) be a bifunction satisfying the following assumptions:

  1. 1)

    \( \Phi (x,x)=0,~\forall x\in \mathcal {C};\)

  2. 2)

    \(\Phi \) is monotone, i.e., \(\Phi (x,y)+\Phi (y,x)\le 0, ~\forall x\in \mathcal {C};\)

  3. 3)

    For each \(x,y,z\in \mathcal {C}, ~\limsup _{t\rightarrow 0}\Phi (tz+(1-t)x,y)\le \Phi (x,y);\)

  4. 4)

    For each \(x\in \mathcal {C}, ~y\rightarrow \Phi (x,y)\) is convex and lower semi continuous.

Lemma 2.10

[15] Let \(\Phi :\mathcal {C}\times \mathcal {C}\rightarrow \mathbb {R}\) be a bifunction satisfying Assumption 2.9. For any \(r>0\) and \(x\in \mathcal {H},\) define a mapping \(U^\Phi _r:\mathcal {H}\rightarrow \mathcal {C}\) as follows

$$\begin{aligned} U^{\Phi }_r(x)=\left\{ z\in \mathcal {C}\,:\,\Phi (z,y)+\frac{1}{r}\Big \langle y-z, z-x\Big \rangle \ge 0, ~~ \forall y\in \mathcal {C}\right\} . \end{aligned}$$

Then, we have the following

  1. (1)

    \(U^{\Phi }_r\) is nonempty and single valued;

  2. (2)

    \(U^{\Phi }_r\) is firmly nonexpansive;

  3. (3)

    \(F(U^{\Phi }_r)=EP(\Phi )\) is closed and convex.

Definition 2.11

Assume that \(T:\mathcal {H}\rightarrow \mathcal {H}\) is a nonlinear operator with \(F(T)\ne \emptyset .\) Then \(I-T\) is said to be demiclosed at zero if for any \(\{x_n\}\) in \(\mathcal {H},\) the following implication holds:

$$\begin{aligned} x_n\rightharpoonup x \text{ and } (I-T)x_n\rightarrow 0\implies x\in F(T). \end{aligned}$$

Lemma 2.12

[54] Suppose \(\{\lambda _n\}\) and \(\{\theta _n\}\) are two nonnegative real sequences such that

$$\begin{aligned} \lambda _{n+1}\le \lambda _n + \phi _n,~~ \forall n\ge 1. \end{aligned}$$

If \(\sum _{n=1}^{\infty }\phi _n<\infty ,\) then \(\lim _{n\rightarrow \infty }\lambda _n\) exists.

Lemma 2.13

[3] Let \(\{a_n\}\) be a sequence of non-negative real numbers, \(\{\gamma _n\}\) be a sequence of real numbers in (0, 1) with conditions \(\sum _{n=1}^{\infty }\gamma _n=\infty \) and \(\{d_n\}\) be a sequence of real numbers. Assume that

$$a_{n+1}\le (1-\gamma _n)a_n+\gamma _nd_n,~~ n\ge 1.$$

If \(\limsup _{k \rightarrow \infty }d_{n_k}\le 0\) for every subsequence \(\{a_{n_k}\}\) of \(\{a_n\}\) satisfying the condition\(\liminf _{k \rightarrow \infty }(a_{{n_k}+1}-a_{n_k})\ge 0,\) then \(\lim _{n \rightarrow \infty }a_n=0.\)

Lemma 2.14

[44] Each Hilbert space H satisfies the Opial condition, that is, for any sequence \(\{x_n\}\) with \(x_n\rightharpoonup x,\) the inequality \(\liminf _{n\rightarrow \infty }||x_n-x||< \liminf _{n\rightarrow \infty }||x_n-y||\) holds for every \(y\in H\) with \(y\ne x.\)

3 Proposed Method

In this section, we present our proposed method and discuss its features. We begin with the following assumptions under which our strong convergence result is obtained.

Assumption 3.1

Suppose that the following conditions hold:

  1. (a)

    The feasible sets \(\mathcal {C}\) and \(\mathcal {Q}\) are nonempty, closed and convex subsets of the real Hilbert spaces \(\mathcal {H}_1\) and \(\mathcal {H}_2\), respectively.

  2. (b)

    \(A:\mathcal {H}_1 \rightarrow \mathcal {H}_1\) and \(B:\mathcal {H}_2 \rightarrow \mathcal {H}_2\) are pseudomonotone and uniformly continuous.

  3. (c)

    The mapping \(A:\mathcal {H}_1\rightarrow \mathcal {H}_1\) and \(B:\mathcal {H}_2 \rightarrow \mathcal {H}_2\) satisfies the following property: whenever \(\{x_n\}\subset \mathcal {C}, ~x_n\rightharpoonup x^*,\) one has \(\Vert Ax^*\Vert \le \liminf _{n\rightarrow \infty }\Vert Ax_n\Vert \) and whenever \(\{x_n\}\subset \mathcal {Q}, ~x_n\rightharpoonup x^*,\) one has \(\Vert Bx^*\Vert \le \liminf _{n\rightarrow \infty }\Vert Bx_n\Vert ,\) respectively.

  4. (d)

    \(\mathcal {F}_1:\mathcal {H}_1 \rightarrow \mathcal {H}_3\) and \(\mathcal {F}_2:\mathcal {H}_2 \rightarrow \mathcal {H}_3\) are bounded linear operators.

  5. (e)

    \(\Phi _1:\mathcal {C}\times \mathcal {C}\rightarrow \mathbb {R},\hspace{0.1cm} \Phi _2:\mathcal {Q}\times \mathcal {Q}\rightarrow \mathbb {R}\) are bifunctions satisfying Assumption 2.9 and \(\Phi _2\) is upper semi continuous in the first argument.

  6. (f)

    \(\mathcal {T}_a =\{T_1(s)\,:\,0\le s<\infty \}\) and \(\mathcal {T}_b=\{T_2(u)\,:\,0\le u<\infty \}\) are one-parameter nonexpansive semigroups on \(\mathcal {H}_1\) and \(\mathcal {H}_2,\) respectively.

  7. (g)

    The solution set \(\Gamma =\{x\in EP(\Phi _1)\cap VI( \mathcal {C}, A)\cap F(\mathcal {T}_a),~y\in EP(\Phi _2)\cap VI(\mathcal {Q}, B)\cap F(\mathcal {T}_b)\,:\,\mathcal {F}_1x=\mathcal {F}_2y\} \ne \emptyset .\)

  8. (h)

    \(\{\alpha _n\}\subset (0,1),\) \( \sum _{n=1}^{\infty }\alpha _n=+\infty ,~\lim _{n\rightarrow \infty }\alpha _n=0,~ 0<\lim \inf _{n\rightarrow \infty }\beta _n\le \limsup _{n\rightarrow \infty }\beta _n<1,~0<\liminf _{n\rightarrow \infty }\gamma _n\le \limsup _{n\rightarrow \infty }\gamma _n<1.\)

  9. (i)

    Let \(\{\epsilon _n\}\) and \(\{\zeta _n\}\) be positive sequences such that \(\lim _{n\rightarrow \infty }\frac{\epsilon _n}{\alpha _n}=0\) and \(\lim _{n\rightarrow \infty }\frac{\zeta _n}{\alpha _n}=0,\) respectively.

  10. (j)

    Let \(\{\sigma _n\}\) and \(\{\mu _n\}\) be nonnegative sequences such that \(\sum _{n=1}^{\infty }\sigma _n<+\infty \) and \(\sum _{n=1}^{\infty }\mu _n<+\infty ,\) respectively, \( \{t_{n,1}\},\{t_{n,2}\}\subset (0,+\infty ), \liminf r_{n,1}>0,\liminf r_{n,2}>0\).

Algorithm 3.2

Step 0: Choose sequences \(\{\beta _n\}^{\infty }_{n=1}, \{\gamma _n\}^{\infty }_{n=1},\{\theta _n\}^{\infty }_{n=1}\) and \(\{\tau _n\}^{\infty }_{n=1}\) such that the conditions from Assumption 3.1 (h)–(i) hold. Select an initial point \((x_0,y_0)\in \mathcal {H}_1\times \mathcal {H}_2,\) let \(\eta \ge 0,\) \( ~a_i \in (0,1), i=1,2,\) \(\lambda _1>0\), \(\rho _1>0\), \(\theta>0,~ \tau >0\) and set \(n:=1.\)

Step 1: Given the iterates \(x_{n-1},y_{n-1}\) and \(x_n,y_n\) for each \(n \ge 1,\) choose \(\theta _n\) such that \(0\le \theta _n \le \bar{\theta }_n\) and \(\tau _n\) such that \(0\le \tau _n \le \bar{\tau }_n\), where

$$\begin{aligned} \bar{\theta }_n:= {\left\{ \begin{array}{ll} \min \left\{ \theta , \frac{\epsilon _n}{\Vert x_n-x_{n-1}\Vert }\right\} &{} \text{ if } x_n \ne x_{n-1}\\ \theta &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$
(3.1)

Step 2: Compute

$$w_n=(1-\alpha _n)\Big (x_n+\theta _n(x_n-x_{n-1})\Big )$$

and

$$\varphi _n=(1-\alpha _n)\Big (y_n+\tau _n(y_n-y_{n-1})\Big ).$$

Step 3: Compute

$$\begin{aligned}{} & {} z_n=w_n-\eta _n\mathcal {F}^*_1(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n),\\{} & {} \phi _n=U^{\Phi _1}_{r_{n,1}}z_n,\\{} & {} u_n=P_\mathcal {C}(\phi _n-\lambda _n A\phi _n),\\{} & {} v_n=u_n-\lambda _n (Au_n-A\phi _n),\\{} & {} x_{n+1}=(1-\beta _n)v_n+\beta _n\frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_n~ds \end{aligned}$$

and

$$\begin{aligned} \lambda _{n+1}={\left\{ \begin{array}{ll} \min \left\{ \frac{a_1||u_n-\phi _n||}{||Au_n-A\phi _n||},~\lambda _n+\sigma _n\right\} &{} \text{ if } Au_n\ne A\phi _n\\ \lambda _n+\sigma _n&{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$
(3.2)

Step 4: Compute

$$\begin{aligned} \bar{\tau }_n:= {\left\{ \begin{array}{ll} \min \left\{ \tau , \frac{\zeta _n}{\Vert y_n-y_{n-1}\Vert }\right\} &{} \text{ if } y_n \ne y_{n-1}\\ \tau &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$
(3.3)

Step 5 Compute

$$k_n=\varphi _n+\eta _n \mathcal {F}^{*}_2(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n).$$

Step 6: Compute

$$\begin{aligned}{} & {} \psi _n=U^{\Phi _2}_{r_{n,2}}k_n,\\{} & {} s_n= P_\mathcal {Q} (\psi _n-\rho _n B\psi _n),\\{} & {} b_n=s_n-\rho _n(Bs_n-B\psi _n),\\{} & {} y_{n+1}=(1-\gamma _n)b_n+\gamma _n\frac{1}{t_{n,2}}\int _{0}^{t_{n,2}} T_2(u)b_n~du \end{aligned}$$

and

$$\begin{aligned} \rho _{n+1}={\left\{ \begin{array}{ll} \min \left\{ \frac{a_2||s_n-\psi _n||}{||Bs_n-B\psi _n||},~\rho _n+\mu _n\right\} &{} \text{ if } Bs_n\ne B\psi _n\\ \rho _n+\mu _n&{} \text{ otherwise }, \end{array}\right. } \end{aligned}$$
(3.4)

where the step size \(\eta _n\) is chosen such that for small enough \(\epsilon >0,\)

$$\eta _n\in \left[ \epsilon , ~~\frac{2\Vert \mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\Vert ^2}{\Vert \mathcal {F}^{*}_2(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2}-\epsilon \right] ,$$

if \(\mathcal {F}_1w_n\ne \mathcal {F}_2\varphi _n\); otherwise, \(\eta _n=\eta .\)

Set \(n:=n+1\) and go back to Step 1.

Remark 3.3

The step sizes generated in (3.2) and (3.4) are allowed to increase per iteration. This reduces their dependence on the initial step sizes. When n is large enough the step size may not increase. We assume that Algorithm 3.2 does not terminate in a finite number of iterations.

Remark 3.4

By conditions (h) and (i), from (3.1) we observe that

$$\begin{aligned} \lim _{n\rightarrow \infty }\theta _n||x_n - x_{n-1}|| = 0 ~~ \text {and}~~ \lim _{n\rightarrow \infty }\frac{\theta _n}{\alpha _n}||x_n - x_{n-1}|| = 0. \end{aligned}$$
(3.5)

Similarly, from (3.3) we have

$$\begin{aligned}\lim _{n\rightarrow \infty }\tau _n||y_n - y_{n-1}|| = 0 ~~ \text {and}~~ \lim _{n\rightarrow \infty }\frac{\tau _n}{\alpha _n}||y_n - y_{n-1}|| = 0. \end{aligned}$$

Remark 3.5

We note that condition (c) of Assumption 3.1 is weaker than the sequentially weakly continuity condition.

We present an example which satisfies condition (c) of Assumption 3.1.

Example 3.6

Let \(A:\ell _2(\mathbb {R})\rightarrow \ell _2(\mathbb {R})\) be an operator defined by

$$\begin{aligned} Ax^*=x^*\Vert x^*||,~~\forall x^*\in \ell _2. \end{aligned}$$

Suppose that \(\{x_n\}\subset \ell _2(\mathbb {R})\) such that \(x_n\rightharpoonup x^*.\) Then, by the weakly lower semi-continuity of the norm we obtain

$$\begin{aligned} \Vert x^*\Vert \le {\underset{n\rightarrow +\infty }{\liminf }}\Vert x_n\Vert . \end{aligned}$$

Thus,

$$\begin{aligned}&\Vert Ax^*\Vert =\Vert x^*\Vert ^2\le \Big ({\underset{n \rightarrow +\infty }{\liminf }}\Vert x_n\Vert \Big )^2\le {\underset{n \rightarrow +\infty }{\liminf }}\Vert x_n\Vert ^2={\underset{n \rightarrow +\infty }{\liminf }}\Vert Ax_n\Vert . \end{aligned}$$

Hence, A satisfies condition (c) of Assumption 3.1.

Remark 3.7

Since the sequences of step sizes generated by the algorithm in (3.2) and (3.4) are well defined and the limits \(\lim _{n\rightarrow \infty }\lambda _n\) and \(\lim _{n\rightarrow \infty }\rho _n\) exist (see Lemma 4.1). Then, the limit

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }\left( 1-\frac{\lambda _n^2a_1^2}{\lambda _{n+1}^2}\right) =1-a_1^2>0. \end{aligned}$$
(3.6)

Thus, there exists \(n_{0_1}> 0\) such that for all \(n> n_{0_1},\) we have \(\Big (1-\frac{\lambda _n^2a_1^2}{\lambda _{n+1}^2}\Big )>0.\)

Similarly, we have that

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }\left( 1-\frac{\rho _n^2a_2^2}{\rho _{n+1}^2}\right) =1-a_2^2>0, \end{aligned}$$
(3.7)

and there exists \(n_{0_2}> 0\) such that for all \(n> n_{0_2},\) we have \(\Big (1-\frac{\rho _n^2a_2^2}{\rho _{n+1}^2}\Big )>0.\) Now, we set \(n_0=\max \{n_{0_1}, n_{0_2}\}.\)

Remark 3.8

From the definition of \(\eta _n,\) that is,

$$\begin{aligned} \eta _n\in \left[ \epsilon , ~~\frac{2\Vert \mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\Vert ^2}{\Vert \mathcal {F}^{*}_2(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2}-\epsilon \right] \end{aligned}$$

we have

$$\begin{aligned} (\eta _n+\epsilon )\Big [\Vert \mathcal {F}^*_2(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2\Big ]\le 2\Vert \mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\Vert ^2. \end{aligned}$$

Expanding the last inequality, we have

$$\begin{aligned}&\eta _n\cdot \epsilon \Big [\Vert \mathcal {F}^*_2(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\Vert )^2\Big ]\nonumber \\ \le&\eta _n\Big (2\Vert \mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\Vert ^2 -\eta _n\Big [\Vert \mathcal {F}^*_2(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2\Big ]\Big ). \end{aligned}$$
(3.8)

4 Convergence Analysis

Lemma 4.1

Let \(\{\lambda _n\}\) and \(\{\rho _n\}\) be sequences generated by Algorithm 3.2. Then, we have \(\lim _{n\rightarrow \infty }\lambda _n=\lambda ,\) where \(\lambda \in [\min \{\frac{a_1}{K_1},\lambda _1\},\lambda _1+b_1], b_1=\sum _{n=1}^{\infty }\sigma _n\) for some \(K_1>0\) and\(\lim _{n\rightarrow \infty }\rho _n=\rho ,\) where \(\rho \in [\min \{\frac{a_2}{K_2},\rho _1\},\rho _1+b_2],b_2=\sum _{n=1}^{\infty }\mu _n\) for some \(K_2>0.\)

Proof

Since A is uniformly continuous, we obtain from (2.1) that for any given \(\epsilon >0,\) there exists a constant \(M<+\infty \) such that \(\Vert Au_n-A\phi _n\Vert \le M\Vert u_n-\phi _n\Vert +\epsilon .\) Thus, when \(Au_n-A\phi _n\ne 0\) for all \(n\ge 1\) we have

$$\begin{aligned} \frac{a_1\Vert u_n-\phi _n\Vert }{\Vert Au_n-A\phi _n\Vert }\ge \frac{a_1\Vert u_n-\phi _n\Vert }{M\Vert u_n-\phi _n\Vert +\epsilon } \ge \frac{a_1\Vert u_n-\phi _n\Vert }{(M+\epsilon _1)\Vert u_n-\phi _n\Vert } =\frac{a_1}{K_1}, \end{aligned}$$

where \(\epsilon =\min \{\epsilon _1\Vert u_n-\phi _n\Vert \,:\, n\in \mathbb {N}\}\) for some \(\epsilon _1>0\) and \(K_1=M+\epsilon _1.\) Hence, from the definition of \(\lambda _{n+1},\) the sequence \(\{\lambda _n\}\) is bounded below by \(\min \{\frac{a_1}{K_1},\lambda _1\}\) and above by \(\lambda _1 + b_1.\) By Lemma 2.12, it follows that \(\lim _{n\rightarrow \infty }\lambda _n\) denoted by \(\lambda =\lim _{n\rightarrow \infty }\lambda _n\) exists. Clearly, we have \(\lambda \in [\min \{\frac{a_1}{K_1},\lambda _1\},\lambda _1+b_1].\)

Similarly, we have \(\lim _{n\rightarrow \infty }\rho _n=\rho ,\) and \(\rho \in \text{ min }\{\frac{a_2}{K_2},\rho _1\},\rho _1+b_2.\) \(\square \)

Lemma 4.2

Let \(\big \{(x_n,y_n)\big \}\) be a sequence generated by Algorithm 3.2 under Assumption 3.1. Then

$$\begin{aligned} \Vert z_n-x^*\Vert ^2+\Vert k_n-y^*\Vert ^2\le \Vert w_n-x^*\Vert ^2+\Vert \varphi _n-y^*\Vert ^2. \end{aligned}$$

Proof

Let \((x^*,y^*)\in \Gamma .\) Then, by applying Lemma 2.5, we have

$$\begin{aligned} \Vert z_n-x^*\Vert ^2=&\Vert w_n-\eta _n\mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)-x^*\Vert ^2 \nonumber \\ =&\Vert w_n-x^*\Vert ^2+\eta _n^2\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-F_2\varphi _n)\Vert ^2-2\eta _n\left\langle w_n-x^*,~\mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\right\rangle \nonumber \\ =&\Vert w_n-x^*\Vert ^2+\eta _n^2\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-F_2\varphi _n)\Vert ^2-2\eta _n\left\langle \mathcal {F}_1w_n-\mathcal {F}_1x^*,~\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\right\rangle \nonumber \\ =&\Vert w_n-x^*\Vert ^2+\eta _n^2\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-F_2\varphi _n)\Vert ^2-\eta _n\Vert \mathcal {F}_1w_n-\mathcal {F}_1x^*\Vert ^2\nonumber \\&-\eta _n\Vert \mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\Vert ^2 +\eta _n\Vert \mathcal {F}_2\varphi _n-\mathcal {F}_1x^*\Vert ^2. \end{aligned}$$
(4.1)

Similarly, we have

$$\begin{aligned} \Vert k_n-y^*\Vert ^2=&\Vert \varphi _n+\eta _n\mathcal {F}_2^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)-y^*\Vert ^2 \nonumber \\ =&\Vert \varphi _n-y^*\Vert ^2+\eta _n^2\Vert \mathcal {F}_2^*(\mathcal {F}_1w_n-F_2\varphi _n)\Vert ^2-\eta _n\Vert \mathcal {F}_2\varphi _n-\mathcal {F}_2y^*\Vert ^2\nonumber \\&-\eta _n\Vert \mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\Vert ^2 +\eta _n\Vert \mathcal {F}_1w_n-\mathcal {F}_2y^*\Vert ^2. \end{aligned}$$
(4.2)

Adding (4.1) and (4.2), we have

$$\begin{aligned}&\Vert z_n-x^*\Vert ^2+\Vert k_n-y^*\Vert ^2\\ =&\Vert w_n-x^*\Vert ^2+\Vert \varphi _n-y^*\Vert ^2+\eta _n^2\Big [\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-F_2\varphi _n)\Vert ^2\\&+\Vert \mathcal {F}_2^*(\mathcal {F}_1w_n-F_2\varphi _n)\Vert ^2\Big ] -\eta _n\Big [\Vert \mathcal {F}_1w_n-\mathcal {F}_1x^*\Vert ^2+\Vert \mathcal {F}_2\varphi _n-\mathcal {F}_2y^*\Vert ^2\Big ]\\&-2\eta _n\Vert \mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\Vert ^2 +\eta _n\Big [\Vert \mathcal {F}_1w_n-\mathcal {F}_2y^*\Vert ^2+\Vert \mathcal {F}_2\varphi _n-\mathcal {F}_1x^*\Vert ^2\Big ]. \end{aligned}$$

By (3.8) and the fact that \(\mathcal {F}_1x^*=\mathcal {F}_2y^*,\) we have

$$\begin{aligned}&\Vert z_n-x^*\Vert ^2+\Vert k_n-y^*\Vert ^2\nonumber \\ =&\Vert w_n-x^*\Vert ^2+\Vert \varphi _n-y^*\Vert ^2-\eta _n\bigg [2\Vert \mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\Vert ^2\nonumber \\&-\eta _n\Big (\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2+\Vert \mathcal {F}_2^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2\Big )\bigg ]\nonumber \\ =&\Vert w_n-x^*\Vert ^2+\Vert \varphi _n-y^*\Vert ^2-\eta _n\cdot \epsilon \Big [\Vert \mathcal {F}^*_2(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2 +\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2\Big ]\nonumber \\&\le \Vert w_n-x^*\Vert ^2+\Vert \varphi _n-y^*\Vert ^2, \end{aligned}$$
(4.3)

which is the desired result.\(\square \)

Lemma 4.3

Let \(\big \{(x_n,y_n)\big \}\) be a sequence generated by Algorithm 3.2 under Assumption 3.1. Then

$$\begin{aligned} \Vert v_n-x^*\Vert ^2\le \Vert z_n-x^*\Vert ^2-\Vert z_n-\phi _n\Vert ^2-\left( 1-\frac{\lambda _n^2a_1^2}{\lambda _{n+1}^2}\right) \Vert u_n-\phi _n\Vert ^2 \end{aligned}$$

and

$$\begin{aligned} \Vert b_n-y^*\Vert ^2\le \Vert k_n-y^*\Vert ^2-\Vert k_n-\psi _n\Vert ^2-\left( 1-\frac{\rho _n^2a_2^2}{\rho _{n+1}^2}\right) \Vert s_n-\psi _n\Vert ^2. \end{aligned}$$

Proof

Let \((x^*,y^*)\in \Gamma .\) Since \(U^{\Phi _1}_{r_{n,1}}\) is firmly nonexpansive, it follows from Lemma 2.8 that

$$\begin{aligned} \Vert \phi _n-x^*\Vert ^2=\Vert U^{\Phi _1}_{r_{n,1}}z_n-x^*\Vert \le \Vert z_n-x^*\Vert ^2-\Vert z_n-\phi _n\Vert ^2. \end{aligned}$$
(4.4)

Similarly, we have

$$\begin{aligned} \Vert \psi _n-y^*\Vert ^2=\Vert U^{\Phi _2}_{r_{n,2}}k_n-y^*\Vert \le \Vert k_n-y^*\Vert ^2-\Vert k_n-\psi _n\Vert ^2. \end{aligned}$$

From (3.2), we obtain

$$\begin{aligned} \lambda _{n+1}=\min \left\{ \frac{a_1\Vert u_n-\phi _n\Vert }{\Vert Au_n-A\phi _n\Vert },\lambda _n+\sigma _n\right\} \le \frac{a_1\Vert u_n-\phi _n\Vert }{\Vert Au_n-A\phi _n\Vert }, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert Au_n-A\phi _n\Vert \le \frac{a_1}{\lambda _{n+1}}\Vert u_n-\phi _n\Vert ,~~\forall n\ge 1. \end{aligned}$$
(4.5)

Similarly, we have

$$\begin{aligned} \Vert Bs_n-B\psi _n\Vert \le \frac{a_2}{\rho _{n+1}}\Vert s_n-\psi _n\Vert ,~~\forall n\ge 1. \end{aligned}$$

From the definition of \(v_n\) in Step 3 and Lemma 2.5, we have

$$\begin{aligned} \Vert v_n-x^*\Vert ^2\le&\Vert u_n-\lambda _n(Au_n-A\phi _n)-x^*\Vert ^2\nonumber \\ =&\Vert u_n-x^*\Vert ^2+\lambda _n^2\Vert Au_n-A\phi _n\Vert ^2-2\lambda _n\langle Au_n-A\phi _n, u_n-x^*\rangle \nonumber \\ =&\Vert \phi _n-x^*\Vert ^2+\Vert u_n-\phi _n\Vert ^2+2\langle u_n-\phi _n,\phi _n-x^*\rangle \nonumber \\ {}&+\lambda _n^2\Vert Au_n-A\phi _n\Vert ^2-2\lambda _n\langle Au_n-A\phi _n,u_n-x^*\rangle \nonumber \\ =&\Vert \phi _n-x^*\Vert ^2+\Vert u_n-\phi _n\Vert ^2-2\langle u_n-\phi _n, u_n-\phi _n\rangle \nonumber \\&+2\langle u_n-\phi _n, u_n-x^*\rangle -2\lambda _n\langle Au_n-A \phi _n, u_n-x^*\rangle +\lambda _n^2\Vert Au_n-A\phi _n\Vert ^2\nonumber \\ =&\Vert \phi _n-x^*\Vert ^2-\Vert u_n-\phi _n\Vert ^2+2\langle u_n-\phi _n, u_n-x^*\rangle \nonumber \\&-2\lambda _n\langle A u_n-A\phi _n, u_n-x^*\rangle +\lambda _n^2\Vert Au_n-A\phi _n\Vert ^2. \end{aligned}$$
(4.6)

Since \(u_n=P_{\mathcal {C}}(\phi _n-\lambda _nA\phi _n)\) and \(x^*\in \mathcal {C},\) we obtain from the characteristic property of \(P_{\mathcal {C}}\) that

$$\langle u_n-\phi _n+\lambda _nA\phi _n, u_n-x^*\rangle \le 0.$$

This implies that

$$\begin{aligned} \langle u_n-\phi _n,u_n-x^*\rangle \le -\lambda _n\langle A\phi _n, u_n-x^*\rangle . \end{aligned}$$
(4.7)

Also since \(u_n\in \mathcal {C}\) and \(x^*\in \Gamma \) we have

$$\begin{aligned} \langle Au_n,~~u_n-x^*\rangle \ge 0,~~ \forall n\ge 0. \end{aligned}$$
(4.8)

Applying (4.4), (4.5), (4.7) and (4.8) in (4.6), we obtain

$$\begin{aligned} \Vert v_n-x^*\Vert ^2\le&\Vert \phi _n-x^*\Vert ^2-\Vert u_n-\phi _n\Vert ^2\nonumber \\&-2\lambda _n\langle A\phi _n, u_n-x^*\rangle -2\lambda _n\langle Au_n-A\phi _n, u_n-x^* \rangle +\lambda _n^2\Vert Au_n-A\phi _n\Vert ^2\nonumber \\ =&\Vert \phi _n-x^*\Vert ^2-\Vert u_n-\phi _n\Vert ^2-2\lambda _n\langle Au_n, u_n-x^*\rangle +\lambda _n^2\Vert Au_n-A\phi _n\Vert ^2\nonumber \\ \le&\Vert \phi _n-x^*\Vert ^2-\Vert u_n-\phi _n\Vert ^2+\lambda _n^2\frac{a_1^2}{\lambda _{n+1}^2}\Vert u_n-\phi _n\Vert ^2\nonumber \\ =&\Vert z_n-x^*\Vert ^2-\Vert z_n-\phi _n\Vert ^2-\left( 1-\frac{\lambda _n^2a_1^2}{\lambda _{n+1}^2}\right) \Vert u_n-\phi _n\Vert ^2. \end{aligned}$$
(4.9)

Following the same line of argument, we have

$$\begin{aligned} \Vert b_n-y^*\Vert ^2\le \Vert k_n-y^*\Vert ^2-\Vert k_n-\psi _n\Vert ^2-\left( 1-\frac{\rho _n^2a_2^2}{\rho _{n+1}^2}\right) \Vert s_n-\psi _n\Vert ^2, \end{aligned}$$
(4.10)

which completes the proof. \(\square \)

Lemma 4.4

Let \(\{(x_n,y_n)\}\) be a sequence generated by Algorithm 3.2 satisfying Assumption 3.1. Then \(\{(x_n,y_n)\}\) is bounded.

Proof

Let \(x^*\in \Gamma . \) From the definition of \(w_n\) and Lemma 2.5, we have

$$\begin{aligned} \Vert w_n-x^*\Vert&=\Vert (1-\alpha _n)(x_n+\theta _n(x_n-x_{n-1}))-x^*\Vert \nonumber \\&=\Vert (1-\alpha _n)(x_n-x^*)+(1-\alpha _n)\theta _n(x_n-x_{n-1})-\alpha _nx^*\Vert \nonumber \\&\le (1-\alpha _n)\Vert x_n-x^*\Vert +(1-\alpha _n)\theta _n\Vert x_n-x_{n-1}\Vert +\alpha _n\Vert x^*\Vert \nonumber \\&=(1-\alpha _n)\Vert x_n-x^*\Vert +\alpha _n\Big [(1-\alpha _n)\frac{\theta _n}{\alpha _n}\Vert x_n-x_{n-1}\Vert +\Vert x^*\Vert \Big ]. \end{aligned}$$
(4.11)

By (3.5), we have

$$\underset{n\rightarrow \infty }{\lim }\Big [(1-\alpha _n)\frac{\theta _n}{\alpha _n}\Vert x_n-x_{n-1}\Vert +\Vert x^*\Vert \Big ]=\Vert x^*\Vert .$$

Thus, there exists a constant \(M_1>0\) such that \((1-\alpha _n)\frac{\theta _n}{\alpha _n}\Vert x_n-x_{n-1}\Vert +\Vert x^*\Vert \le M_1\) for all \(n\in \mathbb {N}.\) Thus, from (4.11) it follows that

$$\begin{aligned} \Vert w_n-x^*\Vert \le (1-\alpha _n)\Vert x_n-x^*\Vert +\alpha _nM_1. \end{aligned}$$

Consequently, we have

$$\begin{aligned} \Vert w_n-x^*\Vert ^2\le (1-\alpha _n)^2\Vert x_n-x^*\Vert ^2+2\alpha _n(1-\alpha _n)M_1\Vert x_n-x^*\Vert +\alpha _n^2M_1^2. \end{aligned}$$
(4.12)

Following similar procedure, we have

$$\begin{aligned} \Vert \varphi _n-y^*\Vert ^2\le (1-\alpha _n)^2\Vert y_n-y^*\Vert ^2+2\alpha _n(1-\alpha _n)M_2\Vert y_n-y^*\Vert +\alpha _n^2M_2^2. \end{aligned}$$
(4.13)

Adding (4.12) and (4.13), we obtain

$$\begin{aligned} \nonumber&\Vert w_n-x^*\Vert ^2+\Vert \varphi _n-y^*\Vert ^2\nonumber \\ \le&(1-\alpha _n)^2\Big [\Vert x_n-x^*\Vert ^2+\Vert y_n-y^*\Vert ^2\Big ]\nonumber \\&+2\alpha _n(1-\alpha _n)\Big (M_1\Vert x_n-x^*\Vert +M_2\Vert y_n-y^*\Vert \Big ) +\alpha _n^2(M_1^2+M_2^2)\nonumber \\ \le&(1-\alpha _n)\Big [\Vert x_n-x^*\Vert ^2+\Vert y_n-y^*\Vert ^2\Big ]\nonumber \\&+2\alpha _n\Big (M_1\Vert x_n-x^*\Vert +M_2\Vert y_n-y^*\Vert \Big ) +\alpha _n(M_1^2+M_2^2)\nonumber \\ =&(1-\alpha _n)\Big [\Vert x_n-x^*\Vert ^2+\Vert y_n-y^*\Vert ^2\Big ]+\alpha _nc_n, \end{aligned}$$
(4.14)

where \(c_n=2(M_1\Vert x_n-x^*\Vert +M_2\Vert y_n-y^*\Vert )+M_1^2+M^2_2.\) From STEP 3, and by applying Lemma 2.5, (4.9) together with Remark 3.6, we have

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2=&\Big \Vert (1-\beta _n)v_n+\beta _n\frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-x^*\Big \Vert ^2\nonumber \\ =&\Big \Vert (1-\beta _n)(v_n-x^*)+\beta _n\Big (\frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-x^*\Big )\Big \Vert ^2\nonumber \\ =&(1-\beta _n)\Vert v_n-x^*\Vert ^2+\beta _n\Big \Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-x^*\Big \Vert ^2\nonumber \\&-\beta _n(1-\beta _n)\Big \Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-v_n\Big \Vert ^2 \nonumber \\ =&(1-\beta _n)\Vert v_n-x^*\Vert ^2+\beta _n\Big \Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-\frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)x^*ds\Big \Vert ^2\nonumber \\&-\beta _n(1-\beta _n)\Big \Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-v_n\Big \Vert ^2\nonumber \\ \le&(1-\beta _n)\Vert v_n-x^*\Vert ^2+\beta _n\Vert v_n-x^*\Vert ^2-\beta _n(1-\beta _n)\Big \Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-v_n\Big \Vert ^2\nonumber \\ =&\Vert v_n-x^*\Vert ^2-\beta _n(1-\beta _n)\Big \Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-v_n\Big \Vert ^2\nonumber \\ \le&\Vert z_n-x^*\Vert ^2-\Vert z_n-\phi _n\Vert ^2-\Big (1-\frac{\lambda _n^2a_1^2}{\lambda _{n+1}^2}\Big )\Vert u_n-\phi _n\Vert ^2\nonumber \\&-\beta _n(1-\beta _n)\Big \Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-v_n\Big \Vert ^2 \end{aligned}$$
(4.15)
$$\begin{aligned} \le&\Vert z_n-x^*\Vert ^2. \end{aligned}$$
(4.16)

Similarly, from STEP 5, and by applying Lemma 2.5, (4.10) together with Remark 3.6, we have

$$\begin{aligned} \Vert y_{n+1}-y^*\Vert ^2 \le&\Vert k_n-y^*\Vert ^2-\Vert k_n-\psi _n\Vert ^2-\Big (1-\frac{\rho _n^2a_2^2}{\rho _{n+1}^2}\Big )\Vert s_n-\psi _n\Vert ^2\nonumber \\&-\gamma _n(1-\gamma _n)\Big \Vert \frac{1}{t_{n,2}}\int _{0}^{t_{n,2}}T_2(u)b_ndu-b_n\Big \Vert ^2\end{aligned}$$
(4.17)
$$\begin{aligned} \le&\Vert k_n-y^*\Vert ^2. \end{aligned}$$
(4.18)

From (4.3), (4.14), (4.16) and (4.18), we have

$$\begin{aligned} \Vert x_{n+1}-x^*\Vert ^2+\Vert y_{n+1}-y^*\Vert ^2&\le \Vert z_n-x^*\Vert ^2+\Vert k_n-y^*\Vert ^2\\ {}&\le \Vert w_n-x^*\Vert ^2+\Vert \varphi _n-y^*\Vert ^2\\&\le (1-\alpha _n)\Big [\Vert x_n-x^*\Vert ^2+\Vert y_n-y^*\Vert ^2\Big ]+\alpha _nc_n\\&\le \text{ max }~~\{\Vert x_n-x^*\Vert ^2+\Vert y_n-y^*\Vert ^2,~~c_n\}\\&\vdots \\&\le \text{ max }~~\{\Vert x_{n_0}-x^*\Vert ^2+\Vert y_{n_0}-y^*\Vert ^2,~~c_{n_0}\}. \end{aligned}$$

Thus, \(\big \{(x_n,y_n)\big \}\) is bounded. Consequently, \(\{z_n\},\{v_n\},\{k_n\}\) and \(\{b_n\}\) are also bounded. \(\square \)

Lemma 4.5

Let \(\big \{(x_n,y_n)\big \}\) be a sequence generated by Algorithm 3.2 under Assumption 3.1. Then,

$$\begin{aligned}&\Vert x_{n+1}-x^*\Vert ^2+\Vert y_{n+1}-y^*\Vert ^2\\ \le&(1-\alpha _n)\Big [\Vert x_n-x^*\Vert ^2+\Vert y_n-y^*\Vert ^2\Big ]+\alpha _nd_n\\ \nonumber&-\eta _n\cdot \epsilon \Big [\Vert \mathcal {F}^*_2(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2\Big ]\\&-\Vert z_n-\phi _n\Vert ^2-\Vert k_n-\psi _n\Vert ^2-\left( 1-\frac{\lambda _n^2a_1^2}{\lambda _{n+1}^2}\right) \Vert u_n-\phi _n\Vert ^2 -\left( 1-\frac{\rho _n^2a_2^2}{\rho _{n+1}^2}\right) \Vert s_n-\psi _n\Vert ^2\\&-\beta _n(1-\beta _n)\Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-v_n\Vert ^2-\gamma _n(1-\gamma _n)\Vert \frac{1}{t_{n,2}}\int _{0}^{t_{n,2}}T_2(u)b_ndu-b_n\Vert ^2, \end{aligned}$$

where \(d_n=[2(1-\alpha _n)\Vert x_n-x^*\Vert \frac{\theta _n}{\alpha _n}\Vert x_n-x_{n-1}\Vert +\theta _n\Vert x_n-x_{n-1}\Vert \cdot \frac{\theta _n}{\alpha _n}\Vert x_n-x_{n-1}\Vert +2\Vert x^*\Vert \Vert w_n-x_{n+1}\Vert +2\langle x^*, x^*-x_{n+1}\rangle ]+[2(1-\alpha _n)\Vert y_n-y^*\Vert \frac{\tau _n}{\alpha _n}\Vert y_n-y_{n-1}\Vert +\tau _n\Vert y_n-y_{n-1}\Vert \cdot \frac{\tau _n}{\alpha _n}\Vert y_n-y_{n-1}\Vert +2\Vert y^*\Vert \Vert \varphi _n-y_{n+1}\Vert +2\langle y^*, y^*-y_{n+1}\rangle ].\)

Proof

Let \((x^*,y^*)\in \Gamma . \) From Lemma 2.5 and the definition of \(w_n,\) we have

$$\begin{aligned} \Vert w_n-x^*\Vert ^2 =&\Vert (1-\alpha _n)(x_n-x^*)+(1-\alpha _n)\theta _n(x_n-x_{n-1})-\alpha _nx^*\Vert ^2\nonumber \\ \le&\Vert (1-\alpha _n)(x_n-x^*)+(1-\alpha _n)\theta _n(x_n-x_{n-1})\Vert ^2+2\alpha _n\langle -x^*,~~w_n-x^*\rangle \nonumber \\ \le&(1-\alpha _n)^2\Vert x_n-x^*\Vert ^2+2(1-\alpha _n)\theta _n\Vert x_n-x^*\Vert \Vert x_n-x_{n-1}\Vert +\theta _n^2\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&+2\alpha _n\langle -x^*,~~w_n-x_{n+1} \rangle +2\alpha _n\langle -x^*,~~x_{n+1}-x^*\rangle \nonumber \\ \le&(1-\alpha _n)\Vert x_n-x^*\Vert ^2+\alpha _n\Big [2(1-\alpha _n)\Vert x_n-x^*\Vert \frac{\theta _n}{\alpha _n}\Vert x_n-x_{n-1}\Vert \nonumber \\&+\theta _n\Vert x_n-x_{n-1}\Vert \cdot \frac{\theta _n}{\alpha _n}\Vert x_n-x_{n-1}\Vert \nonumber \\&+2\Vert x^*\Vert \Vert w_n-x_{n+1}\Vert +2\langle x^*, x^*-x_{n+1}\rangle \Big ]. \end{aligned}$$
(4.19)

Following the same line of argument, we have

$$\begin{aligned} \Vert \varphi _n-y^*\Vert ^2 \le&(1-\alpha _n)\Vert y_n-y^*\Vert ^2+\alpha _n\Big [2(1-\alpha _n)\Vert y_n-y^*\Vert \frac{\tau _n}{\alpha _n}\Vert y_n-y_{n-1}\Vert \nonumber \\&+\tau _n\Vert y_n-y_{n-1}\Vert \cdot \frac{\tau _n}{\alpha _n}\Vert y_n-y_{n-1}\Vert +2\Vert y^*\Vert \Vert \varphi _n-y_{n+1}\Vert +2\langle y^*, y^*-y_{n+1}\rangle \Big ]. \end{aligned}$$
(4.20)

Adding (4.19) and (4.20) we have

$$\begin{aligned} \Vert w_n-x^*\Vert ^2+\Vert \varphi _n-y^*\Vert ^2\le (1-\alpha _n)\Big [\Vert x_n-x^*\Vert ^2+\Vert y_n-y^*\Vert ^2\Big ]+\alpha _nd_n. \end{aligned}$$
(4.21)

From (4.3), (4.15), (4.17) and (4.21), we have

$$\begin{aligned}&\Vert x_{n+1}-x^*\Vert ^2+\Vert y_{n+1}-y^*\Vert ^2\\ \le&\Vert z_n-x^*\Vert ^2+\Vert k_n-y^*\Vert ^2-\Vert z_n-\phi _n\Vert ^2-\Vert k_n-\psi _n\Vert ^2-\Big (1-\frac{\lambda _n^2a_1^2}{\lambda _{n+1}^2}\Big )\Vert u_n-\phi _n\Vert ^2\\&-\Big (1-\frac{\rho _n^2a_2^2}{\rho _{n+1}^2}\Big )\Vert s_n-\psi _n\Vert ^2-\beta _n(1-\beta _n)\Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-v_n\Vert ^2\\ {}&-\gamma _n(1-\gamma _n)\Vert \frac{1}{t_{n,2}}\int _{0}^{t_{n,2}}T_2(u)b_ndu-b_n\Vert ^2\\&\le \Vert w_n-x^*\Vert ^2+\Vert \varphi _n-y^*\Vert ^2-\eta _n\cdot \epsilon \Big [\Vert \mathcal {F}^*_2(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2\Big ]\\&-\Vert z_n-\phi _n\Vert ^2-\Vert k_n-\psi _n\Vert ^2-\Big (1-\frac{\lambda _n^2a_1^2}{\lambda _{n+1}^2}\Big )\Vert u_n-\phi _n\Vert ^2-\Big (1-\frac{\rho _n^2a_2^2}{\rho _{n+1}^2}\Big )\Vert s_n-\psi _n\Vert ^2\\&-\beta _n(1-\beta _n)\Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-v_n\Vert ^2-\gamma _n(1-\gamma _n)\Vert \frac{1}{t_{n,2}}\int _{0}^{t_{n,2}}T_2(u)b_ndu-b_n\Vert ^2\\&\le (1-\alpha _n)\Big [\Vert x_n-x^*\Vert ^2+\Vert y_n-y^*\Vert ^2\Big ]+\alpha _nd_n\\ {}&-\eta _n\cdot \epsilon \Big [\Vert \mathcal {F}^*_2(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n)\Vert ^2\Big ] -\Vert z_n-\phi _n\Vert ^2-\Vert k_n-\psi _n\Vert ^2\\ {}&-\Big (1-\frac{\lambda _n^2a_1^2}{\lambda _{n+1}^2}\Big )\Vert u_n-\phi _n\Vert ^2-\Big (1-\frac{\rho _n^2a_2^2}{\rho _{n+1}^2}\Big )\Vert s_n-\psi _n\Vert ^2\\ {}&-\beta _n(1-\beta _n)\Vert \frac{1}{t_{n,1}}\int _{0}^{t_{n,1}}T_1(s)v_nds-v_n\Vert ^2-\gamma _n(1-\gamma _n)\Vert \frac{1}{t_{n,2}}\int _{0}^{t_{n,2}}T_2(u)b_ndu-b_n\Vert ^2, \end{aligned}$$

which is the required result. \(\square \)

Now we are in a position to state the main result of this work.

Theorem 4.6

Let \(\{(x_n,y_n)\}\) be a sequence generated by Algorithm 3.2 such that Assumption 3.1 holds. Then, the sequence \(\{(x_n,y_n)\}\) converges strongly to \( (\hat{x},\hat{y})=P_{\Gamma }(0_{\mathcal {H}_1},0_{\mathcal {H}_2})\in \Gamma .\)

Proof

Let \( (\hat{x},\hat{y})=P_{\Gamma }(0_{\mathcal {H}_1},0_{\mathcal {H}_2})\in \Gamma .\) Then, it follows from Lemma 4.5 that

$$\begin{aligned} \Vert x_{n+1}-\hat{x}\Vert ^2+\Vert y_{n+1}-\hat{y}\Vert ^2\le (1-\alpha _n)\Big [\Vert x_n-\hat{x}\Vert ^2+\Vert y_n-\hat{y}\Vert ^2\Big ]+\alpha _n\hat{d}_n, \end{aligned}$$
(4.22)

where \(\hat{d}_n= [2(1-\alpha _n)\Vert x_n-\hat{x}\Vert \frac{\theta _n}{\alpha _n}\Vert x_n-x_{n-1}\Vert +\theta _n\Vert x_n-x_{n-1}\Vert \cdot \frac{\theta _n}{\alpha _n}\Vert x_n-x_{n-1}\Vert +2\Vert \hat{x}\Vert \Vert w_n-x_{n+1}\Vert +2\langle \hat{x}, \hat{x}-x_{n+1}\rangle ]+[2(1-\alpha _n)\Vert y_n-\hat{y}\Vert \frac{\tau _n}{\alpha _n}\Vert y_n-y_{n-1}\Vert +\tau _n\Vert y_n-y_{n-1}\Vert \cdot \frac{\tau _n}{\alpha _n}\Vert y_n-y_{n-1}\Vert +2\Vert \hat{y}\Vert \Vert \varphi _n-y_{n+1}\Vert +2\langle \hat{y}, \hat{y}-y_{n+1}\rangle ].\) Now, we claim that the sequence \(\{\Vert x_n-\hat{x}\Vert +\Vert y_n-\hat{y}\Vert \}\) converges to zero. To show this, by Lemma 2.13 it suffices to show that \(\limsup _{k\rightarrow \infty }\hat{d}_{n_k}\le 0\) for every subsequence \(\{\Vert x_{n_k}-\hat{x}\Vert +\Vert y_{n_k}-\hat{y}\Vert \}\) of \(\{\Vert x_n-\hat{x}\Vert +\Vert y_n-\hat{y}\Vert \}\) satisfying

$$\begin{aligned} \underset{k\rightarrow \infty }{\liminf }\left( \left( \Vert x_{n_{k+1}}-\hat{x}\Vert +\Vert y_{n_{k+1}}-\hat{y}\Vert \right) -\left( \Vert x_{n_k}-\hat{x}\Vert +\Vert y_{n_k}-\hat{y}\Vert \right) \right) \ge 0. \end{aligned}$$
(4.23)

Suppose that \(\{\Vert x_{n_k}-\hat{x}\Vert +\Vert y_{n_k}-\hat{y}\Vert \}\) is a subsequence of \(\{\Vert x_n-\hat{x}\Vert +\Vert y_n-\hat{y}\Vert \}\) such that (4.23) holds. Again, from Lemma 4.5, we obtain

$$\begin{aligned}&\eta _{n_k}\cdot \epsilon \Big [\Vert \mathcal {F}^*_2(\mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k})\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k})\Vert ^2\Big ]\\ {}&+\Vert z_{n_k}-\phi _{n_k}\Vert ^2+\Vert k_{n_k}-\psi _{n_k}\Vert ^2\\ {}&+\Big (1-\frac{\lambda _{n_k}^2a_1^2}{\lambda _{n_{k+1}}^2}\Big )\Vert u_{n_k}-\phi _{n_k}\Vert ^2+\Big (1-\frac{\rho _{n_k}^2a_2^2}{\rho _{n_{k+1}}^2}\Big )\Vert s_{n_k}-\psi _{n_k}\Vert ^2\\&+\beta _{n_k}(1-\beta _{n_k})\Vert \frac{1}{t_{n_{k,1}}}\int _{0}^{t_{n_{k,1}}}T_1(s)v_{n_k}ds-v_{n_k}\Vert ^2\\ {}&+\gamma _{n_k}(1-\gamma _{n_k})\Vert \frac{1}{t_{n_{k,2}}}\int _{0}^{t_{n_{k,2}}}T_2(u)b_{n_k}du-b_{n_k}\Vert ^2\\\le&(1-\alpha _{n_k})\Big [\Vert x_{n_k}-\hat{x}\Vert ^2+\Vert y_{n_k}-\hat{y}\Vert ^2\Big ]-\Big [\Vert x_{n_{k+1}}-\hat{x}\Vert ^2+\Vert y_{n_{k+1}}-\hat{y}\Vert ^2\Big ]+\alpha _{n_k}\hat{d}_{n_k}. \end{aligned}$$

From (4.23) and the condition on \(\alpha _{n_k}\) we have

$$\begin{aligned}&\underset{k\rightarrow \infty }{\lim }\Big (\eta _{n_k}\cdot \epsilon \Big [\Vert \mathcal {F}^*_2(\mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k})\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k})\Vert ^2\Big ]\\ {}&+\Vert z_{n_k}-\phi _{n_k}\Vert ^2+\Vert k_{n_k}-\psi _{n_k}\Vert ^2\\ {}&+\Big (1-\frac{\lambda _{n_k}^2a_1^2}{\lambda _{n_{k+1}}^2}\Big )\Vert u_{n_k}-\phi _{n_k}\Vert ^2+\Big (1-\frac{\rho _{n_k}^2a_2^2}{\rho _{n_{k+1}}^2}\Big )\Vert s_{n_k}-\psi _{n_k}\Vert ^2\\&+\beta _{n_k}(1-\beta _{n_k})\Vert \frac{1}{t_{n_{k,1}}}\int _{0}^{t_{n_{k,1}}}T_1(s)v_{n_k}ds-v_{n_k}\Vert ^2\\ {}&+\gamma _{n_k}(1-\gamma _{n_k})\Vert \frac{1}{t_{n_{k,2}}}\int _{0}^{t_{n_{k,2}}}T_2(u)b_{n_k}du-b_{n_k}\Vert ^2\Big )=0. \end{aligned}$$

From (3.6), (3.7) and the conditions on the control parameters, we have

$$\begin{aligned} \underset{k \rightarrow \infty }{\lim }\Vert z_{n_k}-\phi _{n_k}\Vert =0,~\underset{k\rightarrow \infty }{\lim }\Vert k_{n_k}-\psi _{n_k}\Vert =0,~\underset{k\rightarrow \infty }{\lim }\Vert u_{n_k}-\phi _{n_k}\Vert =0,~\underset{k\rightarrow \infty }{\lim }\Vert s_{n_k}-\psi _{n_k}\Vert =0,\end{aligned}$$
(4.24)
$$\begin{aligned} \underset{k \rightarrow \infty }{\lim }\Big \Vert \frac{1}{t_{n_{k,2}}}\int _{0}^{t_{n_{k,2}}}T_2(u)b_{n_k}du-b_{n_k}\Big \Vert =0,~ \underset{k \rightarrow \infty }{\lim }\Big \Vert \frac{1}{t_{n_{k,1}}}\int _{0}^{t_{n_{k,1}}}T_1(s)v_{n_k}ds-v_{n_k}\Big \Vert =0. \end{aligned}$$
(4.25)

Also, we have

$$\begin{aligned} \underset{k\rightarrow \infty }{\lim }\Big [\Vert \mathcal {F}^*_2(\mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k})\Vert ^2+\Vert \mathcal {F}_1^*(\mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k})\Vert ^2\Big ]=0 \end{aligned}$$

which implies that

$$\begin{aligned}&\underset{k\rightarrow \infty }{\lim }\Vert \mathcal {F}^*_2(\mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k})\Vert =0,\\&\underset{k\rightarrow \infty }{\lim }\Vert \mathcal {F}_1^*(\mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k})\Vert =0,\\&\underset{k\rightarrow \infty }{\lim }\Vert \mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k}\Vert =0. \end{aligned}$$

From the definition of \(z_{n_k}, k_{n_k}\) and the previous inequality we have

$$\begin{aligned} \Vert z_{n_k}-w_{n_k}\Vert =\eta _{n_k}\Vert \mathcal {F}_1^*(\mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k})\Vert \rightarrow 0,~\text {as}~~k\rightarrow \infty .\nonumber \\ \Vert k_{n_k}-\varphi _{n_k}\Vert =\eta _{n_k}\Vert \mathcal {F}_2^*(\mathcal {F}_1w_{n_k}-\mathcal {F}_2\varphi _{n_k})\Vert \rightarrow 0,~\text {as}~~k\rightarrow \infty . \end{aligned}$$
(4.26)

Also, from the definition of \(v_{n_k},b_{n_k}\) and (4.24), we have

$$\begin{aligned} \Vert v_{n_k}-u_{n_k}\Vert =\lambda _{n_k}\Vert Au_{n_k}-A\phi _{n_k}\Vert \le \frac{\lambda _{n_k}a_1}{\lambda _{n_{k+1}}}\Vert u_{n_k}-\phi _{n_k}\Vert \rightarrow 0,~\text {as}~k\rightarrow \infty .\\ \Vert b_{n_k}-s_{n_k}\Vert =\rho _{n_k}\Vert Bs_{n_k}-B\psi _{n_k}\Vert \le \frac{\rho _{n_k}a_2}{\rho _{n_{k+1}}}\Vert s_{n_k}-\psi _{n_k}\Vert \rightarrow 0,~\text {as}~k\rightarrow \infty .\\ \end{aligned}$$

From (4.25) and Lemma 2.3 we have

$$\begin{aligned} \nonumber \Vert v_{n_k}-T_1(v)v_{n_k}\Vert \le&\Big \Vert v_{n_k}-\frac{1}{t_{n_{k,1}}}\int _{0}^{t_{n_{k,1}}}T_1(s)v_{n_k}ds\Big \Vert \nonumber \\&+\Big \Vert \frac{1}{t_{n_{k,1}}}\int _{0}^{t_{n_{k,1}}}T_1(s)v_{n_k}ds-T_1(v)\frac{1}{t_{n_{k,1}}}\int _{0}^{t_{n_{k,1}}}T_1(s)v_{n_k}ds\Big \Vert \nonumber \\&+\Big \Vert T_1(v)\frac{1}{t_{n_{k,1}}}\int _{0}^{t_{n_{k,1}}}T_1(s)v_{n_k}ds-T_1(v)v_{n_k}\Big \Vert \rightarrow 0,~\text {as}~k\rightarrow \infty . \end{aligned}$$
(4.27)

Similarly, we have

$$\begin{aligned} \underset{k \rightarrow \infty }{\lim }\Vert b_{n_k}-T_2(b)b_{n_k}\Vert =0. \end{aligned}$$

From the definition of \(x_{n_{k+1}}\) and (4.25), we have

$$\begin{aligned}\Vert x_{n_{k+1}}-v_{n_k}\Vert&=\Big \Vert (1-\beta _{n_k})v_{n_k}+\beta _{n_k}\frac{1}{t_{n_{k,1}}}\int _{0}^{t_{n_{k,1}}}T_1(s)v_{n_k}ds-v_{n_k}\Big \Vert \\&=\beta _{n_k}\Big \Vert \frac{1}{t_{n_{k,1}}}\int _{0}^{t_{n_{k,1}}}T_1(s)v_{n_k}ds-v_{n_k}\Big \Vert \rightarrow 0,~\text {as}~k\rightarrow \infty . \end{aligned}$$

Similarly, we have

$$\begin{aligned} \underset{k \rightarrow \infty }{\lim }\Vert y_{n_{k+1}}-b_{n_k}\Vert =0. \end{aligned}$$

Now, from Step 2 and by Remark 3.4, we get

$$\begin{aligned} \Vert w_{n_k}-x_{n_k}\Vert&=\Vert (1-\alpha _{n_k})(x_{n_k}+\theta _{n_k}(x_{n_k}-x_{{n_k}-1}))-x_{n_k}\Vert \nonumber \\&=\Vert (1-\alpha _{n_k})(x_{n_k}-x_{n_k})+(1-\alpha _{n_k})\theta _{n_k}(x_{n_k}-x_{{n_k}-1})-\alpha _{n_k}x_{n_k}\Vert \nonumber \\&\le (1-\alpha _{n_k})\Vert x_{n_k}-x_{n_k}\Vert +(1-\alpha _{n_k})\theta _{n_k}\Vert x_{n_k}-x_{{n_k}-1}\Vert +\alpha _{n_k}\Vert x_{n_k}\Vert \rightarrow 0,\quad k\rightarrow \infty . \end{aligned}$$
(4.28)

Similarly, we have

$$\begin{aligned} \underset{k \rightarrow \infty }{\lim }\Vert \varphi _{n_k}-y_{n_k}\Vert =0. \end{aligned}$$
(4.29)

From (4.24)–(4.29) we have

$$\begin{aligned} \underset{k \rightarrow \infty }{\lim }\Vert x_{n_k}-\phi _{n_k}\Vert =0,\underset{k \rightarrow \infty }{\lim }\Vert x_{n_{k+1}}-w_{n_k}\Vert =0,\underset{k \rightarrow \infty }{\lim }\Vert y_{n_{k+1}}-\varphi _{n_k}\Vert =0. \end{aligned}$$
(4.30)

From (4.28) and (4.30) we have

$$\begin{aligned} \underset{k \rightarrow \infty }{\lim }\Vert x_{n_{k+1}}-x_{n_k}\Vert =0. \end{aligned}$$
(4.31)

Similarly, from (4.29) and (4.30)

$$\begin{aligned} \underset{k\rightarrow \infty }{\lim }\Vert y_{n_{k+1}}-y_{n_k}\Vert =0. \end{aligned}$$
(4.32)

To complete the proof, we show that \(w_{\omega }\big (x_n,y_n\big )\subset \Gamma ,\) where \(w_{\omega }\big (x_n,y_n\big )\) is the set of weak limits of \(\big \{(x_n,y_n)\big \}.\) Since \(\big \{(x_n,y_n)\big \}\) is bounded we have that \(w_{\omega }\big (x_n,y_n\big )\) is nonempty. Let \((x^*,y^*)\in w_{\omega }\big (x_n,y_n\big )\) be an arbitrary element. From (4.26), (4.28) and (4.29) we have \(x^*\in w_{\omega }(x_n)\) and \(y^*\in w_{\omega }(y_n).\) Then there exists a subsequence \(\{x_{n_k}\}\) of \(\{x_n\}\) such that \(x_{n_k}\rightharpoonup x^*\) as \(k\rightarrow \infty .\) Since \(\lim _{k\rightarrow \infty }\Vert x_{n_k}-\phi _{n_k}\Vert =0,\) we have that \(\phi _{n_k}\rightharpoonup x^*\in \mathcal {C}\) as \(k\rightarrow \infty .\) From the characteristic property of \(P_{\mathcal {C}},\) we have

$$\begin{aligned} \langle x-u_{n_k},~~ \phi _{n_k}-\lambda _{n_k}A\phi _{n_k}-u_{n_k},\rangle \le 0,~~x\in \mathcal {C}, \end{aligned}$$

which implies that

$$\begin{aligned} \frac{1}{\lambda _{n_k}}\left\langle \phi _{n_k}-u_{n_k},~~x-u_{n_k}\right\rangle \le \left\langle A\phi _{n_k},~x-u_{n_k}\right\rangle ,~~ \forall x\in \mathcal {C}. \end{aligned}$$

Consequently, we have

$$\begin{aligned} \frac{1}{\lambda _{n_k}}\left\langle \phi _{n_k}-u_{n_k},~ x-u_{n_k}\right\rangle +\left\langle A\phi _{n_k},~~u_{n_k}-\phi _{n_k}\right\rangle \le \left\langle A\phi _{n_k},~~x-\phi _{n_k}\right\rangle ,~~\forall x\in \mathcal {C}. \end{aligned}$$
(4.33)

Applying the fact that \(\lim _{k \rightarrow \infty }\Vert \phi _{n_k}-u_{n_k}\Vert =0\) and \(\lim _{k\rightarrow \infty }\lambda _{n_k}=\lambda >0\) to (4.33), we have

$$\begin{aligned} 0\le \underset{k\rightarrow \infty }{\liminf }\left\langle A\phi _{n_k},~~x-\phi _{n_k}\right\rangle ,~~ \forall x\in \mathcal {C}. \end{aligned}$$
(4.34)

Also, we have that

$$\begin{aligned} \left\langle Au_{n_k},~ x-u_{n_k}\right\rangle =\left\langle Au_{n_k}-A\phi _{n_k},~ x-\phi _{n_k}\right\rangle +\left\langle A\phi _{n_k},~ x-\phi _{n_k}\right\rangle +\left\langle Au_{n_k},~ \phi _{n_k}-u_{n_k}\right\rangle . \end{aligned}$$

Since A is uniformly continuous on \(\mathcal {H}\) and \(\lim _{k \rightarrow \infty }\Vert \phi _{n_k}-u_{n_k}\Vert ,\) we have

$$\begin{aligned} \underset{k\rightarrow \infty }{\lim }\Vert A\phi _{n_k}-Au_{n_k}\Vert =0. \end{aligned}$$
(4.35)

From (4.34)–(4.35), we have

$$\begin{aligned} 0\le \underset{k\rightarrow \infty }{\liminf }\left\langle Au_{n_k},~x-u_{n_k}\right\rangle ,~~ \forall x\in \mathcal {C}. \end{aligned}$$
(4.36)

Let \(\{\delta _k\}\) be a sequence of positive numbers such that \(\delta _{k+1} \le \delta _k, ~ \forall k\ge 1 \text { and } \delta _k \rightarrow 0 \text { as } k \rightarrow \infty .\) Then, for each \(k\ge 1,\) we denote by \(N_k\) the smallest positive integer such that

$$\begin{aligned} \langle Au_{n_j},x-u_{n_j} \rangle +\delta _k \ge 0, ~~\forall j \ge N_k, \end{aligned}$$
(4.37)

where the existence of \(N_k\) follows from (4.36). We have that \(\{N_k\}\) is increasing since \(\{\delta _k\}\) is decreasing. Furthermore, since \(\{u_{n_k}\}\subset \mathcal {C}\) we can suppose \(Au_{N_k} \ne 0\) (otherwise, \(u_{N_k}\) is a solution) and we set for each \(k \ge 1,~~ h_{N_k}= \frac{Au_{N_k}}{\Vert Au_{N_k}\Vert ^2}.\) Then we have that \(\langle Au_{N_k}, h_{N_k} \rangle =1~~\text {for ~each}~~ k\ge 1.\) Thus, by (4.37), we have that

$$ \langle Au_{N_k},x+\delta _kh_{N_k}-u_{N_k} \rangle \ge 0, $$

which implies by the pseudo-monotonicity of A that

$$\begin{aligned} \langle A(x+\delta _kh_{N_k}), x+\delta _kh_{N_k}-u_{N_k} \rangle \ge 0. \end{aligned}$$
(4.38)

Since \(u_{n_k}\subset C,\) the sequence \(\{u_{n_k}\}\) converges weakly to \(x^*\in \mathcal {C}.\) If \(Ax^*=0,\) then \(x^*\in VI(\mathcal {C}, A).\) On the contrary, we suppose \(Ax^*\ne 0.\) Since A satisfies condition (c), we have

$$ 0<\Vert Ax^*\Vert \le \liminf _{k \rightarrow \infty }\Vert Au_{n_k}\Vert . $$

Since \(\{u_{N_k}\} \subset \{u_{n_k}\},\) we obtain that

$$\begin{aligned} 0&\le \limsup _{k \rightarrow \infty }\Vert \delta _kh_{N_k}\Vert = \limsup _{k \rightarrow \infty }\left( \frac{\delta _k}{\Vert Au_{n_k}\Vert }\right) \le \frac{\underset{k\rightarrow \infty }{\limsup }\ \delta _k}{ \underset{k \rightarrow \infty }{\liminf }\Vert Au_{n_k}\Vert }=0. \end{aligned}$$

Therefore, \(\lim _{k \rightarrow \infty } \Vert \delta _kh_{N_k}\Vert =0.\) Letting \(k \rightarrow \infty \) in (4.38) gives

$$\begin{aligned} \langle A x, x-x^*\rangle \ge 0,~~\forall x\in \mathcal {C}, \end{aligned}$$

which implies by Lemma 2.7 that \(x^*\in VI(\mathcal {C}, A)\). By similar argument, we have that \(y^*\in VI(\mathcal {Q},B).\)

Now, to show that \(x^*\in F(\mathcal {T}_a)\) and \(y^*\in F(\mathcal {T}_b).\) On the contrary, we suppose that \(T_1(v)x^*\ne x^*\) and \(T_2(b)x^*\ne y^*\) for all \(v\ge 0\) and \(b\ge 0.\) Then, it follows from the Opial condition of Hilbert space and from (4.27) that

$$\begin{aligned} \underset{k \rightarrow \infty }{\liminf }\Vert v_{n_k}-x^*\Vert&<\underset{k \rightarrow \infty }{\liminf }\Vert v_{n_k}-T_1(v)x^*\Vert \\&\le \underset{k \rightarrow \infty }{\liminf }\Big \{\Vert v_{n_k}-T_1(v)v_{n_k}\Vert +\Vert T_1(v)v_{n_k}-T_1(v)x^*\Vert \Big \}\\&\le \underset{k \rightarrow \infty }{\liminf }\Big \{\Vert v_{n_k}-T_1(v)v_{n_k}\Vert +\Vert v_{n_k}-x^*\Vert \Big \}\\&= \underset{k \rightarrow \infty }{\liminf }\Vert v_{n_k}-x^*\Vert , \end{aligned}$$

which is a contradiction. Thus, it follows that \(T_1(v)x^*=x^*\) for all \(v\ge 0\) which implies that \(x^*\in F(\mathcal {T}_a).\) Similarly, \(y^*\in F(\mathcal {T}_b).\)

Next, from (4.24) we have that \(\lim _{k \rightarrow \infty }\Vert \phi _{n_k}-z_{n_k}\Vert =\lim _{k \rightarrow \infty }\Vert U^{\Phi _1}_{r_{{n_k},1}}z_{n_k}-z_{n_k}\Vert =0,\) and since \(z_{n_k}\rightharpoonup x^*\) it follows from the demiclosed property of nonexpansive mappings that \(x^*\in EP(\Phi _1).\) Similarly, we have that \(y^*\in EP(\Phi _2).\) Since \(\mathcal {F}_1x^*-\mathcal {F}_2y^*\in w_{\omega }(\mathcal {F}_1w_n-\mathcal {F}_2\varphi _n),\) it follows from the weakly lower semi-continuity of the norm that

$$\begin{aligned} \Vert \mathcal {F}_1x^*-\mathcal {F}_2y^*\Vert \le \underset{n\rightarrow \infty }{\liminf }\Vert \mathcal {F}_1w_n-\mathcal {F}_2\varphi _n\Vert =0. \end{aligned}$$

Hence, we have that \((x^*,y^*)\in \Gamma .\) Since \((x^*,y^*)\in w_{\omega }\big (x_n,y_n\big )\) was chosen arbitrarily, it follows that \(w_{\omega }\big (x_n,y_n\big )\subset \Gamma .\) To conclude, we show that

$$\begin{aligned} \underset{k \rightarrow \infty }{ \limsup }\Big (\Big \langle \hat{x},~\hat{x}-x_{n_{k+1}}\Big \rangle +\Big \langle \hat{y},~\hat{y}-y_{n_{k+1}}\Big \rangle \Big )\le 0. \end{aligned}$$

By the boundedness of \(\{(x_{n_k}, y_{n_k})\},\) it follows that there exists a subsequence \(\{(x_{n_{k_j}}, y_{n_k})\}\) of \(\{(x_{n_k}, y_{n_k})\}\) which converges weakly to some \((\bar{x}, \bar{x})\in \mathcal {H},\) and such that

$$\begin{aligned} \underset{j\rightarrow \infty }{\lim }\Big (\left\langle \hat{x},~\hat{x}-x_{n_{k_j}}\right\rangle + \left\langle \hat{y},~\hat{y}-y_{n_{k_j}}\right\rangle \Big )=\underset{k \rightarrow \infty }{\limsup }\Big (\left\langle \hat{x},~\hat{x}-x_{n_{k}}\right\rangle + \left\langle \hat{y},~\hat{y}-y_{n_{k}}\right\rangle \Big ). \end{aligned}$$
(4.39)

From (4.39) and the fact that \( (\hat{x},\hat{y})=P_{\Gamma }(0_{\mathcal {H}_1},0_{\mathcal {H}_2})\in \Gamma \) we have

$$\begin{aligned}&\underset{k \rightarrow \infty }{\limsup }\Big (\left\langle \hat{x},~~\hat{x}-x_{n_k}\right\rangle + \left\langle \hat{y},~~\hat{y}-y_{n_k}\right\rangle \Big )\nonumber \\ =&\underset{j \rightarrow \infty }{\lim }\Big (\left\langle \hat{x},~~\hat{x}-x_{n_{k_j}}\right\rangle + \left\langle \hat{y},~~\hat{y}-y_{n_{k_j}}\right\rangle \Big )\nonumber \\ =&\left\langle \hat{x},~~\hat{x}-\bar{x}\right\rangle + \left\langle \hat{y},~~\hat{y}-\bar{y}\right\rangle \le 0. \end{aligned}$$
(4.40)

From (4.31), (4.32) and (4.40), it follows that

$$\begin{aligned}&\underset{k \rightarrow \infty }{\limsup }\Big (\left\langle \hat{x},~~\hat{x}-x_{n_k+1}\right\rangle + \left\langle \hat{y},~~\hat{y}-y_{n_k+1}\right\rangle \Big )\nonumber \\ =&\underset{k \rightarrow \infty }{\limsup }\Big (\left\langle \hat{x},~~\hat{x}-x_{n_k}\right\rangle + \left\langle \hat{y},~~\hat{y}-y_{n_k}\right\rangle \Big )\nonumber \\ =&\left\langle \hat{x},~~\hat{x}-\bar{x}\right\rangle + \left\langle \hat{y},~~\hat{y}-\bar{y}\right\rangle \le 0. \end{aligned}$$
(4.41)

Thus, by (4.30) and (4.41) we have \(\limsup _{k\rightarrow \infty } \hat{d}_{n_k} \le 0.\) Now, applying Lemma 2.13 to (4.22) we have \(\{\Vert x_n-\hat{x}\Vert +\Vert y_n-\hat{y}\Vert \}\) converges to zero, which implies that \(\lim _{n\rightarrow \infty }\Vert x_n-\hat{x}\Vert =0\) and \(\lim _{n\rightarrow \infty }\Vert y_n-\hat{y}\Vert =0.\) Therefore, \((\{x_n\},\{y_n\})\) converges strongly to \((\hat{x},\hat{y})\). \(\square \)

Fig. 1
figure 1

Example 5.1: Case 1

Full size image
Fig. 2
figure 2

Example 5.1: Case 2

Full size image
Fig. 3
figure 3

Example 5.1: Case 3

Full size image
Fig. 4
figure 4

Example 5.1: Case 4

Full size image
Fig. 5
figure 5

Example 5.2: Case 1

Full size image
Fig. 6
figure 6

Example 5.2: Case 2

Full size image
Fig. 7
figure 7

Example 5.2: Case 3

Full size image
Fig. 8
figure 8

Example 5.2: Case 4

Full size image

5 Numerical Experiment

In this section, we discuss the numerical behavior of our method, (Proposed Alg.) Algorithm 3.2 in comparison with the method in Appendix A proposed by Latif and Eslamian [31] (Latif and Eslamian Alg.), which is the only related result we could find in the literature. We plot the graph of errors against the number of iterations in each case of both examples using \(\vert x_{n+1}-x_{n}\vert < 10^{-4}\) and \(\Vert x_{n+1}-x_{n}\Vert < 10^{-4}\) in Example 5.1 and Example 5.2 respectively as the stopping criterion. The numerical computations are reported in Figs. 1, 2, 3, 4, 5, 6, 7, and 8 and Tables 1 and 2 with all implementations performed using Matlab 2021 (b).

In our computation, we choose \(\theta =3.5,~\tau =2.44,~\lambda _1=1.5,~\rho _1=1.8,~a_1=0.8, a_2=0.9, ~\epsilon _n=\zeta _n=\frac{1}{(2n+1)^3},~\alpha _n=\frac{3}{2n+1},~~\beta _n=\frac{1}{4},~\gamma _n=\frac{1}{4},~ ~~\rho _n=\sigma _n=\frac{100}{(n+1)^2}, \eta =0.5, r_{n,1}=2.8, r_{n,2}=3.5, t_{n,1}=4.5, t_{n,2}=5.5, s=u=1.5.\) For Appendix A, we choose \(\alpha = 0.85, \varsigma _n=\kappa _n=\frac{1}{6},~\xi _n=\delta _n=\frac{1-\alpha _n}{2}.\)

Example 5.1

Let \(\mathcal {H}_1=\mathcal {H}_2=\mathcal {H}_3=\mathbb {R}\) the set of all real numbers with the inner product \(\langle x,y\rangle =xy,~\forall x,y\in \mathbb {R}\) and induced norm \(|\cdot |.\) For \(r_i>0,~i=1,2,\) consider \(\mathcal {C}=[-10,10]\) and \(\mathcal {Q}=[0,20].\) We define the bifunction \(\Phi _1:\mathcal {C}\times \mathcal {C}\rightarrow \mathbb {R}\) and \(\Phi _2:\mathcal {Q}\times \mathcal {Q}\rightarrow \mathbb {R}\) as follows:

$$\begin{aligned} U^{\Phi _1}_{r_{1}}(u)=\frac{u}{3r_1+1},~~ \forall x\in \mathcal {C} \end{aligned}$$

and

$$\begin{aligned} U^{\Phi _2}_{r_{2}}(v)=\frac{v}{r_2+1},~~ \forall y\in \mathcal {Q}. \end{aligned}$$

Let \(\mathcal {F}_1x=2x\) and \(\mathcal {F}_2x=5x\) which implies that \(\mathcal {F}_1^*x=2x\) and \(\mathcal {F}_2^*x=5x.\) Next we define \(A:\mathcal {H}_1\rightarrow \mathcal {H}_1\) as \(Ax=2x\) and \(B:\mathcal {H}_2\rightarrow \mathcal {H}_2\) as \(Bx=3x.\) We define the mappings \(T_1(s):\mathbb {R}\rightarrow \mathbb {R}\) and \(T_2(u):\mathbb {R}\rightarrow \mathbb {R}\) as follows; \(T_1(s)x=10^{-s}x\) and \(T_2(u)y=10^{-2u}y.\) Clearly, we observe that \(T_1(s)\) and \(T_2(u)\) are nonexpansive semigroups.

We choose \(\mathcal {V}_1=x_0, \mathcal {V}_2=y_0\) and consider the following cases for the numerical experiments of this example.

Case 1: Take \((x_0,y_0)=(-13.5,8.0)\) and \((x_1,y_1)=(5.7,-9.1).\)

Case 2: Take \((x_0,y_0)=(15.1,7.9)\) and \((x_1,y_1)=(6.4,81.3).\)

Case 3: Take \((x_0,y_0)=(10.9,-11.8)\) and \((x_1,y_1)=(-37.2,26.8).\)

Case 4: Take \((x_0,y_0)=(-14.9,-9.8)\) and \((x_1,y_1)=(-25.2,-17.7).\)

Table 1 Numerical Results for Example 5.1
Full size table

Example 5.2

Let \(\mathcal {H}_1=\mathcal {H}_2=\mathcal {H}_3=( l _2(\mathbb {R}), \Vert \cdot \Vert _2),\) where \( l _2(\mathbb {R}):=\{x=(x_1,x_2,\ldots ,x_n,\ldots ),\) \( x_i\in \mathbb {R}\,:\,\sum _{i=1}^{\infty }|x_i|^2<+\infty \}, ||x||_2=\sqrt{(\sum _{i=1}^{\infty }|x_i|^2)}\) and \(\langle x,y \rangle = \sum _{i=1}^\infty x_iy_i\) for all \(x\in \ell _2(\mathbb {R}).\) For \(r_i>0,~i=1,2,\) we define the sets \(\mathcal {C}:=\{x\in \ell _2\,:\,\Vert x\Vert \le 1\}\) and \(\mathcal {Q}:=\{y\in \ell _2\,:\,\Vert y\Vert \le 1\}.\) Let \(\mathcal {F}_1:\mathcal {H}_1\rightarrow \mathcal {H}_2,\) \(\mathcal {F}_2:\mathcal {H}_2\rightarrow \mathcal {H}_3\) be defined by \(\mathcal {F}_1x=\frac{x}{3}\) and \(\mathcal {F}_2x=\frac{2x}{5}\) respectively which implies that \(\mathcal {F}_1^*y=\frac{y}{3}\) and \(\mathcal {F}_2^*y=\frac{2y}{5}.\) Clearly, \(\mathcal {F}_1\) and \(\mathcal {F}_2\) are bounded linear operators. We define \(\Phi _1:\mathcal {C}\times \mathcal {C}\rightarrow \mathbb {R}\) and \(\Phi _2:\mathcal {Q}\times \mathcal {Q} \rightarrow \mathbb {R}\) by \(\Phi _1(x,y) =\langle L_1x, y-x \rangle \) and \(\Phi _2(x,y) =\langle L_2x, y-x \rangle ,\) where \(L_1x =\frac{x}{3}\) and \(L_2x =\frac{x}{2}.\) Observe that \(\Phi _1\) and \(\Phi _2\) satisfy Assumption 2.9. After simple calculation and applying Lemma 2.10, we obtain

$$U^{\Phi _1}_{r_1} (u) = \frac{3u}{r_1+3},~~ \forall x\in \mathcal {C},$$

and

$$U^{\Phi _2}_{r_2} (v)=\frac{2v}{r_2+2}, ~~ \forall y\in \mathcal {Q}.$$

Let \(A:\mathcal {H}_1\rightarrow \mathcal {H}_1\) be defined by \(A(x_1,x_2,x_3,\dots )=(x_1e^{-x_1^2},0,0,\dots )\) and \(B:\mathcal {H}_2\rightarrow \mathcal {H}_2\) as \(B(x_1,x_2,x_3,\dots )=(5x_1e^{-x_1^2},0,0,\dots ).\) Clearly, we see that A and B are pseudomonotone mappings. We define the mappings \(T_1(s):\mathbb {R}\rightarrow \mathbb {R}\) and \(T_2(u):\mathbb {R}\rightarrow \mathbb {R}\) as follows; \(T_1(s)x=10^{-5s}x\) and \(T_2(u)y=10^{-3u}y.\) Clearly, we observe that \(T_1(s)\) and \(T_2(u)\) are nonexpansive semigroups.

We choose \(\mathcal {V}_1=x_0, \mathcal {V}_2=y_0\) and consider different initial values as follows:

Case 1: \(x_0 = (\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \dots ),\) \(y_0 = (\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \dots );\) \( x_1 = (\frac{1}{3}, \frac{1}{9}, \frac{1}{27},\dots ),\) \(y_1 = (\frac{1}{3}, \frac{1}{9}, \frac{1}{27},\dots );\)

Case 2: \(x_0 = (\frac{1}{2}, \frac{1}{6}, \frac{1}{18}, \dots ),\) \(y_0 = (\frac{1}{2}, \frac{1}{4},\frac{1}{8}, \dots );\) \(x_1 = (-\frac{1}{3}, \frac{1}{6}, -\frac{1}{18}, \dots ),\) \(y_1 = (-\frac{1}{3}, \frac{1}{6}, -\frac{1}{18}, \dots );\)

Case 3: \(x_0 = (\frac{3}{8}, \frac{3}{16}, \frac{3}{32}, \dots ),\) \(y_0 = (\frac{5}{9}, \frac{5}{18}, -\frac{5}{36}, \dots );\) \(x_1 = (-\frac{1}{3}, \frac{1}{9}, -\frac{1}{27}, \dots ),\) \( y_1 = (\frac{1}{2}, \frac{1}{6}, \frac{1}{12}, \dots );\)

Case 4: \(x_0 = (\frac{3}{8}, \frac{3}{16}, \frac{3}{32},\dots ),\) \(y_0 = (\frac{5}{9}, \frac{5}{18}, \frac{5}{36},\dots );\) \(x_1 = (\frac{1}{9}, \frac{1}{18}, \frac{1}{36},\dots ),\) \(y_1 = (-\frac{7}{12}, \frac{7}{24}, -\frac{7}{36}).\)

Table 2 Numerical Results for Example 5.2
Full size table

6 Conclusion

In this paper, we studied the split equalities of the VIP, EP and FPP of nonexpansive semigroups. We introduced a Tseng’s extragradient method with self-adaptive step size for approximating a common solution of the split equalities of the VIP, EP and FPP of nonexpansive semigroups in the framework of real Hilbert spaces when the cost operator of the VIP is pseudomonotone and non-Lipschitz. Without the sequential weak continuity condition on the cost operator, we obtained a strong convergence result of our proposed method. While the cost operator is non-Lipschitz, our algorithm does not involve any linesearch procedure and our strong convergence result was obtained without the usual “two cases approach" widely used in many papers. Finally, we presented some numerical experiments of our proposed method in comparison with a related method in the literature to show the applicability of our method. Our result improves, extends and generalizes several other results in the literature.