Robust estimation for multivariate wrapped models

Abstract

A weighted likelihood technique for robust estimation of multivariate Wrapped distributions of data points scattered on a $p-$dimensional torus is proposed. The occurrence of outliers in the sample at hand can badly compromise inference for standard techniques such as maximum likelihood method. Therefore, there is the need to handle such model inadequacies in the fitting process by a robust technique and an effective downweighting of observations not following the assumed model. Furthermore, the employ of a robust method could help in situations of hidden and unexpected substructures in the data. Here, it is suggested to build a set of data-dependent weights based on the Pearson residuals and solve the corresponding weighted likelihood estimating equations. In particular, robust estimation is carried out by using a Classification EM algorithm whose M-step is enhanced by the computation of weights based on current parameters’ values. The finite sample behavior of the proposed method has been investigated by a Monte Carlo numerical study and real data examples.

1 Introduction

Multivariate circular observations arise commonly in all those fields where a quantity of interest is measured as a direction or when instruments such as compasses, protractors, weather vanes, sextants or theodolites are used [24]. Circular (or directional) data can be seen as points on the unit circle and represented by angles, provided that an initial direction and orientation of the circle have been chosen.

These data might be successfully modeled by using appropriate wrapped distributions such, e.g, the Wrapped Normal or the Wrapped Cauchy on the unit circle. The reader is pointed to [9, 19, 25] for modeling and inferential issues on circular data. Wrapping can be explained as the geometric translation of a distribution with support on $\mathbb {R}$ to a space defined on a circular object, e.g., a unit circle [25].

When data come in a multivariate setting, we might extend the univariate wrapping around the circle by using a component-wise wrapping of multivariate distributions around a $p-$dimensional torus. Let

$$\begin{aligned} \mathcal {M}=\left\{ m(\varvec{x}; \varOmega )= c_p |\Sigma |^{-\frac{1}{2}} h(d(\varvec{x};\varvec{\mu },\Sigma )), \varOmega =(\varvec{\mu },\Sigma ), \varvec{\mu } \in \mathbb {R}^p, \Sigma \in PDS(p) \right\} \end{aligned}$$

be the elliptically symmetric family of distributions where PDS(p) is the set of all positive-definite symmetric $p\times p$ matrices, $c_p$ is a normalization constant depending on $p>1$, $h(\cdot )$ is a non-negative scalar function, called density generating function, and $d(\varvec{x};\varvec{\mu },\Sigma ) = \left[ (\varvec{x} - \varvec{\mu })^\top \Sigma ^{-1}(\varvec{x} - \varvec{\mu })\right] ^{1/2}$ is the Mahalanobis distance. For example, the multivariate Normal distribution and the multivariate Student $t_\nu$ distribution belong to this family choosing $h(d)=\exp (-d^2/2)$ and $h(d)=(1+d^2/\nu )^{-(p+\nu )/2}$, respectively, as density generating function. As particular case, the multivariate Cauchy distribution can be obtained for $\nu =1$. Let $\varvec{X}$ be a multivariate random variable whose distribution belongs to the family of elliptically symmetric distributions. Then, the distribution of $\varvec{Y} = \varvec{X} \ \text {mod} \ 2\pi$ is

$$\begin{aligned} M^\circ (\varvec{y})= \sum _{\varvec{j} \in \mathbb {Z}^p} [M(\varvec{y} + 2 \pi \varvec{j}; \varOmega )- M(2 \pi \varvec{j}; \varOmega ) ], \end{aligned}$$

with density function

$$\begin{aligned} m^\circ (\varvec{y})= \sum _{\varvec{j} \in \mathbb {Z}^p} m(\varvec{y} + 2 \pi \varvec{j}; \varOmega ), \end{aligned}$$

$\varvec{y} \in (0,2\pi ]^p$, $\varOmega =(\varvec{\mu },\Sigma )$, where $M(\cdot )$ and $m(\cdot )$ are the distribution and density function of $\varvec{X}$, respectively, and the modulus operator mod is applied component-wise. As a special case, let $\varvec{X}$ be multivariate Normal, i.e. $\varvec{X} \sim N_p(\varvec{\mu }, \Sigma )$. Then, the distribution of $\varvec{Y} = \varvec{X} \ \text {mod} \ 2\pi$ is Wrapped Normal and denoted as $WN_p(\varvec{\mu },\Sigma )$. An appealing property of the Normal distribution that carries over to the Wrapped Normal is its closure with respect to convolution [7, 19]. This property will be particularly relevant in the implementation of our methodology.

Given an i.i.d. sample $\varvec{y}_1, \ldots , \varvec{y}_n$ of size n from $\varvec{Y}$ on the p-torus, likelihood based inference about the parameters of Wrapped distributions can be trapped in numerical and computational hindrances since the log-likelihood function

$$\begin{aligned} \ell (\varOmega ) = \sum _{i=1}^n \log \left[ \sum _{\varvec{j} \in \mathbb {Z}^p} m(\varvec{y}_i + 2 \pi \varvec{j}; \varOmega ) \right] , \end{aligned}$$

involves the evaluation of an infinite series. [2] proposed an Iterative Reweighted Maximum Likelihood Estimating Equations algorithm in the univariate setting, that is available in the R package circular [4]. Algorithms based on the Expectation-Maximization (EM) method have been used by [15] for parameter estimation in autoregressive models of Wrapped Normal distributions and by [10, 32] and [14] in a Bayesian framework according to a data augmentation approach to estimate the missing unobserved wrapping coefficients. An innovative estimation strategy based on EM and Classification EM algorithms has been discussed in [28]. In order to perform maximum likelihood estimation, the wrapping coefficients are treated as latent variables.

We can think of $\varvec{y}_i = \varvec{x}_i \mod 2\pi$ where $\varvec{x}_i$ is a sample from a random variable whose distribution belongs to the elliptically symmetric family of distributions. The EM algorithm works with the complete log-likelihood function given by

$$\begin{aligned} \ell _C(\varOmega ) = \sum _{i=1}^n \sum _{\varvec{j} \in \mathbb {Z}^p} v_{i\varvec{j}}\log m(\varvec{y}_i + 2 \pi \varvec{j}; \varOmega ), \end{aligned}$$

(1)

that is characterized by the missing unobserved wrapping coefficients $\varvec{j}$ and $v_{i\varvec{j}}$ is an indicator of the ith unit having the $\varvec{j}$ vector as wrapping coefficients. The EM algorithm iterates between an Expectation (E) step and a Maximization (M) step. In the E-step, the conditional expectation of (1) is obtained by estimating the $v_{i\varvec{j}}$ with the posterior probability that $\varvec{y}_i$ has $\varvec{j}$ as wrapping coefficient based on current parameters’ values, i.e.

$$\begin{aligned} v_{i\varvec{j}} = \frac{m(\varvec{y}_i + 2 \pi \varvec{j}; \varOmega )}{\sum _{\varvec{b} \in \mathbb {Z}^p} m(\varvec{y}_i + 2 \pi \varvec{b}; \varOmega )} \ , \qquad \varvec{j} \in \mathbb {Z}^p, \quad i=1,\ldots ,n. \end{aligned}$$

In the M-step, the conditional expectation of (1) is maximized with respect to $\varOmega$. The reader is pointed to [28] for computational details about such maximization problem for the multivariate Wrapped Normal distribution.

An alternative estimation strategy is based on the CEM-type algorithm. The substantial difference is that the E-step is followed by a C-step (where C stands for classification) in which $v_{i\varvec{j}}$ is estimated as either 0 or 1 and so that each observation $\varvec{y}_i$ is associated to the most likely wrapping coefficients $\varvec{j}_i$ with $\varvec{j}_i = \arg \max _{\varvec{b} \in \mathbb {Z}^p} v_{i\varvec{b}}$.

When the sample data is contaminated by the occurrence of outliers, it is well known that maximum likelihood estimation, also achieved through the implementation of the EM or CEM algorithm, is likely to lead to unreliable results [13]. Then, there is the need for a suitable robust procedure providing protection against those unexpected anomalous values. There have been few attempts to deal with outliers in circular data analysis for univariate distributions, mainly focused on the Von Mises distribution [2, 20, 21, 33]. On the contrary, the robust technique proposed here is based on multivariate Wrapped distributions and, to the best of our knowledge, there are no competiting techniques of robust estimation for multivariate models.

An attractive solution to develop a robust estimation algorithm for multivariate wrapped distributions would be to modify the likelihood equations in the M-step. Such a modification could be achieved by the introduction of a set of weights aimed to bound the effect of those observations deviating from the assumed model. Here, it is suggested to evaluate weights according to the weighted likelihood methodology ([26]). Weighted likelihood is an appealing robust technique for estimation and testing [5]. The methodology leads to a robust fit and gives the chance to detect outliers and possible substructures in the data. Furthermore, the weighted likelihood methodology works in a very satisfactory fashion when combined with the EM and CEM algorithms, as in the case of mixture models [17, 18].

The remainder of the paper is organized as follows. Section 2 gives brief but necessary preliminaries on weighted likelihood. The weighted CEM algorithm for robust fitting of multivariate Wrapped models on data on a $p-$dimensional torus is described in Sect. 3, while some theoretical properties are discussed in Sect. 3.1. Section 4 reports the results of some numerical studies, whereas a real data example is discussed in Sect. 5. Concluding remarks end the paper.

2 Preliminaries on weighted likelihood

Let $\varvec{y}_1, \ldots , \varvec{y}_n$ be a random sample of size n drawn from a r.v. $\varvec{Y}$ with distribution function F and probability (density) function f. Let $\mathcal {M} = \{ M(\varvec{y}; \varvec{\theta }), \varvec{\theta } \in \Theta \subseteq \mathbb {R}^d, d \ge 1, \varvec{y} \in \mathcal {Y} \}$ be the assumed parametric model, with corresponding density $m(\varvec{y};\varvec{\theta })$, and $\hat{F}_n$ the empirical distribution function. Assume that the support of M is the same as that of F and independent of $\varvec{\theta }$. A measure of the agreement between the true and assumed model is provided by the Pearson residual function $\delta (\varvec{y})$, with $\delta (\varvec{y})\in [-1,+\infty )$, [23, 26], defined as

$$\begin{aligned} \delta (\varvec{y}) = \delta (\varvec{y}; \varvec{\theta }, F) = \frac{f(\varvec{y})}{m(\varvec{y}; \varvec{\theta })} - 1 \ . \end{aligned}$$

(2)

The finite sample counterpart of (2) can be obtained as

$$\begin{aligned} \delta _n(\varvec{y}) = \delta (\varvec{y}; \varvec{\theta }, \hat{F}_n) = \frac{\hat{f}_n(\varvec{y})}{m(\varvec{y}; \varvec{\theta })} - 1 \ , \end{aligned}$$

(3)

where $\hat{f}_n(\varvec{y})$ is a consistent estimate of the true density $f(\varvec{y})$. In discrete families of distributions, $\hat{f}_n(\varvec{y})$ can be driven by the observed relative frequencies [23], whereas in continuous models one could consider a non parametric density estimate based on the kernel function $k(\varvec{y};\varvec{t},h)$, that is

$$\begin{aligned} \hat{f}_n(\varvec{y})=\int _\mathcal {Y}k(\varvec{y};\varvec{t},h)d\hat{F}_n(\varvec{t}) \ . \end{aligned}$$

(4)

Moreover, in the continuous case, the model density in (3) can be replaced by a smoothed model density, obtained by using the same kernel involved in non-parametric density estimation [8, 26], that is

$$\begin{aligned} \hat{m}(\varvec{y}; \varvec{\theta })=\int _\mathcal {Y}k(\varvec{y};\varvec{t},h)m(\varvec{t};\varvec{\theta }) \ d\varvec{t} \ \end{aligned}$$

leading to

$$\begin{aligned} \delta _n(\varvec{y}) = \delta (\varvec{y}; \varvec{\theta }, \hat{F}_n) = \frac{\hat{f}_n(\varvec{y})}{\hat{m}(\varvec{y}; \varvec{\theta })} - 1 \ . \end{aligned}$$

(5)

By smoothing the model, the Pearson residuals in (5) converge to zero with probability one for every $\varvec{y}$ under the assumed model and it is not required that the kernel bandwidth h goes to zero as the sample size n increases. Large values of the Pearson residual function correspond to regions of the support $\mathcal {Y}$ where the model fits the data poorly, meaning that the observation is unlikely to occur under the assumed model. The reader is pointed to [3, 8, 26] and references therein for more details.

Observations leading to large Pearson residuals in (5) are supposed to be down-weighted. Then, a weight in the interval [0, 1] is attached to each data point, that is computed accordingly to the following weight function

$$\begin{aligned} w(\delta (\varvec{y})) = \min \left\{ 1, \frac{\left[ A(\delta (\varvec{y})) + 1\right] ^+}{\delta (\varvec{y}) + 1} \right\} \ , \end{aligned}$$

(6)

where $[\cdot ]^+$ denotes the positive part and $A(\delta )$ is the Residual Adjustment Function (RAF, [8, 23, 29]). The weights $w(\delta _n(\varvec{y}))$ are meant to be small for those data points that are in disagreement with the assumed model. Actually, the RAF plays the role to bound the effect of large Pearson residuals on the fitting procedure. $A(\cdot )$ is an increasing, twice differentiable, function in $[-1,\infty )$, such that $A(0)=0$ and $A'(0)=1$.

The weight function (6) might be based on the families of RAF stemming from the Symmetric Chi-squared divergence [26], the Generalized Kullback-Leibler divergence [30]

$$\begin{aligned} A_{gkl}(\delta , \tau )=\frac{\log (\tau \delta +1)}{\tau }, \ 0\le \tau \le 1; \end{aligned}$$

(7)

or the Power Divergence Measure [11, 12]

$$\begin{aligned} A_{pdm}(\delta , \tau ) = \left\{ \begin{array}{lc} \tau \left( (\delta + 1)^{1/\tau } - 1 \right) &{} \tau < \infty \\ \log (\delta + 1) &{} \tau \rightarrow \infty \ . \end{array} \right. \end{aligned}$$

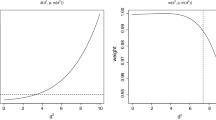
In the latter case, special cases are maximum likelihood (ML, $\tau = 1$, as the weights become all equal to one), Hellinger distance (HD, $\tau = 2$), Kullback–Leibler divergence (KL, $\tau = \rightarrow \infty$) and Neyma-s Chi-Square (NCS, $\tau = -1$). The RAF stemming from the Power Divergence Measure are illustrated in the left panel of Fig. 1. The resulting weight function (6) is unimodal and declines smoothly to zero as $\delta (\varvec{y})\rightarrow -1$ or $\delta (\varvec{y})\rightarrow \infty$, as displayed in the right panel of Fig. 1. See also [29] for further ways of defining RAFs.

Fig. 1

RAF from Power Divergence Measure (left) and corresponding weight function (right) for different values of $\tau$

According to the chosen RAF, robust estimation can be based on a Weighted Likelihood Estimating Equation (WLEE), defined as

$$\begin{aligned} \sum _{i=1}^n w(\delta _n(\varvec{y}_i); \varvec{\theta }, \hat{F}_n) s(\varvec{y}_i; \varvec{\theta }) = 0 \ , \end{aligned}$$

(8)

where $s(\varvec{y}_i;\varvec{\theta })$ is the individual contribution to the score function. Therefore, weighted likelihood estimation can be thought as a root solving problem. Finding the solution of (8) requires an iterative weighting algorithm.

Remark 1

Several functions could be defined to bound the effect of large Pearson residuals rather than using the RAF. However, the use of the RAF is strictly connected to weighted likelihood estimation. First, this choice is motivated by historical reasons, in the spirit of the work by [23, 26], among others. Then, the special role played by the RAF is justified in light of the connection between weighted likelihood estimation and minimum disparity estimation. Actually, the RAF arises naturally from a minimum disparity estimation problem, although the construction of the WLEE does not depend on the availability of an objective function [3].

Remark 2

As pointed out in [29], values of the Pearson Residuals in the interval $(0, \infty )$ are related to outliers, while values in $(-1,0)$ to inliers. RAFs can act on this last interval in opposite ways. For instance, the RAF related to the HD leads to downweighting while the Negative Exponential Disparity (see [23]) leads to an upweigthing of the observations. Since inliers represent a minor issue for data in p–dimensional torus, we decided to modify our RAFs in the interval $(-1,0)$ setting them equal to the identity function. The plots of the modified RAFs together with the corresponding weights are reported in Fig. 2. We used these RAFs in our simulations and examples.

Fig. 2

Modified RAF from Power Divergence Measure (left) and corresponding weight function (right) for different values of $\tau$

The corresponding weighted likelihood estimator $\hat{\varvec{\theta }}^w$ (WLE) is consistent, asymptotically normal and fully efficient at the assumed model, under some general regularity conditions pertaining the model, the kernel and the weight function [3, 5, 26]. Its robustness properties have been established in [23] in connection with minimum disparity problems. It is worth remarking that under very standard conditions, one can build a simple WLEE matching a minimum disparity objective function, hence inheriting its robustness properties.

In finite samples, the robustness/efficiency trade-off of weighted likelihood estimation can be tuned by varying the smoothing parameter h in Eq. (4). Large values of h lead to Pearson residuals all close to zero and weights all close to one and, hence, large efficiency, since $\hat{f}_n(\varvec{y})$ is stochastically close to the postulated model. On the other hand, small values of h make $\hat{f}_n(\varvec{y})$ more sensitive to the occurrence of outliers and the Pearson residuals become large for those data points that are in disagreement with the model. On the contrary, the shape of the kernel function $k(\varvec{y};\varvec{t},h)$ has a very limited effect.

For what concerns the tasks of testing and setting confidence regions, a weighted likelihood counterpart of the classical likelihood ratio test, and its asymptotically equivalent Wald and Score versions, can be established. Note that, all share the standard asymptotic distribution at the true model, according to the results stated in [5], that is

$$\begin{aligned} \varLambda (\varvec{\theta })=2\sum _{i=1}^nw_i\left[ \ell (\hat{\varvec{\theta }}^w; \varvec{y}_i)-\ell (\varvec{\theta }; \varvec{y}_i)\right] {\mathop {\rightarrow }\limits ^{p}}\chi ^2_p \ , \end{aligned}$$

with $w_i= w(\delta _n(\varvec{y}_i); \hat{\varvec{\theta }}^w, \hat{F}_n)$. Profile tests can be obtained as well.

3 A weighted CEM algorithm

As previously stated in the “Introduction” [28] provided effective iterative algorithms to fit a multivariate Wrapped distribution on the p-dimensional torus. Here, robust estimation is achieved by a suitable modification of their CEM algorithm, consisting in a weighting step before performing the M-step, in which data-dependent weights are evaluated according to (6) yielding a WLEE (8) to be solved in the M-step.

In the special case of the multivariate Wrapped Normal distribution, the construction of Pearson residuals in (5) involves a multivariate Wrapped Normal kernel with covariance matrix $h \varLambda$. Since the family of multivariate Wrapped Normal is closed under convolution, then the smoothed model density is still Wrapped Normal with covariance matrix $\Sigma +h\varLambda$. Here, we set $\varLambda = \Sigma$ so that h can be a constant independent of the variance-covariance structure of the data. The problem becomes more challenging if other elliptically symmetric distributions are considered, since smoothed densities require numerical evaluations.

The weighted CEM algorithm is structured as follows:

• 0 Initialization. Starting values can be obtained by maximum likelihood estimation evaluated over a randomly chosen subset. The subsample size is expected to be as small as possible in order to increase the probability to get an outliers’ free initial subset but large enough to guarantee estimation of the unknown parameters. A starting solution for $\varvec{\mu }$ can be obtained by the circular mean, whereas the diagonal entries of $\Sigma$ can be initialized as $-2\log (\hat{\rho }_r)$, where $\hat{\rho }_r$ is the sample mean resultant length and the off-diagonal elements by $\rho _c(\varvec{y}_r, \varvec{y}_s) \sigma _{rr}^{(0)} \sigma _{ss}^{(0)}$ ($r \ne s$), where $\rho _c(\varvec{y}_r, \varvec{y}_s)$ is the circular correlation coefficient, $r=1,2,\ldots ,p$ and $s=1,2,\ldots ,p$, see [19] pag.176,equation8.2.2. In order to avoid the algorithm to be dependent on initial values, a simple and common strategy is to run the algorithm from a number of starting values using the bootstrap root searching approach as in [26]. A criterion to choose among different solutions will be illustrated in Sect. 5.

• 1. E-step. Based on current parameters’ values, first evaluate posterior probabilities

  $$v_{i\varvec{j}} = \frac{m(\varvec{y}_i + 2 \pi \varvec{j}; \varOmega )}{\sum _{\varvec{b} \in \mathbb {Z}^p} m(\varvec{y}_i + 2 \pi \varvec{b}; \varOmega )} \ , \qquad \varvec{j} \in \mathbb {Z}^p, \quad i=1,\ldots ,n \ ,$$

• 2. C-step. Set $\varvec{j}_i = \arg \max _{\varvec{b} \in \mathbb {Z}^p} v_{i\varvec{b}}$ and $v_{i\varvec{j}}=1$ for $\varvec{j}=\varvec{j}_i$, and $v_{i\varvec{j}}=0$ otherwise. Note that, at each iteration the classification algorithm provides also an estimate of the original unobserved sample obtained as $\hat{\varvec{x}}_i = \varvec{y}_i + 2 \pi \varvec{j}_i$, $i = 1, \ldots , n$.

• 3. W-step (weighting step). Based on current parameters’ values, compute Pearson residuals according to (5) and evaluate the weights as

  $$\begin{aligned} w_i=w(\delta _n(\varvec{y}_i), \varOmega , \hat{F}_n). \end{aligned}$$

• 4. M-step. Update parameters’ values by solving the WLEE

  $$\begin{aligned} \sum _{i=1}^n w_i s(\varvec{y}_i+ 2 \pi \varvec{j}_i; \varvec{\theta }) = \sum _{i=1}^n w_i s(\hat{\varvec{x}_i}; \varvec{\theta }) =\varvec{0} \ , \end{aligned}$$

  conditionally on $\varvec{j}_i$ $(i = 1,\ldots ,n)$, with $s(\varvec{x}; \varvec{\theta })=\partial \log m(\varvec{x}; \varvec{\theta })/\partial \theta ^\top$. In the Normal case, the WLEE returns weighted mean and variance-covariance matrix with weights $w_i$, given by

  $$\begin{aligned} \hat{\varvec{\mu }}_i&= \frac{\sum _{i=1}^n w_i \hat{\varvec{x}}_i}{\sum _{i=1}^n w_i}, \\ \hat{\Sigma }&= \frac{\sum _{i=1}^n w_i(\hat{\varvec{x}}_i - \hat{\varvec{\mu }}_i) (\hat{\varvec{x}}_j - \hat{\varvec{\mu }}_j)^\top }{\sum _{i=1}^n w_i}. \end{aligned}$$

3.1 Properties

The WLEE to be solved in the M-step is of the type (8). Let denote it by $\varPsi _n=\varvec{0}$. Let $\theta _f$ be such that $f(\varvec{y})$ is close to $m^\circ (\varvec{y}; \varvec{\theta }_f)$, that is $\varvec{\theta }_f$ is implicitly defined by

$$\begin{aligned} \varPsi =\int w(\delta (\varvec{y}))s(\varvec{y}+2\pi \varvec{j}; \varvec{\theta }_f) \ dF(\varvec{y}) = \varvec{0}, \end{aligned}$$

given $\varvec{j}$. We have the following results:

• (i)
  $$\begin{aligned} \sqrt{n}\left( \varPsi _n- \varPsi \right) {\mathop {\rightarrow }\limits ^{d}} N(0, V(\theta )) \end{aligned}$$
• (ii)
  $$\begin{aligned} \hat{\theta }^w{\mathop {\rightarrow }\limits ^{a.s.}} \theta _f \end{aligned}$$
• (iii)
  $$\begin{aligned} \sqrt{n}\left( \hat{\theta }^w- \theta _f\right) {\mathop {\rightarrow }\limits ^{d}} N(0, B^{-1}(\theta _f)V(\theta _f)B^{-1}(\theta _f)) \end{aligned}$$

with

$$\begin{aligned} V(\theta )&= \lim _{n \rightarrow \infty } \mathbb {V}ar \left[ \int k((y - Y)/h) A'(\delta (y)) s(y;\theta ) \ dy \right] \\&= \mathbb {V}ar \left[ A'(\delta (Y)) s(Y;\theta ) \right] \end{aligned}$$

and

$$\begin{aligned} B(\theta ) = \int A(\delta (y)) \nabla _2 m(y;\theta ) \ dy - \int A'(\delta (y))(\delta (y) + 1) s(Y;\theta ) s^\top (Y;\theta ) m(y;\theta ) \ dy \ , \end{aligned}$$

where $V(\theta )$ is finite and positive definite and $B(\theta )$ is non-zero for $\theta = \theta _f$. At the true model, $B^{-1}(\theta _f)V(\theta _f)B^{-1}(\theta _f)$ coincides with the inverse of the expected Fisher information matrix and the WLE recovers full efficiency. Details about the assumptions and proofs can be found in [3, 22].

In particular, one can also relax the mathematical device of evaluating integrals and their approximations given by sums on a trimmed set to avoid numerical instabilities due the occurrence of small (almost null) densities in the tails that would affect the denominator of Pearson residuals. As stated in [22], trimming is not necessary and could not be considered, especially in those models where the tails decay exponentially.

4 Numerical studies

The finite sample behavior of the proposed weighted CEM has been investigated by some numerical studies based on 500 Monte Carlo trials each, in the Normal case, with data drawn from a $WN_p(\varvec{\mu },\Sigma )$. We set $\varvec{\mu }=0$, whereas in order to account for the lack of affine equivariance of the Wrapped Normal model [28], we considered different covariance structures $\Sigma$ as in [6]. In particular, for fixed condition number $CN = 20$, we obtained a random correlation matrix R. Then, the correlation matrix R has been converted into the covariance matrix $\Sigma = D^{1/2} R D^{1/2}$, with $D=\text {diag}(\sigma ^2\varvec{1}_p)$, where $\sigma$ is a chosen constant and $\varvec{1}_p$ is a p-dimensional vector of ones. Outliers have been generated by shifting a proportion $\epsilon$ of randomly chosen data points by an amount $k_\epsilon$ in the direction of the smallest eigenvalue of $\Sigma$. We considered sample sizes $n=50,100,500$, dimensions $p=2,5$, contamination level $\epsilon =0, 5\%, 10\%, 20\%$, contamination size $k_\epsilon =\pi /4, \pi /2, \pi$ and $\sigma =\pi /8, \pi /4, \pi /2$.

For each combination of the simulation parameters, we compare the performance of CEM and weighted CEM algorithms. The weights used in the W-step are computed using the Generalized Kullback–Leibler RAF in Eq. (7) with $\tau = 0.1$. According to the strategy described in [5], the bandwidth h has been selected by setting $\varLambda = \Sigma$, so that h is a constant independent of the scale of the model. Here, h is obtained so that any outlying observation located at least three standard deviations away from the mean in a component-wise fashion, is attached a weight not larger than 0.12 when the rate of contamination in the data has been fixed equal to $20\%$. The algorithm has been initialized according to the root search approach described in [26] based on 15 subsamples of size 10. It is worth remarking here that there are not other robust proposals to be compared with our method, to the best of our knowledge.

The weighted CEM is assumed to have reached convergence when at the $(k+1)$–th iteration

$$\begin{aligned} \max \left( \sqrt{2(1-\cos (\hat{\varvec{\mu }}^{(k)}-\hat{\varvec{\mu }}^{(k+1)}))}, \max |\hat{\Sigma }^{(k)}-\hat{\Sigma }^{(k+1)} | \right) <10^{-6} \end{aligned}$$

where differences are element-wise and $\max |\hat{\Sigma }^{(k)}-\hat{\Sigma }^{(k+1)}|$ denotes the maximum absolute difference in any of the components of the matrix $\hat{\Sigma }^{(k)}-\hat{\Sigma }^{(k+1)}$. The algorithm has been implemented so that $\mathbb {Z}^p$ is replaced by the Cartesian product $\times _{s=1}^p \varvec{\mathcal {J}}$ where $\varvec{\mathcal {J}} = (-J, -J+1, \ldots , 0, \ldots , J-1, J)$ for some J providing a good approximation. Here we set $J=3$. The algorithm runs on R code [31] available from the authors upon request.

Fitting accuracy has been evaluated according to

• (i) the average angle separation ([9])

  $$\begin{aligned} {\text {AS}}(\hat{\varvec{\mu }}) = \frac{1}{p} \sum _{i=1}^p (1 - \cos (\hat{\mu }_i - \mu _{i})) \ , \end{aligned}$$

  which ranges in [0, 2], for the mean vector;

• (ii) the divergence

  $$\begin{aligned} \varDelta (\hat{\Sigma }) = {\text {trace}}(\hat{\Sigma } \Sigma ^{-1}) - \log (\det (\hat{\Sigma } \Sigma ^{-1})) - p \ , \end{aligned}$$

for the variance-covariance matrix. Here, we only report the results stemming from the challenging situation with $n=100$ and $p=5$.

Figure 3 displays the average angle separation whereas Fig. 4 gives the divergence to measure the accuracy in estimating the variance-covariance matrix for the weighted CEM (in dark grey) and CEM (in light grey). The weighted CEM exhibits a fairly satisfactory fitting accuracy both under the assumed model (i.e. when the sample at hand is not corrupted by the occurrence of outliers) and under contamination. The robust method outperforms the CEM method, especially in the estimation of the variance–covariance components. The algorithm results in biased estimates for both the mean vector and the variance–covariance matrix only for the large contamination rate $\epsilon =20\%$, with small contamination size and a large $\sigma$. Actually, in this data constellation outliers are not well separated from the group of genuine observations. A similar behavior has been observed for the other sample sizes. Complete results are made available in the “Supplementary Material”.

Fig. 3

Distribution of average angle separation for $n=100$ and $p=5$ using weighted CEM (in dark grey) and the CEM (in light grey). The contamination rate $\epsilon$ is given on the horizontal axis. Increasing contamination size $k_\epsilon$ from left to right, increasing $\sigma$ from top to bottom

Fig. 4

Distribution of the divergence measure for $n=100$ and $p=5$ using the weighted CEM (in dark grey) and the CEM (in light grey). The contamination rate $\epsilon$ is given on the horizontal axis. Increasing contamination size $k_\epsilon$ from left to right, increasing $\sigma$ from top to bottom

4.1 Monitoring the smoothing parameter

As pointed out in Sect. 2, in finite samples the robustness/efficiency trade-off of weighted likelihood estimation can be tuned by varying the smoothing parameter h used in kernel density estimation. In the numerical studies above, h has been selected according to an objective criterion (see Section 4.1 in [26] for the details). However, practitioners are advised to monitor the behavior of weighted likelihood estimation as h varies in a reasonable range [16]. Here, the procedure is illustrated over a sample of size $n = 100$ from the previous numerical studies with $\sigma = \frac{\pi }{4}$, $\epsilon = 10\%$, $k_\epsilon = \frac{\pi }{2}$.

Figure 5 shows the trajectories of the weights at convergence corresponding to different values of h in the range [0.001, 0.25]. In particular, the weights relative to the generated outliers are in dark grey, whereas those for the genuine observations are displayed in light grey. Outliers are correctly downweighted for several values of h and, as expected, beyond a certain value the analysis becomes not robust. On the other side, weights corresponding to genuine observations rapidly goes to unity for increasing h. The (red) dashed line indicates the value of h used in the simulation study. Such a value correctly downweights the outlying observations.

Fig. 5

Final weights of contaminated observations (dark grey) and uncontaminated observations (light grey) computed with respect to the smoothing parameter h. The dashed (red) line indicates the value used in the simulation study

5 Real data example: protein data

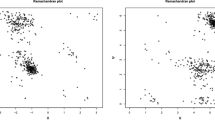
The data under consideration [27] contain bivariate information about 63 protein domains that were randomly selected from three remote Protein classes in the Structural Classification of Proteins (SCOP). In the following, we consider the data set corresponding to the 39th protein domain. A bivariate Wrapped Normal has been fitted to the data at hand by using the weighted CEM algorithm, based on a Generalized Kullback-Leibler RAF with $\tau =0.25$ and $J=6$. The tasks of bandwidth selection and initialization have been resolved according to the same strategy described above in Sect. 4.

The inspection of the data suggests the presence of at least a couple of clusters that make the data non homogeneous.

Fig. 6

Protein data. Fitted means ($+$) and $95\%$ confidence regions corresponding to three different roots from weighted CEM ($J=6$)

Fig. 7

Protein data. Weights corresponding to three different roots from weighted CEM

Figure 6 displays the data on a flat torus together with fitted means and $95\%$ confidence regions corresponding to three different roots of the WLEE (that are illustrated by different colors): one root gives location estimate $\varvec{\mu }_1=(1.85, 2.34)$ and a positive correlation $\rho _1=0.79$; the second root gives location estimate $\varvec{\mu }_2=(1.85, 5.86)$ and a negative correlation $\rho _2=-0.80$; the third root gives location estimate $\varvec{\mu }_3=(1.61, 0.88)$ and correlation $\rho _3=-0.46$. The first and second roots are very close to maximum likelihood estimates obtained in different directions when unwrapping the data: this is evident from the shift in the second coordinate of the mean vector and the change in the sign of the correlation. In both cases the data exhibit weights larger than 0.5, except in few cases, corresponding to the most extreme observations, as displayed in the first two panels of Fig. 7. In none of the two cases the bulk of the data corresponds to an homogeneous sub-group. On the contrary, the third root is able to detect an homogeneous substructure in the sample, corresponding to the most dense region in the data configuration. A weight close to zero is attached to almost half of the data points, as shown in the third panel of Fig. 7. These findings still confirm the ability of the weighted likelihood methodology to tackle such uneven patterns as a diagnostic of hidden substructures in the data. In order to select one of the three roots we have found, we consider the strategy discussed in [1], that is, we select the root leading to the lowest fitted probability

$$\begin{aligned} \text {Prob}_{\hat{\varOmega }}\left( \delta _{n}(\mathbf{y} ; {\hat{\varOmega }}, {\hat{F_{n}}})< -0.95 \right) . \end{aligned}$$

This probability has been obtained by drawing 5000 samples from the fitted bivariate Wrapped Normal distribution for each of the three roots. The criterion correctly leads to choose the third root, for which an almost null probability is obtained, wheres the fitted probabilities for the first and second root are 0.204 and 0.280, respectively.

6 Conclusions

In this paper an effective strategy for robust estimation of multivariate Wrapped models on a $p-$dimensional torus has been presented. The method inherits the good computational properties of the CEM algorithm developed in [28] jointly with the robustness properties stemming from the employ of Pearson residuals and the weighted likelihood methodology. In this respect, it is particularly appealing the opportunity to work with a family of distribution that is close under convolution and allows to parallel the procedure one would have developed on the real line by using the multivariate normal distribution. The proposed weighted CEM works satisfactory at least in small to moderate dimensions, both on synthetic and real data. It is worth stressing that the method can be easily extended to other multivariate wrapped models.