1 Introduction

Let \(Y_1,\ldots ,Y_n\) be a time series of counts like the weekly number of people falling ill in epidemiology, the number of transactions per minute in finance, or jobs sent to a server during an hour. Zhu [28] extends the Poisson integer valued GARCH (more briefly called INGARCH) model, which has been put forward by [12, 14], among others, to scenarios where the conditional distribution of \(Y_t\) given the past of the process exhibits overdispersion. In the arising NBINGARCH model this conditional distribution is assumed to belong to the negative binomial family,

$$\begin{aligned} Y_t|{\mathcal {F}}_{t-1}\sim NB(r,p_{t}). \end{aligned}$$

Here, \({\mathcal {F}}_{t-1}\) is the \(\sigma \)-algebra describing the information provided by the past of the process up to time \(t-1\), \(r\in \mathbb {N}\) is the constant number of successes, and \(p_t\) is the time-varying probability of success. He assumes a linear model for the inverse odds \(\lambda _t=(1-p_t)/p_t\), which is regressed on past values \(Y_{t-1},\ldots ,Y_{t-p}, \lambda _{t-1},\ldots ,\lambda _{t-q}\). The negative binomial is a natural extension of the Poisson and covers a broad variety of overdispersed unimodal distributions. Zhu [28] studies Yule–Walker estimators for the parameter \(\theta =(\alpha _0,\ldots ,\alpha _p)'\) of NBINGARCH(p, 0) models, also called NBINARCH(p) models, and conditional least squares and conditional maximum likelihood estimators for the parameter of NBINGARCH(p, q) models for given values of r.

A first approach for robust fitting of NBINGARCH(p, q) models has been published by [27]. Like these authors we parameterize the negative binomial distribution in terms of the conditional mean \(\mu _t\ge 0\) and the parameter \(\kappa =1/r\ge 0\). The conditional mean and variance of \(Y_t\) are

$$\begin{aligned} \mu _{t}= & {} E(Y_t|{\mathcal {F}}_{t-1})= r \lambda _{t} = r \frac{1-p_{t}}{p _{t}}\\ \text{ and } \sigma ^{2}_{t}= & {} Var(Y_t|{\mathcal {F}}_{t-1})= r \lambda _{t} + r \lambda _{t}^{2}=\mu _t+\kappa \mu _t^2, \end{aligned}$$

respectively, i.e., \(\kappa \) measures the amount of overdispersion. The conditional Poisson model corresponds to the limiting special case \(\kappa =0\). An analogous parametrization has also been used by [1] in the context of generalized linear models for independent observations because of its greater numerical stability. While \(\kappa \) can take any positive value, r is usually restricted to be an integer. The linear model of [28] mentioned above can be expressed equivalently in terms of \(\mu _t\) as

$$\begin{aligned} \mu _t={\alpha }_0+\sum _{i=1}^p{\alpha }_iY_{t-i}+\sum _{j=1}^q{\beta }_j\mu _{t-j}, \end{aligned}$$

with \(\alpha _0,\ldots ,\alpha _p,\beta _1,\ldots ,\beta _q\) being positive parameters.

The interest of [27] is in transaction counts, where very large numbers of observations are available for model fitting. Accordingly, they focus on scenarios with at least \(n=1000\) observations. Moreover, they usually fix the dispersion parameter \(\kappa \) at the true value in their simulations. Our interest is also in scenarios with only a few hundred observations, where robust joint estimation of the shape parameter \(\kappa \) and the regression parameters \(\beta _1,\ldots ,\beta _q\) measuring the effects of unobserved past conditional means becomes very difficult. We avoid the latter and focus on the simpler class of NBINARCH(p) models, where we regress on past observations, only. NBINARCH models offer the advantage that the observed process \((Y_t:t\in \mathbb {N}_0)\) forms a p-th order Markov chain, which implies some simplifications in practice. Furthermore, Xiong and Zhu recommend the MCD [24] for dealing with outlying past observations, although the MCD has been designed for multivariate elliptically symmetric continuous measurements [17]. This may eliminate observations from the estimating equations although just a single preceding value is spurious. We instead shrink outlying past values towards an estimate of the marginal mean to avoid unnecessary eliminations.

The rest of the paper is organized as follows. In Sect. 2, we investigate robust versions of method of moment estimators, which are useful to get a first idea about a suitable model and its order p. In Sect. 3, we discuss robustifications of conditional maximum likelihood estimators for NBINARCH models. Section 4 illustrates the methods by a data example and Sect. 5 concludes.

2 Estimation derived from method of moments

Moment type estimators are computationally tractable even in case of high model orders if the moments are estimated individually without the need of multidimensional optimization. A possible drawback arises if the parameters of interest are nonlinear transforms of the moments used, since estimation errors can increase a lot in this transformation then. Nevertheless, moment type estimators are convenient for getting a first idea about suitable model orders and for initialization of more complex estimators like those discussed in the next section.

Here and in the following, we make use of popular \(\psi \)-functions as proposed by Huber and by Tukey. The Huber \(\psi \)-function compromises least squares and least absolute deviations,

$$\begin{aligned} \psi _c(x)= x \min \Big (1,\frac{c}{|x|}\Big ). \end{aligned}$$
(1)

Tukey’s biweight \(\psi \)-function is

$$\begin{aligned} \psi _{c}(x)=x\left( c^2-x^2\right) ^2 I_{[-c,c]}\left( x\right) , \end{aligned}$$
(2)

where \(I_A\) is the indicator function of a set A. The \(\psi \)-functions are applied to standardized values \((y-\mu )/\sigma \). The tuning constant c regulates the robustness and the efficiency of the estimators. For both these \(\psi \)-functions, larger values of c increase the efficiency but reduce the robustness to outliers. The Poisson and the negative binomial distributions do not form location-scale families and the tail behaviour depends on the parameters, so that suitable choices of the tuning constant in principle depend on the parameters.

For our calculations we need the formula for the conditional probabilities corresponding to the negative binomial distribution in terms of \(\mu _t\) and \(\kappa \), which is

$$\begin{aligned} P(Y_t=y_t|{\mathcal {F}}_{t-1})=\frac{\displaystyle \varGamma (y_t+1/\kappa )}{\displaystyle y_t!\ \varGamma (1/\kappa )}(\kappa \mu _t+1)^{-1/\kappa }\left( \frac{\displaystyle \kappa \mu _t}{\displaystyle \kappa \mu _t+1}\right) ^{y_t}, \; y_t\in \mathbb {N}_0. \end{aligned}$$

2.1 Conditions for mean and second-order stationarity

Many of [28] formulae simplify if the parametrization in terms of \(\kappa \) and the regression parameters \(\theta =(\alpha _0,\ldots ,\alpha _p)'\) for the conditional mean is used. The necessary and sufficient condition for the NBINARCH(p) model to be stationary in the mean stated in his Theorem 1 then becomes that all roots of the equation

$$\begin{aligned} 1-\sum _{i=1}^{p}\alpha _i z^{-1}=0 \end{aligned}$$

lie inside the unit circle. Under this assumption, the marginal mean is

$$\begin{aligned} \mu =E(Y_t)=\frac{\displaystyle \alpha _0}{\displaystyle 1-\sum _{i=1}^p\alpha _i}, \end{aligned}$$
(3)

as in the limiting conditional Poisson case. The additional condition for second-order stationarity is that all roots of \(1-C_1z^{-1}-\cdots -C_pz^{-p}=0\) lie inside the unit circle, where

$$\begin{aligned} C_u= & {} (1+\kappa )\left( \alpha _u^2-\alpha _u\sum _{v=1}^{p-1}\sum _{|i-j|=v}\alpha _i\alpha _jb_{vu}\right) ,\quad u=1,\ldots ,p-1,\\ C_p= & {} (1+\kappa )\alpha _p^2, \end{aligned}$$

with \(b_{vu}\) being the elements of the inverse of the matrix \((\beta _{vu})_{v,u=1}^{p-1}\), \(\beta _{vv}=\sum _{|i-v|=v}\alpha _i-1\) and \(\beta _{vu}=\sum _{|i-v|=u}\alpha _i\), \(v\ne u\). Like in the standard AR(p) model, the autocorrelation function \((\rho _Y(h), h\in \mathbb {N})\) then satisfies

$$\begin{aligned} \rho _Y(h)=\sum _{i=1}^p\alpha _i\rho _Y(|h-i|),\quad h\ge 1. \end{aligned}$$
(4)

The above conditions simplify if p is small. An NBINARCH(2) model is mean stationary iff \(\alpha _1+\alpha _2<1\), and it is second-order stationary iff additionally

$$\begin{aligned} (1+\kappa )\left[ \alpha _1^2+\alpha _2^2+\frac{\displaystyle 2\alpha _1^2\alpha _2}{\displaystyle 1-\alpha _2}\right] <1. \end{aligned}$$

The restrictions for \(\alpha _1\) and \(\alpha _2\) to achieve second-order stationarity are thus more stringent for larger values of \(\kappa \).

In the simplest interesting case, the second-order stationary NBINARCH(1)-model, the marginal mean, variance and the autocorrelations are

$$\begin{aligned} \mu= & {} E(Y_t)=\frac{\displaystyle \alpha _0}{\displaystyle 1-\alpha _1},\\ \sigma ^2= & {} Var(Y_t)=\frac{\displaystyle \mu +\kappa \mu ^2}{\displaystyle 1-\alpha _1^2(1+\kappa )},\\ \rho _Y(h)= & {} \alpha _1^{h-1},\quad h\ge 1. \end{aligned}$$

Note that the model is overdispersed in case of \(\alpha _1>0\), \(E(Y_t)<Var(Y_t)\), even if \(\kappa =0\), imposing a tendency to overestimate \(\kappa \) if autocorrelation is neglected.

2.2 Definition of the estimators

Zhu [28] studies Yule–Walker (YW) estimation of \(\alpha _1,\ldots ,\alpha _p\) based on the ordinary sample autocovariances in NBINARCH(p) models. He suggests combining them with a method of moments (MoM) estimator of \(\alpha _0\) based on the formula (3) for the marginal mean \(\mu \). A moment type estimator of \(\kappa \) [4, 8, 19] can be obtained solving

$$\begin{aligned} \frac{\displaystyle 1}{\displaystyle n-2p-1}\sum _{t=p+1}^n\left( \frac{\displaystyle y_t-\mu _t}{\displaystyle \sigma _t}\right) ^2=1, \end{aligned}$$
(5)

where \(p+1\) is the dimension of \(\theta \). Remember that \(\sigma _t^2=\mu _t+\kappa \mu _t^2\).

We can use the autocorrelation \((\rho _Y(h), h\in \mathbb {N})\) instead of the autocovariance function to write down the Yule–Walker estimators. We plug the sample autocorrelations \(\hat{\rho }_Y(1),\ldots ,\hat{\rho }_Y(p)\) into the equations (4) for \(\rho _Y(1)\),\(\ldots \),\(\rho _Y(p)\) and solve for the unknown parameters \(\alpha _1,\ldots ,\alpha _p\), imposing the basic positivity restriction. A suitable model order p can be identified from the partial autocorrelation function, as it is zero for all lags \(h>p\). The partial autocorrelations can be estimated from estimates of the ordinary autocorrelations using the Durbin-Levinson algorithm, setting negative estimates to 0 because of the positivity restrictions.

Fried et al. [15] find Spearman’s rank autocorrelation to work well in case of Poisson INARCH models, being rather efficient but more robust than the sample autocorrelations. We study YW estimation of NBINARCH models, applying Spearman’s rank correlation to all pairs \((Y_t,Y_{t-h})\), \(t=h+1,\ldots ,n\), for \(h=1,\ldots ,p\), and plugging the resulting autocorrelation estimates \(\hat{\rho }_R(h)\), \(h=1,\ldots ,p\), into (4).

Suitable score transforms can improve the asymptotical efficiencies of rank based autocorrelation estimators in case of autoregressive models with continuous innovation densities; see e.g. [16]. Let \(R_t\) be the rank of \(Y_t\) and J a score function, which is often chosen as the quantile function \(F^{-1}\) of a suitable distribution function F. Using this notation, the concept of empirical autocorrelation can be applied to the transformed ranks \(J(R_t/(n+1))\), \(t=1,\ldots ,n\). The negative binomial distribution functions \(F_{\mu ,\kappa }\) do not form a location-scale family and there is no linear relationship between the quantiles of different negative binomials. A suitable score function will thus depend on \(\mu \) and \(\kappa \), which will be unknown in practice. We investigate rank estimators with negative binomial (NB) scores, applying a stepwise approach: for initialization we calculate estimates \(\hat{\mu },\hat{\kappa }\) of the negative binomial parameters under the simplifying assumption of observing independent data. Then estimate \(\alpha _1,\ldots ,\alpha _p\) from ranks transformed by the quantile function \(J=F_{\hat{\mu },\hat{\kappa }}^{-1}\). Thereafter use these NB scores estimators to estimate \(\alpha _0\) and \(\kappa \) as described below. The process can be iterated using the new estimates of \(\mu \) and \(\kappa \) to improve on the estimates of \(\alpha _1,\ldots ,\alpha _p\).

A robust method of moments type estimator of \(\alpha _0\) can be derived by estimating the marginal mean \(\mu \) for a given value of \(\kappa \) modifying the Huber or the Tukey M-estimator for the Poisson distribution investigated by [5, 11], respectively. Setting \(\sigma ^2=\mu +\kappa \mu ^2\), we can solve

$$\begin{aligned} \frac{\displaystyle 1}{\displaystyle n}\sum _{t=1}^n\psi _c\left( \frac{\displaystyle y_t-\mu }{\displaystyle \sigma }\right) =a, \end{aligned}$$
(6)

where \(a=a(\mu ,\kappa )=E\psi _c\left( (Y_1-\mu )/\sigma \right) \) is a bias correction to achieve Fisher consistency. In our calculations, we fix the value of \(\kappa \) at an initial estimate and ignore the effects of the temporal dependence in this part of the algorithm for simplicity. Elsaied and Fried [11] suggest the tuning constants \(c=1.8\) for the Huber and \(c=5.5\) for the Tukey M-estimator in case of independent Poisson data. Since negative binomial distributions are more heavy-tailed than the Poisson, we choose larger tuning constants \(c\ge 2\) and \(c\ge 6\), respectively.

Moreover, we suggest a robustification of the moment type estimator of \(\kappa \) based on equation (5), applying a robust \(\psi \)-function and solving

$$\begin{aligned} \frac{\displaystyle 1}{\displaystyle n-2p-1}\sum _{t=p+1}^n\psi _c^2\left( \frac{\displaystyle y_t-\mu _t}{\displaystyle \sigma _t}\right) =d, \end{aligned}$$
(7)

where d is the expectation of the term on the left hand side. Since our interest in this equation is in a robust estimate of the amount of overdispersion \(\kappa \), a rather large tuning constant like \(c=10\) can be chosen for the Tukey \(\psi \)-function here to restrict the resulting negative bias, setting \(d(n,p)=1\), which is its limiting value as \(c\rightarrow \infty \).

We combine the ideas presented above as follows, initializing with an a-priori guess of \(\kappa \) (e.g. \(\kappa =0\)) and estimating \(\alpha _1,\ldots ,\alpha _p\) by plugging the first p Spearman rank autocorrelations into the YW equations. In steps 1 and 3 we use the R (R Core Team [21]) function optimise to minimize the squared difference between the terms on the left and the right hand side of the corresponding estimation equation.

  1. 0.

    Estimate \(\alpha _1,\ldots ,\alpha _p\) using the YW equations and the first p Spearman rank autocorrelations.

  2. 1.

    Estimate \(\mu \) from (6) using the current estimate of \(\kappa \).

  3. 2.

    Estimate \(\alpha _0\) from (3) using the current estimates of \(\mu \) and \(\alpha _1,\ldots ,\alpha _p\).

  4. 3.

    Estimate \(\kappa \) from (7) using the current estimate of \(\theta =(\alpha _0,\ldots ,\alpha _p)'\).

  5. 4.

    (Optional) Estimate \(\alpha _1,\ldots ,\alpha _p\) using the YW equations by plugging in the NB score transforms of the first p Spearman rank autocorrelations based on the current estimates of \(\mu \) and \(\kappa \).

Steps 1.–4. can be iterated until some convergence criterion is met. We found the changes of the parameter estimates to be very small after the second iteration. We call the estimator obtained after the first iteration the 1-step NB scores estimator.

The estimators of \(\mu \) and \(\kappa \) corresponding to (6) and (7), respectively, can be shown to be consistent at least for known values of the other parameters, using similar arguments as for the joint estimator of all model parameters presented in the next section. In the next subsection we will inspect the performance of the estimators presented here via simulations.

2.3 Simulations

We evaluate the performance of the estimators derived from methods of moments, applying them to time series of length \(n=200\) and \(n=500\) from several NBINARCH(1) and NBINARCH(2) models. We consider first order models with parameters

$$\begin{aligned} (\alpha _0,\alpha _1,\kappa )\in&\{(0.55,0.3,0.3), (0.55,0.7,0.0), (0.55,0.7,0.3), (0.55,0.7,0.7),&\\&(1.5,0.2,0.0), (1.5,0.8,0.2), (1.5,0.2,0.8), (1.5,0.6,0.8)\}.&\end{aligned}$$

The two models with \(\kappa =0\) correspond to Poisson INARCH models with low or high lag-one autocorrelation, \(\alpha _1=0.2\) or \(\alpha _1=0.7\). Two other models with \(\kappa \in \{0.2,0.3\}\) correspond to moderate deviations from the Poisson case, again one of them with low and one with high lag-one autocorrelation. Four other models with \(\kappa \in \{0.7,0.8\}\) correspond to substantial deviations from the Poisson case, two of them with low and two with high lag-one autocorrelation, combined with a small or a moderately large intercept \(\alpha _0\in \{0.55,1.5\}\). Varying these models, we also consider eight second order models with parameters \((\alpha _0,\alpha _1,\alpha _2,\kappa )\) in

$$\begin{aligned}&\{(0.55,0.7,0.2,0.0), (0.55, 0.7,0.1,0.3),(0.55, 0.6,0.1,0.7), (0.55,0.3,0.2,0.3),&\\&(1.5,0.0,0.2,0.0), (1.5,0.5,0.3,0.8), (1.5,0.7,0.1,0.2), (1.5,0.1,0.2,0.8)\}.&\end{aligned}$$

We consider time series of length \(n\in \{200,500\}\) and four different data scenarios for each of these models, namely clean time series without outliers, time series with 5% additive outliers of size either 4 marginal standard deviations or 8 marginal standard deviations, rounded to the nearest integer, at time points chosen independently from a uniform distribution, and time series with 5% additive outliers occurring as a block at the end of the time series. The latter scenario resembles the onset of a level shift.

For each of these 128 combinations of an NBINARCH model, an outlier scenario and a sample size, we generate 1000 time series and fit NBINARCH(2) models. From the derived estimates we calculate the empirical mean square errors (MSE) for the estimation of each of the parameters \(\alpha _0,\alpha _1,\alpha _2\) and \(\kappa \), and take the efficiency (as measured by the ratio of the MSEs) relatively to the estimator with the smallest MSE for the respective scenario among those considered here. Then we calculate summary measures like the average mean square error or the median relative efficiency of an estimator over sets of data scenarios.

Table 1 summarizes the simulation results for the estimation of \(\alpha _1\) and \(\alpha _2\) by showing the average root of the mean square error and the median relative efficiencies separately for the scenarios without outliers, with isolated additive outliers of size \(4\sigma \) or \(8\sigma \), or with a patch of outliers. We set the tuning constant of the Tukey score function to \(c=6\) if not stated otherwise. Results for \(c=7\) are quite similar and not shown here.

The YW estimators based on the ordinary sample autocorrelations offer little advantage as compared to the rank based estimators considered here in terms of efficiency in clean data scenarios, and they are usually inferior in the outlier scenarios. Transforming the ranks by the NB scores improves the efficiency of the rank based YW estimators in case of clean data, but reduces their robustness against outliers to some extent. Similarly, the 1-step NB scores estimator shows somewhat better efficiencies in case of clean data but somewhat larger MSE in case of outliers as compared to Spearman’s rank autocorrelation. This difference appears to be smaller for the larger sample size \(n=500\).

The significance of the coefficients of the sample partial autocorrelation function is commonly checked by comparing their absolute values to the 97.5% percentile of the standard normal distribution divided by the square root of the sample size. We apply this rule to the different estimators of \(\alpha _2\) and calculate the percentage of time series for which the estimate of \(\alpha _2\) is found to be significant separately for 1st and 2nd order models. This gives us an idea of the size and the power of such tests based on the different estimators, see Table 1. The rank based tests work similarly well as the one based on the ordinary sample autocorrelations in case of clean data and better in the presence of outliers. Spearman’s rank autocorrelation can be recommended as it works well in case of all outlier scenarios considered here if \(n=200\), and it shows the least size distortions in case of \(n=500\) with outliers.

Table 1 Results for Yule–Walker type estimators of \(\alpha _1\) and \(\alpha _2\) if \(n=200\) (left) or \(n=500\) (right): ordinary sample acf (SC), rank-based Spearman acf (RC), NB scores based on Tukey M-estimation of \((\mu ,\kappa )\) with tuning constant c (NB0\({}_c\)) and after 1 iteration (NB1\({}_c\))
Full size table

Table 2 shows the results for the estimation of \(\alpha _0\) and \(\kappa \). Combining the Tukey M-estimator of the marginal mean with Spearman’s rank autocorrelation leads to the most stable results for \(\alpha _0\) among the methods considered here, followed by the estimators based on the NB scores transformed ranks. Increasing the tuning constant to \(c=7\) (not shown here) improved the efficiency for \(\alpha _0\) in case of clean data and patchy outliers, but increased the MSE in case of isolated outliers. The iterated NB scores estimator gives the best results for the estimation of \(\kappa \). Starting the iterated estimator from Spearman’s rank autocorrelation (not shown here) leads to rather similar results.

These findings indicate that the partial autocorrelation estimates arising from Spearman’s rank autocorrelation can be used to get a first idea about a suitable NBINARCH model order p even in the presence of some outlier contamination. Simple yet quite robust estimates of the autoregressive parameters \(\alpha _1,\ldots ,\alpha _p\) can then be obtained by applying the Yule–Walker equations to the first p Spearman rank autocorrelations, and of \(\alpha _0\) by combining these estimates \(\hat{\alpha }_1,\ldots ,\hat{\alpha }_p\) with Tukey’s M-estimator of the marginal mean using a tuning constant \(c\ge 6\). Finally, estimate \(\kappa \) solving Eq. (7) using the estimates \(\hat{\mu }_t=\hat{\alpha }_0+\hat{\alpha }_1y_{t-1}+\cdots +\hat{\alpha }_py_{t-p}\) and \(\hat{\sigma }_t=\hat{\mu }_t+\kappa \hat{\mu }_t^2\).

Table 2 Results for method of moments type estimators of \(\alpha _0\) and \(\kappa \) if \(n=200\) (left) or \(n=500\) (right): ordinary moments and sample autocorrelations (MoM), Tukey M-estimator with Spearman acf (TR), Tukey M-estimator and NB scores estimation of \((\mu ,\kappa )\) with tuning constant c (NB0\({}_c\)) and after 1 iteration (NB1\({}_c\))
Full size table

3 Joint M-estimation

In Sect. 2 we have seen that rank based autocorrelation estimators perform similarly well as ordinary sample autocorrelations in terms of efficiency in NBINARCH models, while being more robust. Now we investigate whether the efficiency and robustness of these simple estimators can be improved further if we robustify the conditional maximum likelihood estimators for a given model order p. We expect substantial improvements in particular concerning the estimation of \(\alpha _0\), as the simple method of moment type estimator \(\hat{\mu }/(1-\hat{\alpha }_1-\cdots -\hat{\alpha }_p)\) suffers from the non-linear effects of estimation errors in \(\hat{\alpha }_1,\ldots ,\hat{\alpha }_p\), especially if the sum of these parameters is close to 1. This can possibly be improved by joint estimation of \(\alpha _0,\alpha _1,\ldots ,\alpha _p\) as considered in the following but for the price of larger computational costs. We focus on first order models for the reason of simplicity. After reviewing conditional maximum likelihood estimation we summarize the estimation approach of [27], before explaining ours. Then we compare the estimators in a simulation study, including also some of the estimators which showed the best performance in Sect. 2.

3.1 Conditional maximum likelihood estimation

The score equations of the conditional maximum likelihood estimator (CMLE) for the parameter vector \(\omega =(\theta ',\kappa )'\), with \(\theta =(\alpha _0,\ldots ,\alpha _p)'\), are

$$\begin{aligned} \frac{\displaystyle \partial \ell (\omega )}{\displaystyle \partial \omega }= & {} \left( \sum _{t=1}^nS_{t,\theta }'(\omega ),\sum _{t=1}^nS_{t,\kappa }(\omega )\right) '=0, \text{ where }\\ S_{t,\theta }(\omega )= & {} \frac{\displaystyle y_t-\mu _t}{\displaystyle \mu _t+\kappa \mu _t^2}\frac{\displaystyle \partial \mu _t}{\displaystyle \partial \theta },\\ S_{t,\kappa }(\omega )= & {} -\kappa ^{-2}\left( \frac{\displaystyle \partial \ln \varGamma (y_t+1/\kappa )}{\displaystyle \partial (y_t+1/\kappa ) }- \frac{\displaystyle \partial \ln \varGamma (1/\kappa )}{\displaystyle \partial \kappa }-\ln (\kappa \mu _t+1)-\frac{\displaystyle \kappa (y_t-\mu _t)}{\displaystyle \kappa \mu _t+1}\right) \\= & {} -\frac{\displaystyle 1}{\displaystyle \kappa ^2}\left( G(y_t+1/\kappa )-G(1/\kappa )-\ln (\kappa \mu _t+1)-\frac{\displaystyle \kappa (y_t-\mu _t)}{\displaystyle \kappa \mu _t+1}\right) ,\\ \frac{\displaystyle \partial \mu _t}{\displaystyle \partial \theta }= & {} \left( 1,y_{t-1},\ldots ,y_{t-p}\right) '=\tilde{X}_t. \end{aligned}$$

Hereby, G(u) denotes the digamma function, \(G(u)=\partial \ln \varGamma (u)/\partial u\). Solving the score equations can be initialized using the Poisson quasi-likelihood estimator of \(\theta \), which corresponds to the assumption \(\kappa =0\), and the moment estimator of \(\kappa \) defined in (5).

3.2 M-estimation using multivariate outlyingness

Xiong and Zhu [27] robustify the first of the above score equations of the CML estimator using the Pearson residuals \(r_t=(y_t-\mu _t)/\sigma _t\) and Mallow’s quasi-likelihood estimator proposed by Cantoni and Ronchetti (2001),

$$\begin{aligned} \sum _{t=p+1}^n\left[ \frac{\displaystyle \psi (r_t)w_t}{\displaystyle \sigma _t}\frac{\displaystyle \partial \mu _t}{\displaystyle \partial \theta }-a_t(\theta )\right] =0, \end{aligned}$$

where \(a_t(\theta )=E\left[ \psi (r_t)w_t(\sigma _t)^{-1}\partial \mu _t/\partial \theta \right| {\mathcal {F}}_{t-1}]\) is a bias correction to achieve Fisher consistency. They consider weights \(w_t=\sqrt{1-h_{t,t}}\) based on the diagonal elements \(h_{t,t}\) of the hat matrix \(H=X(X'X)^{-1}X'\), with \(X=(\tilde{X}_1,\ldots ,\tilde{X}_{n-p})'\), as well as hard rejection weights \(w_t=I(D_t^2\le \chi _p^2(0.95))\) based on the squared Mahalanobis distances \(D_t^2\) measuring multivariate outlyingness.

For estimation of \(\kappa \), they suggest the weighted maximum likelihood estimator proposed by [1], using the estimation equation

$$\begin{aligned} 0=\sum _{t=p+1}^n\left[ \frac{\displaystyle \psi (r_t)}{\displaystyle r_t}S_{t,\kappa }(\omega ) w_t-b_t(\kappa )\right] \end{aligned}$$

with another Fisher consistency correction \(b_t(\kappa )=E(S_{t,\kappa } w_t\psi (r_t)/r_t|{\mathcal {F}}_{t-1})\).

Xiong and Zhu [27] perform a simulation study for time series consisting of \(n=1000\) observations without, or with up to 40 isolated, or a patch of 52 subsequent outliers. Based on this they recommend hard rejection weights using the minimum covariance determinant (MCD) estimator [25] in combination with Tukey’s \(\psi \)-function for both, the estimation of \(\theta \) and \(\kappa \), using constants \(c_1=7\) and \(c_2=6\), respectively.

Using multivariate outlyingness allows taking positive correlations among the regressors into account, but it may downweight the contribution of many observations substantially although just one of its regressor components looks suspicious; see the R-package cellWise [22], and the references cited therein for related discussions. Moreover, the MCD has been designed for (continuous) unimodal elliptically symmetric but not for discrete data, see e.g. [17]. Indeed, methods based on subsets of the observations like the MCD may have problems with many identical values, as they can occur in count data; see Duerre et al. (2015) for a discussion in the context of robust autocorrelation estimation. These are possible drawbacks of the method by Xiong and Zhu.

3.3 M-estimation using componentwise shrinking

We propose another variant of robust M-estimation for NBINARCH(p) models, combining the M-estimation approaches developed by [10] for the limiting Poisson INARCH model and by [1] for the negative binomial regression model.

We robustify the CML estimator along the same lines as in [10] in the Poisson case, applying M-estimation to the Pearson residuals \(r_t=(y_t-\mu _t)/\sigma _t\),

$$\begin{aligned} \sum _{t=p+1}^ns_{t,0}(y_t,\omega )= \sum _{t=p+1}^n\left( \frac{\displaystyle \psi \left( r_t\right) }{\displaystyle \sigma _t}-c_{t,0}\right)= & {} 0,\\ \sum _{t=p+1}^ns_{t,i}(y_t,\omega )= \sum _{t=p+1}^n\left( \frac{\displaystyle \psi \left( r_t\right) }{\displaystyle \sigma _t}\left[ \sigma \psi \left( \frac{\displaystyle y_{t-i}-\mu }{\displaystyle \sigma }\right) +\mu \right] -c_{t,i}\right)= & {} 0,\quad i=1,\ldots ,p. \end{aligned}$$

Hereby, we use bias corrections \(c_{t,0}=c_{t,0}(\omega )=E_\omega (\psi ((Y_t-\mu _t)/\sigma _t)/\sigma _t|{\mathcal {F}}_{t-1})\) and \(c_{t,i}=c_{t,i}(\omega )=E_\omega \left( \psi ((Y_t-\mu _t)/\sigma _t)\left[ \sigma \psi \left( \frac{\displaystyle Y_{t-i}-\mu }{\displaystyle \sigma }\right) +\mu \right] /\sigma _t\big |{\mathcal {F}}_{t-1}\right) \), \(i=1,\ldots ,p\). While [27] downweight the whole vector \(S_{t,\theta }(\omega )\) in the score equation according to a measure of the multivariate outlyingness of the corresponding regressor values, including the component for the intercept, we shrink each regressor towards the center of its distribution. Note that replacing \(c_{t,i}(\omega )\) by its expectation \(c_{i}(\omega )=E(c_{t,i}(\omega ))\) is simpler and asymptotically equivalent because of the general ergodic theorem [18] and Slutsky’s Lemma.

For estimation of \(\kappa \) we also make use of the M-estimator of [1]. To obtain starting values for an iterative scheme to solve these equations, [1] recommend plugging in the estimates resulting from Poisson M-estimation into the equation for \(\kappa \) and then to iterate. Alternatively, we can use the estimator of \(\kappa \) proposed in the previous section.

In the Appendix we prove the consistency of the joint estimator \(\hat{\omega }_n=(\hat{\theta }_n',\hat{\kappa }_n)'\) and conjecture its asymptotic normality,

$$\begin{aligned} \sqrt{n}(\hat{\omega }_n-\omega ^{(0)})\rightarrow N\left( 0,A(\omega ^{(0)})^{-1}B(\omega ^{(0)})A(\omega ^{(0)})^{-1}\right) , \end{aligned}$$

with \(A(\omega ^{(0)})=E(\partial s_t(Y_t,\omega )/\partial \omega )_{\omega ^{(0)}}\), \(B(\omega ^{(0)})= E(s_t(Y_t,\omega ^{(0)})\times s_t(Y_t,\omega ^{(0)})')\), \(s_{t}(y_t,\omega )=(s_{t,0}(y_t,\omega ),\ldots ,s_{t,p}(y_t,\omega ))'\), and \(\omega ^{(0)}=(\theta ^{(0)}{}',\kappa ^{(0)})'\) being the true parameter vector. The matrices \(A(\omega ^{(0)})\) and \(B(\omega ^{(0)})\) can be estimated using their empirical counterparts as in [10], replacing the unknown parameters by their robust estimations and the expectations by the corresponding averages across the realizations; the arising estimate inherits some robustness when using a bounded \(\psi \)-function with a bounded derivative.

3.4 Simulations

We perform some simulations to compare the performance of the CML estimator, the robust method of moments estimator based on Spearman’s rank autocorrelation combined with the Tukey M-estimator of the marginal mean, the 1-step NB scores transformed rank estimator, as well as our Tukey M-estimator and [27] M-estimators using the hat matrix or the MCD. We consider the performance in scenarios without outliers as well as with an increasing number of isolated or patchy additive outliers with the same size. We focus on scenarios similar to those inspected by [27] with time series of length \(n=1000\). This is in part due to problems when running their algorithms with the recommended MCD for shorter series lengths n, presumably caused by the discreteness of the data. We applied several estimators for initialization of our joint M-estimator, namely the estimators presented in Sect. 2, in particular that using the ordinary Spearman rank autocorrelations, and the robust Poisson INARCH estimator of [10] assuming \(\kappa =0\). We can combine these possibilities to check for the possibility of multiple roots. The solutions obtained by the different initializations in the following simulations can usually be regarded as identical.

3.4.1 Scenarios without outliers

First we inspect the efficiency in case of data without outliers, generating 1000 time series of length \(n=1000\) from an NBINARCH(1) model with parameter \(\omega =(0.55,0.4, 0.3)\), see Fig. 1. The initial method of moments estimators achieve about 50% efficiency for \(\alpha _1\) and about 30% efficiency for \(\alpha _0\). The 1-step NB scores rank estimator improves on this as its efficiencies are about 90% for \(\alpha _1\) and 60% for \(\alpha _0\). The estimator of [27] with a recommended tuning constant c about 6 or 7 achieves an efficiency of more than 70% using hard rejection based on the MCD and even about 80% efficiency when using soft rejection based on the hat matrix. Our estimator shows a stronger dependence on c. It achieves high efficiencies of about 90% when using \(c=10\), like Xiong and Zhu’s method, while for \(c=7\) it is somewhat less efficient than their estimator.

Fig. 1
figure 1

Simulated efficiencies for \(\alpha _0\) (left) and \(\alpha _1\) (right) as a function of the tuning constant in case of \(n=1000\) data points from an NBINARCH(1) process with parameters \(\alpha _0=0.55\), \(\alpha _1=0.4\) and \(\kappa =0.3\)

Full size image

Figure 2 compares normal qq-plots of our joint M-estimator with \(c=10\) and of the conditional maximum likelihood estimator in case of time series of length \(n=200\), \(n=500\) or \(n=1000\). The finite-sample distributions of both estimators are right-skewed for \(\alpha _0\) if \(n=200\) but reasonably close to normality for the larger sample sizes, with little difference between the estimators.

Fig. 2
figure 2

Normal qq-plots for the CML (upper panel) and our joint Tukey M-estimator (lower panel) of \(\alpha _0\) (top) and \(\alpha _1\) (bottom) in case of \(n=200\) (left), \(n=500\) (middle) or \(n=1000\) (right) data points from an NBINARCH(1) process with parameters \(\alpha _0=0.55\), \(\alpha _1=0.4\) and \(\kappa =0.3\)

Full size image

3.4.2 Scenarios with an increasing number of isolated outliers

Now we analyze the behavior of the estimators in the presence of outliers. In a first experiment we generate a time series of length \(n=300\) from an NBINARCH(1) model with parameters \(\alpha _0=0.55\), \(\alpha _1=0.4\) and \(\kappa =0.3\) and include a single additive outlier of increasing size. Figure 3 shows the arising sensitivity curves of several estimators for estimation of \(\alpha _0\) and \(\alpha _1\), corresponding to the difference between the estimated value with and without this outlier, multiplied by n. Except for the CMLE, the other estimators show bounded sensitivities, with the effects being largest for the 1-step NB score estimator, followed by our joint M-estimator.

Fig. 3
figure 3

Sensitivities of the estimators of \(\alpha _0\) (left) and \(\alpha _1\) (right) against a single additive outlier of increasing size in case of data generated from an NBINARCH(1) process with parameters \(\alpha _0=0.55\), \(\alpha _1=0.4\) and \(\kappa =0.3\)

Full size image

Next we include an increasing number of 4,8,...,40 isolated additive outliers of size 5 or 10 at positions chosen at random, analyzing 500 time series for each scenario. Figure 4 depicts the resulting biases as a function of the number of outliers. The lack of robustness of the CMLE and the Poisson quasi-likelihood estimator manifests itself in an increasingly large positive (negative) bias for \(\alpha _0\) (\(\alpha _1\)), particularly for the larger outlier size. Spearman’s rank autocorrelation is negatively biased for \(\alpha _1\), and the resulting estimator for \(\alpha _0\) thus positively biased, which explains its moderately large efficiency for large sample sizes observed before. The 1-step NBscore transform estimator reduces this bias in case of clean data but is more affected by the outliers. Our Tukey M-estimator shows some bias for the estimation of \(\alpha _1\) in case of the smaller outlier size considered here, but performs better than the other estimators otherwise, except for M-estimator with hard-thresholding based on the MCD  [27]. These two estimators perform similarly well although we have chosen a larger tuning constant \(c=10\) for our estimator to obtain a high efficiency in case of clean data, instead of the \(c=6\) recommended by Xiong and Zhu for their estimator. Qualitatively similar results have been obtained for time series with parameters \(\alpha _0=1\), \(\alpha _1=0.6\) and \(\kappa =0.3\) (not shown here).

Fig. 4
figure 4

Simulated biases for \(\alpha _0\) (left) and \(\alpha _1\) (right) in case of an increasing number of 4,8,...,20,24,...,36,40 isolated additive outliers of size 5 (top) or 10 (bottom) at randomly chosen positions in time series of length \(n=1000\) generated from an NBINARCH(1) process with parameters \(\alpha _0=0.55\), \(\alpha _1=0.4\) and \(\kappa =0.3\)

Full size image

3.5 Scenarios with a patch of additive outliers

We also investigate scenarios with a patch of consecutive additive outliers of the same size, which can arise for instance because of a temporary disturbance or a temporary level shift. Figure 5 depicts the results obtained for an increasing number of 4, 8, ..., 52 additive outliers of identical size 5 or 10 starting at time point 250 in NBINARCH(1) time series with parameters \(\alpha _0=0.55\), \(\alpha _1=0.4\), \(\kappa =0.3\). A patch of consecutive outliers imposes a positive bias on non-robust estimators of \(\alpha _1\), which can then lead to a negative bias for the estimation of \(\alpha _0\). This can be seen for the 1-step NB scores rank estimator, which shows a similarly strong bias for \(\alpha _1\) as the QMLE and the CML here. Estimation using Spearman’s rank autocorrelation performs better than this in terms of bias and similar to our Tukey M-estimator with a tuning constant \(c=10\), which is large relatively to the height of the shift. Application of the latter with a smaller tuning constant \(c=6\) resists these outliers better and similarly well as the M-estimator with hard rejection proposed by [27] in the scenarios considered here. The version of their estimator applying soft-thresholding based on the hat matrix shows considerable problems for the estimation of the intercept here, and this also applies to the version using the MCD in case of the smaller outlier size.

Fig. 5
figure 5

Simulated biases for \(\alpha _0\) (left) and \(\alpha _1\) (right) in case of an outlier patch consisting of an increasing number of 4,8,...,52 additive outliers of size 5 (top) or 10 (bottom) in time series of length \(n=1000\) generated from an NBINARCH(1) process with parameters \(\alpha _0=0.55\), \(\alpha _1=0.4\) and \(\kappa =0.3\) (top) or \(\alpha _0=1\), \(\alpha _1=0.6\) and \(\kappa =0.3\) (bottom)

Full size image

4 Data example

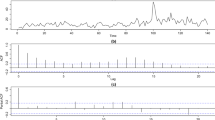
For illustration we analyze the number of campylobacterosis infections from January 1990 to the end of October 2000 in the north of the Province of Québek, Canada. There is one observation every 4 weeks, that is 13 observations per year. [12] used this data set shown in Fig. 6 to exemplify the INGARCH model with a conditional Poisson distribution. Under the same basic model assumption, [13] found a possible level shift at time \(t=84\) and a so-called spiky outlier at time \(t=100\) by applying an iterative procedure for the detection and elimination of different types of intervention effects. Later on, [20] found evidence that the conditional distribution might be better described by a negative binomial than by a Poisson distribution, albeit their estimate of the overdispersion parameter was small (\(\hat{\kappa }\approx 0.0297\)). In consequence, the findings of [13] might have been influenced by using the wrong conditional distribution, and in turn the findings of [20] might be in part due to extraordinary effects in these data, which might have been estimated incorrectly or even been missed. We re-analyze these data using robust methods to get additional insights. Further work is needed to include structural changes or covariate information into the methods presented in Sect. 3. We instead concentrate on the methods presented in Sect. 2.2 as they can be modified easily to account for a level shift:

Fig. 6
figure 6

Number of campylobacterosis infections (dots), conditional mean fitted by robustified method of moments (bold solid line), and 95% as well as 99% percentiles of the conditional negative binomial distributions (solid line and dashed line)

Full size image
  1. 1.

    First we want to get an idea about suitable model orders, taking a possible level shift after observation number \(t=84\) into account, i.e., in the middle of the seventh year of the observation period. For this we calculate Spearman’s rank autocorrelation and also the ordinary sample autocorrelation from the first six years of data. Both types of autocorrelation point at the suitability of an INARCH(1) model without a seasonal effect, with the estimates of \(\alpha _1\) being about 0.44 and thus substantially larger than their asymptotical standard error under the assumption of white noise, which is about 0.11. Calculating the ordinary sample autocorrelation at lag 1 or the conditional maximum likelihood estimate of \(\alpha _1\) from the full data set leads to a much larger value than this, namely about 0.64, which is just within the range of a 95% confidence interval based on the first six years.

  2. 2.

    Second we fit an INARCH(1) model with a level shift after \(t=84\) to the data, i.e., we allow for a change of the intercept \(\alpha _0\). In order to make use of the full data set in spite of a possible level shift, we split the time series into several non-overlapping subsequences and estimate the parameters of interest from each of them separately. This approach has been analysed by [23] for estimation of the Hurst parameter and by [3] for estimation of the variance. Here, we split the time series into five subsequences of length 28 each, which fits well to the total sample size of 140 and also to a possible level shift right at the end of the third subsequence. Due to the robustness properties of ranks we expect the effect of a single spiky outlier on the estimate to be small and take the average of the estimates obtained from the five subsequences as our final estimate. The average lag one Spearman rank autocorrelation is \(\hat{\alpha }_1=0.368\), which is again large as compared to the asymptotic standard error 0.085 under white noise and very close to the value 0.369 obtained by [20] using an iterative procedure for detecting and modelling different types of intervention effects. The robust Tukey type method of moments estimate of \(\alpha _0\) derived from the first three subsequences is 5.27, and the estimate of the change in intercept because of a level shift, derived from the difference with the estimate calculated from the fourth and fifth subsequence, is 4.20. A parametric bootstrap confidence interval for the height of the shift is [3.04, 6.69].

  3. 3.

    It remains to estimate \(\kappa \), taking the conditional mean function \(\mu _t=5.27+4.20I(t>84)+0.368y_{t-1}\) derived in step 2 into account. The robustified method of moments type estimate with the tuning constant \(c=10\) is \(\tilde{\kappa }=0.0179\). Application of a parametric bootstrap, generating 200 time series from a Poisson INARCH model with the same conditional mean function, leads to a bootstrap p-value of 0.01, so that this estimate is small but significantly different from 0. In another parametric bootstrap we generate 1000 time series for each of several INARCH(1) models, all with the conditional mean function estimated for the real data but different values of \(\kappa =0.001,\ldots ,0.1\). In a bootstrap confidence interval we include all values of \(\kappa \) for which the estimate \(\tilde{\kappa }=0.0179\) lies between the 2.5% and the 97.5% percentile of the estimates obtained from the corresponding simulated data sets, resulting in the interval [0.006, 0.093]. For a larger tuning constant \(c=12\) we get a larger estimate \(\tilde{\kappa }=0.0303\), which is very close to the estimate 0.0297 obtained by [20] applying a sequential outlier detection and modelling procedure.

    Our robust method of moment type estimator \(\tilde{\kappa }\) of \(\kappa \) is obviously biased, with a bias which is larger for smaller tuning constants c. The smaller estimate obtained for \(c=10\) might thus be due to a negative bias, but the difference to the less robust estimates could also be due to outlier effects. To correct the bias of \(\tilde{\kappa }\) we can multiply it with a correction factor \(f_c(\theta ,\kappa )\), which will likely depend on the true parameters \(\theta =(\alpha _0,\alpha _1)\) and \(\kappa \) as well. To derive suitable finite sample correction factors we generate 1000 NBINARCH(1) time series with the same length \(n=140\), the same parameters and the same level shift as found for the real data, and estimate the value of \(\kappa \) for each of them. Then we set \(f_c(\tilde{\theta },\tilde{\kappa })\) to the ratio between the value of \(\kappa \), from which these artificial data sets have been generated, and the average of these estimates. Multiplication of \(\tilde{\kappa }\) with this factor gives a new bias-reduced estimate. Since \(f_c(\tilde{\theta },\tilde{\kappa })\) only approximates the factor \(f_c({\theta },{\kappa })\) needed, we can iterate this process until it stabilizes after a few steps. This leads us to an estimate of about 0.04, a little larger than those reported before but well within the bootstrap CI.

Overall our analysis confirms that a NBINGARCH model describes this data set well after taking a possible level shift at observation 84 and an outlier at time 100 into account. Figure 6 illustrates that all observations except for a few ones at or right after time point 100 are below or at least close to the respective 95% percentile of the fitted 1-step ahead predictive distribution. The observations at \(t=100\) and \(t= 101\) are far outlying as compared even to the 99% percentile. Note that the differences between these percentiles and those obtained by a Poisson INARCH(1) model with the same conditional mean sequence is at most 2 in case of the 95% and at most 3 in case of the 99% percentile, so that a Poisson model suits most purposes here.

5 Conclusions

We have proposed robustifications of method of moments and ML-estimation for fitting INARCH models with conditional negative binomial distributions. The former avoid multidimensional optimizations and are useful for getting information about a suitable model and as initial estimates for calculation of the more efficient and robust joint M-estimators of the autoregressive parameters.

Our proposal of negative binomial scores increases the efficiency of rank based autocorrelation and partial autocorrelation estimators in the NBINARCH model substantially but reduces its robustness. Similar findings are known for van der Waerden scores under Gaussian model assumptions. If robustness against outliers is important, we prefer the ordinary Spearman’s rank (partial) autocorrelation. Our joint M-estimation approach is an alternative to the one suggested by [27]. Our method seems to be computationally simpler, so that it can be applied to moderately large data sets, where we encountered problems for the Xiong and Zhu’s algorithm. A drawback of our approach is that the choice of tuning constants to achieve both high efficiency and high robustness against different outlier scenarios (like isolated and patchy outliers) seems to be more difficult. Nevertheless, in our experiments it achieves better efficiency and robustness than the Yule–Walker estimates based on Spearman’s rank autocorrelation if the model order is known.

For illustration we have analyzed a famous data set from the literature, the campylobacterosis data studied e.g. by [12]. In doing so we have modified the robust method of moment estimators such that patterns of change like a level shift found in these data by several authors (e.g. [13]) can be incorporated in the estimation. The results obtained agree well with those obtained by [20] applying sophisticated stepwise detection and correction procedures.