Abstract
Numerous methods exist for solving the Lambert problem, the two-point boundary value problem (BVP) governed by two-body dynamics. Many applications would benefit from a solution to a perturbed Lambert problem; a few studies have attempted to solve one. Establishing a larger pool of alternative solution methods gives practitioners greater latitude in choosing the solution that best suits their needs. To that end, a novel Lambert-type BVP is constructed in this work that includes oblateness by way of Vinti’s potential, rendering the problem mathematically unperturbed. This BVP is first defined and then converted to a system of equations that is amenable to an iterative solution. The formulation, which is valid for both the zero- and multiple-revolution problems, couples oblate spheroidal (OS) universal variables and OS equinoctial orbital elements together to sow robustness across all orbital regimes, only excepting orbits that are sufficiently rectilinear. For the first time, the solution space is broadly explored, exposing multiple new insights of significant practical use. Initial guess and root-solve techniques are offered to solve the system of equations. When assessed at Earth for robustness, accuracy, and computational efficiency, the zero-revolution algorithm excels across all three performance metrics, with runtimes averaging only about 15 times slower than a typical two-body Lambert solver. The multiple-revolution algorithm, while not yet evaluated as extensively, also exhibits high levels of performance, the formulation generally characterizing the existence of solutions around oblate bodies more accurately than its Keplerian counterpart.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
After more than 200 years of study, the Lambert problem, a gravitational two-body boundary value problem (BVP), is considered one of the most fundamental and well understood problems of astrodynamics [1, 2]. Each solution draws a ballistic arc between two given terminal positions for a specified time of flight (TOF), and each arc traces the path of a conic. The Lambert problem is a two-point BVP, and while it is limited in the fidelity of the gravitational model, it still enjoys broad use across the entire discipline. For example, preliminary orbit determination (OD) and uncorrelated track (UCT) association support critical tasks tied to the maintenance of the space object catalog and the space situational awareness (SSA) mission [3, 4]. Preliminary OD also supports satellite operators wishing to initiate a track of their satellite. Other applications include guidance, targeting, rendezvous, and maneuver planning efforts that are essential to the design of Earth and interplanetary missions. Practicing astrodynamicists benefit from publicly available source code that solves the Lambert problem, including Gooding’s benchmark [5] Fortran implementation, as well as recent ones like that proposed by Izzo [6] or Russell [7], wherein seminal and competitive Lambert solution methods are also reviewed.
For decades, practitioners have been able to get by with the level of fidelity included in a traditional Lambert solver, but these solvers are nonetheless rendered less effective for some important applications. For example, consider the demands of active space debris removal (ASDR), which was studied by Cerf [8]. This type of mission would typically be solved as a long-duration, multi-leg mission, often requiring a spacecraft to make many revolutions (revs) around the Earth. In ASDR, a spacecraft may need to rendezvous with many pieces of debris over the course of 100s of revolutions, where the unknown sequence of encounters is optimized. Under the hood, each rendezvous in turn requires the design of spacecraft maneuvers in the form of a guess, usually furnished by a Lambert solver. While the Lambert solver offers a good approximation for short orbit transfers and certain Earth-centered problems, over many revolutions, the effects of dynamical forces that are typically neglected accumulate, giving rise to large errors in a Lambert solution that subsequently stress or even break the optimizer. A rendezvous sequence generated from a standard Lambert algorithm can completely fall apart under the real dynamics, raising questions on how these issues can be mitigated.
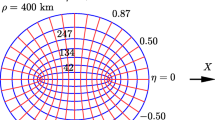
Different strategies exist for addressing the described drawbacks that can be encountered with traditional Lambert solvers. Some may seek alternative optimizers that are less sensitive to the quality of a guess, but other strategies aim to lift the burden off the optimizer and place it squarely on the Lambert solver itself, i.e. improving the guess passed on to the optimizer without changing the optimization algorithm. The present work investigates the latter option, though it is generally worth considering both approaches since these architectures can fall in completely different regions on the speed versus robustness trade space. Computational speed and robustness are important because a Lambert solver may be called a billion times for one study. With typical Lambert runtimes around a microsecond, a billion calls could take about 20 minutes, and a 0.1% fail rate would lead to a million failures [7]. Beginning with the early work of Andrus [9] and Engels and Junkins [10], the literature shows considerable interest in recent years in improving Lambert guesses [11,12,13,14,15,16], pursuing solutions to perturbed Lambert problems that include other phenomena in the BVP dynamics. The unperturbed Lambert problem is considered to be quite challenging, and the level of difficulty in solving the problem only increases with the addition of perturbations. For this reason, it is common to limit the fidelity to include only the most dominant perturbation [11, 10], which for the Earth and many bodies is due to oblateness or the \(J_2\) spherical harmonic coefficient. Figure 1 gives a notional illustration of the ballistic arc connecting two terminal positions over many revolutions when the object is influenced by a large equatorial bulge. Instead of tracing out an ellipse in a fixed orbital plane over multiple revolutions, the object’s path is characterized by a distinct drift of the orbital plane. A few studies have looked at including additional perturbations [12,13,14,15,16], but they all use a classical, unperturbed Lambert solver to warm start their perturbed Lambert algorithms.
The perturbed Lambert problem can be solved in a number of ways. A straightforward approach may use a shooting method (SM) to differentially correct the unperturbed Lambert solution to target the desired final position. Shooting methods commonly use numerical integration in the trajectory propagation step, though advanced implementations leverage the speed of analytical propagators [12, 17] and, with additional effort, an associated analytical state transition matrix (STM) [17], where the propagator and STM employed in the shooting method for these two studies are based on Vinti’s asymmetric gravitational potential [18]. Whether these shooting method components are computed numerically or analytically, the approach is still limited by the number of spacecraft revolutions undertaken in transit and can fail to converge when the number of revolutions is too high, numerical integration posing the additional disadvantage that the runtime increases with the number of revs. A multiple shooting method [17], which breaks long arcs into shorter ones, can remove this limitation, but trade-offs can be expected between computational speed and robustness, and also the difficulty of implementation. A single shooting method can be combined with a continuation method that nudges \(J_2\) from zero (unperturbed) up to \(1.08 \times 10^{-3}\) (Earth-perturbed) to help circumvent the limitations on the number of spacecraft revolutions [11], but again, similar trade-offs persist. With these ideas in mind, the development of techniques to solve perturbed Lambert problems continues to be a major challenge and an active area of research.
The present study takes a markedly different approach to solving the \(J_2\)-perturbed Lambert problem. Instead of leveraging the two-body Lambert solution and adding perturbations on top of it, the symmetric Vinti potential [18,19,20] is used to define a novel unperturbed BVP that already includes the effects due to \(J_2\) and a partial \(J_4\). This approach is inspired by the historically significant utility of exactly solvable problems, which typically betray a special structure or symmetry that can be exploited for gains in computational efficiency [21]. Since the present problem is unperturbed, a solution may be developed without recourse to a shooting or other perturbation method, therefore holding promise for significant speedups in runtime, possibly with a more favorable trade in robustness than seen for other methods. A problem formulation and solution is sought and developed that is broadly applicable, not limited by the orbital regime or number of spacecraft revolutions. To achieve this goal, the study is broken down into two parts: the first part defines and sets up the BVP to be solved; the second part presents a specific method of solving the BVP and includes descriptions of the solution space and various performance results and examples. These ideas borrow heavily from universal Vinti orbit propagation methods concurrently developed by the author [22], solving the initial value problem (IVP) governed by Vinti’s symmetric potential. This approach establishes techniques required to avoid computational difficulties commonly encountered in orbital mechanics and conveniently unifies solutions for bounded (elliptical) and unbounded (hyperbolic) Vinti trajectories. The analytical propagator developed by Biria [22] is notably validated against numerically integrated solutions to lend confidence to the correctness of the dynamics modeled in the BVP. Note that various solution methods packaged with publicly available source code exist for the Vinti IVP [18, 23,24,25,26].
A Lambert solution method presented in Bate et al. [1], notable for its robustness and applicability across all orbital regimes, uses universal variables (UVs) similar to those used by the author to solve Vinti’s IVP [22]. Therefore, much of the implementation of the author’s UV Vinti solution may be directly reused in a congruent BVP solver if an approach is chosen that is similar to the one in Bate et al. [1]. This choice allows the new BVP solver to inherit all of the benefits of the author’s Vinti IVP formulation. Battin [27] notes that this particular unperturbed Lambert solution method was proposed by John Deyst of the MIT Instrumentation Laboratory, presumably in the early 1960s. The solution method of the current investigation essentially augments Deyst’s algorithm to accommodate \(J_2\) effects. Deyst’s approach requires a root-solve of a certain system of equations. A main result of this paper is the conversion of the proposed BVP into a specific system of equations that aligns with those that Deyst identified for the two-body BVP. Then, a method is offered for iteratively solving this system of equations. Comparisons are made to the two-body BVP to illustrate the different ways that oblateness changes the solution space. Practitioners can benefit from this additional insight. Performance is also assessed through a number of examples, and strengths and pitfalls are identified.
For improved readability, an outline of the paper structure is offered before moving on. First, in Sect. 2, the kinematic equations developed in prior work are reviewed and all quantities are defined. The next three sections respectively address the formulation, exploration, and solution of the BVP. Specifically, a novel formulation of a Lambert-type BVP under Vinti’s potential is derived in Sect. 3, the BVP solution space is explored in Sect. 4, and a solution method for this BVP is proposed and evaluated in Sect. 5. Concluding remarks are offered in Sect. 6.
2 Review of Kinematic Equations
Recall Vinti’s symmetric gravitational potential [19, 20] expressed in terms of oblate spheroidal (OS) coordinates \(\rho ,\phi ,\eta \) as
where \(\mu \) is the gravitational parameter of the primary body, \(\rho \) is the semiminor axis of the instantaneous oblate spheroid that intersects the spacecraft, \(\phi \) is the right ascension, and \(\eta \) is tied to latitude, approximately the sine of the declination in an Earth application. A free parameter c is fit to the oblateness coefficient, \(J_2\), of the spherical harmonic expansion as \(c^2 = R_e^2 J_2\), where \(R_e\) is the equatorial radius. Refer to Vinti [19, 20] for formal definitions of these quantities. The analytical solution to Vinti’s integrable IVP can be stated classically as \(\textbf{x}= {\tilde{\mathbf {{f}}}} ( t, t_0, \textbf{x}_0)\), where \({\tilde{\textbf{f}}}\) is a vector-valued, nonlinear function representing a solution to the kinematic equations, such as offered by Vinti [20] or Getchell [26], t is the time, \(\textbf{x}= [\textbf{r}^\top \;\;\; \textbf{v}^\top ]^\top = [x\;\;\; y\;\;\; z\;\;\; {\dot{x}}\;\;\; {\dot{y}}\;\;\; {\dot{z}}]^\top \) is the Earth-centered inertial (ECI) state, \(\textbf{r}\) and \(\textbf{v}\) are the position and velocity vectors, and the subscript “\(0\)” denotes initial conditions (ICs).
The kinematic equations contained in \({\tilde{\textbf{f}}}\) explicitly depend on anomalistic angles, but it is possible to develop alternative formulations with inherent advantages. For example, Biria [22] developed an alternative form of the kinematic equations that depends on the difference in anomalistic and other angles, and rigorous testing found that algorithms based on the new equations perform with heightened robustness in popular orbital regimes, among other benefits. The new form is referred to in this work as the “differential form” because the underlying equations depend on the difference in anomalistic and other angles instead of depending on the angles themselves. Letting \({\Delta }t = t - t_0\) be the time of flight, the differential form of Vinti’s IVP can be stated as \(\textbf{x}= \textbf{f} ( {\Delta }t, \textbf{x}_0)\) Biria [22]. This ostensibly small adjustment to the form of the kinematic equations has large consequences. The refinement enables a novel formulation of the BVP governed by Vinti’s potential, and it is considered foundational to the present work.
The differential form of the third-order kinematic equations [22] expressed in spheroidal UVs [28] is repeated here for convenience as
where subscripts indicating ICs have been changed from “\(0\)” to “\(1\)” to be consistent with typical BVP notation. The IC subscript convention applies only to \(\rho _1\) and \(\sigma _1\), where \(\sigma \) is tied to the dot product of the OS position and relative OS velocity [22, 28]. Equations (2), (3), and (4) govern anomalistic motion in the OS orbital plane, OS apsidal drift, and OS nodal drift, respectively. Next, over the remainder of the section, the large number of quantities introduced in Eqs. (2–4) are all defined.
The solution of the IVP yields six constants of integration [18]: \(\alpha _1\) or \(\varepsilon \) is the total energy, \(\alpha _2\) is closely related to the total angular momentum, \(\alpha _3\) is the polar component of angular momentum, \(\tau = -\beta _1\) is the time of OS periapsis passage, \(\omega = \beta _2\) is the argument of OS periapsis, and \({\Omega }= \beta _3\) is the right ascension of the OS ascending node (spheroidal RAAN). The usual formulas [18] relate the \(\alpha _j\) constants to a set of orbital elements termed the prime constants [18]: \(p_0\) is the prime OS semi-latus rectum, \(\gamma _0\) is the inverse of the prime OS semimajor axis \(a_0\), where \(\gamma _0 = -1/a_0\) for elliptical orbits, and \(S_0 = \sin ^2 i_0\), where \(i_0\) is the prime OS inclination. When these elements appear without the “0” subscript, they denote a different set termed the mutual constants [18] that are related to the two quartics, \(F\left( \rho \right) \) and \(G\left( \eta \right) \), noting that \(Q = \sin I\) and a capital “I” denotes the mutual OS inclination. Specifically, p, \(\gamma \), \(A_1\), and \(B_1\) result from factoring the \(F\left( \rho \right) \) quartic, and Q and \(Q_1\) result from factoring the \(G\left( \eta \right) \) quartic. The mutual OS eccentricity, e, is derived from p and \(\gamma \). The factoring of the quartics also yields \(\gamma _1\) and \(S_1\), two additional quantities defined by the relations \(\gamma _1 \gamma = \gamma _0\) and \(S_1 S = S_1 Q^2 = S_0\), respectively [26]. By convention, and because the mutual constants are used to set up the Vinti theory, references to OS elements in this work denote the mutual constants, not the prime constants, and elements should generally be interpreted as spheroidal or OS unless noted otherwise. From Getchell’s formulation [26], the \(A_n\) constants arise from the expansion of a quadratic in \(\rho \), and the \(C_n\), \(C_{1n}\), and \(C_{2n}\) constants arise from different expansions leading to expressions in terms of \(Q_1\), where odd \(C_n\) are zero, \(C_0 = 0\), \(C_2 = 1\), \(C_4 = Q_1/2\), \(C_6 = 3Q_1^2/8\), \(C_{1n}\) and \(C_{2n}\) are given by
\(d_m\) are zero for odd \(m\), \(d_2 = Q_1/2\), \(d_4 = 3 Q_1^2/8\), and \(d_6 = 5 Q_1^3/16\).
The time of flight and a number of important angular quantities are introduced in Eqs. (2–4) as well. First, note that the time of flight, \({\Delta }t \equiv t_2 - t_1\), appears explicitly on the left-hand side (LHS) in Eq. (2), where the \({\Delta }\) symbol denotes the difference of two quantities or expressions, in this context marking how much a quantity changes during the time \({\Delta }t\). For example, the LHS quantities in Eqs. (3) and (4) denote two angular differences that accrue over \({\Delta }t\). The OS apsidal drift [22], \({\Delta }\omega ^\prime \), tracks the drift of the OS perifocal frame [28] in the OS orbital plane, and the OS nodal drift [22], \({\Delta }{\Omega }^\prime \), tracks the drift of the OS equinoctial frame [23]. Note that \(\omega ^\prime \) is a different argument of OS periapsis [25] (\(\omega ^\prime \ne \omega \)) and \({\Omega }^\prime \) is a different spheroidal RAAN [29] (\({\Omega }^\prime \ne {\Omega }\)). The right-hand side (RHS) in Eq. (2) contains additional angular variables. The \(W_n\) and \(T_n\) symbols are recursive functions defined by Getchell [26] and the computation of their differential forms is discussed extensively by Biria [22]. Notably, \({\Delta }W_0 = {\Delta }f\) is the change in OS true anomaly and \({\Delta }T_0 = {\Delta }\psi \) that of the true argument of OS latitude. Related to the OS anomalistic angles are the UVs [28] in Eq. (2): \({\hat{x}}\), where \({\hat{x}}= \sqrt{a}{\Delta }E\) for elliptical orbits and E is the eccentric anomaly, \({\hat{z}}= -\gamma {\hat{x}}^2\), and the Stumpff functions [1, 28], \(C\left( {\hat{z}}\right) \) and \(S\left( {\hat{z}}\right) \).
3 Defining a BVP Under Vinti’s Potential as a Universal System of Equations
A congruent IVP and BVP are governed by the same dynamical system, which in this work is generated by Vinti’s symmetric, integrable potential. Consequently, when posing a boundary value problem instead of an initial value problem under the Vinti potential, the BVP may be formulated in part by rearranging many of the equations developed for the analytical universal Vinti propagator [22] into a new system of equations. To derive this system of equations, the general problem is first defined. From there, a good starting point is to define the orbital plane, and then to examine the OS Lagrange coefficients developed by Biria [28]. The section concludes with procedures for enabling multiple-revolution (multi-rev) solutions and obtaining terminal velocity vectors after the root-solve. The root-solve itself is addressed in a later section.
3.1 Problem Definition
In general, the BVP is stated as: Given terminal position vectors \(\textbf{r}_1\) and \(\textbf{r}_2\), the desired time of flight \({\Delta }t_*\), the direction of motion (DOM), and the number of complete revolutions N, find the terminal velocity vectors \(\textbf{v}_1\) and \(\textbf{v}_2\). Under Keplerian dynamics, the DOM is traditionally translated to a binary variable \({\tilde{d}}_k \in \{-1,1\}\) that divides the solution space into two branches according to the range of the transfer angle, \({\Delta }f_k\). The binary variable indicates short-way (SW) solutions (\(0 \le {\Delta }f_k \le \pi \)) or long-way (LW) solutions (\(\pi< {\Delta }f_k < 2\pi \)) with \({\tilde{d}}_k = 1\) or \({\tilde{d}}_k = -1\), respectively Russell [7], where the subscript k denotes Keplerian motion. Alternatively, the retrograde factor, \(K \in \{-1,1\}\), another binary variable, can define the DOM instead, where \(K = 1\) for direct orbits and \(K = -1\) for retrograde orbits, noting from Russell [7] that if a Lambert algorithm accepts K as an input, then \({\tilde{d}}_k\) must be determined in the first step. While the DOM is still a required input under Vinti’s potential, it is translated in a different way that is explained in a later section. To identify multi-rev solutions, N is used as a parameter, where the signed integer \({\tilde{N}} \in {\mathbb {Z}}\) described by Russell [7] is adopted in this work to distinguish by its sign between short-period (SP) and long-period (LP) solutions. Using the same convention, \({\tilde{N}} < 0\) corresponds to an SP solution, \({\tilde{N}} > 0\) to an LP solution, and \(N = |{\tilde{N}}|\). Note that \({\Delta }t\), determined from the OS time of flight equation, is distinct from the input \({\Delta }t_*\). The difference between the computed and desired times of flight, \({\Delta }t - {\Delta }t_*\), in the end is root-solved as part of a larger root-solve procedure.
3.2 Mapping Terminal Positions to Oblate Spheroidal Geometry
Since Vinti’s potential is defined in OS coordinates, both position vector boundary conditions (BCs) must be mapped to Vinti’s OS geometry. This map is simple, where Vinti’s equations [18] apply for \(i= 1, 2\) as
with \(r_i = \Vert \textbf{r}_i \Vert \), and the equation for the OS position unit vectors from Biria [28] applies as
The particular definition of the OS position vectors leading to the above unit vectors is directly connected to the OS equinoctial basis vectors [23].
3.3 OS Orbital Plane Orientation
In contrast to the two-body Lambert problem, the given position vectors do not define the orbital plane. In fact, because the plane rotates, the OS position vectors still do not define the OS orbital plane. In other words, \({\hat{{\varvec{\rho }}}}_1\) is in the orbital plane at \(t_1\) and \({\hat{{\varvec{\rho }}}}_2\) is in the orbital plane at \(t_2\). Choosing \({\hat{{\varvec{\rho }}}}_{1}\) as common to both the ECI and rotating frames, rotate \({\hat{{\varvec{\rho }}}}_{2}\) about the polar axis by the OS RAAN drift, \({\Delta }{\Omega }^\prime \), according to
so that both vectors lie in the orbital plane, where the secondary index “1” denotes \(t_1\) and “2” denotes \(t_2\). Now that \({\hat{{\varvec{\rho }}}}_{2}\) is in the same rotating reference frame as \({\hat{{\varvec{\rho }}}}_{1}\), and both vectors lie in the orbital plane, the transfer angle subtended by \({\hat{{\varvec{\rho }}}}_{1}\) and \({\hat{{\varvec{\rho }}}}_{21}\) is actually the change in true argument of OS latitude, \({\Delta }\psi \), which can be computed from the dot product and cross product to retain accuracy. Specifically, \(\cos {\Delta }\psi \) and \(\sin {\Delta }\psi \) are obtained as
respectively, and, using Eq. (9), basic trigonometry determines the angle \({\Delta }\psi \) as
where \({\tilde{d}}_\psi \) is the SW/LW indicator for \({\Delta }\psi \), distinct from \({\tilde{d}}_f\), the SW/LW indicator for \({\Delta }f\) with the same direction of motion. The indicators are \(+1\) for SW (\(0 \le {\Delta }(\cdot ) \le \pi \)) and \(-1\) for LW (\(\pi< {\Delta }(\cdot ) < 2\pi \)). It makes sense to define the direction of motion by specifying the orbit as direct or retrograde with K first, since that determines the direction of the node, and then derive \({\tilde{d}}_\psi \) from K and the cross product of the OS terminal positions,
which is not a unit vector, as
The traditional transfer angle, the change in OS true anomaly (\({\Delta }f= {\Delta }W_0\)), and \({\tilde{d}}_f\) can be determined as
The mutual OS inclination can be obtained from the OS angular momentum direction, \({\hat{\textbf{w}}}_1\), which is a unit vector, as
Note that I is not explicitly needed, only \(\sin I\) and \(\cos I\), so that computing the arctangent may be avoided:
3.4 OS Lagrange Coefficients
Biria [28] defined and derived OS Lagrange coefficients, \({\tilde{F}}\), \({\tilde{G}}\), \(\dot{{\tilde{F}}}\), and \(\dot{{\tilde{G}}}\), under Vinti’s potential in terms of various differential anomalistic angles. Equating the expressions for these coefficients in terms of \({\Delta }f\) and \({\hat{x}}\) gives
where \(h_i= \rho _i^2 {\dot{f}}_i\) for \(i=1,2\) and \({\dot{f}}_i\), the time derivative of the OS true anomaly, is defined by Biria and Russell [23] as
which is also repeated in Eq. (42) for convenience. Adapting Deyst’s approach [1], several useful relationships can now be obtained. Solving Eq. (16) for \({\hat{x}}\) yields
Careful manipulation of Eq. (18) leads to a more useful alternative form of the equation. To derive this alternative equation, recall from Biria [28] that the OS conic equation can be written in terms of \({\Delta }f\) as
Then, rearrange Eq. (22) as
divide Eq. (23) by \(p\rho _1\) to obtain
and subtract \(1/\rho _1\) from both sides of Eq. (24) to yield
Next, manipulate the LHS of Eq. (18), multiplying the entire LHS by
but canceling that operation out by multiplying both terms inside the square brackets by the reciprocal of Eq. (26), yielding
Bringing the factor \(1/\sqrt{p}\rho _1\) inside the square brackets, canceling terms, and applying some trigonometric identities in Eq. (27) gives
Finally, recognizing that the RHS of Eq. (25) appears in Eq. (28), substitute Eq. (25) into Eq. (28) and substitute the result into the LHS of Eq. (18) to obtain the desired alternative form of Eq. (18) as
After substituting Eq. (21) into Eq. (29), canceling \(h_2/p\) on both sides, multiplying both sides by \(\rho _1\rho _2\), and defining the auxiliary variables \({\tilde{A}}\) and \({\tilde{y}}\), adapted from Bate et al. [1], as
and
the resulting equation can be simplified to a more compact form as
Note that \({\tilde{A}}\) should be computed differently to avoid the indeterminate form for small values of \({\Delta }f\) as
When \(1 + \cos {\Delta }f\le 10^{-2}\), \({\tilde{A}}\) should be computed from Eq. (30), where the threshold of \(10^{-2}\) is recommended by Russell [7] to mitigate the loss of precision that arises when \(\cos {\Delta }f\approx -1\). Substituting Eq. (31) into Eq. (21) yields a compact form for \({\hat{x}}\) in terms of \({\tilde{y}}\) and \({\hat{z}}\) as
Finally, Eq. (17) can be related to the time of flight by observing
and substituting Eq. (35) into Eq. (2) to obtain
Note that Eq. (36) requires \({\Delta }\psi \) and \({\Delta }f\) explicitly in the secular terms, computed from inverse trigonometric functions, unlike the two-body Lambert problem that requires only \(\cos {\Delta }f\), not the angle itself.
Looking back over the preceding analysis, Eqs. (36), (3), (4), (14), (10), (13), (32), and (34) can be viewed as a system of eight equations in the eight unknowns \({\hat{z}}\), \({\Delta }\omega ^\prime \), \({\Delta }{\Omega }^\prime \), I, \({\Delta }\psi \), \({\Delta }f\), \({\tilde{y}}\), and \({\hat{x}}\), respectively. Due to the nature of the specific functional relationships between the variables, it is not required to iterate on all eight variables. To see why, consider first the following simpler system of three equations in three unknowns governing the two-body Lambert problem:
which Bate et al. [1] state as Eqs. 5.3-1, 5.3-2, and 5.3-3 in their book. The three unknowns are, using classical orbital elements, \(p_k\), \(a_k\), and \({\Delta }E_k\) or, in universal form, \({\tilde{y}}_k\), \({\hat{x}}_k\), and \({\hat{z}}_k\), recalling that \({\hat{z}}_k= {\Delta }E_k^2\) for elliptical orbits. Bate et al. [1] point out that iterating on \(a_k\) does not lead to a straight forward root-solve algorithm because guessing \(a_k\) does not uniquely determine \(p_k\) or \({\Delta }E_k\). But iterating on either \(p_k\) or \({\hat{z}}_k\) does lead to a straight forward root-solve algorithm because guessing \(p_k\) or \({\hat{z}}_k\) uniquely determines the remaining two variables. Iterating on \(p_k\) leads to the so-called p-iteration method [1]: guess the first variable, \(p_k\); the second variable, \(a_k\), is determined from \(p_k\) and the problem geometry, \({\Delta }f_k\); the third variable, \({\Delta }E_k\) in the elliptical case, is determined from \(p_k\) and \(a_k\), and the time of flight equation is used to check the trial value of \(p_k\). Alternatively, Bate et al. [1] describe the following universal approach credited to John Deyst: guess the first variable, \({\hat{z}}_k\); the second variable, \({\tilde{y}}_k\), is determined from \({\hat{z}}_k\) and the problem geometry, \({\Delta }f_k\); the third variable, \({\hat{x}}_k\), is determined from \({\hat{z}}_k\) and \({\tilde{y}}_k\), and the time of flight equation is used to check the trial value of \({\hat{z}}_k\). Interested readers can refer to Bate et al. [1] for the details, but the key takeaway is that, due to the nature of the functional relationships, it is not required to iterate on all three variables in the two-body Lambert problem. Rather, if the iteration variables are chosen carefully, then a solution method can be devised that iterates on a single variable to satisfy the time of flight equation.
A very similar argument is applied to the system of eight equations in eight unknowns governing the oblate Lambert problem. If the iteration variables are chosen carefully, then a solution method can be devised that iterates on only three variables to satisfy the OS time of flight, OS apsidal drift, and OS nodal drift equations, which refer to Eqs. (36), (3), and (4), respectively. First, guess the three iteration variables \({\hat{z}}\), \({\Delta }\omega ^\prime \), and \({\Delta }{\Omega }^\prime \)The fourth variable, I, is determined from Eq. (14), depending on \({\Delta }{\Omega }^\prime \) and the problem geometry. The fifth variable, \({\Delta }\psi \), is determined from Eq. (10), also depending on \({\Delta }{\Omega }^\prime \) and the problem geometry. The sixth variable, \({\Delta }f\), is determined from Eq. (13), depending on \({\Delta }\omega ^\prime \) and \({\Delta }\psi \). The seventh variable, \({\tilde{y}}\), is determined from Eq. (32), depending on \({\hat{z}}\) and \({\Delta }f\). The eighth variable, \({\hat{x}}\), is determined from Eq. (34), depending on \({\hat{z}}\) and \({\tilde{y}}\). It follows that guessing \({\hat{z}}\), \({\Delta }\omega ^\prime \), and \({\Delta }{\Omega }^\prime \) uniquely determines the remaining five variables. Finally, the OS time of flight equation is used to check the trial value of \({\hat{z}}\), the OS apsidal drift equation is used to check the trial value of \({\Delta }\omega ^\prime \), and the OS nodal drift equation is used to check the trial value of \({\Delta }{\Omega }^\prime \). Additional details are given in Sect. 5.
To summarize, as the two-body Lambert problem can be reduced from three equations in three unknowns to one equation iterating on \({\hat{z}}_k\) [1], the present system can be reduced to three equations, Eqs. (36), (3), and (4), iterating on the three unknowns \({\hat{z}}\), \({\Delta }\omega ^\prime \), and \({\Delta }{\Omega }^\prime \). It is not known if the system of equations can be further reduced, although three equations appears to be the minimum.
These three equations can be viewed as a generalization of Lambert’s equation to include \(J_2\), in one sense by generalizing the time of flight equation, which is the traditional Lambert equation, and in another sense by adding two equations to the dynamical system to account for the drift of the node and apse line. These additional two equations may be considered present but degenerate in the classical Lambert problem, where \({\Delta }{\omega }^\prime = {\Delta }\Omega ^\prime = 0\), and nondegenerate in the BVP defined by the Vinti potential. In fact, as \(J_2 \rightarrow 0\), \(({\Delta }\omega ^\prime , {\Delta }{\Omega }^\prime ) \rightarrow 0\) in Eqs. (3–4), respectively, and Eq. (36) reduces to the traditional Lambert time-of-flight equation, \(\sqrt{\mu }{\Delta }t = {\hat{x}}^3 S + {\tilde{A}}\sqrt{{\tilde{y}}}\), which is plainly embedded as the first two terms in Eq. (36). A consideration of the fundamental frequencies of the respective dynamical models hints at the observed properties described above. The two-body problem is fully degenerate [30], possessing only the one frequency, and this property manifests as a single Lambert root-solve function in the traditional Lambert problem. Vinti’s potential, generating what Wiesel [30] describes as a full spectrum of frequencies, defines a nondegenerate dynamical system, and this property manifests as three OS Lambert root-solve functions in the congruent BVP. Remarkably, all of these results are obtained without perturbation methods.
3.5 Adapting the Equations to Enable Multi-Rev Solutions
To enable N-rev solutions, add \(2N \pi \) to \({\Delta }f\), modifying Eq. (13) to yield
If \({\Delta }f_\textrm{tot}\) is below or above the valid range for N, then add or subtract \(2\pi \), respectively, for both \({\Delta }f_\textrm{tot}\) and \({\Delta }\psi _\textrm{tot}\). With this approach, the search for \({\hat{z}}\) is bounded between \(4N^2\pi ^2\) at the left end (LE) and \((2N+2)^2\pi ^2\) at the right end (RE) for a given N, and the kinematic equations must use the total angles in the secular terms, meaning \(2N\pi < {\Delta }f_\textrm{tot} \le (2N+2)\pi \). Put another way, the range requirement of \({\Delta }f\) is absolute, while that of \({\Delta }\psi \) is relative to \({\Delta }f\).
3.6 Obtaining Terminal Velocity Vectors After the Root-Solve
The OS Lagrange coefficients can be rewritten in terms of \({\tilde{A}}\) and \({\tilde{y}}\), noting \(\dot{{\tilde{F}}}\) is not required, as
The coefficients are defined in a rotating frame, which means the frame's rotation rates are required [23] for \(i=1,2\) as
where Eq. (43) was derived in Biria [22] and
are given in many references [23, 26]. Alternative, singular forms of Eq. (43) are not recommended because they contain \(1 - \eta _i^2\) in the denominator, which goes to zero when the spacecraft is on a pole (\(\eta _i= 1\)). The resulting indeterminate forms and catastrophic cancellation must be resolved with special mitigation techniques. For example, a conservative heuristic defines \(1 - \eta _i^2\le 10^{-2}\) as the condition where \(\eta _i\) is too close to unity and the subtraction operation loses too much precision. Other conditions may be more appropriate depending on the application, Biria and Russell [23] recommending the alternative condition \(1 - |\eta _i| < 10^{-7}\) with a different goal in mind. In any case, when the user-defined condition is satisfied, \(1 - \eta _i^2\) may be obtained by computing \(\alpha _2^2 - \alpha _3^2\) first as
Then, noting that
Eq. (45) can be substituted into Eq. (46) to obtain
where \(\sqrt{G(\eta _i)} = \sqrt{G_i} = {\dot{\eta }}_i\left( \rho _i^2 + c^2 \eta _i^2\right) \). Now, the simplest terminal velocity component anticipated is \({\dot{z}}_1= \rho _1{\dot{\eta }}_1+ {\dot{\rho }}_1\eta _1\), which requires \({\dot{\eta }}_1\), obtained from
Alternatively, \(Q\cos \psi _1\) can be determined by computing the sign of \(Q\cos \psi _1\) separately from its magnitude as
which can be multiplied by \(\sqrt{Q^2 - \eta _1^2}\) to obtain
Similar to the two-body Lambert problem, numerical difficulties appear for \(N\pi \) transfers in \({\Delta }\psi \) because the position vectors do not geometrically define the inclination. An indeterminate form arises in Eq. (48), while in Eq. (50), the signs of the signum arguments could be inaccurate, and Q, obtained from Eq. (15), also loses accuracy from the cross product.
From the definitions in Biria [28], the usual formulas can actually still be used to obtain the terminal velocities, but they must be generalized for rotating frames like Eq. 29 in Biria [22]. Following that logic, the OS relative velocities in the perifocal frame can be computed as
where the superscript P denotes the OS perifocal frame, all other vectors are in ECI coordinates, Rodrigues’ formula is used to obtain the rotation matrix \(R({\Delta }\omega ^\prime )\) from an axis-angle representation as
the position vector \({\varvec{\rho }}_{20}\) denotes \({\varvec{\rho }}_2\) as viewed in the perifocal frame, computed as
the notation \(I_{3 \times 3}\) denotes the identity matrix in Eq. (52), and the subscript \(\times \) the skew symmetric matrix equivalent for the cross product expressed as
The axis-angle representation is convenient here because the angular momentum vector is easily adopted as the rotation axis, which directly enables the use of \({\Delta }\omega ^\prime \) as the rotation angle, notably defining the rotation in terms of physical quantities. Adding the centripetal term to Eq. (51) gives inertial OS velocities for \(i= 1, 2\) as
where the angular velocity vectors are given by
OS RAAN at the terminal points are determined as
and differencing the rotation rates in Eq. (42) yields an expression for the instantaneous apsidal rotation rate, \({\dot{\omega }}^\prime _i\), as
Finally, by rearranging Eq. 27 in Biria [22], the terminal inertial velocities in ECI coordinates, \(\textbf{v}_i\), can be computed as
Equations (51–58) draw useful connections to the two-body Lambert problem, but they also present two issues. The appearance of the singular element \({\Omega }^\prime _i\) in Eq. (56) implies numerical difficulties for nearly equatorial orbits and motivates an alternative approach based on equinoctial elements. More importantly, the division by \({\tilde{G}}\) in Eq. (51) implies an inability to compute velocities when half-rev transfers in \({\Delta }f\) are encountered, specifically an ambiguity in the velocity direction in the OS perifocal frame, analogous on some level to the traditional Lambert problem. But since the OS perifocal frame is rotating, intuition suggests that the singularity in Eq. (51) is non-physical and merely the result of the formulation or approach. To verify this assertion, begin from considerations of the OS orbital inclination, as could equivalently be done for the two-body case. The OS inclination is defined in Eq. (14), which traces back to the cross product \({\hat{{\varvec{\rho }}}}_{1}\times {\hat{{\varvec{\rho }}}}_{21}\) that appears in Eqs. (10) and (11). When \({\hat{{\varvec{\rho }}}}_{1}\) and \({\hat{{\varvec{\rho }}}}_{21}\) are parallel or anti-parallel, then the OS rotating orbital plane, and thus the OS inclination, is undefined. But under Vinti’s potential, the angle subtended by these vectors is \({\Delta }\psi \), which suggests that \({\Delta }\psi \), not \({\Delta }f\), is the transfer angle associated with half-rev singularities. Under Keplerian dynamics, \({\Delta }\omega ^\prime = 0\), and so the half-rev singularity becomes associated with \({\Delta }f\) instead, viewed here through the lens of a degenerate dynamical system. When considering Vinti’s potential, then, there appears to be no obvious physical singularity associated with half-rev transfers in \({\Delta }f\), thus verifying the earlier assertion. If this physical singularity is labeled a half-rev singularity, regardless of the dynamics, then the observation could be made that, in summary, the half-rev singularity in \({\Delta }f\) seems to have disappeared under Vinti’s potential, appearing in \({\Delta }\psi \) instead. Note that the full-rev singularity exists in both variables, in \({\Delta }\psi \) because of the same cross product and in \({\Delta }f\) because of the division by \({\tilde{y}}\), which is evident later in Eqs. (62) and (63). A logical next step is to pursue a different formulation devoid of singularities when \({\Delta }f= \pi \). Such an alternative approach is proposed next to avoid both stated \({\Omega }^\prime _i\) and \({\Delta }f\)-half-rev issues.
To avoid computing \({\Omega }^\prime _i\), the velocities can be obtained entirely in terms of OS equinoctial elements instead. From Biria and Russell [23], compute the following: \({\hat{\textbf{f}}}_1, {\hat{\textbf{g}}}_1, {\varvec{\dot{{\hat{\textrm{f}}}}}}_1, {\varvec{\dot{{\hat{\textrm{g}}}}}}_1\) via Eqs. 125–128, \(\cos L_1, \sin L_1\) from Eq. 90–91, and \({\dot{L}}_i\) from Sect. 9. Compute \({\dot{\rho }}_i\) from Eq. 21 in Vinti [29] and \({\dot{\eta }}_i= {\dot{\psi }}_iQ \cos \psi _i\). To avoid inverse trigonometric functions, obtain \(\cos L_2, \sin L_2\) from standard angle sum identities after computing \({\Delta }L\) from Eq. (70) in Appendix A in [22]. Then propagate [22] \(p_{11},p_{21}\) via Eq. (71) in Appendix A to obtain \(p_{12},p_{22}\), which determine \({\hat{\textbf{f}}}_2, {\hat{\textbf{g}}}_2, {\varvec{\dot{{\hat{\textrm{f}}}}}}_2, {\varvec{\dot{{\hat{\textrm{g}}}}}}_2\) as before. Finally, compute \(\textbf{v}_i\) by applying to each terminal point Eqs. 133 and 134 in Biria and Russell [23]. See Appendix A for computational details. Notice that as \(J_2 \rightarrow 0\), all equations reduce to the two-body equations.
4 Properties and Comparisons of the Lambert Solution Space with Oblateness Effects
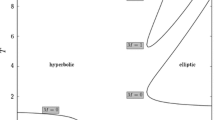
The examination of the solution space, which should be independent of the root-solve technique, is divided into two parts: zero-rev and multi-rev. The simpler zero-rev case is explored first. Once basic properties are established, attention is drawn to the multi-rev case, which adds a significant layer of complexity.
4.1 Visualization Strategy and Example Setup
Under the Vinti potential, many of the properties observed under two-body dynamics continue to hold. Properties are interpreted from the Vinti and Keplerian \({\Delta }t\)-\({\hat{z}}\) curves [1], such as in the top panels in Fig. 2, where each point on the curve corresponds to a feasible Lambert-type transfer orbit between a fixed \(\textbf{r}_1\) and \(\textbf{r}_2\) in the computed transfer time \({\Delta }t\). Short-way transfers are depicted on the left and long-way transfers on the right. These transfers are automatically feasible for the Keplerian dynamics because the root-solve is one-dimensional. However, it is important to emphasize their feasibility for Vinti dynamics. To obtain this curve for Vinti dynamics, the three-dimensional root-solve of Eqs. (36) and (3–4) is collapsed onto one dimension by ensuring that the root-solve of Eqs. (3–4) for \({\Delta }\omega ^\prime \) and \({\Delta }{\Omega }^\prime \) is converged for each \({\hat{z}}\) on the curve (see the next section for root-solve details). This extra step enables the direct comparisons between Vinti and Keplerian dynamics in Fig. 2 and helps visualize the solution space. The terminal position vectors for Fig. 2 are generated by propagating the set of osculating Keplerian element ICs in Table 1 through the time of flight given in Table 2, or roughly 14,156 sec, under Vinti dynamics, resulting in the approximate terminal positions \({\textbf{r}_1= [5372.789 , 4437.582 , 668.070]^\top }\) km and \({\textbf{r}_2= [-6903.967 , -892.533 , 1480.227]^\top }\) km. All examples in the present work use Earth parameters \(\mu = 3.986004415 \times 10^{5}\) km\(^3\) /sec\(^2\), \(R_e = 6378.137\) km, and \(J_2 = 1.082636022984 \times 10^{-3}\)
4.2 Zero-Rev Solution Space
Now that the analysis framework and example is set up, the top panels in Fig. 2 can be discussed in more depth. In this example, SW transfers are direct while LW ones are retrograde. The SW transfers, being direct orbits, have an inclination close to the value in Table 1. Ignoring the multi-rev cases for now, note that the SW and LW solutions are distinct, possessing the same general properties as observed for two-body dynamics. For either case, and noting the logarithmic scale on the vertical axis, \({\Delta }t \rightarrow \infty \) as \({\hat{z}}\rightarrow (2\pi )^2\), a limiting parabola with finite p (the orbit approaches a different limiting parabola when the asymptote is approached from the other direction). As \({\hat{z}}\) is decreased from this value, it obtains the value for the well-known minimum-energy ellipse, which can be obtained analytically for Keplerian dynamics [2]. The minimum-energy spheroidal ellipse is marked with a blue square and the Keplerian ellipse with a red “x”. The two energy values are distinct, occurring for different TOF and \({\hat{z}}\) values, and only appearing to be identical at this scale. While the minimum energy, \(\varepsilon _{\textrm{min}}\), retains the same value for all N and directions of motion under Keplerian dynamics [7] (\(\varepsilon _{k,\textrm{min}} =\) constant), this property does not hold under Vinti dynamics because \({\Delta }f\), and thus the chord length in the perifocal frame, changes with \({\hat{z}}\), N, and K. As \({\hat{z}}\) is decreased further, the curves intersect the vertical axis when \({\hat{z}}= 0\), corresponding to the parabolic transfer, and \({\hat{z}}\) then obtains negative values for a range of hyperbolic transfers. The curves for SW transfers steeply intersect the horizontal axis at some negative \({\hat{z}}\) as \({\Delta }t \rightarrow 0\), corresponding to a straight line (\(p = \infty \)) relative to the OS orbital plane, while \({\Delta }t \rightarrow 0\) asymptotically for LW hyperbolic transfers, theoretically equaling zero for the limiting rectilinear hyperbola (\(p = 0\)) [1], although noting that the formulation completely breaks down well before that limit [26] with the forbidden zone [31] boundary sitting at \(210 \lessapprox \rho \lessapprox 297\) km for Earth. At this scale, there is almost no discernible difference between the dynamical models, except for the LW hyperbolic transfers in the top panel in Fig. 2b, the curves visibly approaching the horizontal asymptote at different rates. This discrepancy is attributed to periapsis approaching Earth’s center (\(\rho _{p} < 235.2\) km and \(r_{p_k} < 249.7\) km when \({\hat{z}}= -52.008\) rad\(^2\)), so that the effect of \(J_2\) increases as \({\hat{z}}\) decreases. Zooming in would reveal more discrepancies, and, as shown in a later section, these differences only become more exaggerated as N increases because the implied longer portion of the transfer time spent near periapsis allows errors to accumulate.
Alternatively, the difference between the two curves, denoted as \({\Delta }t_\textrm{err}\), can be plotted as in the second row of panels in Fig. 2, which clearly quantifies the discrepancies. The TOF error appears to blow up near the \({\hat{z}}\)-full-rev asymptotes. As \({\hat{z}}\) is decreased, \({\Delta }t_\textrm{err}\) for the long-way solution goes negative as the curve approaches the asymptote, the traditional Lambert solution overestimating the required transfer TOF by \(\approx \) 17.0 sec at the LE. For the short-way solution, the TOF error curve exhibits a hook-like characteristic toward the left end, going slightly negative in a small region between \(\approx [-4.54, -0.49]\) rad\(^2\), and otherwise remaining positive. The traditional Lambert solution underestimates the required SW transfer TOF by \(\approx \) 5.6 sec at the LE (\({\hat{z}}= -13.0656\) rad\(^2\)) near where the \({\Delta }t\)-\({\hat{z}}\) curve intersects the horizontal axis. Note that the LE has the largest p for which the Vinti-Lambert algorithm converges, so p is not infinite (\(p \approx 266,469\) km, \({\Delta }t \approx 92.2\) sec).
The next four rows of panels in Fig. 2 illustrate some of the characteristics of the other six main root-solved quantities: two transfer angles, two orbital drift angles, the orbital inclination, and the periapsis radius. Because the root-solve of Eqs. (3–4) is converged, the values of \({\Delta }t\), \({\Delta }f\), \({\Delta }\psi \), \({\Delta }{\Omega }^\prime \), \({\Delta }\omega ^\prime \), I, and \(\rho _p\) can be directly read off the plots for a given \({\hat{z}}\). Results in Fig. 2 confirm basic expectations, that the first five root-solved quantities vary under Vinti dynamics while remaining constant under Keplerian dynamics, for which \({\Delta }\psi _k = {\Delta }f_k\) is constant because \({\Delta }{\Omega }_k = {\Delta }\omega _k = 0\) and \(i_k\) is constant because the orbital plane is inertially invariant.Footnote 1 Periapsis, denoted \(\rho _p\) (spheroidal) or \(r_{p_k}\) (spherical), behaves similarly under either dynamical model. What immediately stands out is that the long-way Vinti transfers exhibit strong deviations away from the Keplerian transfers as the orbit becomes more hyperbolic. Evidently, because these transfers pass through periapsis and the periapsis radius is small, approaching 235 km at the left endpoint, \(J_2\) considerably warps the inclination, which shoots up 15\(^\circ \) to become more equatorial, and significantly contributes to the turning angle. Since the Vinti-Lambert solver was not intended to work for such a low periapsis radius, a few of the very hyperbolic transfers were more closely examined to assess whether the solutions were even remotely accurate or representative of the intended dynamics. Comparisons were made between the associated universal Vinti propagator and numerically integrated Vinti trajectories, and results indicated that the substantial increase in orbital drift and inclination still faithfully capture the Vinti dynamics to sub-kilometer accuracy. With a spacecraft on such trajectories traveling through a minimum radial distance close to 235 km, these scenarios are not practical, but the sub-kilometer level of accuracy is still considered sufficient to at least qualitatively characterize some of the corners of the solution space. This exercise is viewed more as an important test of the limitations of the formulation and the algorithm, and also a testament to the formulation’s integrity.
4.3 Multi-Rev Solution Space
Figure 2 also reveals some preliminary, novel characteristics of multi-rev scenarios that appear even for very low N, limited to 1 or 2 revs in this data set. Qualitatively, curves for the Vinti transfer angles, drift angles, and inclination are observed to have either an arctangent (\(\arctan \)) or arccotangent (\(\textrm{arccot}\)) shape for each N, appearing to approach distinct horizontal asymptotes as \({\hat{z}}\) approaches either vertical asymptote. While the Lambert solutions approach the same limiting parabolas at the \({\hat{z}}\) asymptotes for each N under Keplerian dynamics, \(J_2\) causes the limiting parabolas to change slightly for each N (different p, I). When switching from the SW to LW solution space, the I curve, having the observed property \(I > i_k\) for all examples considered, changes with increasing N from increasingly inclined \(\arctan \) shapes to progressively more equatorial \(\textrm{arccot}\) shapes. Similarly, the maximum \({\Delta }\psi \) and \({\Delta }\omega ^\prime \) increases with N, switching from \(\arctan \) shapes (SW case) to \(\textrm{arccot}\) shapes (LW case). The minimum \({\Delta }f\) decreases with N, switching from \(\textrm{arccot}\) shapes (SW case) to \(\arctan \) shapes (LW case), while the maximum \(|{\Delta }{\Omega }^\prime |\) increases with N, maintaining an \(\textrm{arccot}\) shape regardless of the solution family but changing from negative to positive when switching from direct to retrograde solutions.
Having covered some basics of the low-rev cases, the discussion is now focused on some general properties of multi-rev scenarios, using the low-rev results as illustrative examples. The multi-rev case adds a significant layer of complexity and poses interesting consequences to transfer design, particularly with regard to the existence of solutions and repercussions of incorrectly determining existence. An important property of the traditional Lambert solver is its ability to determine the existence of multi-rev transfers by identifying the minimum TOF, \({\Delta }t_\textrm{min}\). As illustrated in the zero-rev case, the required transfer TOF does not agree in general between Vinti and Keplerian dynamics, and this discrepancy extends to \({\Delta }t_\textrm{min}\) for the multi-rev case (\({\Delta }\textrm{TOF}\equiv {\Delta }t_\textrm{min}- {\Delta }t_{k,\textrm{min}}\ne 0\)), where the traditional Lambert solver generally overestimates or underestimates \({\Delta }t_\textrm{min}\) for an N-rev transfer, corresponding to a potential false negative or false positive, respectively, in terms of the existence of multi-rev solutions given \({\Delta }t_*\). Existence can be determined from the \({\Delta }t\)-\({\hat{z}}\) curves or, alternatively, a rough idea may be obtained for low revs by referencing the second row of panels in Fig. 2. While ostensibly there is no difference in the TOF error trends in Fig. 2, a positive or negative TOF error at \({\hat{z}}_{{\Delta }t_\textrm{min}}\), indicated by the red \(+\) symbols, can be interpreted as a false positive or false negative, respectively. For the short-way transfers, \({{\Delta }t_\textrm{err}}({\hat{z}}_{{\Delta }t_\textrm{min}})<0\) for \(N = 1, 2\), the error being larger or more negative for \(N = 2\) at \(\approx -17.84\) sec versus \(\approx -4.58\) sec for \(N = 1\). The long-way transfers exhibit the opposite trend: \({{\Delta }t_\textrm{err}}({\hat{z}}_{{\Delta }t_\textrm{min}})>0\) for \(N = 1, 2\), the error being larger or more positive for \(N = 2\) at \(\approx 33.55\) sec versus \(\approx 14.03\) sec for \(N = 1\). If obtained directly from the \({\Delta }t\)-\({\hat{z}}\) curves, the minimum TOF for short-way transfers is overestimated by 17.42 sec for \(N = 2\) and 4.58 sec for \(N = 1\) (false negative), while for long-way transfers it is underestimated by 33.93 sec for \(N = 2\) and 14.03 sec for \(N = 1\) (false positive).
In this example, \(J_2\) is thus observed to decrease \({\Delta }t_\textrm{min}\) for direct transfers and increase it for retrograde transfers, corresponding to a respective minimum TOF advance or delay, apparently depending on the orbital regime. It seems reasonable to suspect that the trend observed is directly caused by the orbital inclination, acting through the well-known apsidal and nodal drift phenomena and the secular effect on the mean anomaly, in addition to some interplay with periapsis distance and the length of time spent closer to periapsis. That is not to say that direct transfers always experience a minimum TOF advance and retrograde ones experience a delay; rather, the actual trends are thought to be much more nuanced. For instance, in this example, since the inclination is roughly 30 deg away from being equatorial in either case, the apsidal drift should impact the transfer time to a similar degree and in the same “direction” (\({\Delta }\omega ^\prime > 0\)) for either inclination, and therefore cannot be the dominant cause of the observed trend. By process of elimination, some combination of nodal drift and periapsis considerations are thought to be causing the trend, but it is not clear how. These trends hint at underlying physical mechanisms affecting the minimum TOF and are explored further in the next section.
4.4 Minimum TOF Advance or Delay with Practical Considerations
Preliminary notions of the physical mechanisms controlling trends in the existence of multi-rev solutions were probed in the previous section. It is shown in the following that the impact of accumulated errors from neglecting oblateness can be considerably more profound, even at Earth, and the impact on transfer existence exemplifies in different ways how neglecting \(J_2\) can lead to erroneous conclusions. Multiple examples are examined to investigate more broadly, though not exhaustively, how inclination can affect the solution space.
4.4.1 Very-High-Rev Example
An illustration of this problem for a 100-rev transfer is offered in Fig. 3 using a log scale as in Fig. 2. BCs are generated from Tables 1–2, leading to approximate terminal positions \({\textbf{r}_1= [5558.706 , 3761.031 , 1990.162]^\top }\) km at one end and \({\textbf{r}_2= [-3077.908 , -514.361 , -6285.426]^\top }\) km at the other. With \(\textbf{r}_1\) and \(\textbf{r}_2\) fixed, the \({\Delta }t\)-\({\hat{z}}\) slice of the solution space in Fig. 3a appears to retain the same basic shape with \(J_2\) effects, but now with a more pronounced discrepancy. It is evident from a glance that the two Lambert solvers predict a significantly different minimum TOF: the Keplerian Lambert solver indicates a minimum of 6.32 days while the more accurate Vinti one indicates a 6.66-day minimum, which is a difference of \(\approx \) 8.1 hours. The minimum-time 100-rev short-way Vinti transfer has the following approximate orbital elements: \(\rho _p= 6173\) km, \(a = 6916\) km, \(e = 0.11\), \(I = 80.75^\circ \), \({\Delta }E = 166.0^\circ \), \({\Delta }f= 153.8^\circ \), \({\Delta }\psi = 131.6^\circ \), \({\Delta }{\Omega }^\prime = -8.2^\circ \), and \({\Delta }\omega ^\prime = -22.2^\circ \). Since the transfer is only \(\approx \) 9.25 deg away from being polar, the nodal drift should not significantly affect the transfer time, even for 100 revs. In fact, the plot clearly shows a time delay, implying that the apsidal drift (\({\Delta }\omega ^\prime < 0\)) is not only causing the delay, but is also great enough to overcome other effects. Ignoring other effects, the apsidal drift induces a time delay because, relative to the Keplerian solution, the transfer angle grows when \({\Delta }\omega ^\prime < 0\), or roughly when \(63.4^\circ< I < 116.6^\circ \), and shrinks when \({\Delta }\omega ^\prime > 0\), or roughly when \(I < 63.4^\circ \) or \(I > 116.6^\circ \). It is straightforward to connect apsidal drift to a change in transfer angle because the drift is in the OS orbital plane, leading to the simple angle summation in Eq. (13). In contrast, \({\Delta }{\Omega }^\prime \) is not easily connected to a change in transfer angle, operating through Eqs. (8–12). In the present case, \({\Delta }f_k = 130.0^\circ \) and \({\Delta }E_k = 154.1^\circ \), the latter being cubed in Eq. (36) and larger with \(J_2\) effects, leading to the longer TOF and 8.1-hour discrepancy.
Direct comparison of Lambert solution spaces under Vinti and Keplerian dynamics for 100-rev short-way transfers at Earth with fixed \(\textbf{r}_1, \textbf{r}_2\). The minimum predicted TOF for existence of solutions differs by \(\approx \) 8 hours; a 6.5-day transfer exists under Keplerian dynamics, but not under the more realistic Vinti dynamics. The minimum predicted energy differs by \(\approx \) 1 km\(^2\)/sec\(^2\)
Figure 3b highlights another interesting feature of Vinti dynamics that does not exist in the two-body case. As stated earlier, all transfers for the same BCs share the same minimum energy under Keplerian dynamics, but this property vanishes with \(J_2\) effects. In this example, a 100-rev transfer not only requires a lot more time, but also much more energy (\({\Delta }\varepsilon _\textrm{min}\approx \) 1.02 km\(^2\)/sec\(^2\)) to execute compared to the two-body prediction, the Vinti energy curve appearing to reside inside a Keplerian energy envelope. The inverse was found to occur for BCs leading to a \({\Delta }t_\textrm{min}\) advance rather than a delay, where the Keplerian energy curve resides within a Vinti energy envelope and the Vinti transfer requires less energy (\({\Delta }\varepsilon _\textrm{min} < 0\)). Note that the envelope findings apply to the left end of the curves, not necessarily generalizing to the entire energy curve that includes regions where \({\Delta }t \rightarrow \infty \). In these regions, the inner curve was observed to pierce the “envelope”, and it is not clear without further analysis whether this is an inaccuracy resulting from the third-order Vinti approximation, numerical inaccuracy due to large TOF, a different source of inaccuracy, or a property of the exact Vinti dynamics. These observations are based on a few numerical examples and warrant further study.
4.4.2 Multi-Rev Inclination Sweep
While the preceding results are illuminating, they still fall short of a broader mapping and characterization of the Lambert solution space with \(J_2\), which is better achieved with the inclination sweep presented in Fig. 4. These results emerge from a sweep across the domain of direct, short-way transfers with \(N =\) 20 revs, covering eight separate BVPs or BC pairs generated from the values in Tables 1 and 2. Various methods would be considered appropriate ways to choose these BVPs, and the specific thought process employed is discussed here for interested readers. Choosing 20 complete revs is somewhat arbitrary, but with a main goal of ensuring that inclination-induced \(J_2\) effects would be visible in the results. Upon finding that such \(J_2\) effects are easily observed with 20 revs, it follows that, for this type of investigation, a sweep at a moderate N like 20 revs is preferred to the very high N of the 100-rev example shown in Fig. 3.
With N selected, the next decision concerns how to constrain the geometry. Since the Keplerian solution space is being compared to the Vinti solution space, it would help, if possible, if the Keplerian solution space were constant while varying the inclination. For example, it seems that an appropriate approach could keep the in-plane geometry constant, under Keplerian dynamics, for the entire parameter sweep, to isolate the effects of varying I. However, there is a secondary goal, which is to demonstrate that, while the transfer angle is a simple function of the fraction of the orbit traversed when under Keplerian dynamics (and independent of I), this property does not hold under Vinti dynamics. Specifically, the inclination affects how long it takes to traverse through a certain orbit fraction, in addition to how long it takes to complete a certain number of revs (i.e., the orbital period varies). Now, a good way to accomplish both goals stated above is to use the same procedure to generate the BCs for Figs. 2 and 3, and then hold \(\textbf{r}_1\) and the number of revs fixed for all cases while varying I. With some trial and error, choosing 20.4 revs led to favorable results that exposed interesting features of the solution space. The choice kept \({\Delta }f_k\) constant enough for the purposes of the first stated goal, spanning only \(\approx \) 9\(^\circ \), which is considered an insignificant change in the in-plane orbital geometry. Secondly, the choice demonstrates that holding the ICs and number of revs fixed at 20.4 revs over varying inclinations requires varying times of flight, and also results in varying transfer angles. In summary, an attempt is made to keep \({\Delta }f_k\) nearly the same for each case in Fig. 4, though this consistency in the in-plane geometry is balanced against a desire for \({\Delta }t_0\) to propagate each IC consistently through 20.4 revs under Vinti dynamics. For brevity, the sweep does not extend into the retrograde domain, which would include an additional eight BVPs, nor does it include the other half of the solution space for the selected BVPs, the long-way counterparts excluded from Fig. 4 that would also happen to be retrograde.
Now that the BVPs are selected, the results in Fig. 4 are explored and discussed. Each column or subfigure of Fig. 4 is organized like Fig. 2 but without the periapsis panes, and Figure 4 as a whole can be analyzed by stepping from the left to right subfigures, \(i_k\) increasing from \(\approx \) 12\(^\circ \) to exactly \(90^\circ \). While some behaviors are maintained from the low-rev examples in Fig. 2, others vary considerably. As \(i_k\) is walked up to the polar case, the \(\arctan \) behavior in I is retained, but notice the variations in I decreasing from a spread of \(\approx \) 22\(^\circ \) in Fig. 4a (LE: \(\rho _p\approx 4984\) km; RE: \(\rho _p\approx 1762\) km) down to \(0^\circ \) in Fig. 4h (LE: \(\rho _p\approx 4524\) km; RE: \(\rho _p\approx 2691\) km). The spread variation is not only caused by the greater strength of \(J_2\) close to the equator, but also its accumulated effect over many revs. The concentration of mass closer to the equator and away from the poles can be inferred from Fig. 4 in other ways, where the effect on \({\Delta }f\) over 20 revs is markedly unintuitive. Specifically, while \({\Delta }f\) is observed in Fig. 2 to vary monotonically with \({\hat{z}}\) for low revs, \({\Delta }f\) does not necessarily vary monotonically with \({\hat{z}}\) for high revs. In Fig. 4a, b, for example, an \(\textrm{arccot}\) shape in the trend for \({\Delta }f\) that may have been anticipated from Fig. 2 instead appears as if slightly corrupted by \(J_2\). In contrast, the trend in \({\Delta }\psi \) retains the \(\arctan \) shape seen in Fig. 2, the spread in \({\Delta }\psi \) decreasing, as observed for I, from \(\approx 24^\circ \) in Fig. 4a down to \(0^\circ \) in Fig. 4h. The constant \({\Delta }\psi \) observed for the polar case in Fig. 4h is not an intuitive result, and it is viewed as an instructive special case warranting further explanation. First, consider that the OS inclination is expected to be constant in the polar case because a polar transfer orbit is only possible with a \(90^\circ \) inclination. To understand why \({\Delta }\psi \) is constant in the polar transfer solution space, consider that \({\Delta }{\Omega }^\prime = 0\) for all \({\hat{z}}\), leading to the condition \({\hat{{\varvec{\rho }}}}_{21}= {\hat{{\varvec{\rho }}}}_{22}\). It follows that \({\Delta }\psi \), the angle subtended by \({\hat{{\varvec{\rho }}}}_{1}\) and \({\hat{{\varvec{\rho }}}}_{21}\), is equal to the angle subtended by \({\hat{{\varvec{\rho }}}}_{1}\) and \({\hat{{\varvec{\rho }}}}_{2}\), analogous to how \({\Delta }f_k\) is the angle subtended by \(\textbf{r}_1\) and \(\textbf{r}_2\) under Keplerian dynamics. For polar Vinti transfers, then, the \({\Delta }\psi \) transfer angle is solely dependent on the BCs or supplied geometry in the same way that \({\Delta }f_k\) is in general under Keplerian dynamics. A remarkable condition follows: \({\Delta }\psi \approx {\Delta }f_k\) for all \({\hat{z}}\). Of course, \({\Delta }f\) still varies with \({\hat{z}}\) at the polar inclination because \({\Delta }\omega ^\prime \ne 0\). At \(i_k \approx \) 38\(^\circ \) (Fig. 4c), \({\Delta }f\) is seen to vary the least, by \(\approx \) 3\(^\circ \).
For orbit drift angles, \({\Delta }{\Omega }^\prime \) retains an \(\textrm{arccot}\) shape that decreases in magnitude and spread as \(i_k\) increases. In contrast, \({\Delta }\omega ^\prime \) is observed to have a sort of inflection point (IP) captured in Fig. 4d. It does not coincide with a transition from positive to negative drift, but does seem to coincide with when \({\Delta }\textrm{TOF}\) is almost minimized, suggesting that some balance of \(J_2\) effects occurs in this regime that may be connected to \({\Delta }f\) obtaining an \(\arctan \) shape after the IP. The apsidal drift retains an \(\arctan \) shape before the IP (with a noticeable maximum almost coinciding with the minimum \({\Delta }f\) in Fig. 4a) and an \(\textrm{arccot}\) shape after. Within \(\approx \) 5\(^\circ \) of the IP, it is not known if the symmetric binomial shape with positive drift seen here is common for Vinti transfers in this regime. A deeper understanding of the IP may be obtained with further study. Equatorial trends were omitted for brevity.
The hypothesis that the inclination may serve as a major physical lever contributing to a minimum TOF advance or delay is further supported in Fig. 4, where strong correlations are observed between I and \({\Delta }\textrm{TOF}\), with values given in each subfigure caption. A \({\Delta }t_\textrm{min}\) advance is observed for low \(i_k\), reaching nearly 58 min in Fig. 4a, transitioning through a minimum \({\Delta }t_\textrm{min}\) discrepancy near the \(i_{k_0} =\) 55\(^\circ \) case with \({\Delta }\textrm{TOF}\approx \) 2 min, and then growing to a \({\Delta }t_\textrm{min}\) delay of \(\approx \) 18 min for the polar case. It is suspected that \({\Delta }\textrm{TOF}= 0\) at some \(i_k\) between 38.4\(^\circ \) and 48.6\(^\circ \), probably near 46\(^\circ \), though no attempt is made to find this exact inclination where the estimate of \({\Delta }t_\textrm{min}\) agrees between the two dynamical models. Evidently, the potential for false negatives and false positives is substantial and one situation does not appear to be more common than the other.
4.4.3 Practical Considerations
Turning to some practical considerations, suppose, now referring to Fig. 3, that a 6.5-day transfer is desired to satisfy mission requirements, indicated by the green horizontal dashed line. Here, a traditional Lambert solver erroneously claims a 100-rev transfer exists, a false positive. Without the insight of the Vinti-Lambert solver, it would be tempting to use the 6.5-day solutions as guesses in a perturbed Lambert algorithm, but Fig. 3 clearly shows that would be pointless. In fact, for a typical approach, such as a shooting method, the algorithm would waste valuable time trying to find a solution that does not exist, and the algorithm would ultimately fail for an unknown reason. These unexpected, undiagnosable failures can occur whenever \({\Delta }\textrm{TOF}> 0\), observable in Figs. 3 and 4. Turning to Fig. 4a, suppose a 31-hour transfer is desired. Here, a standard Lambert solver erroneously claims a 20-rev transfer does not exist, a false negative, and does not return a 20-rev solution to the shooting method, noting that \(N_{k,\textrm{max}}\) may be several revs lower and the 20-rev case may not even be attempted in an algorithm that first identifies \(N_{k,\textrm{max}}\). Practically speaking, this situation is not catastrophic, but, when performing broad searches, for example, it does imply a statistically significant probability of overlooking good many-rev solutions that may save a large amount of fuel or be otherwise favorable.
The false negative scenario underscores the importance of developing good alternatives to using a traditional Lambert solution as a guess, because the two-body Lambert guess can literally skip over useful parts of the solution space without giving any clue to the user that much better transfers may exist. That being said, the results of the present study do point to potentially useful mitigation techniques, such as heuristics based on the inclination, that do not even require the practitioner to implement a Vinti-Lambert solver. Heuristics for the whole solution space would require more study, but something could be said for direct short-way transfers supported by Fig. 4. For example, in multi-rev cases, if an SM reaches a maximum number of iterations and \(i_k>\) 45\(^\circ \), the user can be informed that a transfer likely does not exist. If \(i_k<\) 45\(^\circ \) and the two-body Lambert guess returns \(N_{k,\textrm{max}}\), the user can be warned that an alternative guess is recommended, if not executed, to determine if solutions are being overlooked for \(N > N_{k,\textrm{max}}\). These techniques can be refined and improved with further investigation, noting the \(i_k\) threshold, which could be more of a region than a hard boundary, may depend on \(\{c, N, {\Delta }f\}\).
The analytical BVP solver presented in the current work, which operates under Vinti dynamics, is seen in Figs. 3 and 4 to offer new insights that directly inform mission design, a way for practitioners to determine the existence of more realistic transfers and weed out infeasible ones. In simple diagrams, it also attributes to a physical cause some of the difficulties encountered in applications like ASDR, and it motivates, more generally, some of the risks assumed when neglecting \(J_2\) in preliminary analyses.
5 A Method for Solving the BVP Defined by the Vinti Potential
Having converted the BVP to a system of equations and explored major parts of the solution space, an elementary method is now proposed and employed to solve that system of equations. While the system of equations can be solved in multiple ways, only one method is explored in the current work.
5.1 Initial Guesses for the Unknowns
There are multiple ways to obtain an initial guess, but one of the advantages of adapting Deyst’s algorithm to the Vinti BVP is that the Keplerian orbital elements (KOEs) from a robust two-body BVP solver can be used directly to generate a guess. This approach stands distinctly apart from any existing initial guess techniques in perturbed Lambert solvers, which typically ingest the two-body position and velocity instead of the orbital elements, working in the highly nonlinear ECI space instead of the more linear orbital element space. As such, KOEs offer a decent estimate of the secular drift rates in \({\Omega }^\prime \) and \(\omega ^\prime \) if \(e_k < 1\) as
with zero rates otherwise. Multiplying these rates by \({\Delta }t\) yields decent initial guesses for \({\Delta }{\Omega }^\prime \) and \({\Delta }\omega ^\prime \) as
The maximum of either \(\eta _i\) determines \(I_\textrm{min}\) as \(\arcsin \eta _{i,\textrm{max}}\), so \(i_k\) may be replaced with \(I_\textrm{min}\) if \(i_k < I_\textrm{min}\). For multi-rev cases, further improve the guess by computing I from Eqs. (8) and (14) and iterating a few times on all four equations, replacing \(i_k\) with I in Eq. (60) and computing \({\Delta }\omega ^\prime _0\) and its rate outside the loop.
When guessing \({\hat{z}}\), simply set \({\hat{z}}_0 = {\hat{z}}_k\), where \(\{{\hat{z}}, {\hat{z}}_k\}\) have the same range for \(N > 0\) (not the same minimum TOF) and the same upper bound with otherwise similar trends for \(N = 0\). While notably overcoming one of the main drawbacks of the universal approach, which lacks a good guess for \({\hat{z}}_k\), this method warrants some words of caution. For the zero-rev case, this guess tends to avoid the issue of guessing a value of \({\hat{z}}\) that places \(\rho _p\) inside the Vinti forbidden zone [31], which would require a step rejection and some way of handling it, a new issue that does not exist under Keplerian dynamics. On the other hand, the effect of \(J_2\) is very small over zero revs, so it is expected that \({\hat{z}}\approx {\hat{z}}_k\) when converged, implying a large reduction in the number of iterations and a significant speedup. Checks on the minimum value \({\hat{z}}_\textrm{min}\) for the short-way solution must be retained [1], ensuring that \({\tilde{y}}\ge 0\), but note that \({\hat{z}}_\textrm{min}\) will generally be different between the dynamical models because nearly rectilinear Vinti trajectories passing through the forbidden zone have an unknown analytical representation, leading to the stricter condition \(\rho _p> c\). In practice, robustness was observed to remain high when \(\rho _p> 2,500\) km. Note, too, that the value of \({\tilde{A}}\) is updated on each iteration, so \({\hat{z}}_\textrm{min}\) can fluctuate: the same \({\hat{z}}\) value rejected on one iteration could be valid on the next iteration if \({\tilde{A}}\) is sufficiently different. For multi-rev scenarios, it seems possible to guess \({\hat{z}}\) in the wrong bin, meaning that the user may request an LP solution, but inadvertently seed the guess with an SP \({\hat{z}}\) value that is outside the bounds on \({\hat{z}}\). In this example, the value of \({\hat{z}}_k\) for the LP solution, which is to the left of \({\hat{z}}_k({\Delta }t_{k,\textrm{min}})\), lies to the right of \({\hat{z}}({\Delta }t_\textrm{min})\), because the \({\hat{z}}\) values at the minimum TOF can differ greatly between the two dynamical models. One mitigation technique in this scenario would be to reset \({\hat{z}}_0\) to its value at \({\Delta }t_\textrm{min}\) within some tolerance.
Nonexistence of two-body solutions does not preclude the existence of Vinti or perturbed counterparts, as was demonstrated in an earlier section. If the two-body Lambert solver fails to find a solution for a desired N, even if the time of flight is below the minimum, a robust Vinti-Lambert solver must still pursue a solution with a different initial guess. Armellin et al. [11] noted the benefit of avoiding a Keplerian initial guess in some circumstances in favor of an alternative technique, but while their approach may be useful in this situation, this alternative is not explored in the current study and is left to future work.
5.2 An Elementary Vinti-Lambert Algorithm
After normalizing by \(r_1+ r_2\) to obtain canonical units [7] with \(\mu = 1\), the algorithm begins with the evaluation of Eqs. (6) and (7) for \(\rho _i, \eta _i, {\hat{{\varvec{\rho }}}}_{i}\), where repeated constants are also stored. Next, from the previous section, compute initial guesses for \({\Delta }{\Omega }^\prime \), \({\Delta }\omega ^\prime \) from Eqs. (60–61) after a single Keplerian Lambert call (or an alternative if the solver fails), noting that all variables have an implicit subscript j to denote iterates that is generally dropped to reduce notational clutter. Then, compute \({\Delta }\psi \), \({\Delta }f\), \(\cos I\), \(Q = \sin I\) from Eqs. (8–15) and \({\tilde{A}}\) from Eq. (33) or (30). The previous steps are all done before guessing \({\hat{z}}\). If \(N = 0\), guess \({\hat{z}}= {\hat{z}}_k\); otherwise, \(N > 0\) and the bottom of the \({\Delta }t\)-\({\hat{z}}\) curve must be found first. Once found, guess \({\hat{z}}= 0.9 {\hat{z}}({\Delta }t_\textrm{min})\) for the LP solution or \({\hat{z}}= 1.1 {\hat{z}}({\Delta }t_\textrm{min})\) for the SP solution. With all initial guesses in place, the root-solve begins. For \(N = 0\), a 1D Newton-Raphson method iterating on \({\hat{z}}\) is used to root-solve Eq. (36) with analytical partial derivatives of the Keplerian Lambert problem [1], considered a good enough approximation; deriving partial derivatives of the Vinti-Lambert problem is considered outside the scope of this work. As implemented, a truncated version of Eq. (36), \({\Delta }t = ({\hat{x}}^3 S + {\tilde{A}}\sqrt{{\tilde{y}}})/\sqrt{\mu \gamma _1}\), is used until \({\Delta }{\hat{z}}_j < 1\) to help with convergence (derivatives including \(\sqrt{\mu \gamma _1}\) as well), after which Eq. (36) is used in its entirety, the derivatives subsequently including one extra term, \(A_1/\sqrt{\mu \gamma _1} \cdot \textrm{d} {\hat{x}}/\textrm{d} {\hat{z}}\), one of the major contributors to \(O(J_2)\) terms. Before Eq. (36) and its approximate derivatives can be evaluated, though, a root-solve of Eqs. (3–4) is required, performed as a nested root-solve via the method of successive approximations (MSA) [32] while noting that a 2D MSA root-solve at this step could be a viable alternative. First, compute \(C({\hat{z}}), S({\hat{z}})\), followed by Eq. (32) and Eq. (34) for \({\tilde{y}}, {\hat{x}}\), respectively. If \({\Delta }{\hat{z}}_j > 1\), the truncated Eq. (36) can be evaluated at this point, but typically after one iteration, \({\Delta }{\hat{z}}_j < 1\), which requires many additional computations. In this case, two nested loops are used, one checking convergence of \({\Delta }\omega ^\prime \), the inner one checking \({\Delta }{\Omega }^\prime \), implicitly requiring that \({\Delta }f\), and subsequently \({\tilde{A}}\), be updated on each iteration. Specifically, with this setup, \({\tilde{y}}, {\hat{x}}\) must be updated at the beginning of the \({\Delta }\omega ^\prime \) loop. Then, compute
At this point, check the forbidden zone condition and reject the \({\hat{z}}\) step if violated. If not, from Biria and Russell [23], obtain \(A_1, B_1, \gamma _1, p_0, S_1\), and \(Q_1 = C_2\) from Eqs. 143–148 and \({\alpha _i = \{ \varepsilon , \sqrt{\mu p_0}, h_z \}}\) from Step 4 (p. 287). Next, follow steps in Biria’s UV Vinti propagator [22] to compute \(A_n\), \({\Delta }W_{n}\), \(C_n\), \(C_{1n}\), \(C_{2n}\), \(Q^nT_{n_1}\), \({\Delta }(Q^nT_{n})\), and ultimately \({\Delta }R_{1_j}, {\Delta }R_{2_j}, {\Delta }R_{3_j}, {\Delta }N_{1_j}, {\Delta }N_{4_j}\), which enables the determination of \({\Delta }\omega ^\prime \) from Eq. (3) and \({\Delta }{\Omega }^\prime \) from Eq. (4). Relative to the propagation steps, a key difference in the Vinti-Lambert solver is that the initial \(Q\cos \psi _1\) must be obtained from Eq. (48) and \(\sigma _1, e\sin f_1\), and \(e\cos f_1\) from
where \(h_1= \rho _1^2 {\dot{f}}_1\) and Eqs. (42) and (17) give \({\dot{f}}_1\) and \({\tilde{G}}\), respectively. Once the updated value of \({\Delta }{\Omega }^\prime \) is calculated, \({\Delta }\psi , {\tilde{d}}_\psi \) are updated from Eqs. (8–12). Careful attention must be paid to quadrant ambiguities. If \({\tilde{d}}_\psi = -1\), then \({\Delta }\psi = 2\pi + {\Delta }\psi \) so that \(0 \le {\Delta }\psi < 2\pi \) initially. Then, compute \({\Delta }f, {\tilde{d}}_f\) from Eq. (13), but adjusted so that if \({\Delta }f< 0\), \(2\pi \) is added to \({\Delta }f, {\Delta }\psi \), and if \({\Delta }f> 2\pi \), \(2\pi \) is subtracted from \({\Delta }f, {\Delta }\psi \), maintaining the correct relative difference between the two angles while ensuring \(0 \le {\Delta }f< 2\pi \). For multi-rev cases, apply Eq. (40) to compute the total angular displacements \({\Delta }f_\textrm{tot}, {\Delta }\psi _\textrm{tot}\). With the updated \({\Delta }\psi \), compute \(Q, \cos I\) from Eq. (15). If \({\Delta }{\Omega }^\prime \) has not converged to within some tolerance, then return to the computation of \(A_1, B_1\) and repeat. Otherwise, exit the inner loop, compute \({\tilde{A}}\), and check \({\Delta }\omega ^\prime \) against its value on the previous iteration. If \({\Delta }\omega ^\prime \) has not converged to within some tolerance, return to the beginning of the loop, compute \({\tilde{y}}, {\hat{x}}\), Eq. (62), and continue through the MSA loops. Otherwise, exit the loop, finally evaluate Eq. (36), and update \({\hat{z}}\). This entire process is repeated until \({\hat{z}}\) converges to within some tolerance.
For \(N > 0\), the minimization of the \({\Delta }t\)-\({\hat{z}}\) curve is solved with a golden section search on \({\hat{z}}\), followed by a root-solve of Eq. (36) via the bisection method. Gradient-free root-solve methods offer both simplicity and robustness in this part of the algorithm. Future implementations employing more efficient root-solve algorithms and better initial guesses are expected to enjoy significant performance boosts. Regardless of N, after the root-solve converges, the algorithm concludes with the evaluation of Eqs. (41–50) and the equinoctial element approach detailed in Appendix A to obtain the terminal velocities.
5.3 Performance Evaluation
Performance of the above algorithm is evaluated for robustness, accuracy, and speed in Fig. 5. All measures of performance consider all combinations of SW/LW zero-rev transfers and direct/retrograde orbits for each eccentricity regime (ER), which is a specific range of \(e_{k}\). Since 500,000 BC-\({\Delta }t_*\) pairs are run for each of 4 direction/inclination combinations, and there are 5 ERs, each performance metric is measured from 10 million scenarios, constructed as follows. The ER number on the horizontal axis refers to the uniformly sampled ERs given in Table 3, chosen to broadly test and stress the algorithm, in order as: broad elliptical, \(e_{k} \rightarrow 1\) from below, \(e_{k}\) near unity, broad hyperbolic, and limited hyperbolic, the last one depending on direction. For each ER, the ICs in the last line of Table 1 are transformed to ECI coordinates to obtain \(\textbf{r}_1\), where the square brackets indicate uniformly sampled quantities and \(f_{k_0}\) is computed differently according to \(e_{k}\). If \(e_{k} < 1\), then \(f_{k_0} =\) [0; 360\(^\circ \)]; if \(e_{k} \ge 1\), then \({f_{k_0} = [-f_{k\infty } + 0.01^\circ ;\; f_{k\infty } - 0.01^\circ - {\Delta }f_k]}\), where \(f_{k\infty } = \arccos ( -1/e_k)\). The ICs are analytically propagated under Keplerian dynamics with UVs by a transfer angle \({\Delta }f_k =\) [0; 180\(^\circ \)] for SW ERs 1–5, \({\Delta }f_k =\) \([180^\circ ;\; 2 ( f_{k\infty } - 0.01^\circ )]\) for LW ERs 1–4, or \({\Delta }f_k =\) [180\(^\circ \); 360\(^\circ \)] for LW ER 5 to obtain \(\textbf{r}_2\), where \({\Delta }t_* = {\Delta }t_0\) is obtained iteratively in the process.
All performance metrics are then measured from this data set. Robustness is interpreted in Fig. 5a as the percentage of Lambert calls that converge when expected, so that the identification of problematic scenarios (full-rev, low \(r_p\), etc.) are treated as successes and do not reduce the robustness measure. Robustness is observed to be high, ranging between 99.22 and 99.99% over all ERs, averaging 99.76% overall. In Fig. 5b, c, accuracy is also compared side-by-side with a Keplerian UV Lambert solver as a benchmark, where average miss distance is used as a proxy for the accuracy of \(\textbf{v}_1\), and \(\textbf{v}_2\) is assumed to have similar accuracy. Miss distance is defined here as the difference between the BC \(\textbf{r}_2\), taken as truth, and the predicted value of \(\textbf{r}_2\) resulting from the analytical UV Vinti propagation of the initial state \(\textbf{x}_1= [\textbf{r}_1^\top \;\, \textbf{v}_1^\top ]^\top \), where \(\textbf{v}_1\) is the output of either the Vinti or Keplerian Lambert solver. Figure 5c considers all cases, including unreasonably long TOF, and is only presented for completeness; Fig. 5b is considered a more useful measure of accuracy that only includes cases with \({\Delta }t_* < 1\) year, which, while still a large TOF limit, has the benefit of still stressing the algorithm. As such, Vinti-Lambert accuracy is found to be remarkably high, SW transfers boasting an average miss distance of \(\approx \) 44 mm across all ERs. LW transfers exhibit lower accuracy, averaging \(\approx \) 10 km miss distance across all ERs and 7.5 m ignoring ERs 2–3. This LW trend likely stems from the increased likelihood that transfers will pass through periapsis, noting that they must pass through periapsis for hyperbolic transfers, with nearly parabolic transfers appearing particularly stressing. Relative to a standard Keplerian Lambert solver, the Vinti-Lambert solver improves the accuracy by as much as 9 orders of magnitude on average in some eccentricity regimes. In ERs 2–3, the discrepancy may be caused by qualitative disagreement between physical models, one predicting an escape trajectory where the other predicts a bounded one. Note that because the integrals are only evaluated to \(O(J_2^3)\), the entire Vinti transfer orbit solution is of that accuracy, including the orbital elements. This property stands in contrast to analytical solutions to the IVP, for which half of the orbital elements, p, e, and I, can be obtained exactly (to double-precision accuracy) despite the lower accuracy of the integral approximations.
Computational speed is evaluated on an HP EliteBook 830 G5 laptop computer with an Intel Core i5-8350U CPU operating at a base speed of 1.9 GHz with 16 GB of RAM. The maximum speed at which a single one of these cores is capable of operating is 3.6 GHz, and the CPU operated at this maximum speed during tests, where the UV Vinti-Lambert algorithm is benchmarked in runtime against a UV Keplerian Lambert algorithm. Both algorithms are implemented in Fortran 90 and compiled with Intel Fortran Compiler Classic for Windows in 64-bit mode with O3 and Qip optimization settings enabled. For the described BC-\({\Delta }t_*\) pairs, the Vinti-Lambert algorithm implemented in this study only takes 18.0 \(\mu \)s on average to compute \(\textbf{v}_1, \textbf{v}_2\). The Vinti-Lambert solver is found to be only 15.4 times slower than the Keplerian Lambert solver, which takes an average of 1.2 \(\mu \)s on the same machine. Considering a typical universal Lambert call runs at \(\approx \) 1 \(\mu \)s and the Vinti-Lambert solver is running about 15 times slower, a two-body initial guess is considered a wise use of computational resources as the performance gains are thought to outweigh the cost of assigning, on average, \(\approx \) 6.5–7% of the runtime to calculating the initial guess. Multi-rev runtimes were not assessed as rigorously, but a Lambert call for the 100-rev scenario in Fig. 3a (Tables 1 and 2) was measured to take \(\approx \) 4 ms (LP), with runtimes generally seen to be on the order of milliseconds for any N. Based on published performance data, the Vinti-Lambert zero-rev algorithm is estimated to run at least 1,000 times faster than comparable perturbed Lambert solvers [11, 14], depending on the method, though the other algorithms were not independently implemented. Note that implementing more efficient root-solve algorithms than those presented in this work, which prioritized simplicity and robustness, is likely to yield significant additional Vinti-Lambert speedups. Such improvements to the oblate Lambert algorithm are expected to lead to multi-rev runtimes on the order of zero-rev runtimes, with the only performance losses resulting from the need to obtain both LP and SP solutions, as well as the formal minimization step to find \({\hat{z}}({\Delta }t_\textrm{min})\). For additional perspective, note that the Vinti-Lambert solver implemented in this work for zero revs is only 4.3 times slower than the author’s UV Vinti propagator [22], whose runtime is estimated to be near the best achievable Vinti-Lambert runtime.
6 Conclusions
The classical Lambert problem is generalized to include the physical effects of a celestial body’s equatorial bulge, generalizing Lambert’s equation to a system of three equations that together define a new boundary value problem (BVP). This novel BVP is governed by Vinti’s symmetric gravitational potential, which causes the problem to remain unperturbed despite the inclusion of \(J_2\) effects, enabling the reduction to a system of equations via geometrical arguments and the oblate spheroidal (OS) Lagrange coefficients. Geometric connections are drawn between the orbital reference frames of the two BVPs to show how generalizing the classical Lambert inertial frame to a rotating frame enables, in an approximate sense, the definition of the Vinti-Lambert problem. Like the recent third-order universal solution to Vinti’s initial value problem, the \(O(J_2^3)\) Vinti-Lambert formulation leverages OS equinoctial elements, OS universal variables (UVs), and the differential form of the equations of motion, collectively working to avoid indeterminate forms, angle ambiguities, and singular elements for all orbital regimes excluding a region around the forbidden zone. The Vinti-Lambert solution space is visualized, discussed, and extensively mapped for the first time for both zero- and multi-rev cases, and then directly compared to the classical Lambert solution space, leading to multiple new insights that distinguish this BVP from the classical Lambert problem. In particular, the advance or delay of the multi-rev minimum time of flight is shown to be a key contributor to shooting method pitfalls, while at the same time pointing to how the pitfalls can be mitigated. Some preliminary understanding of the effects of \(J_2\) on minimum energy are observed as well, the investigation generally leaving ample room for future solution space exploration, including the study of corner cases and bifurcations.
As part of this study, an elementary, iterative method is presented for obtaining a solution to the zero-rev and multi-rev oblate BVP. Performance is rigorously evaluated at Earth for the zero-rev case over a broad range of orbital regimes, demonstrating, on average, robustness of 99.8%, accuracy boosts between three and nine orders of magnitude relative to Keplerian dynamics for times of flight less than 1 year, and computational efficiency with runtimes around 18 \(\mu \)s, only 15.4 times slower than a classical UV Lambert solver. These high performance levels stand to benefit numerous applications. More extensive testing of the multi-rev case is left to future work, though multi-rev runtimes were consistently observed to peak on the order of milliseconds for cases with any number of revs examined in this study. While some areas of potential improvement have been identified, this study presents a novel algorithm for the solution of the oblate Lambert problem demonstrating both efficiency and robustness in comparison to existing methods in the literature.
Notes
The phrase “inertially invariant” is used to draw a distinction between the invariance of the orbital plane in the inertial frame under Keplerian dynamics and the invariance of the orbital plane in the relative frame under Vinti dynamics.
References
Bate, R.R., Mueller, D.D., White, J.E.: Fundamentals of Astrodynamics. Dover Publications Inc, Mineola (1971)
Battin, R.H.: An Introduction to the Mathematics and Methods of Astrodynamics, Revised AIAA Education Series. American Institute of Aeronautics and Astronautics Inc, Reston (1999)
Roscoe, C.W.T., Schumacher, J.P.W., Wilkins, M.P.: Parallel track initiation for optical space surveillance using range and range-rate bounds. In: AAS/AIAA Astrodynamics Specialist Conference, vol 150, pp 989–1008, Paper AAS 13-767. Univelt, Inc., San Diego (2014)
Schumacher, P.W., Gaebler, J., Roscoe, C.W.T., Wilkins, M.P.: Parallel initial orbit determination using angles-only observation pairs. Celest. Mech. Dyn. Astr. 130, 60 (2018). https://doi.org/10.1007/s10569-018-9852-6
Gooding, R.H.: A procedure for the solution of Lambert’s orbital boundary-value problem. Celest. Mech. Dyn. Astron. 48(2), 145–165 (1990). https://doi.org/10.1007/BF00049511
Izzo, D.: Revisiting Lambert’s problem. Celest. Mech. Dyn. Astron. 121(1), 1–15 (2015). https://doi.org/10.1007/s10569-014-9587-y
Russell, R.P..: On the solution to every Lambert problem. Celest. Mech. Dyn. Astr. 131, 50 (2019). https://doi.org/10.1007/s10569-019-9927-z
Cerf, M.: Multiple space debris collecting mission—debris selection and trajectory optimization. J. Optim. Theory Appl. 156(3), 761–796 (2013). https://doi.org/10.1007/s10957-012-0130-6
Andrus, J.F.: First-order effects of the Earth’s oblateness upon coasting bodies. Celest. Mech. 15(2), 217–224 (1977). https://doi.org/10.1007/BF01228463
Engels, R.C., Junkins, J.L.: The gravity-perturbed Lambert problem: a ks variation of parameters approach. Celest. Mech. 24(1), 3–21 (1981). https://doi.org/10.1007/BF01228790
Armellin, R., Gondelach, D., Juan, J.F.S.: Multiple revolution perturbed Lambert problem solvers. J. Guid. Control Dyn. 41(9), 2019–2032 (2018). https://doi.org/10.2514/1.G003531
Der, G.J..: The superior Lambert algorithm. In: Advanced Maui Optical and Space Surveillance Technologies (AMOS) Conference, Maui, HI (2011)
Woollands, R.M., Younes, A.B., Junkins, J.L.: New solutions for the perturbed Lambert problem using regularization and Picard iteration. J. Guid. Control Dyn. 38(9) 1548–1562 (2015). https://doi.org/10.2514/1.G001028
Woollands, R.M., Read, J.L., Probe, A.B., Junkins, J.L.: Multiple revolution solutions for the perturbed Lambert problem using the method of particular solutions and Picard iteration. J. Astronaut. Sci. 64, 361–378 (2017). https://doi.org/10.1007/s40295-017-0116-6
Woollands, R.M., Read, J.L., Probe, A.B., Junkins, J.L.: Unified Lambert tool for massively parallel applications in space situational awareness. J. Astronaut. Sci. 65, 29–45 (2018). https://doi.org/10.1007/s40295-017-0118-4
Yang, Z., Luo, Y.Z., Zhang, J., Tang, G.J.: Homotopic perturbed Lambert algorithm for long-duration rendezvous optimization. J. Guid. Control Dyn. 38(11), 2215–2223 (2015). https://doi.org/10.2514/1.G001198
Der, G.J..: An analytic perturbed Lambert algorithm for short and long durations. In: AAS/AIAA Astrodynamics Specialist Conference. Advances in the Astronautical Sciences, vol 156, Paper AAS 15-538. Univelt, Inc., San Diego (2016)
Der, G.J., Bonavito, N.L. (eds.): Orbital and Celestial Mechanics, Progress in Astronautics and Aeronautics, vol. 177. American Institute of Aeronautics and Astronautics, Reston (1998)
Vinti, J.P.: New method of solution for unretarded satellite orbits. J. Res. Natl. Bureau Stand. 63B(2), 105–116 (1959). https://doi.org/10.6028/jres.063B.012
Vinti, J.P.: Theory of an accurate intermediary orbit for satellite astronomy. J. Res. Natl. Bureau Stand. 65B(3), 169–201 (1961). https://doi.org/10.6028/jres.065B.017
Lipton, M., Mirollo, R., Strogatz, S.H.: The Kuramoto model on a sphere: explaining its low-dimensional dynamics with group theory and hyperbolic geometry. Chaos 31(9), 093113 (2021). https://doi.org/10.1063/5.0060233
Biria, A.D.: Revisiting universal variables for robust, analytical orbit propagation under the Vinti potential. J. Astronaut. Sci. 70, 29 (2023). https://doi.org/10.1007/s40295-023-00385-9
Biria, A.D., Russell, R.P.: Equinoctial elements for Vinti theory: generalizations to an oblate spheroidal geometry. Acta Astronaut. 153(1), 274–288 (2018). https://doi.org/10.1016/j.actaastro.2017.11.013
Biria, A.D., Russell, R.P.: A satellite relative motion model including \(J_2\) and \(J_3\) via Vinti’s intermediary. Celest. Mech. Dyn. Astron. 130(3), (2018). https://doi.org/10.1007/s10569-017-9806-4
Biria, A.D., Russell, R.P.: Analytical solution to the Vinti problem in oblate spheroidal equinoctial orbital elements. J. Astronaut. Sci. 67(1), 1–27 (2020). https://doi.org/10.1007/s40295-019-00179-y
Getchell, B.C.: Orbit computation with the Vinti potential and universal variables. J. Spacecr. Rockets 7(4), 405–408 (1970). https://doi.org/10.2514/3.29954
Battin, R.H.: Astronautical Guidance. McGraw-Hill Electronic Sciences Series. McGraw-Hill Book Company Inc, New York (1964)
Biria, A.D.: The lagrange coefficients of Vinti theory. Celest. Mech. Dyn. Astron. 132(5), (2020). https://doi.org/10.1007/s10569-020-09966-4
Vinti, J.P.: Improvement of the spheroidal method for artificial satellites. Astron. J. 74(1), 25–34 (1969). https://doi.org/10.1086/110770
Wiesel, W.E.: Numerical solution to Vinti’s problem. J. Guid. Control Dyn. 38(9), 1757–1764 (2015). https://doi.org/10.2514/1.G000661
Lang, T.J.: Spheroidal solution for unbounded orbits about an oblate planet. Master’s thesis, Massachusetts Institute of Technology, Cambridge, MA (1969)
Ford, L.R.: The solution of equations by the method of successive approximations. Am. Math. Mon. 32(6), 272–287 (1925). https://doi.org/10.2307/2299139
Funding
Open access funding provided by SCELC, Statewide California Electronic Library Consortium.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Appendix A: Equinoctial Approach to Compute Terminal Velocity Vectors
Appendix A: Equinoctial Approach to Compute Terminal Velocity Vectors
To avoid computing \({\Omega }^\prime _i\), the velocities can be obtained entirely in terms of OS equinoctial elements instead. First, knowing \({\hat{\textbf{w}}}_1\) from Eq. (14), compute \(p_{11},p_{21}\) from Biria [22] as
Next, from Biria and Russell [23], compute the following: \({\hat{\textbf{f}}}_1, {\hat{\textbf{g}}}_1, {\varvec{\dot{{\hat{\textrm{f}}}}}}_1, {\varvec{\dot{{\hat{\textrm{g}}}}}}_1\) via Eqs. 24, 127, and 128, \(\cos L_1, \sin L_1\) from Eqs. 90–91, and \({\dot{L}}_i\) from Sect. 9, where the equation numbers refer to that reference. For convenience, and with \(i= 1, 2\), these equations are repeated here in order as
and
Then, compute \({\dot{\eta }}_i\) from Eq. (48) or (50) and \(\sigma _i\) and \({\dot{\rho }}_i\) from
where the expression for \(\sigma _i\) is new and that for \({\dot{\rho }}_i\) is derived from Biria [28]. Note that, alternatively, \({\dot{\eta }}_2\) does not need to be computed from Eq. (48) or (50) and \(\sigma _2\) does not need to be computed from Eq. (69). By using angle sum identities to determine \(Q\cos \psi _2\) and \(e\sin f_2\) in Eq. (48) and Eq. (69), respectively, \({\dot{\eta }}_2\) can be determined directly from \({\dot{\eta }}_2= {\dot{\psi }}_2Q \cos \psi _2\) and the computation of \(\sigma _2\) can be bypassed. Next, to avoid inverse trigonometric functions, obtain \(\cos L_2, \sin L_2\) from standard angle sum identities after computing \({\Delta }L\) from Biria [22] as
Then, propagate \(p_{11},p_{21}\) via Eq. 63 in Biria in [22], repeated here for convenience as
to obtain \(p_{12},p_{22}\), which determine \({\hat{\textbf{f}}}_2, {\hat{\textbf{g}}}_2, {\varvec{\dot{{\hat{\textrm{f}}}}}}_2, {\varvec{\dot{{\hat{\textrm{g}}}}}}_2\) as before in Eqs. (65–66). Finally, compute \(\textbf{v}_i\) by applying to each terminal point Eqs. 133 and 134 in Biria and Russell [23], repeated here as
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Biria, A.D. The Oblate Lambert Problem: Geometric Formulation and Solution of an Unperturbed, Generalized Lambert Problem Governed by Vinti’s Potential. J Astronaut Sci 70, 38 (2023). https://doi.org/10.1007/s40295-023-00388-6
Accepted:
Published:
DOI: https://doi.org/10.1007/s40295-023-00388-6